СПОСОБ УПРАВЛЕНИЯ ТРАЕКТОРИЕЙ СТВОЛА СКВАЖИНЫ (ЕГО ВАРИАНТЫ) Российский патент 1994 года по МПК E21B7/08 

Изобретение относится к области бурения наклонно-направленных скважин.

Известен способ управления траекторией ствола скважины, включающий наложение на инструмент продольных колебаний с частотой, равной частоте вращения, и управление кривизной и направлением ствола скважины.

Поскольку в известном техническом решении применяется асимметричный инструмент, то у такого инструмента режущие свойства лезвий примерно одинаковы, а геометрическая осевая симметрия нарушена: имеется ненулевое осевое расстояние между вершинами режущих кромок, отличаются главные углы в плане, т. е. углы наклона режущих кромок относительно оси инструмента.

Интенсивность искривления траектории ствола скважины таким инструментом весьма слаба. Такие инструменты успешно применяются для прямолинейного бурения скважин.

В связи с изложенным известный способ управления траекторией ствола скважины не позволяет обеспечить достаточно высокой интенсивности зенитного искривления ствола скважины.

Целью изобретения является устранение указанного недостатка и обеспечение возможности резкого повышения интенсивности искривления.

Указанная цель достигается тем, что у инструмента, на который наложены продольные колебания с частотой, равной частоте его вращения, хотя бы один из породоразрушающих элементов затупляют или заменяют на опорный элемент, а кривизной ствола скважины управляют в соответствии с зависимостью
Y_c = Δ S ^. k [ ] , где Δ S - амплитуда продольных колебаний инструмента;
Y_с - величина зенитного смещения;
S - средняя величина подачи на оборот инструмента;
l - общая длина проходки участка искривления, причем
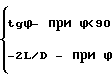
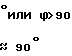
K= где ϕ - угол наклона режущей кромки и оси инструмента;
D - диаметр инструмента;
L - расстояние от режущей части до полюса поворота.

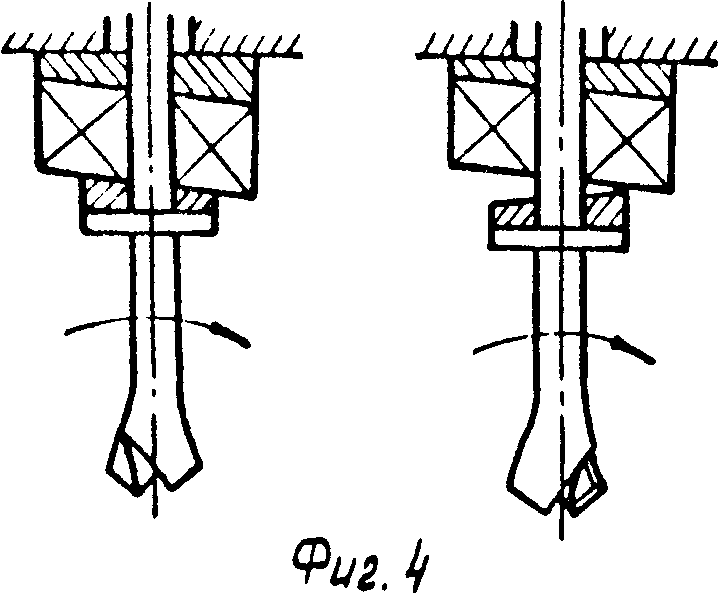
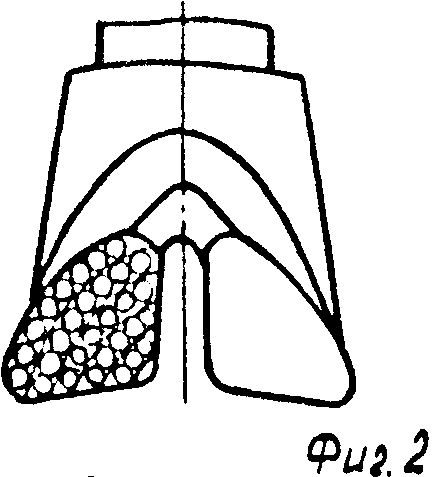
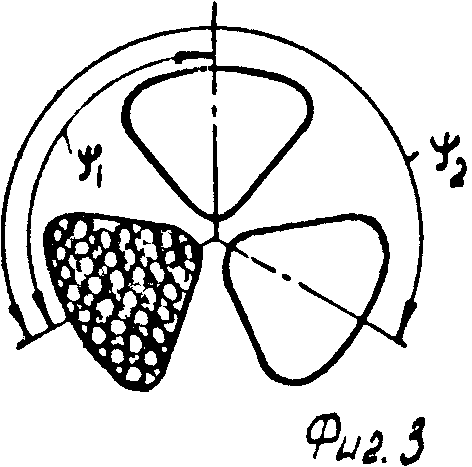
Например, используют бурильный резец, одно из лезвий которого затуплено (фиг. 1.1), или шарошечное долото, у которого одна или две шарошки заменены на гладкие ролики (фиг. 2, 3). Продольные же вибрации с частотой, равной частоте вращения, создаются за счет перекоса подшипника привода вращения (фиг. 4).

Примем, что перекос подшипника привода вращения приводит к следующему закону периодического изменения подачи на оборот инструмента
S = S_o + ΔS sin (Ψ - Ψ_o), где Ψ_о - произвольный угол сдвига фазы.

Для уяснения сущности заявляемого способа рассмотрим некоторые математические модели процессов бурения инструментами различного типа. Допустим сначала, что диссимметрия породоразрушающих свойств элементов бурильного инструмента настолько значительна, что процесс бурения динамически устойчив, т. е. быстрых поперечных автоколебаний его не возникает, а инерционными силами можно пренебречь.

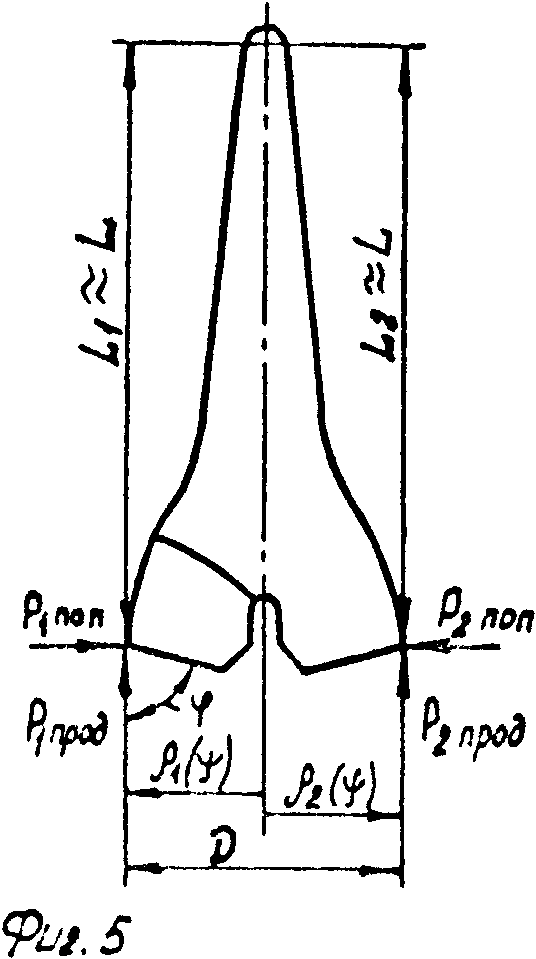
Сначала рассмотрим двухэлементные инструменты, например, бурильный резец (фиг. 5). Если в первом приближении пренебречь тангенциально-поперечными силами и перемещениями, дающими составляющие погрешности второго порядка малости при динамической устойчивости процесса, то уравнение статического равновесия бурильного резца выразится следующим образом:
Р_1поп^. L₁ - P_1прод ρ₁(ϑ)=
= Р_2поп^. L₂ - Р_2прод ρ₂(ϑ), (1) где Р_1поп и Р_2поп - радиальные составляющие силы на лезвиях 1 и 2 бурильного резца; а Р_1прод и Р_2прод - продольные составляющие сил на этих лезвиях;
ρ₁(ϑ) и ρ₂(ϑ) - текущие радиус-векторы вершин лезвий 1 и 2;
ϑ - текущий угол поворота бурильного резца; ϑ = ω_вр t;
L₁ ≈ L₂ = L - расстояние от вершин лезвий до полюса поворота.

При достаточно большом L>>D и при ϕ<90^о моментами от продольных сил можно пренебречь. Тогда уравнение статического равновесия (1) выразится как
Р_1поп = Р_2поп, (2) при этом оно дополняется геометрическим соотношением
ρ₁(ϑ) + ρ₂(ϑ) = D (3) Силы, входящие в уравнение статического равновесия, приблизительно пропорциональны площадям Δ₁ и Δ₂ разрушаемого слоя породы и коэффициентам породоразрушающей способности элементов бурильного инструмента К_r1 и К_r2
Р_1поп = К_r1^. Δ₁ = K_r1^.h₁ δ₁; (4)
Р_2поп = К_r2^. Δ₂ = K_r2^. h₂ δ₂, (5) где h₁ - высота; δ₁ - ширина разрушаемого слоя породы.

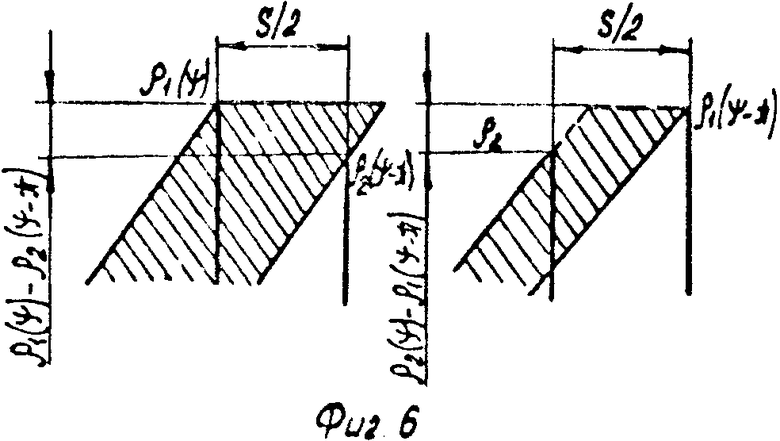
Из фиг. 6 нетрудно видеть, что
Δ₁= ρ₁(ϑ)·(S/2+(ρ₁(ϑ)-ρ₂(ϑ-Π))/tg ϕ) (6)
Δ₂= ρ₂(ϑ)·(S/2+(ρ₂(ϑ)-ρ₁(ϑ-Π))/tg ϕ) (7)
Подставляя равенства (6), (7), (4), (5), (3) в (2) и исключая ρ₂(ϑ), получим нелинейное разностное уравнение относительно ρ₁(ϑ): K_r1ρ₁(ϑ)(S/2+(ρ₁(ϑ)-ρ₂(ϑ-Π)-D)/tg ϕ)= = K_r2(D-ρ₁(ϑ))(S/2+(D-ρ₁(ϑ)-ρ₁)/tg ϕ (8)
Численные решения нелинейного разностного уравнения (8) показывают, что при K_r1≠K_r2; и при
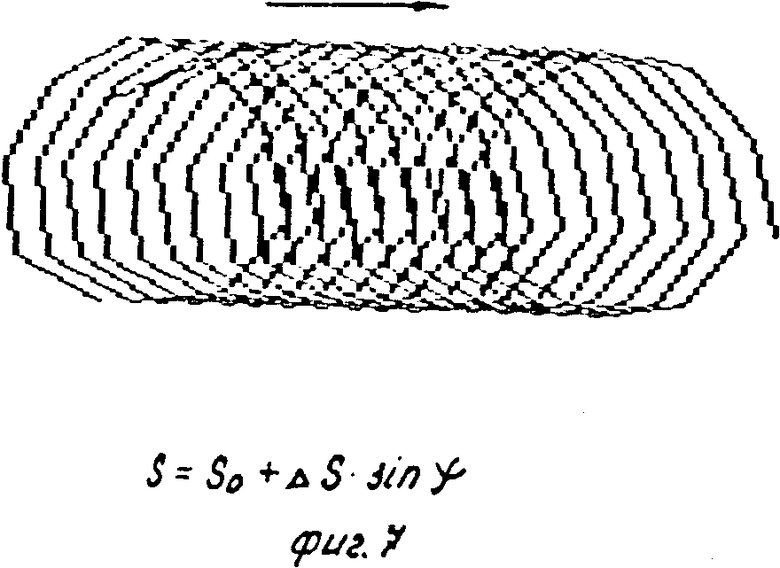
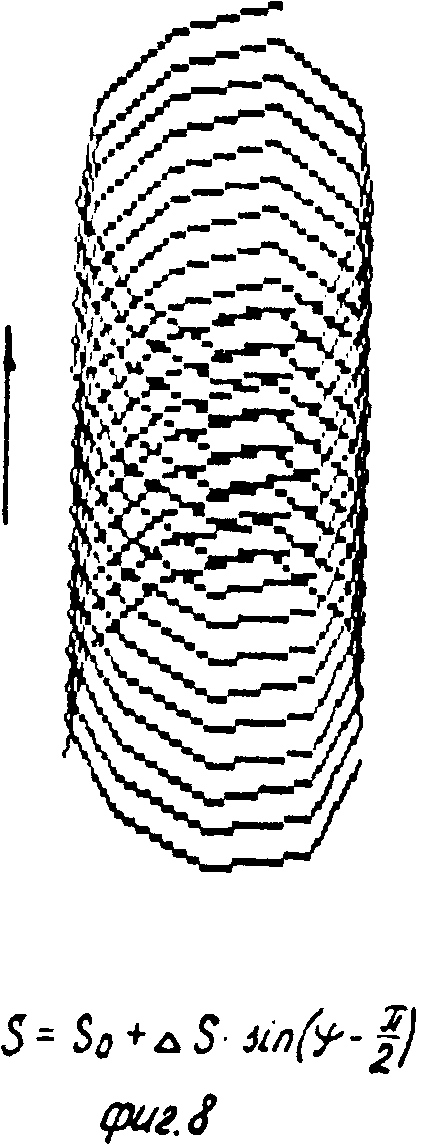
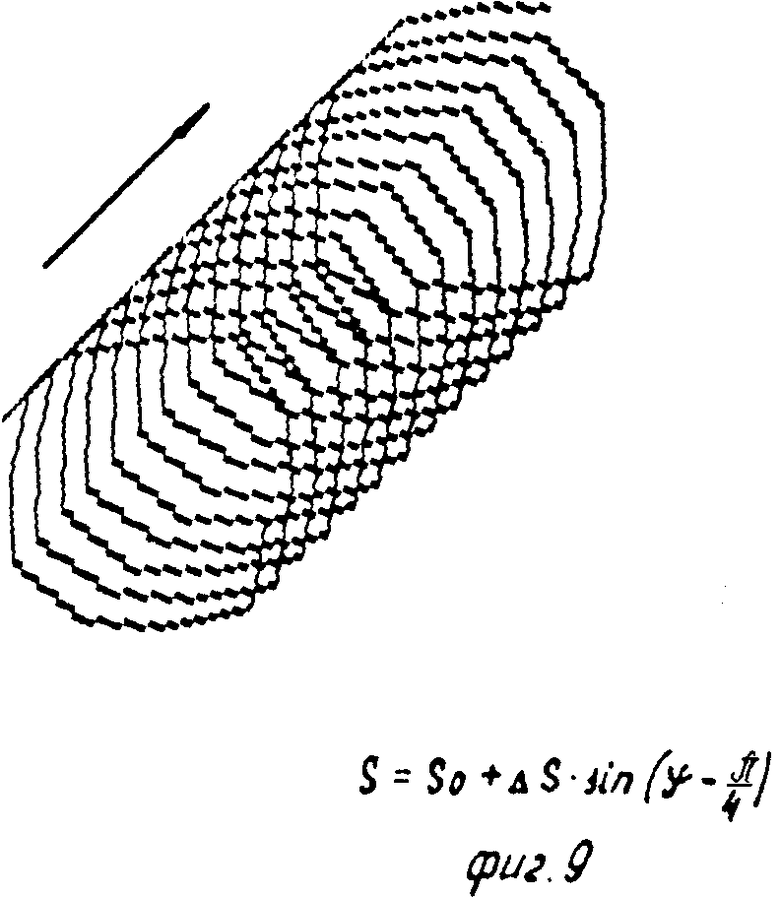
S = S_o + ΔS ^. sin (ϑ - ϑ_o), (9) где ϑ_о - произвольный угол сдвига фазы, т. е. при наличии продольных колебаний бурильного инструмента с амплитудой Δ S и с частотой, равной частоте вращения (ϑ = = ω_вр t), наблюдается поперечное смещение бурильного инструмента, т. е. зенитное искривление скважины, направление которого зависит от сдвига фаз ϑ_опродольных колебаний (фиг. 7, 8, 9).

Можно заметить, что искривление наблюдается в том угловом направлении, в котором оказывается элемент бурильного инструмента с большей разрушающей способностью в моменты, когда скорость проходки S оказывается максимальной. Численные расчеты показывают, что интенсивность искривления тем больше, чем больше соотношения K_r1/K_r2 или K_r2/K_r1.

В частности, при K_r2>>K_r1 (или K_r1>>K_r2) уравнение (8) вырождается в линейное разностное уравнение
ρ₁(ϑ)= D-ρ₁(ϑ-Π)+(S₀/2)tg ϕ + (ΔS/2)tg ϕ·sin(ϑ-ϑ₀) (10) Для уравнения (10) несложно получить аналитическое решение, которое содержит неограниченно растущий член
(ΔS/2)tg 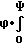cos(ϑ-ϑ₀-u)·{ (1+(-1)^[u/Π])/2} du=
= (ΔS/2)tgϕ [Ψ/Π] = (ΔS/2)tgϕ [2l/S] , (11) где ϑ - угол в радианах, на который повернется вокруг своей оси инструмент за все время проходки, когда осуществляется искривление скважины;
l - длина проходки, на которой осуществляется искривление скважины, являющейся оценкой сверху максимальной интенсивности искривления трассы скважины.

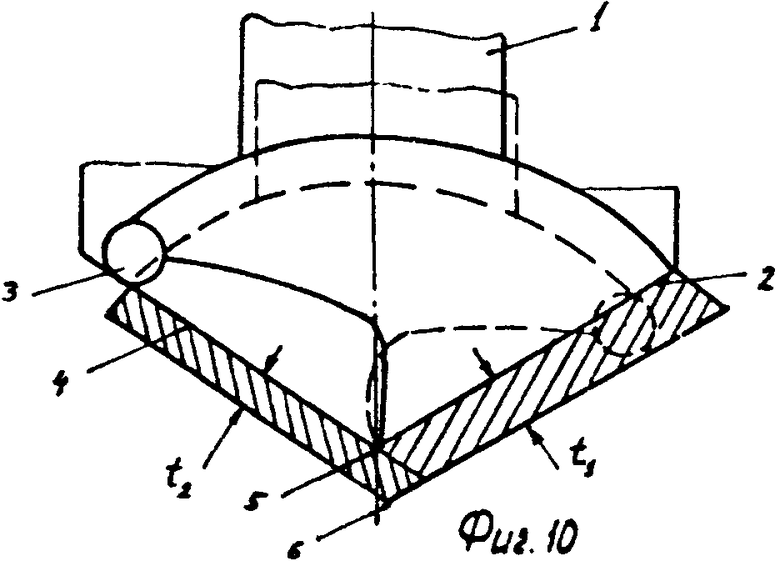
Для пояснения физического смысла изложенного рассмотрим (фиг. 10) положение бурильного резца в какой-то момент обработки. Резец (1) (показан схематично) заточен так, что режущее лезвие 2 режет породу, а затупленной кромкой 3 опирается по поверхности резания.

Пусть в этот момент бурильный резец кроме подачи S получит приращение подачи ΔS, т. е. ему сообщают продольные колебания с амплитудой Δ S. Режущая кромка (2) срезает слой породы глубиной t₁, а кромка (3) опирается на поверхность 4 резания. Вследствие подачи S + Δ S кромка 3 начинает перемещаться по поверхности 4 резания влево. Крайняя точка 5 режущей кромки (2) переместится с оси отверстия в точку 6.

При повороте резца (1) на 180^о ему сообщается подача S- Δ S. Режущая кромка (2) продолжает резать породу, а кромка 3 опирается на поверхность резания. Резец имеет подачу S- ΔS, следовательно срезает слой породы t₂ меньше слоя t₁. Кромка 3 перемещается по поверхности 4 резания вправо, но ввиду того, что подача в этот момент меньше максимальной на величину 2 Δ S, резец переместится вправо на величину Δ₂, меньшую, чем Δ₁. Т. е. суммарное смещение оси скважины за один оборот составит
Δ = Δ₁ - Δ₂. Это максимальная величина смещения оси за один оборот бурильного инструмента.

Отметим, что полученными оценками максимальной интенсивности искривления нельзя пользоваться при ϕ≈ 90^о. В случае применения бурильного инструмента с ϕ= 90^о необходимо в уравнении статического равновесия инструмента (1) положить Р_1поп= Р_2поп= 0.

Проделав аналогичные приведенным выкладки, для этого случая при К_2прод>>К_1прод (или K_1прод>>К_2прод) из уравнения (1) можно получить уравнение
ρ₁(ϑ)= D- ρ₁(ϑ-π)-S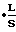, (12) которое математически аналогично уравнению (10), в котором (tg ϕ) заменен выражением (-2L/D).

Решение уравнения (12) аналогично решению уравнения (10), однако искривление идет в противоположном направлении, т. е. в направлении, диаметрально противоположном угловому положению, в котором оказывается элемент бурильного инструмента с большой породоразрушающей способностью в моменты, когда скорость проходки максимальна.

Аналогичные математические модели могут быть построены и для многоэлементного бурильного инструмента, например, твердосплавных и алмазных буровых коронок, шарошечных долот и т. д. Например, для трехшарошечного долота, у которого одна шарошка имеет максимальную разрушающую способность, а две других заменены гладкими роликами (фиг. 3), породоразрушающей способностью которых можно пренебречь, получим уравнение ρ₁(ϑ)-(D/2)= -{ (sinϑ₁)/(sin(ϑ₂-ϑ₁)} [ρ₁(ϑ -ϑ₂)- (D/2)+{ (S·ϑ₂)/2Π} ·K] +{ (sinϑ₂)/(sin(ϑ₂-ϑ₁)} [ρ₁(ϑ -ϑ₁)- -(D/2)+{ (S·ϑ₁)/2Π} ·K] где k= tg ϕ, при ϕ≠90^о и L>>D,
или k= - 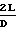при ϕ = 90^о.

Можно отметить, что при ϑ₂= π вид и решение уравнения (13) совпадает с видом и решением уравнений (10) и (12). Численные же решения уравнения (13) в общем случае также показывают возникновение искривления трассы скважины при наличии продольных колебаний бурильного инструмента с частотой, равной частоте вращения (фиг. 11). Указанная цель достигается также тем, что продольные колебания, частота которых равна частоте вращения, сообщают бурильному инструменту с одинаковыми в среднем породоразрушающими способностями элементов, у которого тем не менее породоразрушающие способности различных элементов в разные моменты времени не равны из-за спонтанно возникающих быстрых поперечных вибраций бурильных инструментов. Такая кинематическая несимметрия породоразрушающих свойств элементов бурильного инструмента возникает вследствие того, что кинематические углы резания, например, бурильного резца различаются из-за появления переносной скорости движения центра бурильного резца. Однако, в этом случае амплитуду медленных продольных колебаний, частоты которых равна частоте вращения, дополнительно быстро изменяют с частотой, равной частоте поперечных автоколебаний бурильного инструмента.

Таким образом, бурильному инструменту сообщают амплитудно-модулированные продольные колебания, так называемые биения, несущая частота которых равна частоте быстрых поперечных автоколебаний инструмента, а огибающая этих биений имеет период, равный периоду вращения инструмента.

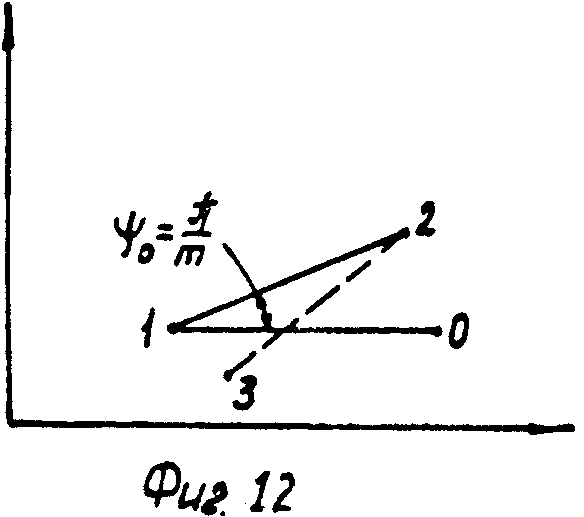
Для составления соответствующей математической модели (фиг. 12) используем то обстоятельство, что при быстрых поперечных автоколебаниях бурильного резца мгновенные значения K_τ1>>K_τ2 или в другие моменты K_τ1<<K_τ2.

Тогда при π·2k/m<ϑ≅(2k+1)·π/m неподвижно второе лезвие, а при π·(2k+1)<ϑ<π·(2k+2) неподвижно первое лезвие. Декартовы координаты радиус-вектора первого лезвия в точках качения пронумеруем нечетными числами, а декартовы координаты радиус-вектора второго лезвия в этих точках пронумеруем четными точками. Не нарушая общности, можно положить tg ϕ = 1, тогда имеем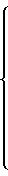
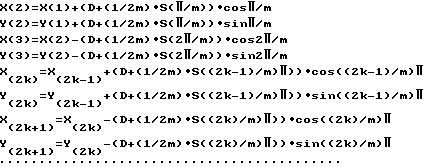
Далее квазикинематическую модель (14) можно решать алгоритмически.

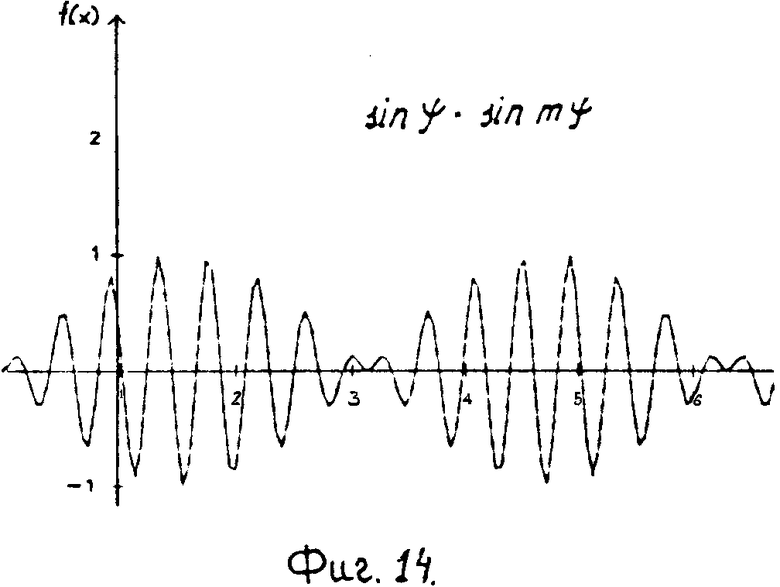
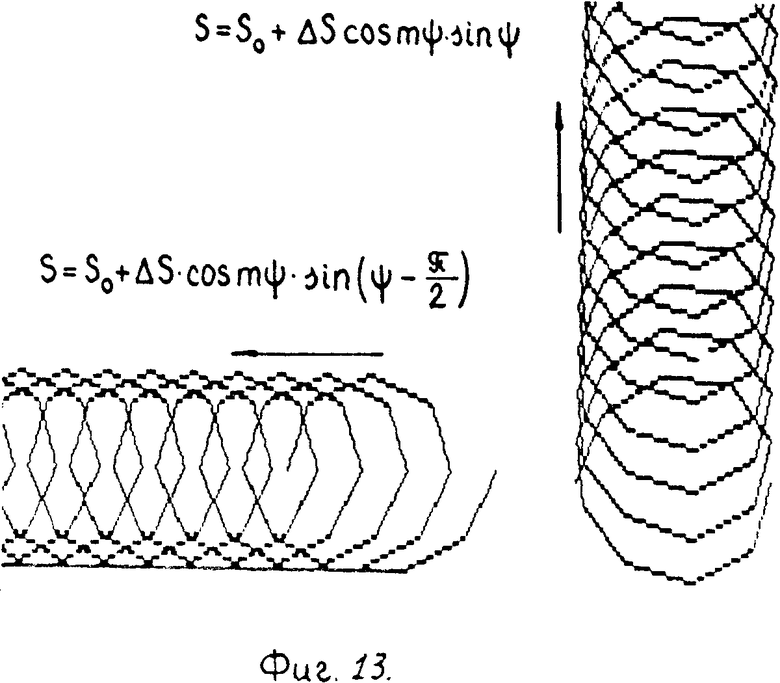
Численные решения (фиг. 13) показывают, что при наложении модулированных продольных колебаний вида (фиг. 14)
S = S_o + ΔS cos m ϑ ^. sin(ϑ - ϑ_o) наблюдается искривление трассы скважины в направлении, зависящем от сдвига фазы ϑ_о.

Отметим, что физическая сущность искривления при бурении геометрически симметричным инструментом с модулированными продольными колебаниями аналогично физической сущности искривления при бурении геометрически симметричного инструмента с медленными продольными колебаниями.

Действительно, рассмотрим двухлезвийный симметричный инструмент только в те моменты, когда лезвие 1 не режет, а опирается на поверхность дна скважины. Т. е. процесс бурения будем наблюдать как бы в стробоскоп с частотой вспышек, равной частоте быстрых поперечных автоколебаний. При таком "стробоскопическом" рассмотрении этот процесс подобен процессу бурения, когда одно из лезвий абсолютно затуплено. Если при этом на инструмент наложить продольные биения, несущая частота которых равна частоте поперечных автоколебаний, а период огибающей равен периоду вращения, то в стробоскоп мы увидим примерно следующую картину: в моменты, когда "нережущее" лезвие 1 находится в левой половине скважины, скорости проходки максимальны, а в моменты, когда "нережущее" лезвие 1 находится в правой половине скважины, скорости проходки минимальны. Очевидно, будет наблюдаться такой же эффект искривления как и на фиг. 10. Картина, наблюдаемая в стробоскоп, практически не изменится, если фазу вспышек его изменить на половину периода. Только наблюдать мы будем, что когда "нережущее" лезвие 2 находится в правой половине, скорости проходки минимальны, а когда "нережущее" лезвие 2 находится в левой половине, скорости проходки максимальны.

Очевидно, что наблюдение процесса в любые моменты времени дает один и тот же физический результат - смещение и дальнейшее искривление траектории в одну и ту же сторону.

Хотя, для осуществления заявляемого способа в этой его части требуется вибратор более сложного типа, отпадает необходимость искусственного нарушения симметрии бурильного инструмента.

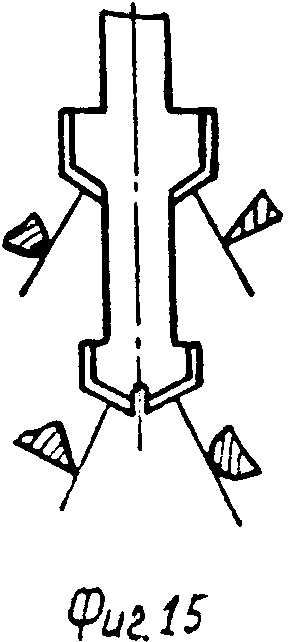
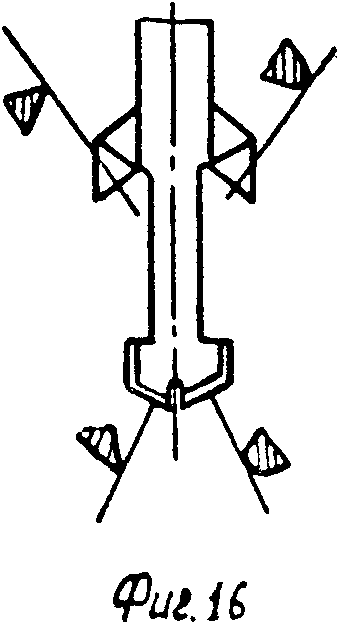
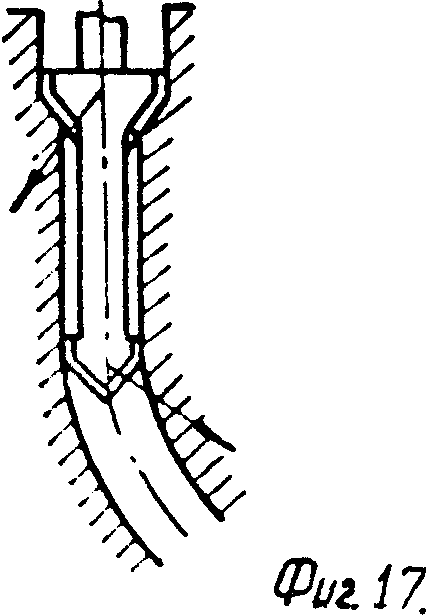
Наконец, поставленная цель достигается также тем, что в качестве породоразрушающего инструмента используют двухступенчатый инструмент, которому сообщают продольные колебания с частотой, равной частоте вращения. Двухступенчатый инструмент выполняют, например, в виде двух разнесенных в продольном направлении буровых коронок разных диаметров, причем затупленные или опорные элементы одной ступени (или коронки) располагают оппозитно относительно упомянутых элементов другой ступени (фиг. 15), а углы в плане обеих ступеней назначают одинаковыми. Если же одна буровая коронка имеет угол в плане ϕ <90^о, а другая - ϕ≥ 90^о, то их ориентируют одинаковым образом (фиг. 16). Действительно, при такой ориентации буровых коронок двухступенчатого бурильного инструмента каждая из несимметричных буровых коронок при наложении продольных колебаний с частотой, равной частоте вращения, стремится сместиться в сторону, противоположную смещению другой буровой коронки. Это резко интенсифицирует набор кривизны (фиг. 17).

При этой модификации способа кривизной скважины можно дополнительно управлять, изменяя осевое расстояние между бурильными коронками. А при необходимости управление направлением возможно и за счет изменения взаимного углового расположения буровых коронок.

Сравнительный анализ заявляемого технического решения с известными свидетельствуют о достижении нового положительного эффекта, заключающегося в обеспечении возможности резкого повышения интенсивности ее искривления. Новый положительный эффект обеспечивается благодаря новым техническим действиям, что позволяет сделать вывод о соответствии заявленного решения критерию "Существенные отличия". Достижение положительного эффекта обосновано теоретически и подтверждено лабораторными экспериментами.

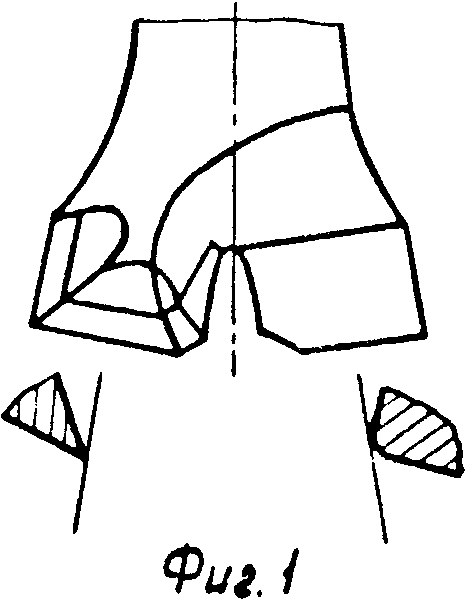
На фиг. 1 изображен геометрически несимметричный бурильный резец, одно из лезвий которого искусственно затуплено; на фиг. 2 и 3 - то же, вид сбоку и снизу геометрически несимметричного трехшарошечного долота, у которого две шарошки заменены на гладкие ролики, породоразрушающей способностью которых можно пренебречь; на фиг. 4 - схема создания продольных вибраций бурильного инструмента, частота которых равна частоте вращения, за счет создания перекоса подшипника привода вращения; на фиг. 5 - расчетная схема для составления уравнения статического равновесия бурильного резца; на фиг. 6 - расчетная схема для определения толщины слоя разрушаемой породы; на фиг. 7 - траектория вершины режущей кромки бурильного резца, одно из лезвий которого затуплено, в проекции на плоскость, перпендикулярную оси вращения при нулевом сдвиге фаз продольных колебаний; на фиг. 8 - искривление траектории этого резца при сдвиге фаз, равном π/2; на фиг. 9 - искривление траектории этого резца при сдвиге фаз, равном π/4; на фиг. 10 - схема образования искривления трассы скважины за один оборот бурильного инструмента; на фиг. 11 - искривление траектории шарошечного инструмента, у которого две шарошки заменены опорным элементом; на фиг. 12 - схема движения динамически неустойчивого симметричного бурильного резца; на фиг. 13 - его траектории в проекции на плоскость, перпендикулярную оси вращения; на фиг. 14 - график амплитудно-модулированных продольных колебаний с несущей частотой, равной частоте быстрых поперечных автоколебаний, и с периодом огибающей, равным периоду вращения инструмента; на фиг. 15, 16, 17 - схемы образования кривизны трассы скважины при проходке скважин двухступенчатым бурильным инструментом, например пикобуром.

Приведенные примеры осуществления способа были реализованы в ходе проведения лабораторных экспериментов. Управление кривизной и направлением трассы скважин производилось при бурении заготовок из плексиглаза уменьшенными моделями бурильных резцов (фиг. 1) из стали Р18, диаметром 5-15 мм, частота вращения составляла 10 Гц, средняя скорость проходки составляла 0,2 мм за один оборот инструмента.

П р и м е р 1. Требовалось искривить скважину в заданном направлении на 10^о на длине 30 мм. Применялась модель бурильного резца диаметром 6 мм, образующая коническое дно скважины с углом при вершине конуса 120^о, одно из острых лезвий которого было притуплено надфилем с образованием радиуса кривизны 0,05-0,1 мм. Во время бурения создавались продольные колебания бурильного резца с частотой, равной частоте его вращения (10 Гц) и с амплитудой, равной 0,04 мм. При этом удалось обойтись без применения специального вибратора за счет размещения в узел подшипника привода вращения двух клиновидных прокладок (фиг. 4), одна из которых закреплялась в корпусе привода вращения, а другая - на вращающемся шпинделе, перепады толщин клиновых прокладок составляли 0,04 мм. Причем край с большой толщиной прокладки, установленной на вращающемся шпинделе, совпадал по направлению с незатупленным лезвием бурильного резца, а край с большой толщиной прокладки, установленной в корпусе привода вращения, был повернут в том направлении, в котором требовалось искривить скважину.

П р и м е р 2. Требовалось искривить скважину в обратном направлении на ту же величину. Все параметры, приведенные в первом примере, были сохранены, при этом прокладку, закрепленную в корпусе привода вращения, развернули на 180^о и снова закрепили.

П р и м е р 3. Требовалось искривить скважину в обратном направлении. Все параметры, приведенные в первом примере, были сохранены, однако был применен бурильный резец, дающий плоское дно скважины.

П р и м е р 4. Требовалось искривить скважину в заданном направлении на 30^о на длине 30 мм. Все параметры, приведенные в первом примере, были сохранены кроме величины затупления одной из режущих кромок и амплитуды продольных колебаний. Одна из режущих кромок бурильного резца была затуплена профилем до полного исключения резания ею, а амплитуда продольных колебаний была доведена до 0,1 мм путем смены прокладок. Скважина искривилась в том же направлении, что и в первом примере, но в три раза интенсивнее.

П р и м е р 5. Требовалось искривить скважину в заданном направлении на 90^о на 100 мм. Применялся двуступенчатый бурильный инструмент, диаметр первой ступени составлял 10 мм, диметр второй 15 мм. Применялось также шарнирное закрепление инструмента на вращающейся штанге. Амплитуда продольных вибраций составляла 0,1 мм. Продольное расстояние между бурильными резцами первой и второй ступеней составляло 50 мм. Одно из лезвий каждого бурильного резца было затуплено до полного исключения резания этим лезвием.

Эксперимент проводился в двух вариантах:
- в первом, бурильные резцы имели одинаковый положительный наклон лезвий ϕ= 30^о, но острые кромки резцов первой и второй ступеней были расположены оппозитно;
- во втором варианте, острые кромки резцов первой и второй ступеней были направлены одинаково, но наклон лезвий резца первой ступени составлял ϕ = 30^о, так, что дно скважины было коническим и вогнутым, а наклон лезвий резца второй ступени составлял ϕ = -30^о так, что дно скважины было выпукло-коническим.

В обоих вариантах эксперимент дал идентичные результаты.

П р и м е р 6. Требовалось искривить скважину при проходке геометрически симметричным бурильным резцом, дающим плоское дно, с диаметром 8 мм, а через 50 мм проходки изменить направление искривления на противоположное.

Использовался электромеханический вибратор со специальной электронной приставкой для амплитудной модуляции входного сигнала. Сначала бурильный резец перемещали и вращали с частотой 10 Гц и сообщали ему продольные колебания той же частоты и с амплитудой 0,1 мм, при этом с помощью емкости датчика и тензостанции измеряли частоту поперечных вибраций бурильного резца, которая оказалась равна 250 Гц. На этом заходном участке L₁= 10 мм скважина еще была прямолинейной. Затем амплитуду продольных колебаний стали изменять с частотой 250 Гц за счет периодического прерывания входного сигнала. На этом участке скважина стала искривляться влево и на длине 30 мм отклонилась на 10^о. Затем изменили фазу медленных продольных колебаний на 180^о, не прекращая изменения их амплитуды с частотой 250 Гц. На этом участке длиной 50 мм скважина искривилась в обратную сторону и отклонилась на 15^о. Очевидно, в этом варианте осуществления способа для его эффективного использования необходимо применение средств обратной связи.

Технические преимущества указанных вариантов предлагаемого способа по сравнению с существующими заключаются в том, что появляется возможность производить искривление скважин с недостижимой ранее интенсивностью, что расширяет технологические возможности бурения в целом. (56) Авторское свидетельство СССР N 765494, кл. Е 21 В 7/04, 1978.

Использование: при бурении направленных скважин с использованием ударно-вращательных машин. Сущность изобретения: способ управления траекторией ствола скважины включает наложение на инструмент продольных колебаний с частотой, равной частоте вращения. При использовании осесимметричного инструмента затупляют или заменяют на опорный элемент один из породоразрушающих элементов и кривизной ствола скважины управляют в соответствии с приведенной в формуле изобретения зависимостью. При использовании двухступенчатого породоразрушающего инструмента кривизной дополнительно управляют путем изменения осевого расстояния между ступенями инструмента или изменением угла между разрушающими или затупленными элементами инструмента. Для повышения интенсивности зенитного искривления инструменту сообщают амплитудно-модулированные продольные колебания, несущую частоту которых выбирают равной частоте его быстрых поперечных автоколебаний, а частоту огибающей - равной частоте его вращения. В этом случае направлением зенитного искривления управляют, изменяя фазу огибающей, а интенсивностью искривления управляют, изменяя фазу несущих колебаний. 3 з. п. ф-лы, 17 ил.

1. Способ управления траекторией ствола скважины, включающий наложение на инструмент продольных колебаний с частотой, равной частоте вращения, управление кривизной и направлением ствола, отличающийся тем, что, с целью повышения интенсивности зенитного искривления ствола скважины, один из породоразрушающих элементов осесимметричного инструмента затупляют или заменяют на опорный элемент, а кривизной ствола скважины управляют в соответствии с зависимостью
Y₀= ΔS·K,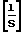
где Δ S - амплитуда продольных колебаний инструмента;
Y - величина зенитного смещения;
S - средняя величина подачи на оборот инструмента;
I - общая длина проходки участка искривления,
причем K=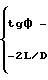
где ϕ - угол наклона режущей кромки к оси инструмента;
D - диаметр инструмента;
L - расстояние от режущей части до полюса поворота. 2. Способ по п. 1, отличающийся тем, что в качестве породоразрушающего инструмента используют двухступенчатый инструмент, имеющий общую ось симметрии и вращения ступеней, разные диаметры и одинаковые углы резания в плане, причем затупленные или опорные элементы одной ступени породоразрушающего инструмента располагают оппозитно относительно упомянутых элементов другой его ступени, а кривизной ствола скважины дополнительно управляют путем изменения осевого расстояния между ступенями породоразрушающего инструмента или изменением угла между разрушающими и затупленными или опорными элементами породоразрушающего инструмента. 3. Способ по п. 1, отличающийся тем, что в качестве породоразрушающего инструмента используют двухступенчатый инструмент, имеющий общую ось симметрии и вращения ступеней, разные диаметры и различные главные углы в плане, которые на одной ступени меньше 90^o, а на другой - больше 90^o, затупленные или опорные элементы каждой из ступеней расположены с одной стороны их общей оси, причем кривизной ствола скважины дополнительно управляют путем изменения осевого расстояния между ступенями породоразрушающего инструмента или изменением угла между разрушающими и затупленными или опорными элементами породоразрушающего инструмента. 4. Способ управления траекторией ствола скважины, включающий наложение на инструмент продольных колебаний с частотой, равной частоте вращения, управление кривизной и направлением ствола скважины, отличающийся тем, что, с целью повышения интенсивности зенитного искривления ствола скважины, инструменту сообщают амплитудно-модулированные продольные колебания, несущую частоту которых выбирают равной частоте его быстрых поперечных автоколебаний, а частоту огибающей - равной частоте его вращения, причем направлением зенитного искривления управляют, изменяя фазу огибающей, а интенсивностью искривления управляют, изменяя фазу несущих колебаний.