Изобретение относится к геофизическим методам исследования скважин, в частности к способам акустического каротажа.
Известен способ акустического каротажа скважин, в котором при непрерывном перемещении скважинного прибора и периодическом возбуждении излучателей преобразованные сигналы каждой посылки суммируют с сигналами, накопленными в оперативном запоминающем устройстве, нескольких предыдущих посылок, и по окончании накапливания заданного числа посылок записывают суммарный сигнал на магнитный носитель [1] .
Недостатком известного способа акустического каротажа скважин является низкая производительность каротажных работ из-за невысокой частоты посылок зондирующих акустических сигналов.
Также известен способ акустического каротажа скважин, состоящий в непрерывном перемещении скважинного прибора и периодическом возбуждении излучателей, приеме сигналов и суммировании сигналов нескольких посылок, при этом увеличивают частоту посылок зондирующих импульсов, модулируют их по фазе бинарной псевдослучайной периодической последовательностью, принятые сигналы каждой посылки подвергают синхронной фазовой демодуляции с помощью той же последовательности и суммируют их друг с другом в пределах ее периода [2] .
Недостатком известного способа акустического каротажа скважин является отсутствие полного подавления корреляционных шумов, так как они определяются уровнем боковых лепестков периодической автокорреляционной функции излучаемой последовательности.
Наиболее близким по технической сущности к заявляемому объекту является способ акустического каротажа, который состоит в том, что модуляцию зондирующих сигналов осуществляют в пределах не менее трех периодов модулирующей М-последовательностью с последующим дополнительным возбуждением в исследуемой среде последовательности акустических импульсов с нулевой начальной фазой через временной интервал, не меньший периода М-последовательности. При этом длительность возбуждаемой последовательности равна не менее, чем двум периодам модулирующей М-последовательности. Амплитуда акустических импульсов равна амплитуде зондирующих сигналов, а частота следования акустических импульсов равна частоте следования импульсов в М-последовательности. Затем осуществляют преобразование принятых дополнительно возбужденных сигналов в цифровой код и суммирование с результатом корреляционной обработки сигналов предшествующих посылок [3] .
Недостатком известного способа акустического каротажа является низкая производительность каротажных работ и неполное использование энергии излученных сигналов при их выделении, что приводит к понижению отношения сигнал/случайный шум.
Целью изобретения является увеличение производительности путем повышения скорости каротажа.
Цель достигается благодаря тому, что в способе акустического каротажа, основанном на непрерывном перемещении скважинного прибора и периодической посылке в исследуемую среду зондирующих сигналов в виде акустических импульсов, модулированных псевдослучайной периодической последовательностью, корреляционной обработке принятых сигналов, предусмотрены следующие отличия: излучение как минимум одного периода псевдослучайной периодической последовательности, период которой состоит из единичных акустических импульсов с начальными фазами О и π и пропусков излучения; число единичных акустических импульсов и пропусков излучения в периоде последовательности устанавливают равным
K= (q(2n+1)-1)/(q-1), K+= (q2n+qn)/2, K-= (q2n-qn)/2, где К - общее число единичных акустических импульсов с начальными фазами О и π и пропусков излучения; К+ - число единичных акустических импульсов с начальной фазой О; К -- число единичных акустических импульсов с начальной фазой π; q = pm, p - простое число; n и m - натуральные числа; длительности пропуска излучения и временного интервала , на котором излучают единичный акустический импульс, устанавливают равными; закон следования единичных акустических импульсов и пропусков излучения в периоде последовательности формируют таким образом, чтобы периодическая автокорреляционная функция модулирующей последовательности не содержала ненулевых боковых лепестков на протяжении периода; выполняют корреляцию принятых сигналов с одним периодом модулирующей последовательности, при этом выделяют сигналы на М+2, где М - число периодов в излучаемой последовательности, временных интервалах, каждый из которых по длительности равен периоду последовательности, и синхронно их накапливают на временном интервале, равном длительности исследуемого отклика среды.
Кроме того, предложенный способ отличается тем, что закон следования единичных акустических импульсов и пропусков излучения в период последовательности формируют путем генерирования линейной рекуррентной псевдослучайной последовательности чисел, преобразования чисел, которые являются квадратичными вычетами, в единичные акустические импульсы с начальной фазой О, чисел, которые являются квадратичными невычетами, в единичные акустические импульсы с начальной фазой π, а чисел нуль - в пропуски возбуждения.
Таким образом, наличие в заявляемом способе акустического каротажа отличительных признаков от прототипа позволяет сделать вывод, что он удовлетворяет критерию "новизна".
При изучении других известных технических решений в данной области техники признаки, отличающие заявляемое техническое решение от прототипа, не были выявлены, а поэтому можно сделать вывод, что заявляемый объект соответствует критерию "существенные отличия".
Достижение положительного эффекта при осуществлении заявляемого способа обеспечивается выбором структуры излучаемых сигналов, характеризующихся отсутствием корреляционных шумов при выделении сигналов и увеличением количества энергии, используемой для выделения сигналов, поскольку регистрируются и обрабатываются сигналы, вызванные полным излучением последовательности.
Для обеспечения отсутствия или минимального уровня корреляционных шумов при выделении сигналов в периоде излучаемой последовательности устанавливают общее число К единичных акустических импульсов и пропусков излучения, число К+ акустических импульсов с начальной фазой О и число К- - акустических импульсов с начальной фазой π равными:
K= (q(2n+1)-1)/(q-1), K+= (q2n+qn)/2, K-= (q2n-qn)/2, (1) для q = pm; p - простое число; n и m - натуральные числа.
Для получения структуры периодов последовательностей с идеальными периодическими автокорреляционными функциями производят следующие действия: в конечном поле Галуа GF(q) находят неприводимый полином вида
x3 - ax2 - bx - c = 0. (2) Для этого можно воспользоваться таблицами неприводимых полиномов, приведенными, например, в работе: Гилл А. Линейные последовательностные машины. М. : Наука, 1974, с. 263-276, табл. II 4; на основании выбранного неприводимого полинома вида (2) для заданного q строят соответствующее ему рекуррентное уравнение
Sj = a ˙ Sj-1 + b˙ Sj-2 + c ˙ Sj-3 , (3) где Sj, Sj-1, Sj-2, Sj-3 - вычисляемые и предшествующие во времени элементы. Для вычисления элементов последовательности задают значения ее начальных условий, например Sj-3= Sj-2 = 0, Sj-1 = 1.
Построение рекуррентных уравнений на базе неприводимых полиномов описано в ряде работ, например Цирлер Н. Линейные возвратные последовательности. - В кн. : Кибернетический сборник. М. : Изд-во иностр. лит. , 1963, вып. 6, с. 55-79; на основании рекуррентного уравнения (3) формируют q-ичную псевдослучайную последовательность числа; из полученной таким образом q-ичной псевдослучайной последовательности чисел { Sj} формируют последовательность { αj} , состоящую из символов -1, 0, +1 и обладающую идеальной периодической автокорреляционной функцией.
Для этого применяют правило:
αj= 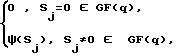 (4) где αj - j-й элемент формируемой последовательности,
(4) где αj - j-й элемент формируемой последовательности,
j = 0, 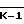 ,
,
Ψ (Sj) - индекс числа Sj, устанавливаемый на основании теоремы о квадратичных вычетах (см. , например, Варакин Л. Е. Теория сложных сигналов. М. : Советское радио, 1970, с. 238-239, где показано, что квадратичные вычеты определяются из тождества x2≡ Sj(mod q), при этом значения Sj, при которых сравнение x2≡ Sj имеет решения, называются квадратичными вычетами и им присваивается символ +1, а значения Sj, при которых сравнение не имеет решений, называются квадратичными невычетами и им присваивается значение -1). Индексы чисел приведены в ряде работ, например. Виноградов И. М. Основы теории чисел. М. : Наука, 1981, с. 176; для подтверждения идеальности периодической автокорреляционной функции, полученного периода последовательности, состоящего из символов +1, 0, -1, проверяют выполнение соотношений (1).
При совпадении расчетного числа символов +1, -1 и 0 по формулам (1) и сформированного числа символов по правилу (4) процесс формирования периода последовательности завершен. Вычислением периодической автокорреляционной функции последовательности можно подтвердить ее идеальность; в случае, если в сформированном периоде последовательности расчетное, согласно (1), количество символов +1, -1, 0 не совпадает со значениями количества символов +1, -1, 0 в сформированном по правилу (4) периоде последовательности, то вместо этого правила формирования периода последовательности применяют следующее правило: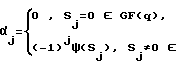
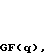



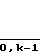 (5)
(5)
Анализ решающих правил (4) и (5) показывает их идентичность, отличие состоит в том, что при использовании решающего правила (5) символы, находящиеся на нечетных позициях в сформированной последовательности, инвертируются по знаку, то есть символ +1 заменяется на -1, а символ -1 заменяется на +1.
После этого, как и в случае пользования правилом (4), выполняют проверку расчетного количества символов +1, -1, 0 в периоде последовательности по формулам (1) и сформированного числа элементов +1, -1, 0 в периоде последовательности на основании решающего правила (5) и при их совпадении, вычислением периодической автокорреляционной функции последовательности подтверждают ее идеальность.
Таким образом, сформированная последовательность по правилам (4) или (5) обладает идеальной периодической функцией автокорреляции, что в математическом виде можно записать
Rk= 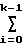 ai·ai+k=
ai·ai+k= 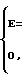
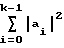



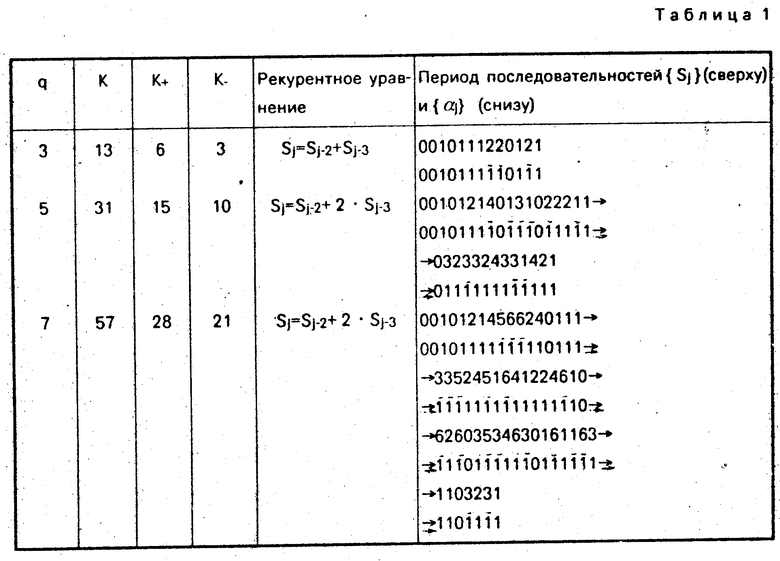
На основании изложенного в табл. 1 даны примеры периодов последовательностей с идеальной структурой для К = 13, 31 и 57.
В табл. 1 символы - 1 последовательностей { αj} для удобства написания отмечены чертой сверху 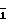 . В приведенных примерах последовательности { αj} получены из последовательностей { Sj} для q = 3 и q = 7 (К = 13 и К = 57) по правилу (4), а для q = 5 (К = 31) - по правилу (5). При этом использовались следующие замены ненулевых чисел Sj символами +1 и -1: для q = 3 Ψ (1) = 1; Ψ (2) = -1; для q = 5 Ψ (1) = Ψ (4) = 1, Ψ (2) = Ψ (3) = -1; для q = 7 Ψ (1) = Ψ (2) = Ψ (4) = 1, Ψ(3) = Ψ (5) = Ψ (6) = -1.
. В приведенных примерах последовательности { αj} получены из последовательностей { Sj} для q = 3 и q = 7 (К = 13 и К = 57) по правилу (4), а для q = 5 (К = 31) - по правилу (5). При этом использовались следующие замены ненулевых чисел Sj символами +1 и -1: для q = 3 Ψ (1) = 1; Ψ (2) = -1; для q = 5 Ψ (1) = Ψ (4) = 1, Ψ (2) = Ψ (3) = -1; для q = 7 Ψ (1) = Ψ (2) = Ψ (4) = 1, Ψ(3) = Ψ (5) = Ψ (6) = -1.
Анализ показывает, что приведенные в табл. 1 последовательности обладают идеальной периодической автокорреляционной функцией.
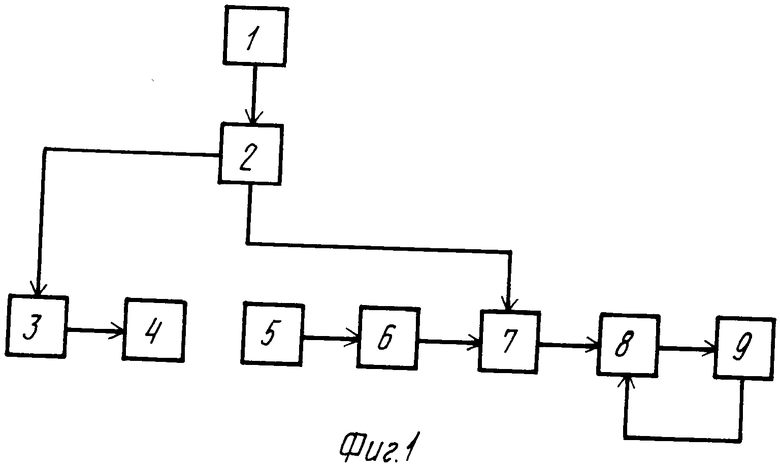
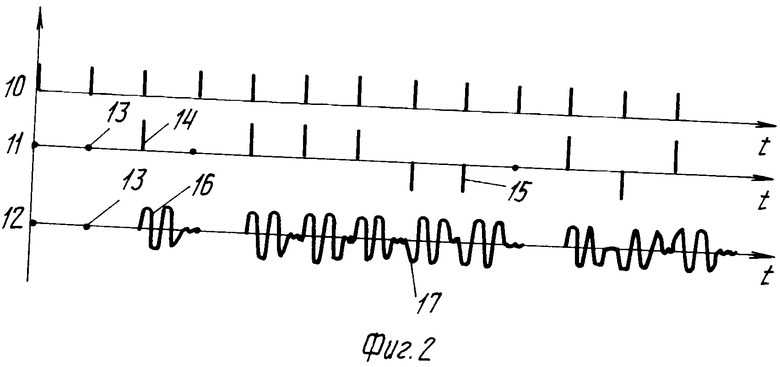
На фиг. 1 представлена структурная схема устройства для осуществления способа; на фиг. 2 приведены временные диаграммы, иллюстрирующие способ.
Устройство (фиг. 1) содержит тактовый генератор 1, генератор 2 псевдослучайной периодической последовательности, формирователь 3 импульсов возбуждения излучателя, излучатель 4, приемник 5, аналого-цифровой преобразователь 6, умножитель 7, сумматор 8 и оперативное запоминающее устройство (ОЗУ) 9.
На фиг. 2 изображены сигналы 10 на выходе тактового генератора, сигналы 11 на выходе тактового генератора псевдослучайной периодической последовательности, сигналы 12 на выходе излучателя, пропуски 13 излучения, единичный дельтаобразный импульс 14, соответствующий символу +1, единичный дельтаобразный импульс 15, соответствующий символу -1, единичный акустический импульс 16 с начальной фазой О и единичный акустический импульс 17 с начальной фазой π .
Для реализации способа используются общеизвестные средства, так, например, в качестве тактового генератора 1 используют высокостабильный генератор импульсов, частота которого определяется кварцевым элементом, генератор 2 псевдослучайной периодической последовательности выполнен по а. с. СССР N 1499437, кл. H 03 K 3/64, формирователь 3 импульсов возбуждения излучателя выполнен по схеме узла импульсного излучения (Ивакин Б. Н. и др. Акустический метод исследования скважин. М. : Недра, 1978, с. 144-145), в котором применена мостовая схема разрядных тиристоров, позволяющая манипулировать фазой разрядного тока на излучатель 4, в качестве которого используется магнитострикционный преобразователь или электроискровой разрядник. В качестве приемника 5, аналого-цифрового преобразователя 6, умножителя 7, сумматора 8 и оперативного запоминающего устройства 9 применены общеизвестные элементы.
Способ осуществляют следующим образом. Тактовый генератор 1 формирует непрерывную последовательность импульсов, частота следования (1/ Δτ) которых определяет частоту посылок зондирующих акустических импульсов и пропусков излучения. Выбор величины Δτ определяется, исходя из условия Δτ ≫  , где F - ширина спектра единичного акустического сигнала, а также скоростью заряда накопительного конденсатора формирователя 3 импульсов возбуждения излучателя. Практически Δτ выбирают в пределах 0,5-10 мс, за это время накопления энергия в формирователе 3 полностью преобразовывается излучателем 4 в упругие колебания и накопительный конденсатор формирователя 3 успеет зарядиться.
, где F - ширина спектра единичного акустического сигнала, а также скоростью заряда накопительного конденсатора формирователя 3 импульсов возбуждения излучателя. Практически Δτ выбирают в пределах 0,5-10 мс, за это время накопления энергия в формирователе 3 полностью преобразовывается излучателем 4 в упругие колебания и накопительный конденсатор формирователя 3 успеет зарядиться.
Тактовые импульсы поступают на вход генератора 2 псевдослучайной периодической последовательности. Период генерируемой им последовательности равен τ, а частота следования импульсов и пропусков равна 1/ Δτ. При этом общая длительность формируемой псевдослучайной периодической последовательности равна М периодам, где М - натуральное число. Длительность периода псевдослучайной последовательности устанавливают из условия τ ≥τиo, где τиo - длительность исследуемого отклика среды. Для обеспечения отсутствия интерференционных (корреляционных) помех длительность периода псевдослучайной последовательности должна быть больше максимальной длительности полного акустического сигнала, регистрируемого на одну посылку зондирующего акустического импульса. Исходя из заданных таким образом τ, Δτ, τиo , определяют возможное минимальное число символов в периоде последовательности, равное целой части отношения τ /Δτ , и на его основании выбирают необходимое число символов в последовательности по формуле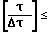 N= (q(2n+1)-1)/(q-1), где q = pm; p - простое число; m и n - натуральные числа. При этом число символов +1 равно K+= (q2n+qn)/2 , число символов -1 равно K-= (q2n-qn)/2, а число символов 0 равно Ко = К - К+ - К-. При выборе числа символов в периоде последовательности необходимо учитывать, что увеличение q дает возможность получать периоды большей длины при одновременном уменьшении числа символов О в периоде последовательности. Структура периода последовательности определяется рекуррентным уравнением (3), полученным на основании неприводимого полинома вида (2). При этом закон следования единичных акустических импульсов и пропусков излучения в периоде последовательности формируют путем генерирования линейной псевдослучайной рекуррентной последовательности чисел, преобразования чисел, которые являются квадратичными вычетами, в единичные акустические импульсы с начальной фазой О, чисел, которые являются квадратичными невычетами, в единичные акустические импульсы с начальной фазой π, а чисел нуль - в пропуски излучения. Устанавливают длительности пропусков излучения и временные интервалы, на которых излучают единичные акустические импульсы равными между собой. Общая длительность псевдослучайной периодической последовательности, т. е. число периодов последовательности, определяется из необходимой энергии излучения для получения заданного отношения сигнал/шум.
N= (q(2n+1)-1)/(q-1), где q = pm; p - простое число; m и n - натуральные числа. При этом число символов +1 равно K+= (q2n+qn)/2 , число символов -1 равно K-= (q2n-qn)/2, а число символов 0 равно Ко = К - К+ - К-. При выборе числа символов в периоде последовательности необходимо учитывать, что увеличение q дает возможность получать периоды большей длины при одновременном уменьшении числа символов О в периоде последовательности. Структура периода последовательности определяется рекуррентным уравнением (3), полученным на основании неприводимого полинома вида (2). При этом закон следования единичных акустических импульсов и пропусков излучения в периоде последовательности формируют путем генерирования линейной псевдослучайной рекуррентной последовательности чисел, преобразования чисел, которые являются квадратичными вычетами, в единичные акустические импульсы с начальной фазой О, чисел, которые являются квадратичными невычетами, в единичные акустические импульсы с начальной фазой π, а чисел нуль - в пропуски излучения. Устанавливают длительности пропусков излучения и временные интервалы, на которых излучают единичные акустические импульсы равными между собой. Общая длительность псевдослучайной периодической последовательности, т. е. число периодов последовательности, определяется из необходимой энергии излучения для получения заданного отношения сигнал/шум.
Дельтаобразные единичные импульсы положительной (символ +1) и отрицательной (символ -1) полярности поступают на формирователь 3 импульсов возбуждения излучателя, в котором они вызывают формирование импульсов, подаваемых на излучатель 4. Вследствие этого излучателем 4 будут возбуждены акустические импульсы с начальной фазой О и π в зависимости от модулирующей псевдослучайной периодической последовательности, поступающей с генератора 2.
Скважинный прибор с излучателем и приемником непрерывно перемещают и периодически осуществляют посылку в исследуемую среду зондирующих сигналов в виде акустических импульсов, модулированных псевдослучайной периодической последовательностью.
Акустические сигналы, прошедшие через горные породы, поступают на приемник 5 и преобразовываются им в электрические, после чего их преобразовывают в аналого-цифровом преобразователе 6 в цифровой код. После этого осуществляют корреляцию принятых акустических сигналов на временном интервале, равном сумме длительности излученных М периодов псевдослучайной последовательности, где М - натуральное число исследуемого отклика среды τиo с одним периодом модулирующей псевдослучайной периодической последовательности. После выполнения корреляции выделяют сигналы на М+2, где М - число периодов в излучаемой последовательности, временных интервалах, каждый из которых по длительности равен периоду последовательности, и синхронно их накапливают на временном интервале, равном длительности исследуемого отклика среды.
При этом в умножителе 7 при корреляционной обработке осуществляется операция синхронной фазовой демодуляции сигнала в аналоговом виде. Предложенный метод синхронного накопления выделенных сигналов на М+2 интервалах длиной в период позволяет устранить корреляционные шумы, осложняющие полезные сигналы без потерь возбужденной энергии. В известных способах акустического каротажа теряется энергия крайних периодов последовательностей с целью устранения корреляционных шумов. Этот недостаток ликвидирован в заявляемом объекте.
П р и м е р. Рассматриваемый пример иллюстрируется временными диаграммами, представленными на фиг. 2. В рассматриваемом варианте способа излучают псевдослучайную последовательность, состоящую из одного периода, содержащего 13 символов.
Тактовый генератор 1 формирует непрерывную последовательность 10 импульсов, частота следования 1/ Δτ которых определяет частоту посылок акустических импульсов и пропусков излучения. Параметры Δτ выбирают так, как это было описано выше. Тактовые импульсы 10 поступают на вход генератора 2 псевдослучайной периодической последовательности, период генерируемой им последовательности состоит из 13 дельтаобразных импульсов с начальными фазами О и π и пропусков, а частота следования импульсов и пропусков равна 1/ Δτ. Для генерирования такого периода псевдослучайной последовательности при q = 3 выбирают неприводимый полином вида X3 + 2X + 2 в поле Галуа GF(q). На его основании получают рекуррентное уравнение Sj = Sj-2 + Sj-3. Тогда при начальных условиях Sj-3 = Sj-2 = 0, Sj-1 = 1 будет сформирован следующий период псевдослучайной последовательности чисел 0 0 1 0 1 1 1 2 2 0 1 2 1. Поскольку при q = 3 число 1 является квадратичным вычетом, а число 2 - квадратичным невычетом, то указанную числовую последовательность можно преобразовать в следующую последовательность символов 0 0 1 0 1 1 1 -1 -1 0 1 -1 1. Указанные значения символов кодируются и заносятся в память генератора 2, который формирует один период последовательности 11, состоящей из 6 дельтаобразных единичных положительных импульсов 14, 3 дельтаобразных единичных отрицательных импульсов 15 и 4 пропусков излучения 13, что соответствует расчетным значениям по формулам (1). Периодическая автокорреляционная функция такой последовательности равна . . . 9 000 000 000 000 9. . . , то есть не имеет боковых лепестков. Время излучения периода такой последовательности должно превышать длительность исследуемого отклика среды. Импульсная последовательность 11 с генератора 2 подается на формирователь 3 импульсов возбуждения излучателя, где происходит формирование мощных импульсов тока соответствующей полярности, подаваемых на излучатель 4, который генерирует в среде последовательность 12 акустических импульсов, промодулированных по фазе последовательностью 11. В результате в генерируемой последовательности 12 излучателем 4 будет содержаться 4 пропуска излучения 13, 6 единичных акустических импульсов 16 с начальной фазой О, соответствующих единичным положительным дельтаобразным импульсам 14, 3 единичных акустических импульса 17 с начальной фазой π , соответствующих единичным отрицательным дельтаобразным импульсам 15. Устанавливают длительность каждого пропуска излучения 13 равной длительности временного интервала, на котором возбуждают акустический импульс с начальной фазой О или π.
Скважинный прибор с излучателем и приемником непрерывно перемещают и периодически осуществляют посылку в исследуемую среду зондирующих сигналов в виде акустических импульсов, модулированных псевдослучайной периодической последовательностью 11.
Акустические сигналы, прошедшие через горные породы, поступают на приемник 5 и преобразовываются им в электрические, после чего их преобразовывают в аналого-цифровом преобразователе 6 в цифровой код. После этого осуществляют корреляцию принятых акустических сигналов на временном интервале, равном сумме длительности излученного периода псевдослучайной периодической последовательности и исследуемого отклика среды τио, с периодом псевдослучайной периодической последовательности 11. Положим, единичный акустический импульс 16 с начальной фазой О вызывает отклик среды Х1, Х2, Х3, Х4, Х5, а единичный акустический импульс 17 с начальной фазой π вызывает отклик среды 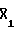 ,
, 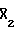 ,
, 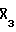 ,
, 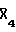 ,
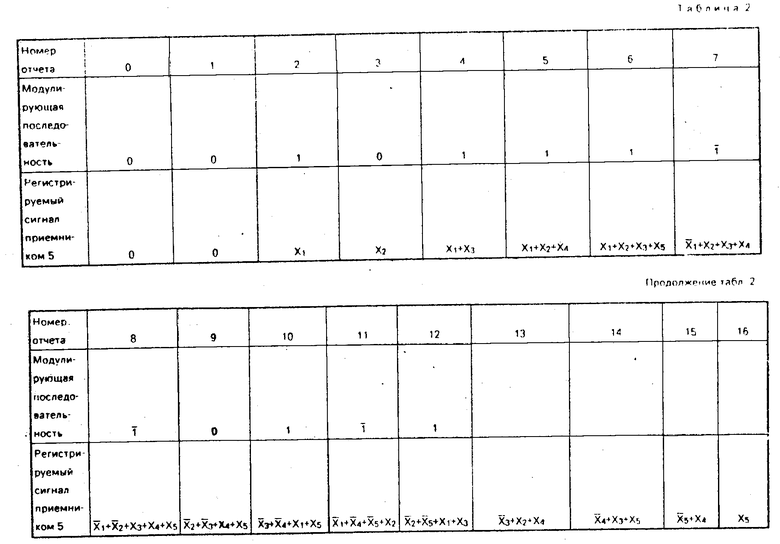
, 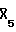 , где черта сверху над Х означает инвертирование полярности. Здесь для простоты отсчеты отклика среды задаются через временные интервалы, соответствующие временным интервалам следования акустических импульсов и пропусков излучения, то есть равными Δτ. В табл. 2 приведен зарегистрированный приемником 5 сигнал на возбуждение последовательности 12.
, где черта сверху над Х означает инвертирование полярности. Здесь для простоты отсчеты отклика среды задаются через временные интервалы, соответствующие временным интервалам следования акустических импульсов и пропусков излучения, то есть равными Δτ. В табл. 2 приведен зарегистрированный приемником 5 сигнал на возбуждение последовательности 12.
В результате выполнения корреляции между зарегистрированным сигналом приемником 5 (табл. 2) и импульсной последовательностью 11, модулирующей возбуждаемый сигнал, получен сигнал корреляционного преобразования. При этом на отсчетах 12. . . 16 содержится полезный сигнал, осложненный корреляционными шумами (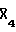 + Х5;
+ Х5; 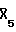 ; 0;
; 0; 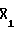 ; Х1 +
; Х1 + 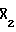 ), а на остальных отсчетах - корреляционные шумы. Сложение (накопление) сигналов на отсчетах 38, 0. . . 11 и 12. . . 24 и 25. . . 37 позволяет выделить полезный сигнал, не осложненный корреляционными шумами, а именно 9Х1, 9Х2, 9Х3, 9Х4, 9Х5. Этот сигнал соответствует полной возбужденной энергии в последовательности (9 единичным акустическим импульсам) и не содержит корреляционных шумов.
), а на остальных отсчетах - корреляционные шумы. Сложение (накопление) сигналов на отсчетах 38, 0. . . 11 и 12. . . 24 и 25. . . 37 позволяет выделить полезный сигнал, не осложненный корреляционными шумами, а именно 9Х1, 9Х2, 9Х3, 9Х4, 9Х5. Этот сигнал соответствует полной возбужденной энергии в последовательности (9 единичным акустическим импульсам) и не содержит корреляционных шумов.
Предложенный способ акустического каротажа по сравнению с прототипом позволяет повысить производительность каротажных работ за счет уменьшения числа возбуждаемых последовательностей и использования всех периодов излучаемой последовательности при корреляционной обработке, это одновременно позволяет улучшить в выделенных сигналах отношение сигнал/случайный шум.
Предложенный способ может найти также применение в межскважинном прозвучивании при использовании мощного излучателя, построенного, например, на электромеханическом принципе.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АКУСТИЧЕСКОГО КАРОТАЖА | 1990 |
|
RU2012019C1 |
| Способ сейсмической разведки | 1990 |
|
SU1749862A1 |
| Способ сейсмической разведки | 1989 |
|
SU1749860A1 |
| Способ пространственной сейсморазведки | 1989 |
|
SU1803897A1 |
| Способ сейсмической разведки | 1990 |
|
SU1805414A1 |
| Способ пространственной сейсморазведки | 1989 |
|
SU1749861A1 |
| Способ сейсмической разведки | 1989 |
|
SU1679431A1 |
| Устройство синхронизации источников сейсмических сигналов | 1991 |
|
SU1787278A3 |
| Способ возбуждения сейсмических сигналов | 1981 |
|
SU1140070A1 |
| СПОСОБ СЕЙСМОРАЗВЕДКИ | 1991 |
|
RU2009527C1 |
Использование: при геофизических исследованиях скважин, в частности при акустическом каротаже. Сущность изобретения: выполняют модуляцию зондирующих акустических импульсов псевдослучайной периодической последовательностью. При этом излучают как минимум один период псевдослучайной периодической последовательности. Он состоит из единичных акустических импульсов с начальными фазами О и π , а также пропусков излучения. Число единичных акустических импульсов и пропусков излучения в периоде последовательности устанавливают равными K=(q(2n+1)-1)/(q-1) , K+=(q2n+qn)/2 , K-=(q2n+qn)/2, где K - общее число единичных акустических импульсов с начальными фазами О и π и пропусков излучения в периоде последовательности; K+ - число единичных акустических импульсов с начальной фазой О; K- - число единичных акустических импульсов с начальной фазой π ; q=pm ; p - простое число; n и m - натуральные числа. Длительности пропусков излучения и временные интервалы, на которых излучают акустические импульсы, равны. Закон следования единичных акустических импульсов и пропусков излучения в периоде последовательности задают таким, чтобы периодическая автокорреляционная функция модулирующей последовательности не содержала ненулевых боковых лепестков на протяжении периода. Корреляцию принятых сигналов выполняют с одним периодом модулирующей последовательности, при этом выделяют сигналы на M + 2 временных интервалах, где M - число периодов в излучаемой последовательности. Каждый временной интервал по длительности равен периоду последовательности, а выделенные сигналы синхронно накапливают на временном интервале, равном длительности исследуемого отклика среды. 1 з. п. ф-лы, 2 ил. , 2 табл.
(q2n+1 - 1) / (q - 1),
а количества единичных акустических импульсов с начальной фазой 0 и π соответственно равные (q2n + qn) / 2 и (q2h - qn) / 2, где q = pm;
p - простое число;
m и n - натуральные числа,
при этом генерируют реккурентную псевдослучайную последовательность чисел, преобразовывают числа, соответствующие квадратичным вычетам, в единичные акустические импульсы с начальной фазой 0, числа, соответствующие квадратичным невычетам, - в единичные акустические импульсы с начальной фазой π, а числа "0" - в пропуски излучения, причем длительность пропуска излучения задают равной временному интервалу, на котором излучают единичный акустический импульс, зарегистрированные приемником сигналы коррелируют с одним периодом модулирующей последовательности, при этом выделенные при корреляции сигналы на M + 2 временных интервалах, каждый из которых равен длине периода последовательности, где M - число периодов в излучаемой последовательности, синхронно суммируют.
Авторы
Даты
1994-04-30—Публикация
1990-06-04—Подача