Изобретение относится к области измерений штамповых испытаний твердых деформируемых тел, в частности грунтов и строительных материалов.
Известен прессиометрический способ определения модуля деформации грунтов [1, с. 38-49]. Этот метод является разновидностью методов испытания статической нагрузкой и заключается в обжатии участка скважины равномерным радиальным давлением и измерении образующихся при этом перемещений грунта. Модуль деформации определяют по прессиометрическому графику экспериментальной зависимости между давлением и перемещениями в пределах линейного участка с использованием аналога формулы Ляме. Практика измерений показывает, что случайная ошибка в определении модуля деформации прессиометрических испытаний превышает соответствующую ошибку штамповых испытаний в среднем в 1,5 раза. Поэтому прессиометрический способ определения модуля деформации классифицируется как грубый.
Наиболее близким техническим решением по совокупности признаков к предложенному изобретению является способ определения модуля деформации с помощью жестких штампов [1, с. 9-17], включающий вдавливание заданной нагрузкой в исследуемую среду плоских штампов круглой или прямоугольной формы в плане, и определение модуля деформации согласно измеренным осадкам штампов с использованием аналога формулы Буссинеска.
Однако несмотря на простоту приборов и оборудования, методы испытаний плоскими штампами имеют ряд существенных недостатков. Главный из них - низкая представительность получаемых результатов для характеристики свойств грунтов по разрезу отложений. Результаты испытаний на поверхности оснований, имея обычно случайный характер, распространяются на всю толщу грунтового массива. Далее, контактные давления под плоским штампом характеризуются значительной неоднородностью, обусловленной резким ростом градиентов при подходе к краям штампа. В результате по периметру штампа возникают остаточные пластические деформации, определяемые прочностными свойствами грунта и не характеризующие его уплотняемость (упругую сжимаемость). Зачастую выявляются несоответствия между теоретическими решениями и экспериментальными данными, особенно при использовании штампов малых размеров. Следует отметить еще, что при малых размерах плоских штампов существенное влияние на результаты испытаний оказывают случайные погрешности, связанные с неровным прилеганием подошвы штампа, возможным эксцентриситетом приложения нагрузки и т.д. Поэтому статические испытания по вдавливанию плоских штампов с целью определения модуля деформации должны включать многократное проведение опытов со статистической обработкой результатов. Кроме того, испытания грунтов с помощью плоских штампов весьма трудоемки и являются дорогостоящими, вследствие чего широкое применение этого метода при изысканиях для строительных площадок под объекты массовой застройки, а тем более при инженерно-геологических съемках, до сих пор ограничиваются.
Задачей изобретения является разработка способа определения модуля деформации с помощью статических испытаний материалов заглубленными разноугольными коническими штампами, обеспечивающего повышение точности, надежности и достоверности результатов испытаний. Эти испытания пригодны как на Земле, так и на других планетах; как для полевых, так и для лабораторных исследований. Они отличаются простотой и портативностью, дешевизной и высокой скоростью исполнения, легко поддаются автоматизации и позволяют получать непрерывные механические характеристики по грунтовому разрезу с минимальными трудо- и энергозатратами. Применение конусных штампов в установках для статических испытаний грунтов имеет особенно важное значение для дорожного строительства, которое отличается большой протяженностью трасс и требует определения свойств грунтов в очень большом числе точек.
Поставленная задача решается тем, что в способе определения модуля деформации с помощью штампа, включающем вдавливание заданной нагрузкой в исследуемую среду жесткого штампа, измерение его перемещений и определение модуля деформации, отличительными от прототипа признаками является то, что производят вдавливание в исследуемую среду заглубленного конического штампа, а модуль деформации определяют по следующей формуле:
где ΔP и ΔW - соответствующие изменения нагрузки (H) и осадки (м) при статических испытаниях в пределах фазы линейного деформирования исследуемого материала; a - радиус заглубленной части конического штампа (м), q(α,ν) - безразмерный коэффициент, рассчитываемый по формуле
q(α,ν) = K(α)•[1+A(α)•ν-B(α)•ν2],
в которой α - угол при вершине конического штампа;
ν - коэффициент Пуассона исследуемого материала;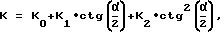
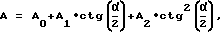
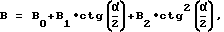
ctg(α/2) = h/a - относительное заглубление конуса;
Ki, Ai, Bi (i = 0, 1, 2) - числовые параметры, найденные нами по результатам решения осесимметричной контактной задачи теории упругости для заглубленного в полупространство жесткого конуса.
Отметим, что попытка решения контактной задачи для заглубленного конуса с фиксированным углом α = 53,14o при вершине (относительное заглубление h/a = 2,0) было предпринято ранее А.Я.Александровым и Ю.И.Соловьевым [2] с использованием метода контурных интегралов. Однако в этой работе не указано значение коэффициента Пуассона ν, при котором авторами получен числовой результат. Кроме того, использование метода контурных интегралов в работе [2] предполагало пренебрежение горизонтальными перемещениями в точках контакта штампа с основанием. Это ограничение привело к малоправдоподобному распределению контактных напряжений по боковой поверхности конуса (эпюры нормальных и касательных напряжений оказались практически идентичными). Полученный в [2] результат не может быть признан вполне достоверным и обобщен для конусов с различными углами при вершине, а также сред, имеющих разные значения ν.
Изобретение поясняется фиг. 1-5.
На фиг. 1 представлена расчетная схема контактной задачи о вдавливании центральной силой жесткого конуса, заглубленного в упругое основание.
Фиг. 2 иллюстрирует дискретизацию контактной поверхности с использованием треугольных и четырехугольных плоских граничных элементов, принятую при численном решении пространственной задачи теории упругости о вдавливании заглубленного конуса в испытываемый материал.
На фиг. 3 приведены эпюры касательных τ и нормальных σ контактных напряжений для заглубленного конического штампа (h/a = 2,0), отнесенные к среднему напряжению σср = P/S, P - внешняя вертикальная нагрузка на штамп; S - площадь контактной поверхности.
На фиг. 4 по результатам численного решения контактной задачи построены графики безразмерной функции q(α,ν), характеризующей осадку разноугольных конусов, заглубленных в упругое основание.
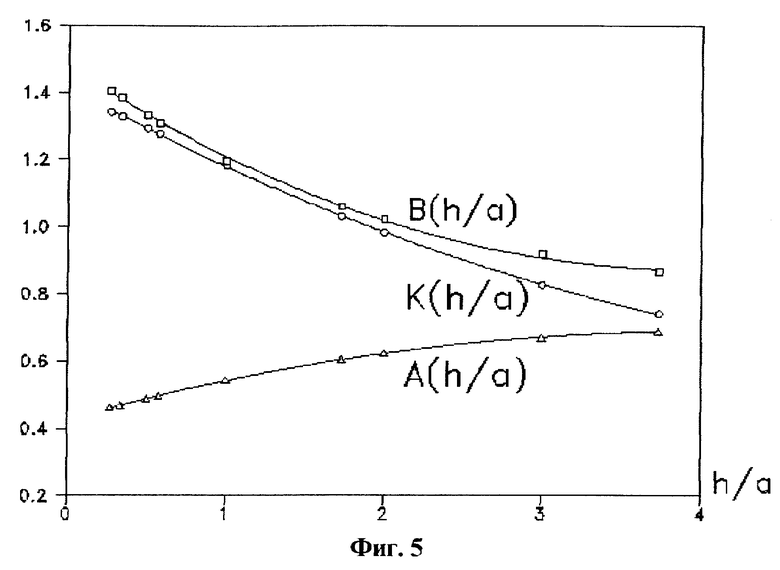
На фиг. 5 показано изменение параметров функции q(α,ν), от угла при вершине конуса α = 2arccrtg(h/a).
Способ определения модуля деформации включает вдавливание заглубленного конического штампа 1 (штанги с конусным наконечником-индентором) в исследуемый материал вертикальным усилием P, передаваемым нагрузочным устройством (не показано) (фиг. 1). В свою очередь, измерительное устройство (не показано) обеспечивает определение вертикальных перемещений (осадок) W штампа. Наличие линейной связи между нагрузкой и осадкой для абсолютного большинства твердых деформируемых сред (грунты и горные породы, строительные материалы и др.) в определенном диапазоне деформирования позволяет, используя методы теории упругости, по наклону прямолинейного участка кривой W = W(P) определить модуль деформации исследуемой среды. В виду инвариантности модуля деформации по отношению к используемому индентору указанный угловой коэффициент помимо коэффициента Пуассона ν должен функционально зависеть и от формы индентора, в данном случае от угла раскрытия конуса α и его заглубления h = a•ctg(α/2). Поэтому линейная связь между нагрузкой и осадкой приводит к формуле для определения модуля деформации
E = k • P/W,
где k = q(α,ν)/πa; q(α,ν) - безразмерная функция жесткости системы "штамп-упругое основание"; a - характерный линейный масштаб (в нашем случае радиус конуса). Множитель π в знаменателе используется для придания расчетным формулам такой же структуры, как и в формуле для случая круглого штампа с плоской подошвой.
Для определения функциональной зависимости q = q(α,ν) рассмотрим пространственную контактную задачу теории упругости для заглубленного конического штампа, вдавливаемого осевой силой P в упругое однородное основание, деформационные свойства которого характеризуются модулем деформации E и коэффициентом Пуассона ν. В качестве расчетной модели основания используем линейно-деформируемое полупространство, ослабленное полостью, границы которой находятся в полном соответствии с контактной поверхностью конического штампа. Считаем, что штамп спаян с полупространством по поверхности конической выемки глубиной h и радиусом а (угол при вершине конуса α = 2arcctg(h/a). Расчетная схема задачи и используемые обозначения приведены на фиг. 1.
В силу осевой симметрии заглубленный абсолютно жесткий конический штамп будет смещаться только вертикально. Напряженное состояние упругого полупространства (линейно-деформируемого основания) характеризуется радиальной pr и вертикальной pz составляющими вектора контактных напряжений (тангенциальные напряжения prz в силу осевой симметрии отсутствуют) и зависят только от вертикальной координаты. Записанная с использованием теоремы взаимности Бетти система интегральных уравнений пространственной контактной задачи для заглубленного осесимметричного штампа, включающая уравнение равновесия, имеет вид:
где W - вертикальное перемещение конуса; pr (N), pz (N) - проекции вектора контактного напряжения в точке N на оси цилиндрической системы координат; P - результирующая внешних сил, приложенных к конусу в направлении оси z; Ur (k)(K,N), V(k)(K,N) - перемещения точек упругого полупространства, которые определяются по формулам
Uij (K, N) - фундаментальное решение Р.Миндлина [3], представляющее перемещение в точке N полупространства в j-ом направлении от единичной сосредоточенной силы, приложенной в точке К полупространства по i-му направлению; Г - контактная поверхность штампа, точки N ∈ Г и K ∈ Г ; значения индексов i, j = 1, 2, 3.
Нормальные p(n) и касательные p(τ) контактные напряжения после решения системы (1) легко вычисляются с использованием известных соотношений:
p(n) = prcosθ+pzsinθ,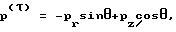
где θ - угол между внешней нормалью к контактной поверхности и горизонтальной плоскостью.
Ввиду отсутствия по настоящее время точного аналитического решения рассматриваемой контактной задачи, решаем ее численно с использованием прямого метода граничных элементов [4] в сочетании с кусочно-постоянной аппроксимацией функции контактных напряжений. Контактную поверхность конуса и полупространства разбиваем на плоские граничные элементы, узлы которых образуются при пересечении горизонтальных (равноотстоящих) и вертикальных (проходящих через ось конуса и составляющих между собой равные углы) плоскостей. Регулярная сетка граничных элементов умеренной густоты иллюстрируется на фиг. 2. (вид сбоку (а) и снизу (б)). На каждом граничном элементе функции контактных напряжений усредняются. При этом осредненные величины контактных усилий выражаются только через осевое жесткое смещение штампа. Размерность гранично-элементной задачи равна (2М+1) относительно значений W и pr (m), pz (m) = 1,2,...М, где М - общее число граничных элементов вдоль образующей конуса.
В соответствии с разработанным алгоритмом автоматизированно дискретизируется поверхность контакта заглубленной части конуса с исследуемой средой, формируется и решается система линейных алгебраических уравнений метода граничных элементов для различных значений коэффициента Пуассона ν и внешнего силового воздействия P. В практических расчетах образующая конуса разбивалась горизонтальными плоскостями на М = 10 участков, а по угловой координате на 400 меридиональных поясов, определяемых углами Δϕ = 2π/400. Вычисление регулярных интегралов осуществлялось по кубатурным формулам наивысшей степени точности, сингулярных - полуаналитическим методом с выделением особенности. Отметим, что, увеличивая число граничных элементов по угловой координате, получаем решения с необходимой степенью точности.
На фиг. 3 в качестве примера по данным экстраполяции численного решения контактной задачи представлены эпюры нормальных и касательных контактных напряжений в меридиональном сечении конического штампа, имеющего заглубление h = 2a(α/2 = 26,57o) и вдавливаемого в упругое полупространство с коэффициентом Пуассона ν = 0,3. В центрах десяти участков равной длины на образующей конуса определены значения нормальных σ и касательных τ контактных напряжений, отнесенные к среднему напряжению σср = P/S, S - площадь контактной поверхности.
По результатам расчета осадок заглубленных в упругое полупространство конусов с различными углами при вершине (α/2 = 15o; 18,43o; 26,57o; 30o; 45o ; 60o; 63,43o; 71,57o; 75o) были определены (фиг. 4) значения безразмерной функции
при изменении коэффициента ν от 0,2 до 0,5 с шагом 0,05, что достаточно подробно охватывает реально возможный интервал изменения объемной сжимаемости многих сред (ν = 0,2 - бетон; ν = 0,27 - крупноблочные грунты; ν = 0,3 - пески и супеси; ν = 0,35 - cуглинки; ν = 0,42 - глины [1, с.15]). Регрессионный анализ расчетных данных показал, что при фиксированном угле раствора конуса α значения q с большой степенью точности могут быть представлены (фиг. 4) параболической зависимостью
q(α,ν) = K(α)•[1+A(α)•ν-B(α)•ν2], (3)
для параметров которой составлена расчетная таблица. В целях большего удобства при пользовании формулы (3) на фиг. 5 представлены вспомогательные графические зависимости K(α), A(α), B(α), полученные по результатам квадратической аппроксимации табличных данных. Соответствующие формулы имеют вид:
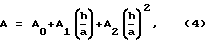

где h/a = ctg(α/2) - относительное заглубление конуса; Ki, Ai, Bi (i = 0, 1, 2) - числовые параметры, обеспечивающие аппроксимацию с абсолютной погрешностью, не превышающей ε = 10-5.
Полученные зависимости (3) и (4), определяющие связь W - P для заглубленных разноугольных конусов, так же, как и в случае плоских штампов, теперь обычным образом используем для вычисления модуля деформации по формуле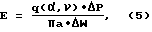
где ΔP и ΔW - соответствующие изменения нагрузки и осадки при статических испытаниях в пределах фазы линейного деформирования испытываемого материала. Указанная зависимость для определения модуля деформации является следствием формулы (2), причем вместо значений P и W использованы их приращения, поскольку осадка на начальных стадиях нагружения всегда будет связана с погрешностями из-за неплотного прилегания штампа и основания, обмятия неровностей и т.п.
Методика проведения и обработки результатов испытаний статических нагружений заглубленных конусов с помощью формулы (5) во многом подобна применению штампов с плоской подошвой и заключается в приложении к коническому штампу начального давления с последующим нагружением ступенями ΔP, величина которых должна зависеть от зернового состава, степени влажности и плотности испытываемых материалов, их консистенции, пористости и др.
В отличие от испытаний плоскими штампами, когда осадка должна определяться в нескольких точках их кромки, при вдавливании конуса достаточно определять его осевое перемещение.
Подчеркнем важную особенность статических испытаний при использовании теоретического решения (5), состоящую в том, что производится вдавливание конуса, предварительно заглубленного в деформируемую среду. Так например, при испытаниях грунтов нарушенного сложения формование образцов проводится с закладкой вкладышей, образующих после их удаления конические полости. В образцах грунтов естественного сложения выемка создается специальным приспособлением типа спирального бура. Вблизи стен приямков, а также для установления анизотропных свойств грунта конус может вдавливаться как в горизонтальном, так и в вертикальном направлениях.
Отметим, что по резкому перегибу экспериментальной кривой W = W(P) так же, как и для штампов с плоской подошвой, с помощью конического штампа может быть определено критическое давление (соответствующее пределу пропорциональности). Таким образом, использование статического нагружения конического штампа можно отнести к совершенствованию не только существующих способов определения деформационных параметров, но и контроля прочностных свойств материалов.
Изобретение иллюстрируется следующим примером.
Пусть требуется определить модуль деформации упругосжимаемой среды по результатам вдавливания заглубленного конического штампа, имеющего угол α = 100o при вершине и радиус а = 5 см. Штамп вдавливается в мелкозернистый песок (коэффициент Пуассона ν = 0,333) вертикальной силой P = 15 кН. Полученное в результате измерения индикатором часового типа значение осадки конуса W1 = 0,42937 см.
Согласно представленному способу сначала вычисляем относительное заглубление штампа h/a = ctg(α/2) = ctg(50o) = 0,8391. По формулам (4) или по графикам на фиг. 5 находим коэффициенты
К = 1,2143; A = 0,52591; B = 1,24754
и далее значение g (100o; 0,333) = 1,25896. Рассчитанный по формуле (5) модуль деформации грунта будет E = 28 МПа.
Таким образом, предлагаемый способ определения модуля деформации по результатам вдавливания заглубленного конуса обеспечивает
- возможность использования традиционного оборудования (нагрузочных и измерительных устройств), применяемого при стандартных испытаниях материалов статическими нагрузками;
- значительные преимущества в технике проведения экспериментов, так как позволяет с большей надежностью, чем для штампов с плоской подошвой, осуществлять полный контакт с испытываемым материалом;
- учет сопоставимого уровня касательных и нормальных напряжений в зоне контакта благодаря реализации распорной системы усилий между штампом и исследуемой средой;
- адекватную интерпретацию результатов испытаний вследствие реализации напряженных состояний пространственного типа вблизи конусов различной формы;
- совершенствование существующих способов определения важнейшего параметра сжимаемости грунтов, с учетом которого построены регламентируемые нормативными документами методы расчета оснований сооружений по деформациям, а также контроль прочностных свойств материалов;
- проведение как полевых, так и лабораторных испытаний грунтов разноугольными конусами, что повышает информационность и достоверность экспериментальных результатов;
- существенную экономию при инженерных изысканиях в строительстве за счет снижения габаритов измерительной техники;
- учет процесса контактного взаимодействия ниже поверхности основания, что важно для повышения надежности оценок характеристик сжимаемости материалов, однако отсутствует при использовании плоских штампов, устанавливаемых на поверхности и не испытывающих влияния вышележащего массива.
Источники информации
1. Швец В.Б., Лушников В.В., Швец Н.С. Определение строительных свойств грунтов (справочное пособие). - Киев: Будивельник, 1981.
2. Александров А.Я., Соловьев Ю.И. Решение пространственной осесимметричной задачи теории упругости при помощи контурных интегралов/Прикл. математика и механика. - 1964. - Вып.5. - С. 914 - 919.
3. Миндлин P. , Чень Д. Сосредоточенная сила в упругом полуполупространстве/Механика (Сб.сокр.пер.). - 1952. - N 4(14). - С. 118-141.
4. Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов. - М.: Мир, 1987. - С. 196-254.
| название | год | авторы | номер документа |
|---|---|---|---|
| АМОРТИЗАТОР | 1998 |
|
RU2141064C1 |
| СПОСОБ УПРАВЛЕНИЯ РАБОЧИМ ОРГАНОМ ЗЕМЛЕРОЙНО-ТРАНСПОРТНОЙ МАШИНЫ | 1997 |
|
RU2131961C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ МАТЕРИАЛЬНОЙ СРЕДЫ | 2014 |
|
RU2566400C1 |
| СПОСОБ ДИНАМИЧЕСКОЙ БАЛАНСИРОВКИ ПРЕИМУЩЕСТВЕННО КАРДАННОГО МЕХАНИЗМА МАШИНЫ | 1995 |
|
RU2109260C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК ГРУНТА | 1997 |
|
RU2135689C1 |
| АРМАТУРНЫЙ КАРКАС СТРОИТЕЛЬНОЙ КОНСТРУКЦИИ | 1998 |
|
RU2137892C1 |
| СПОСОБ УСТРОЙСТВА ДОРОЖНОГО ПОКРЫТИЯ | 1999 |
|
RU2144106C1 |
| АРМАТУРНЫЙ ЭЛЕМЕНТ | 2000 |
|
RU2171342C1 |
| БАЛКА | 2000 |
|
RU2172372C1 |
| ДИНАМИЧЕСКИЙ ПЛОТНОМЕР ГРУНТА | 1995 |
|
RU2097487C1 |



Изобретение относится к области измерений и испытаний деформируемых тел, в частности грунтов и строительных материалов. Согласно изобретению способ включает в себя вдавливание заданной нагрузки в исследуемый материал жесткого конуса и измерение его перемещений в процессе внедрения в материал. Модуль деформации определяется по измеренным параметрам согласно предложенной расчетной формуле. При этом используются данные статических испытаний материала в пределах его линейной деформации. Изобретение позволяет повысить информативность и достоверность опытных результатов за счет применения в испытаниях загубленных разноугольных конических штампов. 5 ил.
Способ определения модуля деформации по результатам испытаний материалов статическими нагрузками, включающий вдавливание заданной нагрузкой в исследуемую среду жесткого штампа, измерение его перемещений и определение модуля деформации, отличающийся тем, что в исследуемую среду производят вдавливание заглубленного конического штампа, а модуль деформации определяют по формуле
где ΔP и ΔW - соответствующие друг другу изменения нагрузки (H) и осадки (м) при статических испытаниях в переделах фазы линейного деформирования исследуемого материала;
a - радиус заглубленной части конического штампа (м);
q(α,ν) - безразмерный коэффициент, рассчитываемый по формуле
q(α,ν) = K(α)•[1+A(α)•ν-B(α)•ν2],
в которой α - угол при вершине конического штампа, град;
ν - коэффициент Пуассона исследуемого материала;
K = K0+K1•ctg(α/2)+K2•ctg2(α/2),
A = A0+A1•ctg(α/2)+A2•ctg2(α/2),
B = B0+B1•ctg(α/2)+B2•ctg2(α/2),
ctg(α/2) = h/a - относительное заглубление конуса;
Ki, Ai, Bi (i = 0, 1, 2) - числовые параметры.
| Швец В.Б | |||
| и др | |||
| Определение строительных свойств грунтов (справочное пособие) | |||
| - Киев: Будивельник, 1981, с.9-17 | |||
| US 5463896 A, 1995-11-07 | |||
| RU 94019498 A1, 1995-11-10 | |||
| RU 94023277 A1, 1997-04-10. |
Авторы
Даты
2000-02-20—Публикация
1998-09-15—Подача