Настоящее изобретение относится к устройству с лазером для воспроизведения изображений, в котором посылаемый лазером луч имеет определенную длину когерентности L с заданной длиной волны λ и в котором на пути распространения лазерного луча расположена первая структура, позволяющая производить для отдельных фотонов лазерного луча фазовые сдвиги в соответствии с заданным распределением.
Самыми известными и наиболее распространенными на сегодняшний день устройствами с лазером для воспроизведения изображений являются лазерные принтеры, у которых в соответствии с выводимой на печать информацией с помощью лазерного луча заряжаются участки поверхности фоточувствительного барабана, а затем на барабан в освещенных лазерным лучом местах наносится прилипающее к нему покрытие из тонера, который затем в свою очередь переносится при печатании на бумагу.
В других устройствах, известных, например, из DE 19501525 C1, лазер используется для последовательного освещения точек телевизионного изображения на экране. Из-за инерции зрительного восприятия отдельные точки сливаются, благодаря чему наблюдатель воспринимает визуальную информацию в виде видеоизображения.
В обоих типах устройств лазеры используются в первую очередь для достижения высокого поточечного разрешения, что становится возможным в основном благодаря высокой параллельности лазерных лучей. Еще одним преимуществом лазера по сравнению с другими источниками света являeтся высокая плотность энергии излучения, предпочтительная прежде всего для видеосистем указанного типа, что позволяет с достаточно высокой яркостью воспроизводить изображение также при очень большой площади проекции на экране с диагональю более 1,50 м или даже на киноэкране.
Подобные преимущества лазера основываются на вынужденном, или стимулированном, излучении фотонов, следствием которого, как очевидно, является также высокая когерентность испускаемого лазером луча. Указанное, в иных случаях положительное, свойство когерентности создает помехи при воспроизведении изображения, поскольку может приводить к появлению интерференционных структур, проявляющихся на воспроизводимом изображении в виде блестящих точек. Такие явления интерференции, называемые спеклами, искажают воспроизводимое изображение и не допустимы для оптимального его воспроизведения.
В обзорной статье "Speckle Reduction in Coherent Information Processing" авторов Toshiaki Iwai и Toshimitsu Asakura, Proceedings of the IEEE, т. 84, N 5, май 1996, описаны различные возможности по уменьшению спеклов. При этом особый интерес представляет график, показывающий постоянный рост количества публикаций с 1970 по 1990 г., явно указывая на тот факт, что удовлетворительного решения проблемы уменьшения спеклов до сих пор еще не найдено.
В указанной обзорной статье содержатся теоретические расчеты по уменьшению спеклов. Кроме того, предлагаются различные способы по нарушению пространственной или временной когерентности лазерных лучей. В частности, при этом исходят из того предположения, что спеклы сглаживаются вследствие локальных или пространственных изменений лазерного луча, снижающих контрастность спеклов.
Попытка локального нарушения когерентности была предпринята в уже указанном патенте DE 19501525 C1 при помощи фазовой пластинки. Данная фазовая пластинка, помещаемая на пути распространения лазерного луча, накладывает на различные части светового пучка лазерного луча различные фазы в пределах порядка величин, соизмеримого с длиной волны. В частности, отдельные участки на фазовой пластинке стохастически распределены с целью получения различной разности фаз, вследствие чего можно было бы предположить, что фазы отдельных частей светового пучка распределяются аналогично свету обычных источников света.
Экспериментально было подтверждено, что с помощью подобной фазовой пластинки возможно существенно уменьшить спеклы. Однако было отмечено, что отдельные структуры на фазовой пластинке, обеспечивающие соответствующую величину фазового сдвига для части светового пучка, обусловливают новые проявления дифракции. Поэтому световые пучки с дифракционным максимумом любого порядка приходится коллимировать, пропуская их через линзу, из-за чего, как очевидно, в результате этой дифракции немного ухудшается показатель лазерного светового пучка (показатель, представляющий собой произведение значения среднего отклонения лучей в пучке от средней оси пучка лучей на синус среднего угла расходимости, т. е. среднего значения угла, который лучи в пучке образуют со средней осью пучка лучей (radiation product)). Кроме того, по наблюдениям растр фазовой пластинки был заметен на проецируемом изображении, что, по-видимому, указывает на наличие, несмотря на фазовую пластинку, еще достаточно высокой регистрируемой глазом контрастности спеклов.
Однако недостаток уменьшенного показателя светового пучка можно было бы устранить путем использования вместо отдельной фазовой пластинки экрана с рассеивающими элементами, у которого с помощью статистического рассеивания различный фазовый сдвиг обеспечивается за счет различий в оптической длине пути. Тем не менее опыты показали, что подобные экраны, в которых разница в оптической длине пути для различных фотонов лазерного луча составляет порядка нескольких длин волн, не приводят к требуемому результату устранения спеклов.
Таким образом, можно было бы предположить, что лазерный луч, у которого возникают спеклы, и по другим своим физическим свойствам существенно отличается от лучей других источников света, у которых до сих пор не наблюдалось спеклов. Еще одной физической величиной, характеризующей источник света, является длина когерентности. У обычного видимого излучения значения длины когерентности, как правило, существенно меньше в сравнении с лазерным излучением.
В заявке WO 96/08116 говорится о том, что при использовании импульсного лазера с длительностью импульса в 1 пс, т.е. с длиной когерентности 0,3 мм, наблюдалась существенно меньшая контрастность спеклов, чем при освещении того же экрана гелий-неоновым лазером. Однако априори нельзя понять, связан ли данный наблюдавшийся эффект с меньшей длиной когерентности или со специальной конструкцией лазера. В остальном же, хотя длина когерентности и изменяется пульсацией, в принципе для получения достаточной яркости каждый импульс обладает значительно большей плотностью фотонов, чем при излучении в непрерывном режиме, вследствие чего интерференция за счет большого количества фотонов должна были бы даже усилиться. Единственный эффект, который мог бы уменьшить спеклы, основывается на большей ширине спектра Δλ. Но, как следует из известного уравнения Δλ = λ2/L, где L означает длину когерентности, и с учетом того факта, что ширина интерференционного максимума в основном пропорциональна длине волны λ, данное спектральное уширение не может объяснить наблюдавшееся уменьшение спеклов при пульсации на основе существовавшего до сих пор понимания причин возникновения спеклов.
В частности, данные измерений, приведенные в заявке WO 96/08116, еще показывают наличие небольшой спекл-структуры. Если верна трактовка, согласно которой спекл-структура в основном зависит от выбранной длины когерентности, то тогда и другие источники света, например газоразрядная лампа с аналогичной длиной когерентности (1 пс соответствует L≈0,3 мм) могла бы создавать схожую спекл-структуру. Однако об этом ничего не известно.
Из сказанного выше следует, что в механизме возникновения спеклов понятными являются практически лишь несколько моментов, вследствие чего любой метод уменьшения спеклов в основном базируется лишь на экспериментальных данных.
С технической точки зрения недостаток всего сказанного выше состоит в том, что описанный в литературе метод уменьшения спеклов необязательно может быть применим не только к иным, но и даже к аналогичным устройствам. Из-за отсутствия общей теории возникновения спеклов, на основании которой можно было бы сделать заключение о соответствующих механизмах уменьшения спеклов, может даже иметь место случай, когда метод уменьшения спеклов, случайно оказавшийся эффективным на опытном образце, при серийном производстве натолкнется на непреодолимые трудности. Таким образом, в отношении ни одного из известных способов нельзя с абсолютной уверенностью предположить, что он обеспечит достаточно высокую воспроизводимость результатов.
В основу настоящего изобретения была положена задача усовершенствовать известное из уровня техники устройство таким образом, чтобы обеспечить эффективное, общеприменимое и воспроизводимое уменьшение спеклов.
Указанная задача решается благодаря распределению фазового сдвига лазерного луча, при котором полученное в результате этого распределения среднеквадратическое значение разницы в оптической длине пути при указанном фазовом сдвиге больше длины когерентности L, умноженной на коэффициент 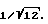
Такое решение является неожиданным. Согласно DE 19501525 C1 можно было бы ожидать, что средний фазовый сдвиг должен был бы быть соизмерим с длиной волны. Сделать заключение о какой-либо связи с длиной когерентности на основании указанной публикации невозможно.
Известные из WO 96/08116 результаты уменьшения спеклов могли бы, как уже говорилось выше, привести к заключению, что причиной уменьшения спеклов является конструкция специального типа лазера. Изложенное выше в этой связи дает повод сомневаться в эффективности такого уменьшения спеклов, поскольку исходя из высокой плотности фотонов и совпадения по фазе собственно следовало бы ожидать, что в один и тот же временной интервал все еще достаточное количество фотонов будeт когерентными.
Изобретение отличается, в частности, тем, что получаемые за счет фазового сдвига различия в длине пути в целом должны составлять не менее 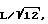 что вообще не является очевидным из технического решения, предложенного в заявке WO 96/08116.
что вообще не является очевидным из технического решения, предложенного в заявке WO 96/08116.
Предлагаемое техническое решение основывается на новых соображениях, необходимых для соответствующей интерпретации результатов собственных экспериментов заявителя. Последние более подробно поясняются ниже при описании примеров выполнения. Прежде всего из данного решения вытекает, что для его осуществления можно отказаться от требуемых согласно DE 19501525 C1 небольших структур, применяемых для изменения фазы частей светового пучка, и поэтому изобретение может использоваться без признанных негативными возникающих из-за небольших структур явлений дифракции, приводящих к ухудшению показателя светового пучка.
Поскольку указанное техническое решение возникло на основе общих теоретических рассуждений относительно возникновения спеклов, которые соответствуют всем проведенным в этой связи экспериментам, нет никакого повода сомневаться в возможности перенесения указанного решения на самые различные устройства, такие как лазерные принтеры, видеоаппаратура или другие устройства для воспроизведения изображений. Поэтому воспроизводимость уменьшения спеклов согласно изобретению обеспечивается с максимально возможной надежностью.
Как упоминалось выше, необходимые согласно изобретению фазовые сдвиги могут не только стохастически распределяться, но и следовать некоторым функциональным закономерностям, что явно отличает данное изобретение прежде всего от встречающихся обычно в литературе методов уменьшения спеклов с помощью стохастического размывания изображения спекл-структур. Фазовые сдвиги могут быть получены, например, и с помощью зеркал, за счет соответствующего расположения которых различные фотоны будут проходить путь различной длины.
Однако устройство можно реализовать также очень простым путем с помощью предпочтительного варианта выполнения, в котором первая структура выполняется из прозрачного материала со стохастически включенными в него частицами, имеющими по сравнению с окружающим их материалом более высокий показатель преломления, причем возникающая в результате этого разница в показателях преломления приводит к фазовым сдвигам.
Таким путем можно, например, получить структуру с небольшими прозрачными частицами, имеющими более высокий показатель преломления и находящимися внутри связывающего эти частицы материала. В частности, для ее изготовления можно использовать имеющиеся в продаже обычные материалы, предусмотрев, например, размещение первой структуры на экране, причем толщина экрана согласно изобретению должна быть подобрана таким образом, чтобы среднеквадратическое значение фазового сдвига позволяло получить оптическую длину пути, большую указанного значения 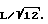
Следовательно, толщину структуры, т.е. тот путь, который лазерный луч проходит в этой структуре, можно соответствующим образом подбирать для всевозможных материалов, реализуя предлагаемое согласно изобретению техническое решение. Однако толщину, например, экрана, в существенной степени определяет выбранный показатель преломления. Для практического использования, в частности для лазерных видеосистем с обычными лазерами, как было установлено, толщина первых структур может быть реализована в разумных пределах, составляющих до нескольких миллиметров, если разница в показателе преломления частиц в соответствии с предпочтительным вариантом выполнения изобретения по сравнению с показателем преломления окружающего их материала превышает 0,1.
Из сказанного выше следует, что частицы, приводящие к стохастическому фазовому сдвигу, также не должны быть слишком большими, чтобы устанавливалась адекватная разность фаз на основании показателя преломления или различий в оптической длине пути. В этом отношении в соответствии с предпочтительным вариантом выполнения изобретения предполагается, что размер частиц в направлении распространения света должен быть меньше 0,5 мм, в частности по крайней мере размер некоторых из частиц должен быть менее 0,1 мм.
Выше уже говорилось о том, что первая структура должна иметь лишь незначительную протяженность в направлении распространения лазерного луча. Для обеспечения этого еще в одном из предпочтительных вариантов предусматривается наличие у первой структуры зеркала для увеличения фазового сдвига за счет увеличения длины волны лазерного луча.
В другом предпочтительном варианте выполнения изобретения для воспроизведения изображения используется экран, причем первая структура, по крайней мере частично, расположена в самом экране или в одном слое экрана.
Благодаря такому варианту при конструировании первой структуры не обязательно сохранять показатель лазерного пучка. Таким образом обеспечивается большая свобода выбора при создании первой структуры. Зона экрана при этом не играет существенной роли, поскольку экран, например видеосистемы, сам должен рассеивать свет, чтобы зрители могли видеть видеоизображение с различных направлений, и от экрана даже требуется уменьшенный показатель пучка.
Можно использовать особо малые первые структуры, если длина когерентности благодаря предлагаемому согласно изобретению решению сама очень мала. Поэтому согласно предпочтительному варианту выполнения предусматривается использовать в качестве лазера импульсный лазер с длительностью импульса менее 10 пс. Длина когерентности вычисляется обычно умножением длительности импульса на скорость света. Это означает, что длина когерентности в подобном лазере составляет 3 мм. Таким образом, при длительности импульса меньше 10 пс первую структуру можно реализовать в целом в пределах нескольких сантиметров и менее.
При столь малых длинах когерентности для ощутимого уменьшения спеклов целесообразно использовать лазеры с шириной полосы усиления более 100 ГГц, прежде всего более 300 ГГц.
В частности, было установлено, что для видеосистем можно добиться существенного улучшения, если в еще большей степени уменьшить ширину импульса, а тем самым и длину когерентности. В соответствии с этим в предпочтительном варианте выполнения изобретения предусматривается использование в устройстве по меньшей мере одного лазера, излучающего в красной, зеленой или синей областях спектра при длительности импульса менее 4 пс и прежде всего менее 2 пс, если этот лазер излучает в красной области спектра, менее 3 пс и прежде всего менее 1,5 пс, если этот лазер излучает в зеленой области спектра, и менее 2 пс и прежде всего менее 1 пс, если этот лазер излучает в синей области спектра.
Этот вариант выполнения позволяет получить длину когерентности порядка до 0,3 мм. При этом также достигается особое преимущество, заключающееся в том, что первую структуру можно выполнить очень малых размеров.
Однако при этом, в частности у видеосистем с размещенными на пути лазерного луча оптическими элементами, неожиданно было выявлено и еще одно преимущество.
От подобных оптических элементов можно ожидать, что они также будут приводить к небольшим разностям фаз фотонов в различных местах, что, таким образом, при соответствующем конструктивном исполнении данных оптических элементов в качестве первой фазосдвигающей структуры позволяет отказаться от применения соответствующих отдельных структурных элементов для получения разности фаз согласно изобретению.
В качестве оптической системы в этом отношении может служить, например, расширяющая оптическая система или линза Френеля, устанавливаемые перед экраном по ходу луча и использовавшиеся первоначально для других целей, например для увеличения угла отклонения развертываемого в соответствии с определенным видеостандартом лазерного луча.
Существенным для осуществления изобретения является выбор соответствующей длины когерентности. Как следует из преобразования Фурье конечного цуга волн длиной L в вакууме, конечная длина волны всегда отражает ширину спектра Δλ, связанную с длиной когерентности L соотношением L = λ2/Δλ. Однако априори необязательно, чтобы каждая ширина спектра Δλ непременно приводила к уменьшению длины когерентности. Как неожиданно было установлено, что, однако, становится понятным с учетом упоминавшейся уже выше и более подробно описываемой ниже модели, ширину спектра Δλ достаточно выбрать соответственно большой, чтобы можно было реализовать согласно изобретению связанную с этой шириной длину когерентности.
С этой целью в устройстве в соответствии с предпочтительным вариантом выполнения изобретения предусмотрена вторая структура, которая имеет являющиеся источниками локальных квантовомеханических возмущений кристаллиты или элементы и которая позволяет за счет таких локальных квантовомеханических возмущений фотонов сократить в лазерном луче, прежде всего путем увеличения ширины спектра Δλ длин волн лазера, длину когерентности. В соответствии с этим получаемая из отношения L = λ2/Δλ длина когерентности уменьшается за счет увеличения ширины спектра Δλ.
Известно, что спектр фотонов может быть расширен за счет отдачи энергии молекулам или атомам при прохождении света через материал. Соответствующие эффекты, например эффект Рамана, обычно незначительны, и поэтому их лишь условно можно использовать для увеличения ширины спектра.
Однако более подробные исследования показывают, что локальные квантовомеханические возмущения можно получить и с помощью специальных соответствующим образом сконструированных структур. Но для понимания возникающих при этом эффектов необходимы более основательные теоретические исследования, подробно рассматриваемые ниже при описании примеров выполнения изобретения.
Используемый основной принцип подобных структур состоит в том, что фотоны в лазерном луче на время локализуются в узком диапазоне, в результате чего на основе соотношения неопределенностей возникает небольшое уширение спектральных линий. При соответственном количестве подобных ожидаемых согласно принципам квантовой механике возмущений возникает соответствующая ширина спектра, с помощью которой за счет уширения спектральных линий можно обеспечить эффективное уменьшение длины когерентности.
Как и в случае с длительностью импульса, в отношении данной ширины спектра Δλ также можно указывать оптимальные значения для определенных устройств. Исходя из выкладок, аналогичных приведенным выше относительно длительности импульса, в соответствии с предпочтительным вариантом выполнения изобретения задаваемая длиной когерентности лазерного луча или ее уменьшением с помощью второй структуры ширина Δλ распределения спектральных линий с длиной волны λ больше 0,5 нм.
Однако в соответствии с данным вариантом выполнения требуемая ширина Δλ распределения спектральных линий достигается не только исключительно за счет второй структуры. Можно также подобрать лазеры с требуемой шириной спектра. В частности, в качестве лазеров с большой шириной Δλ спектральных линий можно использовать волоконные лазеры.
Поскольку на основании различий в показателе преломления можно реализовать как первую, так и вторую структуры, в соответствии еще с одним из предпочтительных вариантов выполнения изобретения первую и вторую структуры можно также объединить в одну общую структуру. Тем самым уменьшающие спеклы структуры можно прежде всего выполнить очень маленькими, что позволит найти для них место, например, даже в лазерном принтере.
В частности, для второй структуры в соответствии с предпочтительным вариантом выполнения изобретения было установлено, что в ней целесообразно предусмотреть множество расположенных на пути распространения луча фазосдвигающих элементов, обладающих малой протяженностью в направлении хода луча, которая не превышает двадцатикратной и прежде всего двукратной длины волны. За счет этого уширение спектральных линий в результате квантовомеханических локальных возмущений становится настолько большим, что для устанавливаемой ширины Δλ требуется лишь небольшое количество подобных элементов.
Вследствие в основном гауссового уширения как результата возмущения в отдельном элементе можно ожидать, что общее уширение при большом количестве таких элементов будет возрастать лишь пропорционально корню из их количества. Однако этого можно избежать. Гораздо более эффективного уширения спектральных линий во второй структуре можно достичь в соответствии с предпочтительным вариантом выполнения за счет упорядоченной формы и равномерного расположения фазосдвигающих элементов на таком расстоянии, при котором локальные квантовомеханические возмущения при формировании матрицы рассеяния, характеризующей возмущения от нескольких элементов, синфазно складываются.
Как более подробно рассмотрено ниже при описании примеров выполнения, ширина спектральных линий, получаемая в этом случае с помощью второй структуры, пропорциональна количеству фазосдвигающих элементов, а не корню из их количества. Таким образом, для установления требуемой ширины необходимо значительно меньше элементов, благодаря чему вторая структура может иметь более простую конструкцию и быть более дешевой в изготовлении.
Как и в случае определения длины когерентности у импульсных лазеров с помощью длительности импульса, для ширины спектральных линий также могут быть указаны оптимальные значения. Соответственно этому, если в предпочтительном варианте изобретения предусмотрен по меньшей мере один лазер, излучающий в красной, зеленой или синей областях спектра, то ширина спектра Δλ для отдельных цветов составляет:
Δλ > 1,3 нм для красной области спектра,
Δλ > 0,9 нм для зеленой области спектра и
Δλ > 0,75 нм для синей области спектра.
Первая структура может изготавливаться также из спеченного гранулята. В частности, для состоящих из частиц структур в соответствии с предпочтительным вариантом выполнения изобретения было установлено, что прежде всего целесообразно использовать зерна с размером менее 0,5 мм, в частности менее 0,1 мм.
Было установлено, что для объединения первой и второй структур в одну особенно предпочтительно использовать частицы, состоящие по крайней мере из двух фаз с различным показателем преломления. Обусловлено это тем, что с помощью этих двух фаз можно реализовать и вторую структуру, в то время как сами зерна будут брать на себя существенную функцию первой структуры. Тем самым можно простым способом получить вышеназванную объединенную структуру для первой и второй структур.
Формирование второй структуры в состоящем из частиц материале экрана, как уже подробно говорилось выше, в соответствии с предпочтительным вариантом выполнения является оптимальным лишь в том случае, когда протяженность по меньшей мере одной зоны между двумя границами фаз в направлении пути распространения лазерного луча составляет менее 20 длин волны и прежде всего менее 2 длин волны.
Для соблюдения указанного требования к объединенной структуре для первой и второй структур в предпочтительном варианте наиболее пригоден политетрафторэтилен (тефлон). Тефлон поставляется, в частности, также в виде гранулята, который может подвергаться спеканию. Стандартным способом можно получать указанную величину зерна, составляющую менее 0,5 мм. Кроме того, зерна содержат так называемые кристаллиты диаметром порядка до 1 мкм, которые в виде включений присутствуют в аморфной фазе. Диаметр порядка ≈ 1 мкм также обеспечивает получение оптимальной второй структуры с требуемым порядком величин, несколько превышающим двукратную длину волны. Тем самым тефлон представляет собой материал, позволяющий оптимально соблюсти предъявляемые к структурам требования.
В отношении свойств тефлона в этой связи особо следует сослаться на следующие публикации: C.J. Speerschneider и C.H. Li "A Correlation of Mechanical Properties and Microstructure of Polytetrafluoroethylene at Various Temperatures", Journal of Applied Physics, т. 34, N 10, октябрь 1963, стр. 3004-3007, и Solomon Fischer и Norman Brown, "Deformation of polytetrafluoroethylene from 78 to 298 K and the effects of environmental grazing", Journal of Applied Physics, т. 44, N 10, октябрь 1973, стр. 4322-4327.
Тефлон является также хорошим объемным рассеивателем, поэтому он наиболее пригоден для использования в качестве материала для изготовления экранов, что в предпочтительном варианте выполнения изобретения, где первой структурой является экран или слой экрана, обеспечивает достижение ряда преимуществ. Одно из преимуществ тефлона состоит в том, что внушавшее опасения ухудшение показателя лазерного пучка вследствие объемного рассеяния тефлона при изготовлении экрана из этого материала не играет никакой роли.
В частности, от экрана требуется определенное распределение углов рассеяния излучения, чтобы зрители могли видеть с различных направлений видеоизображение, воспроизводимое, например, с помощью лазера.
В отношении конструкции экрана следует отметить, что возможны также следующие варианты выполнения, базирующиеся на других соображениях, касающихся, в частности, небольших длин когерентности порядка нескольких миллиметров и меньше.
В одном из таких вариантов предусматривается, что толщина d экрана или его слоя, определяемая в направлении распространения излучаемого лазером для формирования изображения луча, больше критической толщины dkrit, вычисляемой на основании среднего расстояния b между создаваемыми лазерным лучом на поверхности слоя или экрана и известными как спеклы интерференционными максимумами по следующей формуле: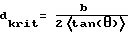
где  означает среднее значение тангенса угла θ рассеяния для распределения углов рассеяния, характеризующего отклонение лазерного луча частицами, соответственно структурами.
означает среднее значение тангенса угла θ рассеяния для распределения углов рассеяния, характеризующего отклонение лазерного луча частицами, соответственно структурами.
Таким образом, по сравнению с уровнем техники указанное решение является неожиданно простым и основано на выборе соответствующей толщины экрана или слоя.
Приведенная формула базируется на представлении о том, что свет возникающих на довольно большой глубине спеклов рассеивается имеющимися в этом месте структурами, и поэтому в интерференционных минимумах на поверхность экрана из его поверхности также выходит свет. Тем самым эффективно снижается контрастность спеклов. Приведенное уравнение для dkrit простым образом вытекает из данного представления, как более подробно описано ниже. При значительно большей толщине экрана или нанесенного на него слоя в отношении dkrit другие слои способствуют снижению контрастности спеклов, которые вследствие этого должны полностью размываться.
Это решение является очень простым и недорогим в реализации, что обеспечивается в первую очередь благодаря следующим вариантам выполнения изобретения.
Размер спекла определяется в основном диаметром луча. Как можно вычислить исходя из простого рассмотрения на основе интерференционной оптики (см. M.I. Yoder, D.G. Youmans: "Laser radar wavelength selection and trade-offs", SPIE, т. 999, Laser Radar III (1988), стр. 72-83) при расстоянии S от лазера до экрана, а также при диаметре D и эффективной длине волны λ в спектре лазерного излучения размер спекла составляет λStanθ/D. Однако поскольку размер спекла не может быть больше диаметра, подобная оценка справедлива только при условии, что D2>λS.
В подобных случаях в соответствии с предпочтительным вариантом выполнения изобретения при расстоянии S от экрана до лазера, а также диаметре D и эффективной длине волны λ исходящего от лазера луча справедлива зависимость D2>λS, а толщина d экрана или слоя больше 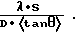
Данная толщина слоя может быть примерно в два раза больше dkrit, благодаря чему ожидается и значительно лучшее размывание спеклов и, следовательно, меньшая их контрастность.
В соответствии с еще одним предпочтительным вариантом выполнения изобретения толщина d имеет величину, при которой функциональная характеристика величины контраста K(d) в зависимости от толщины d принимает значение меньше 0,20, в частности меньше или равное 0,05, причем указанная функциональная характеристика величины контраста измеряется по формуле 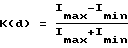 в зависимости от возникающей максимальной интенсивности света Imax и минимальной интенсивности света Imin в равномерно освещаемой лазерным лучом зоне при соответствующей толщине слоя d на поверхности экрана.
в зависимости от возникающей максимальной интенсивности света Imax и минимальной интенсивности света Imin в равномерно освещаемой лазерным лучом зоне при соответствующей толщине слоя d на поверхности экрана.
Эта толщина, как показывает опыт, также существенно превышает dkrit, но ожидается существенно меньшая контрастность спеклов. В дополнение к вышеназванной физической характеристике контрастности спеклов в зависимости от толщины в данном варианте изобретения учитывается и физиология глаза. Обусловлено это тем, что, как было установлено, спеклы ниже границы контраста, которая определена выше через максимальную и минимальную интенсивности света, при значении в 0,2 почти не воспринимаются, а при значении, в частности, 0,05 вообще не воспринимаются глазом. Тем самым толщина слоя в соответствии с данным вариантом выполнения подобрана таким образом, что спеклы эффективно гасятся, поскольку они перестают восприниматься глазом.
Для практической реализации вышеуказанного варианта можно провести измерения функциональной характеристики для оценки различных материалов. Однако для снижения затрат на измерения можно оценить требуемую толщину и в соответствии с другим предпочтительным вариантом выполнения изобретения.
Согласно данному варианту толщина экрана должна составлять 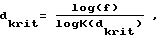 где f означает число меньше 0,20, в частности меньше или равное 0,05, а
где f означает число меньше 0,20, в частности меньше или равное 0,05, а 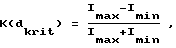 где Imax означает максимальную, а Imin означает минимальную световые интенсивности в пределах равномерно освещаемой лазером области на экране толщиной dkrit.
где Imax означает максимальную, а Imin означает минимальную световые интенсивности в пределах равномерно освещаемой лазером области на экране толщиной dkrit.
Все вышеназванные варианты выполнения изобретения можно реализовать простым образом, если выполнить экран из спеченного политетрафторэтилена (материала Teflon® ).
При этом в соответствии с предпочтительным вариантом выполнения изобретения толщина d должна быть больше 0,1 мм, в частности больше 1 мм и прежде всего больше 3 мм. При подобной толщине у различных лазеров с различной длиной когерентности перестает наблюдаться сколь-нибудь существенная контрастность спеклов. Однако, как неожиданно было установлено, толщина, необходимая для полного исчезновения контрастности спеклов, зависит от длины когерентности. Оптимальная толщина определяется в зависимости от длины когерентности используемого лазерного луча в соответствии с предпочтительным вариантом выполнения изобретения, согласно которому излучение лазера имеет длину когерентности L, а толщина d экрана или слоя составляет d≥(0,04 см·L)1/2±25%. В частности, на экране из материала Teflon®, изготовленном из порошкового исходного материала с размером зерен в пределах от 20 до 800 мкм в виде экрана толщиной 4 мм, при использовании лазерного излучения с длиной когерентности 4 см (согласно данным фирмы-изготовителя лазера) спеклы более не наблюдались.
Ниже изобретение более подробно поясняется на примерах его выполнения со ссылкой на прилагаемые чертежи, на которых показано:
на фиг. 1 - устройство с лазером для воспроизведения изображения, показанное на примере видеосистемы,
на фиг. 2 - принципиальная схема, поясняющая возникновение и устранение спеклов,
на фиг. 3 - вариант выполнения первой структуры правильной формы для уменьшения спеклов, предназначенной для устройства по фиг. 1,
на фиг. 4 - другой вариант выполнения первой структуры правильной формы для уменьшения спеклов, предназначенной для устройства по фиг. 1,
на фиг. 5 - первая структура, которую можно, например, предусмотреть в экране, обеспечивающем воспроизведение стереоизображений,
на фиг. 6 - схематичное изображение структур в изготовленном из материала Teflon® экране для устройства по фиг. 1,
на фиг. 7 - вторая структура регулярной формы для изменения ширины спектра лазерного луча,
на фиг. 8 - технологическая схема изготовления структуры по фиг. 7,
на фиг. 9 - схема, поясняющая контрастность спеклов экрана при заданной толщине слоя d, и
на фиг. 10 - диаграмма контраста как функции отношения интенсивности света в интерференционном максимуме к интенсивности света в интерференционном минимуме.
На фиг. 1 в качестве примера показано устройство с лазером и экраном для показа изображений. В данном примере генерируются цветные видеоизображения, поэтому предусмотрены не один, а три лазера 10, 20, 30, излучающие свет с соответствующей длиной волны основных цветов для формирования точек видеоизображения. Однако исходящие от лазеров 10, 20, 30 лазерные лучи 12, 22, 32 в данном примере еще не модулированы для регулировки яркости и цветокоррекции точек видеоизображения, поскольку в данном случае для некоторых исследований использовались газовые лазеры, управление которыми нельзя осуществлять непосредственно с помощью видеочастоты. При использовании лазерных диодов вместо газовых лазеров 10, 20, 30 интенсивность лазерных лучей 12, 22, 32 изменяется непосредственно за счет модуляции лазеров информацией, предназначенной для воспроизведения точек изображения.
Кроме того, было установлено, что для не связанного с высокими затратами уменьшения спеклов благодаря их большой ширине спектра предпочтительно применять, в частности, волоконные лазеры, как более подробно описано ниже.
Однако для модуляции газовых лазеров 10, 20, 30 на пути распространения лазерных лучей 12, 22, 32 установлены специальные модуляторы 14, 24, 34. Модуляторы изготавливаются из кристаллов DKDP, изменяющих направление поляризации лазерных лучей 12, 22, 32, благодаря чему последние с помощью установленного за ними поляризационного фильтра модулируются по интенсивности в зависимости от управляющего напряжения. Далее лазерные лучи 12, 22, 32 с помощью системы 38 зеркал сводятся в полный световой пучок 40, который в таком виде проходит через последующие элементы системы.
Полный световой пучок 40 с помощью дефлектора, состоящего из зеркального барабана 41 и качающегося зеркала 42, развертывается по строкам и кадрам на экране 43, последовательно освещая на этом экране 43 отдельные точки формируемого видеоизображения. При этом с помощью модуляторов 14, 24, 34 обеспечивается соответствующая яркость и цветность каждой точки изображения.
Используемая в лазерном телевидении технология развертки луча известна из обычного телевидения, где используются кинескопы. Однако применяемая в данном случае технология отличается от обычной тем, что вместо электронного луча используется полный световой пучок 40, а обычное магнитное отклонение луча в кинескопах заменено механической разверткой с помощью зеркального барабана 41 и качающегося зеркала 42.
Однако развертка не ограничивается использованием представленных механических средств. Она может осуществляться, например, и с помощью акустооптики.
Кроме того, на фиг. 1 представлены расширяющая оптическая система 44 и линза Френеля 45, используемые в данном примере для увеличения размера изображения даже несмотря на небольшие углы отклонения луча. Однако данные оптические элементы могут быть сконструированы и таким образом, чтобы создавать с помощью линзы Френеля 45 или линз расширяющей оптической системы 44 различные локальные фазовые сдвиги, согласованные с длиной когерентности лазера, при этом данные элементы выполняют аналогично тому, как это подробнее поясняется ниже со ссылкой на фиг. 3 и 4.
Благодаря когерентности генерируемого лазерами полного светового пучка 40 он наилучшим образом пригоден для создания интерференции. Указанное свойство лазерных лучей, которое в иных случаях может расцениваться как положительное, например в таких областях, как интерференционная оптика или голография, в видеопроекторе согласно фиг. 1 является крайней нежелательным. Обусловлено это тем, что любое небольшое отклонение в траектории светового пучка приводит к появлению интерференции, проявляющейся в виде блестящих точек внутри каждой точки видеоизображения, так называемых спеклов. Спеклы в целом создают помехи для зрителя, и поэтому для получения приемлемого видеоизображения их в любом случае следует устранять или подавлять.
Обычно появление спеклов описывается в литературе как однофотонная интерференция, возникающая, как это принято рассматривать в оптике, вследствие распространения единичной волны в состоянии фотона в результате простого сложения волн. Однако подобное упрощенное представление противоречит следующим экспериментально полученным результатам:
1. на рассеивающем экране спеклы видны, а на гладком отражающем экране не видны;
2. рассеивающий экран со стохастическими фазовыми сдвигами порядка одной или нескольких длин волны в любом случае дает высококонтрастные спеклы;
3. волоконный лазер, вызывающий в обычном режиме появление спеклов на экране и работающий ниже порога мощности вынужденного излучения, воспроизводит изображение без спеклов.
То, что эти наблюдения противоречат простому сложению волн в том виде, в каком оно известно по однофотонной интерференции, подробнее обосновывается ниже. При этом величины, начинающиеся с прописных букв x, y и z, обозначают соответствующие векторы.
К п. 1:
Если исходить из того, что из-за высокой когерентности лазера фотон, выходящий из точки x1 лазера, и фотон, выходящий из точки x2 лазера, излучаются каждый соответственно с волновым числом k = 2π/λ и что эти фотоны имеют постоянное соотношение фаз вследствие стимулированного излучения, то при простой суперпозиции волн локально получился бы следующий интерференционный член:
cos{k|z-x1|-k|z-x2|},
причем независимо от того, отражает ли экран лучи или рассеивает. Такой независимости не наблюдалось. Подобное представление, на основании которого можно было бы сделать заключение о том, что на отражающем экране видны спеклы, противоречило бы и описывающим световое излучение уравнениям Максвелла.
К п. 2:
Как следует из представленного выше интерференционного члена, стохастические разности фаз порядка одной длины волны должны были бы приводить к исчезновению интерференционного члена. Это не соответствует наблюдениям, поскольку с помощью фазовых пластинок не удавалось полностью устранить спеклы.
К п. 3:
Различие между генерацией некогерентного оптического излучения и генерацией когерентного оптического излучения указывает на наличие эффекта оптической плотности. Плотность потока фотонов при генерации когерентного излучения существенно выше.
Вывод, который можно сделать из пункта 3, позволяет предположить существование явлений многофотонной интерференции, которые в литературе, посвященной спеклам, вообще не упоминаются. Это обстоятельство, возможно, привело к тому, что проблема спеклов при воспроизведении изображений до настоящего времени не нашла удовлетворительного решения.
Многофотонная интерференция рассматривается ниже на примере наиболее простой модели интерференции двух фотонов. При этом не учитываются несущественные значения нормирующих коэффициентов, принципиально не влияющие на результат. В последующем рассматривается двухфотонная волновая функция 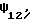 модуль квадрата которой показывает вероятность обнаружения двух фотонов в одной общей точке или в различных отстоящих друг от друга точках. Вероятность, отличающаяся от нуля, является важной предпосылкой к тому, чтобы интерференция двух фотонов вообще могла иметь место.
модуль квадрата которой показывает вероятность обнаружения двух фотонов в одной общей точке или в различных отстоящих друг от друга точках. Вероятность, отличающаяся от нуля, является важной предпосылкой к тому, чтобы интерференция двух фотонов вообще могла иметь место.
В первом случае при интерференции двух фотонов в различных точках x1 и x2, откуда исходят фотоны с волновыми числами k1 и k2, для двухфотонной волновой функции получают следующее выражение: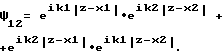
Второй член является результатом симметризирования первого на основе статистики Бозе, которой подчиняются фотоны согласно принципам квантовой механики.
Вероятность присутствия обоих фотонов в точке z вычисляется на основании этого по следующей формуле:
Ψ12Ψ
Если сравнить данное выражение с приведенным выше, основывающемся на нереалистичной интерпретации явления как однофотонной интерференции, представляющей собой сумму волновой функции, то можно видеть, что возможная интерференция зависит от ширины спектра (k1-k2), а не только лишь от самого волнового вектора k. Это означает, что при лазерном излучении высокой когерентности, т.е. при достаточно малом значении (k1-k2), косинус равен 1, и интерференция отсутствует, т. е. отсутствуют спеклы на отражающих поверхностях. И наоборот, при наличии на пути распространения луча рассеивающих структур может возникать интерференция, как это поясняется ниже на примере по фиг. 2.
На фиг. 2 показаны две точки x1 и x2 и две точки y1 и y2, в которых, например в двух точках на экране 43, находятся рассеивающие элементы. Буквой z в этом случае также обозначена точка, в которой должно проверяться, способны ли в принципе два фотона интерферировать. Этой точкой z может быть, например, еще один центр рассеяния на экране 43, или же ею может служить сетчатка глаза наблюдателя.
В принципе для составления двухфотонной волновой функции следовало бы сложить все составляющие, образуемые различными фотонами, выходящими из точек x1, x2 в выходном сечении лазера и проходящими через точки y1 и y2 к точке z. Однако для понимания механизма возникновения спеклов интерес в данном случае представляют только те члены, у которых состояние фотонов на отрезках z-y1 и z-y2 однозначно описывается волновыми числами k1 и k2. Для наглядного представления подобного состояния отдельные отрезки траектории луча на фиг. 2 обозначены соответствующими волновыми числами k1 и k2.
Соответствующий квадрат амплитуды дает следующий интерференционный член двухфотонной волновой функции:
cos{k1|y1-x1|+k2|y2-x2|-k1|y1-x2|-k2|y2-x1|} 1.0
Этот член постоянно равен единице, если x1=x2, т.е. если способные интерферировать в точке z фотоны в основной своей части излучаются из одной и той же точки выходного сечения лазера и из точек, отстоящих друг от друга на расстояния, при которых разность фаз в выражении 1.0 кратна 2π. Таким образом, в случае с двухфотонной интерференцией уже выходное сечение лазера можно рассматривать в качестве структуры, на базе которой может возникать интерференция.
Для дальнейшего рассмотрения следует остановиться на аппроксимации приведенного выше выражения, описывающего функциональное поведение интерференционного члена в отношении точек y1 и y2. При этом принимается, что точки x1 и x2 лежат в одной плоскости, расположенной перпендикулярно плоскости чертежа, а y1 и y2 являются двумя точками, лежащими в плоскости, проходящей параллельно первой и также перпендикулярной плоскости чертежа, причем обе эти плоскости удалены друг от друга на расстояние A. Кроме того, предполагается, что векторы точек x1, y1, x2 и y2 лежат в плоскости чертежа, а величины X1, X2, Y1, Y2 являются соответствующими спроецированными составляющими этих векторов на плоскость, в которой лежат точки x1, y1, x2, y2. При очень большом расстоянии A по отношению к составляющим X1, Y1, X2, Y2 для любой произвольно взятой пары составляющих X и Y в соответствующих плоскостях можно использовать следующую аппроксимацию: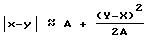
Тогда для аргумента после получения среднего значения по x1 и x2, без учета постоянной фазы, на основании этого усреднения в аргументе косинуса получают выражение вида: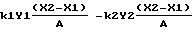
где <X1-X2> в качестве среднего значения для точек x1 и x2 выходного сечения лазера примерно равно диаметру D лазерного луча.
Таким образом, способные интерферировать пары фотонов в основном возникают на таких расстояниях на экране, которые дают в фазе целое кратное 2π, т. е. они в основном удалены друг от друга на расстояние порядка Aλ/<x2-x1>. Тем самым состоящий из пар фотонов свет, идущий от плоскости y, по способности интерферировать можно в целом сравнить с решеткой. Однако данная способность частично подавляется возможным неравномерным рассеянием со стороны рассеивающих элементов, что в таком случае приводит к возникновению спеклов.
В отличие от описанного случая у отражающей поверхности подобные интерференционные максимумы на большом удалении снова сводятся в полный луч, поэтому данный пример объясняет, почему спеклы могут наблюдаться только у рассеивающих поверхностей.
Следует отметить, что в приведенном выражении 1.0 для косинуса разность фаз вообще не сказывается на различиях в длине пути лучей y1-z и y2-z. Отсюда следует, что сдвигами фаз в экране с величинами порядка длины волны до выхода фотонов как фактором, влияющим на данный член, можно пренебречь. Таким образом, возникающие из-за многофотонной интерференции спеклы с помощью сдвига фазы порядка длины волны согласно данному наблюдению полностью устранить нельзя.
Далее, на основании приведенной интерпретации можно заключить, что лазер, работающий вне диапазона стимулированного излучения, не обнаруживает более наличия спеклов: приведенные наблюдения для x1 и x2 в одной плоскости применимы только в отношении лазера, работающего в режиме генерации когерентного оптического излучения, поскольку только в таком случае фазовое состояние в выходном сечении лазера однозначно определено. В отличие от этого в режиме генерации некогерентного оптического излучения у волоконного лазера точки x1 и x2 возникновения фотонов смещены относительно друг друга в направлении стекловолокна, вследствие чего в направлении распространения лазерного луча данные точки x1 и x2 существенно удалены друг от друга, и поэтому при интегрировании по x1 и x2 в результате усреднения выражение с косинусом исчезает.
Эти примеры, рассмотренные на моделях, могут объяснить возникновение спеклов в соответствии с результатами экспериментов, но не приводят еще априори к нахождению решения проблемы спеклов.
Согласно изобретению для устранения спеклов предлагается различными путями обеспечить для фотонов соответствующие сдвиги фаз. Для пояснения следует рассмотреть особо выделенную на фиг. 2 локальную зону 50. Если бы в этом месте вблизи от x1 можно было изменить длину пути фотонов на величину ΔA, чтобы выходящие из x1 фотоны вне зависимости от ситуации с волновыми числами k1 и k2 проходили более длинный путь, то в выражении 1.0 появилась бы следующая дополнительная фаза:
(k1-k2)ΔA
Таким образом, в спектре длин волн при распределении ΔA с определенной шириной > (2π/k1-k2) пропадает интерференционный член 1.0, и спеклы не должны были бы больше появляться.
Это означает, что для эффективного устранения спеклов необходимо соблюдать следующее условие: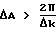 1.1
1.1
Чем больше ΔA, тем эффективнее подавление спеклов. Рекомендуемая нижняя граница, кроме указанного уравнения 1.1, определяется, в частности, неравенством 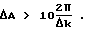
Однако при ближайшем рассмотрении оказывается, что точная нижняя граница эффективного подавления спеклов существенно зависит от распределений, эффективных для изменения длины пути фотонов. Приведенные ниже примеры позволяют пояснить это еще более наглядно.
Подавление спеклов может производиться и в других точках, отличных от точки 50. Так, например, экран, как это описано ниже на примерах, может характеризоваться стохастическим распределением оптической длины пути с гауссовой шириной ΔA. В этом случае статистическое уширение в точках y1 и y2 происходит два раза, т.е., поскольку ширина гауссовых функций складывается в квадрате, из соотношения 1.0 вытекает следующее неравенство: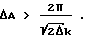
Другое граничное значение для длины когерентности, при котором наступает эффективное уменьшение спеклов, получается далее при равномерном распределении фаз, например, в точке 50. При равномерном распределении среднеквадратическое значение, как известно, равно общей ширине, деленной на 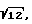 и поэтому для эффективного уменьшения спеклов при всех возможных распределениях в качестве самой нижней границы для заданной ширины Δk лазерного излучения справедливо следующее неравенство:
и поэтому для эффективного уменьшения спеклов при всех возможных распределениях в качестве самой нижней границы для заданной ширины Δk лазерного излучения справедливо следующее неравенство: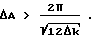
Однако существенным во всех указанных уравнениях является то, что необходимое увеличение длины пути всегда обратно пропорционально Δk. Поэтому ширина спектра лазерного луча должна быть по возможности максимально большой, если эффективное уменьшение спеклов необходимо получить при небольших значениях разности в длине пути ΔA.
С этой целью, например, можно выбрать лазер с очень большой шириной спектра. В частности, волоконные лазеры обладают подобной большой шириной спектра, и поэтому необходимую для уменьшения спеклов разность в длине пути ΔA можно выдержать в разумных границах в миллиметровом диапазоне и ниже.
Кроме того, у импульсного лазера в зависимости от длительности импульса также получается достаточно большая ширина. Соответствующее уширение в результате преобразования Фурье конечного цуга световых волн длиной L определяется по следующей формуле:
Δk = 2π/L 1.2
При этом, однако, необходимо учитывать, что указанную ширину не следует путать с гауссовой шириной. Данная ширина конечного цуга волн получается из нулей трансформанты Фурье.
Гауссову ширину в данном случае нельзя указать в общем виде. Однако следует исходить из того, что лазерный импульс не имеет строго прямоугольной формы, из-за чего полученная с помощью преобразования Фурье ширина не соответствует в точности действительному спектру. Поэтому зависимость согласно уравнению 1.2, тем не менее, соответствует практическим условиям. Однако при общих расчетах длины когерентности по уравнению 1.2 следует проявлять осторожность, поскольку составляющие менее 1/10 максимальной интенсивности, как показано на примере по фиг. 5-7, еще могут использоваться для эффективного уменьшения спеклов.
Поэтому для формулировки условия для оптической длины пути в зависимости от длины когерентности с целью уменьшения спеклов можно принимать только наименьший возможный предел для среднеквадратического ΔA. Это означает, что в целом для 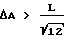 можно ожидать эффективного уменьшения спеклов. Однако в принципе справедливо следующее правило: чем больше выбранное значение ΔA, тем эффективнее подавляются спеклы.
можно ожидать эффективного уменьшения спеклов. Однако в принципе справедливо следующее правило: чем больше выбранное значение ΔA, тем эффективнее подавляются спеклы.
Если предусматриваемая разница в оптической длине пути должна оставаться в пределах нескольких миллиметров, то в соответствии с приведенным выше уравнением при импульсном режиме работы лазера длительность импульса следует выдерживать по возможности менее 10 пс, т.е. 3 мм оптической длины пути за импульс.
В частности, для примера по фиг. 1 в зависимости от цвета излучения лазеров 10, 20, 30 были установлены следующие значения:
- 4 пс и прежде всего менее 2 пс для лазера, излучающего в красной области спектра,
- 3 пс и прежде всего менее 1,5 пс для лазера, излучающего в зеленой области спектра, и
- 2 пс и прежде всего менее 1 пс для лазера, излучающего в синей области спектра.
Поскольку ширина спектра обычно измеряется не в волновых числах, а в зависимости от длины волны, особенно важна также следующая зависимость, вытекающая из уравнения 1.2 и касающаяся известного соотношения волнового числа и длины волны: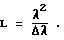
С помощью данного выражения легко определяется и ширина Δλ спектра лазера, при которой при заданной разнице в оптической длине пути ожидается уменьшение спеклов. Лишь при незначительной разнице в оптической длине пути, чтобы можно было, например, использовать тонкий экран 43, оптимальными значениями для примера по фиг. 1 являются Δλ > 1,3 нм для лазера, излучающего в красной области спектра, Δλ > 0,9 нм для лазера, излучающего в зеленой области спектра, и Δλ > 0,75 нм для лазера, излучающего в синей области спектра. Это соответствует длине когерентности примерно в 0,3 мм, вследствие чего можно ожидать, что с помощью данных значений будет обеспечено эффективное уменьшение спеклов уже на обычном "жемчужном" экране для диапроекции.
Подобные параметры ширины линий можно простым путем получить также с помощью волоконных лазеров, благодаря чему последние и являются предпочтительными для применения в примере по фиг. 1.
Однако в будущем планируется также проекция стереоизображений с использованием различной поляризации света. Это может быть достигнуто с помощью специальных очков и раздельного воспроизведения одного изображения для каждого глаза зрителя с использованием света с различной поляризацией. Однако для сохранения состояния поляризации при этом нельзя будет использовать указанные в качестве примера "жемчужные" экраны. Поэтому удлинение пути луча на величину ΔA в данном случае придется реализовывать иным образом.
Как пояснялось выше на примере по фиг. 2, в точке 50 в соответствии с фиг. 2 можно также предусмотреть изменение оптической длины пути для уменьшения спеклов.
Пример выполнения этого варианта схематично показан на фиг. 3. На данном чертеже изображена призма 52, установленная согласно фиг. 1 соответственно между модулятором 14, 24 или 34 и системой 38 сведения лучей. Размещение призмы 52 перед системой 38 сведения наиболее целесообразно, поскольку в этом случае не возникают обусловленные наличием призмы и требующие коррекции хроматические аберрации, которые могли бы возникнуть при ее размещении за системой 38 сведения вследствие различий в отклонении лазерных лучей 12, 22, 23 в полном световом пучке 40.
В зависимости от местоположения x1, соответственно x2 фотона в лазерном луче согласно фиг. 2 в призме наблюдаются различные разности фаз, которые могут взаимоуничтожаться при получении среднего значения в соответствии с уравнением 1.0, если эти различные разности фаз, обусловленные призмой 52, достаточно велики.
В примере по фиг. 3 максимальная разность фаз по диаметру D ≈ <x1-x2> лазерного луча 32 составляет, как показано, 2w(n-1), где n означает показатель преломления материала. При использовании стеклянной призмы с углом 90o и примерном диаметре лазерного луча D = 2 мм можно, таким образом, в результате сдвига фазы за счет показателя преломления от одного фронта импульса лазерного луча 32 к другому получить среднюю эффективную разницу в оптической длине пути порядка 2 мм. При большей длине когерентности лазерного луча появляющиеся спеклы должны в результате приобретать эллиптическую форму, а при существенно меньших значениях в данном случае следует ожидать полос.
То обстоятельство, что спеклы в результате не гасятся полностью, а проявляются лишь в виде полос, связано с тем, что сдвиги фаз при использовании призмы 52 действуют только в одном направлении. Для полного гашения спеклов следовало бы установить на различных направлениях по крайней мере три разные призмы 52.
В отличие от этого в примере по фиг. 4 требуется только один элемент 54. Он выполнен в виде практически вращательно-симметричного купола с наружной поверхностью 56 и полостью 57. Наружная поверхность 56 и внутренняя, находящаяся в полости 57 поверхность 58 имеют такую форму, что преломляющийся в материале элемента 54 луч проходит параллельно экваториальной плоскости 60. Тем самым обеспечивается сохранение лазерным лучом 32 своей формы при его прохождении через данный элемент 54. Однако и в этом случае, как и в примере по фиг. 3, отдельные фотоны в зависимости от их точки входа в оптический элемент 54 проходят путь различной длины, что приводит к эффективным фазовым сдвигам. Согласно оценкам с помощью данного оптического элемента с такими же соотношениями размеров, что и показанные на фиг. 4, и при диаметре луча 2 мм можно получить разницу в оптической длине пути порядка нескольких десятых миллиметра, что является достаточным для эффективного уменьшения спеклов при вышеназванной ширине спектра.
Вместо использованного в примере по фиг. 4 элемента со сложной в изготовлении формой для параллельного прохождения всех световых пучков в полости 52, можно, если допустить некоторое расширение луча, использовать для уменьшения спеклов и простую полусферу из светопреломляющего материала или же скорректировать при необходимости ожидаемое расширение лазерного луча с помощью дополнительной оптической системы.
Примеры по фиг. 3 и 4 показывают, что достигаемой в преломляющих материалах разности фаз достаточно для получения соответствующего изменения оптической длины пути. Подобных изменений фаз можно ожидать и от линзы Френеля 45, от расширяющей оптической системы 44, а при определенных условиях даже и от системы 38 сведения. Указанные изменения вполне могут составлять порядка нескольких десятых миллиметра, что при соответствующим образом подобранной длине когерентности лазера будет достаточным для использования данных систем в качестве первой структуры для уменьшения спеклов.
На фиг. 5 схематично изображен экран 43, который также можно использовать для воспроизведения без спеклов стереоскопических изображений. При этом с целью упростить пояснение принципа уменьшения спеклов не показана рассеивающая структура для расширения телесного угла для различных наблюдателей.
Экран 43 по фиг. 5 состоит в основном из светоделительного, или частично пропускающего, зеркала 62 и еще одного зеркала 64. Между зеркалами 64 и 62 находится светопреломляющий прозрачный материал 66, который, во-первых, придает экрану 43 устойчивость, а, во-вторых, позволяет при заданной длине когерентности сделать зеркало более тонким, поскольку показатель преломления материала 66 увеличивает необходимые изменения фаз.
При попадании полного светового пучка 40 на светоделительное зеркало 62 часть его лучей отражается. Другая часть отражается, попадая на зеркало 64, что тем самым приводит к появлению разницы в оптической длине пути. В частности, происходит также распределение по оптической длине пути, поскольку определенная часть лазерных лучей, как показано на фиг. 5, отражается многократно. Благодаря этому в выходящем потоке световых лучей возникает требуемое различие в оптической длине их пути, позволяющее избежать спеклов.
Экран требуемого типа может быть выполнен, например, из листового стекла с двухсторонней шероховатой поверхностью, на которое напыляются зеркала 62 и 64. Для более тонких и легких экранов 43 может использоваться имеющаяся в продаже майларовая пленка с зеркальным покрытием с одной стороны, на другую сторону которой может быть нанесено покрытие с частичным отражением. Неровность поверхности для рассеяния лучей в различные направления может достигаться при этом путем неоднородной термообработки различных мест майларовой пленки, при которой она коробится на небольших участках.
Несколько вариантов, являющихся альтернативными экрану, показанному на фиг. 5, можно получить, например, снабдив его рассеивающими элементами, которые, однако, могут своим рассеянием изменять поляризацию света и не допускать поэтому возможность показа стереоизображений.
Подобные экраны могут формоваться из спеченного гранулята или же из фазосдвигающих частиц, соответственно изменяющих оптическую длину пути. У зерен с диаметром δ обусловливаемые зерном различия в оптической длине пути составляют примерно от 0 до δ, благодаря чему при разнице в показателе преломления Δn относительно окружающего зерно пространства при прохождении луча через зерно можно ожидать максимальных различий в оптической длине пути (Δn-1)δ, что примерно соответствует среднеквадратическому изменению оптической длины пути при условии равномерного распределения примерно в (Δn-1)δ/121/2. При толщине d экрана лазерный луч проходит в среднем примерно сквозь d/δ зерен. Среднеквадратичные отклонения по длине волны суммируются у нескольких зерен в квадратичной зависимости, вследствие чего в данном случае при толщине d экрана 43 ожидается среднее квадратическое отклонение, примерно составляющее: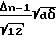
Опыты показали, что наиболее пригодным для гашения спеклов материалом является Teflon®, который спекают из гранулята и из которого формованием изготавливают экраны. Ожидаемый показатель преломления материала Teflon® составляет от 1,2 до 1,4.
В вышеназванных опытах по уменьшению спеклов использовались экраны 34 из материала Teflon® со средним размером зерна δ ≈ 0,4 мм.
Таким образом, в соответствии с приведенным выше уравнением изготовленный из гранулированного материала Teflon® экран с размером зерна δ ≈ 0,4 мм, показателем преломления 1,4 и толщиной 4 мм должен был бы давать различия в оптической длине пути в соответствии со среднеквадратическим значением ΔA ≈ 0,15 мм. Это означает, что исходя из теоретических выкладок, сделанных выше при описании фиг. 2, подобный экран мог бы гасить спеклы лазерного излучения с длиной когерентности 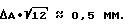
Фактически было установлено, что спеклы на таком экране не воспринимались визуально уже при указываемой фирмой-изготовителем лазера длине когерентности в 4 см. Это противоречит ожидаемому результату. Хотя приведенная выше оценка квадратичной разницы в оптической длине пути является очень грубой, тем не менее более точные расчеты, в которых при рассмотрении учитывались и различия в длинах волн, обусловленные рассеянием лучей зернами, показали, что оцениваемая величина слишком мала, максимум в 2-3 раза. Это означает, что все еще имеется большое несоответствие между теоретически рассчитанной длиной когерентности, при которой возможно наблюдавшееся уменьшение спеклов, и длиной когерентности, указываемой фирмой-изготовителем лазера.
Поэтому можно предположить, что Teflon® обладает дополнительным эффектом, благодаря которому происходит более эффективное гашение спеклов. С целью выяснить это предположение была исследована зависимость от длины когерентности. Для волоконного лазера с длиной волны приблизительно 500 нм, шириной спектра 2 нм, т.е. с длиной когерентности примерно 0,2 мм, было установлено, что спеклы перестают зрительно восприниматься уже при толщине слоя Teflon® в 1 мм. Однако лазер с длиной когерентности 4 см давал при этой толщине явно видимые спеклы. Из этого следует, что надежное гашение спеклов происходит в зависимости от длины когерентности, и поэтому должны быть справедливы подробно описанные выше на примере моделей варианты.
Разрешение этого несоответствия следует искать в самом материале Teflon®. Обусловлено это тем, что Teflon® обладает очень сложной структурой, схематично показанной на фиг. 6.
На фиг. 6 схематично показаны зерна 67 тефлонового экрана, которым должен соответствовать вышеназванный показатель преломления 1,2-1,4. Однако, как уже известно из указанной в начале описания литературы, сами зерна 67 также обладают некоторой структурой. Иными словами, в них заключены так называемые кристаллиты 68, присутствующие в виде включений в аморфной фазе 69. В использованном материале Teflon® кристаллиты 68, согласно наблюдениям, имели длину порядка 100 мкм при очень малой толщине от нескольких мкм и менее до 1 мкм. Между кристаллитами 68 имеются включения воздуха (n = 1).
В промежутках между кристаллитами 68 находится аморфный материал 69, разница в показателе преломления которого по сравнению с кристаллитами 68 должна составлять по собственным измерениям заявителя порядка 0,1. Однако из-за небольшого показателя преломления от этой состоящей из кристаллитов 68 и аморфного материала 69 второй структуры не следует ожидать изменения оптической длины пути.
Тем не менее данная вторая структура, образованная кристаллитами и аморфным материалом, может влиять на длину когерентности исходя из следующих соображений.
О волне, имеющей определенную длину, можно, о чем наглядно свидетельствует преобразование Фурье, говорить лишь в том случае, если эта волна распространяется от отрицательной области бесконечности к положительной. При наличии какой-либо помехи, например, когда цуг волн ограничен импульсным излучением или когда направляемый волной квант в локально ограниченной области пространства переходит в другое состояние, следует, напротив, ожидать спектрального уширения.
Данное свойство нашло свое отражение во всеобщем принципе неопределенности, согласно которому длина волны де Бройля связана с ее импульсом.
Так, например, волна, распространяющаяся только по ограниченной области пространства, т. е. по длине когерентности, всегда спектрально уширена, как это видно из следующих расчетов.
Для единичного фотона с цугом волн, имеющим длину когерентности L, и с волновым вектором k0, волна которого по длине L нормирована на число фотонов, равное 1, получают следующую зависимость: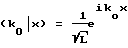 для -L/2≅x≅L/2, в остальных случаях нуль.
для -L/2≅x≅L/2, в остальных случаях нуль.
Известным образом путем преобразования Фурье с использованием оператора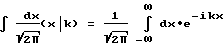
в k-пространстве получают следующее выражение: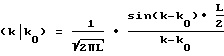
Таким образом получают спектр, ширина которого определяется длиной когерентности L. Данный эффект спектрального уширения, как уже было описано выше, может быть использован с помощью импульсных лазеров.
Для дальнейшего рассмотрения следует ввести распределение P:
P(k,k0) = |(k|k0)2|2,
которое обычно описывает вероятность детектирования возникшего с волновым вектором k0 фотона с волновым вектором k.
Далее для лучшего понимания длины когерентности следует предварительно остановиться на следующих моментах.
В локальном пространстве длина когерентности показывает, на каком расстоянии два фотона при постоянном соотношении фаз еще могут интерферировать друг с другом, поскольку интерференция предполагает наложение амплитуд обоих фотонов в одном месте и в одно и то же время. Аналогичное объяснение следует и для k-пространства: постоянное соотношение фаз может сохраняться только в случае, когда два цуга волн имеют приблизительно одинаковое волновое число. При слишком большом уширении спектра из-за слишком быстро изменяющегося во времени соотношения фаз любая зависящая от фазы суперпозиция пропадает.
Данное пояснение ясно показывает, что для нарушения когерентности вовсе необязательно получить очень короткий цуг волн, а важно лишь то, насколько расширен спектр. В случае двух волн бесконечной длины с различным волновым числом относительные фазы при различиях в оптической длине пути пропадают при разности фаз 2 π или кратной ей, и поэтому для любой ширины спектра можно также получить величину, эквивалентную понятию длины когерентности и называемую ниже эффективной длиной когерентности.
В соответствии с данным подходом эффективная длина когерентности L' для любого распределения вычисляется по следующей формуле:
(k-k0)когерентность·L′= 2π.
Существенной величиной является при этом среднее значение разности волновых векторов. Однако это среднее значение нужно еще соответствующим образом определить.
При каждом достаточно быстро уменьшающемся в направлении бесконечности распределении гауссову ширину можно определить по следующей формуле: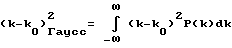
где k0 означает среднее значение распределения k. Очевидно, что указанная гауссова ширина не может быть задана в рассчитанном выше распределении, поскольку подынтегральная функция из-за члена sin2(k-k0)L/2 при больших волновых числах k все еще дает большие составляющие.
Причиной возникновения высоких волновых чисел являются крутые фронты при ±L/2 в локальном пространстве. Однако такое принятое для расчета крутое нарастание с физической точки зрения нереально. Поэтому целесообразно проводить интегрирование, беря интеграл для расчета гауссовой ширины лишь до ограниченного количества колебаний. Возникающая из-за этого неопределенность относительно пути интегрирования может быть устранена следующим образом.
Как уже отмечалось выше, значение гауссова интеграла в существенной степени зависит от крутизны нарастания, соответственно спада фронтов, что может быть учтено за счет ограниченной длины интегрирования. Однако следует также ожидать, что учитываемая для длины когерентности ширина будет изменяться в зависимости от формы.
Поэтому следует ввести коэффициент формы, или формфактор, F для учета различных граничных параметров на высоких частотах: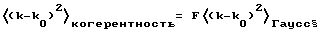
Из этого с помощью приведенного выше уравнения для распределения вероятностей P получают следующее отношение: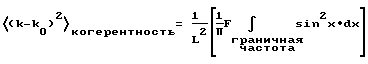
Выражение в квадратных скобках не содержит более никаких физических величин и может поэтому рассматриваться только как зависимая от граничной частоты постоянная, по крайней мере для бесконечно больших областей интегрирования.
Для вычисления значения в квадратных скобках в данном случае не хватает лишь одной величины для формфактора F. Однако ее легко получить, сделав логичное предположение о том, что эффективная длина когерентности L' при принятом выше цуге волн равна фактической длине когерентности L. Тем самым приходят к следующему результату: при указанных функциональных взаимосвязях значение выражения в квадратных скобках следует принять за равное (2π)2, чтобы L' = L.
Описанный выше подход позволяет устранить расходящиеся в иных случаях интегралы, встречающиеся в последующих вычислениях, и получить конечные, рациональные с точки зрения физики результаты.
Как следует из приведенных выше расчетов, у конечного цуга волн и/или при конечной ширине спектра получается эффективная длина когерентности, т.е. длина, сверх которой при различии двух произвольных путей фотона интерференции более наступить не может.
С точки зрения квантовой механики это понятно, исходя из принципа неопределенности. Уширение спектрального распределения означает уширение импульса, влияющее на ограниченную локальную неопределенность при обнаружении фотона.
С другой стороны, принцип неопределенности обусловлен тем, что при пространственном ограничении процесса измерения следует ожидать уширения импульса за счет его поглощения измерительным прибором. Поскольку для принципиальной достоверности принципа неопределенности тип измерительного процесса не имеет значения, сущность физического процесса обусловлена не самим измерительным прибором, а помехами, создаваемыми им по отношению к измеряемой частице. Аналогично процессу измерения от любой помехи в таком случае следует ожидать подобного уширения импульса.
Приводимые ниже расчеты можно полностью произвести и без введения квантовомеханического импульса. Вместо этого в рассматриваемом случае везде используется волновой вектор k. Несмотря на это данные расчеты совпадают с квантовомеханической интерпретацией, поскольку k согласно формуле Планка пропорционален импульсу волны.
Частица с волновым вектором k0 с амплитудой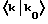
обнаруживается в виде частицы с волновым вектором k. Это вычисляется при помощи преобразования из локального пространства в виде: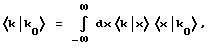
причем локальная помеха вводится с помощью матрицы рассеяния S в виде: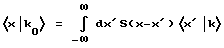
Из данного уравнения следует, что в том случае, если матрица рассеяния S дает составляющую, которая лишь в узкой области пространства отличается от нуля, то амплитуда 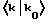 содержит интегралы, аналогичные тем, которые появлялись у спектра для конечной длины когерентности. Поэтому и математически ожидается изменение эффективной длины когерентности при локальных помехах. Уширения спектра в результате локальных помех, таких как поглощение и излучение фотона молекулами или атомами, наблюдались экспериментально, например при комбинационном рассеянии света (эффект Рамана), и ниже более подробно рассматриваться не будут.
содержит интегралы, аналогичные тем, которые появлялись у спектра для конечной длины когерентности. Поэтому и математически ожидается изменение эффективной длины когерентности при локальных помехах. Уширения спектра в результате локальных помех, таких как поглощение и излучение фотона молекулами или атомами, наблюдались экспериментально, например при комбинационном рассеянии света (эффект Рамана), и ниже более подробно рассматриваться не будут.
Однако из данных уравнений можно заключить, что уширения спектра с небольшой эффективной длиной когерентности следует ожидать и тогда, когда фотон локально находится в состоянии, отличном от состояния излучения, но может в этом случае наблюдаться в исходном состоянии. Например, в таком случае можно было бы ожидать также уширения спектра при прохождении фотона через локально ограниченный элемент, в котором фотон будет иметь несколько отличающийся волновой вектор из-за отличного от 1 показателя преломления.
На основании данных выкладок можно рассчитать эффективную длину для тонкого отдельного элемента, а именно, для случая с фотоном с амплитудой A, длиной когерентности L и волновым вектором k0, который в находящемся в точке x = b элементе толщиной а и показателем преломления n имеет волновой вектор nk0. Состояние для подобного цуга волн в локальном пространстве в данном случае можно представить в следующем виде: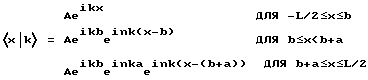
В данном уравнении фазы записаны в виде множителей таким образом, чтобы сразу сделать очевидным, что абсолютная величина и фаза на каждой граничной поверхности принимают требуемые значения, обеспечивая непрерывность волны. Если обобщить показатели, то получается следующая картина, существенно упрощающая дальнейшие расчеты: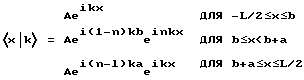
Для амплитуды 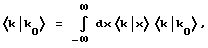 за исключением тривиальных множителей, таких как A·A, получается следующее выражение при Δk = k0-k:
за исключением тривиальных множителей, таких как A·A, получается следующее выражение при Δk = k0-k: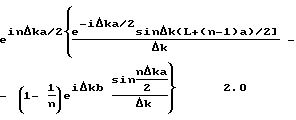 2.0
2.0
С помощью приведенных выше уравнений для эффективной длины когерентности L' в приближении a << L, исходя из вышеназванного выражения для определения эффективной длины когерентности, получают простую зависимость следующего вида: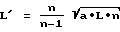
Таким образом, эффективная длина когерентности из-за помех значительно короче собственно длины когерентности. Однако при очень больших длинах когерентности данный эффект очень незначителен. Пространственная помеха от элемента толщиной a должна действовать в пределах значительно меньше 1 мкм, чтобы получить измеримый эффект.
Другая оценка вытекает из рассмотрения действия нескольких элементов. Если через 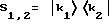 обозначить квантовомеханическую матрицу рассеяния для отдельного элемента, с помощью которой квантовомеханическое состояние с волновым вектором k2 переводится в состояние с волновым вектором k1, то для m элементов общая матрица имеет следующий вид:
обозначить квантовомеханическую матрицу рассеяния для отдельного элемента, с помощью которой квантовомеханическое состояние с волновым вектором k2 переводится в состояние с волновым вектором k1, то для m элементов общая матрица имеет следующий вид: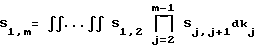
Данный интеграл просто вычислить при следующих условиях. Длина L в этом случае снова принимается за очень большую по сравнению с толщиной элемента a, благодаря чему член sinΔkL в выражении 1.0 можно будет аппроксимировать с помощью функции δ. Кроме того, во всех S-матрицах опускаются постоянные фазы, поскольку в данных расчетах интерес представляют только абсолютные значения квадратов матриц. Кроме того, у различных элементов, расположенных соответственно на расстоянии bj от нулевой точки, амплитуда 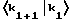 в соответствии с выражением 2.0 может быть взята с корректным для проведения интегрирования нормированием в следующем виде:
в соответствии с выражением 2.0 может быть взята с корректным для проведения интегрирования нормированием в следующем виде: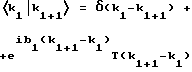
При этом δ-функция Дирака соответствует содержащему sin(kL) первому слагаемому, а функция T соответствует слагаемому с членом sin(ka) в уравнении 2.0.
В этом случае после интегрирования для амплитуды получают следующее выражение: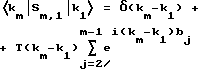
Интегрирование упрощается в основном за счет преобладающего вклада, вносимого δ-функциями. Таким образом, суммирование по различным элементам заключается лишь в сложении фаз на основании различного местоположения bj элементов толщиной a.
Для расчета ширины спектра по волновым векторам необходимо снова рассчитать следующее выражение: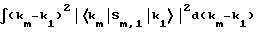
Составляющие δ-функций при этом не вносят никакого вклада, а участвуют только квадраты сумм фаз. При определении численного значения интеграла интегрирование по суммам фаз дает m элементов при условии статистического распределения местонахождения b отдельных элементов. С другой стороны, для особого случая получают значение m2, когда разности пути bj, умноженные на волновой вектор, отличаются у отдельных элементов на целое кратное 2π.
Таким образом, для длины когерентности получают следующее общее уравнение для m элементов: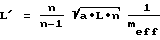
где meff означает эффективное количество элементов, которое в стохастическом случае равно корню из количества элементов, но в случае выбора расстояния между элементами в соответствии с указанной величиной фазового угла, равной целому кратному от 2π, может увеличиться вплоть до значения m.
Тем самым становится более понятным поведение света в тефлоне, поскольку действующая в нем эффективная длина когерентности в соответствии с рассмотренными закономерностями должна под влиянием кристаллитов 68 уменьшиться.
Рассмотренное выше касалось элемента с показателем преломления n в вакууме. В данном случае, однако, важно лишь отличие показателя преломления кристаллитов 68 от аморфного материала. При измеренном значении разности показателей преломления, равном 0,1, выражение n/(n-1) должно в таком случае быть примерно равным 10. Значение для a в подкоренном выражении должно усредняться исходя из различного расположения кристаллитов 68 относительно траектории светового пучка и толщины. Исходя из S-матричной зависимости 1/a среднее значение при этом следует находить через 1/a, т.е. меньшие толщины дают при усреднении наибольшую составляющую. Соответствующая оценка для схематично показанной на фиг. 6 структуры тефлона приводит к получению значения, составляющего 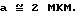
Очевидно, что при длине кристаллитов 68 в среднем 100 мкм на пути распространения лазерного луча располагаются лишь приблизительно шестьдесят кристаллитов 68, вследствие чего следует исходить из meff, приблизительно равного 8. С этими значениями для длины когерентности в 4 см падающего на экран 43 лазерного луча 40 эффективная длина когерентности приблизительно равна 0,4 мм в тефлоне, что оптимально согласуется с приведенной выше оценкой средней длины пути, равной примерно 0,5 мм, для экспериментально найденной толщины в 4 мм для гашения спеклов.
Из приведенных уравнений следует еще один вывод. В материалах с аналогичной второй структурой средняя разность фаз зависит от корня из значения толщины. С другой стороны, изменение длины когерентности в зависимости от meff зависит от обратной величины корня из толщины, и поэтому из условия L<ΔA для эффективного уменьшения спеклов при данной длине когерентности L вытекает критическая толщина dkrit: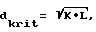
выше которой возможно эффективное уменьшение спеклов.
При этом в общем случае к означает постоянную материала размером одной длины, причем в эту постоянную входят зависимость от показателя преломления, разности показателей преломления, размеры зерна и т.д. Вместо проведения сложных расчетов по названным параметрам данная формула для материалов, имеющих как первую структуру для получения траектории определенной длины, так и вторую структуру для уменьшения длины когерентности, позволяет измерять постоянную материала при одной длине когерентности и оценивать соответствующие толщины для других длин когерентности.
Если бы в экране 43 не было второй структуры, то для среднего квадратического отклонения была бы справедлива степенная зависимость с дробным показателем, благодаря чему можно было бы принять dkrit ~ L2.
Для указанного материала тефлон с размером зерна 0,4 мм была определена постоянная материала к = 0,4 мм ± 25%. Указываемая большая погрешность связана прежде всего с тем, что толщина, при которой более не наблюдались спеклы, определялась субъективно.
Как следует из представленных выше расчетов, длину когерентности можно в дальнейшем уменьшать гораздо эффективнее, если использовать регулярные вторые структуры, расстояние между отдельными элементами у которых в основном выдерживается таким образом, что оно составляет целое кратное разности фаз 2π.
Подобная вторая структура 70, которую в видеопроекторе по фиг. 1 предпочтительно располагать между модуляторами 14, 24, 34 и блоком 38 сведения, чтобы не нужно было учитывать хроматическую аберрацию, показана на фиг. 7. Процесс ее изготовления более подробно поясняется ниже на примере фиг. 8.
Структура состоит из кремниевой подложки 72, на которой травлением получено несколько элементов 74. Затем кремнию давали окислиться, благодаря чему полученные элементы 74 состояли из прозрачного оксида кремния. Время окисления было выбрано с таким расчетом, чтобы на подложке также образовался кремнийдиоксидный слой 76 с толщиной, при которой он действует как диэлектрическое зеркало для падающего лазерного луча 32.
Над структурой 70 расположено еще одно зеркало 78, которое в сочетании с диэлектрическим зеркалом 76 многократно отражает лазерный луч 32 от одной поверхности к другой. В зеркале 78 предусмотрены два отверстия 80 и 82, через которые входит и выходит лазерный луч 32.
Кроме того, на фиг. 7 показаны отрезки a и b, относящиеся к приведенным выше математическим расчетам.
Следует отметить, что показанные на фиг. 7 размеры воспроизведены без соблюдения масштаба. В то время как лазерный луч 32 может иметь диаметр в несколько миллиметров, толщина элементов 74 должна по возможности выдерживаться в пределах от 2 до 20 длин волны, чтобы длина когерентности в соответствии с изложенным выше была по возможности минимальной. Кроме того, высота элементов 76 должна быть по возможности максимальной, чтобы лазерный луч 32 как можно равномернее проходил через вторую структуру, образованную элементами 74.
В журнале "Physikalische Blatter" 52, 1966, N 7 и 8, стр. 661-664, в статье "Photonische Bandstruktur in makro-porosem Silizium" описан метод, позволяющий изготавливать указанные выше элементы толщиной в 2,3 мкм и высотой почти до 0,1 мм. Этот метод поясняется на примере фиг. 8.
Сначала поверхность высоколегированной донорной примесью кремниевой пластинки 86 структурируется, например литографским методом. В настоящем примере для образования второй структуры, изменяющей длину когерентности, необходимо получение полоскового рисунка поверхности в отличие от указанной выше статьи, где описывается получение микропор.
Затем элементы 74 вытравливают электрохимическим методом в растворе 90 плавиковой кислоты. Большая высота элементов 74 при их небольшой ширине достигается за счет того, что травление осуществляют только в местах с высокой концентрацией электронов в кремнии. Для получения свободных электронов подложку облучают сзади ультрафиолетовым излучением 92'. Наибольшая концентрация электронов достигается в тех местах, где вначале, например литографским способом, было выполнено углубление. Чем больше углубление, тем выше эффект локально-избирательного вытравливания при изготовлении элементов 74.
Во избежание электрополировки кремниевой пластинки 86 следует использовать малые токи с напряжением от 1 до 2 В, которые регулируются с помощью стабилизатора 94 напряжения и контролируются с помощью измерительного прибора 96. Характеристика требуемых параметров тока и напряжения приводится в указанной выше статье.
Приведенные ниже выкладки предоставляют также следующие возможности по конструктивному оформлению экрана.
Из интерференционной оптики известно, что размер спекла в основном зависит от размера интерферирующих структур. При этом размеры наименьшей структуры в интерференционной картине в основном определяются наибольшей способствующей появлению интерференции площадью. В условиях проекции изображения в примере по фиг. 1 эта площадь задается диаметром D лазерного луча. Согласно оценке на основе приведенной литературы размер спекла должен был бы в соответствии с этим равняться λS/D, где λ означает длину волны, S означает расстояние от лазеров 10, 20, 30 до экрана 43, а D означает диаметр попадающего на экран лазерного луча. На фиг. 9 появление спекла 92 обозначено на схеме в каждом случае тремя стрелками, отходящими от различных точек называемого спеклом 92 явления интерференции.
Поскольку рассеивающие элементы 67 распределены в материале экрана 43 равномерно, можно исходить из того, что в сечении, перпендикулярном нормали к поверхности экрана 43, из каждого слоя будут появляться аналогичные картины спеклов. Такая ситуация отражена на фиг. 9 в виде расположенных на большей глубине спеклов 92. Диаметр этих спеклов практически не будет отличаться от находящихся на поверхности, поскольку S при обычной толщине d экрана порядка нескольких миллиметров и расстоянии до экрана порядка нескольких метров, исходя из приведенной выше формулы, изменится лишь незначительно. Однако положение спеклов на рассматриваемой различной глубине может быть различным. На фиг. 9 показан самый неблагоприятный случай, при котором расположенные на глубине и лежащие на поверхности экрана спеклы 92, если смотреть со стороны экрана, накладываются друг на друга.
Таким образом, для уменьшения спеклов глубина d должна быть достаточно большой, а именно такой, чтобы возникающий более глубоко в экране 43 свет от спеклов 92 попадал и в места интерференционных минимумов на поверхности, размывая контраст. Это означает, что свет от спеклов, возникающих в экране 43 на большей глубине, должен отражаться примерно до половины среднего расстояния d между спеклами.
Распределение отражаемого с большей глубины d до поверхности экрана 43 света с полной интенсивностью I можно для любого угла рассеяния θ нормированного на 1 распределения углов рассеяния f(θ) определить для каждого рассеивающего элемента 67 по следующей формуле: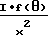
где x означает длину пути светового луча от рассеивающего элемента 67 к поверхности. При угле θ и очень малой толщине d, при которой другими видами рассеяния отражаемого к поверхности света можно пренебречь, x можно представить как d/cosθ.
Эффективное уменьшение спеклов за счет попадания дополнительного света в интерференционные минимумы при b/2 между поверхностными спеклами 92 достигается в том случае, если согласно фиг. 9 распределение углов рассеяния в среднем происходит в соответствии с 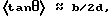 т.е. если в приближении можно принять, что:
т.е. если в приближении можно принять, что: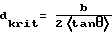
причем среднее значение для tanθ вычисляется из следующего отношения: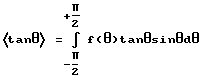
а интегрирование 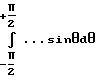 дает интеграл телесного угла полусферы для рассеяния в направлении поверхности.
дает интеграл телесного угла полусферы для рассеяния в направлении поверхности.
Таким образом определяется толщина экрана dkrit, начиная с которой можно ожидать уменьшения спеклов. При большей толщине экрана спеклы уменьшаются в еще большей степени, поскольку в этом случае идущая от более глубоких слоев часть света, которой также нельзя пренебрегать, обеспечивает еще большее уменьшение контраста между интерференционными максимумами и интерференционными минимумами.
В случае, когда D2>λS, спеклы, возникающие вследствие конечного диаметра D лазерного луча, меньше самого диаметра D луча. Следовательно, следует ожидать, что диаметр D луча существенным образом определяет размер спекла, поэтому для величины b можно произвести оценку, исходя из того, что b примерно равно двойному диаметру спекла. Обусловлено это тем, что у отдельных структур интерференция является очень неопределенной, вследствие чего характеристика функции может быть аппроксимирована с помощью простых функций синуса, соответственно косинуса. В таком случае расстояние между двумя максимумами примерно равно двойной ширине максимума. Из этого следует, что для эффективного подавления спеклов следует выбирать: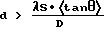
Выше уже неоднократно упоминалось понятие контраста. Контраст K спекла при толщине d ниже определяется по следующей формуле: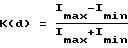
где Imax означает интенсивность света в одном спекле, а Imin означает интенсивность света в интерференционном минимуме. Эта величина показана на фиг. 10 в зависимости от отношения Imin/Imax. На графике видно, что при увеличении Imin, т. е. при большей толщине d, интерференционные явления благодаря этой толщине еще больше "смазываются" светом, идущим с большей глубины, и контраст резко снижается.
Было установлено, что при значениях K(d) функции контраста ниже 0,2, в частности ниже 0,05, контраст спеклов физиологически перестает восприниматься.
Таким образом, если требуется не только уменьшить спеклы, но и полностью устранить их с физиологической точки зрения, то в этом случае можно измерять величину контраста K(d) в зависимости от толщины, а затем подбирать толщину d экрана 43 таким образом, чтобы K(d) было меньше 0,2, в частности меньше 0,05.
В менее трудоемком, поясняемом ниже способе приблизительного определения оптимальной толщины слоя используется контраст при критической толщине dkrit. Для определения контраста K(dkrit) он либо математически оценивается исходя из вышеприведенных выкладок при критической толщине слоя dkrit с дополнительным учетом не рассматривавшегося до сих пор отражения и многократного рассеяния исходящего от рассеивающих элементов светового пучка 50, либо просто измеряется контраст K(dkrit) при критической толщине dkrit.
Поскольку величины K контраста в приближенном методе перемножаются, общий контраст составляет: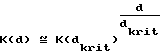
Таким путем легко оценить толщину, при которой контрасты физиологически больше не воспринимаются, а именно: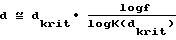
При этом число f описывает, в какой степени необходимо подавлять контрастность спеклов на экране 43. В соответствии с рассмотренным выше f, таким образом, означает число меньше 0,2, в частности меньше или равное 0,05, если контрастность спеклов должна быть ниже границы восприятия.
Из вышеприведенных примеров следует, что согласно изобретению имеется множество возможностей для уменьшения спеклов. При этом важно, чтобы оптическая длина пути отдельных фотонов согласовывалась с длиной когерентности. Для получения длины когерентности с величиной, наиболее пригодной для практических условий, ее можно рассчитать в соответствии с требуемыми условиями путем подбора лазеров 10, 20, 30 или продолжительностей импульса, а также с помощью второй структуры.
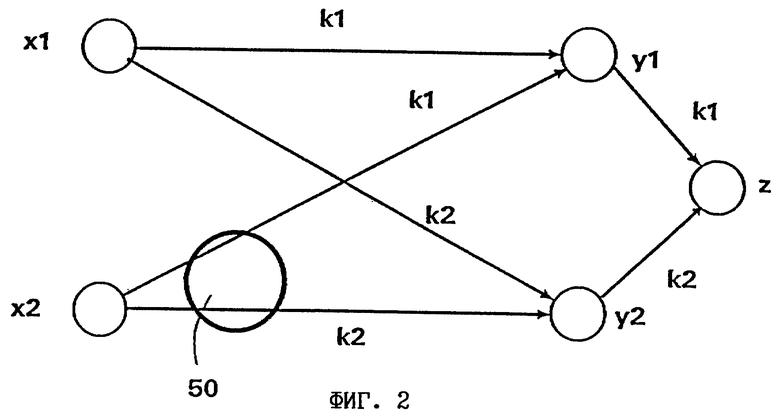
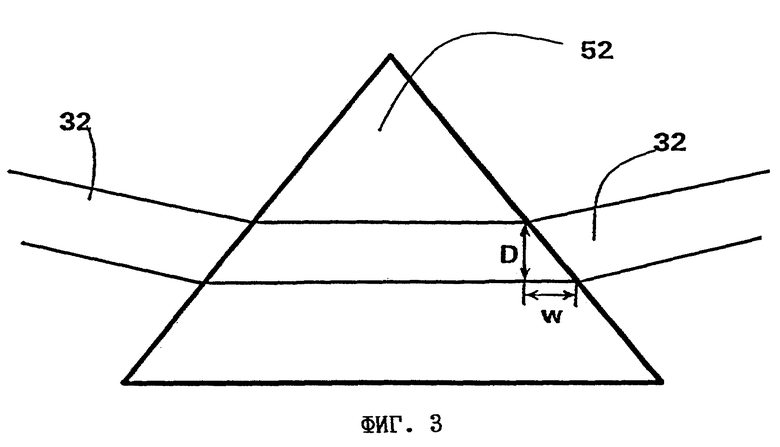
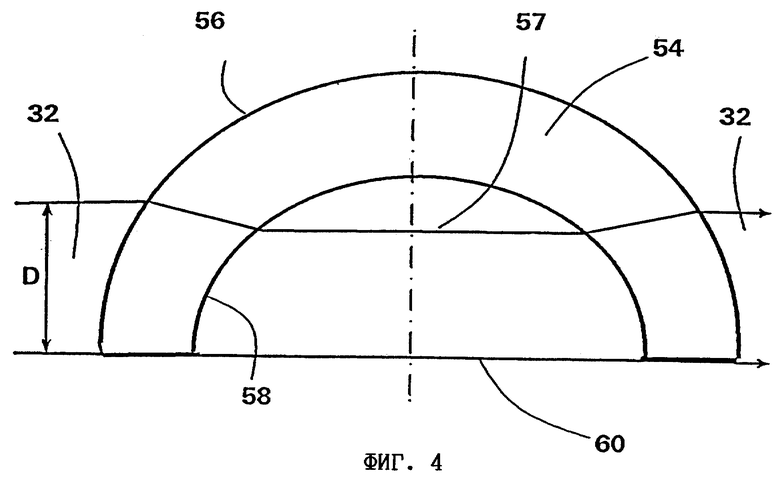
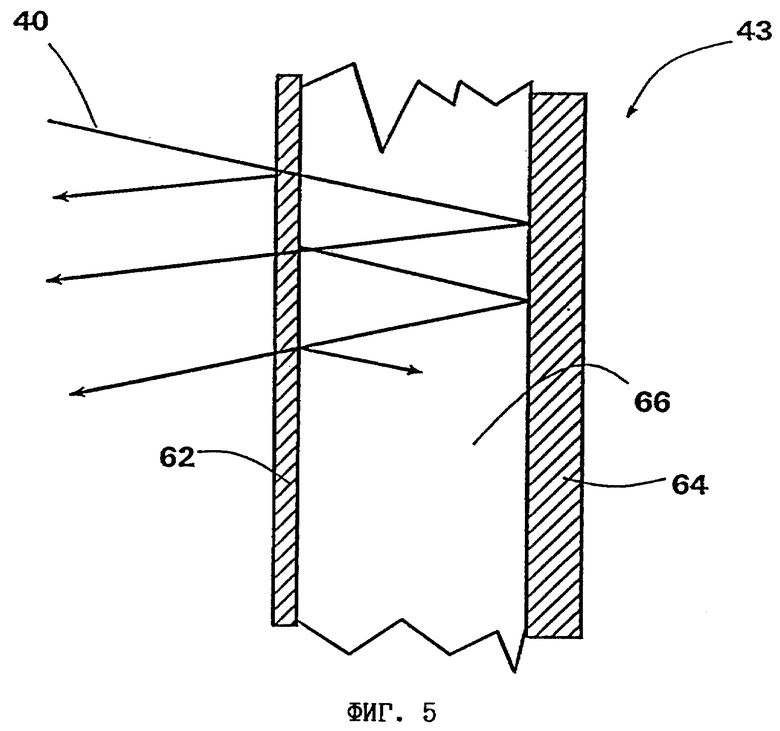
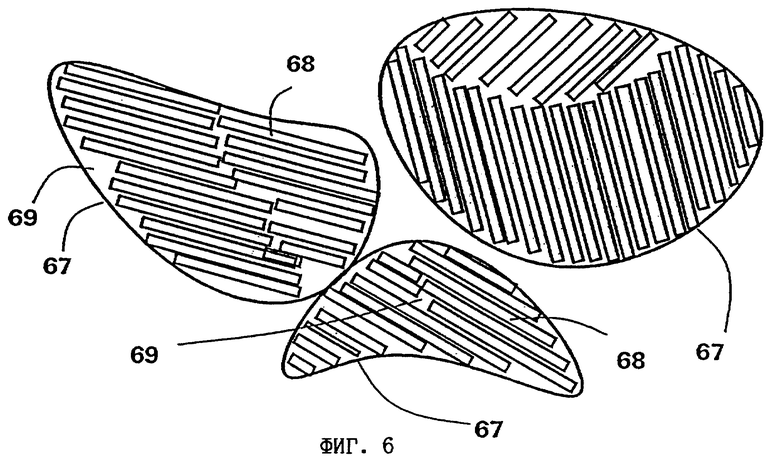
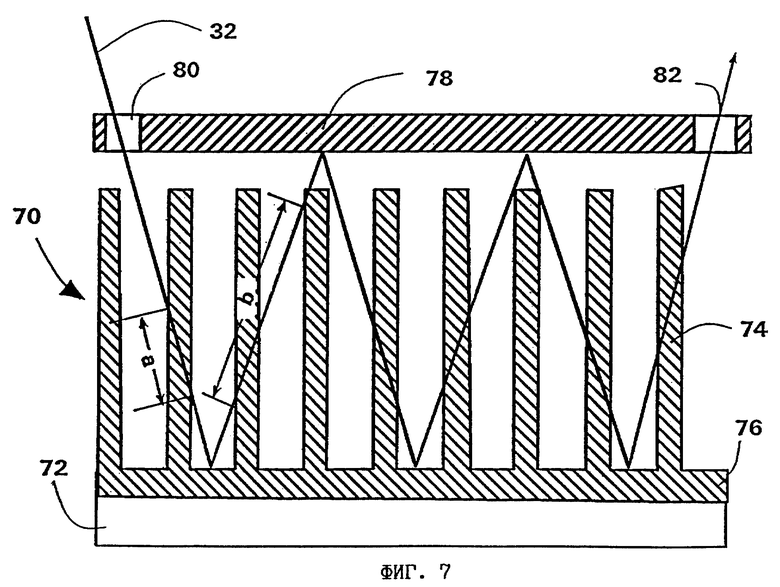
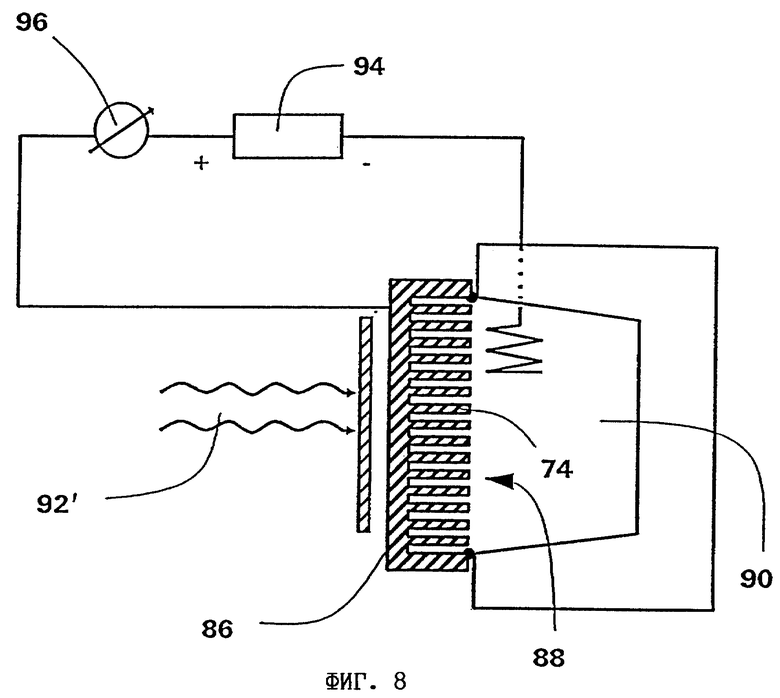
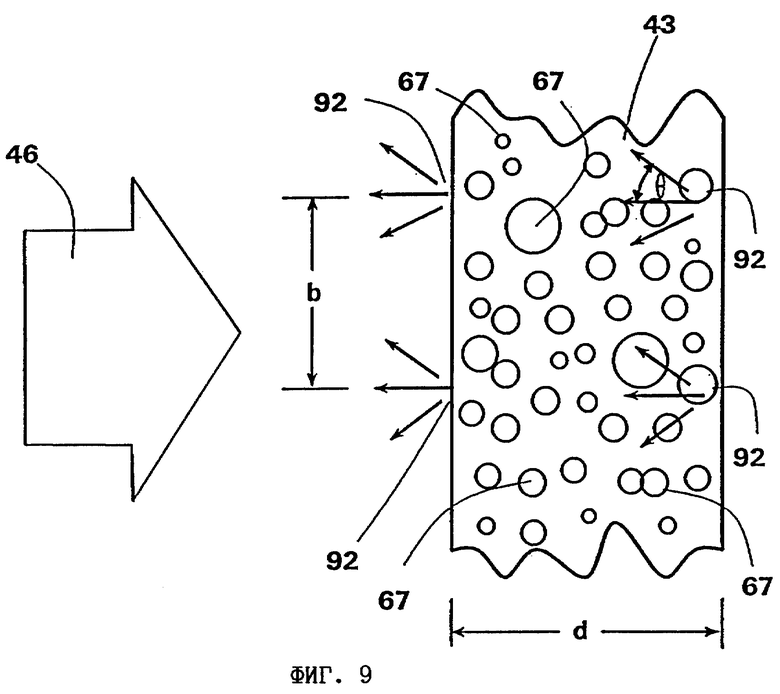
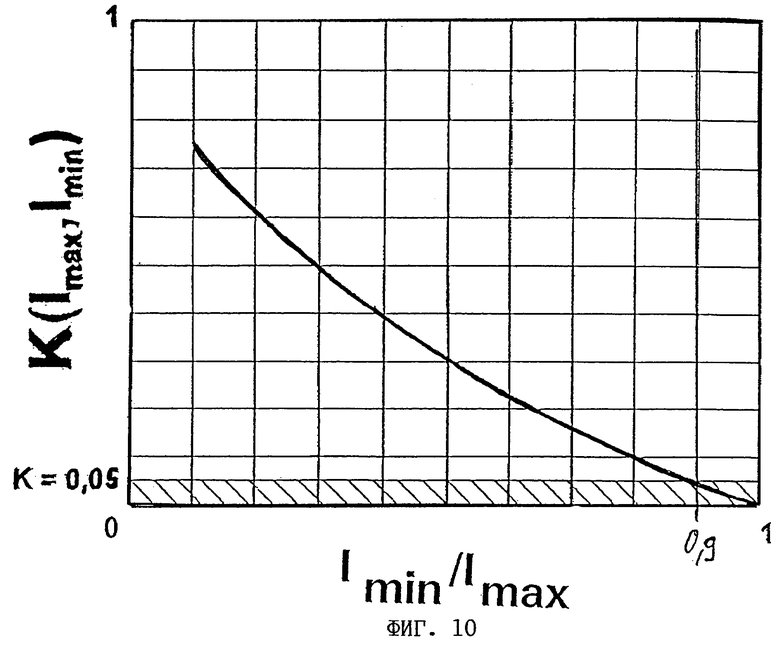
Устройство содержит первую структуру, осуществляющую для отдельных фотонов лазерного луча, имеющего когерентность L, фазовые сдвиги в соответствии с заданным распределением. Полученное в результате фазового сдвига среднеквадратическое значение разницы в оптической длине пути больше длины когерентности L, умноженной на коэффициент 1/(12)1/2. Первая структура может быть выполнена из прозрачного материала с включенными в него частицами, имеющими более высокий показатель преломления. Устройство может содержать вторую структуру, содержащую элементы, позволяющие уменьшить длину когерентности лазерного луча. Обеспечивается уменьшение спеклов. 19 з.п. ф-лы, 10 ил.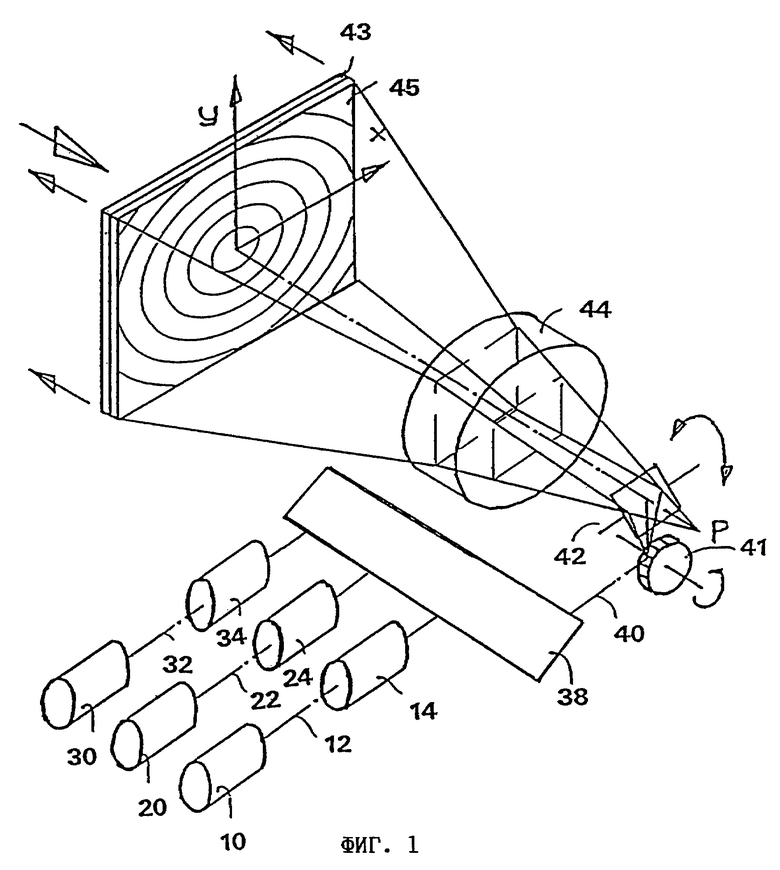
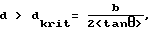
где <tanθ> означает среднее значение тангенса угла θ рассеяния для характеризующего отклонения лазерного луча (40) частицами (67) распределения углов рассеяния.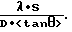
17. Устройство по п.15 или 16, отличающееся тем, что толщина d имеет величину, при которой характеристика функции величины контраста K(d) в зависимости от толщины d принимает значение меньше 0,20 прежде всего меньшее или равное 0,05, при этом указанная функциональная характеристика величины контраста измеряется по формуле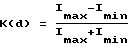
в зависимости от возникающей максимальной световой интенсивности Imax и минимальной световой интенсивности Imin в равномерно освещаемой лазерным лучом (40) области при соответствующей толщине d слоя на поверхности экрана (43).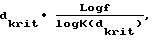 где f обозначает число меньшее 0,20 и прежде всего меньшее или равное 0,05, а
где f обозначает число меньшее 0,20 и прежде всего меньшее или равное 0,05, а 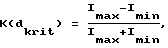 где Imax обозначает максимальную, а Imin обозначает минимальную световую интенсивность в пределах равномерно освещаемой лазером (10, 20, 30) области на экране (43) толщиной dkrit.
где Imax обозначает максимальную, а Imin обозначает минимальную световую интенсивность в пределах равномерно освещаемой лазером (10, 20, 30) области на экране (43) толщиной dkrit.
d ≥ (0.04 см · L)1/2 ± 25%.
| Подвеска для узкогорлых полых изделий | 1974 |
|
SU589179A1 |
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
| Система коррекции и коллимации пучка излучения полупроводникового лазера | 1989 |
|
SU1640663A1 |
| Оптическая система для расширения, коллимации и выравнивания интенсивности лазерного гауссова пучка | 1988 |
|
SU1561062A1 |
Авторы
Даты
2001-01-27—Публикация
1997-10-31—Подача