Изобретение относится к ультразвуковой технике, а именно к выполненным в виде стержней, пластин или оболочек волноводным акустическим трансформаторам. использующимся для переноса потока энергии упругих продольных волн внутри своих границ заданного профиля, а также для изменения (увеличения) плотности потока переносимой энергии за счет изменяющейся (уменьшающейся) в направлении распространения волн площади сечения.
Заявленное устройство может быть также использовано в качестве понижающего волнового акустического трансформатора.
Известен класс волноводных акустических трансформаторов, объединенных общим признаком: функции изменения площади их сечения в направлении распространения волн являются элементарными функциями координаты на оси симметрии их профилей [1-7]. Под профилем подразумевается сечение волноводного акустического трансформатора по оси его симметрии. Геометрические пространственные тела основных типов таких акустических трансформаторов образованы:
- вращением профиля вокруг оси симметрии для стержней круглого сечения и оболочек кольцевого сечения [8];
- плоскопараллельным перемещением профиля по нормали к оси симметрии для пластин [6].
Линии, которые очерчивают профиль и не являются при этом линиями, параллельными оси симметрии, как это имеет место для наружных границ некоторых оболочек, также могут быть представлены графиками элементарных функций с координатой оси симметрии профиля в качестве аргумента. Далее для однозначности толкования под функцией профиля волноводного трансформатора будет пониматься монотонная функция
h(x) {H ≥ h(x) > 0},
где 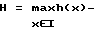 хорда полупрофиля - части профиля, расположенной в первом квадранте комплексной плоскости координат z(x,у), то есть x = Rez{x:0≤x≤∞}, y = Imz{y:0≤y≤j∞}. Соответственно, второй полупрофиль, осесимметричный первому, будет располагаться во втором квадранте этой плоскости, то есть будет зеркальным отображением первого относительно действительной оси.
хорда полупрофиля - части профиля, расположенной в первом квадранте комплексной плоскости координат z(x,у), то есть x = Rez{x:0≤x≤∞}, y = Imz{y:0≤y≤j∞}. Соответственно, второй полупрофиль, осесимметричный первому, будет располагаться во втором квадранте этой плоскости, то есть будет зеркальным отображением первого относительно действительной оси.
Очевидно, что функция профиля, представленная в таком виде, задает в функции площадей сечения в виде, например:
s(x) = πh2(x)- для стержней круглого сечения;
s(x) = πh(x)[2H-h(x)]- для оболочек кольцевого сечения постоянного наружного диаметра;
s(x) = πh1(x)[2h2(x)-h1(x)]- для оболочек кольцевого сечения увеличивающегося наружного диаметра [4];
s(x)= 2wh(x) - для пластин шириной w.
При этом ориентация относительно координат, в которых резонансная длина волновода l откладывается по оси его симметрии x, а у = h(x)
то есть, с увеличением координаты x, растет и значение плотности потока переносимой волноводным трансформатором энергии.
Использование в практике расчета волноводных акустических трансформаторов некоторых элементарных функций в качестве функций профиля было обусловлено возможностью аналитического решения в этих случаях волнового уравнения для одномерных гармонических колебаний. Известно, что наиболее распространенными для этого элементарными функциями, различающимися кривизной графиков, являются:
- экспоненциальная, катеноидальная, гиперболическая, обладающие положительной кривизной графика относительно оси аргументов;
- линейная, обладающая нулевой кривизной;
- параболическая, Бесселева, обладающая отрицательной кривизной;
- Гауссова и полиномиальная (или Фурье-типа), обладающие знакопеременной кривизной.
В принятой ориентации они выглядят, соответственно, как:
hexp(x) = He-αx, (2)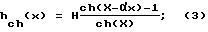
hhup(x) = H(1+αx)-1; (4)
hlin(x) = H(1-αx); (5)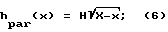
hBes(x) = H(1-αx)β; (7)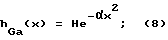
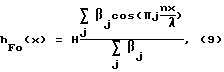
где α- независимая переменная (параметр);
λ- длина волны колебаний в материале трансформатора:
β- вектор коэффициентов Фурье размером j ≥ 3 [7].
Достижению указанного ниже технического результата при использовании волноводных акустических трансформаторов с такими функциями профиля препятствует следующее обстоятельство. Известно, что область возможных значений коэффициентов усиления
(где ξs, ξS- амплитуды колебательного смещения меньшего и большего по площади, соответственно, торцов акустического трансформатора, работающего в резонансном режиме) при одинаковых соотношениях площадей торцов ограничена сверху теоретическим коэффициентом трансформации канонического акустического волноводного трансформатора с функцией профиля ступенчатой формы без галтелей и скруглений:
hst(x) = H[1-αϑ(x-0,25λ)], (11)
где α[0,1]- независимая переменная (параметр);
ϑ(x)- функция Хевисайда.
Этот предельный теоретический коэффициент усиления равен отношению площадей торцов канонического "хевисайдовского" трансформатора [1, 2]: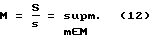
Таким образом, используя для оценки качеств акустических волноводных трансформаторов различных, в том числе, приведенных выше форм, тривиальный критерий подобия: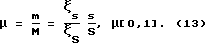
Аналогично [2, 5] можно показать, что они обладают малой относительной трансформацией, что не дает возможности использовать их с большими абсолютными значениями коэффициента трансформации без потери жесткости к изгибным колебаниям [5, 6] и рассеяния передаваемой энергии неосновными модами колебаний.
Известен класс акустических волноводных трансформаторов с большей устойчивостью к возникновению изгибных колебаний и, соответственно, с более высокими значениями относительной трансформации μ. Этот класс объединен следующим общим признаком. Функции профилей трансформаторов этого класса являются кусочно-гладкими и/или кусочно-непрерывными функциями с точками разрыва I рода. Фрагменты таких функций, являющиеся аналитическими функциями на отрезках, могут иметь различные знаки кривизны. Примерами профилей трансформаторов этого класса являются:
- галтельный [2, 6], цилиндрическо-катеноидальный [5], имеющие участки положительной кривизны функции профиля и особые точки разрыва I рода и перелома, соответственно;
- цилиндрическо-конусный и конусно-цилиндрический [9-11], функции профиля которых имеют точки перелома и нулевую кривизну на участках;
- ампульно-цилиндрический [2] , имеющий участок отрицательной кривизны функции профиля и точку перелома.
Функции профилей их, соответственно, следующие:

где X≈λ, α- независимые переменные (параметры);
h=h(l);
r - радиус галтели;
x = 0,25λ и x = 0,125λ- особые точки.

где X<0.25λ, α- независимые переменные (параметры).


где X>0,25λ, α- независимые переменные (параметры).
Несмотря на то, что эти волноводные трансформаторы по своим значениям μ приближаются к каноническому ступенчатому более чем трансформаторы предыдущего класса, они также обладают недостатком в отношении достижения указанной ниже цели. Этот недостаток заключается в низком значении "фактора качества" - нетривиального критерия подобия, имеющего вид [6]: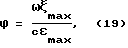
где ξmax, εmax- максимальные абсолютные значения амплитуды колебательного смещения и деформации, соответственно;
ω- резонансная угловая частота колебаний;
с - скорость звука в материале волновода.
Фактор качества наилучшим образом характеризует волноводный акустический трансформатор данной формы [6] и дает его комплексную оценку с учетом абсолютной трансформации (усиления), определяемой ξmax, и устойчивости к механическому разрушению, зависящей от εmax. Низкие значения ϕ трансформаторов рассматриваемого класса обусловлены малыми величинами их поперечного сечения вблизи плоскости, которой принадлежит координата с максимальным значением ε, а также наличием там же концентраторов механических напряжений, образованных точками перелома функции профиля с положительным скачком ее первой производной или участками с положительной кривизной и малыми радиусами кривизны. Эти свойства, в свою очередь, обусловлены необходимостью резкого изменения площади сечения трансформатора на коротком участке для получения высокой абсолютной трансформации при минимальной разнице площадей торцов. Зависимость величин коэффициентов концентрации напряжений (деформаций) K от формы и соотношения размеров концентраторов, например, для валов и пластин с галтелями, известна [12, 13] . Также известно о фактах более вероятного разрушения акустических волноводных трансформаторов с концентраторами напряжений [2] (см. фиг.1).
Учитывая принятые ранее допущения о том, что колебания в рассматриваемых колебательных системах гармонические и приняты все ограничительные меры к тому, чтобы считать волну плоской, можно привести выражение для фактора качества ϕ к виду, позволяющему сравнивать между собой волноводы различных типов, в том числе содержащие явно выраженные концентраторы механических напряжений, изготовленные из одного материала, аналогично тому, как это было проделано выше для μ, сделав относительными величинами параметры, зависящие от свойств материала волновода. В качестве волновода канонической формы здесь следует принять волновод с функцией профиля h(x)=h. Действительно, такой волновод, в противоположность "хевисайдовскому" волноводу ступенчатой формы, не имеет сосредоточенных концентраторов напряжений и вообще не концентрирует энергию волны. Тогда, заменив значения всех констант и переменных, входящих в выражение для ϕ их отношениями к соответствующим параметрам волновода канонической формы c0, ξmax,0 и εmax,0 можно записать: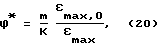
где K[1,∞]- коэффициент концентрации механических напряжений (деформаций), действующих в плоскости, которой принадлежит координата с максимальным значением относительной, средней по сечению деформации.
Пользуясь критерием ϕ*, можно показать, что факторы качества у волноводных акустических трансформаторов, функции профилей которых являются кусочно-гладкими или кусочно-непрерывными с резкими изменениями h(x) на коротких участках оси, даже ниже, чем у предыдущего класса трансформаторов.
Такие трансформаторы, как цилиндрическо-конический или цилиндрическо-катеноидальный, не имеющие выраженных концентраторов напряжений, то есть, обладающие высоким запасом прочности, в то же время не обладают высокой относительной трансформацией. Коническо-цилиндрический и ампульно-цилиндрический, наоборот, обладая достаточным μ, имеют сильные концентраторы напряжений в местах особых точек, которые можно считать участками с положительной кривизной и бесконечно малым радиусом кривизны. Для канонического ступенчатого трансформатора, который но совокупности признаков также можно отнести к данному классу, ϕ* вообще имеет нулевое значение. Галтельные трансформаторы могут изменять фактор качества в широком диапазоне в зависимости от радиуса галтели r, наиболее используемые значения для которого 0,6-0,8(H - h) [2]. Оценка волноводных акустических трансформаторов по критерию "относительного фактора качества" позволяет сделать вывод о том, что установление противоположно-экстремальных значений радиусов кривизны на соседствующих участках функции профиля с разными знаками кривизны приводят к одному и тому же результату - снижению ϕ*.
Исходя из этого, становится ясно. что оптимум находится в области акустических трансформаторов с гладкими функциями профиля, резко изменяющими абсолютное значение на сравнительно коротком диапазоне аргумента.
Следующим классом акустических волноводных трансформаторов являются трансформаторы, функция профиля которых представляет из себя аналитическую на всем диапазоне их длины, кусочно-гладкую, непрерывно дифференцируемую функцию, составленную из конгруэнтных в точках сопряжения фрагментов и обладающую не менее, чем однократно изменяющимся знаком кривизны. Известный пример таких трансформаторов - ампульный (по Э. Эйснеру), составленный из последовательно сопряженных функций положительного аргумента, как минимум одна из которых является гауссовой функцией [6]. Трансформаторы этого класса обладают высокими значениями ϕ*. Общее выражение для функции "эйснеровского" профиля трансформатора при априорном выборе параметров может быть представлено, например, в виде двух последовательно сопряженных гауссовых функций:
где α,β- независимые переменные (параметры);
Y - ордината асимптоты первого фрагмента функции;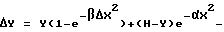 поправка к ординате максимума второго фрагмента функции, обеспечивающая гладкое сопряжение;
поправка к ординате максимума второго фрагмента функции, обеспечивающая гладкое сопряжение;
X - абсцисса точки сопряжения;
ΔX- поправка к абсциссе точки сопряжения, обеспечивающая гладкое сопряжение;
с ≤ 0,01 - значение первой производной функции профиля в точке сопряжения, практически удовлетворяющее условию конгруэнтности и признакам, изложенным в [6].
При значениях ϕ-1m≈1, (α = 0, X = 0,25λ) такой трансформатор вырождается в цилиндрическо-гауссовый, форма которого является наиболее предпочтительной.
Наиболее близким из этого же класса трансформаторов к заявленному по совокупности признаков в отношении поставленной цели является волноводный акустический трансформатор (концентратор) [14] , функция профиля которого представляет из себя аналитическую на всем диапазоне длины, непрерывно дифференцируемую функцию, обладающую однократно изменяющимся знаком кривизны, составленную из последовательно конгруэнтно сопряженных прямой h(x) = H, дуг окружностей радиусов r1, r2 и прямой h(x) = h, принятый за прототип.
Прототип фактически представляет собой галтельный трансформатор с галтелью радиуса r1, единственная точка перелома функции профиля которого ликвидирована путем наружного скругления по радиусу r2, причем проекция радиального сопряжения на ось x не превышает 0,06λ. Функция профиля прототипа, формализованная в соответствии с признаками, изложенными в [14], например, при условии r1 + r2 ≤ H - h, имеет вид:
где a = 0,06λ- константа;
X - абсцисса начала скругления.
Очевидно, что в предельных случаях, например, при r1 = 0 прототип вырождается в галтельный трансформатор с радиусом галтели r = H-h, а при r2 = 0 приобретает "абсолютный" концентратор напряжений, так же как и канонический ступенчатый трансформатор.
Причиной, препятствующей достижению технического результата, являющегося целью изобретения, при использовании описанного волноводного акустического трансформатора (концентратора), принятого за прототип, является недостаток, присущий всему классу акустических трансформаторов, к которому принадлежит прототип. Это неразрешенное с помощью известных признаков, описывающих функцию профиля трансформатора, противоречие между механической прочностью, определяемой относительным фактором качества ϕ*, и величиной изменения плотности потока передаваемой энергии, характеризуемой относительной трансформацией μ.
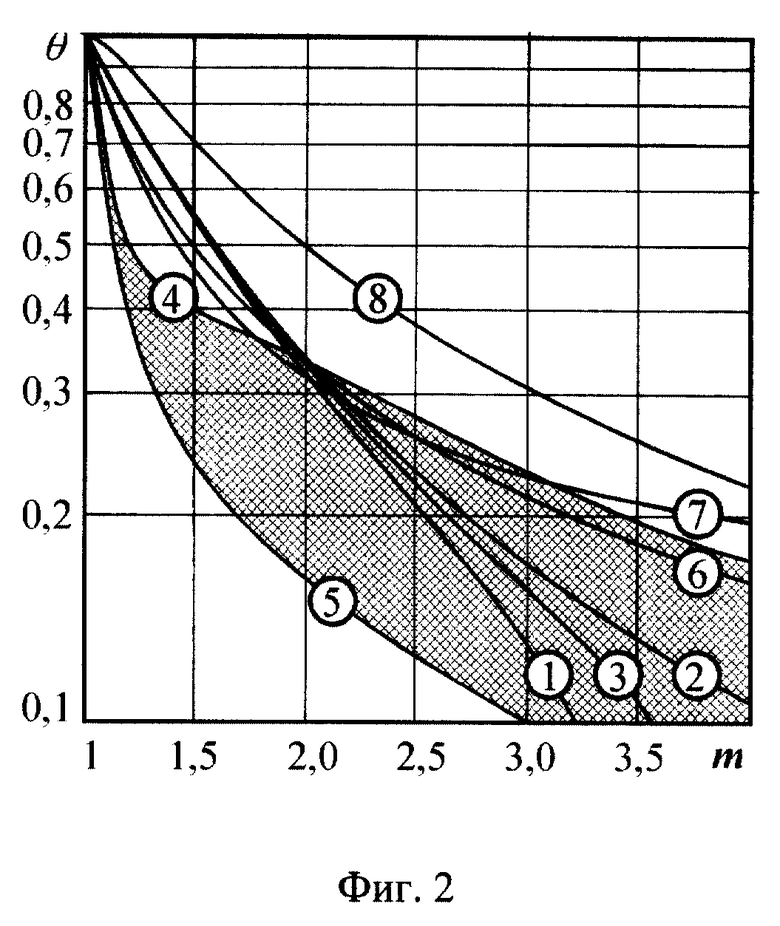
Так, при значениях абсолютной трансформации 0 ≤ m ≤ 2,5 прототип с хордой профиля H = 0,125λ превосходит по значению относительного фактора качества ϕ* галтельный трансформатор с тем же соотношением размеров и радиусом галтели r = 0,8(H - h), а при 2,5 <m - уступает ему (см. фиг. 2).
Сущность изобретения заключается в следующем. Обеспечение условий передачи акустической энергии от источника колебаний к нагрузке посредством волноводных акустических трансформаторов с минимальным риском разрушения последних и максимальным коэффициентом трансформации является одной из основных задач при расчете и проектировании ультразвуковых колебательных систем. При правильном выборе материала волноводного акустического трансформатора эти условия обеспечиваются исключительно выбором геометрической формы волновода, которая в свою очередь, как было сказано выше, однозначно характеризуется функцией его профиля. Прогресс в области волноводных акустических трансформаторов в основном определялся новыми методами проектирования, а также технологическими средствами изготовления волноводов сложной формы.
В области проектирования большое значение имеет выбор критерия сравнительной оценки волноводов, который еще на этом этапе позволил бы оптимизировать их конструкцию. В известном обзоре Эйснера [6] при анализе различных волноводных акустических трансформаторов часто делаются оговорки о преимущественном диапазоне коэффициентов усиления, в котором те или иные формы различных волноводных акустических трансформаторов, несмотря на значение ϕ, предпочтительнее, что свидетельствует о некотором несовершенстве его критерия. Фактически критерий Эйснера является двухпараметрическим.
Унифицировать критерий оптимальности при оценке качества различных волноводных акустических трансформаторов можно следующим образом: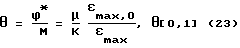
Такой безразмерный нетривиальный критерий θ показывает отношение ϕ* к максимально возможному при заданном соотношении площадей торцов различных волноводных акустических трансформаторов коэффициенту усиления. Нижняя граница диапазона изменения θ соответствует значению этого критерия, принадлежащего ступенчатому волноводу, имеющему галтель с нулевым радиусом - "абсолютный" концентратор напряжений.
Пользуясь критерием θ, можно для каждого значения m сравнить различные волноводные акустические трансформаторы. Очевидно, что лучшим оказывается тот, у которого больше значение критерия.
Технический результат - повышение коэффициента трансформации волноводного акустического трансформатора при одновременном повышении устойчивости к механическому разрушению.
Указанный технический результат при реализации изобретения достигается тем, что в известном волноводном акустическом трансформаторе, функция профиля которого представляет собой аналитическую на всем диапазоне длины, непрерывно дифференцируемую функцию, обладающую однократно изменяющимся знаком кривизны, отличие состоит в том, что функция профиля описывается уравнением эквилипии потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения.
Функция профиля такого волноводного акустического трансформатора может быть задана, например, в виде множества на комплексной плоскости z(x,y):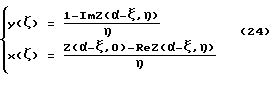
где Z(ζ)- функция конформного отображения комплексной области прямоугольника ζ(ξ,η) на область полупрофиля ступенчатого трансформатора z(x,y);
α- параметр на конформном инварианте ζ(ξ,η), задающий положение узла смещений;
η - параметр на конформном инварианте ζ(ξ,η), задающий ординату эквилинии потока поля волнового вектора.
Известно, что при помощи метода конформных отображений решаются задачи теории упругости [15, 16] . Задача передачи и трансформации акустической энергии упругой волны внутри волноводного акустического трансформатора также является задачей теории упругости. Соответствующее поле волнового вектора [17] удовлетворяет условиям уравнения Лапласа, так как в условиях плоской волны поток энергии во внешнюю среду через границы волновода незначителен, и им можно пренебречь, а источники и стоки энергии внутри волновода отсутствуют по определению.
Варьируя независимыми параметрами α и η в (24), а также соотношением h и H канонического трансформатора, можно выбирать функцию профиля в широких пределах формы. Такой выбор профиля достаточен для удовлетворения требований к волноводным акустическим трансформаторам во всех областях их применений. Он позволяет при обеспечении высокого значения коэффициента трансформации удалить плоскость максимальных деформаций от концентратора механических напряжений.
Таким образом, сравнение заявленного волноводного акустического трансформатора с прототипом, являющимся наиболее близким аналогом из технических решений, характеризующих известный заявителю уровень техники в области предмета изобретения, показывает, что заявленный способ обладает существенным по отношению к указанному техническому результату отличительным признаком.
При исследовании отличительных признаков описываемого трансформатора заявителем не выявлено каких-либо известных аналогичных решений, касающихся выбора функции профиля из семейства эквилиний потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения.
На фиг. 1 приведена фотография волноводного акустического трансформатора с галтелью малого радиуса, разрушенного в результате превышения предела циклической прочности материала механическим напряжением в зоне концентратора напряжений.
На фиг. 2 в графическом виде приведен результат сравнения наиболее распространенных форм волноводных акустических трансформаторов по критерию θ, где 1 - конический; 2 - экспоненциальный; 3 - Гауссовый; между 4 и 5 - область галтельных волноводных акустических трансформаторов; 6 - конгруэнтный с сопряженными галтелью и округлением (прототип); 7 - цилиндрическо-Гауссовый.
График заявленного трансформатора показан под номером 8.
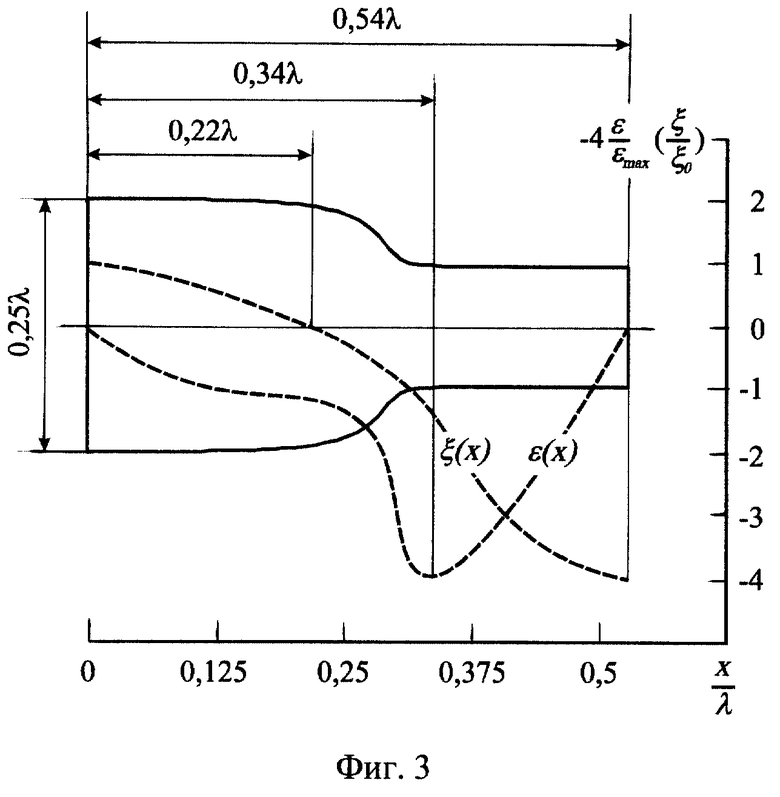
На фиг. 3 изображен профиль заявленного трансформатора в виде стержня круглого сечения с параметрами: H = 1 = 0,125λ; η = 0,8; m = 4; α = 1,92. Кривыми показаны графики функций ε(x) и ξ(x) в масштабах ε/εmax и ξ/ξ0 соответственно, полученные путем численного решения дифференциального уравнения вида: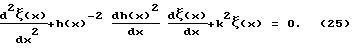
В подтверждение возможности осуществления изобретения с получением вышеуказанного технического результата ниже приводится описание конкретного примера реализации заявленного трансформатора в соответствии с совокупностью его признаков.
Волноводный акустический трансформатор в виде стержня переменного сечения (фиг. 3) имеет в качестве функции профиля аналитическую на всем диапазоне длины, непрерывно дифференцируемую функцию, обладающую однократно изменяющимся знаком кривизны, описываемую уравнением одной из эквилиний потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения.
Алгоритм установления вида функции профиля волноводного акустического трансформатора, опирающийся на известный уровень знаний и подтверждающий возможность осуществления изобретения, следующий. Конформное отображение комплексной области прямоугольника ζ(ξ,η) высотой π на область полупрофиля ступенчатого трансформатора z(x,y), например, при H = 1; h <1; λ = 8 и уступом (разрывом функции I рода) при x = 0 [15] осуществляется посредством выражения вида: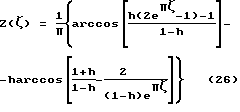
При этом получаемое в соответствии с (24) точечное множество, задающее функцию профиля (уравнение эквилинии потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения) на комплексной плоскости z(x,y), будет иметь вид: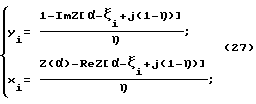
где i = 0.1...n.
Функцию, заданную на точечном множестве, можно преобразовать в аналитическую на всем диапазоне длины, непрерывно дифференцируемую функцию, путем, например, приближения интерполяционным многочленом либо путем полиномиального сглаживания по методу наименьших квадратов с требуемой погрешностью. Используя полученную аналитическую функцию, можно вновь произвести дискретизацию функции профиля с требуемым постоянным значением шага аргумента x, например, с целью использования ее для программирования станка с числовым программным управлением, на котором будет изготавливаться данный волноводный акустический трансформатор.
Волноводный акустический трансформатор работает следующим образом.
Плоская акустическая волна распространяется в нем, через границу с максимальным значением хорды полупрофиля. Если отсутствуют условия для стока энергии с противоположной границы (с минимальным значением хорды полупрофиля), а приток энергии осуществляется при частоте колебаний, равной резонансной частоте, и в количестве, компенсирующим ее рассеяние внутри трансформатора, то в нем устанавливается стоячая акустическая волна. Когда появляются условия для передачи энергии колебаний в нагрузку, например, при погружении второго конца трансформатора в вязкую среду, рассеивающую акустическую энергию, в трансформаторе появляется бегущая волна, переносящая эту энергию. При этом данный волноводный акустический трансформатор будет играть роль концентратора, так как его функция профиля в этом случае является монотонно убывающей, следовательно, плотность потока поля волнового вектора в нем растет по направлению к нагрузке.
Так как боковой границей трансформатора является эквилиния потока поля волнового вектора, принадлежащая семейству эквилиний профиля ступенчатого трансформатора, обладающего наивысшим теоретическим значением коэффициента усиления, то значение последнего может быть сколь угодно максимально к нему приближено выбором параметра η.
При этом зона действия максимального значения деформации и пропорционального ему значения механического напряжения может быть удалена от концентратора механических напряжений - сечения с минимальным значением радиуса кривизны функции профиля - путем соответствующего подбора независимого параметра α. Это обеспечивает устойчивость такого волноводного акустического трансформатора к механическому разрушению под воздействием циклических нагрузок.
Подтверждение возможности достижения технического результата изобретения при использовании волноводного акустического трансформатора заявленного профиля дает его сравнительная оценка с помощью универсального критерия θ (23) с известными, перечисленными выше трансформаторами различных классов, в том числе с прототипом. Результаты такого сравнения в графической форме приведены на фиг. 2.
Расчет коэффициентов концентрации механических напряжений при этом выполнен следующим образом.
Из дифференциальной геометрии известно выражение для функции радиуса кривизны плоской кривой (в данном случае функции профиля):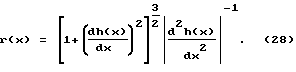
Ясно, что картины векторных полей деформаций, испытываемых трансформатором при статической и переменной нагрузках на его торцы, идентичны и различаются только значениями модулей векторов.
Деформация вдоль функции профиля, которую трансформатор при любом заданном соотношении H и h испытывает при статической нагрузке, вычислена как разность модулей соседних комплексных чисел, получаемых из (27), совокупность которых составляет эту кривую: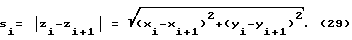
Соответственно, дискретное значение коэффициента концентрации механических напряжений: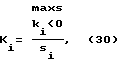
где k = 1/r - кривизна профиля.
Полученная таким образом функция K(x), заданная на точечном множестве, преобразована в аналитическую на всем диапазоне длины, непрерывно дифференцируемую функцию аналогично h(x).
Функция, описывающая зависимость коэффициента концентрации механических напряжений от радиуса кривизны профиля и соотношения экстремальных значений его хорд K(r, H, h), формализована путем постановки в соответствие r(x) из (28) и K(x).
Результаты сравнения, приведенные на фиг. 2, однозначно показывают в пользу заявленного волноводного акустического трансформатора.
Таким образом, вышеизложенные сведения свидетельствуют о возможности осуществления заявленного изобретения с помощью описанных в заявке или известных ранее средств и методов, а также о способности достижения указанного выше технического результата при воплощении совокупности признаков изобретения.
Источники информации
1. Теумин И.И. Ультразвуковые колебательные системы.- М.: Машгиз, 1959. -331 с.: ил.
2. Марков А.И. Ультразвуковое резание труднообрабатываемых материалов. - М.: Машиностроение. - 1968.- 365 с.: ил.
3. Авторское свидетельство СССР 227736, кл. В 06 В 1/08, 1967.
4. Патент РФ 2068741, кл. В 06 В 1/00, 1996.
5. Грачев А. А. и др. Ультразвуковая микросварка / Л.Л. Грачев. А.П. Кожевников, В. Л. Лебига, А.А. Россошинский. - М.: Энергия, 1977.- 184 с.: ил.
6. Физическая акустика/ Мод ред. У. Мэзона. Том 1, Часть Б.- М.: Мир, 1967.-362 с.: ил.
7. Ультразвуковые концентраторы Фурье-типа из титановых сплавов //Асташкин и др. - в кн.: Создание и применение аппаратуры для ультразвуковых технологических процессов в машиностроении, часть I /Под ред. А.И. Маркова. - М.: Знание, 1978, с.45-50.
8. Патент РФ 2046135, кл. С 12 Н 1/06, А 23 L 2/70, 1995.
9. Патент РФ 1797221, кл. В 24 В 39/04, 1996.
10. Патент РФ 2056926, кл. В 01 F 11/02, 1996.
11. Муханов И.И. Импульсная упрочняюще-чистовая обработка деталей машин ультразвуковым инструментом. - М.: Машиностроение, 1978.- 44 с.: ил.
12. Коллинз Дж. Повреждение материалов в конструкциях. Анализ, предсказание, предотвращение. - М.: Мир, 1984.- 624 с.: ил.
13. Петерсон Р. Коэффициенты концентрации напряжений. Графики и формулы для расчета конструктивных элементов на прочность. - М.: Мир, 1977.
14. Заявка на полезную модель 97114204/20 (015387), кл. В 06 В, 1997. Решение о выдаче свидетельства от 19 ноября 1997 г.
15. Лаврик В.И.. Савенков В.H. Справочник по конформным отображениям. - Киев: Наукова думка, 1970.- 251 с.: ил.
16. Галин Л.А. Упруго-пластические задачи. - М.: Наука, 1984.- 231 с.: ил.
17. Горелик Г.С. Колебания и волны. - М.: Ф-МЛ.-1959.- 572 с.: ил.
| название | год | авторы | номер документа |
|---|---|---|---|
| АКУСТИЧЕСКИЙ ТРАНСФОРМАТОР | 2006 |
|
RU2311971C1 |
| ИНТЕГРИРУЮЩИЙ АКУСТИЧЕСКИЙ ВОЛНОВОДНЫЙ ТРАНСФОРМАТОР (КОНЦЕНТРАТОР) | 2009 |
|
RU2402386C1 |
| ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ИЗЛУЧАТЕЛЬ ПЛОСКОЙ УЛЬТРАЗВУКОВОЙ ВОЛНЫ | 2009 |
|
RU2402113C1 |
| ВИБРОУДАРНЫЙ ИНСТРУМЕНТ С УЛЬТРАЗВУКОВЫМ ВОЗБУЖДЕНИЕМ | 1998 |
|
RU2179919C2 |
| СПОСОБ КАВИТАЦИОННОЙ ОБРАБОТКИ ЖИДКИХ СРЕД И РЕАКТОР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2228217C1 |
| УЛЬТРАЗВУКОВОЙ ВИБРОУДАРНЫЙ ИНСТРУМЕНТ | 2004 |
|
RU2259912C1 |
| КАВИТАЦИОННЫЙ РЕАКТОР | 2006 |
|
RU2290990C1 |
| АКУСТИЧЕСКАЯ ЯЧЕЙКА СОНОХИМИЧЕСКОГО РЕАКТОРА | 2008 |
|
RU2392047C1 |
| СПОСОБ ОЧИСТКИ ПРОВОЛОКИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2429086C1 |
| УСТРОЙСТВО ДЛЯ ПРИГОТОВЛЕНИЯ МАСЛЯНО-ВОДНОЙ ЭМУЛЬСИИ | 2000 |
|
RU2183986C2 |
Использование: для изменения (увеличения) плотности потока переносимой энергии за счет изменяющейся (уменьшающейся) в направлении распространения волн площади сечения. Сущность: в волноводном акустическом трансформаторе функция профиля представляет собой аналитическую на всем диапазоне длины непрерывно дифференцируемую функцию, обладающую однократно изменяющимся знаком кривизны, и описывается уравнением эквилинии потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения. Выбор конкретной функции профиля осуществляется рекурсивно путем максимизации безразмерного нетривиального критерия вида
где K[1,∞] - коэффициент концентрации механических напряжений (деформаций), действующих в плоскости, которой принадлежит координата с максимальным значением деформации εmax; m - коэффициент трансформации; М - коэффициент трансформации ступенчатого трансформатора с площадями входного и выходного торцов. соответственно равными площадям входного и выходного торцов выбираемого трансформатора; εmax,0 - максимальное значение деформации трансформатора, площади торцов, которого равны друг другу и площади меньшего торца рассчитываемого трансформатора. Технический результат: повышение коэффициента трансформации при одновременном повышении устойчивости к механическому разрушению. 3 ил.
Волноводный акустический трансформатор, отличающийся тем, что функция его профиля описывается уравнением эквилинии потока поля волнового вектора в осевом сечении ступенчатого волноводного акустического трансформатора, не принадлежащей границе этого сечения.
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Ротационный колун | 1919 |
|
SU227A1 |
| ТЕУМИН И.И | |||
| Ультразвуковые колебательные системы | |||
| - М.: Машгиз, 1959, с.331 | |||
| ПАРОВАЯ ИЛИ ГАЗОВАЯ ТУРБИНА | 1914 |
|
SU278A1 |
Авторы
Даты
2002-06-10—Публикация
2000-08-07—Подача