СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ ДЛЯ СЕЙСМИЧЕСКОЙ ИНТЕРПРЕТАЦИИ Российский патент 2002 года по МПК G01V1/30 

Настоящее изобретение имеет главным образом отношение к созданию способа количественной оценки и визуализации тонких эффектов сейсмической настройки для тонкого (маломощного) пласта. Раскрытый в настоящем изобретении способ предусматривает разложение сейсмического отраженного сигнала на его частотные компоненты за счет использования дискретного (или другого ортонормального) преобразования Фурье для длины (длительности), зависящей от толщины пласта, которая должна быть определена. После разложения за счет использования указанного дискретного преобразования, полученные в результате коэффициенты организуют и индицируют таким образом, что выявляется и усиливается характеристическое выражение области частот событий отражения от тонкого пласта. Это позволяет визуализировать вариации в толщине подстилающего слоя, которые иным образом не могут быть выявлены. Настоящее изобретение позволяет сейсмическому интерпретатору анализировать и отображать в виде карты (картографировать) геологические и стратиграфические характеристики нижних горизонтов в виде функции пространственного положения, времени пробега волны и частоты, в такой степени, которая ранее была недостижима.

По всем стандартам геофизика разведки является относительно молодой наукой, так как самые ранние работы в этой области появились в 20-е годы, а обновленный СМР подход только в 50-е. Однако с самого ее появления геофизика разведки стала в нефтяной отрасли доминирующим подходом при нахождении залежей нефти. Несмотря на то, что геофизика разведки заключает в себе три широких области, а именно, гравитационную, магнитную и сейсмическую разведку, в настоящее время сейсмический метод является доминирующим до такой степени, что другие виды разведки практически не применяются. На практике простой подсчет числа сейсмических разведывательных партий в поле стал принятой мерой оценки состояния всей нефтяной отрасли.

Сейсмическая съемка отображает попытку картографирования нижних горизонтов земли за счет посылки энергии звука в толщу земли и регистрации "эхо-сигналов", которые возвращаются от подстилающих слоев горной породы. Источником направленной вниз звуковой энергии может быть взрыв или сейсмические вибраторы на поверхности земли, или же пневмопушки на морской поверхности. В ходе проведения сейсмической разведки источник энергии перемещают по поверхности над представляющей интерес геологической структурой. При каждой детонации источника его записывают в большом числе точек на поверхности земли. Множество комбинаций взрыв/запись затем объединяют для создания почти непрерывного профиля нижних горизонтов, которые могут простираться на многие километры. При двухмерной (2-D) сейсмической съемке точки регистрации сигнала обычно лежат на прямой линии, в то время как при трехмерной (3-D) съемке точки регистрации распределены по поверхности в виде решетки. При самом простом объяснении можно полагать, что 2-D сейсмическая линия дает поперечное сечение каждого слоя, существующего под местом регистрации, а 3-D съемка дает "куб" данных или объем, который, по меньшей мере концептуально, является 3-D картиной нижних горизонтов, лежащих под зоной съемки. Следует иметь в виду, что имеется возможность извлечения индивидуальной 2-D линии съемки из 3-D объема данных.

Сейсмическая съемка образована очень большим числом индивидуальных сейсмических записей или трасс. При типичной 2-D съемке обычно имеется несколько десятков тысяч трасс, в то время как при 3-D съемке число индивидуальных трасс может составлять многие миллионы. Сейсмическая трасса представляет собой цифровую запись энергии звука, отраженной от неоднородностеи в нижних горизонтах, причем частичное отражение происходит всякий раз при изменении акустического импеданса материалов нижних горизонтов. Цифровые выборки обычно получают с интервалами 0,004 сек (4 мс), хотя часто используют также и интервалы 2 мс и 1 мс. Следует иметь в виду, что каждая выборка на сейсмической трассе связана с временем пробега волны, а в случае отраженной энергии - с временем двойного пробега волны. Кроме того, положение каждой трассы сейсмической съемки на поверхности земли тщательно региструется и обычно является частью самой трассы (является частью заголовка информации трассы). Это позволяет в дальнейшем коррелировать сейсмическую информацию, которая содержится в трассах, со специфическими местоположениями нижних горизонтов, в результате чего получают средство оконтуривания сейсмических данных и извлечения из них атрибутов (характерных признаков) для отображения в виде карты (для картографирования). Сигнал, который посылают в толщу земли, именуется сейсмическим колебанием или сейсмическим импульсоидом. Вид сейсмического колебания зависит от того, является ли источником пневмопушка, динамит или вибратор. Термин "сигнатура источника" или "импульс источника" обычно используют для описания сейсмической характеристики записи конкретного сейсмического колебания.

Генерируемый на поверхности земли сейсмический импульс источника немедленно начинает распространение от точки возникновения, в том числе и в толщу земли, встречая блоки горной породы в нижних горизонтах и проходя через них. У каждой поверхности раздела между двумя различными горными породами имеется вероятность сейсмического отражения. Величина сейсмической энергии, отраженной от определенной поверхности раздела, которая зависит от контраста акустического импеданса между блоками горной породы и от коэффициента отражения, является известной мерой оценки контраста. Можно полагать, что коэффициент отражения является отношением амплитуды отраженной волны к амплитуде падающей волны. В терминах свойств горной породы:

где акустический импеданс блока горной породы определен как математическое произведение плотности горной породы, (причем ρ₁ и ρ₂ являются соответственно плотностями верхних и нижних блоков горной породы) на скорость прохождения сигнала в указанной горной породе. V₁ и V₂ соответствуют скоростям в верхнем и нижнем блоках горной породы. (Строго говоря это выражение является совершенно справедливым только если импульсоид пересекает поверхность раздела горной породы при вертикальном падении. Однако на практике обычно принимают, что требование вертикальности удовлетворяется, если импульсоид пересекает поверхность раздела с отклонением ориентировочно 20^o от вертикали).

Отраженная энергия, которую регистрируют на поверхности земли, может быть отображена концептуально как свертка сейсмического имлульсоида с отражательной функцией нижних горизонтов, в виде так называемой "модели свертки". Короче говоря, модель свертки предназначена для объяснения сейсмического сигнала, зарегистрированного на поверхности, в виде математической свертки направленного вниз (в толщу земли) импульсоида источника с отражательной функцией, которая отображает коэффициенты отражения у поверхностей раздела между различными слоями горной породы в нижних горизонтах. Это может быть выражено уравнением:
х(t)=w(t)•е(t)+n(t)
где х (t) представляет собой зарегистрированную сейсмограмму, w (t) является сейсмическим импульсоидом источника, е (t) является отражательной функцией земли, а n (t) представляет собой случайный шум окружающей среды. "*" представляет собой математическую свертку. Дополнительно модель свертки требует, в частности, (1) чтобы импульсоид источника оставался инвариантным при его прохождении через нижние горизонты (то есть, чтобы он был стационарным и неизменным) и (2) чтобы записанная на поверхности земли сейсмическая трасса могла быть представлена в виде арифметической суммы отдельных сверток импульсоида источника с каждой поверхностью раздела в нижних горизонтах (принцип "суперпозиции", при котором отражение импульсоида и распространение сигнала являются линейной системой). Несмотря на то, что лишь немногие верят в то, что модель свертки полностью описывает механику распространения волны, эта модель является достаточно точной для решения многих задач, что делает ее очень полезной на практике. Некоторые детали построения модели свертки обсуждаются в главе 2.2 публикации "Обработка сейсмических данных", Ozdogan Yilmaz, Society of Exploration Geophysicists, 1987, описание которой включено здесь в качестве ссылки.

Сейсмические данные, которые получены и обработаны надлежащим образом, дают богатую информацию разведчику - специалисту нефтяной компании, работой которого является локализация возможных мест бурения скважин. Например, сейсмический профиль дает разведчику широкий взгляд на структуру слоев горной породы нижних горизонтов и часто позволяет выявить важные характеристики, связанные с захватом и хранением углеводородов, среди многих других такие характеристики как сбросы, складки, антиклинали, несоответствия и подстилающие соляные куполы и рифы. В ходе компьютерной обработки сейсмических данных обычно получают оценки скорости сигнала в нижних горизонтах, а также обнаруживают и индицируют близкие к поверхности земли неоднородности. В некоторых случаях сейсмические данные могут быть использованы для непосредственной оценки пористости горной породы, насыщения ее водой и для оценки содержания углеводородов. Менее очевидно, что атрибуты сейсмического колебания, такие как фаза, пиковая амплитуда, отношение пика к впадине и множество других, часто эмпирически могут быть коррелированы с известным содержанием углеводородов, причем эта корреляция применима для сейсмических данных, собранных для новых районов разведки. Короче говоря, сейсмические данные обеспечивают лучшую из имеющейся структурной и стратиграфической информации относительно нижних горизонтов, без проведения бурения скважины.

Сейсмические данные связаны однако с одним принципиальным ограничением: блоки горной породы, которые относительно "тонкие", часто не имеют достаточной (четкой) разрешающей способности. Более конкретно, в то время как сейсмические отраженные данные могут обеспечивать отображение, близкое к "геологическому поперечному сечению" нижних горизонтов, если литографические слои являются относительно "толстыми", то сейсмическое изображение, которое получают от "тонких" слоев, является намного менее четким. Это явление известно специалистам как проблема сейсмической разрешающей способности.

Сейсмическая разрешающая способность в данном контексте относится к вертикальному разрешению в пределах единственной сейсмической трассы и может быть определена как минимальное расстояние между двумя сейсмическими рефлекторами в нижних горизонтах, которые могут быть опознаны на сейсмической записи как отдельные поверхности раздела, а не как единое составное отражение. В качестве примера можно указать, что блок нижних горизонтов может быть опознан в идеале на сейсмическом сечении как комбинация двух величин: отдельного отражения, исходящего (полученного) от вершины блока, и второго отдельного отражения, с возможной противоположной полярностью, исходящего от основания блока. В идеальном случае как вершина, так и основание блока видны на записанной сейсмограмме как отдельные и изолированные рефлекторы, которые могут быть индивидуально "разнесены по времени" (то есть отмаркированы и идентифицированы) в сейсмическом сечении, причем сейсмические данные в интервале между двумя разнесенными по времени пиками содержат информацию относительно промежуточного блока горной породы. С другой стороны, если сейсмический блок не является достаточно толстым (мощным), то возвратные отражения от вершины и основания блока перекрываются, в результате чего создается интерференция между двумя событиями отражения и возникает размытие изображения нижних горизонтов. Размытое изображение нижних горизонтов является одним из примеров феномена, известного специалистам как проблема "тонкого пласта".

На фиг. 1 показано в самом общем виде, как возникает проблема тонкого пласта при использовании аксиом модели свертки. Рассмотрим вначале отражение от "толстого" пласта, показанное на фиг.1а. В левой части фиг.1а показан импульсоид источника, генерируемый на поверхности земли. Импульсоид источника распространяется в неизменном виде через толщу земли по траектории Р1, до тех пор, пока он не встречает поверхность раздела "А" блока горной породы. (Следует иметь в виду, что траектории волны на этой фиг.1а в действительности являются вертикальными, но для лучшего понимания показаны наклонными. Это обычно используется на практике). Когда направленное вниз сейсмическое колебание встречает поверхность раздела "А", часть его энергии отражается назад в направлении к поверхности земли по пути Р2 и регистрируется на поверхности как отраженное событие R1. Следует иметь в виду, что импульсоид R1 имеет обратную полярность по сравнению с полярностью импульсоида источника, что отображает отрицательный коэффициент отражения поверхности раздела "А". Эта обратная полярность показана только в качестве примера, так как специалисты знают, что коэффициенты отражения могут иметь любую полярность.

Оставшаяся часть направленной вниз энергии (после частичного отражения у поверхности раздела "А") продолжает движение через толстый пласт, пока она не сталкивается с поверхностью раздела "В" у основания толстого литографического блока. При достижении поверхности раздела "В" часть энергии импульсоида проходит глубже в толщу земли по пути Р5, а остальная энергия отражается по траектории Р4 к поверхности земли, где она регистрируется как отражение R2. Обратите внимание, что отражение от поверхности раздела "В" происходит позже по времени, чем отражение от поверхности раздела "А". Точное разделение по времени между двумя событиями зависит от толщины слоя между двумя поверхностями раздела и от скорости распространения звука в этом слое, причем более толстые слои или более медленные скорости создают большее временное разделение между отражениями от вершины и основания слоя. Оценкой толщины слоя является время, которое требуется сейсмическому импульсоиду для прохождения этой толщины.

На поверхности земли регистрируют в действительности композитное (составное) отражение от толстого пласта, которое является арифметической суммой (суперпозицией) двух возвратных отражений, с учетом разделения по времени этих двух событий. Так как два отраженных импульсоида не имеют временного перекрытия, то на полученной сейсмической записи четко индицируются оба события, несущие информацию о двух дискретных (отдельных) горизонтах. (Следует иметь в виду, что разделение по времени между двумя отраженными событиями отображено на фиг.1а не в масштабе. Специалистам известно, что временное разделение в действительности в два раза превышает характеристику толщины слоя по времени).

Обратимся теперь к рассмотрению фиг.1b, на которой показано отражение от тонкого пласта. И в этом случае импульсоид источника генерируют на поверхности земли и направляют его по пути Р6, пока он не встречает поверхность раздела "С" блока горной породы. (Как и предыдущем случае, траектории волны на фигуре в действительности являются вертикальными). Как это показано на фиг.1b, когда направленное вниз сейсмическое колебание встречает поверхность раздела "С", часть его энергии отражается по траектории Р7 назад в направлении к поверхности земли, где она регистрируется как отражение R3. Остальная часть энергии продолжает движение вниз через тонкий пласт, пока не столкнется с поверхностью раздела "D". При достижении поверхности раздела "D" часть энергии импульсоида проходит глубже в толщу земли по траектории Р10, в то время как остальная часть его энергии отражается по пути Р9 назад к поверхности земли, где она регистрируется как отражение R4.

И в этом случае отражение от поверхности раздела "D" происходит позже по времени, чем отражение от поверхности раздела "С", однако разделение по времени между двумя отражениями в случае тонкого пласта меньше, потому что меньше расстояние, которое должна пробежать волна перед ее отражением от поверхности раздела "D". В действительности разделение по времени между двумя отражениями настолько мало, что возвратные (идущие к поверхности земли) импульсоиды перекрываются. Так как и в этом случае композитное отражение от тонкого слоя является арифметической суммой двух возвратных отражений, то зарегистрированный в действительности сигнал является событием, которое не четко отображает отражение от вершины и основания блока, поэтому его интерпретация является достаточно сложной. Указанное неопределенное композитное отраженное событие является примером типичной проблемы тонкого пласта.

Нет необходимости говорить о том, что толщина разведанного пласта нижних горизонтов имеет существенное экономическое значение для разведчика нефтяной компании, потому что, при прочих равных условиях, чем больше толщина литографического блока, тем больше объем углеводородов, которые потенциально он может содержать. Принимая во внимание важность точного определения толщины слоя, нет ничего удивительного в том, что предложено множество подходов для решения проблемы тонкого пласта.

Первым подходом, который применяется почти повсеместно, является укорочение длины сейсмического импульсоида, так как более длинные импульсоиды обычно обеспечивают худшее разрешение, чем короткие. В ходе обработки данных фаза записанного сейсмического импульсоида часто может быть укорочена драматическим образом за счет применения хорошо известной техники обработки сигнала. Например, специалистам хорошо известно, что обычное прогнозируемое обратное преобразование свертки может быть использовано для очистки спектра импульсоида. Аналогично, известная техника обработки импульсоида, в том числе обратное преобразование свертки сигнатуры источника, а также ряд других подходов, могут быть альтернативно применены в попытке достижения аналогичного конечного результата, а именно, получения более компактной формы колебания. Несмотря на то, что любой из указанных видов обработки может привести к драматическим изменениям характера сейсмического сечения и может существенно укоротить длину импульсоида, часто приходится применять дополнительные операции обработки сигнала.

Даже самые лучшие виды обработки сигнала в конечном счете только откладывают неизбежное: вне зависимости от того, насколько компактен импульсоид, всегда найдутся представляющие экономический интерес слои горной породы, которые слишком тонкие для этого импульсоида, чтобы он мог их определить надлежащим образом. Поэтому применяется другой широкий подход, который направлен скорее на анализ характера композитного отражения. Этот подход основан на наблюдении, что даже в том случае, когда имеется только единственное композитное отражение и толщина слоя не может быть непосредственно определена, все еще может быть получена информация при помощи записанных сейсмических данных, которая косвенно может быть использована для оценки действительной толщины литографического блока.

Например, на фиг.4а показана знакомая "сжатая" сейсмическая модель, на которой толщина представляющего интерес стратиграфического блока (причем эта толщина измерена по времени пробега импульсоида) уменьшается до полного исчезновения (то есть "сжимается") на левом конце чертежа. На фиг.4b приведен набор полученных математически синтетических сейсмограмм, вычисленных по этой модели, которые иллюстрируют освобожденную от шумов свертку сейсмического импульсоида, с поверхностями раздела, которые охватывают указанный слой. Обратите внимание на то, что на самом правом краю фиг.4b, композитный сигнал, записанный по первой трассе, показывает, что рефлектор четко ограничен отрицательным отражением у вершины блока и положительным отражением у его основания. При перемещении влево по фиг.4b индивидуальные отражения у вершины и основания начинают сливаться в единое композитное отражение и исчезают при стремлении толщины интервала к нулю. Обратите однако внимание на то, что характер композитного отражения все еще продолжает изменяться даже после дегенерации событий в единственное отражение. Таким образом, хотя и имеется мало прямых визуальных свидетельств того, что отражение возникло от двух поверхностей раздела, изменения в отражениях при уменьшении толщины подсказывают, что в них содержится информация, которая связана с толщиной тонкого пласта.

Пионерская работа Уидесса в 1973 году (Widess. "Насколько тонок тонкий пласт? ", Геофизика, т. 38, стр. 1176 - 1180) обосновала популярный подход к анализу тонкого пласта, при котором используют калибровочные кривые, которые получают с использованием как амплитуды пик-впадина композитного отраженного от тонкого пласта события, так и разделения по времени пик-впадина, что позволяет получить оценку ориентировочной толщины "тонкого" слоя. (См. также публикацию Neidell and Poggiagliomi, "Стратиграфические модели и их интерпретация - геофизические принципы и технологии", в сборнике "Применения сейсмической стратиграфии для разведки углеводородов", A. A. P.G. Memoir 26, 1977). Необходимой операцией в процессе калибровки является установление амплитуды "настройки" для рассматриваемого отражения от тонкого пласта, причем эту амплитуду настройки получают при такой толщине слоя, при которой возникает максимальная конструктивная интерференция между отражениями от вершины и основания блока. По крайней мере в теории, ширина настройки зависит только от доминирующей длины волны импульсоида λ и равняется λ/2, когда коэффициенты отражения от вершины и основания блока имеют одинаковые знаки, и равняется λ/4, когда коэффициенты отражения имеют противоположные знаки.

По той причине, что подходы калибрационного типа являются гибкими, они с успехом используются при самых разных направлениях разведки. Однако эти основанные на амплитуде и времени калибрационные методы сильно зависят от тщательности проведения сейсмической обработки для установки точной фазы импульсоида и для контроля относительных амплитуд при переходе от одной сейсмической трассы к другой. Однако специалисты в сейсмической обработке знают, насколько трудно получить сейсмическое сечение, в котором везде поддерживаются относительные амплитуды. Кроме того, описанный выше и основанный на калибровке метод не годится для исследования отражений от тонкого пласта при широкой 3-D съемке; этот метод лучше всего работает при его применении для изолированного рефлектора на единственной сейсмической линии. Достаточно сложной задачей является выработка калибровочной кривой для единичной линии; но намного сложнее найти калибровочную кривую, которая подходит для всей решетки 3-D сейсмических данных.

В связи с изложенным, как это хорошо известно в области сейсмической обработки и сейсмической интерпретации, существует необходимость в создании способа, лишенного указанных выше проблем, позволяющего извлекать полезную информацию относительно тонкого пласта из полученных обычным образом сейсмических данных. Кроме того, этот способ также должен преимущественно обеспечивать атрибуты для последующего стратиграфического и структурного анализа. Следует признать, как это сделали авторы настоящего изобретения, что существует реальная потребность в создании способа обработки сейсмических данных, который учитывает и позволяет разрешить описанные выше проблемы.

Перед тем, как приступить к описанию настоящего изобретения, следует однако отметить, что последующее описание, данное со ссылкой на сопроводительные чертежи, приведено только в качестве примера (или преимущественных вариантов осуществления изобретения) и не имеет ограничительного характера. Специалисты в данной области, которых касается настоящее изобретение, могут применить настоящее изобретение в других формах, которые не выходят однако за рамки приложенной формулы изобретения. Наконец, несмотря на то, что раскрытое здесь изобретение иллюстрируется со ссылкой на различные аспекты модели свертки, изложенные далее методы не основаны ни на какой частной модели записанной сейсмической трассы и работают одинаковым образом хорошо при существенных отклонениях от стандартной модели свертки.

В соответствии с настоящим изобретением раскрыто новое средство использования дискретного преобразования Фурье для отображения и картографирования тонких пластов и других боковых разрывов (нарушений сплошности) горной породы для обычных 2-D и 3-D сейсмических данных. Более конкретно, настоящее изобретение мотивировано тем наблюдением, что отражение от тонкого пласта имеет характеристическое выражение в области частот, которое несет информацию о толщине пласта; гомогенный тонкий пласт вводит периодическую последовательность отметок (зарубок) в амплитудный спектр композитного отражения, причем эти отметки раздвинуты на расстояние, которое инверсно пропорционально временной (измеренной за счет замера времени пробега импульсоида) толщине тонкого пласта. Кроме того, если коэффициенты преобразования Фурье получены надлежащим образом, то это характеристическое выражение может быть использовано интерпретатором для отслеживания отражений тонкого пласта в 3-D объеме и для оценки толщины и протяженного тонкого пласта в такой степени, которая ранее была недостижима. В более общем виде, раскрытый здесь способ может быть применен для обнаружения и идентификации вертикальных и боковых разрывов в локальной массе горной породы. Кроме того, полезность способа в соответствии с настоящим изобретением усиливается за счет применения нового способа очистки частотной области, который подчеркивает геологическую информацию, присутствующую в спектре. Наконец, настоящее изобретение направлено также на обнаружение сейсмических атрибутов, которые могут коррелировать. с представляющими интерес структурными и стратиграфическими характеристиками нижних горизонтов, что дает возможность получения количественных величин, которые могут быть нанесены на карту разведчиками и использованы для прогнозирования наличия углеводородов в нижних горизонтах или другого накопления минералов.

В качестве общего основания в соответствии с настоящим изобретением преимущественно используется относительно короткое дискретное преобразование Фурье для определения частотных компонентов сейсмической трассы. Как известно специалистам, вычисление преобразования Фурье для временных серий, даже если они имеют исключительно действительные значения, приводит к получению комплексных коэффициентов преобразования Фурье в виде "А+Bi", где "i" отображает "мнимое" число или квадратный корень минус единицы. Кроме того, хорошо известно, что выражение "А+Bi" может быть записано в виде:
A+Bi = re^-θ
где

θ = tan^-1(B/A).
Выражение "θ" известно как фазовый угол (или просто как "фаза") комплексной величины А+Bi, выражение "г" как амплитуда, а выражение |A+Bi| как модуль, именуемое также абсолютным значением. Частотный спектр получают из коэффициентов преобразования Фурье путем вычисления комплексного значения каждого коэффициента преобразования. Кроме того, цифровое значение ("размер") каждого коэффициента в частотном спектре пропорционально мощности этой частоты в исходных данных. Наконец, после применения преобразования Фурье к некоторым определенным временным сериям, получают результирующие серии комплексных коэффициентов в частотной области, в то время как не преобразованные данные лежат во временной области.

Настоящее изобретение основано на том общем наблюдении, что частотный спектр, вычисленный при помощи преобразования Фурье для всей трассы, имеет тенденцию походить на спектр импульсоида источника, в то время как спектры более коротких окон имеют тенденцию отображения подстилающей геологической информации. Это происходит потому, что длинные окна анализа заключают в себе большие геологические вариации, которые образуют с течением времени "белую" (или случайную и некоррелированную) отражательную функцию, которая имеет "плоский" спектр амплитуды. Поэтому форма частотного спектра, вычисленного из полной сейсмической трассы, в большой степени зависит от частотного содержания импульсоида источника (См., например, Главу 2. 2. 1. в публикации "Обработка сейсмических данных", Ozdogan Yilmaz, Society of Exploration Geophysicists, 1987, включенную здесь в качестве ссылки). С другой стороны, в том случае, когда окно анализа настолько короткое, что земная отражательная функция не является белой, то тогда результирующий спектр Фурье имеет компоненты, которые зависят как от импульсоида, так и от локальной геологии. Можно сказать, что такие малые окна геологически действуют как фильтр, ослабляя спектр импульсоида источника и создавая при этом не стационарные спектры малых окон.

Упомянутые идеи отображены в общем виде на фиг.2, где показана типичная сейсмическая трасса и некоторые частотные спектры, вычисленные из нее. В верхней части фиг.2 показан частотный спектр преобразования Фурье для всей сейсмической трассы. Этот спектр имеет вид типичного импульсоида поля. Однако спектры, вычисленные для более коротких окон и показанные на фиг.2 внизу, являются не стационарными и имеют тенденцию к отображению подстилающей геологии, которая потенциально может изменяться драматическим образом в течение очень коротких интервалов.

Важность этого наблюдения для настоящего изобретения иллюстрируется фиг. 3, на которой в общем виде показаны два представительных спектра. Левый частотный спектр отображает типичный широкополосный спектр импульсоида источника. Однако правый частотный спектр отображает в общем виде выражение в частотной области для композитного отражения от тонкого пласта. В этом последнем случае геология тонкого пласта имеют тенденцию действовать как фильтр в частотной области и вносит собственный вклад в частотное содержимое отраженного импульсоида. Как это показано в общем виде на фиг.3, авторы настоящего изобретения обнаружили, что гомогенный тонкий пласт воздействует на амплитудный спектр отраженного события за счет ввода в него "отметок" (зарубок) или узких полос ослабления частот, имеющих характерный внешний вид. Гомогенный пласт представляет собой пласт с постоянной скоростью распространения сигнала и плотностью на всем его протяжении. Кроме того, расстояние между введенными таким образом отметками равно инверсной "временной толщине" тонкого пласта, причем под временной толщиной понимают промежуток времени, который требуется импульсоиду для прохождения слоя в одном направлении (что равно толщине слоя, поделенной на скорость сигнала). Таким образом, ослабленные частоты в амплитудном спектре могут быть использованы для идентификации отражения от тонкого пласта и для измерения его толщины.

Обратимся теперь к рассмотрению фиг.4, на которой полученные в предыдущем параграфе результаты распространены на анализ упрощенной 2-D геологической модели, для которой исследовано выражение частотной области для тонкого пласта. На фиг. 4а показана типичная "сжатая" отражательная функция (геологическая модель). На фиг.4с показано изображение в градациях серого амплитуд частотного спектра преобразования Фурье, вычисленных из модели. Это изображение получено путем создания временных серий в 50 положениях, размещенных с равными промежутками в объеме модели, каждое из которых имеет только два не нулевых значения: одно соответствует коэффициенту отражения у вершины слоя, а другое - коэффициенту отражения у основания слоя. Затем было произведено вычисление стандартного дискретного преобразования Фурье для временных серий, с последующим вычислением комплексной величины каждого коэффициента.

На фиг. 4с более светлые участки соответствуют большим объемам амплитудных спектров, в то время как более темные участки отображают меньшие величины. При этом "отметки" в амплитудных спектрах показаны более темными значениями на графике. Эта фиг.4с отображает, в самом буквальном смысле, преобразование Фурье для геологии, а более конкретно, характерную сигнатуру, которая наложена на импульсоид за счет этого события. Наиболее существенным в этом графике в связи с настоящим изобретением является то, что по мере уменьшения толщины модели промежуток между отметками увеличивается. Кроме того, для данной модели отметки являются периодическими, с периодом, равным временной толщине слоя. Таким образом, если указанная сигнатура, а именно, наличие периодической частоты отметок, может быть локализована в сейсмической съемке, то это является несомненным свидетельством наличия тонкого пласта.

В соответствии с первым аспектом настоящего изобретения, предлагается система для интерпретации сейсмических данных, содержащих связанные с существованием тонкого пласта события, в которой данные разлагают на серии преобразований Фурье для 2-D линий и 3-D объемов, в результате чего усиливают отображение слоев указанного тонкого пласта. В данном варианте используют окно единичного преобразования Фурье, которое изолированно применяют для того участка сейсмической трассы, который пересекает зону интереса. Этот вариант показан главным образом на фиг.5 в применении к 3-D сейсмическим данным, однако специалисты поймут, что тот же самый способ может быть преимущественно применен и для 2-D набора сейсмических трасс, чтобы получить усиление отображения отражений тонкого пласта, которые в нем содержатся.

На первом этапе получают набор пространственных, связанных друг с другом, сейсмических трасс. Эти трассы могут представлять собой, только для целей иллюстрации, одну или несколько коротких записей, монтаж сейсмических трасс с постоянным смещением, СМР монтаж сейсмических трасс, VSP съемку, двухмерную сейсмическую линию, двухмерные расположенные одна над другой сейсмические линии, выделенные из 3-D сейсмической съемки, или, что предпочтительно, 3-D участок 3-D сейсмической съемки. Более того, настоящее изобретение может быть также применено для 2-D или 3-D съемки, в которой данные транспонированы, то есть имеют "смещенные" или пространственные оси (оси "X" или "Y" для 3-D данных), которые ориентированы таким образом, что заменяют вертикальную ось или ось "времени". В более общем виде, любой 3-D объем цифровых данных может быть обработан при помощи раскрытых в соответствии с настоящим изобретением способов. С учетом изложенного, для упрощения, вертикальная ось в дальнейшем именуется осью времени, несмотря на то, что специалисты поймут, что цифровые выборки могут и не быть разделены временными блоками. Вне зависимости от выбора, настоящее изобретение наиболее эффективно при его применении для группы сейсмических трасс, которые имеют пространственную связь с некоторыми геологическими характеристиками нижних горизонтов. Вновь только в целях иллюстрации, последующее обсуждение будет проведено в терминах трасс, которые содержатся в стопке трасс при 3-D съемке, хотя может быть также использована любая набранная группа пространственно связанных сейсмических трасс.

Как это показано в общем виде на фиг.5, затем выбирают зону интереса в пределах определенного 3-D объема. Зоной интереса может быть, например, волнистая область, ограниченная двумя выделенными рефлекторами, как это показано на фиг.5. В этом случае рефлектор преимущественно уплощен или превращен в опорный уровень (то есть сделан плоским за счет сдвига по времени индивидуальных трасс вверх или вниз) до начала анализа, а также, вероятно, реконструирован палинспастически. Обычно может быть задан специфический связанный временной интервал (например, от 2200 до 2400 мс), в результате чего получают "куб" или, что более точно, "ящик" сейсмических данных в пределах 3-D объема, а именно, субобъем. Дополнительно, боковая протяженность зоны интереса может быть ограничена заданием пределов трасс "in-line" и "cross-line" (в продольном и поперечном направлениях). Возможно применение и других методов задания зоны интереса, что известно авторам настоящего изобретения.

Селекция и экстракция данных, которые соответствуют зоне интереса, известна как операция нахождения подмножества данных (фиг.5). Критерием, которым пользуются при выборе зоны интереса, является желание иметь возможно более короткую (по времени) зону. Это связано с изложенной ранее общей философией, в соответствии с которой спектры преобразования Фурье с длинным окном имеют тенденцию походить на импульсоид источника, а спектры преобразования Фурье с коротким окном имеют тенденцию содержать больше связанной с геологией информации. Следует иметь в виду, что имеется "скрытое" расширение окна, которое часто автоматически и неожиданным образом применяется к окнам преобразования Фурье, а именно, расширение размера окна до длины степени два. Это удлинение окна производится для повышения эффективности вычислений, так как окна с длительностью степени два являются кандидатами для применения алгоритма быстрого преобразование Фурье (FFT). Однако в соответствии с настоящим изобретением не используется эта широко распространенная практика, а применяется алгоритм более общего дискретного преобразования Фурье (хотя он и имеет менее эффективные вычислительные возможности), что позволяет сохранять минимальное возможное значение длительности окна анализа. Принимая во внимание вычислительную мощность современных компьютеров, имеется мало причин для того, чтобы не применять преобразование только данных в пределах зоны интереса.

Указанная на фиг.5 операция COMPUTE ("вычислить"), в применении к настоящему изобретению, содержит по меньшей мере одну операцию, а именно, вычисление дискретного преобразования Фурье для зоны интереса. Результирующие коэффициенты спектрального разложения зоны интереса затем хранят как часть выходного объема спектрального разложения (как "куб настройки") для последующего рассмотрения. Следует иметь в виду, что имеется одна трасса (то есть набор коэффициентов преобразования Фурье) в выходном объеме куба настройки для каждой сейсмической трассы, обработанной как часть входных данных. Следует также иметь в виду, что в этом преимущественном выходном построении срезы горизонтальной плоскости через объем содержат коэффициенты, соответствующие единственной общей частоте Фурье.

Опционно, операция COMPUTE может содержать дополнительные операции, которые потенциально улучшают качество выходного объема и последующего анализа. Прежде всего весовая функция может быть применена к сейсмическим данным в пределах зоны интереса ранее вычисления преобразования. Задачей весовой функции является сжатие или сглаживание данных в пределах окна Фурье анализа, в результате чего уменьшаются искажения в частотной области, которые могут возникать в окне анализа типа "вагона". Использование весовой функции ранее преобразования хорошо известно специалистам. Преимущественной весовой функцией в соответствии с настоящим изобретением является Гауссовская по форме, которая по многим причинам оптимальна для настоящего применения. С учетом изложенного следует иметь в виду, что потенциально могут быть использованы и другие весовые функции.

Кроме того, так как именно амплитудный спектр обычно представляет наибольший интерес для разведчика, то амплитудный спектр может быть вычислен из коэффициентов преобразования, после их перемещения во вспомогательную зону хранения. Альтернативно, фазовый спектр или любой другой производный атрибут может быть вычислен из коэффициентов преобразования перед их отправкой на хранение, причем эти вычисления производились авторами настоящего изобретения.

Наконец, как часть операции вычисления, индивидуальное частотное масштабирование может быть применено для каждой плоскости (то есть частоты) в выходном объеме. Как это показано в общем виде на фиг.10, авторы настоящего изобретения пришли к выводу о предпочтительности раздельного масштабирования для каждого частотного среза в выходном объеме, чтобы получить одинаковое усредненное значение перед его рассмотрением. Этот вид масштабирования является одним из видов, которые могут быть применены, однако авторы настоящего изобретения предпочитают этот метод потому, что он позволяет выделять геологическое содержание запомненных частотных спектров за счет общей информации импульсоида.

После вычисления и запоминания спектров они готовы для использования при геофизической разведке тонких пластов. Следует иметь в виду, что при последующей индикации данных важно, чтобы каждый спектр был организован и рассмотрен при таком же пространственном соотношении с другими спектрами, что и трассы, из которых они вычислены. Это означает, что присутствующие в не преобразованных данных пространственные соотношения должны быть сохранены в соотношениях коэффициентов преобразования. Преимущественный метод рассмотрения коэффициентов преобразования начинается с их формирования в пределах 3-D "объема" (куба настройки), естественно, при условии, что входные данные первоначально были взяты из 3-D объема. Однако следует иметь в виду, что вертикальная ("z") ось уже не является "временной", какой она было до преобразования, а скорее условно отображает теперь единицы измерения частоты, при запоминании коэффициентов преобразования Фурье.

На фиг. 5 показано, что последней операцией является рассмотрение куба настройки, аналогично любому виду рассмотрения обычного 3-D объема сейсмических данных. С учетом изложенного авторы настоящего изобретения пришли к выводу о том, что рассмотрение последовательных горизонтальных срезов в пределах объема коэффициентов является предпочтительным для локализации и визуализации эффектов тонкого пласта. Обратите внимание на то, что при использовании куба настройки горизонтальный срез отображает все коэффициенты, которые соответствуют единственной частоте Фурье, и поэтому является поперечным сечением постоянной частоты. Кроме того, в качестве дополнительного средства при анализе данных, которые содержатся в пределах этого объема, авторы настоящего изобретения преимущественно применяют анимацию ("оживление") серии горизонтальных видов в пределах объема. В том случае, когда зона интереса является скорее участком индивидуальной сейсмической линии, а не объема, результирующее изображение, которое является набором спектров преобразования Фурье пространственно связанных сейсмических трасс, которые индицируются в их исходном пространственном соотношении, может считаться кубом настройки, хотя технически оно может не быть "кубом" данных.

Анимация последовательных горизонтальных срезов в пределах спектрального объема является предпочтительным методом рассмотрения и анализа коэффициентов преобразования, причем указанная анимация преимущественно осуществляется на компьютерном мониторе имеющей высокую скорость рабочей станции. Как это хорошо известно специалистам, анимация в форме интерактивного панорамирования в пределах объема является быстрым и эффективным средством рассмотрения больших объемов данных. Объем данных может быть рассмотрен по горизонтальным, вертикальным или наклонным срезам, каждый из которых представляет собой единственный вид данных. Однако более важно в контексте настоящего изобретения быстрое рассмотрение последовательных горизонтальных срезов, одного за другим, при котором получают диагностическое средство для съемки большого объема данных и для идентификации в нем отражений тонкого пласта, о чем речь пойдет ниже. Следует иметь в виду, что для раскрытого метода предпочтительно иметь порядок следования срезов в терминах частоты (при ее четком нарастании или убывании), когда производят анимацию и рассмотрение указанных срезов.

В соответствии со вторым аспектом настоящего изобретения, предлагается система для обработки сейсмических данных, позволяющая усиливать сейсмические записи связанных с существованием тонкого пласта событий, в которой данные разлагают на серии преобразований Фурье для 2-D линий и 3-D объемов, за счет использования серий перекрывающихся преобразований Фурье для короткого окна, в результате чего усиливают отображение слоев указанного тонкого пласта. Этот вариант показан главным образом на фиг.6 в применении к 3-D сейсмическим данным, однако специалисты поймут, что тот же самый способ может быть преимущественно применен и для 2-D набора сейсмических трасс, чтобы усилить отображения отражений тонкого пласта, которые в нем содержатся. Как это показано на фиг.6 и как обсуждалось ранее, первый этап данного варианта предусматривает картографирование интерпретатором временных границ сейсмической зоны интереса. Как это было описано ранее, в результате картографирования можно получить куб сейсмических данных или прямоугольный элемент инивидуальной сейсмической линии.

В соответствии с настоящим изобретением не применяют преобразование Фурье с единственным окном для каждой трассы, а используют вместо этого серии преобразований Фурье с перекрывающимися короткими окнами. Длительность окна и степень перекрытия изменяют для конкретного применения, однако и в данном случае длина окна не должна быть равной степени "2", а скорее должна быть выбрана так, чтобы получить наилучшее изображение подстилающей геологии. Следует иметь в виду, что опционно к данным до проведения преобразования может быть применена весовая функция в пределах каждого короткого окна, причем, как и ранее, предпочтительной является Гауссовская весовая функция.

Как это показано на фиг.6, после проведения вычисления каждого преобразования Фурье для короткого окна, полученные из него коэффициенты хранятся изолированно внутри индивидуального куба настройки, который сохраняет связь с исходным коротким окном. Следует иметь в виду, что может существовать столько кубов настройки, сколь имеется перекрывающихся окон в анализе. Масштабирование, если оно применяется, то применяется изолированно для каждой частотной плоскости в каждом кубе настройки.

Каждый куб настройки короткого окна, полученный при помощи скользящего окна, теперь может быть проанализирован индивидуально точно также, как это было предложено ранее для первого варианта. И в этом случае каждый куб преимущественно рассматривают при помощи горизонтальных срезов или изображений постоянной частоты, в результате чего получают средство визуализации геологических изменений при изменении частоты. Кроме того, так как теперь имеется набор кубов настройки, вычисленных для различных временных точек трассы, то в действительности получают набор кубов настройки, которые перекрывают диапазон глубин нижних горизонтов.

Наконец, в соответствии с третьим аспектом настоящего изобретения, предлагается система для обработки сейсмических данных, позволяющая усиливать сейсмические записи связанных с существованием тонкого пласта событий, в которой данные разлагают на серии преобразований Фурье для 2-D линий и 3-D объемов, за счет использования преобразования Фурье для короткого окна, с последующей реорганизацией в кубы настройки с единственной частотой, в результате чего усиливают отображение слоев указанного тонкого пласта.

Как это показано в общем виде на фиг.7, первые операции в данном варианте повторяют операции предшествующих двух вариантов, а именно, данные вначале интерпретируют, а затем разбивают на подмножества. После этого из сейсмических данных в пределах зоны интереса вычисляют серии преобразований Фурье для перекрывающихся коротких окон, с опционным предшествующим преобразованию применением весовой функции или применением сжатия внутри каждого окна. Как и в предыдущем варианте, накапливают коэффициенты от каждого преобразования короткого окна. Однако в данном случае вычисленные коэффициенты преобразования Фурье не рассматривают в виде кубов настройки, а реорганизуют в кубы энергии единичной частоты, которые затем анализируют в горизонтальной или вертикальной плоскости для выделения эффектов тонкого пласта.

Более конкретно, реорганизация в соответствии с настоящим изобретением концептуально предусматривает извлечение из всех кубов настройки каждого горизонтального среза, который соответствует определенной частоте. После этого эти индивидуальные срезы с одной и той же частотой "складывают в стопку" таким образом, что самый верхний срез содержит коэффициенты, вычисленные из самого верхнего скользящего окна, следующий срез содержит коэффициенты, вычисленные из следующего за верхним скользящего окна, и т.д. Следует иметь в виду, что после реорганизации объем коэффициентов будет организован в блоки "х-у" и блок времени. Это вызвано тем, что по вертикальной оси отложено "время" скользящего окна, что и дает особый коэффициент.

Для использования информации при помощи кубов настройки с единственной частотой, образованных в предшествующей операции, сейсмический интерпретатор должен выбрать соответствующую им частоту и сейсмический объем (например, он может выбрать объем коэффициента, соответствующий 10 Гц и/или объем для 11 Гц, и т. д. ). Каждый куб постоянной частоты может быть рассмотрен в виде сверху или в виде по горизонтали, или любым иным образом, в результате чего получают средство визуализации геологических изменений в боковом направлении для определенной частоты.

Важно отметить, что, для всех упомянутых ранее вариантов, тот факт, что исходные не преобразованные трассы являются пространственно связанными, обеспечивает дополнительное преимущество. Более конкретно, хорошо известно, что коэффициенты преобразования Фурье короткого окна сами по себе достаточно зашумлены и обладают плохим частотным разрешением в сравнении с преобразованием длинного окна. Один из подходов, который использован в соответствии с настоящим изобретением для повышения надежности преобразованных данных, заключается в применении Гауссовской весовой функции к данным до их преобразования. Однако другим важным подходом в соответствии с настоящим изобретением является индикация коэффициентов в пределах объема в таком же пространственном соотношении, что и входные данные. Так как индицируемые указанным образом трассы содержат пространственно коррелированную информацию, то их индикация рядом друг с другом позволяет наблюдать визуально "сглаживание" шумов и выявлять подстилающую информацию когерентного сигнала.

Наконец, несмотря на то, что настоящее изобретение обсуждается здесь в терминах дискретного преобразования Фурье, в действительности преобразование Фурье является только одним из ряда дискретных временных преобразований данных, которые могут быть использованы совершенно аналогично. Основные операции, а именно, (1) вычисление преобразования короткого окна, (2) объединение результирующих коэффициентов в объем и (3) исследование объема для нахождения эффектов тонкого пласта, могут быть осуществлены при самых разнообразных дискретных преобразованиях данных, отличающихся от преобразования Фурье. При таких преобразованиях объемы настройки образуют за счет группирования коэффициентов, соответствующих одной и той же базовой функции. Таким образом, в случае использования в дальнейшем "куба настройки единственной частоты" речь идет не только о кубе настройки, образованном обычными коэффициентами преобразования Фурье, но и о любом другом кубе настройки, образованном коэффициентами функции на том же базисе.

Специалистам известно, что дискретное преобразование Фурье является только одним из множества дискретных линейных унитарных преобразований, которые удовлетворяют следующим требованиям: (1) они являются линейными операторами, которые (2) точно инвертируемы, и (3) их базисная функция образует ортонормальный набор. В терминах уравнения, если х(k), k=1, L, отображает временные серии, а Х (n) представляет собой ее "n-ное" преобразованное значение, n=1, L, то прямое преобразование для временных серий для этого класса преобразований может быть записано как: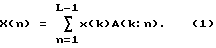

где A (k: n) отображает ядро прямого преобразования или набор базисных функций. Кроме того, имеется инверсное преобразование, которое позволяет от преобразованных значений вернуться к исходным данным:

где В (k:n) отображает ядро обратного преобразования. В соответствии с требованиями ортонормальности внутренние произведения между двумя базисными функциями должны быть равны нулю, а значение каждой базисной функции должно быть равно единице. Это требование в сжатом виде может быть выражено следующими уравнениями: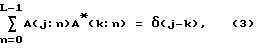


где

и A* (k: n) представляет собой комплексное сопряжение для A(k:n). Для дискретного преобразования Фурье базисные функции, которые соответствуют прямому преобразованию длины L, обычно выбирают в виде набора комплексных показательных функций:
A(k;n) = {e^-2πikn/L, k = 0,L-1} (5)
В этом случае имеется L базисных функций ( или базисных векторов), по одной базисной функции для каждого значения "n":
n=-(L/2), ..., 0, ..., (L/2-1)
Суммируя, можно сказать, что каждый коэффициент преобразования Х (n), вычисленный из окна данных, соответствует определенной базисной функции, а объем настройки образован набором всех коэффициентов преобразования, соответствующих определенной зоне интереса, которые хранятся во вспомогательной зоне хранения в таком же пространственном соотношении, что и трассы, из которых было рассчитано каждое окно.

В качестве другого специфического примера можно указать, что дискретное преобразование Уелша (Walsh) может быть использовано вместо преобразования Фурье, причем коэффициенты Уелша аналогичным образом группируются, индицируются и анализируются. Аналогично описанному ранее, преобразование Уелша может быть вычислено в пределах перекрывающихся серий скользящих окон, а полученные при этом коэффициенты могут быть организованы и накоплены в кубах настройки. В данном случае расчетные коэффициенты преобразования отображают не частоту, а величину, именуемую "секвенцией". При этом кубы настройки "единичной секвенции" могут быть образованы из коэффициентов преобразования Уелша совершенно аналогично тому, как это происходит при образовании кубов настройки Фурье. В дальнейшем эти кубы настройки " одной и той же частоты" (или в более общем виде, одной и той же базисной функции) будут именоваться кубами настройки единственной ортонормальной базисной функции.

Наконец, несмотря на то, что дискретное преобразование Фурье является преобразованием, которое характеризуется набором ортонормальных базисных функций, применение не тривиальной весовой функции к базисным функциям ранее вычисления преобразования разрушает их ортонормальность. В соответствии с принятой теорией, весовую функцию, которая применена в пределах окна, следует рассматривать как примененную к базисным функциям, а не к данным, в результате чего целостность подстилающих данных сохраняется. Однако базисные функции, которые были ортогональными до применения весовой функции, обычно не являются таковыми после ее применения. С учетом изложенного, вне зависимости от того, применена весовая функция к данным или к базисным функциям, конечный результат вычисления после преобразования будет одним и тем же.

Одной из возможностей исключения незначительной теоретической дилеммы, которая возникает при использовании весовой функции с дискретным ортонормальным преобразованием, является выбор такой комбинации ортонормальное преобразование/вес, которая не так подвержена указанному воздействию. Например, локальное косинусное (или локальное синусное) преобразование является дискретным ортонормальным преобразованием, для которого выбирают весовую функцию в виде гладкого сужения специальной формы, при этом ортонормальность базисных функций сохраняется за счет некоторой потери разрешающей способности по частоте. Кроме того, логическое обоснование локального косинусного/синусного преобразования служит естественным теоретическим мостиком к области общих преобразований импульсоида.

На фиг.1 приведена схема, которая иллюстрирует в общем виде проблему тонкого пласта.

На фиг. 2 показана типичная сейсмическая трасса и проведено сравнение спектров длинного и короткого окон, вычисленных из нее.

На фиг.3 показано в общем виде, как выражается в частотной области воздействие сейсмического импульсоида на тонкий пласт.

На фиг. 4 показана простая сейсмическая сжатая модель, отклик свертки и отображение в частотной области указанного отклика свертки.

На фиг.5 приведена схема, которая отображает общий подход в соответствии с предпочтительным вариантом настоящего изобретения.

На фиг. 6 схематично показано, как предпочтительный вариант настоящего изобретения может быть использован при разведке.

На фиг. 7 схематично показан другой предпочтительный вариант настоящего изобретения.

На фиг. 8 показана схема, которая иллюстрирует предпочтительный вариант настоящего изобретения.

На фиг. 9 показана схема, которая описывает появление тонкого пласта в ходе анимации срезов постоянной частоты.

На фиг.10 иллюстрируется общий подход, который используется для масштабирования срезов постоянной частоты, чтобы выявить геологическое содержание преобразованных данных.

На фиг. 11 показана схема, которая иллюстрирует другой предпочтительный вариант настоящего изобретения.

В соответствии с настоящим изобретением предлагается способ обработки сейсмических данных с использованием дискретного преобразования Фурье, за счет которого повышается полезность указанного преобразования для обнаружения тонких пластов.

В соответствии с первым аспектом настоящего изобретения предлагается способ усиления и рассмотрения эффектов тонкого пласта с использованием дискретного преобразования Фурье, причем вычисляют единичное преобразование Фурье для окна, перекрывающего зону интереса, а полученные при этом коэффициенты индицируют в дальнейшем иным образом. Положим, как это показано на фиг. 5, что х(k.j.nt) отображает 3-D объем сейсмических данных, где k=1,k и j= 1, j отображают показатели, идентифицирующие специфическую трассу в пределах заданного 3-D объема. В качестве примера можно указать, что эти показатели могут быть номерами продольного и поперечного положений, хотя возможны и иные схемы расположения. Переменная "nt" использована для отображения временного (или глубинного) положения в пределах каждой сейсмической трассы, nt=0, NTOT - 1 - полное число выборок в каждой индивидуальной трассе. Временное разделение между последовательными значениями х(k.j.nt) ( то есть частота выборок) обозначено как Δt, причем Δt обычно измеряют в миллисекундах. Поэтому каждая трасса в 3-D объеме содержит запись (NTOT) ^*Δt миллисекунд данных, причем первую выборку обычно берут при "нулевом " времени. С учетом изложенного можно понять, что сейсмические данные, которые подходят для анализа в соответствии с настоящим изобретением, не упорядочены в терминах "времени". Например, выборки сейсмических данных, обработанные программой миграции глубины, хранят (сохраняют) в пределах сейсмической трассы в порядке нарастающей глубины Δz. Однако настоящее изобретение полностью применимо и к таким выборкам данных. Поэтому в последующем описании понятие Δt (и "время") будут использоваться в широком смысле, как относящиеся к разделению между последовательными цифровыми выборками, вне зависимости от возможной формы измерения разделения.

В качестве первой операции разведчик или сейсмический интерпретатор выбирает зону интереса в пределах 3-D объема. Это может быть осуществлено, например, путем преобразования в цифровую форму временных пиков сейсмических событий, или в таблице оцифровки или, что чаще, на сейсмической компьютерной рабочей станции. При обнаружении события разведчик пытается найти такую же характеристику рефлектора (например, пик, впадину, момент пересечения нулевой линии и т.п.) для каждой сейсмической трассы; конечной задачей является выработка компьютерного файла, который содержит информацию о времени и локализации поверхности, которая позволяет отслеживать событие в пределах 2-D сечения или 3-D объема. Как это показано на фиг.11, при наличии такой информации может быть разработана компьютерная программа для считывания пиков и нахождения зоны интереса для любой трассы в пределах объема данных и/или для осуществления способа в соответствии с настоящим изобретением. Эта программа может быть введена в компьютер, например, при помощи магнитного диска, ленты, оптического диска или CD-ROM.

Альтернативно, интерпретатор может просто задать постоянное время начала и окончания, которые ограничивают представляющее интерес событие в пределах всего объема, в результате создавая представляющий интерес "куб", причем понятие "куб" использовано здесь в родовом смысле для отображения 3-D суб-объема исходного 3-D объема разведки. В качестве примера в последующем обсуждении предполагается, что был извлечен 3-D суб-объем, хотя можно понять, что такая же техника, которая обсуждается далее, может быть адаптирована и для не постоянного по времени окна. Вновь в качестве примера использованной техники предполагается, что временная зона интереса после экстракции простирается от первой выборки в 3-D суб-объеме до последней выборки с номером "N". Аналогично предполагается также, что зона интереса присутствует на каждой трассе в суб-объеме, хотя известно, что часто зона интереса занимает только часть 3-D объема.

После выбора зоны интереса следующей операцией является выбор длины окна "L" преобразования Фурье. В самом общем виде длина преобразования не должна быть длиннее, чем это совершенно необходимо для окружения (захвата) зоны интереса. Обычно длину преобразования Фурье выбирают из соображений эффективности вычислений и обычно ограничивают целым числом степени 2 (например, 32, 64, 128 и т.д.), что позволяет использовать эффективный алгоритм вычисления FFT, а не менее эффективное преобразование Фурье со смешанными корнями или намного менее эффективное дискретное преобразование Фурье. Однако в контексте настоящего изобретения не рекомендуется увеличивать выбранную длину окна, как это делается обычно, до целого числа степени 2; вместо этого следует использовать дискретное преобразование Фурье. С учетом изложенного, следует понимать, что в дальнейшем изложении при любом упоминании дискретного преобразования Фурье при возможности может быть произведено вычисление FFT. В противном случае может быть выбрано общее дискретное преобразование Фурье или некоторый его вариант со смешанными корнями, если выбранная длина окна не является целым числом степени 2.

Перед началом преобразований Фурье следует создать вспомогательный объем хранения для вычисленных коэффициентов Фурье. Объем хранения L компьютерных слов должен быть задан для запоминания вычисленных коэффициентов преобразования для каждой трассы, причем еще больший объем хранения требуется в случае запоминания значений сейсмических данных или преобразованных результатов с двойной (или более высокой) точностью. Для объяснения можно сказать, что преобразование Фурье серий в реальном масштабе времени длины L требует запоминания L/2 значений комплексных данных, для каждого из которых обычно требуются два компьютерных слова хранения. (В действительности только [(L/2)-1] значений комплексных данных, а не L, так как серии в реальном масштабе коэффициентов преобразования Фурье, которые соответствуют положительным и отрицательным частотам, непосредственно связаны друг с другом и образуют комплексные сопряженные пары. Кроме того, существует два действительных значения: коэффициент при нуле ("dc") герц и коэффициент при частоте Найквиста, оба из которых могут быть запомнены в виде единственной комплексной величины. Наконец, если L представляет собой нечетное целое число, то число значений данных равно [(L+1)/2]. Если всего имеется (J умножить на К) сейсмических трасс в зоне (кубе) интереса, то требуется как минимум общий объем вспомогательного хранения, измеренный в компьютерных словах, равный произведению L, J и К. Положим, что решетка A(k.j.nt) отображает зону вспомогательного хранения для данного варианта осуществления изобретения.

При первой операции вычисления, как это показано на фиг.8, значения данных в пределах зоны интереса экстрагируют из входной трассы х (j, k, nt), взятой в суб-объеме:
у(nl)=х(j,k, nt), nl=0, L-1
и применяют опционно весовую функцию:
у(nl)=у(nl)w (nl), nl=0, L=1,
в которой решетка у (nl) представляет собой зону временного хранения. (Следует иметь в виду, что в данном варианте длина окна анализа равна длине зоны хранения). Весовая функция w (t) или окно данных, как некоторые его именуют, может принимать различные формы. Некоторыми из самых популярных окон данных являются окна Хамминга, Ханнинга, Парцена, Бартлетта и Блекмана. Каждая из указанных функций окна имеет определенные преимущества и недостатки. Однако авторы настоящего изобретения нашли, что оптимальным для данного применения по многим причинам является использование Гауссовского окна. Гауссовская весовая функция может быть определена следующими соотношениями:
w(nl) = σ_τe^{-(nl-1/2)2/σ}, nl = 0, L-1 (6)
где

Как правило, весовая функция должна быть в ее диапазоне действительной функцией, не равной нулю.

После применения весовой функции производят вычисление дискретного преобразования Фурье в соответствии со следующим стандартным выражением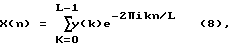

n=-(L/2), ..., 0, ..., (L/2-1),
где Х (n) отображает комплексный коэффициент преобразования Фурье при частоте f(n), которая зависит от длины окна L. Известно, что при помощи преобразования Фурье получают коэффициенты, которые дают оценку спектральной амплитуды при следующих частотах Фурье: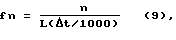

n=-(L/2), ..., 0, ..., (L/2-1)
Следует иметь в виду, что номинальная частота выборок Δt может и не соответствовать той частоте выборок, при которой получены данные в поле. Например, широко распространенной практикой является повторная выборка сейсмической трассы с более высокой частотой выборок для экономии памяти, когда имеется мало полезной информации при самых высоких частотах записи. С другой стороны, для одной из сейсмических трасс может быть произведена выборка при малой частоте выборок, в сочетании с другими линиями, определенными с более высокой частотой выборок. В любом случае, номинальная частота выборок данных может не точно отражать ее истинную спектральную ширину полосы. При простой модификации предыдущего выражения может быть получена контингенция:
f_n=(n/L)F_max, n=-(L/2), ..., 0, ..., (L/2-1)
в которой F_mах представляет собой самую высокую частоту, которая имеется в данных.

Так как сейсмическая трасса представляет собой "действительную" функцию (то есть не мнимую), то ее преобразование Фурье является симметричным и коэффициенты Фурье соответствуют положительным и отрицательным частотам, связанным следующими выражениями:
RE[X(f_n)]=RE[X(f-_n)]
и
IM[X(f_n)]=-IM[X(f-_n)]
где RE [Z] представляет собой функцию, которая экстрагирует действительную часть комплексной величины z, a IM [Z] представляет собой функцию, которая экстрагирует ее мнимую часть. В соответствии с указанными выражениями в каждом окне преобразования Фурье получают только значения (L/2-1). Поэтому из соображений специфичности в последующем обсуждении будут рассматриваться только положительные частоты, хотя понятно, что аналогичные результаты могут быть получены и при использовании только отрицательных частот.

Следующая операция процесса предусматривает размещение вычисленных значений комплексной частоты в решетке вспомогательного хранения. Эти трассы заполняют вычисленными значениями комплексной частоты следующим образом:
А (j, k, i)=X(i), i=0, L/2
где "j" и "k" совпадают с показателями, соответствующими исходной трассе данных. На практике решетка А (j, k, i) может не храниться целиком одновременно в RAM (в запоминающем устройстве с произвольной выборкой ЗУПВ), а может быть локализована, полностью или частично, на магнитной ленте или диске, на оптическом диске или на другом средстве хранения. Кроме того, так как данный вариант преимущественной индикации тонкого пласта требует использования скорее частотного спектра, а не комплексных значений, то удобно одновременно производить вычисление комплексной величины при помещении каждого коэффициента во вспомогательную решетку хранения:
A(j,k,i) = |X(i)|, i = 0, L/2.
Однако во многих случаях комплексные коэффициенты необходимы и полезны, как это показано на фиг.8; тогда комплексные коэффициенты преимущественно хранят во вспомогательной решетке хранения.

Описанную процедуру повторяют для каждой трассы в заданном суб-объеме, заполняя вспомогательную решетку хранения коэффициентами преобразования, подготовленными для их рассмотрения разведчиком. Однако до рассмотрения результатов данные вновь преимущественно масштабируют иным образом, в результате чего выделяют геологическую информацию в коэффициентах преобразования по отношению к вкладу импульсоида. Общая методика, которая применяется при указанном масштабировании частотной области, иллюстрируется фиг.10. Раскрытый здесь метод масштабирования предназначен для выравнивания средней спектральной амплитуды в каждом частотном срезе, в результате чего возникает тенденция получения очищенного спектра импульсоида. Как это показано на фиг. 8, пусть Т (j, k, i) представляет собой вспомогательную решетку хранения, в которой может храниться целиком куб настройки. Для данного частотного среза i может быть вычислена средняя спектральная амплитуда:

Спектральную величину вычисляют потому, что Т (j, k, i) является потенциально комплексным значением. В следующей операции значения в этом конкретном частотном срезе устанавливают таким образом, что их среднее значение равно некоторому заданному пользователем постоянному значению, представленному переменной AVG, в соответствии с выражением:
Т (j, k, i)-[AVG/TAVG] (j, k, i), j=1, J, k=1, K
в котором первичную запись используют для указания того, что решетка T(j, k, i) была модифицирована. На практике для AVG устанавливают некоторое специфическое цифровое значение, например, 100. Эту операцию масштабирования повторяют изолированно для каждого частотного среза i=0, L/2 в объеме куба настройки. По завершении этой операции каждый срез имеет одну и ту же усредненную амплитуду, при этом достигается некоторый спектральный баланс. Следует иметь в виду, что данная форма масштабирования с единственной частотой представляет собой только один из многих алгоритмов масштабирования, которые в соответствии с настоящим изобретением могут быть применены к данным кубов настройки. В качестве примера можно указать, что вместо вычисления арифметического среднего для элементов в срезе, может быть использована также другая оценка центральной тенденции или любой другой статистики (например, медиана, мода, геометрическое среднее, дисперсия и т.п.). В качестве другого примера можно указать, что вместо установки среднего значения в каждом частотном срезе, равным некоторой одной и той же постоянной, каждый срез может иметь различные постоянные средние значения, в результате чего усиливаются некоторые частоты в спектре и подавляются другие.

Если проинвертировать данные куба настройки после масштабирования назад во временную область, используя стандартное обратное преобразование Фурье, то можно получить спектрально сбалансированную версию оригинальных входных сейсмических трасс. Пусть Х (к) отображает масштабированный набор коэффициентов преобразования, полученных при помощи раскрытого ранее процесса, взятых из местоположения (j, k) в пределах масштабированной решетки куба настройки. Тогда может быть получена спектрально очищенная версия входных данных в соответствии со следующим выражением: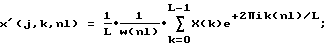

n1=0; L-1 (11)
в котором х' (j, k, nl) отображает модифицированную теперь (спектрально сбалансированную) версию входных данных х (j, k, nl). Делитель w (nl) использован для удаления эффектов весовой функции, которая была применена до осуществления преобразования. Этот элемент может быть опущен, если вес не применялся при прямом преобразовании Фурье.

Однако вместо инвертирования масштабированного куба настройки, он преимущественно может быть использован как средство разведки для обнаружения тонких пластов. После обработки всех трасс и их помещения во вспомогательную зону хранения, горизонтальные (имеющие постоянную частоту) амплитудные срезы Si (j, k), соответствующие i-той частоте, могут быть экстрагированы из А (j, k, i) для последующего рассмотрения и/или анимации:
Si(j,k) = |A(j,k,i)|
Когда производят анимацию (быстрое последовательное рассмотрение) указанных трасс, то тонкие пласты могут быть опознаны как такие события, которые последовательно чередуются между высокими и низкими амплитудными значениями. Кроме того, для многих видов тонких пластов существуют характерные картины перемещающихся отметок, которые четко говорят о том, что событие вызвано тонким пластом. Следует иметь в виду, что для раскрытого здесь способа предпочтительно производить, в случае анимации и рассмотрения срезов, их упорядочение по частоте (при ее четком нарастании или убывании).

На фиг. 9 показан источник этой диагностической подвижной картины. На фиг. 9а показана геологическая модель тонкого пласта линзового типа, а на фиг. 9b приведено стилизованное преобразование Фурье для этой модели, где нанесены только отметки. Как указывалось ранее, отметки являются периодическими, с периодом, который равен обратной временной толщине модели у этой точки. Теперь представьте модель фиг.9а, как отображающую 2-D поперечное сечение 3-D (дискового типа) радиально симметричной модели, а фиг.9b - как аналогично радиально симметричный набор одномерных преобразований Фурье указанной 3-D модели. Если плоскость постоянной частоты, именуемую Plane 1, пропустить через объем указанным образом, то в виде сверху в этой плоскости можно обнаружить кольцевую область малой амплитуды, соответствующую первой отметке. Плоскость Plane 2 проходит через две отметки и дает две кольцевых области малой амплитуды. Наконец, плоскость Plane 3 проходит через три отметки и дает три кольцевых области малой амплитуды. Если теперь рассматривать эти срезы при их быстром чередовании в порядке нарастания частоты, то появляется визуальное впечатление картины "бычьего глаза", в которой кольца перемещаются наружу от центра. Эта картина перемещающихся отметок является характерной (диагностической) для тонких пластов.

Если тонкий пласт не является кольцевым, то наблюдают другую картину. Вместо концентрических кругов появляется серия отметок, которые уходят от более толстых зон в направлении тонких зон. Например, пусть модель фиг.9 представляет собой поперечное сечение канала потока линзовой формы. При последовательном рассмотрении частотных срезов будет наблюдаться по всей длине канала картина перемещающихся наружу отметок, которые движутся от центра канала к его периферии.

Следует иметь в виду, что если тонкий пласт не является гомогенным, например, если он содержит ступенчатое нарастание или уменьшение скорости, то он может не давать характерную картину "отметок" гомогенного тонкого пласта, а скорее создавать некоторое выражение в другой частотной области. В таких случаях предпочтительным методом идентификации характеристического отклика является создание модели события и вычисление преобразования Фурье, как это было ранее показано на фиг.4b. При наличии такой информации разведчик может затем произвести анализ анимированного куба настройки для моментов предсказуемого отклика.

Картина отметок является не только качественной индикацией гомогенного тонкого пласта, но и дает также количественную оценку события тонкого пласта. Обратите внимание на то, что на фиг.9 отметки ограничены в боковом направлении самыми внешними краями модели. Поэтому при панорамировании стопки частотных срезов и при определении самых внешних пределов перемещения отметок может быть получена количественная оценка события тонкого пласта.

Описанное является удивительным визуальным эффектом, который легко может наблюдаться в имеющихся объемах сейсмических данных. Так как типичное событие не тонкого пласта имеет некоторый определенный и медленно изменяющийся амплитудный спектр, то отклик тонкого пласта существенно отличается от него и легко может быть обнаружен. Следует иметь в виду, что в случае вычисления единственного окна для полной зоны интереса, действительное положение по времени (то есть глубина) тонкого пласта в пределах зоны интереса не имеет особого значения. При любом расположении тонкого пласта в пределах временной зоны интереса, спектр для этого окна будет содержать характерную картину подвижных отметок. Специалисты легко поймут, что перемещение местоположения события во времени не изменяет амплитудный спектр. Это перемещение скорее вводит изменение фазы, которое не видно при рассмотрении и вычислении амплитудного спектра. Вместо индикации амплитудных спектров в анимированном виде сверху в данном варианте можно использовать также любое число других атрибутов, вычисленных из комплексных значений, хранящихся в кубе настройки. Например, фаза комплексных коэффициентов преобразования дает другое средство идентификации событий тонкого пласта и, в более общем случае, боковых разрывов массы горной породы. Фазовый куб настройки может быть вычислен следующим образом: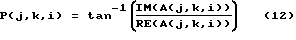

где Р (j, k, i) содержит фазовую часть комплексных коэффициентов преобразования Фурье для каждой точки в исходном кубе настройки. Специалисты давно используют фазовые сечения для выделения нечетких отражателей, причем фазовые сечения помогают выделять неразрывности в сейсмических данных. Однако в соответствии с настоящим изобретением боковые разрывы в спектральном фазовом отклике несут информацию о боковой вариабельности локальной массы горной породы, первым примером которой является усечение тонких пластов. При рассмотрении в анимированном виде сверху фазовые величины вблизи боковой кромки являются относительно "нестабильными", с отличающейся от нормальной первой производной. Поэтому границы тонких пластов и, в более общем случае, боковые разрывы в массе горной породы (например, сбросы, трещины, несоответствия и т.п.) будут иметь фазу, которая контрастирует с окружающими фазовыми значениями, и поэтому относительно просто могут быть идентифицированы. Это поведение может быть использовано изолировано для идентификации боковых границ или совместно с кубом настройки амплитудного спектра для нахождения вариабельности локальной массы горной породы.

Наконец, в соответствии с настоящим изобретением предусмотрено, что раскрытая в нем технология куба настройки может обеспечить дополнительное понимание отраженных сейсмических данных. Может быть произведен вывод на индикацию и исследование куба настройки (который содержит фазовые или амплитудные данные), чтобы получить эмпирические корреляции с подстилающими содержаниями горной породы, со свойствами горной породы, с подстилающей структурой или стратиграфией слоя. Альтернативно, может быть произведена дополнительная манипуляция значений преобразования Фурье, хранящихся в кубе настройки, для выработки новых сейсмических атрибутов, которые могут быть полезны при установках положения разведки. В качестве примера можно указать, что атрибуты, которые могут быть вычислены из значений куба настройки, включают в себя среднюю спектральную амплитуду или фазу, а также множество других атрибутов. Важность этого аспекта настоящего изобретения лучше всего может быть показана следующим образом. В области сейсмической интерпретации известно, что пространственные вариации признака сейсмического рефлектора часто могут быть эмпирически скоррелированы с изменениями литологии резервуара или с содержанием жидкости. Так как точный физический механизм, который приводит к возникновению этой вариации характера отражения точно неизвестен, то принятой практикой является вычисление интерпретаторами множества сейсмических атрибутов, с последующим их нанесением на график или карту и поиском атрибута, который имеет некоторое предсказуемое значение. Атрибуты, полученные при помощи вычислений из куба настройки, отображают локализованные анализы свойств отражателя (при их вычислении из короткого окна) и как таковые потенциально обладают существенной важностью в продвижении интерпретации.

В соответствии со вторым аспектом настоящего изобретения, предлагается способ обработки сейсмических данных, позволяющий усиливать эффекты, связанные с существованием тонкого пласта, при использовании дискретного преобразования Фурье, в соответствии с которым производят вычисление преобразований Фурье серии скользящих коротких окон, расположенных в окне, перекрывающем зону интереса, и после этого по-новому выводимых на индикацию. Этот способ показан в общем виде на фиг.6 и более детально на фиг.8. Концептуально, данный вариант настоящего изобретения может быть представлен как создающий серии кубов настройки описанного выше типа, по одному кубу настройки для каждого положения окна преобразования Фурье, заданному пользователем.

И в этом случае х (k, j, n) отображает 3-D объем сейсмических данных, a "L" - длину выбранного преобразования Фурье короткого окна. В соответствии с данным вариантом "L" обычно выбирают существенно короче, чем длина зоны интереса N. Как и раньше, длину окна преобразования Фурье следует выбирать не на основании вычислительной эффективности, а скорее так, чтобы получить лучшее отображение определенных классов событий тонкого пласта в нижних горизонтах. В качестве примера можно указать, что разумной стартовой длиной преобразования является такая длина, которая достаточна для перекрытия "самого толстого" тонкого пласта в зоне интереса. Следует иметь в виду, что может возникать необходимость увеличения этой минимальной длины в таких обстоятельствах, например, когда форма волны особенно не компактна. В этом последнем случае минимальная длина окна может быть увеличена до длины импульсоида, измеренной в выборках.

Переменное целое число NS используют для отображения инкремента в выборках, который применяют для последующих окон. Например, если NS равно 1, то преобразование Фурье короткого окна вычисляют в каждом возможном стартовом положении в зоне интереса, с последующими скользящими окнами, которые отличаются только на одну выборку. Если NS равно 2, то последовательные окна имеют одинаковые величины данных за исключением двух, и вычисление преобразований будет производиться в каждом другом (втором) стартовом положении в зоне интереса.

Коэффициенты преобразования Фурье в соответствии с данным вариантом вычисляют следующим образом. Начиная с вершины зоны интереса для определенной сейсмической трассы производят вычисление серий преобразований Фурье скользящего окна длиной L для каждого возможного положения в пределах указанной зоны интереса. Как это показано на фиг.8, переменное целое число "М" принимают в качестве переменной счетчика, которая отображает номер текущего скользящего окна. Первоначально устанавливают М, равным единице, для указания положения первого скользящего окна.

Теперь для трассы локализации (j, k) в пределах суб-объема х (j, k, i) сейсмических данных, могут быть экстрагированы и перемещены для кратковременного хранения данные для М-ного скользящего окна, причем это скользящее окно начинается при номере выборки (М-1)*(NS:
у(n1)=х (j, k, (М-1)*NS+nl), nl=0, L-1
После этого данные преобразуются при помощи преобразования Фурье. Как это показано ранее, до проведения преобразования весовая функция опционно может быть применена к данным. Для фиксированного значения М применение предыдущих вычислений к каждой трассе в суб-объеме дает куб настройки для этого определенного положения окна. Аналогично, при задании инкремента для М и при пропускании полного объема данных через алгоритм, получают другой полный куб настройки, который вычислен для положения окна, начинающегося на NS выборок ниже предыдущего окна.

Теперь коэффициенты преобразования Фурье могут быть размещены во вспомогательной зоне хранения и могут храниться до тех пор, пока они не выводятся на индикацию. Выработанное выше представление может быть слегка изменено для учета того факта, что для каждой индивидуальной трассы могут быть применены несколько окон. Пусть А_M (j, k, i) отображает объем накопленных коэффициентов преобразования Фурье, взятых из всех трасс в зоне интереса для М-ного вычисленного положения окна. Следует иметь в виду, что объем памяти, необходимый для хранения этой решетки, существенно возрастает. Теперь полный объем памяти зависит от числа скользящих окон, вычисленных для каждой трассы, например, NW, и должен составлять по меньшей мере число слов хранения, равное произведению NW L, J и К:
Объем памяти =(NW) (L) (J) (К)
Как упоминалось ранее, возможно не полностью хранить А_M (j, k, i) в RAM, а хранить его частично в RAM, а частично на диске.

Используя введенное ранее представление о решетке и вновь предполагая, что в X(i) хранится преобразование Фурье взвешенных данных, можно указать, что коэффициенты преобразования для М-ного окна трассы (i, j) хранятся в местоположении решетки:
A_М(j, k, i)=X(i),i-0, L/2
И в этом случае индивидуальные частотные срезы в пределах различных кубов настройки, хранящихся в А_М (j, k, i), преимущественно масштабируют при помощи показанной на фиг.8 процедуры, ранее их исследования для поиска артефактов тонкого пласта. В каждом случае горизонтальные частотные срезы масштабируют индивидуально, при этом их среднее значение равняется некоторой постоянной, в результате чего спектры очищаются.

После обработки сейсмических трасс в зоне интереса, может быть индивидуально произведено исследование каждого куба настройки для поиска эффектов тонкого пласта. Как и ранее, эффекты тонкого пласта могут быть идентифицированы в амплитудных спектрах за счет рассмотрения серий горизонтальных срезов, соответствующих различным частотам. Более того, это может быть осуществлено изолированно для куба настойки, соответствующего положению каждого окна, в результате чего получают некоторую общую индикацию относительно временной и пространственной протяженности особого события тонкого пласта.

В соответствии с третьим аспектом настоящего изобретения, предлагается способ усиления эффектов тонкого пласта, при использовании дискретного преобразования Фурье аналогично описанному выше для второго аспекта, но при наличии дополнительной операции организации коэффициентов преобразования Фурье в объемы единичной частоты, ранее вывода на индикацию и проведения анализа. Это способ в общем виде иллюстрируется фиг.7. Как это раскрыто ранее для второго аспекта настоящего изобретения, вспомогательная решетка хранения А_М (j, k, i) заполняется коэффициентами преобразования Фурье, которые преимущественно подвергаются масштабированию.

Пусть F (j, k, m) отображает объем единичной частоты, экстрагированный из А_M (j, k, i). Всего будет L/2+1 различных объемов ((L+1/2) значений, если L нечетное), по одному для каждой частоты Фурье, полученной за счет преобразования длиной "L". Объем, который соответствует "i"-той частоте Фурье, экстрагируют из А_М (j, k, i) следующим образом:
F(j, k, m)=A_М (j, k, i), m=1, NW, j=1, J, k=1, К
В действительности решетку F (j, k, m) концептуально можно считать образованной горизонтальными срезами в каждом из объемов окна скольжения, сложенных стопкой в порядке нарастания номера короткого окна "M".

Преимущество указанной организации данных для целей опознания тонкого пласта заключается в том, что при этом получают средство, при помощи которого может быть найдено положение события тонкого пласта во времени и в пространстве. Ранее указывалось, что временное положение тонкого пласта в пределах зоны интереса не воздействует на его отклик: тонкие пласты вблизи вершины зоны интереса и тонкие пласты вблизи основания зоны интереса дают одинаковые характеристические амплитудные спектры. Это выгодно для идентификации тонких пластов, однако является недостатком при определении их потенциала накопления углеводородов, так как более высокие поднятия пласта обычно являются предпочтительными.

Однако в соответствии с данным вариантом настоящего изобретения объем срезов одной и той же частоты имеет "время" по его вертикальной оси, а переменная М является номером, который ориентировочно соответствует расстоянию вниз от сейсмической трассы. Указанная организация дополнительно дает возможность установления ориентировочной временной длительности события тонкого пласта.

Для примера положим, что данное событие тонкого пласта имеет отметку 10 Гц в частотной области. При этом каждое короткое окно преобразования Фурье, которое содержит этот тонкий пласт, будет иметь такую же отметку. Если производить анализ объема срезов 10 Гц, то получим набор срезов, который содержит эту отметку. Таким образом, при рассмотрении последовательных срезов в объеме постоянной частоты имеется возможность локализации во времени представляющего интерес рефлектора. Что более важно, если известно, что определенная отметка появляется, например, при 10 Гц, то куб настройки 10 Гц может быть анимирован и рассмотрен как средство определения боковой протяженности тонкого пласта, при этом наблюдаемые в этом частотном кубе настройки границы отметок определяют границы пласта.

В предшествующем описании речь шла об операциях, проводимых над обычными сейсмическими данными. Однако специалисты легко поймут, что настоящее изобретение может быть преимущественно применено и в других областях для локализации не углеводородов, а других минералов в нижних горизонтах. В качестве примера можно указать, что описанный здесь подход может быть использован для обработки и/или анализа многокомпонентных сейсмических данных, данных поперечной волны, магнито-теллурических данных, данных разведки поперечного шурфа, полной формы волны акустического каротажа, а также основанного на модели цифровой имитации любого из указанных явлений. Короче говоря, способ в соответствии с настоящим изобретением в потенциале может быть применен для любых единичных геофизических временных серий, однако преимущественно его применяют к набору пространственно связанных временных серий, которые содержат события тонкого пласта. Специалисты легко поймут, что использованный в тексте описания термин "сейсмическая трасса" использован в родовом смысле и применим в общем для любых геофизических временных серий.

Несмотря на то, что были описаны предпочтительные варианты осуществления изобретения, совершенно ясно, что в них специалистами в данной области могут быть внесены изменения и дополнения, которые не выходят однако за рамки приведенной далее формулы изобретения и соответствуют его сущности.

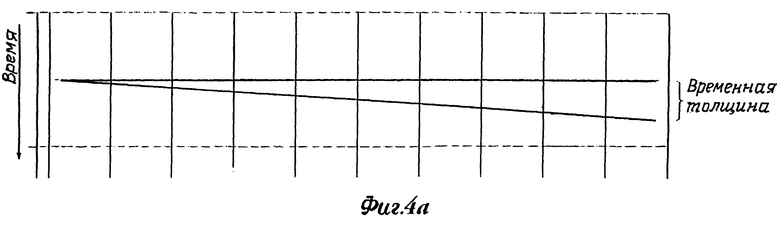
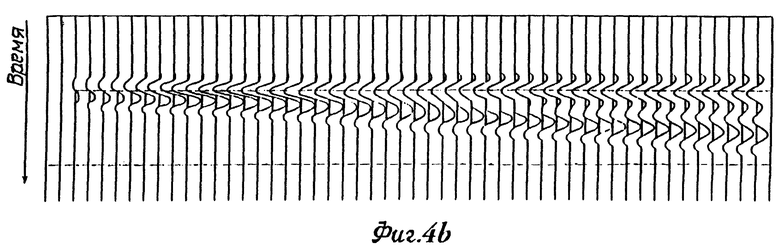
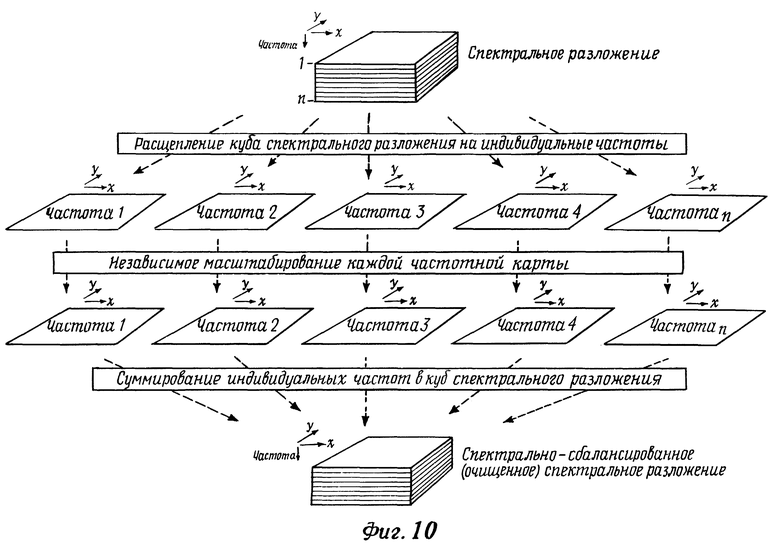
Изобретение направлено главным образом на создание способа обработки сейсмических данных, позволяющего добиться улучшения количественной оценки и визуализации малых эффектов настройки сейсмического тонкого пласта и других боковых нарушений сплошности горной породы. Отражение от тонкого пласта имеет характерное выражение в частотной области, которое может дать информацию о толщине пласта. Это отражение содержит периодическую последовательность отметок в его амплитудном спектре, причем указанные отметки раздвинуты на расстояние, которое обратно пропорционально временной толщине тонкого пласта. Кроме того, это характерное выражение может быть использовано для отслеживания отражений тонкого пласта в пределах 3-D объема и для оценки их толщин и боковой протяженности. Сущность изобретения: получают отображение набора сейсмических трасс, распределенных по заданному объему земли, выбирают часть указанного объема. Преобразуют по меньшей мере один из участков сейсмических трасс с использованием дискретного ортонормального преобразования, которое дает множество коэффициентов преобразования. Полученные коэффициенты организуют в куб настройки, который может быть использован совместно с компьютером для идентификации локализации углеводородов. Может быть получена карта для разведки нефти и газа. 6 c. и 25 з.п. ф-лы, 16 ил.

1. Способ обработки сейсмических данных, отличающийся тем, что он включает в себя следующие операции: (а) получение отображения набора сейсмических трасс, распределенных в пределах заданного объема толщи земли, причем указанные сейсмические трассы содержат цифровые выборки, которые являются характерными по меньшей мере по времени, положению и амплитуде; (б) выбор части указанного объема и содержащихся в нем сейсмических трасс для ограничения зоны интереса в пределах указанного объема; (в) преобразование по меньшей мере одного из участков указанных сейсмических трасс в пределах указанной зоны интереса с использованием дискретного ортонормального преобразования, причем указанное дискретное ортонормальное преобразование дает множество коэффициентов преобразования; (г) организация указанных коэффициентов преобразования в куб настройки, используемый при сейсмической разведке, причем указанный куб настройки может быть использован совместно с компьютером для идентификации потенциальной локализации углеводородов. 2. Способ по п.1, отличающийся тем, что он дополнительно включает в себя следующую операцию: (д) вывод на индикацию по меньшей мере одного из участков указанного куба настройки. 3. Способ по п.1, отличающийся тем, что он дополнительно включает в себя следующую операцию: (е) запоминание указанных коэффициентов преобразования в форме, удобной для индикации в виде куба настройки. 4. Способ по п.1, отличающийся тем, что указанное дискретное ортонормальное преобразование в операции (в) характеризуется наличием множества ортонормальных базисных функций и применено к окну, которое содержит указанные цифровые выборки, для получения множества коэффициентов преобразования, объединенных с указанными ортонормальными базисными функциями. 5. Способ по п.1, отличающийся тем, что указанное дискретное ортонормальное преобразование представляет собой преобразование Фурье. 6. Способ по п. 4, отличающийся тем, что весовую функцию применяют в пределах указанного окна, содержащего цифровые выборки, ранее применения преобразования за счет указанного дискретного ортонормального преобразования. 7. Способ по п.6, отличающийся тем, что указанная весовая функция представляет собой Гауссовскую весовую функцию. 8. Способ по п.4, отличающийся тем, что указанное дискретное ортонормальное преобразование в операции (в) характеризуется наличием множества ортонормальных базисных функций и применено к окну, которое содержит указанные цифровые выборки, для получения множества коэффициентов преобразования, объединенных с указанными ортонормальными базисными функциями, а операция (г) включает в себя операцию масштабирования указанных коэффициентов преобразования в пределах указанного куба настройки. 9. Способ по п.8, отличающийся тем, что операция масштабирования указанных коэффициентов преобразования в пределах указанного куба настройки включает в себя следующие операции: (i) выбор базисной функции из указанных в операции (в); (ii) выбор по меньшей мере двух коэффициентов преобразования, соответствующих базисной функции операции (i); (iii) вычисление комплексной величины всех коэффициентов преобразования, выбранных в операции (ii); (iv) вычисление статистической величины из всех величин коэффициентов преобразования, вычисленных в операции (iii); (v) вычисление величины масштабирования из статистической величины; (vi) умножение указанных коэффициентов преобразования операции (ii) на указанную величину масштабирования. 10. Способ по п.9, отличающийся тем, что указанная статистическая величина представляет собой арифметическое среднее всех вычисленных указанным образом величин коэффициентов преобразования. 11. Способ по п.2, отличающийся тем, что операция (д) включает в себя операцию записи визуально различимых изображений, отображающих указанный куб настройки на главным образом плоской среде. 12. Способ по п.11, отличающийся тем, что он дополнительно включает в себя операцию использования указанных визуально различимых изображений для идентификации структурных и осадочных характеристик нижних горизонтов, обычно связанных с захватом и накоплением углеводородов. 13. Способ по п. 12, отличающийся тем, что он дополнительно включает операцию вывода на индикацию по меньшей мере одного из участков указанного куба настройки, при которой осуществляют запись визуально различаемых изображений, отображающих указанный куб настройки на главным образом плоской среде и операцию использования этих изображений для идентификации структурных и осадочных характеристик нижних горизонтов, обычно связанных с захватом и накоплением углеводородов, которые содержатся по меньшей мере в одном тонком пласте. 14. Способ по п.3, отличающийся тем, что операция (д) включает в себя операцию запоминания по меньшей мере одного из участков указанного куба настройки в запоминающем устройстве с произвольной выборкой компьютера. 15. Способ по п.2, отличающийся тем, что операция (д) включает в себя следующие операции: (i) выбор ортонормальной базисной функции; (ii) выбор по меньшей мере двух коэффициентов преобразования, соответствующих указанной ортонормальной базисной функции: (iii) определение положения для каждого выбранного коэффициента преобразования; (iv) вывод на индикацию указанных коэффициентов преобразования в местоположениях, представительных для указанных положений. 16. Способ по п.15, отличающийся тем, что операции (i) - (iv) повторяют для множества ортонормальных базисных функций. 17. Способ обработки сейсмических данных с использованием цифрового компьютера, при котором производится обработка пространственно связанных сейсмических трасс в цифровой форме, причем трассы характеризуются по меньшей мере временем, положением и амплитудой, причем цифровой компьютер запрограммирован для выбора части указанного набора пространственно связанных сейсмических трасс для выделения зоны интереса, отличающийся тем, что он включает в себя следующие операции: (а) преобразование по меньшей мере одного из участков указанных сейсмических трасс в пределах зоны интереса с использованием преобразования Фурье, которое характеризуется множеством ортонормальных базисных функций и которое применяют к окну, содержащему указанные цифровые выборки, для получения множества коэффициентов преобразования, объединенных с указанными ортонормальными базисными функциями; (б) организация указанных коэффициентов преобразования в объем спектрального разложения; (в) применение масштабирующего значения к указанным коэффициентам преобразования для получения масштабированного объема разложения, причем этот масштабированный объем разложения является представительным для среднего объема, полученного при помощи следующих операций: (i) выбор базисной функции из функций, полученных в операции (а); (ii) выбор по меньшей мере двух коэффициентов преобразования, соответствующих базисной функции по п.(в) (i); (iii) вычисление комплексных величин для всех коэффициентов преобразования, выбранных по п.(в) (ii), и (iv) вычисление среднего значения из всех величин коэффициентов преобразования по п.(в) (iii); (г) вывод на индикацию указанного масштабированного объема разложения. 18. Способ обработки сейсмических данных, отличающийся тем, что он включает в себя следующие операции: (а) получение отображения набора пространственно связанных сейсмических трасс, распределенных в пределах заданного объема толщи земли, причем указанные сейсмические трассы содержат цифровые выборки, которые характеризуются по меньшей мере временем, положением и амплитудой; (б) выбор части указанного объема и указанных пространственно связанных сейсмических трасс, содержащихся в нем, для ограничения зоны интереса в пределах указанного объема; (в) очерчивание окна в пределах указанной зоны интереса, причем это окно имеет номер стартовой выборки и включает в себя множество цифровых выборок; (г) преобразование по меньшей мере одного из участков указанных пространственно связанных сейсмических трасс в пределах зоны интереса с использованием дискретного ортонормального преобразования, которое характеризуется множеством ортонормальных базисных функций и которое применяют к указанному окну, содержащему указанные цифровые выборки по п.(в), для получения множества коэффициентов преобразования, объединенных с указанными ортонормальными базисными функциями; (д) организация указанных коэффициентов преобразования в куб настройки, причем указанный куб настройки и коэффициенты преобразования в нем объединены с указанным номером стартовой выборки указанного окна по п.(в); и (е) вывод на индикацию указанного куба настройки, причем операции (в), (г) и (е) повторяют по меньшей мере для одного или нескольких заданных окон, для получения множества кубов настройки. 19. Способ по п.18, отличающийся тем, что операция (е) включает в себя следующие операции: (i) выбор ортонормальной базисной функции; (ii) выбор куба настройки из указанного множества кубов настройки; (iii) экстрагирование из указанного выбранного куба настройки множества коэффициентов преобразования, объединенных с указанной выбранной ортонормальной базисной функцией; (iv) повтор операций (ii) и (iii) по меньшей мере еще для одного выбранного куба настройки; (v) организация указанных экстрагированных коэффициентов преобразования в куб настройки единственной ортонормальной базисной функции; (vi) вывод на индикацию указанного куба настройки единственной ортонормальной базисной функции. 20. Способ по п. 19, отличающийся тем, что операцию (v) осуществляют путем упорядочения указанных экстрагированных коэффициентов преобразования при помощи указанного номера стартовой выборки, объединенного с указанным заданным окном. 21. Способ по п.19, отличающийся тем, что указанное дискретное ортонормальное преобразование представляет собой преобразование Фурье, причем операцию (v) осуществляют путем организации указанных экстрагированных коэффициентов преобразования в куб настройки единственной частоты. 22. Способ по п. 18, отличающийся тем, что в пределах указанного окна применяют весовую функцию, содержащую цифровые выборки, ранее осуществления преобразования при помощи указанного дискретного ортонормального преобразования. 23. Способ по п.22, отличающийся тем, что указанная весовая функция представляет собой Гауссовскую весовую функцию. 24. Способ по п. 18, отличающийся тем, что операция (е) дополнительно включает в себя операцию записи визуально различимых изображений, отображающих один или несколько из указанных кубов настройки на главным образом плоской среде. 25. Способ по п.24, отличающийся тем, что он дополнительно включает в себя операцию использования указанных визуально различимых изображений для идентификации структурных и осадочных характеристик нижних горизонтов, обычно связанных с захватом и накоплением углеводородов. 26. Способ обработки сейсмических данных, отличающийся тем, что он включает в себя следующие операции: (а) обращение при помощи компьютера к набору данных, который включает в себя сейсмические трассы, распределенные в пределах заданного объема толщи земли, причем указанные сейсмические трассы содержат цифровые выборки, которые характеризуются по меньшей мере временем, положением и амплитудой; (б) выбор множества пространственно связанных сейсмических трасс; (в) выбор зоны интереса в пределах указанного выбранного множества пространственно связанных сейсмических трасс; (г) преобразование по меньшей мере одного из участков указанных пространственно связанных сейсмических трасс в пределах зоны интереса с использованием дискретного ортонормального преобразования и получение множества коэффициентов преобразования; (д) организация указанных коэффициентов преобразования в куб настройки; (е) вычисление множества значений сейсмических атрибутов из указанных коэффициентов преобразования куба настройки; и (ж) вывод на индикацию указанных значений сейсмических атрибутов в местоположениях, отображающих положения в пределax указанного куба настройки. 27. Карта для разведки нефти и газа, полученная способом по п.26, предназначенная для использования при разведке углеводородов, когда сейсмические данные, содержащие отраженную сейсмическую энергию, записывают как функцию времени в пределах заданного объема толщи земли, для получения множества пространственно связанных сейсмических трасс, содержащих выборки, которые характеризуются по меньшей мере временем, положением и амплитудой, отличающаяся тем, что указанная карта содержит: (а) главным образом плоскую среду для записи на ней визуально различимых изображений; и (б) по меньшей мере одно визуально различимое изображение на указанной главным образом плоской среде, причем указанное визуально различимое изображение отображает указанные вычисленные значения сейсмического атрибута. 28. Способ выработки сейсмических атрибутов для использования при разведке углеводородов, отличающийся тем, что он включает в себя следующие операции: (а) получение отображения набора сейсмических трасс, распределенных в пределах заданного объема толщи земли, причем указанные сейсмические трассы содержат выборки, которые характеризуются по меньшей мере временем, положением и амплитудой; (б) выбор части указанного объема и указанных сейсмических трасс, содержащихся в нем, для ограничения зоны интереса в пределах указанного объема; (в) преобразование по меньшей мере одного из участков указанных сейсмических трасс в пределах указанной зоны интереса с использованием очень короткой временной функции дискретного ортонормального преобразования и получение коэффициентов преобразования; (г) организация указанных коэффициентов преобразования в куб настройки; (д) вычисление множества сейсмических атрибутов из указанных коэффициентов преобразования в указанном кубе настройки. 29. Способ по п.28, отличающийся тем, что он дополнительно включает в себя следующие операции: (е) масштабирование указанных коэффициентов преобразования в пределах указанного куба настройки; и (ж) инвертирование указанного куба настройки с использованием инверсной функции дискретного ортонормального преобразования для получения отфильтрованной версии указанного преобразованного участка указанных пространственно связанных сейсмических трасс. 30. Способ по п.29, отличающийся тем, что указанная функция преобразования по п. (в) содержит множество ортонормальных базисных функций, причем операция (е) включает в себя следующие операции: (i) выбор одной из базисных функции и по меньшей мере двух соответствующих ей коэффициентов преобразования; (ii) вычисление комплексной величины указанных выбранных коэффициентов преобразования; (iii) вычисление статистического значения из указанной комплексной величины; (iv) вычисление значения масштабирования из указанного статистического значения; (v) применение указанного значения масштабирования к указанным выбранным коэффициентам преобразования. 31. Способ по п.30, отличающийся тем, что указанное статистическое значение является арифметическим средним указанных комплексных величин коэффициентов преобразования.