Предлагаемое изобретение относится к области измерительной техники, в частности к области измерения параметров модуляции сигналов.
Известно устройство для измерения глубины амплитудной модуляции [А.с. СССР №347694, МПК G 01 R 29/06, опубл. 1972], содержащее аттенюатор, усилители, логарифмирующие цепочки, детектор, фильтры нижних частот и вычислительный блок с индикатором. В этом устройстве осуществляется выделение напряжений, пропорциональных максимальной и минимальной амплитудам AM-сигнала, и вычисление глубины AM с помощью функциональных преобразователей (логарифмирующие цепочки и переворачивающее устройство, состоящее из логарифмирующей цепочки и дифференцирующего усилителя). При использовании устройства возникают трудности выделения огибающей AM-сигнала с малыми искажениями. Применение функциональных преобразователей обуславливает сложность схемы и низкую точность измерения.
Наиболее близким по технической сущности к заявленному устройству является выбранный в качестве прототипа “Цифровой измеритель глубины модуляции” [А.с. СССР №424089, МПК G 01 R 29/06, опубл. 1974], содержащий входное устройство, блок синхронизации, преобразователь аналог-код, цифровое сравнивающее устройство, два реверсных счетчика, блок переноса, цифровой логометр, индикатор и блок управления. Амплитудно-модулированный сигнал частоты с выхода входного устройства поступает на входы блока синхронизации и преобразователя аналог-код. Блок синхронизации выделяет моменты времени, соответствующие максимальному значению напряжения несущей частоты и запускает в эти моменты преобразователь аналог-код. Последний преобразует мгновенные значения напряжения несущей частоты в цифровые коды, поступающие на схему сравнения, где производится их поочередное сравнивание, а выделенные максимальные и минимальные значения напряжения (AMAX и AMIN) записываются соответственно в регистры максимального и минимального значений. Регистры соединены соответственно со входами вычислительного блока, который осуществляет расчет глубины амплитудной модуляции по формуле:
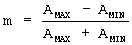 .
.
Результат вычисления выводится на цифровом индикаторе. Устройство лишено методической погрешности, связанной с нелинейностью AM-детектора, т.к. расчет глубины AM ведется по мгновенным значениям ВЧ-сигнала. Однако устройство имеет сложную схему синхронизации и не может измерять девиацию частоты.
Целью предлагаемого изобретения является расширение функциональных возможностей, а именно реализация одновременного измерения глубины амплитудной модуляции и девиации частоты сложных модулированных сигналов.
Поставленная цель достигается тем, что в цифровой измеритель модуляции, содержащий индикатор, преобразователь аналог-код и входное устройство, первый вход которого является входом измерителя, а выход соединен с первым входом преобразователя аналог-код, введены преобразователь частота-код и вычислитель, причем вход преобразователя частота-код соединен с выходом входного устройства, а выход преобразователя частота-код соединен со вторым входом вычислителя, первый вход которого соединен с выходом преобразователя аналог-код, первый выход вычислителя соединен с индикатором, второй выход вычислителя соединен со вторым входом преобразователя аналог-код, а третий выход вычислителя соединен со вторым входом входного устройства.
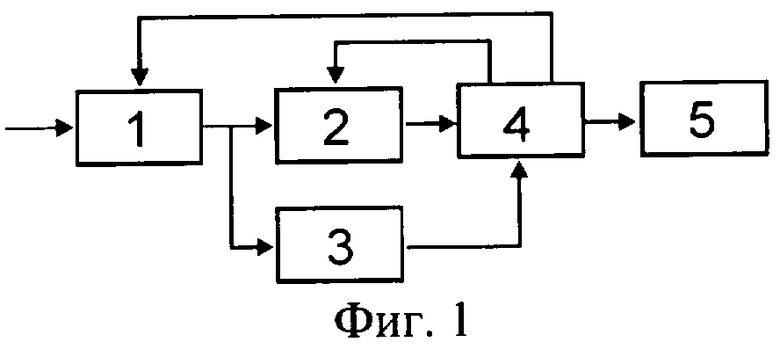
Структурная схема приведена на фиг.1.
Цифровой измеритель модуляции содержит входное устройство 1, преобразователь 2 аналог-код, преобразователь 3 частота-код, вычислитель 4 и индикатор 5. Причем выход входного устройства 1 соединен со входом преобразователя 3 частота-код и первым входом преобразователя 2 аналог-код, выход которого соединен с первым входом вычислителя 4, первый выход вычислителя соединен с индикатором, второй выход соединен со вторым входом преобразователя 2 аналог-код, а третий выход со вторым входом входного устройства 1, выход преобразователя 3 частота-код соединен со вторым входом вычислителя.
Входное устройство 1 представляет собой согласованный усилитель-аттенюатор с регулируемым коэффициентом передачи. При необходимости во входном устройстве 1 может осуществляться перенос частоты в область более низких частот. Преобразователь 2 аналог-код представляет собой аналого-цифровой преобразователь (АЦП), работающий в режиме стробирования. Преобразователь 3 частота-код формирует код несущей частоты входного сигнала. Вычислитель 4 задает частоту дескритизации АЦП, управляет коэффициентом усиления входного устройства, а также обрабатывает дискретизированный массив данных с выхода АЦП. Вычислитель 4 имеет стандартную конфигурацию и связи, характерные для любых микропроцессорных устройств. Он содержит процессор, оперативное и постоянное запоминающие устройства, устройства ввода-вывода. Индикатор 5 отображает измеренные значения глубины AM и девиации частоты.
Принцип работы измерителя основан на обработке дискретизированного массива данных при помощи преобразования Гильберта.
Преобразование Гильберта позволяет найти для сигнала X(t), ортогональный ему сигнал X1(t). Используя эти сигналы, можно найти огибающую (мгновенную амплитуду) и мгновенную частоту сигнала X(t) по формулам:

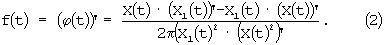
Таким образом, необходимость выделения моментов времени, соответствующих максимальному значению напряжения несущей, отсутствует, соответственно становится не нужным и синхронизирующее устройство.
При стробировании с частотой дискретизации fд несущая частота сигнала fВЧ на выходе преобразователя определяется выражением: fСП=fВЧ-nfд, где n=ent(fBЧ/fд) - целое число. После дискретизации с указанными условиями минимальная и максимальная частоты в спектре AM-сигнала будут определяться в соответствии с выражениями:
fMIN=fСП-FМАХ, fMAX=fСП+fМАХ,
где fMAX максимальная частота модулирующего колебания. Если при дискретизации в окно преобразования попадает не целое число периодов несущей частоты и/или частоты модулирующего сигнала, то происходит растекание спектра (явление Гиббса). Для уменьшения этого эффекта целесообразно применение временных окон.
Спектр сигнала на выходе АЦП должен быть расположен в диапазонах частот: от 0 до fд/2 или от fд/2 до fд-fд/N, однако из-за явления Гиббса происходит расширение спектра. Чтобы учесть это явление, необходимо уменьшить снизу и сверху границы допустимых частот на величину bfд/N, где N - количество дискретизированных точек в массиве данных. Тогда скорректированные диапазоны частот будут от bfд/N до fд/2-bfд/N или от fд/2+bfд/N до fд-(b+1)fд/N. Коэффициент b можно выбрать, например, равным 7.
Требования к точности преобразователя частота-код не высокие, так как значение несущей частоты используется только для изменения частоты дискретизации таким образом, чтобы спектр сигнала на выходе АЦП лежал в допустимых границах. Погрешность преобразователя частота-код, если она велика, может быть учтена путем дополнительного сужения границ допустимых частот, тогда скорректированные диапазоны частот будут от bfд/N+Δ fВЧ до fд/2-bfд/N-Δ fВЧ или от fд/2+bfд/N+Δ fВЧ до fд-(b+1)fд/N-Δ fВЧ, где Δ fВЧ - абсолютная погрешность измерения частоты.
Аналогично, путем сужения границ допустимых частот можно учесть погрешность установки частоты дискретизации. Тогда для b=7 получим условия работоспособности:
а) от 7fд/N+Δ fВЧ+nΔ fд до fд/2-7fд/N-Δ fВЧ-nΔ fд;
б) от fд/2+7fд/N+Δ fВЧ+nΔ fд до fд-8fд/N-Δ fВЧ-nΔ fд,
где Δ fд - абсолютная погрешность установки частоты дискретизации.
Пример проверки правильности выбора частоты дискретизации:
Пусть fВЧ=100,5 МГц, FMAX=10 кГц, fд=955,5 кГц, АМ-сигнал, N=512 (количество точек в массиве данных). Тогда n=ent(fВЧ/fд)=105,
fСП=fВЧ-nfд=172,5 кГц, fMIN=fСП-FMAX=162,5 кГц, fMAX=fСП+FMAX=182,5 кГц, Если Δ fд/fд=Δ fВЧ/fВЧ=10-5, тогда Δ fВЧ=fВЧ·10-5=1005 Гц, Δ fд=fд·10-5=9,555 Гц.
Проверим выполнение условия работоспособности:
a) fMIN>7fд/N+Δ fВЧ+nΔ fд≈15.1 кГц и fMAX<fд/2-7fд/N-Δ fВЧ-nΔ fд≈462.7 кГц;
б) fMIN>fд/2+7fд/N+Δ fВЧ+nΔ fд≈492.9 кГц и fMAX<8fд/N-Δ fВЧ-nΔ fд≈938.6 кГц. Выполняется первое условие, что говорит о правильном выборе частоты дискретизации. Если ни одно условие не выполняется, то необходимо изменить частоту дискретизации.
Рассмотрим алгоритм работы вычислителя по шагам:
1. Измерение несущей частоты входного сигнала fВЧ.
2. Перебор допустимых для АЦП частот дискретизации и выбор такой fд, чтобы выполнялось одно из условий:
а) bfд/N+Δ fВЧ+nΔ fд до fд/2-bfд/N-Δ fВЧ-nΔ fд;
б) fд/2+bfд/N+Δ fВЧ+nΔ fд до fд-bfд/N-Δ fВЧ-nΔ fд.
3. Дискретизация сигнала с частотой fд и получение массива X[iTд], где i∈ [0, N-1] - номер элемента в массиве мгновенных значений X[iТд].
4. Нахождение максимального значения из массива AMAX=МАХ(X[iТд]). Если P1>AMAX/MАХацп>P2, то изменение коэффициента передачи входного устройства не производится. Здесь: P1 и Р2 - максимальный и минимальный коэффициент использования динамического диапазона АЦП (можно выбрать P1=0.9, Р2=0.5); МАХацп - предел шкалы АЦП. При необходимости изменения коэффициента передачи повторяются 3-й и 4-й шаги алгоритма. Правильный выбор коэффициента передачи обеспечит более полное использование рабочего диапазона АЦП, что будет способствовать высокой точности оцифровки.
5. Наложение на дискретизированный массив временного окна Хемминга и получение массива Xw[iТд].
6. Нахождение преобразования Гильберта от массива Xw[iТд].
Преобразование Гильберта находится через прямое (FFT) и обратное (RFT) преобразование Фурье:
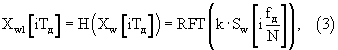
где 
k=-j если i=0,1,2,3,... N/2;
k=j если i=N/2+1, N/2+2, N/2+3,... N-1.
7. Нахождение огибающей
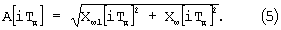
Для восстановления амплитуды A[iTд] каждый элемент массива необходимо разделить на функцию (массив коэффициентов) окна Хемминга. Из-за краевых эффектов, которые возникают при попадании в окно преобразования нецелого количества периодов входного сигнала, около 25% от начала и конца функции A[iTд] целесообразно отбросить.
8. Для симметричной формы огибающей A[iTд] коэффициент амплитудной модуляции находим по формуле 
где АMAX=МАХ(A[iТд]); AMIN=MIN(A[iTд]).
9. Для нахождения частотной модуляции необходимо вычислить производную от массивов Хw, Хw1. Производную можно найти, используя прямое и обратное преобразование Фурье:
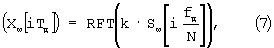
где 
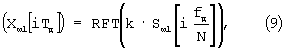
где 
Здесь k=jω i если i=0,1,2,3,... N/2;
k=-jω (N-i) если i=N/2+1, N/2+2, N/2+3,... N-1.
10. После нахождения производных закон изменения частоты fСП будет описываться формулой:
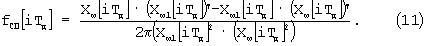
Из-за краевых эффектов, которые возникают при попадании в окно преобразования нецелого количества периодов входного сигнала, около 25% от начала и конца массива fСП[iTд] целесообразно отбросить.
11. Для симметричной формы модулирующего сигнала девиация частоты

где fСПMAX=MAX(fСП[iTд]), fСПMIN -MIN(fСП[iTд]).
Устройство работает следующим образом. Сигнал поступает на входное устройство 1, представляющее собой согласованный усилитель-аттенюатор с регулируемым коэффициентом передачи. Затем сигнал одновременно поступает на преобразователь 2 аналог-код и преобразователь 3 частота-код. В зависимости от уровня сигнала, оцифрованного преобразователем 2 аналог-код, вычислитель 4 задает требуемый коэффициент передачи входного устройства. В зависимости от значения несущей частоты вычислитель 4 задает частоту дискретизации (стробирования) fд таким образом, чтобы сигнал на выходе преобразователя аналог-код находился в требуемом диапазоне частот. Массив оцифрованных данных Х[iТд] с выхода преобразователя 2 аналог-код поступает на вычислитель 4, который реализует представленный выше алгоритм работы. Найденные значения девиации частоты и глубины модуляции отображаются на индикаторе 5.
Если полоса сигнала НЧ много меньше fд/2, то целесообразно отфильтровать демодулированный сигнал при помощи цифрового фильтра. Для этого нужно добавить процедуру цифровой фильтрации между 7 и 8 шагами для AM, а также между 10 и 11 шагами для ЧМ-сигнала, что позволит уменьшить погрешность. Целесообразна реализация фильтра через прямое и обратное преобразование Фурье. Моделирование показало, что наименьшую погрешность дают временные окна, спадающие к нулю на краях, например, для окна Хемминга можно выбрать a=0.5001. При использовании 12-битного АЦП (преобразователь аналог-код) и случайном шуме на уровне 1 бита относительная погрешность измерения глубины AM не превосходит 0,1%, а относительная погрешность измерения девиации частоты не превосходит 0,7%.
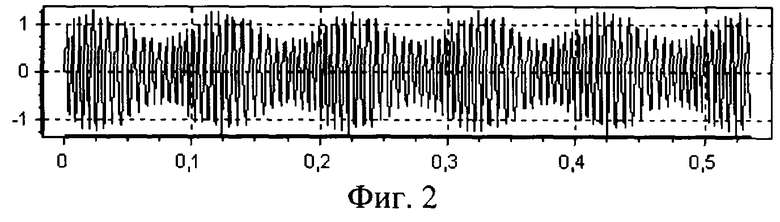
Результаты моделирования представлены на фиг.2-5. На вход АЦП подавался комбинированный AM и ЧМ модулированный сигнал: fВЧ=100,5 МГц, F=10000 Гц, fд=955500 Гц, М=30%, Fд=30000 Гц. Фазы модуляции AM и ЧМ отличались на π /2, N=512.
По оси ОХ на каждом из графиков отложено время в миллисекундах.
На фиг.2 показан массив данных X[iTд]. По оси OY отложена относительная амплитуда.
На фиг.3 показан массив данных Xw[iTд] (наложено окно Хемминга). По оси OY отложена относительная амплитуда.
На фиг.4 показан массив данных A[iTд] (демодулированный AM-сигнал). По оси OY отложена относительная амплитуда.
На фиг.5 показан массив данных fСП[iTд] (демодулированный ЧМ-сигнал). По оси OY отложена мгновенная частота fСП в герцах.
Наибольший эффект от использования предложенного изобретения может быть достигнут в измерительных комплексах, содержащих в своей структуре персональный компьютер (ПК). При использовании современных АЦП, вставляемых в свободный слот ПК и работающих в режиме стробирования, компьютер обеспечивает всю дальнейшую обработку и представление данных. Значительное упрощение аналоговой части измерителя достигнуто за счет усложнения алгоритма цифровой обработки, что позволило расширить функциональные возможности.
Предложенный цифровой измеритель модуляции может измерять:
- AM-сигнал;
- ЧМ-сигнал;
- AM-сигнал с паразитной ЧМ;
- ЧМ-сигнал с паразитной AM;
- сигнал со сложной модуляцией несущей AM и ЧМ.
Использование в цифровом измерителе модуляции недорогой цифровой схемотехнической базы приводит к снижению стоимости и повышению надежности устройства. Применение АЦП с относительно невысокой частотой дискретизации (0,5... 5 МГц), работающего в режиме стробирования, также снижает стоимость.
Предложенное устройство было реализовано и апробировано для измерения параметров простых и сложных (комбинированных) AM- и ЧМ-сигналов. Результаты измерения девиации ЧМ-сигнала показали, что влиянием паразитной AM (глубиной до 95%) можно пренебречь. Аналогичные результаты были получены и при измерении глубины AM в присутствии паразитной ЧМ. Во всех экспериментах проводилось одновременное измерение глубины AM и девиации частоты с допустимой для большинства практических задач погрешностью.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ МОДУЛЯЦИИ | 2010 |
|
RU2424534C1 |
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК | 2012 |
|
RU2520956C2 |
| Цифровой измеритель коэффициента амплитудной модуляции | 2020 |
|
RU2768206C2 |
| СПОСОБ ПЕЛЕНГАЦИИ РАДИОСИГНАЛОВ И ПЕЛЕНГАТОР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2419805C1 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР СИГНАЛОВ С ЧАСТОТНОЙ МОДУЛЯЦИЕЙ | 2012 |
|
RU2522039C1 |
| СПОСОБ ЦИФРОВОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ | 2010 |
|
RU2434304C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ | 1992 |
|
RU2111496C1 |
| СПОСОБ ИЗМЕРЕНИЯ РЕЗОНАНСНОЙ ЧАСТОТЫ | 2013 |
|
RU2541119C1 |
| УСТРОЙСТВО РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 1999 |
|
RU2154896C1 |
| ИЗМЕРИТЕЛЬ ДЕВИАЦИИ ЧАСТОТЫ ЧАСТОТНО-МОДУЛИРОВАННЫХ КОЛЕБАНИЙ | 1991 |
|
RU2019843C1 |



Изобретение относится к области измерительной техники, в частности к области измерения параметров модуляции. Измеритель содержит индикатор, преобразователь аналог-код и входное устройство. Первый вход входного устройства является входом измерителя, а выход соединен с первым входом преобразователя аналог-код. Введены преобразователь частота-код и вычислитель. Вход преобразователя частота-код соединен с выходом входного устройства. Выход преобразователя частота-код соединен со вторым входом вычислителя. Первый вход вычислителя соединен с выходом преобразователя аналог-код, первый выход - с индикатором, второй выход - со вторым входом преобразователя аналог-код, а третий выход - со вторым входом входного устройства. Технический результат - возможность одновременного измерения глубины амплитудной модуляции и девиации частоты сложных модулированных сигналов. 5 ил.
Цифровой измеритель модуляции, содержащий индикатор, преобразователь аналог-код и входное устройство, первый вход которого является входом измерителя, а выход соединен с первым входом преобразователя аналог-код, отличающийся тем, что в него введены преобразователь частота-код и вычислитель, причем вход преобразователя частота-код соединен с выходом входного устройства, а выход преобразователя частота-код соединен со вторым входом вычислителя, первый вход которого соединен с выходом преобразователя аналог-код, первый выход вычислителя соединен с индикатором, второй выход вычислителя соединен со вторым входом преобразователя аналог-код, а третий выход вычислителя соединен со вторым входом входного устройства.
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ ГЛУБИНЫ МОДУЛЯЦИИ | 1970 |
|
SU424089A1 |
| Устройство для измерения глубины модуляции | 1979 |
|
SU788043A1 |
| Устройство для измерения частоты последовательного резонанса пьезорезонаторов многорезонаторного дифференциальномостового пьезоэлектрического фильтра | 1981 |
|
SU953598A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| ЕР 1083433 А2 14.03.2001. | |||
Авторы
Даты
2005-03-10—Публикация
2003-05-05—Подача