Изобретение относится к геодезии и может найти применение при кадастровом учете земельных угодий со сложным рельефом.
Известен аналитический способ определения площади земельных участков [см. например, “Инженерная геодезия”, учебник под редакцией Д.Ш.Михелева, Высшая школа, М., 2000 г., стр.335-337 - аналог]. При аналитическом способе определения площадей применяют формулы геометрии, тригонометрии и аналитической геометрии. При этом оцениваемую площадь разбивают на простейшие геометрические фигуры, преимущественно треугольники (прямоугольники), а площадь участка находят как сумму площадей отдельных фигур (S) вычисляемых: для треугольника по двум сторонам l1, l2 и углу β , заключенному между ними:
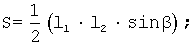 ;
;
или по формуле Герона:
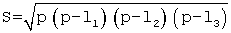
где р - полупериметр сторон треугольника, равный 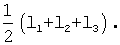
В способе-аналоге площадь участка вычисляют по результатам измерений перечисленных параметров на местности. Результирующая ошибка (стр.337 аналога) определения площади полигона с n вершинами составляет величину:
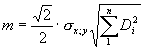
где σ x,y - среднеквадратическая ошибка определения координат x, y точек вершин полигона при условии, что 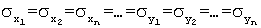
Di - расстояние от начала координат до i-ой точки вершины полигона.
Таким образом, к недостаткам способа-аналога следует отнести:
- увеличение результирующей ошибки при усложнении рельефа, т.е. необходимость разбиения полигона на большее число простейших фигур;
- большой объем, трудоемкость наземных измерений, неоперативность работ;
- трудности реализации способа в сложно-пересеченной и горной местности.
В последние годы совершенствуются методы определения площади земельных участков по цифровым моделям местности (ЦММ). Цифровой моделью местности называют совокупность точек местности с известными координатами в трехмерном пространстве x, y, h. Существуют различные методы формирования массивов ЦММ, отличающиеся друг от друга различной точностью и степенью детализации элементов рельефа. Точность ЦММ обычно увязывают с требуемой точностью решения инженерно-геодезических задач. При этом рельеф аппроксимируют криволинейными поверхностями различного порядка. При получении аналитического выражения аппроксимирующей поверхности h(x, y) площадь рельефа вычисляют как поверхностный интеграл от этой функции в области Ф [см., например, П.С.Пискунов, “Дифференциальное и интегральное исчисление для вузов”, учебник, 5-е издание, том 2, Наука, М.,1964 г., § 7 “Вычисление площади поверхности”, стр.73-74 - аналог]
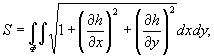
Ближайшим аналогом является способ вычисления поверхности рельефа [см., например, Н.П.Булгаков, Е.М.Рывина, Г.А.Федотов “Прикладная геодезия”, учебник. Недра, М., 1990 г., §16. Математические модели местности, стр.42-44], при котором разделяют массив ЦММ на фрагменты, каждый из которых приурочивается к определенной форме рельефа: склон, гора, котловина, лощина, седловина, хребет, выбирают в пределах фрагмента необходимое число точек ЦММ с известными координатами xm, ym, hm и методом наименьших квадратов решают следующую систему уравнений:
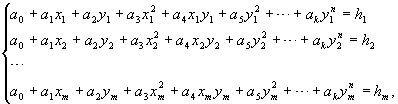
где а0, а1... ak - неизвестные коэффициенты уравнения аппроксимирующей поверхности;
k - число неизвестных коэффициентов;
m - число уравнений.
Как правило, число уравнений при решении системы обычно превышает число неизвестных коэффициентов m>k. Поэтому ввиду сложности аналитических решений в практике инженерных расчетов обычно ограничиваются аппроксимирующей поверхностью второго порядка. Кроме того, сам метод наименьших квадратов уже предполагает уклонение аппроксимирующих функций от исходных точек ЦММ, т.е. ошибки метода добавляются к ошибкам отсчетов ЦММ.
Разбиение на фрагменты с вычислением аппроксимирующей поверхности каждого фрагмента существенно увеличивает трудоемкость операций и не обеспечивает автоматизацию вычислительного процесса.
Задача, решаемая заявляемым способом, состоит в повышении точности и автоматизации вычислительного процесса расчета площади рельефа по массиву ЦММ путем аппроксимации рельефа бесконечной суммой гармоник тригонометрического ряда Фурье с использованием как существующих, так и вновь разработанных специализированных математических программ для ПЭВМ.
Решение поставленной задачи обеспечивается тем, что в способе определения площади рельефа, включающем получение цифровой модели местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты h(x, y) от пространственных координат, разбиение матрицы ЦММ на фрагменты, вычисление аппроксимирующей функции для поверхности фрагмента, расчет площади как поверхностного интеграла аппроксимирующей функции, дополнительно вычисляют двумерный пространственный спектр Фурье матрицы фрагмента ЦММ:

представляют аппроксимирующую поверхность бесконечной суммой гармоник тригонометрического ряда Фурье:
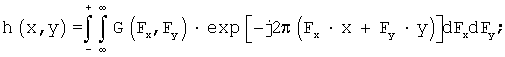
выражают квадраты частных производных тригонометрического ряда через огибающие автокорреляционных функций b(х), b(y) как
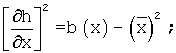
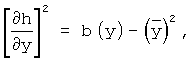
а площадь рельефа определяют численным интегрированием функции вида:
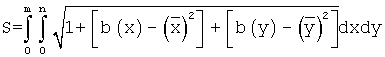
по специализированной программе для ПЭВМ, где m, n - число строк, столбцов матрицы ЦММ; 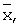
 - средние значения матрицы ЦММ по координатам x, y.
- средние значения матрицы ЦММ по координатам x, y.
Изобретение поясняется чертежами, где фиг.1 - визуализированное изображение фрагмента ЦММ;
фиг.2 - визуализированный двумерный пространственный спектр Фурье анализируемого фрагмента;
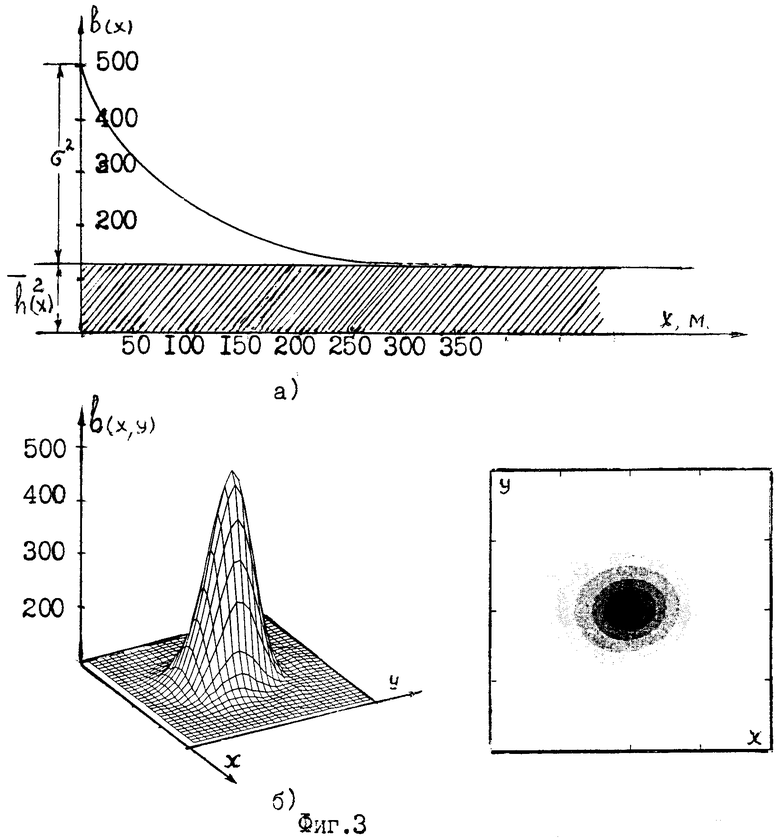
фиг.3 - автокорреляционные функции сигнала h(x, y): а) по координате x; б) вид автокорреляционной функции в аксонометрии;
фиг.4 - сечение рельефа поверхности, по которому проводились отладка программы в примере реализации;
фиг.5 - функциональная схема устройства, реализующая способ.
Техническая сущность изобретения состоит в следующем.
Для достижения заданных точностей вычисления функций часто используют их разложение в бесконечный ряд.
Из математики известно [см., например, Г.Корн, Т.Корн “Справочник по математике для научных работников и инженеров”, пер. с англ., Наука, Физматгиз, М., 1970 г., стр.144], что наибольшую точность вычислений обеспечивает аппроксимация функций бесконечным тригонометрическим рядом, коэффициенты разложения которого суть коэффициенты Фурье. В настоящее время существуют пакеты программ специализированного математического обеспечения, как то: ER MAPPER 5.0 [“Пакет программ для обработки изображений в науках о Земле”, GENASYS Inc. San Diego, USA, p.283-294], MATHCAD 6.0 PLUS [издание 2-е стереотипное, М.: Информ. Издат. Дом ФИЛИНЪ, 1997 г., стр.412], реализующих алгоритмы быстрого Фурье - преобразования (БПФ) от цифровых массивов информации.
В соответствии с теорией спектрального оценивания [см., например, С.П.Марпл “Цифровой спектральный анализ и его приложения”, пер. с англ., М.: Мир, 1990 г., стр.181] устойчивые результаты, малые флуктуации и высокая точность достигаются при условии, когда:
Q· Te·B>1
где Q - показатель качества, среднеквадратическая ошибка вычислений, если она равна 10%, то Q=0,1;
Тe=N· Т, полный интервал записи данных из N отсчетов длительностью Т каждого отсчета;
В - эффективное разрешение по частоте.
Перечисленные данные позволяют по имеющемуся массиву ЦММ с известной дискретизацией отсчетов (разрешению Δ x, Δ y, Δ h) априори рассчитать ошибку вычисления площади рельефа из условия аппроксимации рельефа бесконечным тригонометрическим рядом Фурье.
На основании теоремы отсчетов Котельникова-Шеннона [см., например, Дуда Р., Харт П. “Распознавание образов и анализ сцен”, пер. с англ., Наука, М., 1976 г., стр.319-335] интервал дискретизации отсчетов должен удовлетворять условию:

где Fmax - максимальная частота пространственного спектра, определяемая степенью изрезанности анализируемого рельефа.
Если принять за изрезанность холмистого рельефа размер диаметра подошвы наименьшего холма (L), то для обеспечения среднеквадратической ошибки вычисления площади рельефа 1% соотношение между длиной диаметра L и шагом дискретизации Δ x, (Δ y) должно составлять величину: 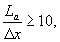 т.е. не менее десяти дискретных отсчетов на минимальный элемент кривизны (шероховатости) рельефа. Космические средства наблюдения позволяют в настоящее время получать стереоизображение подстилающей поверхности с разрешением 5-7 м на отсчет [см., например, “MOMS-2P camera”, ФРГ, описание, НПО “Энергия”, “РАКА”, 1994 г.]. Таким образом, предлагаемый способ обеспечивает среднеквадратическую ошибку вычислений ≤ 1% при всхолмленности рельефа 50-70 м (по расстоянию между соседними вершинами холмов), что охватывает практически все возможные рельефы, пригодные для сельхоз эксплуатации. Процедура вычислений реализуется следующей последовательностью операций. Массив ЦММ h(x,y) вводят в ПЭВМ. Стандартной программой БПФ (см. выше ER MAPPER или MATHCAD) вычисляют двумерный пространственный спектр Фурье обрабатываемого участка (фрагмента):
т.е. не менее десяти дискретных отсчетов на минимальный элемент кривизны (шероховатости) рельефа. Космические средства наблюдения позволяют в настоящее время получать стереоизображение подстилающей поверхности с разрешением 5-7 м на отсчет [см., например, “MOMS-2P camera”, ФРГ, описание, НПО “Энергия”, “РАКА”, 1994 г.]. Таким образом, предлагаемый способ обеспечивает среднеквадратическую ошибку вычислений ≤ 1% при всхолмленности рельефа 50-70 м (по расстоянию между соседними вершинами холмов), что охватывает практически все возможные рельефы, пригодные для сельхоз эксплуатации. Процедура вычислений реализуется следующей последовательностью операций. Массив ЦММ h(x,y) вводят в ПЭВМ. Стандартной программой БПФ (см. выше ER MAPPER или MATHCAD) вычисляют двумерный пространственный спектр Фурье обрабатываемого участка (фрагмента):

Затем обратным Фурье-преобразованием представляют рельеф h(x,y) бесконечным тригонометрическим рядом:

Учитывая, что отрицательных частот не существует, тригонометрический ряд представляют в виде:

Вычисляют частные производные рельефа по координатам x, y:
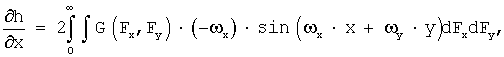
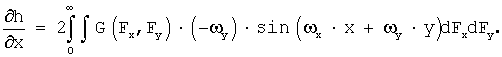
Непосредственно, аналитически, данные интегральные суммы вычислить затруднительно. По своему физическому смыслу, если h(x, y) есть сигнал, то частные производные 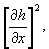
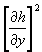 (скорость в квадрате) есть скорость флуктуации мощности процесса в функции пространственных координат. Известно [см., например, Заездный А.М., М., 1969 г., стр. 91-94], что скорость флуктуации мощности в функции пространственных координат отражает автокорреляционная функция сигнала b(x, y). Автокорреляционная функция сигнала связана с энергетическим спектром E(Fx, Fy) обратным преобразованием Фурье:
(скорость в квадрате) есть скорость флуктуации мощности процесса в функции пространственных координат. Известно [см., например, Заездный А.М., М., 1969 г., стр. 91-94], что скорость флуктуации мощности в функции пространственных координат отражает автокорреляционная функция сигнала b(x, y). Автокорреляционная функция сигнала связана с энергетическим спектром E(Fx, Fy) обратным преобразованием Фурье:
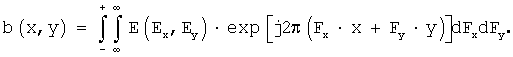
В свою очередь энергетический спектр сигнала вычисляют как квадрат пространственного спектра Фурье:
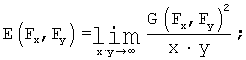
Известно [см., там же, Заездный А.М.], что значение автокорреляционной функции в нуле равно средней мощности процесса 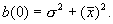 На фиг.3, а представлена автокорреляционная функция по одной из координат и фиг.3, б - вид двумерной функции автокорреляции b(x, y) в аксонометрии.
На фиг.3, а представлена автокорреляционная функция по одной из координат и фиг.3, б - вид двумерной функции автокорреляции b(x, y) в аксонометрии.
Огибающую автокорреляционной функции, характеризующую скорость флюктуации мощности процесса, соответственно вычисляют как 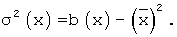
Таким образом, определение площади рельефа сводится к вычислению двойного интеграла от функции:
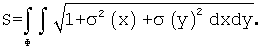
Полученное соотношение не противоречит физическому смыслу. Если поверхность гладкая, то дисперсии σ 2(x), σ 2(y) равны нулю, а площадь равна произведению сторон участка S=x· y. Если поверхность сильно изрезана (большая дисперсия), то чем больше “шероховатость” рельефа, тем больше его площадь.
Значения σ 2(x), σ 2(y) рассчитывают непосредственно по массиву дискретных отсчетов ЦММ численным методом. Представляя пространственный спектр канонической функцией вида 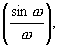 получено, что огибающие автокорреляционных функций b(x), b(y) имеют зависимость вида:
получено, что огибающие автокорреляционных функций b(x), b(y) имеют зависимость вида: 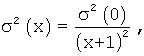

Приведенные выше функциональные соотношения реализуются следующей специализированной программой для ПЭВМ.


Пример реализации способа.
Заявляемый способ может быть реализован на базе устройства по схеме фиг.5. Функциональная схема устройства фиг.5 содержит орбитальный комплекс наблюдения 1 типа космического аппарата (КА) “Ресурс” с установленной на его борту оптической системой стереосъемки типа MOMS-2P (ФРГ) с каналами 2, 3 формирования стереоизображения. Съемка запланированных участков местности и включение каналов 2, 3 осуществляет бортовой комплекс управления (БКУ) 4 по командам, передаваемым из центра управления полетом (ЦУП) 5 по радиолинии управления 6. Информацию стереоизображений подстилающей поверхности 7 записывают на бортовой видеомагнитофон 8 и в сеансах видимости КА с наземных пунктов сбрасывают посредством телеметрической системы 9 по автономному каналу связи 10 на наземные пункты приема информации 11, где осуществляется запись массивов информации на видеомагнитофон 12 типа “Арктур”.
Предварительную обработку информации, выделение кадров по служебным признакам и формирование ЦММ осуществляют в Картографическом центре 13 Министерства Природных Ресурсов. Скомпонованные массивы ЦММ по запросам потребителей передаются в Региональные центры кадастрового учета 14, где ведется архив 15 ЦММ региона на базе стримеров, типа FT-120. Программный расчет площади рельефа участков осуществляют на ПЭВМ 16 в стандартном наборе элементов: процессора 17, ОЗУ 18, винчестера 19, дисплея 20, принтера 21, клавиатуры 22. Расчетные значения площадей участков помещают в базу региональных данных с выводом на сайт сети “Интернет” 23.
Программу вычисления площади рельефа записывают на винчестер 19. На электронной карте ЦММ высота (глубина) рельефа обычно квантуется в стандартной шкале от 0 до 255 уровней.
Обрабатываемый участок может иметь произвольную конфигурацию. Для его обработки следует выполнить выделение границы участка, “залив” окрестности белым цветом (255). Предполагается, что на обрабатываемом участке максимально возможная высота 255 не достигается. Если это не так, следует использовать изображение местности, выполненное в другом масштабе глубины. Для вычисления площади поверхности обрабатываемого участка необходимо указать масштаб по горизонтали, вертикали и глубине, то есть указать, чему соответствует в метрах один пиксель по горизонтали (Δ x), по вертикали (Δ y) и одна единица глубины (Δ h).
Отладка программы вычислений проводилась на сильно изрезанном рельефе древесного полога, представленного функцией яркости изображения I(x, y) фиг.1. Вершины крон деревьев отражают падающий световой поток зеркально, а промежутки между деревьями диффузно. В результате изображение древесного полога в виде функции яркости I(x, y) (каждая точка которого квантуется в шкале 0... 255 уровней) является аналогом ЦММ h(x, y). Поскольку реальные диаметры крон составляют 5... 10 м, то рельеф анализируемой поверхности оказывается сильно изрезанным. Обработке подвергался участок |m× n|=[111× 102| элементов. Изображение вводилось в ПЭВМ путем сканирования снимка сканером типа “Panasonic” с разрешением 1000 точек на дюйм. Уровень яркости изображения находился в интервале Imax=135 Imin=23, среднее значение яркости 64.
Стандартной процедурой MATHCAD вычислялся двумерный пространственный спектр Фурье участка изображения, иллюстрированный фиг.2. Рассчитывались числовые характеристики матрицы I(x, y) |111× 106| элементов, которые составили: дисперсия по x 1407, дисперсия по y 1458.
Поскольку отсканированное изображение имело одинаковое разрешение по x, y, то автокорреляционные функции практически симметричны.
Расчетное значение площади рельефа составило величину S=73697,82 м2, при площади его проекции 9801,00.
Реальная площадь сильно изрезанного рельефа отличается от площади квадрата анализируемого плоского участка в 7,5 раз. Эффективность способа определяется такими показателями как точность, достоверность, документальность, оперативность. При использовании аэрокосмических средств получения ЦММ высокого пространственного разрешения преимущества заявляемого способа перед аналогами по перечисленной гамме показателей очевидны.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ РЕЛЬЕФА | 2004 |
|
RU2251075C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ РЕЛЬЕФА | 2004 |
|
RU2253089C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРИРОСТА ЗАПАСА НАСАЖДЕНИЙ | 2004 |
|
RU2277325C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛНОТЫ ДРЕВОСТОЕВ | 2005 |
|
RU2294622C2 |
| Способ идентификации загрязнений морской поверхности | 2015 |
|
RU2664255C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЗАГРЯЗНЕНИЙ МОРСКОЙ ПОВЕРХНОСТИ | 2016 |
|
RU2632176C1 |
| СПОСОБ ЭКОЛОГИЧЕСКОГО ЗОНИРОВАНИЯ ТЕРРИТОРИИ | 1998 |
|
RU2132606C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНОМАЛИЙ МОРСКОЙ ПОВЕРХНОСТИ | 2017 |
|
RU2675072C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ЗЕМЛЕТРЯСЕНИЯ | 2001 |
|
RU2183844C1 |
| СПОСОБ ОЦЕНКИ БИОМАССЫ РАСТИТЕЛЬНОСТИ | 1999 |
|
RU2155472C1 |



Изобретение относится к геодезии и может быть использовано в процессе кадастрового учета земель со сложным рельефом. Заявленный способ включает съемку запланированных участков местности с борта космического аппарата, на котором устанавливают оптическую систему стереосъемки. Получают массив цифровых моделей местности аэрокосмическими средствами с высоким пространственным разрешением. Разбивают матрицу ЦММ участка местности на фрагменты. Вычисляют двумерный пространственный спектр и рассчитывают автокорреляционную функцию сигнала фрагмента по координатам b(х), b(y). Определяют площадь рельефа численным интегрированием по специализированной программе для ПЭВМ поверхностного интеграла S=S[b(x), b(y)] в зависимости от расчетных величин b(x), b(y). Технический результат: повышение точности, достоверности, документальности. 5 ил.

Способ определения площади рельефа, включающий съемку запланированных участков местности с борта космического аппарата, получение цифровой модели местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты h(x, y) от пространственных координат, разбиение матрицы ЦММ на фрагменты, вычисление аппроксимирующей функции для поверхности фрагментов, расчет площади как поверхностного интеграла аппроксимирующей функции, отличающийся тем, что на борту космического аппарата устанавливают оптическую систему стереосъемки с каналами формирования стереоизображения, включение которых осуществляется бортовым комплексом управления по командам, передаваемым из центра управления полетом по радиолинии управления, полученную информацию стереоизображений подстилающей поверхности записывают на бортовой видеомагнитофон и сбрасывают посредством телеметрической системы по автономному каналу связи на наземные пункты приема информации, вводят полученные изображения в ПЭВМ путем сканирования снимков, вычисляют двумерный пространственный спектр Фурье матрицы фрагмента ЦММ, представляют аппроксимирующую поверхность бесконечной суммой гармоник тригонометрического ряда Фурье, выражают квадраты частных производных тригонометрического ряда через огибающие автокорреляционных функций b(x), b(y) как

а площадь рельефа определяют численным интегрированием функции вида:

по специализированной программе для ПЭВМ, где m - число строк матрицы ЦММ; 
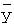 - средние значения матрицы ЦММ по координатам x, y.
- средние значения матрицы ЦММ по координатам x, y.
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКОЙ ПЛОЩАДИ ЗЕМЕЛЬНОГО УЧАСТКА | 2000 |
|
RU2166731C1 |
| СПОСОБ ПРЕДСКАЗАНИЯ ЗЕМЛЕТРЯСЕНИЙ | 1997 |
|
RU2120647C1 |
| СПОСОБ ПРЕДСКАЗАНИЯ ЗЕМЛЕТРЯСЕНИЙ | 1998 |
|
RU2130195C1 |
| US 4727488 А, 23.02.1988. | |||
Авторы
Даты
2005-06-27—Публикация
2004-05-31—Подача