Данное изобретение относится к анализу цифровых изображений, а в особенности к конструированию вычислительных сеток из таких изображений.
Описание предшествующего уровня техники
Цифровые изображения часто анализируют, чтобы получить сетки для дальнейших вычислений. К примеру, сейсмические изображения анализируют, чтобы получить геологические сетки, используемые для моделирования нефти, текущей в подземных резервуарах. Аналогично, медицинские изображения человеческого мозга анализируют, чтобы получить сетки, используемые для моделирования кровотока в артериях. Несколько иным примером является морфинг, т.е. преобразование изображений, при котором сетки, выделенные из одного изображения, могут использоваться для эффективного кодирования различий в последующих изображениях. Во всех этих применениях изображение анализируют для конструирования сетки.
Изображения и построение сеток сегодня
Характерно, что такие применения часто состоят из следующей последовательности этапов:
(1) Обрабатывают изображение, чтобы усилить вызывающие интерес характерные черты.
(2) Находят кривые или поверхности в изображениях, которые ограничивают вызывающие интерес области.
(3) Заполняют пространство, определенное этими областями, вычислительной сеткой.
(4) Моделируют некий процесс на заполняющей пространство сетке.
Для применения к медицинским изображениям см. Cebral, J.R., and Luhner, R., From Medical Images to CFD Meshes, Proceedings of the 8th International Meshing Roundtable, p.321-331, Sandia, 1999. Для применения к сейсмическим изображениям см. Garrett, S., Griesbach, S., Johnson, D., Jones, D., Lo, M., Orr, W., and Sword, C., Earth Model Synthesis, First Break, v.l5, no.1, p.13-20, 1997.
По разным причинам каждый этап в этой последовательности сегодня часто выполняют независимо, с малым вниманием к требованиям последующих шагов. Например, общепринято на этапе (2) вырабатывать ограничивающие кривые или поверхности с бульшим числом деталей, чем может быть представлено используемой на этапе (4) заполняющей пространство сеткой. По обыкновению сейсмические отражения, представляющие геологические пограничные слои, отображают с более высоким разрешением, чем можно практически использовать в сетках для моделирования нефтяных резервуаров. Это ведет к проблеме "перемасштабирования", указанной Garrett et al. (1997).
Это расхождение в разрешении часто сопровождается расхождением в структуре данных. К примеру, двумерная кривая, представленная простым связанным списком линейных сегментов на этапе (2), может стать относительно сложной сеткой треугольников на этапе (3). Такие расхождения сегодня подрывают последовательность анализа и могут привести к несоответствиям между изображением, обработанным на этапе (1), и сеткой, используемой на этапе (4), которые трудно оценить количественно.
Расхождения эти дорогостоящи. В примере с анализом сейсмических изображений одна итерация данной последовательности сегодня может потребовать месяцев работы. Эта высокая стоимость затрудняет выполнение множества итераций при попытке оценить неопределенности в результатах анализа.
Одна причина расхождений в разрешении и структуре данных лежит в реализации последовательности анализа. Исторически перечисленные выше четыре этапа могут выполняться отдельными компьютерными программами, разработанными независимо и используемыми разными специалистами. В настоящее время все четыре этапа в данной последовательности может выполнять один человек или небольшая группа, и имеется потребность, чтобы эти этапы были объединены в большей степени.
Другой причиной расхождений является отсутствие методики. Этап (4) моделирования часто требует численного решения дифференциальных уравнений в частных производных (ДУЧП, PDEs). В прошлом эти решения были осуществимы только для структурированных сеток, в которых элементы могут быть проиндексированы как простые массивы. Преобразование неструктурированной сетки, выработанной на этапе (3), в структурированную сетку создает дополнительные несоответствия между обработанным изображением и сеткой, используемой в моделировании. Однако недавние достижения в численных методах решения ДУЧП на неструктурированных сетках подсказывают, что этого преобразования и получающихся несоответствий можно избежать.
Формирование сеток с помощью решеток
Точность большинства вычислений, выполняемых на сетках, зависит от регулярности сеточных элементов. Моделирование, выполненное на треугольных сетках с высокой регулярностью, имеющих почти равносторонние треугольники, является более точным, чем то, которое выполнено на нерегулярных сетках с длинными тонкими треугольниками.
Это одна причина, по которой популярна триангуляция Делонэ. При заданном наборе узлов, представляющих местоположения узлов для двумерной сетки, триангуляция Делонэ этих узлов по сравнению со всеми иными возможными триангуляциями дает треугольники, в наибольшей степени близкие к равносторонним. Однако триангуляция Делонэ сама по себе не гарантирует регулярной сетки. Для этого необходимо тщательно выбирать местоположения узлов сетки.
(Для обзора двумерной и трехмерной триангуляции Делонэ в применении к проблеме построения сеток см. Bern, М., and Eppstein, D., Mesh Generation and Optimal Triangulation, in Computing in Euclidean Geometry, Du, D.-Z. and Hwang, F.K. eds., World Scientific, 1995.)
За рамками области анализа изображений проблема выбора оптимальных расположений сеточных узлов изучена хорошо. Одно решение для этой проблемы основано на наблюдении, что триангуляция набора узлов, определенного простой кристаллической решеткой, дает сетку с высокой регулярностью. (См. Mello, U.T., and Cavalcanti, P.R., A Point Creation Strategy for Mesh Generation Using Crystal Lattices as Templates, Proceedings of the 9th International Meshing Roundtable, p.253-261, Sandia, 2000.) Однако равномерная решетка узлов может лишь в редких случаях совмещаться с границами объектов, для которых нужно получить сетки. Поэтому некоторые решения начинаются с приблизительно равномерной решетки, а затем используются численные модели физических сил между атомами или пузырьками для автоматического перемещения сеточных узлов (атомов или пузырьков) в более оптимальные местоположения. (См. Shimada, К., Physically-Based Mesh Generation: Automated Triangulation of Surfaces and Volumes via Bubble Packing, Ph.D. thesis, Massachusetts Institute of Technology, 1993, и Shimada, К., and Gossard, D.C., Bubble Mesh: Automated Triangular Meshing of Non-Manifold Geometry by Sphere Packing, в Proceedings of the Third Symposium on Solid Modeling and Applications, p.409-419. Патент США №6124857 на имя Itoh, Т., Inoue, К., Yamada, A., and Shimada, K., Meshing Method and Apparatus, 2000, расширяет эту работу на получение сеток из четырехугольников. (См. Bossen, F.J., and Heckbert, P.S., A Plant Method for Anisotropic Mesh Generation, Proceedings of the 5th International Meshing Roundtable, p.63-74, Sandia, 1996.)
Во всех этих примерах получение сетки на основе решетки начинается с геометрической модели, которая точно определяет внутренние и наружные границы объектов, для которых строятся сетки. Таким образом, существует необходимость в системе и методике построения сеток, способных решить проблемы, где такие границы неизвестны заранее.
Патенты США, указанные в этом описании
4908781 на имя Levinthal, С., and Fine, R., Computing Device for Calculating Energy and Pairwise Central Forces of Particle Interactions, 1990.
5596511 на имя Toyoda, S., Ikeda, H., Hashimoto, E., and Miyakawa, N., Computing Method and Apparatus for a Many-Body Problem, 1997.
6124857 на имя Itoh, Т., Inoue, К., Yamada, A., and Shimada, K., Meshing Method and Apparatus, 2000.
Другие ссылки, указанные в данном описании
Bentley, J.L., and Friedman, J.H., Data Structures for Range Searching, Computing Surveys, Vol.11, no.4, 1979.
Bern, M., and Eppstein, D., Mesh Generation and Optimal Triangulation, в Computing in Euclidean Geometry, Du, D.-Z. and Hwang, F.K. eds., World Scientific, 1995.
Bossen, F.J., and Heckbert, P.S., A Plant Method for Anisotropic Mesh Generation, Proceedings of the 5th International Meshing Roundtable, p.63-74, Sandia, 1996.
Byrd, R.H., Nocedal, J., and Schnabel, R.B., Representations of Quasi-Newton Matrices and Their Use in Limited Memory Methods, Technical Report NAM-03, Northwestern University, Department of Electrical Engineering and Computer Science, 1996.
Cebral, J.R., and Luhner, R., From Medical Images to CFD Meshes, Proceedings of the 8th International Meshing Roundtable, p.321-331, Sandia, 1999.
Garrett, S., Griesbach, S., Johnson, D., Jones, D., Lo, M., Orr, W., and Sword, C., Earth Model Synthesis, First Break, v.15, no.1, p.13-20, 1997.
Mello, U.T., and Cavalcanti, P.R., A Point Creation Strategy for Mesh Generation Using Crystal Lattices as Templates, Proceedings of the 9th International Meshing Roundtable, p.253-261, Sandia, 2000.
Shimada, K., Physically-Based Mesh Generation: Automated Triangulation of Surfaces and Volumes via Bubble Packing, Ph.D. thesis, Massachusetts Institute of Technology, 1993.
Shimada, K., and Gossard, D.C., Bubble Mesh: Automated Triangular Meshing of Non-Manifold Geometry by Sphere Packing, в Proceedings of the Third Symposium on Solid Modeling and Applications, p.409-419, 1995.
Сущность изобретения
В соответствии с различными вариантами осуществления данного изобретения способ генерирования решетки узлов по отношению к характерным чертам в цифровом изображении содержит процесс инициализации решетки и процесс оптимизации совмещения этой решетки по отношению к характерным чертам изображения. Процесс оптимизации работает путем корректирования узлов решетки с целью получения экстремума составной функции пространственных координат узлов решетки. Составная функция может быть взвешенной комбинацией первой функции попарных расстояний между узлами и второй функции, выделенной из изображения (например, вычисленной из выборок изображения вблизи узлов решетки).
Из оптимизированной решетки может генерироваться сетка. Эта сетка может использоваться в любом из множества применений. К примеру, сетка может использоваться для моделирования процесса, связанного с изображением. В качестве другого примера, сетка может использоваться для сжатия изображения или последующих изображений в последовательности изображений (например, в видеопотоке).
В некоторых вариантах осуществления оптимизированная решетка может использоваться для кодирования информации, связанной с изображением, с генерированием или без генерирования промежуточной сетки. Предполагается любой из различных типов связанной информации.
Задачи и преимущества
Одной задачей по меньшей мере некоторых вариантов осуществления данного изобретения является способ, который позволяет заменить описанную выше (при описании предшествующего уровня техники) последовательность анализа изображений более эффективной последовательностью:
(1) Обрабатывают изображение, чтобы усилить вызывающие интерес характерные черты.
(2) Заполняют пространство вычислительной сеткой, совмещенной характерными чертами с характерными чертами изображения.
(3) Моделируют некий процесс на заполняющей пространство сетке.
Вместо нахождения границ областей в изображениях, а затем построения сеток в этих областях, просто конструируют сетку, которая совмещается с границами.
Дополнительными задачами некоторых вариантов осуществления данного изобретения являются использование данного способа для построения:
- сеток с высокой регулярностью, пригодных для дальнейших вычислений, таких как решение дифференциальных уравнений в частных производных; и
- градуированных сеток, в которых плотность сеточных узлов изменяется в зависимости от сложности изображения или как функция, определенная пользователем; и
- трехмерных сеток, где доступны трехмерные изображения.
Эти и другие задачи и преимущества разных вариантов осуществления изобретения станут понятны из рассмотрения нижеследующего описания и чертежей.
Перечень чертежей
Фиг.1 - поток данных среди первичных компонентов в способе по данному изобретению.
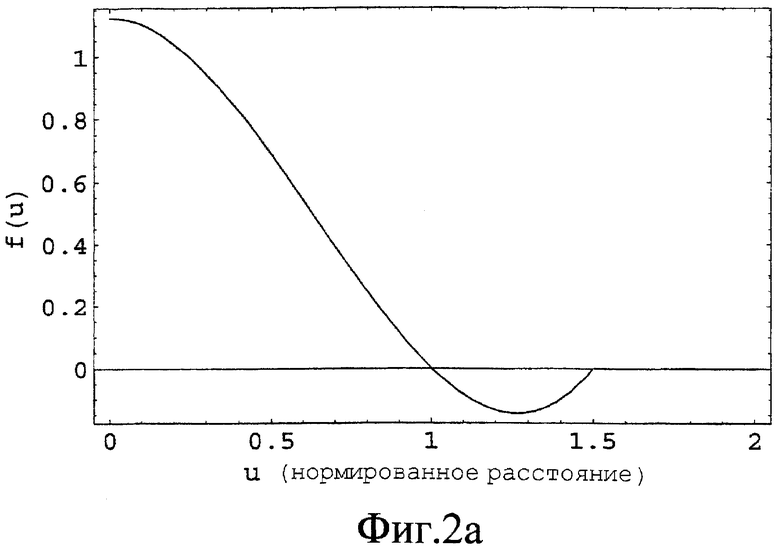
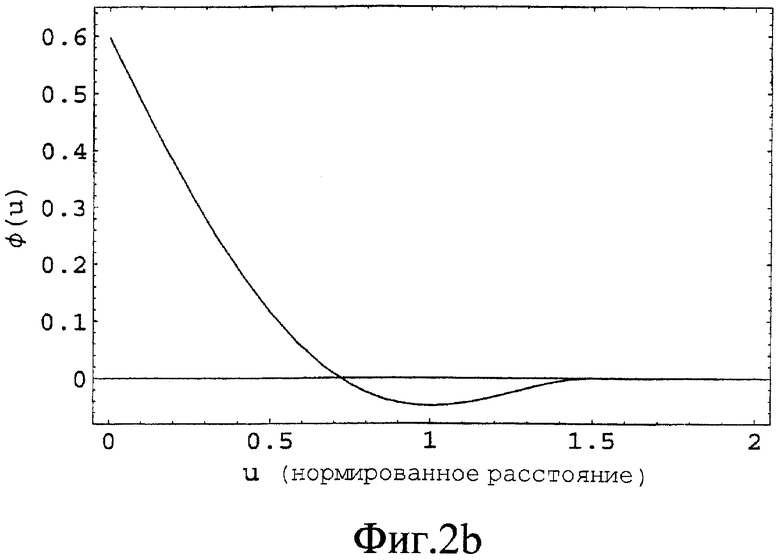
Фиг.2 - двухточечные функции силы (фиг.2а) и потенциала (фиг.2b) от нормированного расстояния между любыми двумя атомами.
Фиг.3 - вклады для номинальных расстояний 4 (фиг.3а) и 8 (фиг.3b) одного атома в дискретное поле потенциалов атомов.
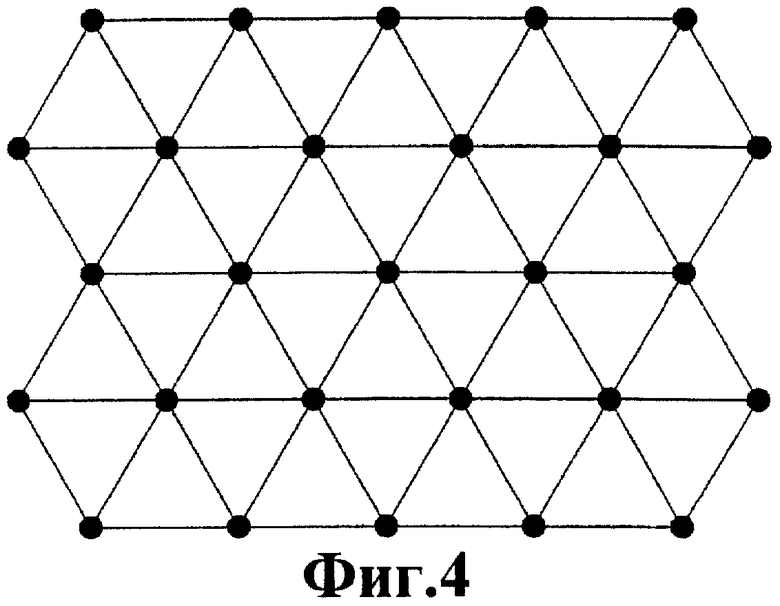
Фиг.4 - гексагональная двумерная решетка атомов, которую триангулировали.
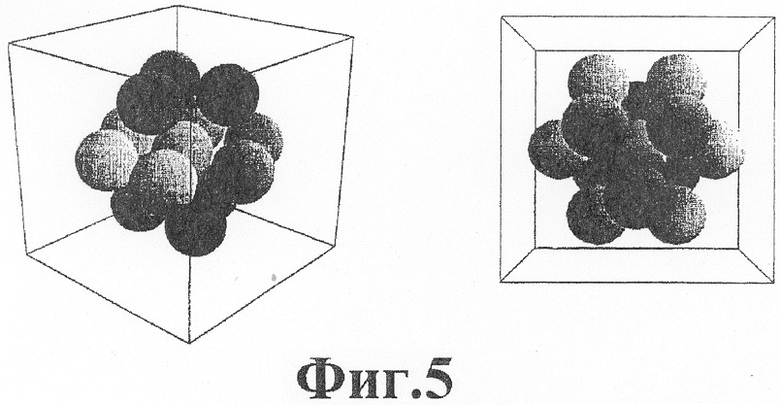
Фиг.5 - гранецентрированная спереди кубическая трехмерная решетка атомов.
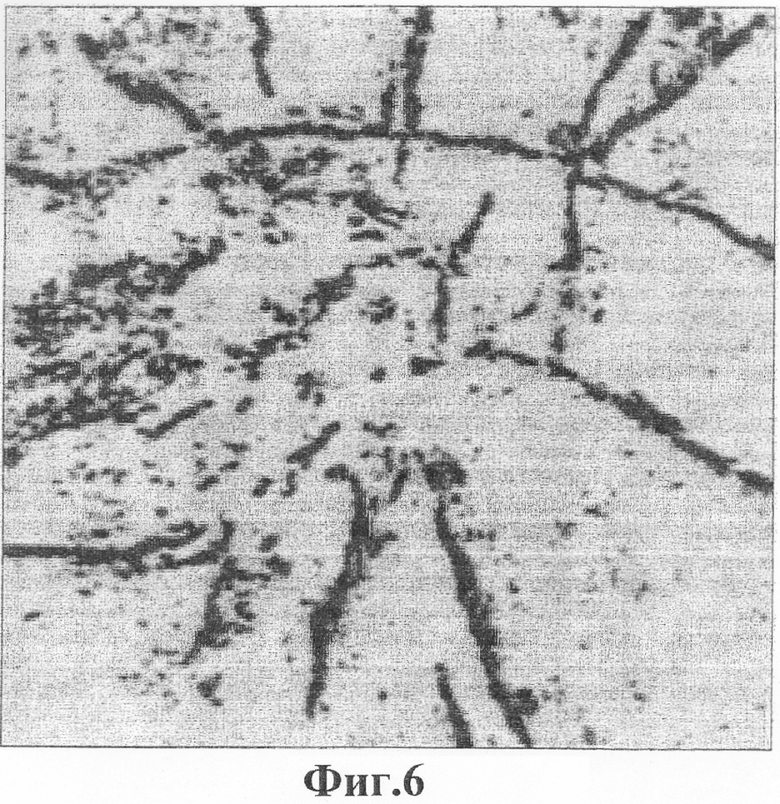
Фиг.6 - сейсмическое изображение, которое обработано, чтобы усилить дефекты, разрывы в подземной геологии.
Фиг.7 - функция номинального расстояния, которая представляет желаемый переменный промежуток между атомами в решетке.
Фиг.8 - начальное псевдорегулярное распределение атомов в решетке; каждый атом помечен кружком с диаметром, пропорциональным функции номинального расстояния, оцененной в местоположении атома.
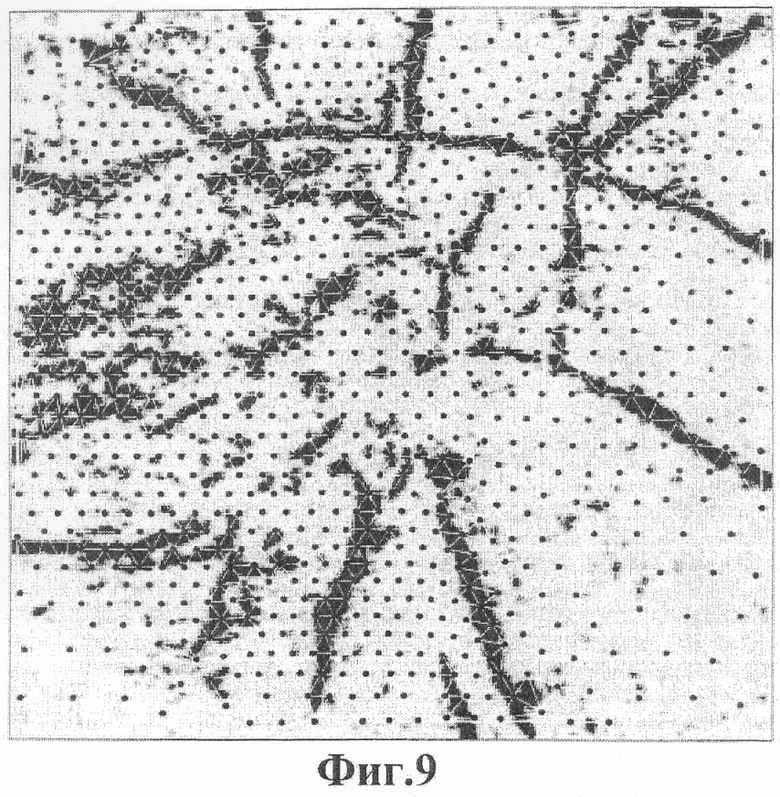
Фиг.9 - сетка, соответствующая псевдорегулярной исходной решетке для сейсмического изображения.
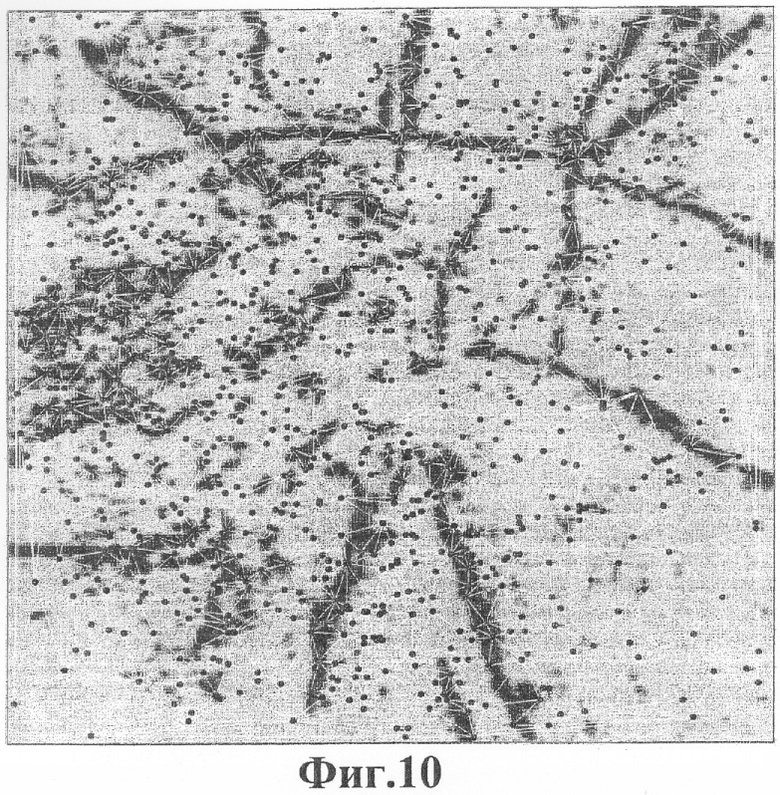
Фиг.10 - сетка, соответствующая псевдослучайной исходной решетке для сейсмического изображения.
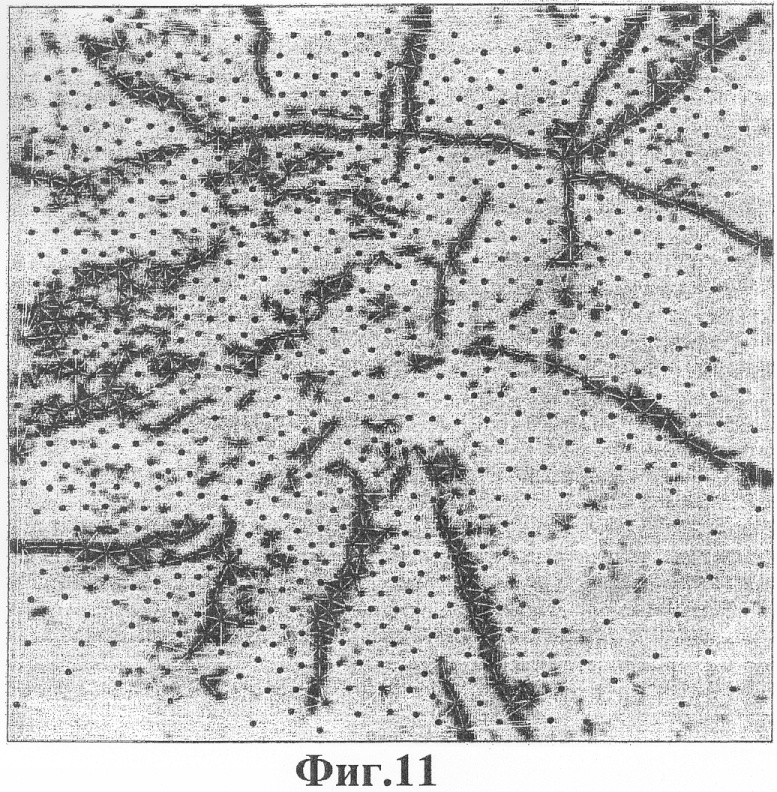
Фиг.11 - сетка, соответствующая оптимизированной решетке для сейсмического изображения.
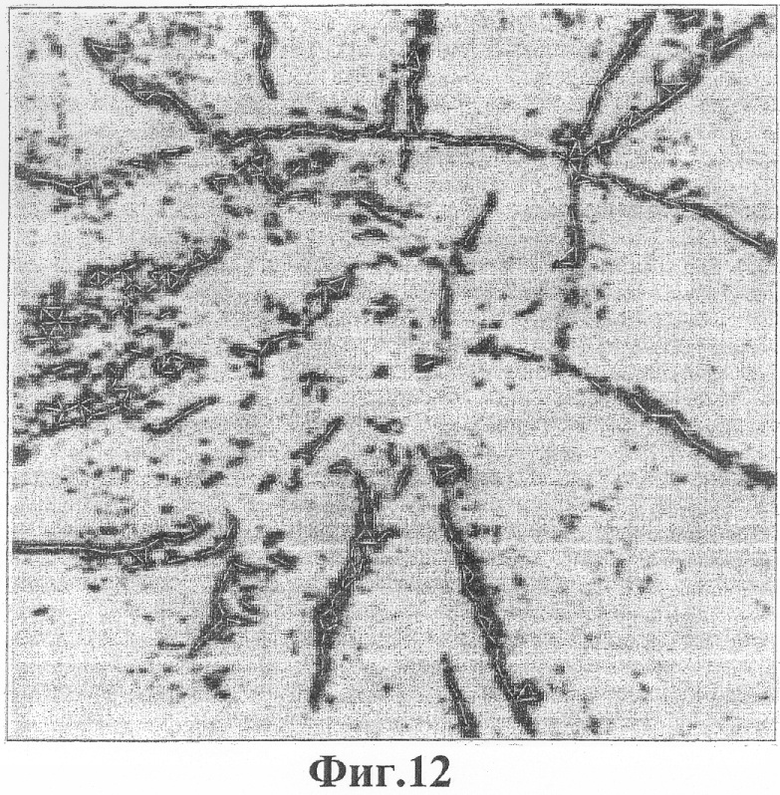
Фиг.12 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в сейсмическом изображении.
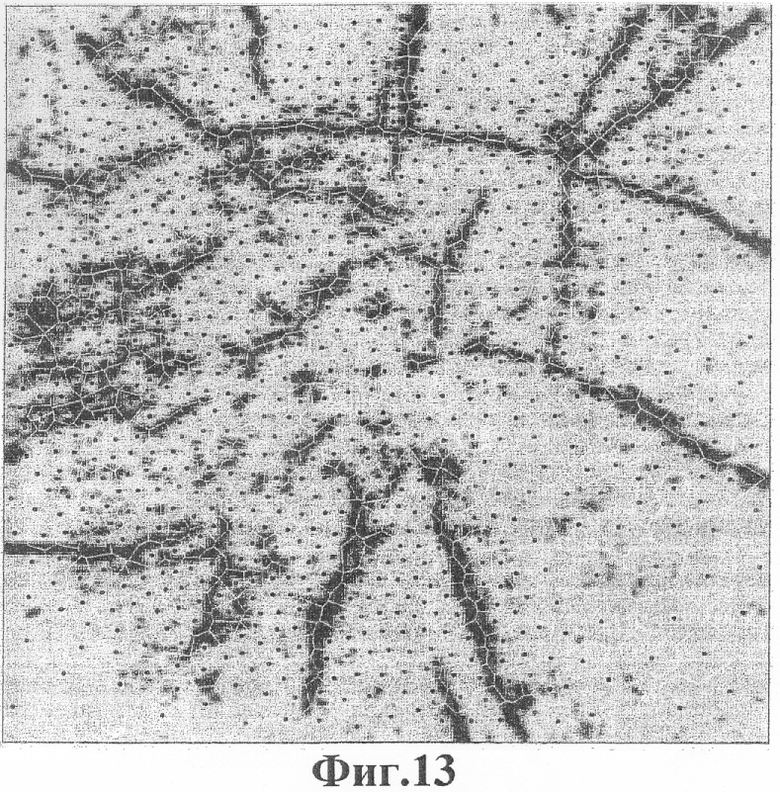
Фиг.13 - сетка Вороного, соответствующая оптимизированной решетке, в которой атомы отталкиваются характерными чертами в сейсмическом изображении.
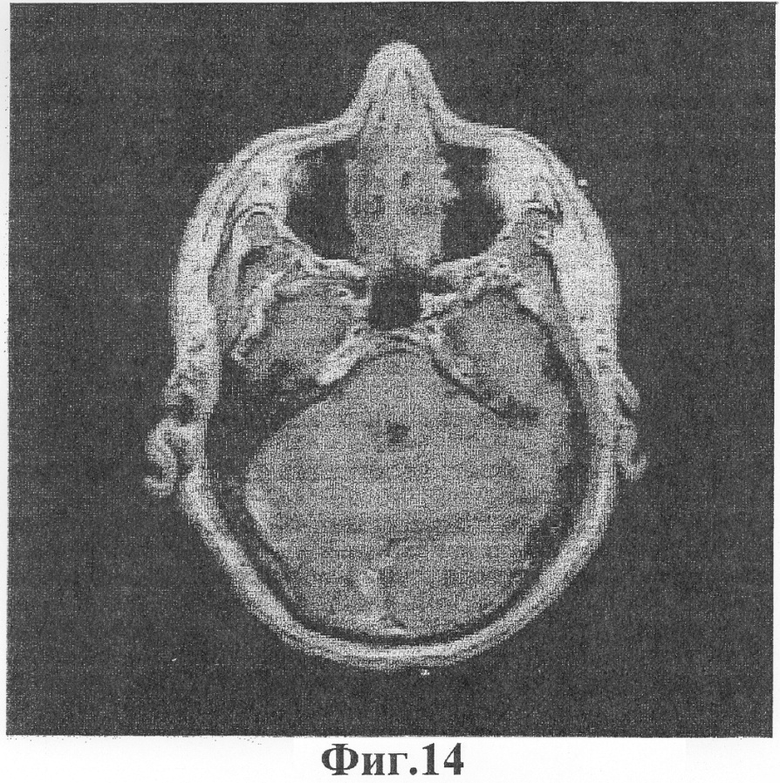
Фиг.14 - магниторезонансное изображение (МРИ, MRI) человеческой головы.
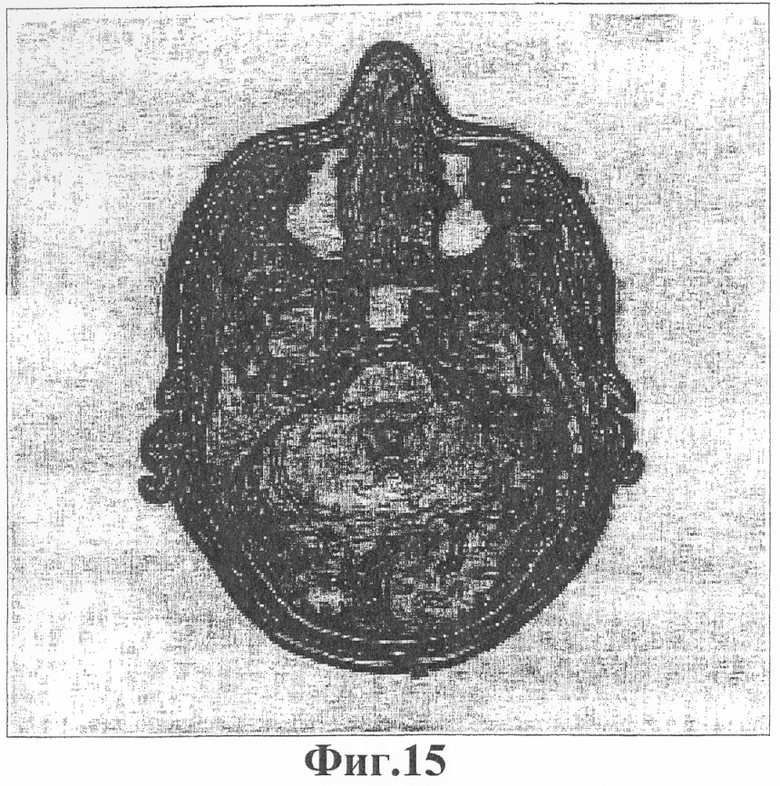
Фиг.15 - изображение человеческой головы, обработанное для усиления краевых характерных черт.
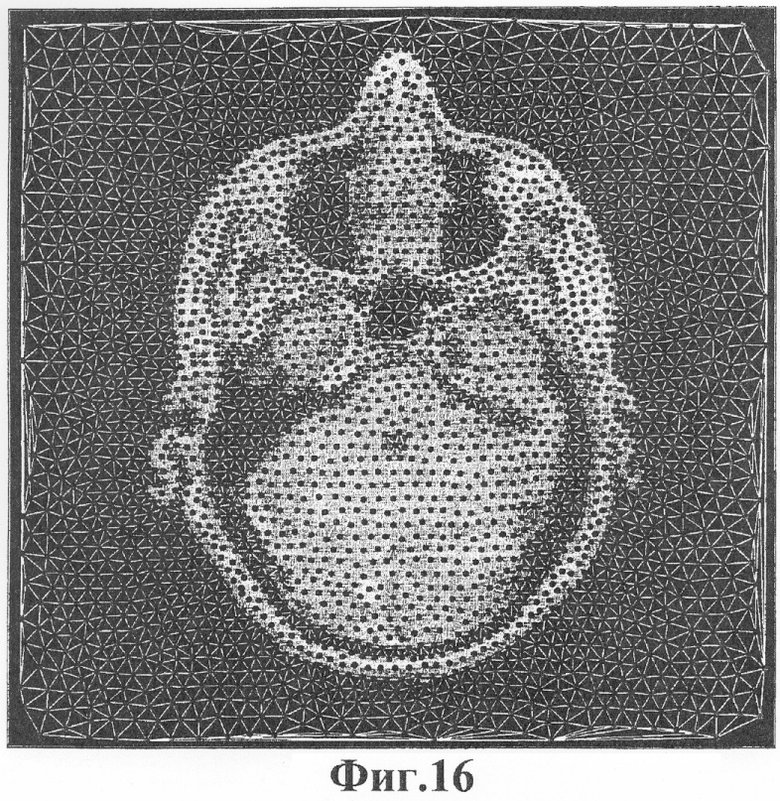
Фиг.16 - сетка, совмещенная с характерными чертами изображения человеческой головы.
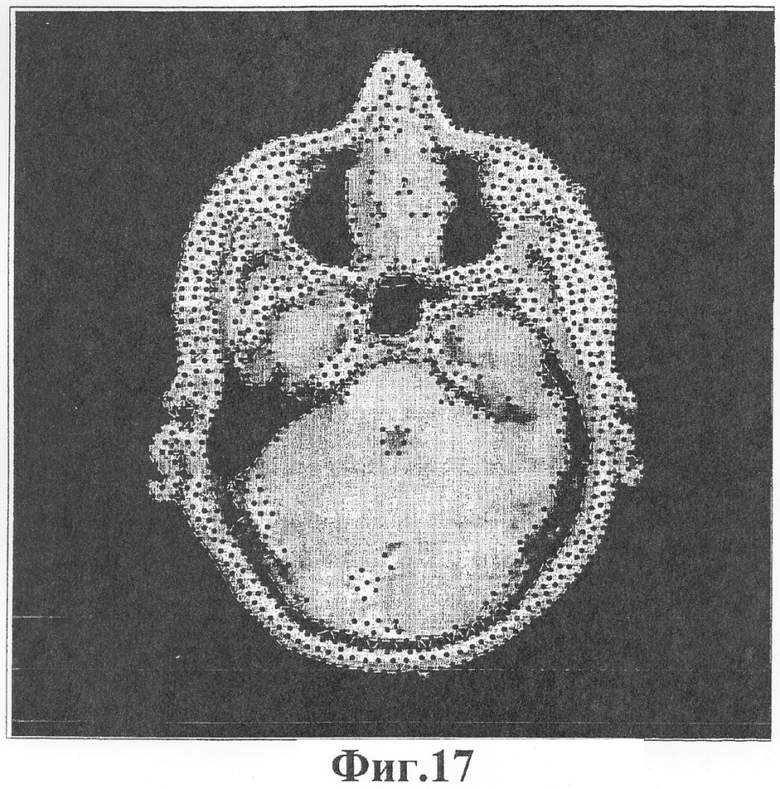
Фиг.17 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в изображении человеческой головы.
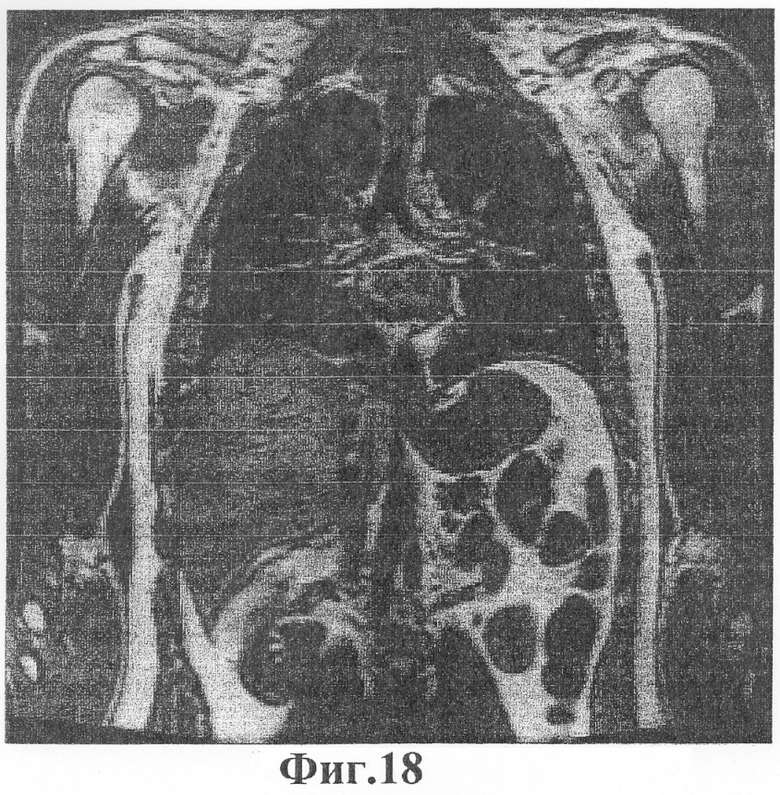
Фиг.18 - магниторезонансное изображение (МРИ) человеческого торса.
Фиг.19 - изображение человеческого торса, обработанное для усиления краевых признаков.
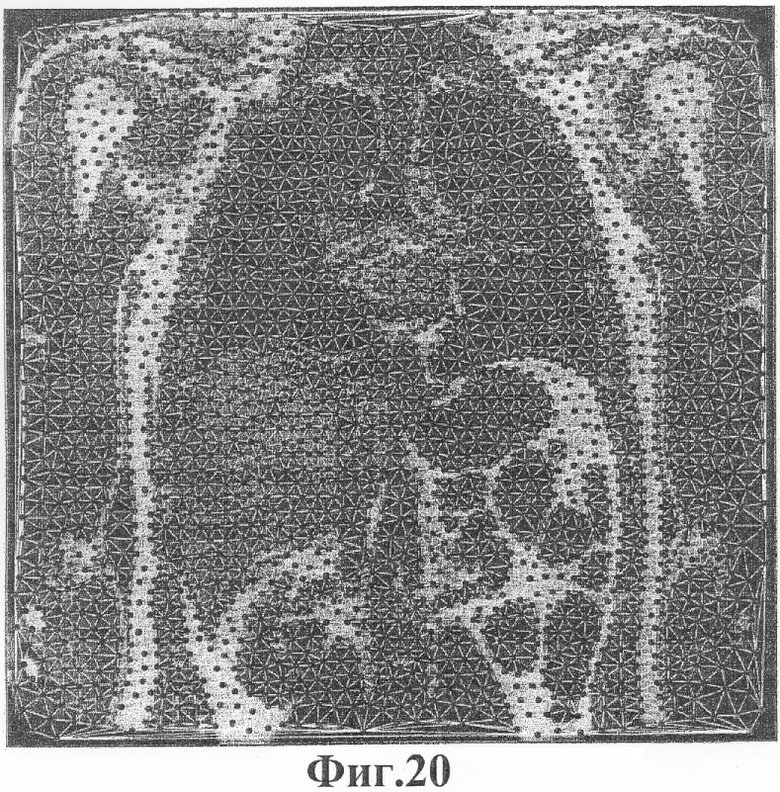
Фиг.20 - сетка, совмещенная с характерными чертами изображения человеческого торса.
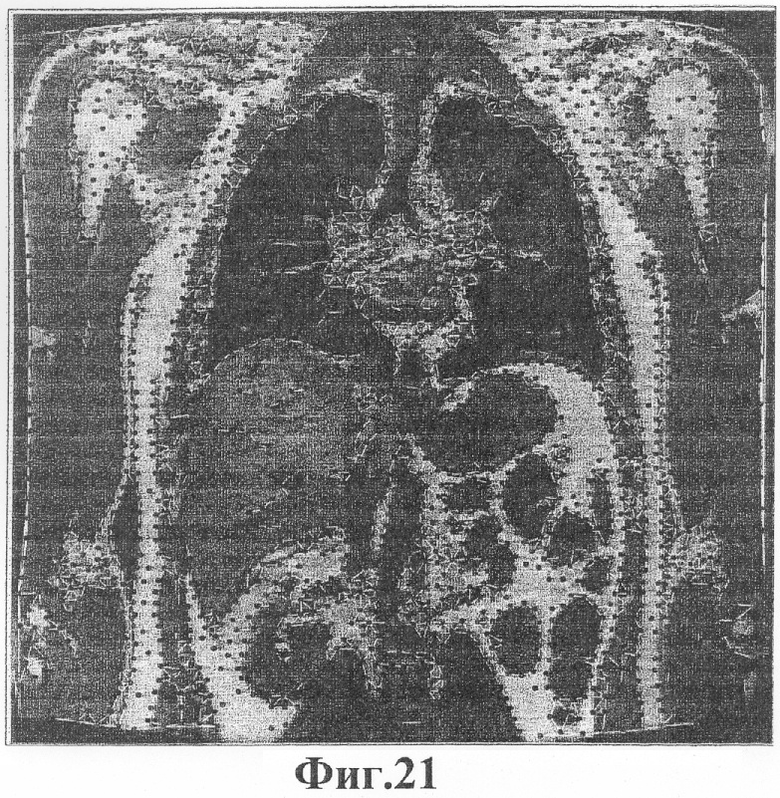
Фиг.21 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в изображении человеческого торса.
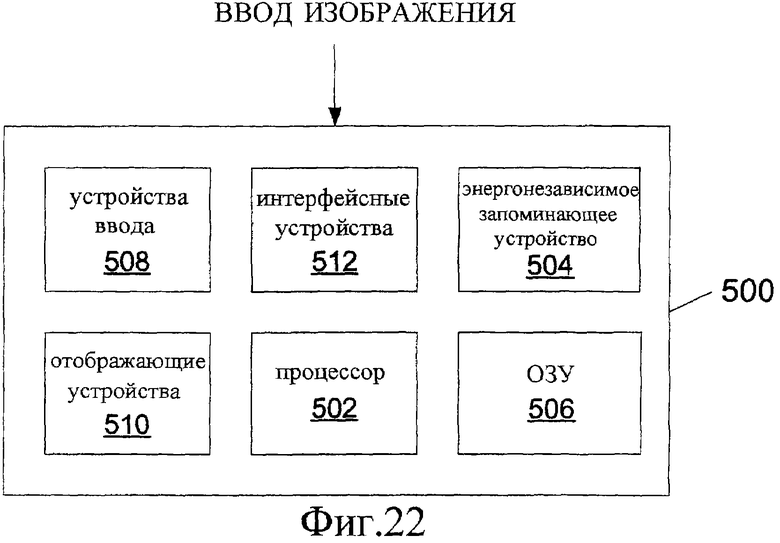
Фиг.22 - компоненты вычислительного устройства, использованные для реализации способа по данному изобретению.
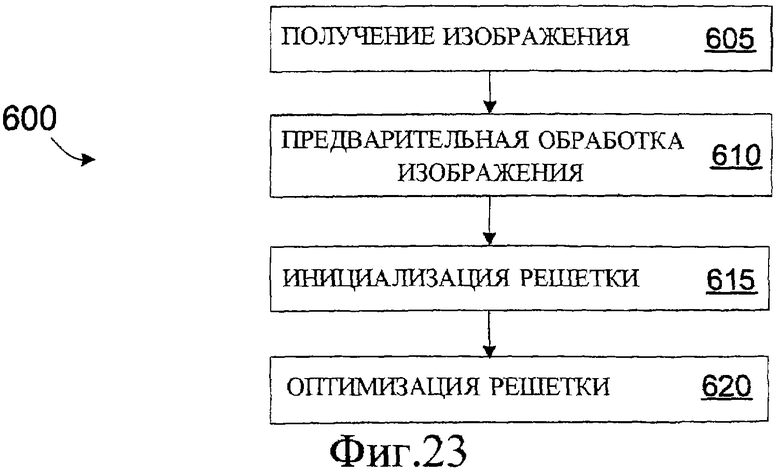
Фиг.23 - вариант осуществления способа по данному изобретению.
Хотя изобретение допускает различные модификации и альтернативные формы, конкретные варианты его осуществления показаны посредством примеров на чертежах и будут здесь описаны подробно. Следует понимать, однако, что чертежи и их подробное описание не предназначены для ограничения изобретения раскрытыми конкретными формами, но напротив, изобретение охватывает все модификации, эквиваленты и альтернативные варианты, отвечающие сущности и объему настоящего изобретения, как оно определено приложенной формулой изобретения.
Подробное описание предпочтительных вариантов осуществления
Здесь описывается способ генерирования решетки узлов, который учитывает характерные черты в цифровом изображении. Этот способ содержит инициализацию, а затем оптимизацию решетки узлов. В одном наборе вариантов осуществления узлы оптимизированной решетки стремятся совместиться (совпасть) с характерными чертами в изображении. Во втором наборе вариантов осуществления узлы оптимизированной решетки стремятся выстроиться вблизи характерных черт в изображении, но не совпасть с ними. В других вариантах осуществления узлы оптимизированной решетки могут стремиться совместиться с некоторыми характерными чертами и не совместиться с другими характерными чертами в том же самом изображении.
Здесь и далее заявители называют узлы решетки атомами. Заявители описывают процесс инициализации решетки в терминах атомных структур кристаллов. Подобным же образом они описывают оптимизацию решетки в терминах минимизации потенциальной энергии атомной решетки. Эти физические модели делают данное описание более легким для понимания, но атом в контексте данного изобретения является просто узлом.
Фиг.1 иллюстрирует более подробно поток данных между первичными компонентами данного способа. Компонент 100 ввода данных вырабатывает изображение, которое обрабатывают где-то в другом месте для выделения вызывающих интерес характерных черт. Здесь изображение либо получают непосредственно как результат этой обработки, либо загружают из компьютерной памяти. Инициализатор 200 решетки создает исходную решетку атомов, которая охватывает изображение. Оптимизатор 300 решетки перемещает атомы так, чтобы решетка совместилась с характерными чертами в изображении. Компонент 400 вывода данных потребляет оптимизированную решетку атомов, либо передавая ее на какую-то иную обработку, либо сохраняя ее в компьютерной памяти.
Оптимизатор 300 решетки содержит минимизатор 310 порождающей функции и вычислитель 320 потенциальной энергии. Минимизатор 310 обобщенной функции итеративно ищет минимум функции многих переменных. Во время этого поиска данный минимизатор требует повторных оценок данной функции и ее частных производных по каждой переменной. Здесь переменными являются пространственные координаты атомов в решетке. При заданных координатах атомов и изображении вычислитель 320 потенциальной энергии оценивает потенциальную энергию решетки и частную производную этой энергии по координате каждого атома.
Вычисление потенциальной энергии
Атом в двумерном пространстве имеет координаты x и y, а атом в трехмерном пространстве имеет координаты x, y и z. Вектор х обозначает пространственные координаты x и y (или x, y и z) узла в двумерном (или трехмерном) пространстве. Пусть заданы два атома с местоположениями xi и xj, тогда выражение |xi-xj| обозначает расстояние между ними. В предпочтительном варианте осуществления норма |·| вектора, используемая для вычисления этого межатомного расстояния, является эвклидовой нормой. Однако вместо нее может использоваться любая из множества других норм.
Двухточечные потенциальные функции
Для эффективности вычислений заявители моделируют взаимодействие между атомами с помощью простой двухточечной силовой функции, такой, что полная сила, прикладываемая к атому его соседями, является просто суммой сил, прикладываемых каждым из них. Даже при этом упрощении имеется много обоснованных вариантов выбора для двухточечной силовой функции.
Чтобы избежать ситуации, когда два или более атомов имеют те же самые или почти те же самые координаты, сила между ними может быть отталкивающей (положительной), если они находятся слишком близко друг к другу. Аналогично, чтобы предотвратить большие пустые пространства без атомов, сила между двумя атомами может быть притягивающей (отрицательной), если они находятся слишком далеко друг от друга. Для облегчения численных вычислений эта сила может быть ограничена. Для предотвращения того, чтобы каждый атом в решетке воздействовал на каждый другой атом с некоторой силой, эта сила может быть нулевой за пределами расстояния отсечки. Далее, силовая функция может быть непрерывной как функция межатомного расстояния. Силовая функция, предложенная Shimada (1993), имеет эти свойства. Таким образом, в одном наборе вариантов осуществления заявители используют силовую функцию Симада, что описано ниже. Однако можно применять любую из множества силовых функций, соответствующих этим свойствам.
Пусть d обозначает номинальное расстояние между двумя атомами, т.е. расстояние, на котором сила переходит от отталкивающей к притягивающей. Тогда сила f между двумя атомами, расположенными в xi и xj, может быть задана кубическим полиномом:
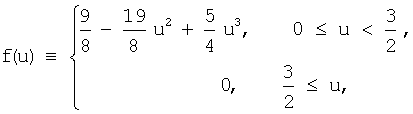
где u - нормированное расстояние между двумя атомами, определяемое выражением
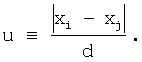
Коэффициенты этой полиномиальной функции гарантируют, что сила ограниченна и непрерывна, что она равна нулю при u=1 и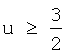 
, и что она положительна для 0≤u<1 и отрицательна для 
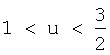. Фиг.2а иллюстрирует эту силовую функцию.
Вообще, сила, действующая на атом, является вектором. Здесь направление этого вектора определяется знаком f(u) и местоположениями xi и хj, двух атомов.
Более удобно работать со скалярным потенциалом, чем со множеством компонентов вектора силы. Поэтому, следуя общеизвестному соглашению, заявители определяют силу как градиент скалярного потенциала, взятый со знаком "минус":
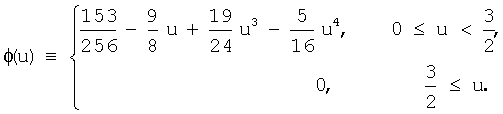
Постоянная интегрирования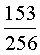 
выбрана так, чтобы φ(u) была непрерывна при 
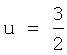. Фиг.2b иллюстрирует эту потенциальную функцию. Как ожидается, потенциальная функция φ(u) имеет минимум на нормированном расстоянии u=1, где силовая функция f(u) равна нулю.
Потенциальные энергии и потенциальные поля
При заданной потенциальной функции φ(u) от нормированного расстояния и заявители определяют потенциальную энергию атомов следующей суммой потенциалов попарного взаимодействия:
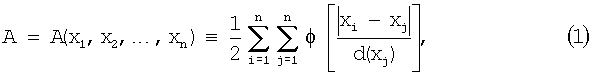
где x1, x2, ..., xn являются координатами n атомов в решетке, а d(x) - функция номинального межатомного расстояния от положения х. Функция d(x) номинального расстояния не обязательно должна быть постоянной; но чтобы гарантировать гладко изменяющуюся решетку, заявители требуют, чтобы она была гладкой. Конкретно, они требуют, чтобы |▿d|≪1, так что d(xi)≈d(xj) для |xi-xj|/d меньше, чем расстояние 3/2 отсечки потенциальной функции φ(u). Далее, множитель 1/2 компенсирует появление φ[|xi-xj|/d(xj)]≈φ[|xi-xj|/d(xi)] дважды в определении полной потенциальной энергии А.
Можно также определить потенциальную энергию А атомов в терминах потенциального поля атомов:
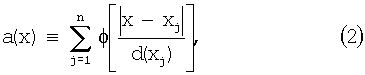
так что
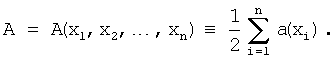
Иными словами, потенциальная энергия атомов определяется как половина суммы значений, полученных оцениванием потенциального поля атомов в координатах атомов.
Аналогично, определяют потенциальную энергию изображения:
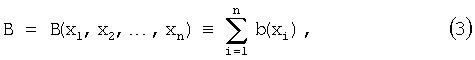
где b(x) - потенциальное поле изображения, основанное на входном изображении.
Во многих контекстах потенциальное поле изображения представляет собой просто изображение (или сглаженный вариант изображения), обычно представленный двумерным (или трехмерным) массивом чисел, хранящимся в компьютерной памяти. Здесь заявители используют термин "потенциальное поле", чтобы подчеркнуть (а позже применить) сходство между потенциальными полями атомов и изображения.
В одном наборе вариантов осуществления предполагается, что изображение обработано так, что потенциальное поле изображения достигает минимального значения (например, b(x)≈-1) в пределах вызывающих интерес характерных черт и максимального значения (например, b(x)≈0) в не вызывающих интерес областях. В этом случае минимизация потенциальной энергии В изображения эквивалентна перемещению атомов в минимумы, соответствующие вызывающим интерес характерным чертам в изображении.
Во втором наборе вариантов осуществления предполагается, что изображение обработано так, что потенциальное поле изображения достигает максимального значения (например, b(x)≈1) в пределах вызывающих интерес характерных черт и минимального значения (например, b(x)≈0) в не вызывающих интерес областях. В этом случае минимизация потенциальной энергии В изображения эквивалентна перемещению атомов в максимумы, соответствующие вызывающим интерес характерным чертам в изображении.
В третьем наборе вариантов осуществления потенциальное поле изображения может достигать максимального значения (например, b(х)≈1) вдоль первого поднабора характерных черт изображения, минимального значения (например, b(x)≈-1) вдоль второго поднабора характерных черт изображения и промежуточного значения (например, b(x)≈0) вне этих характерных черт изображения.
В более общем виде заявители перемещают атомы с целью минимизации следующей взвешенной суммы потенциальных энергий атомов и изображения:
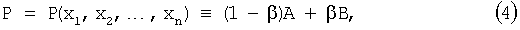
которую называют полной потенциальной энергией. Масштабирующий множитель β определяет относительные вклады А и В в полную потенциальную энергию Р. Когда β=0, атомы стремятся к совершенно регулярной решетке, которая не совмещена с изображением. Когда β=1, атомы восприимчивы только к значениям выборок изображения; т.е. атомы перемещаются только на основании их притяжения к минимумам в изображении и/или их отталкивания от максимумов в изображении. Таким образом, атомы стремятся скапливаться в минимумах и освобождать максимумы в изображении, давая очень нерегулярную решетку. Обычно выбирают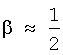 
и получаем решетку, которая приблизительно регулярна и учитывает характерные черты изображения.
В терминах потенциальных полей а(х) и b(х) полная потенциальная энергия составляет:
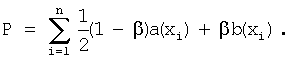
В терминах полного потенциального поля, определенного как
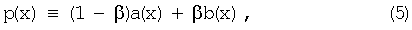
полная потенциальная энергия равна
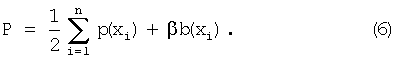
Как и для функции d(x) номинального расстояния, масштабирующий множитель β в уравнениях (5) и (6) может быть гладко изменяющейся функцией от положения х. (Что касается d(x), гладкость подразумевает, что производные от β(х) пренебрежимо малы.) Это обобщение обеспечивает баланс между регулярностью решетки и ее восприимчивостью (т.е. притяжением к или отталкиванием от) к пространственно меняющимся характерным чертам изображения. Восприимчивость решетки к характерным чертам изображения может быть важнее в одной части изображения, нежели в какой-либо иной его части. Для простоты заявители определяют здесь β как постоянный масштабирующий множитель.
Полная потенциальная энергия Р является неквадратичной функцией от координат x1, x2, ..., хn атомов со множеством локальных минимумов. (К примеру, отметим, что взаимное изменение координат любых двух атомов не меняет Р.) Поэтому любой поиск минимума, обычно близкого к координатам исходной решетки, должен быть итеративным. При эффективном итеративном поиске нужно неоднократно оценивать частные производные от Р по отношению к координатам атомов. Рассмотрим, к примеру, изменение в Р по отношению к х-координате i-го атома:
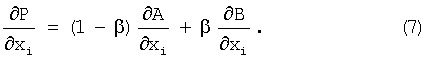
При оценивании частной производной ∂А/∂хi потенциальной энергии атомов вспоминают, что выражение φ[|xi-xj|/d(xj)]≈φ[|xi-xj|/d(xi)] появляется дважды в двойной сумме уравнения (1).
Поэтому,
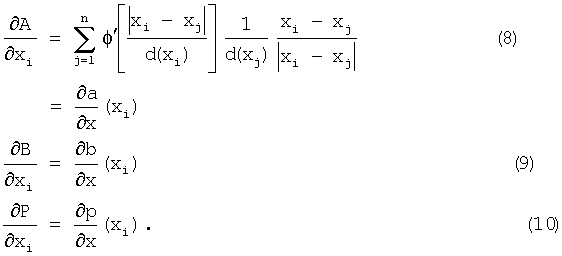
Аналогичные результаты можно легко получить для частных производных по координате у (а для трехмерного случая - z) - каждого атома.
Вычисление
Вычисление полной потенциальной энергии Р требует вычисления ее компонентов А и В. Чтобы вычислить потенциальную энергию В изображения согласно уравнению (3), нужно оценить потенциальное поле b(х) изображения для местоположения х=xi каждого атома. Изображения обычно дискретизируют равномерно, и простейшим и наиболее эффективным приближением к b(xi) является значение потенциального поля b(х) изображения в выборке изображения, ближайшей к узлу xi. Возможны и более точные приближения (интерполяции), но заявители использовали эту простую и быструю интерполяцию к ближайшему соседу во всех показанных здесь примерах. Уравнение (3) предполагает, что стоимость (вычислительная сложность) вычисления В - О(n), где n - число атомов.
Наоборот, двойная сумма в уравнении (1) предполагает, что стоимость наиболее прямого метода вычисления А составляет O(n2). В практических применениях n достаточно велико, так что стоимость O(n2) вычисления А становится много больше, чем стоимость O(n) оценивания В. Для снижения стоимости вычисления А можно применить представленную конструкцию потенциальной функции φ(u), которая равна нулю для нормированных расстояний и больших, чем расстояние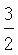 
отсечки. Только атомы, ближайшие к атому, расположенному в положении х=хi, вносят вклад в потенциальное поле a(xi) атомов в этом положении.
Это замечание приведет к задаче определения того, какие атомы-соседи находятся в пределах расстояния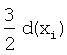 
от каждого атома, расположенного в x=xi. Решение этой задачи нетривиальное, потому что атомы перемещаются неоднократно во время оптимизации решетки.
К примеру, если формируют списки соседних атомов, по одному списку для каждого атома, нужно обновлять эти списки (или по меньшей мере проверять, не требуют ли они обновления) при любых перемещениях атомов. Для решеток с плотностью, близкой к постоянной, стоимость формирования и обновления таких списков, использующих простые структуры данных, представляет собой O(mn), где m - среднее число соседних атомов в пределах расстояния отсечки. Для решеток с переменной плотностью требуются более сложные структуры данных, и стоимость становится O(mnlogn). (См., например, Bentley, J.L., and Friedman, J.H., Data Structures for Range Searching, Computing Surveys, Vol.11, no.4, 1979. См. также патент США №4908781 на имя Levinthal, С., and Fine, R., Computing Device for Calculating Energy and Pairwise Central Forces of Particle Interactions, 1990, и патент США №5596511 на имя Toyoda, S., Ikeda, H., Hashimoto, E., and Miyakawa, N., Computing Method and Apparatus for a Many-Body Problem, 1997.)
Представленное выражение для потенциальной энергии А атомов в терминах потенциального поля а(х) атомов предлагает более простое решение. Заявители интерпретируют уравнение (2) как рецепт для вычисления потенциального поля а(х) атомов, которое дискретизируют подобно потенциальному полю b(х) изображения. Конкретно, представляют а(х) с помощью двумерного или трехмерного массива, имеющего те же самые размерности, что и массив, использованный для представления изображения h(x). Сначала инициализируют а(х) нулем для всего дискретного набора х. Затем для каждого атома, расположенного в положении х=хj, суммируют нарастающим итогом дискретизированную потенциальную функцию φ[|x-xj|/d(xj)]. Это суммирование нарастающим итогом ограничивается пространственно до выборок внутри круга (или сферы) радиуса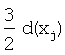 
с центром в положении хj, где вклад дискретизированной потенциальной функции ненулевой.
Фиг.3а и 3b иллюстрируют две такие потенциальные функции для номинальных расстояний d=4 и d=8 соответственно. Уровни серого между черным и белым соответствуют значениям дискретизированной функции между -0,05 и 0,05 соответственно. Потенциальное поле а(х) атомов представляет собой просто результат суммирования нарастающим итогом множества таких функций. Для вычислительной эффективности эти дискретизированные потенциальные функции могут быть заранее вычислены и затабулированы для различных номинальных расстояний d. Затем, задавая d(x) для любого местоположения х, соответствующие значения потенциальной функции можно эффективно определить путем табличного просмотра (или путем табличного просмотра и интерполяции).
Предпочтительный вариант осуществления
Представленный анализ предлагает два совершенно разных алгоритма для вычисления полной потенциальной энергии и ее частных производных. Предпочтительный вариант осуществления данного изобретения использует уравнения (2) и (5) для вычисления полного потенциального поля р(х), а затем использует уравнение (6) для вычисления полной потенциальной энергии и уравнение (10) для вычисления ее частных производных. Нижеследующий листинг псевдокодов подробнее описывает этот алгоритм.
АЛГОРИТМ 1: ВЫЧИСЛИТЬ Р,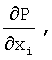 
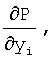И 
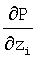
101: инициализируют полное потенциальное поле р(х)=βb(х)
102: для всех местоположений xj=x1, x2, ..., xn атомов {
103: для всех х таких, что |x-xj|< {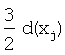
104: суммируют р(х)=р(х)+(1-β)φ[|x-xj|/d(xj)] нарастающим итогом
105: }
106: }
107: инициализируют полную потенциальную энергию Р=0
108: для всех местоположений xj=x1, x2, ..., xn атомов {
109: суммируют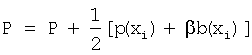 
110: вычисляют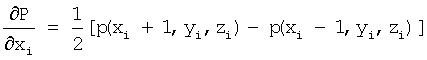 
111: вычисляют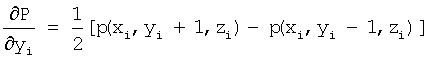 
112: вычисляют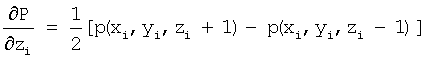 
113: }
Строки 101-106 вычисляют полное потенциальное поле р(х), дискетизированное так же, как потенциальное поле b(х) изображения. При задании этого поля строки 107-113 вычисляют полную потенциальную энергию Р и ее частные производные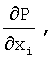 
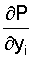и 
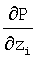. В строке 109 значения полного потенциального поля и потенциального поля изображения в местоположении xi можно аппроксимировать, как упомянуто выше, путем выбора соответствующих значений поля в ближайшем положении выборки изображения либо посредством любой желаемой схемы интерполяции. Частные производные в строках 110-112 вычисляют из полного потенциального поля с помощью простых приближений центрированных конечных разностей; однако вместо этого могут использоваться альтернативные (например, более высокого порядка) численные приближения производных. Для определенности, в этом листинге предполагается трехмерное координатное пространство. Для двумерного пространства координаты z и частные производные 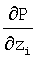просто игнорируются.
В предположении, что местоположения атомов согласуются с функцией d(x) номинального расстояния, вычислительная сложность Алгоритма 1 составляет O(N), где N - число выборок в изображении. Вспомним, что дискретизировали полное потенциальное поле так же, как и изображение, и что каждый атом вносит вклад в виде пространственно ограниченной потенциальной функции (наподобие функции на фиг.3) в те выборки в полном потенциальном поле, которые лежат ближе всего к этому атому. Поэтому стоимость суммирования нарастающим итогом вкладов от всех атомов пропорциональна числу выборок N в этом поле.
Стоимость этого алгоритма сравнима со стоимостью обычной обработки изображений, и он требует структуры данных не сложнее, чем простой массив, который представляет изображение. Более того, для функций d(x) непостоянного номинального расстояния стоимость та же самая, что и для постоянного номинального расстояния d.
Альтернативный вариант осуществления
Альтернативный вариант осуществления данного изобретения не вычисляет полного потенциального поля. Вместо этого он использует уравнения (7), (8) и (9), чтобы вычислить его частные производные. Нижеследующий листинг псевдокодов описывает этот алгоритм подробнее.
АЛГОРИТМ 2: ВЫЧИСЛИТЬ Р,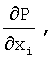 
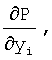И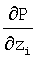
201: инициализируют полную потенциальную энергию Р=0
202: для всех местоположений xj=x1, x2, ..., хn атомов {
203: суммируют P=P+βb(xi) нарастающим итогом
204: инициализируют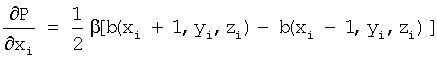 
205: инициализируют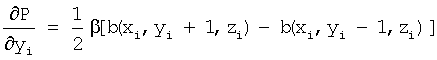 
206: инициализируют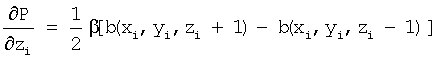 
207: для всех местоположений хj атомов таких, что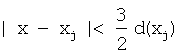 
{
208: суммируют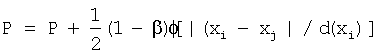 
нарастающим итогом
209: вычисляют Δ=(1-β)φ'[|xi-xj|/d(xi)]/[d(xi)|xi-xj|]
210: суммируют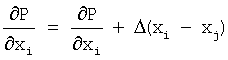 
нарастающим итогом
211: суммируют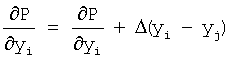 
нарастающим итогом
212: суммируют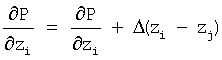 
нарастающим итогом
213: }
214: }
Для каждого атома строка 203 суммирует нарастающим итогом потенциальную энергию В изображения, а строка 208 суммирует нарастающим итогом потенциальную энергию А атомов для каждого соседнего атома в полную потенциальную энергию Р. Аналогично, строки 204-206 и 210-212 суммируют нарастающим итогом вклады от частных производных полной энергии изображения и атомов в частные производные полной потенциальной энергии.
Строка 207 подразумевает использование вспомогательной структуры данных, которая позволяет быстро определять соседние атомы, ближайшие к атому, расположенному в х=хi. Эта структура данных должна переформировываться или каким-то образом обновляться при любом перемещении атомов. Атомы перемещаются неоднократно при любом итерационном поиске координат атомов, которые минимизируют полную потенциальную энергию. Поэтому стоимость поддержания этой структуры данных может быть значительной. Для наиболее эффективных структур данных стоимость выше для функций d(x) непостоянного номинального расстояния, нежели для постоянного номинального расстояния d.
Инициализация решетки
Как отмечено выше, полная потенциальная энергия Р является неквадратичной функцией координат атомов со множеством локальных минимумов. Во время оптимизации решетки итеративно перемещают атомы при поиске минимума. На практике не ищут и не находят глобальный минимум. Вместо этого заявители находят оптимизированную решетку атомов, которая близка к исходной решетке. Поэтому желательно, чтобы исходная решетка:
- минимизировала (локально) потенциальную энергию атомов,
- была в высокой степени регулярной, и
- была совместима с функцией d(x) номинального расстояния.
Постоянное номинальное расстояние
Для постоянного номинального расстояния d можно легко построить исходную решетку с этими свойствами. Фиг.4 иллюстрирует такую решетку для двумерного пространства. В этой идеальной решетке атомы могут соединяться для образования равносторонних треугольников. Расстояние между любым атомом и его шестью ближайшими соседями является просто постоянным номинальным расстоянием d. На этом расстоянии сила, прикладываемая любым атомом к другому, в точности равна нулю, и потенциальная энергия атомов локально минимизируется.
Фиг.5 иллюстрирует регулярную решетку для трехмерного пространства. Это гранецентрированная кубическая (ГЦК, FCC) решетка, в которой атомы размещены в горизонтальных слоях, которые выглядят как двумерная решетка по фиг.4, но каждый слой слегка сдвинут для заполнения свободного пространства между слоями выше и ниже. Для ясности на фиг.5 атомы различных слоев визуализированы сферами, окрашенными в разные оттенки серого. Расстояние между любым атомом и его двенадцатью ближайшими соседями равно постоянному номинальному расстоянию d.
В противоположность равносторонним треугольникам, которые могут заполнять двумерное пространство полностью (как на фиг.4), равносторонние тетраэдры не могут заполнить трехмерное пространство. Тем не менее, атомы в решетке ЦСК можно триангулировать, чтобы получить в высокой степени регулярные тертаэдры.
Переменное номинальное расстояние
Исходное размещение атомов более трудно для функции d(х) непостоянного номинального расстояния.
Первая сложность состоит в том, что эта функция d(x) должна вычисляться, если она не определена иным образом. В качестве примера того, как можно вычислить эту функцию, рассмотрим изображение (например, потенциальное поле b(x) изображения), отображенное на фиг.6. Это изображение является горизонтальным срезом трехмерного сейсмического изображения (не показано), которое было обработано для выделения дефектов, разрывов в подземной геологии. Темные линейные характерные черты на этом изображении представляют следы дефектов, которые пересекают этот горизонтальный срез. Эти дефекты приблизительно вертикальны, почти ортогональны к этому горизонтальному срезу.
Фиг.7 показывает результат сглаживания сейсмического изображения с целью получения оценки функции d(x) номинального расстояния. Самые темные области на этом чертеже соответствуют минимальному расстоянию d=6 выборок, а самые светлые области соответствуют максимальному расстоянию d=18 выборок. Эти минимальное и максимальное расстояния были заданы явно на основании уровня детализации, который наблюдали в сейсмическом изображении. Расстояния оказываются меньше в средней левой части изображения и больше в нижней правой части. Среднее расстояние составляет приблизительно 9,7 выборок.
В некоторых применениях функция d(x) номинального расстояния может быть явно задана или построена интерактивно с помощью компьютерной программы, предназначенной для раскраски изображения. Что касается настоящего изобретения, то реальный способ, которым вычисляется функция d(x), не является существенным. Как утверждалось выше, заявители требуют только, чтобы эта функция была гладкой, т.е. чтобы |▿d|≪1.
Вторая сложность состоит в том, чтобы размещение атомов в решетке соответствовало функции d(x) номинального расстояния. Заявители описывают здесь два алгоритма для этого размещения.
Предпочтительный вариант осуществления
Предпочтительный вариант осуществления данного изобретения использует алгоритм генерирования псевдорегулярных решеток. Нижеследующий листинг псевдокодов подробнее описывает этот алгоритм.
АЛГОРИТМ 3: ИНИЦИАЛИЗИРОВАТЬ ПСЕВДОРЕГУЛЯРНУЮ РЕШЕТКУ
301: инициализируют подобный изображению массив булевых флагов w(x)=false (ложно)
302: формируют пустой список атомов
303: формируют пустую очередь атомных узлов
304: соединяют местоположение xi центра изображения к этой очереди
305: пока очередь не пустая {
306: извлекают и удаляют xi первого узла из очереди
307: если xi лежит в координатных границах изображения {
308: устанавливают сфера = сферическая область диаметром γd(xi) с центром в xi
309: если для всех выборок внутри сферы w(x)=false (ложно) {
310: для всех выборок внутри сферы устанавливают w(x)=true (истинно)
311: присоединяют атом с координатами xi к списку
312: присоединяют идеальные узлы для соседних атомов к концу очереди
313: }
314: }
315: }
Массив w(x), инициализированный в строке 301, является временным рабочим массивом с размерностями, равными размерностям изображения. Его единственное назначение состоит в том, чтобы пометить местоположения атомов в решетке по мере их генерирования алгоритмом. (Проверка в строке 309 гарантирует, что местоположения, помеченные таким образом, не будут помечаться снова.) В предпочтительном варианте осуществления данного изобретения этот массив может быть тем же самым, что и массив, используемый для сохранения полного потенциального поля р(х) в Алгоритме 1, так что не потребуется дополнительной памяти. Фиг.8 показывает пример массива w(x), вычисленного для функции номинального расстояния по фиг.7.
Каждая круговая область на фиг.8 имеет центр в местоположении атома и диаметр, пропорциональный значению функции d(x) номинального расстояния в этом местоположении атома. Постоянная пропорциональность имеет множитель γ в строке 308 этого алгоритма. Выбором значения этого множителя, меньшего, чем единица, разрешают некоторым атомам в исходной решетке быть ближе друг к другу, чем подразумевается функцией d(х) номинального расстояния, с учетом того, что остальные атомы будут удалены. Заявители определили экспериментально, что множитель γ=0,8 дает псевдорегулярные решетки, совместимые со сглаженными функциями d(х) номинального расстояния.
Идеальные узлы в строке 312 являются местоположениями соседних атомов в регулярных решетках, показанных на фиг.4 и 5. (Расстояния до этих соседних атомов не масштабируются множителем γ.) Поэтому для постоянной d Алгоритм 3 дает регулярную решетку, подобную одной из этих. Для непостоянной d(x) он дает псевдорегулярную решетку.
В любом случае обработка идеальных узлов в очереди заставляет решетку расти вовне из первого узла, помещенного в очередь. Поэтому первый узел действует как семя, из которого растет решетка. Строка 304 Алгоритма 3 выбирает, чтобы первый узел был центром изображения. Можно использовать альтернативные местоположения семян. К примеру, если желательна сетка для моделирования потока жидкости, тогда местоположения одного или более источников жидкости могут использоваться в качестве источника роста решетки. В качестве другого примера в качестве местоположения семени можно выбрать центр масс характерных черт в изображении.
Сетка, показанная на фиг.9, является триангуляцией Делонэ для псевдорегулярной решетки, созданной с помощью Алгоритма 3 и функции номинального расстояния, показанной на фиг.7. Хотя большинство треугольников в этой сетке исходной решетки являются в высокой степени регулярными, полная триангуляция Делонэ, показанная здесь, дает некоторое количество длинных тонких треугольников вблизи выпуклого каркаса узлов решетки. Такие нерегулярные треугольники вблизи границ сетки можно просто игнорировать в последующих вычислениях.
Альтернативный вариант осуществления
Альтернативный вариант осуществления данного изобретения использует совершенно отличный алгоритм для генерирования псевдослучайных исходных решеток. Нижеследующий листинг псевдокодов подробнее описывает этот алгоритм.
АЛГОРИТМ 4: ИНИЦИАЛИЗИРОВАТЬ ПСЕВДОСЛУЧАЙНУЮ РЕШЕТКУ
401: формируют пустой список атомов
402: для всех х, дискретизированных изображением {
403: устанавливают d=d(x)
404: если двумерная, устанавливают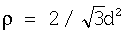 
405: если трехмерная, устанавливают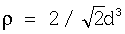 
406: генерируют псевдослучайное число г, равномерно распределенное в [0:1)
407: если r<р, добавляют атом, расположенный в х, в список
408: }
Строка 404 (для двумерных изображений) или 405 (для трехмерных изображений) этого алгоритма вычисляет номинальную плотность ρ решетки, соответствующую значению функции d(x) номинального расстояния. В двумерном пространстве плотность решетки обратно пропорциональна квадрату расстояния между атомами; в трехмерном пространстве она обратно пропорциональна кубу расстояния. Постоянные пропорциональности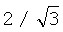 
(строка 404) и 
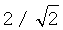(строка 405) соответствуют идеальным решеткам, показанным на фиг.4 и 5 соответственно.
Плотность решетки является вероятностью того, что атом находится в любом местоположении, дискретизированном изображением. Строки 406 и 407 используют генератор псевдослучайных чисел, чтобы добавить к решетке атом с этой вероятностью. Данный алгоритм использует обыкновенное компьютерное программное обеспечение для генерирования псевдослучайного числа, равномерно распределенного в интервале [0:1).
Данный псевдослучайный алгоритм проще и быстрее, чем псевдорегулярный Алгоритм 3. Он также генерирует исходные решетки, которые полностью изотропны, без предпочтительных направлений или плоскостей симметрии, характерных для псевдорегулярных решеток. В зависимости от применения, это может быть, а может и не быть преимуществом.
К сожалению, псевдослучайная исходная решетка в высокой степени нерегулярна. Атомам в такой решетке не характерен геометрический шаблон, что делает полезное в иных отношениях выражение "псевдослучайная решетка" оксюмороном.
Фиг.10 показывает сетку, соответствующую псевдослучайной исходной решетке, сгенерированной для сейсмического изображения с помощью Алгоритма 4. Хотя эта сетка статистически совместима с функцией номинального расстояния, показанной на фиг.7, она в высокой степени нерегулярна, со множеством треугольников, которые далеки от равносторонних. Оптимизация решетки сделает эту псевдослучайную решетку более регулярной, но потребует больше работы (больше итераций), нежели оптимизация псевдорегулярной исходной решетки, показанной на фиг.9.
Оптимизация решетки
Оптимизатор решетки перемещает атомы в исходной решетке, чтобы получить оптимизированную решетку. В одном наборе вариантов осуществления оптимизированная решетка и регулярна, и в большей степени совмещена с характерными чертами изображения, чем исходная решетка. Другими словами, атомы в оптимизированной решетке вдали от характерных черт изображения стремятся к псевдорегулярной структуре, которая учитывает функцию номинального расстояния, тогда как атомы вблизи характерных черт изображения стремятся совпасть с этими характерными чертами. В другом наборе вариантов осуществления оптимизированная решетка и регулярна, и более разрежена вдоль характерных черт изображения, чем исходная решетка. Оптимизатор решетки использует обыкновенное компьютерное программное обеспечение для минимизации произвольной функции многих переменных. Оптимизатор решетки применяет это программное обеспечение, чтобы минимизировать полную потенциальную энергию решетки, которая является функцией координат атомов.
Возможны разные варианты выбора для минимизатора обобщений функции. В предпочтительном варианте осуществления используют минимизатор с ограниченной памятью Бройдена-Флетчера-Гольдфарба-Шано (O-БФГШ, L-BFGS). (См., к примеру, Byrd, R.H., Nocedal, J., and Schnabel, R.B., Representations of Quasi-Newton Matrices and Their Use in Limited Memory Methods, Technical Report NAM-03, Northwestern University, Department of Electrical Engineering and Computer Science, 1996. Отметим, в частности, простую двуцикловую рекурсию на стр.17.) Подобно другим минимизаторам, способ O-БФГШ итеративно оценивает функцию и ее частные производные в процессе поиска минимума.
Минимизатор O-БФГШ требует больше компьютерной памяти, но меньше оценок функции, чем метод сопряженных градиентов, другой общеизвестный метод. Однако требуемая дополнительная память незначительна по сравнению с памятью, требуемой для представления изображения. Более того, каждая оценка функции (вычисление полной потенциальной энергии решетки) оказывается значительно более дорогостоящим, нежели стоимость других вычислений, выполняемых минимизатором. Поэтому минимизатор O-БФГШ хорошо подходит для этого изобретения.
Предпочтительный вариант осуществления
Предпочтительный вариант осуществления данного изобретения использует нижеследующий алгоритм для оптимизации решетки.
АЛГОРИТМ 5: ОПТИМИЗИРОВАТЬ РЕШЕТКУ
501: получают координаты x1, x2, ..., xn атомов исходной решетки
502: конструируют вычислитель потенциальной энергии
503: конструируют минимизатор
504: вычисляют полную потенциальную энергию Р исходной решетки
505: делают {
506: устанавливают Р0=Р
507: случайным образом нарушают порядок x1, х2, ..., xn
508: делают {
509: устанавливают Pi=P
510: разрешают минимизатору уменьшить Р посредством корректировки x1, х2, ..., xn
511: } пока Pi-P>∈|Pi|
512: } пока P0-P>∈|P0|
Этот алгоритм начинается в строке 501 с исходной решетки атомов, такой как псевдорегулярная решетка, выработанная Алгоритмом 3, или псевдослучайная решетка, генерированная Алгоритмом 4. Затем он формирует (строка 502) вычислитель потенциальной энергии, ответственный за вычисление полной потенциальной энергии Р и ее частных производных. Далее он конструирует (строка 503) минимизатор, который будет использовать вычислитель полной энергии для минимизации Р. (Конструирование вычислителя потенциальной энергии и минимизатора включает в себя выделение памяти и инициализацию нескольких переменных и таблиц.) Затем он вычисляет (строка 504) полную потенциальную энергию Р исходной решетки.
Остальная часть алгоритма содержит два вложенных цикла. Внутренний цикл, начинающийся в строке 508, разрешает минимизатору регулировать координаты x1, x2, ..., xn атомов, чтобы уменьшить полную потенциальную энергию Р. Этот цикл продолжается до тех пор, пока уменьшение Р не станет незначительным, что определено малым пороговым значением ∈ в строке 511. Обычно пороговое значение составляет ∈=0,001.
Вспомним, что полная потенциальная энергия является функцией со многими локальными минимумами. Внутренний цикл начинается с текущих координат атома и стремится к минимуму, ближайшему к этим координатам. Наблюдали, что этот локальный минимум может иметь полную потенциальную энергию больше, чем другой минимум поблизости.
Внешний цикл, начинающийся в строке 505, разрешает алгоритму перемещаться от одного локального минимума к другому до тех пор, пока уменьшение полной потенциальной энергии Р не станет незначительным. Случайные возмущения координат атомов в строке 507 малы, обычно не более 10% от номинального расстояния d(xi), для каждого местоположения xi атома. Использовали обыкновенный генератор псевдослучайных чисел для вычисления этих возмущений. Последующие итерации внутреннего цикла обычно дают значительное уменьшение в полной потенциальной энергии Р.
Внутренний и внешний циклы в Алгоритме 5 используют одну и ту же проверку на сходимость. Оба цикла завершаются, когда уменьшение полной потенциальной энергии Р становится незначительным. Альтернативные критерии сходимости являются обыкновенными в численной оптимизации, и выбор здесь не важен. К примеру, можно завершать эти циклы, когда максимальное изменение в координатах атома меньше, чем некоторое пороговое значение.
Фиг.11 показывает результат оптимизации исходной псевдорегулярной решетки для сейсмического изображения, когда это изображение обработано таким образом, чтобы иметь значения около минус единицы вдоль характерных черт изображения и около нуля вдали от признаков изображения. Вспомним уравнение (4), которое устанавливает, что полная потенциальная энергия Р представляет собой взвешенную сумму потенциальных энергий атомов и изображения. В данном примере использовали вес изображения β=0,3. Результирующая оптимизированная решетка как в высокой степени регулярна (опять-таки, игнорируя треугольники около выпуклого каркаса узлов решетки), так и хорошо совмещена с характерными чертами изображения.
Для изображений с малыми или узкими характерными чертами может быть полезно выполнять первые несколько итераций Алгоритма 5, используя слегка сглаженный вариант изображения. Эти первые итерации дают возможность атомам перемещаться к характерным чертам, которые иначе могут быть пропущены, потому что они расположены слишком далеко от местоположений исходной решетки. Атомы притягиваются сначала к сглаженным характерным чертам, а затем в последующих итерациях - к характерным чертам с высоким разрешением в исходном несглаженном изображении.
Выделение кривых и поверхностей
В заполняющей пространство сетке кривые (в двумерном случае) или поверхности (в трехмерном случае) появляются неявно. Например, в двумерной сетке, показанной на фиг.11, любая последовательность смежных линейных краев треугольников представляет кривую. В трехмерной тетраэдрической сетке любая совокупность смежных треугольных поверхностей тетраэдров представляет поверхность. Разумеется, большинство таких кривых или поверхностей не представляет интереса, потому что они не совмещаются с характерными чертами изображения.
Фиг.12 выделяет те края треугольников, которые получаются наиболее совмещенными с дефектами в сейсмическом изображении. Показанные здесь края были выбраны просто потому, что все значения выборок изображения под ними были ниже заданного порогового значения (-0,2). Никаких попыток не делалось, чтобы вызвать соединения между отдельными краями. Тем не менее, многие края соединяются и образуют непрерывные кривые.
Заполняющая пространство сетка облегчает более трудоемкие алгоритмы выделения кривых или поверхностей, чем простое сравнение с пороговым значением, использованное в данном примере. Как одно из следствий данного изобретения, заявители предвидят разработку новых алгоритмов выделения. В противоположность алгоритмам выделения (или сегментации), обычно используемым сегодня, эти новые алгоритмы будут вырабатывать кривые или поверхности, гарантированно совмещенные с заполняющей пространство сеткой.
Альтернативные решетки и сетки
В предыдущих примерах потенциальное поле изображения определялось так, чтобы атомы притягивались к характерным чертам изображения. В некоторых ситуациях желательно создать псевдорегулярную решетку, в которой атомы отталкиваются от характерных черт изображения.
Такую решетку можно получить с помощью Алгоритма 5 оптимизации с той же самой потенциальной функцией атомов, но с потенциальным полем изображения, которое достигает максимального значения (к примеру, единицы) вдоль характерных черт изображения, а минимального значения (к примеру, нуля) вдали от характерных черт изображения. Фиг.13 иллюстрирует результат такой оптимизации для сейсмического изображения. Атомы в оптимизированной решетке стремятся выстроиться поблизости от характерных черт изображения (а не совпасть с ними).
Фиг.13 иллюстрирует также сетку Вороного, сгенерированную из оптимизированной решетки. Сетка Вороного представляет собой двойную триангуляцию Делонэ. Так, атомы лежат внутри элементов сетки, а не в вершинах элементов сетки. Из-за того, что атомы в оптимизированной решетке стремятся выстроиться поблизости от характерных черт изображения, границы элементов сетки Вороного стремятся наложиться на эти характерные черты.
Сетки Вороного имеют многочисленные применения, в том числе моделирование потоков жидкости. Зачастую сетки Вороного приводят к решениям в конечных разностях для уравнений в частных производных, тогда как симплексные треугольные/тетраэдрические сетки приводят к решениям в конечных элементах. Оба типа решений широко используются в настоящее время. В обоих типах желательно иметь границы элементов сетки совмещенными с характерными чертами изображения, потому что эти характерные черты часто соответствуют разрывам в физических свойствах.
В более общем случае может быть желательно создать псевдорегулярную решетку из атомов, которые притягиваются к некоторым характерным чертам в изображении и отталкиваются от остальных характерных черт. Например, может быть выгодно поместить коммуникационные приемопередатчики в регулярных шаблонах, локальная плотность которых соответствует плотности человеческого населения. Может быть также желательно, чтобы те же самые приемопередатчики располагались в зонах больших высот (к примеру, на вершинах горных хребтов) и избегали зон с малой высотой (например, каньоны и речные долины). Таким образом, потенциальное поле изображения может включать в себя максимумы и минимумы, равно как и промежуточные плато.
Дополнительные примеры
Способ по данному изобретению можно также применять к медицинским изображениям. Фиг.14 показывает магнитно-резонансное изображение (МРИ) человеческой головы. Это цифровое изображение свободно доступно в Национальной библиотеке медицины как часть проекта визуализации человека (Visual Human Project).
Фиг.15 показывает изображение после обработки с целью усиления краев, разрывов в первоначальном МРИ. Использовался простой и общеизвестный алгоритм Превита для усиления краев. Это изображение с усиленными краями можно использовать в качестве потенциального поля b(x) изображения в способе по данному изобретению.
Фиг.16 показывает сетку, оптимизированную для совмещения с изображением по Фиг.15. Как и для сейсмического изображения, непостоянная функция d(x) номинального расстояния вычислялась путем сглаживания изображения. Значения номинального расстояния простираются от минимума d=4 до максимума d=12. Масштабирующий множитель изображения β=0,4.
Фиг.17 выделяет линейные сегменты в сетке, которые в наибольшей степени совмещаются с краями в изображении. Показанные сегменты выбирались с помощью того же самого алгоритма простого сравнения с порогом, который использовался для сейсмического изображения.
Фиг.18, 19, 20 и 21 предоставляют другой пример медицинского изображения. Как и изображение головы, это изображение человеческого торса свободно доступно в Национальной библиотеке медицины. Обработка изображения и оптимизация решетки для этого изображения точно такие же, как и для изображения головы, за исключением того, что значения номинального расстояния здесь простираются от минимума d=5 до максимума d=15.
Компьютерные системы, запоминающий носитель данных и вариант осуществления способа
Отметим, что способ по настоящему изобретению, предназначенный для генерирования псевдорегулярных решеток, которые учитывают характерные черты в цифровом изображении, может быть реализован в любой из различных компьютерных систем, таких как настольные компьютеры, миникомпьютеры, рабочие станции, многопроцессорные системы, параллельные процессоры различных видов, распределенные вычислительные сети и т.д. Способ по настоящему изобретению может быть реализован в одной или более программ или программных модулей, которые сохраняются на любой из множества запоминающих носителей данных, таких как постоянное запоминающее устройство (ПЗУ) на компакт-диске (CD-ROM), магнитный диск, запоминающее устройство на цилиндрических магнитных доменах, полупроводниковое запоминающее устройство (например, любой из множества типов оперативного запоминающего устройства (ОЗУ) или ПЗУ). Далее, эти одна или более программ и/или результатов, которые они генерируют, можно передавать по любой из множества сред передачи данных, таких как оптическое волокно, металлический провод, свободное пространство и/или через любую из множества сетей, таких как Интернет и/или коммутируемая телефонная сеть общего пользования (КТСОП, PSTN).
Фиг.22 иллюстрирует один вариант 500 осуществления компьютерной системы, функционально применимой для выполнения способа генерирования решетки по настоящему изобретению. Компьютерная система 500 может включать в себя процессор 502, запоминающее устройство (к примеру, оперативное запоминающее устройство 506 и/или энергонезависимые запоминающие устройства 504), одно или более устройств 508 ввода, одно или более отображающих устройств 510 и одно или более интерфейсных устройств 512. Эти составляющие подсистемы могут соединяться между собой согласно любой из множества конфигураций. Энергонезависимые запоминающие устройства 504 могут включать в себя такие устройства, как ленточные приводы, дисководы, полупроводниковое ПЗУ или электрически стираемое программируемое ПЗУ (EEPROM) и т.д. Устройства 508 ввода могут включать в себя такие устройства как клавиатура, мышь, графический планшет, трэкбол, сенсорный планшет и/или световое перо. Отображающие устройства 510 могут включать в себя такие устройства как мониторы, проекторы, укрепляемые на голове дисплеи (шлемы виртуальной реальности) и т.д. Интерфейсные устройства 512 могут быть выполнены для получения данных цифрового изображения по сети от одного или более устройств сбора данных и/или от одного или более удаленных компьютеров или устройств хранения.
Любое из множества устройств сбора данных может использоваться в зависимости от типа изображаемого объекта или процесса. Одно или более устройств сбора данных могут воспринимать любые из множества видов механической энергии (к примеру, акустическая энергия, смещение и/или напряжения/деформации) и/или электромагнитной энергии (к примеру, световая энергия, радиоволновая энергия, ток и/или напряжение).
Процессор 502 может быть сконфигурирован для считывания программных команд и/или данные из ОЗУ 506 и/или энергонезависимых запоминающих устройств 504 и сохранения результатов вычислений в ОЗУ 506 и/или энергонезависимых запоминающих устройствах 504. Программные команды предписывают процессору 502 оперировать входным изображением на основании любой комбинации описанных здесь вариантов осуществления способа. Входное изображение может подаваться в компьютерную систему 500 посредством любого из множества механизмов. Например, входное изображение может быть введено в энергонезависимую память 504 и/или ОЗУ 506 с помощью одного или более интерфейсных устройств 512. В качестве другого примера, входное изображение может подаваться в компьютерную систему 500 через такой запоминающий носитель данных, как диск или магнитная лента, которое загружают в одно из энергонезависимых запоминающих устройств 504. В этом случае входное изображение должно быть предварительно записано на запоминающий носитель данных компьютерной системой 500 или какой-нибудь другой компьютерной системой.
Отметим, что входное изображение не обязательно должно представлять собой необработанные данные с датчика, полученные устройством сбора данных. Например, входное изображение может быть результатом одной или более операций предварительной обработки набора необработанных данных с датчика. Эти одна или более операций предварительной обработки могут выполняться компьютерной системой 500 и/или одной или более другими компьютерными системами. Более того, входное изображение может быть совершенно независимо от данных с датчика, как в случае, когда изображение генерируется проектировщиком с помощью пакета автоматизированного проектирования (CAD).
Фиг.23 иллюстрирует один вариант 600 осуществления способа генерирования решетки узлов, которая является псевдорегулярной и которая учитывает характерные черты в цифровом изображении. На этапе 605 изображение (к примеру, изображение объекта и/или процесса) может быть получено в такое локально доступное запоминающее устройство, как энергонезависимое запоминающее устройство 504 и/или ОЗУ 506 компьютерной системы 500. На этапе 610 изображение можно предварительно обработать, чтобы усилить или выявить вызывающие интерес характерные черты изображения. Если вызывающие интерес характерные черты достаточно различимы на изображении, которое получено на этапе 605, то этап 610 можно опустить. (Как упомянуто выше, изображение, которое получено на этапе 605, может быть уже подвергнуто операциям предварительной обработки.)
Настоящее изобретение предполагает использование любого желаемого способа или комбинации способов обработки для предварительной обработки на этапе 610. Например, изображение может быть подвергнуто обнаружению краев, сверточной фильтрации, преобразованию Фурье, нелинейной фильтрации, заданию пороговых значений и т.д. Предварительная обработка может генерировать потенциальное поле изображения, дискретизированное как цифровое изображение. Далее, предварительная обработка может оперировать изображением с целью генерирования функции d(x) номинального расстояния. Предварительная обработка может быть автоматической или реагировать на вводы пользователя. К примеру, пользователь может выделять вызывающие интерес характерные черты и/или области в изображении.
На этапе 615 в пространстве, покрываемом изображением, можно инициализировать решетку узлов, совместимую с функцией d(x) номинального расстояния. Эту решетку можно инициализировать способами Алгоритма 3 или Алгоритма 4. В одном альтернативном варианте осуществления исходную решетку, совместимую с функцией номинального расстояния, можно генерировать из такой "легкой" решетки как прямоугольная решетка или равносторонняя решетка, путем исполнения нескольких итераций оптимизации решетки с масштабирующим параметром β, равным нулю. Однако, чтобы избежать разрывов решетки, расстояние между атомами в этой "легкой" решетке может быть установлено равным минимуму функции номинального расстояния. В другом альтернативном варианте осуществления исходную решетку можно генерировать из "легкой" решетки исполнением нескольких итераций оптимизации решетки с ненулевым значением для масштабирующего параметра β и с функцией d(x) расстояния, заменяющей потенциальное поле b(x) изображения.
На этапе 620 исходную решетку узлов можно оптимизировать посредством Алгоритма 5. Оптимизированная решетка узлов может использоваться в любом из множества применений. К примеру, эту решетку можно триангулировать с целью генерирования заполняющей пространство сетки, а эта сетка может использоваться для осуществления основанного на сетке моделирования (такого как моделирование резервуаров), алгоритма кодирования изображения, метода анализа сигналов и т.д. В некоторых вариантах осуществления оптимизированная решетка может использоваться прикладной программой без введения этапа генерирования сетки.
Заключение, ответвления и объем
Представленные выше примеры демонстрируют полезность способа по данному изобретению при генерировании решетки узлов, которая одновременно является псевдорегулярной и реагирующей на характерные черты в цифровом изображении. Оптимизированная решетка может иметь переменную плотность, соответствующую пространственно-переменному уровню детализации в изображении.
Примеры показали также, что триангуляция такой решетки может дать заполняющую пространство сетку, которая хорошо совмещается с характерными чертами изображения. В высокой степени регулярные элементы в этой сетке делают ее пригодной основой для последующих вычислений, таких как моделирование потока жидкости.
Представленную комбинацию каркасной решетки и изображения можно использовать в качестве основы для усовершенствованных алгоритмов выделения характерных черт.
Хотя показанные выше примеры представляют двумерные изображения, способ по данному изобретению в равной мере применим и к трехмерным изображениям. При необходимости разница между двумерными и трехмерными уравнениями и алгоритмами отмечалась при их описании. Способ по настоящему изобретению естественно обобщается на N-мерные изображения, где N - любое целое больше нуля.
Изображения в примерах равномерно дискретизировались на прямоугольной двумерной сетке. Однако предусматриваются различные варианты осуществления, когда данный способ работает с меняющимися топологиями изображений. К примеру, двумерное изображение можно дискретизировать на поверхности сферы. Таким образом, в одном варианте осуществления способ по настоящему изобретению может генерировать псевдорегулярную решетку узлов на такой сферической поверхности, согласующуюся с функцией расстояния, определенной на этой поверхности, а затем совмещаемую с характерными чертами изображения, отображенными на этой поверхности. Предполагается множество топологий в разных измерениях.
Способ по данному изобретению представлен в терминах задачи минимизации. Очевиден математический факт, что минимизация функции f эквивалентна максимизации ее отрицательного варианта -f. Таким образом, подразумеваются альтернативные варианты осуществления, где оптимизацию решетки выполняют путем максимизации составной функции, содержащей комбинацию первой функции межатомных расстояний между узлами (т.е. атомами) в решетке и второй функции положений этих узлов решетки.
Хотя приведенное выше описание содержит много конкретных деталей, их не следует истолковывать как ограничение объема изобретения. Напротив, они просто предоставляют иллюстрации предпочтительных в настоящее время вариантов осуществления данного изобретения. Например, простая полиномиальная двухточечная потенциальная функция может быть заменена другой функцией с аналогичными свойствами. Аналогично, множество алгоритмов можно использовать для инициализации решетки атомов в дополнение к двум представленным выше алгоритмам.
Таким образом, объем данного изобретения следует определять приложенной формулой изобретения и ее законными эквивалентами, а не примерами вариантов осуществления, представленными выше.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО, СПОСОБ И СИСТЕМА ДЛЯ РЕКОНСТРУКЦИИ 3D-МОДЕЛИ ОБЪЕКТА | 2015 |
|
RU2642167C2 |
| АВТОМАТИЧЕСКАЯ ТРЕХМЕРНАЯ СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЯ СЕРДЦА ПО КОРОТКОЙ ОСИ, ПОЛУЧЕННОГО МЕТОДОМ МАГНИТНО-РЕЗОНАНСНОЙ ТОМОГРАФИИ С ОТЛОЖЕННЫМ КОНТРАСТИРОВАНИЕМ | 2009 |
|
RU2503061C2 |
| ОПРЕДЕЛЕНИЕ ПУТИ ДВИЖЕНИЯ ФЛЮИДА | 2014 |
|
RU2619803C2 |
| СИСТЕМЫ И СПОСОБЫ ПРОГНОЗИРОВАНИЯ СТРУКТУРЫ И СВОЙСТВ АТОМАРНЫХ ВЕЩЕСТВ И ИХ СПЛАВОВ | 2019 |
|
RU2727631C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С СУБДИФРАКЦИОННЫМ РАЗРЕШЕНИЕМ | 2013 |
|
RU2533502C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ГЕНЕРИРОВАНИЯ ДАННЫХ, ХАРАКТЕРИЗУЮЩИХ ПИКСЕЛЬНЫЙ ПУЧОК | 2016 |
|
RU2734115C2 |
| Основанная на модели сегментация анатомической структуры | 2014 |
|
RU2647194C2 |
| СИСТЕМА ДЛЯ АНАЛИЗА И ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ ШУМА ДЫХАТЕЛЬНЫХ ПУТЕЙ | 2003 |
|
RU2314751C2 |
| МЕТОД ОПРЕДЕЛЕНИЯ ЗОНЫ ДВИЖЕНИЯ И САМОСТОЯТЕЛЬНОГО ОБЪЕЗДА ПРЕПЯТСТВИЙ ДЛЯ БЕСПИЛОТНОГО ТРАНСПОРТНОГО ОБОРУДОВАНИЯ В ПОДЗЕМНЫХ ЗАМКНУТЫХ ПРОСТРАНСТВАХ | 2022 |
|
RU2803671C1 |
| СПОСОБ СОЗДАНИЯ СИГНАТУРЫ ДЛЯ ДРАГОЦЕННОГО КАМНЯ С ИСПОЛЬЗОВАНИЕМ РЕНТГЕНОВСКОЙ ВИЗУАЛИЗАЦИИ | 2015 |
|
RU2690707C2 |
Изобретение относится к анализу цифровых изображений с помощью вычислительных сеток. Техническим результатом является обеспечение возможности процесса инициализации решетки и процесса оптимизации конфигурации этой решетки по отношению к характерным чертам изображения. Результат достигается путем оптимизации и коррекции узлов решетки с целью обеспечения экстремума составной функции пространственных координат узлов решетки. Узлы решетки интерпретируются как атомы. Каждый узел решетки вносит вклад в виде потенциальной функции в потенциальное поле атомов. Изображение представляет потенциальное поле. Составная функция является взвешенной суммой потенциальных полей атомов и изображения, оцененной в узлах решетки. 6 н. и 49 з.п. ф-лы, 25 ил.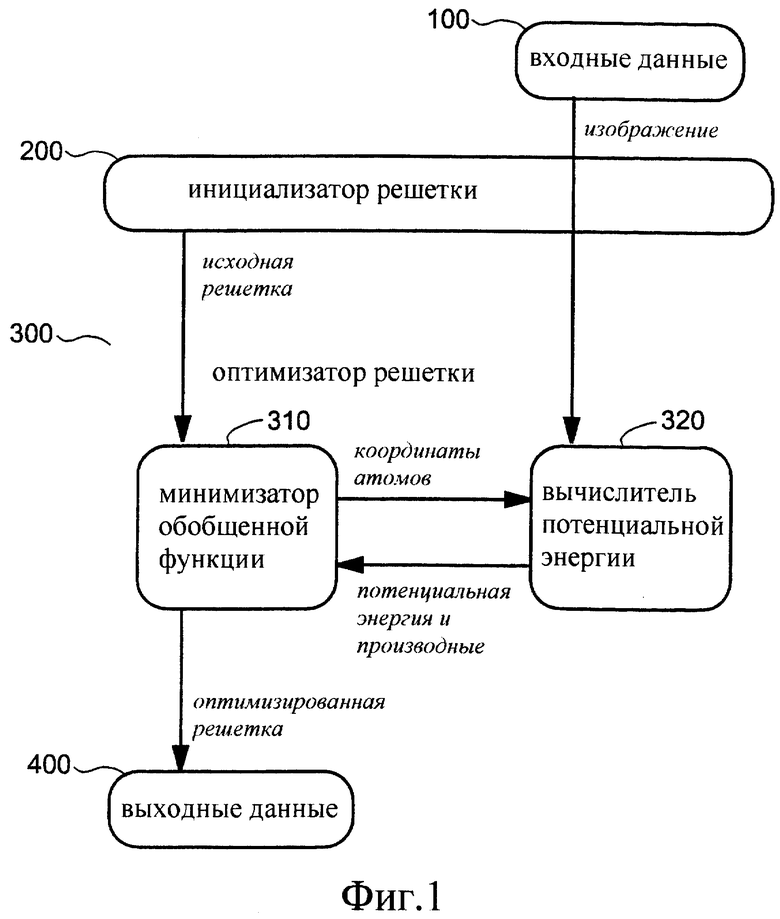
| СПОСОБ ОПРЕДЕЛЕНИЯ НАЧАЛЬНЫХ И ТЕКУЩИХ ЗАПАСОВ ГАЗА ГАЗОКОНДЕНСАТНОГО МЕСТОРОЖДЕНИЯ | 1999 |
|
RU2148153C1 |
| АССОЦИАТИВНАЯ ЗАПОМИНАЮЩАЯ СРЕДА | 1996 |
|
RU2102796C1 |
| JP 10153520, 09.06.1998 | |||
| JP 3030071, 08.02.1991. | |||
