Изобретение относится к специализированным средствам вычислительной техники и может быть использовано для создания генераторного оборудования, а также при решении краевых задач математической физики.
Известен генератор функций, содержащий матрицу вычислителей, первую группу блоков деления, блок синхронизации, регистр сдвига, Р-1 группу блоков элементов И, Р-2 групп блоков деления, первый и второй блоки памяти, матрицу операционных блоков, Р-2 элементов задержки и кольцевой регистр сдвига (см. авторское свидетельство СССР №1753463, кл. G 06 F 1/02, 1990).
Однако известный генератор предназначен для генерирования дискретных базисных функций, описываемых собственными векторами положительно определенной симметрической матрицы, и не формирует аналоговые ортогональные функции.
Известно также устройство для воспроизведения ортогональных колебаний, содержащее интегратор, умножители, первые и вторые интеграторы, усилители (см. авторское свидетельство СССР №1368899, кл. G 06 G 7/26, 1986).
Однако известное устройство формирует только один класс функций, являющийся решением полученного авторами дифференциального уравнения, и не способно генерировать ортогональные функции различных классов.
Наиболее близким по технической сущности к предлагаемому изобретению является устройство, содержащее пять интеграторов, два блока перемножения, сумматор, блок деления и инвертор, причем вход первого интегратора является входом устройства, а выход соединен с первым входом первого блока перемножения и с входом второго интегратора, выход которого подключен к первому входу второго блока перемножения, выход которого соединен с первым входом сумматора, выход которого соединен со вторым входом второго блока перемножения и с входом третьего интегратора, выход которого соединен с входом четвертого интегратора и с вторым входом первого блока перемножения, выход которого подключен к второму входу сумматора, выход первого интегратора подключен к входу пятого интегратора, выход которого соединен с первым входом блока деления, выход которого подключен к входу интегратора, выход которого подключен к четвертому входу сумматора, выход четвертого интегратора соединен со вторым входом блока деления, выход четвертого интегратора соединен также с третьим входом сумматора и является выходом устройства (см. авторское свидетельство СССР №822216, кл. G 06 G 7/40, 1979).
Однако это устройство предназначено для воспроизведения только одного класса ортогональных функций, описываемых присоединенными полиномами Лежандра, и не способно формировать ортогональные функции других классов.
Целью изобретения является расширение функциональных возможностей за счет воспроизведения всех классов ортогональных функций, являющихся решением дифференциальных уравнений второго порядка.
Поставленная цель достигается тем, что в известное устройство, содержащее три интегратора, два блока перемножения, сумматор и инвертор, причем вход первого интегратора является входом устройства, выход первого блока перемножения соединен с первым входом сумматора, выход второго блока перемножения соединен с вторым входом сумматора, введены три блока перемножения, аналого-цифровой преобразователь, пять цифроаналоговых преобразователей первой группы, три цифроаналоговых преобразователя второй группы и два блока памяти, причем первая группа адресных входов первого и второго блоков памяти является группой входов установки класса формируемых функций, вторая группа адресных входов первого и второго блоков памяти является группой входов установки порядкового номера формируемой функции, выход первого интегратора подключен к входу аналогоцифрового преобразователя, выходы которого подключены к третьей группе адресных входов первого блока памяти, входы цифроаналоговых преобразователей первой группы подключены к соответствующим информационным выходам первого блока памяти, выход первого цифроаналогового преобразователя первой группы соединен с первым входом первого блока умножения, второй вход которого подключен к выходу сумматора, выход второго цифроаналогового преобразователя первой группы соединен с первым входом второго блока умножения, второй вход второго блока умножения подключен к выходу инвертора, выход третьего цифроаналогового преобразователя первой группы соединен с первым входом третьего блока умножения, вторые входы третьего и четвертого блоков умножения подключены к выходу третьего интегратора, первый вход четвертого блока умножения соединен с выходом пятого блока умножения, первый вход которого подключен к выходу четвертого цифроаналогового преобразователя первой группы, а второй вход которого подключен к выходу пятого цифроаналогового преобразователя первой группы, выход третьего блока перемножения соединен с третьим входом сумматора, выход четвертого блока перемножения соединен с четвертым входом сумматора, выход сумматора подключен к входу второго интегратора, выход которого соединен с входом третьего интегратора и входом инвертора, входы цифроаналоговых преобразователей второй группы подключены к соответствующим информационным выходам второго блока памяти, выход первого цифроаналогового преобразователя второй группы подключен к входу установки начального состояния первого интегратора, выход второго цифроаналогового преобразователя второй группы подключен к входу установки начального состояния второго интегратора, выход третьего цифроаналогового преобразователя второй группы подключен к входу установки начального состояния третьего интегратора, выход третьего интегратора является выходом устройства.
Линейный дифференциальный оператор второго порядка общего вида может быть записан как:

(см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.363, соотношение (9.1)).
Дифференциальное уравнение второго порядка может быть записано в форме:

(см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.365, соотношение (9.6)).
Здесь λ - некоторая постоянная, а ω(х) - известная функция х, называемая плотностью или весовой функцией.
Потребуем, чтобы ω(х)>0, исключая, может быть, изолированные точки, в которых ω(х)=0. Функция uλ(x), при некотором λ, удовлетворяющая уравнению (1) с заданными граничными условиями, называется собственной функцией, которая соответствует собственному значению λ.
В теории дифференциальных уравнений удобно определить сопряженный оператор  :
:
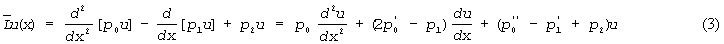
Сравнение уравнений (1) и (3) дает необходимое и достаточное условие того, чтобы  :
:

При выполнении условия (4):
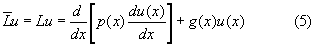
оператор L называется самосопряженным. Здесь p0(x) заменено на p(x), а p2(x) на g(x) (см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.363, соотношение (9.2), с.364, соотношение (9.3), (9.4)).
Теория линейных самосопряженных дифференциальных уравнений второго порядка носит общий характер, так как всегда можно привести несамосопряженный оператор к самосопряженному виду (см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.364, второй абзац).
Самосопряженный оператор характеризуется следующими свойствами:
- его собственные значения вещественны;
- его собственные функции ортогональны
(см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.370, первый абзац).
При приведении уравнений к самосопряженному виду значение их коэффициентов и параметров могут быть легко определены (см. Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.365, второй абзац снизу). При этом собственная функция uλ{x) должна удовлетворять определенным граничным условиям.
Соотношение (2) с учетом (5) может быть записано в виде:
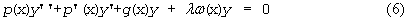
или иначе
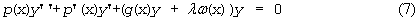
Дифференциальное уравнение второго порядка может быть записано в виде:
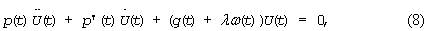
где 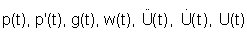 - функции времени, λ - собственное значение.
- функции времени, λ - собственное значение.
Собственные функции U(t), соответствующие собственным значениям λ, при определенных значениях p(t), p'(t), g(t), ω(t), задаваемых классом колебаний, согласно сказанному выше, являются ортогональными между собой и могут быть использованы в системах связи в качестве переносчиков.
Значения функций p, p', g, ω известны для всех классов классических колебаний и могут быть легко рассчитаны для любых классов колебаний, описываемых функциями, являющимися решениями дифференциальных уравнений второго порядка.
Значения коэффициентов и параметров для классических колебаний представлены, например, в источнике: Г.Афкен. Математические методы в физике. - М.: Атомиздат, 1970, с.366, таблица 9.1.
Эти значения представлены в таблице 1. Кроме коэффициентов и параметров для классических колебаний, в предпоследней строке таблицы представлены их значения для колебаний, формируемых аналогом и являющихся решениями полученного авторами дифференциального уравнения второго порядка.
На фиг.1 представлена структурная схема предлагаемого устройства для воспроизведения ортогональных функций.
Устройство содержит интеграторы 1, 3, 4, сумматор 2, инвертор 5, умножители 6, аналого-цифровой преобразователь 7, первый блок 8 памяти, цифроаналоговые преобразователи 9 первой группы, второй блок 10 памяти, цифроаналоговые преобразователи 11 второй группы.
Устройство работает следующим образом. Перед началом формирования ортогональных функций на группу входов установки класса формируемых функций подается код, соответствующий требуемому классу. Например, для формирования функций Лежандра на эту группу входов подается код 0...001, для формирования функций Чебышева первого рода - 0...010, для формирования функций Чебышева второго рода - 0...011 и т.д. Этот код подается по шине на первую группу адресных входов первого блока 8 памяти и второго блока 10 памяти.
Блок 8 памяти представляет собой обычное постоянное запоминающее устройство (ПЗУ), в котором память разбита на зоны, соответствующие каждому классу функций, формируемых предлагаемым устройством. Каждая зона, в свою очередь, разбита на области, соответствующие номеру формируемой функции. Подачей кода на вторую группу адресных входов блока 8 памяти можно осуществить выбор номера функции, которую будет формировать устройство. Осуществляя подачу сигнала текущего времени, преобразованного в цифровую форму, на третью группу адресных входов блока 8 памяти, на выходах цифроаналоговых преобразователей 9, входы которых подключены к информационным выходам блока 8 памяти, можно сформировать значения коэффициентов и параметров p(t), p'(t), g(t), λi, ω(t).
Второй блок 10 памяти также представляет собой ПЗУ, память которого разбита на зоны, соответствующие классу функций, каждая из которых включает в себя области, соответствующие номеру формируемой функции. При подаче кодов класса функции и номера функции на первую и вторую группу адресных входов блока 10 памяти на выходах цифроаналоговых преобразователей 11, входы которых подключены к информационным выходам блока 10 памяти, кратковременно формируются начальные условия интеграторов 1, 3 и 4, подаваемые на входы начальной установки интеграторов.
С учетом сказанного, с подачей кода класса функции на первую группу адресных входов и кода номера требуемой функции на вторую группу адресных входов блока 8 памяти и блока 10 памяти на выходах цифроаналоговых преобразователей 11.1, 11.2 и 11.3 кратковременно сформируются и запишутся соответственно в первый интегратор 1, второй интегратор 3 и третий интегратор 4 начальные условия. Например, в случае формирования функций, аналогичных формируемым прототипом (см. авторское свидетельство СССР №822216, кл. G 06 G 7/40, 1979) на выходе цифроаналогового преобразователя 11.1 появится единица, на выходе цифроаналогового преобразователя 11.2 появится ноль, на выходе цифроаналогового преобразователя 11.3 появится одно из значений
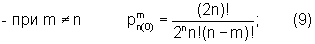

в зависимости от номера функции.
При подаче постоянного напряжения - U на вход интегратора 1 на его выходе формируется сигнал текущего времени t, поступающий на вход аналого-цифрового преобразователя 7. Код текущего времени с его выходов подается на третью группу адресных входов первого блока 8 памяти. В результате, в соответствии с последней строкой таблицы 1, на выходе преобразователя 9.1 формируется сигнал 1-t2, на выходе преобразователя 9.2 формируется сигнал - 2t, на выходе преобразователя 9.3 формируется сигнал -  на выходе преобразователя 9.4 формируется постоянный уровень, соответствующий собственному значению λ (где λ=n(n+1)), на выходе преобразователя 9.5 формируется единица. В результате на выходе перемножителя 6.5, первый вход которого подключен к выходу преобразователя 9.4, а второй - к выходу преобразователя 9.5 формируется сигнал n(n+1).
на выходе преобразователя 9.4 формируется постоянный уровень, соответствующий собственному значению λ (где λ=n(n+1)), на выходе преобразователя 9.5 формируется единица. В результате на выходе перемножителя 6.5, первый вход которого подключен к выходу преобразователя 9.4, а второй - к выходу преобразователя 9.5 формируется сигнал n(n+1).
На выходе умножителя 6.1 появляется сигнал 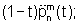
на выходе умножителя 6.2 появляется сигнал - 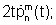
на выходе умножителя 6.3 появляется сигнал - 
на выходе умножителя 6.4 появляется сигнал 
Каждый из этих сигналов поступает на соответствующий вход сумматора. В результате на выходе сумматора 2 формируется колебание, описываемое функцией  а на выходе второго интегратора 3 формируется сигнал, описываемый функцией
а на выходе второго интегратора 3 формируется сигнал, описываемый функцией 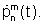 Таким образом, с выхода третьего интегратора 4 снимается колебание, описываемое требуемой функцией вида
Таким образом, с выхода третьего интегратора 4 снимается колебание, описываемое требуемой функцией вида  то есть присоединенным полиномом Лежандра соответствующего порядка.
то есть присоединенным полиномом Лежандра соответствующего порядка.
Аналогично осуществляется работа устройства и при формировании других видов колебаний.
Например, при формировании колебаний, идентичных генерируемым аналогом (см. авторское свидетельство СССР №1368899, кл. G 06 G 7/26, 1986), являющихся решением полученного авторами дифференциального уравнения второго порядка
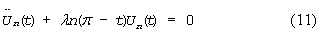
Код этого класса функций и номер требуемой функции подается на первую и вторую группу адресных входов блока 8 и блока 10 памяти соответственно. На выходах цифро-аналоговых преобразователей 11.1, 11.2 и 11.3 кратковременно сформируются и запишутся соответственно в первый интегратор 1, второй интегратор 3 и третий интегратор 4 начальные условия:

где k - номер формируемой функции.
При подаче постоянного напряжения + U на вход интегратора 1 на его выходе формируется сигнал (π-t), поступающий на вход аналого-цифрового преобразователя 7. Код, соответствующий значениям (π-t), с его выходов подается на третью группу адресных входов первого блока 8 памяти. В результате, в соответствии с предпоследней строкой таблицы 1, на выходе цифроаналогового преобразователя 9.1 формируется единица, на выходе преобразователя 9.2 формируется ноль, на выходе преобразователя 9.3 формируется сигнал λn(π-t)-λn, на выходе преобразователя 9.4 формируется значение λn, на выходе преобразователя 9.5 формируется единица. В результате на выходе перемножителя 6.5, первый вход которого подключен к выходу преобразователя 9.4, а второй - к выходу преобразователя 9.5, формируется сигнал λn, где λт - решение уравнения
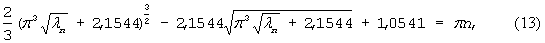
где n - порядковый номер формируемой функции (см. авторское свидетельство СССР №1368899, кл. G 06 G 7/26, 1986).
Так как второй вход блока перемножения 6.1 подключен к выходу сумматора 2, на котором формируется сигнал 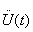 , а вторые входы блоков перемножения 6.3 и 6.4 подключены к выходу третьего интегратора 4, на котором формируется сигнал U(t), то сигнал U(t) является решением полученного дифференциального уравнения (11).
, а вторые входы блоков перемножения 6.3 и 6.4 подключены к выходу третьего интегратора 4, на котором формируется сигнал U(t), то сигнал U(t) является решением полученного дифференциального уравнения (11).
Использование изобретения позволяет расширить функциональные возможности известных устройств, так как может воспроизводить все классы ортогональных функций, являющихся решениями дифференциальных уравнений второго порядка, что дает возможность генерировать колебания, которые обеспечивают повышение помехоустойчивости уплотняемых каналов в системах связи, увеличение пропускной способности, а также решать краевые задачи математической физики.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 2011 |
|
RU2446437C1 |
| УСТРОЙСТВО ДЛЯ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ МЕХАНИЗМОВ | 2013 |
|
RU2531474C1 |
| МОДУЛЯТОР ДИСКРЕТНОГО СИГНАЛА ПО ВРЕМЕННОМУ ПОЛОЖЕНИЮ | 2008 |
|
RU2393640C1 |
| МНОГОКАНАЛЬНАЯ СИСТЕМА ДЛЯ ПРЕДУПРЕЖДЕНИЯ О ВОЗНИКНОВЕНИИ СЕЙСМИЧЕСКИХ ТОЛЧКОВ И ЦУНАМИ | 2008 |
|
RU2363963C1 |
| УСТРОЙСТВО ДЛЯ ГЕОЭЛЕКТРОРАЗВЕДКИ С ПОВЫШЕННОЙ ПОМЕХОУСТОЙЧИВОСТЬЮ, ЧУВСТВИТЕЛЬНОСТЬЮ И ТОЧНОСТЬЮ ИЗМЕРЕНИЙ | 2009 |
|
RU2408038C1 |
| УСТРОЙСТВО ДЛЯ ГЕОЭЛЕКТРОРАЗВЕДКИ | 2008 |
|
RU2366983C1 |
| СТОХАСТИЧЕСКИЙ ГЕНЕРАТОР ФУНКЦИЙ УОЛША | 2009 |
|
RU2421770C1 |
| МНОГОКАНАЛЬНАЯ СИСТЕМА ДЛЯ СЕЙСМИЧЕСКИХ ИССЛЕДОВАНИЙ | 2020 |
|
RU2722462C1 |
| МОДУЛЯТОР ДИСКРЕТНОГО СИГНАЛА ПО ВРЕМЕННОМУ ПОЛОЖЕНИЮ | 2018 |
|
RU2677358C1 |
| ЧАСТОТНЫЙ МОДУЛЯТОР | 2008 |
|
RU2354065C1 |
Изобретение относится к специализированным средствам вычислительной техники и может быть использовано для создания генераторного оборудования, а также при решении краевых задач математической физики. Техническим результатом является расширение функциональных возможностей за счет воспроизведения всех классов ортогональных функций, являющихся решениями дифференциальных уравнений второго порядка. Устройство содержит три интегратора, блоки перемножения, сумматор, инвертор, аналого-цифровой преобразователь, пять цифро-аналоговых преобразователей первой группы, три цифроаналоговых преобразователя второй группы и два блока памяти. 1 ил., 1 табл.
Устройство для воспроизведения ортогональных функций, содержащее три интегратора, два блока перемножения, сумматор и инвертор, причем вход первого интегратора является входом устройства, выход первого блока перемножения соединен с первым входом сумматора, выход второго блока перемножения соединен со вторым входом сумматора, отличающееся тем, что в него введены три блока перемножения, аналого-цифровой преобразователь, пять цифроаналоговых преобразователей первой группы, три цифроаналоговых преобразователя второй группы и два блока памяти, причем первая группа адресных входов первого и второго блоков памяти является группой входов установки класса формируемых функций, вторая группа адресных входов первого и второго блоков памяти является группой входов установки порядкового номера формируемой функции, выход первого интегратора подключен к входу аналого-цифрового преобразователя, выходы которого подключены к третьей группе адресных входов первого блока памяти, входы цифроаналоговых преобразователей первой группы подключены к соответствующим информационным выходам первого блока памяти, в котором хранятся значения коэффициентов и параметров p(t), p'(t), g(t), λi, w(t), где p(t), p'(t), g(t), w(t) - значения воспроизводимой функции, а λi - постоянная для данного класса функции, всех классов классических колебаний, описываемых функциями, являющимися решениями дифференциальных уравнений второго порядка, выход первого цифроаналогового преобразователя первой группы соединен с первым входом первого блока умножения, второй вход которого подключен к выходу сумматора, выход второго цифроаналогового преобразователя первой группы соединен с первым входом второго блока умножения, второй вход второго блока умножения подключен к выходу инвертора, выход третьего цифроаналогового преобразователя первой группы соединен с первым входом третьего блока умножения, вторые входы третьего и четвертого блоков умножения подключены к выходу третьего интегратора, первый вход четвертого блока умножения соединен с выходом пятого блока умножения, первый вход которого подключен к выходу четвертого цифроаналогового преобразователя первой группы, а второй вход которого подключен к выходу пятого цифроаналогового преобразователя первой группы, выход третьего блока перемножения соединен с третьим входом сумматора, выход четвертого блока перемножения соединен с четвертым входом сумматора, выход сумматора подключен к входу второго интегратора, выход которого соединен с входом третьего интегратора и входом инвертора, входы цифро-аналоговых преобразователей второй группы подключены к соответствующим информационным выходам второго блока памяти, в котором хранятся начальные условия для интеграторов всех классов классических колебаний, описываемых функциями, являющимися решениями дифференциальных уравнений второго порядка, выход первого цифроаналогового преобразователя второй группы подключен к входу установки начального состояния первого интегратора, выход второго цифроаналогового преобразователя второй группы подключен к входу установки начального состояния второго интегратора, выход третьего цифроаналогового преобразователя второй группы подключен к входу установки начального состояния третьего интегратора, выход третьего интегратора является выходом устройства.
| Устройство для воспроизведенияпОлиНОМА лЕжАНдРА | 1979 |
|
SU822216A1 |
| ГЕНЕРАТОР НЕСУЩИХ КОЛЕБАНИЙ | 1997 |
|
RU2115166C1 |
| ГЕНЕРАТОР ЕРМАКОВА-КАЖДАНА ПОЛНОГО СПЕКТРА ОРТОГОНАЛЬНЫХ ФУНКЦИЙ КАЖДАНА С ДИСКРЕТНЫМИ СДВИГАМИ (ВАРИАНТЫ) | 2001 |
|
RU2213995C2 |
| Устройство для воспроизведения ортогональных колебаний | 1986 |
|
SU1368899A1 |
| JP 10307708, 17.11.1998 | |||
| US 4021648 А, 03.05.1977 | |||
| АРФКЕН Г | |||
| Математические методы в физике | |||
| - М.: Атомиздат, 1970, с.363-366. | |||
Авторы
Даты
2006-08-27—Публикация
2005-01-11—Подача