СПОСОБ ИЗМЕРЕНИЯ РЕЧНОЙ СЕТИ ПО ЧИСЛЕННОСТИ ВОДОТОКОВ Российский патент 2006 года по МПК G01C13/00 

Изобретение относится к гидрологии рек и водосборным бассейнам речных сетей и может быть использовано при оценке водных ресурсов.

Известен способ измерения речной сети (см. книгу: Географические закономерности гидрологических процессов юга Восточной Сибири / А.Н.Антипов, Н.В.Абасов, Т.В.Бережных и др. - Иркутск: Изд-во Института географии СО РАН, 2003. - 208 с. - С.32), включающий измерения и применение результатов измерений элементарных водотоков как первого и определяющего звена речной сети, по их численности (мощности первичных элементарных водотоков).

Недостатком этого способа является то, что все первичные элементарные водотоки, то есть первичные притоки реки, считаются одинаковыми по свойствам и параметрам и поэтому попадают в одно общее множество первичных водотоков, характеризующее мощность речной сети.

Известен также способ измерения речной сети (см. книгу: Географические закономерности гидрологических процессов юга Восточной Сибири / А.Н.Антипов, Н.В.Абасов, Т.В.Бережных и др. - Иркутск: Изд-во Института географии СО РАН, 2003. - 208 с. - С. 38), включающий классификацию первичных водотоков по Р.Хортону как относящиеся к низшему порядку (присваивается низший порядок единица самым малым неразветвленным водотокам), измерение водотоков, группировку их по различным порядкам, применение результатов измерений в расчетах коэффициента бифуркации речной сети как отношения между количествами притоков смежных порядков. При этом по значению коэффициента бифуркации судят об индивидуальных свойствах речной системы, зависящих от геологических особенностей местности либо со спецификой влагооборота водосборного бассейна речной системы (сети).

Недостатком прототипа является то, что введение группировки по порядкам Р.Хортона хотя и кажется естественным по структуре речной сети, но только запутывает процесс применения результатов измерений первичных элементарных водотоков. Часто оказывается ситуация, когда основные параметры водотоков (притоков) - площадь водосбора и длина - не учитываются и элементарные водотоки иногда имеют большие по значению площадь водосбора, чем притоки более высоких порядков. Таким образом, группировка первичных, вторичных, третичных и других притоков по структуре речной сети оказывается недостаточно точным для описания речной сети многими показателями, в том числе и коэффициентом бифуркации.

Технический результат - повышение точности количественного описания речной системы и учета водных ресурсов.

Этот технический результат достигается тем, что дополнительно к группировке водотоков реки по порядкам примыкания притоков к водотоку более высшего порядка по Р.Хортону уточняют значения длины и площади водосборов каждого притока реки в речной сети по результатам полевых или иных измерений, проведенных в каждой группе Р.Хортона, затем принимают множество водотоков для статистического моделирования, состоящее по крайней мере из одной группы Р.Хортона, вычисляют и принимают шаг группировки отдельно по интервалам длины притока и отдельно по интервалам площади водосбора, затем уточняют шаги группировки по результатам исключения из множества уникальных притоков, после этого распределяют притоки этого принятого для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора, определяют параметры статистических моделей по устойчивым законам распределения, а по математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети.

Для статистического моделирования принимают множество водотоков, как правило, состоящее из притоков первого и второго порядков, то есть по двум группам Р.Хортона, которые и определяют значительную долю мощности речной сети. Это же множество характеризует и качество всей речной системы.

Для возможности сопоставления математических закономерностей по рядам распределения численности притоков многих речных сетей принимают общий шаг группировки по интервалу длины притока или площади водосбора, например, равный целому числу 1 км или 4 км², полученные для наиболее крупной речной сети из нескольких сравниваемых. Ниже приведен пример моделирования по реке Буй. Сравнение показывает, что интервалы (шаги) изменения длины притока и площади водосбора можно принять и для других рек, находящихся на территории Республики Марий Эл. По-видимому, для рек Российской Федерации потребуются несколько шкал длины и площади.

Для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора определяют параметры статистических моделей по устойчивым законам распределения, причем для идентификации применяют общую математическую закономерность распределения притоков по интервалам длины притоков и площади водосбора по формуле:

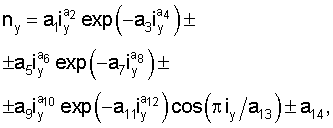
где y - показатели притока реки (длина притока L, км, или площадь водосбора S, км²),

n_y - число попаданий притоков в тот или ной интервал значений показателя, шт.,

i_y - код интервала изменения показателя, то есть место расположения интервалов значений показателя: код интервала длины притока i_L или код интервала значений площади водосбора i_S,

а₁...a₁₄ - параметры статистической модели, при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а₄=1, a₈=1, а₁₂=1, а₆=0, а₁₀=0 или а₁₄=0).

По математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети по изменениям статистических показателей адекватности найденных математических закономерностей ко множеству учтенных измеренных значений длины притока и площади водосбора.

Сущность технического решения заключается в том, что речная сеть состоит из самой реки и множества притоков, причем притоки группируются по порядку структуры речной сети. За системообразующую часть речной сети принимаются по крайней мере притоки первого порядка. Но из-за совпадения порядка значений длины и площади водосбора в основное множество для последующего статистического моделирования можно принять совокупность притоков первого и второго порядков. Для малых рек, как показали наши исследования, следует принять шаг группировки значений длины и площади водосборов не менее 15 элементарных первичных водотоков, что определяется известными в статистике ограничениями по численности элементов статистической выборки, используемой при группировке ее членов по интервалам. Если все речные сети на данной территории будут иметь одинаковый шаг группировки, например по длине 1 км и по площади водосбора 4 км², то их можно будет сопоставлять по математическим закономерностям распределения притоков. В итоге это само распределение численности основной части притоков реки становится действенным средством не только для последующих различных гидрологических расчетов, в том числе и расчетов по обоснованию различных мероприятий на территории речной системы, но и оценки качества всей речной сети по параметрам адекватности моделей фактически измеренным значениям.

Положительный эффект достигается тем, что речная сеть получает четкое статистическое описание по распределению длины и площади водосбора, дополняющее структурное описание по порядкам Р.Хортона, то есть существенно дополняется информационное описание речной сети и появляется возможность оценки качества речной сети (худшие значения показателей адекватности математического распределения показывают низкое качество речной системы). Это позволяет проводить гидрологические расчеты по вероятностным математическим моделям, а не только по средним и максимальным значениям гидрологических показателей. В итоге мощный аппарат вероятностной динамики может быть применен и в гидрологии и при оценке водных ресурсов, что поднимет эти науки на принципиально новый и более высокий научный уровень. Одновременно появляется возможность сравнения качества водосборных бассейнов по статистическим показателям адекватности закономерностей распределения первичных притоков фактически измеренным значениям длины и площади водотоков первого и второго порядков по интервалам их распределения.

Новизна технического решения заключается в том, что впервые предложено дополнять группировку по порядкам Р.Хортона группировкой по интервалам изменения длины притока и площади водосборов основной части притоков реки (как правило, по сумме притоков первого и второго порядков по Р.Хортону), и эта основная часть речной системы в целом характеризует свойства всей речной сети. К существенной новизне относится также применение устойчивых законов распределения, в том числе и предложенного нами биотехнического закона, для системного описания речной сети в виде распределений численности притоков по интервалам длины притока и площади водосбора. Существенным является также оценка качества речной сети по показателям адекватности распределений фактическим распределениям значений длины и площади основной части притоков реки.

Предлагаемое техническое решение обладает существенными признаками, мировой новизной и значительным положительным эффектом. Материалов, порочащих новизну технического решения, нами не обнаружено.

Способ измерения речной сети включает в себя следующие действия.

Важное значение приобретает необходимость дополнительных измерений для уточнения показателей длины и площади каждого водотока реки. Дело в том, что существующая концепция гидрологии считает достаточным при определении водных ресурсов измерение только крупных притоков реки, не обращая достаточного внимания на мелкие и первичные водотоки. В итоге возникло техническое противоречие: для гидрологических расчетов достаточна та информация, которая существует в справочниках, но для оценки речной сети требуется на порядок (то есть не менее в 10 раз) повысить добротность и точность сведений о каждом, пусть даже мельчайшем, притоке. Главное в измерениях речной сети становится не вычисление максимального или среднего расхода речной воды, а измерение структуры и параметров каждого элемента речной сети. Эти структурные параметры и определяют, собственно говоря, все возможные значения гидрологических показателей, в том числе и предельно возможные по орографическим и системным признакам.

Поэтому дополнительно к группировке водотоков реки по порядкам примыкания притоков к водотоку более высшего порядка по Р.Хортону уточняют значения длины и площади водосборов каждого притока реки в речной сети по результатам полевых или иных измерений, проведенных в каждой группе Р.Хортона. Затем принимают множество водотоков для статистического моделирования, состоящее, по крайней мере, из одной группы Р.Хортона. Таким образом, статистическое множество может включать любую группу Р.Хортона. Например, можно включить в статистическую выборку притоки третьего порядка и т.д. Но лучше всего принять притоки первого порядка или сумму первого и второго порядка.

Затем вычисляют и принимают шаг группировки отдельно по интервалам длины притока и отдельно по интервалам площади водосбора, затем уточняют шаги группировки по результатам исключения из множества уникальных притоков, после этого распределяют притоки этого принятого для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора. После этого определяют параметры статистических моделей по устойчивым законам распределения, а по математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети.

Для статистического моделирования принимают множество водотоков, состоящее, как правило, из притоков первого и второго порядков, то есть по двум группам Р.Хортона, которые и определяют значительную долю мощности речной сети. Это же множество характеризует и качество всей речной системы.

Для возможности сопоставления математических закономерностей по рядам распределения численности притоков многих речных сетей принимают общий шаг группировки по интервалу длины притока или площади водосбора, например, равный целому числу 1 км или 4 км², полученные для наиболее крупной речной сети из нескольких сравниваемых. Ниже приведен пример моделирования по реке Буй. Сравнение показывает, что интервалы (шаги) изменения длины притока и площади водосбора можно принять и для других рек, находящихся на территории Республики Марий Эл. По-видимому, для рек Российской Федерации потребуются несколько шкал длины и площади.

Для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора определяют параметры статистических моделей по устойчивым законам распределения, причем для идентификации применяют общую математическую закономерность распределения притоков по интервалам длины притоков и площади водосбора по формуле:

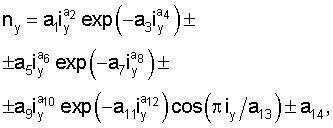
где y - показатели притока реки (длина притока L, км, или площадь водосбора S, км²),

n_y - число попаданий притоков в тот или ной интервал значений показателя, шт.,

i_y - код интервала изменения показателя, то есть место расположения интервалов значений показателя: код интервала длины притока i_L или код интервала значений площади водосбора i_S,

а₁...a₁₄ - параметры статистической модели, при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а₄=1, a₈=1, а₁₂=1, а₆=0, а₁₀=0 или а₁₄=0).

По математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети по изменениям статистических показателей адекватности найденных математических закономерностей к множеству учтенных измеренных значений длины притока и площади водосбора и структуре самой статистической закономерности. Здесь много возможностей оценки качества речной сети и некоторые из них будут показаны на примере.

Способ измерения речной сети выполняется, например, при измерении параметров притоков средней реки, следующим образом.

Вначале по литературным и справочным данным составляется табличная модель значений длины и площади водосбора реки и ее притоков. Эта табличная модель до сих пор не применялась для статистического моделирования речной сети и применялась в основном только для ориентировочных гидрологических расчетов, главным образом для вычислений максимальных расходов речной воды во время весенних половодий.

Поэтому дополнительно к группировке водотоков реки по порядкам примыкания притоков к водотоку более высшего порядка по Р.Хортону уточняют значения длины и площади водосборов каждого притока реки в речной сети по результатам полевых или иных измерений, проведенных в каждой группе Р.Хортона. Затем принимают множество водотоков для статистического моделирования, состоящее по крайней мере из одной группы Р.Хортона, например в совокупности притоки первого и второго порядков. После этого вычисляют и принимают шаг группировки отдельно по интервалам длины притоков и отдельно по интервалам площади водосбора этих же притоков. Статистически эти действия в гидрологии рек не применялись. Поэтому обладают новизной.

Затем уточняют шаги группировки по результатам исключения из множества уникальных притоков, после этого распределяют притоки этого принятого для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора. После этого определяют параметры статистических моделей с использованием ПЭВМ и специальных программных средств по устойчивым законам распределения, а по математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети.

Для статистического моделирования принимают множество водотоков, как правило, состоящее из притоков первого и второго порядков, то есть по двум группам Р.Хортона, которые и определяют значительную долю мощности речной сети. Это же множество характеризует и качество всей речной системы.

Для возможности сопоставления математических закономерностей по рядам распределения численности притоков многих речных сетей принимают общий шаг группировки по интервалу длины притока или площади водосбора, например, равный целому числу 1 км или 4 км², полученные для наиболее крупной речной сети из нескольких сравниваемых. Ниже приведен пример моделирования по реке Буй. Сравнение показывает, что интервалы (шаги) изменения длины притока и площади водосбора можно принять и для других рек, находящихся на территории Республики Марий Эл. По-видимому, для рек Российской Федерации потребуются несколько шкал длины и площади.

Для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора, определяют параметры статистических моделей по устойчивым законам распределения, причем для идентификации применяют общую математическую закономерность распределения притоков по интервалам длины притоков и площади водосбора по формуле:

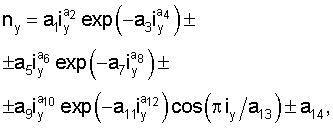
где y - показатели притока реки (длина притока L, км, или площадь водосбора S, км²),

n_y - число попаданий притоков в тот или ной интервал значений показателя, шт.,

i_y - код интервала изменения показателя, то есть место расположения интервалов значений показателя: код интервала длины притока i_L или код интервала значений площади водосбора i_S,

а₁...a₁₄ - параметры статистической модели, при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а₄=1, a₈=1, а₁₂=1, а₆=0, а₁₀=0 или а₁₄=0).

По математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают качество всей речной сети по изменениям статистических показателей адекватности найденных математических закономерностей к множеству учтенных измеренных значений длины притока и площади водосбора, а также по структуре самой статистической закономерности.

Для измерения качества речной сети применяется статистический показатель Δ_max, то есть максимальная относительная погрешность. Чем меньше значение погрешности, тем качественнее речная сеть, так как она лучше проявляется как биотехническая закономерность.

Другой показатель предлагается для оценки качества структуры речной сети. Для этого запишем вышеприведенную формулу в виде

n_y=n₁±n₂±n₃,

где n₁ - первая составляющая, характеризующее естественное изменение речной сети по параметрам длины и площади, n₂ - вторая составляющая стрессового возбуждения речной сети (как биологического организма) на внешние воздействия (как правило, антропогенные изменения), n₃ - третья составляющая волнового возмущения речной сети на различные прошлые катастрофы (природные катастрофы в недалеком прошлом или антропогенные катастрофы от нарушений структуры речной сети, например, от сводки прибрежных лесов и др.).

При этом третья волновая составляющая по своей структуре имеет вид

n₃=a cos(πi_y/p_0.5±a₁₄),

где а - амплитуда колебательного изменения структуры речной сети по отдельным группам значений длины или площади, р_0.5 - половина периода колебательно-цикличного возмущения (измеряется кодами или натуральными значениями учтенных показателей речной сети - длины притоков или площади водосборов).

Показатель качества речной сети по отношению к своему водосборному бассейну определяется коэффициентом приспособляемости, равным

k=n₃/n₁.

По этому показателю качество речной сети определяется отношением колебательного возмущению третьей составляющей статистической закономерности по измеренному показателю площади водосбора к первой естественной составляющей. При этом показатель длины притоков можно не учитывать, так как размер по длине недостаточно полно отражает природный объект. Поэтому лучше всего применять оценку по площади водосбора.

Пример. Для группировки значений длины и площади водосбора в табл. 1 приведены исходные данные, полученные после уточняющих измерений натурными и картографическими способами по речной сети реки Буй, расположенной в основном на территории Республики Марий Эл.

Таблица 1
Речная сеть бассейна реки Буй№ п/пНаименование водотокаПорядок водотокаДанные до проведения исследованияДанные после ИсследованияДлина L, кмПлощадь S, км²Длина L, кмПлощадь S, км²Исток р. Буй, юг села Помосъял11 л. пр в Помосъял13,010,82,452,8022 пр. пр из Елеево1--3,507,8033 л. пр. р.Корем из Егорково1--6,5023,6044 пр. пр. из полей напр. Иштры1--0,954,0055 л. пр. из Иштры1--1,555,2566 л. пр. из Иштры1--0,751,6577 пр. пр. из р.Ляжмори11,2-2,058,7988 пр. пр. от трассы1--1,004,4799 пр. пр. из Юлтышки11,8-1,154,501010 л. пр. р.Сереньга211,240,611,2011,50111 л. пр. 10-го пр из Соловьево12,3-2,509,50122 л. пр. 10-го пр. Ворошилово1--2,404,161311 л. пр. р.Касмер из Сюдумари11,810,56,6011,001412 пр. пр. из Писминер1--0,951,60Продолжение табл.11513 пр. пр. р.Шалген1--1,003,251614 пр. пр. из Азянково1--1,603,501715 л. пр. из Арып Мурзы1--3,6012,41816 пр. пр. от леса1--2,455,601917 пр. пр. из Б.Коршуны2--1,003,30201 пр. пр. 17-го пр.1--0,401,602118 пр. пр.1--0,400,902219 л. пр. из М.Мунамари1--1,503,152320 л. пр. из Б.Вочармы1--3,9512,102421л. пр. р.Собака322,8144,222,00144,00251 пр. пр. из Чагино15,510,13,5010,10262 л. пр. 21-го в Б.Гари11,8-1,801,60273 пр. пр. 21-го пр.12,7-1,104,10284 пр. пр. 21-го пр.1--0,602,20295 л. пр. 21-го пр. ниже Моркинерь11,1-1,101,20306 пр. пр. 21-го пр р.Орья25,527,07,7027,00311 л. пр. 6 пр. из кордона1--1,501,80322 пр. пр. 6-го пр.1--0,801,50333 пр. пр. 6-го пр. из Меркуши1--2,004,50347 пр. пр. из Козлоял25,114,85,0015,00351 пр. пр. 7-го пр1--0,402,90368 пр. пр. 21-го пр. из Калеево1--1,5010,30379 пр. пр. 21-го пр.1--1,603,003810 л. пр. 21-го пр. из Вошмы16,318,15,5018,103911 пр. пр. из родника1--0,351,504022 пр. пр. р.Буй1--0,654,304123 пр. пр. из Таловки1--3,006,004224 л. пр. из Орсюбы12,27,64,757,604325 л. пр. р.Сюбинка328,559,528,5059,50441 л. пр. 25-го пр.1--1,004,30452 пр. пр. 25-го пр.11,5-1,601,90463 пр. пр. 25-го пр.11,5-1,602,00474 пр. пр. 25-го пр. р.Кужнурка13,5-3,706,30485 л. пр. 25-го пр.10,8-0,301,10496 л. пр. 25-го пр.10,3-0,301,75507 л. пр. 25-го пр. из Пижинерь15,1-5,1011,005126 л. пр. р.Буй1--1,802,105227 пр. пр. р.Буй1--2,303,005328 пр. пр. р.Алежурка23,620,23,6020,20541 пр. пр. 28-го пр.1-00,952,205529 л. пр. р.Мазарка325,1110,025,10110,00561 пр. пр. 29-го пр.11,1-1,101,00572 л. пр. 29-го пр.10,7-0,701,50583 л. пр. 29-го пр. р.С.Мазарка14,816,24,8016,20594 л. пр. 29-го пр.1--2,7510,25605 л. пр. 29-го пр.1--1,101,90616 л. пр. 29-го пр.1--0,952,40627 л. пр. 29-го пр.16,618,56,6018,506330 пр. пр. из Кугерь22,014,82,2515,00

Окончание табл.1641 л. пр. 30-го пр.1- 1,757,256531 л. пр. выше р.Чамки16,213,46,2013,406632 л. пр. р.Чамка из В.Чамки17,916,67,9016,606733 пр. пр. р.Буй1--1,502,106834 л. пр. р.Чамка из Александров.310,030,210,0031,00691 л. пр. 34-го пр.24,5-3,505,30701 пр. пр. 1-го пр.10,8-0,803,007135л. пр. выше Шуеть25,4-4,5010,80721 пр. пр. 16-го пр.10,7-0,702,307336 л. пр. в М.Шуеть24,09,04,009,00741 л. пр. 36-го пр.10,6-0,601,277537 пр. пр. из Федорищева3--4,006,30761 пр. пр. 37-го пр.2--1,500,85771 пр. 1 пр. 37-го пр.1--0,901,80782 пр. пр-37-го пр.2--1,500,907938 пр. пр. из Сарда1--1,801,958039 пр. пр. из Б.Ошки21,6-2,006,20811 пр. 39-го пр.1--1.702,508240 л. пр. из Новоройского16,218,06.2018,008341 л. пр. выше Щино1--3,256,758442 пр. пр. из Рожденсвенское1--1,201,958543 л. пр. из ур. Касьянове25,516,35,5016,30861 пр.пр. 43-го пр.10,8-0,802,00872 пр.пр. 43-го пр.11,8-1,804,50883 л. пр. 43-го пр.1--2,203,208944 пр. пр. из Пестово1--0,502,759045 л. пр. из Петровское11,8-1,803,0091р.Буй498,8893,298,80893,20

По формуле Г.А.Стреджеса получаем для 91-6=85 точек статистической выборки 7 интервалов. При этом в статистическую выборку включаются водотоки 1-го и 2-го порядков, так как они мало отличаются по значениям измеряемых (исследуемых) показателей друг от друга. Поэтому из группировки на 7 интервалов исключаем притоки 3-го порядка и саму реку Буй (4-й порядок). Тогда размах значений длины притоков будет равен 11,2-0,3=10,9. Делим это значение размаха на 7 интервалов и получаем шаг группировки, равный 10,9/7=1,56 км. Округляя до удобных значений, получим шаг группировки 1,5 км.

Размах площади равен 27,0-0,85=26,15 км². Тогда интервал шага будет равен 26,15/7=3,74 км². Округляем и получаем шаг группировки по площади для притоков реки Буй, равный 4,0 км.

Теперь можем принять два варианта оси абсцисс - по середине интервалов, например, по площади (2, 4, 6 и т.д.) и по кодам интервалов 1, 2, 3 и т.д. Если будет получена статистическая (математическая) зависимость по одной из этих двух шкал, то второй вариант закономерности будет определен простым подставкой значений аргумента. Пусть принимается код интервалов длины i_L и площади водосбора i_S.

После распределения значений длины притоков получим статистический ряд: 37, 24. 10, 6, 5. 2, 0, 1. Здесь замечаем, что один из интервалов имеет нулевое значение числа наблюдений. Этого не должно быть, поэтому приток под №10 (табл. 1) требует дальнейших уточняющих полевых измерений (в общем случае исследований). Из сопоставления также видно, что до уточняющих измерений площадь водосбора была равна даже 40,6 км². Это означает, что у этого притока могут оказаться неучтенные притоки (засохшие или засыхающие), которые проявляются только во время весеннего половодья.

Исключение наблюдения №10 дает новый шаг группировки (7,9-0,3)/7=1,09 км. Округленно принимаем шаг длины водотока, равный 1,00 км (измерения при уточняющих полевых исследованиях выполнены с точностью 10 м, поэтому значения длины приводим с двумя знаками после запятой). Тогда статистический ряд преобразуется к виду: 25, 26, 10, 9, 4, 3, 5, 2. Эту статистическую выборку примем для последующего статистического моделирования идентификацией биотехнического закона.

Для ряда из 84 значений площади водосбора получили статистический ряд: 43, 18, 9, 5, 6, 2, 1.

Длина притоков. После идентификации была получена закономерность изменения длины притоков первого и второго порядков у реки Буй (табл. 2)

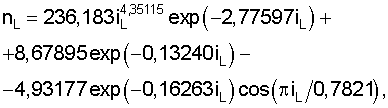
где n_L - расчетное число водотоков в одном интервале изменения длины притоков, i_L - код (номер) группы водотоков в одном интервале длины.

Таблица 2
Распределение притоков по интервалам длины водотока речной сети реки Буй, шт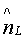Код i_LИнтервал длиныФакт Расчетные значенияСоставляющие моделиn_LεΔ, %n₁n₂аn₃10,00-1,002525.0-0.00-0.0014.717.604.19-2.6921,00-2,002626.0-1.8y-14-0.0018.706.653.56-0.6432,00-3,001010.0-3.6е-15-0.006.805.833.032.6343,00-4,0099.0-1.8е-15-0.001.485.112.57-2.4154,00-5,0044.02.7е-150.000.244.482.190.7265,00-6,0033.0-6.7е-15-0.000.033.921.860.9676,00-7,0055.08.9е-160.000.003.441.58-1.5687,00-8,0022.0-1.8е-15-0.000.003.011.341.01

Здесь: 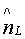- фактические значения показателя; n_L - расчетные значения показателя; ε - остаток, то есть разница 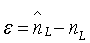; Δ - относительная погрешность, вычисляемая по формуле 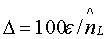. При этом достоверность формулы оценивается по значению Δ_max (в табл. 2 все значения относительной погрешности равны нулю), которое в таблице подчеркнуто. Доверительная вероятность будет равна 100-Δ_max.

Площадь водосбора. Идентификацией также была получена статистическая модель изменения площади притоков первого и второго порядков реки Буй по площади водосбора (табл. 3)

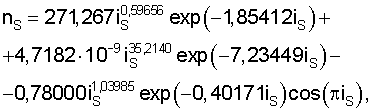
где n_S - расчетное число водотоков в одном интервале изменения площади водосбора притоков, i_S - код группы водотоков, распределившихся в один интервал значений площади водосбора.

Таблица 3
Распределение притоков по интервалам площади водосбора реки Буй, штКод i_SИнтервал площадиФакт Расчетные значенияСоставляющие моделиn_SεΔ, %n₁n₂аn₃10,00-4,004343.0-6.4e-7-0.0042.480.000.52-0.5224,00-8,001818.0-2.9e-7-0.0018.720.000.720.7238,00-12,0099.05.7e-70.008.160.110.73-0.73412,00-16,0055.05.3e-60.003.632.030.660.66516,00-20,0066.0l.0e-50.001.663.780.56-0.56620,00-24,0022.06.5e-60.000.781.680.450.45724,00-28,0011.01.4e-60.000.370.280.35-0.35

Как и предыдущее уравнение, модель распределения численности притоков реки Буй имеет 100-ю доверительную вероятность, поэтому закономерность у конкретной речной сети по популяции водотоков вполне существует. Такие статистические закономерности, получаемые по предлагаемому способу измерения речной сети конкретной реки, вполне можно использовать в гидрологических расчетах, а также при обосновании мероприятий природообустройства и рационального природопользования.

Оценка качества речной сети. Относительная погрешность статистических закономерностей в обоих случаях равна нулю. Поэтому вышеприведенные конкретные закономерности можно считать за математические функциональные зависимости. Это факт показывает, что река Буй имеет высокое качество по основной части речной сети - по множеству из притоков первого и второго порядков водотоков.

Теперь рассмотрим коэффициенты приспособляемости k₁=n₂/n₁, и k₂=n₃/n₁ реки Буй. По отношению к первой составляющей статистической закономерности изменения площади водосбора второй и третьей составляющих получаем значения этого коэффициента приспособляемости речной сети реки Буй к своему водосборному бассейну, которые приведены в табл. 4.

В этой же таблице приведены значения коэффициента значимости каждой из составляющих, вычисляемые как отношение составляющей к теоретическому значению показателя по формулам:

α₁=n₁/n_S;

α₂=n_2/n_S,

α₃=n₃/n_S.

При этом сумма значений этих трех коэффициентов равна единице, то есть α₁+α₂+α₃=1, поэтому активность третьей составляющей принимается с учетом знака перед третьей составляющей статистической модели.

Таблица 4
Коэффициенты приспособляемости речной сети реки Буй по площади к водосборному бассейнуКод группы i_SИнтервал площади водосбора, км²Коэффициент активности составляющих моделиКоэффициент приспособляемостиα₁=n₁/n_Sα₂=n₂/nSα₃=n₃/n_Sk₁=n₂/n₁k₂=n₃/n₁10,00-4,000.9880.000+0.0120.000-0.01224,00-8,001.0400.000-0.0400.0000.03838,00-12,000.9070.012+0.0810.013-0.089412,00-16,000.7260.406-0.1320.5590.182516,00-20,000.2770.630+0.0932.277-0.337620,00-24,000.3900.840-0.2252.1540.577724,00-28,000.3700.280+0.3500.757-0.946

Из данных табл. 4 видно, что группы притоков в каждом интервале значений площади водосбора ведут себя по-разному. Наиболее активны водотоки первых двух групп, то есть водотоки, располагающиеся по площади от нуля до 8,00 км². Далее активность по естественной составляющей снижается и достигает 37,0% для 7-й группы. Таким образом, речная сеть реки Буй обладает хорошими свойствами, имея множество естественных мелких притоков.

Значимость второй составляющей получает максимум для притоков 6-й группы. Но при этом отрицательное влияние оказывает волновая составляющая, поэтому по сумме двух не первых составляющих максимум стрессового возбуждения имеет 5-я группа с активностью 0,630+0,093=0,723. Высокую значимость по антропогенному влиянию имеют также и притоки групп 4, 6 и 7. Поэтому необходимо особое внимание с позиций природообустройства и экологических позиций обращать внимание на притоки, у которых площадь водосбора находится в интервале от 12 до 28 км.

По приспособляемости речной сети к территории имеют притоки пятой группы (максимум коэффициента 2.277).

Циклическое и волновое возмущение нарастает от группы с малым кодом к группе с высоким кодом. Наименьшее влияние на речную сеть по колебательному возмущению оказывают мелкие притоки, в особенности первых двух групп, это указывает на то, что необходимо природоохранными мерами всячески увеличивать численность мелких притоков, имеющих площадь водосбора от нуля до 8 км². Одновременно повышение значимости и приспособляемости более крупных притоков, расположенных в пределах площади водосбора от 12 до 28 км², показывает, что они могут превратиться в обычные водотоки, не имеющие биотехническое значение.

Предлагаемый способ может быть применен к любой речной системе, то есть к реке со многими притоками (теоретически не менее 15, так как чем меньше количество притоков, тем труднее группировать водотоки по интервалам длины и площади). Этот способ можно назвать как метод измерения речной сети распределением численности притоков по ступеням площади их водосбора. Поэтому способ применим, прежде всего, к крупным и средним рекам с большим числом водотоков (десятки, сотни и тысячи).

Изобретение относится к гидрологии рек и может быть использовано при оценке водных ресурсов. Сущность: измеряют количество водотоков. Группируют водотоки по порядкам примыкания к водотоку более высокого порядка, согласно Р.Хортону. Уточняют значения длины и площади водосбора каждого притока реки по результатам полевых или иных измерений, проведенных в каждой группе Р.Хортона. Принимают множество водотоков, состоящее, по крайней мере, из одной группы водотоков Р.Хортона, для статистического моделирования. Вычисляют шаг группировки отдельно по интервалам длины притока и отдельно по интервалам площади водосбора. Уточняют шаги группировки по результатам исключения из множества уникальных притоков. После этого распределяют притоки принятого для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора. Определяют параметры статистических моделей по устойчивым законам распределения. По математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают речную сеть. Технический результат: повышение точности измерений. 5 з.п. ф-лы.

1. Способ измерения речной сети по численности водотоков, включающий измерение численности водотоков для уточнения распределения их по интервалам длины и площади водосбора, группировку водотоков по различным порядкам Р.Хортона, отличающийся тем, что дополнительно к группировке водотоков реки по порядкам примыкания притоков к водотоку более высшего порядка по Р.Хортону уточняют значения длины и площади водосборов каждого притока реки в речной сети по результатам полевых или иных измерений, проведенных в каждой группе Р.Хортона, затем принимают множество водотоков для статистического моделирования, состоящее, по крайней мере, из одной группы водотоков Р.Хортона, вычисляют и принимают шаг группировки отдельно по интервалам длины притока и отдельно по интервалам площади водосбора, затем уточняют шаги группировки по результатам исключения из множества уникальных притоков, после этого распределяют притоки этого принятого для статистического моделирования множества по интервалам длины учтенных притоков и площади их водосбора, определяют параметры статистических моделей по устойчивым законам распределения, а по математическим закономерностям распределений численности притоков по интервалам длины и площади водосбора оценивают речную сеть.2. Способ измерения речной сети по численности водотоков по п.1, отличающийся тем, что для статистического моделирования принимают множество водотоков речной сети, состоящее как правило из притоков первого и второго порядка по первым двум группам Р.Хортона, которые определяют также и значительную долю мощности речной сети.3. Способ измерения речной сети по численности водотоков по п.1, отличающийся тем, что после уточнения показателей длины и площади у водотоков речной сети ориентировочный или уточненный шаг группировки по интервалам длины водотока и интервалам площади водосбора вычисляют по формуле Г.А.Стреджеса в виде

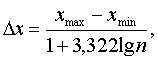
где x_max, x_min - соответственно максимальное и минимальное значение влияющей переменной (длины притока или площади водосбора); n - число членов статистической выборки, то есть количество учтенных водотоков, при этом выражение в знаменателе формулы характеризует число групп наблюдений m, поэтому для удобства применения значения параметров распределения n и m по Г.А.Стреджесу приведены в таблице.

n15-2425-4445-8990-179180-359360-719720-1439m567891011

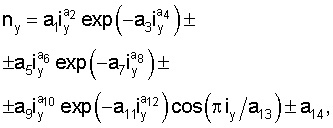
где y - показатели притока реки (длина притока L, км, или площадь водосбора S, км²;

n_y - число попаданий притоков в тот или иной интервал значений показателя, шт.;

i_y - код интервала изменения показателя, т.е. место расположения интервалов значений показателя: код интервала длины притока i_L или код интервала значений площади водосбора i_S;

a₁...a₁₄ - параметры статистической модели, при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а₄=1, a₈=1, a₁₂=1, a₆=0, а₁₀=0 или a₁₄=0).