Предложенное изобретение относится к обработке сигналов, более конкретно к обработке сигналов для последовательно поступающих значений, например значений выборок аудиоданных или значений выборок видеоданных, которые, в частности, пригодны для приложений кодирования без потерь.
Предложенное изобретение также подходит для алгоритмов сжатия для дискретных значений, которые имеют аудио- и/или видеоинформацию, в частности для алгоритмов кодирования, которые включают в себя преобразование в частотную область, или временную область, или область местоположения, за которыми следует кодирование, например энтропийное кодирование в форме кодирования Хафмана или арифметического кодирования.
Современные способы аудиокодирования, например, MPEG уровня 3 (MP3) или MPEG AAC применяют преобразования, например так называемое модифицированное дискретное косинусное преобразование (МДКП), чтобы получать блочное частотное представление аудиосигнала. Подобный аудиокодер получает обычно поток дискретных по времени значений выборок аудиосигнала. Поток значений выборок аудиосигнала подвергается взвешиванию функцией окна, чтобы получать взвешенный блок, например, 1024 или 2048 значений выборок аудиосигнала. Для взвешивания функцией окна используются различные функции окна, например синусоидальное окно и т.д.
Взвешенные функцией окна дискретные по времени значения выборок аудиоданных затем преобразуются посредством набора фильтров в спектральное представление. В принципе, для этого может использоваться преобразование Фурье или, из-за особых причин, некоторый производный тип преобразования Фурье, например быстрое преобразование Фурье (БПФ) или МДКП. Блок спектральных значений аудиоданных на выходе набора фильтров может, по мере необходимости, подвергаться дальнейшей обработке. В случае вышеописанных аудиокодеров осуществляется так называемое квантование спектральных значений аудиоданных, причем шаг квантования выбирается таким образом, чтобы шумы квантования, обусловленные квантованием, находились ниже психоакустического порога маскирования, то есть были замаскированными. Квантование представляет собой кодирование с потерями. Чтобы получить дальнейшее сокращение объема данных, квантованные спектральные значения затем кодируются, например, путем энтропийного кодирования Хафмана. За счет добавления вспомогательной информации, например масштабирующих коэффициентов и т.д., из энтропийно кодированных квантованных спектральных значений посредством мультиплексора битового потока формируется битовый поток, который сохраняется или передается.
В аудиодекодере битовый поток посредством демультиплексора битового потока разделяется на кодированные квантованные спектральные значения и вспомогательную информацию. Энтропийно кодированные квантованные спектральные значения сначала подвергаются энтропийному декодированию, чтобы получить квантованные спектральные значения. Квантованные спектральные значения затем подвергаются обратному квантованию, чтобы получить декодированные спектральные значения, содержащие шумы квантования, которые лежат ниже психоакустического порога маскирования и поэтому становятся неслышимыми. Эти спектральные значения затем преобразуются посредством набора фильтров синтеза во временное представление, чтобы получить дискретные по времени декодированные значения выборок аудиосигнала. В наборе фильтров синтеза должен применяться алгоритм преобразования, обратный вышеупомянутому алгоритму преобразования. Кроме того, после обратного частотно-временного преобразования взвешивание функцией окна должно осуществляться в обратном направлении.
Для того чтобы достичь хорошей избирательности по частоте, современные аудиокодеры в типовом случае применяют перекрытие блоков, как показано на фиг.6а. Сначала, например, берутся 2048 дискретных по времени значений выборок аудиосигнала и подвергаются взвешиванию функцией окна посредством устройства 402. Окно, реализуемое устройством 402, имеет длину окна, равную 2N значений выборок, и выдает на выход блок из 2N значений выборок. Чтобы получить перекрытие окон, сначала посредством устройства 404, которое на фиг.6а показано отдельно от устройства 402 только для наглядности, формируется второй блок из 2N взвешенных функцией окна значений выборок. Однако введенные в устройство 404 2048 значений выборок не являются дискретными по времени значениями выборок аудиосигнала, непосредственно примыкающими к первому окну, а содержат вторую половину значений выборок, взвешенных функцией окна с помощью устройства 402, и дополнительно только 1024 "новых" значений выборок. Перекрытие символически представлено на фиг.6а с помощью устройства 406, которое обеспечивает степень перекрытия 50%. Как 2N взвешенных значений выборок, выданных устройством 402, так и 2N взвешенных значений выборок, выданных устройством 404, затем подвергаются обработке в соответствии с алгоритмом МДКП посредством устройства 408 или 410. Устройство 408 выдает, согласно известному алгоритму МДКП, N спектральных значений для первого окна, в то время как устройство 410 выдает также N спектральных значений, но для второго окна, причем между первым окном и вторым окном имеется перекрытие 50%.
В декодере N спектральных значений первого окна, как показано на фиг.6b, подаются на устройство 412, которое выполняет обратное модифицированное дискретное косинусное преобразование. То же самое справедливо для N спектральных значений второго окна. Они подаются на устройство 414, которое также выполняет обратное модифицированное дискретное косинусное преобразование. Как устройство 412, так и устройство 414 выдают соответственно 2N значений выборок для первого окна и 2N значений выборок для второго окна.
В устройстве 416, как обозначено на фиг.6b аббревиатурой TDAC (компенсация наложения спектров во временной области), учитывается тот факт, что оба окна перекрываются. В частности, значение выборки y1 второй половины первого окна, то есть с индексом N+k, суммируется с значением выборки y2 первой половины второго окна, то есть с индексом k, так что на выходе, то есть в декодере, получается N декодированных временных значений выборок.
Следует отметить, что за счет функции устройства 416, которая также называется функцией суммирования, взвешивание функцией окна, проводимое в схематично представленном на фиг.6а кодере, в известной степени учитывается автоматически, так что в декодере, представленном на фиг.6b, в явном виде не производится никакого "инверсного взвешивания функцией окна".
Если обозначить функцию окна, реализуемую устройством 402 или 404 как w(k), где индекс k представляет собой временной индекс, то должно выполняться условие, что вес окна w(k) в квадрате, суммированный с весом окна w(N+k) в квадрате, дает 1, причем k изменяется в пределах от 0 до N-1. Если применяется синусное окно, вес которого соответствует первой полуволне функции синуса, то это условие всегда выполняется, так как квадрат синуса и квадрат косинуса для каждого угла в сумме дают 1.
Недостаток способа взвешивания функцией окна, описанного со ссылкой на фиг.6а, с последующим применением функции МДКП заключается в том обстоятельстве, что взвешивание функцией окна реализуется посредством умножения дискретных по времени значений выборок, в предположении синусного окна, с использованием числа с плавающей запятой, так как синус угла в пределах от 0 до 180 градусов, исключая угол 90 градусов, не дает целого числа. И в случае, когда взвешиванию функцией окна подвергаются целочисленные значения выборок, после взвешивания функцией окна возникают также числа с плавающей запятой.
Поэтому, и без применения психоакустического кодера, то есть, когда должно быть реализовано кодирование без потерь, на выходе устройств 408 или 410 необходимо квантование, чтобы иметь возможность проведения до некоторой степени обозримого энтропийного кодирования.
Таким образом, современные известные целочисленные преобразования для аудио- и/или видеокодирования без потерь реализуют за счет разложения применяемых при этом преобразований на Givens-вращения и применения схем поднятия для каждого Givens-вращения. Тем самым на каждом шаге вводится ошибка округления. Для последующих ступеней Givens-вращений ошибка округления все больше аккумулируется. Получающаяся в результате ошибка аппроксимации становится, особенно для аудиокодирования без потерь, проблематичной, в частности, если применяются длинные преобразования, которые вырабатывают, например, 1024 спектральных значения, как это имеет место, например, для известного МДКП с перекрытием и суммированием. В частности, в высокочастотной области, где аудиосигнал и без того имеет в типовом случае очень малое содержание энергии, ошибка аппроксимации может быстро становиться большей по величине, чем действительный сигнал, так что такие применения в отношении кодирования без потерь и, в частности, в отношении достижимой эффективности кодирования являются проблематичными.
Целочисленные преобразования, то есть алгоритмы преобразования, которые вырабатывают целочисленные выходные значения, основываются, в аспекте аудиокодирования, в частности, на известном ДКП-IV, которое не учитывает постоянную составляющую, в то время как целочисленные преобразования применительно к изображениям скорее базируются на ДКП-II, которое содержит режимы, специально предусмотренные для постоянной составляющей. Такие целочисленные преобразования известны, например, из следующих работ: Y.Zeng, G.Bi, Z.Lin, "Integer sinusoidal transforms based on lifting factorization", Proc. ICASSP'01, May 2001, p.1.181-1.184; K.Komatsu, K.Sezaki, "Reversible Discrete Cosine Trasnsform", Proc. ICASSP, 1998, V.3, p.1.769-1.772; P.Hao, Q.Shi, "Matrix factorizations for reversible integer mapping", IEEE Trans. Signal Processing, V.49, p.2.314-2.324; J.Wang, J.Sun, S.Yu, "1-d and 2-d transforms from integers to integers", Proc. ICASSP'03, Hongkong, April 2003.
Как изложено в указанных работах, описанные в них целочисленные преобразования основываются на разложении преобразования на Givens-вращения и на применении известной схемы поднятия к Givens-вращениям, что влечет за собой проблему накопления ошибок округления. Это объясняется, в частности, тем, что в пределах одного преобразования должно многократно осуществляться округление, например, после каждого шага поднятия, так что особенно при длинных преобразованиях, которые сопровождаются соответственно большим количеством шагов поднятия, особенно часто должна проводиться операция округления. Как представлено, это приводит в результате к накоплению ошибок, а также к относительно высоким затратам на обработку, так как всегда после каждого шага поднятия осуществляется округление, чтобы выполнить следующий шаг поднятия.
Далее, со ссылкой на фиг.9-11, еще раз представлено разложение взвешивания функцией окна по алгоритму МДКП, как оно описано в документе DE 10129240 А1, причем это разложение взвешивания по алгоритму МДКП на Givens-вращения с матрицами поднятия и соответствующими округлениями, предпочтительным образом, может комбинироваться с принципом, изображенным на фиг.1 для преобразования и на фиг.2 для обратного преобразования, чтобы получить полную целочисленную аппроксимацию МДКП, то есть целочисленное МДКП, согласно настоящему изобретению, причем на примере МДКП может быть реализован как принцип прямого преобразования, так и принцип обратного преобразования.
На фиг.3 показана обобщенная диаграмма соответствующего изобретению предпочтительного способа обработки дискретных по времени значений выборок, которые представляют аудиосигнал, чтобы получить целочисленные значения, на основе которых работает алгоритм целочисленного преобразования МДКП. Дискретные по времени значения выборок, посредством показанного на фиг.3 устройства, подвергаются взвешиванию функцией окна и дополнительно могут преобразовываться в спектральное представление. Дискретные по времени значения выборок, которые подаются на вход 10 устройства, взвешиваются посредством функции окна w с длиной, соответствующей 2N дискретным по времени значениям выборок, чтобы на выходе 12 получить целочисленные взвешенные значения выборок, которые пригодны для того, чтобы посредством преобразования, в частности устройством 14 для выполнения целочисленного ДКП, перевести их в спектральное представление. Целочисленное ДКП выполняется для того, чтобы из N входных значений сформировать N выходных значений, что отличается от функции МДКП 408 по фиг.6а, которая из 2N взвешенных значений выборок на основе уравнения МДКП вырабатывает только N спектральных значений.
Для взвешивания оконной функцией дискретных по времени значений выборок сначала в устройстве 16 выбираются два дискретных по времени значения выборок, которые совместно представляют вектор дискретных по времени значений выборок. Дискретное по времени значение выборки, которое выбирается с помощью устройства 16, расположено в первой четверти окна. Другое дискретное по времени значение выборки находится во второй четверти окна, как это более детально представлено с помощью фиг.5. К сформированному устройством 16 вектору применяется затем матрица вращения размерности 2 х 2, причем эта операция проводится не непосредственно, а посредством множества так называемых матриц поднятия.
Матрица поднятия имеет то свойство, что она имеет только один элемент, который зависит от окна w и не равен "1" или "0".
Факторизация волновых преобразований шагами поднятия представлена в публикации "Factoring Wavelet Transforms Into Lifting Steps", Ingrid Daubechies, Wim Sweldens, Preprint, Bell Laboratories, Lucent Technologies, 1996. В обобщенном смысле, схема поднятия представляет собой простое соотношение между идеально реконструируемыми парами фильтров, которые содержат одинаковые фильтры нижних частот или верхних частот. Каждая пара комплементарных фильтров может быть факторизована шагами поднятия. В частности, это справедливо для Givens-вращений. Можно рассмотреть случай, при котором полифазная матрица соответствует Givens-вращению. Тогда справедливо равенство:

Каждая из трех стоящих в правой части равенства матриц поднятия имеет в качестве элементов главной диагонали значение "1". Кроме того, в каждой матрице поднятия один элемент второстепенной диагонали равен "0" и один элемент второстепенной диагонали зависит от угла поворота α.
Вектор затем умножается на третью матрицу поднятия, то есть на крайнюю справа матрицу поднятия в приведенном выше равенстве, чтобы получить результирующий вектор. Это представлено на фиг.3 устройством 18. Затем первый результирующий вектор округляется с использованием любой функции округления, которая отображает множество действительных чисел на множество целых чисел, как представлено на фиг.3 устройством 20. На выходе устройства 20 получается округленный первый результирующий вектор. Округленный первый результирующий вектор вводится теперь в устройство 22 для его умножения на среднюю, то есть вторую, матрицу поднятия, чтобы получить второй результирующий вектор, который вновь округляется в устройстве 24, чтобы получить округленный второй результирующий вектор. Округленный второй результирующий вектор вводится теперь в устройство 26 для его умножения на приведенную слева в вышеуказанном уравнении, то есть на первую, матрицу поднятия, чтобы получить третий результирующий вектор, который, в итоге, вновь округляется в устройстве 28, чтобы получить на выходе 12 целочисленные взвешенные функцией окна значения выборок, которые затем, если желательно их спектральное представление, должны обрабатываться устройством 14, чтобы получить на спектральном выходе 30 целочисленные спектральные значения.
Предпочтительным образом, устройство 14 выполняется как устройство целочисленного ДКП.
Дискретное косинусное преобразование согласно типу 4 (ДКП-IV) с длиной N определяется следующим равенством:
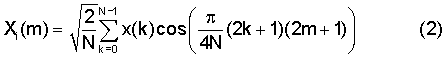
 Коэффициенты ДКП-IV образуют ортогональную матрицу размера N x N. Каждая ортогональная матрица размера N x N может быть разложена на N(N-1)/2 Givens-вращений, как это представлено в публикации P.P.Vaidyanathan, "Multirate Systems And Filter Banks", Prentice Hall, Englewood Cliffs, 1993. Следует отметить, что существуют и другие разложения.
Коэффициенты ДКП-IV образуют ортогональную матрицу размера N x N. Каждая ортогональная матрица размера N x N может быть разложена на N(N-1)/2 Givens-вращений, как это представлено в публикации P.P.Vaidyanathan, "Multirate Systems And Filter Banks", Prentice Hall, Englewood Cliffs, 1993. Следует отметить, что существуют и другие разложения.
Относительно классификации различных алгоритмов ДКП можно сослаться на работу H.S.Malvar, "Signal Processing With Lapped Transforms", Artech House, 1992. В общем, алгоритмы ДКП различаются по виду их базовой функции. В то время как алгоритм ДКП-IV, который здесь рассматривается в качестве предпочтительного, включает в себя несимметричные базовые функции, то есть четверть волны косинусоиды, 3/4 волны косинусоиды, 5/4 волны косинусоиды, 7/4 волны косинусоиды и т.д., дискретное косинусное преобразование, например, типа II (ДКП-II) имеет асимметричные и центрально симметричные базовые функции. 0-ая базовая функция имеет постоянную составляющую, первая базовая функция представляет собой полуволну косинусоиды, вторая базовая функция представляет собой полную косинусоиду и т.д. На основе того факта, что ДКП-II, в частности, учитывает постоянную составляющую, оно применяется при видеокодировании, но не при аудиокодировании, так как для аудиокодирования, в противоположность видеокодированию, постоянная составляющая не релевантна.
Далее описано, каким образом угол поворота α Givens-вращения зависит от оконной функции взвешивания.
МДКП с длиной окна 2N может быть сокращено до косинусного преобразования типа IV с длиной N. Это реализуется тем, что проводится операция TDAC в явном виде во временной области, и затем применяется ДКП-IV. При 50% перекрытии перекрывается левая половина окна для блока t с правой половиной предыдущего блока, то есть блока t-1. Перекрывающаяся часть двух следующих друг за другом блоков t-1 и t во временной области, то есть перед преобразованием, обрабатывается следующим образом, то есть между входом 10 и выходом 12 по фиг.3:
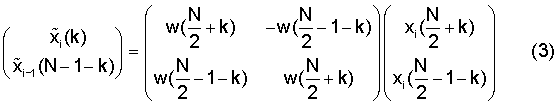
Обозначенные тильдой значения представляют собой значения на выходе 12 на фиг.3, в то время как значения х без тильды в вышеприведенном уравнении представляют собой значения на входе 10 или после устройства 16 для выбора. Индекс k изменяется от 0 до N/2-1, и w представляет собой оконную функцию взвешивания.
Из условия TDAC для оконной функции взвешивания w следует следующая взаимосвязь:

Для определенного угла αk, где k=0, ..., N/2-1, эта предварительная обработка во временной области может описываться как Givens-вращение, как оно выполняется.
Угол α Givens-вращения зависит, следовательно, от оконной функции взвешивания w:

Следует отметить, что могут использоваться любые оконные функции взвешивания w, если они выполняют это условие TDAC.
Далее со ссылкой на фиг.4 описываются каскадный кодер и декодер. Дискретные по времени значения выборки от х(0) до x(2N-1), которые выделяются посредством окна, сначала выбираются таким образом с помощью устройства 16 на фиг.3, что выбираются значение выборки х(0) и значение выборки x(N-1), то есть значение выборки из первой четверти окна и значение выборки из второй четверти окна, чтобы сформировать вектор на выходе устройства 16. Пересекающиеся стрелки схематично представляют умножения поднятия с последующими округлениями устройств 18, 20, или 22, 24, или 26, 28, чтобы на входе блоков ДКП-IV получить целочисленные взвешенные оконной функцией значения выборок.
Когда первый вектор обработан, как описано выше, затем второй вектор из значений выборок x(N/2-1) и x(N/2), то есть вновь значение выборки из первой четверти окна и значение выборки из второй четверти окна, выбирается и обрабатывается посредством описанного на фиг.3 алгоритма. Аналогично этому обрабатываются все другие пары значений выборок из первой и второй четверти окна. Та же самая обработка проводится для третьей и четвертой четверти первого окна. После этого на выходе 12 имеется 2N взвешенных целочисленных значений выборок, которые теперь, как изображено на фиг.4, вводятся в преобразование ДКП-IV. В частности, взвешенные целочисленные значения выборок второй и третьей четверти вводятся в ДКП. Взвешенные целочисленные значения выборок первой четверти окна обрабатываются в предыдущем ДКП-IV вместе с взвешенными целочисленными значениями выборок четвертой четверти предыдущего окна. Аналогично этому четвертая четверть взвешенных целочисленных значений выборок на фиг.4 вместе с первой четвертью следующего окна вводятся в преобразование ДКП-IV. Среднее показанное на фиг.4 целочисленное преобразование ДКП-IV 32 вырабатывает N целочисленных спектральных значений от y(0) до y(N-1). Эти целочисленные спектральные значения могут теперь, например, просто энтропийно кодироваться, не требуя промежуточного квантования, так как взвешивание функцией окна и преобразование дают целочисленные выходные значения.
В правой половине фиг.4 представлен декодер. Декодер, состоящий из обратного преобразования и "инверсного оконного взвешивания", работает обратно по отношению к кодеру. Известно, что для обратного преобразования относительно ДКП-IV может применяться инверсное ДКП-IV, как показано на фиг.4. Выходные значения декодера ДКП-IV 34, как показано на фиг.4, теперь подвергаются инверсной обработке с соответствующими значениями предыдущего преобразования или последующего преобразования, чтобы из целочисленных взвешенных значений выборок на выходе устройства 34 или предыдущего и последующего преобразований вновь выработать дискретные по времени значения выборок аудиосигнала от х(0) до х(2N-1).
Операция на стороне выхода осуществляется посредством инверсного Givens-вращения, то есть таким образом, чтобы блоки 26, 28, или 22, 24, или 18, 20 проходились в противоположном направлении. Это более детально представлено с помощью второй матрицы поднятия уравнения (1). Если (в кодере) второй результирующий вектор формируется посредством перемножения округленного первого результирующего вектора с второй матрицей поднятия (устройство 22), то получается следующее выражение:
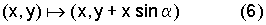
Значения х, y в правой стороне равенства (6) являются целыми числами. Однако это не имеет места для значения выражения x sin α. В этой связи нужно ввести функцию округления r, как это представлено следующим равенством:
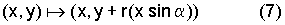
Эту операцию выполняет устройство 24.
Инверсное отображение (в декодере) определяется следующим образом:
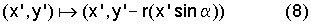
С помощью знака "минус" перед операцией округления показано, что целочисленная аппроксимация шага поднятия может обращаться, не вводя ошибок. Применение этой аппроксимации на каждом из трех шагов поднятия приводит к целочисленной аппроксимации Givens-вращения. Округленное вращение (в кодере) может претерпевать обращенное вращение (в декодере), не вводя ошибки, а именно тем, что инверсно округленные шаги поднятия проходятся в обратном порядке, то есть когда при декодировании алгоритм по фиг.3 проходится снизу вверх.
Если функция округления r является центрально симметричной, то инверсно округленное вращение идентично округленному вращению на угол -α и записывается следующим образом:

Матрица поднятия для декодера, то есть для инверсного Givens-вращения, получается в этом случае непосредственно из равенства (1), при этом только выражение "sin α" заменяется на выражение "-sin α".
Ниже со ссылкой на фиг.5 еще раз рассмотрено разложение обычного МДКП с перекрывающимися окнами 40-46. Окна 40-46 перекрываются, соответственно, на 50%. На каждое окно сначала выполняются Givens-вращения в пределах первой и второй четверти окна или в пределах третьей и четвертой четверти окна, как это схематично показано на фиг.5 стрелкой 48. Затем повернутые значения, то есть взвешенные функцией окна целочисленные значения выборок, вводятся в ДКП, реализующее преобразование из N в N (ДКП из N в N) таким образом, что всегда вторая и третья четверть окна или, соответственно, четвертая и первая четверть последующего окна совместно преобразуются в спектральное представление посредством ДКП-IV.
Затем обычные Givens-вращения разлагаются в матрицы поднятия, которые выполняются последовательно, причем после каждого умножения на матрицу поднятия выполняется шаг округления таким образом, что числа с плавающей запятой округляются непосредственно после их образования, так что перед каждым умножением результирующего вектора на матрицу поднятия результирующий вектор содержит только целые числа.
Выходные значения остаются, таким образом, всегда целочисленными, причем предпочтительным является также применение целочисленных входных значений. Это не является каким-то ограничением, так как любые значения выборок, например, сигнала с импульсно-кодовой модуляцией (ИКМ), как они сохранены, например, на компакт-диске (CD), являются целочисленными значениями, диапазон значений которых варьируется согласно длительности бита, то есть в зависимости от того, являются ли дискретные по времени цифровые входные значения 16-битовыми значениями или 24-битовыми значениями. Однако в том виде, как это выполнено, весь процесс является инвертируемым, то есть инверсные вращения выполняются в обратной последовательности. Таким образом, существует целочисленная аппроксимация МДКП с совершенной реконструкцией, то есть преобразование без потерь.
Показанное преобразование формирует на выходе целочисленные выходные значения вместо чисел с плавающей запятой. Оно обеспечивает совершенную реконструкцию, так что не вводятся никакие ошибки, если выполняется прямое, а затем обратное преобразование. Это преобразование, согласно предпочтительному варианту осуществления изобретения, заменяет модифицированное дискретное косинусное преобразование. Однако и другие способы преобразования могут выполняться в целочисленном виде, если возможны разложение на вращения и разложение вращений на шаги поднятия.
Целочисленное МДКП имеет большинство полезных свойств МДКП. Оно имеет структуру с перекрытием, за счет чего получается лучшая частотная избирательность, чем при блочных преобразованиях без перекрытия. На основе функции TDAC, которая учитывается уже при взвешивании функцией окна перед преобразованием, сохраняется критичное взятие выборок, так что общее число спектральных значений, которые представляют аудиосигнал, равно общему числу входных значений выборок.
Сравнение с нормальным МДКП, которое вырабатывает значения выборок с плавающей запятой, показывает при описанном предпочтительном целочисленном преобразовании, что только в спектральной области, в которой имеется низкий уровень сигнала, шум повышен по сравнению с нормальным МДКП, в то время как такое повышение шума не заметно при значительных уровнях сигнала. Зато целочисленная обработка обеспечивает эффективную реализацию в аппаратных средствах, так как применяются только шаги умножения, которые без труда могут разлагаться на шаги сдвига и суммирования, которые просто и быстро могут быть реализованы аппаратными средствами. Разумеется, также возможна реализация с помощью программного обеспечения.
Целочисленное преобразование обеспечивает хорошее спектральное представление аудиосигнала и при этом остается в области целых чисел. Если оно применяется к тональным частям аудиосигнала, то это приводит в результате к хорошей концентрации энергии. Тем самым можно сформировать эффективную схему кодирования без потерь, просто за счет того, что показанные на фиг.3 взвешивание функцией окна и преобразование каскадно связываются с энтропийным кодером. В частности, предпочтительным является поэтапное кодирование с применением значений перехода, как используется в MPEG AAC. Предпочтительным является то, что все значения масштабируются с понижением на определенную степень двух, пока они не будут согласованы с желательной кодовой таблицей, и затем отброшенные менее значимые биты дополнительно кодируются. По сравнению с альтернативой применения более крупных кодовых таблиц описанный вариант является более благоприятным в отношении требований к объему памяти для запоминания кодовых таблиц. Кодер, по существу, без потерь мог бы также быть получен благодаря тому, что определенные из наименее значимых битов просто отбрасываются.
В частности, для тональных сигналов энтропийное кодирование целочисленных спектральных значений обеспечивает высокий выигрыш при кодировании. Для переходных частей сигнала выигрыш при кодировании является низким, а именно ввиду равномерного спектра переходных сигналов, то есть ввиду незначительного числа спектральных значений, которые равны или близки к нулю. Как описано в работе J.Herre, J.D.Johnston: "Enhancing the Performance of Perceptual Audio Coders by Using Temporal Noise Shaping (TNS)" 101. AES Convention, Los Angeles, 1996, Preprint 4384, эта равномерность спектра применяется, однако, в том, что в частной области используется линейное предсказание. Альтернативным вариантом является прогнозирование в разомкнутом контуре. Другая альтернатива обеспечивается устройством прогнозирования с замкнутым контуром. Первый вариант, то есть устройство прогнозирования с разомкнутым контуром, называется TNS. Квантование после прогнозирования приводит к адаптации результирующих шумов квантования к временной структуре аудиосигнала и за счет этого предотвращает возникновение опережающего эха в психоакустических аудиокодерах. Для аудиокодирования без потерь подходит вторая альтернатива, то есть с устройством прогнозирования с замкнутым контуром, так как прогнозирование в замкнутом контуре обеспечивает более точную реконструкцию входного сигнала. Если этот метод применяется к вырабатываемому спектру, после каждого шага фильтра прогнозирования должно выполняться округление, чтобы оставаться в области целых чисел. За счет применения инверсного фильтра и той же самой функции округления можно снова точно восстановить первоначальный спектр.
Чтобы использовать избыточность между двумя каналами для сокращения данных, может также использоваться кодирование средней-боковой областей без потерь, если применяется округленное вращение на угол π/4. По сравнению с альтернативой вычисления суммы и разности левого и правого каналов стереосигнала округленное вращение имеет преимущество по получению энергии. Применение так называемых методов совместного стереокодирования может для каждой полосы включаться или исключаться, как это выполняется также согласно стандарту MPEG AAC. Другие углы поворота также могут учитываться для того, чтобы иметь возможность более гибко сократить избыточность между двумя каналами.
В частности, показанный на фиг.3 принцип преобразования обеспечивает целочисленную реализацию МДКП, то есть целочисленное МДКП, которое работает без потерь по отношению к прямому преобразованию и обратному преобразованию. Кроме того, за счет этапов округления 20, 24, 28 и соответствующих этапов округления в целочисленном ДКП (блок 14 на фиг.3) все еще возможна целочисленная обработка, то есть обработка с более грубо квантованными значениями, чем они, например, формировались при умножении с плавающей запятой с матрицей поднятия (блоки 18, 22, 26 на фиг.3).
Это приводит к тому, что все целочисленное МДКП также может выполняться эффективным вычислительным образом.
Отсутствие потерь этого целочисленного МДКП, говоря в общем, отсутствие потерь всего алгоритма кодирования, обозначаемого как кодирование без потерь, объясняется тем, что сигнал, когда он кодируется, чтобы получить кодированный сигнал, и когда он снова декодируется, чтобы получить кодированный/декодированный сигнал, выглядит точно так, как первоначальный сигнал. Иными словами, первоначальный сигнал идентичен кодированному/декодированному первоначальному сигналу. Это явно противоположно так называемому кодированию с потерями, при котором, как в случае аудиокодеров, которые работают на психоакустической основе, за счет процесса кодирования и особенно за счет процесса квантования, которое управляется психоакустической моделью, данные безвозвратно теряются.
Однако, разумеется, вводятся ошибки округления. Так проводятся этапы округления, как показано на фиг.3 в блоках 20, 24, 28, которые, разумеется, вводят ошибку округления, которая вновь "исключается" только в декодере, когда выполняются обратные операции. Таким образом, принципы кодера/декодера без потерь принципиально отличаются от концепций кодера/декодера с потерями тем, что в случае концепций кодера/декодера без потерь ошибка округления вводится таким образом, что она может вновь исключаться, в то время как в случае концепции кодера/декодера с потерями это не имеет места.
Однако если рассматривается кодированный сигнал, то есть в примере кодеров с преобразованием - спектр блока временных значений выборок, то округление при прямом преобразовании или, в общем случае, квантование такого сигнала приводит к тому, что в сигнал вводится ошибка. Тем самым на идеальный спектр сигнала без ошибок накладывается ошибка округления, которая в типовом случае, например в примере по фиг.3, представляет собой белый шум, который равномерно окружает все частотные составляющие рассматриваемой области спектра. Этот наложенный на идеальный спектр белый шум представляет собой, таким образом, ошибку округления, которая возникла, например, из-за округления в блоках 20, 24, 28 во время взвешивания функцией окна, то есть предварительной обработки сигнала, перед собственно обработкой ДКП в блоке 14. Особенно следует отметить то, что для требования отсутствия потерь вся ошибка округления обязательно должна кодироваться, то есть должна переноситься к декодеру, так как декодеру необходима вся введенная в кодере ошибка округления, чтобы вновь обеспечить корректное восстановление без потерь.
Ошибка округления, правда, не создает проблем, если возникает не в спектральном представлении, то есть когда спектральное представление только переносится в сохраненном виде и вновь декодируется посредством корректно согласованного инверсного декодера. В таком случае всегда выполняется критерий отсутствия потерь, независимо от того, сколько ошибок округления введено в спектр. Если, однако, со спектральным представлением, то есть с идеальным спектральным представлением, подверженным влиянию ошибок округления, первоначального сигнала что-то предпринимается, например формируются уровни масштабируемости и т.д., то все эти вещи функционируют тем лучше, чем меньше ошибка округления.
Таким образом, при кодировании/декодировании также существует требование, что сигнал, с одной стороны, должен быть восстанавливаемым без потерь посредством специального декодера, что сигнал, однако, должен иметь наименьшую возможную ошибку округления в спектральном представлении, чтобы сохранить в значительной степени гибкость, что спектральное представление также может вводиться в неидеальные декодеры без потерь или могут формироваться уровни масштабирования и т.д.
Как уже отмечено, ошибка округления проявляется как белый шум по всему рассматриваемому спектру. С другой стороны, особенно в применениях, характеризуемых высоким качеством, особенно интересных в варианте без потерь, а также в аудиоприложениях с очень высокими частотами выборок, например 96 кГц, аудиосигнал имел бы разумное содержание только в определенной спектральной области, которая могла бы доходить максимум до 20 кГц. В типовом случае область, в которой концентрируется максимальная энергия аудиосигнала, будет областью между 0 и 10 кГц, в то время как в области выше 10 кГц энергия сигнала уже значительно спадает. Однако для шума, введенного округлением, это соотношение является безразличным. Он накладывается на весь рассматриваемый спектральный диапазон энергии сигнала. Это приводит к тому, что в спектральных областях, то есть в типичном случае, в высоком спектральном диапазоне, где аудиосигнал отсутствует или имеется лишь очень малое количество энергии аудиосигнала, будет иметь место только ошибка округления. Ошибка округления, в частности, ввиду своего недерминированного характера, к тому же вызывает проблемы при кодировании, то есть может кодироваться только при относительно высоких битовых затратах. Битовые затраты, в особенности в некоторых приложениях без потерь, не играют, правда, решающей роли. Однако для того, чтобы расширить возможности применения кодирования без потерь, и в этом случае имеет значение возможность работы с высокой битовой эффективностью, чтобы преимущество, присущее применениям без потерь, заключающееся в отсутствии снижения качества, также объединять с соответствующей битовой эффективностью, как это известно из концепций кодирования с потерями.
Хотя в контексте применений без потерь ошибка округления, таким образом, не создает проблем ввиду того, что она может быть исключена при декодировании, однако большое значение имеет обеспечение того, чтобы декодирование без потерь или восстановление вообще могло осуществляться. С другой стороны, как указано выше, ошибка округления несет ответственность за то, что спектральное представление становится содержащим ошибки, то есть искажается по сравнению с идеальным спектральным представлением неокругленного сигнала. Для определенных случаев применения, при которых действительно применяется спектральное представление, то есть кодированный сигнал, а именно, когда из кодированного сигнала, например, вырабатываются различные уровни масштабирования, является желательным получить кодированное представление с по возможности малой ошибкой округления, из которой, однако, не может быть исключена ошибка округления, которая требуется для восстановления.
Задача настоящего изобретения состоит в том, чтобы создать принцип обработки входных значений, характеризуемый сниженными вводимыми искажениями.
Эта задача решается устройством обработки, по меньшей мере, двух входных значений, согласно пункту 1 формулы изобретения, или способом обработки, по меньшей мере, двух входных значений, согласно пункту 11 формулы изобретения, или компьютерной программой, согласно пункту 12 формулы изобретения.
В основе настоящего изобретения лежит знание того, что снижение ошибки округления может быть достигнуто за счет того, что всегда в условиях, когда именно два значения должны округляться и два округленных значения затем комбинируются, например, путем суммирования с еще одним третьим значением, ошибка округления снижается за счет того, что сначала оба значения суммируются в неокругленном состоянии, то есть в представлении с плавающей запятой, и только после этого суммарное выходное значение суммируется с третьим значением. По сравнению с обычным способом действия, при котором каждое значение обрабатывается отдельно, принцип, лежащий в основе изобретения, приводит к тому, что один процесс суммирования и один процесс округления могут быть сэкономлены, так что принцип, лежащий в основе изобретения, наряду с тем, что сокращается ошибка округления, способствует более эффективному выполнению алгоритма.
В предпочтительном варианте осуществления заявленного изобретения принцип, лежащий в основе изобретения, используется для снижения ошибки округления, когда два вращения, полученные разложением на шаги поднятия, "наталкиваются" друг на друга, то есть когда имеет место ситуация, при которой сначала первое значение с третьим значением должны быть "повернуты" совместно, а потом результат этого первого вращения вновь должен быть повернут с вторым значением.
Другой случай применения соответствующего изобретению принципа снижения ошибки округления существует тогда, когда перед ступенью поднятия концепции многомерного поднятия включены Butterflies ("бабочки"), как это имеет место, когда N-точечное ДКП расщепляется на два ДКП половинной длины, то есть с N/2 точками. В этом случае перед собственно многомерным поднятием реализуется ступень "бабочка", а после многомерного поднятия - ступень вращения. В частности, требуемые для ступени "бабочка" округления могут комбинироваться с округлениями первой ступени поднятия концепции многомерного поднятия, чтобы сократить ошибку округления.
После того как число ступеней округления при целочисленном МДКП с целочисленным взвешиванием функцией окна/предварительной обработкой и многомерной обработкой поднятия для преобразования, в сравнении с уровнем техники, итак уже сильно сокращено без применения изобретения, соответствующий изобретению принцип, особенно в этой ситуации, способствует значительному сокращению еще остающейся, но и так уже низкой ошибки округления. Это приводит к тому, что, например, спектр имеет весьма малое отклонение относительно идеального спектра, обусловленное имеющейся, но однако сильно сниженной ошибкой округления.
Настоящее изобретение может комбинироваться, особенно в контексте кодирования/декодирования, без помех со спектральным формированием ошибки округления, причем остающаяся еще ошибка округления спектрально формируется таким образом, что она "помещается" в частном диапазоне кодируемого сигнала, в котором сигнал имеет высокую энергию, и, тем самым, ошибки округления по существу нет в тех областях, в которых сигнал имеет низкую энергию. В то время, как согласно уровню техники, при кодировании без потерь и, в частности, при кодировании без потерь на основе целочисленных алгоритмов ошибка округления по всему спектру сигнала распределена как белый шум, на идеальный спектр ошибка округления накладывается в форме окрашенного шума, а именно таким образом, что энергия шума, обусловленного округлением, присутствует там, где сигнал имеет свою максимальную энергию, и тем самым шум, обусловленный ошибкой округления, также имеет малую энергию или вообще отсутствует там, где кодируемый сигнал сам также не содержит энергии. Благодаря этому можно избежать неблагоприятного случая, когда ошибка округления, представляющая собой трудно кодируемый стохастический сигнал, является в некотором частотном диапазоне единственным сигналом и тем самым бесполезно повышает битовую скорость.
Если рассматривается аудиосигнал, в случае которого энергия сосредоточена в низкочастотном диапазоне, то устройство округления выполняется таким образом, чтобы реализовать спектральное формирование для низкочастотной фильтрации сформированной ошибки округления, чтобы на высоких частотах кодированного сигнала не имелось ни энергии сигнала, ни энергии шума, в то время как ошибка округления отображается на диапазон, где сигнал имеет высокую энергию.
В частности, для применений кодирования без потерь это решение имеет отличия от уровня техники, при котором ошибка округления подвергается высокочастотной фильтрации, чтобы вывести ошибку округления за пределы слышимого диапазона. Это соответствует, таким образом, случаю, при котором спектральный диапазон, в котором находится ошибка округления, отфильтровывается либо электронными средствами, либо самим органом слуха, чтобы исключить ошибку округления. Для кодирования/декодирования без потерь ошибка округления обязательно требуется в декодере, так как в противном случае применяемый в декодере алгоритм, являющийся инверсным алгоритму кодирования без потерь, приведет к искажениям.
Принцип спектрального формирования ошибки округления предпочтительным образом используется в приложениях, характеризуемых отсутствием потерь, с высокой частотой выборки, так как, в частности, в случаях, где спектры теоретически продолжаются до частот выше 40 кГц (ввиду применения сверхдискретизации), в высоком частотном диапазоне, в котором по существу нет энергии сигнала, то есть в котором может быть реализовано очень эффективное кодирование, реализуется та же ситуация, что и в случае нецелочисленного кодирования, при котором в высоком частотном диапазоне энергия сигнала также равна "нулю".
За счет того, что большое число нулей кодируется очень эффективным способом, и того, что ошибка округления, которую проблематично кодировать, смещается в диапазон, который в типовом случае может кодироваться очень точно, полная скорость передачи данных сигнала снижается, по сравнению со случаем, когда ошибка округления в виде белого шума распределяется по всему частотному диапазону. Кроме того, эффективность кодирования - и тем самым эффективность декодирования - повышается, так как для кодирования и декодирования более высокого частотного диапазона не должно затрачиваться время на вычисления. Таким образом, этот принцип приводит к тому, что может быть реализована более быстродействующая обработка на стороне кодера и, соответственно, на стороне декодера.
В одной форме выполнения принцип формирования или снижения ошибки аппроксимации применяется при инвертируемом целочисленном преобразовании, в частности при целочисленном МДКП. Здесь существуют две области использования, в частности, с одной стороны, многомерное поднятие, с помощью которого МДКП может быть в значительной степени упрощено, что касается требуемых этапов округления, а с другой стороны, операции округления, требуемые при целочисленном взвешивании функцией окна, в том виде как они проявляются при предварительной обработке перед собственно ДКП.
Для спектрального формирования ошибки округления используется принцип обратной связи по ошибке, при котором ошибка округления смещается в частотный диапазон, в котором сигнал, который обрабатывается в текущий момент, имеет наибольшую энергию сигнала. В случае аудиосигналов и, в частности, видеосигналов это будет низкий частотный диапазон, так что система обратной связи по ошибке будет иметь свойства низкочастотной фильтрации. Тем самым обеспечивается меньше ошибок округления в более высоком частотном диапазоне, в котором обычно имеется меньше сигнальных составляющих. В более высоком диапазоне преобладают ошибки округления согласно предшествующему уровню техники, которые затем должны кодироваться и, таким образом, повышают необходимое для кодирования количество битов. Предпочтительным образом эта ошибка округления снижается на высоких частотах, что непосредственно снижает число битов, требуемое для кодирования.
Предпочтительные примеры выполнения заявленного изобретения ниже пояснены более подробно со ссылками на чертежи, на которых представлено следующее:
Фиг.1 - блок-схема принципа обработки сигнала с последовательностью дискретных значений со спектральным формированием ошибки округления;
Фиг.2a - известный принцип спектрального формирования с высокочастотной фильтрацией ошибки квантования;
Фиг.2b - принцип формирования с низкочастотной фильтрацией ошибки округления;
Фиг.2с - блок-схема, согласно примеру выполнения, блока спектрального формирования/округления;
Фиг.3 - блок-схема предпочтительного варианта устройства обработки дискретных по времени значений выборок для получения целочисленных значений, из которых могут определяться целочисленные спектральные значения;
Фиг.4 - схематичное представление разложения МДКП и инверсного МДКП на Givens-вращения и две операции ДКП-IV;
Фиг.5 - представление для наглядной иллюстрации разложения МДКП с 50% перекрытием на вращения и операции ДКП-IV;
Фиг.6а - блок-схема известного кодера с МДКП и 50% перекрытием;
Фиг.6b - блок-схема известного декодера для декодирования значений, сформированных согласно фиг.10а;
Фиг.7 - представление поднятия при взвешивании функцией окна согласно фиг.3;
Фиг.8 - "несортированное" представление поднятия согласно фиг.7 для взвешивания функцией окна перед собственно преобразованием;
Фиг.9 - применение спектрального формирования для взвешивания функцией окна согласно фиг.3, 7 и 8;
Фиг.10а-с - блок-схема устройства для преобразования согласно предпочтительному варианту осуществления настоящего изобретения;
Фиг.11 - устройство инверсного преобразования согласно предпочтительному варианту осуществления настоящего изобретения;
Фиг.12 - представление преобразования двух следующих друг за другом блоков значений, как оно применяется для заявленного изобретения;
Фиг.13 - детальное представление многомерного шага поднятия с матрицей прямого преобразования;
Фиг.14 - детальное представление многомерного инверсного шага поднятия с матрицей обратного преобразования;
Фиг.15 - представление настоящего изобретения для разложения ДКП-IV длины N на два ДКП-IV длины N/2;
Фиг.16 - применение соответствующего изобретению принципа в рамках преобразования с многомерным поднятием по фиг.10;
Фиг.17 - представление двух следующих друг за другом этапов поднятия для уменьшения ошибок округления в соответствии с изобретением;
Фиг.18 - представление соответствующего изобретению принципа уменьшения ошибок округления для двух следующих друг за другом шагов поднятия; и
Фиг.19 - предпочтительная комбинация принципа по фиг.18 с принципом по фиг.16.
На фиг.1 представлено устройство для обработки сигнала с последовательностью дискретных значений, который вводится через сигнальный вход 200 в устройство 202 для обработки. Сигнал в типовом случае сформирован таким образом, чтобы иметь первый частотный диапазон, в котором сигнал имеет высокую энергию, и чтобы иметь второй частотный диапазон, в котором сигнал имеет сравнительно низкую энергию. Если первый сигнал является аудиосигналом, то он в первом частотном диапазоне, то есть в низкочастотном диапазоне, будет иметь высокую энергию, а в высокочастотном диапазоне - низкую энергию. Если же сигнал является видеосигналом, то он также в низкочастотном диапазоне будет иметь высокую энергию, а в высокочастотном диапазоне - низкую энергию. В противоположность аудиосигналу, частотный диапазон у видеосигнала является областью пространственных частот, пусть тогда будут рассматриваться последовательные видеокадры, для которых также существует временная частота, относящаяся, например, к выбранной области изображения в последовательных кадрах.
Устройство 202 для обработки, в принципе, выполнено таким образом, чтобы обрабатывать последовательность дискретных значений, чтобы получить последовательность обработанных значений, среди которых, по меньшей мере, одно обработанное значение не является целочисленным. Эта последовательность нецелочисленных дискретных значений вводится в устройство 204 для округления последовательности обработанных значений, чтобы получить последовательность округленных обработанных значений. Устройство 204 для округления выполнено так, что обеспечивает воздействие на спектральное формирование ошибки округления, обусловленной округлением, таким образом, чтобы спектрально сформированная ошибка округления в первом частотном диапазоне, то есть в частотном диапазоне, где первоначальный сигнал имеет высокую энергию, также имела высокую энергию и чтобы спектрально сформированная ошибка округления во втором частотном диапазоне, то есть в частотном диапазоне, где первоначальный сигнал имеет низкую энергию, также имела низкую энергию или вообще не имела энергии. В принципе, энергия спектрально сформированной ошибки округления в первом частотном диапазоне, таким образом, выше, чем энергия спектрально сформированной ошибки округления во втором частотном диапазоне. Спектральное формирование, однако, не вносит изменений в общую энергию ошибки округления.
Предпочтительным образом, устройство для формирования имеющей ошибки последовательности округленных обработанных значений связано непосредственно или через дополнительные комбинации обработки/округления с устройством 206 для преобразования в спектральное представление. Так, имеющая ошибки последовательность округленных обработанных значений может непосредственно вводиться в устройство 206 для преобразования в спектральное представление, чтобы получить непосредственный спектр имеющей ошибки последовательности округленных обработанных значений. В одном примере выполнения устройство для обработки реализует шаг поднятия или матрицу поднятия и устройство для округления, обеспечивающее округление нецелочисленных результатов шага поднятия. В этом случае за устройством 204 следует дополнительное устройство для обработки, которое выполняет второй шаг поднятия и за которым вновь следует устройство для округления, после которого вновь следует третье устройство для обработки, которое реализует третий шаг поднятия, причем затем вновь осуществляется обработка, так что завершаются все три шага поднятия. Таким образом, из первоначальной имеющей ошибки последовательности округленных обработанных значений на выходе устройства 204 вырабатывается выведенная имеющая ошибки последовательность округленных обработанных значений, которая затем, в итоге, предпочтительно также посредством целочисленного преобразования, преобразуется в спектральное представление, как представлено блоком 206. Выходной сигнал спектрального представления на выходе блока 206 имеет спектр, который, в противоположность уровню техники, больше не имеет распределенной ошибки округления, а имеет ошибку округления, которая является спектрально сформированной, а именно таким образом, что там, где собственно "полезный спектр" имеет высокую энергию сигнала, также имеет место высокая энергия округления, в то время как в частотных диапазонах, в которых отсутствует энергия сигнала, в лучшем случае также отсутствует и энергия ошибки округления.
Этот спектр затем подается в устройство 208 для энтропийного кодирования спектрального представления. Устройство для энтропийного кодирования может использовать некоторый метод кодирования, например кодирование Хафмана, арифметическое кодирование и т.д. В частности, для кодирования большого числа спектральных линий, которые равны "нулю" и которые примыкают друг к другу, подходит кодирование длин серий, которое, естественно, неприменимо в уровне техники, так как при этом в подобных частотных диапазонах должен кодироваться собственно детерминированный сигнал, который, однако, имеет белый спектр и поэтому полностью не пригоден для средств кодирования любого типа, так как отдельные спектральные значения полностью некоррелированы друг с другом.
Далее, со ссылками на фиг.2а, 2b, 2с, описан предпочтительный вариант осуществления устройства 204 для округления со спектральным формированием.
На фиг.2а представлена известная система с обратной связью по ошибке для спектрального формирования ошибки квантования, как она описана в книге "Digitale Audiosignalverarbeitung", U.Zoelzer, Teubner-Verlag, Stuttgart, 1997. Входное значение x(i) подается на входной сумматор 210. Выходной сигнал сумматора 210 подается на квантователь 212, который выдает квантованное выходное значение y(i) на выход устройства спектрального формирования. Во втором сумматоре 214 определяется разность между значением после квантователя 212 и значением перед квантователем 212, то есть ошибка округления e(i). Выходной сигнал второго сумматора 214 подается в устройство 216 задержки. Ошибка e(i), задержанная на единицу времени, вычитается из входного значения с помощью сумматора 210. Тем самым осуществляется оценка посредством высокочастотной фильтрации первоначального сигнала е(n) ошибки.
Если вместо устройства задержки z-1, обозначенного на фиг.2а ссылочной позицией 216, применяется z-1(-2 + z-1), то реализуется оценка посредством высокочастотной фильтрации второго порядка. Подобные спектральные формирования ошибки квантования в определенных примерах осуществления применяются для того, чтобы "вырезать" ошибку квантования из воспринимаемого диапазона, то есть, например, из диапазона низкочастотной фильтрации сигнала x(n), чтобы ошибка квантования не воспринималась.
Вместо этого, как показано на фиг.2b, проводится оценка посредством низкочастотной фильтрации, чтобы спектральное формирование ошибки реализовывать не вне воспринимаемого диапазона, а именно в воспринимаемом диапазоне. Для этого выходной сигнал сумматора 210, как представлено на фиг.2b, вводится в блок 218 округления, который реализует некоторую функцию округления, которая может представлять собой округление с избытком, округление с недостатком, округление усечением, округление с избытком/недостатком, относительно ближайшего целого числа, следующего ближайшего, следующего за следующим ближайшего целого числа и т.д. В цепи обратной связи по ошибке, таким образом, между сумматором 214 и сумматором 210 находится, дополнительно к звену задержки 216, еще один блок 220 обратной связи с импульсным откликом h(n) или с передаточной функцией H(z). Выходная последовательность, подвергнутая z-преобразованию, то есть Y(z), связана с входной последовательностью X(z) представленным на фиг.2b уравнением:

В представленном уравнении x(n) является входным сигналом сумматора 210, а y(n) - выходным сигналом блока 218 округления.
Кроме того, справедливо следующее уравнение:
y(n)=round (x'(n))
В приведенном уравнении "round" представляет функцию округления, которая реализуется блоком 218. Кроме того, справедливо следующее уравнение, в котором "*" обозначает операцию свертки:

В Z-области получается следующее:

После того как E(z) определено в качестве ошибки округления, она подвергается спектральной фильтрации с помощью фильтра (1 - z-1 H(z)). В соответствии с изобретением затем используется передаточная функция типа низкочастотного полосового фильтра.
Простейшая передаточная функция типа низкочастотного полосового фильтра может быть получена, если, например, установлено H(z)= -1. В этом простом примере ошибка округления из предыдущей операции округления просто суммируется со значением, подлежащим округлению, прежде чем будет применена следующая операция округления. Тем самым реализуется простая и очень эффективная и, следовательно, предпочтительная для заявленного изобретения низкочастотная фильтрация ошибки округления.
Реализация представлена на фиг.2с. В частности, представлено устройство 202 для манипулирования первоначальной последовательностью целочисленных дискретных значений, которое вырабатывает на выходе последовательность нецелочисленных дискретных значений y0, y1, y2, ..., yi. Затем, в противоположность предшествующему уровню техники, округляется не каждое значение, как это, например, представлено с помощью блоков 20, 24, 28 на фиг.3, или с помощью блоков 104, 110, 142 на фиг.10, или с помощью блоков 126, 132, 150 на фиг.11. Вместо этого нецелочисленные дискретные значения последовательности y0, y1, y2, y3, ..., фильтруются с помощью показанной на фиг.2с "схемы" независимо друг от друга с характеристикой низкочастотного полосового фильтра в цепи обратной связи, так что в результате реализуется описанное спектральное формирование. Элементы, идентичные элементам, показанным на фиг.2b, представлены с теми же самыми ссылочными позициями.
Кроме того, на фиг.2с представлена параллельная реализация, то есть реализация, в которой подлежащие округлению значения предоставляются параллельно. Разумеется, это представление является всего лишь схематичным. Значения y0, y1, y2, ..., могут представляться последовательно, чтобы затем получить последовательные выходные значения, причем в этом случае достаточно единственного выполнения структуры из элементов 210, 214, 216, 218, 220. Только из соображений наглядности, изображены повторяющиеся структуры элементов 214, 218, 210, 220.
Показанное на фиг.2с устройство 204 для округления действует, таким образом, для того, чтобы прежде всего вычислить округленное значение [y0]. Затем вычисляется ошибка i0 округления. Затем ошибка i0 округления взвешивается (фильтруется) посредством блока 220 с передаточной функцией H(z), которая, предпочтительно, равна -1, и суммируется в сумматоре 210. Эта отфильтрованная ошибка округления добавляется к следующему значению последовательности yi, после чего результат сумматора 210 округляется в блоке 218, чтобы получить округленное следующее значение [y1]. Затем с помощью сумматора 214 снова определяется ошибка округления, в частности, с применением округленного значения [y1] и первоначального значения y1, причем эта полученная ошибка округления значения i1 снова фильтруется в блоке 220, чтобы провести ту же самую процедуру для следующего значения y2 последовательности.
Здесь следует отметить, что направление является безразличным. Это означает, что можно также переходить от значений yi с большими индексами к значениям yi с меньшими индексами, то есть в противоположном направлении, как показано на фиг.2с стрелками, которые проходят от блока 220 к сумматору 210. Таким образом, порядок следования, то есть переход от низких к высоким индексам последовательности или от высоких к низким индексам последовательности, не играет никакой роли.
В частности, в случае применения целочисленного МДКП спектральное формирование ошибки округления предпочтительно выполняется особенно эффективно при следующих условиях:
- К нескольким соседним значениям независимо добавляется ошибка округления.
- В случае соседних значений речь идет (в широком смысле) о временных сигналах, которые затем посредством преобразования преобразуются в спектральное представление, то есть переводятся в частотную область.
Ниже более подробно поясняется, в каких частях целочисленного МДКП предпочтительно используется спектральное формирование ошибки округления.
Первый предпочтительный случай применения заключается во взвешивании функцией окна перед собственно преобразованием, то есть для округления, которое на фиг.3 определяется блоками 20, 24, 28. Операция поднятия, как она воспринимается каждым отдельным значением выборки x1, ..., xN и как она описывается с помощью фиг.3, может также быть наглядно представлена с помощью диаграммы, показанной на фиг.7. При этом представлены применения трех матриц поднятия, то есть соответствующее умножение на коэффициент для значения выборки, по каждому значению выборки, так что получается последовательность "сверху вниз", "снизу вверх" и "сверху вниз".
В случае обозначений на фиг.7 следует отметить, что когда стрелка появляется на горизонтальной линии, это означает, что осуществляется сложение. Такое сложение, например, обозначено на фиг.7 ссылочной позицией 27. Если сравнить фиг.4 с фиг.7, то единственная разница состоит в том, что х(0) на фиг.4 соответствует х1 на фиг.7. Также хN на фиг.7 соответствует x(N-1) на фиг.4. Кроме того, x(N/2-1) на фиг.4 соответствует хN/2 на фиг.7, а также x(N/2) на фиг.4 соответствует хN/2+1 на фиг.7, так что реализуются "бабочки", показанные на фиг.4, посредством которых соответствующее значение из первой четверти окна взвешивается значением из второй четверти окна согласно шагам поднятия, в то время как, аналогичным образом, значение из третьей четверти окна обрабатывается значением четвертой четверти окна по процедуре систематики "вниз-вверх-вниз", как представлено на фиг.7.
Соответственно осуществляется обработка для пары значений хN/2 и хN/2+1. Здесь снова применяется последовательность "вниз-вверх-вниз", причем за шагом "вниз" 29а следует шаг "вверх" 29b, за которым вновь следует шаг "вниз" 29с.
На фиг.7 показано, таким образом, целочисленное взвешивание функцией окна посредством поднятия. Это вычисление может без труда сортироваться в обратном направлении, без изменения результата, как представлено на фиг.8. Так могут, разумеется, сначала проводиться все шаги "вниз" (все шаги 29а). Затем могут проводиться все шаги "вверх" (29b) и, наконец, все шаги "вниз" (29с), так что получается блок "вниз" 31а, блок "вверх" 31b и снова блок "вниз" 31с. Следует отметить, что фиг.8 соответствует фиг.7, однако в другом представлении, которое в большей степени способствует пониманию настоящего изобретения.
Фиг.9 показывает принцип, при котором округление проводится со спектральным формированием. Принцип вычисления поднятия, иллюстрируемый на фиг.9, соответствует фиг.1 в том, что входные значения х1, xN/2 изображают исходную последовательность целочисленных дискретных значений на входе 200. Блоки оценки cs1, cs2, ..., csk в блоке "вниз" 31а образуют совместно устройство 202 для обработки. Блок, обозначенный [.]/Формирование Шума, представляет устройство 204 для округления, показанное на фиг.1. На выходе этого блока получается теперь имеющая ошибки последовательность округленных обработанных значений.
В примере выполнения, показанном на фиг.9, последовательность имеющих ошибки округленных обработанных значений суммируется с другой последовательностью от xN/2+1 до xN, чтобы получить новую последовательность целочисленных дискретных значений, которая вновь обрабатывается (посредством блоков s1, sk в блоке "вверх" 31b), чтобы затем снова реализовать округление в блоке "вверх" 31b посредством элемента 204b. Затем вновь, как в блоке "вниз" 31а, а также как в случае сумматора 205а, предусмотрен поэлементный сумматор 205b, чтобы получить новую последовательность, которая вновь вводится в блок 202с обработки, причем выходной сигнал блока 202с обработки является нецелочисленным и в последующем блоке 204с округления округляется, чтобы вновь суммироваться в последующем сумматоре 205с с последовательностью, вводимой в блок 202b обработки.
На выходе получается, в случае примера выполнения, представленного на фиг.9, блок значений выборок, взвешенный функцией окна, который, в соответствии с систематикой, изображенной на фиг.4, вводится в соответственно смещенные блоки ДКП-IV. Эти смещенные блоки ДКП обеспечивают преобразование, позволяющее преобразовать имеющую ошибки последовательность округленных обработанных значений в спектральное представление. Блоки ДКП-IV на фиг.4 представляют собой, таким образом, реализацию устройства 206, показанного на фиг.1. Аналогично этому, блоки для выполнения инверсного целочисленного ДКП-IV представляют аналогичные устройства для преобразования во временное представление.
Далее со ссылками на фиг.10-15 поясняется применение многомерного поднятия, чтобы представить целочисленную реализацию устройства для преобразования в спектральное представление 206 по фиг.10а и, соответственно, аналогичную целочисленную реализацию инверсного преобразования (для декодера). Принцип многомерного поднятия представлен в патентной заявке Германии, зарегистрированной под номером 103318038.
На фиг.10а показано устройство для преобразования дискретных значений в преобразованное представление с целочисленными значениями. Дискретные значения вводятся в устройство посредством первого входа 100а, а также второго входа 100b. Посредством первого входа 100а вводится первый блок дискретных значений, в то время как посредством второго входа 100b вводится второй блок дискретных значений. Дискретные значения представляют собой аудиоданные или данные изображений, соответственно видеоданные. Как изложено ниже, первый блок дискретных значений и второй блок дискретных значений могут действительно включать в себя два последовательных во времени блока значений аудиовыборок. Первый и второй блоки дискретных значений могут также включать в себя два представленные дискретными значениями изображения, или остаточные значения после прогнозирования, или разностные значения при дифференциальном кодировании и т.д. В качестве альтернативы, оба блока дискретных значений могут подвергаться предварительной обработке, как, например, при целочисленной реализации МДКП, где первый блок и второй блок дискретных значений выработаны посредством Givens-вращений из значений выборок, действительно подвергнутых взвешиванию функцией окна. Первый и второй блоки дискретных значений могут быть, таким образом, получены из исходных аудиоданных или данных изображения посредством некоторой предварительной обработки, например вращениями, перестановками, плюс/минус-поворотами ("бабочками"), масштабированиями. Несмотря на это, первый и второй блоки дискретных значений, хотя они не являются непосредственно значениями аудиовыборок или дискретизированными значениями изображения, однако, содержат аудиоинформацию и, соответственно, информацию изображения.
Первый блок дискретных значений вводится через вход 100а в устройство 102 для обработки первого блока дискретных значений с применением первого правила преобразования, чтобы на выходе устройства 102 получить первый блок преобразованных значений, как показано на фиг.10а. Этот первый блок преобразованных значений в типовом случае будет не целочисленным, а будет включать в себя значения с плавающей запятой, как это имеет место в типовом случае в результате некоторого правила преобразования, например преобразования Фурье, преобразования Лапласа, БПФ, ДКТ, ДСТ, МДКП, МДСП или некоторого другого преобразования, как, например, преобразование элементарных волн с любой базовой функцией. Первый блок преобразованных значений вводится в устройство 104 для округления первого блока преобразованных значений, чтобы на выходе получить первый блок округленных преобразованных значений. Устройство 104 предназначено для округления с использованием некоторой функции округления, например округления с усечением или округления с избытком или недостатком, осуществляемого в зависимости от значения с плавающей запятой.
Правило округления, которое реализуется устройством 104, обеспечивает то, что первый блок округленных преобразованных значений снова содержит только целочисленные значения, точность которых определяется применяемым в устройстве 104 правилом округления. Первый блок округленных преобразованных значений, так же как второй блок дискретных значений, который подается на второй вход 100b, поступает на устройство 106 для суммирования, чтобы получить второй блок суммарных значений. Если рассматривается пример аудиосигнала, то можно видеть, что посредством устройства 106 спектральные значения из первого блока округленных преобразованных значений суммируются с временными значениями из второго блока дискретных значений. Если дискретные значения второго блока представлены, например, как значения напряжения, то рекомендуется, чтобы первый блок округленных преобразованных значений также был представлен как амплитуды напряжений, то есть как значения с размерностью В. В этом случае нет никаких проблем с размерностями при суммировании. Для специалистов, однако, понятно, что с первым блоком округленных преобразованных значений или, соответственно, со вторым блоком дискретных значений могут осуществляться любые операции нормирования размерностей в такой степени, чтобы как первый блок округленных преобразованных значений, так и второй блок дискретных значений были, например, безразмерными.
Второй блок суммарных значений подается на устройство 108 для обработки второго блока суммарных значений с применением второго правила преобразования, чтобы получить второй блок округленных преобразованных значений. Если правило преобразования, которое применяется в устройстве 102, представляет собой, например, преобразование из временной области в частотную область, то второе правило преобразования, которое применяется в блоке 108, является, например, правилом преобразования из частотной области во временную область. Это соотношение может, однако, быть обратным, так что первый и второй блоки дискретных значений являются, например, спектральными значениями, и с помощью устройства 102 обработки с применением правила обработки формируются временные значения, в то время как с помощью устройства обработки с применением инверсного правила обработки, то есть устройства 108, вновь получаются спектральные значения. Первое и второе правила обработки могут, таким образом, представлять собой правила прямого и обратного преобразования, причем инверсное правило преобразования является правилом обратного преобразования или правилом прямого преобразования.
Второй блок преобразованных значений, как показано на фиг.10а, вводится в устройство 110 для округления, чтобы получить второй блок округленных преобразованных значений, который в итоге вводится в устройство 112 для вычитания, чтобы вычесть второй блок округленных преобразованных значений из первого блока дискретных значений, который вводится через первый вход 108а, для получения блока целочисленных выходных значений преобразованного представления, который выдается на выход 114. Посредством обработки блока целочисленных выходных значений преобразованного представления с применением любого третьего правила преобразования, которое также применяется в устройстве 102 или отличается от него, и последующего округления блока преобразованных выходных значений для получения блока округленных преобразованных выходных значений, и посредством последующего суммирования блока округленных преобразованных выходных значений и второго блока суммарных значений можно получить другой блок целочисленных выходных значений преобразованного представления, который с полученным на выходе 114 блоком целочисленных выходных значений обеспечивает полное преобразованное представление первого и второго блоков дискретных значений.
Однако и без последних трех этапов обработки, округления и суммирования, в которых используется блок целочисленных выходных значений преобразованного представления на выходе 114, уже можно получить часть общего преобразованного представления, а именно, например, первую половину, которая, будучи подвергнутой инверсной обработке, обеспечивает возможность обратного вычисления первого и второго блоков дискретных значений.
Здесь следует отметить, что, в зависимости от правила преобразования, первое, второе и, при необходимости, третье правило преобразования могут быть идентичными. Это имеет место, например, в случае ДКП-IV. Если бы в качестве первого правила преобразования использовалось быстрое преобразование Фурье (БПФ), то в качестве второго (инверсного) правила преобразования могло бы применяться обратное быстрое преобразование Фурье (ОБПФ), которое не идентично БПФ.
Из вычислительных соображений предпочтительным является обеспечение правил преобразования в форме матрицы, которая в случае, если число дискретных значений первого блока равно числу дискретных значений второго блока, становится квадратной матрицей размера N x N, если число дискретных значений первого блока и число дискретных значений второго блока, соответственно, равно N.
Устройства 104 и 110 для округления в одном примере выполнения выполнены таким образом, чтобы осуществлять округление согласно функции округления, которая выдает округленные результаты, точность которых ниже, чем вычислительная точность у вычислителя, который выполняет функции, показанные на фиг.10а. Относительно функции округления следует указать на то, что она только в предпочтительном варианте осуществления отображает нецелочисленное число на ближайшее большее или меньшее целое число. Функция округления может также осуществлять отображение на другие целые числа, как, например, число 17,7 на число 10 или на число 20, если функция округления обуславливает снижение точности округляемого числа. В приведенном выше примере неокругленное число является числом с одним разрядом после запятой, в то время как округленное число является числом, которое больше не содержит разряда после запятой.
Хотя на фиг.10а показано устройство 102 для обработки с применением первого правила преобразования и устройство 108 для обработки с применением второго правила преобразования в виде отдельных устройств, следует отметить, что в конкретной реализации может иметься только один функциональный блок преобразования, который под управлением со стороны специального средства управления процессом обработки сначала преобразует первый блок дискретных значений, а затем, в соответствующий момент времени алгоритма, второй блок суммарных значений подвергает инверсному преобразованию. Тогда первое и второе правила преобразования были бы идентичными. То же самое справедливо для обоих устройств 104, 110 для округления. Также и они не обязательно должны быть предусмотрены как отдельные устройства, а могут быть реализованы одним функциональным блоком округления, который, вновь под управлением средства управления процессом, согласно требованию алгоритма, сначала округляет первый блок преобразованных значений, а затем округляет второй блок преобразованных значений.
В первом примере выполнения первый блок преобразованных значений и второй блок преобразованных значений представляют собой целочисленные значения выборок, взвешенные функцией окна, как они получены на выходе блока 28 на фиг.3. Целочисленное ДКП в блоке 14 на фиг.3 затем реализуется посредством показанного на фиг.1 целочисленного алгоритма таким образом, что преобразованное представление в примере с аудиосигналом, к которому относится фиг.3, изображает целочисленные спектральные значения на выходе 30 показанного на фиг.3 устройства.
Ниже с помощью фиг.10b представлено устройство для инверсного преобразования, соответствующее фиг.10а, в котором, наряду с блоком целочисленных выходных значений на выходе блока 112 на фиг.10а, также применяется второй блок суммарных значений на выходе устройства 106, показанного на фиг.10а. С учетом описанного ниже более подробно со ссылкой на фиг.11, это соответствует случаю, когда имеются только блоки 150 и 130, но не блок 124 преобразования.
На фиг.10b показано устройство для инверсного преобразования блока целочисленных выходных значений преобразованного представления, как оно получается на выходе 114 на фиг.10а, и второго блока суммарных значений. Второй блок суммарных значений вводится на вход 120 показанного на фиг.10b устройства для инверсного преобразования. Блок выходных значений преобразованного представления вводится на другой вход 122 устройства для инверсного преобразования.
Второй блок суммарных значений вводится в устройство 130 для обработки этого блока с применением второго правила преобразования, если последнее примененное правило преобразования при кодировании было вторым правилом преобразования. Устройство 130 выдает на выходе первый блок преобразованных значений, который подается в устройство 132 для округления, которое на выходе вновь вырабатывает первый блок округленных преобразованных значений. Первый блок округленных преобразованных значений затем посредством устройства 134 вычитается из блока выходных значений преобразованного представления, чтобы получить первый блок дискретных значений на первом выходе 149 устройства по фиг.10b.
Этот первый блок дискретных значений подается на устройство 150 для обработки этого блока с применением первого правила преобразования, чтобы получить второй блок преобразованных значений на выходе устройства 150. Этот второй блок преобразованных значений вновь округляется в устройстве 152, чтобы получить второй блок округленных преобразованных значений. Этот второй блок округленных преобразованных значений вычитается из введенного на входной стороне второго блока суммарных значений, который введен через вход 120, чтобы на выходе 136 получить второй блок дискретных значений.
Что касается соотношений между первым, вторым и третьим правилами преобразования, а также конкретной реализации отдельных функциональных блоков на фиг.10b посредством общих функциональных блоков и соответствующих средств управления процессом и промежуточного хранения, дается ссылка на примеры выполнения, приведенные на фиг.10а.
Ниже, со ссылкой на фиг.10с, представлен предпочтительный пример выполнения показанного на фиг.10а в обобщенном виде устройства для преобразования преобразованного представления. Пример выполнения по фиг.10с включает в себя дополнительное преобразование/округление, по сравнению с фиг.10а, чтобы из второго блока суммарных значений сформировать другой блок целочисленных выходных значений.
Первый вход 100а включает в себя N входных линий х0,..., хN-1, предназначенных для ввода N значений первого блока дискретных значений. Второй вход 100b также включает в себя N входных линий, предназначенных для ввода N значений хN, ..., х2N-1 второго блока дискретных значений. Устройство 102 по фиг.10а показано на фиг.10с как преобразователь ДКП-IV. Преобразователь ДКП 102 предназначен для того, чтобы из N входных значений сформировать N выходных значений, каждое из которых округляется, как показано устройством 104 на фиг.10с, с помощью правила округления, которое обозначено как "[.]". Устройство 106 суммирования выполнено таким образом, что обеспечивается суммирование по каждому значению. Это означает, что выходное значение устройства с индексом 0 суммируется с первым значением второго блока дискретных значений, имеющим индекс N. В общем случае, значение первого блока округленных преобразованных значений на выходе устройства 104 округления с i-ым порядковым номером суммируется по отдельности с дискретным значением второго блока выходных значений с (N+i)-ым порядковым номером, причем i является переменным индексом, который изменяется в пределах от 0 до N-1.
Устройство 108 обработки с применением второго правила преобразования также обозначается как преобразователь ДКП-IV. Устройство 112 для вычитания также выполнено, в случае показанного на фиг.10с предпочтительного варианта осуществления, для поэлементного вычитания, а именно таким образом, что значения второго блока округленных преобразованных значений по отдельности вычитаются из первого блока дискретных значений. В случае показанного на фиг.10с варианта осуществления предпочтительным является, когда значение второго блока с (N+i)-ым порядковым номером вычитается из значения первого блока с i-ым порядковым номером, причем i изменяется в пределах от 0 до N-1. В качестве альтернативы, могут проводиться и другие суммирования/вычитания, например таким образом, что значение блока с (N-1)-ым порядковым номером вычитается из значения другого блока с N-ым порядковым номером, если это соответственно учитывается при инверсном преобразовании.
Устройство 112 вычитания выдает на выходе блок целочисленных выходных значений преобразованного представления, таким образом, целочисленные выходные значения от у0 до уN-1 преобразованного представления. Для того чтобы, если желательно, получить и остальные целочисленные выходные значения преобразованного представления, то есть другой блок от уN до у2N-1, блок целочисленных выходных значений преобразованного представления, которое подается на выход 114, подвергается преобразованию с применением третьего правила преобразования посредством блока 140 прямого преобразования, причем его выходные значения вновь округляются, как представлено посредством устройства 142 округления, чтобы теперь провести суммирование этих значений со вторым блоком суммарных значений на выходе сумматора 106, как это представлено ссылочной позицией 144 на фиг.10с. Выходные значения сумматора 144 представляют тогда другой блок 146 целочисленных выходных значений преобразованного представления, которые обозначены символами от уN до у2N-1.
Ниже со ссылками на фиг.11 представлено устройство для инверсного преобразования преобразованного представления в соответствии с примером выполнения. При этом следует отметить, что посредством устройства, показанного на фиг.11, без потерь в обратном направлении выполняются операции, выполняемые устройством, представленным на фиг.10с. Фиг.11 соответствует фиг.10b с точностью до дополнительного каскада преобразования/округления, чтобы из второго блока преобразованных выходных значений сформировать второй блок суммарных значений, который в примере выполнения, показанном на фиг.10b, вводится на вход 120. Следует отметить, что функция сумматора реализуется обращенным образом функцией вычитателя. Кроме того, следует отметить, что пара сумматор/вычитатель (144 на фиг.10с и 128 на фиг.11) может нагружаться входными величинами, инвертированными по знаку, так что сумматор 144 в случае, если подается группа входных величин, по сравнению с показанным случаем, с отрицательным знаком, выполняет собственно операцию вычитания, если это учитывается в противоположном ему компоненте (128 на фиг.11), который тогда должен был бы выполнять операцию сложения.
Показанные на фиг.11 вычитатель 128, сумматор 134, а также другой вычитатель 154 вновь выполнены таким образом, чтобы выполнять поэлементное сложение/вычитание, причем вновь применяется та же обработка согласно порядковым номерам, как изложено выше для фиг.10с. Если бы на фиг.10с использовалось другое применение порядковых номеров, чем показано на чертеже, то это должно быть принято во внимание для фиг.11.
На выходе вычитателя 134 имеется уже первый блок дискретных значений, которые обозначены значениями от х0 до хN-1. Чтобы получить и остальную часть обратно преобразованного представления, первый блок дискретных значений подается на преобразователь 150, который работает в соответствии с первым правилом преобразования, выходные значения которого округляются с помощью блока 152 округления и вычитаются из второго блока разностных значений на выходе вычитателя 128, чтобы получить также второй блок дискретных значений 156, которые обозначены символами от хN до х2N-1.
Ниже со ссылками на фиг.12-15 дается математическое обоснование устройств, которые представлены на фиг.10а, 10b, 10с и 11. Посредством представленного устройства для преобразования или инверсного преобразования создаются способы преобразования для аудиокодирования без потерь, при которых ошибка аппроксимации снижается. Кроме того, затраты на вычисления учитываются в значительной степени тем, что вычисления больше не основываются на известных решениях, состоящих в применении схемы поднятия на каждое Givens-вращение, причем здесь постоянно применяются тривиальные суммарно-разностные "бабочки". Именно они повышают существенным образом вычислительные затраты по сравнению с первоначальной нецелочисленной версией преобразования, подлежащей последующему отображению.
Обычно схема поднятия применяется, чтобы получить инвертируемую целочисленную аппроксимацию Givens-вращения.

Эта целочисленная аппроксимация реализуется тем, что функция округления применяется после каждого суммирования, то есть каждого этапа поднятия.
Схема поднятия может также использоваться для инвертируемой целочисленной аппроксимации определенных операций масштабирования. В публикации R.Geiger, G.Schuller, "Integer low delay and MDCT filter banks", Proc. of the Asilomar Conf. on Signals, Systems and Computers, 2002, представлено и описано следующее разложение поднятия матрицы масштабирования размером 2 х 2 с детерминантом, равным 1:
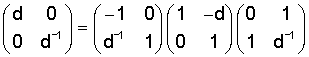
Это разложение поднятия, которое является одномерным, то есть относится только к матрице масштабирования размером 2 х 2, расширено на многомерный случай. По отдельности все значения из вышеописанного уравнения заменены на матрицы размером n x n, причем n, то есть число дискретных значений блока, больше или равно 2. Тем самым получается, что для каждой любой n x n-матрицы Т, которая предпочтительно должна быть инвертируемой, возможно следующее разложение на блочные матрицы размером 2n x 2n, причем En описывает единичную матрицу n x n:
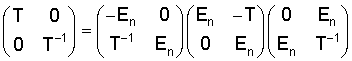
Наряду с простыми операциями, как перестановки или умножения на -1, все три блока этого разложения имеют следующую общую структуру:
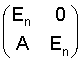
Для этой блочной матрицы размером 2n x 2n может применяться обобщенная схема поднятия, которая ниже обозначается как многомерное поднятие.
Для вектора значений x = (x0, ..., x2n-1) применение этой блочной матрицы дает следующее  уравнение:
уравнение:

Следует отметить, что в правой части этого уравнения имеется вектор, размерность которого, то есть число строк, равна 2n. Первые n компонентов, то есть компоненты от 0 до n-1, соответствуют значениям от x0 до xn-1. Вторые n компонентов, то есть вторая половина вектора, который получается в правой части приведенного выше уравнения, равны сумме второго блока дискретных значений, то есть значениям от хn до х2n-1, однако теперь просуммированным с произведением матрицы А, которая соответствует матрице преобразования по фиг.10а, 10b, 10с и 11, и первого блока дискретных значений x0, ..., xn-1. Матрица преобразования представляет первое, второе и третье правило преобразования.
Подобно обычной схеме поднятия с матрицами размера 2 х 2 формы
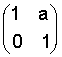
эти матрицы размера 2n x 2n могут применяться для инвертируемой целочисленной аппроксимации преобразования Т следующим образом. Для целочисленных входных значений (x0, ..., x2n-1) округляются значения с плавающей запятой (у0, ..., уn-1) = А·(x0, ..., xn-1), а именно до целочисленных значений, прежде чем они будут суммироваться с целочисленными значениями (xn, ..., x2n-1). Инверсное представление блочной матрицы получается в следующем виде:
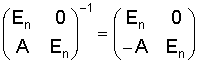
Таким образом, этот процесс может быть инвертирован без ошибок за счет того, что просто применяются та же самая матрица А и та же самая функция округления, и за счет того, что результирующие значения вместо суммирования при прямой обработке теперь вычитаются. Прямая обработка представлена на фиг.13, в то время как обратная обработка представлена на фиг.14. Следует отметить, что матрица преобразования на фиг.13 идентична матрице преобразования на фиг.14, что является предпочтительным ввиду простоты реализации.
После того как значения (x0, ..., xn-1) на этапе прямой обработки, которая показана на фиг.13, не модифицируются, они все еще доступны для использования на инверсном этапе, то есть на этапе обратной обработки по фиг.14. Следует отметить, что отсутствуют какие-либо специальные ограничения для матрицы А. Поэтому она не обязательно должна быть инвертируемой.
Для того чтобы получить инвертируемую целочисленную аппроксимацию известного МДКП, МДКП на первом этапе разлагается на Givens-вращения, причем этот этап представляет собой этап взвешивания функцией окна, и на последующий этап ДКП-IV. Это разложение обсуждено ниже со ссылкой на фиг.3 и детально описано в DE 10129240 А1.
В противоположность уровню техники, согласно которому преобразование ДКП-IV разлагается на несколько ступеней Givens-вращения, преобразование остается, как оно есть, и затем округляется.
Известным образом, тем самым, проводится целочисленная аппроксимация преобразования ДКП-IV посредством нескольких ступеней, основанных на поднятии Givens-вращений. Число Givens-вращений определяется лежащим в основе обработки применяемым быстродействующим алгоритмом. Так, число Givens-вращений задается равным 0 (N log N) для преобразований длины N. Этап взвешивания функцией окна каждого разложения МДКП состоит только из N/2 Givens-вращений или из 3N/2 шагов округления. Так, в особенности в случае преобразований большой длины, как это применяется в приложениях аудиокодирования (например, 1024), целочисленное преобразование ДКП-IV вносит основной вклад в ошибку аппроксимации.
Рассматриваемое решение применяет описанную многомерную схему поднятия. Тем самым число шагов округления в ДКП-IV сокращается до 3N/2, то есть равно числу шагов округления на этапе взвешивания функцией окна, а именно по сравнению с примерно числом 2N log2 N шагов округления при традиционном решении на основе поднятий.
Преобразование ДКП-IV одновременно применяется на двух блоках сигналов. Возможный вариант этого приведен на фиг.12, где, например, два последовательных по времени блока значений выборок подвергаются преобразованию ДКП-IV. Оба блока, которые подвергаются обоим преобразованиям, также могут представлять собой значения выборок из двух каналов многоканального сигнала.
Разложение из вышеописанного многомерного уравнения поднятия применяется к правилу преобразования, которое также может рассматриваться как матрица размера N x N. Так как инверсия, в частности, при ДКП-IV вновь представляет собой ДКП-IV, получается следующее разложение для показанного на фиг.12 принципа:

Перестановки умножений на -1 могут быть выделены в собственную блочную матрицу, так что получается следующее соотношение:
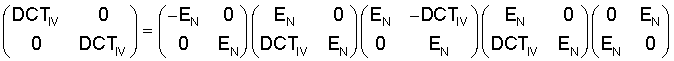
Тем самым может быть получено применение одного преобразования к двум блокам сигналов, то есть к двум блокам дискретных значений, предпочтительно с тремя многомерными шагами поднятия:

Приведенное выше уравнение графически представлено на фиг.10с на примере выполнения. Инверсное преобразование, в том виде, как оно выполнено, соответственно проиллюстрировано на фиг.11.
С помощью этого решения два преобразования ДКП-IV длины N могут быть реализованы инвертируемым способом, причем необходимы только 3N шага округления, то есть 3N/2 шага округления на преобразование.
Преобразование ДКП-IV в трех многомерных шагах поднятия может иметь различные реализации, например в виде реализации с плавающей запятой или с фиксированной запятой. Оно должно быть неоднократно инвертируемым. Оно должно лишь точно одинаковым образом выполняться в прямом и обратном процессе обработки. Это приводит к тому, что данный принцип становится пригодным для преобразований большой длины, например, 1024, как оно применяется в современных приложениях аудиокодирования.
Полная сложность вычислений равна 1,5-кратной сложности вычислений нецелочисленной реализации обоих преобразований ДКП-IV. Эта сложность вычислений все равно заметно ниже, чем для обычных, основанных на поднятии целочисленных реализаций, которые примерно вдвое более сложны, чем обычное преобразование ДКП-IV, так как эти реализации должны применять тривиальные процедуры вида плюс-минус-"бабочки" на применяемой схеме поднятия, чтобы реализовать получение энергии, как описано в работе R.Geiger, T.Sporer, J.Koller, K.Brandenburg, "Audio Coding based on Integer Transforms", 111th AES Convention, New York, 2001.
Представленное решение вычисляет, по меньшей мере, два преобразования ДКП-IV в известной мере одновременно, то есть в рамках одного преобразования. Это может быть реализовано, например, тем, что вычисляется преобразование ДКП-IV для двух последовательных блоков аудиосигнала или двух последовательных блоков сигнала изображения. В случае двухканального стереосигнала это тоже может быть реализовано таким образом, что преобразование ДКП-IV левого и правого каналов вычисляется в одной операции преобразования или инверсного преобразования. Первая версия приводит к дополнительной задержке на один блок в системе. Вторая версия возможна в применении к стереоканалам или, вообще говоря, для многоканальных сигналов.
В качестве альтернативы, если обе опции нежелательны, если, однако, должны сохраняться нормальные длины обработки блоков из N значений, то преобразования ДКП-IV длины N могут разлагаться на два преобразования ДКП-IV длины N/2. В этой связи следует сослаться на работу Y.Zeng, G.Bi, Z.Lin, "Integer sinusoidal transforms based in lifting factorization", Proc. ICASSP'01, May 2001, pp.1.181-1.184, где выполняется такое разложение. Дополнительно к обоим преобразованиям ДКП-IV длины N/2 требуются еще некоторые дополнительные шаги Givens-вращений. В этом алгоритме, кроме того, применяются блочная матрица

то есть N/2-плюс-минус-"бабочка", блочная диагональная матрица с N/2 Givens-вращениями и, кроме того, некоторые матрицы перестановок. При применении этих дополнительных шагов N/2 Givens-вращений многомерный подход с использованием поднятий может также применяться для вычисления только одного преобразования ДКП-IV длины N. Основная структура этого алгоритма показана на фиг.15, где, наряду с собственно шагом преобразования, на котором применяются два преобразования ДКП-IV длины N/2, сначала имеется шаг "бабочки", чтобы вычислить первый и второй блоки дискретных значений, которые теперь имеют всего лишь длину N/2. На выходе, кроме того, предусмотрена ступень вращения, чтобы из блока выходных значений преобразованного представления и дополнительного блока выходных значений преобразованного представления, которые, однако, теперь имеют всего лишь N/2 значения каждый, получить выходные значения y0,...,yN-1, которые равны выходным значениям операции ДКП-IV по фиг.12, как это очевидно из сравнения индексов на входе и на выходе на фиг.15 и фиг.12.
До сих пор представлялось только применение многомерного поднятия на блочных матрицах следующей формы:
T 0
0 T-1
Однако также возможно другие блочные матрицы разложить на многомерные шаги поднятия. Например, может применяться следующее разложение, чтобы реализовать комбинацию из каскада с нормированными плюс-минус-"бабочками" и двух блоков преобразования ДКП-IV посредством трех шагов многомерных поднятий:
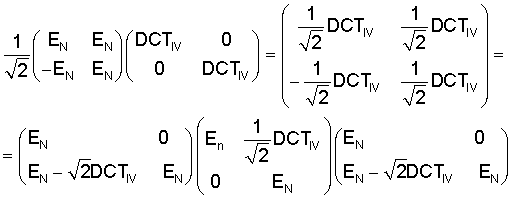
Из приведенного выше уравнения видно, что первое правило преобразования, которое применяется в левой скобке уравнения, и второе правило преобразования, которое применяется в средней скобке уравнения, а также третье правило преобразования, которое применяется в последней скобке уравнения, не должны быть идентичными. Кроме того, из приведенного выше уравнения видно, что могут разлагаться не только блочные матрицы, в которых заполнены только главные диагонали, но также могут обрабатываться полностью заполненные матрицы. Кроме того, следует отметить, что отсутствует ограничение, заключающееся в том, что правила преобразования, которые применяются при преобразовании в преобразованное представление, должны быть идентичными или даже должны иметь некоторое соотношение друг с другом таким образом, что, например, второе правило преобразования является правилом обратного преобразования относительно первого правила преобразования. В принципе, могли бы также применяться три отличающихся друг от друга правила преобразования, если это учитывается при инверсном представлении.
В этой связи следует еще раз сослаться на фиг.10с и фиг.11. При преобразовании дискретных значений в преобразованное представление устройство 102 должно быть выполнено таким образом, чтобы реализовывать некоторое правило 1 преобразования. Кроме того, устройство 108 может также быть выполнено таким образом, чтобы применять некоторое иное или то же самое правило преобразования, которое обозначено как правило 2 преобразования. Кроме того, устройство 140 может быть выполнено таким образом, чтобы в общем случае применять некоторое правило 3 преобразования, которое не обязательно должно быть одинаковым с первым или вторым правилом преобразования.
При инверсном преобразовании преобразованного представления должно быть, однако, найдено соответствие с представленными на фиг.10с правилами 1-3 преобразования, чтобы первое устройство 124 для преобразования выполняло не любое правило преобразования, а правило 3 преобразования, которое выполняется в блоке 140 на фиг.10с. Соответственно, устройство 130 на фиг.11 должно выполнять правило 2 преобразования, которое также выполняется блоком 108 на фиг.10с. Наконец, устройство 150 на фиг.11 должно выполнять правило 1 преобразования, которое также выполняется устройством 102 на фиг.10с, чтобы получить инверсное преобразование без потерь.
На фиг.16 показана модификация принципа, описанного на фиг.10с. В частности, округления в элементах 104, 110, 142 для прямого преобразования или в элементах 126, 132, 152 при обратном преобразовании больше не выполняются поэлементным способом, а вместо этого осуществляется спектральное формирование ошибки округления.
Из сравнения фиг.10с с фиг.16 можно видеть, что предпочтительным является заменить блок 104 блоком 204а, а блок 204b применить вместо блока 110 округления. Это используется потому, что данный принцип имеет преимущество особенно в том случае, когда последующее преобразование производится в частотной области, где белые шумы ошибки округления, если не производится спектральное формирование, вызывают проблемы. Если бы после округления в блоке 142 не производилось больше никакого частотного преобразования, то спектральное формирование в блоке 142 не обеспечивало бы никакого преимущества. Однако это имеет место для блока 204а, так как за счет преобразования в блоке 108 вновь осуществляется частотное преобразование. Спектральное формирование в блоке 204b также имеет преимущество, состоящее в том, что посредством последнего блока 140 вновь осуществляется преобразование. Однако, как видно из фиг.16, образованная шумом ошибка округления входит уже в выходной блок 114, так что уже в блоке 204b вместо спектрального формирования ошибки округления может выполняться обычное округление, как это показано на фиг.10с, блоками 110.
Производится ли в конце второго преобразования, то есть преобразования 108, округление согласно спектральному формированию или обычным образом, то есть с ошибкой округления, имеющей белое спектральное распределение, зависит от конкретного случая применения.
Таким образом, независимое округление определенного количества, например, k значений заменяется округлением со спектральным формированием, которое также обозначается как "зависимое округление".
Из вышеприведенного обсуждения со ссылкой на фиг.16 следует, что спектральное формирование ошибки округления также можно использовать и при целочисленном ДКП, требующемся для целочисленного МДКП. Однако при этом, как отмечено, следует учитывать, что спектральное формирование путем обратной связи по ошибке только тогда имеет преимущество, когда в случае округляемых значений речь идет о временных значениях, которые посредством последующего шага преобразования переводятся в частотную область. Поэтому, как представлено с помощью многомерного поднятия на фиг.16, на первых обоих шагах спектральное формирование имеет преимущество, а на третьем шаге оно не обязательно будет иметь преимущество.
Следует отметить, что фиг.16 показывает соответствующий фиг.10с случай в кодере. Соответствующий фиг.16 случай в декодере получается непосредственно из сравнения фиг.16 и фиг.11. Непосредственно соответствующий фиг.16 декодер получается из фиг.11 за счет того, что все блоки работают идентично, кроме обоих блоков 132, 152 округления. Эти оба блока округления работают, согласно фиг.11, как независимые блоки округления и в декодере были бы заменены блоками 204а, 204b зависимого округления, которые, например, имеют структуру, показанную на фиг.2с. В частности, следует отметить то, что в декодере может применяться точно тот же алгоритм округления спектральным формированием, что и в кодере.
Принцип, иллюстрируемый на фиг.2b и 2с, в частности, для H(z)="-1", подходит также, в частности, для того, чтобы реализовать соответствующее изобретению снижение ошибки округления при целочисленных преобразованиях.
Согласно изобретению, такое снижение ошибки округления возможно только в том случае, если два значения с плавающей запятой округляются и суммируются с одним и тем же значением, а не с разными значениями. Подобная ситуация показана на фиг.17. Здесь имеется, прежде всего, первый шаг поднятия с последовательностью "вниз-вверх-вниз" между членами поднятия x1 и x3. Кроме того, существует еще вторая последовательность поднятия с известной последовательностью "вниз-вверх-вниз", но между членами поднятия x2 и x3. В частности, полученное в первой операции поднятия значение x3 применяется для того, чтобы использоваться в качестве слагаемого во втором шаге поднятия, как это можно видеть на фиг.17. Вновь следует отметить, что если стрелка имеется на горизонтальной линии, то это представляет суммирование. Иными словами, значение, которое как раз округляется, добавляется к значению, соответствующему горизонтальной линии.
Более конкретно, в примере, показанном на фиг.17, значение x1 сначала взвешивается (блок 250), а затем индивидуально округляется (блок 252). Выходной сигнал блока 252 добавляется к значению x3 (блок 254). Затем результат суммирования 254 вновь взвешивается (блок 256) и вновь округляется (блок 258). Результат этого округления 258 затем добавляется к x1 (260). Результат суммирования 260 вновь взвешивается (блок 262) и округляется (блок 264), чтобы суммироваться с текущим значением x3 (блок 266). Соответственно, значение x2 сначала взвешивается (блок 270), а затем округляется блоком 272. Результат блока 272 добавляется к текущему значению x3 (блок 274). Затем результат вновь взвешивается (блок 276) и округляется (блок 278), чтобы результат блока 278 добавить к текущему значению x2 (280). Результат этого суммирования 280 вновь взвешивается (блок 282), и взвешенный результат округляется (блок 284), чтобы результат блока 284 округления просуммировать с текущим значением x3 (блок 286), чтобы получить результирующее значение для x3. Из фиг.17 можно видеть, что сначала первое значение, а именно результат блока 262, округляется и затем суммируется с x3. Кроме того, второе значение, а именно результат блока 270, также округляется (блок 272) и затем суммируется с значением x3 (сумматор 274). Таким образом, имеет место ситуация, когда друг за другом два значения с плавающей запятой округляются и суммируются с одним и тем же значением, а не с разными значениями. В примере по фиг.17 результат третьего и четвертого шагов поднятия суммируется с одним и тем же значением, а именно с x3, то есть суммирование производится с функцией округления [.]:
[x1·cs1] + [x2·cs2].
Если ошибка третьего шага поднятия при округлении вводится в четвертый шаг поднятия, то в этом случае можно применить ошибку третьего шага, и возникает только одна ошибка округления, вместо двух ошибок округления. В вычислительных операциях это получается из следующего соотношения:

В вычислительном смысле введение ошибки округления в следующий этап округления в этом случае идентично суммированию значений с последующим округлением. Эта ситуация изображена на фиг.18, причем фиг.18 соответствует фиг.17, однако оба отдельных блока округления 264, 272 и оба отдельных сумматора 266, 274 заменены на один блок 268, который выполнен таким образом, чтобы обеспечить реализацию приведенного выше уравнения. Поэтому результаты обоих блоков 262 и 270 сначала в неокругленной форме суммируются, а затем округляются. Тем самым ошибка округления в наилучшем случае сокращается наполовину. На выходе блока 268 получается теперь только единственное значение, которое суммируется с помощью сумматора 269 с значением x3.
Комбинация снижения и формирования ошибки округления может также иметь место в том случае, когда, например, набор Givens-вращений и многомерный шаг поднятия следуют друг за другом, как показано на фиг.19. Для этого, например, для значений от х1 до х4 последний шаг последовательности "вниз-вверх-вниз" проводится для множества значений, например шаг "вниз" 31с по фиг.9. Эти значения должны теперь добавляться к соответствующим значениям, к которым также должны добавляться округленные значения на фиг.16, то есть значения на выходе блока 204а. В этом случае предпочтительным является суммировать сначала неокругленные значения, а именно посредством показанного на фиг.19 сумматора 203, чтобы затем суммарные значения в блоке 204 на фиг.19 округлить и при этом одновременно подвергнуть формированию шума так, что затем получается лишь простая ошибка округления, и выходные значения после суммирования посредством сумматора 106 становятся в меньшей степени подверженными влиянию ошибок. Ситуация, показанная на фиг.19, получается в том случае, когда фиг.9 располагается слева рядом с фиг.16, в частности, если вместо преобразования ДКП-IV с N значениями применяется преобразование ДКП-IV с N/2 значениями.
В соответствии с изобретением является предпочтительным комбинировать снижение ошибок округления с формированием ошибок округления. В случае снижения ошибок округления множество входных значений обрабатывается и совместно округляется, причем округленные значения суммируются в одно значение, в то время как в случае спектрального формирования ошибки округления округленные значения округляются независимо друг от друга и суммируются с соответственно различными другими значениями.
Кроме того, следует отметить, что ситуация на фиг.19 может возникнуть и в том случае, когда, как представлено на фиг.15, применяются преобразования ДКП-IV с N/2 значениями. При этом перед каскадом преобразования, то есть перед обоими блоками ДКП, имеется каскад, обозначенный на фиг.15 как каскад-"бабочка", посредством которого входные значения от х0 до хN/2-1 соответственно взвешиваются и округляются, чтобы затем суммироваться с теми же значениями, с которыми также суммируются значения каскада преобразования ДКП-IV. Кроме того, следует отметить, что ступень преобразования на фиг.15 представлена только схематично. Оба представленных схематично на фиг.15 блока преобразования ДКП-IV в практической реализации были бы заменены компонентами, показанными на фиг.16, если на фиг.16 вместо значения хN-1 записывается хN/2-1, и записывается хN/2, и если вместо значения хN/2-1 записывается хN-1.
На фиг.19 показана предпочтительная реализация, в частности, для моноприложений, то есть для случая, при котором должно использоваться одно преобразование ДКП-IV с N/2 значениями.
В зависимости от заданных условий соответствующий изобретению способ округления может быть реализован аппаратными средствами или программным обеспечением. Реализация может осуществляться на цифровом носителе записи, в частности на дискете, или на компакт-диске со считываемыми электронным способом управляющими сигналами, которые могут взаимодействовать с программируемой компьютерной системой для выполнения способа. В общем случае изобретение предусматривает, таким образом, компьютерный программный продукт с программным кодом, сохраненным на машиночитаемом носителе для осуществления соответствующего изобретению способа, если компьютерный программный продукт выполняется на компьютере. Иными словами, изобретение также представляет компьютерную программу с программным кодом для осуществления способа, когда компьютерная программа выполняется на компьютере.
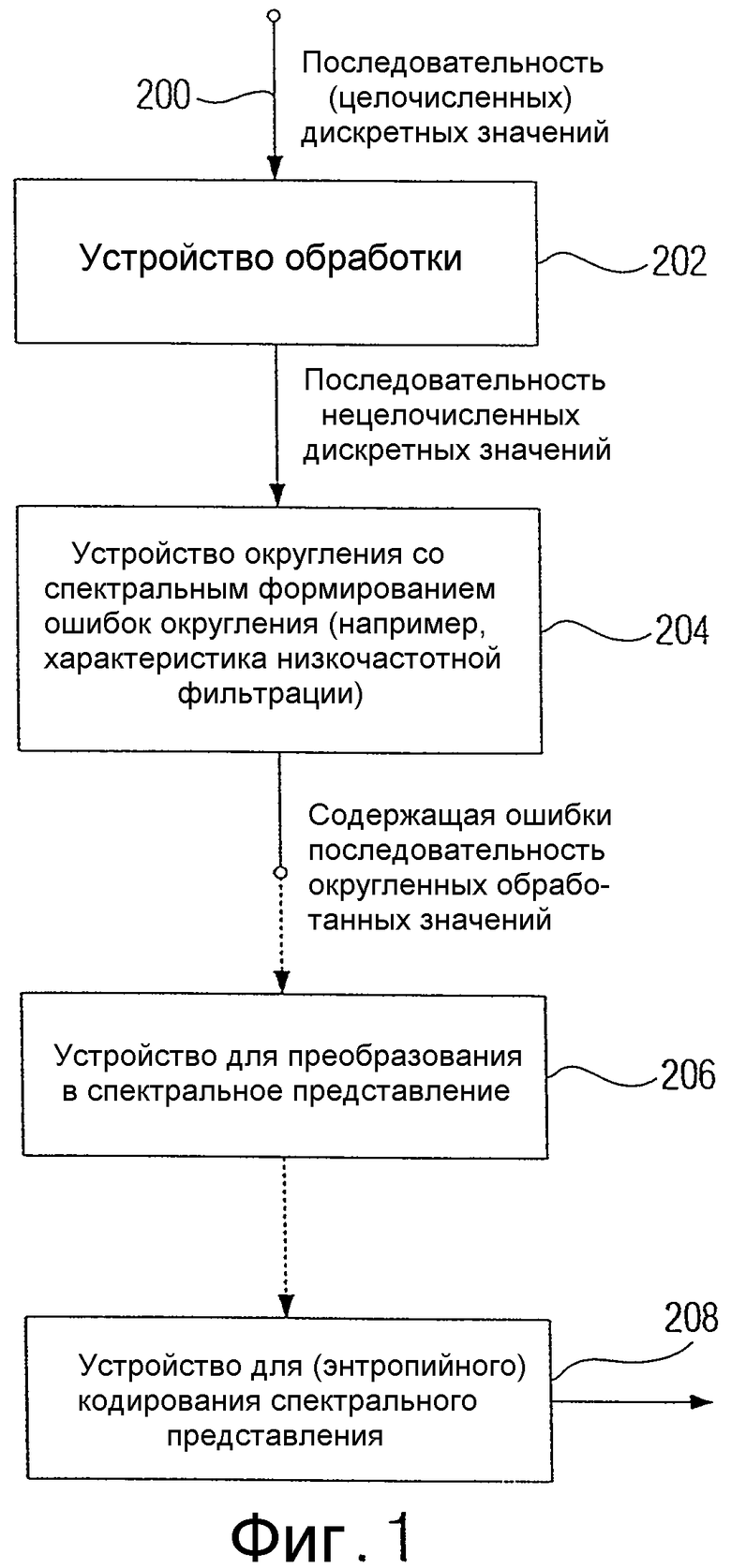
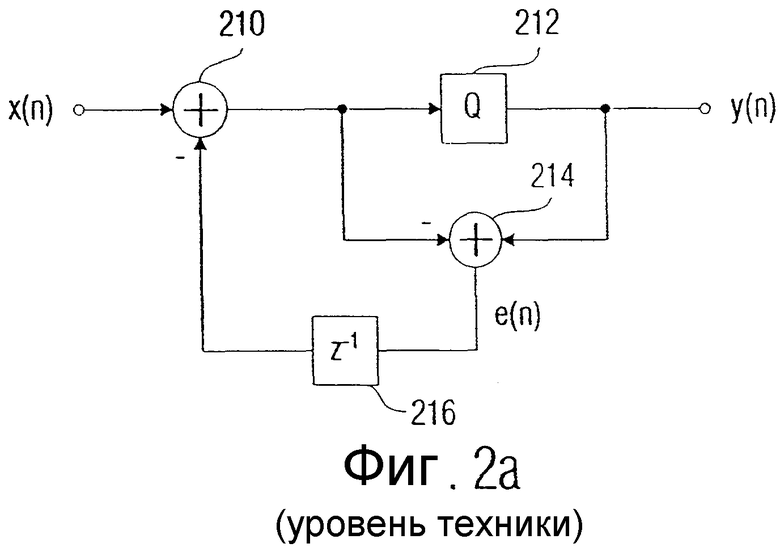
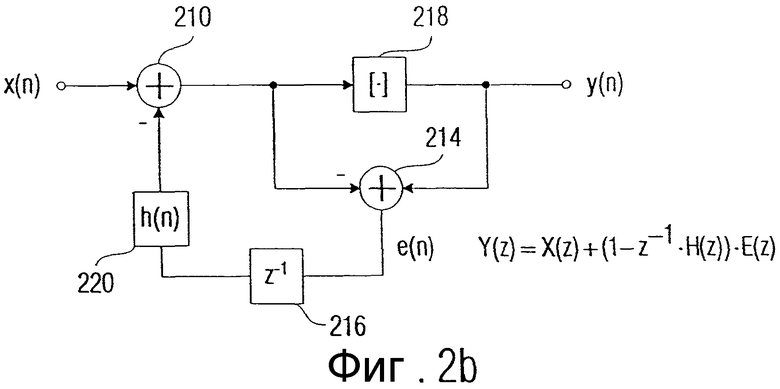
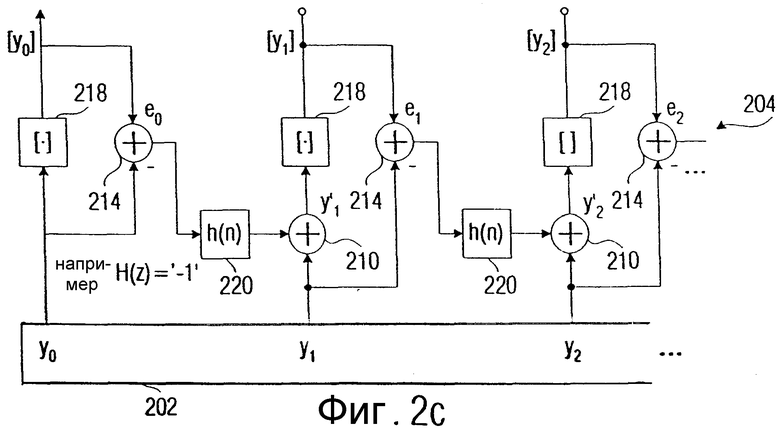
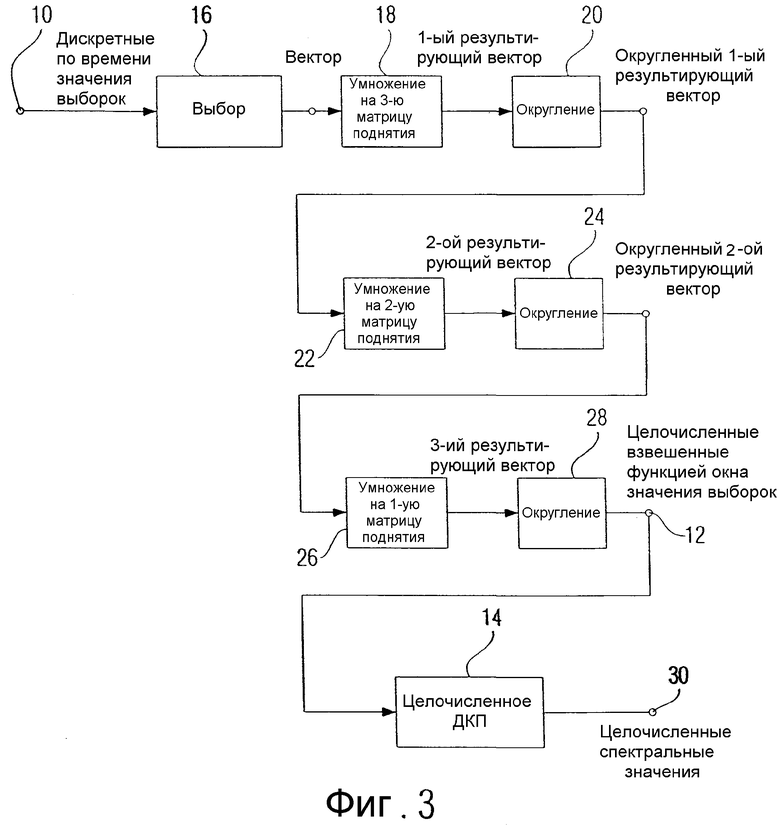






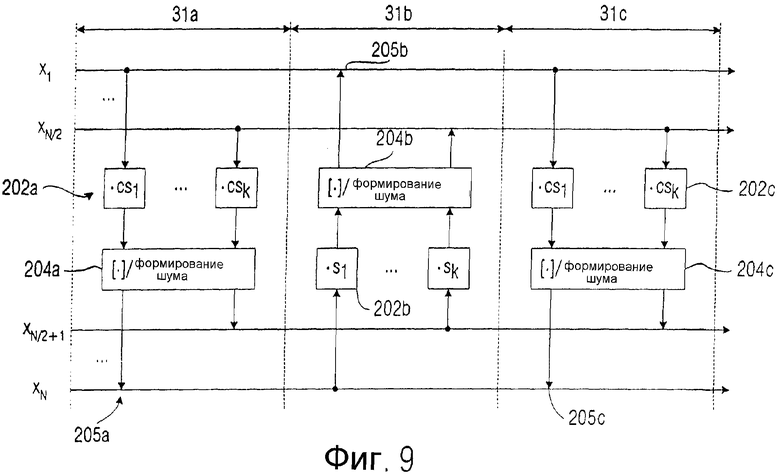
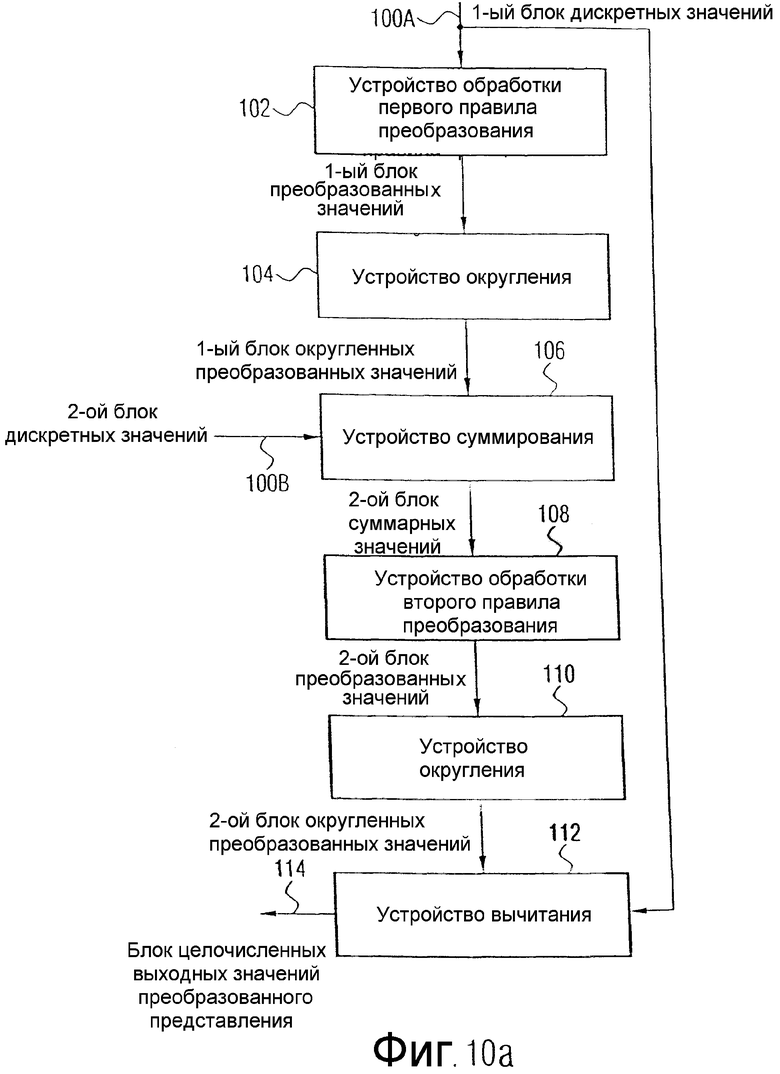

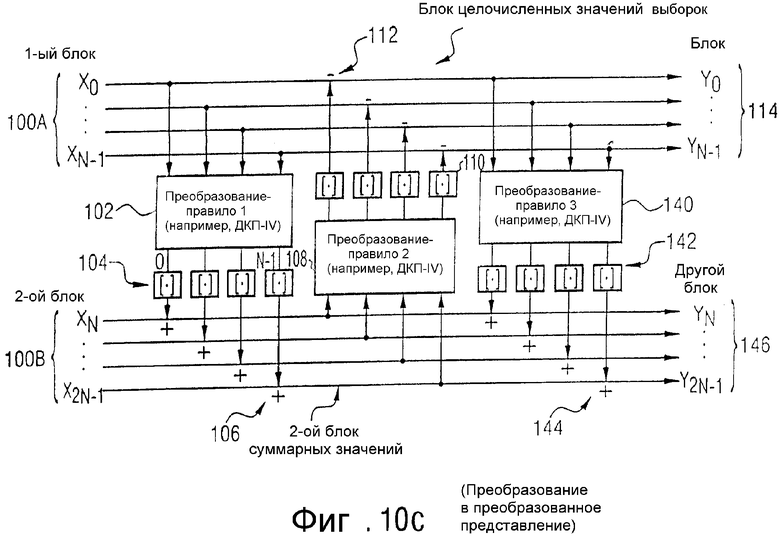
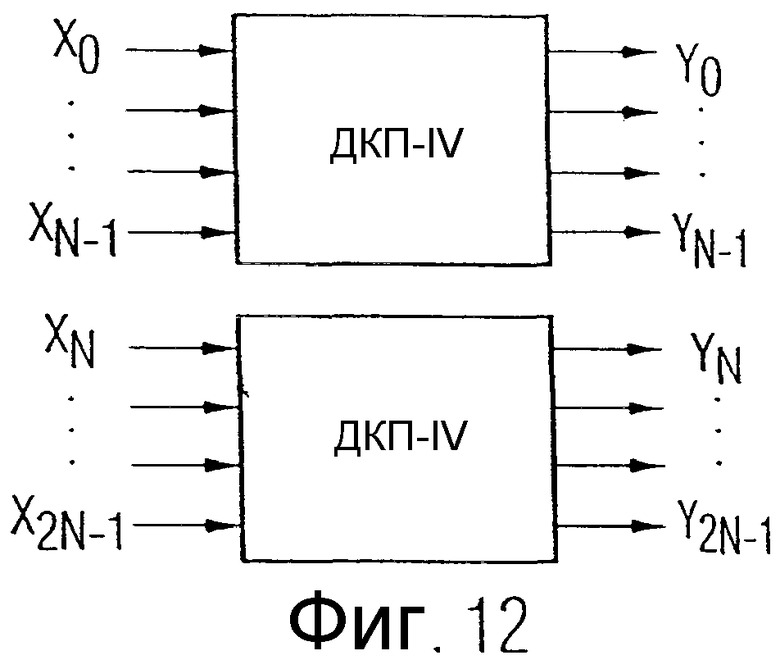
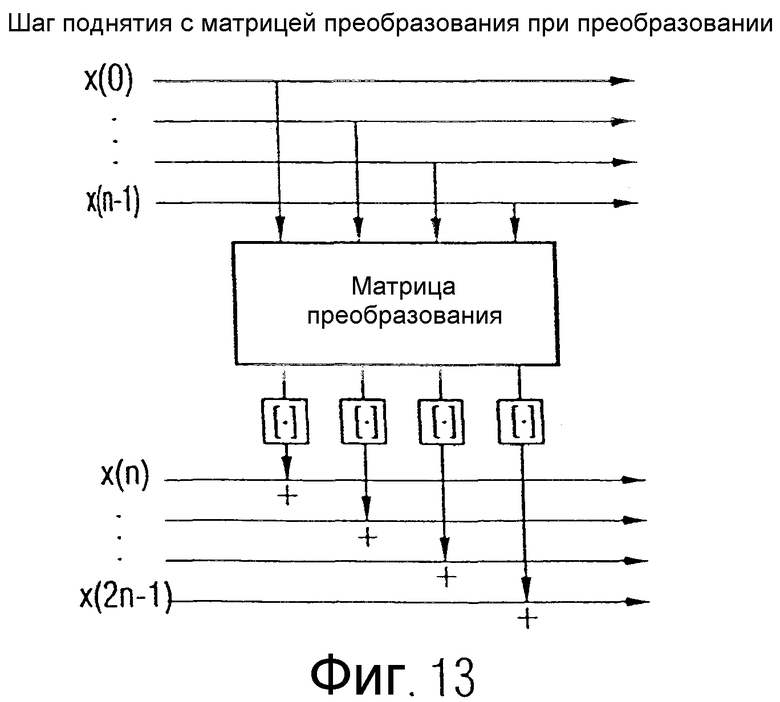
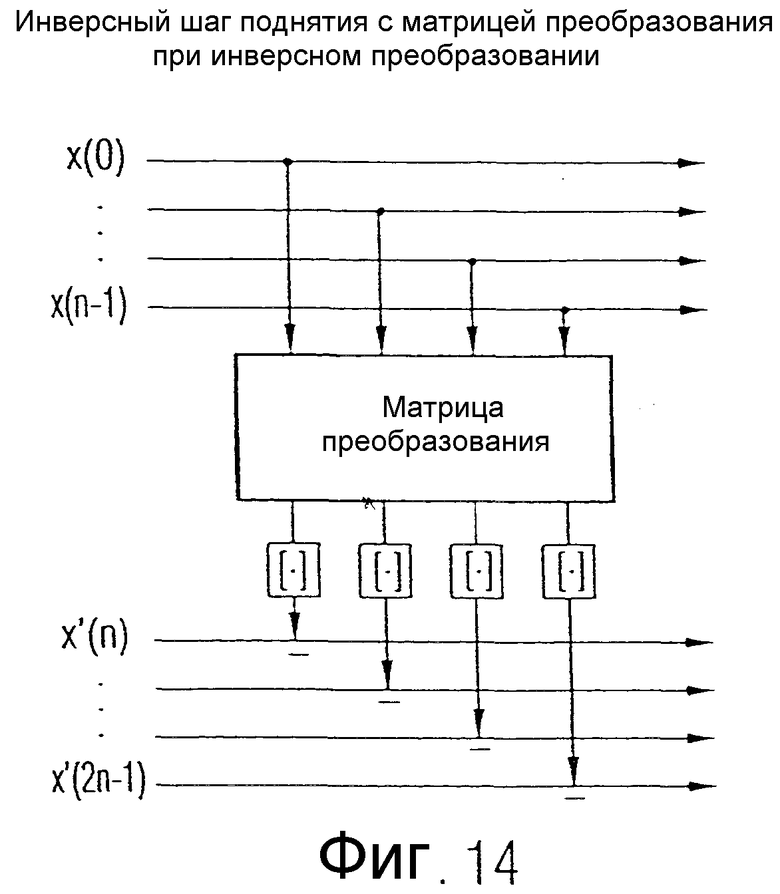
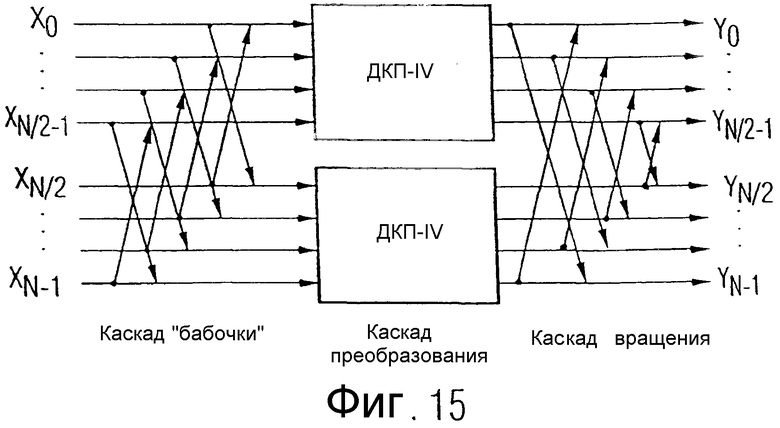
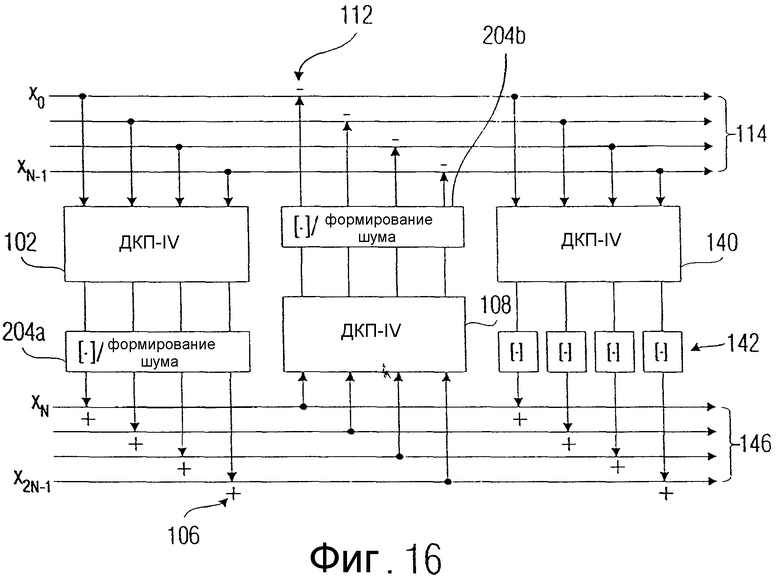
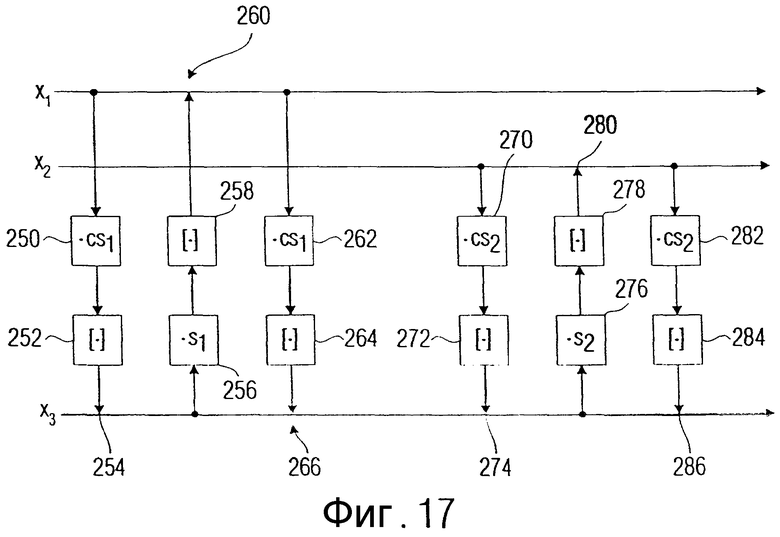
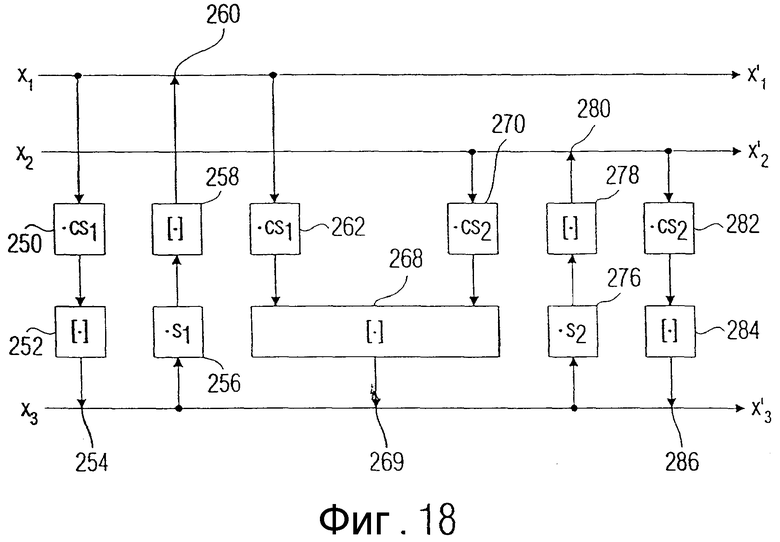

Изобретение относится к вычислительной технике и может быть использовано для обработки сигналов для последовательно поступающих значений. Техническим результатом является снижение ошибки округления. Устройство содержит средство для формирования первого нецелочисленного входного значения и второго нецелочисленного входного значения, причем первое нецелочисленное входное значение формируется из первого исходного значения и третьего исходного значения посредством первого шага поднятия и второго шага поднятия и последующего взвешивания, второе нецелочисленное входное значение формируется посредством взвешивания второго исходного значения; средство для комбинирования первого и второго нецелочисленных входных значений и для округления нецелочисленного результирующего значения. 5 н. и 9 з.п. ф-лы, 24 ил.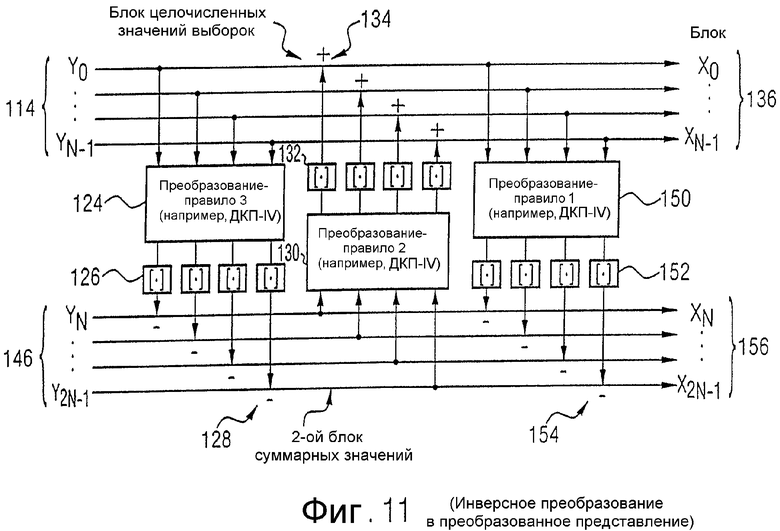
формирования (250, 252, 254, 256, 258, 260, 262) первого нецелочисленного входного значения из первого исходного значения (x1) и третьего исходного значения (х3) посредством первого шага поднятия и второго шага поднятия и последующего взвешивания (262), формирования второго нецелочисленного входного значения посредством взвешивания (270) исходного второго входного значения (х2);
комбинирования (268) первого нецелочисленного входного значения и второго нецелочисленного входного значения для получения нецелочисленного результирующего значения и округления нецелочисленного результирующего значения для получения округленного результирующего значения.
средство (202) для формирования первого нецелочисленного входного значения и второго нецелочисленного входного значения, причем первое нецелочисленное входное значение формируется взвешиванием первого исходного значения (x1), а второе нецелочисленное входное значение вычисляется путем преобразования из последовательности исходных входных значений, которой принадлежит первое исходное значение (x1); и средство (203, 204) для комбинирования первого нецелочисленного входного значения и второго нецелочисленного входного значения для получения нецелочисленного результирующего значения и для округления нецелочисленного результирующего значения для получения округленного результирующего значения.
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ХАРТЛИ-ФУРЬЕ | 1999 |
|
RU2190874C2 |
| Арифметическое устройство для процессора быстрого преобразования Фурье | 1986 |
|
SU1363245A1 |
| DE 10129240 A1, 02.01.2003 | |||
| US 6058215 A, 02.05.2000 | |||
| JP 2002091943, 29.03.2002 | |||
| US 6421464 B1, 16.07.2002. | |||
Авторы
Даты
2008-04-27—Публикация
2004-09-28—Подача