ДИФРАКЦИОННОЕ ПРОФИЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ ЧАСТИЧНО ПРОСТРАНСТВЕННО КОГЕРЕНТНОГО СВЕТОВОГО ПУЧКА Российский патент 2009 года по МПК G02B27/09 G02B27/42 

Область техники, к которой относится изобретение

Настоящее изобретение относится к формированию заданных распределений интенсивности в пучках излучения, испускаемых многомодовыми лазерами и другими частично пространственно когерентными источниками излучения, а также к улучшению качества подобных распределений.

Уровень техники

Многие мощные лазеры, используемые в промышленных целях, в том числе импульсные эксимерные лазеры, генерируют оптическое излучение (далее для краткости называемое также "светом"), которое включает в себя большое количество взаимно некоррелированных поперечных мод (типов колебаний). В отличие от света, испускаемого обычными He-Ne или полупроводниковыми лазерами, свет, испускаемый подобными источниками, обладает частичной пространственной когерентностью (см. F. Gori, Opt. Commun., 34, p.301, 1980; A. Starikov and E. Wolf, J. Opt. Soc. Am., 72, p.923, 1982; S. Lavi, R. Prochaska and E. Keren, Appl. Opt, 27, p.3696, 1988).

Распределение интенсивности в лазерном пучке в плоскости, перпендикулярной направлению его распространения, представляет собой важное свойство почти для всех промышленных применений лазеров. Например, профиль пучка излучения импульсных эксимерных лазеров в типичном случае далеко не идеальный: в нем могут наблюдаться резкие флуктуации интенсивности; пучок не всегда обладает вращательной симметрией и может иметь значительную эллиптичность; распределение интенсивности может изменяться от импульса к импульсу.

В типичном случае (хотя и не всегда) распределение интенсивности в пучке многомодового лазера в дальней зоне имеет, с хорошей степенью приближения, такую же форму кривой Гаусса, что и аналогичное распределение пучка одномодового лазера. Фундаментальное различие, однако, заключается в том, что многомодовый пучок весьма далек от дифракционного предела, т.е. его расходимость выше, чем у пучка одномодового лазера с той же длиной волны и с теми же начальными размерами. Кроме того, в распространяющемся пучке излучения мощного многомодового лазера часто обнаруживаются сильные локальные флуктуации интенсивности, не наблюдаемые в пучках высококачественных одномодовых лазеров.

Гауссовское распределение интенсивности не всегда является идеальным. Во многих применениях лазеров предпочтительно иметь в плоскости, перпендикулярной направлению распространения, распределение, которое является равномерным в некоторой области например, в пределах круга или квадрата. В частности, пучки квадратного сечения желательны в применениях, когда освещаемое поле состоит из квадратных пикселов, тогда как круглые в сечении пучки равномерной интенсивности полезны при сверлении различных материалов с помощью лазеров. Могут быть полезны и другие профили: в экспериментах по термоядерному синтезу сферический объект облучается пучками, подаваемыми по различным направлениям, причем в идеальном случае каждый пучок должен равномерно освещать соответствующую полусферу. Для этого требуется пучок круглого сечения с интенсивностью, увеличивающейся по косинусному закону от центра к краям с последующим падением до нуля.

Пучки, испускаемые мощными полупроводниковыми лазерами с торцевым излучением, также часто состоят из большого количества поперечных мод. Особое свойство данных лазеров заключается в том, что пучок является частично пространственно когерентным в направлении испускающего свет волновода, но (почти) когерентным в противоположном направлении. В типичном случае качество пучка в направлении волновода является низким: наблюдаются сильные локальные осцилляции, которые желательно устранить.

Разрабатываются и другие яркие полупроводниковые источники света, не основанные на полностью вынужденном излучении. В качестве примера могут быть названы светодиоды с резонансной полостью, которые занимают промежуточное положение между лазерами и обычными светодиодами (СД). Испускаемое излучение в этом случае состоит из большого числа когерентных мод резонатора, причем поле, соответствующее суперпозиции этих мод, является полностью некогерентным, или квазиоднородным. Когда подобный источник установлен в передней фокальной плоскости положительной линзы, формируются частично когерентные квазиколлимированные световые поля. Однако распределение интенсивности, в частности, в дальней зоне не является идеальным. Очень часто пучок коллимируется (проецируется) линзой таким образом, что интенсивность в дальней зоне (в плоскости изображения) приближенно соответствует изображению поверхности источника. Термин "приближенно" использован потому, что апертура линзы срезает высокие пространственные частоты в угловом спектре первичного поля. Другими словами, формируемое изображение подвергается низкочастотной фильтрации, что обычно не позволяет обеспечить заданный профиль.

Пучок излучения, формируемый торцевой поверхностью многомодового оптического волокна, также соответствует частично пространственно когерентному полю, которое тоже требует модифицирования (т.е. профилирования).

Когда ставится цель достижения высокой мощности оптического излучения, особенно в случае полупроводниковых источников света, обычно единственный источник излучения заменяют одномерным или двумерным набором индивидуальных, взаимно некоррелированных источников (лазеров или СД). В этом случае в плоскости изображения линзы формируется набор световых пятен, даже если желательно иметь равномерно освещенную область.

Задача формирования заданного распределения интенсивности когерентного светового пучка либо в дальней зоне, либо на некотором конечном расстоянии от источника в принципе может решаться с применением традиционной преломляющей оптики. С этой целью перед источником устанавливают асферическую преломляющую поверхность, причем профиль поверхности оптимизируют таким образом, чтобы распределение энергии в целевой плоскости имело желательную форму (см. Р.W.Rhodes and D.L Shealy, Appl. Opt., 19, p.3545, 1980).

Известное решение представлено на фиг.1. Распределение интенсивности лазерного пучка профилируется с помощью асферической линзы 102. Вариант (а) соответствует идеальной ситуации: идеально согласованный по направлению гауссовский пучок 101 формирует распределение 103 интенсивности с плоской вершиной в фокальной плоскости линзы. Если оптимизированная поверхность имеет вращательную симметрию, ее можно изготовить, например, посредством алмазного точения. Если же преломляющая поверхность не обладает указанной симметрией, ее изготовление с применением современных технологий представляет значительные трудности.

С другой стороны, даже если такая поверхность может быть изготовлена с высокой точностью, эффективность выполнения ею своей функции будет чувствительной как к форме распределения падающего излучения, так и к качеству совмещения осей падающего пучка и оптического элемента. Такая чувствительность обусловлена тем, что форма поверхности оптимизируется на основе геометрической оптики. Данная реальная ситуация иллюстрируется фиг.1b: отклонение 104 от расчетного распределения интенсивности в падающем пучке или погрешность юстировки приводят к нежелательным искажениям результирующего распределения 105 интенсивности. Отсюда следует, что локальное изменение распределения интенсивности в плоскости элемента имеет прямое локальное влияние на распределение интенсивности в плоскости наблюдения.

Дифракционная оптика (см. J. Turunen and F. Wyrowski, eds. Diffractive Optics for Industrial and Commercial Applications, Wiley-VCH, Berlin, 1997; далее данная монография упоминается как Diffractive Optics) подтвердила свою эффективность при решении многих проблем, связанных с изменением профиля когерентных лазерных пучков. Так, исходный гауссовский профиль распределения интенсивности может быть преобразован почти в любой заданный профиль (например, в однородный или с повышенной интенсивностью на краях) в дальней зоне или на конечном расстоянии путем введения в пучок элемента, плоского на макроуровне, но обладающего поверхностной микроструктурой. Подобный элемент модулирует фазу или амплитуду или оба эти параметра (см. Diffractive Optics, chapter 6).

Дифракционная оптика предлагает и решения проблемы вышеупомянутых распределений, не обладающих вращательной симметрией. Действительно, поскольку микроструктура формируется посредством технологии микролитографии, конкретная форма этой микроструктуры не имеет большого значения с производственной точки зрения. Тем не менее оптическая функция вводимого элемента остается аналогичной функции асферической линзы, так что проблемы чувствительности профиля пучка к изменениям в распределении падающего излучения или взаимной настройке оптических осей не устраняются. Дифракционная оптика позволяет уменьшить влияние названных погрешностей путем придания микроструктуре некоторого заданного рассеяния, однако данный выигрыш достигается ценой снижения эффективности преобразования (см. Diffractive Optics, chapter 6).

Исходным положением при разработке обычных дифракционных элементов для управления профилем пучка является полная пространственная когерентность (см. W.В.Veldkamp and С.J.Kastner, Appl. Opt., 21, p.879, 1982; C.-Y.Han, Y.Ishii, K.Murata, Appl. Opt., 22, p.3644, 1982; M.Т.Eisman, A.M.Tai and J.N.Cederquist, Appl. Opt., 28, p.2641, 1989; N. Roberts, Appl. Opt., 28, p.31, 1989). Даже при том, что ни один лазер не отвечает полностью данному положению, оно приемлемо для всех тех лазеров, которые испускают излучение, соответствующее, по существу, единственному типу поперечных мод (хотя при этом могут существовать несколько продольных мод, т.е. излучение не является полностью монохроматическим). Однако допущение о полной пространственной когерентности неприменимо, если в пучке одновременно присутствует более одной поперечной моды. В этом случае известные решения рассматриваемого типа не всегда срабатывают, так что некоторые проблемы, обусловленные изменениями формы пучка и допусками на согласование осей, сохраняются.

В документе US 4790627 А описан способ профилирования пространственно некогерентных широкополосных лазерных пучков для экспериментов по лазерному термоядерному синтезу. Главная решаемая задача состоит в уменьшении аберраций лазерной системы с использованием поглотителя, изменяющего профиль пучка, и проецирования требуемого профиля. В документе US 4521075 А рассматривается, по существу, та же проблема; однако здесь для преобразования пространственно когерентного широкополосного пучка в широкополосный, но, по существу, некогерентный пучок предложено решение, предусматривающее применение ступенчатых дифракционных решеток. Документ US 6157756 А, 1998 соответствует уровню техники в отношении профилирования полностью когерентного лазерного пучка в лазерную линию с большим углом расхождения. Используемая световолоконная решетка является периодической, но не микроструктурной, причем ее функционирование не основано на частичной когерентности.

В документе US 4410237 A, G02B 5/18, 1980, описан способ профилирования (т.е. изменения профиля) полностью когерентных лазерных пучков и оптический элемент для осуществления данного способа. Эти решения (которые можно рассматривать в качестве ближайших аналогов изобретения) предназначены для формирования пучка с различными профилями в двух взаимно ортогональных плоскостях и предусматривают введение в пучок излучения оптического элемента, состоящего из прозрачной дифракционной решетки с центрально-симметричным профилем и двух последовательно установленных призм для сжатия преобразуемого пучка. Известный оптический элемент имеет довольно сложную конструкцию и непригоден для профилирования частично когерентных пучков.

Раскрытие изобретения

Настоящее изобретение предлагает способ управления распределением (способ профилирования) распределений интенсивности многомодовых оптических полей с использованием дифракционных элементов (см. Diffractive Optics). Изобретение основано на, по существу, периодических дифракционных элементах и на использовании частичной пространственной когерентности многомодового пучка, т.е. того свойства светового пучка, которое ранее рассматривалось как создающее проблемы.

Настоящее изобретение решает рассмотренные трудности, свойственные уровню техники. Оно характеризуется тем, что профиль (форма) преобразованного распределения интенсивности является независимым от поперечной настройки по отношению к падающему пучку при приемлемых отклонениях профиля падающего пучка от расчетного профиля.

Порядок использования частичной пространственной когерентности будет описан далее.

Если имеет место наложение двух полностью взаимно коррелированных пучков (например, полученных путем расщепления одного лазерного пучка), их комплексные амплитуды суммируются. Распределение интенсивности представляет собой интерференционную картину: если пучки имеют одинаковую интенсивность, наблюдаются полосы с яркими максимумами и с минимумами, имеющими нулевую интенсивность. Если же имеет место наложение двух взаимно некоррелированных пучков (например, пучков от двух различных лазеров), суммируются распределения интенсивности и интерференция отсутствует. В рамках теории оптической когерентности рассмотренные случаи являются хорошо изученными предельными вариантами. Свет, испускаемый многомодовыми источниками света, не подпадает ни под один из рассмотренных вариантов. Действительно, если многомодовый пучок разделить на две части с последующей их рекомбинацией, будет наблюдаться интерференция, но различимость интерференционных полос падает с увеличением количества мод, а минимумы имеют ненулевую интенсивность. Настоящее изобретение использует эту ограниченную способность частично пространственно когерентного света к интерференции и применяет ее для профилирования многомодовых световых пучков. Основная идея заключается в том, что частичная когерентность падающего излучения облегчает использование периодических дифракционных элементов, которые разделяют падающий пучок на несколько пучков в рамках профилирования многомодовых пучков. Данная операция может рассматриваться как распространение рассмотренных принципов двухлучевой интерференции на многомодовые пучки.

Таким образом, поставленные технические задачи решены созданием способа управления распределением интенсивности частично пространственно когерентного поля оптического излучения на конечном расстоянии от его источника или в дальней зоне с использованием оптического элемента, установленного в указанном поле. Способ по изобретению характеризуется тем, что используемый для управления элемент выполнен дифракционным и периодическим в одном или в двух направлениях, ортогональных по отношению к направлению распространения падающего на него оптического излучения.

Настоящее изобретение охватывает также оптический элемент, устанавливаемый в пучок оптического излучения для управления распределением его интенсивности на конечном расстоянии от источника излучения или в дальней зоне. Оптический элемент по изобретению является дифракционным и периодическим в одном или в двух направлениях, ортогональных по отношению к направлению распространения падающего на него исходного пучка оптического излучения. При этом оптический элемент по изобретению выполнен с возможностью профилирования распределения интенсивности многомодовых пучков, формируемых лазерами, светодиодами или оптическими волокнами, в плоскости, перпендикулярной указанному направлению распространения.

Предпочтительно выполнить оптический элемент таким образом, что его поступательное перемещение в плоскости, перпендикулярной направлению распространения пучка, не оказывает заметного влияния на профилированный пучок, если только падающий пучок полностью перекрывается рабочей поверхностью указанного элемента. Кроме того, оптический элемент по изобретению способен осуществлять усреднение быстрых флуктуаций интенсивности в многомодовых лазерных пучках и улучшать воспроизводимость профиля пучка. В предпочтительных вариантах своего выполнения оптический элемент способен осуществлять профилирование полей, формируемых многомодовыми лазерами, светодиодами или многомодовыми оптическими волокнами, с получением однородного или иного распределения интенсивности в пределах заданной зоны в плоскости, перпендикулярной направлению распространения и находящейся в дальней зоне или на конечном расстоянии от источника.

Альтернативно, оптический элемент по изобретению может быть выполнен с возможностью осуществлять преобразование полей, формируемых наборами взаимно некоррелированных многомодовых лазеров, светодиодов и многомодовых оптических волокон, в поле с однородной интенсивностью или иным профилем в пределах заданной зоны в плоскости, перпендикулярной направлению распространения. В качестве альтернативы, данный элемент выполняется из условия обеспечения равномерной освещенности полусферического объекта.

Известно, что пучки излучения, испускаемые многими многомодовыми лазерами, могут быть охарактеризованы с приемлемой точностью с помощью так называемой модели гауссиана Шелла (Gaussian Schell model; далее сокращенно МГШ). Функция взаимной спектральной плотности (см. L. Mandel and E. Wolf. Coherence and Quantum Optics, Cambridge University Press, Cambridge, 1995), которая описывает корреляции для источника, соответствующего МГШ, имеет вид

где w₀ (полуширина профиля интенсивности на уровне 1/е²) и σ₀ (среднеквадратическое значение степени когерентности в плоскости источника) являются константами, а общая степень когерентности описывается отношением α=σ₀/w₀. Отношение α и, следовательно, σ₀ могут быть определены путем измерения расходимости в дальней зоне, поскольку угол дифракции в дальней зоне (на уровне 1/е²) находится из θ=λ/(πw₀β), где λ - это длина волны света, а β=(1+α^-2)-^1/2. Даже при том, что МГШ не является абсолютно точной для любого реального источника света, ее точность достаточна для задач, решаемых настоящим изобретением, в том числе применительно ко многим источникам, для которых дифракционная картина в дальней зоне не соответствует точно распределению Гаусса.

Краткое описание чертежей

Фиг.1 иллюстрирует уровень техники. Варианты (а) и (b) соответствуют идеальной и реальной ситуациям.

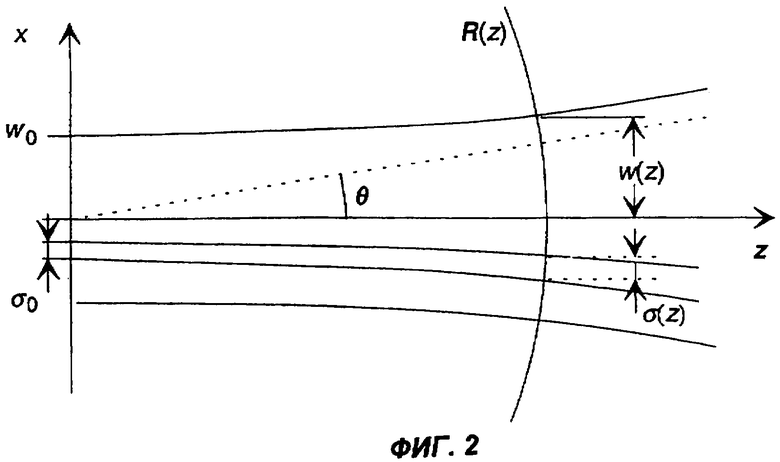
На фиг.2 представлено распространение пучка, соответствующего МГШ, в свободном пространстве.

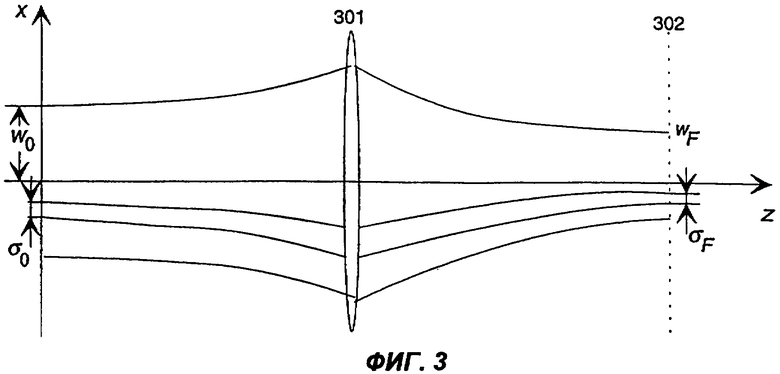
Фиг.3 иллюстрирует осуществление преобразования Фурье для источника, описываемого МГШ, посредством тонкой линзы.

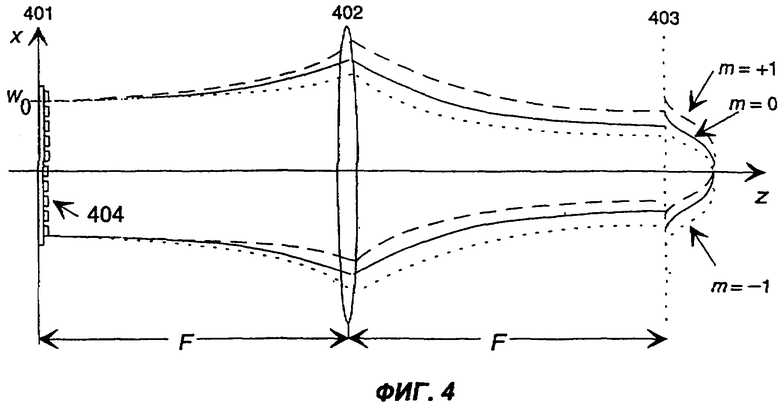
Фиг.4 иллюстрирует профилирование пучка, соответствующего МГШ, посредством тонкой линзы и периодического дифракционного элемента.

Фиг.5 иллюстрирует интерференцию частично пространственно когерентных пучков при использовании геометрии, аналогичной представленной на фиг.3.

На фиг.6 представлены распределения интенсивности, построенные методом численного моделирования распределений интенсивности в плоскости 302 на фиг.3 в предположении, что дифракционный элемент разделяет пучок на девять составляющих равной интенсивности.

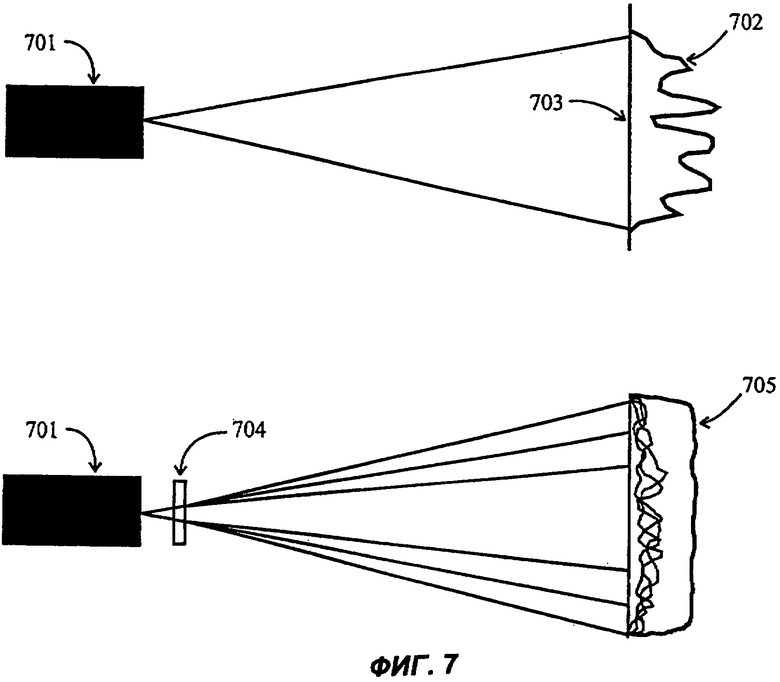
Фиг.7 иллюстрирует повышение однородности пучка многомодового полупроводникового лазера.

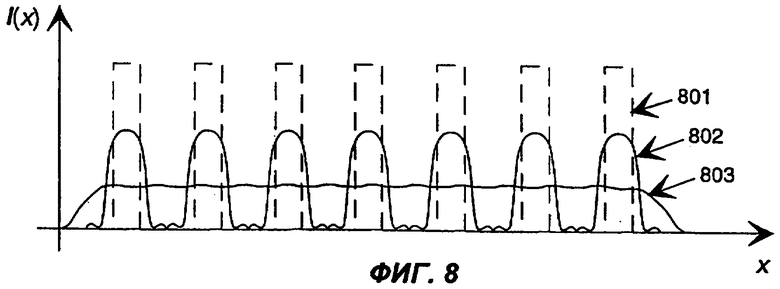
Фиг.8 иллюстрирует комбинирование нескольких взаимно некоррелированных световых пучков, испускаемых независимыми источниками света, с получением распределения с практически плоской вершиной в плоскости изображения источников.

Осуществление изобретения

Далее настоящее изобретение будет описано со ссылками на фиг.2-8.

Фиг.2 иллюстрирует распространение пучка, соответствующего МГШ, в свободном пространстве (или в однородном диэлектрике). На данной фигуре иллюстрируются, в частности, величины w₀ и σ₀; представлены также в графической форме так называемые параметры распространения, т.е. w(z) (полуширина на уровне 1/е²), σ(z) (значение ширины когерентности) и R(z) (радиус кривизны). Известно, что данные величины описываются следующими соотношениями (см. А.Т.Friberg and R.J.Sudol, Opt. Commun., 41, p.297, 1982):

Угол θ (см. фиг.2) соответствует уже упоминавшейся полуширине распределения интенсивности в дальней зоне на уровне 1/е². После прохождения через тонкую линзу пучок, соответствующий МГШ, распространяется, как сферическая волна с радиусом кривизны R(z).

Фиг.3 иллюстрирует ситуацию, когда излучение источника, описываемого МГШ, подвергается преобразованию Фурье посредством тонкой линзы 301 (с фокальной длиной F) в соответствии со стандартной 2F-геометрией преобразования Фурье в плоскости 302 для случая R(F)=∞, т.е. волновой фронт является плоским. Использование уравнений (1)-(3) позволяет управлять данной геометрией путем поиска параметров пучка в Фурье-плоскости, а также значений когерентности таким образом, чтобы ширина пучка и область когерентности соответствовали аналогичным параметрам в плоскости линзы. Используя дополнительно известный закон преобразования сферической волны тонкой линзой, можно определить параметры выходного пучка. Описанная процедура может быть расширена на распространение пучка в рамках МГШ через произвольную параксиальную линзовую систему (см. А. Т. Friberg and J. Turunen, J. Opt. Soc. Am., A 5, p.713, 1988).

Фиг.4 иллюстрирует профилирование пучка, соответствующего МГШ, посредством тонкой линзы 402 и периодического дифракционного элемента 404. На фиг.4 показана, в частности, геометрия падения пучка, соответствующего МГШ, на периодический дифракционный элемент 404, который разделяет плоскую волну на ряд пучков, распространяющихся в слегка различных направлениях.

Дифракционный элемент является периодическим по одной или двум координатам, причем аналогично обычной дифракционной решетке он создает различные порядки дифракции с направлениями распространения, соответствующими уравнению дифракционной решетки. Периоды решетки d_x и d_y по координатам х и y в типичном случае выбираются такими, что угловые смещения δθ_х≈λd_x и δθ_y≈λd_y имеют меньшие значения, чем углы δθ_х и δθ_у расхождения по координатам х и у в дальней зоне.

Описанным образом можно получить набор частично перекрывающихся пучков, соответствующих МГШ и центрированных относительно направлений распространения порядков дифракции. Подобный набор показан на фиг.5, которая иллюстрирует интерференцию частично пространственно когерентных пучков при использовании геометрии, аналогичной представленной на фиг.3, для случая, когда дифракционная решетка формирует двумерный набор порядков дифракции (в форме эллипсов). Центральные точки эллипсов соответствуют пространственным частотам порядков дифракции. В результате взаимного наложения сформированные частично коррелированные поля образуют область почти постоянной интенсивности в пределах окружности (обозначенной штриховой линией). В отличие от когерентных пучков эти пучки интерферируют только частично, как это будет показано далее. Для облегчения понимания будет рассмотрена только двумерная геометрия, хотя это рассмотрение может быть легко расширено на трехмерный вариант.

Обозначим комплексные амплитуды, ассоциированные с порядками дифракции в выходной плоскости дифракционного элемента, через Т_m, где m∈М - это номер порядка дифракции, а М - это набор таких порядков, для которых эффективность дифракции η_m=|Т_m|² существенно выше нуля.

Тогда взаимная спектральная плотность поля непосредственно за оптическим элементом имеет вид

где n - это также номер порядка дифракции, a d- период решетки по координате х. Распределение интенсивности в фокальной плоскости линзы (с фокусным расстоянием F) по координате u имеет вид:

Интегрируя уравнения (1), (5) и (6), получаем окончательный результат

где w_F=λF/πw₀β, σ_F=σ₀=w_F/w₀ и u₀=λF/d.

Фиг.6 иллюстрирует в форме графиков результаты численного моделирования на основе уравнения (7) для распределений интенсивности в плоскости 302 на фиг.3. Задача заключается в трансформировании исходного гауссовского распределения интенсивности в распределение с плоской вершиной при использовании дифракционного элемента, который способен разделить полностью когерентную плоскую волну на девять порядков дифракции, имеющих равную интенсивность: m=-4,...,+4. Для графиков на фиг.6а и 6b степень когерентности соответственно составляла α=1/5 и α=1/10, а значения σ₀ соответственно w₀/5 и w₀/10.

Когда значение d достаточно велико, угловое расстояние δθ между порядками намного меньше, чем угол θ расхождения; при этом u₀<<w_F. В этом предельном случае оптический элемент почти не оказывает влияния на распределение интенсивности в дальней зоне. При уменьшении d распределение, соответствующее преобразованию Фурье, сначала расширяется, а затем при w_F>u₀, разделяется на разрешенные пики. При правильном выборе d (точнее, отношения w₀/d) реализуется оптимальный вариант, при котором достигается наивысшая однородность распределения интенсивности. При этом уменьшение степени когерентности соответствует уменьшению периода дифракционной решетки, поскольку приводит к увеличению ширины пучка w_F. Следует также отметить, что суммарная энергия во всех случаях остается неизменной: уменьшение d приводит к расширению пучка при одновременном уменьшении его максимальной интенсивности.

Период d решетки является самым мощным инструментом для изменения профиля пучка (количество порядков М имеет меньшее значение). В том случае, когда источник анизотропен (например, его распределение интенсивности является периодическим), целесообразно оптимизировать d отдельно по координатам х и у. Такая ситуация иллюстрируется фиг.5, соответствующей наблюдению в плоскости, перпендикулярной направлению распространения пучка. Поскольку источник является анизотропным, анизотропной является и дифракционная картина в дальней зоне. Однако благодаря правильному выбору периодов решетки по координатам х и у картина в дальней зоне преобразуется к форме, обладающей вращательной симметрией. Если это необходимо, можно использовать различное количество пучков по двум ортогональным направлениям.

Как это иллюстрируется на фиг.6 результатами численного моделирования, оптический элемент, способный преобразовать гауссовский пучок в пучок с равномерной интенсивностью, формирует набор гауссовских пучков, распространяющихся в различных направлениях, соответствующих порядкам дифракции. Углы между порядками выбираются такими, чтобы они составляли существенную долю θ, но не настолько большими, чтобы эти порядки разрешались. Выбор δθ/θ определяется значением α частичной когерентности. При этом оптимизация осуществляется независимо для каждого случая с использованием численного моделирования и на основе компромисса между однородностью пучка и сложностью дифракционной структуры. Тот же принцип применим и при построении других элементов для профилирования пучков, в том числе для повышения интенсивности на краю пучка (что достигается соответствующим подбором эффективности для индивидуальных порядков). Для облегчения понимания рассматривались в основном одномерные распределения; однако путем очевидного распространения описанных принципов могут быть легко реализованы и соответствующие двумерные распределения.

На фиг.7 и 8 в качестве примеров проиллюстрированы другие эффективные варианты осуществления изобретения и их применения.

Фиг.7 качественно иллюстрирует использование дифракционного элемента 704 в качестве дифракционного разделителя пучков для повышения однородности пучка многомодового полупроводникового лазера 701 с сильно выраженной неоднородностью распределения, изменяющейся во времени. На схеме (а) распределение 702 интенсивности на экране 703 является неоднородным. На схеме (b) дифракционный элемент 704 формирует набор пучков (для большей наглядности показано только три пучка), распространяющихся по слегка различным направлениям. Распределение интенсивности в каждом отдельном пучке аналогично распределению 702, однако взаимное наложение частично пространственно когерентных пучков создает пучок 705 с улучшенной однородностью.

В этом случае частично когерентный пучок разделяется на несколько пучков, которые распространяются по слегка отличающимся направлениям таким образом, что не происходит значительного расширения распределения, причем имеет место только частичная интерференция между пучками. Как следствие, возникает тенденция к усреднению флуктуации, так что результирующий пучок является более однородным, чем исходный пучок. Подобный подход удобен, в частности, для повышения качества импульсов излучения эксимерного лазера с целью достижения лучшей воспроизводимости профиля импульсов. Он также пригоден для повышения однородности пучков многомодовых полупроводниковых лазеров (как это иллюстрируется фиг.6).

Фиг.8 иллюстрирует проецирование нескольких дискретных, взаимно некоррелированных источников света (типа источников 404 на фиг.4) в плоскость наблюдения. Источники могут представлять собой как лазеры, так и СД. Если проекционная линза имеет дифракционно-ограниченную апертуру и не усекает существенно угловой спектр источников, будет получено изображение 801 набора источников. На практике получается слегка уширенное распределение 802.

Однако часто представляется предпочтительным получение, вместо дискретного набора, более или менее непрерывного распределения интенсивности, например, равномерно освещенной зоны квадратной или прямоугольной формы. Такое распределение может быть получено способом, предлагаемым настоящим изобретением: изображение каждого источника "размножается" по координатам х и у так, чтобы промежутки между дискретными источниками оказались заполненными. Изображения различных источников могут взаимно налагаться, поскольку эти источники являются взаимно некоррелированными. Таким образом, какая-либо интерференция отсутствует, и результат соответствует некогерентной сумме 803 различных распределений интенсивности.

Изобретение относится к способу управления распределением интенсивности поля волны или волн частично когерентного или некогерентного оптического излучения на конечном расстоянии от его источника или в дальней зоне и устройству, реализующему заявленный способ. При этом при реализации заявленного способа используется установленный в указанном поле оптический элемент, содержащий дифракционную решетку, которая выполнена периодической по одной или двум координатам х, у, ортогональным по отношению к направлению распространения падающего на нее оптического излучения, с возможностью разделения указанного поля на частично перекрывающиеся пучки, центрированные относительно направлений распространения порядков дифракции. Технический результат: получение равномерного распределения интенсивности в многомодовом лазерном пучке при помощи дифракционного элемента. 2 н. и 9 з.п. ф-лы, 8 ил.

1. Способ управления распределением интенсивности поля волны или волн частично когерентного или некогерентного оптического излучения на конечном расстоянии от его источника или в дальней зоне с использованием установленного в указанном поле оптического элемента, содержащего дифракционную решетку, которая выполнена периодической по одной или двум координатам х, у, ортогональным по отношению к направлению распространения падающего на нее оптического излучения, с возможностью разделения указанного поля на частично перекрывающиеся пучки, центрированные относительно направлений распространения порядков дифракции.2. Способ по п.1, отличающийся тем, что используют частично когерентное поле излучения и обеспечивают однородность распределения его интенсивности в результате взаимного наложения частично пространственно когерентных пучков за счет выбора отношения w₀/d, где d - период дифракционной решетки и w₀ - полуширина профиля интенсивности указанной волны на уровне 1/е².3. Способ по п.1, отличающийся тем, что посредством дифракционной решетки, имеющей различные периоды по координатам х и у, формируют двумерный набор порядков дифракции в форме эллипсов, центральные точки которых соответствуют пространственным частотам порядков дифракции частично коррелированных полей.4. Способ по п.3, отличающийся тем, что указанный двумерный набор порядков дифракции формируют при взаимном наложении частично коррелированных полей с образованием области почти постоянной интенсивности в пределах указанного наложения.5. Способ по п.1, отличающийся тем, что при управлении распределением интенсивности поля оптического излучения нескольких дискретных взаимно некоррелированных источников света изображение каждого источника "размножают" посредством дифракционной решетки, периодической по двум координатам, так, чтобы перекрыть промежутки между дискретными источниками по указанным координатам.6. Оптический элемент, устанавливаемый в поле волны или волн частично когерентного или некогерентного оптического излучения для управления распределением интенсивности указанного поля на конечном расстоянии от его источника или в дальней зоне и содержащий дифракционную решетку, которая выполнена периодической по одной или двум координатам х, у, ортогональным по отношению к направлению распространения падающего на нее оптического излучения, с возможностью разделения указанного поля на частично перекрывающиеся пучки, центрированные относительно направлений распространения порядков дифракции.7. Элемент по п.6, отличающийся тем, что период или периоды дифракционной решетки по одной или по двум координатам выбраны из условия обеспечения взаимного наложения частично пространственно когерентных пучков, формируемых многомодовыми лазерами, светодиодами и/или многомодовыми оптическими волокнами, в плоскости, перпендикулярной направлению распространения излучения.8. Элемент по п.7, отличающийся тем, что периоды дифракционной решетки оптимизированы отдельно по координатам х и у.9. Элемент по п.7, отличающийся тем, что период или периоды дифракционной решетки выбран (выбраны) из условия обеспечения однородности распределения интенсивности частично когерентного поля в плоскости, перпендикулярной направлению распространения и расположенной на конечном расстоянии от его источника или в дальней зоне, за счет взаимного наложения частично пространственно когерентных полей.10. Элемент по п.6, отличающийся тем, что выполнен с возможностью осуществлять преобразование полей, формируемых наборами взаимно некоррелированных многомодовых лазеров, светодиодов или многомодовых оптических волокон, в поле с однородной интенсивностью или иным профилем в пределах заданной зоны в плоскости, перпендикулярной направлению распространения, за счет "размножения" изображения каждого источника посредством дифракционной решетки, периодической по координатам х и у, так, чтобы перекрыть промежутки между дискретными источниками по указанным координатам.11. Элемент по п.6, отличающийся тем, что выполнен с возможностью обеспечения равномерной освещенности полусферического объекта.