Область техники
Данное изобретение в целом относится к беспроводным системам связи. Более конкретно, варианты осуществления изобретения имеют отношение к созданию и использованию кодовых книг на основе унитарных матриц.
Уровень техники
Структурированные способы предварительного кодирования с ограниченной обратной связью и замкнутым контуром в системах со многими входами и многими выходами (MIMO, multiple-input multiple-output) были разработаны для эффективной передачи данных от мобильной станции (MS, mobile station) к базовой станции (BS, base station) при беспроводной связи между ними. Такие способы не требуют полной обратной связи для передачи либо весовой матрицы W предварительного кодирования, либо канальной матрицы Н. Вместо этого для каждой пары передающей антенны с номером Nt и пространственного потока с номером Mt строится матричная кодовая книга, которая формируется из набора матриц предварительного кодирования. И базовая станция, и мобильная станция имеют доступ к матричной кодовой книге. Следовательно, для того чтобы осуществить обратную связь с базовой станцией, мобильной станции нужно только передать указатель на матрицу предварительного кодирования, которая содержится в матричной кодовой книге. Такой указатель (индекс) обычно формируется в виде строки битов, где каждый бит имеет двоичное значение. Набор матриц, или кодовую книгу, можно построить так, чтобы достигнуть желаемого компромисса между рабочими характеристиками и пропускной способностью линии обратной связи.
Когда содержимое кодовой книги фиксировано, количество битов обратной связи, которые необходимы для построения указателя к кодовой книге, не растет с увеличением размера матрицы W предварительного кодирования, как это происходит при других существующих подходах. Было показано, что способы, направленные на структурированное предварительное кодирование кодовых книг, могут достигать близких к оптимальным характеристик предварительного кодирования MIMO, требуя достаточно малого количества битов для обратной связи.
Центральным элементом способов, направленных на структурированное предварительное кодирование MIMO, является разработка кодовых книг на основе унитарных матриц. Предпочтительно, такие кодовые книги строятся таким образом, чтобы матрицы, или кодовые слова, которые образуют кодовую книгу, распределялись в грассмановском многообразии максимально равномерно. В математике грассманианом называют пространство из всех k-мерных подпространств n-мерного векторного пространства V. Одним из подходов к построению оптимальной кодовой книги является подход, который способен лучше максимизировать минимальное хордальное расстояние для кодовой книги. Используемый здесь термин «хордальное расстояние» относится к расстоянию между матрицами или кодовыми словами в многомерном пространстве, содержащем грассмановское многообразие.
В то время как кодовая книга, сформированная на основе случайного вычисления и распределения кодовых слов внутри грассмановского многообразия, представляет собой наилучшую возможную кодовую книгу в смысле минимального хордального расстояния, на практике невозможно построить такую кодовую книгу для систем с большим количеством передающих антенн и пространственных потоков. С учетом этого ограничения был предложен блочно-циркулянтный способ построения, также называемый способом построения Хохвальда (Hochwald), в качестве систематического способа построения, который позволяет избежать вычислительных затрат способа прямого случайного поиска. Способ Хохвальда предоставляет кодовые книги, близкие к оптимальным, которые способствуют эффективному хранению и извлечению кодовых слов, содержащихся в них, что является следствием неинтенсивной в вычислительном плане параметризации кодовой книги. Кроме того, блочно-циркулянтная структура расстояния также делает возможным так называемый способ подпространственного слежения в процессе предварительного кодирования на основе MIMO-OFDM (Orthogonal Frequency Division Multiplexing - мультиплексирование с ортогональным частотным разделением). В схеме Хохвальда кодовая книга полностью определена, когда предоставлены первое кодовое слово Рl и диагональная матрица Q поворота. Другие кодовые слова в кодовой книге задаются следующим выражением (здесь 2L - количество элементов кодовой книги, и каждое кодовое слово является матрицей размера NtxMt):

где Q - диагональная матрица, полностью параметризуемая целочисленным вектором 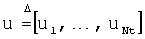 :
:
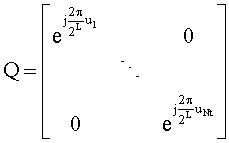
Кроме того, при этом построении первое кодовое слово P1 выбирается в виде подматрицы Nt×Mt матрицы DNt дискретного преобразования Фурье (DFT - Discrete Fourier Transform) размерностью Nt×Nt, в которой элемент (m, n) определяется как 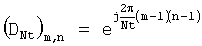 ,
,
где 1≤m, n≤Nt. Если обозначить с-ый столбец матрицы DN как dc, то первое кодовое слово будет набором из Mt столбцов, параметризованных набором индексов столбцов 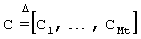 ,
,
то есть P1=[dc1, …, dCNt]. В таблице 1, приведенной ниже, для примера показан выбор 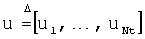 и
и 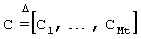 для различного числа передающих антенн Nt, от двух до четырех, и числа пространственно мультиплексированных потоков данных Mt, при условии, что Nt>Mt. Отметим, что выбор величины 2L, т.е. размера кодовой книги, является результатом компромисса между рабочими характеристиками и количеством требуемых битов обратной связи.
для различного числа передающих антенн Nt, от двух до четырех, и числа пространственно мультиплексированных потоков данных Mt, при условии, что Nt>Mt. Отметим, что выбор величины 2L, т.е. размера кодовой книги, является результатом компромисса между рабочими характеристиками и количеством требуемых битов обратной связи.
 Индексы столбцов
Индексы столбцов
Вектор поворота
Отметим, что каждый индекс столбца 0<=c<=Nt-1, с=[0] обозначает первый столбец матрицы D дискретного преобразования Фурье, с=[1] обозначает второй столбец матрицы D и т.д.
К сожалению, кодовые книги, сформированные из кодовых слов, которые генерированы в соответствии со способом построения Хохвальда, подвержены различным нежелательным ограничениям. Среди этих ограничений есть требование, чтобы энергии любых двух элементов в пределах одного матричного кодового слова были равными, и суммарная энергия каждого отдельного кодового слова была равна суммарной энергии каждого другого отдельного кодового слова. Хотя такие ограничения допускают прямое применение способа построения Хохвальда, их принудительное применение приводит к такому распределению кодовых слов кодовой книги в грассмановском многообразии, которое может быть улучшено. Поэтому было бы предпочтительно создать способ выполнения построения Хохвальда, который не имел бы ограничений известного способа.
Сущность изобретения
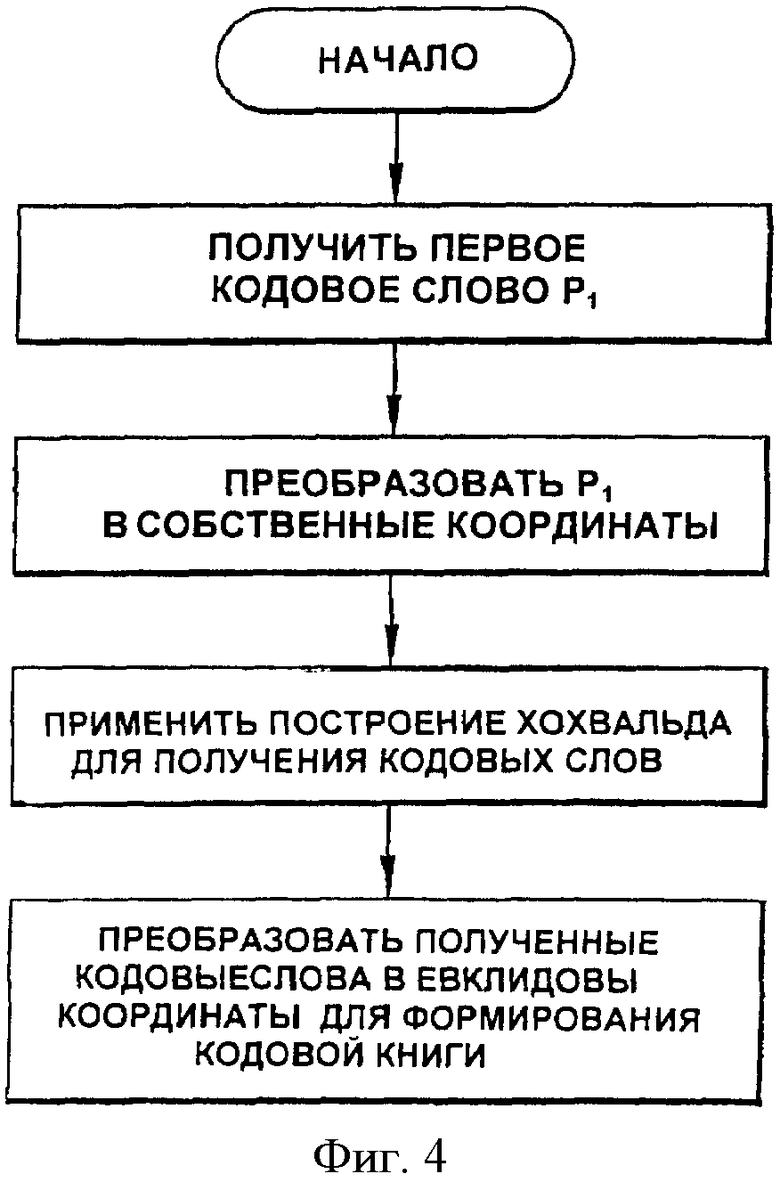
В соответствии с примером осуществления настоящего изобретения способ формирования кодовой книги включает получение первого кодового слова P1 в евклидовых координатах, преобразование первого кодового слова в собственные координаты, применение построения Хохвальда к первому кодовому слову в собственных координатах для получения множества кодовых слов в собственных координатах и преобразование множества кодовых слов в собственных координатах в множество кодовых слов в евклидовых координатах для формирования кодовой книги.
В соответствии с другим примером осуществления изобретения структура данных, реализованная на материальном носителе, содержит первое кодовое слово P1 и множество кодовых слов Pl, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом P l=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица.
В соответствии с другим примером осуществления изобретения мобильная станция содержит средства для хранения кодовой книги, при этом кодовая книга содержит первое кодовое слово P1 и множество кодовых слов P l, l=2…2L, где 2L - количество кодовых слов множества, при этом P l=VQlVHP1, где V - унитарная матрица, которая содержит собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, и средства доступа к первому кодовому слову и множеству кодовых слов.
В соответствии с еще одним примером осуществления изобретения базовая станция содержит средства для хранения кодовой книги, при этом кодовая книга содержит первое кодовое слово P1 и множество кодовых слов P l, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом P l=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, и средства доступа к первому кодовому слову и множеству кодовых слов.
В соответствии с еще одним примером осуществления изобретения предлагается программа из машиночитаемых инструкций, материально реализованная на носителе информации и исполняемая процессором цифровой обработки данных для выполнения действий, направленных на передачу информации, при этом действия включают получение информационной матрицы и доступ к кодовой книге для выбора одного из множества индексов, который соответствует информационной матрице, а кодовая книга содержит первое кодовое слово P1 и множество кодовых слов P l, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом P l=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, причем каждое из первого кодового слова и множества кодовых слов соответствует единственному индексу из множества индексов, и передачу этого индекса из указанного множества индексов.
В соответствии с еще одним примером осуществления изобретения предлагается программа из машиночитаемых инструкций, материально реализованная на носителе информации и исполняемая процессором цифровой обработки данных для выполнения действий, направленных на прием информации, при этом действия включают прием индекса и доступ к кодовой книге для выбора одного из множества кодовых слов, которое соответствует индексу, а кодовая книга содержит первое кодовое слово P1 и множество кодовых слов P l, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом P l=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, причем каждое из первого кодового слова и множества кодовых слов соответствует единственному индексу из множества индексов.
Краткое описание чертежей
Фиг.1 - алгоритм варианта осуществления настоящего изобретения.
Фиг.2 - иллюстрация типичного распределения энергии между кодовыми словами кодовой книги в собственном и евклидовом пространстве.
Фиг.3 - схема базовой станции и мобильной станции, которые используют кодовую книгу.
Фиг.4 - алгоритм способа согласно изобретению.
Подробное описание
В примере осуществления настоящего изобретения представлен способ на основе преобразования собственных координат для улучшения минимального хордального расстояния для кодовых книг, которые формируют с помощью способа построения Хохвальда.
Это частично достигается путем ослабления по меньшей мере одного ограничения построения Хохвальда, чтобы обеспечить более близкое к оптимальному распределение кодовых слов в многомерном грассмановском многообразии. Как отмечалось ранее, использование способа построения Хохвальда приводит к кодовой книге, в которой распределение энергии среди различных элементов в каждом отдельном матричном кодовом слове равномерно и фиксировано от одного матричного кодового слова к другому. То есть для любых двух матричных кодовых слов Pl1 и Pl2 элемент (i, j) каждого кодового слова имеет одинаковую энергию, т.е.
I|(Pl1)i,j|2=|(Pl2)i,j|2.
В примере осуществления настоящего изобретения это ограничение снимается, чтобы обеспечить способ формирования кодовых книг с лучшими характеристиками хордального расстояния. А именно, ограничение ослабляется так, чтобы получить кодовые книги, в которых минимальное хордальное расстояние более близко к максимуму по сравнению со случаями, в которых это ограничение не ослабляется. Изложенный здесь способ преобразования собственных координат устраняет отмеченное выше ограничение, используя преимущество свойства сдвига энергии, присущее преобразованиям собственных координат, в то же время сохраняя выгодные возможности построения Хохвальда, например блочно-циркулянтное распределение расстояния кодовых слов и простую параметризацию.
В последующем описании примера осуществления изобретения делаются ссылки на сопроводительные чертежи, которые образуют часть описания и на которых показан в качестве иллюстрации пример того, как может быть осуществлено изобретение. Надо понимать, что можно использовать и другие примеры, поскольку в рамках настоящего изобретения могут быть сделаны структурные и функциональные изменения.
Как упоминалось выше, пример осуществления настоящего изобретения раскрывает способ, который использует преобразование собственных координат для предоставления систематического пути устранения ограничения, связанного с фиксированным распределением энергии в построении Хохвальда. Такой способ делает ближе к максимуму минимальное хордальное расстояние кодовой книги, которая построена согласно этому способу.
Из уравнения (1) очевидно, что все остальные кодовые слова P l=QlP1 для l=2, …, 2L выводятся из первого кодового слова Р1. Это наблюдение делает очевидным преимущество, которое можно получить от устранения ограничения на фиксированное распределение энергии, позволяя кодовому слову P1 быть произвольной унитарной матрицей, а не столбцами матрицы дискретного преобразования Фурье, как определено в построении Хохвальда.
Однако устранение такого ограничения полностью не устраняет недостатки построения Хохвальда, так как распределение энергии по-прежнему фиксировано от одного кодового слова к другому. Это так, даже если энергия более не распределяется равномерно в пределах одного кодового слова, как в случае построения Хохвальда. Поэтому замены первого кодового слова P1 на произвольную унитарную матрицу недостаточно, чтобы наиболее выгодно оптимизировать построение кодовой книги.
Поэтому в примере осуществления настоящего изобретения используется преобразование собственных координат для достижения изменений в распределении энергии среди различных матричных кодовых слов. Во-первых, так как Q является диагональной матрицей, ее можно представить в виде части собственного разложения некоторой матрицы S:

где V - это унитарная матрица размером NtxNt, которая состоит из результирующих собственных векторов. Далее матрицу Q можно заменить матрицей S в уравнении (1), чтобы прийти к усовершенствованному построению Хохвальда:
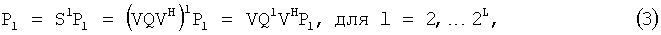
где параметризация матрицы V собственных векторов обсуждается ниже более подробно.
Обратимся к фиг.1, где проиллюстрирован алгоритм примера осуществления усовершенствованного построения Хохвальда согласно настоящему изобретению. Сначала первое кодовое слово P1 преобразуют в первое кодовое слово в собственных координатах в блоке 11 путем применения эрмитовой собственной матрицы VH к P1, чтобы получить VHP1 Затем в блоке 13 построение Хохвальда применяют к первому кодовому слову в собственных координатах, VHP1, чтобы получить l-ое кодовое слово в собственных координатах, QlVHP1. Затем l-ое кодовое слово в собственных координатах преобразуют обратно в евклидовы координаты с помощью матрицы V в блоке 15, чтобы сформировать каждое окончательное кодовое слово как Pl=VQlVHP1.
Поскольку эта методика применяет построение Хохвальда к первому кодовому слову, преобразованному в собственную систему координат, промежуточные кодовые слова QlVHP1 для l=1, …, L все еще имеют то же распределение энергии в собственных координатах, которое определено V. Однако окончательные кодовые слова
Pl=VQlVHP1 будут иметь другие распределения энергии после преобразования в евклидовы координаты. Для векторных кодовых книг иногда удобно удалить фазу первого элемента в каждой кодовой книге при помощи выражения 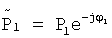 для l=2, …, 2L, где φl - фаза первого элемента P
l. В этом альтернативном представлении кодовой книги, которое является точным эквивалентом исходной кодовой книги, первый элемент каждого кодового слова вещественен.
для l=2, …, 2L, где φl - фаза первого элемента P
l. В этом альтернативном представлении кодовой книги, которое является точным эквивалентом исходной кодовой книги, первый элемент каждого кодового слова вещественен.
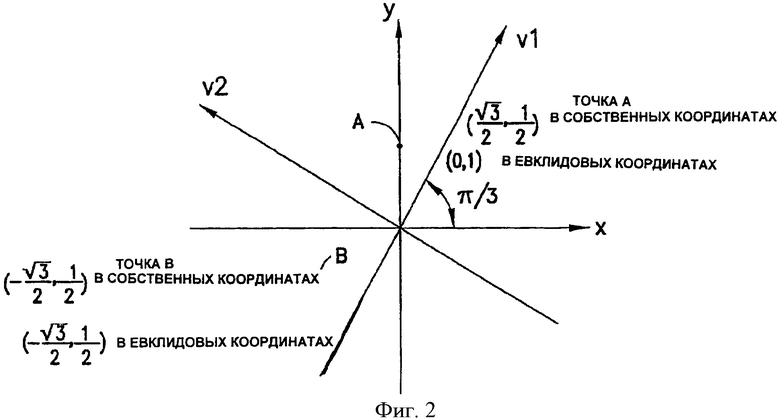
На фиг.2 проиллюстрирован типичный вид различных распределений энергии среди элементов кодового слова, вызванный свойствами сдвига энергии, присущими преобразованию собственных координат. Точки А и В являются элементами в пределах одного кодового слова, полученного в соответствии с примером осуществления настоящего изобретения. Оси x и y представляют евклидово пространство, а собственные вектора v1 и v2 представляют собственное пространство. Координаты точки А равны ((sqrt (3)/2), 1/2) в собственном пространстве и (0, 1) в евклидовом пространстве. Подобным же образом координаты точки В равны (-(sqrt (3)/2), 1/2) в собственном пространстве и (-(sqrt(3)/2), -1/2) в евклидовом пространстве. В результате видно, что распределение энергии точек А и В одинаково в пространстве собственных координат, которое задано посредством собственных векторов v1 и v2, но различно в пространстве евклидовых координат.
Остается показать как параметризуется собственная матрица V. Здесь мы дополнительно наложим структуру Хаусхолдера (Householder) на V, чтобы обеспечить очень простую параметризацию V, то есть:

где w=а-e1 и e1=[1 0…0]Т и 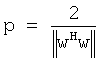 . Здесь I - единичная матрица, а надстрочный индекс Н обозначает эрмитово сопряжение. С такой дополнительной параметризацией вектора а кодовая книга теперь однозначно определена, когда получены три вектора u, с и а. Обозначим эту кодовую книгу как Р(u, с, а). Поиск оптимальной кодовой книги, которая параметризована тремя этими векторами, описывается следующим уравнением:
. Здесь I - единичная матрица, а надстрочный индекс Н обозначает эрмитово сопряжение. С такой дополнительной параметризацией вектора а кодовая книга теперь однозначно определена, когда получены три вектора u, с и а. Обозначим эту кодовую книгу как Р(u, с, а). Поиск оптимальной кодовой книги, которая параметризована тремя этими векторами, описывается следующим уравнением:
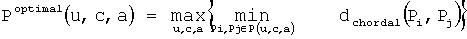
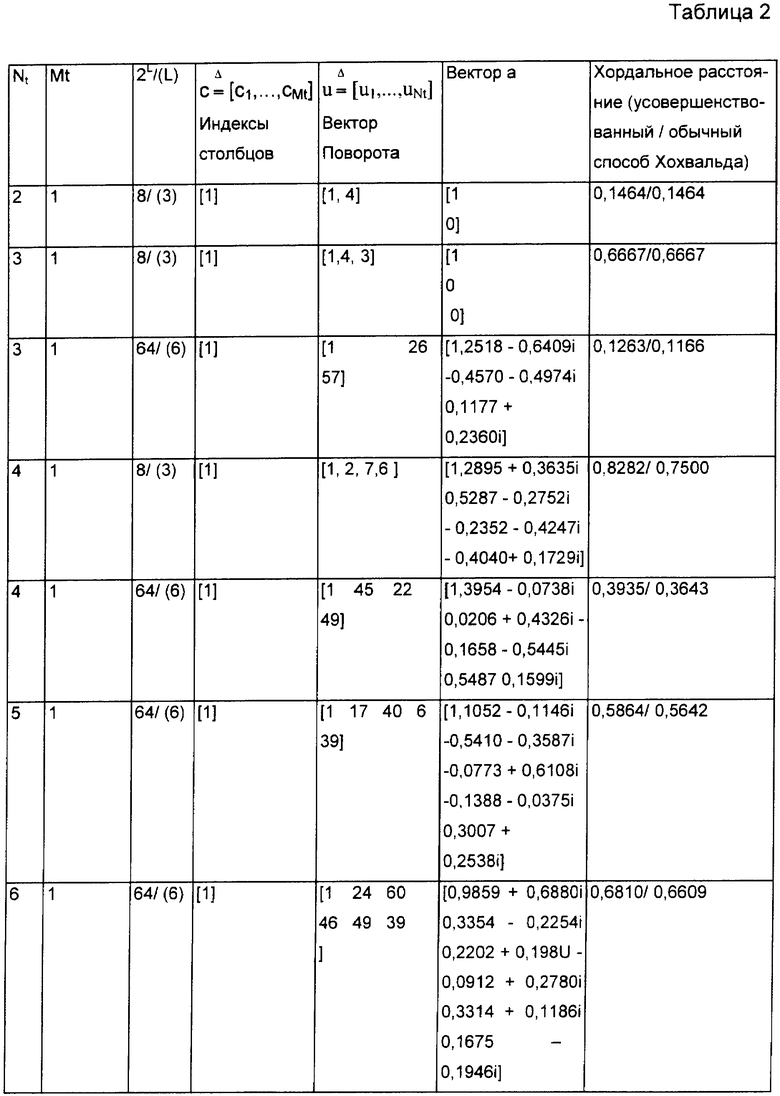
Здесь dchordal(Pi, Pj) - хордальное расстояние между двумя кодовыми словами Pi, Pj. Оптимальные кодовые книги для разных конфигураций антенн показаны в таблице 2. Таблица 2 иллюстрирует эффективность способа согласно настоящему изобретению, показывая параметры нескольких кодовых книг, которые используют описанное здесь усовершенствованное построение Хохвальда. Заметим, что первое кодовое слово Р1 остается сформированным в виде столбцов дискретного преобразования Фурье, как и в случае обычного применения построения Хохвальда. Собственный вектор "а" добавлен в качестве дополнительного параметра. В примере осуществления настоящего изобретения практически выполняется совместная оптимизация вектора а и первого кодового слова P1, которое, как отмечалось выше, является произвольной унитарной матрицей. Особый интерес имеет последний столбец, где указано максимальное минимальное хордальное расстояние между кодовыми словами кодовой книги, которая использует усовершенствованное построение Хохвальда согласно настоящему изобретению в сравнении со стандартным построением Хохвальда. Во всех случаях минимальное хордальное расстояние улучшается вследствие осуществления способа согласно настоящему изобретению.
Отметим, что каждый индекс столбца 0<=c<=Nt-1, с=[0] означает первый столбец матрицы D дискретного преобразования Фурье, с=[1] означает второй столбец матрицы D и т.д.
Отметим, что в таблице 2 вектор а точно определен как состоящий из вещественной и мнимой части. Настоящее приложение распространяется на все реализации вектора а, а также на отклонения от значений вектора а, намеренные либо случайные, которые могли бы возникнуть в процессе работы, такие, что реализованный вектор а находится достаточно близко к значению, указанному выше, чтобы иметь возможность использовать кодовую книгу.
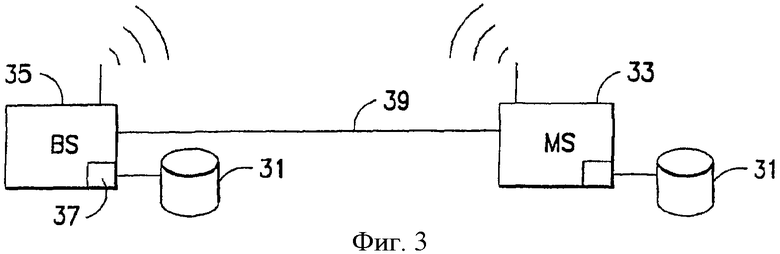
После вычисления кодовая книга, построенная в соответствии с примером осуществления настоящего изобретения, может использоваться так, как проиллюстрировано на фиг.3. Базовая станция 35 связывается беспроводным способом с мобильной станцией 33. Мобильная станция 33 является любым мобильным устройством, способным к беспроводной связи, которое включает, но этим не ограничивается, беспроводные телефоны, карманные персональные компьютеры (КПК), персональные вычислительные устройства и тому подобное. И базовая станция 35, и мобильная станция 33 образованы из цифрового сигнального процессора 37 (DSP) или другого вида процессора для обработки данных для доступа к цифровым данным и работы с ними. DSP 37 соединен с устройством 31 памяти, которое способно хранить цифровые данные. Кодовая книга согласно настоящему изобретению предпочтительно хранится в каждом устройстве 31 памяти, которое индивидуально соединено с базовой станцией 35 и мобильной станцией 33.
DSP 37 мобильной станции 33 выбирает индекс для кодового слова, соответствующего информации, которую мобильная станция 33 желает передать базовой станции 35. Примеры вида данных, которые соответствуют кодовым словам кодовой книги, включают, но этим не ограничиваются, канальную информацию в виде канальных матриц, подтверждение приема данных, весовые матрицы предварительного кодирования и результаты измерений отношения сигнал/помеха на пространственных потоках. Предпочтительно, индекс является строкой данных, состоящей из некоторого количества двоичных битов b. Так как каждое кодовое слово соответствует одному и только одному индексу, максимальное количество кодовых слов в кодовой книге равно 2b.
В типичном случае не будет существовать кодового слова, которое будет точно равно информации, которую нужно передать. Обычно такая информация представляется в виде матрицы так, чтобы сформировать информационную матрицу. Именно поэтому методика настоящего изобретения помогает равномерно распределять или, более точно, максимизировать минимальное хордальное расстояние между кодовыми словами. При этом можно передать информацию, посылая индекс кодового слова, которое ближе всего в многомерном грассмановском многообразии к информационной матрице, такой как, например, канальная матрица, с минимальной потерей точности. DSP 37 мобильной станции работает для выполнения вычисления или вычислений, предписанных программно или аппаратно кодированной логикой, чтобы выбрать из кодовой книги кодовое слово, которое ближе всего к информации, которую нужно передать, для получения индекса, который соответствует выбранному таким образом кодовому слову.
Полученный таким образом индекс обычно передается мобильной станцией 33 через по меньшей мере одну передающую антенну 41 по контуру 39 обратной связи на базовую станцию 35. Базовая станция 35 принимает переданный индекс с помощью по меньшей мере одной приемной антенны 43. Как отмечалось, базовая станция 35 также оборудована DSP 37, который соединен с запоминающим устройством 31, в котором хранится кодовая книга 45. Используя принятый индекс, DSP 37 базовой станции работает посредством выполнения программно или аппаратно кодированной логики для того, чтобы извлечь соответствующее кодовое слово из кодовой книги 45.
Как отмечалось выше, это изобретение можно осуществить с помощью компьютерного программного обеспечения, исполняемого процессором для обработки данных мобильной станции 33, или с помощью аппаратных схем, или с помощью сочетания программного обеспечения и аппаратных схем. Мобильная станция может быть одним из компонентов беспроводной системы связи. Дополнительно в этом отношении нужно отметить, что различные блоки логического алгоритма, показанного на фиг.1, могут представлять этапы работы программы или взаимосвязанные логические цепи, блоки и функции или сочетание этапов работы программы и логических цепей, блоков и функций для выполнения определенных задач.
На фиг.4 проиллюстрирован алгоритм примера осуществления способа согласно изобретению.
Несмотря на то, что описание было дано в контексте конкретных примеров, специалистам должно быть очевидно, что может иметь место ряд модификаций и различных изменений в этом описании. Таким образом, в то время как изобретение было детально показано и описано в отношении одного или нескольких предпочтительных вариантов его осуществления, специалистам понятно, что возможны определенные модификации или изменения вида и конфигурации без выхода за рамки изобретения.
Изобретение относится к беспроводным системам связи, более конкретно, варианты осуществления изобретения имеют отношение к созданию и использованию кодовых книг на основе унитарных матриц. Способ формирования кодовой книги включает получение первого кодового слова P1 в евклидовых координатах, преобразование первого кодового слова в собственные координаты, применение построения Хохвальда к первому кодовому слову в собственных координатах для получения множества кодовых слов в собственных координатах и преобразование множества кодовых слов в собственных координатах в множество кодовых слов в евклидовых координатах для формирования кодовой книги. Технический результат - обеспечение формирования кодовых книг, близких к оптимальным, которые способствуют эффективному хранению и извлечению кодовых слов. 4 н. и 18 з.п. ф-лы, 2 табл., 4 ил.
1. Способ формирования кодовой книги, включающий:
получение первого кодового слова P1 в евклидовых координатах;
преобразование указанного первого кодового слова в собственные координаты;
применение построения Хохвальда к указанному первому кодовому слову в собственных координатах для получения множества кодовых слов в собственных координатах; и
преобразование указанного множества кодовых слов в собственных координатах в множество кодовых слов в евклидовых координатах для формирования указанной кодовой книги.
2. Способ по п.1, в котором указанное первое кодовое слово является унитарной матрицей.
3. Способ по п.1, в котором преобразование указанного первого кодового слова включает применение эрмитовой собственной матрицы VH для получения VHP1, где V - унитарная матрица размером Nt×Nt, a P1 - матрица размером Nt×Mt.
4. Способ по п.3, в котором указанное множество кодовых слов в собственных координатах задают как QlVHP1, где l=2…2L, 2L - число кодовых слов в указанном множестве, a Q - диагональная матрица.
5. Способ по п.4, в котором Q является частью собственного разложения матрицы S, S=VQVH, где V - унитарная матрица, содержащая собственные вектора.
6. Способ по п.5, в котором преобразование указанного множества кодовых слов в собственных координатах содержит применение указанной унитарной матрицы к каждому из указанного множества кодовых слов в собственных координатах для получения указанного множества кодовых слов в евклидовых координатах, так что Pl=VQlVHP1, где l=2…2L.
7. Способ по п.6, в котором матрицу V параметризуют как
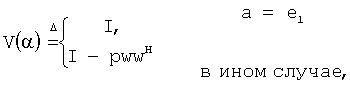
где а - вектор, w=a-e1 и e1=[1 0…0]T, 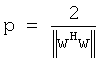 , I - единичная матрица, а надстрочный индекс Н обозначает эрмитово сопряжение.
, I - единичная матрица, а надстрочный индекс Н обозначает эрмитово сопряжение.
8. Способ по п.7, в котором первое кодовое слово P1 параметризуют как P1(c)=[dc1, …, dCNt], где с определяют как 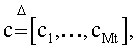
a dc1 - столбец с номером c1 матрицы дискретного преобразования Фурье DNt размером Nt×Nt, в которой элемент (m, n) определяют как 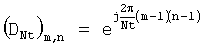
где 1≤m, n≤Nt.
9. Способ по п.7, в котором матрицу Q поворота параметризуют как
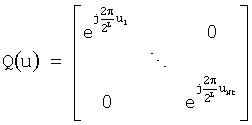 , где и определяют как
, где и определяют как 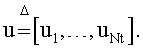
10. Способ по п.7, в котором указанный собственный вектор "а" задают как [1,2518-0,6409i, -0,4570-0,4974i, 0,1177+0,2360i], "с" задают как [1], "u" задают как [1, 26, 57] для шестибитной кодовой книги, где количество пространственных потоков равно 1, а количество передающих антенн равно 3.
11. Способ по п.7, в котором указанный собственный вектор "а" задают как [1,3954-0,0738i, 0,0206+_0,4326i, -0,1658-0,5445i, 0,5487-0,1599i], "с" задают как [1], "и" задают как [1, 45, 22, 49] для шестибитной кодовой книги, где количество пространственных потоков равно 1 и количество передающих антенн равно 4.
12. Способ по п.3, в котором параметр оптимальной кодовой книги формируют как
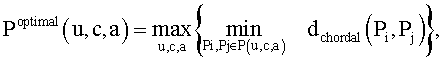
где dchordal(Pi, Pj) - хордальное расстояние между двумя кодовыми словами Pi, Pj.
13. Устройство для хранения множества кодовых слов и для доступа к ним, содержащее:
средство для хранения кодовой книги, содержащей:
первое кодовое слово P1 и
множество кодовых слов Pl, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом Pl=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица; и
средства для доступа к указанному первому кодовому слову и указанному множеству кодовых слов.
14. Устройство по п.13, дополнительно содержащее множество индексов, каждый из которых соответствует отдельному кодовому слову из указанных первого кодового слова и множества кодовых слов.
15. Устройство по п.13, содержащее средство для передачи, по меньшей мере, одного индекса из указанного множества индексов.
16. Устройство по п.13, представляющее собой мобильную станцию.
17. Устройство по п.13, представляющее собой компонент беспроводной сети.
18. Машиночитаемый носитель информации, содержащий машиночитаемые инструкции, исполняемые посредством процессора цифровой обработки данных для выполнения действий, направленных на передачу информации, которые включают:
получение информационной матрицы;
доступ к кодовой книге для выбора одного из множества индексов, соответствующего указанной информационной матрице, при этом указанная кодовая книга содержит:
первое кодовое слово P1 и
множество кодовых слов Pl, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом Pl=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, причем каждое из указанных первого кодового слова и множества кодовых слов соответствует единственному индексу из указанного множества индексов; и
передачу указанного индекса из указанного множества индексов.
19. Машиночитаемый носитель по п.18, в которой указанная информационная матрица является канальной матрицей.
20. Машиночитаемый носитель по п.18, который располагается в компоненте системы беспроводной связи.
21. Машиночитаемый носитель информации, содержащий машиночитаемые инструкции, исполняемые посредством процессора цифровой обработки данных для выполнения действий, направленных на прием информации, которые включают:
прием индекса и
доступ к кодовой книге для выбора одного из множества кодовых слов, соответствующего указанному индексу, при этом указанная кодовая книга содержит:
первое кодовое слово P1 и
множество кодовых слов Pl, l=2…2L, где 2L - число кодовых слов в указанном множестве, при этом Pl=VQlVHP1, где V - унитарная матрица, содержащая собственные вектора, Q - диагональная матрица и VH - эрмитова собственная матрица, причем каждое из указанных первого кодового слова и множества кодовых слов соответствует единственному индексу из указанного множества индексов.
22. Машиночитаемый носитель по п.21, который располагается в компоненте системы беспроводной связи.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| ПОИСК В ГЛУБИНУ ПО АЛГЕБРАИЧЕСКОЙ ШИФРОВАЛЬНОЙ КНИГЕ ДЛЯ БЫСТРОГО КОДИРОВАНИЯ РЕЧИ | 1996 |
|
RU2175454C2 |
| СНИЖЕНИЕ РАЗРЕЖЕННОСТИ В КОДИРОВАННЫХ РЕЧЕВЫХ СИГНАЛАХ | 1998 |
|
RU2239239C2 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
Авторы
Даты
2009-12-20—Публикация
2006-01-05—Подача