Область техники, к которой относится изобретение
Настоящее изобретение относится к способу для передачи управляющей информации нисходящей линии связи и к способу для формирования кодового слова для нее.
Уровень техники
Из основных правил теорий абсолютных кодов далее поясняются некоторые вещи, необходимые для описания настоящего изобретения.
Когда типичный двоичный код коррекции ошибок представляется как [n, k, d], "n" означает число битов кодированного кодового слова, "k" означает число информационных битов перед кодированием, а "d" означает минимальное значение из расстояний между кодовыми словами. Здесь, поскольку кодовое слово является двоичным кодом, длина кодового слова составляет 2n, а общее число кодированных кодовых слов составляет 2k. С другой стороны, двоичный код коррекции ошибок для удобства может быть выражен просто как код [n, k].
В дальнейшем в этом документе "n", "k" и "d" имеют вышеупомянутые значения, если не заявлено иное.
Кодовая скорость R задается как значение, делящее число информационных битов на число битов кодового слова (т.е. R=k/n).
Расстояние Хэмминга - это число битов, соответствующие битовые значения которых различаются в двоичных кодах, имеющих идентичное число битов. Если расстояние Хэмминга "d" равно или больше (2a+1), ровно "a" ошибок может быть скорректировано. Например, два кодовых слова - это "101011" и "110010", расстояние Хэмминга между этими двумя кодовыми словами составляет 3, и одна ошибка может быть скорректирована.
Минимальное значение из расстояний между любыми двумя кодовыми словами, принадлежащими коду, задается как минимальное расстояние. Минимальное расстояние - это один из важных показателей для того, чтобы оценивать производительность кода. Вышеуказанное расстояние Хэмминга может использоваться в качестве расстояния между двумя кодовыми словами. По мере того как расстояние между кодовыми словами, формируемыми через процесс кодирования, становится больше, поскольку вероятность того, что соответствующее кодовое слово, как определяется, является отличающимся кодовым словом, становится меньшей, производительность кодирования повышается. Производительность кода определяется посредством расстояния между кодовыми словами, имеющими самую плохую производительность, т.е. минимального расстояния между кодовыми словами. Следовательно, код, в котором минимальное расстояние максимизировано, демонстрирует хорошую производительность.
Между тем, система 3GPP LTE (стандарт долгосрочного развития Партнерского проекта третьего поколения) предлагает, чтобы информация, указывающая формат канала управления в ходе передачи управляющей информации, передавалась через физический канал индикатора формата управления (PCFICH). PCFICH требует передавать код, имеющий очень низкую кодовую скорость, чтобы минимизировать возникновение ошибок в ходе передачи, поскольку информация о формате, передающем управляющую информацию, передается посредством него.
Тем не менее, при формировании кода с большой длиной, имеющего очень низкую кодовую скорость, трудно задавать минимальное расстояние между кодовыми словами, равным максимальному значению.
Сущность изобретения
Техническая задача
Задачей настоящего изобретения, разработанного для того, чтобы решить проблему, является предоставление способа составления кода так, что минимальное расстояние между кодами максимизировано, и одновременного формирования кода с большой длиной, имеющего низкую кодовую скорость, и способа передачи управляющего сигнала с использованием его.
Для этой задачи код с большой длиной формируется посредством повторения абсолютного кода. Когда код заранее определенной длины не может быть сформирован посредством простого повторения абсолютного кода, соответствующая корректировка выполняется для того, чтобы формировать код, имеющий заранее определенную длину, при одновременном удовлетворении условия, что минимальное расстояние между кодами максимизировано.
Другой задачей настоящего изобретения является предоставление способа передачи управляющей информации нисходящей линии связи с использованием кода, формируемого посредством вышеописанного способа.
Техническое решение
Задача настоящего изобретения может решаться посредством предоставления способа передачи управляющей информации через нисходящую линию связи посредством системы. Способ включает в себя: передачу управляющей информации через канал управления нисходящей линии связи; и передачу информации о числе символов OFDM (мультиплексирование с ортогональным частотным разделением каналов), занимаемых управляющей информацией в канале управления нисходящей линии связи, с использованием заданного кода, при этом заданный код - это одно из следующего:
(0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1),
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0),
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1) и
(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
согласно информации о числе OFDM-символов, занимаемых посредством управляющей информации.
Информацией о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи, может быть индикатор формата управления (CFI), и информация о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи, может передаваться через физический канал индикатора формата управления (PCFICH). Заданный код может быть (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, занимаемых посредством управляющей информации, равно 1, (1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, занимаемых посредством управляющей информации, равно 2, и (1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, занимаемых посредством управляющей информации, равно 3.
В другом аспекте настоящего изобретения, предусмотрен способ приема управляющей информации через нисходящую линию связи посредством абонентского устройства (UE). Способ включает в себя: прием информации о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи, с использованием заданного кода; и прием управляющей информации через канал управления нисходящей линии связи с использованием заданного кода, при этом заданный код - это одно из следующего:
(0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1),
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0),
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1) и
(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
согласно числу OFDM-символов, занимаемых посредством управляющей информации.
В дополнительном аспекте настоящего изобретения, предусмотрен способ формирования кодового слова. Способ включает в себя: получение информации о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи; и формирование кодового слова согласно полученной информации, при этом кодовое слово формируется посредством повторения любого из симплексных кодов (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) 11 раз и прореживания ("прокалывания") последнего одного бита.
В еще одном другом аспекте настоящего изобретения, предусмотрен способ формирования кодового слова. Способ включает в себя: получение информации о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи; и формирование кодового слова согласно полученной информации, при этом кодовое слово формируется посредством повторения любого из симплексных кодов (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) 9 раз и вставки любого из кодов Хемминга (0, 1, 1, 0, 1), (1, 0, 1, 1, 0), (1, 1, 0, 1, 1) и (0, 0, 0, 0, 0).
В еще одном другом аспекте настоящего изобретения, предусмотрен способ формирования кодового слова. Способ включает в себя: получение информации о числе OFDM-символов, занимаемых посредством управляющей информации в канале управления нисходящей линии связи; и формирование кодового слова согласно полученной информации, при этом полученная информация выражается как 2 информационных бита, и кодовое слово формируется посредством повторения любого из симплексных кодов (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) 10 раз и вставки информационных битов.
Преимущества
Согласно аспектам настоящего изобретения, длинный код, имеющий низкую кодовую скорость, может быть сформирован простым способом, при этом минимальное расстояние между кодами максимизировано.
Кроме того, управляющая информация может передаваться с низкой частотой ошибок посредством представления информации о числе OFDM-символов, занимаемых посредством управляющей информации, с использованием сформированного кода.
Описание чертежей
Прилагаемые чертежи, которые включены для того, чтобы обеспечивать дополнительное понимание изобретения, иллюстрируют варианты осуществления изобретения и вместе с описанием служат для того, чтобы пояснять принципы настоящего изобретения.
На чертежах:
Фиг.1 является схемой для пояснения процесса формирования кода с большой длиной, имеющего низкую кодовую скорость, согласно примерному варианту осуществления настоящего изобретения.
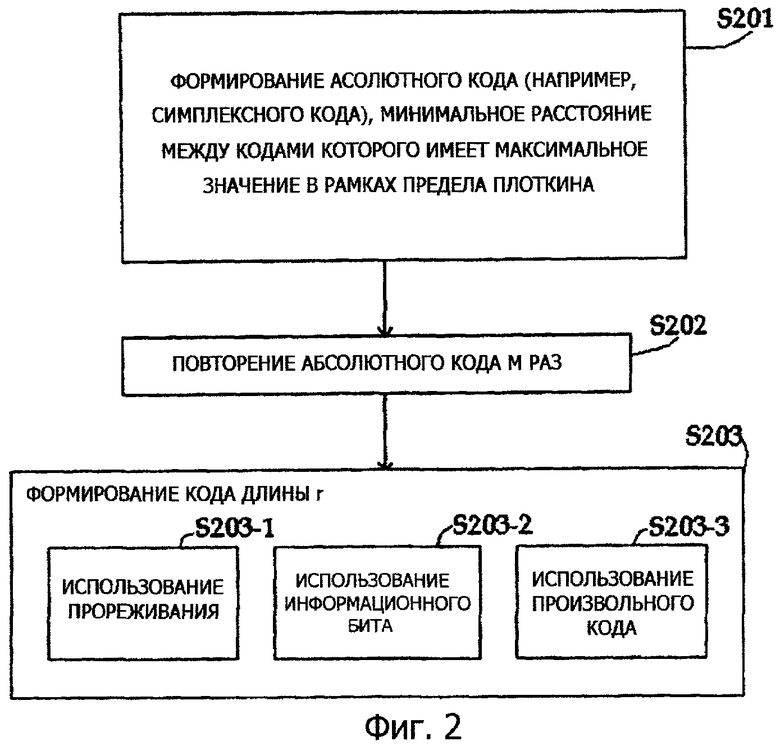
Фиг.2 является блок-схемой последовательности операций способа, схематично иллюстрирующей процесс формирования кода с большой длиной, имеющего низкую кодовую скорость, согласно примерному варианту осуществления настоящего изобретения.
Фиг.3a-3c являются схемами для пояснения взаимосвязи между позицией прореживания симплексного кода и информационным битом согласно примерному варианту осуществления настоящего изобретения.
Фиг.4a-4c являются схемами для пояснения примеров построчного или постолбцового преобразования абсолютного кода с точки зрения преобразования с помощью информационного бита согласно примерному варианту осуществления настоящего изобретения.
Фиг.5a-5b являются схемами для пояснения процесса передачи управляющей информации с использованием кода [32, 2] согласно примерному варианту осуществления настоящего изобретения.
Оптимальный режим осуществления изобретения
Далее подробно описаны предпочтительные варианты осуществления настоящего изобретения со ссылками на прилагаемые чертежи. Подробное описание, которое приведено ниже со ссылкой на прилагаемые чертежи, имеет намерение пояснять примерные варианты осуществления настоящего изобретения вместо того, чтобы показывать единственные варианты осуществления, которые могут быть реализованы согласно изобретению.
Последующее описание предоставляет конкретные подробности для полного понимания вариантов осуществления изобретения. Тем не менее, специалисты в данной области техники должны понимать, что изобретение может осуществляться на практике без этих подробностей.
В других случаях, известные структуры и функции не описаны подробно или могут быть показаны в форме блок-схемы, чтобы исключать излишнее затруднение понимания описания вариантов осуществления изобретения. Где бы то ни было, одинаковые номера ссылок используются на чертежах для того, чтобы ссылаться на одинаковые или аналогичные элементы. При формировании длинного кода, имеющего низкую кодовую скорость, предусмотрен способ для составления кода так, что минимальное расстояние между кодами максимизировано, и одновременного формирования длинного кода простым способом, и способ для передачи управляющего сигнала с использованием его. Для этой цели, условие, что минимальное расстояние между кодами максимизировано, рассматривается подробно.
В последующем описании настоящего изобретения принцип нормированного минимального расстояния вводится в качестве способа для сравнения различных технологий кодирования. А именно в двоичном коде коррекции ошибок [n, k, d] значение, делящее минимальное расстояние "d" на число "n" битов кодового слова, задается как нормированное минимальное расстояние, и нормированное минимальное расстояние выражается как d для удобства описания.
Таким образом, нормированное минимальное расстояние может быть выражено следующим образом:
уравнение 1
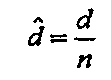
В дальнейшем в этом документе поясняется предел Плоткина, чтобы учитывать условия для задания минимального расстояния между кодами, равным максимальному значению. Подробное описание предела Плоткина раскрывается подробно в "John G. Proakis, Wiley Encyclopedia of Telecommunications, Wiley Interscience, New Jersey, 2003, vol.2, pp 929-935".
Предел Плоткина вкратце обобщается следующим образом.
Когда общий двоичный код коррекции ошибок выражается как [n, k, d], "n" означает число битов кодированного кодового слова, "k" означает число информационных битов перед кодированием, а "d" означает минимальное значение из расстояний между кодовыми словами. Вышеописанный предел Плоткина может быть выражен следующим образом:
уравнение 2

Предел Плоткина, выраженный так, как указано в уравнении 2, также может быть выражен на основе минимального расстояния d следующим образом:
уравнение 3
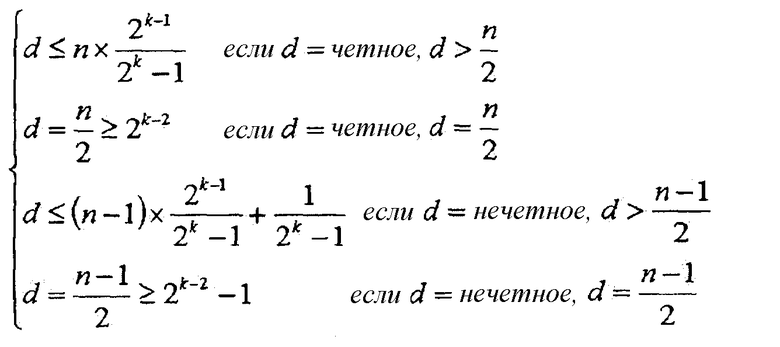
Способ для формирования кода, выражаемый, в общем, как [n, k, d], далее рассматривается в отношении вышеприведенного уравнения 3 согласно примерному варианту осуществления настоящего изобретения. Если минимальное расстояние d больше половины длины кода (т.е. d>n/2), желательно проектировать оптимальный код так, чтобы удовлетворять вышеописанному пределу Плоткина.
При этом в примерном варианте осуществления настоящего изобретения предполагается, что формируемый код имеет низкую кодовую скорость (т.е. n>2k). Когда n=2k, ортогональный код может быть сформирован, и минимальное расстояние ортогонального кода составляет n/2. Следовательно, имеет смысл считать допустимыми только следующие два случая относительно предела Плоткина при низкой кодовой скорости в этом примерном варианте осуществления настоящего изобретения.
уравнение 4
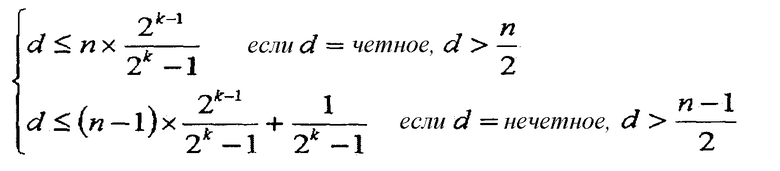
При вышеописанных условиях, указанных в уравнении 4, случаи, где минимальное расстояние d является четным числом и нечетным числом, описываются далее.
Во-первых, при условии, что минимальное расстояние d является четным числом, максимальное значение минимального расстояния d равно 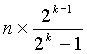 , как известно из первого выражения уравнения 4.
, как известно из первого выражения уравнения 4.
При рассмотрении нормированного минимального расстояния 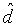 , получаемого посредством деления минимального расстояния на число битов кодового слова, максимальное значение нормированного минимального расстояния
, получаемого посредством деления минимального расстояния на число битов кодового слова, максимальное значение нормированного минимального расстояния 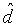 составляет
составляет 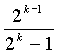 .
.
Следовательно, если полный код может быть составлен посредством повторения кода, нормированное минимальное расстояние 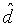 которого составляет
которого составляет 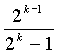 , поскольку максимальное значение минимального расстояния удовлетворяется, составленный код может быть оптимальным кодом с точки зрения минимального расстояния.
, поскольку максимальное значение минимального расстояния удовлетворяется, составленный код может быть оптимальным кодом с точки зрения минимального расстояния.
Затем, при условии, что минимальное расстояние является нечетным числом, максимальное значение минимального расстояния d составляет  , как известно из второго выражения уравнения 4. В таком случае максимальное значение нормированного минимального расстояния
, как известно из второго выражения уравнения 4. В таком случае максимальное значение нормированного минимального расстояния  становится
становится  .
.
Следовательно, когда полный код может быть составлен посредством повторения кода, нормированное минимальное расстояние 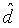 которого аппроксимируется к
которого аппроксимируется к 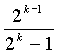 , максимальное значение минимального расстояния удовлетворяется, и составленный код становится оптимальным кодом с точки зрения минимального расстояния.
, максимальное значение минимального расстояния удовлетворяется, и составленный код становится оптимальным кодом с точки зрения минимального расстояния.
Примером кода, нормированное минимальное расстояние которого равно  , является симплексный код.
, является симплексный код.
Симплексный код имеет свойство [2k-1, k, 2k-1], и каждое нормированное расстояние между кодовыми словами является таким же, как 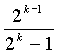 . Симплексный код может геометрически представляться как вершины в единичном кубе размерности (2k-1). Двойным кодом симплексного кода является код Хемминга, имеющий минимальное расстояние 3.
. Симплексный код может геометрически представляться как вершины в единичном кубе размерности (2k-1). Двойным кодом симплексного кода является код Хемминга, имеющий минимальное расстояние 3.
Симплексный код также известен как код сдвигового регистра максимальной длины, m-последовательность или последовательность псевдослучайного шума (PN). Когда код - это двоичный код, выраженный как +1 и -1, и число кодовых слов равно M, корреляционная функция между различными кодовыми словами является равной -1/(m-1) (где M является четным числом), или -1/M (где M является нечетным числом). В симплексном коде максимальная корреляционная функция между различными кодовыми словами среди двоичных кодов с одинаковым числом кодовых слов минимизируется.
Полный код, представляемый как [n, k, d] согласно примерному варианту осуществления настоящего изобретения, формируется следующим образом. Сначала, симплексный код [2k-1, k, 2k-1] формируется как абсолютный код и повторяется до тех пор, пока длина полного кода не становится равной n. Затем, длинный код, нормированное минимальное расстояние которого равно  , может быть сформирован.
, может быть сформирован.
В некоторых случаях, тем не менее, длина полного кода n не может быть кратной длине абсолютного кода 2k-1. В примерном варианте осуществления настоящего изобретения, предлагается способ для формирования кода, имеющего длину n, когда длина полного кода n не является кратной длине абсолютного кода 2k-1.
Фиг.1 является схемой для пояснения процесса формирования кода с большой длиной, имеющего низкую кодовую скорость, согласно примерному варианту осуществления настоящего изобретения.
Как проиллюстрировано на фиг.1, рассматривается случай, где длина кода n не является кратной 2k-1. А именно, допускается, что n=m(2k-1)+r (где m - это число повторений абсолютного кода).
Когда вышеупомянутая взаимосвязь удовлетворяется, способ для формирования кода, имеющего длину n, предлагается следующим образом.
Во-первых, симплексный код, удовлетворяющий [2k-1, k, 2k-1], формируется как абсолютный код. Затем, формируется код, повторяющий абсолютный код ровно m раз. Наконец, r битов формируются посредством прореживания симплексного кода или посредством использования любых других кодов, максимальное расстояние которых максимизировано.
В качестве способа для формирования r битов, когда k является небольшим числом, код, допускающий максимизирование минимального расстояния, может рассматриваться посредством поиска по всем возможным случаям. Общее допущение для r битов заключается в том, что r меньше длины абсолютного кода 2k-1. Тем не менее, r может быть больше 2k-1 согласно конкретному примерному варианту осуществления настоящего изобретения, который описан ниже.
После того, как абсолютный код, имеющий длину 2k-1, повторяется, процесс для корректировки заданных битов, чтобы формировать код, имеющий длину n, может быть различным, и это подробно описано далее.
Вышеописанный процесс формирования кода описан ниже с точки зрения минимального расстояния.
Сначала, предел Плоткина минимального расстояния при низкой кодовой скорости должен рассматривать только следующие два случая (где n=m(2k-1)+r).
уравнение 5

Когда длина кода n (=m(2k-1)+r) не является кратной длине абсолютного кода, способ формирования кода следующий.
То есть предусмотрена часть, составленная посредством повторения симплексного кода, удовлетворяющего [2k-1, k, 2k-1], m раз, и часть кода [r, k], получаемая посредством добавления r битов. Добавленные [r, k] могут быть составлены разными способами, и желательно удовлетворять следующему минимальному расстоянию (в дальнейшем в этом документе, называемому dr для удобства описания) от предела Плоткина.
уравнение 6

где dr имеет целочисленное значение.
Код [r, k] может быть составлен разными способами, например, посредством прореживания заданных битов в симплексном коде, используемом для повторения, или с помощью других кодов, отличных от симплексного кода. Тем не менее, при корректировке r битов важно формировать код, аппроксимирующийся к пределу Плоткина для минимального расстояния, указываемого в уравнении 6.
С другой стороны, значимый диапазон значения r рассматривается в дальнейшем.
Как описано выше, код, имеющий длину r, может быть составлен посредством прореживания заданных битов в симплексном коде, используемом для повторения, или с помощью других кодов, отличных от симплексного кода. Когда код, имеющий длину r, сформирован с использованием кода, отличного от симплексного кода, так что минимальное расстояние между кодами максимизировано, нет необходимости ограничения значения r конкретным диапазоном. Другими словами, значение r может быть меньше или больше длины абсолютного кода 2k-1. Если значение r больше 2k-1, любой код, удовлетворяющий такому условию, что минимальное расстояние между кодами максимизировано в рамках предела Плоткина, может быть сформирован.
С другой стороны, когда другой код, отличный от симплексного кода, не используется, поскольку длина кода n равна m(2k-1)+r, r меньше (2k-1). Следовательно, диапазон r варьируется согласно k. Нет необходимости рассматривать случай, где r меньше k. В этом случае, поскольку r меньше числа k битов, которые должны быть фактически переданы, используется, кодирование, выполняемое посредством добавления избыточных битов, не имеет смысла. Следовательно, значимым диапазоном r становится [k, 2k-2], если только код, отличный от симплексного кода, не используется для того, чтобы формировать код, имеющий длину r.
Тем не менее, если r равен k (т.е. r=k), тогда желательно передавать данный информационный бит (систематический бит), чтобы максимизировать минимальное расстояние.
В дальнейшем в этом документе, способ для формирования длинного кода, имеющего низкую кодовую скорость, описывается как основной вариант осуществления для удобства описания.
Фиг.2 является блок-схемой последовательности операций способа, схематично иллюстрирующей процесс формирования кода с большой длиной, имеющего низкую кодовую скорость, согласно примерному варианту осуществления настоящего изобретения.
Ссылаясь на фиг.2, абсолютный код, минимальное расстояние между кодами которого имеет максимальное значение в рамках предела Плоткина, формируется на этапе S201. Типичным кодом, удовлетворяющим вышеуказанному условию, может быть симплексный код.
Тем не менее, если есть другие коды, максимальное расстояние которых между кодами имеет максимальное значение в рамках предела Плоткина, эти коды могут использоваться.
Абсолютный код повторяется m раз на этапе S202. Когда код, максимальное расстояние которого между кодами максимизировано, повторяется, такое условие, что минимальное расстояние максимизировано в рамках предела Плоткина, удовлетворяется аналогично абсолютному коду с точки зрения нормированного минимального расстояния.
Тем не менее, когда длина кода n не является кратной длине абсолютного кода, другая длина r формируется на этапе S203. Хотя может быть много способов для формирования кода, имеющего длину r, желательно задавать код, имеющий длину r, так, чтобы иметь минимальное расстояние максимального значения в рамках предела Плоткина с точки зрения нормированного минимального расстояния.
Для этой цели, заданные биты в абсолютном коде, используемом для повторения, прореживаются так, как показано на этапе S203-1. Если другая длина r равна числу информационных битов, информационный бит используется в качестве кода длины r, как показано на этапе S203-2. Если длина r равна длине любого произвольного кода, удовлетворяющего условию максимально-минимального расстояния в рамках предела Плоткина, произвольный код используется в качестве кода длины r, как показано на этапе S203-3.
В дальнейшем в этом документе, поясняются способы для формирования кода длины r согласно варианту осуществления настоящего изобретения, например, способ, использующий прореживание, и различные модификации способа формирования кода.
Кроме того, поясняется способ для формирования кода [32,2] (или кода (32, 2)) посредством применения способа формирования кода к 3GPP LTE-системе и способ для передачи управляющего сигнала с использованием кода [32,2].
Сначала описывается способ для формирования кода длины r с помощью прореживания согласно варианту осуществления настоящего изобретения.
Способ для формирования кода длины r с помощью прореживания
Оптимальный способ формирования кода с помощью прореживания в случае, когда длина кода n не является кратной (2k-1), описывается подробно. Сначала абсолютный код короткой длины формируется, а затем абсолютный код повторяется так, чтобы абсолютный код мог быть больше длины кода n. Лишние биты прореживаются из абсолютного кода. Способ для оптимального выбора местоположения прореживания в процессе прореживания предлагается следующим образом.
При формировании кода [r, k], максимальное расстояние которого максимизировано в рамках предела Плоткина, рассматривается способ для составления симплексного кода [2k-1, k, 2k-1] с помощью прореживания. Число битов прореживания равно 2k-1-r, и условие для определения местоположений прореживания (2k-1-r) битов состоит в том, чтобы максимально поддерживать минимальное расстояние в рамках предела Плоткина.
Местоположение прореживания может быть определено различными способами. В качестве простого и достоверного примера могут быть проверены все возможные местоположения прореживания. Таким образом, если число (2k-1-r) местоположений прореживания является небольшим и, таким образом, число возможных местоположений прореживания является небольшим, все возможные случаи могут быть протестированы. В этом случае, оптимальные местоположения прореживания могут быть определены посредством проверки того, удовлетворяется ли условие, что минимальное расстояние максимально поддерживается в рамках предела Плоткина при одновременном варьировании местоположений прореживания.
Может использоваться фиксированное местоположение прореживания. Если число битов прореживания равно 2k-1-r, рассматривается способ для последовательного прореживания 2k-1-r битов от местоположения первого бита. Подробнее, (2k-1-r) битов, соответствующих числу битов прореживания, прореживаются от местоположения первого бита из симплексного кода [2k-1, k, 2k-1]. Тем не менее, поскольку этот способ не может обеспечивать условие, что минимальное расстояние максимально поддерживается в рамках предела Плоткина, необходимо проверять, удовлетворяет ли код, формируемый после прореживания, вышеуказанному условию.
В дальнейшем в этом документе, поясняется то, удовлетворяется ли условие минимального расстояния при прореживании последовательных битов от первого местоположения в прореживании симплексного кода. Если длина кода n равна m(2k-1)+r, значимый диапазон r составляет [k, 2k-2] (от k до 2k-2, оба включительно).
Предполагается, что k равно 2. Поскольку k равно 2, r меньше 3 (=22-1), и рабочий диапазон r равен [2, 2] (от 2 до 2, оба включительно). Следовательно, рассматривается только случай, где r=2. В этом случае, исходные два информационных бита используются в качестве кода длины r, и это демонстрирует результат, идентичный случаю, когда первый бит прореживается из симплексного кода [3, 2, 2].
Это поясняется со ссылкой на фиг.3a-3c.
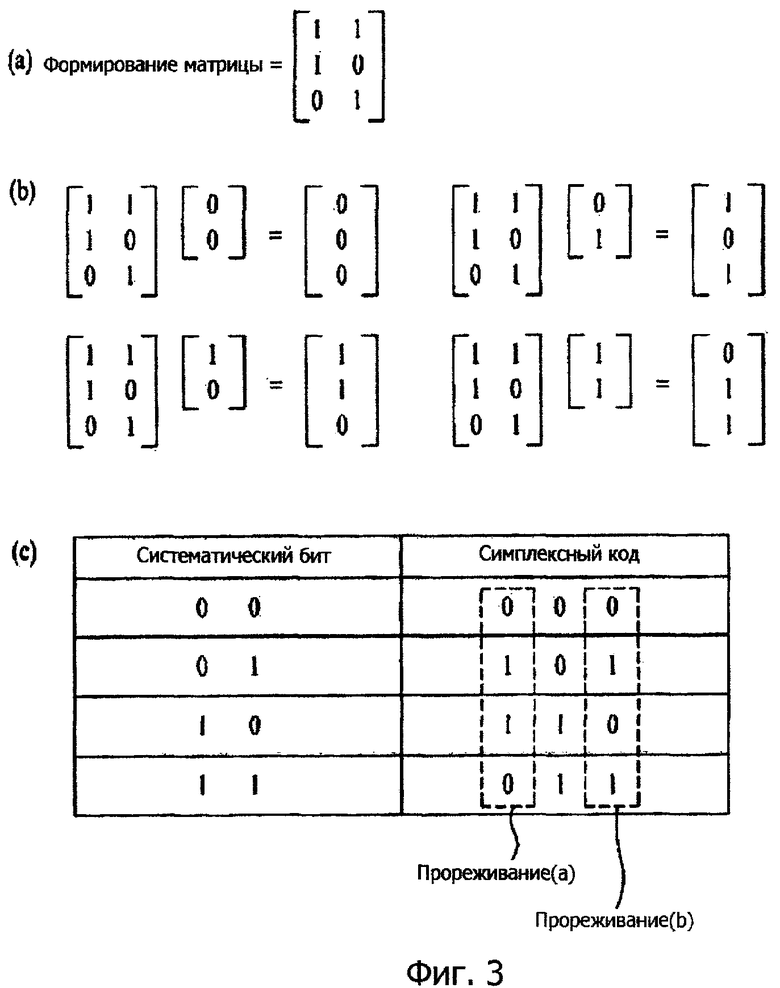
Фиг.3a-3c являются схемами для пояснения взаимосвязи между местоположением прореживания симплексного кода и информационным битом.
Матрица, используемая для того, чтобы формировать симплексный код [3, 2, 2], проиллюстрирована на фиг.3a. На фиг.3b процесс для формирования симплексных кодов (0, 0, 0), (1, 0, 1), (1, 1, 0), (0, 1, 1) относительно информационных битов (0, 0), (0, 1), (1, 0), (1, 1), соответственно, проиллюстрирован.
При формировании кода длины r, информационный бит эффективно использовать только, когда r=2. Это демонстрирует результат, идентичный случаю, когда первый бит симплексного кода [3, 2, 2] прореживается так, как показано посредством прореживания (a) на фиг.3c.
Когда первый бит симплексного кода [3, 2, 2] прореживается или только информационный бит используется, предел Плоткина может быть выражен следующим образом:
уравнение 7

При условии предела Плоткина, указанном в уравнении 7, желательно, чтобы интеграл dr удовлетворял максимальному значению 1.
Между тем, когда первый бит прореживается из симплексного кода [3, 2, 2] или только информационный бит используется, поскольку минимальное расстояние между кодами равно 1, как известно из фиг.3c, условие, что минимальное расстояние максимизировано в рамках предела Плоткина, удовлетворяется.
Следовательно, если k=2 и r=2 при формировании кода длины r с помощью прореживания, предлагается, чтобы первый бит прореживался из симплексного кода [3, 2, 2], и это демонстрирует результат, идентичный случаю, когда информационный бит используется в качестве кода длины r.
Затем, допускается, что k=3.
Если k равно 3, r меньше 7 (=23-1), и рабочий диапазон r составляет [3, 6] (от 3 до 6, оба включительно). Следовательно, рассматриваются только случаи, где r равно 3, 4, 5 и 6.
Если r равно 6, можно формировать код длины r посредством прореживания первого бита из симплексного кода [7, 3, 4]. В этом случае, предел Плоткина может вычисляться следующим образом:
уравнение 8

Затем интеграл dr имеет верхний предел 24/7 или 21/7 и поэтому максимальное целочисленное значение dr равно 3.
Случай, где d является либо четным числом, либо нечетным числом, рассматривается для предела Плоткина, и затем другой случай естественным образом извлекается. В дальнейшем в этом документе поясняется только случай, где d является четным числом.
При вычислении минимального расстояния посредством прореживания первого бита из симплексного кода [7, 3, 4] получается минимальное расстояние 3. В таком случае следует понимать, что условие предела Плоткина удовлетворяется.
Следовательно, если k=3 и r=6 при формировании кода длины r с помощью прореживания согласно примерному варианту осуществления настоящего изобретения, предлагается прореживать первый бит из симплексного кода [7, 3, 4].
Затем, рассматривается случай, где k=3 и r=5. В этом случае, поясняется способ для прореживания двух последовательных битов, т.е. первого и второго битов из симплексного кода [7, 3, 4]. Предел Плоткина вычисляется следующим образом:
уравнение 9
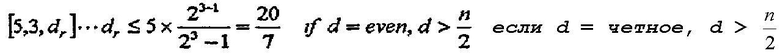
Как описано выше, поскольку рассматривается только случай, где d является четным числом, максимальное значение интеграла dr равно 2, как известно из уравнения 9.
Между тем, поскольку минимальное расстояние, когда первый и второй биты прореживаются из симплексного кода [7, 3, 4] равно 2 вышеупомянутое условие предела Плоткина удовлетворяется.
Следовательно, если k=3 и r=5 при формировании кода длины r с помощью прореживания, предлагается формировать код посредством прореживания двух последовательных битов, т.е. первого и второго битов из симплексного кода [7, 3, 4].
Затем, рассматривается случай, где k=3 и r=4.
В этом случае, рассматривается способ для формирования кода посредством прореживания трех последовательных битов, т.е. первого-третьего битов из симплексного кода [7, 3, 4]. Предел Плоткина вычисляется следующим образом:
уравнение 10
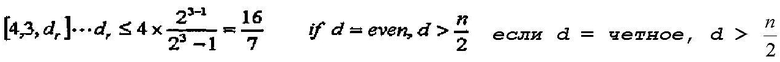
Следует понимать, что максимальное значение интеграла dr равно 2 из вышеприведенного уравнения 10.
При вычислении минимального расстояния посредством прореживания первого-третьего битов из симплексного кода [7, 3, 4], получается минимальное расстояние в 2, и условие предела Плоткина удовлетворяется.
Следовательно, если k=3 и r=4 при формировании кода длины r с помощью прореживания, предлагается формировать код посредством прореживания трех последовательных битов, т.е. первого-третьего битов из симплексного кода [7, 3, 4].
Наконец, рассматривается случай, где k=3 и r=3. В этом случае, рассматривается способ для формирования кода посредством прореживания четырех последовательных битов, т.е. первого-четвертого битов из симплексного кода [7, 3, 4]. В этом случае, предел Плоткина вычисляется следующим образом:
уравнение 11
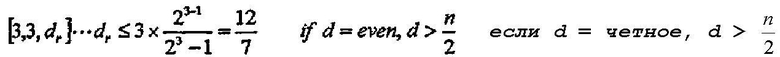
Следует понимать, что максимальное значение интеграла dr равно 1 из вышеприведенного уравнения 11.
Поскольку минимальное расстояние, вычисляемое посредством прореживания четырех последовательных битов из симплексного кода [7, 3, 4], равно 1, вышеупомянутое условие предела Плоткина удовлетворяется.
Вышеописанный случай, где r равен k, также может поясняться в качестве случая, где три информационных бита (или систематических бита) используются в качестве кода длины r.
Следовательно, если k=3 и r=3 при формировании кода длины r, предлагается прореживать четыре последовательных бита с первого-четвертого битов из симплексного кода [7, 3, 4] или использовать информационный бит в качестве кода длины r.
Способы для формирования кода длины r с помощью прореживания, когда k=2 и k=3, могут быть обобщены так, чтобы способы могли применяться к случаям, где k равно 4 или более.
Таким образом, даже когда k составляет 4 или более, можно формировать код [r, k] посредством последовательного прореживания (2k-1-r) битов от местоположения первого бита из симплексного кода [2k-1, k, 2k-1].
Модификация 1
Тем не менее, местоположения прореживания, прореживаемые последовательно от первого бита из (2k-1-r) битов, не означают единственные местоположения, которые максимизируют минимальное расстояние в рамках предела Плоткина. В некоторых случаях, код длины r, минимальное расстояние которого максимизировано в рамках предела Плоткина, может быть сформирован, даже когда соответствующие биты прореживаются в других местоположениях.
Например, при прореживании одного бита, когда k=2 и r=2, последний бит может прореживаться вместо первого бита так, что код длины r, значение dr которого становится максимальным значением в рамках предела Плоткина. Таким образом, следует принимать во внимание, что dr равно 1, даже когда местоположение прореживания одного бита является третьим битом, как указано посредством прореживания (b) на фиг.3c.
Модификация 2
Когда полный код симплексного кода, нормированное минимальное расстояние которого имеет максимальное значение, выражается как матрица, характеристика минимального расстояния не варьируется, даже когда местоположение или строки, или столбца или местоположения как строки, так и столбца переставляются.
Следовательно, при повторении симплексного кода m раз оптимальная характеристика минимального расстояния не варьируется, даже когда местоположения строки и столбца кода, имеющего небольшую длину, варьируются. Соответственно, можно получать требуемое оптимальное минимальное расстояние несмотря на то, является форма симплексного кода варьируемой или фиксированной.
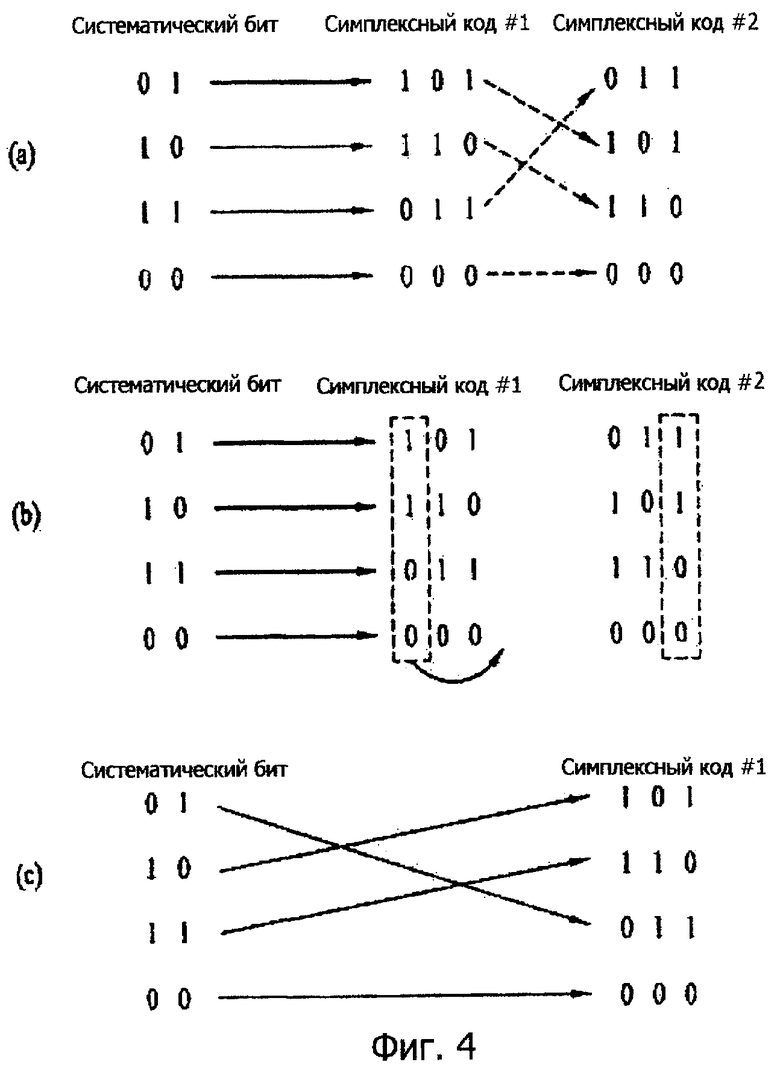
Фиг.4a-4c являются схемами для пояснения примеров построчного или постолбцового преобразования симплексного кода с точки зрения преобразования с помощью информационного бита.
Как описано выше, даже если местоположение столбца или строки симплексного кода в качестве абсолютного кода, используемого для повторения, переставляется при формировании кода длины n, характеристика минимального расстояния не варьируется. В этом случае, перестановка столбца или строки симплексного кода может означать, что взаимосвязь преобразования с информационным битом изменена.
Таким образом, когда информационные биты (0, 1), (1, 0), (1, 1) и (0, 0) преобразуются в симплексные коды #1 (1, 0, 1), (1, 1, 0), (0, 1, 1) и (0, 0, 0) соответственно, как показано на фиг.4a, симплексные коды #2, строка которых переставляется, могут использоваться вместо симплексных кодов #1.
Идентичный результат может быть описан в другом аспекте следующим образом. Как проиллюстрировано на фиг.4b, когда первый столбец симплексных кодов #1 переставляется с их третьим столбцом и когда вторые и третьи столбцы симплексных кодов #1 переставляются с их первыми и вторыми столбцами соответственно, формируется кодовая матрица, которая является такой же, как симплексные коды #2, проиллюстрированные на фиг.4a.
Перестановка столбца или строки симплексного кода может соответствовать изменению преобразования между информационным битом и симплексным кодом, как проиллюстрировано на фиг.4c. А именно, в симплексных кодах #2 информационные биты (0, 1), (1, 0), (1, 1) и (0, 0) преобразуются в симплексные коды (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) соответственно.
Модификация 3
Коды, максимальное расстояние которых максимизировано, могут модифицироваться различными способами.
Сначала, поскольку расстояние между кодами не варьируется, даже когда 0 и 1 обмениваются, код может модифицироваться посредством обмена 0 и 1 формируемого кода.
Во-вторых, когда полный код выражается в матрице так, что каждый код занимает каждую строку матрицы, характеристика минимального расстояния не варьируется, даже когда местоположение столбца или строки или местоположения столбца и строки переставляются. Следовательно, можно изменять код посредством обмена столбца или строки или как столбца, так и строки кодовой матрицы ранее сформированного кода.
В вышеприведенном описании, когда длина полного кода не является кратной абсолютному коду при формировании кода с большой длиной, имеющего низкую кодовую скорость, с использованием абсолютного кода, имеющего характеристику минимального расстояния, рассматривались способы для корректировки другой части длины и различные модификации этих способов.
В дальнейшем в этом документе поясняется пример применения вышеупомянутых способов формирования кода к 3GPP LTE-системе, например способа для формирования кода (32,2) и передачи управляющей информации с использованием кода (32,2).
Пример, применяемый к коду (32,2)
Индикатор формата канала управления (CFI), указывающий объем управляющей информации из символов мультиплексирования с ортогональным частотным разделением каналов (OFDM) в одном OFDM-кадре в 3GPP LTE, состоит из 2 битов. Поскольку CFI передается через физический канал индикатора формата управления (PCFICH) по 16 символам квадратурной фазовой манипуляции (QPSK), необходимо 32 бита кодирования. Следовательно, необходим код [32,2].
Поскольку производительность кода пропорциональна расстоянию между кодами, код, имеющий превосходную производительность, имеет большое расстояние между кодами. Код, расстояние которого максимально разнесено, называется максимально разнесенным (MDS) кодом. MDS-код может быть симплексным кодом в качестве примера кода [3,2] и кодом Хемминга в качестве примера кода [5,2].
Симплексный код [3,2] является следующим:
{000, 101, 011, 110}.
В симплексном коде [3,2] можно обмениваться 0 и 1. А именно, когда 0 и 1 обмениваются, вышеупомянутый кодовый набор может использоваться как {111, 010, 100, 001}, а измененный код также удовлетворяет характеристике симплексного кода [3,2].
Местоположение каждого бита в симплексном коде [3,2] может взаимно обмениваться. Это имеет такой же результат, как случай, когда каждый столбец симплексного кода изменяется в описании со ссылкой на фиг.4b. Другими словами, когда первым и вторым битами обмениваются из вышеупомянутого кодового набора, кодовый набор {000,011,101,110} получается, и этот код также имеет характеристику симплексного кода [3,2].
Код Хемминга [5,2] является следующим: {00000, 01101, 10011, 11110} или {00000, 01011, 10110, 11101}.
Также можно обмениваться 0 и 1 и обмениваться местоположением каждого бита.
Между тем, поскольку трудно непосредственно формировать длинный код, имеющий низкую кодовую скорость, такой как код [32,2], рассматривается способ для формирования полного кода посредством процесса повторения абсолютного кода, как описано выше.
Абсолютный код использует симплексный код [3,2]. После того как абсолютный код повторен, битовая часть, формируемая, поскольку вся длина 32 не является кратной 3, может обрабатываться посредством следующих способов, например, способа, использующего прореживание, описанное в основном варианте осуществления и его примерах модификации, способа, использующего информационный бит, и способа, использующего код Хемминга [5,2].
Сначала поясняется способ для повторения симплексного кода [3,2] и прореживания одного бита.
Согласно примерному варианту осуществления настоящего изобретения, симплексный код [3,2] повторяется 11 раз, и один бит прореживается, тем самым формируя код [32,2].
Местоположение прореживания одного бита может быть любым местоположением 33 битов. Тем не менее, желательно, что конечный код, формируемый с использованием способа прореживания, удовлетворяет условию, что его минимальное расстояние максимизировано в рамках предела Плоткина.
Симплексный код [3,2] может использовать кодовую комбинацию, такую как {000, 101, 011, 110}. Этот абсолютный код может использоваться как модифицированные формы до тех пор, пока свойство минимального расстояния не варьируется. Например, предусмотрен способ для перестановки столбца и/или строки кода, способ для обмена 0 и 1 кода и способ для обмена 0 и 1 кода и затем обмена строки и/или столбца кода.
При повторении симплексного кода [3,2] можно выборочно использовать симплексные коды 11 раз из различных симплексных кодов [3,2].
Во-вторых, поясняется способ для повторения симплексного кода [3,2] и вставки 2 информационных битов.
Согласно примерному варианту осуществления настоящего изобретения, симплексный код [3,2] повторяется 10 раз и затем 2 информационных бита добавляются, тем самым формируя код [32,2].
Местоположения добавленных информационных битов могут быть последней частью кода [32,2]. Альтернативно, добавленные биты размещаются в произвольных местоположениях из 30 битов. Эти 2 информационных бита могут добавляться последовательно или добавляться отдельно.
Симплексный код [3,2], используемый для повторения, может использовать кодовую комбинацию, такую как {000, 101, 011, 110}. Альтернативно, можно использовать различные формы в пределах диапазона без изменения характеристики минимального расстояния, как описано выше. Например, предусмотрен способ для перестановки столбца и/или строки кода, способ для обмена 0 и 1 кода и способ для обмена 0 и 1 кода и последующей перестановки строки и/или столбца кода.
При повторении симплексного кода [3,2] можно выборочно использовать симплексные коды 10 раз из различных симплексных кодов [3,2].
В завершение, поясняется способ для повторения симплексного кода [3,2] и добавления кода Хемминга [5,2].
В этом примерном варианте осуществления, симплексный код [3,2] повторяется 9 раз и затем добавляется код Хемминга [5,2], тем самым формируя код [32,2].
Добавленные биты кода Хемминга [5,2] позиционируются в произвольных местоположениях из 27 битов. 5 битов могут добавляться последовательно или добавляться отдельно.
Симплексный код [3,2], используемый для повторения, может использовать кодовую комбинацию, такую как {000, 101, 011, 110}. Альтернативно, можно использовать другие формы вместо абсолютного кода, если характеристика минимального расстояния не варьируется, как описано выше. Например, есть способ для перестановки столбца и/или строки кода, способ для обмена 0 и 1 и способ для обмена 0 и 1 и последующей перестановки строки и/или столбца кода.
Дополненный код Хемминга [5,2] может использовать любой из следующих абсолютных кодов:
{00000, 01101, 10011, 11110},
{00000, 01101, 11011, 10110},
{00000, 10101, 01011, 11110},
{00000, 10101, 11011, 01110},
{00000, 11101, 01011, 10110},
{00000, 11101, 10011, 01110},
{01000, 00101, 10011, 11110},
{01000, 00101, 11011, 10110},
{01000, 10101, 00011, 11110},
{01000, 10101, 11011, 00110},
{01000, 11101, 00011, 10110},
{01000, 11101, 10011, 00110},
{10000, 00101, 01011, 11110},
{10000, 00101, 11011, 01110},
{10000, 01101, 00011, 11110},
{10000, 01101, 11011, 00110},
{10000, 11101, 00011, 01110},
{10000, 11101, 01011, 00110},
{11000, 00101, 01011, 10110},
{11000, 00101, 10011, 01110},
{11000, 01101, 00011, 10110},
{11000, 01101, 10011, 00110},
{11000, 10101, 00011, 01110},
{11000, 10101, 01011, 00110}.
Следует понимать, что код Хемминга [5,2] имеет минимальное расстояние в 3. Поскольку минимальное расстояние в 3 равно значению, получаемому посредством прибавления минимального расстояния 2 симплексного кода [3,2] к минимальному расстоянию 1 кода длины r, условие, что минимальное расстояние между кодами максимизировано в рамках предела Плоткина, удовлетворяется.
В этом примерном варианте осуществления, код Хемминга [5,2] может использоваться посредством модификации вышеописанного абсолютного кода, при этом одновременно удовлетворяя характеристике кода Хемминга. В качестве возможных модификаций предусмотрены способ изменения порядка кода Хемминга [5,2], способ обмена 0 и 1 в коде Хемминга [5,2], способ обмена 0 и 1 в коде Хемминга [5,2] и последующего изменения порядка кода, способ обмена местоположениями битов в коде Хемминга [5,2], способ для обмена местоположениями битов в коде Хемминга [5,2] и последующего изменения порядка кода, способ для обмена 0 и 1 в коде Хемминга [5,2] и последующего обмена местоположениями битов и способ обмена 0 и 1, обмена местоположениями битов и изменения порядка кода.
При повторении симплексного кода [3,2] можно выборочно использовать симплексные коды 10 раз из различных симплексных кодов [3,2].
Примеры кода [32,2], формируемого посредством вышеописанных способов, могут быть выражены следующим образом:
Вышеупомянутые четыре кода могут быть сформированы посредством одного из следующих способов.
Во-первых, четыре кода [32,2], показанные в таблице, могут быть сформированы посредством повторения каждого из (0, 1, 1), (1, 0, 1), (1, 1, 0), (0, 0, 0) 11 раз и последующего прореживания последнего одного бита из последнего симплексного кода. Как описано в вышеупомянутой модификации 1, если r=2 и k=2, случаи, где первый бит симплексного кода [3,2] прореживается и последний бит симплексного кода [3,2] прореживается, удовлетворяют условию, что минимальное расстояние максимизировано в рамках предела Плоткина. Следовательно, оптимальный код может быть сформирован.
Во-вторых, когда эти симплексные коды [3,2] (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) преобразуются в информационные биты (0, 1), (1, 0), (1, 1) и (0, 0) соответственно, как проиллюстрировано на фиг.4c, эти симплексные коды [3,2] (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) повторяются 10 раз и затем соответствующие информационные биты вставляются.
В-третьих, четыре кода [32,2], показанные в таблице, могут быть сформированы посредством повторения этих симплексных кодов [3,2] (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) 9 раз и последующего добавления (0, 1, 1, 0, 1), (1, 0, 1, 1, 0), (1, 1, 0, 1, 1) и (0, 0, 0, 0, 0) в качестве кода Хемминга [5,2].
В дальнейшем в этом документе поясняется способ для передачи управляющей информации с использованием сформированного кода [32,2].
Фиг.5a и 5b являются схемами для пояснения процесса передачи управляющей информации с использованием кода [32,2] согласно примерному варианту осуществления настоящего изобретения.
Информация о числе OFDM-символов, занимаемых посредством управляющей информации, из OFDM-символов в рамках одного OFDM-кадра в 3GPP LTE-системе передается через PCFICH, и вышеописанный код [32,2] используется. На фиг.5a, управляющая информация передается более чем за 2 OFDM-символа в рамках одного OFDM-кадра. Информация о числе OFDM-символов, занимаемых посредством управляющей информации, может быть выражена посредством кода [32,2], как показано в таблице.
Если число OFDM-символов, занимаемых посредством управляющей информации, существует как только 3 случая, то только 3 кода могут быть использованы из этих 4 кодов, показанных в таблице.
Фиг.5b иллюстрирует пример с использованием только первой, второй и третьей строк из кода [32,2], показанного в таблице, когда управляющая информация занимает OFDM-символы 1, 2 и 3.
Подробное описание примерных вариантов осуществления настоящего изобретения приведено для того, чтобы давать возможность специалистам в данной области техники реализовывать и осуществлять на практике изобретение. Хотя изобретение описано в отношении примерных вариантов осуществления, специалисты в данной области техники должны принимать во внимание, что различные модификации и изменения могут быть сделаны в настоящем изобретении без отступления от сущности или объема изобретения, описываемого в прилагаемой формуле изобретения.
Следовательно, необходимо понимать, что этот патент не должен быть ограничен конкретными вариантами осуществления, описанными в данном документе, а получать право на самый широкий объем, согласованный с принципами и новыми признаками, раскрытыми в данном документе.
Промышленная применимость
Настоящее изобретение предоставляет способ для формирования кода с большой длиной, имеющего низкую кодовую скорость, и способ для передачи управляющей информации с использованием его. Эти способы могут непосредственно применяться к коду [32,2], используемому для PCFICH в 3GPP LTE-системе. Способы для формирования кода с большой длиной, имеющего низкую кодовую скорость, посредством повторения и прореживания абсолютного кода, вставки информационного бита и использования произвольных кодов, отличных от абсолютного кода, могут по-разному применяться в качестве способа для формирования кода, используемого для того, чтобы передавать конкретную информацию о том, какая серьезная ошибка может возникать, и использования кода даже в системах связи, отличных от 3GPP LTE-системы.

Изобретение относится к беспроводной связи, а именно к способам передачи управляющей информации нисходящей линии связи и способам формирования кодового слова для нее, и может быть использовано в системах связи. Технический результат заключается в повышении производительности и уменьшении частоты ошибок при передаче. Для этого при формировании длинного кода, имеющего низкую кодовую скорость, абсолютный код, минимальное расстояние которого между кодами максимизировано, повторяется заданное число раз, и биты повторенного кода корректируются, таким образом условие минимального расстояния между кодами длинного кода удовлетворяется, при этом код формируется достаточно просто. 5 н. и 16 з.п. ф-лы, 5 ил., 1 табл.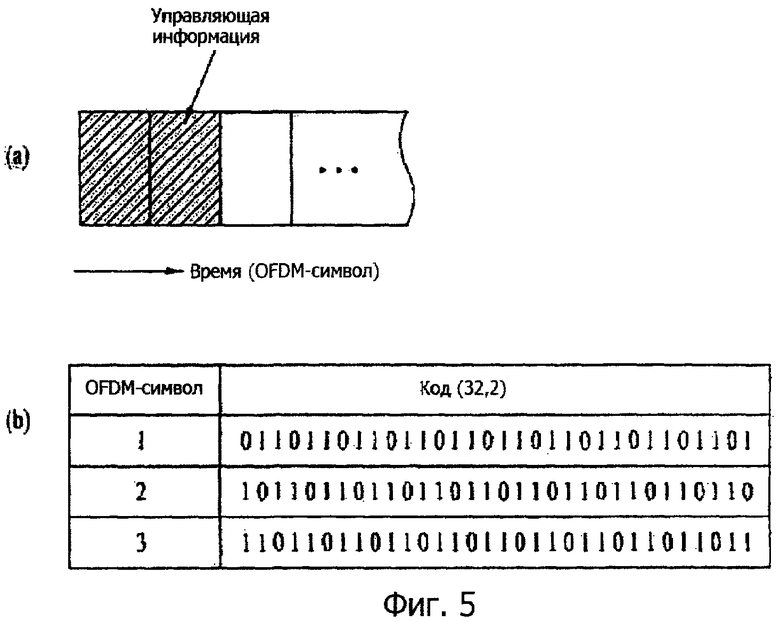
1. Способ передачи управляющей информации нисходящей линии связи в системе беспроводной связи, при этом способ содержит этап, на котором:
передают информацию из сети, указывающую число символов мультиплексирования с ортогональным частотным разделением каналов (OFDM), содержащих управляющую информацию в канале управления нисходящей линии связи с использованием заданного кода,
при этом заданный код является одним из следующего: (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), (1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), (1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1) и (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
согласно информации, указывающей число OFDM-символов, содержащих управляющую информацию.
2. Способ по п.1, дополнительно содержащий этап, на котором передают управляющую информацию через канал управления нисходящей линии связи.
3. Способ по п.1, в котором информация, указывающая число OFDM-символов, содержащих управляющую информацию в канале управления нисходящей линии связи, является индикатором формата управления (CFI).
4. Способ по п.1, в котором информацию, указывающую число OFDM-символов, содержащих управляющую информацию в канале управления нисходящей линии связи, передают через физический канал индикатора формата управления (PCFICH).
5. Способ по п.1, в котором заданным кодом является:
(0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, содержащих управляющую информацию, равно 1,
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, содержащих управляющую информацию, равно 2, и
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, содержащих управляющую информацию, равно 3.
6. Способ приема управляющей информации нисходящей линии связи в системе беспроводной связи, при этом способ содержит этапы, на которых:
принимают информацию в абонентском устройстве (UE), указывающую число символов мультиплексирования с ортогональным частотным разделением каналов (OFDM), содержащих управляющую информацию в канале управления нисходящей линии связи, причем информацию передают от сети с использованием заданного кода; и
принимают управляющую информацию через канал управления нисходящей линии связи с использованием заданного кода,
при этом заданный код является одним из следующего: (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), (1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), (1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1) и (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
согласно числу OFDM-символов, содержащих управляющую информацию.
7. Способ по п.6, в котором информация, указывающая число OFDM-символов, содержащих управляющую информацию, является индикатором формата управления (CFI).
8. Способ по п.6, в котором информацию, указывающую число OFDM-символов, содержащих управляющую информацию, принимают через физический канал индикатора формата управления (PCFICH).
9. Способ по п.6, в котором заданным кодом является:
(0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, содержащих управляющую информацию, равно 1,
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, содержащих управляющую информацию, равно 2, и
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, содержащих управляющую информацию, равно 3.
10. Способ формирования кодового слова для передачи управляющей информации нисходящей линии связи в системе беспроводной связи, при этом способ содержит этап, на котором:
формируют последовательность согласно числу символов мультиплексирования с ортогональным частотным разделением каналов (OFDM), содержащих управляющую информацию в канале управления нисходящей линии связи,
при этом последовательность формируют посредством повторения одного из симплексных кодов (0, 1,1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) одиннадцать раз и прореживания последнего бита последовательности.
11. Способ по п.10, в котором последовательностью является: (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, содержащих управляющую информацию, равно 1,
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, содержащих управляющую информацию, равно 2, и
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, содержащих управляющую информацию, равно 3.
12. Способ по п.10, в котором число OFDM-символов, содержащих управляющую информацию, указывают посредством индикатора формата управления (CFI).
13. Способ по п.10, дополнительно содержащий этап, на котором передают последовательность через физический канал индикатора формата управления (PCFICH).
14. Способ формирования кодового слова для передачи управляющей информации нисходящей линии связи в системе беспроводной связи, при этом способ содержит этап, на котором:
формируют последовательность согласно числу символов мультиплексирования с ортогональным частотным разделением каналов (OFDM), содержащих управляющую информацию в канале управления нисходящей линии связи,
при этом последовательность формируют посредством повторения одного из симплексных кодов (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) девять раз и вставки одного из кодов Хемминга (0, 1, 1,0, 1), (1, 0, 1, 1, 0), (1, 1,0, 1, 1) и (0, 0, 0, 0, 0) в последовательность.
15. Способ по п.14, в котором последовательность является: (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, содержащих управляющую информацию, равно 1,
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, содержащих управляющую информацию, равно 2, и
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, содержащих управляющую информацию, равно 3.
16. Способ по п.14, в котором число OFDM-символов, содержащих управляющую информацию, указывают посредством индикатора формата управления (CFI).
17. Способ по п.14, дополнительно содержащий этап, на котором передают последовательность через физический канал индикатора формата управления (PCFICH).
18. Способ формирования кодового слова для передачи управляющей информации нисходящей линии связи в системе беспроводной связи, при этом способ содержит этап, на котором:
формируют последовательность согласно числу символов мультиплексирования с ортогональным частотным разделением каналов (OFDM), содержащих управляющую информацию в канале управления нисходящей линии связи,
при этом последовательность формируют посредством повторения одного из симплексных кодов (0, 1, 1), (1, 0, 1), (1, 1, 0) и (0, 0, 0) десять раз и вставки двух информационных битов в последовательность.
19. Способ по п.18, в котором последовательностью является: (0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1), когда число OFDM-символов, содержащих управляющую информацию, равно 1,
(1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0), когда число OFDM-символов, содержащих управляющую информацию, равно 2, и
(1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1), когда число OFDM-символов, содержащих управляющую информацию, равно 3.
20. Способ по п.18, в котором число OFDM-символов, содержащих управляющую информацию, указывают посредством индикатора формата управления (CFI).
21. Способ по п.18, дополнительно содержащий этап, на котором передают последовательность через физический канал индикатора формата управления (PCFICH).
| УСТРОЙСТВО И СПОСОБ ДЛЯ ПЕРЕДАЧИ БИТОВ УКАЗАТЕЛЯ КОМБИНАЦИИ ТРАНСПОРТНОГО ФОРМАТА ДЛЯ РЕЖИМА ЖЕСТКОГО РАЗДЕЛЕНИЯ В СИСТЕМЕ МОБИЛЬНОЙ СВЯЗИ МНОЖЕСТВЕННОГО ДОСТУПА С КОДОВЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ | 2002 |
|
RU2251797C2 |
| УСТРОЙСТВО И СПОСОБ ГЕНЕРАЦИИ ПОСЛЕДОВАТЕЛЬНОСТИ ПРЕАМБУЛЫ В СИСТЕМЕ СВЯЗИ ОМЧР | 2003 |
|
RU2278474C2 |
| US 2003108025 А1, 12.06.2003 | |||
| US 2003063595 A1, 03.04.2003 | |||
| WO 2006008359 A1, 26.01.2006 | |||
| US 2003118083 A1, 26.06.2003. | |||
Авторы
Даты
2011-08-10—Публикация
2008-05-09—Подача