Изобретение относится к акустооптике и может быть использовано в приборах отклонения и модуляции лазерных пучков и, в частности, при разработке элементов ввода информации в устройствах оптической обработки радиосигналов.
Принцип действия широкополосных анизотропных акустооптических дефлекторов основан на использовании особенностей геометрии акустооптического взаимодействия при анизотропной дифракции [1]. Известно, что в таких дефлекторах центральная частота диапазона зависит от параметров материала, из которого изготовлена фотоупругая среда дефлектора (физических свойств кристалла) и направления распространения акустической волны [2, 3, 4]. Подбор среза акустооптического кристалла является единственным известным способом изменения центральной частоты широкополосного анизотропного СВЧ-дефлектора [2, 3, 4, 5]. Однако необходимость изменения среза кристалла при смене центральной частоты анизотропного дефлектора приводит к уменьшению коэффициента акустооптического качества М2 и, следовательно, снижению дифракционной эффективности от максимальных величин, возможных для данного акустооптического кристалла [2, 3, 6]. Это является существенным недостатком способа изменения центральной частоты с помощью выбора среза кристалла в анизотропных акустооптических дефлекторах.
Задача изобретения заключается в реализации возможности выбора центральной частоты диапазона анизотропного акустооптического дефлектора без изменения геометрии среза кристалла, являющегося фотоупругой средой дефлектора.
Поставленная задача достигается тем, что способ изменения центральной частоты диапазона акустооптического анизотропного дефлектора включает возбуждение акустической волны в фотоупругой среде акустооптического анизотропного дефлектора посредством многоэлементного электроакустического преобразователя, период следования элементов которого выбирают в соответствии с предварительно установленной зависимостью центральной частоты диапазона акустооптического анизотропного дефлектора от периода следования элементов многоэлементного преобразователя, и настройку акустооптического анизотропного дефлектора путем изменения угла падения света на фотоупругую среду для работы с одним из боковых акустических лепестков диаграммы направленности многоэлементного преобразователя, при этом зависимость центральной частоты диапазона анизотропного акустооптического дефлектора от периода следования элементов преобразователя определяют на основе полученных для заданного интервала периодов следования элементов преобразователя частотно-угловых характеристик акустооптического анизотропного дефлектора с многоэлементным электроакустическим преобразователем.
Предлагаемое изобретение поясняется чертежами: на фиг.1 представлена векторная диаграмма взаимодействия плоской монохроматической световой волны с акустической волной для анизотропной дифракции в отрицательном одноосном кристалле, где 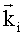 - волновой вектор падающей обыкновенной световой волны,
- волновой вектор падающей обыкновенной световой волны, 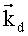 - волновой вектор дифрагированной необыкновенной световой волны,
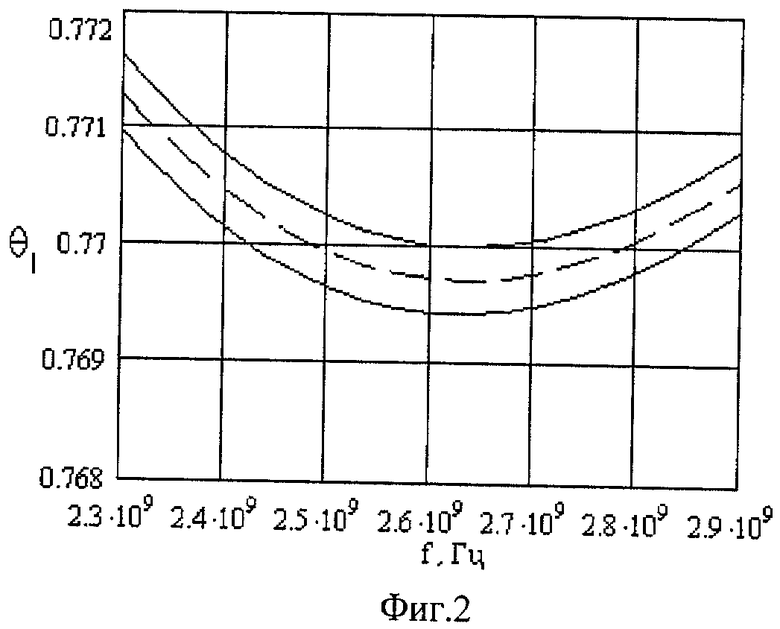
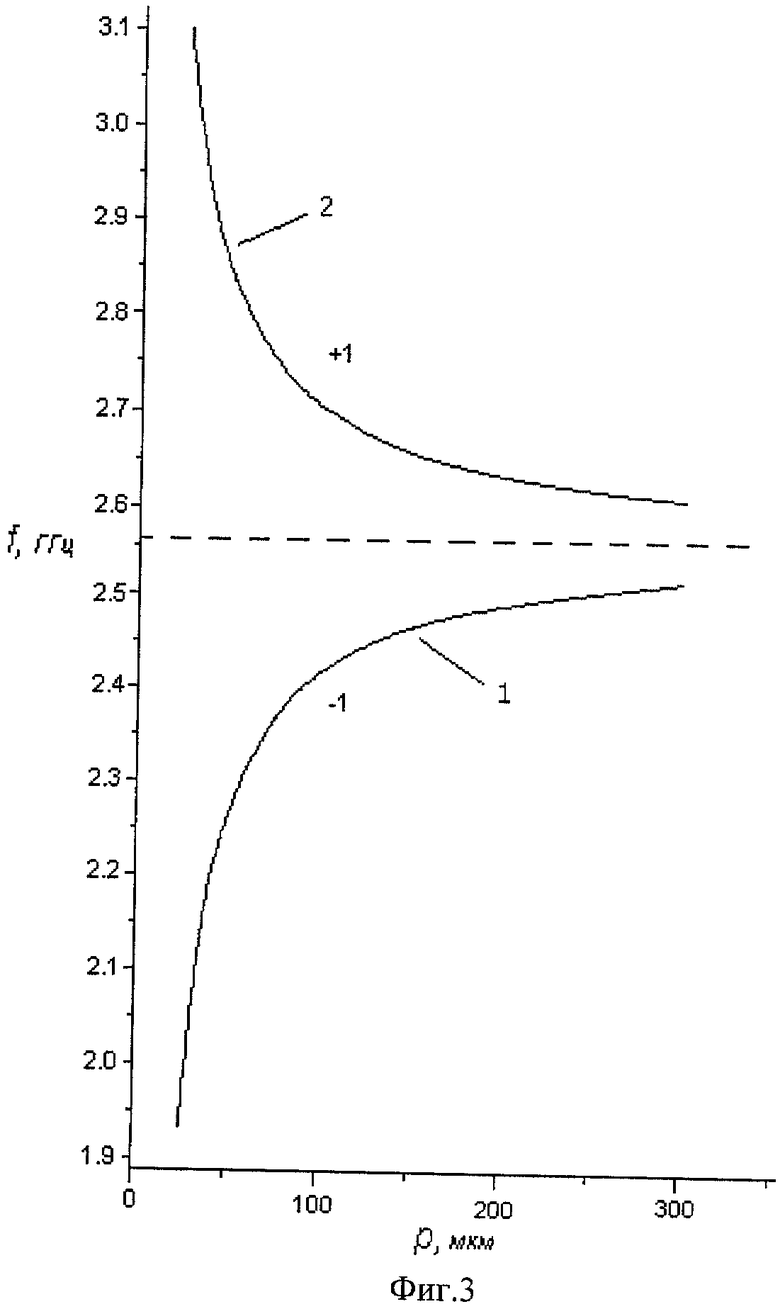
- волновой вектор дифрагированной необыкновенной световой волны, 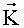 - волновой вектор акустической волны, β - угол между направлением распространения акустической волны и осью Y кристалла, θi - угол падения световой волны, θd - угол дифракции, θl - угол падения света относительно оси Y кристалла; на фиг.2 изображена рассчитанная частотно-угловая характеристика для анизотропного дефлектора на ниобате лития YZ+1200 среза с многоэлементным преобразователем длиной 2 мм и периодом 200 мкм; на фиг.3 - зависимость центральной частоты диапазона дефлектора от периода многоэлементного преобразователя, где кривая 1 показывает настройку дефлектора для работы на акустическом лепестке, соответствующем «-1» гармонике периодического преобразователя, кривая 2 - настройку дефлектора для работы на акустическом лепестке, соответствующем «+1» гармонике.
- волновой вектор акустической волны, β - угол между направлением распространения акустической волны и осью Y кристалла, θi - угол падения световой волны, θd - угол дифракции, θl - угол падения света относительно оси Y кристалла; на фиг.2 изображена рассчитанная частотно-угловая характеристика для анизотропного дефлектора на ниобате лития YZ+1200 среза с многоэлементным преобразователем длиной 2 мм и периодом 200 мкм; на фиг.3 - зависимость центральной частоты диапазона дефлектора от периода многоэлементного преобразователя, где кривая 1 показывает настройку дефлектора для работы на акустическом лепестке, соответствующем «-1» гармонике периодического преобразователя, кривая 2 - настройку дефлектора для работы на акустическом лепестке, соответствующем «+1» гармонике.
Предлагаемый способ осуществляют следующим образом. В анизотропном кристалле выбранного среза, соответствующего максимальным значениям коэффициента акустооптического качества м2, с помощью многоэлементного электроакустического преобразователя возбуждают акустические волны, на которых при выполнении условия Брэгга и происходит широкополосная анизотропная дифракция падающего на кристалл монохроматического пучка света. Диаграмма направленности многоэлементного преобразователя имеет несколько акустических лепестков, интенсивность которых зависит от геометрических параметров многоэлементного преобразователя. При изменении частоты подаваемого на преобразователь электромагнитного сигнала происходит изменение направления распространения возбуждаемых преобразователем боковых акустических лепестков. Интервал изменения углов распространения определяется как частотой входного сигнала, так и периодом следования электродов многоэлементного преобразователя. Существует период многоэлементного преобразователя, при выборе которого изменение угла направления распространения акустического лепестка с изменением частоты и изменение угла падения света с частотой, необходимого для выполнения условия Брэгга, позволяют получить широкополосную дифракцию в диапазоне с центральной частотой, отличной от центральной частоты анизотропного акустооптического дефлектора с одноэлементным преобразователем. При этом значение центральной частоты диапазона акустооптического анизотропного дефлектора зависит от периода следования элементов многоэлементного электроакустического преобразователя, и поэтому период преобразователя выбирают в соответствии с этой зависимостью. Кроме того, центральная частота диапазона акустооптического анизотропного дефлектора зависит от направления поворота бокового акустического лепестка, на котором происходит дифракция, при изменении частоты электромагнитного сигнала. В результате дефлектор с многоэлементным преобразователем с конкретным периодом может работать в диапазонах с разными центральными частотами. В зависимости от требуемой центральной частоты дефлектор настраивают для работы с одним из боковых лепестков диаграммы направленности многоэлементного преобразователя путем изменения угла падения светового пучка на кристалл.
Зависимость центральной частоты диапазона акустооптического анизотропного дефлектора от периода следования элементов многоэлементного преобразователя устанавливают на основе частотно-угловых характеристик акустооптического анизотропного дефлектора с многоэлементным преобразователем, полученных теоретически или экспериментально для заданного интервала периодов.
Проанализируем частотно-угловую характеристику анизотропного дефлектора с многоэлементным преобразователем. В работе [1] исходя из законов сохранения энергии и импульса получено выражение зависимости оптимального угла падения световой волны от частоты для эффективной анизотропной дифракции θi:
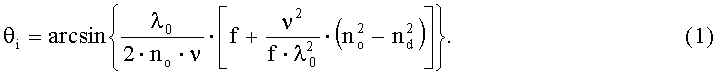
где λ0 - длина волны света в вакууме, ν - скорость упругой волны в кристалле, f - частота этой волны, no - показатель преломления падающей обыкновенной световой волны, nd - показатель преломления дифрагированной необыкновенной световой волны.
Метод расчета частотно-угловой характеристики основан на анализе оптических индикатрис показателей преломления обыкновенной и необыкновенной световых волн в кристалле и нахождении показателя преломления дифрагированной световой волны nd. На сегодняшний день самым перспективным материалом в качестве фотоупругой среды дефлекторов для работы в СВЧ-диапазоне является ниобат лития (LiNbO3). Этот материал обладает наименьшим коэффициентом затухания акустических волн Г при относительно высоком коэффициенте акустооптического качества М2 по сравнению с другими материалами, применяемыми в высокочастотных дефлекторах [6]. Поэтому как пример, в качестве фотоупругой среды был выбран именно кристалл ниобата лития. На фиг.1 изображена векторная диаграмма происходящей в плоскости YZ анизотропной дифракции на упругой волне, распространяющейся в направлении, составляющем угол β с осью Y. Для ниобата лития при β≈120° такая геометрия взаимодействия позволяет получить наиболее высокий коэффициент акустооптического качества [2].
Найдем выражение для показателя преломления дифрагированной волны nd, в котором в качестве параметров выступают зависящие от частоты направление упругой волны β и модуль ее волнового вектора K=2π·f/ν. Концы возможных волновых векторов дифрагированного света при заданных значениях этих параметров на фиг.1 отображаются точками 2, 4, 6 и 8. Искомая величина определяется значениями координат этих точек. Например, для точки 2:

Чтобы отыскать координаты точки 2, решим совместно систему уравнений:
1) уравнение окружности, которой принадлежит точка 1

2) уравнение эллипса, на котором расположена точка 2

3) уравнение прямой, проходящей через точки 1 и 2

4) уравнение для длины отрезка, соединяющего точки 1 и 2
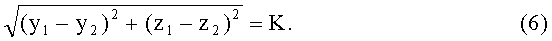
Система сводится к уравнению четвертой степени относительно неизвестной координаты y2:
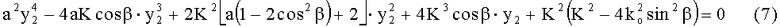
Здесь использованы обозначения: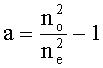 , где n0 - показатель преломления обыкновенной волны, ne - минимальная величина показателя преломления необыкновенной волны,
, где n0 - показатель преломления обыкновенной волны, ne - минимальная величина показателя преломления необыкновенной волны, 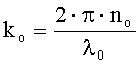 - модуль волнового вектора падающего света, λ0 - длина волны падающего света в вакууме,
- модуль волнового вектора падающего света, λ0 - длина волны падающего света в вакууме, 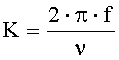 - модуль волнового вектора упругой волны, ν - скорость упругой волны, f - частота упругой волны. В общем случае это уравнение имеет четыре корня, которые определяют модули волновых векторов дифрагированного света, соответствующих точкам 2, 4, 6 и 8.
- модуль волнового вектора упругой волны, ν - скорость упругой волны, f - частота упругой волны. В общем случае это уравнение имеет четыре корня, которые определяют модули волновых векторов дифрагированного света, соответствующих точкам 2, 4, 6 и 8.
Используя введенные обозначения и уравнение (4), выражение (2) можно переписать

Следует отметить, что параметры уравнения (7) β и К в случае использования для возбуждения ультразвуковой волны многоэлементного преобразователя не являются независимыми. Направление распространения ультразвуковой волны β определяется срезом кристалла α и параметрами многоэлементного преобразователя. На высоких частотах для синфазного преобразователя оно задается выражением

где ρ - период многоэлементного преобразователя. В случае использования противофазного преобразователя значение величины р должно быть в два раза больше реального периода. Выбор знака "+" или "-" зависит от того на акустическом лепестке какой пространственной гармоники соответственно "+1" или "-1" происходит акустооптическое взаимодействие. Скорость же ультразвуковой волны ν вследствие анизотропии упругой среды сама зависит от направления распространения β. Для рассматриваемой геометрии акустооптического взаимодействия в ниобате лития [7]

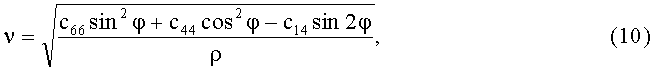
где с14, c44, с66 - упругие константы ниобата лития, ρ - его плотность, 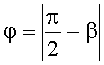 .
.
Таким образом, и частота f, и скорость ν, и показатель преломления дифрагированной волны nd, входящие в качестве параметров в выражение (1), зависят от угла β. Поэтому предлагаемый алгоритм нахождения частотно-угловой характеристики имеет вид:
1) Задаем срез кристалла α.
2) Выбираем пределы и шаг изменения направления распространения упругой волны β.
3) Для каждого заданного значения β по формуле (10) определяем величину скорости упругой волны ν.
4) С учетом найденной скорости упругой волны ищем ее частоту, работая на которой многоэлементный преобразователь излучает акустический лепесток в направлении β:

5) При заданных величинах параметров α, β и ρ находим модуль волнового вектора упругой волны:

6) Решаем уравнение четвертой степени (7), полученное из указанной выше системы геометрических уравнений, и определяем показатель преломления дифрагированной световой волны nd для конкретного значения направления распространения ультразвука β.
7) Подставляя найденные значения ν, f и nd в формулу (1), получаем угол Брэгга для падающей световой волны θi.
8) Этот угол отсчитывается относительно нормали к направлению упругой волны (фиг.1), которое изменяется при смене частоты волны. Поэтому в заключение вычисляем требуемый угол падения света относительно оси Y кристалла θl:

9) Откладывая вдоль осей координат величины, найденные в п.4 и п.8, для всего диапазона изменений угла β, получаем частотно-угловую характеристику анизотропного акустооптического дефлектора с многоэлементным преобразователем заданного периода.
Как пример, на фиг.2 показана рассчитанная частотно-угловая характеристика для анизотропного дефлектора на ниобате лития YZ+120° среза с многоэлементным преобразователем длиной 2 мм и периодом 200 мкм. Область углов, в которой снижение эффективности акустооптического взаимодействия не превышает 3 дБ, ограничена сплошными линиями. Полоса частот составляет величину около 420 МГц при центральной частоте 2633 МГц.
Анализ частотно-угловых характеристик анизотропных дефлекторов на ниобате лития YZ+120° среза с преобразователями одинаковой длины и различными периодами следования электродов позволил установить зависимость центральной частоты диапазона дефлектора от периода многоэлементного преобразователя. Для геометрии взаимодействия, соответствующей точке 2 (фиг.1), эта зависимость показана на фиг.3. Центральная частота анизотропного дефлектора на ниобате лития YZ+120 среза с одноэлементным преобразователем отмечена на фиг.3 пунктирной линией и равна 2563 МГц. Необходимо отметить, что направление распространения упругой волны при рассмотренных значениях периода изменяется от 116° до 123°, что близко к оптимальной с точки зрения эффективности дифракции величине 120°.
Для экспериментальной проверки предлагаемого способа был изготовлен опытный образец анизотропного дефлектора на кристалле ниобата лития YZ+120° среза с синфазным спиральным преобразователем, состоящим из 10 витков медного провода диаметром 100 мкм, намотанного с периодом 200 мкм. С помощью этого преобразователя в кристалле возбуждалась медленная сдвиговая волна, на которой и происходила дифракция пучка света от He-Ne лазера. По результатам измерений центральная частота дефлектора составила 2,49 ГГц, а абсолютная полоса частот - 420 МГц при дифракции падающего оптического пучка на акустическом лепестке, соответствующем «-1» гармонике. Настройка дефлектора путем изменения угла падения света для работы с акустическим лепестком диаграммы направленности преобразователя, соответствующим «+1» гармонике, обеспечивала работу устройства в полосе 410 МГц с центральной частотой 2,63 ГГц. Полученные экспериментально величины центральных частот анизотропного дефлектора хорошо совпадают со значениями, рассчитанными теоретически (фиг.3).
Список используемой литературы
1. Dixon R.W. Acoustic diffraction of light in anisotropic media // IEEE J. Quantum Electron. 1967. Vol. QE-3. №.2. P.85-93.
2. Демидов А.Я., Задорин А.С., Пуговкин А.В. Широкополосная аномальная дифракция света на гиперзвуке в кристалле LiNbO3 // Акустооптические методы и техника обработки информации: межвузовский сборник. Ленинград: ЛЭТИ, ЛИАП, 1980. С.106-111.
3. Балакший В.И., Парыгин В.Н., Чирков Л.Е. Физические основы акустооптики. М.: Радио и связь, 1985. 280 с.
4. US patent №5576880. G02F 1/33. Acousto-optic Bragg cell / I-Cheng Chang. Date of Patent - Nov. 19, 1996.
5. Advances in acousto-optics - 2000, / Special issue., Pure & Appl. Opt., v.3, #4, P. S1-S101, 2001.
6. Акустические кристаллы: Справочник / Под ред. М.П.Шаскольской. М.: Наука, 1982, 632 с.
7. Кайно Г. Акустические волны: Устройства, визуализация и аналоговая обработка сигналов / Пер. с англ. Под ред. О.В.Руденко. М.: Мир, 1990, 656 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Акустооптический элемент Брэгга | 2018 |
|
RU2677117C1 |
| СПОСОБ ОТОБРАЖЕНИЯ КАРТИНЫ ПОЛЯ СТОЯЧЕЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ В МНОГОЭЛЕМЕНТНОМ ЭЛЕКТРОАКУСТИЧЕСКОМ ПРЕОБРАЗОВАТЕЛЕ | 2012 |
|
RU2530478C2 |
| КОЛЛИНЕАРНЫЙ ОПТИЧЕСКИЙ ФИЛЬТР | 2002 |
|
RU2208825C1 |
| АКУСТООПТИЧЕСКИЙ МОДУЛЯТОР СВЕТА | 2010 |
|
RU2448353C1 |
| НЕКОЛЛИНЕАРНЫЙ ОПТИЧЕСКИЙ ФИЛЬТР | 2002 |
|
RU2208824C1 |
| АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР | 1997 |
|
RU2136032C1 |
| АКУСТООПТИЧЕСКИЙ СПЕКТРОАНАЛИЗАТОР | 2012 |
|
RU2512617C2 |
| СПОСОБ ОТКЛОНЕНИЯ СВЕТОВОГО ПУЧКА | 1973 |
|
SU363873A1 |
| МНОГОЭЛЕМЕНТНЫЙ ЭЛЕКТРОАКУСТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ | 1995 |
|
RU2085983C1 |
| УСТРОЙСТВО ДЛЯ ЭЛЕКТРОННОГО ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ГОЛОГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ | 1996 |
|
RU2115148C1 |
Изобретение относится к акустооптике и может быть использовано в приборах отклонения и модуляции лазерных пучков. Способ включает возбуждение акустической волны в фотоупругой среде акустооптического анизотропного дефлектора посредством многоэлементного электроакустического преобразователя. Период следования элементов преобразователя выбирают в соответствии с предварительно установленной зависимостью центральной частоты диапазона акустооптического анизотропного дефлектора от периода следования элементов многоэлементного преобразователя. Осуществляют настройку акустооптического анизотропного дефлектора путем изменения угла падения света на фотоупругую среду для работы с одним из боковых акустических лепестков диаграммы направленности многоэлементного преобразователя. Зависимость центральной частоты диапазона анизотропного акустооптического дефлектора от периода следования элементов преобразователя определяют на основе полученных для заданного интервала периодов следования элементов преобразователя частотно-угловых характеристик акустооптического анизотропного дефлектора с многоэлементным электроакустическим преобразователем. Технический результат заключается в обеспечении возможности выбора центральной частоты диапазона анизотропного акустооптического дефлектора без изменения геометрии среза кристалла. 3 ил.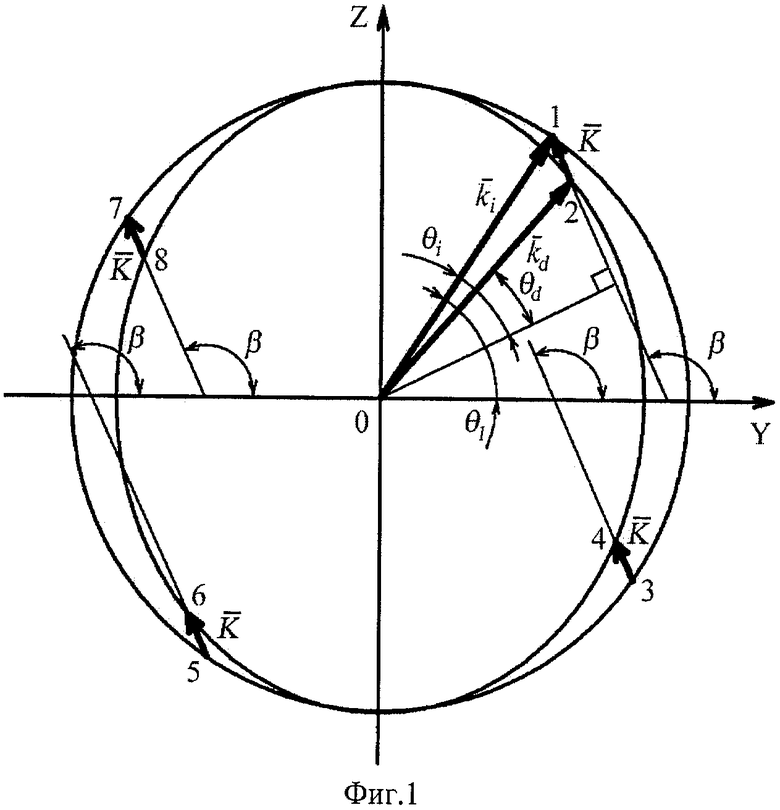
Способ изменения центральной частоты диапазона акустооптического анизотропного дефлектора, включающий возбуждение акустической волны в фотоупругой среде акустооптического анизотропного дефлектора посредством многоэлементного электроакустического преобразователя, период следования элементов которого выбирают в соответствии с предварительно установленной зависимостью центральной частоты диапазона акустооптического анизотропного дефлектора от периода следования элементов многоэлементного преобразователя, и настройку акустооптического анизотропного дефлектора путем изменения угла падения света на фотоупругую среду для работы с одним из боковых акустических лепестков диаграммы направленности многоэлементного преобразователя, при этом зависимость центральной частоты диапазона анизотропного акустооптического дефлектора от периода следования элементов преобразователя определяют на основе полученных для заданного интервала периодов следования элементов преобразователя частотно-угловых характеристик акустооптического анизотропного дефлектора с многоэлементным электроакустическим преобразователем.
| US 5576880 А, 19.11.1996 | |||
| АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР | 1997 |
|
RU2136032C1 |
| US 20080180782 A1, 31.07.2008 | |||
| Способ коррекции угла брэгга в ультразвуковых дефлекторах светового луча | 1978 |
|
SU744422A1 |
| WO 2004109370 A2, 16.12.2004. | |||
Авторы
Даты
2012-09-20—Публикация
2011-03-17—Подача