Изобретение относится к цифровой вычислительной технике, а именно к цифровым вычислительным системам для обработки входной информации о характеристиках боевых средств разнородных группировок, ее преобразовании, выбора необходимой стратегии, формирования критериев противоборства с выявлением исхода (победа, поражение, паритет) боевых действий, оценки своих потерь и нанесенного противнику ущерба при выборе оптимальных и других стратегий обеими сторонами. Оно может быть использовано командным составом Вооруженных Сил в процессе его обучения и переучивания, проведения командно-штабных учений и непосредственно для планирования групповых боевых действий (ГБД) с разнородными группировками. Техническим результатом является расширение арсенала технических средств для повышения эффективности и результативности боевых действий за счет планирования способа и создания устройства выбора оптимальной стратегии целераспределения по разнородным групповым объектам.
Предлагаемый способ и реализующее его устройство также могут быть использованы и при организации борьбы с террористическими бандами при охране и обороне важных государственных объектов.
Известен способ [1-4], который раскрывает динамику боя одной группировки против другой и позволяет до его проведения назвать будущего победителя. Однако не известен способ ведения боевых действий (БД) разнородных группировок с оценкой его результативности. В приведенных источниках, во-первых, не рассматриваются БД сторон, состоящих из группировок, включающих разнородные боевые средства (БСр) с неодинаковыми характеристиками, поэтому не может быть осуществлен и выбор правильной стратегии групповых БД. Во-вторых, не оценивается цена достигнутой победы, отсутствует количественная оценка нанесения максимального ущерба противнику при победе или поражении от него. Третьим недостатком при ведении БД является существующее смещение акцентов в сторону соотношения количества БСр сторон, а не соотношения интенсивностей ведения поражающего огня сторонами, не учет которого приводит не только к снижению боевой эффективности и даже к поражению одной из сторон при групповых БД в случае неправильно выбранной стратегии.
Известен способ [5], устраняющий эти недостатки, но он учитывает ведение БД стороной А против двух разнородных группировок стороны В. В данном способе не рассматривается ситуация, при которой сторона А тоже включает две разнородные группировки. Отсюда ряд неопределенностей. Во-первых, не известна стратегия ведения БД двух разнородных группировок стороны А против двух разнородных группировок другой стороны В: то ли стороне А вначале необходимо уничтожить более сильную группировку, а затем слабую, либо наоборот; рассматривать ли вариант распределения БСр стороной А на одновременное уничтожение обеих группировок противника;
планировать ли БД стороне А таким образом, чтобы каждая группировка вела автономное боевое противоборство с одной их группировок неприятеля.
Вторым недостатком способа [5] является не учет выбора стратегии стороной В, несомненно влияющей на результативность БД. Возникает ситуация, требующая рассмотрения знания противником выбора своей оптимальной стратегии.
Третьим недостатком способа служит отсутствие для данного сценария оценки исхода предстоящих БД до их проведения (на чьей стороне будет победа), прогнозирования цены победы над противником (оценки своих потерь), в случае поражения - нанесения максимального ущерба противнику с определением количества оставшихся у него непораженных БСр при разных стратегиях сторон А и В.
Имеются патенты [6-9], направленные на создание аппаратуры приема и реализации целеуказания, которые не устраняют выявленные недостатки и не решают сформулированную авторами задачу.
Поэтому возникает потребность в разработке такого способа и устройства, которые позволили бы устранить выявленные недостатки.
В отличие от известных способов ведения групповых боевых действий (ГБД) повышение боевой эффективности в предлагаемом изобретении осуществляется за счет учета:
- показателей БСр состава всех группировок сторон;
- разнородности группировок обеих сторон;
- выбора оптимальной стратегии ведения ГБД стороной А;
- выбора оптимальной стратегии противоборствующей стороной В;
- влияния выбора других стратегий на результативность ГБД противоборствующих сторон;
- исхода предстоящих боевых действий до их проведения (на чьей стороне будет победа), прогнозирования цены победы над противником (оценки своих потерь), в случае поражения - нанесения максимального ущерба противнику с определением количества оставшихся у него непораженных БСр при разных стратегиях сторон А и В.
1. Согласно изобретению технический результат достигается тем, что коммутируют информацию о показателях всех боевых средств каждой из группировок сторон, записывают ее в первый блок памяти, отличающийся тем, что ее пересылают в арифметический блок определения коэффициентов превосходства для каждой из применяемых ими стратегий, записывают их значения во второй блок памяти, передают их в блок сравнения, в котором сравнивают с пороговым значением, в случае превосходства принимают решение о победе стороны А, в противном случае - о поражении, превосходящие пороговое значение величины коэффициентов превосходства посылают в блок определения максимума для выбора оптимальной стратегии для стороны А, информацию о показателях боевых средств передают в вычислительный блок, в котором определяют остатки боевых средств сторон после завершения боевых действий и пересылают в третий блок памяти, с помощью блока выбора результатов боевых действий через сигналы с блока управления воздействуют на второй и третий блоки памяти и передают информацию о результатах в блок визуализации, с которого осуществляются считывание и выбор оператором оптимальной стратегии, прогнозирования исхода боевых действий и их результатов.
Сущность способа заключается в следующем.
Известно математическое описание двустороннего боя с помощью дифференциальных уравнений динамики боя [1-4]. При этом каждая из двух сторон А и В включает группировку из однородных боевых средств (БСр).
Представляет интерес рассмотрение двусторонних БД с разнородными группировками, когда сторона А имеет две разнородные группировки А1 и А2. Противостоящая ей сторона В включает также две разнородные группировки B1 и В2. Показателями БСр стороны А до начала (t≤0) групповых БД будут:
M1, М2 - первоначальное количество боевых средств группировок A1 и А2;
µ11=p11 f11, µ12=p12 f12 - интенсивности поражающего огня БСр группировки A1, пропорциональные вероятностям поражения целей одним выстрелом p11, p12 и скорострельностям БСр f11, f12, осуществляемым по БСр группировок B1 и В2;
µ21=p21 f21, µ22=р22 f22 - интенсивности поражающего огня БСр группировки А2, пропорциональные вероятностям поражения целей одним выстрелом р21, р22 и скорострельностям БСр f21, f22, осуществляемым по БСр группировок B1 и В2.
В процессе ГБД (t>0) убывающие величины M1, М2 в момент времени t обозначаются m1(t), m2(t).
Группировки B1 и В2 стороны В имеют аналогичные показатели: N1, λ11=p11f11, n1(t), λ12=p12f12, n2(t), и N2, λ21=p21f21, λ22=p22f22, n2(t) ведения БД по БСр группировок A1 и А2 стороны А.
При одновременном начале БД группировок A1 и A2 с группировками B1 и B2 в зависимости от исходных данных возникают следующие проблемные вопросы:
- на чьей стороне будет победа?
- существует ли критерий (математическое выражение), подставив в которое исходные данные до начала ГБД, можно ответить на первый вопрос?
- какой ценой досталась победа, т.е. сколько осталось БСр у победившей стороны?
- в случае поражения стороны А, какая ее стратегия приводит к нанесению максимального ущерба противнику, и каков он?
- каким образом на результатах БД сказывается выбор своей оптимальной стратегии?
- каким образом на результатах БД сказывается выбор противником оптимальной стратегии?
- каким образом на результатах БД сказывается отклонение сторон от оптимальных стратегий.
В существующей литературе [1-4] при ведении БД между двумя сторонами с однородными БСр ответы на первые два вопроса имеются. Наличие разнородных группировок у сторон затрудняет получение ответа на все поставленные вопросы. Сценарий боевого противоборства (БПб) сторон, имеющих по две разнородные группировки, предполагает доступность ведения БД для каждой из группировок обеих противостоящих сторон.
Обоснование оптимальной стратегии БД для обеих сторон должно предусматривать выполнение следующих основных этапов:
1) формирование таблицы исходных данных (показателей) БСр противостоящих сторон;
2) формирование вариантов взаимодействия (выработки стратегии) для собственных группировок A1 и А2;
3) учет формирования вариантов взаимодействия группировок B1 и B2 для стороны В;
4) выбор критерия оптимальности ведения БД;
5) выбор метода моделирования двусторонних БД;
6) оценка результатов БД для разных вариантов БПб;
7) обоснование алгоритма и оптимальной стратегии БД сторон.
Раскроем содержание каждого из этапов.
1. Для наглядности оценки влияния каждого из вариантов на результаты БПб придадим характеристикам БСр численные значения, приведенные в таблице 1.
2. Рассмотрим стратегии (варианты взаимодействия) группировок A1 и А2 в совместных групповых БД.
Возможные варианты взаимодействия группировок БПб обеих сторон показаны в таблице 2, в которой введены обозначения следующих вариантов взаимодействия группировок A1 и А2 на первом этапе БД (столбец 1):
А→В2 - вариант, когда группировки A1 и А2 совместно ведут БД против группировки В2;
A1→B1; А2→В2 - вариант БД, когда группировка A1 ведет БД против группировки B1, группировка А2 - против В2;
A1→B2; A2→B1 - вариант перекрестных БД, когда группировка A1 ведет БД против группировки В2, группировка А2 - против B1;
A→B1 - вариант, когда группировки A1 и А2 ведут БД против группировки B1.
После завершения первого этапа БД оставшиеся БСр группировок стороны А будут совместно действовать на втором этапе против не уничтоженной группировки противника.
3. Формирование вариантов взаимодействия группировок B1 и B2 для стороны В аналогично вариантам ведения БД стороной А, являющееся отображением вариантов стороны А. Таких вариантов 4 (столбцы 2-5). В результате имеем матрицу 4×4=16 вариантов взаимодействия группировок (стратегий) каждой из сторон А и В (для стороны А - столбец 1, для стороны В - строка 1 таблицы 2).
Для краткости каждую из 16 стратегий удобно записать в виде Sγ или Si-j. В первом случае γ=1,16; во втором i=1,4; j=1,4. Например, стратегии сторон, отмеченные в 1-й строке и 2-м столбце таблицы 2:S{A→B2; A1←B}, возможно кратко записать S1, либо S1-1. Стратегии сторон, отмеченные в 4-й строке и 5-м столбце таблицы 2:S{A→B1; A2←B}, можно записать как S16, или S4-4.
4. Критерий оптимальности K(Si-j) ведения БД сторон должен удовлетворять следующим условиям:
- возможность прогнозирования результатов БД:

- отражать влияние стратегии на результаты БД: чем выше величина K(Sγ), тем предпочтительнее стратегия Sγ, другими словами, неравенство
K(S1)>K(S2)>…>K(Sm-1)>K(Sm)
ведет к предпочтительности стратегий
S1>S2 >…>Sm-1>Sm;
- учитывать влияние стратегий обеих сторон на результаты БД.
В качестве критерия оптимальности можно выбрать математические выражения F1 или F2:
- величина F1(Mi, Nj, µij, λji, Sγ)=К1, полученная путем моделирования двусторонних БД, точна, но сложна и неудобна при использовании;
- величина F2(Mi, Nj, µij, λji, Sγ)=К2, отражающая коэффициент превосходства используемой стратегии в БД обеими сторонами, менее точна, но проста, наглядна и удобна при расчетах.
Итак, в качестве критерия F2=К2 возьмем отношение боевых потенциалов БСр сторон - коэффициентов превосходства, которыми характеризуется каждая группировка, использующая выбранную стратегию.
Например, для стратегий S1-1, S4-4, критерии примут вид
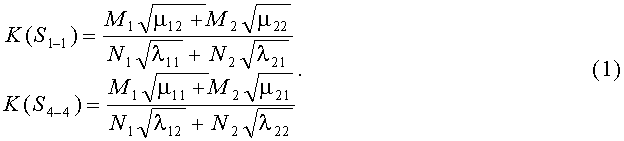
В таблице 3 к критериям (1) добавлены остальные 14 для обозначения разных стратегий сторон. Там же приведены их численные значения по исходным данным таблицы 1.
Из количественных значений, приведенных в таблице 3, должны быть сделаны следующие выводы:
- для стороны А оптимальной является стратегия S{A→B2}, так как K{S1-1} среди других значений, приведенных в первом столбце таблицы 3 наибольшее (K{S1-1}=1.082→max) в случае использования стороной В наихудшей стратегии S{A1←B};
- при выбранной стратегии победа будет на стороне А в связи с тем, что K{S1-1}=1.082>1;
- использование противником также оптимальной стратегии S{A2←B} снижает критерий K{S1-1}=1.082 до K{S1-4}=1.034, но, по-прежнему, с победой стороны А, т.к. K{S1-4}=1.034>1 (победа будет обеспечена стороне А, но с большими потерями);
- отклонение стороны А от оптимальной стратегии S1-1, например, к S4-1, ведет к уменьшению критерия K{S4-1}=1.024<1.082 (при этом, по-прежнему, победа будет на стороне А);
- использование противником оптимальной стратегии S{А2←В} снижает неоптимальный критерий K{S4-1}=1.024 до K{S4-4}=0.979<1, что ведет к поражению стороны А;
В общем случае критерий превосходства K(SA, SB) стороны А над стороной В с учетом соответствующих коэффициентов целераспределения r1, r2 БСр группировок A1, А2 и ρ1, ρ2 БСр группировок B1, В2 представляется в следующем виде:
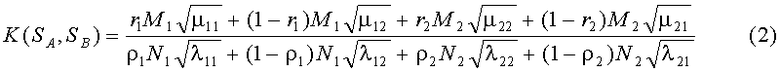
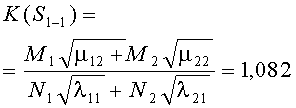
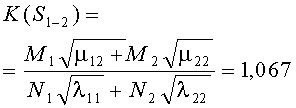
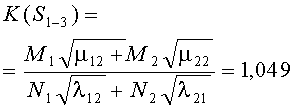
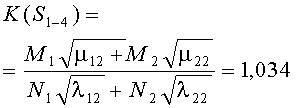
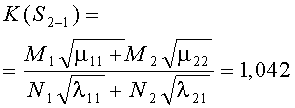
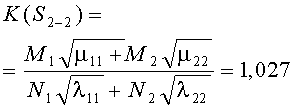
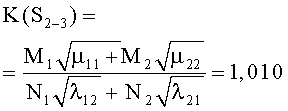
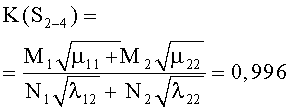
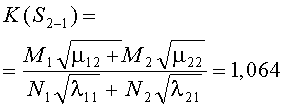
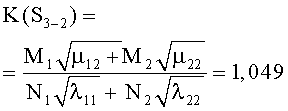
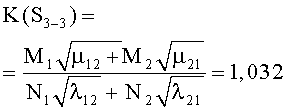
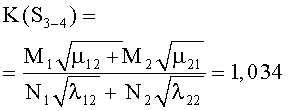
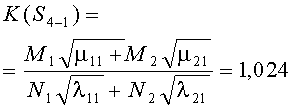
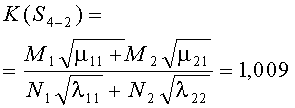
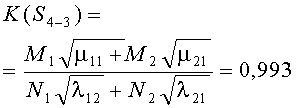
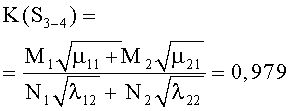
Из приведенного аналитического соотношения первый критерий K(S1-1) формулы (1) получается как частный случай формулы (2) при значениях r1=0, r2=1; ρ1=1, ρ2=0. Второму критерию K(S4-4) формулы (1) соответствуют следующие значения коэффициентов распределения БСр r1=1, r2=0; ρ1=0, ρ2=1.
Придавая коэффициентам распределения r1, r2; ρ1, ρ2 значения 0 или 1, можно полностью заполнить таблицу 3. Другими словами, выбор численных значений коэффициентов распределения БСр r1, r2; ρ1, ρ2 характеризует выбор стратегий БД группировок обеих сторон.
5. Описание динамики двусторонних боевых действий (БД) при их моделировании производят с помощью следующих дифференциальных уравнений Ланчестера:
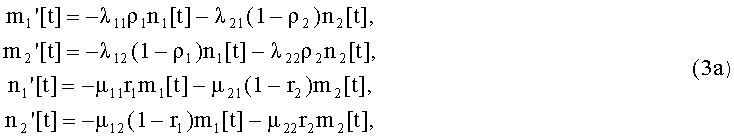
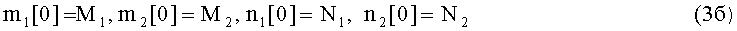
с численными значениями исходных данных, взятыми из таблицы 1
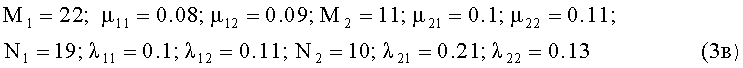
Решение дифференциальных уравнений (3а) в общем виде для всех стратегий S1÷S16 было получено авторами, но из-за громоздкости выражений целесообразно его продемонстрировать на конкретном сценарии для стратегий S1-1 сторон при r1=0, r2=1, ρ1=1, ρ2=0. Полученное аналитическое выражение можно представить в следующем виде:
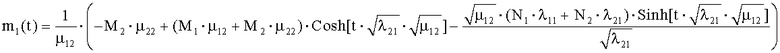
m2(t)=M2;
n1(t)=N1
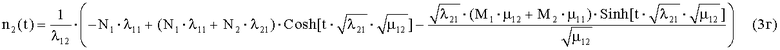
Окончание первого этапа БПб определяется равенством n2[t1∞], решение которого фиксирует время его окончания
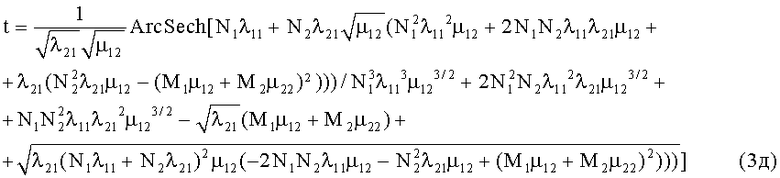
Для приведенных исходных данных (3в) в момент t1∞=3.63 фиксируется численность оставшихся БСр сторон М1=13, М2=11, N1=19, N2=0.
Динамика второго этапа будет проходить без группировки В2 с обновленными исходными данными (4б) и описываться следующими дифференциальными уравнениями
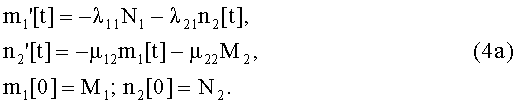
Исходные данные 2-го этапа БД
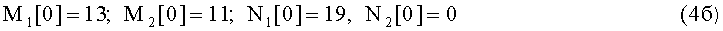
Решение дифференциальных уравнений (4а) в общем виде (4в) может быть представлено в следующем виде:
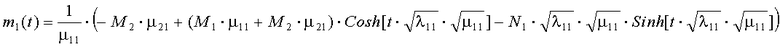 ;
;
m2(t)=M2;
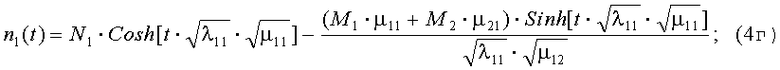
n2(t)=0.
Фиксирование окончания второго этапа БПб t2∞ определяется решением уравнения n1[t]=0. В этот момент находится и численность БСр {M1=3, М2=11, N1=0, N2=0}. Остаток БСр стороны А после завершения БПб для стратегий S{A→B2 и А1←В} составляет M∞=3+11=14, у стороны В N2∞=N1∞=0.
6. Оценка результатов БД для разных вариантов БПб. По аналогии с расчетом рассмотренных стратегий S1-1 были определены результаты боевых действий для остальных стратегий S1-2÷S4-4, которые сведены в таблицу 4. В скобках повторно показаны значения коэффициентов превосходства стороны А, взятые из таблицы 3.
7. Обоснование оптимальной стратегии S{A→B2} БД стороной А, принятое по максимальному значению K{S1-1}=1.082, приводит к максимальному значению остатков своих БСр M∞=14.
Таблица 4 убедительно подтверждает правильность и обоснованность выдвигаемых авторами предложений:
во-первых, критерий K{SA, SB} соответствует требованиям, изложенным в п.4;
во-вторых, в предложенном способе не только рассматривается выбор стратегии SA (1-й столбец таблицы 4) стороной А, оптимальной для которой является стратегия S{A→B2} с остатком БСр М∞=14 (2-я строка, 2-й столбец таблицы), но и учитывается использование противоборствующей стороной В наихудшей стратегии S{A1←В}. Применение стороной В наилучшей стратегии S{А2←В} приводит к снижению остатка БСр стороны А до М∞=6 (строка 2, столбец 4);
в-третьих, пренебрежение, отклонение от оптимальной стратегии вместо S{A→B2} и использование худшей стратегии S{A→B1} - (строка 5, столбец 1) стороной А, ведет не только к снижению остатка БСр с М∞=14 до М∞=8 (строка 5, столбец 2), но и к полному разгрому стороны А М∞=0 в случае применения оптимальной стратегии S{A2←B} стороной В с остатком своих средств N∞=8 (строка 5, столбец 5);
в-четвертых, предложенный способ указывает на возможность дезинформации противника с целью выбора им неоптимального варианта ведения групповых БД с разнородными группировками.
На фиг.1 приведена структурная схема устройства, предназначенного для осуществления предлагаемого способа, а на фиг.2 представлены границы остатков БСр при выборе следующих стратегий:
S1-1 - лучшей с позиций стороны А и худшей для стороны В; S1-4 - лучшей со стороны А и лучшей в плане противоборства с позиций стороны В; S1-2, S1-3 - лучшей по отношению к стороне А при промежуточных стратегиях (между лучшей и наихудшей), выбранных стороной В; S4-1 - худшей по отношению к обеим сторонам А и В; S4-4 - худшей со стороны А и лучшей со стороны В; S4-2, S4-3 - худшей по отношению к стороне А при выбранных стороной В промежуточных стратегиях.
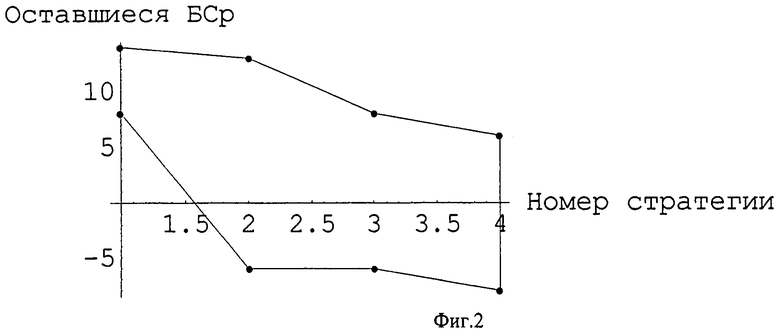
2. Устройство для реализации способа по п.1, изображенное на фиг.1, содержащее коммутатор 1 и первый блок 2 памяти, отличающееся тем, что в его состав введены арифметический блок 3, второй блок 4 памяти, блок 5 сравнения, блок 6 выбора максимума, блок 7 визуализации, вычислительный блок 8, третий блок 9 памяти, блок 10 выбора результатов боевых действий и блок 11 управления, при этом выход коммутатора 1 подключен к информативному входу первого блока 2 памяти, соединенного своим выходом 12 со входом 12 арифметического блока 3, выход 13 которого соединен со входом 13 второго блока 4 памяти, подключенного своим выходом ко входу блока 5 сравнения, выход 14 которого подключен ко входу 14 блока 6 выбора максимума и ко входу 14 второго блока 4 памяти, выход 15 блока 6 выбора максимума подключен ко входу 15 второго блока 4 памяти, соединенного своими выходами 16, 17, 18 с аналогичными входами блока 7 визуализации, выход 12 первого блока 2 памяти подключен ко входу 12 вычислительного блока 8, соединенного через третий блок 9 памяти с аналогичным входом 19 блока 7 визуализации, блок 10 выбора результатов БД соединен своим выходом со входом блока 11 управления, соединенного своими управляющими выходами с управляющими входами всех 1-10 блоков.
Работа устройства происходит следующим образом.
В соответствии с фиг.1 исходные значения показателей БСр всех группировок сторон A (A1, A2) и В (B1, B2), приведенные в таблице 1, поступают на входы коммутатора 1, и по управляющему сигналу с блока 11 управления подаются на вход первого блока 2 памяти. С выхода 12 первого блока памяти по управляющему сигналу с блока 11 управления значения показателей БСр поступают на входы 12 арифметического блока 3, в котором по формуле (1) вычисляется коэффициент превосходства K(S1-1) стороны А для стратегий S1-1 (в нашем случае K(S1-1)=1.082 - см. таблицу 3, 2-я строка, 2-й столбец). Данное значение по сигналу с блока 11 управления с выхода 13 арифметического блока 3 поступает на вход второго блока 4 памяти. Аналогичным путем по командам, посылаемым с блока 11 управления согласно формул таблицы 3, происходит вычисление в арифметическом блоке 3 остальных коэффициентов превосходства K(S1-2), …, K(S4-4) и запись их в соответствующие ячейки второго блока 4 памяти. В таблице 3 приведены значения всех 16 коэффициентов превосходства, зависимых от применяемых сторонами А и В стратегий БД.
По команде «К{16 стратегий}», выбранной на блоке 10 выбора результатов БД, поступающий на вход блока 11 управления сигнал осуществляет считывание со второго блока 4 памяти 16 коэффициентов превосходства (согласно таблице 3). Данные значения по входу 16 поступают на блок визуализации, представляющий командиру прогнозируемую картину БД в виде матрицы 4×4.
При необходимости конкретизации победного вектора стратегий S* используют следующее неравенство:

в котором Δ представляет собой погрешность ошибок округления, определяющих гарантированную победу. С этой целью с выхода второго блока памяти значения K(S1-16) поступают на вход блока 5 сравнения, осуществляющего проверку неравенства (5). Для стратегий S*, удовлетворяющих этому неравенству, коэффициенты превосходства по входу 14 записываются во второй блок 4 памяти. Определение оптимальной стратегии So находят путем решения уравнения и проверки выполнения следующего правила:
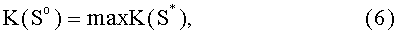
осуществляемого в блоке 6 выбора максимума из всех значений K(S*), поступаемых с выхода 14 блока сравнения. Максимальное значение K(So), фиксирующее оптимальную стратегию So, передается с выхода 15 блока 6 на аналогичный вход второго блока 4 памяти. При этом для просмотра величин K(S*), K(So) необходимо на блоке 10 выбора результатов БД выбрать команды «Победные стратегии» или «Оптимальная стратегия». В результате через блок 11 управления сигнал поступает на управляющий вход второго блока 4 памяти, с которого и передается соответственно с выходов 17, 18 на аналогичные входы блока 7 визуализации. Командир (оператор) считывает с блока 7 визуализации значения K(S*) или K(So), утвердившись в возможности победы только при стратегиях S*, либо при одной So.
При этом значения показателей БСр с выхода 12 первого блока 2 памяти поступают также и на вход 12 вычислительного блока 8, в котором по формулам (3а)÷(3д) и (4а)÷(4в) происходит вычисление остатков своих БСр M∞ и средств противника N∞ для всей матрицы, применяемых сторонами стратегий S1-16. Вся матрица остатков БСр записывается в третий блок 9 памяти. При необходимости знания цены победы по команде «Остаток БСр» с блока 10 сигнал передается на блок 11 управления. По сигналу блока 11 управления на управляющий вход третьего блока 9 памяти обеспечивают передачу матрицы остатков БСр в блок визуализации по входу 19, считывание которой позволит командиру принять наилучшее решение по участию своих группировок в боевых действиях.
Синхронизация работы блоков осуществляется с помощью блока 11 управления.
Реализация предложенного способа и устройства на первом этапе возможна в виде аппаратно-программного комплекса на ноутбуке, а на втором - в виде автономного прибора.
Источники информации
1. Жиров А.Ю. Военно-прикладная математика. Вероятностные основы оценки эффективности боевых и обеспечивающих действий авиации. - Монино: ВВА им. Ю.А.Гагарина, 2004. С.80-118.
2. Иванов П.И. и др. Основы и применение методов прикладной математики в военном деле. - Монино: ВВА им. Ю.А.Гагарина, 1991. С.186-224.
3. Вентцель Е.С. Введение в исследование операций. - М.: Сов. Радио,1964, 391 с.
4. Абчук В.А., Матвейчук Ф.А., Томашевский Л.П. Уравнения динамики боя/Справочник по исследованию операций. - М.: Военное изд-во министерства Обороны СССР, 1979, с.322-325.
5. Черноскутов А.И., Климов С.М. и др. Способ и устройство целераспределения по групповым объектам. Решение о выдаче патента на изобретение от 25.08.10 г., G06F 17/00, G0F 5/04, F41G 7/34, F41G 7/00.
6. Пархоменко О.Л. (RU) и др. Аппаратура приема и реализации целеуказания, патент №2236666, F41G 7/00.
7. Даниленко А.И. (RU) и др. Многопозиционная система определения местоположения объектов, патент №2073380, G01S 5/00.
8. Космическая автоматизированная система контроля за подвижными объектами. (RU), патент №2284550, G01S 13/06.
9. Беляев Б.Г. (RU) и др. Способ обнаружения групповых объектов, патент №2157550, G01S 5/00.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ОЦЕНКИ ВЛИЯНИЯ ЛОЖНЫХ БОЕВЫХ СРЕДСТВ В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2011 |
|
RU2547637C2 |
| СПОСОБ И УСТРОЙСТВО ОЦЕНКИ ВЛИЯНИЯ ЗАПАЗДЫВАНИЯ ВВОДА РЕЗЕРВА В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2012 |
|
RU2496084C1 |
| СПОСОБ И УСТРОЙСТВО ВЫБОРА СТРАТЕГИИ ЦЕЛЕРАСПРЕДЕЛЕНИЯ ПО ГРУППОВЫМ ОБЪЕКТАМ | 2010 |
|
RU2469386C2 |
| СПОСОБ ВЫБОРА ЭФФЕКТИВНОЙ СТРАТЕГИИ В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2017 |
|
RU2682374C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ ПО ВЫБОРУ ЭФФЕКТИВНОЙ СТРАТЕГИИ В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2017 |
|
RU2677386C1 |
| СПОСОБ ВЫБОРА ОПТИМАЛЬНОЙ СТРАТЕГИИ В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2017 |
|
RU2694019C2 |
| СПОСОБ И УСТРОЙСТВО ВЫБОРА РАЦИОНАЛЬНОЙ СТРАТЕГИИ В БОЕВЫХ ДЕЙСТВИЯХ ГРУППИРОВОК СТОРОН С ОДНОРОДНЫМИ БОЕВЫМИ СРЕДСТВАМИ | 2013 |
|
RU2571613C2 |
| СПОСОБ И УСТРОЙСТВО ЦЕЛЕРАСПРЕДЕЛЕНИЯ ПО ГРУППОВЫМ ОБЪЕКТАМ | 2008 |
|
RU2419140C2 |
| СПОСОБ И УСТРОЙСТВО ОБРАБОТКИ ИНФОРМАЦИИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ВЫБОРА РАЦИОНАЛЬНЫХ СТРАТЕГИЙ В БОЕВЫХ ДЕЙСТВИЯХ РАЗНОРОДНЫХ ГРУППИРОВОК | 2015 |
|
RU2602395C1 |
| Способ обработки информации, направленный на повышение эффективности боевых действий с разнородными группировками | 2016 |
|
RU2649849C1 |
Изобретение относится к области цифровых вычислительных систем для обработки входной информации о характеристиках боевых средств разнородных группировок. Техническим результатом является расширение арсенала технических средств для повышения эффективности боевых действий за счет планирования способа и создания устройства выбора оптимальной стратегии в боевых действиях разнородных группировок. Коммутируют информацию о показателях всех боевых средств каждой из группировок сторон, записывают ее в первый блок памяти, пересылают ее в арифметический блок определения коэффициентов превосходства для каждой из применяемых ими стратегий, записывают их значения во второй блок памяти, передают их в блок сравнения, в котором сравнивают с пороговым значением, в случае превосходства принимают решение о победе стороны А, в противном случае - о поражении, превосходящие пороговое значение величины коэффициентов превосходства посылают в блок определения максимума для выбора оптимальной стратегии для стороны А, информацию о показателях боевых средств передают в вычислительный блок, в котором определяют остатки боевых средств сторон после завершения боевых действий и пересылают в третий блок памяти, с помощью блока выбора результатов боевых действий через сигналы с блока управления воздействуют на второй и третий блоки памяти и передают информацию о результатах в блок визуализации, с которого осуществляются считывание и выбор оператором оптимальной стратегии, прогнозирования исхода боевых действий и их результатов. 2 н.п. ф-лы, 2 ил., 4 табл.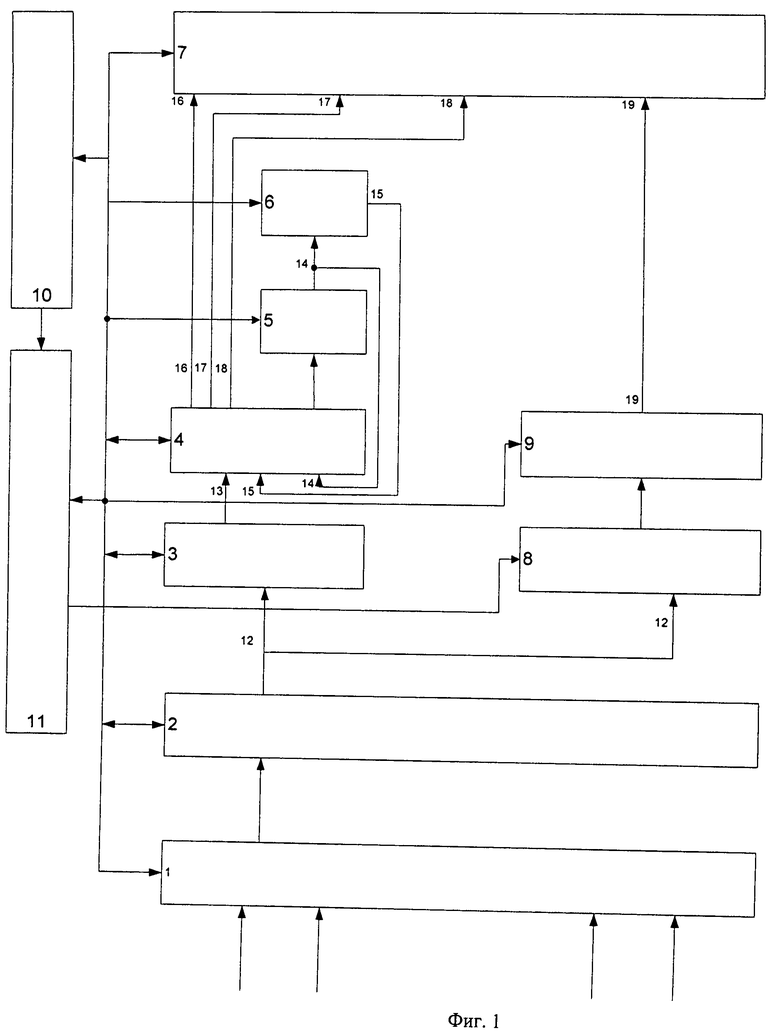
1. Способ выбора стратегии в боевых действиях разнородных группировок, заключающийся в том, что коммутируют информацию о показателях всех боевых средств каждой из группировок сторон, записывают ее в первый блок памяти, отличающийся тем, что информацию пересылают в арифметический блок определения коэффициентов превосходства для каждой из применяемых ими стратегий, записывают их значения во второй блок памяти, передают их в блок сравнения, в котором сравнивают с пороговым значением, в случае превосходства принимают решение о победе стороны А, в противном случае - о поражении, превосходящие пороговое значение величины коэффициентов превосходства посылают в блок определения максимума для выбора оптимальной стратегии для стороны А, информацию о показателях боевых средств передают в вычислительный блок, в котором определяют остатки боевых средств сторон после завершения боевых действий и пересылают в третий блок памяти, с помощью блока выбора результатов боевых действий через сигналы с блока управления воздействуют на второй и третий блоки памяти и передают информацию о результатах в блок визуализации, с которого осуществляют считывание и выбор оператором оптимальной стратегии прогнозирования исхода боевых действий и их результатов.
2. Устройство для реализации способа по п.1, содержащее коммутатор и первый блок памяти, отличающееся тем, что в его состав введены арифметический блок, второй и третий блоки памяти, блок сравнения, блок выбора максимума, блок визуализации, вычислительный блок, блок выбора результатов боевых действий и блок управления, при этом выход коммутатора подключен к информативному входу первого блока памяти, соединенного своим выходом со входом арифметического блока, выход которого соединен со входом второго блока памяти, подключенного своим выходом ко входу блока сравнения, выход которого подсоединен ко входу блока выбора максимума и ко входу второго блока памяти, выход блока выбора максимума подключен ко входу второго блока памяти, соединенного своими выходами с аналогичными входами блока визуализации, выход первого блока памяти подключен ко входу вычислительного блока, соединенного через третий блок памяти с аналогичным входом блока визуализации, блок выбора результатов боевых действий соединен своим выходом со входом блока управления, подключенного своими управляющими выходами с управляющими входами всех блоков.
| СПОСОБ ЛЕЧЕНИЯ МОЧЕКАМЕННОЙ БОЛЕЗНИ У СОБАК | 2009 |
|
RU2419440C2 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ МАТРИЧНЫХ ИГР | 0 |
|
SU304585A1 |
| СИСТЕМА ИНДИВИДУАЛЬНОГО УЧЕТА И СОРТИРОВКИ РАНЕНЫХ | 1994 |
|
RU2105350C1 |
| US 7155423 B1, 26.12.2006. | |||
Авторы
Даты
2012-11-20—Публикация
2011-09-20—Подача