Изобретение относится к бурению горизонтальных скважин и может быть использовано при их проводке.
Известна "Методика выбора комплекса мероприятий для предупреждения ликвидации осложнений, связанных с нарушением устойчивости пород в процессе бурения" (РД 39-0147009-723-88 [1]). Она предназначена для оперативной оценки геологических условий бурения, позволяет прогнозировать зоны возможных осложнений. По данной " Методике" для обеспечения устойчивости пробуренных и не закрепленных обсадными трубами участков ствола скважины, следует выбирать необходимую плотность бурового раствора на основании суммарной информации о градиентах поровых давлений.
Недостаток указанной "Методики" заключается в том, что она не учитывает влияния угла падения пластов или угла наклона горных пород к горизонту, что сужает область ее применения.
Известен способ управления процессом углубления и промывки скважины (см. «Поисковая работа по созданию системы методического и программного обеспечения проектирования, планирования и управления процессами углубления и промывки скважин», ВНИИКРнефть, ВНИИБТ, Краснодар, 1991, с.189-190 [2]).
В работе приведена зависимость между временем устойчивости стенок скважины, плотностью бурового раствора, поровым давлением и углом падения пластов (ф.6-37).
Однако данная зависимость (ф.6-37) имеет свои вполне определенные границы применимости и справедлива только при проводке вертикальных скважин.
К недостатку следует отнести то, что при проводке наклонно направленных скважин случаются нарушения устойчивости стенок скважины, то есть известная зависимость не учитывает постоянно изменяющийся зенитный угол искривления скважины.
Следствием этого могут быть затяжки при подъеме инструмента, посадки и проработки при его спуске, недоходы обсадных колонн и другое.
Наиболее близким к заявляемому по своей технической сущности является способ повышения эффективности бурения наклонно направленных горизонтальных скважин на участках с интенсивным искривлением за счет предупреждения осложнений, связанных с нарушением устойчивости стенок скважины (RU 2061835 [3]). В соответствии с этим способом, при бурении участков ствола с интенсивным искривлением в вертикально направленных скважинах, промывку производят буровым раствором, плотность которого рассчитывают с учетом суммарного угла, характеризующегося углом падения пластов и зенитным углом искривления скважины, по математической зависимости. В случае если величина расчетной плотности γi бурового раствора окажется больше заданной, эталонной γэт, принятой по данным ранее пробуренной скважины, то величину последней (γэт) корректируют (увеличивают) добавкой утяжелителя. В случае, когда γi меньше γэт, то процесс бурения продолжают на плотности γэт. Критерием оптимального управления бурением является поддержание такой плотности бурового раствора (γi) в любой момент бурения, которая обеспечит необходимое время устойчивого состояния стенок скважины.
Недостатком известного способа является невозможность его использования в пластах с ярко выраженной анизотропией механических и прочностных свойств.
Заявляемый в качестве изобретения способ определения устойчивости ствола горизонтальных скважин направлен на обеспечение устойчивости стенок скважины в любой момент бурения скважины в анизотропной слоистой породе, а также на упрощение необходимых испытаний образцов в условиях одноосного сжатия.
Указанный результат достигается тем, что способ определения устойчивости ствола горизонтальных скважин включает извлечение кернов из скважин, изготовление из них образцов цилиндрической формы, ось вращения которых образует с осью керна угол φ, величина которого определяется выражением:
φ=1/2(π/2-ρ),
где ρ - угол внутреннего трения породы, который определяют путем предварительного изготовления из кернового материала, отобранного из исследуемого интервала глубины, цилиндрических образцов, вырезанных под углами α1 и α2 относительно оси керна, которые подвергают одноосному сжатию с созданием напряжений N1 и N2 до полного разрушения по заданной программе и по полученным значениям N1 и N2 из соотношений:
1/2N1sin2α1=k+N1sin2α1tgρ,
l/2N2sin2α2=k+N2sin2α2tgρ,
где k - коэффициент сцепления,
вычисляют угол внутреннего трения,
приложение к образцам вдоль оси вращения одноосного сжимающего напряжения N, величину которого определяют по формуле:
N=-2(q+Pc),
где N - одноосное сжимающее напряжение, Па,
q - горное давление на данной глубине скважины, величина которого определяется по формуле
q=-γпh,
где γп - средняя плотность вышележащих горных пород, т/м3,
h - глубина скважины, м,
Pc - давление на забое скважины, равное произведению плотности бурового раствора на глубину h, Па,
измерение изменения величины осевой деформации образца со временем для каждой из различных величин прикладываемых напряжений N, при этом вычисляют скорость деформации и по снижению скорости деформации со временем при постоянном напряжении N делают вывод об устойчивости скважин и допустимости использования бурового раствора с плотностью γб.р.
γб.р.=-(q+N/2)/h,
а при постоянстве скорости деформации или ее росте - о недопустимости такого использования.
Для достижения заявленного результата авторами была создана математическая модель зависимости устойчивости стволов горизонтальных скважин от их геометрии, т.е. зависимость возникающих в окрестности скважины напряжений от степени анизотропии упругих и прочностных свойств породы, в которой осуществляется проводка скважины.
Для изотропной среды и равнокомпонентного горного давления распределение напряжений в окрестности скважины, (фиг.1), не зависит от ее угла наклона и определяется решением задачи Ламе.

где σr, σθ, σz - радиальное, кольцевое и осевое напряжения, действующие в окрестности скважины, фиг.1, Па;
q - горное давление (q<0), Па;
Рс - давление в скважине (Рс>0), Па;
Rc - радиус скважины, м;
r - расстояние от оси скважины, м.
Касательные напряжения
τ=1/2(σr-σφ) равны 
Нормальные напряжения, действующие в грунтовом скелете на произвольную площадку, равны

где P - давление в рассматриваемой точке пласта. Вокруг вертикальной скважины в трансверсально изотропной среде возникает такое же распределение напряжения, как и в изотропной среде.
При наклонной скважине картина меняется. Напряжения по контуру наклонной скважины в анизотропном пласте не являются постоянными, как в случае изотропной среды (для вертикальной скважины), а меняются от точки к точке, причем их величина зависит от модулей упругости породы и угла наклона скважины.
Несущая способность горных пород обусловлена в основном сопротивлением сдвигу и отрыву. Критическая величина сопротивления сдвигу в среде, которую в среднем считают однородной по всем направлениям, на данной ориентированной площадке, т.е. критерий местного разрушения, представляется в виде τ≥[τ], где [τ] - предел прочности и
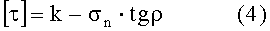
где k - коэффициент сцепления;
σn - нормальное напряжение на площадке;
ρ - угол трения - прочностные характеристики породы.
Если в породе имеются площадки ослабления (плоскость напластования), то разрушение начинается в первую очередь по ним, т.к. предел прочности [τ] на них значительно ниже, чем в других направлениях. В этом случае под k и ρ следует понимать коэффициент сцепления и угол трения на плоскостях напластования. Для наклонных скважин это означает, что разрушение начнется в первую очередь в тех точках на ее контуре, где касательное напряжение в плоскостях напластования достигают величины [τ]. При увеличении угла наклона скважины предельные касательные напряжения будут захватывать все большую область на контуре скважины. При достижении угла наклона определенной величины наступает момент, когда порода вблизи скважины уже не выдерживает действующих напряжений и разрушается. Это состояние, а следовательно, и соответствующие ему напряжения и угол наклона скважины будут предельными. Для потери устойчивости стенок скважины недостаточно, чтобы разрушение породы началось в одной точке или малой области контура скважины, необходимо, чтобы захваченная разрушением область стала достаточно большой. Таким образом, необходимо найти точку (или области), в которой в плоскости напластования раньше всего достигается состояние предельного равновесия, характеризуемое критерием [τ]=k-σп·tgρ.
На фиг.2 схематично показан участок наклонной скважины, пробуренной в горной породе, обладающей горизонтальным напластованием, где Z - вертикальная ось, Z' - ось скважины, θ - угол наклона скважины к вертикали, φ - угол между большой полуосью эллипса, получаемого в сечении наклонной скважины горизонтальной плоскостью (перпендикулярной оси Z), и рассматриваемой точкой - точкой, в которой в плоскости напластования раньше всего достигается состояние предельного равновесия, характеризуемого критерием (4).
Примем следующие обозначения: Po>0 - пластовое давление;
ΔP=Po-Pc - депрессия; xyz - декартовая система координат, связанная с напластованием (ось z - вертикальная ось, перпендикулярная к напластованию); rφz' - полярная система координат, связанная со скважиной; угол φ отсчитывается от оси x; τ - абсолютная величина касательных напряжений в плоскости предполагаемых ослаблений (горизонтальной плоскости); σп - напряжения, нормальные к плоскости предполагаемых ослаблений.
Для построения критерия разрушения необходимо знать касательные напряжения в плоскостях ослаблений и напряжения, нормальные к ней. Напряженное состояние в грунтовом скелете на контуре скважины для проницаемых пород согласно (1) и (3) определяется как

где Sz, Sr, Sφ - напряжения в грунтовом скелете в окрестности скважины, Па.
Абсолютная величина касательных напряжений в плоскости предполагаемых ослаблений (горизонтальной плоскости) при этом может быть вычислена путем преобразований компонент тензора напряжений к системе координат, связанной со слоистостью следующим образом

Сжимающие напряжения, нормальные к плоскости предполагаемых ослаблений, будут

Следовательно, наиболее опасными точками контура будут те точки, для которых раньше всего выполняется условие τ=[τ], где [τ] определяется соотношением (4).
В этих точках комбинация

где τ, Sn определяются (6) и (7), будет максимальной. Местонахождения точек локального экстремума комбинации (8) определяются из условия равенства нулю ее производной (по φ):

Уравнение (9) удовлетворяется, если либо

либо

Решение уравнения (10) существует всегда, в то время как действительное решение уравнения (11) для физически возможных значений параметров - нет. Действительно, для 0≤ρ≤π/2,0≤θ≤π/2 преобразуем (11) следующим образом




Действительное решение данного уравнения существует только, если правая часть последнего выражения не превосходит единицу:

Что выполняется при ρ≤0. Само решение имеет вид
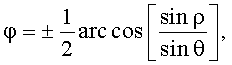

Таким образом, при 0≤θ≤ρ, имеются экстремумы в точках φ=0, φ=π - максимумы, и в точках φ=±π/2 - минимумы, а при 0≤ρ≤π/2 появляются дополнительные максимумы в точках  при этом в точках φ=0, φ=π максимумы сменяются минимумами.
при этом в точках φ=0, φ=π максимумы сменяются минимумами.
После нахождения значений критических углов φ условие разрушения получается подстановкой найденных значений в (8). Окончательно, величина критического угла φ и условие разрушения даются следующими формулами:
для
0≤θ≤ρ

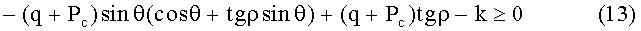
для
ρ≤θ≤π/2


Разрушение начинается, когда действующие по плоскостям ослабления касательные напряжения достигают предела прочности [τ]=k+σntgρ, где σn - нормальное напряжение к плоскости ослабления, а под k и ρ следует понимать модуль сцепления и угол трения на плоскостях напластования.
Горизонтальная скважина является предельным случаем наклонной скважины, когда угол наклона θ равен 90°. Поэтому для горизонтальной скважины с учетом того, что она бурится в проницаемых породах, остаются справедливыми соотношения (5) - (7), (14), (15), если в них положить θ=90°.
Тогда для касательного напряжения, действующего в плоскости напластования, для различных точек на контуре скважины из (6) получаем
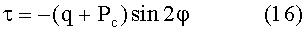
где угол φ отсчитывается от вертикальной оси поперечного сечения скважины.
Сжимающие напряжения, нормальные к плоскости напластования, согласно (7) равны

Согласно (15) касательное напряжение на контуре горизонтальной скважины (при θ=0) достигает максимума в точке, смещенной относительно вертикальной оси поперечного сечения скважины на угол

Из модели следует, что для горизонтальной скважины на контуре скважины в точке, расположенной под углом φ к оси скважины, возникают напряжения τ и Sn:


В цилиндрическом образце породы на площадке, расположенной под углом α к оси цилиндрического образца, возникают касательные и нормальные напряжения, которые определяются по формулам:


Таким образом, если к цилиндрическому образцу, отвечающему углу наклона скважины θ=π/2 (горизонтальная скважина), приложить сжимающее напряжение N=-2(q+Pc), то на плоскостях напластования возникнут касательные напряжения, вычисляемые по формуле (22), совпадающие с касательными напряжениями (19), действующими в плоскостях напластования в окрестности горизонтальной скважины.
Значение угла внутреннего трения ρ, необходимое для определения угла φ, при котором касательное напряжение на контуре достигает максимума, см. (18), для исследуемой породы определяется при испытании на одноосное сжатие двух образцов, вырезанных из керна горной породы под различными углами α1 и α2 к оси керна (например, под углами 30° и 45°).
В цилиндрическом образце, нагруженном одноосным сжатием напряжением N, на площадке, расположенной под углом α к направлению сжатия, касательные и нормальные напряжения соответственно равны:

Разрушение на данной площадке начнется, когда действующие на ней касательные напряжения достигают предела прочности [τ]=k+σntgρ, где σn - нормальное напряжение к плоскости ослабления, а под k и ρ следует понимать модуль сцепления и угол трения породы в плоскостях напластования.
Тогда с учетом (24) условие достижения на данной площадке предельного состояния будет:

Напряжения одноосного сжатия, приводящие к разрушению каждого из двух образцов, обозначим через N1 и N2. Тогда условия достижения предельного состояния на площадках ослабления для каждого из образцов будут:

Из уравнений (26) определяем значения прочностных характеристик породы k и ρ.
Изготовление из кернов образцов цилиндрической формы, ось вращения которых образует с осью керна угол φ, град, величина которого определяется выражением:
φ=1/2(π/2-ρ),
необходимо для того, чтобы, как следует из математической модели, при одноосном сжатии цилиндрических образцов иметь возможность создать в них такие же напряжения, которые возникают в плоскостях анизотропии породы в окрестности горизонтальной скважины.
Поскольку величина значения угла внутреннего трения породы ρ, необходимая для определения угла φ, при котором касательное напряжение на контуре достигает максимума, является неизвестной, то она для исследуемой породы определяется экспериментально путем испытания на одноосное сжатие двух образцов, вырезанных из керна горной породы под различными углами α1 и α2 к оси керна (например, под углами 30° и 45°).
Приложение к образцам вдоль оси одноосного сжимающего напряжения N, величину которого определяют по формуле:
N=-2(q+Pc),
где N - одноосное сжимающее напряжение, Па,
q - горное давление на данной глубине скважины (Па), величина которого определяется по формуле
q=-γпh,
где γп - средняя плотность вышележащих горных пород (кг/м3),
h - глубина скважины, м,
Рс - давление на забое скважины, равное произведению плотности бурового раствора на глубину h, (Па), необходимо для того, чтобы, как следует из математической модели, создать в цилиндрических образцах при одноосном сжатии напряжения, равные максимальным напряжениям, возникающим на контуре горизонтальной скважины.
Измерение изменения величины осевой деформации образца со временем для различных величин прикладываемых напряжений N и вычисление для каждой величины прикладываемого напряжения N скорости деформации позволяет для горизонтальной скважины определить допустимую минимальную плотность бурового раствора γmin, при которой не происходит нарушение устойчивости стенок скважины.
γmin=-(q+Nmin/2)/h,
где Nmin - минимальное значение одноосного сжимающего образец напряжения, при котором скорость деформации образца со временем уменьшается, Па.
Сущность заявляемого способа определения устойчивости ствола горизонтальных скважин поясняется чертежами и примерами реализации.
На фиг.1 представлена схема напряжений, возникающих в элементарном объеме вертикальной скважины; на фиг.2 схематично показан участок наклонной скважины, пробуренной в горной породе, обладающей горизонтальным напластованием; на фиг.3 представлена испытательная машина SHIMATZU, на которой производится одноосное испытание образцов горных пород.
Пример 1. В самом общем случае способ реализуется с помощью испытательной машины SHIMATZU, которая представлена на фиг.3. Машина содержит силовую раму, включающую в себя: основную раму с фиксированными боковыми сторонами, состоящую из основания 1, закрепленного на бетонном фундаменте болтами (на фиг.3 не показано), двух резьбовых штанг (ходовых винтов) 2, нижнего крейцкопфа 3; основную раму с подвижной стороной, прикрепляемую к раме с жесткой боковой стороной, состоящую из стола 4, соединенного со штоком гидроцилиндра 5, верхнего крейцкопфа 6, двумя колонками (стойками) 7 зигзагообразной конфигурации; двигателя подъемника 8 нижнего крейцкопфа 3, защитного мата 9 поверхности стола 4, нижней планшайбы 10, оправы 11 для установки верхней планшайбы 12, контроллера измерений 13. Испытываемый образец устанавливается между нижней и верхней планшайбами по определенной технологии.
Образцы устанавливают между планшайбами испытательной машины, так чтобы ось образца и ось машины совпадали. На образцы устанавливают измерительные клещи экстензометров (на фиг.3 не показаны), причем их устанавливают так, чтобы плоскость, в которой находится каждая пара клещей, была строго перпендикулярна оси образца. Затем измеряют расстояние между ножами клещей для осевой деформации и проверяют положение ножей для поперечной деформации (они должны опираться строго на диаметр образца). Далее задают программу нагружения, которая создает постоянную скорость нагружения образца. Для обеспечения режима квазистатического деформирования образца скорость деформирования  должна быть не более 10-61/с.
должна быть не более 10-61/с.
Для линейного участка диаграммы зависимости σ, ε нормальное напряжение будет определяться выражением σ=Еε. С учетом того, что для многих горных пород модуль упругости в плоскости изотропии (напластования) равен Е≈5·104 МПа, то скорость изменения нормального напряжения будет составлять σ≤5·10-2 МПа/с. Для образца диаметром d=L0=40 мм скорость нагружения  определяется выражением:
определяется выражением:
 Следующий образец испытывают так, чтобы скорость деформирования на протяжении всего процесса нагружения не превышала 10-61/с.
Следующий образец испытывают так, чтобы скорость деформирования на протяжении всего процесса нагружения не превышала 10-61/с.
В ходе опыта датчики нагружающей системы и экстензометра регистрируют F(t), Δd(t), Δl(t) (нагрузка на образец, изменение диаметра, изменение расстояния между ножами для продольной деформации).
На установке SHIMATZU задают программу нагружения, по которой в образцах породы возникают напряжения согласно формул (16) и (17), и определяют начало и скорость ползучести породы, соответствующие конкретным значениям глубины скважины, плотности бурового раствора и угла наклона скважины.
Для горизонтальной скважины, когда θ=0, наиболее опасной точкой на контуре скважины является точка, смещенная от вертикальной оси поперечного сечения скважины на угол φ, который равен: φ=1/2(π/2-ρ). В этой точке вычисляем касательное и нормальное напряжения:


Таким образом, если к цилиндрическому образцу, вырезанному под углом φ, приложить одноосное сжимающее напряжение N=-2(q+Pc), то на плоскостях напластования возникнут касательные напряжения, определяемые формулой (29), совпадающие с касательными напряжениями (19), действующими на контуре горизонтальной скважины в точке, наклоненной под углом φ к вертикальной оси.
Способ оценки устойчивости стволов горизонтальных скважин на основе результатов измерений продольного сжатия образца керна на прессе SHIMATZU осуществляют следующим образом.
Сначала из кернового материала, отобранного из исследуемого интервала глубины, изготавливают цилиндрические образцы, выпиленные под углами α1 и α2 относительно оси керна, которые помещают в испытательную машину SHIMATZU и производят одноосное сжатие с созданием напряжений N1 (для образца, вырезанного под углом α1) и N2 (для образца, вырезанного под углом α2) до полного разрушения по заданной программе. По полученным значениям N1 и N2 из соотношения (26)

определяют значения прочностных констант породы - модуль сцепления k и угол внутреннего трения породы ρ, зная который, определяют угол смещения точки на контуре скважины относительно вертикальной оси поперечного сечения скважины, в которой касательное напряжение τ достигает максимума по формуле (16) φ=1/2(π/2-ρ).
Затем из кернового материала вырезают образец цилиндрической формы, ось вращения которого образует с осью керна угол φ=1/2(π/2-ρ). Зная горное давление на заданной глубине (отрицательное) q и давление на забое скважины Рс, испытывают образцы нагрузкой, создающей напряжение в образце величиной N=-2(q+Pc), с измерением продольной деформации образца в зависимости от времени. Затем рассчитывают средние скорости ползучести породы при различных плотностях бурового раствора, для чего общая деформация образца делится на общее время его нагружения при рассматриваемой плотности бурового раствора. На основе полученных данных выявляют допустимую плотность бурового раствора. Если ползучесть образца является ограниченной (скорость деформации образца со временем падает), то плотность такого бурового раствора является допустимой. Но если ползучесть образца носит установившийся характер (скорость деформации образца со временем сохраняется) или нарастающей (скорость деформации образца со временем увеличивается), то при данной плотности бурового раствора следует ожидать потери устойчивости скважины. Затем определяют искомое время до разрушения породы на стенках скважины, для чего определенную предельную деформацию, выявленную при одноосном сжатии, делят на вычисленную скорость ползучести.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ УСТОЙЧИВОСТИ СТВОЛА НАКЛОННЫХ СКВАЖИН | 2011 |
|
RU2472928C2 |
| СПОСОБ ВСКРЫТИЯ ПРОДУКТИВНОГО ПЛАСТА | 1996 |
|
RU2110664C1 |
| Способ направленной разгрузки пласта | 2016 |
|
RU2645684C1 |
| СПОСОБ ОБРАБОТКИ ПРИЗАБОЙНОЙ ЗОНЫ СКВАЖИНЫ | 2005 |
|
RU2285794C1 |
| СПОСОБ ПРОВЕДЕНИЯ АНАЛИЗА ПРОЧНОСТИ НА СЖАТИЕ ГОРНОЙ ПОРОДЫ | 1997 |
|
RU2172834C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛАВНЫХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ В МАССИВЕ ГОРНЫХ ПОРОД И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2029084C1 |
| СПОСОБ ВЫБОРА ПОВЕРХНОСТНО-АКТИВНЫХ ВЕЩЕСТВ ПРИ УВЛАЖНЕНИИ КАМЕННЫХ УГЛЕЙ ПО КОЭФФИЦИЕНТУ ПРОНИЦАЕМОСТИ | 2013 |
|
RU2533562C1 |
| СПОСОБ ВЫБОРА БУРОВОГО РАСТВОРА ДЛЯ СТРОИТЕЛЬСТВА НАКЛОННЫХ И ГОРИЗОНТАЛЬНЫХ СКВАЖИН, ПРОБУРЕННЫХ В НЕУСТОЙЧИВЫХ ГЛИНИСТЫХ ОТЛОЖЕНИЯХ | 2016 |
|
RU2620822C1 |
| Способ определения трещинного коллектора и способ добычи углеводородов | 2021 |
|
RU2797376C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ МАТЕРИАЛА С ХРУПКИМ СКЕЛЕТОМ | 2013 |
|
RU2543709C2 |


Изобретение относится к бурению горизонтальных скважин. Способ определения устойчивости ствола горизонтальной скважины осуществляют следующим образом: извлекают с различной глубины из скважины керны, изготавливают из них образцы цилиндрической формы и подвергают одноосному сжатию вдоль оси вращения до полного разрушения. При этом образцы выпиливают под различными углами к оси керна. Измеряют изменения величины осевой деформации образца со временем для каждой из различных величин прикладываемых напряжений, в зависимости от глубины скважины. Вычисляют скорость деформации и по снижению скорости деформации со временем при постоянном напряжении делают вывод об устойчивости скважин и допустимости использования бурового раствора с определенной плотностью. Предложенный способ обеспечивает возможность определения устойчивости ствола скважины в пластах с ярко выраженной анизотропией механических и прочностных свойств пород, а также упрощение необходимых испытаний образцов в условиях одноосного сжатия. 3 ил.
Способ определения устойчивости ствола горизонтальных скважин, включающий извлечение кернов из скважин, изготовление из них образцов цилиндрической формы, ось вращения которых образует с осью керна угол φ, величина которого определяется выражением:
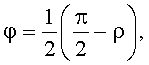
где ρ - угол внутреннего трения породы, который определяют путем предварительного изготовления из кернового материала, отобранного из исследуемого интервала глубины, цилиндрических образцов, выпиленных под углами α1 и α2 относительно оси керна, которые подвергают одноосному сжатию с созданием напряжений N1 и N2 до полного разрушения по заданной программе, и по полученным значениям N1 и N2 из соотношений:
l/2N1sin2α1=k+N1sin2α1tgρ,
l/2N2sin2α2=k+N2sin2α2tgρ,
где k - коэффициент сцепления;
вычисление угла внутреннего трения ρ,
приложение к образцам вдоль оси вращения одноосного сжимающего напряжения N, величину которого определяют по формуле:
N=-2(q+Pc),
где N - одноосное сжимающее напряжение, Па;
q - горное давление на данной глубине скважины, величина которого определяется по формуле:
q=- γпh,
где γп - средняя плотность вышележащих горных пород, т/м3;
h - глубина скважины, м;
Рс - давление на забое скважины, равное произведению плотности бурового раствора на глубину h, Па,
измерение изменения величины осевой деформации образца со временем для каждой из различных величин прикладываемых напряжений N, при этом вычисляют скорость деформации и по снижению скорости деформации со временем при постоянном напряжении N делают вывод об устойчивости скважин и допустимости использования бурового раствора с плотностью γб.р
γб.р=-(q+N/2)/h,
а при постоянстве скорости деформации или ее росте - о недопустимости такого использования.
| RU 2073227 C1, 10.02.1997 | |||
| Способ определения влияния буровых растворов на горные породы | 1989 |
|
SU1619106A1 |
| СПОСОБ УПРАВЛЕНИЯ БУРЕНИЕМ УЧАСТКОВ СТВОЛА СКВАЖИНЫ С ИНТЕНСИВНЫМ ИСКРИВЛЕНИЕМ | 1994 |
|
RU2061835C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЛОКАЛЬНЫХ НАПРЯЖЕНИЙ В ГОРНОЙ ПОРОДЕ | 1999 |
|
RU2215149C2 |
| СПОСОБ ПОВЫШЕНИЯ УСТОЙЧИВОСТИ ГОРНЫХ ПОРОД В ПРИСКВАЖИННОЙ ЗОНЕ | 2007 |
|
RU2341638C1 |
| КЛОЗЕТНЫЙ ПРОМЫВНОЙ БАК | 1929 |
|
SU12933A1 |
| US 5767399 A, 16.06.1998. | |||
Авторы
Даты
2013-01-27—Публикация
2011-02-18—Подача