Изобретение относится к области оптики, автоматики и вычислительной техники, в частности к способу восприятия техническими системами элементов поля изображения макро- и микрообъектов, функциональные и кинематические связи компонент которого многократно снижают влияние дифракционного светорассеяния, параллельно формируют объемные рецептивные поля и многопараметрические сигналы точек поля изображения в реальном масштабе времени, а также обеспечивают с высокой разрешающей способностью восприятие элементов поля трехмерных, спектрально не однородных объектов.
Изобретение может найти широкое применение в области биологии и медицины при прижизненном изучении объемного строения клеточных и субклеточных микроструктур в норме и патологии, а также в области телевидения, навигации и робототехники по формированию сигналов трехмерного восприятия элементов изображения для анализа и управления объектами и процессами в реальном масштабе времени.
Известные способы восприятия поля изображения микрообъектов основаны на трех функционально сочлененных компонентах: формировании изображения и его проецировании на фотоэлектрический преобразователь (ФЭП) или матрицу ФЭП для преобразования оптической информации в электрические сигналы; сканировании поля изображения путем развертки или считывания элементов поля проецированного изображения на фотоэлектрические преобразователи; обработки сигналов ФЭП. В предлагаемом способе перечисленные компоненты рассмотрены как единый объект способа, в котором установленные структурно-функциональные взаимосвязи и последовательности действий приводят к параллельному восприятию элементов поля изображения и быстродействию формирования и логической обработки сигналов с качественно новым информационным содержанием элементов восприятия в процессе микролокального параллельного «просмотра» элементов поля.
Известен способ сканирования поля дискретных объектов произвольной формы, проецированного на ФЭП (например, биологических объектов), основанный на слежении контура объекта путем перемещения поля изображения относительно неподвижно установленного ФЭП в плоскости изображения, и поэлементно строчной развертки участка, ограниченного экстремальными координатами контура объекта [1]. Достоинством такого способа сканирования являются:
- эффективное сжатие поля за счет исключения фоновых участков изображения;
- минимизация оптических искажений благодаря восприятию изображения в центральной части поля зрения оптической системы.
Недостатками указанного способа являются:
- низкие помехоустойчивость и скорость развертки элементов поля и невозможность их обработки для анализа дискретных объектов в реальном масштабе времени;
- функциональная ограниченность способа для восприятия поля объектов, изображения которых представляют текстуру с расплывчатыми границами межобъектного разделения;
- невысокая разрешающая способность и контрастность восприятия элементов изображения, обусловленные дифракционным светорассеянием, ухудшающим раздельное восприятие смежных элементов изображения;
- функциональная ограниченность способа сканирования для трехмерного восприятия элементов поля изображения.
Основные недостатки способа сканирования вызваны последовательным просмотром элементов поля изображения и взаимовлиянием дифракционного межэлементного светорассеяния освещенностей между точками поля изображения. Это приводит к существенным искажениям восприятия объектов: по контрастности; изменению формы; размеров; смещению координат положения. При этом оказывается сложным как однозначный поиск и сканирование объектов, так и воспроизведение ранее воспринятых объектов. Что же касается вопроса разрешающей способности и контрастности, то просмотр и регистрация элементов изображения этим способом не приводит к уменьшению дифракционного и межэлементного светорассеяния воспринимаемых элементов, а следовательно, не улучшает разрешение и межэлементный контраст смежных точек изображения.
Другим способом является способ параллельного сканирования группы элементов поля изображения, спроецированного на дискретное поле, сформированное элементами фотоэлектрических преобразователей (ФЭП), которые образуют матрицу ФЭП с прямоугольным растром распределения, при этом развертку и считывание элементов регистрируемого поля изображения осуществляют путем параллельной многострочной развертки группы строк.
Недостатками указанного способа являются:
- низкая разрешающая способность восприятия элементов поля изображения обусловлена как явлением дифракционного светорассеяния, так и дискретностью распределения фотопреобразующих элементов в матрице, которая приводит к ухудшению межэлементного контраста и появлению фотонечувствительных зон восприятия элементов поля изображения;
- функциональная ограниченность способа для объемного восприятия элементов поля объектов в реальном масштабе времени;
- сложность аппаратурной реализации способа многострочного считывания и обработки элементов поля изображения.
Наиболее близким способом в плане локального просмотра элементов поля изображения, принятым в качестве прототипа, является способ сканирования поля произвольных объектов [2], спроецированного на дискретное поле матрицы, сформированной последовательно распределенными, независимыми, накапливающими сигнал фотоэлектрическими преобразователями (ФЭП) путем поэлементно строчной развертки и считывания информации ФЭП, в рамках которого с целью формирования сигналов адекватно зрительному восприятию, существенного повышения разрешения и быстродействия анализа изображений объектов и упрощения аппаратурной реализации, одновременно с началом развертки и считывания дискретного поля осуществляют преимущественно по треугольной траектории непрерывное перемещение поля изображения объектов относительно дискретного поля матрицы фотопреобразователей, при этом амплитуду сторон треугольного перемещения устанавливают соответственно равной межэлементному и межстрочному расстояниям дискретного поля, а период треугольного перемещения Тт устанавливают из условия достижения целочисленного соотношения Тр/Тт и выполнения Тр/Тт>>1, где Тр - период развертки дискретного поля, причем после каждого цикла развертки и считывания дискретного поля его дополнительно сдвигают относительно поля изображения объектов в направлении диагонали поля на величину δ/n от размера диагонального отрезка δ, определяемого межэлементным и межстрочным расстояниями дискретного поля, а в момент достижения величины дополнительных сдвигов размеру диагонального отрезка δ направление дополнительного сдвига реверсируют.
Анализ прототипа показывает, что введение за время развертки поля высокочастотного непрерывного движения с треугольной траекторией и со сторонами, равными соответственно межэлементному и межстрочному расстояниям дискретного поля матрицы, позволяет непосредственно на ФЭП осуществить по траектории треугольного движения суммирование-усреднение проецированных участков поля изображения на ФЭП матрицы.
Основным недостатком указанного способа является то, что развертка-считывание матрицы элементов фотоэлектрического преобразования и непрерывное перемещение поля изображения являются функционально независимыми процессами. Поэтому, даже при одновременном запуске процесса развертки-считывания матрицы и непрерывного треугольного перемещения поля изображения, фазы проецирования элементов изображения на ФЭП матрицы меняются. То есть воспринимаемые матрицей элементы поля изображения в зависимости от фазы треугольного перемещения относительно развертки-считывания непрерывно меняются, а следовательно, отсутствует стабильность по координате и времени проецирования элемента изображения на ФЭП матрицы. Кроме того, из условия Тр/Тт>>1 очевидно, что в процессе поэлементно-строчной развертки каждый фоторецептор «видит» адекватно траектории треугольного перемещения и размеру ФЭП треугольную полосу с площадью, более чем в три раза превосходящую размер ФЭП. То есть увеличивается минимальный размер воспринимаемой точки, и происходит сглаживание функции межэлементного распределения интенсивности. Рассматривая эти три фактора во взаимосвязи, нетрудно убедиться, что предложенный способ сканирования произвольных объектов не может привести к повышению разрешающей способности и быстродействию анализа изображений объектов.
Анализ состояния. Рассмотрим фрагмент матрицы, сформированный накапливающими сигнал пропорционально освещенности фотоэлектрическими преобразователями одинаковых размеров, межэлементных расстояний и спектральных характеристик, на которую проецируется изображение поля объектов оптической системой (фиг.1). Проецированное «поле изображение - матрица ФЭП» иллюстрирует взаимовлияние в плоскости изображения окрестных смежных точек на формирование сигналов ФЭП матрицы с прямоугольными или круглыми элементами ФЭП. Расстояния между центрами элементов изображения точек установлено в диапазоне W=3.83÷7.02. То есть зрительно точки разделяемы. На фигурах размеры ФЭП приведены меньше размера дифракционных картин точек поля изображения, что наглядно иллюстрирует, что если даже бесконечно уменьшить размер ФЭП, влияние дифракционного светорассеяния смежных элементов присутствует и ограничивает разрешающую способность восприятия величиной λ/2, а размеры ФЭП>0 приводят к дополнительному ухудшению этого разрешения. Независимо друг от друга все ФЭП матрицы преобразуют проецированные на них поле изображения одновременно и параллельно накапливают сигналы за одинаковый интервал времени. Очевидно, что независимо от способа считывания ФЭП и длительности времени накопления оптического сигнала матрицей, составляющая дифракционного светорассеяния по взаимовлиянию освещенностей смежных элементов и их соотношения остается постоянной. При этом минимальный размер элемента поля изображения и дискретность восприятия спроецированного поля объектов непосредственно определяют размеры ФЭП и величины межэлементной «А» и межстрочной «В» "мертвых" зон матрицы (фиг.1). Последний фактор наряду с явлением дифракционного светорассеяния приводит к еще большему уменьшению межэлементного разрешения. На фрагменте матрицы (фиг.1) окружностями с радиусом R0 и R1 обозначены границы дифракционного распределения освещенности в центральном круге Эйри и в первом кольце проецированного оптической системой светящейся точки. Как известно [3], радиус кружка Эйри и радиус первого кольца в безразмерных оптических единицах W соответственно равны: W0=3,83 и W1=7,02. Физические размеры радиуса кружка Эйри и радиуса первого кольца в пространстве изображений, в пространстве предметов и их соотношения в микроскопии определяются выражениями 1÷3:
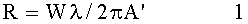 - пространство изображений
- пространство изображений
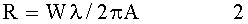 - пространство предметов
- пространство предметов
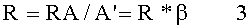
где А' - числовая апертура оптической системы со стороны пространства изображений;
А - числовая апертура со стороны пространства предметов;
β - линейное увеличение оптической системы.
Так как в кружке Эйри и в первом кольце сконцентрированы соответственно около 83,4% и 7,2% энергии, то для оценки интенсивности точки с отбором энергии около 90% область дифракционной картины, проецируемой на ФЭП, охватывает окружность с W1=7,02. Для реальной оценки в микроскопии физических размеров кружка Эйри в условиях достижения максимальной разрешающей способности рассмотрим пример, где в качестве оптической системы взят стандартный объектив микроскопа фирмы "Carl Zeis Iena" с увеличением, равным 100, с апертурой А=1,3 и длиной волны проецируемого поля изображения λ=0,56 мкм. Тогда согласно выражению 2 для пространства предметов радиус кружка Эйри будет R0=0,2627 мкм. Отсюда, для пространства изображений, где проецируется изображение поля объектов на матрицу ФЭП, радиус кружка составит 26,27 мкм. Аналогичным образом, оценивая радиус области, охватывающий энергию кружка Эйри и первого кольца в плоскости изображения, соответственно получим 48,15 мкм. При этом в пространстве изображений удаленного от фокальной плоскости объектива на расстояние 250 мм размер проецированного поля изображения составляет в форме прямоугольника около 50×50 мм2. Из этого примера следует, что для восприятия дискретной матрицей ФЭП такого же размера поля изображения с таким же разрешением приведенного к плоскости объекта, количество фоточувствительных элементов матрицы в плоскости изображения должно быть не менее 75000×75000 (более 900 мегапикселей), чтобы обеспечить эквивалентную оптической, пиксельную разрешающую способность и величину поля зрения. Очевидно, что наряду с расстоянием между смежными точками поля изображения, для восприятия важны также значения отбора их энергии. Выясним целесообразность изолированного восприятия 90% собственной энергии точки в плоскости изображения, когда одновременно в поле присутствуют окружающие смежные точки. Примем, что центры смежных точек отстоят на величину W1≥3,83 и W1≤7,02. То есть смежные точки в поле изображения зрительно воспринимаются раздельно. Теперь, для восприятия 90% энергии дифракционного поля точки, установим в плоскости изображения матрицу с фоточувствительными элементами в диагонали размером 2×48,15 мкм, что обеспечит совместный охват дифракционных зон кружка Эйри и первого кольца точки, эквивалентного W1=7,02. Из положения центров смежных точек ясно (фиг.1), что если проецировать поле изображение на такую матрицу, то для любой точки поля изображения, наряду с энергией самой точки, на ФЭП действуют энергии дифракционных зон смежных точек. То есть в формировании сигнала точки на фоточувствительном элементе матрицы одновременно участвует локальное множество дифракционных картин смежных точек (фиг.1). Это для существующих способов является принципиальным ограничивающим фактором, исключающим возможность непосредственного формирования сигналов на ФЭП матрицы как «чистых» сигналов восприятия изолированных точек с отбором только собственной энергии точки. Это означает, что такой способ увеличения энергии точки с целью повышения разрешающей способности восприятия элементов не приводит к улучшению как оптической, так и пиксельной разрешающих способностей. Кроме того, становится явным другой недостаток, по мере увеличения оптического разрешения сужается размер одновременно воспринимаемого поля объектов. Отсюда можно сделать вывод, что для согласованного отбора энергии точек поля изображения матрицей ФЭП, которая обеспечила бы разрешающую способность восприятия точек эквивалентного критерию Рэлея с сохранением размера поля изображения, необходимо в плоскости изображения для точки ограничиваться энергией кружка Эйри, а размер ФЭП матрицы должен совпадать с размером дифракционного кружка Эйри. Именно этим можно объяснить стремление ведущих мировых фирм разработать в качестве перспективных матриц, прежде всего матрицы, содержащие все большее количество ФЭП с минимальными размерами ФЭП, приближающимися к размеру кружка Эйри в плоскости объекта (хотя при этом сильно ухудшается отношение сигнал-шум ФЭП). Направление развития, которое в конечном итоге может привести к увеличению размера одновременно воспринимаемого поля объектов и непосредственно к улучшению количества пиксельной разрешающей способности, но, к сожалению, не может привести к улучшению предела оптического разрешения. В этой связи уместно заметить, что оптическая разрешающая способность по критерию Рэлея или по критерию абсолютной разрешающей способности справедливы в условиях оценки полей изображения при существующих способах восприятия как параллельное, раздельное восприятие последовательности двух смежных неподвижных точек. Попытки применить аппаратные и математические функции в устройствах формирования изображения для повышения разрешающей способности [4, 5], как правило, приводят к большим затратам вычислительного времени и усложняют конструкцию, лишь немного улучшая контрастно частотную функцию формирования и восприятия образов. Вместе с тем, для оптического диапазона величина λ/2 не является пределом раздельного восприятия элементов изображения. Это подтверждают не только некоторые достижения в области создания оптики с отрицательным показателем преломления и некоторые результаты зрительного восприятия объектов поля изображения, но в решающей степени правомерность этого утверждения вытекает из предлагаемого способа восприятия элементов изображения.
Эти обстоятельства указывают на актуальность разработки нового способа восприятия, который исключил бы взаимовлияние дифракционного светорассеяния на восприятие смежных точек, повысил разрешающую способность и быстродействие восприятия, формировал в каждой точке многопараметрические сигналы, обеспечивающие трехмерное восприятие элементов поля изображения в реальном масштабе времени. Решение этих вопросов, в качестве основных компонентов, требует рассмотреть синергизм: оптики, матрицы фотоэлектрических преобразователей и движения поля изображения как единого целого в процессе способа восприятия.
Указанная цель достигается тем, что формируют матрицу ФЭП путем заполнения плоскости матрицы круглыми или шестигранными изолированными друг от друга ФЭП в виде их плотной гексагональной упаковки, затем их группируют в виде последовательности смежных ФЭП и формируют на матрице не связанные между собой одинаковые гексагональные кольца фотоэлектрических преобразователей (ГКФЭП), при этом ФЭП каждого ГКФЭП по выходу преобразования оптического сигнала в электрический сигнал объединяют и формируют кластер, а номер и координату ФЭП в кластере определяют по номеру и координате фотоэлектрического преобразователя, находящегося в геометрическом центре ГКФЭП кластера, затем кластеры группируют в виде последовательности смежных кластеров и формируют гексагональное кольцо кластеров (ГКК), причем номер и координату смежных кластеров в ГКК определяют по номеру и координате кластера, находящегося в геометрическом центре ГКК, при этом по совокупности ГКК, сформированных на всех кластерах матрицы, формируют гексагонально-кластерно-структурированную матрицу (ГКС), на которую проецируют поле изображения объектов и которое путем поступательно-кругового движения перемещают скачкообразными шагами и формируют замкнутую гексагональную траекторию перемещения элементов поля изображения, которая в плоскости матрицы идентична распределению ФЭП в ГКФЭП кластеров, причем после каждого шага скачкообразного перемещения поля изображения параллельно регистрируют сигналы на выходе всех ГКФЭП кластеров матрицы, а также на ФЭП, расположенном на геометрическом центре кластера и на ФЭП кластера, на который в текущем шаге спроецирован доминантный элемент, координату которого определяют координатой ФЭП центра кластера и номерами векторов первого и текущего шагов скачкообразного перемещения поля, при этом размер единичных шагов перемещения и размер межцентрового расстояния смежных ФЭП матрицы устанавливают равным размеру радиуса кружка Эйри приведенного к плоскости объекта, а с целью кругового обзора точки без дифракционного светорассеяния и оценки ее освещенности по направлениям после каждого текущего шага сигналы одновременно проецированных элементов изображения на кластеры вычитают из сигналов элементов, спроецированных на ФЭП, расположенный в геометрическом центре каждого кластера, а также одновременно вычитают из сигнала доминантного элемента кластера, при этом сигнал доминантного элемента и сигнал разности суммируют и формируют сигнал доминантной точки по направлению (ДТН), а для объемного представления точек с компенсацией дифракционного светорассеяния формируют изображения точек в виде пирамиды, каждая из сторон которой отображает сигнал доминантной точки по направлению с основанием в виде равностороннего шестиугольника, а вершину доминантной точки определяют по значению сигналов ДТН, при этом на каждом новом замкнутом цикле гексагонального перемещения поля в кластерах синхронно сменяют доминантные точки путем изменения направления первого шага перемещения поля на 60°, причем для полного исключения влияния дифракционного светорассеяния на каждом цикле перемещения от смежных элементов, участвовавших в формировании доминантных элементов изображения в кластерах каждого гексагонально кластерного кольца (ГКК), сформированного по совокупности проецированных элементов изображения на кластеры ГКС матрицы, параллельно из центральных кластеров во всех ГКК вычитают одноименные элементы изображения триад смежных кластеров ГКК, расположенных под углом 120° относительно центрального кластера ГКК, а из оставшейся другой триады кластеров ГКК вычитают одноименные элементы изображения из кластера, расположенного в центре ГКК, при этом после вычитания элементов триад кластеров суммируют одноименные сигналы триад и регистрируют сигналы доминантных элементов как сигналы точек объекта без дифракционного светорассеяния.
Сопоставительный анализ заявляемого способа с существующими показывает, что введение ГКС матрицы и соответствующего пошагового скачкообразного перемещения спроецированного на матрицу поля изображения по гексагональной траектории, со сторонами равными радиусу кружка Эйри позволяет осуществить формирование доминантных элементов, а в кластерах ГКК осуществить компенсацию взаимовлияния и уничтожение смежных к доминантным точкам локальную окрестность, исключив влияние дифракционного светорассеяния на доминантные точки, что не обеспечивают способы как поэлементно строчного, так и многострочного параллельного сканирования спроецированного поля объектов на дискретное поле матрицы.
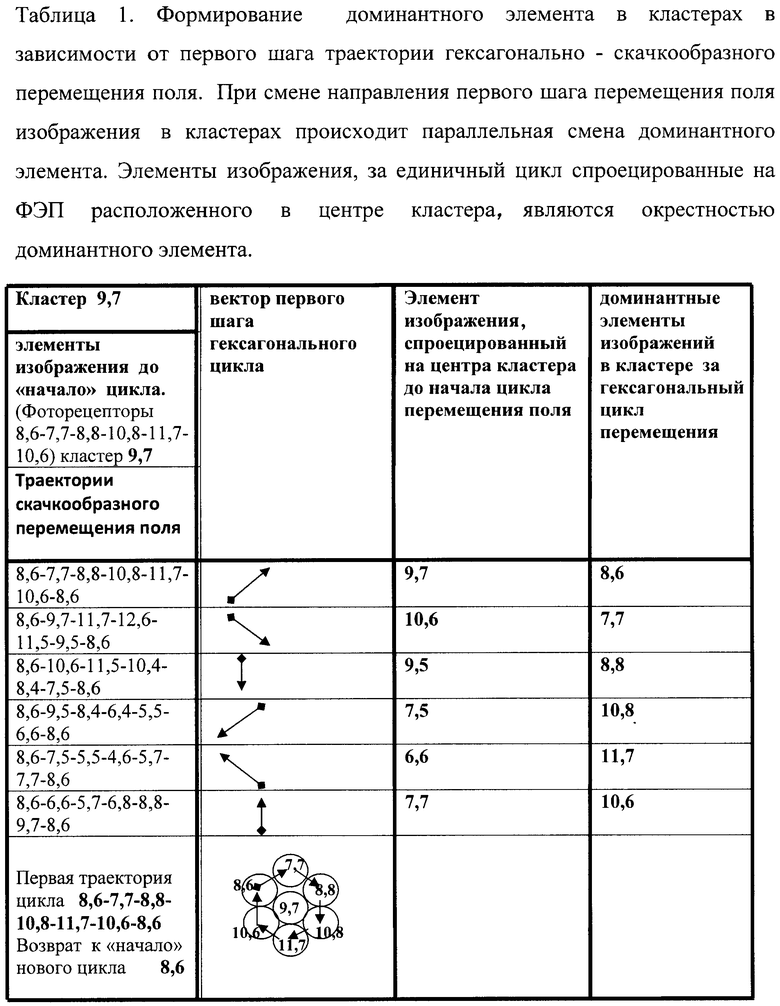
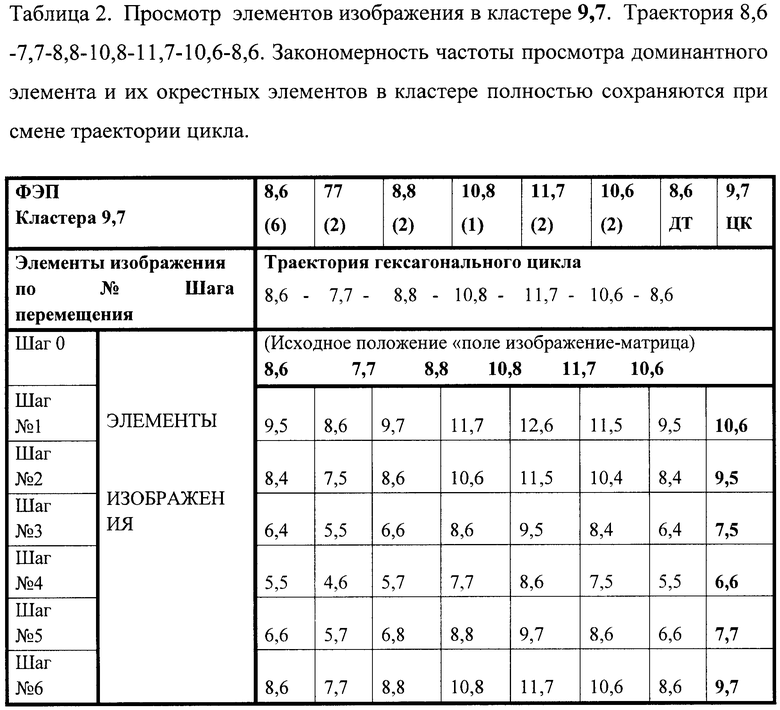
В заявляемом способе формирование гексагонально распределенными фоточувствительными элементами независимых гексагональных кластеров матрицы, на которых одновременно проецируют поле изображения, с возможностью скачкообразного пошагового перемещения всего поля изображения по траектории, адекватной распределению ФЭП в кластерах, формируют на каждом шаге «поле восприятия» кластеров, которое содержит информацию о направлении «обзора» доминантных точек, причем разностные сигналы доминантных элементов и сигналов соответствующих им кластеров задают величину сигнала точки, просмотренного в данном направлении, а разностные сигналы ФЭП, расположенных в центре кластеров и сигналов объединенных выходов кластеров, определяют параллельно дифференциальные сигналы центра каждого кластера. Таким образом, любая доминантная точка изображения объекта «просматривается» в кластерах из шести направлений, охватывающих 360°, причем в момент завершения гексагонального цикла шагов суммарно просмотренные поля в кластерах с центром в координатах доминантных элементов изображения формируют виртуальные поля объемного восприятия точек изображения. Последовательная смена в замкнутом гексагональном цикле первого шага, как следует из таблицы 1, обеспечивает параллельный локальный просмотр поля восприятия кластеров и одновременно формирует новую группу доминантных элементов изображения в кластерах.
Таким образом, в заявляемом способе введение ГКС матриц с гексагональным скачкообразным перемещением поля изображения по матрице с размером шага, равного радиусу кружка Эйри и размеру фоточувствительных элементов ГКС матрицы, приведенные к плоскости объекта, формирует качественно новый тип восприятия элементов, сочетающий параллельное формирование виртуальных рецептивных полей доминантных элементов и обработку информации точек поля изображения по направлениям. Это обеспечивает: в реальном масштабе времени, без дифракционного светорассеяния, формирование сигналов трехмерного восприятия элементов поля изображения и существенное улучшение оптического и пиксельного разрешения, по величине намного меньшее величины λ/2, и в пределе, которые ограничиваются шумовыми составляющими компонентов: оптических элементов, ФЭП матрицы и процесса движения. Таким образом, заявляемый способ в полном объеме соответствует критериям "новизна" и "существенные отличия".
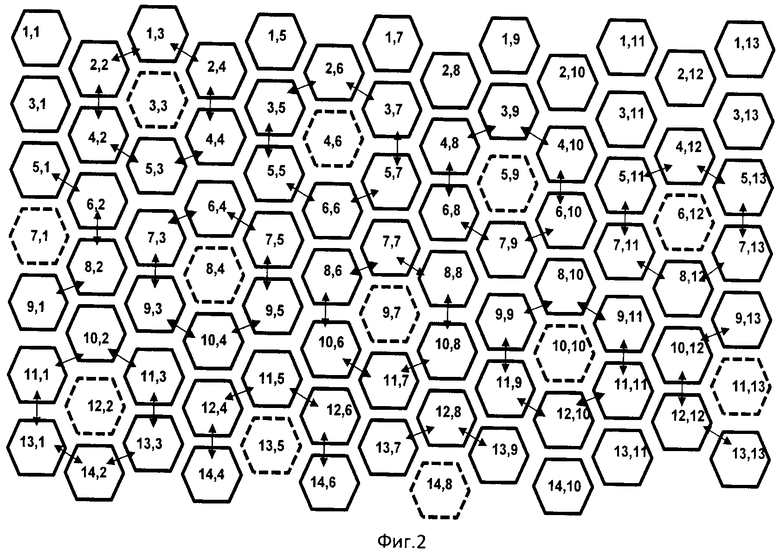
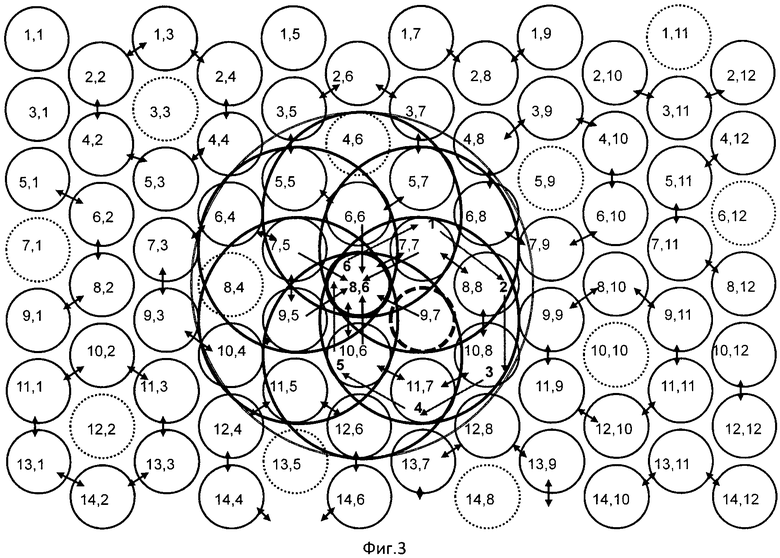
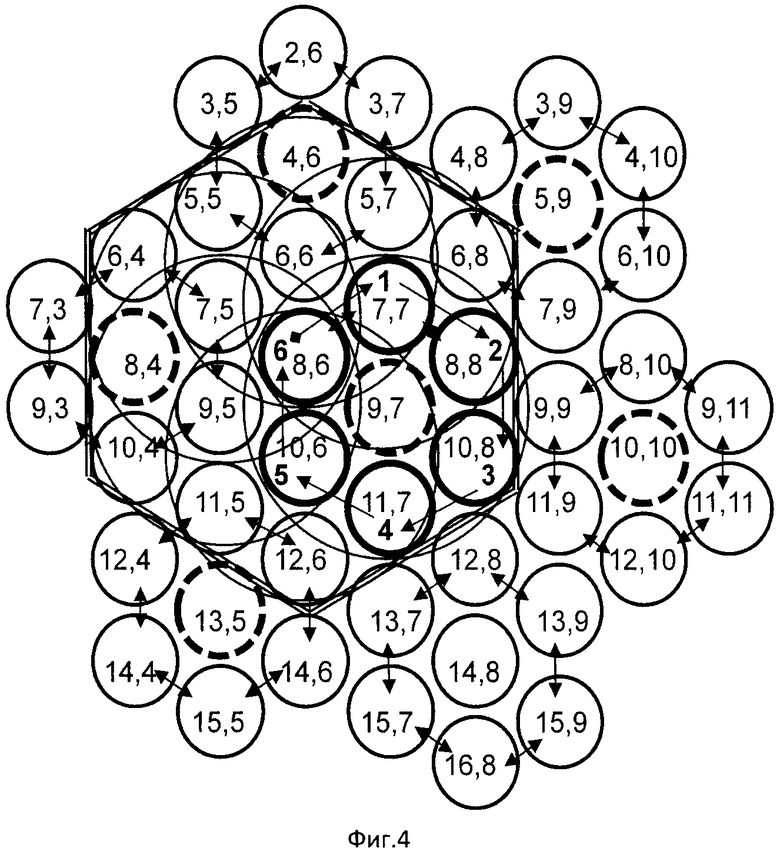
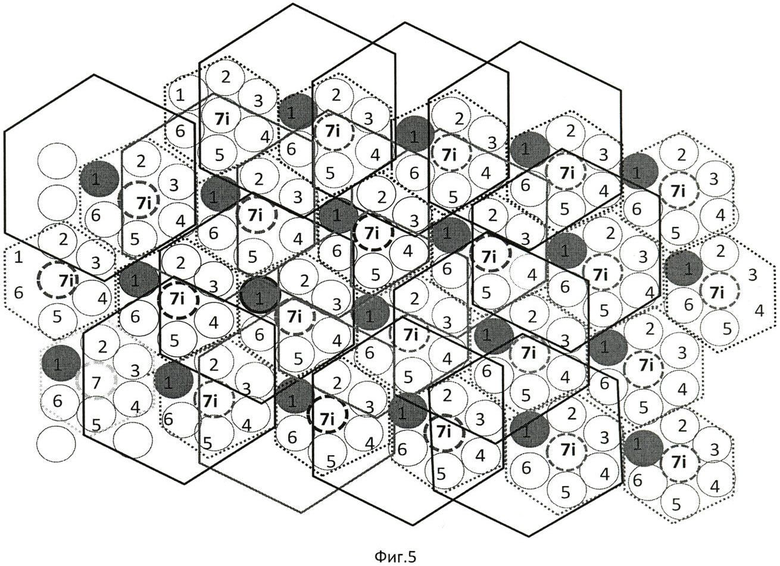
Для пояснения сущности изобретения на Фиг.2 приведена картинг распределения шестиугольных ФЭП в матрице. Двунаправленными стрелками обозначены объединенные выходы ФЭП, которые формируют изолированные кластеры ГКФЭП, совокупность которых образует гексагонально-кластерно-структурированную матрицу. На фиг.3 представлен фрагмент ГКС матрицы в варианте кластеров, сформированных на круглых ФЭП. Кружочками обозначены ФЭП, а цифры внутри указывают координаты ФЭП. Для установления функциональной роли скачкообразного поступательно-кругового перемещения поля изображения в восприятии элементов изображения кластерами на фиг.3 дано фоновое поле изображения объектов, проецированного на ГКС матрицу, в которой выделен кластер 9,7 расположенного в центре ГКК (фиг.4). Для упрощения картины на фиг.4 показаны проецированные за цикл скачкообразного перемещения области восприятия элементов изображения только для кластера 9,7. На фиг.3 границы поля изображения, одновременно воспринимаемые ГКФЭП кластера 9,7, обведены окружностями. На фиг.3 окружностями также обозначены поля изображения, которые последовательно проецируются на кластер 9,7 после каждого скачкообразного шага, выполненного по замкнутому гексагональному циклу перемещения поля. В качестве траектории замкнутого цикла скачкообразного перемещения поля для иллюстрации закономерности восприятия ГКФЭП кластера установлена траектория 8,6-7,7-8,8-10,8-11,7-10,6-8,6, а в таблице 2 приведены координаты элементов изображения, которые при текущем шаге скачкообразного перемещения проецируются на кластер 9,7. На фиг.5 приведены поля, параллельно воспринимаемые кластерами при первом шаге скачкообразного перемещения по вектору 8,6-7,7. Конкретизация траектории, в таблицах 1 и 2, а также изменение вектора первого шага не меняют закономерность частоты просмотра элементов, проецированные на кластеры. На фиг.3 и фиг.4 стрелками 1÷6 указаны векторы перемещения поля, а в скобках рядом с координатами ФЭП кластера числа указывают номер шага перемещения поля. В таблице 2 приведены результаты проецирования элементов равномерно-фонового изображения на кластер 9,7, который иллюстрирует перемещение координат поля изображения по кластеру, в котором объединены выходы ФЭП (8,6;7,7;8,8;10,8;11,7;10,6). В центре кластера расположен ФЭП с координатами 9,7. Траектория скачкообразного замкнутого цикла перемещения поля проходит по траектории 8,6;7,7;8,8;10,8;11,7;10,6;8,6. В скобках, ниже обозначения координаты ФЭП, приведены числа, указывающие количество повторов элемента изображения проецированного на ГКФЭП кластера 9,7. Из таблицы 1 следует, что кластерное «восприятие» элементов поля совместно с замкнутым циклом гексагонального скачкообразного перемещения поля изображения приводит к селективному проецированию элементов и формированию на кластерах доминантных по частоте просмотра элементов поля изображения.
Для прослеживания за скачкообразным перемещением поля проецированного изображения за элементами поля изображения закреплены имена, соответствующие координатам ФЭП кластеров матрицы до начала перемещения поля изображения, которые сохраняют и в процессе гексагональных циклов скачкообразного перемещения поля, что обеспечивает возможность слежения за траекторией перемещения элементов и координат их проецирования на ФЭП матрицы. Доминантные элементы изображения в кластерах априори определяются по таблице 1 стандартных ситуаций, задающей последовательность векторов шагов гексагонального цикла перемещения поля изображения по направлениям. Сигналы восприятия кластера 9,7 на выходе гексагонального кольца ФЭП, обусловленного поступательно-круговым скачкообразным перемещением поля изображения с вектором первого шага (8,6-7,7)1, после каждого шага реализует:

Где - ΣJ(8,6)ср1 - сигнал одновременно проецированных элементов на кластер с центром в координате 9,7.
J(x,y) - сигнал интенсивности проецированного элемента. В скобках, рядом с интенсивностью элемента изображения, указаны координаты элемента.
Из выражений проецированного на ФЭП кластера 9,7 элементов изображения на каждом шаге гексагонального цикла (1÷6) видно, что элементы изображения проецируются на ФЭП кластера 9,7 не с одинаковой частотой. При этом по частоте проецирования элементов изображения формируется виртуальное поле восприятия кластера (ВРП). Центром восприятия кластера является координата элемента изображения, который на каждом шаге перемещения проецируется на фотоэлектрические преобразователи данного кластера, приведенного к координате ФЭП, соответствующей началу цикла. При траектории 8,6-7,7-8,8-10,8-11,7-10,6-8,6 таким элементом на выходе кластера 9,7 является элемент изображения с координатой 8,6. То есть на выходе кластера появляется доминантный элемент 8,6, который при каждом скачкообразном перемещении гексагонального цикла проецируется на кластер 9,7, тогда как остальные элементы, как следует из таблицы 2, проецируются один или два раза. После каждого шага перемещения поля изображения по этой траектории, если исключить доминантный элемент, который является центром распределения частоты проецирования элементов на кластер, относительно доминантного элемента проецируются следующие элементы изображения:

Из номенклатуры элементов, участвующих в определении величины средней интенсивности по 7÷12 и координатного распределения элементов изображения в кластере (фиг.3, фиг.4), следует, что эти средние значения характеризуют освещенности локальных полей относительно доминантного элемента из разных направлений, причем каждое из них характеризует среднюю интенсивность элементов, окрестных к центру виртуального рецептивного поля, по направлениям, которые охватывают 1/6 области общего виртуального рецептивного поля (ВРП). Для траектории цикла 8,6-7,7-8,8-10,8-11,7-10,6-8,6 разностные сигналы доминантного элемента по кластеру 9,7 на каждом шаге цикла перемещения поля и усредненного сигнала направления определяют следующие приращения:
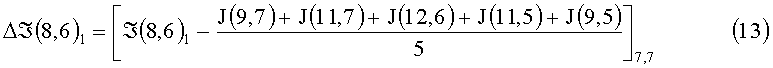
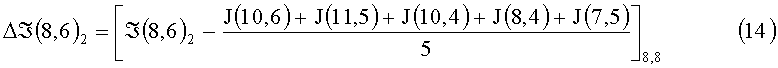
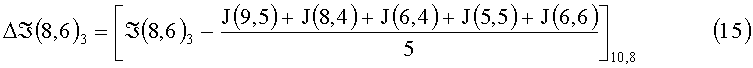
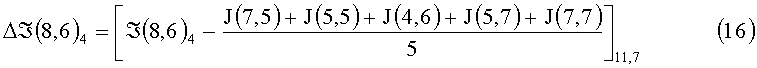
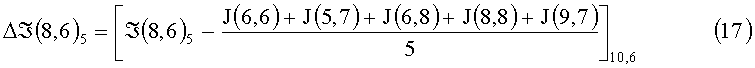
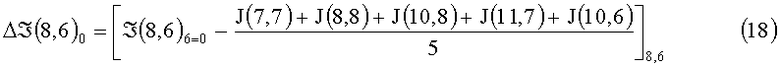
Δℑ(8,6) - разностный сигнал доминантного элемента и усредненного сигнала кластера;
ℑ(8,6) - сигнал доминантного элемента на ФЭП.
Анализируя выражения 13÷18, не трудно заметить, что знак разностного сигнала на каждом шаге перемещения поля характеризует получение доминантным элементом освещенности от окрестных элементов или отдачу освещенности к окрестным в данном направлении. Величина же истинного сигнала доминантного элемента ℑ(8,6)di с учетом получаемой или отдаваемой рассеянной части света по направлению будет:
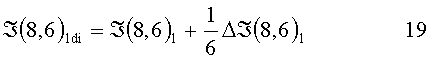

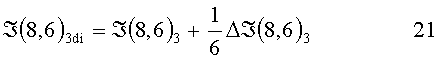
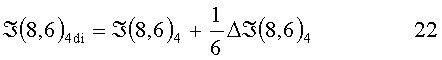
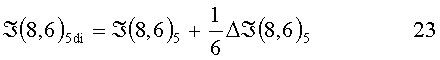
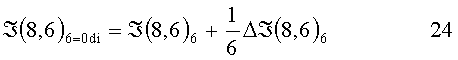
ℑ(8,6)di - доминантный сигнал, истинный по направлению с компенсацией дифракционного светорассеяния.
Тогда общий сигнал доминантного элемента будет:
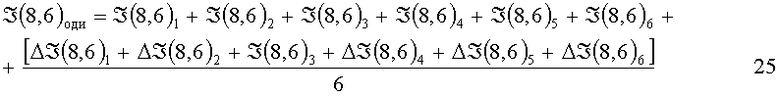
На каком-либо шаге гексагонального цикла равенство разностного сигнала (13÷18) нулю означает, что доминантный элемент поля изображения сколько рассеивает энергии к окрестным элементам, ровно столько же получает от них в данном направлении. Выражения 1÷25, приведенные для кластера 9,7, справедливы для любого кластера ГКС матрицы. Координатные обозначения элементов в этих выражениях несут функциональную нагрузку визуализации поля изображения, спроецированные на ФЭП кластеров в процессе скачкообразных шагов перемещения поля. Эти преобразования при любой траектории с проецированными на кластеры элементами поля изображения на ГКС матрицу во всех кластерах осуществляются автоматически, синхронно, параллельно. Важной особенностью ГКС матриц (фиг.5; таблица 2) является то, что на каждом шаге гексагонального цикла элементы изображения, кроме доминантных элементов, которые проецируются на ФЭП своего кластера, «растаскиваются» по разным кластерам. При этом окрестности центра рецептивного поля кластера за гексагональный цикл представляют круговой обзор доминантных точек с существенно ослабленными окрестными элементами точек. Координатно-селективное по частоте проецирование элементов изображения на кластер и круговой обзор доминантных точек многократно уменьшают влияние дифракционного светорассеяния на разрешающую способность раздельного обнаружения точек и повышают межэлементный контраст восприятия. При этом важно, что каждая точка поля объекта представляет объемный элемент изображения.
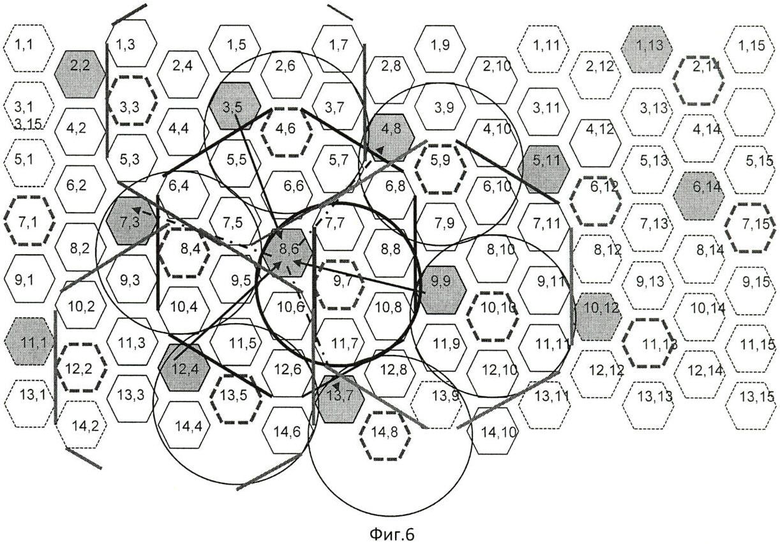
На фиг.6 приведена картина распределения доминантных элементов на ГКС матрице за один замкнутый гексагональный цикл перемещения поля изображения, в процессе выполнения которого возникает параллельно воспринимаемое «разрыхленное» поле доминантных элементов изображения. Внутри ФЭП вместо координатного обозначения указаны номера ФЭП в кластерах; номер кластера и место любого ФЭП в нем можно легко определить по номеру ФЭП матрицы. Так, если дано число, например N=200, то номер кластера определяют i=200/7, где целочисленная часть 28 указывает кластер, а остаток 4 указывает номер ФЭП в кластерах матрицы. Темными окружностями показаны доминантные элементы на ГКС матрице. Равносторонними шестиугольниками показаны поля восприятия каждого кластера, центры которых занимают доминантные элементы.
Для восприятия элементов изображения с максимальной разрешающей способностью необходимо и достаточно шестикратное выполнение замкнутого гексагонального цикла перемещения поля, и провести, как следует из таблицы 1, изменение вектора первого шага на 60° при каждом новом цикле. Так, при гексагональном цикле поступательно-кругового перемещения поля изображения с тактовой частотой шага 50 кГц время шестикратного гексагонального цикла по направлениям перемещения поля равняется 0,72 миллисекунд. То есть время восприятия кадра полного поля изображения с максимальной разрешающей способностью и с обработкой элементов (реализуются выражения 1÷25 для всего поля изображения) потребует времени менее 1 миллисекунд, что особенно важно для четкого восприятия и анализа динамично изменяемых полей изображения объектов. Для сравнения заметим, что такое восприятие, даже если не учитывать затраты на обработку, более чем на порядок быстрее известных способов, а с учетом затрат времени на обработку это преимущество по быстродействию с обработкой сигналов будет 103 раз.
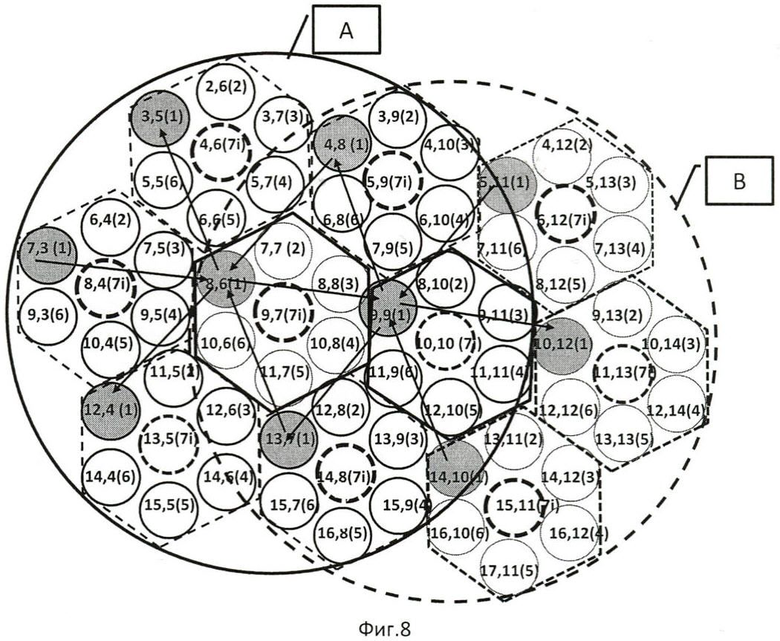
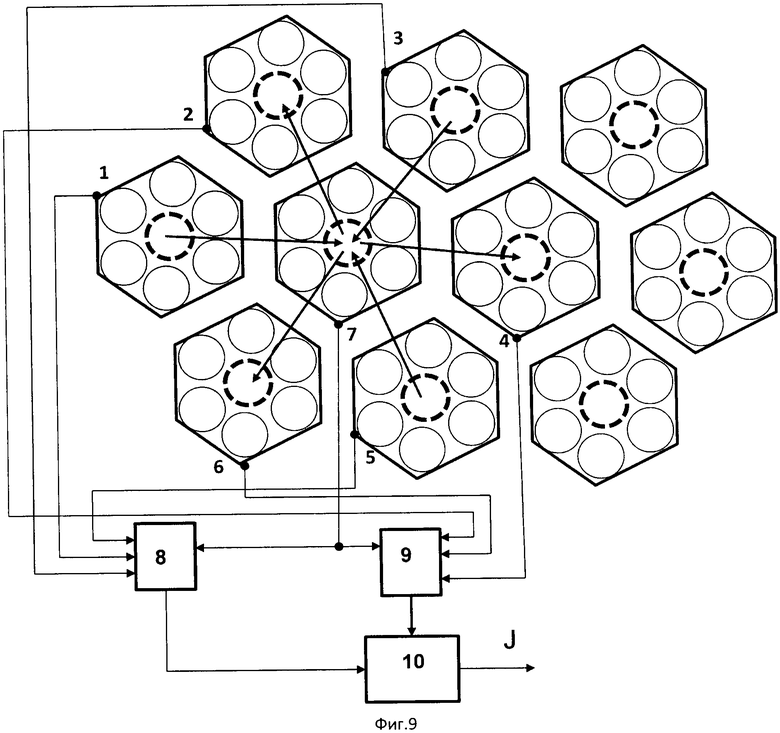
Фиг.(6÷8) иллюстрируют процедуру исключения в ГКК влияния дифракционного светорассеяния смежных элементов изображения на доминантные точки на примере ГКК кластером 9,7 в центре, где доминантным является элемент 8,6. Из картины рецептивного поля кластеров ГКК следует, что доминантный элемент кластера, расположенного в центре ГКК, не «просматривается» в остальных кластерах этого же ГКК. Поэтому для исключения влияния дифракционного светорассеяния смежных элементов, участвовавших в формировании доминантных элементов изображения в кластерах каждого гексагонально кластерного кольца (ГКК), сформированного по совокупности проецированных элементов изображения на ГКФЭП кластеров ГКС матрицы, параллельно из центральных кластеров во всех ГКК вычитают одноименные элементы изображения триад смежных кластеров ГКК, расположенных под углом 120°. Триады кластеров ГКК (Фиг.6, фиг.7) указаны стрелками уходящие и приходящие относительно центрального кластера 9,7 ГКК, а из другой триады кластеров ГКК вычитают одноименные элементы изображения кластера, расположенного в центре ГКК, при этом после вычитании элементов триад кластеров соответственно на блоках 8 и 9 (фиг.9) их суммируют на блоке 10 по одноименным сигналам триад. В результате на выходе остаются только доминантные элементы с их координатами. Таким образом, поле изображения формируется одними точками, эквивалентными кружку Эйри с полной компенсацией дифракционного взаимовлияния смежных точек. В этом случае две точки сливаются воедино при полном совпадении их центров. Таким образом, разрешающая способность ограничивается только шумами компонентов, реализующих предложенный способ восприятия.
Литература
1. Агаджанян Г.М., Красницкий А.П., Корнеев В.Н. «Информатика и технология. Система технического зрения». ОНТИ, г.Пущино, 1996 г.
2. Агаджанян Г.М., Агаджанян А.Ж., Фесенко Е.Е. Способ сканирования поля произвольных объектов и устройство для его реализации. Регистрационный номер №2001130946/09, публ. №2001130946, 2003 г.
3. Скворцов Г.Е., Панов В.А., Поляков Н.И., Федин Л.А. «Микроскопы». Машиностроение, Ленинград, 1969 г.
4. Выставкин А.Н., Пестряков А.В. Банков С.Е., Чеботарев В.М. «Устройство формирования изображения с субдифракционным разрешением». G02B 27/64, 2010 г.
5. П.Дж.Берт. Интеллектуальное восприятие в пирамидальной зрительной машине. «Машинное зрение», ТИИЭР, т.76, №8, 1988 г.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С СУБДИФРАКЦИОННЫМ РАЗРЕШЕНИЕМ | 2013 |
|
RU2533502C1 |
| Устройство для считывания изображений объектов | 1976 |
|
SU638990A1 |
| СПОСОБ СКАНИРОВАНИЯ ЦВЕТНОГО ИЗОБРАЖЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2158486C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С СУБДИФРАКЦИОННЫМ РАЗРЕШЕНИЕМ | 2009 |
|
RU2398253C1 |
| Объектив для ИК-области спектра | 2016 |
|
RU2620202C1 |
| СИСТЕМЫ И СПОСОБЫ МИКРОСКОПИИ СТРУКТУРИРОВАННОГО ОСВЕЩЕНИЯ | 2020 |
|
RU2829111C1 |
| ДИНАМИЧЕСКИЙ ДИСПЛЕЙ ПОЛНОСТЬЮ ОБЪЕМНОГО ИЗОБРАЖЕНИЯ | 2017 |
|
RU2727853C1 |
| ШИРОКОУГОЛЬНЫЙ АТЕРМАЛИЗОВАННЫЙ ИНФРАКРАСНЫЙ ОБЪЕКТИВ С БОЛЬШИМ ЗАДНИМ ОТРЕЗКОМ | 2021 |
|
RU2762997C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЧЕТЫРЕХМЕРНЫХ ЯРКОСТНО-СПЕКТРАЛЬНЫХ ПРОФИЛЕЙ УДАЛЕННЫХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2023 |
|
RU2822085C1 |
| ОБЪЕКТИВ ДЛЯ ИК-ОБЛАСТИ СПЕКТРА | 2015 |
|
RU2604112C2 |

Изобретение относится к способу восприятия техническими системами элементов поля изображения микрообъектов. Техническим результатом является исключение взаимовлияния дифракционного светорассеяния на восприятие смежных точек, повышение разрешающей способности и быстродействия восприятия и обработки элементов изображения, обеспечение трехмерного восприятия элементов поля изображения в реальном масштабе времени. Способ восприятия изображения микрообъектов заключается в том, что формируют матрицу ФЭП круглыми или шестигранными изолированными ФЭП в виде их плотной гексагональной упаковки, группируют их и формируют на матрице не связанные между собой одинаковые гексагональные кольца ФЭП (ГКФЭП), ФЭП каждого ГКФЭП объединяют и формируют кластер, кластеры группируют в виде последовательности смежных кластеров и формируют гексагональное кольцо кластеров (ГКК), по совокупности ГКК формируют гексагонально-кластерно-структурированную матрицу (ГКС), на которую проецируют поле изображения объектов, формируют замкнутую гексагональную траекторию перемещения элементов поля изображения, которая в плоскости матрицы идентична распределению ФЭП в ГКФЭП кластеров, причем после каждого шага перемещения поля изображения регистрируют сигналы на выходе всех ГКФЭП кластеров матрицы, на ФЭП, расположенном на геометрическом центре кластера, и на ФЭП кластера, на который в текущем шаге спроецирован доминантный элемент, регистрируют сигналы доминантных элементов как сигналы точек. 9 ил., 2 табл.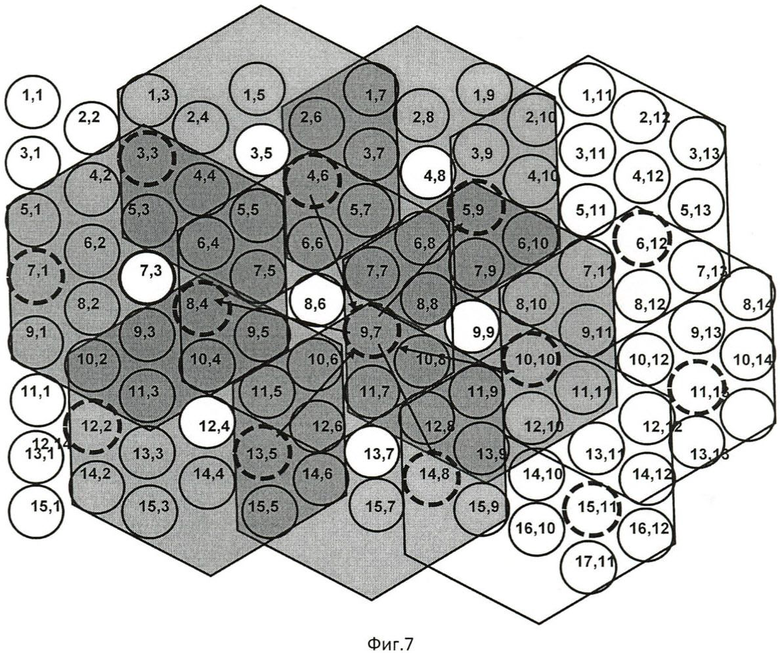
Способ восприятия изображения микрообъектов, заключающийся в том, что формируют матрицу ФЭП путем заполнения плоскости матрицы круглыми или шестигранными изолированными друг от друга ФЭП в виде их плотной гексагональной упаковки, затем их группируют в виде последовательности смежных ФЭП и формируют на матрице не связанные между собой одинаковые гексагональные кольца фотоэлектрических преобразователей ГКФЭП, при этом ФЭП каждого ГКФЭП по выходу преобразования оптического сигнала в электрический сигнал объединяют и формируют кластер, а номер и координату ФЭП в кластере определяют по номеру и координате фотоэлектрического преобразователя, находящегося в геометрическом центре ГКФЭП кластера, затем кластеры группируют в виде последовательности смежных кластеров и формируют гексагональное кольцо кластеров (ГКК), причем номер и координату смежных кластеров в ГКК определяют по номеру и координате кластера, находящегося в геометрическом центре ГКК, при этом по совокупности ГКК, сформированных на всех кластерах матрицы, формируют гексагонально-кластерно-структурированную матрицу (ГКС), на которую проецируют поле изображения объектов, которое затем путем поступательно-кругового движения перемещают скачкообразными шагами и формируют замкнутую гексагональную траекторию перемещения элементов поля изображения, которая в плоскости матрицы идентична распределению ФЭП в ГКФЭП кластеров, причем после каждого шага скачкообразного перемещения поля изображения параллельно регистрируют сигналы на выходе всех ГКФЭП кластеров матрицы, а также на ФЭП, расположенном на геометрическом центре кластера, и на ФЭП кластера, на который в текущем шаге спроецирован доминантный элемент, координату которого определяют координатой ФЭП центра кластера и номерами векторов первого и текущего шагов скачкообразного перемещения поля, при этом размер единичных шагов перемещения и размер межцентрового расстояния смежных ФЭП матрицы устанавливают равным размеру радиуса кружка Эйри, приведенного к плоскости объекта, а с целью кругового обзора точки без дифракционного светорассеяния и оценки ее освещенности по направлениям, после каждого текущего шага сигналы одновременно проецированных элементов изображения на кластеры вычитают из сигналов элементов, спроецированных на ФЭП, расположенный в геометрическом центре каждого кластера, а также одновременно вычитают из сигнала доминантного элемента кластера, при этом сигнал доминантного элемента и сигнал разности суммируют и формируют сигнал доминантной точки по направлению ДТН, а для объемного представления точек с компенсацией дифракционного светорассеяния формируют изображения точек в виде пирамиды, каждая из сторон которой отображает сигнал доминантной точки по направлению с основанием в виде равностороннего шестиугольника, а вершину доминантной точки определяют по значению сигналов ДТН, при этом на каждом новом замкнутом цикле гексагонального перемещения поля в кластерах синхронно сменяют доминантные точки путем изменения направления первого шага перемещения поля на 60°, причем для полного исключения влияния дифракционного светорассеяния на каждом цикле перемещения от смежных элементов, участвовавших в формировании доминантных элементов изображения, в кластерах каждого гексагонально кластерного кольца ГКК, сформированного по совокупности проецированных элементов изображения на кластеры ГКС матрицы, параллельно из центральных кластеров во всех ГКК вычитают одноименные элементы изображения триад смежных кластеров ГКК, расположенных под углом 120° относительно центрального кластера ГКК, а из оставшейся другой триады кластеров ГКК вычитают одноименные элементы изображения из кластера, расположенного в центре ГКК, при этом после вычитания элементов триад кластеров суммируют одноименные сигналы триад и регистрируют сигналы доминантных элементов как сигналы точек объекта без дифракционного светорассеяния.
| RU 2001130946 A, 20.07.2003 | |||
| 0 |
|
SU293507A1 | |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2013-04-10—Публикация
2012-02-28—Подача