Изобретение относится к электротехнике, в частности к трехфазной электрической сети шестипроводного исполнения. Может быть использовано при проектировании, наладки и эксплуатации шестипроводных линий электропередачи.
Известен способ прогнозирования распределения гармонических составляющих электрической энергии по неразветвленным участкам электроэнергетической системы [патент RU 2210154] [1]. Этот способ предполагает, что известен спектральный состав тока и напряжения для однопроводной линии электропередачи, и на его основе получены математические модели, характеризующие связь между протяженностью однопроводного участка линии электропередачи и частотой.
Однако прогнозирование распределения тока и напряжения по шестипроводной линии электропередачи не может быть описано законами распределения электрической энергии для однопроводной линии электропередачи.
Недостатком данного способа является отсутствие влияния спектрального состава тока и напряжения для многопроводных линий электропередачи.
Задачей изобретения является прогнозирование распределения гармонических составляющих тока и напряжения по неразветвленным участкам шестипроводной линии электропередачи.
Технический результат достигается тем, что способ прогнозирования распределения гармонических составляющих тока и напряжения по неразветвленным участкам шестипроводной линии электропередачи, заключающийся в том, что исследуемую неразветвленную часть шестипроводной линии электропередачи разбивают на однородные участки, определяют спектральные составы напряжения и тока в какой-либо точке исследуемого участка, а также определяют место нахождения источников каждой гармонической составляющей электрической энергии.
На рис.1 представлена расчетная электрическая схема замещения для шестипроводной линии электропередачи.
Предварительно необходимо разбить исследуемую неразветвленную часть шестипроводной линии электропередачи на хотя бы относительно однородные участки.
Для осуществления прогнозирования распределения гармонических составляющих электрической энергии по неразветвленным участкам шестипроводной линии электропередачи достаточно знать спектральные составы напряжения и тока в какой-либо точке исследуемого участка этой системы. Кроме того, необходимо с достаточной достоверностью представлять место нахождения источников каждой гармонической составляющей электрической энергии, что позволит определить направление распространения падающей волны электромагнитной энергии той или иной частоты по шести-проводной линии электропередачи.
В схеме присутствуют продольные параметры линейных проводов ROA'n, LOA'n, COA'n, ROB'n, LOB'n, COB'n, ROC'n, LOC'n, COC'n, ROA"n, LOA"n, COA"n, ROB"n, LOB"n, COB"n, ROC"n, LOC"n, COC"n, а поперечные параметры характеризуются электромагнитными связями между линейными проводами: GOA'B'n, COA'B'n, GOA'A"n, COA'A"n, GOA'B"n, COA'B"n, GOB'A"n, COB'A"n, GOB'C"n, COB'C"n, GOB'B"n, COB'B"n, GOB'C'n, COB'C'n, GOC'C"n, COC'C"n, GOC'A'n, COC'A'n, GOC'A"n, COC'A"n, GOA"B"n, COA"B"n, GOB"C"n, COB"C"n, GOB"C'n, COB"C'n, GOC"A"n, COC"A"n, GOC"A"n, COC"A'n и электромагнитными связями между линейными проводами и поверхностью земли: GOA'On, COA'On, GOB'On, COB'On, GOC'On, COC'On, GOA"On, COA"On, GOB"On, COB"On, GOC"On, COC"On, diA'B"n; diA'A"n, diA'B'n, diA'n, diB'A"n, diB'C"n, diB'B"n, diB'C'n, diB'n, diC'C"n, diC'A'n, diC'A"n, diC'n, diA"B"n, diA"n, diB"C"n, diB"C'n, diB"n, diC"A"n, diC"A'n, diC"n, - точки утечки по соответствующим электромагнитным связям; MOA'B'n, MOA'A"n, MOA'B"n, MOB'C'n, MOB'A"n, MOB'B"n, MOB'C"n, MOC'A'n, MOC'A"n, MOC'C"n, MOA"B"n, MOB"C'n, MOB"C"n, MOC"A'n, MOC"A"n - взаимные индуктивности.
Поскольку напряжение и ток являются функциями времени и длины ЛЭП, то в модели необходимо использовать частные производные.
Так, если в выделенный участок ЛЭП длиной dl входит ток  , то выходит из этого участка в тот же момент времени измененный по величине ток
, то выходит из этого участка в тот же момент времени измененный по величине ток  ; если на входе выделенного участка напряжение определяется величиной
; если на входе выделенного участка напряжение определяется величиной 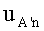 , то в тот же момент времени на выходе напряжение определяется величиной и
, то в тот же момент времени на выходе напряжение определяется величиной и 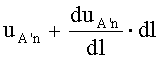 [2].
[2].
Таким образом, в схеме будут присутствовать шесть фазных токов и напряжений, а также пятнадцать линейных напряжений. Тогда рабочая математическая модель для шести проводной линии электропередачи будет состоять из двадцати семи уравнений.
Математическая модель строится на основании законов Кирхгофа.
Для тока в линии A′ справедлив 1-й закон Кирхгофа:

Для напряжения в фазе A′ справедлив 2-ой закон Кирхгофа:


Уравнения для других линий составляются аналогично.
В результате совместных преобразований уравнений (1)-(2) получается дифференциальное уравнение второго порядка для фазы А′:
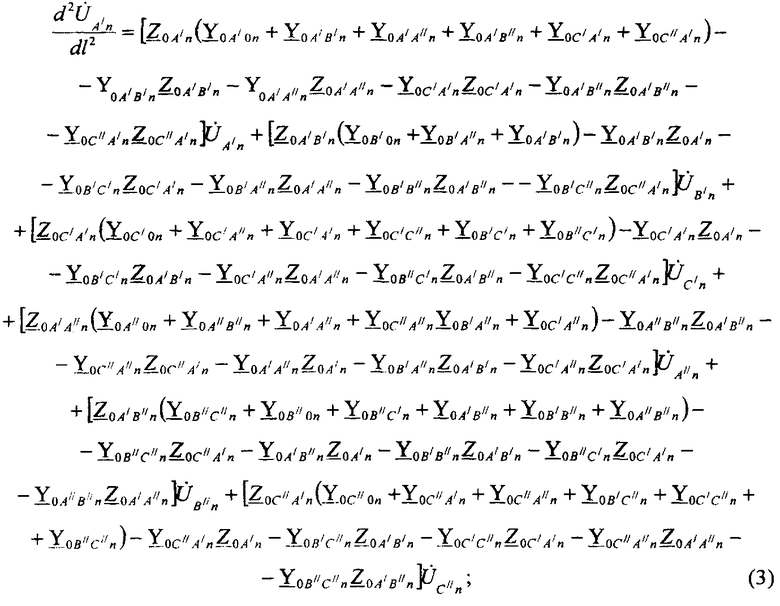
где 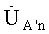 ,
,  ,
,  ,
,  ,
, 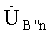 ,
,  - изображения действующих значений напряжений на комплексной плоскости на частоте n-й гармонической составляющей;
- изображения действующих значений напряжений на комплексной плоскости на частоте n-й гармонической составляющей;  - продольные сопротивления каждого провода ЛЭП, расчет которых производится по формуле:
- продольные сопротивления каждого провода ЛЭП, расчет которых производится по формуле:

где rOA'n и xOA'n - удельное активное и индуктивное сопротивление провода A′,
n - номер гармоники; 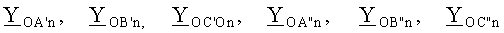 - поперечная проводимость каждого провода линии электропередачи, расчет которых производится по формуле:
- поперечная проводимость каждого провода линии электропередачи, расчет которых производится по формуле:

где COA'n - емкостная проводимость линии; GOA'n - активная проводимость линии.
Уравнения для других линий составляются аналогично.
Таким образом, получаются шесть дифференциальных уравнений второго порядка. Теперь необходимо выполнить их совместное решение. Характеристическое уравнение системы, образованной равенствами (3), выглядит так:
x6+a·x5+b-x4+c·x3+d·х2+е·x+f=0.
Результаты решения характеристического уравнения являются шесть корней x1, x2, x3, x4, х5, x6.
Постоянные распространения электромагнитной волны по однородному участку трехфазной шестипроводной линии электропередачи на частоте n-й гармонической составляющей определяются так:

Общее решение уравнения (3) для фазы А′ будет выглядеть так:

где  - комплексные значения постоянных интегрирования на частоте n-й гармонической составляющей.
- комплексные значения постоянных интегрирования на частоте n-й гармонической составляющей.
Величины фазных токов определяются из дифференциальных уравнений первого порядка. В частности для фазы А′ это уравнение имеет вид:

Из уравнения (7) вычисляются значения фазных токов. Для А′ выглядят следующим образом:

где Δ1A', Δ1B', Δ1C', Δ1A", Δ1B", Δ1C", и Δ - детерминант матриц, полученных из шести уравнений вида (7).
С учетом равенства (6), уравнение тока в линии А′ предстанет в следующем виде:


Из уравнений (6) и (8) следует, что в каждом проводе исследуемого участка ЛЭП будут присутствовать шесть пар волн электромагнитного поля.
Из уравнения (8) собственные волновые сопротивления в линии А′ следует определять так:

Совместное решение уравнений вида (6) и (8) определит уравнения изменения напряжения и тока вдоль однородного участка шестипроводной ЛЭП. Для фазы А′ они выглядят следующим образом:

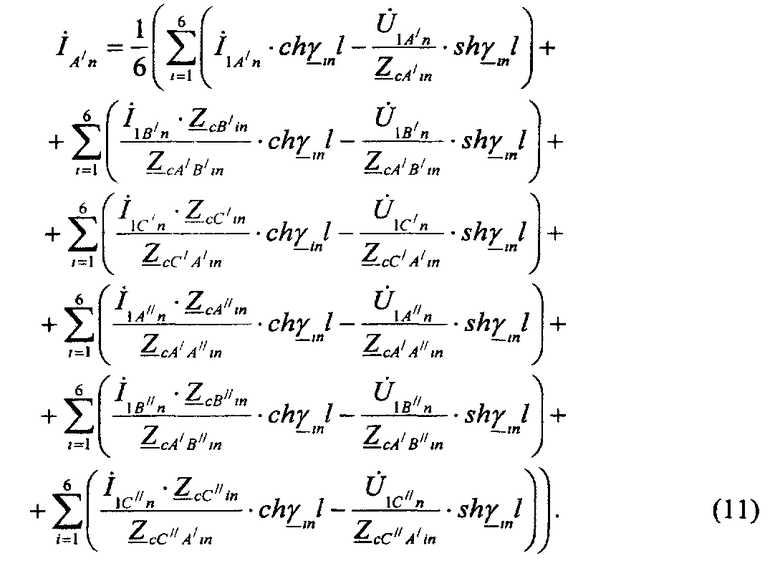
где  и
и  - комплексные значения действующих величин напряжения и тока в начале рассматриваемого участка ЛЭП на частоте n-ой гармонической составляющей.
- комплексные значения действующих величин напряжения и тока в начале рассматриваемого участка ЛЭП на частоте n-ой гармонической составляющей.
Таким образом, описываемый способ позволяет получить представление о спектральных составах тока и напряжения в любом месте анализируемого неразветвленного участка шестипроводной линии электропередачи, а значит и оценить распределение гармонических составляющих электрической энергии.
Источники информации
1. Способ прогнозирования распределения гармонических составляющих электрической энергии по неразветвленным участкам электроэнергетической системы. Патент RU №2210154. Большанин Г.А.
2. Плотников, М.П., Особенности схемы замещения трехфазной двухцепной ЛЭП пониженного качества электрической энергии. Естественные и инженерные науки - развитию регионов Сибири: материалы XI (XXXIII) Всероссийской научно-технической конференции. - Братск: Изд-во БрГУ, 2012. - С.97-98.
3. Большанин, Г.А., К вопросу о волновой теории передачи электрической энергии по линиям электропередач. / Л.Ю. Большанина, Е.Г. Марьясова. // Системы. Методы. Технологии. - 2010. - №3. - С. 71-76.
4. Большанин, Г.А., Особенности распространения электромагнитного поля по линиям электропередачи в условиях пониженного качества электрической энергии. / Л.Ю. Большанина. // Системы. Методы. Технологии. - 2009. - №2. - С.56-59.
Использование: в области электротехники. Технический результат - обеспечение возможности прогнозирования распределения гармонических составляющих тока и напряжения по неразветвленным участкам шестипроводных линий электропередачи. Согласно способу исследуемую неразветвленную часть шестипроводной линии электропередачи разбивают на однородные участки, определяют спектральные составы напряжения и тока в какой-либо точке исследуемого участка, а также определяют место нахождения источников каждой гармонической составляющей электрической энергии. 1 ил.
Способ прогнозирования распределения гармонических составляющих тока и напряжения по линии электропередачи, заключающийся в повышении точности прогнозирования распределения тока и напряжения на любом участке трехфазной шестипроводной линии электропередачи, отличающийся тем, что исследуемую неразветвленную часть шестипроводной линии электропередачи разбивают на однородные участки, определяют спектральные составы напряжения и тока в какой-либо точке исследуемого участка, а также определяют место нахождения источников каждой гармонической составляющей электрической энергии.
| СПОСОБ ПРОГНОЗИРОВАНИЯ РАСПРЕДЕЛЕНИЯ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПО НЕРАЗВЕТВЛЕННЫМ УЧАСТКАМ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ | 2001 |
|
RU2210154C2 |
| ТРЕХФАЗНЫЙ АКТИВНЫЙ ЭЛЕКТРИЧЕСКИЙ ФИЛЬТР | 1995 |
|
RU2121222C1 |
| СПОСОБ ЗАЩИТЫ ЭЛЕКТРИЧЕСКОЙ СЕТИ ОТ ГАРМОНИК ТОКА КРАТНЫХ ТРЕМ | 2009 |
|
RU2399139C1 |
| US 5387821A, 07.02.1995 | |||
Авторы
Даты
2014-09-27—Публикация
2012-12-04—Подача