Изобретение относится к средствам индивидуальной бронезащиты личного состава, в частности к бронированной или пуленепробиваемой одежде, и может быть использовано в военном деле и в специальных подразделениях самостоятельных силовых структур и ведомств.
Известны тканевые бронежилеты (БЖ), основу которых составляют защитные элементы, выполненные в форме груди и спины, которые крепятся на теле при помощи плечевых и поясных ремней либо при помощи специального чехла с передними (на груди) и задними (на спине) карманами, куда вкладываются защитные элементы (бронепанели) [1]. В комплект поставки некоторых моделей БЖ входят дополнительные элементы, предназначенные для защиты паховой области и верхнего плечевого пояса, которые формируют так называемую периферийную защиту.
Все тканевые БЖ выполнены исключительно из защитной структуры на тканевой основе. Конструкция тканевого БЖ состоит из нескольких слоев арамидной ткани, конструктивно собранных в единый защитный экран (бронепанель). Количество слоев в бронепанели может колебаться от 20 до 30 и более, что определяется созданием требуемого уровня защиты. Определенные проблемы при использовании тканевых БЖ связаны со снижением заброневого действия при непробитии. С этой целью используются дополнительные демпфирующие материалы в виде пакетов или пластин, размещенных с внутренней стороны БЖ, прилегающих непосредственно к телу военнослужащего.
По состоянию на сегодняшний день в Вооруженных силах РФ находятся на снабжении тканевые БЖ двух поколений: 90-х гг. (серия БЖ 6Б11) и современного - серия БЖ 6Б23.
Из современных штатных БЖ можно выделить противоосколочный 6Б23, полное наименование которого: бронежилет общевойсковой II уровня защиты противоосколочный 6Б23.
Материалом бронепанелей грудной и спинной секций бронежилета 6Б23 являются тканевые пакеты [2].
Указанный бронежилет является прототипом предлагаемого и имеет следующий основной недостаток, заключающийся в возникновении в организме военнослужащего при непробитии БЖ остаточных изменений, способных привести в дальнейшем даже к летальному исходу. Травматическое воздействие для жестких БЖ удалось исключить путем установки за металлической броней амортизаторов из вспененного полимерного материала, соизмеримого по толщине с высотой тыльной выпуклости защитной пластины от пули. В разработанных в начале 80-х гг. армейских БЖ серии 6Б4 на основе керамических бронематериалов были использованы полугибкие щитки из склеенных тканевых слоев и пенополиуретана. Этим достигалось не только гашение удара, но и распределение его на большую площадь. В последующем за рубежом устройство подобного предназначения получило название антишоковых панелей.
Однако появление в последующем средств индивидуальной бронезащиты из тканей на основе высокопрочных синтетических волокон так называемой «мягкой брони» до предела обострило казалось бы уже полностью решенную проблему заброневой контузионной травмы в случае непробития БЖ. «Мягкая броня» в ряде случаев, позволяя значительно снизить массу БЖ, оказывалась неприемлемой из-за недопустимо высокого травматического воздействия на мягкие ткани биологического объекта (БО) при непробитии БЖ. В отличие от жестких бронеэлементов «мягкая броня» не оказывает практически никакого сопротивления энергетическому воздействию в направлении удара пули и, следовательно, не распределяет сообщенную ей энергию удара поражающего элемента (ПЭ) на большую площадь. Основная часть энергии удара сосредоточивается в пределах места контакта ПЭ с БЖ и передается телу. Опыт показал, что для «мягкой брони» описанные выше способы гашения динамического воздействия оказываются неприемлемыми, а повышение ее жесткости, например, за счет прострачивания, склеивания и др., как правило, снижает ее противопульную стойкость.
Наиболее близким к заявляемому бронежилету является тканевый бронежилет с антишоковым устройством по заявке от 27.11.2007 г. (пат. РФ №2395055) [3].
Технический результат выражается в значительном снижении степени повреждающего воздействия ПЭ на биологический объект через тканевый пакет БЖ в случае его непробития.
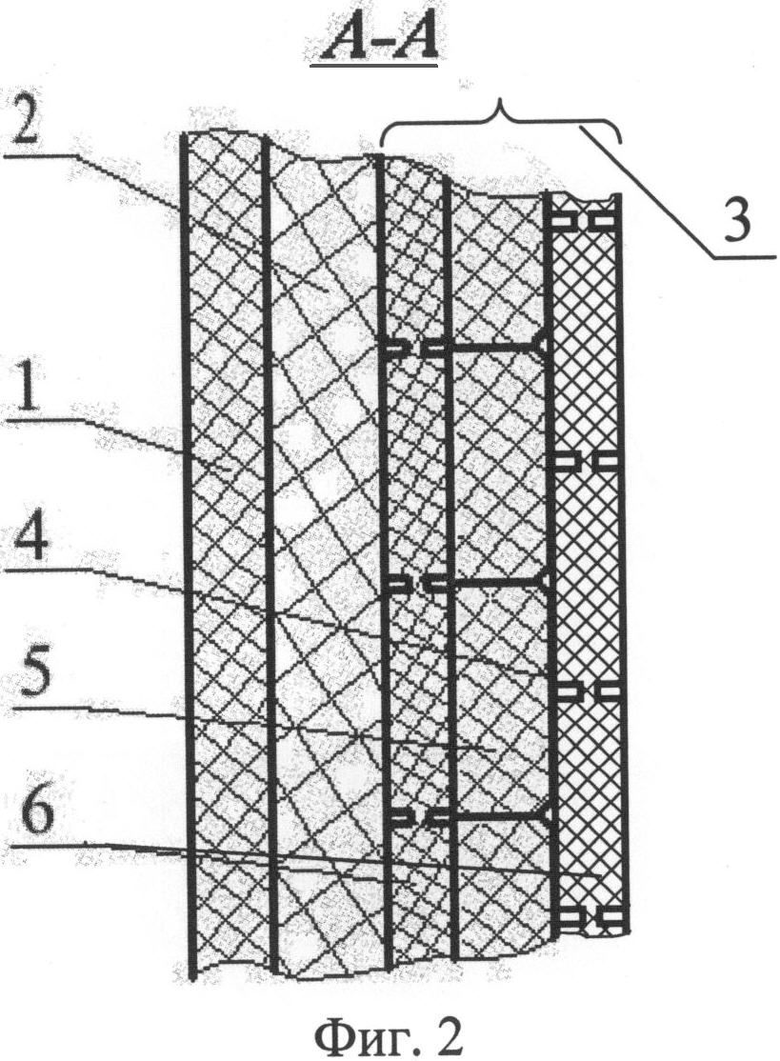
Указанный технический результат достигается за счет того, что на внутренней стороне тканевого пакета БЖ 1 размещается антишоковое устройство (фиг.1), состоящее из амортизатора 2, выполненного из поролона, и подложки 3 (фиг.2). Подложка 3 выполнена в виде секций-компенсаторов удара 4, представляющих собой камеры из прорезиненной ткани ТСВМ с поролоном 5 внутри и облицованных с двух сторон пакетами пластин 6. Тыльный пакет пластин 6 наклеивается на компенсаторы удара 4 таким образом, чтобы центры масс его квадратных элементов располагались напротив угловых точек сочлененных компенсаторов удара 4.
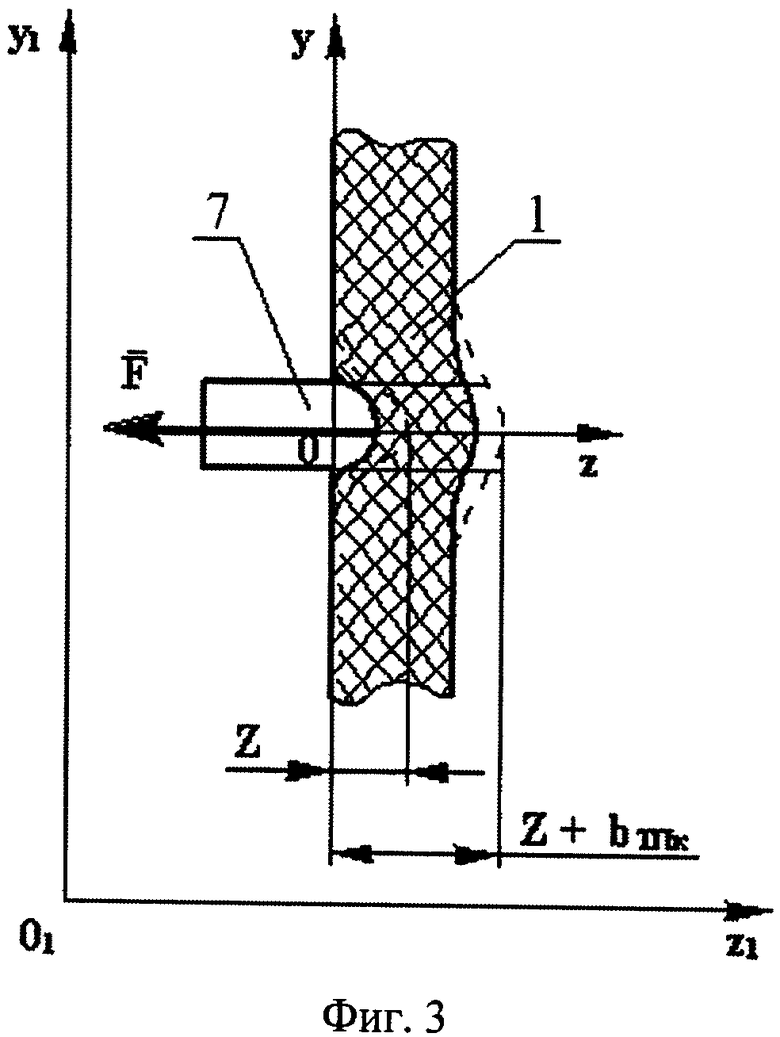
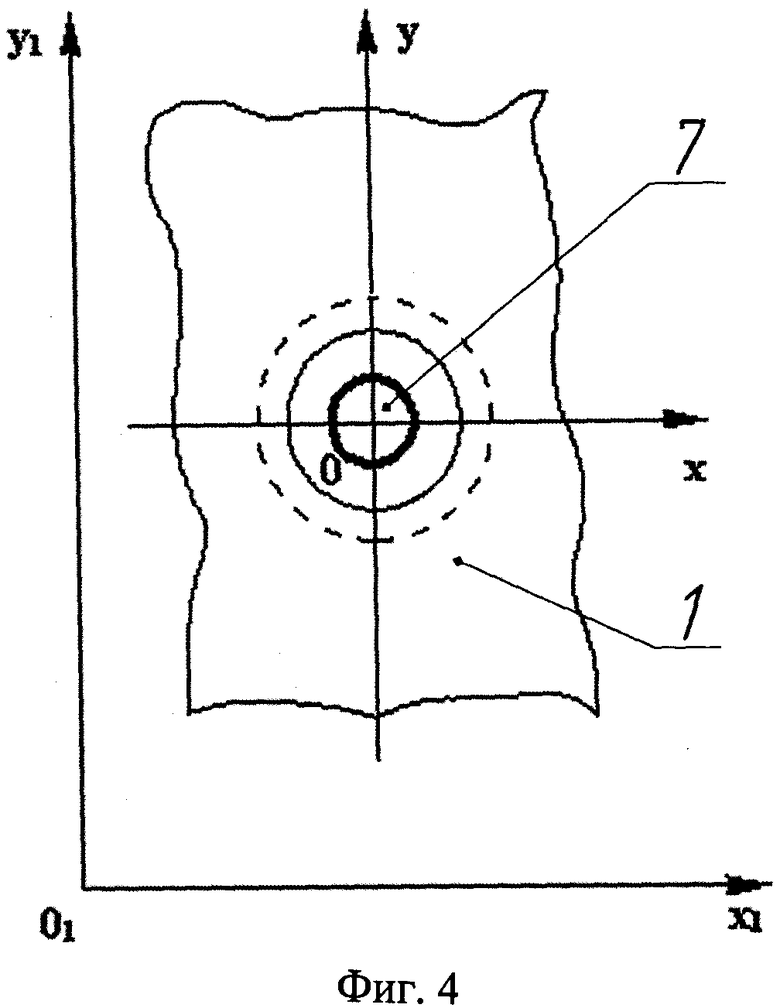
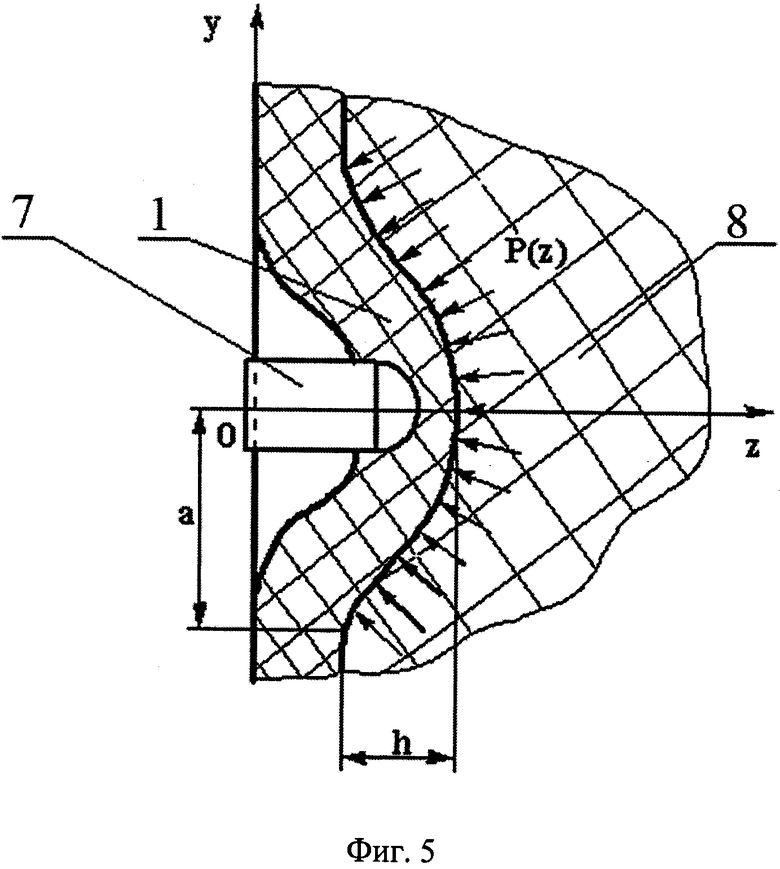
На фиг.1 изображена конструктивная схема построения тканевого бронежилета с антишоковым устройством; на фиг.2 - разрез по А-А на фиг.1; на фиг.3, 4 - расчетная схема процесса взаимодействия поражающего элемента с тканевым пакетом бронежилета; на фиг.5 - схема процесса взаимодействия элементов системы «Поражающий элемент - тканевый пакет бронежилета - биологический объект».
Амортизатор 2 (фиг.2) никакой защитной роли не играет, а обеспечивает удаление тканевого пакета БЖ 1 от подложки 3 с целью реализации прогиба тканевого пакета БЖ 1 во время внедрения в него ПЭ, способствуя тем самым поглощению его кинетической энергии. Толщина его выбирается из условия 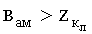
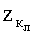
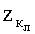
Пакет 6 (фиг.2) представляет собой сборку из нескольких слоев ткани той же основы, что и основная защита БЖ (арамидная ткань ТСВМ), склеенных между собой для обеспечения жесткости, за исключением зоны сгиба из той же ткани, обеспечивающей гибкость пакета слоев с зазором l (см. фиг.1) между ними в половину дуги при изгибе на 90°, что составляет l=1,88 мм. Размеры пакета 6 (b) в виде квадратов (см. фиг.1) выбираются из условия - не менее максимального характерного размера основания каверны временной полости (L или dвх), образуемой в мягких тканях БО при непробитии тканевого БЖ, что по данным экспериментальных и теоретических исследований при непробитии современных тканевых БЖ составляет в=100 мм (см. табл.1, 2). Увеличение размера квадрата ячейки пакета 6 (фиг.1, 2) и размера компенсатора удара 4 приводит к уменьшению гибкости БЖ.
В каждом компенсаторе удара 4 имеется одно или несколько герметично закрытых отверстий, обеспечивающих истечение воздуха из компенсатора удара 4 (дросселирование) при сохранении внутри него постоянное давление воздуха, т.е. Р2=const, при котором отверстия вскрываются или открываются от воздействия поражающего элемента на тканевый пакет БЖ.
Поскольку температурный режим эксплуатации БЖ предусматривает интервал -50…+50°С, то давление воздуха в компенсаторе удара 4 (фиг.2) при температуре -50°С должно соответствовать нормальному (Р0=1·105 Па). Так как компенсатор удара 4 закрыт герметично, то давление воздуха в нем будет зависеть от температуры окружающей среды и будет не меньше атмосферного, т.е. P1≥P0. При погружении в воду в БЖ при прочих равных условиях дополнительная выталкивающая сила (Архимедова сила) будет равна Fnд=(2вПП+вку)Sзρвg, где вПП, вку - толщина пакета пластин и компенсатора удара соответственно; Sз - площадь защиты БЖ (площадь поверхности подложки); ρв - плотность воды; g - ускорение свободного падения.
Принцип работы БЖ с антишоковым устройством при обеспечении защитных свойств заключается в следующем.
При попадании ПЭ в тканевый пакет БЖ 1 (фиг.1, 2) последний вовлекается в движение и по мере развития каверны вместе с поражающим элементом воздействует как минимум на один пакет 6 (см. фиг.2), который находится впереди компенсаторов удара 4.
Вовлеченный в движение пакет 6 воздействует на компенсатор удара 4, сжимая адиабатически воздух, находящийся в нем до некоторого давления Р2, при котором вскрываются или открываются дросселирующие одно или несколько отверстий, обеспечивающих истечение воздуха из компенсатора удара 4 при сохранении давления воздуха внутри компенсатора удара постоянным и равным Р2 до предельного его расхода при полном торможении воздействующих элементов (ПЭ, тканевого пакета БЖ 1 и пакета 6 подложки). Давления воздуха в компенсаторе удара Р2 и диаметр или площадь дросселирующего одного или несколько отверстий определяются соответствующим термодинамическим расчетом.
Для оценки технического результата вначале определим параметры взаимодействия ПЭ с БО в штатном тканевом БЖ при условии его непробития.
Процесс взаимодействия элементов системы «ПЭ - тканевый БЖ - БО» условно разделим на два этапа: - первый - этап вовлечения в движение тканевого пакета в зоне воздействия на него ПЭ. Данный этап взаимодействия заканчивается моментом времени, когда скорости ПЭ и тканевого пакета БЖ в зоне удара сравняются, т.е. скорость проникания ПЭ в тканевый пакет будет равна нулю. На данном этапе силу сопротивления мягких тканей БО можно не учитывать в силу ее малости по сравнению с силой сопротивления тканевого пакета БЖ внедрению ПЭ; - второй - это этап торможения мягкими тканями БО тканевого пакета БЖ и ПЭ, которые двигаются совместно.
Эта задача относится к теории ударного действия ПЭ по подвижной преграде, воздействующей на упругую несжимаемую среду, и решалась при следующих допущениях:
- ПЭ 7 (фиг.3, 4) взаимодействует с тканевым пакетом БЖ 1 по нормали и в процессе внедрения не деформируется (где на фиг.3, 4 01x1y1z1 и 0xyz инерциальная и неинерциальная системы отсчета соответственно);
- вся энергия ПЭ затрачивается на преодоление силы сопротивления тканевого пакета БЖ и на вовлечение его в движение;
- прецессия и нутация ПЭ отсутствуют;
- скорость внедрения ПЭ в тканевый пакет БЖ (Vв) мала (Vв=Vэ-VТП, где Vэ - скорость движения ПЭ, VТП - скорость движения тканевого пакета БЖ в зоне контакта с ним ПЭ), поэтому можно считать, что на ПЭ действует только прочностная составляющая силы сопротивления тканевого пакета, величина которой принимается постоянной;
- во время проникания ПЭ в тканевый пакет БЖ мягкие ткани БО практически не оказывают сопротивления образованию выпучены тканевого пакета БЖ по направлению движения ПЭ;
- развитие деформации тканевого пакета БЖ происходит в виде сферической поверхности от центра удара ПЭ в него;
- толщина тканевого пакета БЖ не изменяется в процессе его вдавливания в мягкие ткани БО, т.к. разрывное удлинение волокон тканей отечественного и зарубежного производства не превышает 5%;
- давление в мягких тканях БО определяется только динамическим воздействием на них.
Используя уравнение движения ПЭ при внедрении в тканевый пакет БЖ, определим силу сопротивления тканевого пакета БЖ внедрению ПЭ при условии его расположения на жестком основании

где mэ - масса ПЭ;
VПСНж - предельная скорость непробития тканевого пакета БЖ при условии его расположения на жестком основании;
вТП - толщина тканевого пакета БЖ.
Предельная скорость непробития тканевого пакета БЖ при условии его расположения на жестком основании (VПСНж) определяется экспериментально или рассчитывается через удельный единичный импульс [4].
Определим параметры взаимодействия элементов системы «ПЭ - тканевый пакет БЖ» для условий свободного положения тканевого пакета (первый этап решения задачи).
Для этого воспользуемся системой уравнений:
- уравнением движения ПЭ в неинерциальной системе отсчета по оси OZ (см. фиг.3):

где VТП - скорость движения тканевого пакета БЖ в точке удара по нему ПЭ в направлении его действия;
- уравнением движения тканевого пакета БЖ в точке попадания в него ПЭ в направлении оси OZ:

где mТП - масса тканевого пакета БЖ, вовлеченного в движение.
Масса тканевого пакета БЖ, вовлекаемого в движение ПЭ, изменяется во времени и при условии, что скорости его продеформированной части в радиальных направлениях от точки удара равны, можно определить как для сферической поверхности, образованной из объема тканевого пакета БЖ, охваченного деформацией, масса которого равна

где zл - координата перемещения лицевой поверхности тканевого пакета БЖ по оси OZ в точке удара ПЭ или радиус продеформированной поверхности БЖ;
ρТП - плотность материала тканевого пакета БЖ.
Решая совместно уравнения (2), (3), можно определить предельную скорость непробития тканевого пакета БЖ при его свободном положении в пространстве
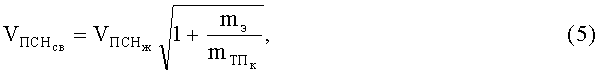
где 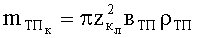
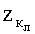
Анализ выражения (5) показывает, что предельная скорость непробития пакета БЖ в свободном состоянии больше, чем при размещении на жестком основании и тем больше, чем легче материал тканевого пакета БЖ и меньше его масса, вовлекаемая в движение.
Оценим параметры движения тканевого пакета БЖ при условии его непробития ПЭ.
Вначале определим время, соответствующее моменту прекращения внедрения ПЭ в тканевый пакет БЖ (tк) (Vв=0, Vэ=VТП).
Подставив уравнение (3) в (2), разделив переменные и проинтегрировав выражение, получим

где Vс - скорость встречи ПЭ с тканевым пакетом БЖ.
Параметры движения тканевого пакета БЖ для момента времени t (время внедрения ПЭ в тканевый пакет БЖ) можно определить, воспользовавшись уравнениями (1), (3), (6). Скорость тканевого пакета в зоне удара в него ПЭ будет равна

Найдем перемещения (прогиб) лицевой поверхности тканевого пакета БЖ в точке удара по нему ПЭ за время 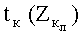
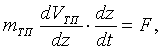
где 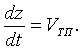
Разделив переменные и проинтегрировав данное уравнение, получим

Подставив выражения (1), (7) в уравнение (8), получим

где 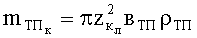
Максимальное перемещение лицевой поверхности тканевого пакета БЖ за время внедрения в него ПЭ будет соответствовать скорости 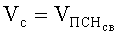
Уравнение (9) можно преобразовать к виду:

где 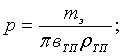
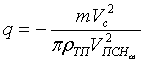
Уравнение (10) является кубическим. Решение данного уравнения осуществляется с применением формулы Кардано.
Тогда координата при перемещении тыльной поверхности тканевого пакета БЖ в точке удара ПЭ с учетом допущения семь будет равна

Для оценки степени поражения биологического объекта в тканевом БЖ рассмотрим второй этап взаимодействия элементов системы «ПЭ - тканевый пакет БЖ-БО» - это этап торможения ПЭ и вовлеченного в движение тканевого пакета БЖ мягкими тканями БО.
Решение задачи осуществлялось при следующих допущениях:
- из составляющих силы сопротивления мягких тканей БО учитывается только инерционная;
- потерями энергии при взаимодействии элементов системы «ПЭ - тканевый пакет БЖ-БО» на трения и нагрев пренебрегаем.
Схема процесса взаимодействия элементов системы «ПЭ - тканевый пакет БЖ-БО» представлена на фиг.5.
Уравнение движения тканевого пакета БЖ 1 с ПЭ 7 при торможении мягкими тканями БО 8 имеет вид:
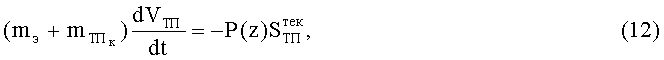
где 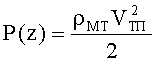
ρМТ - плотность мягких тканей БО;
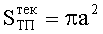
а - текущее значение величины хорды выпучены тканевого пакета БЖ в виде шарового сегмента (см. фиг.5).
Найдем максимальную глубину каверны в мягких тканях при торможении подвижной системы «ПЭ - тканевый пакет БЖ». Для этого воспользуемся уравнением (12), которое можно преобразовать к виду
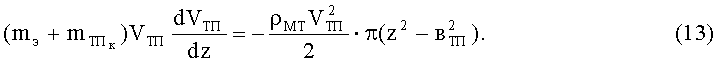
Разделив переменные и проинтегрировав выражение (13), получим
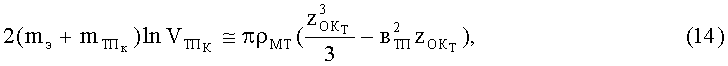
где 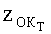
Уравнение (14) можно преобразовать к виду:

где 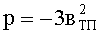
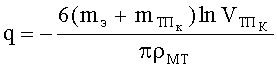
Решение данного кубического уравнения (15) также осуществляется с применением формулы Кардано.
Диаметр выпучены тканевого пакета БЖ по его тыльной поверхности в момент останова его мягкими тканями БО или входной диаметр каверны в них будет равен

Согласно допущению семь высота выпучены тыльной поверхности тканевого пакета БЖ или глубина каверны в мягких тканях БО (см. фиг.5) будет равна

Окончательно объем каверны в мягких тканях БО, образуемый при торможении ими ПЭ и тканевого пакета БЖ будет равен
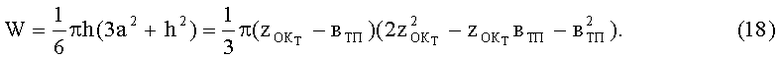
Через параметры каверны в мягких тканях БО можно определить степень контузии (СК) БО.
Размеры временной полости определяются следующими характеристиками: глубиной (H или h), основанием (L или dвх), площадью (S) и объемом (W). При экспериментально-теоретическом методе определения первые три параметра легко устанавливаются непосредственно по рентгенограмме, а последний - объем является расчетной величиной, определяемый как объем эллипсоида вращения по следующей формуле [1].

Значимость всех перечисленных параметров временной полости от величины энергии пули для тканевых БЖ представлена в табл.1, 2.
Результаты анализа экспериментальных и расчетных данных свидетельствуют, что параметры временной полости в значительной степени определяются именно кинетической энергией пули. Как оказалось, размеры ее основания колеблются незначительно при изменении величины энергии пули [1]. В последующем была получена эмпирическая зависимость, связывающая степень тяжести контузионных повреждений (СК) с глубиной (H) и площадью (S) временной полости (ВП) [1].

Используя опытные данные работы [1], авторами предлагаемого изобретения была получена другая эмпирическая зависимость для определения контузионного поражения БО в виде

Условия применимости зависимости (21) - 110≤W≤300 см3.
На основании анализа опытных данных работ [1, 5] и результатов расчета установлено, что при объеме временно пульсирующей полости W<110 см3 СК<2,0, а при W>300 см3 СК>3,1.
Зависимость размеров временной полости от величины кинетической энергии ПЭ достаточно убедительно свидетельствует о том, что параметры временной полости непосредственно характеризуют интенсивность ударного воздействия при непробитии БЖ, а если быть еще точнее, являются показателями именно той части кинетической энергии, которая передается за преграду на подлежащие мягкие ткани БО.
В настоящее время большинство как отечественных, так и зарубежных исследователей однозначно связывают тяжесть заброневой контузионной травмы при непробитии БЖ именно с феноменом образования временной полости, а приведенные выше эмпирические зависимости можно взять за основу при оценке травмобезопасности в БЖ при обстреле.
Рассмотренная математическая модель по расчету параметров взаимодействия элементов системы «ПЭ - тканевый БЖ - БО» позволяет вполне удовлетворительно их прогнозировать расчетным способом. Так, относительная ошибка расчета глубины временной полости в мягких тканях БО (h) и ее диаметра у основания (dвх) не превышает 20%. Результаты расчета параметров взаимодействия элементов системы «ПЭ - тканевый БЖ-БО» приведены в табл.3.
Далее оценим технический результат предлагаемого антишокового устройства БЖ. Вначале оценим защитные свойства предлагаемого БЖ по сравнению со штатным по пулестойкости. Оценку защитных свойств произведем для БЖ 6Б11, в котором тканевый пакет выполнен из 30 слоев ткани ТСВМ-ДЖ (вТП=12 мм, 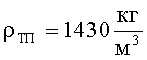
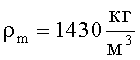
Найдем массу предлагаемого антишокового устройства без учета массы амортизатора 2 и упругого наполнителя 5 компенсаторов удара (фиг.1, 2).
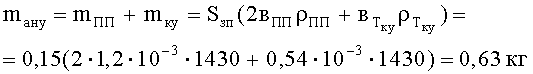
где mПП - масса пакета пластин;
mку - масса компенсаторов удара;
вПП, 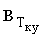
ρПП, 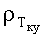
Тогда общая масса предлагаемого БЖ с антишоковым устройством составит 4,33 кг, что не превышает массу штатного БЖ 6Б23, принятого на снабжение в последние годы (масса БЖ 6Б23 составляет 4,5 кг).
При поражении предлагаемой конструкции БЖ пулями стрелкового оружия и осколками боеприпасов его защиту необходимо рассматривать как многослойную, состоящую из тканевого пакета 1, двух пакетов 6 (см. фиг.2) и компенсатора удара 4.
В данном случае предельная скорость сквозного непробития защиты при условии сохранения массы и формы ударника может быть определена по зависимости

где 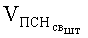
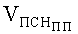
Предельную скорость непробития пакета и одной стенки компенсатора удара пулями пистолета Макарова можно определить по зависимости [6]

где 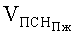
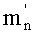
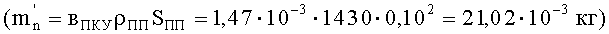
Предельную скорость непробития жестко закрепленного пакета и стенки компенсатора удара можно определить через удельный единичный импульс (iв), который для ткани ТСВМ-ДЖ составляет в среднем 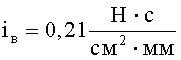
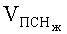

или 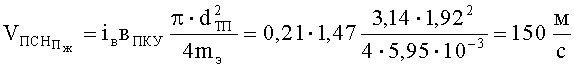
где Sм - площадь Миделевого сечения пули совместно с тканевым пакетом,
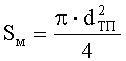
dТП - диаметр выпучены по тыльной поверхности тканевого пакета.
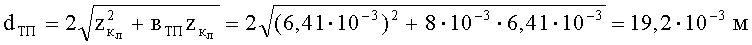
Тогда 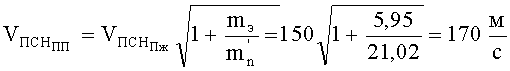
Окончательно предельная скорость непробития защиты предлагаемой конструкции БЖ пулями ПМ составит 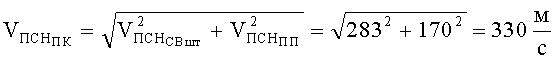
Далее найдем снижение степени контузии личного состава подразделений силовых структур в тканевых БЖ при использовании в антишоковом устройстве подложки в виде компенсаторов удара (КУ) с дросселированием воздуха и без него. Допустим, что температурный интервал использования предлагаемого БЖ от -50 до +50°С.
При поражении предлагаемой конструкции БЖ пулями стрелкового оружия и осколками боеприпасов максимальные напряжения на поверхности мягких тканей БО будут уменьшены до четырех раз по сравнению с избыточным давлением воздуха в компенсаторах удара.
Допустим, что ПЭ воздействует через тканевый пакет БЖ в геометрический центр пакета 6 (см. фиг.2), который находится впереди КУ.
Вначале найдем начальную скорость движения подвижной системы 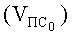
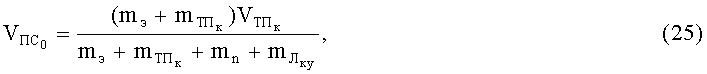
где 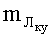
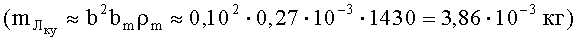
mn - масса пластины пакета;
(mn≈b2bnρm≈0,102·1,2·10-3·1430=17,16·10-3 кг).
Процесс торможения ПЭ и подвижных элементов БЖ разделим на две стадии. I стадия - торможение ПЭ и движущихся элементов БЖ осуществляется при закрытых отверстиях КУ (рассматривается адиабатический процесс сжатия воздуха в КУ).
Уравнение движения подвижной системы БЖ в данном случае имеет вид:

где 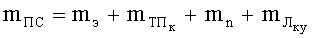
VПС - скорость движения ПЭ и подвижной системы БЖ;
ΔР(x) - избыточное давление воздуха в КУ в зависимости от степени его сжатия;
SКУ - площадь КУ, численно равная площади его фронтальной проекции.

где Р2(х) - давление воздуха в КУ в зависимости от степени его сжатия;
P0 - давление воздуха в окружающей среде (можно брать равным нормальному).
Давление воздуха в КУ с изменением объема воздуха при адиабатическом сжатии определяется выражением [7]
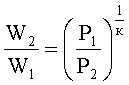

где 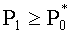
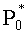
W2 - текущий объем воздуха в КУ при торможении им ПЭ и движущихся элементов БЖ;
W1 - первоначальный объем воздуха в КУ при давлении P1;
к - показатель адиабаты (для воздуха к=1,4).
Давление воздуха в КУ при температуре окружающей среды T1 (ρ1=ρ0, W1=const, процесс изохорный) равно

Текущий объем воздуха в КУ будет равен

где х - деформация КУ.
Из уравнений (27), (28) и (30) получим
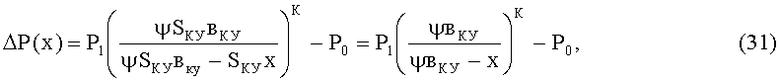
где ψ - коэффициент учета объема упругого наполнителя в КУ (ψ≤1).
Для поролона ψ=0,8, а при его отсутствии ψ=1; вКУ - толщина КУ.
Найдем величину деформации КУ 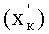
Для случая адиабатического сжатия воздуха в КУ согласно уравнению (28) имеем

Найдем скорость движения ПЭ и вовлеченных в движение элементов БЖ для момента времени, когда давление воздуха в КУ достигает Р2 при допущении, что инерционная масса вовлекаемого в движение воздуха и упругого наполнителя КУ мала и ею можно пренебречь. Для этого воспользуемся уравнением (26) и с учетом зависимости (31) после интегрирования получим
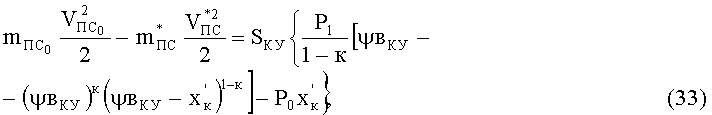
где 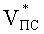
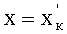
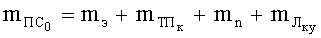
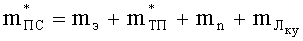
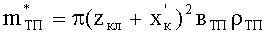
Отсюда
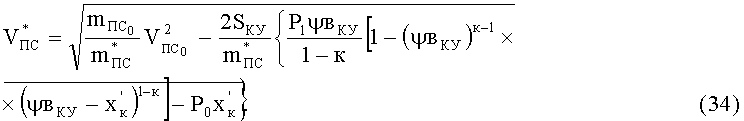
Подставив уравнение (32) в (34), получим
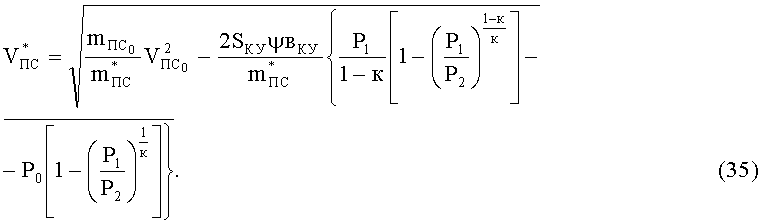
II стадия - торможение ПЭ и вовлеченных в движение элементов БЖ происходит при работе дросселирующего устройства КУ (P2=const, ΔP2=Р2-Р0). Уравнение движения ПЭ и вовлеченных в движение элементов БЖ при воздействии на КУ имеет вид:

Разделив переменные и проинтегрировав выражение (36), получим

где хк - конечное перемещение тканевого пакета БЖ или максимальная степень деформации КУ при его торможении.
Отсюда

Подставив уравнения (32), (35) в выражение (38), получим
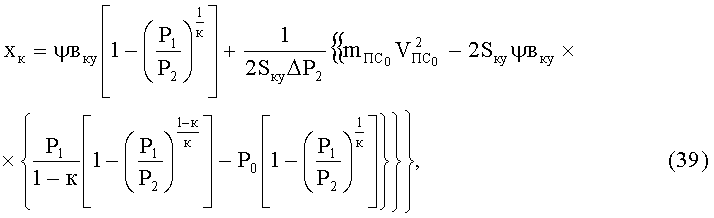
где ΔР2=P2-P0; 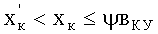
Степень воздействия ПЭ на БО в предлагаемом тканевом БЖ зависит от давления воздуха в КУ P2 и времени торможения ПЭ и вовлеченных в движение элементов БЖ.
Чем меньше давление воздуха в КУ Р2, тем ниже степень контузии БО. Далее задача по оптимизации параметров антишокового устройства со специальным КУ решается следующим образом:
1) зная параметры средства поражения (ПЭ), характеристики тканевого БЖ и условия соударения, определяем начальную скорость воздействия ПЭ и вовлеченных в движение элементов БЖ на КУ по зависимости
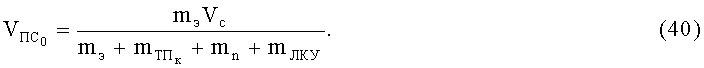
2) задаваясь шагом по избыточному давлению воздуха в КУ(ΔР), определяют Р2 по зависимости (39) при условии, что хк≤ψвКУ. Затем определяется 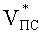
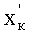
Найдем диаметр дросселирующего отверстия, через которое происходит истечение воздуха из КУ при торможении тканевого пакета БЖ, обеспечивающего постоянное давление воздуха в нем (P2=const).
Вначале найдем время торможения тканевого пакета БЖ на II стадии (при Р2=const), которое равно времени дросселирования воздуха из КУ.
Для этого воспользуемся уравнением (36), проинтегрировав которое, получим

Для случая предельного вытеснения воздуха из КУ (W1=0) время его расхода равно

где ρ1 - плотность воздуха в КУ при температуре Т1;
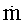
Приравняв уравнения (41) и (42), получим

Отсюда

Для случая истечения воздуха через отверстие из сосуда с критической скоростью Vкр массовый секундный его расход будет равен [7]
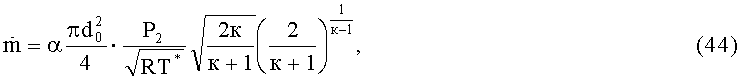
где α - коэффициент расхода воздуха;
d0 - диаметр отверстия, через которое истекает воздух;
Р2 - давление воздуха на входе в отверстие (принимается равным давлению воздуха в КУ);
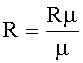
Rµ - универсальная газовая постоянная, 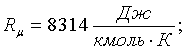
µ - молекулярная масса газа (воздуха);
Т* - температура торможения газа (можно принимать равной температуре воздуха на входе в отверстие, т.е. Т*=T2).
Критическая скорость течения газа через отверстие определяется зависимостью [7]
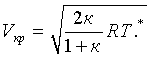
Конечную температуру воздуха в КУ найдем из уравнения его состояния
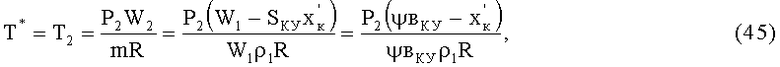
где для воздуха при нормальных условиях (P0=1·105 Па, Т1=293 К)
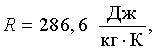
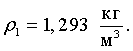
Подставив зависимость (32) в зависимость (45), получим

Конечная плотность воздуха при его давлении Р2 для рассматриваемого процесса равна

Приравняв выражения (43) и (44), получим
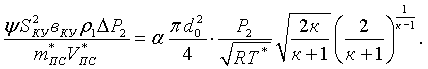
Отсюда
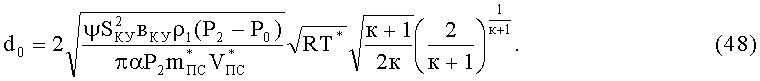
Для оценки амортизирующих свойств КУ без дросселирующих отверстий необходимо установить связь между конечным перемещением тканевого пакета БЖ или степенью деформации КУ и давлением воздуха в нем.
Воспользовавшись уравнением (26) и решая его аналогично тому, как при выводе зависимости (33), получим
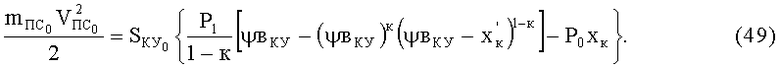
В данном случае ψ можно брать равным единице, т.е. КУ без упругого наполнителя.
Конечное перемещение тканевого пакета БЖ (хк) найдем через давление воздуха в КУ, равное Р2 и соответствующее максимальной деформации КУ.
Используя уравнение (28), получим

С учетом того, что W1=ψSКУвКУ, a W2=W1-SКУхк, уравнение (50) примет вид:

Тогда уравнение (49) примет вид:
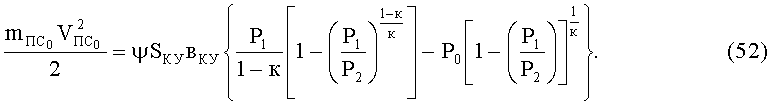
Эффективность использования антишокового устройства оценим в сравнении со штатным тканевым БЖ 6Б11 при поражении 9-мм пулями ПМ на дальности 5 м (дальность 100% непробития штатного БЖ 6Б11). Скорость встречи пули с тканевым пакетом БЖ на этой дальности 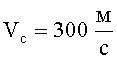
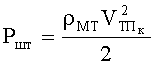
Начальную скорость тканевого пакета предлагаемого БЖ найдем по зависимости (40).
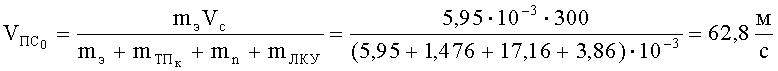
Результаты расчета по оценке оптимальных характеристик предлагаемой конструкции антишокового устройства тканевого БЖ с компенсаторами удара с дросселирующими отверстиями и без них и параметров состояния воздуха в них, а также степени поражения личного состава подразделений силовых структур в тканевых БЖ предлагаемой конструкции на дистанции обстрела 5 м из 9-мм ПМ представлены в табл.4.
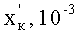
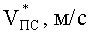
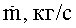
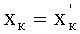
где в табл.4 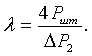
Наиболее рациональной толщиной КУ, с точки зрения приемлемых размеров, следует считать толщину в интервале 15…20 мм. Диаметр дросселирующего отверстия должен составлять не более 40 мм. Тогда максимальное значение отношения площади отверстий к площади КУ будет равно
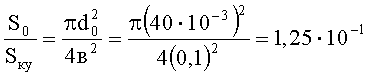
или S0:Sку=1:8.
Таким образом, отношение площади одного или нескольких изначально герметично закрытых отверстий в КУ к фронтальной его площади не должно превышать 1:8.
Анализ данных табл.4 показывает, что при использовании антишокового устройства с КУ без дросселирующих отверстий начальное давление на границе раздела БЖ - мягкие ткани БО при толщине КУ 10…25 мм по сравнению со штатным БЖ 6Б11 уменьшаются в 12…69 раза, а при использовании КУ с дросселирующими отверстиями при том же интервале толщин КУ уменьшается в 20…169 раза.
Предлагаемая конструкция БЖ с антишоковым устройством обеспечивает некоторую плавучесть личного состава подразделений силовых структур. Так, при использовании КУ толщиной от 15…20 мм при общей площади защиты Sз=0,5 м2 выталкивающая сила воды будет равна 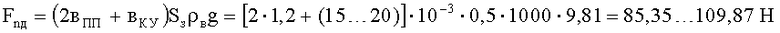
Предлагаемый БЖ с антишоковым устройством не уступает по пулестойкости штатному, значительно снижает степень повреждающего воздействия на БО при непробитии тканевого БЖ различными ПЭ, а при погружении в воду обеспечивает выталкивающую силу практически на уровне двойного веса БЖ, что дает положительный эффект, заключающийся в повышении живучести личного состава подразделений силовых структур в тканевых БЖ.
Источники информации
1. Концептуальные основы создания средств индивидуальной защиты. - Ч. I. Бронежилеты / В.И.Байдак и др. Под общ. ред. В.Г.Михеева. - М.: Вооружение. Политика. Конверсия, 2003. - 338 с.
2. Знахурко В.А. Экипировка военнослужащего. / В.А.Знахурко и др. - Пенза: ПАИИ, 2005. - 148 с.
3. Пат. РФ №2395055, 27.11.2007, F41Н 1/02.
4. Конструкция, теория и расчет артиллерийских снарядов и головных частей. /B.C.Аблов и др. - Пенза: ПВАИУ, 1979. - 504 с.
5. Ивлиев Ю.Г. Заброневая контузионная травма (анализ вероятных механизмов возникновения, методов оценки и способов предотвращения) / Ю.Г.Ивлиев, В.Н.Гривков, В.В.Чивилев // Актуальные проблемы защиты и безопасности: Тр. 4-й Всерос. конф. - СПб.: НПО «Специальные материалы», 2001. - С.324-330.
6. Дерябин П.Н. Физические основы поражения живой силы в бронежилетах и пути повышения ее живучести. /П.Н.Дерябин // Монография. - Пенза: ПАИИ, 2000. - 123 с.
7. Основы теплотехники. /В.В.Бурлов и др. - Пенза: ПАИИ, 2003. - 231 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| ТКАНЕВЫЙ БРОНЕЖИЛЕТ С АНТИШОКОВЫМ УСТРОЙСТВОМ | 2007 |
|
RU2395055C2 |
| БРОНЕЖИЛЕТ С КОМПЕНСАТОРАМИ УДАРА | 2005 |
|
RU2285887C2 |
| АНТИТРАВМАТИЧЕСКИЙ ПАКЕТ | 1996 |
|
RU2125223C1 |
| Способ снижения заброневой травмы пассивной индивидуальной защитой человека от высокоэнергетических поражающих элементов стрелкового оружия и осколков боеприпасов | 2019 |
|
RU2722698C1 |
| Бронезащитный пакет из арамидных тканей с дискретным полимерным покрытием | 2022 |
|
RU2814442C1 |
| БРОНЕЖИЛЕТ, ШЕЙНО-ПЛЕЧЕВАЯ НАКЛАДКА И ЗАЩИТНЫЙ КОМПЛЕКТ | 1995 |
|
RU2072084C1 |
| БАЛЛИСТИЧЕСКИЙ МЯГКИЙ ЗАЩИТНЫЙ ПАКЕТ | 2008 |
|
RU2382317C1 |
| Способ определения травмобезопасности бронешлема при взрыве боеприпаса | 2017 |
|
RU2644901C1 |
| ЖИЛЕТ ЗАЩИТНЫЙ | 1997 |
|
RU2121644C1 |
| СЛОИСТЫЙ БРОНЕЗАЩИТНЫЙ МАТЕРИАЛ | 2013 |
|
RU2522067C1 |
Изобретение относится к средствам индивидуальной бронезащиты личного состава, а именно к бронированной или пуленепробиваемой одежде, и может быть использовано в военном деле и в самостоятельных силовых структурах и ведомствах. Предложен тканевый бронежилет, содержащий грудную и спинную секции, в чехлах которых расположены защитные экраны (тканевые пакеты) из высокопрочной арамидной ткани (ТСВМ или аналог), а на внутренних их поверхностях расположено антишоковое устройство, включающее в себя амортизатор и подложку. Амортизатор обеспечивает удаление тканевого пакета бронежилета от подложки с целью реализации прогиба тканевого пакета во время внедрения в него поражающего элемента. Подложка выполнена в виде компенсаторов удара из секций, представляющих собой камеры из воздухонепроницаемой прорезиненной арамидной ткани с упругим наполнителем внутри, облицованные с двух сторон пакетами пластин, причем тыльный пакет пластин наклеивается на компенсаторы удара таким образом, чтобы центры масс его квадратных элементов располагались напротив угловых точек сочлененных компенсаторов удара. Пакеты пластин представляют собой сборки из слоев ткани той же основы, что и основная защита бронежилета (ТСВМ или аналог), склеенных между собой для обеспечения жесткости, за исключением зоны сгиба. Размеры пластин пакета в виде квадратов выбираются из условия равенства максимальному характерному размеру основания каверны временной полости, образуемой в мягких тканях биологического объекта при непробитии тканевого бронежилета. В каждом компенсаторе удара имеется одно или несколько герметично закрытых отверстий с общей площадью, относящейся к фронтальной площади компенсатора удара не более как 1:8, обеспечивающих истечение воздуха из компенсатора удара при постоянном давлении, при котором отверстия вскрываются от воздействия вовлеченных в движение пластин пакета через основную защиту бронежилета. Изобретение направлено на снижение степени повреждающего воздействия поражающих элементов на биологический объект при непробитии бронежилета без увеличения его массы. 5 ил., 4 табл.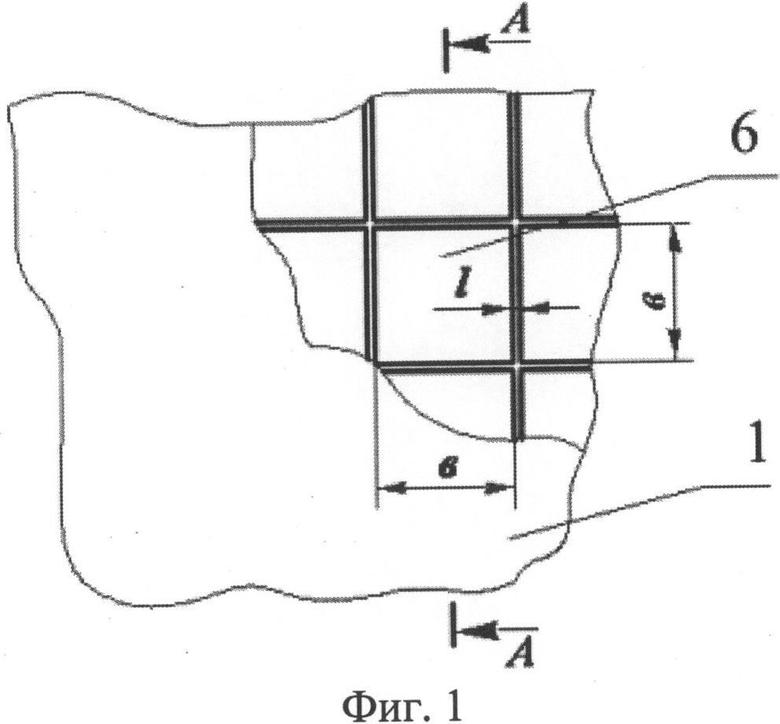
Тканевый бронежилет, содержащий грудную и спинную секции, снабженные размещенными в чехлах пакетами из арамидной ткани ТСВМ, имеющими на своей внутренней поверхности антишоковое устройство, состоящее из амортизатора и подложки, которая состоит из слоя гибко соединенных между собой по периметру квадратных пакетов в виде склеенных между собой слоев арамидной ткани ТСВМ и компенсаторов удара с одним или несколькими дросселирующими отверстиями, отличающийся тем, что подложка дополнительно в свой состав включает пакет пластин из слоя гибко соединенных между собой по периметру квадратных пакетов в виде склеенных между собой слоев арамидной ткани ТСВМ, размещенный на тыльной стороне подложки таким образом, чтобы центры масс его квадратных элементов располагались напротив угловых точек сочлененных компенсаторов удара.
| US 6266819 B1, 31.07.2001 | |||
| БРОНЕЖИЛЕТ С КОМПЕНСАТОРАМИ УДАРА | 2005 |
|
RU2285887C2 |
| US 5060314 A1, 29.10.1991 | |||
| ТКАНЕВЫЙ БРОНЕЖИЛЕТ С АНТИШОКОВЫМ УСТРОЙСТВОМ | 2007 |
|
RU2395055C2 |
Авторы
Даты
2014-10-27—Публикация
2012-07-11—Подача