Общим недостатком типологической основы, базирующейся на биогеоценотическом подходе [4], является недооценка изменчивости лесных экосистем во времени в процессе развития. Типы леса характеризуются признаками и свойствами, присущими спелым или близким к ним возрастным стадиям развития древостоя. При классификации сложных многопородных хвойно-широколиственных лесов, где состав древостоя и облик нижних ярусов зависят от стадии возрастной динамики древостоя, в пределах одного типа лесорастительных условий выделяется значительное число типов леса (производных). Математически подвижное равновесие можно представить в виде точек на плоскости географического ландшафта (рис.1).
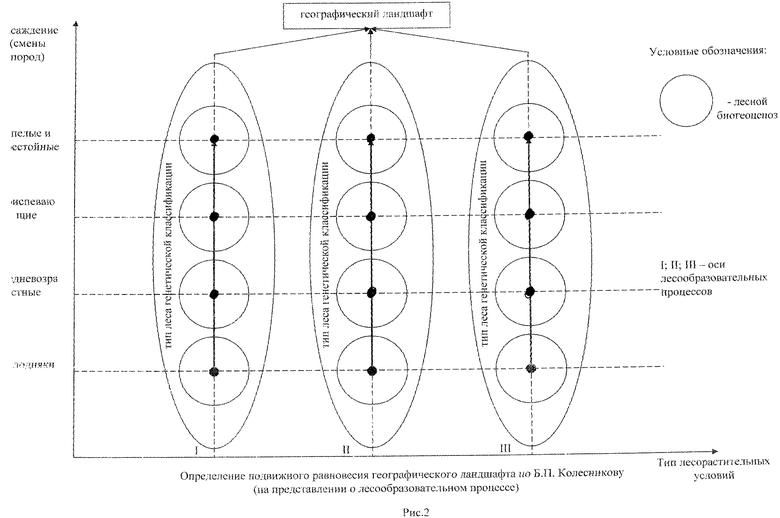
Для географо-генетического направления в лесной типологии, основателем которого является Б.П.Колесников [1], характерно понимание типа леса как крупного таксона. Смены пород, происходящие в процессе естественного восстановления сообществ из-за различий в биолого-экологических свойствах лесообразователей (теневыносливость, интенсивность роста, продолжительность жизненного цикла), отражают типы леса. Типы леса, объединяющие биогеоценозы, находящиеся на различных стадиях возрастных и восстановительных смен, наиболее полно отражают основные стадии лесообразовательного процесса и позволяют мотивированно планировать лесохозяйственные мероприятия. Природно-географическая основа нашла для организации лесного хозяйства кедровых лесов Урала и Дальнего Востока. Математически-подвижное равновесие можно представить в виде точек на прямых линиях географического ландшафта (рис.2). Однако использование природно-географической основы в сложных многопородных хвойно-широколиственных лесах, где в состав древостоя входит несколько основных эдификаторов (сосна, ель, дуб, ясень) невозможно. В пределах типа лесорастительных условий на разных этапах развития древостоя из-за различий в биолого-экологических свойствах эдификаторов выделяется несколько типов леса, а в пределах разных типов лесорастительных условий выделяются однородные типы леса.
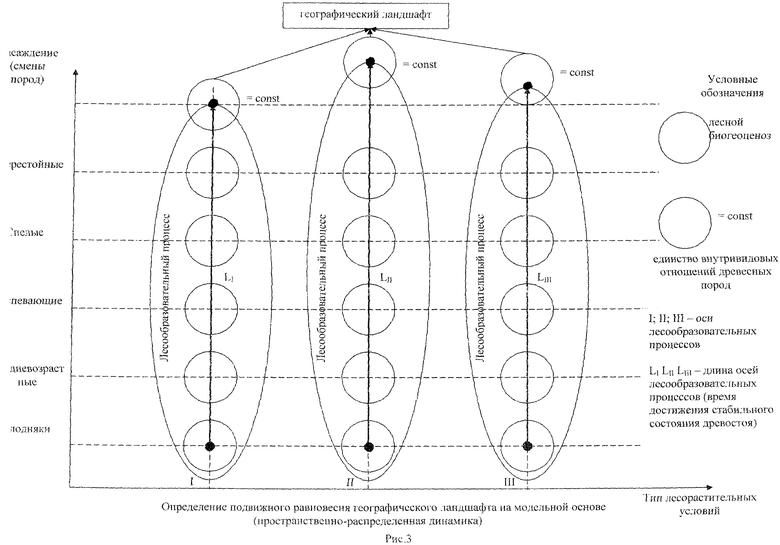
С развитием вычислительной техники появились имитационные модели, позволяющие проанализировать развитие лесного сообщества от его возникновения и до формирования климаксовых лесов. Такие 2-мерные модели леса используются для математического описания пространственно-распределенной динамики различных растительных систем на популяционном и ценотическом уровнях [5, 10] и значительно реже на экосистемном [6] в США, Канаде и Западной Европе. Математически подвижное равновесие можно представить в виде конечных точек на прямых линиях географического ландшафта (рис.3).
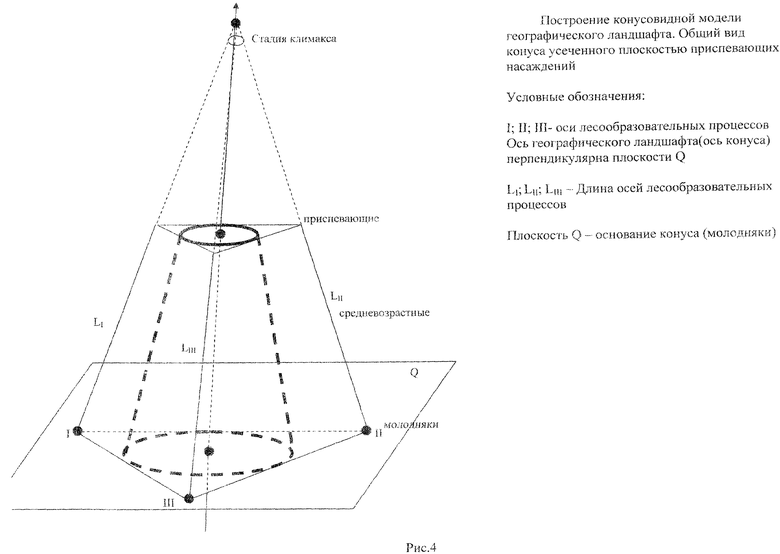
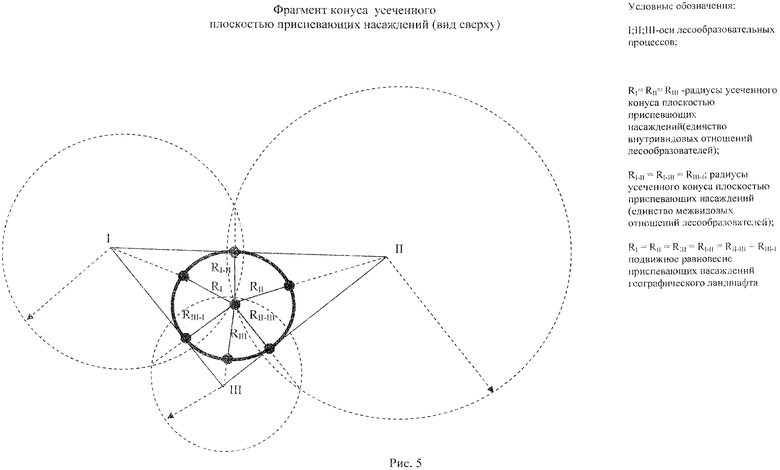
Идейную основу использования биологической сущности лесообразовательного процесса в лесном хозяйстве заложил в своих работах Г.Ф.Морозов [2, 3]. Источник развития или двигательную силу в лесу он видел в «том подвижном равновесии, какое мы всюду наблюдаем в живой природе»[2, с.322]. Подвижное равновесие в сложных многопородных хвойно-широколиственных лесах следует рассматривать как единство внутривидовых и межвидовых отношений лесообразователей, в мере учитывающее пространственную и временную изменчивость. Единственный способ определить подвижное равновесие - разработать модельную основу, которая бы отражала общий закон развития природы, а именно устанавливала равновесное состояние обмена веществом и энергией лесообразователей географического ландшафта. Математически такая основа может быть представлена в виде конуса. Для построения конусовидной модели леса, базирующейся на биологической сущности лесообразовательного процесса необходимо выполнить следующие математические операции: а) все конечные точки осей лесообразовательных процессов и точку оси географического ландшафта объединить в одну (вершина конуса); б) длина оси географического ландшафта должна находиться перпендикулярно к плоскости (основание конуса); в) длина осей лесообразовательных процессов равна времени достижения стадии климакса (const). Математически подвижное равновесие определяется точками на оси географического ландшафта (рис.4, рис.5).
Цель изобретения. Создать способ определения подвижного равновесия географического ландшафта, который включает создание модельной основы, что достигается математическим моделированием биологических процессов в живой природе.
Поставленная цель достигается тем, что на примере Брянского лесного массива разработать конусовидную 3-мерную модель географического ландшафта, базирующуюся на биологической сущности лесообразовательных процессов.
Практическое использование модельной основы для определения подвижного равновесия географического ландшафта требует решения следующих задач:
1. Выявить параметры состава на различных возрастных стадиях и для различных лесорастительных условий.
2. Определить время достижения стабильного состояния состава насаждений для различных лесорастительных условий.
3. Оценить взаимосвязь продуктивности древесных пород и почвенного плодородия в одинаковых лесорастительных условиях.
4. Оценить режим минерального питания древесных пород в зависимости от уровня грунтовых вод.
Для построения модели географического ландшафта нами были использованы марковские модели. Основной конструкцией в этих моделях служит матрица, элементы которой равны вероятностям перехода из одного состояния в другое за определенные промежутки времени. Марковская модель первого порядка - это модель, в которой будущее системы определяется ее текущим состоянием и не зависит от того, каким путем система пришла в это состояние. Последовательность результатов, получаемых из такой модели, часто называют марковской цепью. Название получила по имени выдающегося русского ученого математика Андрея Андреевича Маркова (1856-1922).
Преимущества моделей марковского типа сводятся к следующему:
1. Такие модели довольно легко строить на основе данных по сукцессиям
2. Марковские модели не требуют глубокого понимания внутренних механизмов динамических изменений в системе, но могут помочь выявить те области, где такое понимание имело бы значение
3. Основная матрица переходных вероятностей отображает главные параметры динамических изменений в системе таким образом, который доступен лишь немногим моделям других типов.
4. Результаты анализа марковских моделей легко представить графически, что делает их более наглядными и понятными специалистам по управлению ресурсами
5. Вычислительные потребности при исследовании марковских моделей удовлетворяются с помощью персональных компьютеров.
Среди марковских моделей наибольший интерес для нас представляет модель Хорна [7, 8, 9], основанная на описании сукцессии марковскими процессами. Основной конструкцией в этой модели служит матрица, элементы которой равны вероятностям смены дерева деревом каждого конкретного вида. Модель Хорна, примененная нами, позволяет выявить состав насаждений по числу деревьев на различных возрастных стадиях и для различных лесорастительных условий, а также время достижения стабильного состояния (стадия климакса) для различных лесорастительных условий.
Для установления взаимосвязи между продуктивностью древесных пород и показателями почвенного плодородия в одинаковых лесорастительных условиях проведен сравнительный анализ методами математической статистики, многофакторных корреляций и регрессий.
Режим минерального питания древесных пород в зависимости от уровня грунтовых вод устанавливался путем проведения сопряженных наблюдений за динамикой основных элементов питания в почве и накопления их в хвое и листьях древесных пород.
Для создания модели необходимо: классификация состояний сукцессий по определенным категориям; данные для определения переходных вероятностей или скоростей, с которыми состояние переходит со временем из одной категории данной классификации в другую; данные о начальных условиях, сложившихся в некоторый фиксированный момент времени, обычно после известного возмущения.
Модельными объектами послужили елово-широколиственные леса, расположенные в области распространения мелового рухляка Брянского лесного массива. При характеристике массива Г.Ф.Морозов отмечал, что именно в этой области елово-широколиственные насаждения получили наиболее типичное выражение. Главная отличительная особенность - широкое участие в составе ясеня обыкновенного. В геоморфологическом отношении данная территория представляет собой водораздел между бассейном р. Десна и р. Рессета (бассейн р. Оки).
Фитоценозы формируются в результате сукцессий антропогенного характера (вырубка древостоев) и представлены сообществами разного динамического состояния (от молодняков до перестойных). На основе лесотипологических исследований выделены восстановительно-возрастные ряды нарастающего увлажнения (оси лесообразовательных процессов):
I. Спелые и перестойные насаждения в I ярусе характеризуются преобладанием в составе ели (до 40%). Постоянную примесь составляют дуб (до 30%), ясень, липа и осина (до 20%), береза, клен, вяз (до 10%). Молодняки и средневозрастные характеризуются преобладанием осины в I ярусе. В напочвенном покрове характерно широкое участие мегатрофных представителей со степенью увлажнения (мезофиты). Индикатором и доминантой напочвенного покрова является зеленчук желтый. Этот ряд занимает верхние части склонов водораздела с дерново-карбонатными супесчаными или суглинистыми оподзоленными почвами. Средний уровень грунтовых вод в летний (меженный) период находится в основном на глубине 2-3 м.
II. Спелые и перестойные насаждения в I ярусе характеризуются преобладанием дуба (до 40%). Постоянную примесь составляет ясень (до 30%), ель (до 20%), клен, липа, осина, береза, ольха черная (до 10%). Молодняки и средневозрастные насаждения характеризуются преобладанием в I ярусе березы, реже осины. В травяном покрове наибольшее распространение получили растения, требовательные к плодородию почвы (мегатрофы), и растения мезо-гигрофитной группы. Доминантами напочвенного покрова являются сныть обыкновенная и ясменник пахучий. Ряд занимает средние части склона водораздела, несколько пониженные места с дерново-карбонатными суглинистыми, контактно-оглеенными или глееватыми почвами. Уровень грунтовых вод находится в пределах 1,2-2,0 м.
III. Спелые и перестойные характеризуются преобладанием в I ярусе обыкновенного (до 40%). Постоянную примесь составляют дуб (до 30%), ольха черная (до 20%), ель, вяз, липа, клен, береза (до 10%). Молодняки и средневозрастные насаждения характеризуются преобладанием в I ярусе ольхи черной. В живом напочвенном покрове наибольшее распространение получили растения гигрофитно-мегатрофной группы. Индикаторами и доминантами напочвенного покрова являются пролесник многолетний и крапива двудомная. Положение: нижние части склонов водораздела с перегнойно-карбонатными, глеевыми почвами. Уровень грунтовых вод в меженный период находится на глубине 1,1 м и выше.
Определяющие факторы дифференциации лесорастительной среды: плодородие почвы, уровень грунтовых вод, степень увлажнения. В пределах ряда выделы группировались по возрасту ели и широколиственных пород соответственно группам возраста: молодняки I класса возраста (до 20 лет), молодняки II класса возраста (21-40 лет), средневозрастные (41-80 лет), приспевающие (81-100 лет), (101-140 лет), перестойные - старше 140 лет. В молодняках I класса возраста в подобранных участках периодически проводились уходы за елью и широколиственными породами. В насаждениях старших классов возраста участки подбирались таким образом, чтобы антропогенное воздействие было минимальным. Всего заложено 44 типологических пробных площади.
Применение модели Хорна к практическим ситуациям требует выполнения трех основных условий:
1) Моделируемая система должна допускать классификацию на конечное число состояний;
2) Переходы должны происходить в моменты времени дискретные, но при этом достаточно близкие, чтобы для моделируемой системы время можно было бы считать непрерывным;
3) Вероятности не должны меняться со временем. Исходя из этих условий и разработан метод.
Модель Хорна, ее краткое описание и обоснование применимости к древостоям объекта coздaния модели (Брянский лесной массив).
Генри Хорн разработал модель сукцессии, основанную на теории марковских процессов [7, 8, 9]. Следствием этой модели, как и других марковских моделей сукцессии с вероятностями, является то, что в результате естественной сукцессионной динамики в древостое устанавливается стабильное распределение составляющих пород, не зависящее от начального состояния древостоя.
Автор модели рассматривал сукцессию как процесс замещения дерева деревом в пологе древостоя. Для простоты понимания модели полог древостоя может быть рассмотрен как совокупность независимых ячеек, каждая из которых занята деревом. Для каждого дерева в древостое он оценил вероятность, с которой после определенного промежутка времени (50 лет) данное дерево или останется в древостое, или будет замещено деревом этого же вида или деревом любого другого из видов, встречающихся на данной территории в пологе древостоев. Используя эти принципы, была получена матрица вероятностей смены дерева деревом для конкретного объекта - лесов в районе Принстона (штат Нью-Джерси, США). Модель показала хорошую точность при оценке динамики этих лесов.
Путем картирования одной и той же площади через 50 лет (прямой эксперимент) Хорн определил вероятности смены дерева деревом. Вероятность смены дерева деревом каждого конкретного вида он оценивал путем учета пропорций численности жизнеспособного подроста и деревьев 11 яруса каждого вида под кронами сменяемой древесной породы. Вероятность того, что дерево останется в древостое, была оценена с учетом долговечности дерева. Исходя из вероятностей смены дерева деревом Хорн осуществил прогноз состава насаждений по числу деревьев полога древостоя. На первых стадиях изменение состава весьма значительно, но затем при дальнейших пересчетах по матрице состав мало меняется - насаждение переходит к относительно устойчивому состоянию - климаксу, который характеризуется устойчивым распределением деревьев.
В общем виде модель Хорна будет иметь вид:
Пусть A - переходная матрица сукцессий с шагом 50 лет, тогда
N(t)={N1(t)N2(t)…Nn(t)} - вектор численностей пород, составляющих древостой в год n. Таким образом,
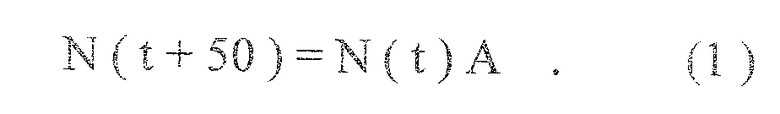
Предельное стабильное состояние древостоя N, характеризующее климаксовую стадию, которая будет наблюдаться через n поколений, можно найти из соотношения:

где

В нашем случае найти вероятности с помощью прямого эксперимента невозможно в связи с большой временной продолжительностью лесной сукцессии.
Нами были выделены восстановительно-возрастные ряды нарастающего увлажнения. Имея насаждение одного ряда на разных стадиях, мы можем преобразовать временной ряд в пространственный. Таким образом, выделив динамику изменения доли породы в составе, мы получаем динамику состава насаждения.
То есть изначально имея состав насаждений на разных временных этапах сукцессии, нам необходимо было получить матрицу этих вероятностей. Например, имея в составе полученный по регрессионной модели процент ели, дуба, ясеня, вяза, липы, клена, березы, осины, ольхи в настоящее время и после 50 лет, нам необходимо определить, какой процент в составе ели останется в насаждении через 50 лет и сменится этим же видом, какой процент сменится дубом, ясенем, вязом, липой, кленом, березой, осиной, ольхой черной. То же можно рассчитать и для других лесообразующих пород. Единственный способ реально выполнить данную задачу - это, используя формулы (1, 2, 3) автора модели [7, 8, 9], решить задачу с несколькими переменными, где переменными будут являться вероятности смены дерева деревом, составляющие переходную матрицу, чтобы результаты расчета по этой матрице совпадали с результатами, полученными по регрессионной модели. Для системы уравнений использовалась разработанная нами программа. В программе полученная система уравнений решалась методом минимальных погрешностей, с помощью которого решается уравнение вида:
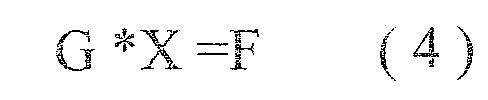
Где G - квадратная, невырожденная (требование метода) матрица, элементами которой являются коэффициенты уравнений (доли пород);
X - вектор решений, элементами которого являются вероятности смены дерева деревом;
F - вектор, элементами которого являются доли пород через 50 лет.
В этом методе основная вычислительная сложность заключается в нахождении матрицы обратной матрице G. Но для матриц, размерность которых не превышает 9, нахождение обратной матрицы для программы не занимает много времени. Так как единственным требованием метода является невырожденность G(det G/=0), то при построении системы уравнений выбирались именно те переходы, которые в совокупности давали бы такие коэффициенты для матрицы, при которых ее определитель как можно больше отличался от нуля.
Для расчета таксационных показателей было заложено 450 круговых пробных площадок: по 30 площадок в каждой из пяти возрастных стадий (молодняки 11 класса возраста, средневозрастные, приспевающие, спелые и перестойные насаждения) для трех восстановительных рядов. Площадки закладывались на участках с минимальным антропогенным воздействием. Древесный полог был разделен на ярусы с учетом разницы в средних высотах. Нижний ярус выделялся и в том случае, когда его запас составлял менее 30 м3 га-1. По данным круговых площадок с точностью до 1% был определен состав насаждений в каждом ярусе для каждой возрастной стадии развития древостоя. Динамику лесовосстановительного процесса оценивали отдельно для каждого восстановительного ряда с применением регрессионного анализа. Характер доли каждой породы в составе в зависимости от возраста был аппроксимирован кривыми. При построении уравнений регрессии использовался метод наименьших квадратов. На основании показателей состава насаждений на разных возрастных стадиях, полученных с помощью регрессионного анализа, были построены переходные матрицы с использованием модели Хорна.
Исходные материалы в молодняках 1 класса возраста были собраны путем закладки 9 постоянных площадей (по три для каждого восстановительного ряда), где проводились сопряженные наблюдения за динамикой основных элементов в почве и накопление их в хвое и листьях в зависимости от уровня грунтовых вод. Использовались пробные площади 1 и 111 восстановительных рядов. Почвенные образцы для анализа отбирались ежемесячно с мая по сентябрь до глубины 40 см по 10-сантиметровым слоям в 5-кратной повторности, что обеспечило вследствие выровненности почвенного покрова относительную погрешность определения азота, фосфора и калия при t0,95 10-20%.
Растительные образцы отбирались по методике И.Верманна [11]. Для установления вариабельности накопления азота, фосфора и калия в хвое и листьях их содержание определялось в 10-ти индивидуальных образцах индивидуального отбора. Отбор хвои и листьев с 10-ти одновозрастных деревьев обеспечивает точность определения 10% при уровне вероятности 0,95. Отобранные образцы помещались на 20 минут в предварительно прогретый сушильный шкаф, а затем досушивались на воздухе. Подготовленные образцы размалывались на мельнице и сжигались в смеси серной и хлорной кислот, в вытяжке определяли: азот - отгонкой в колбе Кьельдаля, фосфор - аскорбиновой кислотой, калий - на пламенном фотометре.
Для установления взаимосвязи между продуктивностью древесных пород и показателями почвенного плодородия проведен сравнительный анализ методами математической статистики, многофакторных корреляций и регрессий. Использовались три постоянные площади 11 восстановительного ряда.
На основании литературных данных, имеющейся информации и собственного опыта из всей совокупности показателей почвенного плодородия выбирали те, которые предположительно наиболее сильно влияют на состояние пород: среднее содержание гумуса в слое 0-40 см, содержание подвижных форм азота, фосфора и калия, pH почвенного раствора. Все эти показатели в той или иной мере связаны с питательным режимом. В качестве результативных показателей были выбраны высота и диаметр.
На основании проведенных этапов исследований составлены 12 регрессионных уравнений, каждое из которых составляет 5-факторную систему, включающую 5 факториальных и 1 результативный. Анализ исходного материала показал, что все оставленные для расчетов факториальные и результативные довольно сильно варьируют. С учетом того что все коэффициенты эксцесса и асимметрии статистически незначимы, допустимо рассматриваемое распределение считать близким к нормальному. Анализ парных корреляций между взятыми факториальными признаками, а также между результативными и факториальными свидетельствует о довольно сложной модели, в которой имеются положительные и отрицательные между отдельными компонентами. Отмечено наличие парных между некоторыми факториальными показателями и отсутствие между факториальными и результативными. Несмотря на это все они оставлены для дальнейших расчетов, поскольку необходимо выявить их совместное влияние на высоту и диаметр древесных пород.
Общее уравнение регрессии имеет вид:
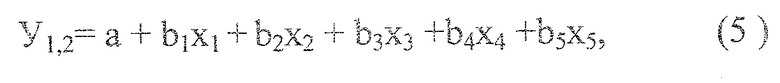
Где y1 и y2 - высота и диаметр деревьев соответственно; x1 - среднее содержание гумуса в слое 0-40 см; x2, x3, x4 - содержание подвижных форм азота, фосфора и калия соответственно; x5 - pH солевой почвенного раствора.
Степень чистого влияния каждого фактора на результативный признак вычислялась по коэффициентам частной корреляции. Достоверность коэффициентов множественной регрессии оценивалась по критерию Стьюдента (t). Суммарное влияние почвенных факторов (x1,…,x5) на результативный признак (y1, y2) оценивалось коэффициентом корреляции (r) и детерминации (r2). На основании t, r, r2 для разных x проведена ранжировка факториальных признаков по степени влияния на результативный признак.
Таким образом, сущность изобретения как технического решения выражена в совокупности существенных признаков, заложена в 4-мерной модели (единство внутривидовых и межвидовых отношений лесообразователей географического ландшафта, в равной мере учитывающее пространственную и временную изменчивость) и математически обеспечивается законом сохранения подвижного равновесия лесообразователей географического ландшафта.
Результат на уровне постановки задачи достигается сохранением подвижного равновесия (параметров устойчивости) лесообразователей географического ландшафта. Технический результат, обеспечиваемый заявленным изобретением, достигается повышением достоверности оценки изменчивости лесных экосистем во времени в процессе их развития.
Источники информации
1. Колесников Б.П. Кедровые леса Дальнего Востока // Тр. ДВФ АН СССР. Сер. ботан. 1956. T. 2 (4). 262 с.
2. Морозов Г.Ф. Избранные труды. Т. 1. - М.: Лесн. Промышл., 1970. - 590 с.
3. Морозов Г.Ф. Избранные труды. Т. 2. - М.: Лесн. Промышл., 1971. - 531 с.
4. Сукачев В.Н. Основы лесной биогеоценологии. М.: Наука, 1964. С.5-49.
5. Bellefleur P. Markov models of forest-type secondary succession in coastal Britist Columbia // Canad. J. Forestry Research. - 1981. - V. 11, # 1. - p.18-19.
6. Debussche M., Godron M., Lepart J., Romane F. An accunt of the use of transition matrix // Agro-Ecosystem. - 1977. - V.3, #1. p.81-92.
7. Horn H.S. Markovian properties of forest succession // Ecology and Evolution of Cammunities / Ed. Cody M/L/. Diamond J.M. Camhrilge. Mass.: Harvard Univ. Press, 1975. P.196-211.
8. Horn H.S. Succession // Theoretical Ecology Principles and Application. One / Ed. May R.M. Oxford: Black-well. 1981. P.253-271.
9. Horn H.S. The ecology of secondary succession // Ann. Rev. Ecol. Syst. 1974. V.5. P.25-37.
10. Leppe E., De Smidt J.T., Glen-Lewin D.C. Marcov models and succession: a test from a heathland in the Netherlands // J. Ecology. - 1985. - V.73. - p.775-791.
11. Wehrmann J. Mmeralsteffornahrung von Kieberabestander in Bayem. - Z., Pflanrenernahrung, Dungung und Boden Kunde, 1959, 84, H.1-3.
Рисунки, прилагаемые к описанию
Рис.1 Определение подвижного равновесия географического ландшафта по В.Н.Сукачеву (биогеоценотический подход)
Рис.2 Определение подвижного равновесия географического ландшафта по Б.П.Колесникову (на представлении о лесообразовательном процессе)
Рис.3 Определение подвижного равновесия географического ландшафта на модельной основе (пространственно-распределенная динамика)
Рис.4 Построение конусовидной модели географического ландшафта. Общий вид конуса, усеченного плоскостью приспевающих насаждений
Рис.5 Фрагмент конуса усеченного плоскостью приспевающих насаждений (вид сверху)
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНОВЛЕНИЯ ХВОЙНЫХ НАСАЖДЕНИЙ | 2004 |
|
RU2267915C1 |
| СПОСОБ ЛЕСОВОДСТВА | 2003 |
|
RU2296458C2 |
| СПОСОБ ТРАНСФОРМАЦИИ ПРОИЗВОДНЫХ МЯГКОЛИСТВЕННЫХ НАСАЖДЕНИЙ В ТЕМНОХВОЙНЫЕ | 2012 |
|
RU2521706C2 |
| СПОСОБ КОМПЛЕКСНОЙ ОЦЕНКИ СОСТОЯНИЯ ЛЕСНЫХ ЭКОСИСТЕМ В РАЙОНАХ ТЕХНОГЕННОГО ВОЗДЕЙСТВИЯ ПРОМЫШЛЕННЫХ ОБЪЕКТОВ | 2011 |
|
RU2489846C2 |
| СПОСОБ ОБНОВЛЕНИЯ И ПЕРЕФОРМИРОВАНИЯ БЕРЕЗОВЫХ НАСАЖДЕНИЙ | 2004 |
|
RU2265994C2 |
| Способ формирования насаждений, выполняющиих защитные, санитарно-гигиенические и оздоровительные функции | 1986 |
|
SU1521383A1 |
| СПОСОБ РЕКОНСТРУКЦИИ НАСАЖДЕНИЙ | 1995 |
|
RU2105464C1 |
| СПОСОБ СОЗДАНИЯ И ФОРМИРОВАНИЯ ХВОЙНОДУБОВОЛИСТВЕННЫХ ЛЕСОВ НА СЕВЕРНОЙ ПОЛОВИНЕ АРЕАЛА ДУБА | 1994 |
|
RU2091006C1 |
| СПОСОБ ЛЕСОПОЛЬЗОВАНИЯ В РАВНИННЫХ ХОЗЯЙСТВЕННО ОСВОЕННЫХ ХВОЙНО-ЛИСТВЕННЫХ ЛЕСАХ | 2005 |
|
RU2311018C2 |
| СПОСОБ ОЦЕНКИ КАЧЕСТВА РУБОК УХОДА | 2001 |
|
RU2211559C2 |
Изобретение относится к области моделирования биологических процессов в живой природе. На участках с минимальным антропогенным воздействием закладывают пробные площади в каждой из пяти возрастных стадий развития древостоя - молодняки 1 класса возраста, средневозрастные, приспевающие, спелые и перестойные насаждения. Разделяют древесный полог на ярусы с учетом разницы в средних высотах. Определяют состав насаждений в каждом ярусе для каждой возрастной стадии развития древостоя. Отбирают в молодняках 1 класса почвенные и растительные образцы для отслеживания динамики основных элементов питания в почве и накопления их в хвое и листьях в зависимости от уровня грунтовых вод. Почвенные образцы отбирают ежемесячно с мая по сентябрь до глубины 40 см по 10-сантиметровым слоям в 5-кратной повторяемости. Растительные образцы отбирают с одновозрастных деревьев для установления вариабельности накопления азота, фосфора и калия в хвое и листьях. Оценку взаимосвязи между продуктивностью древесных пород и показателями почвенного плодородия, и динамики лесовосстановительного процесса осуществляют для каждого восстановительного ряда с использованием уравнения регрессии. Техническим результатом изобретения является повышение достоверности оценки изменчивости лесных экосистем во времени в процессе их развития. 5 ил.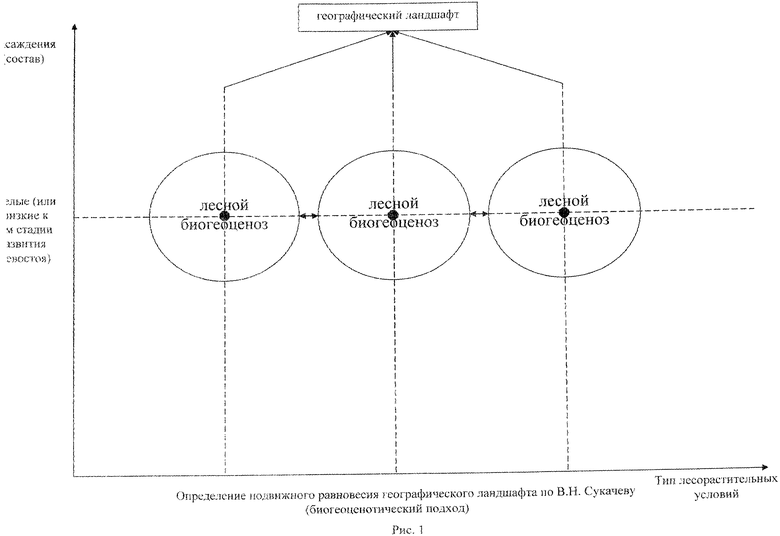
Способ определения подвижного равновесия географического ландшафта, включающий определение параметров устойчивости лесообразователей географического ландшафта, отличающийся тем, что на участках с минимальным антропогенным воздействием закладывают пробные площади в каждой из пяти возрастных стадий развития древостоя - молодняки 1 класса возраста, средневозрастные, приспевающие, спелые и перестойные насаждения, разделяют древесный полог на ярусы с учетом разницы в средних высотах, определяют состав насаждений в каждом ярусе для каждой возрастной стадии развития древостоя, отбирают в молодняках 1 класса почвенные и растительные образцы для отслеживания динамики основных элементов питания в почве и накопления их в хвое и листьях в зависимости от уровня грунтовых вод, при этом почвенные образцы отбирают ежемесячно с мая по сентябрь до глубины 40 см по 10-сантиметровым слоям в 5-кратной повторяемости, а растительные образцы отбирают с одновозрастных деревьев для установления вариабельности накопления азота, фосфора и калия в хвое и листьях, причем оценку взаимосвязи между продуктивностью древесных пород и показателями почвенного плодородия и динамики лесовосстановительного процесса осуществляют для каждого восстановительного ряда с использованием уравнения регрессии:
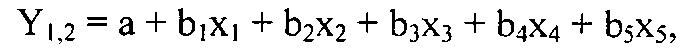
где Y1 и Y2 - высота и диаметр деревьев соответственно;
x1 - среднее содержание гумуса в слое 0-40 см;
x2, x3, x4 - содержание подвижных форм азота, фосфора и калия соответственно;
x5 - pH солевой вытяжки почвенного раствора,
причем параметры устойчивости взаимосвязаны между собой биологической сущностью лесообразовательного процесса и составляют единое целое.
Авторы
Даты
2014-12-20—Публикация
2011-04-11—Подача