Изобретение относится к области измерений, вычислений, импульсной техники и предназначено для прямого и обратного преобразования, а также анализа сигналов произвольной формы.
Известны вейвлет-преобразования Добеши, Морле, FHAT, MHAT, Хаара [1, 2, 3, 4].
С помощью различных базисов можно полнее выявить и подчеркнуть те или иные свойства, содержащиеся в сигналах.
Подавляющее большинство материнских вейвлетов и базисов на их основе являются достаточно сложными функциями [1]. Приложение 1. Стр. 43.
Генерация напряжений, тождественно изменяющихся в соответствие с функциями материнских вейвлетов [1], получение сжатых и сдвинутых таких вейвлетов затруднено, и поэтому для реализации вейвлет-преобразований используют дискретизированные вейвлет-преобразования [4, 5]. При этом скорость, объем и сложность вычислений имеют существенную роль.
Наиболее простым непрерывным быстродействующим вейвлет-преобразованием, требующим минимум операций умножения, является преобразование, основанное на использовании вейвлет-напряжений Хаара, полученных путем сжатия и сдвига (прототип) [2]. Приложение 2. Стр. 64, 65..
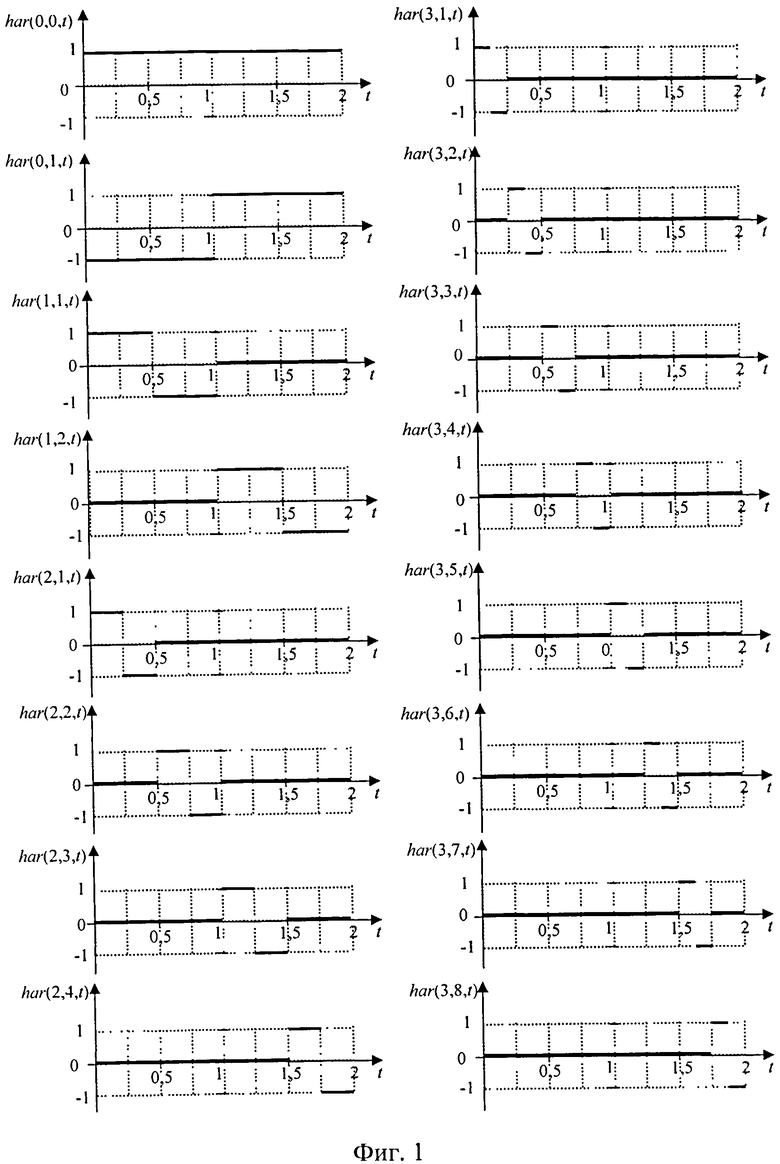
Однако преобразование Хаара при преобразовании непрерывных сигналов обладает существенным недостатком, заключающимся в значительной ступенчатости восстановленного сигнала, обусловленной тем, что вейвлеты Хаара принимают только три значения ±1 и ноль, формирующих безусловный базис [1]. Стр. 17. Графики вейвлет-напряжений Хаара приведены на фиг. 1 [2].
Ступенчатость восстановленного сигнала влечет за собой значительную среднеквадратичную погрешность и существенное уклонение восстановленного сигнала от исходного.
Вейвлет-преобразование Хаара по структуре построения базиса наиболее близко к предлагаемому способу, основанному на использовании пилообразного вейвлет-напряжения, которое в результате сжатия и сдвига формирует ортогональный базис пилообразных вейвлетов.
Базисные вейвлеты Хаара в виде напряжений формируют в результате следующих операций [2]. Стр. 64, 65. Приложение 2.
Первые два вейвлет-напряжения в этом преобразовании har(0, 0, t) и har(0, 1, t) формируют в виде напряжений Уолша Wal(0, t) и Wal(1, t) [2]. Приложение 2.
Для формирования следующих вейвлетов сжимают вейвлет har(0, 1, t) в два раза на промежутке от 0 до 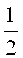
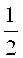
Далее сжимают вейвлет har(1, 1, t) в два раза на промежутке от 0 до 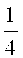
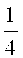
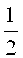
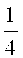
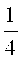
Каждый новый вейвлет формируется в результате нового сжатия и сдвига.
Из графиков напряжений преобразования Хаара фиг. 1 следует, что сжатие и сдвиг напряжений выполнены так, чтобы напряжения от har(0, 0, t) до har(3, 8, t) образовывали ортогональный базис.
Для прямого преобразования напряжений сигнал F(t) умножают на вейвлет-напряжения Хаара, затем вычисляют значения интеграла на промежутке преобразования от напряжений произведений, используя значения этих интегралов, вычисляют коэффициенты преобразования, а при обратном преобразовании вейвлет-напряжения умножают на напряжения, тождественные коэффициентам преобразования, полученные напряжения суммируют и тем самым восстанавливают сигнал.
Для сравнения качественных и количественных характеристик преобразования Хаара и предлагаемого преобразования по пилообразным вейвлет-напряжениям используем среднеквадратичную погрешность [6]
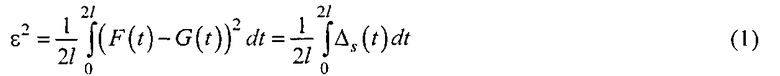
и наибольшее уклонение восстановленного сигнала G(t) исходного F(t)
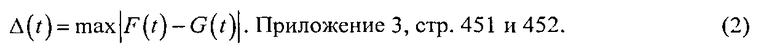
Преобразуемый сигнал представим в следующем виде:
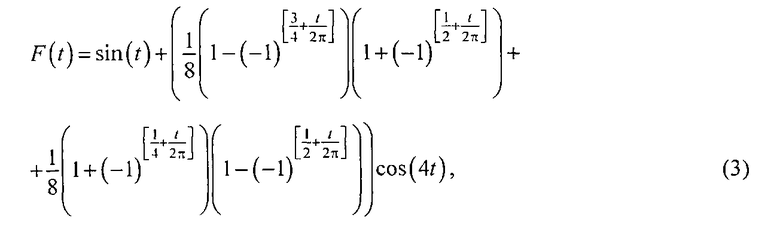
где t - время;
[…] - выделение целой части.
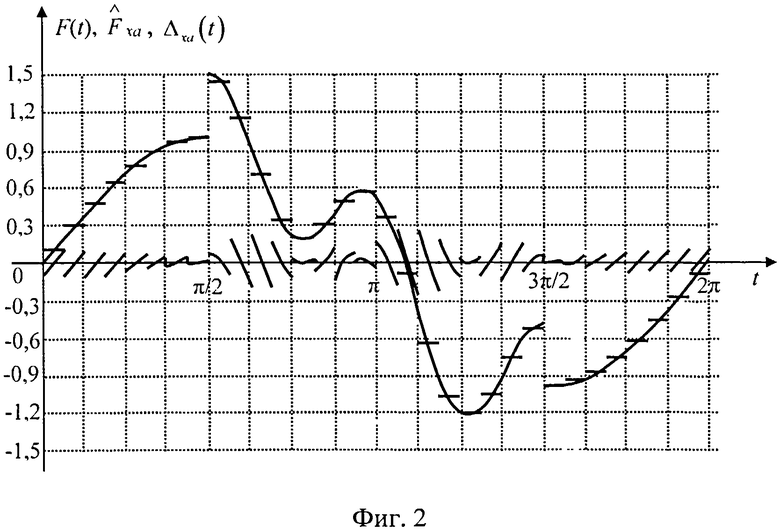
В результате преобразования сигнала F(t) по напряжениям, изменяющимся тождественно функциям Хаара на промежутках от 0 до π и от π до 2π, получены коэффициенты:
Графики исходного сигнала F(t), восстановленного 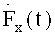
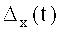
Из графика 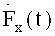
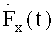

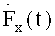
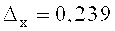
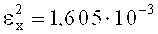
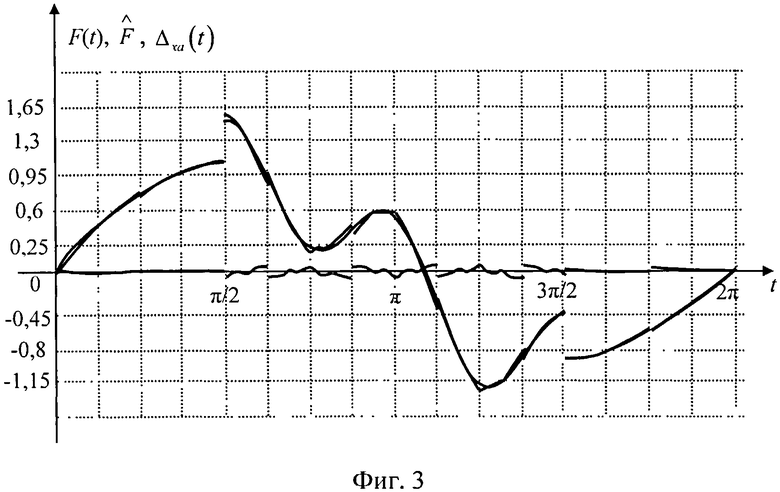
В результате преобразования исходного сигнала F(t) по предлагаемым пилообразным вейвлета-напряжениям (4) на промежутках от 0 до π и от π до 2π получены коэффициенты разложения
Результат преобразования сигнала F(t) по пилообразным вейвлет-напряжениям представлен графиками исходного и восстановленного сигнала на фиг. 3.
Средняя квадратичная погрешность преобразования сигнала F(t) 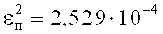
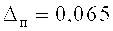
Сравнивая погрешности преобразования по напряжениям Хаара 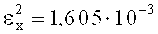
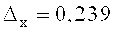
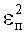
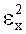
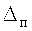

Сравнение результатов преобразований свидетельствует об эффективности предлагаемого преобразования.
Целью изобретения является уменьшение ступенчатости восстановленного сигнала, снижение максимального уклонения восстановленного сигнала 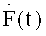
Поставленная цель достигается тем, что в предлагаемом преобразовании из напряжений Уолша с числами секвент 0, 1, 2, 4, 8 формируют пилобразные напряжения с числами секвент 1, 2, 4, 8, 16. Пилообразные напряжения с числами секвент 4, 8, 16 умножают на группы однополярных ортогональных импульсов и тем самым формируют пилообразные ортогональные вейвлет-напряжения, тождественно изменяющиеся в соответствии с равенствами

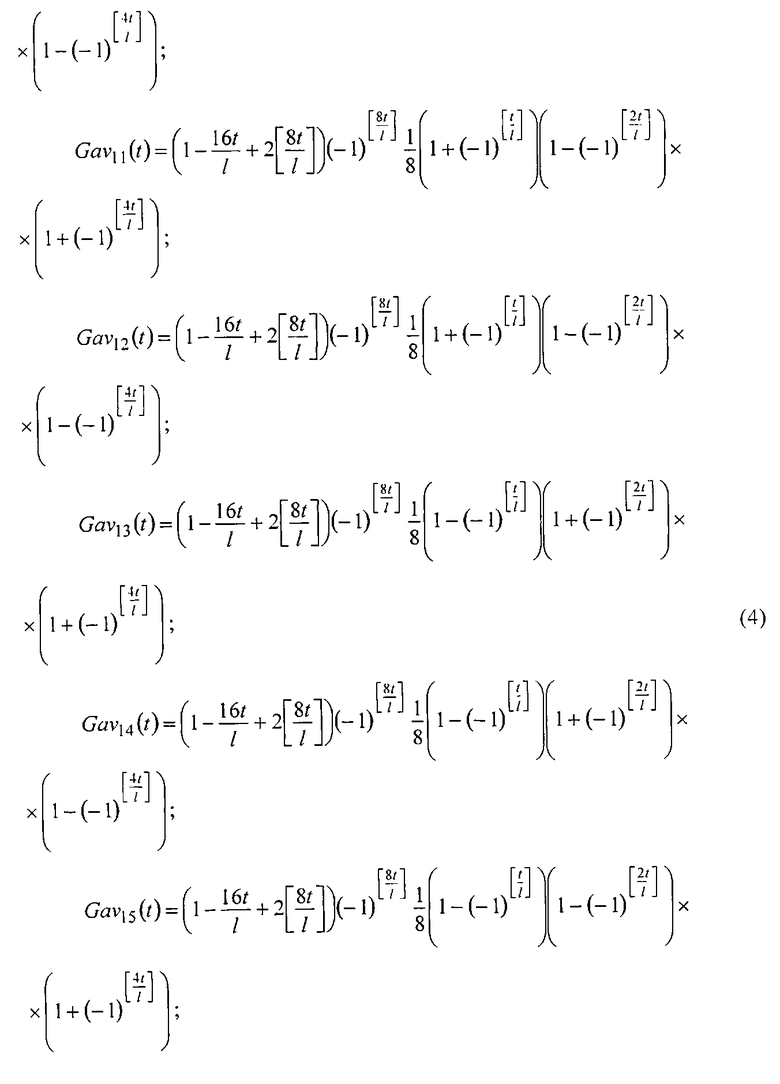
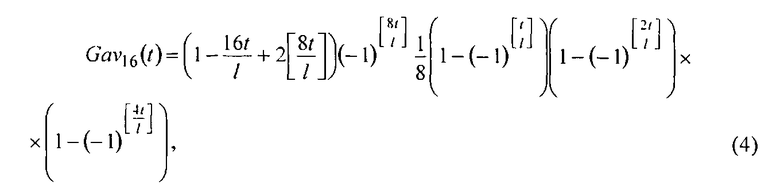
где
t - время;
l - полупериод функции Gav1(t);
[…] - выделение целой части.
Графики пилообразных вейвлет-напряжений (4) приведены на фиг. 4.
Сравнивая структуру расположения функций har(1, k, n) фиг. 1 со структурой расположения пилообразных вейвлетов напряжений (4) фиг. 4, находим, что структура построения напряжений базисных функций одинакова, поэтому способ преобразования Хаара, как наиболее близкий, выбран в качестве прототипа.
Коэффициенты разложения сигнала F(t) по напряжениям (4) определяются из равенств
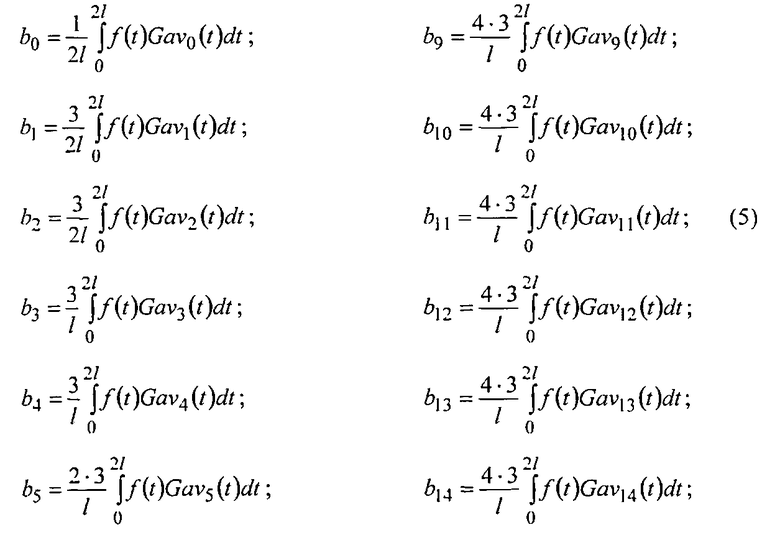
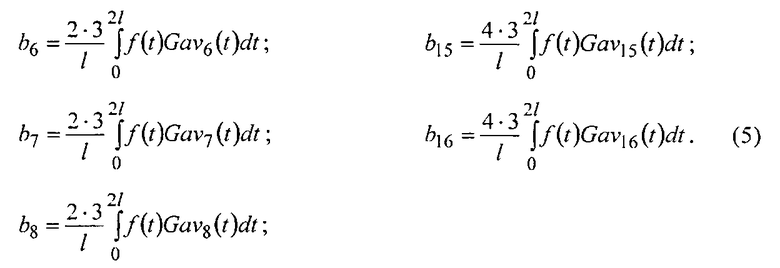
Предлагаемый способ реализуется следующим образом.
Напряжения генератор Уолша [2, (стр. 166)] фиг. 5 (Приложение 4, стр. 166) с числами секвент s=2i-1, где i=0, 1, 2, 4, 8:
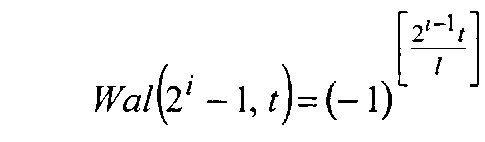 ,
,
где 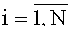
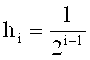
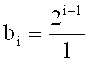
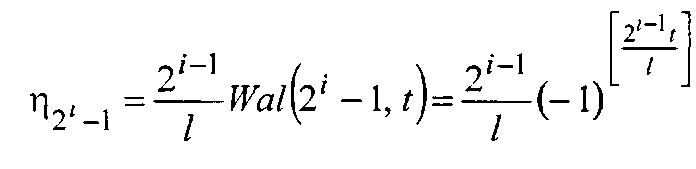 .
.
С помощью интегратора на операционном усилителе [7] (Приложение 5, стр. 127-129) интегрируют напряжения 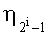
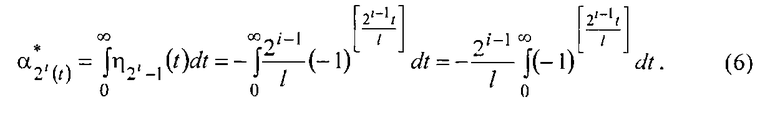
где подынтегральная функция в (6) принимает значения ±1, а интеграл представляет сумму интегралов на промежутках длиной 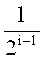
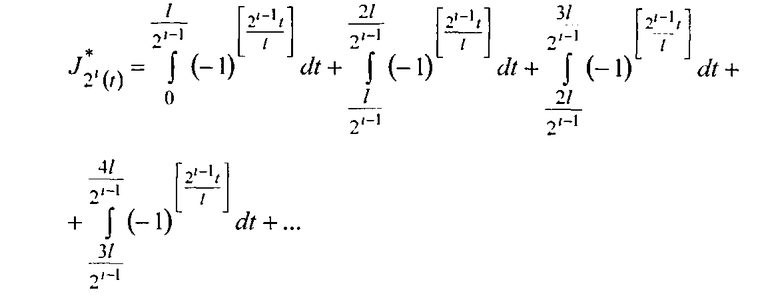
На четных промежутках интегрирования [2(j-1)l, (2j-1)l] подынтегральная функция в (6) принимает значения +1, значения которой записывается в следующем виде:
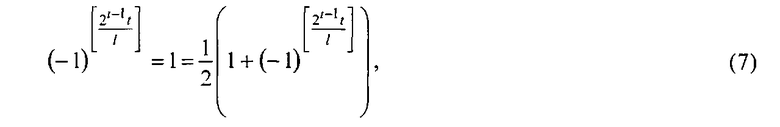
а на нечетных промежутках [(2j-1)l, 2jl]:
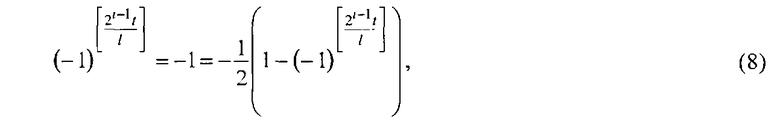
где 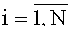
С учетом значений подынтегральной функции из (7) и (8) напряжение (6) принимает вид
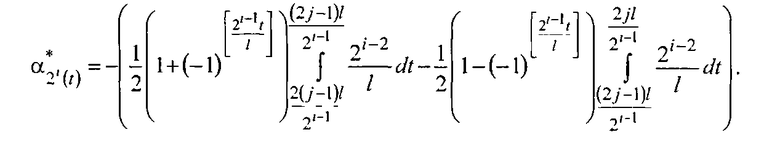
Используя начальное условие интегрирования на каждом промежутке, формируют однополярные пилообразные напряжения
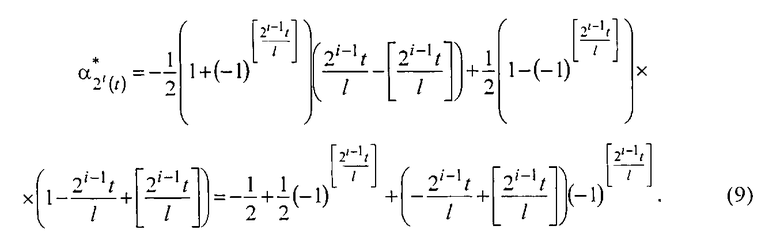
Полученные напряжения (9) суммируют с напряжением 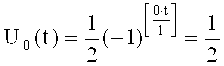
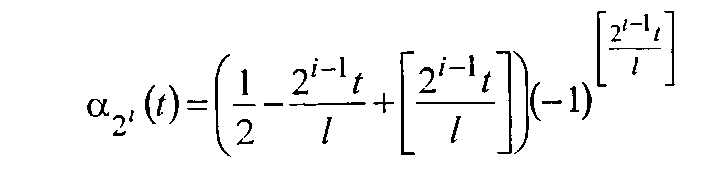
с амплитудой 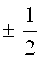
Напряжения 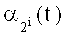
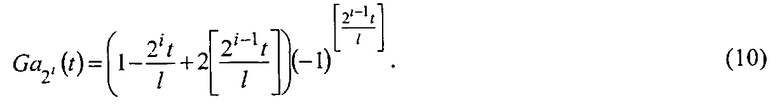
Полагая в (10) i=0, 1, 2, 3, 4, получают пилообразные напряжения
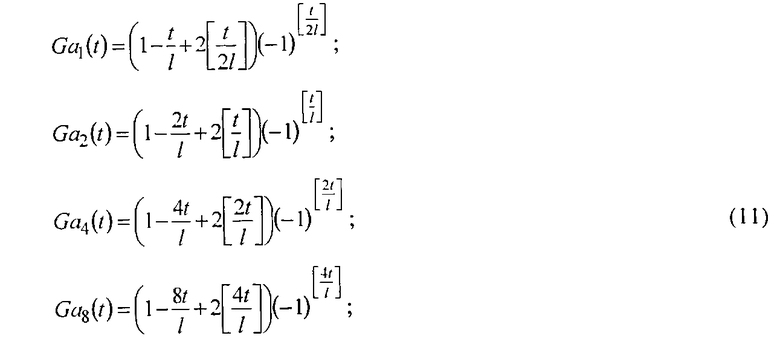
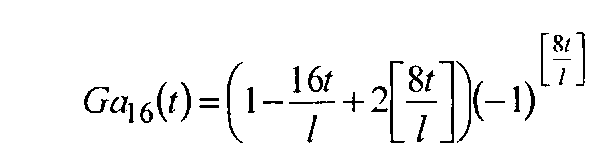
Параллельно напряжения генератора Уолша (Приложение 4) Wal(2i-1, t) суммируют с напряжением 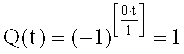

Затем из напряжений 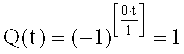
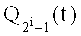
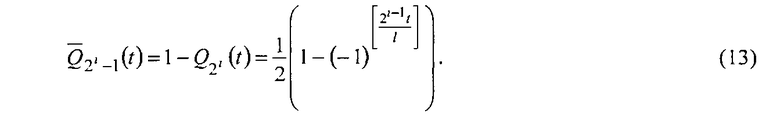
В (12) и (13) полагают i=0, 1, 2, 3, 4, формируют напряжения 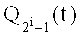
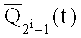
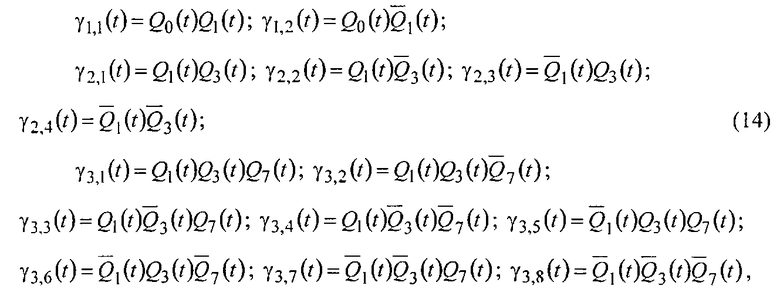
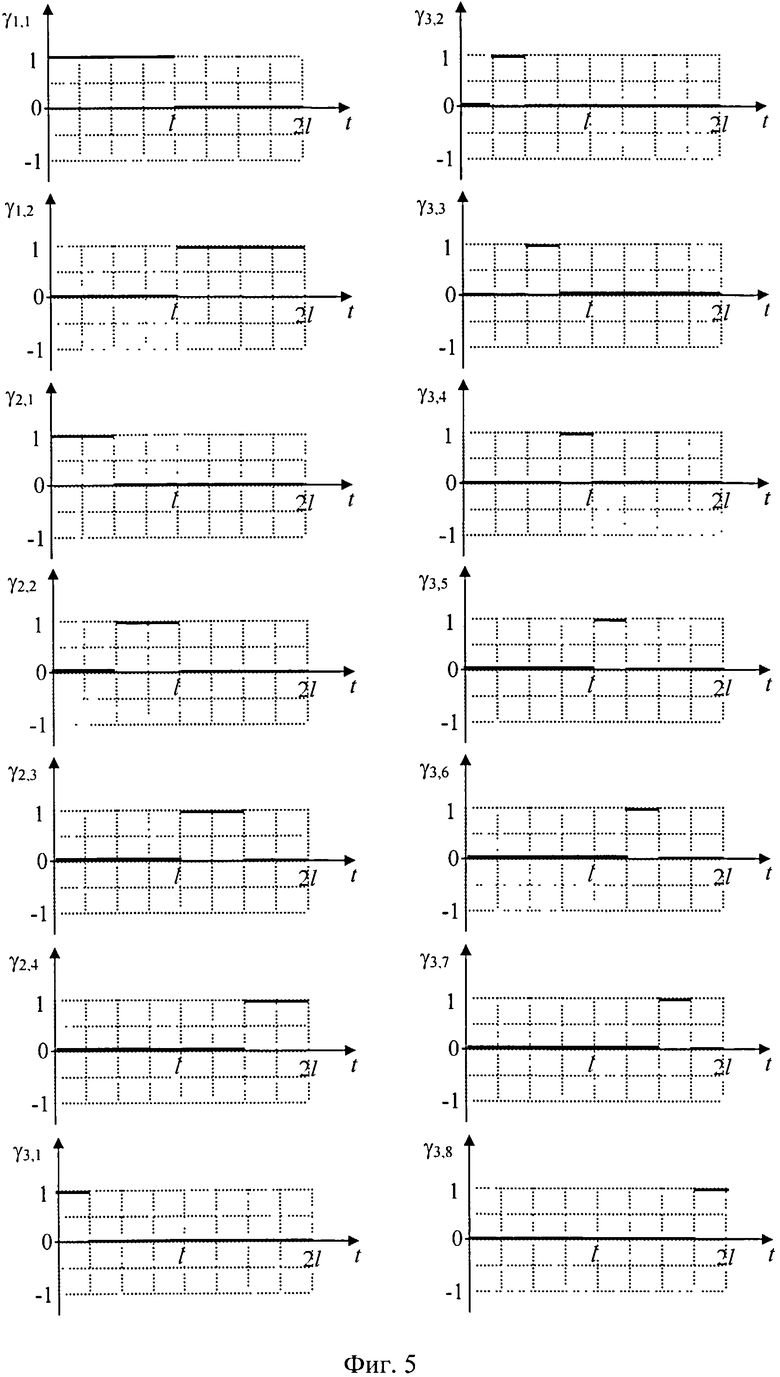
формируют группы однополярных ортогональных напряжений.
График напряжений групп ортогональных однополярных напряжений приведен на фиг. 5.
Напряжения Ga1(t) и Ga2(t) из (11) сохраняют без изменения и обозначают Gav1(t) и Gav2(t), а напряжение Ga4(t) умножают на ортогональные напряжения 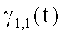
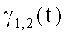
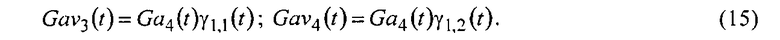
Напряжения Ga8(t) умножают на напряжения группы ортогональных 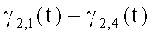
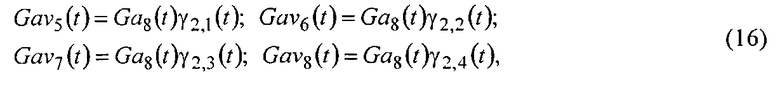
а умножая напряжения Ga16(t) на напряжения 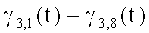
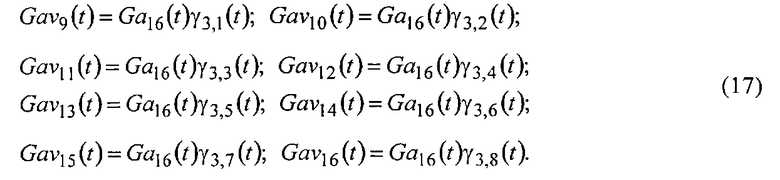
Сформированные напряжения Ga1(t), Ga2(t), (15)-(17) дополняют напряжением 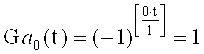
После подстановки в (15)-(17) напряжений из (11) и групп ортогональных импульсов 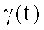
Сформированные напряжения Gav0(t)-Gav16(t) параллельно умножают на напряжение сигнала F(t), например, с помощью схем АD539 [8] (Приложение 6), начиная с 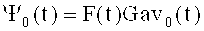
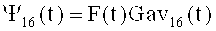
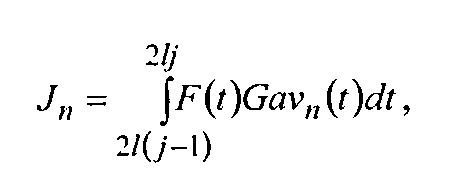 ,
,
где 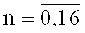
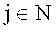
При обратном преобразовании напряжения, соответствующие значениям коэффициентов преобразования bn, параллельно умножают на соответствующие пилообразные вейвлет-напряжения (4), формируют напряжения 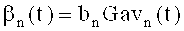
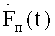
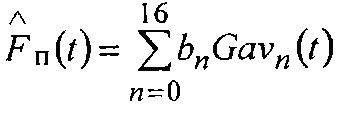 .
.
Источники информации
1. Добеши И. Десять лекций по вейвлетам. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. - 464 С.
2. Хармут Х.Ф. Теория секвентного анализа. Основы и применения. - М.: Мир, 1980.
3. Прэтт У. Цифоровая обработка изображений / Пер. с англ. - М.: Мир. Т. 1, 2. 1982.
4. Сапрыкин В.А., Малый В.В., Лопухин Р.В. Патент РФ №2246132 С2. «Способ и устройство быстрого вычисления вейвлет-преобразования сигнала с произвольным шагом дискретизации масштабных коэффициентов». 10.02.2005.
5. Хамухин А.А. Патент РФ №2437147 С1. «Устройство для вычисления дискретизированного непрерывного сигнала.
6. Смирнов В.И. Курс высшей математики. - М.: Наука, 21 изд. стереот. Т. 2. - 1974. - 656 с.
7. Фолькенберри Л.М. Применение операционных усилителей и линейных ИС. - М.: Мир, 1985. - 572 с.
8. Микросхема AD539 умножения аналоговых сигналов. http://www/analog.com/static/imported-files/data_sheets/AD539/pdf.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и устройство преобразования сигналов произвольной формы с использованием пилообразных ступенчатых вейвлетов | 2017 |
|
RU2682860C2 |
| СПОСОБ И УСТРОЙСТВО ПРЕОБРАЗОВАНИЯ СИГНАЛА ПРОИЗВОЛЬНОЙ ФОРМЫ | 2014 |
|
RU2576591C2 |
| СПОСОБ И УСТРОЙСТВО ПРЕОБРАЗОВАНИЯ СИГНАЛА ПРОИЗВОЛЬНОЙ ФОРМЫ С ИСПОЛЬЗОВАНИЕМ СТУПЕНЧАТЫХ ПИЛООБРАЗНЫХ ФУНКЦИЙ | 2017 |
|
RU2682862C2 |
| УСТРОЙСТВО ДЛЯ УЛУЧШЕНИЯ ЦВЕТОВЫХ ПЕРЕХОДОВ ТЕЛЕВИЗИОННОГО ИЗОБРАЖЕНИЯ | 2006 |
|
RU2301504C1 |
| АНАЛИЗАТОР СПЕКТРА | 2020 |
|
RU2744768C1 |
| КАРДИОМОНИТОР ДЛЯ ВЫЯВЛЕНИЯ ИНФОРМАТИВНЫХ ПАРАМЕТРОВ | 2019 |
|
RU2704437C1 |
| УСТРОЙСТВО ДЛЯ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ МЕХАНИЗМОВ | 2019 |
|
RU2697852C1 |
| АНАЛИЗАТОР СПЕКТРА | 1992 |
|
RU2047895C1 |
| УСТРОЙСТВО ДЛЯ УЛУЧШЕНИЯ ЦВЕТОВЫХ ПЕРЕХОДОВ ТЕЛЕВИЗИОННОГО ИЗОБРАЖЕНИЯ | 2003 |
|
RU2246183C1 |
| Устройство для определения спектральных коэффициентов разложения случайного процесса по функциям Хаара | 1980 |
|
SU935814A1 |
Изобретение относится к области измерений, вычислительной техники и предназначено для прямого и обратного преобразования и фильтрации сигналов произвольной формы. Техническим результатом является уменьшение среднеквадратичной погрешности, максимального уклонения и ступенчатости восстановленного сигнала. Способ заключается в том, что используют ортогональные пилообразные вейвлет-напряжения, которые формируют интегрированием напряжений Уолша, формируют однополярные импульсы из напряжений Уолша, умножают пилообразные напряжения с числами секвент 4, 8 и 16 на однополярные импульсы напряжений, в результате чего формируют пилообразные вейвлет-напряжения, которые умножают на напряжения сигнала, интегрируют эти произведения на промежутках длиной 2l и, используя полученные значения интегралов, вычисляют значения коэффициентов преобразования bn в виде напряжений; при обратном преобразовании сигнала по пилообразным напряжениям: параллельно умножают ортогональные пилообразные напряжения на напряжения, соответствующие значениям коэффициентов разложения; параллельно суммируют полученные напряжения, восстанавливают сигнал либо, положив отдельные коэффициенты bn=0, фильтруют сигнал. 5 ил.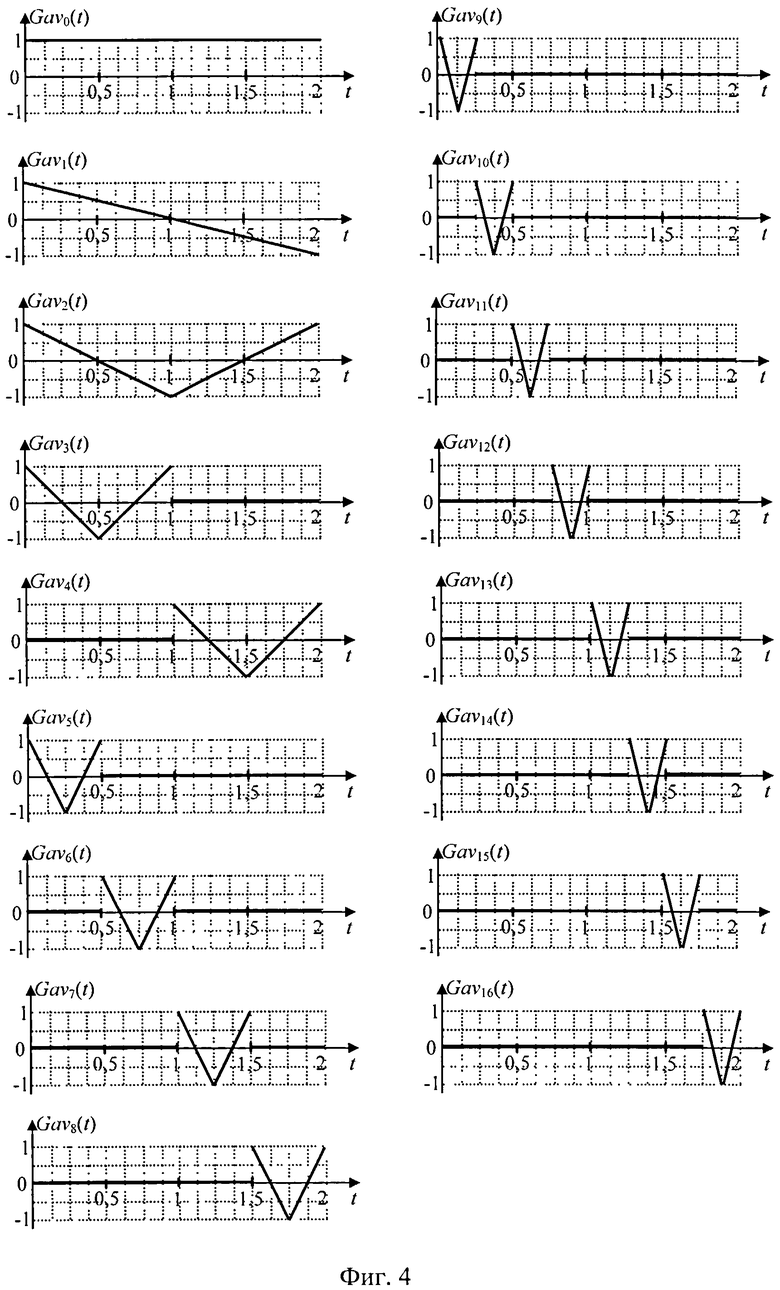
Способ вейвлет-преобразования сигнала произвольной формы, содержащий при прямом преобразовании параллельное формирование напряжений Хаара из напряжений Уолша умножения этих напряжений на напряжение сигнала, интегрирование напряжений от произведений напряжений Хаара на напряжения сигнала, отсчитывание, вычисление и запоминание коэффициентов преобразования Хаара, при обратном преобразовании сигнала умножение коэффициентов преобразования в виде напряжений на соответствующие напряжения Хаара и суммирование полученных напряжений, восстанавливающее сигнал, отличающийся тем, что из напряжений Уолша с числами секвент 0, 1, 2, 4 и 8 путем интегрирования, формируют пилообразные напряжения с числами секвент 1, 2, 4, 8 и 16, пилообразные напряжения с числами секвент 4, 8 и 16 умножают на группы однополярных прямоугольных импульсов, формируют пилообразные вейвлет-напряжения, изменяющиеся в соответствие со следующими равенствами:
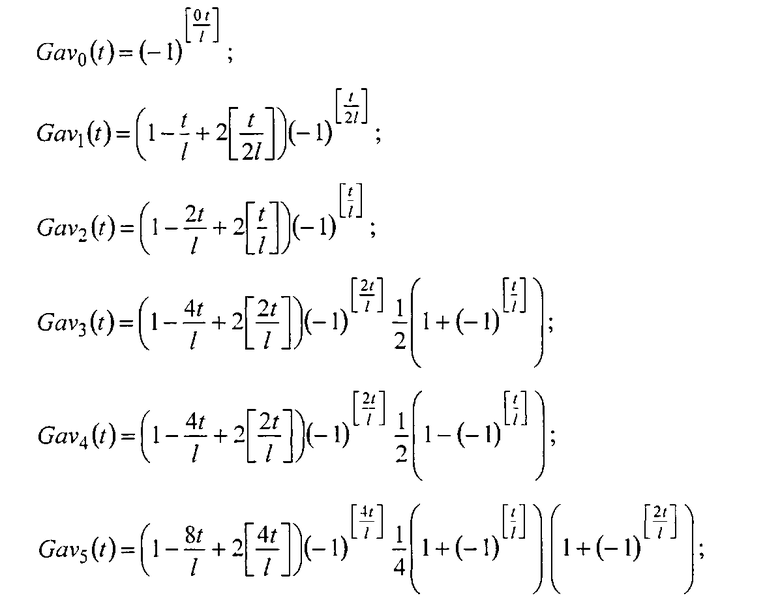
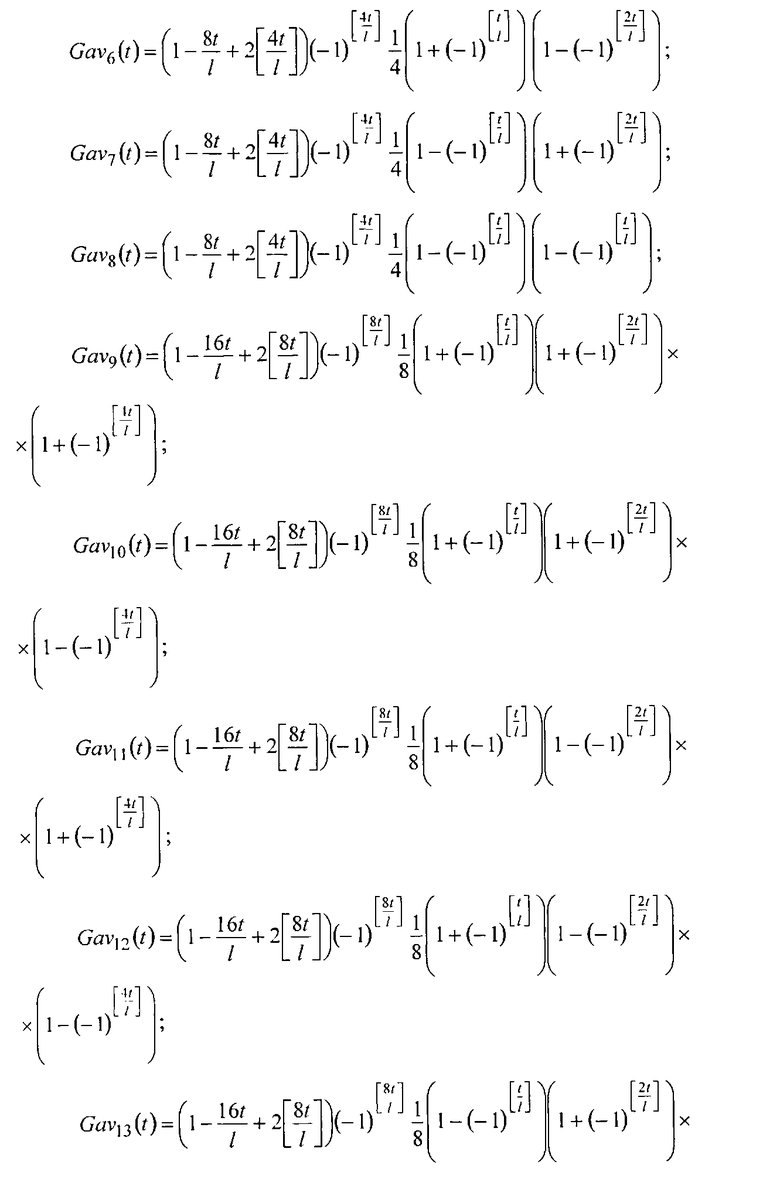
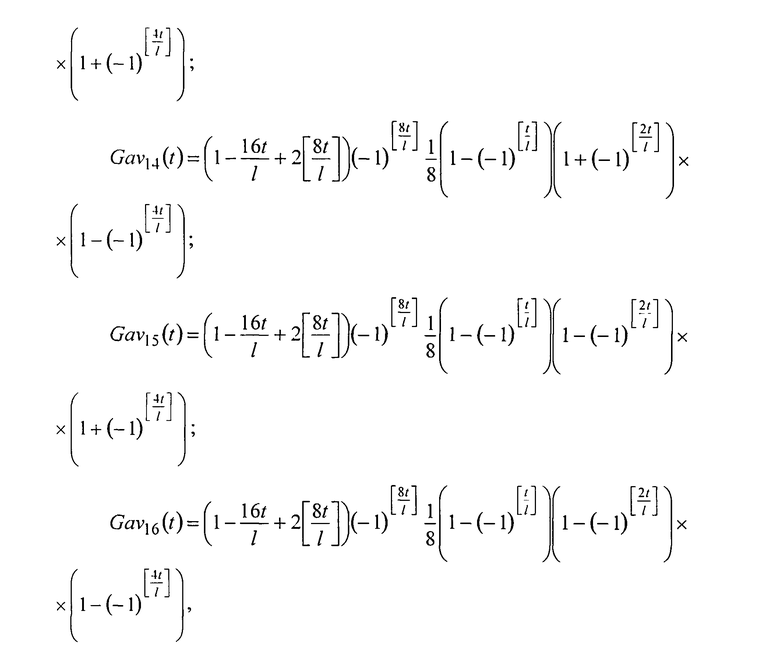
где
t - время;
l - полупериод изменения пилообразного напряжения с числом секвент, равным единице;
[…] - выделение целой части,
- ортогональные пилообразные вейвлет-напряжения от Gav0(t)-Gav16(t) параллельно умножают на напряжения сигнала F(t);
- параллельно вычисляют значения интегралов от произведений напряжения сигнала на вейвлет-напряжения на промежутке длиной 2l;
- из значений интегралов вычисляют коэффициенты преобразования по пилообразным вейвлет-напряжениям bn в виде напряжений в соответствии со следующими равенствами:
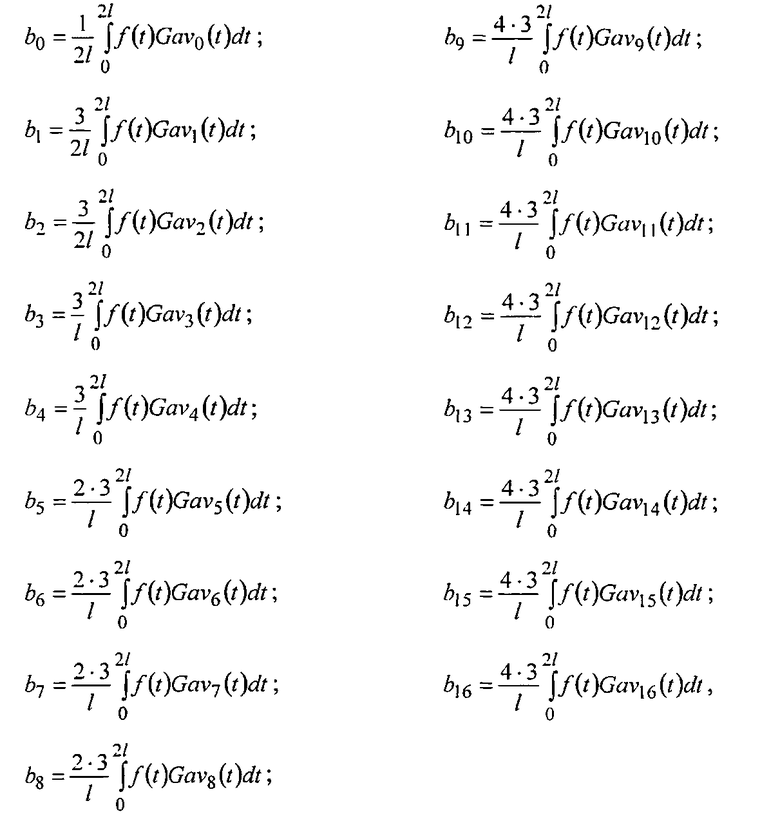
при обратном преобразовании (восстановлении, фильтрации) сигнала по пилообразным вейвлет-напряжениям
параллельно умножают пилообразные вейвлет-напряжения Gav0(t)-Gav15(t) на напряжения b0-b15, полученные напряжения параллельно суммируют, восстанавливают сигнал либо, положив отдельные коэффициенты b0=0, фильтруют сигнал.
| Дренажное устройство паросепараторов | 1939 |
|
SU57033A1 |
| СПОСОБ И УСТРОЙСТВО БЫСТРОГО ВЫЧИСЛЕНИЯ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ СИГНАЛА С ПРОИЗВОЛЬНЫМ ШАГОМ ДИСКРЕТИЗАЦИИ МАСШТАБНЫХ КОЭФФИЦИЕНТОВ | 2003 |
|
RU2246132C2 |
| US 2013191430 A1, 25.07.2013 | |||
| US 2003065489 A1, 03.04.2003 | |||
Авторы
Даты
2015-07-27—Публикация
2014-07-15—Подача