Изобретение относится к области электродинамики и магнетизма ферромагнетиков в их динамическом состоянии и может быть использовано для экспериментальной проверки эффекта возбуждения вихревого электрического поля при движении магнитного поля, создаваемого движением постоянного магнита (электромагнита).
Известное явление электромагнитной индукции [1-3] широко используется в электротехнике. На его основе работают, в частности, трансформаторы переменного тока, в которых изменяется с частотой f переменного тока магнитная индукция B(t)=BOsin(2πft) как функция времени. В классической электродинамике оперируют четырьмя уравнениями Максвелла [4-6], второе из которых имеет вид:
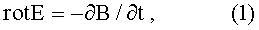
где вектор rot Е - суть соответствующее вихревое электрическое поле, располагаемое в плоскостях, ортогональных вектору магнитной индукции B(t), а сам электрический вихрь коллинеарен виткам соленоида (катушки индуктивности), пронизываемой вектором магнитной индукции, и его направление вращения происходит по известному «правилу буравчика», возбуждая в проводнике соленоида электрический ток действием лоренцевых сил на свободные электроны проводника.
В частности, уравнение (1) говорит о том, что ротор (интеграл по замкнутому контуру) электрического поля Е равен потоку, то есть скорости изменения во времени магнитного поля В=B(t) сквозь этот контур.
Аналогично тому, как движение электрического заряда образует вокруг траектории его движения вихревое магнитное поле, как это следует из известного четвертого уравнения Максвелла, движение магнитного поля с постоянной во времени индукцией BO=const(t), например движение постоянного магнита, вызывает возникновение вихревого электрического поля вокруг траектории движения магнитного поля, что требует введения дополнительного члена во второе уравнение Максвелла, указанное в (1), в форме:
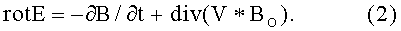
Поскольку магнитная индукция ВО в этом случае не изменяется во времени, то имеем ∂B/∂t=0, однако индукция BO движется в координатном пространстве (вместе с движением постоянного магнита) с постоянной скоростью V, и тогда уравнение (2) в соответствии с положениями векторной алгебры принимает вид:
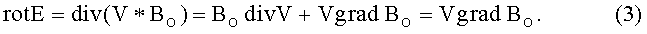
Выражение (3) справедливо, поскольку divV=(∂vx/∂x)+(∂vy/∂y)+(∂vz/∂z)=0 при постоянной скорости магнитного поля с индукцией ВO при произвольном движении постоянного магнита вдоль некоторой прямой (или кривой) в пространстве декартовой системы координат (х, у, z), что нашло свое подтверждение [7] в эксперименте, проведенном заявителем и представленном на рис. 2.
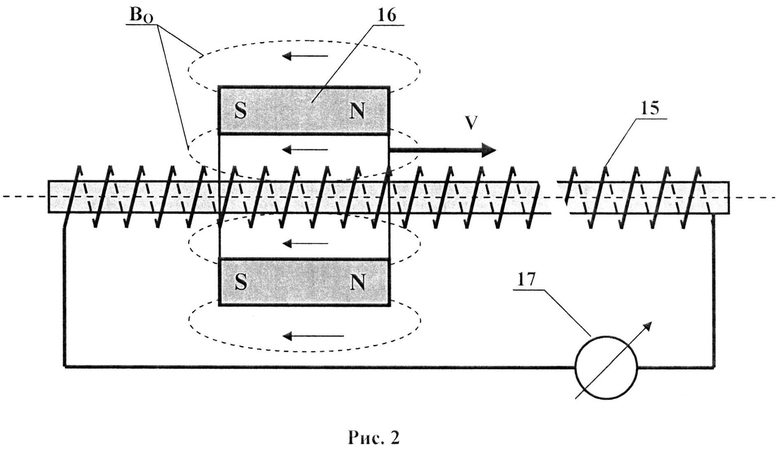
В частности, на рис. 2 представлен проделанный заявителем опыт, подтвердивший возникновение вихревого электрического поля вдоль траектории движения постоянного магнита 16 в форме тороида с намагниченными его торцевыми плоскостями осесимметрично относительно прямого соленоида 15, что индицировалось миллиамперметром постоянного тока 17. При этом изменение направления движения магнита относительно оси соленоида приводило к изменению знака возбуждаемой в соленоиде э.д.с.
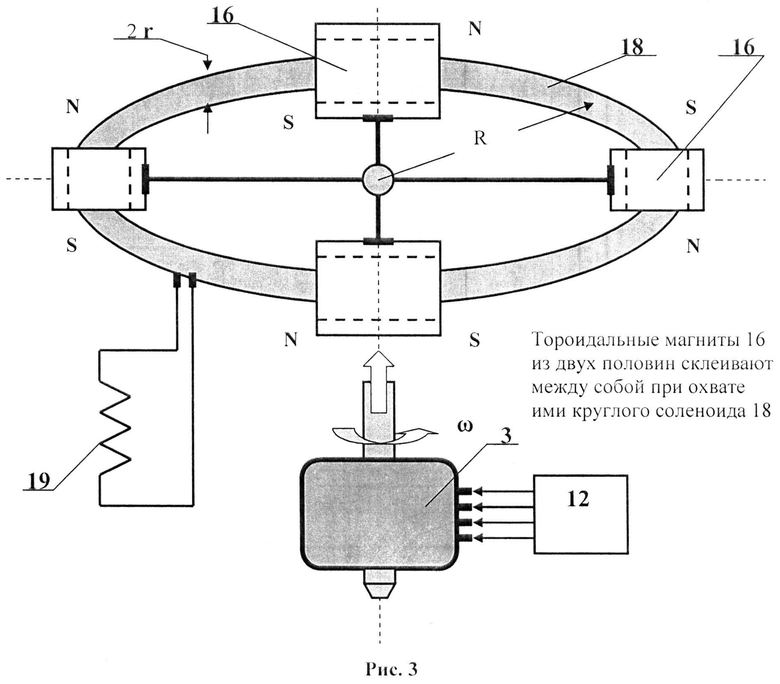
Модификацией данного опыта, рассмотренного в работе [8], является выполнение соленоида 15 (рис. 2) в виде тороида 18 (рис. 3), вдоль круговой оси которого вращаются магниты 16 от синхронного двигателя 3 (как на рис. 1), питание которого осуществляется от генератора многофазного переменного тока 12 (как на рис. 1) с регулируемой частотой колебаний (для изменения угловой скорости вращения магнитов 16), а выводы неподвижного соленоида 18 подключены к нагрузке 19.
Внутри намагниченного по торцам ферромагнитного тороида 16, как видно на рис. 2, магнитное поле практически коллинеарно оси прямого соленоида 15 и охватывает группу витков его катушки с числом витков, равным N, и с длиной каждого из витков, равной 2πr, где r - радиус витка этой катушки. При этом полная длина проводника катушки, находящаяся внутри тела тороидального магнита (между его полюсами), равна L=2πrN. На самом деле и те части витков катушки 15, которые расположены за пределами полюсов вне магнита 16 и вблизи них, также находятся во взаимодействии с его магнитным полем, что видно из выражения (3), определяемого градиентом магнитного поля grad BO. Поэтому согласно закону Фарадея об электромагнитной индукции с учетом модифицированного второго уравнения Максвелла в этой части витков катушки возникает э.д.с. Е=kBOLV, где k - некоторое безразмерное число, определяемое экспериментально и учитывающее краевые эффекты взаимодействия движущегося магнитного поля с витками прямого соленоида 15.
В случае круговой катушки в форме тороида, как это показано на рис. 3, с радиусом оси симметрии его катушки, равном R, получаем выражение для э.д.с. индукции в виде:
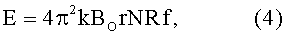
где f=ω/2π=const(t) - частота вращения (об/с) тороидального магнита 16 вокруг оси тороидальной катушки 18 с проводником. На рис. 3 показаны четыре магнита 16, расположенные симметрично относительно тороидального соленоида 18, выводы которого соединены с нагрузкой 19. Это учетверяет возникающую э.д.с. на выводах тороидального соленоида 18.
Число используемых магнитов 16 в конструкции, указанной на рис. 3, может быть увеличено и в пределе может быть представлено намагниченным вдоль образующей ферромагнитным кольцом 1, как это представлено на рис. 1.
В задачу заявляемой схемы (рис. 1) входит обеспечение возможности проверки возбуждения униполярной индукции в соленоиде (одном или нескольких), расположенном осесимметрично относительно вращающегося и намагниченного ферромагнитного тороида. Это является целью изобретения.
Аналоги данного технического решения автором не найдены.
Указанная цель достигается в заявляемой мостовой схеме для проверки возбуждения униполярной индукции в соленоиде, внутри которого движется намагниченный ферромагнетик, образующий вихревое электрическое поле вдоль траектории его движения, включающей ферромагнитный тороид, четыре одинаковых катушки из проводника, включенные последовательно между собой и образующие мостовую схему, к одной диагонали которой подключен регулируемый источник постоянного тока, а другая диагональ мостовой схемы подключена к усилителю постоянного тока, например к входу операционного усилителя с малым дрейфом, ферромагнитный тороид приводится во вращательное движение синхронным двигателем через прижимной ролик, электропитание синхронного двигателя подается от многофазного генератора переменного тока с регулируемой частотой колебаний, причем управление регулируемым источником постоянного тока и многофазным генератором по частоте переменного тока, а также измерение величин тока и частоты колебаний осуществляется с помощью компьютера, в котором осуществляется обработка и индикация получаемой информации по двунаправленным шинам, кроме того, выход усилителя постоянного тока подключен к входу компьютера.
Достижение поставленной цели в заявляемом устройстве объясняется фактором разбаланса мостовой схемы при вращении намагниченного ферромагнитного тороида при возбуждении в четырех катушках, собранных по мостовой схеме, собственных э.д.с. индукции. При этом в диагонали мостовой схемы, подключенной к входу усилителя постоянного тока, индуцируется э.д.с., величина которой пропорциональна произведению тока, поставляемого от регулируемого источника постоянного тока к мостовой схеме, и частоты вращения намагниченного ферромагнитного тороида, а знак этой э.д.с. определяется выбранным направлением указанного тока, запитывающего мостовую схему, и направлением вращения ферромагнитного тороида. Наличие указанной э.д.с. при вращении намагниченного ферромагнитного тороида внутри четырех одинаковых катушек с проводником, соединенных по мостовой схеме, будет свидетельствовать о возбуждении униполярной индукции в катушках из проводника при вращении намагниченного ферромагнитного тороида внутри этих катушек. В состоянии, когда ферромагнитный тороид не вращается, мостовая схема является строго сбалансированной, и никакой разности потенциалов в измерительной его диагонали не возникает, что обеспечивается в исходном состоянии, то есть до приведения намагниченного ферромагнитного тороида во вращательное движение.
Исследование будем проводить по схеме, представленной на рис. 1.
На рис. 1 используются следующие элементы и узлы:
1 - ферромагнитное кольцо в форме тороида со средним радиусом R,
2 - прижимной ролик для приведения ферромагнитного кольца 1 во вращательное движение с угловой скоростью ω,
3 - синхронный двигатель переменного тока, ось которого связана с прижимным роликом 2,
4, 5 и 6 - ролики удержания ферромагнитного кольца 1 в заданном положении, оси которых связаны с неподвижным основанием,
7, 8, 9 и 10 - одинаковые катушки из проводника, соосно размещенные к ферромагнитному кольцу 1 и не связанные с ним механически, закрепленные неподвижно с основанием и образующие симметричную мостовую схему,
11 - регулируемый источник постоянного тока, подключенный в первую диагональ мостовой схемы,
12 - многофазный генератор переменного тока с регулируемой частотой колебаний для электропитания синхронного двигателя 3,
13 - усилитель постоянного тока, входом подключенный ко второй диагонали мостовой схемы,
14 - компьютер для управления и обработки данных с индикацией результатов.
Предварительно рассмотрим произведенный автором эксперимент возбуждения униполярной индукции в схеме, показанной на рис. 2, состоящей из прямого соленоида 15, тороидального магнита 16, намагниченного по его торцевым плоскостям, и измерительного гальванометра (миллиамперметра) постоянного тока 17, подключенного к выводам соленоида 15. При движении магнита с постоянной скоростью V вдоль соленоида регистрировалась э.д.с. одного знака, определяемого направлением движения магнита вдоль оси соленоида. Величина этой э.д.с. возрастала с увеличением скорости протяжки магнита. Это не могло быть объяснено с позиции известного второго уравнения Максвелла, указанного в выражении (1) из-за компенсации возникающих э.д.с., равных по абсолютной величине и противоположных по знаку, возникающих в соответствующих частях соленоида вблизи магнитных полюсов намагниченного тороида. Действительно, из какой-то части катушки магнит выходит, а в другую такую же часть катушки магнит входит, и по закону об электромагнитной индукции в этих одинаковых частях соленоида возникают э.д.с., одинаковые по величине (так как скорость движения магнита одинаковая), но противоположные по знаку, что прямо следует из уравнения (1). Однако поскольку в опыте устойчиво возникала э.д.с., не равная нулю, то это и вызвало необходимость в дополнении второго уравнения Максвелла дополнительным слагаемым, указанным в выражении (2) - в общем виде или в выражении (3) для частного случая неизменности скорости протяжки магнита относительно соленоида. Такого рода дополнение было проведено в свое время для четвертого уравнения Максвелла (для rot В), когда пришлось учитывать действие токов смещения (добавкой слагаемого (1/c2)∂E/∂t). Модификация второго уравнения Максвелла, учитывающая равномерное или переменное движение постоянного магнита в пространстве по прямолинейной или произвольной криволинейной траектории, то есть произвольное движение постоянного магнитного поля, являясь важным вкладом в физическую науку, в частности в электродинамику, определяет единство закономерностей, характерных как для электрического поля (движение заряда создает вихревое магнитное поле), так и для магнитного поля (движение постоянного магнита создает вихревое электрическое поле). Поэтому выявление опытным путем этого единства является важным результатом. Доказательством существования этого единства становится разбаланс мостовой схемы (рис. 1) при вращении ферромагнитного тороида, намагниченного токами от регулируемого источника постоянного тока, в результате которого регистрируется возникновение э.д.с. в измерительной диагонали данной мостовой схемы.
В схеме на рис. 3 прямой соленоид, который не может быть бесконечно длинным для получения постоянного тока, как бы свернут в форму тороидального соленоида, и тогда можно получать постоянный ток от такого неподвижно закрепленного соленоида-тороида при вращении магнитов 16 с постоянной касательной скоростью V=ωR, создаваемой работой синхронного двигателя 3, скорость вращения ротора которого определяется частотой колебаний f, вырабатываемых в многофазном (например, трехфазном) генераторе переменного тока 12.
Будем полагать, что при вращении намагниченного ферромагнитного тороида 1 (рис. 1) с угловой скоростью ω в каждой из четырех одинаковых катушек 7-10 возбуждается э.д.с., равная Е=kBOLV, где V=ωR, R - средний радиус ферромагнитного тороида, L - полная длина проводника в каждой из катушек, а величина магнитной индукции в ферромагнитном тороиде выражается известной формулой:
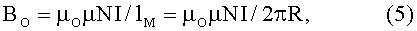
где µO=1,256·10-6 Гн/м - абсолютная магнитная проницаемость вакуума (магнитная постоянная), µ - относительная магнитная проницаемость используемого ферроматериала (безразмерная, порядка нескольких сотен или тысяч), N - число витков в катушке, I - величина протекающего в катушке постоянного тока в заданном направлении, lM=2πR - длина магнитопровода ферромагнитного тороида.
Согласно выражению (4) при движении намагниченного ферромагнетика с магнитной индукцией ВО, определенной в (5), внутри катушек 7-10 в каждой из них возбуждается э.д.с. Е, величина которой (в Вольтах) определяется из выражения:
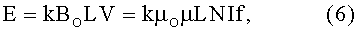
знак которой (+/-) определяется знаком произведения векторов I и f, то есть знаками направления тока в каждой из катушек 4-10 и направления вращения ферромагнитного тороида - соответственно по или против часовой стрелки. В выражении (6) ток I задается в Амперах, а частота f вращения в Герцах (1/с).
Отмечаем, что как показано на рис. 1, направление движения намагниченного ферромагнетика тороида 1, указанное стрелками, одинаково во всех катушках 7-10 (по часовой стрелке), но протекающие токи в катушках 7 и 8 стремятся уменьшить намагниченность находящегося с ними ферромагнетика, а токи в катушках 9 и 10 наоборот стремятся увеличить намагниченность связанного с ними ферромагнетика при условии, что ток от регулируемого источника постоянного тока втекает в катушки 8 и 9, а вытекает из катушек 7 и 10.
Э.д.с. индукции Е, выраженная в (6), суммируется в катушках 9 и 10 с действующих в них напряжениях Ir, где r=ρL/q - активное сопротивление проводника катушек 7-10, одинаковое во всех катушках, ρ - удельное сопротивление проводника сечением q (в мм2), для меди равное ρ=0,017 Ом·мм2/м. Эта э.д.с. для катушек 7 и 8 наоборот вычитается из напряжения Ir. Полагая в первом приближении, что Ir>>Е, используя метод контурных токов, можно записать следующие выражения:
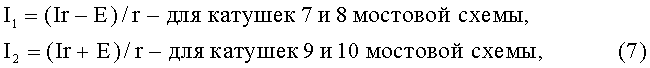
полагая под током I его значение при ω=0 (в исходном состоянии при неработающем синхронном двигателе 3) при подключении мостовой схемы к регулируемому источнику постоянного тока с действующим напряжением U=2Ir, приложенным к первой диагонали мостовой схемы из одинаковых катушек 7-10. С учетом выражений (7) становится понятным указанный выше разбаланс мостовой схемы при вращении ферромагнитного тороида, намагничиваемого токами в катушках 7-10, в соответствующих его частях, связанных с этими катушками.
Тогда легко высчитать потенциалы φA и φC в соответствующих точках А и С мостовой схемы (второй его диагонали, измерительной) и затем вычислить их разность:
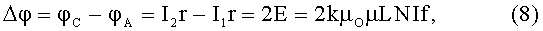
и эта разность потенциалов Δφ действует на входе усилителя постоянного тока 13 и измеряется в спецпроцессоре 14. Более точно разность потенциалов Δφ вычисляется методом последовательных приближений (на основе сходящегося ряда), несколько увеличивая полученный в (8) результат, если действительно соблюдается исходное условие, что Ir>>Е, где ток I определяется как I=U/2r в каждой ветви мостовой схемы при ω=2πf=0.
Нельзя не отметить того факта, что в ферромагнитном тороиде в его неподвижном состоянии (ω=0) возникают в его соответствующих половинах намагниченности BO, соответствующие выражению (5), но в тороиде как целом не возникают замкнутые по кругу магнитные силовые линии, поскольку намагничивание ферромагнетика образует как бы два самостоятельных постоянных магнита с встречными друг другу одноименными магнитными полюсами. Один из таких магнитов образуется от работы тока в катушках 7 и 8, а другой - от действия тока в катушках 9 и 10. При вращении ферромагнитного тороида 1 соответствующие токи I1 в катушках 7 и 8 и I2 в катушках 9 и 10 оказываются не равными, так как I2>I1 согласно выражению (7), поэтому в динамике вращения ферромагнитного тороида в нем присутствует составляющая замкнутого по тору магнитного потока, определяемого разностью токов I2-I1.
Управляя с помощью компьютера 14 значениями тока подмагничивания ферромагнитного тороида 1 от регулируемого источника постоянного тока 11, а также частотой многофазного генератора переменного тока 12 (при одновременном измерении этих величин), можно найти функциональную зависимость разности потенциалов Δφ в измерительной диагонали мостовой схемы из четырех одинаковых катушек 7-10, которая поступает на вход усилителя постоянного тока 13 и далее регистрируется в спецпроцессоре 14, от переменных параметров I и f с учетом знака при произведении этих параметров sign (I∗f), то есть можно составить двумерную таблицу значений: Δφ(I∗f)=sign(I∗f)2kµOµLNIf и отобразить на дисплее персонального компьютера (спецпроцессора 14) семейство линейных функций от параметров I и f.
Ненулевой результат для значений Δφ(I∗f) из (8) при ненулевых параметрах I и f будет свидетельствовать о возникновении униполярной индукции в соленоиде при осесимметричном движении в нем постоянного магнита с заданной скоростью V, что, в свою очередь, доказывает необходимость дополнения второго уравнения Максвелла слагаемым, указанным в общем выражении (2) или в частном выражении (3).
Проверка возможности возбуждения униполярной индукции согласно модифицированного второго уравнения Максвелла представляет существенный теоретический и практический интерес для электродинамики вообще и при решении ее прикладных задач, в частности.
Литература
1. Faradey M. Experimental Researches in Electricity, London, 1841.
2. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред, 2 изд., М., 1982.
3. Джексон Дж. Классическая электродинамика, пер. с англ., М., 1965.
4. Ландау Л.Д., Лифшиц Е.М. Теория поля, 7 изд., М., 1988.
5. Фущич В.И., Никитин А.Г. Симметрия уравнений Максвелла, К., 1983.
6. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика, М., 1985.
7. Меньших О.Ф. Способ возбуждения униполярной индукции, Internet, сайт tele-confi@mail.ru, XIII Международная телеконференция "Актуальные проблемы современной науки", Секция №5 «Проблемы физики,…», опубл. 19.02.2014.
Изобретение относится к электродинамике и и может быть использовано для экспериментальной проверки эффекта возбуждения вихревого электрического поля при движении магнитного поля, создаваемого движением постоянного магнита. Технический результат состоит в обеспечении возможности проверки возбуждения униполярной индукции. Мостовая схема для проверки возбуждения униполярной индукции содержит соленоид, внутри которого движется намагниченный ферромагнетик, образующий вихревое электрическое поле вдоль траектории его движения. Схема содержит ферромагнитный тороид, четыре одинаковых катушки из проводника, включенные последовательно между собой и образующие мостовую схему, к одной диагонали которой подключен регулируемый источник постоянного тока, а другая диагональ мостовой схемы подключена к усилителю постоянного тока. Ферромагнитный тороид приводится во вращательное движение синхронным двигателем через прижимной ролик. Электропитание синхронного двигателя подается от многофазного генератора переменного тока с регулируемой частотой колебаний. Управление регулируемым источником постоянного тока и многофазным генератором по частоте переменного тока, а также измерение величин тока и частоты колебаний осуществляется с помощью компьютера. 3 ил.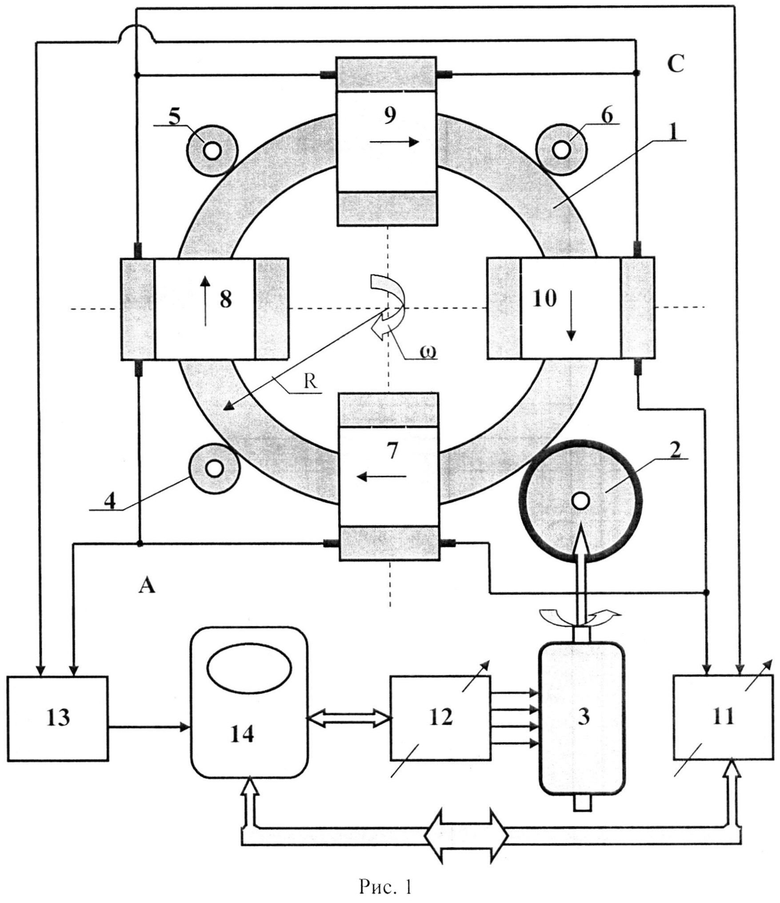
Мостовая схема для проверки возбуждения униполярной индукции в соленоиде, внутри которого движется намагниченный ферромагнетик, образующий вихревое электрическое поле вдоль траектории его движения, включающая ферромагнитный тороид, четыре одинаковых катушки из проводника, включенные последовательно между собой и образующие мостовую схему, к одной диагонали которой подключен регулируемый источник постоянного тока, а другая диагональ мостовой схемы подключена к усилителю постоянного тока, ферромагнитный тороид приводится во вращательное движение синхронным двигателем через прижимной ролик, электропитание синхронного двигателя подается от многофазного генератора переменного тока с регулируемой частотой колебаний, причем управление регулируемым источником постоянного тока и многофазным генератором по частоте переменного тока, а также измерение величин тока и частоты колебаний осуществляется с помощью компьютера, в котором осуществляется обработка и индикация получаемой информации по двунаправленным шинам, кроме того, выход усилителя постоянного тока подключен к входу компьютера.
| УСТРОЙСТВО ДЛЯ РЕГИСТРАЦИИ ВРАЩАТЕЛЬНОГО ЭЛЕКТРОДИНАМИЧЕСКОГО ЭФФЕКТА | 2010 |
|
RU2428678C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ "КРАСНОГО СМЕЩЕНИЯ" ПЛОСКОПОЛЯРИЗОВАННОГО КОГЕРЕНТНОГО ИЗЛУЧЕНИЯ | 2004 |
|
RU2276347C1 |
| УСТРОЙСТВО КОМПЕНСАЦИИ ФАРАДЕЕВСКОГО ВРАЩЕНИЯ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА | 2008 |
|
RU2365957C1 |
| US 5041778 A, 20.08.1991 | |||
Авторы
Даты
2015-08-27—Публикация
2014-03-03—Подача