Изобретение относится к нефтегазодобывающей промышленности и может быть использовано при основании и эксплуатации месторождений, расположенных в зоне распространения многолетне-мерзлых пород.
Известны способы, позволяющие определить температуру горных пород при заранее заданной температуре флюида в скважине - [Ермилов, О.М. Сооружение и эксплуатация газовых скважин в районах крайнего севера. Теплофизические и геохимические акценты. / О.М. Ермилов, Б.В. Дегтярев, А.Р. Курчиков. - Новосибирск: Издательство Сибирского отделения Российской Академии Наук, 2003. - 218 с.].
Главный недостаток известного способа заключается в том, что температура нефти в скважине считается известной, в то время как скважина и горные породы являются одной теплообменной системой и их температуры должны рассчитываться одновременно. Также в решении задачи используется постановка Стефана, в которой сделано предположение, что фазовые переходы происходят при 0°C, в то время как существует постановка Колесникова, где предполагается, что оттаивание происходит в интервале температур, что ближе к отражению реальных характеристик задачи. Также решение задачи известным способом получено при использовании метода последовательной смены стационарных состояний. Однако при высокой температуре теплоносителя в скважине и небольшой льдистости мерзлых пород температурные поля в породе могут сильно отличаться от стационарных, особенно в начальный период и в окрестности подвижной границы.
Известен способ [Кудрявцев С.А. Численные исследования теплофизических процессов в сезонно-мерзлых грунтах / С.А. Кудрявцев // Криосфера земли. - 2003. - Т. IIX. - №4. - С. 102-104] расчета трехмерного температурного поля с учетом фазовых превращений в спектре отрицательных температур. Построение модели базируется на программном комплексе «FEM models». Последняя версия программного комплекса носит название «Thermoground». Минусом данной модели является возможность «проскочить» фазовый переход при неправильно подобранном шаге по времени относительно размера интервала фазовых переходов и упустить пиковый подъем теплоемкости на этом интервале. Температура нефти в скважине также должна быть известна. В заявленном техническом решении используется способ расчета температуры пород, исключающий возможность «проскочить» фазовый переход, который предложен авторами [Инструкция по определению температурного режима вечномерзлых и сезонно-мерзлых грунтов и прогнозированию последствий изменения тепловых условий на поверхности: РД 39-Р-088-91. - Введ. 01.05.91. - Тюмень: Гипротюменнефтегаз, 1991. - 46 с.].
Также известны способы, определяющие температуру флюида в скважине при известной температуре пород, окружающих скважину (включая многолетне-мерзлые). Это минус, т.к. температура нефти и горных пород должна определяться в процессе расчета одновременно. Например, способ расчета температуры нефти при известной температуре горных пород [Мусакаев Н.Г. Математическое моделирование процессов, протекающих в нагнетательной скважине при закачке теплоносителя в пласт / Н.Г. Мусакаев // Нефть и Газ. Известия Вузов ТГНГУ. - 2002. - №4. - С. 12-16]. Способ включает решение квазистационарного уравнения притока тепла.
Известен способ [Бондарев Э.А. Температурный режим нефтяных и газовых скважин / Э.А. Бондарев, Б.А. Красовицкий. - Новосибирск: Наука, 1974. - 87 с.] аналитического решения задачи определения температурного распределения в стволе скважины и конфигурации фронта оттаивания в различные моменты времени. Задача оттаивания вокруг скважины решена в одномерной постановке (изменение температуры происходит только в радиальном направлении). Рассмотрена система двух уравнений: уравнение притока тепла для потока нефти в скважине и условие Стефана, т.е. фазовые переходы происходят при 0°C. Уравнение притока тепла тоже является одномерным, по координате глубины. Для решения использован метод характеристик. Решение приводится отдельно для нефтяной скважины. Предлагаемые системы уравнений довольно громоздки, что не способствует оперативности расчетов.
Известен способ определения размеров и конфигурации зоны оттаивания многолетне-мерзлых пород в приустьевой зоне скважины [RU 2157882 С2, МПК7 E21B 36/00, опубл. 2000], включающий стандартные теплофизические исследования свойств грунтов, термометрических измерений для получения исходных параметров для дальнейших расчетов. Тепловое взаимодействие скважины с многолетне-мерзлыми породами определяют путем решения численными методами на основе математического моделирования для периода времени с момента пуска скважины до окончания сезона летнего оттаивания грунтов нестационарного уравнения теплопроводности. Далее снимают значения температур теплового поля, строят профиль положения фазовой границы пород на различных глубинах и определяют размеры зоны протаивания, для полученной зоны протаивания рассчитывают величину осадки оттаявших пород в приустьевой зоне скважины за расчетный период на различном удалении от скважины по приведенным формулам. По результатам расчетов определяют радиус на различных глубинах и строят масштабный профиль сформировавшейся термокарстовой воронки. Затем в соответствии с рассчитанной величиной осадки оттаявших пород изменяют конфигурацию расчетной области тепловой модели и повторяют вышеописанные операции для следующего годового цикла, при этом циклы расчетов повторяют до достижения заданного момента времени. В случае, если заданный момент времени не совпадает со временем окончания летнего протаивания грунтов, расчет осадки пород и построение масштабного профиля термокарстовой воронки осуществляется на заданный момент времени. Недостатком известного способа является отсутствие теплового потока на нижней границе расчетной области - при глубине 30 метров, т.е. нулевой поток в качестве нижнего граничного условия. Следующим недостатком является особенность численной схемы, позволяющей проскочить фазовый переход, расчеты совершаются при известной температуре флюида в скважине, т.е. без учета динамики теплообмена в системе скважина - горные породы. Известный способ ближе всего к заявленному техническому решению.
Задачей, на решение которой направлено заявляемое техническое решение, является разработка способа, позволяющего учитывать взаимный тепловой обмен скважины и многолетне-мерзлых пород.
Техническим результатом является повышение точности прогнозирования теплового состояния мерзлых пород при эксплуатации скважин, т.е. радиуса оттаивания вокруг скважины и расчет температуры нефти в скважине.
Указанный технический результат достигается тем, что в известном способе определения размеров и конфигурации зоны оттаивания вокруг скважины и температуры нефти в скважине, оборудованной эксплуатационной колонной и расположенной внутри нее колонной насосно-компрессорных труб, включающем проведение стандартных теплофизических исследований свойств грунта и определение на основании полученных исходных данных параметров теплообмена скважины и горных пород путем решения численными методами на основе математического моделирования, особенностью является то, что учитывают теплофизические параметры грунтов вокруг скважины, среднемесячную температуру воздуха, толщину снега, коэффициент теплообмена поверхности земли с воздухом, дебит скважины, обводненность, глубину, температуру пласта на уровне отбора, радиус эксплуатационной колонны и колонны насосно-компрессорных труб, мощность мерзлоты, температуру мерзлоты, затем определяют динамику размера и конфигурации зоны оттаивания вокруг скважины и падение температуры нефти по стволу скважины, устьевую температуру, на основе численных расчетов системы уравнений (1)-(3):
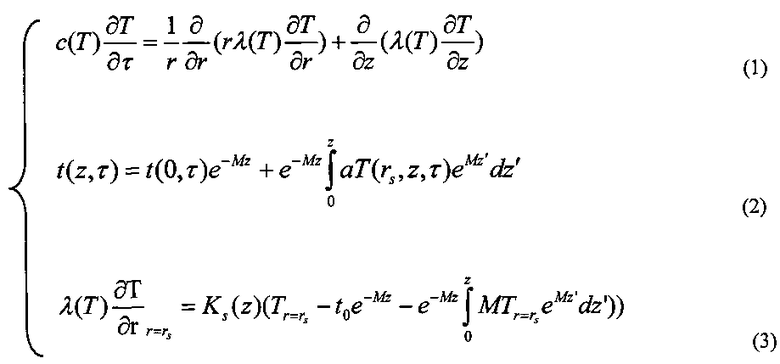
где: 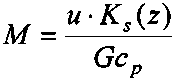
r, z - координаты цилиндрической системы координат,
τ - время, сек,
Т - температура горных пород или T(r, z, τ) впоследствии для упрощения формул будет записываться как Т, °C,
λ(Т) - коэффициент теплопроводности горных пород, Вт/(мK),
с(Т) - эффективная объемная теплоемкость горных пород, Дж/(м3K)
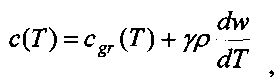
где cgr(T) - объемная теплоемкость породы, зависящая от температуры, Дж/(м3K),
γ - удельная теплота фазового перехода воды, Дж/кг,
ρ - плотность горных пород, кг/м3,
w - влажность мерзлых пород, доли,
t - температура нефти или t(z, τ),
G - дебит жидкости, кг/сек,
Cp - удельная теплоемкость жидкости, Дж/(кгК), которая определяется как
cp=coil·(1-f)+cwat·f,
Coil - удельная теплоемкость нефти, Дж/(кгК),
Cwat - удельная теплоемкость воды, Дж/(кгК),
f - обводненность, доли,
u - периметр сечения движения жидкости, м,
где в уравнении (3):
Ks(z) - коэффициент теплопередачи скважины, Вт/(м2K),
rs - радиус эк, м.
Технический результат достигается тем, что учитывается связь вертикального теплового потока в скважине с горизонтальным потоком тепла от скважины в горные породы: насколько нефть охладилась при подъеме от забоя к устью, настолько прогрелись (протаяли) горные породы вокруг скважины, на основании этого получено сложное интегро-дифференциальное условие на границе скважины и горных пород:
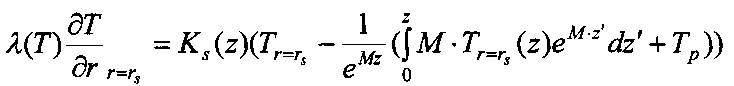
где 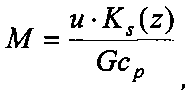
r, z - координаты цилиндрической системы координат,
T - температура горных пород или T(r, z, τ), для упрощения формул записывается как T, °C,
λ(T) - коэффициент теплопроводности горных пород, Вт/(мK),
G - дебит жидкости, кг/сек,
Cp - удельная теплоемкость жидкости, Дж/(кгК),
u - периметр сечения движения жидкости, м,
Ks(z) - коэффициент теплопередачи скважины, Вт/(м2K),
rs - радиус эк, м.
Граничное условие передает информацию о тепловом потоке скважины в многолетне-мерзлые породы и связывает температурное поле флюида в скважине с температурным полем горных пород, которое определяется с помощью численных методов. Способ определяет зону оттаивания вокруг скважины и температуру флюида в скважине. Температура нефти рассчитывают одновременно с температурой горных пород, оттаивание происходит в интервале температур, решается нестационарное уравнение теплопроводности. Заявленное техническое решение также включает квазистационарное уравнение притока тепла, но одновременный расчет температуры нефти и температуры горных пород, включая многолетне-мерзлые. Решение задачи происходит в двумерной области, учтены фазовые переходы в спектре температур.
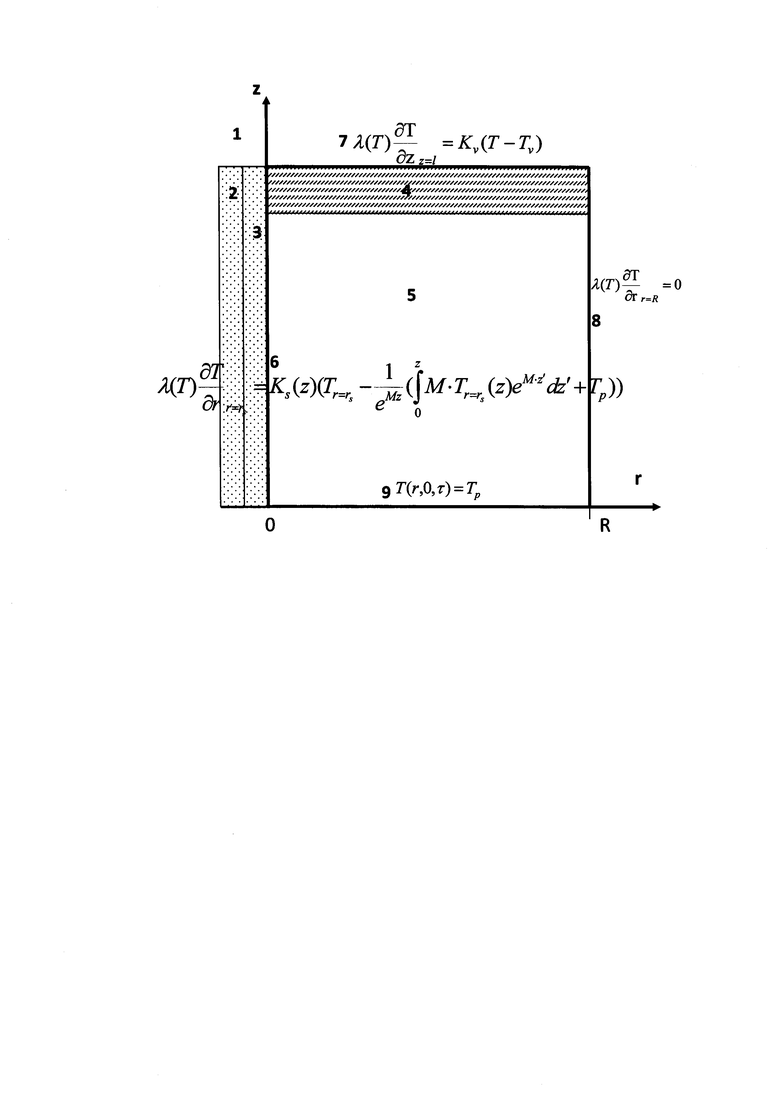
На чертеже представлено схематичное расположение скважины 1 в горных породах, включая расчетную область. Насосно-компрессорные трубы (НКТ) 2, эксплуатационная колонна (ЭК) 3, мерзлые породы обозначены штрихом 4, немерзлые породы - 5, граница скважины и горных пород обозначена 6, граница горных пород с воздухом или поверхность земли - 7, граница области расчета справа - 8, граница области снизу - 9, r, z - координаты цилиндрической системы координат, R - размер расчетной области по радиусу, 0 - начало системы координат.
Скважина 1 состоит из двух вертикальных цилиндрических труб, одна из которых находится внутри другой. НКТ 2 установлена внутри ЭК 3. По внутренней трубе НКТ 2 поднимается нефть от забоя к устью.
Скважину 1 окружают немерзлые 5 и мерзлые породы 4. Мерзлые породы 4 характеризуются мощностью и залегают сплошным массивом от поверхности земли до определенной глубины. В мерзлых породах происходят фазовые переходы, за счет теплового потока от скважины 1 и от поверхности земли 7. Нефть, поднимаясь от забоя к устью, остывает. Это тепло идет в окружающие скважину 1 горные породы, в мерзлых породах 4 начинается оттаивание. Такая задача относится к классу нелинейных относительно температурного поля горных пород и сопряженных относительно граничного условия 6 на скважине 1.
Расчетная область задается в цилиндрической системе координат (ЦСК). Начало координат помещено на забой скважины 1. Рассматриваем двумерную область, где ось скважины 1 совпадает с осью 0z в ЦСК. Область включает породы с положительной и отрицательной температурой.
В результате аналитических преобразований получаем систему уравнений:
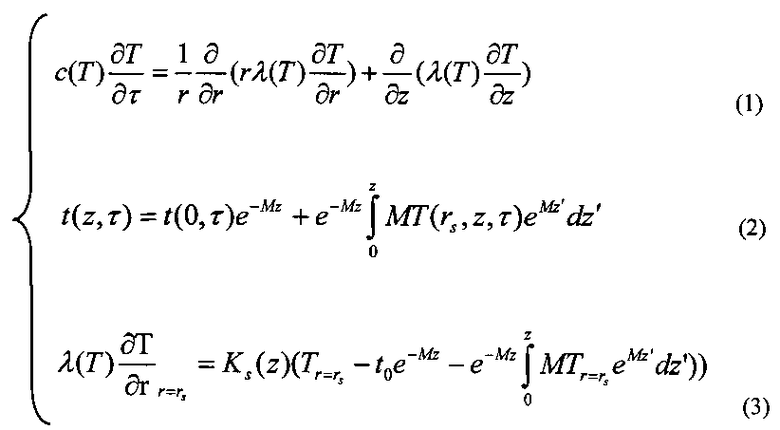
где 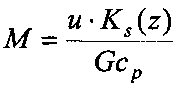
r, z - координаты цилиндрической системы координат,
τ - время, сек,
T - температура горных пород или T(r, z, τ) впоследствии для упрощения формул будет записываться как T, °C,
λ(T) - коэффициент теплопроводности горных пород, Вт/(мK),
c(Т) - эффективная объемная теплоемкость горных пород, Дж/(м3K)
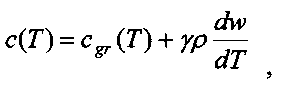
где cgr(T) - объемная теплоемкость породы, зависящая от температуры, Дж/(м3K),
γ - удельная теплота фазового перехода воды, Дж/кг,
ρ - плотность горных пород, кг/м3,
w - влажность мерзлых пород, доли,
t - температура нефти или t(z, τ),
G - дебит жидкости, кг/сек,
Cp - удельная теплоемкость жидкости, Дж/(кгК), которая определяется как
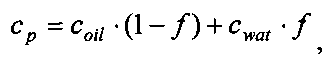
Coil - удельная теплоемкость нефти, Дж/(кгК),
Cwat - удельная теплоемкость воды, Дж/(кгК),
f - обводненность, доли,
u - периметр сечения движения жидкости, м,
Ks(z) - коэффициент теплопередачи скважины, Вт/(м2K),
rs - радиус эк, м.
Уравнение параболического типа (1) описывает тепловое поле горных пород [Инструкция по определению температурного режима вечномерзлых и сезонно-мерзлых грунтов и прогнозированию последствий изменения тепловых условий на поверхности: РД 39-Р-088-91. - Введ. 01.05.91. - Тюмень: Гипротюменнефтегаз, 1991. - 46 с.]. В начальный момент времени температурное поле горных пород имеет вид: T(r, z, 0)=T1(z).
Расчетная область представляет собой фрагмент осевого сечения скважины и массива вмещающих многолетне-мерзлых пород (чертеж) в цилиндрических координатах. Высота (глубина области от поверхности грунта) равна расстоянию от забоя до устья скважины, ширина 25 м.
Рассмотрим условия на границах области для уравнения (1), которые показаны на фиг.
Учет теплового взаимодействия потока нефти с окружающими породами приводит к граничному условию интегро-дифференциального вида (3) - на левой вертикальной границе (6) чертежа. Можно назвать его усовершенствованным граничным условием третьего рода [Фарлоу, С. Уравнения с частными производными для научных работников и инженеров / С. Фарлоу. - М.: Мир. - 1983. - 384 с.]. Чтобы его получить, необходимо было сделать ряд допущений: температура на стенке НКТ 2 скважины 1 равна температуре нефти, температура на внешней стенке ЭК 3 равна температуре горных пород. Тогда коэффициент теплопередачи скважины [Исаченко В.П. Теплопередача / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. - М.: Энергия, 1975. - 486 с.]

В межтрубном пространстве передача тепла осуществляется за счет теплопроводности, свободная конвекция учитывается в виде эквивалентной теплопроводности λэк(z).
Радиус НКТ 2 гораздо меньше глубины скважины 1, поэтому, можно рассматривать тепловое поле нефти как одномерное (в зависимости от глубины). Процесс теплообмена в НКТ 2 происходит гораздо быстрее, чем процесс распространения тепла в горных породах, поэтому уравнение притока тепла можно записать в квазистационарном приближении. Решение (2) уравнения притока тепла [Исаченко, В.П. Теплопередача / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. - М.: Энергия, 1975. - 486 с.] подставлено в граничное условие третьего рода. За счет упрощения задачи в трубе, часть задачи переводится в граничное условие. Здесь вместо обычного подхода с определением температуры нефти заранее предложен нестандартный вариант с использованием решения линейного дифференциального уравнения.
Поля температур нефти и горных пород связаны между собой условием на границе теплообмена (3), которое является главной особенностью заявленного технического решения.
На верхней горизонтальной границе (поверхность земли) (7) чертежа задаются граничные условия 3 рода (Фарлоу С. Уравнения с частными производными для научных работников и инженеров / С. Фарлоу. - М.: Мир. - 1983. - 384 с). Здесь определяется тепловое взаимодействие окружающей среды с многолетне-мерзлыми породами путем задания среднемесячных температур и коэффициентов теплообмена на дневной поверхности.
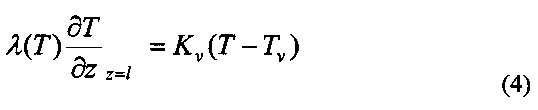
где Kν - коэффициент теплопередачи от поверхности земли через слой снега к воздуху, Вт/(м2K), коэффициент теплопередачи от поверхности земли через слой снега к воздуху [Исаченко, В.П. Теплопередача / В.П. Исаченко, В.А. Осипова А.С. Сукомел. - М.: Энергия, 1975. - 486 с.]:
Tv - температура воздуха, K,
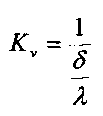
где λ - теплопроводность снега, Вт/(мK),
δ - толщина снега, м,
l - размер области расчета по вертикали.
На правой вертикальной границе области (8) чертежа задано равенство нулю теплового потока:

где R - размер области по радиусу. Значение R можно подобрать с помощью функции влияния точечного источника. Функция влияния мгновенного точечного источника тепла: 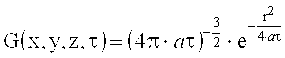 . При a~10-7 м2/с, t~107°C, r~25 м, функция G(x, y, z, t)~10-6. Можно принять R=25 м.
. При a~10-7 м2/с, t~107°C, r~25 м, функция G(x, y, z, t)~10-6. Можно принять R=25 м.
R - это расстояние, при котором функция влияния точечного источника тепла очень мала.
На нижней горизонтальной границе (9) чертежа области задана постоянная температура:

Tp - температура нефтяного пласта.
Численный расчет температур горных пород начинается от забоя скважины, используется метод переменных направлений [Роуч П. Вычислительная гидродинамика / П. Роуч. - М.: Мир, 1980. - 616 с.]. Шаг по координате z 5 м (может уменьшаться до 0.25 м при приближении к дневной поверхности), по r 0.25 м, шаг по времени τ 3 суток.
Предложенный способ определения размеров и конфигурации зоны оттаивания вокруг скважины и температуры нефти в скважине является более точным по сравнению с известными способами, не принимающими во внимание теплообмен в системе скважина - горные породы. Скважина и породы являются одной теплообменной системой, и, поэтому, одновременное определение температуры жидкости в скважине и температурного поля горных пород вокруг нее обеспечивает повышение точности прогнозирования теплового состояния мерзлых пород при эксплуатации скважин, которое используют для выбора расстояния между скважинами, оценки размеров приустьевой воронки. Учет взаимного теплового обмена скважины и многолетне-мерзлых пород позволяет получать более реальные оценки факторов, представляющих угрозу для нормальной работы скважины и кустового оборудования.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЭКСПЛУАТАЦИИ ДОБЫВАЮЩЕЙ СКВАЖИНЫ В УСЛОВИЯХ РАСПРОСТРАНЕНИЯ МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОД | 1999 |
|
RU2170336C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАЗМЕРОВ И КОНФИГУРАЦИИ ЗОНЫ ОТТАИВАНИЯ МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОД В ПРИУСТЬЕВОЙ ЗОНЕ СКВАЖИНЫ | 1998 |
|
RU2157882C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО РЕЖИМА ЭКСПЛУАТАЦИИ СКВАЖИНЫ В МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОДАХ | 1999 |
|
RU2170335C2 |
| СПОСОБ СТАБИЛИЗАЦИИ ТЕПЛОВОГО СОСТОЯНИЯ УСТЬЕВОЙ ЗОНЫ СКВАЖИНЫ В МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОДАХ | 1999 |
|
RU2158353C1 |
| СПОСОБ ТЕПЛОИЗОЛЯЦИИ УСТЬЕВОЙ ЗОНЫ ДОБЫВАЮЩЕЙ СКВАЖИНЫ В МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОДАХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1998 |
|
RU2127356C1 |
| СПОСОБ СТАБИЛИЗАЦИИ СИСТЕМЫ СКВАЖИНА-ПОРОДЫ В КРИОЛИТОЗОНЕ | 2002 |
|
RU2209934C1 |
| СПОСОБ МОНИТОРИНГА ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ СКВАЖИН С МНОГОЛЕТНЕМЕРЗЛЫМИ ПОРОДАМИ | 2013 |
|
RU2526435C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ И ОБЪЕМНОЙ ТЕПЛОЕМКОСТИ ПЛАСТОВ В СКВАЖИНЕ | 2001 |
|
RU2190209C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЕГАЗОВЫХ МЕСТОРОЖДЕНИЙ | 1991 |
|
RU2049913C1 |
| ПОДЗЕМНОЕ ХРАНИЛИЩЕ ДЛЯ РАДИОАКТИВНЫХ ОТХОДОВ | 1993 |
|
RU2065217C1 |
Изобретение относится к нефтегазодобывающей промышленности и может быть использовано при основании и эксплуатации месторождений, расположенных в зоне распространения многолетне-мерзлых пород. Техническим результатом является повышение точности прогнозирования теплового состояния мерзлых пород при эксплуатации скважин, т.е. радиуса оттаивания вокруг скважины и расчет температуры нефти в скважине. В способе учитывают связь вертикального теплового потока в скважине с горизонтальным потоком тепла от скважины в горные породы: насколько нефть охладилась при подъеме от забоя к устью, настолько прогрелись (протаяли) горные породы вокруг скважины, на основании этого получено сложное интегро-дифференциальное условие на границе скважины и горных пород. Температурное поле горных пород определяют с помощью численного моделирования. Температурное поле флюида в скважине находится на основании решения уравнения притока тепла. 1 ил.
Способ определения размеров и конфигурации зоны оттаивания вокруг скважины и температуры нефти в скважине, оборудованной эксплуатационной колонной и расположенной внутри нее колонной насосно-компрессорных труб, включающий проведение стандартных теплофизических исследований свойств грунта и определение на основании полученных исходных данных параметров теплообмена скважины и горных пород путем решения численными методами на основе математического моделирования, отличающийся тем, что учитывают теплофизические параметры грунтов вокруг скважины, среднемесячную температуру воздуха, толщину снега, коэффициент теплообмена поверхности земли с воздухом, дебит скважины, обводненность, глубину, температуру пласта на уровне отбора, радиус эксплуатационной колонны и колонны насосно-компрессорных труб, мощность мерзлоты, температуру мерзлоты, затем определяют динамику размера и конфигурации зоны оттаивания вокруг скважины и падение температуры нефти по стволу скважины, устьевую температуру, на основе численных расчетов системы уравнений (1)-(3):
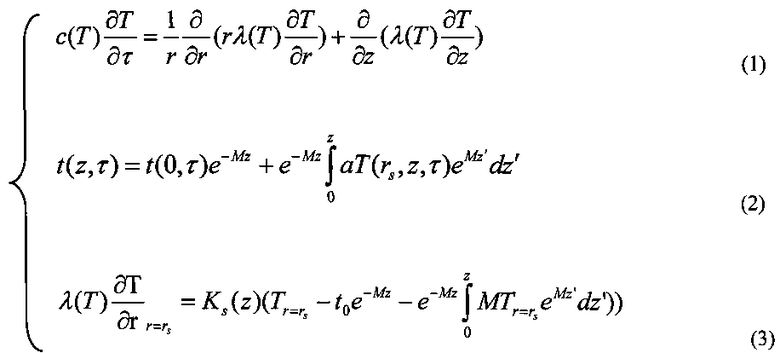
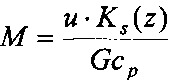
где r, z - координаты цилиндрической системы координат,
τ - время, с,
Т - температура горных пород или T(r, z, τ) впоследствии для упрощения формул будет записываться как Т, °C,
λ(Т) - коэффициент теплопроводности горных пород, Вт/(мK),
с(Т) - эффективная объемная теплоемкость горных пород, Дж/(м3K)
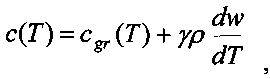
где cgr(T) - объемная теплоемкость породы, зависящая от температуры, Дж/(м3K),
γ - удельная теплота фазового перехода воды, Дж/кг,
ρ - плотность горных пород, кг/м3,
w - влажность мерзлых пород, доли,
t - температура нефти или t(z, τ),
G - дебит жидкости, кг/с,
Ср - удельная теплоемкость жидкости, Дж/(кгК), которая определяется как
cp=coil·(1-f)+cwat·f,
Coil - удельная теплоемкость нефти, Дж/(кгК),
Cwat - удельная теплоемкость воды, Дж/(кгК),
f - обводненность, доли,
u - периметр сечения движения жидкости, м,
где в уравнении (3):
Ks(z) - коэффициент теплопередачи скважины, Вт/(м2K),
rs - радиус эк, м.
| СПОСОБ ОПРЕДЕЛЕНИЯ РАЗМЕРОВ И КОНФИГУРАЦИИ ЗОНЫ ОТТАИВАНИЯ МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОД В ПРИУСТЬЕВОЙ ЗОНЕ СКВАЖИНЫ | 1998 |
|
RU2157882C2 |
| Способ определения прочности многолетнемерзлых горных пород в натурных условиях | 1979 |
|
SU922279A1 |
| Устройство для контроля температуры замороженных пород | 1982 |
|
SU1020577A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО РЕЖИМА ЭКСПЛУАТАЦИИ СКВАЖИНЫ В МНОГОЛЕТНЕМЕРЗЛЫХ ПОРОДАХ | 1999 |
|
RU2170335C2 |
| US 3745822 A1, 17.07.1973 | |||
| US 4343181 A1, 10.08.1982.. | |||
Авторы
Даты
2016-06-27—Публикация
2014-11-26—Подача