Описание изобретения
Изобретение относится к области медицинской диагностической техники и служит для определения плотности биологической ткани в области патологического очага с помощью позитронно-эмиссионного томографа.
Известен диагностический способ визуализации патологического очага с помощью позитронно-эмиссионного томографа, предназначенный для определения местоположения и размеров патологического очага на основе измерения детекторами γ-излучения двух одновременно регистрируемых γ-квантов [1].
Позитронно-эмиссионный томограф (ПЭТ) - это устройство радиоизотопной диагностики, в котором используется внутривенное введение таких радиофармацевтических препаратов (РФП), как излучающие позитроны радиоизотопы 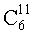
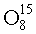
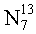

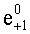
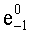
Особенностью этих γ-квантов ћω1 и ћω2 является то, что они излучаются в строго противоположных направлениях.
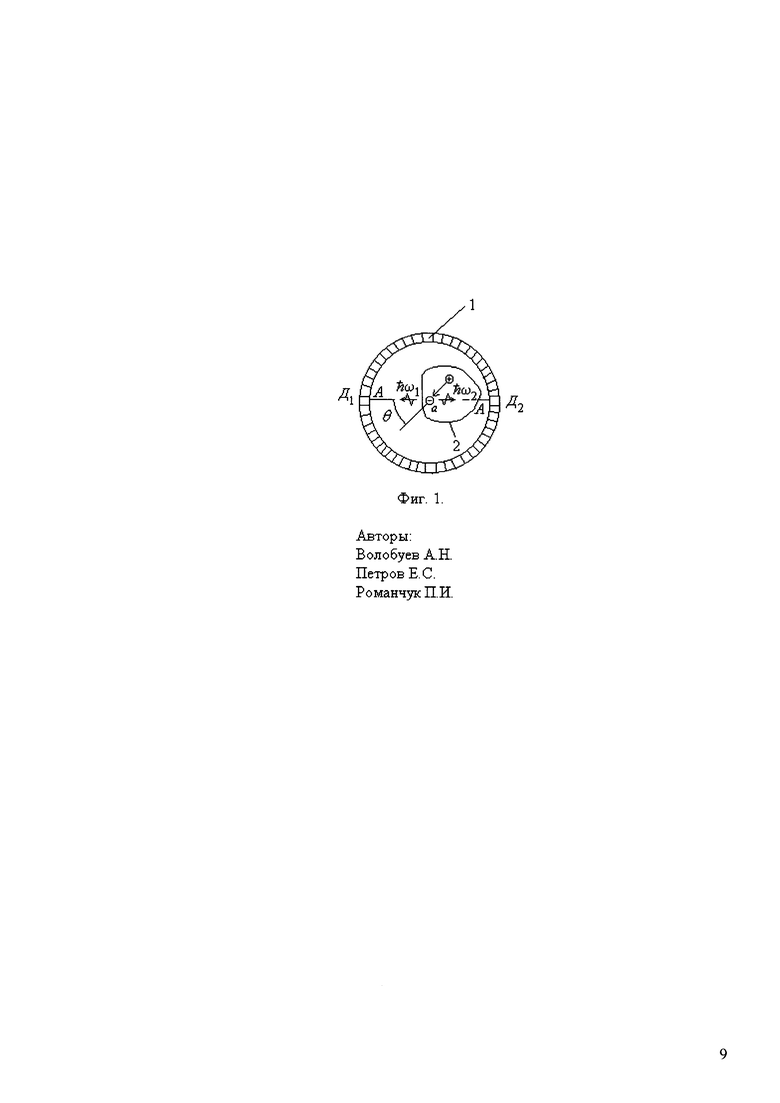
В методе ПЭТ кушетка с пациентом, у которого в тканях имеется патологический участок 2, в котором накопился РФП, помещается в кольцо 1, состоящее из детекторов, регистрирующих γ-кванты. Информационную ценность имеет только событие, когда два излученных в процессе аннигиляции γ-кванта достигают противоположных детекторов одновременно, т.е. оба γ-кванта пролетают одинаковый путь до детекторов. Например, γ-кванты, излученные из точки a патологического очага, достигают двух детекторов γ-излучения Д1 и Д2, расположенных на линии A-A, одновременно, эти сигналы участвуют в построении изображения.
Координата излучающей γ-кванты точки патологического очага, находится на линии, соединяющей детекторы точно посередине между ними. Интенсивность сигнала от детекторов, т.е. количество γ-квантов регистрируемых детекторами в единицу времени, указывает на количество накопленного в патологическом очаге РФП.
Сигналы детекторов, не одновременно регистрирующих γ-кванты, игнорируются. Это связано с тем, что для таких γ-квантов невозможно рассчитать точку их испускания в связи с очень большой скоростью движения квантов.
При перемещении кушетки с пациентом вдоль оси, перпендикулярной плоскости кольца детекторов, получается послойное трехмерное (3D) изображение распределения концентрации РФП в патологическом очаге.
Результаты регистрации γ-квантов всеми, одновременно срабатывающими детекторами, обрабатывается с помощью ЭВМ. При этом получается изображение высокой информативности.
ПЭТ в настоящее время успешно применяется, прежде всего, для раннего обнаружения и визуализации онкологических новообразований, особенно метастазов. С его помощью обнаруживаются патологические очаги, когда структурных изменений еще нет, но течение биохимических реакций в клетках уже нарушено.
Недостатком ПЭТ является отсутствие информации о состоянии патологического очага, в частности плотности ткани в очаге.
В результате квантово-электродинамического расчета процесса аннигиляции были получены две формулы для дифференциального эффективного сечения рассеяния квантов электромагнитного излучения в телесный угол dΩ.
Первая по времени формула была получена Гайтлером [2]. Эта формула имеет вид:
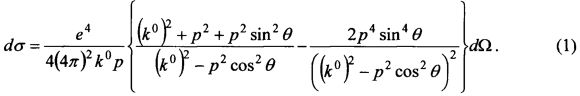
Формула дана в обозначениях [3], где имеется ее подробный вывод. Использована т.н. рациональная система единиц, в которой скорость света и постоянная Планка равны единице c=ћ=1. В этой системе единиц энергия импульса и масса имеют одну и ту же размерность.
В формуле (1) e - заряд электрона (или позитрона с противоположным знаком), k0 - энергия фотона, p - импульс электрона, θ - угол между импульсами электрона и одного из излученных фотонов. Формула (1) получена при условии суммирования по всем направлениям поляризации фотонов.
При выводе (1) использована система отсчета, связанная с центром масс взаимодействующих электрона и позитрона, в которой импульсы электрона и позитрона равны по модулю между собой и противоположны по направлению p1=-p2=p. Импульсы фотонов также равны по модулю между собой и противоположны по направлению k1=-k2 [2, 3]. Отметим, что в этой системе отсчета условия наблюдения обоих фотонов одинаковы.
Вторая формула была предложена несколько позже Фейнманом [4]:
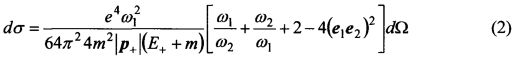
Формула (2) записана в обозначениях [4]. Как и в предыдущем случае, использована рациональная система единиц.
В формуле (2) e1 и e2 - единичные векторы поляризации излученных при аннигиляции фотонов, ω1 и ω2 - частоты излученных фотонов, m - масса электрона (или позитрона), 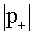
Важнейшим отличительным условием вывода формулы (2) является использование другой системы отсчета по сравнению с выводом формулы (1). Формула (2) выводилась в системе отсчета, в которой электрон покоится, а движется позитрон.
Эта система отсчета в целом эквивалентна системе отсчета, связанной с ПЭТ. Электроны объекта, исследуемого в ПЭТ, в основном находятся в связанном состоянии. Позитроны же возникают в результате β-позитронного распада радиоактивных элементов. Поэтому электроны в системе отсчета, связанной с ПЭТ, можно считать неподвижными (если исключить хаотическое тепловое движение молекул).
Обе формулы (1) и (2) выводились с помощью стандартной диаграммной техники Фейнмана и диаграмм второго порядка теории возмущений. Однако результаты вывода существенно различаются.
Во-первых, формула (1) предполагает довольно сложное угловое распределение аннигиляционных фотонов. Причем это распределение связано только с импульсом электрона, угол θ присутствует только в комплексе с импульсом p. В формуле (2) угловое распределение фотонов отсутствует.
Во-вторых, формула (2) предполагает возможность различной энергии фотонов при аннигиляции, что запрещается выводом формулы (1) вследствие k1=-k2.
Поэтому, прежде всего, возникает вопрос, какова природа углового распределения аннигиляционных фотонов в (1)? Связано ли это распределение с самим процессом аннигиляции, т.е. переходом «вещество-энергия», либо определяется какими-то другими эффектами? Сохранится ли данное угловое распределение фотонов при переходе к другой системе отсчета, например, связанной с ПЭТ?
Для исследования причины угловой зависимости дифференциального эффективного сечения (1) рассмотрим промежуточное выражение вывода, которое еще не просуммировано по направлениям поляризации фотонов [3]:
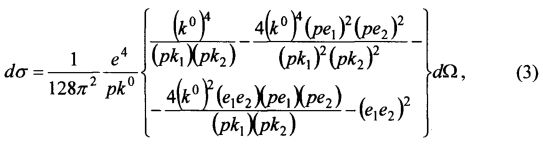
где k1 и k2 - импульсы фотонов. Переменные в квадратных скобках: импульс электрона, импульсы фотонов, единичные векторы поляризации фотонов записаны в виде 4-векторов.
Формулу (3) несложно преобразовать к виду:
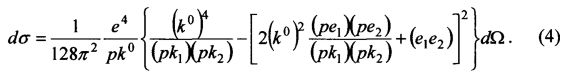
Перейдем в (4) к пространственным векторам, используя правило (ab)=a 0b0-ab, где a и b - трехмерные векторы, компоненты которых изменяются ковариантно, a 0 и b0 - контравариантно изменяющиеся компоненты 4-векторов, в нашем случае энергетические компоненты.
Переходя к трехмерным векторам, а также, учитывая отсутствие контравариантных компонент у поляризационных 4-векторов e0=0, выражение (4) можно представить в виде:
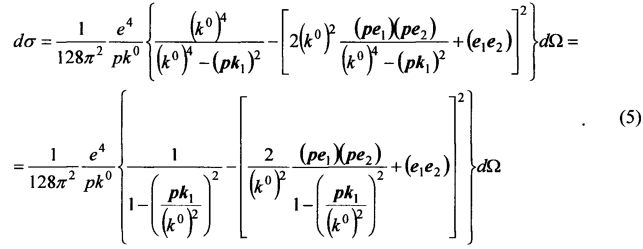
При выводе (5) также использовано условие вылета фотонов в строго противоположных направлениях k2=-k1.
Учитывая 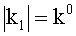
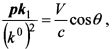 где V - скорость электрона. В результате получим:
где V - скорость электрона. В результате получим:
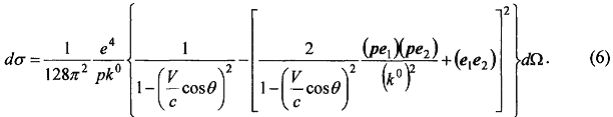
Перейдем в (6) в систему отсчета, предложенную в [4], связанную с электроном (или с ПЭТ). В этом случае p=0, а V - можно рассматривать, как скорость движения позитрона. То же самое относится и к величине p в коэффициенте перед скобками. В данной системе отсчета формула (6) значительно упрощается:

Исследуем вспомогательную задачу.
Наблюдатель 4, находящийся в «неподвижной» (связанной с Землей) системе отсчета, фиг. 2, рассматривает некоторую движущуюся со скоростью V частицу 5, которая в определенный момент времени излучает два противоположно направленных кванта. При V=0 частота квантов равна ω0. Угол между скоростью частицы и направлением распространения одного из квантов равен θ. В направлении наблюдателя частица имеет составляющую скорости Vcosθ.
За счет эффекта Доплера квант, движущийся в направлении наблюдателя, будет обладать повышенной частотой [5]:
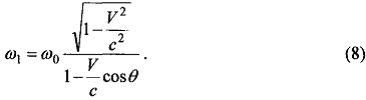
Для кванта, движущегося в противоположном направлении, будет наблюдаться т.н. «красное смещение»:
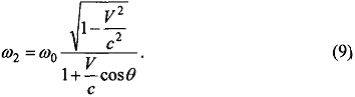
Используя (8) и (9), найдем величину комплекса 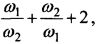 который входит в формулу (2):
который входит в формулу (2):
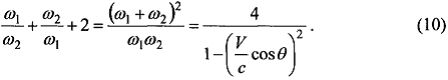
Отметим, что различие в частотах квантов в рассматриваемой задаче определяется различием в условиях наблюдения этих квантов: один квант движется к наблюдателю, другой удаляется от него.
В формуле (7) фактически реализуется рассмотренная вспомогательная задача. При этом под движущейся частицей подразумевается позитрон, а наблюдатель находится на «неподвижном» электроне. Поэтому, подставляя (10) в (7), найдем:
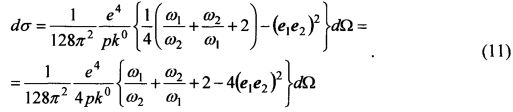
Отметим, что при использовании формулы (10) мы фактически отказались от условия k2=-k1.
Если в коэффициенте перед скобками в формуле (2) принять E+=m=ω1, то формулы (2) и (11) становятся тождественными.
Таким образом, делаем важные выводы.
1. Формулы (1) и (2) полностью эквивалентны.
2. Различие частот фотонов в формуле (2) является следствием эффекта Доплера, который проявляется в результате движения позитрона.
Найдем разность частот излучаемых фотонов, т.е. величину Δω=ω1-ω2, используя формулы (8) и (9):
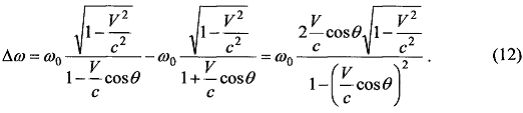
Если угол θ=0, т.е. позитрон движется по линии, соединяющей детекторы γ-излучения Д1 и Д2, разность частот фотонов будет максимально возможной и формула (12) преобразуется к виду:

Учитывая V<<c, найдем:

Величину ω0 можно получить исходя из приближенного равенства ћω0≈mc2. В этом случае:

где 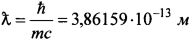 - комптоновская длина волны электрона [6].
- комптоновская длина волны электрона [6].
Целью настоящего изобретения является получение в процессе диагностической процедуры на ПЭТ информации о плотности биологической ткани в патологическом очаге.
Данная цель достигается следующим образом, фиг. 3.
В ПЭТ вводится устройство 3 для измерения разности частот γ-квантов Δω=ω1-ω2, одновременно поступающих на детекторы Д1 и Д2.
Предположим, что в точке a патологического очага происходит аннигиляция электронов и позитронов. Возникшие γ-кванты движутся по разным направлениям, см. фиг. 3. В одном из направлений разность частот фотонов предполагается максимальной Δωmax (при θ=0) и, следовательно, справедлива формула (15).
Таким образом, измеряя с помощью устройства 3, фиг. 3, разность частот фотонов Δω=ω1-ω2, одновременно поступающих на детекторы, используя максимальное значение этой разности за время измерения Δωmax, по формуле (15) - следствии эффекта Доплера, находим скорость позитрона V при его движении в патологическом очаге, которая пропорциональна Δωmax.
Учитывая, что скорость позитрона пропорциональна плотности ткани, через которую он движется ρ~V, получаем необходимую информацию о плотности ткани в патологическом очаге.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Волобуев А.Н. Основы медицинской и биологической физики. Самара: «Самарский дом печати», 2011, С. 636.
2. Гайтлер В. Квантовая теория излучения. М.: Изд-во Иностр. лит., 1956, с. 302-304.
3. Боголюбов Н.Н., Ширков Д.В. Введение в теорию квантовых полей. М.: Наука, 1976, с. 203-205.
4. Фейнман Р. Квантовая электродинамика. Курс лекций. М.: Книжный дом «ЛИБРОКОМ», 2009, с. 135-137.
5. Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1967, с. 156.
6. Яворский Б.М., Детлаф А.А. Справочник по физике. М: Наука, 1990, с. 576.


Изобретение относится к медицине, а именно к медицинской диагностической технике и может быть использовано для определения плотности биоткани в патологическом очаге. С помощью позитронно-эмиссионного томографа, содержащего устройство, измеряющее разность частот γ-квантов, одновременно поступающих на детекторы γ-излучения, измеряют максимальную разность частот указанных γ-квантов. По этой разности частот на основе эффекта Доплера находят скорость позитрона и пропорциональную ей плотность биоткани в патологическом очаге. Способ позволяет измерить плотность биоткани в патологическом очаге за счет использования устройства, позволяющего измерять разность частот γ-квантов, одновременно поступающих на детекторы γ-излучения. 3 ил.
Способ определения плотности биоткани в патологическом очаге с помощью позитронно-эмиссионного томографа, содержащего устройство, измеряющее разность частот γ-квантов, одновременно поступающих на детекторы γ-излучения, отличающийся тем, что измеряется максимальная разность частот γ-квантов, одновременно поступающих на детекторы γ-излучения и по этой разности частот на основе эффекта Доплера находится скорость позитрона и пропорциональная ей плотность биоткани в патологическом очаге.
| СПОСОБ ТОМОГРАФИЧЕСКОГО ИССЛЕДОВАНИЯ ПЛОТНОСТИ ТЕЛА | 1990 |
|
SU1811289A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОТНОСТИ БИОЛОГИЧЕСКИХ ТКАНЕЙ | 2011 |
|
RU2472440C1 |
| СИСТЕМА ПОЗИТРОН-ЭМИССИОННОЙ ТОМОГРАФИИ | 2005 |
|
RU2381525C2 |
| WO 2010004464 A1 14.01.2010 | |||
| WO 2007034357 A2 29.03.2007 | |||
| ВОЛОБУЕВ А.Н | |||
| Основы медицинской и биологической физики | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
Авторы
Даты
2016-10-10—Публикация
2014-12-08—Подача