Изобретение относится к распознаванию радиосигналов на основе анализа скалограммы сигнала и может быть использовано в технических средствах распознавания сигналов в реальных условиях приема при наличии шумов и помех.
Известен способ распознавания сигналов по патенту РФ №2133501 МПК5 G06K 9/00 от 04.02.98, заключающийся в сравнении на выборке длиной Q канальных символов "скользящим окном" всех комбинаций длиной K друг с другом, где K/2 - предполагаемая память помехоустойчивого сверточного кодера, и последующем подсчете частоты появления событий, заключающихся в том, что в двух отрезках кодовой последовательности имеется единственная пара несовпадающих символов, и эти символы одновременно не принадлежат двум различным подансамблям разбиения.
Недостатком этого способа является узкая область его применения, т.к. при использовании данного метода можно выполнять распознавание лишь сигналов, использующих сигнально-кодовые конструкции.
Известен способ распознавания радиосигналов на основе сингулярного разложения псевдо-частотно-временного распределения (псевдо-ЧВР) Вигнера-Вилле [N.M. Marinovic, G. Eichmann. An expansion of Wigner distribution and its applications. - Proc. IEEE ICASSP-85, 1985, pp. 1021-1024]. В указанном способе предварительно на основе псевдо-ЧВР Вигнера формируют матрицы распределения энергии (РЭ) эталонных радиосигналов, выполняют их спектральное разложение, формируют параметры эталонных радиосигналов, затем принимают распознаваемый радиосигнал, дискретизируют и квантуют его, формируют матрицу распределения энергии принятого радиосигнала, выделяют признаки принятого радиосигнала, сравнивают их с параметрами эталонных радиосигналов и по результатам сравнения идентифицируют принятый радиосигнал.
Недостатком этого способа является низкая вероятность правильного распознавания [Дж. Ту, Р. Гонсалес. Принципы распознавания образов. Пер. с англ. - М.: Мир, 1978. - стр. 142] радиосигналов сложной частотно-временной структуры, а также радиосигналов при воздействии на них шумов и помех, что обусловлено особенностями используемого для распознавания псевдо-ЧВР Вигнера-Вилле [Коэн Л. Время-частотные распределения. Обзор // ТИИЭР, 1989, т. 77, №10, с. 72-121].
Снижение вероятности правильного распознавания происходит вследствие появления интерференционного фона и ложных пиков мощности в псевдо-ЧВР Вигнера-Вилле, искажающих реальную картину распределения энергии сигнала в координатах частота - время.
Наиболее близким по технической сущности к заявленному является способ распознавания радиосигналов (по патенту РФ 2261476 МПК: G06K от 26.01.2004) на основе непрерывного вейвлет-преобразования последовательности дискретных квантованных отсчетов радиосигналов. В указанном способе при формировании матрицы распределения энергии эталонных радиосигналов вычисляют непрерывное вейвлет-преобразование последовательности дискретных квантованных отсчетов эталонных радиосигналов, формируют векторы распределения энергии, вычисляют общую ковариационную матрицу, формируют усеченную матрицу собственных векторов, умножают усеченную матрицу собственных векторов на векторы распределения энергии эталонных радиосигналов, из сформированной матрицы распределения энергии принятого радиосигнала формируют вектор распределения энергии и умножают усеченную матрицу собственных векторов на вектор распределения энергии, а результаты вычислений принимают в качестве признаков распознавания принятого радиосигнала.
Недостатком способа-прототипа является сложность выбора наиболее подходящей с точки зрения эффективности выявления особенностей анализируемого сигнала вейвлет-функции, что приводит к снижению контрастности признаков распознавания радиосигнала.
Целью заявленного технического решения является повышение контрастности признаков распознавания радиосигналов - вейвлет-спектрограмм (скалограмм) в условиях приема реального радиосигнала за счет выбора наиболее оптимального вейвлета.
Поставленная цель достигается тем, что в известном способе распознавания радиосигналов, заключающемся в том, что для формирования эталонных матриц распределения энергии (РЭ) вычисляют непрерывное вейвлет-преобразование (НВП), формируются векторы РЭ эталонных радиосигналов, для которых вычисляют общую ковариационную матрицу, вычисляют матрицы собственных значений и собственных векторов ковариационной матрицы, формируют усеченную матрицу собственных векторов, формируют параметры эталонных радиосигналов путем умножения усеченной матрицы собственных векторов на векторы РЭ эталонных радиосигналов, результаты вычислений усредняют, формируется матрица РЭ принятого сигнала путем вычисления НВП и вектор РЭ, усеченную матрицу собственных векторов умножают на вектор РЭ принятого радиосигнала, результаты вычислений принимают в качестве признаков распознавания принятого радиосигнала, в заявленном способе для формирования признаков распознавания радиосигналов по структурно-временному построению выбирается информационная часть сигнала. Выбранный участок сигнала заносится в систему компьютерной математики Matlab, где осуществляется оцифровка и обработка сигнала. Затем оценивается количество наиболее информативных коэффициентов аппроксимации для НВП, формируется вектор сигнала с учетом числа наиболее информативных коэффициентов. С использованием показателей энергетических характеристик сигнала и вейвлетов вычисляется интегральный показатель. По максимальному значению интегрального показателя выбирается вейвлет-функция, обеспечивающая максимальную контрастность признака радиосигнала - скалограммы. Строится скалограмма сигнала путем НВП, которую и принимают в качестве признака распознавания.
Заявленный способ поясняется рисунками и таблицами, на которых показаны:
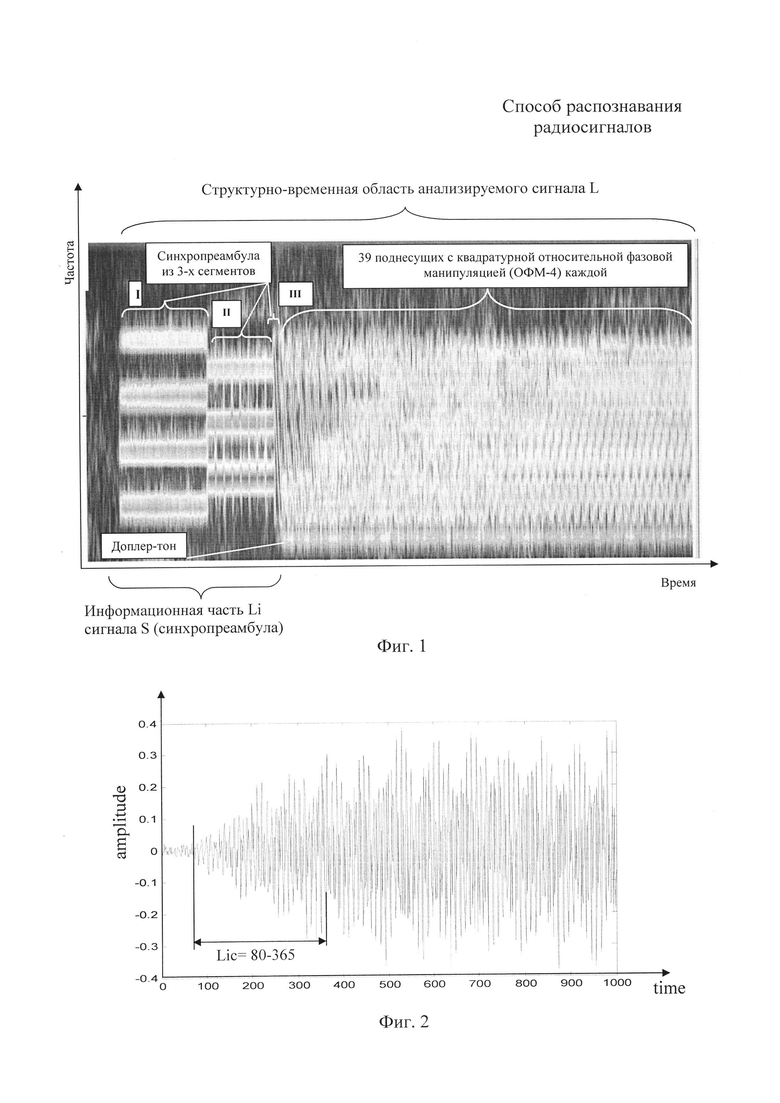
фиг. 1 - спектрограмма сигнала стандарта MIL-STD-188-110А;
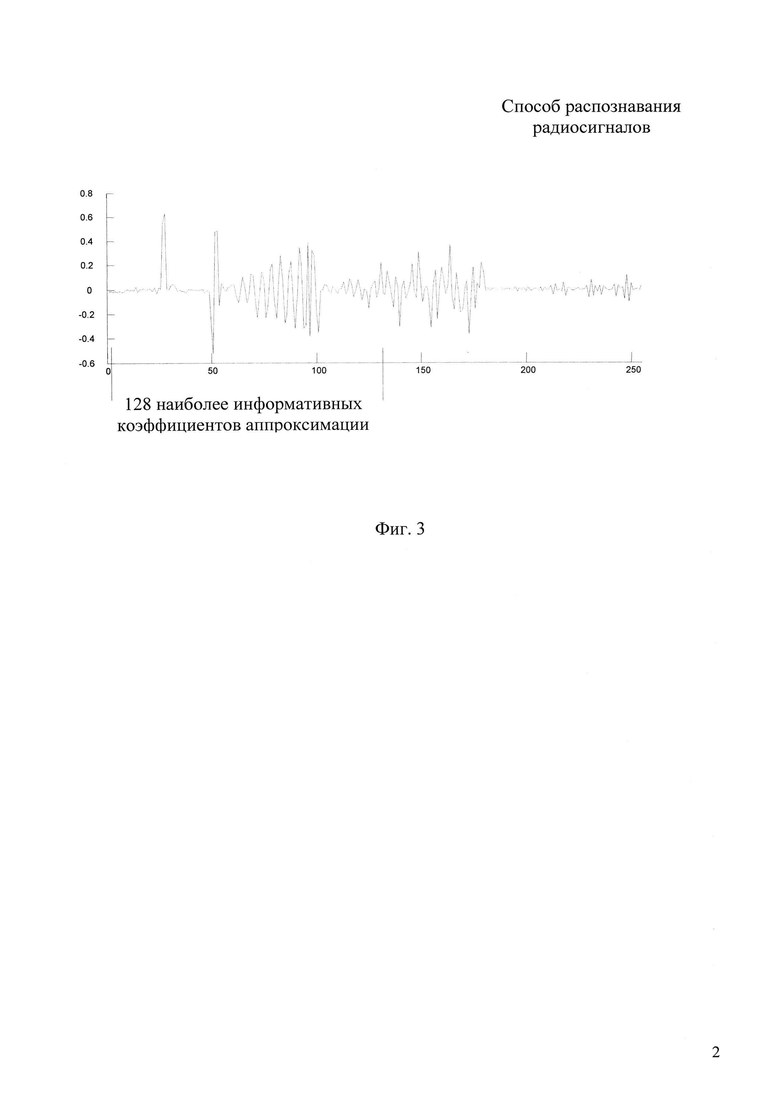
фиг. 2 - осциллограмма информационной части Li сигнала стандарта MIL-STD-188-110A;
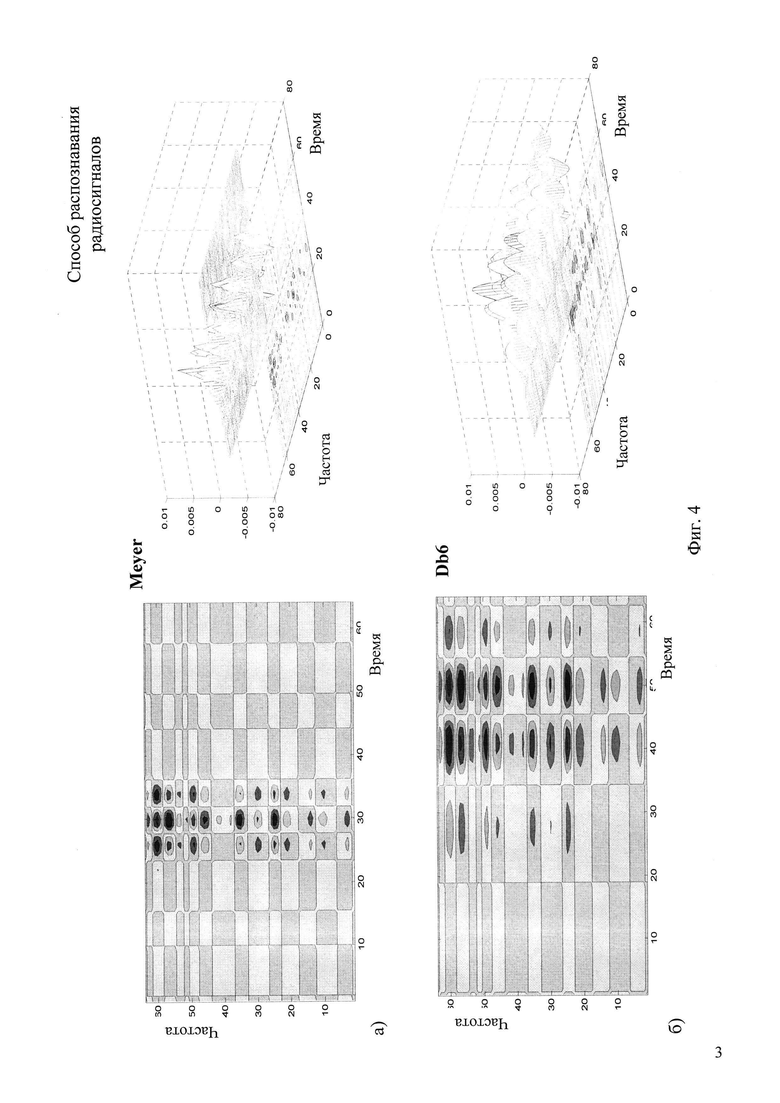
фиг. 3 - осциллограмма информативных коэффициентов аппроксимации (ni) для прямого непрерывного вейвлет-преобразования;
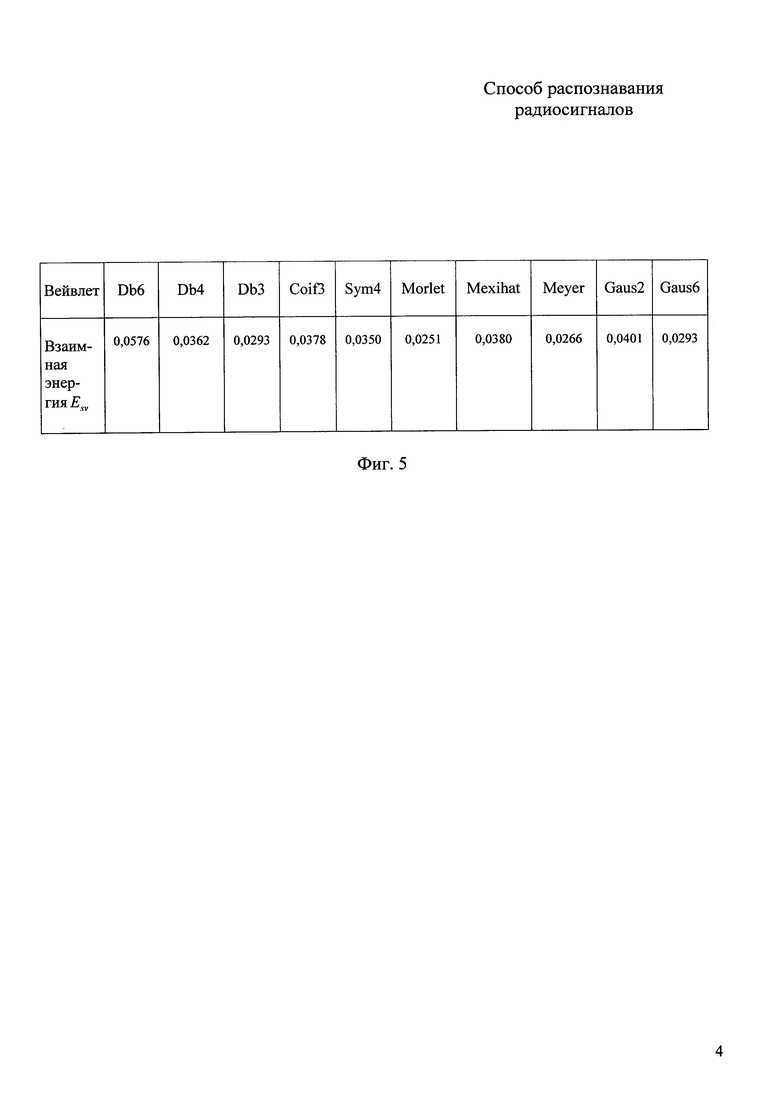
фиг. 4 - контурные графики и 3D-графики матричного (внешнего) умножения вектора сигнала на вектор вейвлета Meyer (а) и на вектор вейвлета Db6 (б);
фиг. 5 - таблица результатов расчета взаимной энергии информационной части Li сигнала S и вейвлета;
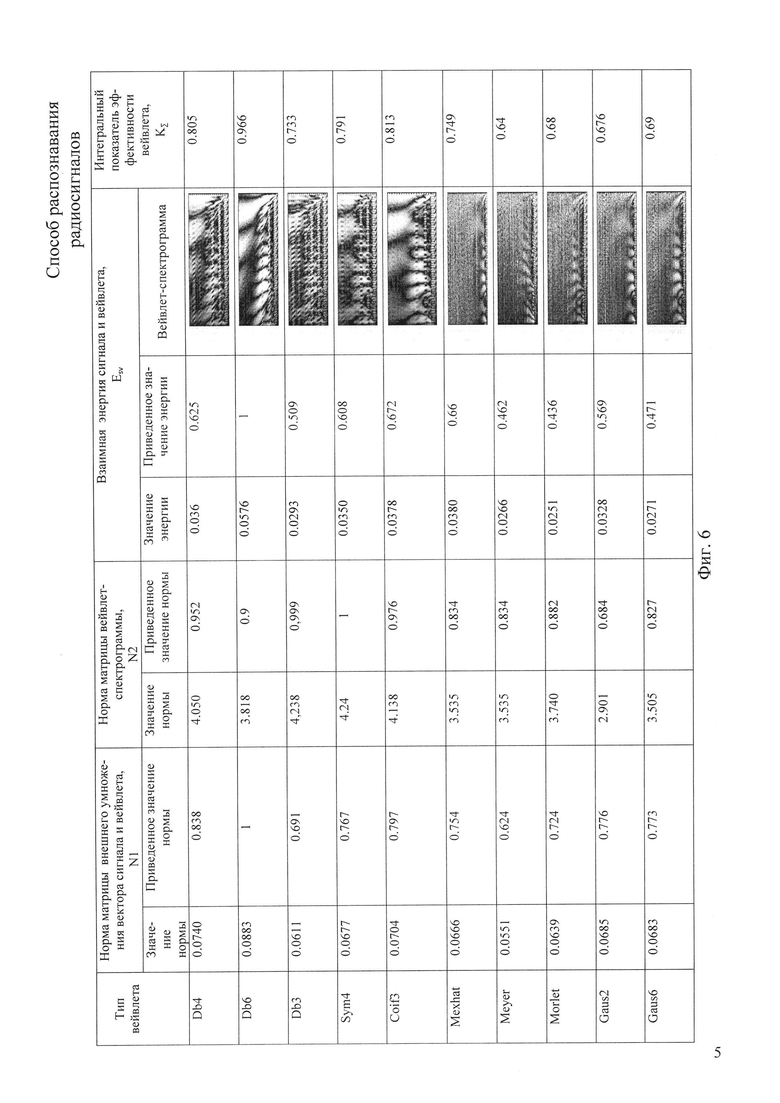
фиг. 6 - аблица результатов расчета интегрального показателя эффективности вейвлета KΣ;
фиг. 7 - блок-схема алгоритма распознавания радиосигнала;
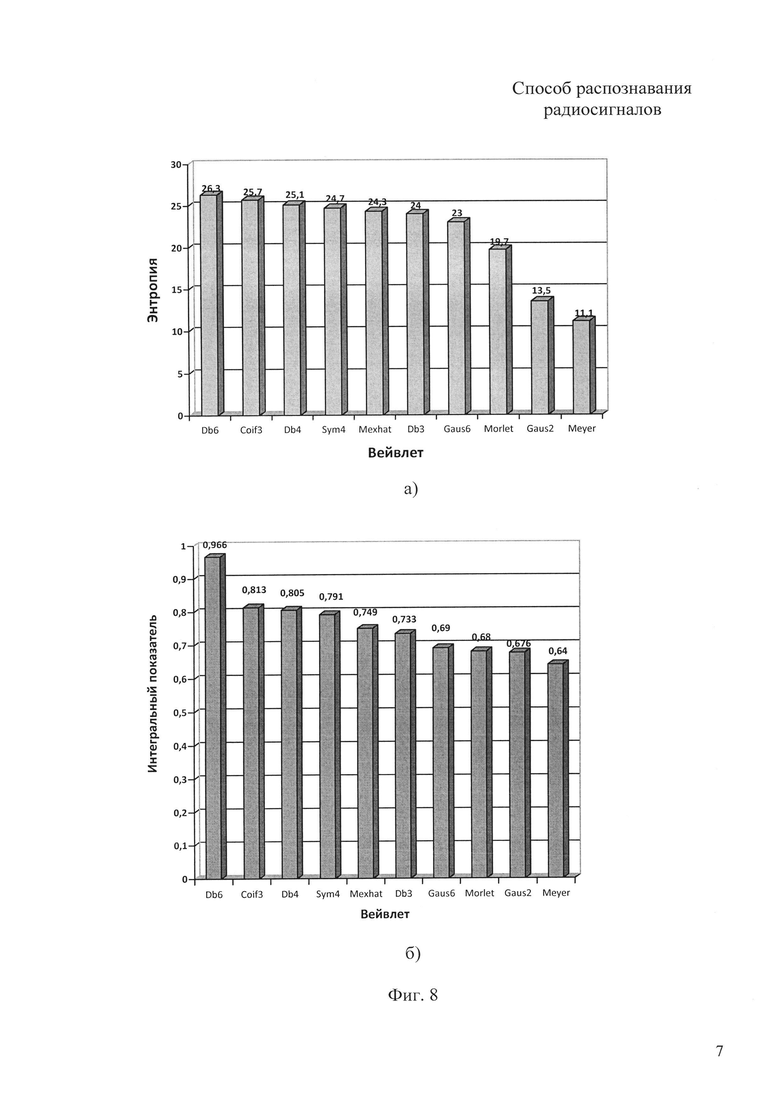
фиг. 8 - диаграммы энтропийной оценки признаковой контрастности скалограммы для различных типов вейвлета (а) и значений интегрального показателя KΣ для различных типов вейвлета (б).
Процесс распознавания включает в себя следующие процедуры: выбор из структурно-временной области L анализируемого сигнала S (фиг. 1) информационной (с точки зрения распознавания и выявления особенностей) части Li, обработку и оцифровку выбранной структурно-временной области в системе компьютерной математики (СКМ) Matlab (Lic), оценку и выбор наиболее информативных коэффициентов аппроксимации для прямого непрерывного вейвлет-преобразования - ni, формирование длины Lcin вектора сигнала S с учетом ni, выбор на основе интегрального показателя KΣ наиболее оптимального с точки зрения повышения признаковой контрастности скалограммы анализируемого сигнала вейвлета - Wi, прямое непрерывное вейвлет-преобразование структурно-временной области сигнала Lic и формирование скалограммы сигнала Swi. Распознавание сигнала осуществляется на основе сравнения параметров матриц скалограмм эталона и анализируемого сигнала одним из известных способов [Способ распознавания радиосигналов (RU 2464633), способ распознавания радиосигналов (RU 2423735)].
Важным условием повышения контрастности признаков распознавания радиосигналов - вейвлет-спектрограмм - является обоснованный выбор вейвлет-функции для анализа исследуемого сигнала.
Энергия сигнала равна интегралу от мощности по всему интервалу существования сигнала [Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988, стр. 74]:
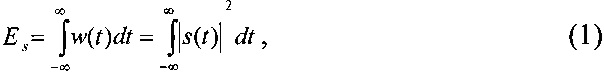
где Es - энергия сигнала s(t);
w(t) - мощность сигнала s(t).
Одним из основных метрических параметров линейного пространства в математике является норма сигнала. Для анализа сигналов часто используются квадратичные нормы [Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988, стр. 25]:

Для случая дискретного сигнала:

где s(n) - дискретные отсчеты сигнала, n=1, 2…∞.
На основании выражения (1) и (2) энергия сигнала определяется:

Энергию взаимодействия сигналов s(t) и v(t) определяет выражение [Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988, стр. 72-73]:

Выражение (6) соответствует удвоенному скалярному произведению сигналов s(t) и v(t) [Давыдов А.В. Сигналы и линейные системы: Тематические лекции. - Екатеринбург: УГГУ, ИГиГ, 1, T2, стр. 9] и определяет энергию взаимодействия во временной области:

При выборе вейвлета для анализа сигнала необходимо обеспечить наибольшее совпадение частотно-временных характеристик сигнала и вейвлета, при этом взаимная энергия сигнала и вейвлета должна стремиться к полной энергии сигнала при идеальном совпадении функции сигнала и вейвлета.
Для оценки совпадения частотно-временных характеристик вейвлета с исследуемым сигналом используется выражение (6), определяющее взаимную энергию через скалярное произведение сигналов.
С использованием матричной лабораторией Matlab и выражения (6) определена энергия реального сигнала, представляющего информационную часть сигнала стандарта MIL-STD-188-110А (фиг. 2).
Листинг в командной строке Matlab:
y=wavread('V12687_all',[80 365]); % формирование сигнала
>>y1=y(1:64, 1:1); % обрезка вектора c 1 по 64 отсчет
z=trace(abs(y1*y1')) % скалярное произведение сигналов (при их полном совпадении соответствует энергии сигнала);
z=0.0824.
В соответствии с выражением (4) энергия сигнала равна квадрату второй нормы этого сигнала.
Листинг в командной строке Matlab:
z1=norm(y1,2)% вторая норма сигнала y1 в соответствии с выражением (5)
z1=0.2870
z2=z1∧2
z2=0.0824.
Полная энергия сигнала, вычисленная через квадрат второй нормы, равна 0.0824 и полностью совпадает с энергией, вычисленной через скалярное произведение [Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988, стр. 29].
Определяется взаимная энергия сигнала и вейвлета Db6 [Дьяконов В.П. - Вейвлеты. От теории к практике. Солон-Р. 2002, стр. 155-158].
Листинг в командной строке Matlab:
[phi,psi,x]=wavefun('db6',4); % формирование вейвлета
Y=[psi,x];
Y1=Y(1:1,46:109); % обрезка вектора вейвлета в соответствии с длиной вектора сигнала.
Y1n=Y1*(max(y1))/(max(Y1)); % нормировка вектора вейвлета по максимуму амплитуды сигнала.
z=trace(abs(y1*Y1n')) % скалярное произведение вектора сигнала и вейвлета:
z=0.0576.
Взаимная энергия сигнала и вейвлета Db6 - Esν равна 0.0576, что значительно меньше полной энергии сигнала.
Результаты вычисления взаимной энергии Esν сигнала и различных наиболее часто используемых в вейвлет-анализе вейвлетов [Дьяконов В.П. - Вейвлеты. От теории к практике. Солон-Р. 2002. - стр. 155-158] приведены в таблице (фиг. 5).
Хорошую оценку совпадения частотно-временных характеристик вейвлета с исследуемым сигналом дает матричное (внешнее) умножение вектора сигнала на вектор вейвлета в соответствии с выражением (7) [Э.Б. Винберг. Курс алгебры: 2-е изд., испр. и доп. - М.: Изд-во «Факториал Пресс», 2001, стр. 318]:
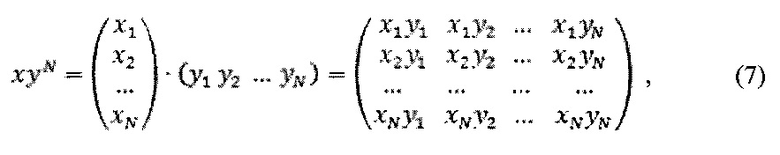
где x1, x2, …xN - дискретные отсчеты значений вейвлет-функции;
y1, y2, …yN - дискретные отсчеты значений сигнала.
Матрица внешнего умножения несет обобщенную информацию о сигналах: диагональ матрицы соответствует умножению функции сигнала на функцию вейвлета в координатной плоскости, что в частотной области соответствует свертке Фурье-образов функций и характеризует степень совпадения функций сигнала и вейвлета, сумма элементов вектора диагонали матрицы есть скалярное умножение сигнала и вейвлета, что соответствует взаимной энергии функций сигнала и вейвлета.
На фиг. 4 представлены результаты матричного (внешнего) умножения вектора сигнала на вектор вейвлета контурным графиком и 3D-графиком с использованием вейвлета Meyer и Db6. Для вейвлета Meyer матрица наполнена слабо, это хорошо видно также на трехмерном графике. Для вейвлета Db6 заполнение матрицы значительно выше.
В соответствии с выражением (3) для оценки матрицы вычисляется вторая норма, которая находит самое большое сингулярное число.
Из графиков, представленных на фиг. 4, очевидно, что норма матриц произведения вектора сигнала на вектор вейвлета будет больше для вейвлета Db6, так как абсолютные значения элементов матрицы имеют большие значения и матрица лучше наполнена. Это подтверждают результаты вычисления второй нормы матрицы для вейвлетов Db6 и Meyer: N1Db6=0.0883; N1Mtyer=0.0551.
Прямое непрерывное вейвлет-преобразование с использованием того или иного вейвлета позволяет получить матрицы спектрограмм (скалограмм) анализируемого сигнала. Оценкой энергии матрицы служит вторая норма N2, которая будет характеризовать эффективность выбранного вейвлета.
Проведенный анализ энергетических характеристик сигнала и вейвлетов позволяет сформировать показатели для их оценки: N1, N2, Esv. Значения этих показателей для целого ряда наиболее часто используемых вейвлетов приведены на фиг. 6. В таблице представлены значения нормы матрицы внешнего умножение вектора сигнала и вейвлета - N1, значения нормы матрицы вейвлет-спектрограммы - N2, значения взаимной энергии сигнала и вейвлета - Esv и их приведенные значения.
Интегральный показатель позволяет проводить комплексную оценку эффективности вейвлет-преобразования с использованием того или иного вейвлета (8):

где N1, N2, Esv - приведенные значения норм соответствующих матриц и взаимной энергии.
Интегральный показатель эффективности вейвлета обосновывает выбор того вейвлета, который обеспечивает наибольшее совпадение частотно-временных характеристик сигнала и вейвлета, при этом взаимная энергия сигнала и вейвлета стремится к полной энергии анализируемого сигнала. Для анализа информационной части Li сигнала стандарта MIL-STD-188-110А таким вейвлетом является Db6, это подтверждают графики, приведенные на фиг. 4, вейвлет спектрограммы на фиг. 6.
Результаты расчета интегрального показателя эффективности вейвлета приведены на фиг. 6.
Заявленный способ реализуют следующим образом (фиг. 7).
Первоначально выбирается информационная (с точки зрения распознавания и выявления особенностей) часть Li сигнала S по структурно-временному построению (фиг. 1).
Выбранный участок сигнала заносится в систему компьютерной математики Matlab для оцифровки (Lic) и дальнейшей обработки (фиг. 2).
Оценивается количество наиболее информативных коэффициентов аппроксимации (ni) для прямого непрерывного вейвлет-преобразования (фиг. 3).
Формируется вектор сигнала Licn с учетом числа наиболее информативных коэффициентов ni.
Формируются интегральный показатель KΣ на основе показателей энергетических характеристик сигнала и применяемых для анализа вейвлетов.
По максимальному значению интегрального показателя KΣ выбирается тип вейвлета Wi, обеспечивающий максимальную контрастность признака распознавания - скалограммы Swi.
Формируется признак распознавания - скалограммы Swi.
Принимается решение о принадлежности Swi к одному из эталонов Swiэ.
Выбор вейвлета для анализа сигнала с использованием интегрального показателя повышает признаковую контрастность, скалограммы имеют больше деталей, при анализе из них удается извлечь больше данных.
Для количественной характеристики признаковой контрастности скалограмм, позволяющей оценивать их информативность, выбрана энтропия.
Энтропия для непрерывного вейвлет-преобразования характеризует размытость анализируемого сигнала по базисным направлениям [Солонина А.И. Цифровая обработка сигналов. Моделирование в MATLAB / А.И. Солонина, С.М. Арбузов. - СПб.: БХВ-Петербург, 2008. - С. 687]. Она принимает меньшие значения, когда основная часть энергии сигналов распределяется на малом числе базисных функций и, наоборот, принимает большие значения, когда основная энергия сигнала распределяется на большом числе базисных функций. В целом это позволяет оценивать информативность скалограммы сигнала.
На фиг. 8 представлена диаграмма энтропийной оценки признаковой контрастности скалограммы для различных типов вейвлета (фиг. 8а) и значения интегрального показателя KΣ (фиг. 8б). Диаграммы показывают, что большему значению интегрального показателя соответствует большее значение энтропии, т.е. скалограмма обладает большей признаковой контрастностью.
Проведенные расчеты (фиг. 8) позволяют сделать заключение о следующих оценках контрастности признаков.
При выборе признаков по алгоритму, реализованному в прототипе, равновероятно используется любая из имеющегося набора вейвлет-функция - Wi, тогда имеем i признаков с различной контрастностью. Среднюю величину контрастности можно рассчитать по формуле:

где 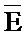
Ei - энтропия i-го признака, i=1, 2, …n;
Pi - вероятность выбора i-го признака.
Для варианта выбора признака, представленного на фиг. 8, средняя контрастность примет значение 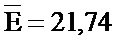
Предлагаемый способ распознавания радиосигналов позволяет за счет оптимального выбора вейвлет-функции однозначно обеспечить максимальную контрастность признака - 26,3. Таким образом, для рассматриваемого варианта распознавания радиосигналов контрастность признака возрастает в среднем на 18%. При выборе худшего по контрастности признака потери в контрастности признака для прототипа составят 58%.
При построении скалограмм на основе непрерывного вейлет-преобразования для решения задачи распознавания по алгоритму, реализованному в прототипе, оценка признаков в зависимости от выбранного вейвлета не производится, что приводит к выбору малоконтрастных признаков.
Предлагаемый способ распознавания за счет использования интегрального показателя для выбора оптимальной вейвлет-функции позволяет обоснованно выбрать наиболее контрастные признаки для исследуемого сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2004 |
|
RU2261476C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2011 |
|
RU2464633C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2010 |
|
RU2423735C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2007 |
|
RU2356064C2 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2010 |
|
RU2430417C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ЗОНДИРУЮЩИХ СИГНАЛОВ МАЛОЗАМЕТНЫХ РАДИОЛОКАЦИОННЫХ СТАНЦИЙ | 2017 |
|
RU2652791C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРИЗНАКОВ ТЕХНИЧЕСКОГО РАСПОЗНАВАНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 2008 |
|
RU2401435C2 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2010 |
|
RU2430416C1 |
| СПОСОБ ДЕТЕКТИРОВАНИЯ СИГНАЛОВ ЯДЕРНОГО КВАДРУПОЛЬНОГО И ЯДЕРНОГО МАГНИТНОГО РЕЗОНАНСА | 2011 |
|
RU2490618C2 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2011 |
|
RU2466455C1 |

Изобретение относится к распознаванию радиосигналов на основе анализа скалограммы сигнала и может быть использовано в технических средствах распознавания сигналов в реальных условиях приема при наличии шумов и помех. Технический результат – повышение контрастности признаков распознавания радиосигналов – вейвлет-спектрограмм (скалограмм) в условиях приема реального радиосигнала за счет выбора наиболее оптимального вейвлета. Способ распознавания радиоизлучений, заключающийся в том, что для формирования признаков распознавания радиосигналов по структурно-временному построению выбирается информационная часть сигнала. Выбранный участок сигнала оцифровывается и обрабатывается. Затем оценивается количество наиболее информативных коэффициентов аппроксимации для непрерывного вейвлет-преобразования, формируется вектор сигнала с учетом числа наиболее информативных коэффициентов. С использованием показателей энергетических характеристик сигнала и вейвлетов вычисляется интегральный показатель. По максимальному значению интегрального показателя выбирается вейвлет-функция, обеспечивающая максимальную контрастность признака радиосигнала - скалограммы. Строится скалограмма сигнала путем непрерывного вейвлет-преобразования, которую и принимают в качестве признака распознавания. 8 ил.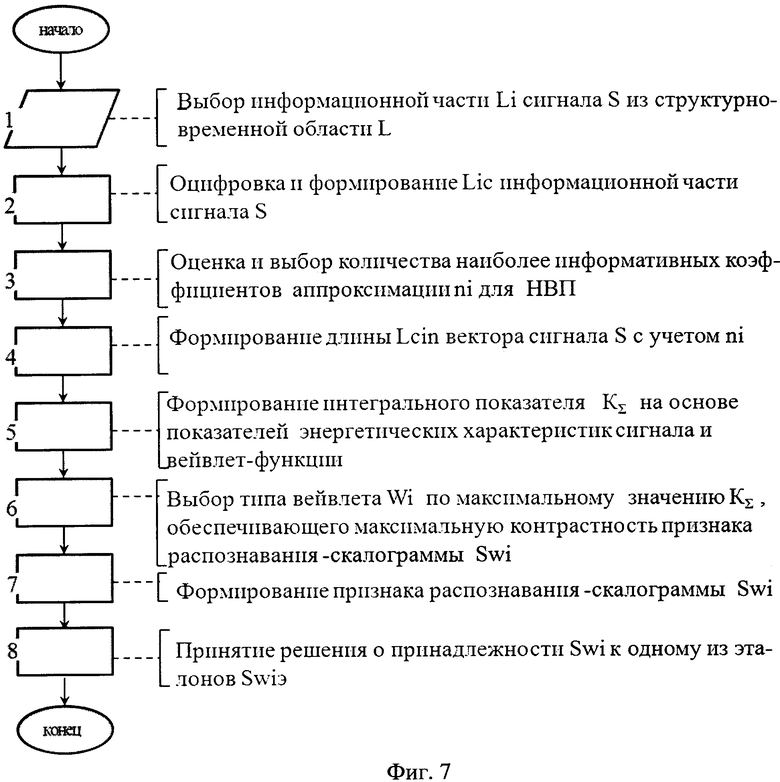
Способ распознавания радиосигналов, заключающийся в том, что для формирования признаков распознавания радиосигналов по структурно-временному построению выбирается информационная часть сигнала, которая заносится в систему компьютерной математики Matlab, где осуществляется оцифровка и обработка сигнала, оценивается количество наиболее информативных коэффициентов аппроксимации для прямого непрерывного вейвлет-преобразования (НВП), формируется вектор сигнала с учетом числа наиболее информативных коэффициентов, затем вычисляется интегральный показатель эффективности вейвлета путем наибольшего совпадения частотно-временных характеристик сигнала и применяемых для анализа сигнала вейвлетов, по максимальному значению интегрального показателя эффективности вейвлета для анализа исследуемого сигнала выбирается вейвлет-функция, с помощью которой путем непрерывного вейвлет-преобразования формируется скалограмма сигнала, которую принимают в качестве признака распознавания радиосигнала.
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2004 |
|
RU2261476C1 |
| СПОСОБ РАСПОЗНАВАНИЯ НЕПАРАМЕТРИЧЕСКОГО СИГНАЛА | 2010 |
|
RU2439679C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2010 |
|
RU2430416C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2011 |
|
RU2466455C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2011 |
|
RU2464633C1 |
| US 5909675 A1, 01.06.1999 | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
Авторы
Даты
2017-03-21—Публикация
2015-09-29—Подача