Изобретение относится к методам спектроскопии высокого разрешения и пространственно-временного анализа оптического излучения со сложной структурой и относительно быстрой эволюцией. Оно может быть использовано при проведении научных и прикладных исследований лазерных систем, в том числе распределенных лазерных систем передачи информации, а также частично когерентных и нестабильных лазерных источников, в особенности с длинными резонаторами и синхронизацией мод.
Спектроскопические методы применяются в различных областях науки и техники, среди прочих, включая лазерную физику, где такими методами осуществляются точные частотные измерения. Наряду с высоким спектральным разрешением, однако, изучаемые явления и процессы требуют также и хорошего разрешения по времени, в силу их динамического характера. Во многих подобных случаях требуемое временное разрешение может составлять от нескольких микросекунд до единиц наносекунд. Большая часть доступных в настоящее время приборов оптической спектроскопии высокого разрешения, однако, основана либо на механических принципах, либо на использовании матричных фотосенсоров, которые не позволяют характеризовать быструю спектральную динамику многих важных процессов, таких как передача информации по оптическим каналам или поведение волоконных лазерных систем.
Уровень техники:
Одним из относительно новых известных способов анализа быстроизменяющихся оптических сигналов является дисперсионное преобразование Фурье [самый близкий US Pat. 8,870,060 не относится к измерительной спектроскопии [1]], основанное на дисперсии групповой скорости оптических импульсов в среде, позволяющей отобразить спектральное распределение интенсивности сигнала во временное.
Этот метод с успехом применяется для анализа многих импульсных источников света, но поскольку он основан на временном растяжении сигнала, его применимость ограничена сигналами с относительно большой скважностью и небольшой длительностью импульса. Кроме этого, практическое спектральное разрешение этого метода не превышает 0,03 нм и он сам по себе не дает картины пространственно-временной эволюции исследуемого излучения.
Значительное расширение возможностей измерительного процесса может быть достигнуто заменой преобразования анализируемого сигнала в физических средах численными методами спектрального анализа, для чего требуется высокоскоростная оцифровка оптического сигнала. В практике спектроскопии хорошо известен принцип оптического гетеродинирования [см., например, Read 1965] [2], который позволяет прямо измерять интенсивность оптического сигнала в пределах полосы пропускания фотодетектора и аналого-цифрового преобразователя. Современные полупроводниковые приборы и цифровые осциллографы позволяют исследовать сигналы с полосой, превышающей 100 ГГц.
В практике обработки сигналов известно использование различных модификаций спектрально-временных методов коэновского класса (например, см. Cohen1966, Cohen2013) [3], [4], используемых для построения двумерных распределений (в идеале, плотности мощности сигнала) в координатах время-частота.
Самым простым, но и наиболее ограниченным в отношении нестационарных сигналов, является т.н. спектрограмма, основанная на оконном преобразовании Фурье. Общий вид распределения коэновского класса для аналитического сигнала ϕ(t)=s(t)+iH{s(t)}, полученного из экспериментального (действительного) сигнала s(t) при помощи преобразования Гильберта, можно записать как:
 ,
,
где Ф(θ,τ) - ядро преобразования, вид которого определяет свойства распределения и которое эквивалентно двумерному фильтрованию в пространстве функции неопределенности исследуемого сигнала.
Для того чтобы полученное распределение имело четкий физический смысл, на ядро обычно налагают ограничения, обеспечивающие неотрицательные значения результата преобразования и соответствие его предельных интегралов по частоте и времени плотности энергии по второй координате.
К настоящему моменту разработаны различные методы оптимизации ядра в зависимости от вида сигнала как итеративные (см. Baraniuk1995) [5], так и прямые (Deprem2015) [6], позволяющие значительно улучшить временное и частотное разрешение спектрального анализа.
Известны различные модификации этого подхода, описанные, например, в патентах США 6,522,996 В1 [7] и 7,035,744[8] В2 или заявке РФ 94017061/09 [9].
Вышеописанные подходы и методы до сих пор не были использованы вместе в составе спектрометрической системы для изучения переходных и быстропротекающих процессов в источниках когерентного и частично-когерентного излучения.
Подобные системы были бы в состоянии выделять отдельные узкополосные или одночастотные составляющие многокомпонентных оптических сигналов и исследовать их быструю эволюцию. Однако они (и реализованные к настоящему времени эксперименты в этом направлении, см. Churkin2016) [10] не позволяют уверенно идентифицировать устойчивые структуры излучения сложных и особенно частично-когерентных систем, в которых несколько таких структур может сосуществовать одновременно и двигаться относительно друг друга с разными групповыми скоростями а также делать это в присутствии шума.
Кроме того, в большинстве известных подходов применяется лишь несколько частных форм преобразования Коэна-Ли, представляющих собой сглаженное преобразование Вигнера = Вилля. В качестве распространенного примера таких форм можно упомянуть т.н. распространение с подавлением интерференции (reduced interference distribution. RID). По самому их смыслу такие методы добиваются уменьшения интерференционных эффектов за счет снижения разрешения.
Раскрытие изобретения
Задача, решаемая изобретением, - создание способа высокоразрешающей спектрально-временной спектроскопии, позволяющего идентифицировать устойчивые структуры излучения сложных и особенно частично-когерентных систем, в которых несколько таких структур может сосуществовать одновременно, но отличаться различной эволюцией их спектра, а также делать это в присутствии шума с возможностью введения обратной связи на исследуемую систему для коррекции ее параметров.
Техническим результатом также является возможность характеризовать лазерные системы со сложным относительно широкополосным излучением на коротких временных интервалах (с шагом в один обход резонатора), с большой точностью по времени и частоте следить за быстропротекающими процессами в оптических системах и управлять ими (например, контролировать лазер с самосканированием длины волны генерации); выявлять в излучении повторяющиеся (когерентные) структуры, которые невозможно обнаружить с помощью известных стандартных методов, и наблюдать их развитие во времени, измерять спектральный состав излучения со спектральным разрешением, значительно превышающим предел общеизвестных спектральных методов, и использовать эти данные в цепи обратной связи для достижения, например, генерации на нескольких частотах сразу.
Поставленная задача решена созданием способа измерения спектрально-временной эволюции излучения, опирающегося на оптическое гетеродинирование для регистрации в реальном времени быстрых процессов в излучении и на частотно-спектральный анализ при помощи коэновских распределений с подбором оптимального ядра преобразования, и дальнейшим использованием выбранной функции ядра для вычисления и представления двумерного частотно-временного распределения.
Для этого:
Из входного излучения получают сигнал оптического гетеродина, смешивая его на фотодетекторе с излучением локального осциллятора с частотой, подобранной так, чтобы весь спектр входного излучения попадал в полосу фотодетектора и последующих компонент. Если спектр входного излучения превышает доступную полосу, выбирают наиболее интересующую его часть.
Запускают непрерывную запись измерений интенсивности сигнала (например, при помощи широкополосного цифрового запоминающего осциллографа).
Регистрируемый сигнал интенсивности s(t) подвергается преобразованию Гильберта для вычисления его аналитического дополнения 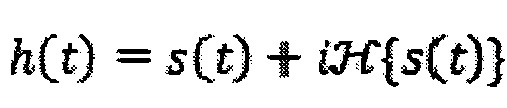 , и в дальнейшей обработке используют полученный аналитический сигнал.
, и в дальнейшей обработке используют полученный аналитический сигнал.
Вычисляют для некоторого начального фрагмента записи зарегистрированного сигнала автокорреляционную функцию 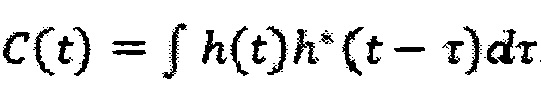 , пользуясь методом быстрого преобразования Фурье
, пользуясь методом быстрого преобразования Фурье  , так как по теореме о свертке (например, см. Katznelson1976 [11] и программную реализацию в Kapinchev2015 [12])
, так как по теореме о свертке (например, см. Katznelson1976 [11] и программную реализацию в Kapinchev2015 [12]) 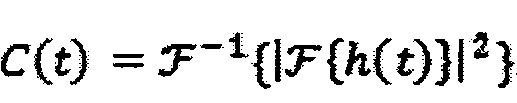 .
.
Для улучшения точности определения, т.е. увеличения контраста и подавления шума применяют частотное фильтрование сигнала, тривиально реализуемое в Фурье-представлении.
По основному периоду полученной автокорреляционной функции вычисляют периодичность основной структуры излучения (т.н. длительности «быстрого времени»).
Поскольку непрерывная регистрация широкополосных сигналов технически возможна лишь в течение небольших промежутков времени, то при необходимости постоянного контроля дальнейшая регистрация может быть синхронизована с основным периодом структуры излучения и осуществляться кусочно по мере обработки записанных данных. Это приводит к пропуску (может быть, большей) части данных об исследуемом сигнале, но позволяет вести непрерывное наблюдение и контроль.
При работе с системами без явно выраженной периодичности может быть необходимо выставлять длительности «быстрого времени» вручную, исходя из конфигурации исследуемой системы (например, длины волоконной линии) и интересующей спектральной полосы сигнала.
Записываемый сигнал разбивают на последовательные интервалы с длиной, равной «быстрому времени», так, чтобы целевая структура располагалась на одном и том же значении «быстрого времени».
Дальнейшая регистрация может быть синхронизована с основным периодом структуры излучения и осуществляться кусочно по мере обработки записанных данных (поскольку скорость обработки, вывода и реакции систем обратной связи обычно значительно ниже скорости записи).
После определения размера окна «быстрого времени» производят выбор оптимального ядра преобразования коэновского класса для исследуемого сигнала. Это может быть сделано выбором из библиотеки заранее рассчитанных функций для ожидаемых видов сигнала либо при помощи одного из неитеративных методов вычисления такого ядра без априорного знания входного сигнала.
Выбранную функцию ядра далее используют для вычисления двумерного спектрально-временного распределения сигнала, проводя его сверстку с выбранным или вычисленным ядром последовательно в каждом промежутке «быстрого времени» в выбранной системе координат.
Это вычисление производится в кусочно-непрерывном режиме, если необходим визуальный вывод в режиме реального времени или автоматическая подстройка параметров оптической системы.
Из полученного набора спектральных распределений, соответствующих последовательным периодам «быстрого времени», составляют двумерную спектрально-временную диаграмму.
Следует заметить, что конкретный вид ядра частотно-временного распределения может одновременно выполнять задачу выделения заранее заданных структур в излучении и подавления всех остальных, что является важной задачей в случае необходимости автоматической подстройки параметров измеряемой системы для получения и стабилизации определенных параметров сигнала (например, вида синхронизации мод излучения).
При использовании предлагаемого метода для контроля или стабилизации параметров измеряемой оптической системы по изменению положения спектральных пиков полученного спектрально-временного распределения формируют сигнал ошибки, который в дальнейшем управляет параметрами оптической системы. Например, по ширине спектрального пика или наличию в спектре высокочастотных составляющих можно судить о качестве синхронизации мод в лазере. Следует заметить, что хотя существуют и альтернативные методы управления оптическими системами, они не обладают достаточным быстродействием для контроля за быстропротекающими процессами (например, самосканирование выходной частоты лазера или эволюция систем с задержанной обратной связью). На Фиг. 1 приведена блок-схема, иллюстрирующая последовательность этапов обработки исследуемого сигнала.
Пример осуществления способа
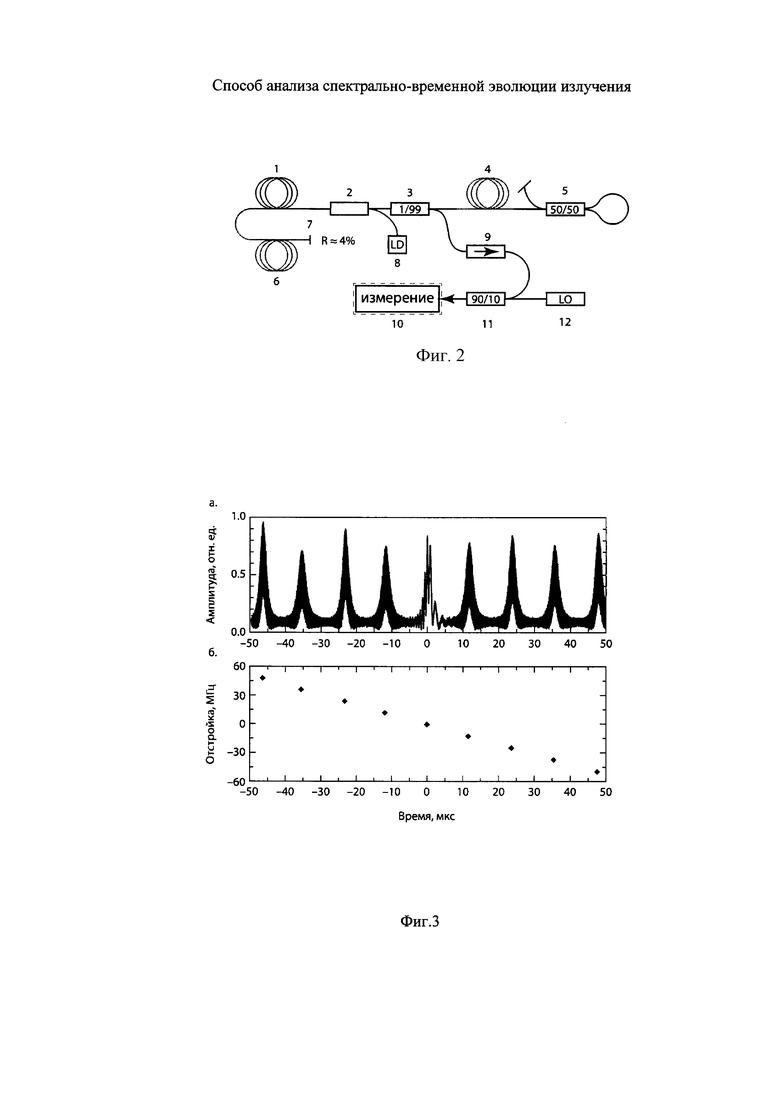
В качестве источника оптического сигнала был использован линейный волоконный лазер с периодическим самосканированием частоты генерации в пределах широкого диапазона, которое обусловлено динамической модуляцией усиления и фазы, в свою очередь происходящей в результате пространственно-неоднородного насыщения усиления в активной среде (см. Фиг. 2),
где
1. Активное волокно
2. Волоконный объединитель пучка накачки
3. Волоконный делитель пучка (1/99%)
4. Пассивное волокно 1
5. Волоконное петлевое зеркало
6. Пассивное волокно 2
7. Волоконный отражатель с коэффициентом отражения 4%
8. Лазерный диод накачки
9. Оптический диод
10. Измерительная схема
11. Волоконный объединитель пучка (10/90%)
12 Локальный осциллятор (одночастотный лазер)
Эта волоконная лазерная система была выбрана для эксперимента, поскольку, с одной стороны, она демонстрирует нетривиальную и довольно быструю динамику излучения, а с другой стороны, стабильное периодическое повторение частотной эволюции и довольно узкая ширина выходной линии позволяют наглядно проиллюстрировать возможности предлагаемого метода, который применим и к более сложным сигналам, в которых могут присутствовать несколько компонент с разными частотами или более широкие линии генерации.
В качестве примера исследован фрагмент выходного сигнала такой системы в конфигурации, обеспечивающей стабильную генерацию импульсов с частотой, самосканируемой в широком диапазоне (до 20 нм). На Фиг. 3а изображен сигнал оптического гетеродина, а на Фиг. 3б - вычисленная разность частот локального осциллятора и исследуемого сигнала.
Для практических применений (например, для высокоточной спектроскопии или сканирующей оптической томографии) представляет интерес поведение излучения на масштабе времени одного импульса.
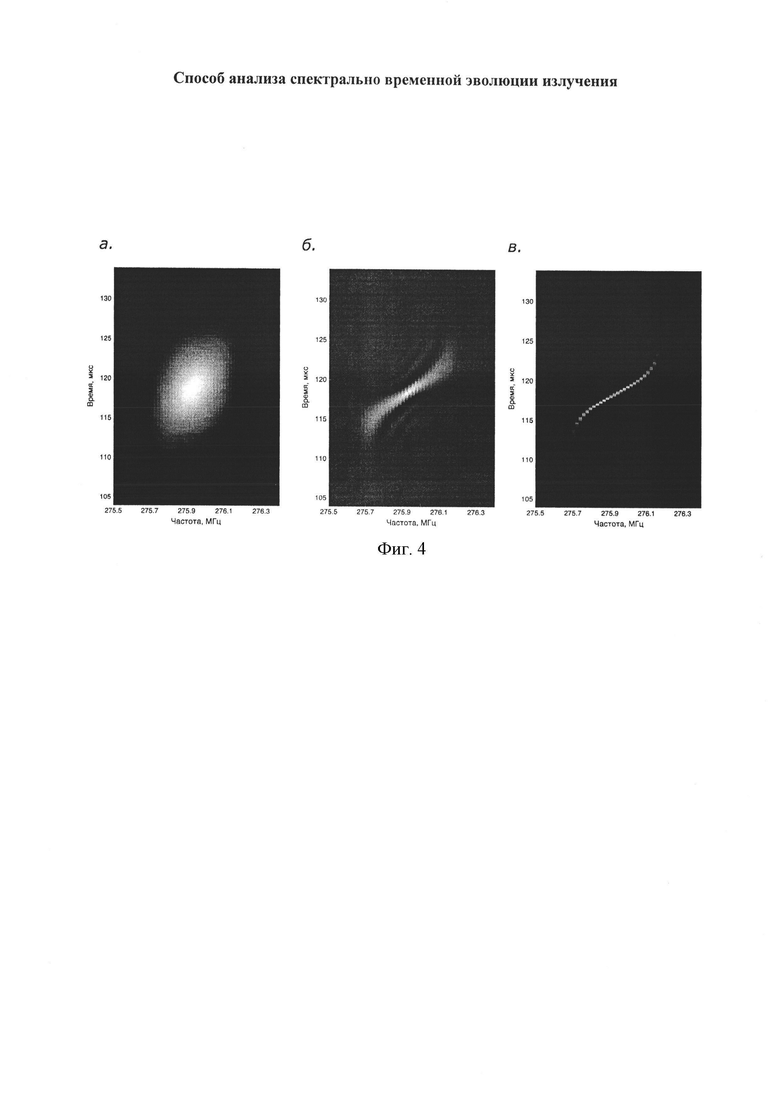
На фиг 4а, б, в представлены результаты анализа оптического сигнала известными методами и предлагаемым.
а. Анализ оптического сигнала экспериментального лазера при помощи спектрограммы.
б. Анализ того же сигнала при помощи распределения Вигнера-Билля.
в. Анализ того же сигнала при помощи предлагаемого метода.
Исследование при помощи большинства традиционных методов не позволяет получить достаточно точную информацию одновременно во временном и спектральном представлении. Например, известная техника оконного преобразования Фурье вносит существенную неопределенность, обусловленную размером окна (см. Фиг. 4а). Разрешение можно существенно улучшить в пределах, определенных фундаментальной неопределенностью частотная полоса - длительность, применяя такие методы, как преобразование Вигнера-Билля и ему подобные (Рис. 4б), но в этом случае или наблюдаются нежелательные интерференционные эффекты от перекрестных членов в соответствующих преобразованиях, или разрешение ухудшается в зависимости от интенсивности сглаживания, которое применяется для их подавления.
В результате применения предлагаемого метода удается избежать как ухудшения разрешения, так и нефизических в данном случае интерференционных составляющих (Фиг. 4в).
Сигнал исследуемого лазера состоит из одночастотных импульсов. На чертежах видно, что предлагаемый метод (в отличие от традиционных) позволяет с большой точностью определить этот факт и количественно измерить эволюцию исследуемого излучения на протяжении индивидуального импульса.
Развитие во времени четко выделенного сигнала позволяет несложными математическими методами (выделение пика) формировать сигнал ошибки, который может быть либо использован для коррекции результатов эксперимента, проводимого при участии такого излучения, либо для контроля параметров резонатора в цепи обратной связи.
Использованные источники информации
1. Патент US 8,870,060.
2. Read1965 W.S. Read and R.G. Turner, «Tracking Heterodyne Detection)), Appl. Opt. 4, 1570 (1965).
3. Cohen1966 L. Cohen, «Generalized Phase-Space Distribution Functions,)) J. Math. Phys., 7 (5), 781-786 (1966).
4. Cohen2013 L. Cohen, «Generalized Phase-Space Distributions)), in book «The Weyl Operator and its Generalization)), Springer Basel 2013, ch. 5, pp. 61-67, doi: 10.1007/978-3-0348-0294-9_5.
5. Baraniuk1995 Douglas L. Jones and Richard G. Baraniuk, "An adaptive optimal-kernel time-frequency representation," IEEE Trans. Signal Process., vol. 43, no. 10, pp. 2361-2371, 1995.
6. Deprem2015 Zeynel Deprem and A. Enis Cetin, "Kernel estimation for time-frequency distributions using epigraph set of L1-norm," In Proc. 23rd European Signal Processing Conference (EUSIPCO 2015), Nice, France 2015.
7. Патент US 6,522,996 В1.
8. Патент US 7,035,744 B2.
9. 3аявка РФ 94017061/09.
10. Churkin2016 S. Sugavanam, S. Fabbri, S. Tai Le, I. Lobach, S. Kablukov, S. Khorev, & D. Churkin, "Real-time high-resolution heterodyne-based measurements of spectral dynamics in fibre lasers," Scientific Reports 6: 23152 (2016), doi: 10. 1038/srep23152.
11. Katznelson1976 Katznelson, Yitzhak (1976), An introduction to Harmonic Analysis, Dover, ISBN 0-486-63331-4.
12. Kapinchev 2015 К.I. Kapinchev, Adrian Bradu, Frederick Barnes, Adrian Podoleanu, "GPU Implementation of Cross-Correlation for Image Generation in Real Time," in Proc. of 9th International Conference on Signal Processing and Communication Systems, 2015, doi: 10.1109/ICSPCS.2015.7391783.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения пространственно-временной эволюции излучения | 2016 |
|
RU2649643C1 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ НАНОВИБРАЦИЙ ПОВЕРХНОСТИ | 2011 |
|
RU2461803C1 |
| СПОСОБ ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЙ ВНУТРЕННЕЙ СТРУКТУРЫ ОБЪЕКТОВ | 2000 |
|
RU2184347C2 |
| Способ и устройство для Фурье-анализа жидких светопропускающих сред | 2021 |
|
RU2770415C1 |
| СПОСОБ ДИСТАНЦИОННОГО БЕСПРОБООТБОРНОГО ОБНАРУЖЕНИЯ И ИДЕНТИФИКАЦИИ ХИМИЧЕСКИХ ВЕЩЕСТВ И ОБЪЕКТОВ ОРГАНИЧЕСКОГО ПРОИСХОЖДЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2567119C1 |
| ИЗМЕРИТЕЛЬ ФАЗОВЫХ ШУМОВ УЗКОПОЛОСНЫХ ЛАЗЕРОВ, ОСНОВАННЫЙ НА СОСТОЯЩЕМ ИЗ РМ-ВОЛОКНА ИНТЕРФЕРОМЕТРЕ МАХА-ЦЕНДЕРА | 2017 |
|
RU2664692C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА РАДИОСИГНАЛОВ | 2014 |
|
RU2566431C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ ГАЗА | 2000 |
|
RU2170922C1 |
| Способ ангиографии в эндоскопической оптической когерентной томографии | 2018 |
|
RU2692225C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДОВОЙ ДИСПЕРСИИ ОПТИЧЕСКИХ ВОЛНОВЕДУЩИХ СИСТЕМ | 2006 |
|
RU2308012C1 |

Способ анализа спектрально-временной эволюции излучения включает в себя получение сигнала оптического гетеродина, измерение интенсивности сигнала, получение аналитической формы сигнала при помощи гильбертова дополнения. Далее вычисляют автокорреляционную функцию методом быстрого преобразования Фурье, определяют периодичность основной структуры во входном излучении, регистрируют входной сигнала, синхронизируя с периодом основной структуры излучения. Производят выбор оптимального ядра преобразования коэновского класса для исследуемого сигнала и составляют двумерную спектрально-временную диаграмму. Способ основан на применении оптического гетеродинирования для смещения анализируемого излучения в радиочастотную область. Технический результат заявленного решения - повышение временного разрешения сигнала при исследовании лазерных систем. 4 ил.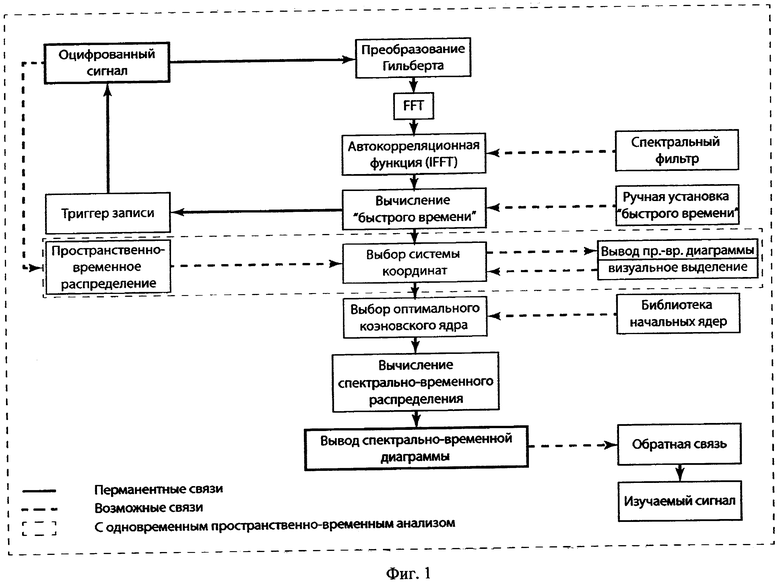
Способ анализа спектрально-временной эволюции излучения, состоящий в том, что из входного излучения получают сигнал оптического гетеродина, смешивая его на фотодетекторе с излучением локального осциллятора, имеющего частоту, подобранную так, чтобы весь спектр входного излучения или, по крайней мере, интересующая часть этого спектра попадал в полосу фотодетектора и последующих компонент, запускают непрерывную запись измерений интенсивности сигнала, получают аналитическую форму записываемого сигнала при помощи гильбертова дополнения, в дальнейшей обработке используют аналитический сигнал, вычисляют для некоторого начального фрагмента записи зарегистрированного сигнала его автокорреляционную функцию, пользуясь методом быстрого преобразования Фурье, по основному периоду полученной автокорреляционной функции вычисляют периодичность основной структуры во входном излучении, т.н. длительность «быстрого времени», или устанавливают величину «быстрого времени» вручную, исходя из конфигурации исследуемой системы и интересующей спектральной полосы сигнала, записываемый сигнал разбивают на последовательные интервалы с длиной, равной "быстрому времени", так чтобы целевая структура располагалась в них на одном и том же значении "быстрого времени", дальнейшую регистрацию входного сигнала синхронизируют с периодом основной структуры излучения, производят выбор оптимального ядра преобразования коэновского класса для исследуемого сигнала, используя либо предварительно рассчитанную библиотеку оптимальных видов коэновского ядра для ожидаемого типа сигнала, либо один из неитеративных методов вычисления такого ядра без априорного знания входного сигнала, и, по мере поступления данных, вычисляют двумерное спектрально-временное распределение сигнала, проводя его свертку с выбранным или вычисленным ядром, последовательно в каждом промежутке «быстрого времени» в выбранной системе координат и из полученного набора спектральных распределений, соответствующих последовательным периодам «быстрого времени», составляют двумерную спектрально-временную диаграмму.
| US 20120093519 A1 19.04.2012 | |||
| US 5684586 A1 04.11.1997 | |||
| US 7301633 B2 27.11.2007 | |||
| Прерыватель электрического тока | 1929 |
|
SU20208A1 |
Авторы
Даты
2018-03-12—Публикация
2016-12-12—Подача