ОБЛАСТЬ ТЕХНИКИ
По меньшей мере в одном аспекте реализации настоящего изобретения по меньшей мере один вариант осуществления изобретения относится к способам выполнения нефтепромышленных операций. В частности, по меньшей мере один вариант осуществления настоящего изобретения относится к способам выполнения стимулирующих операций, таких как перфорация, закачка и/или выполнение гидроразрыва пласта подземной формации, содержащего по меньшей мере один коллектор.
В целях облегчения извлечения углеводородов из нефтяных и газовых скважин, подземные пласты месторождений, окружающие такие скважины, могут стимулироваться с помощью гидравлического разрыва пласта. Гидравлический разрыв пласта может быть использован для создания трещин в подземных пластах месторождений для того, чтобы позволить нефти или газу продвинуться в направлении скважины. Пласт подвергается разрыву путем введения специально подготовленной жидкости (называемой в данном документе "жидкость для гидроразрыва пласта", "жидкость для обработки" или "буровой раствор для гидроразрыва") при высоком давлении и высокой скорости потока в пласт через одну или нескольких скважин.
Гидравлические разрывы пласта могут расходиться от ствола скважины на сотни футов в противоположных направлениях в соответствии с естественным давлением в пласте. При определенных обстоятельствах, они могут образовывать сложную сеть разрывов. Сложные сети разрывов могут включать искусственно образованные и естественные разрывы, которые могут пересекаться или не пересекаться вдоль множественных азимутов, во множественных плоскостях и направлениях, а также во множественных районах.
Структура трещин гидравлических разрывов, созданных при помощи стимуляции разрыва, может быть сложной и образовывать сеть трещин, обозначенную распределением связанных микросейсмических событий. Сложные сети гидравлических разрывов были разработаны для представления созданных гидроразрывов. Примеры моделей и симуляторов разрывов предоставлены в Патенте США/Заявке № 6101447, 7363162, 7788074, 8412500, 20120179444, 20080133186, 20100138196, 20100250215, 6776235, 8584755 и 8066068, содержание которых полностью включено в настоящую заявку посредством ссылки.
Жидкости для гидроразрыва пласта могут закачиваться в ствол скважины таким образом, чтобы обеспечить возникновение требуемых разрывов. Жидкости для гидроразрыва пласта могут включать в себя проппанты для поддержания разрывов в открытом состоянии и облегчения попадания потока жидкости в ствол скважины. Примеры методов образования разрывов и/или использования проппантов представлены в патенте США/Заявке № 6776235, 8066068, 8490700, 8584755, 7581590 и 7451812, содержание которых полностью включено в настоящую заявку посредством ссылки.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
По меньшей мере в одном аспекте реализации настоящее изобретение относится к способу выполнения стимулирующих операций на буровой площадке. Буровая площадка имеет ствол скважины, проникающий в пласт, содержащий в себе разрывы. Способ содержит прогнозирование размещения проппанта в разрывах на основе скважинных данных (включая геометрию разрывов), создание модели неровностей на основе прогнозированного размещения, прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей, определение проводимости разрывов на основе спрогнозированного аппертурного изменения и размещение проппанта в разрывах вместе с жидкостью для воздействия на пласт путем закачивания жидкости для воздействия на пласт, содержащей в себе проппант, в пласт месторождения на основании определенной проводимости разрывов.
В другом аспекте реализации изобретения раскрытие сущности изобретения относится к выполнению стимулирующих операций на буровой площадке. Буровая площадка имеет ствол скважины, проникающий в пласт, содержащий в себе разрывы. Способ содержит определение проппантных параметров разрывов путем прогнозирования размещения проппанта в разрывах на основе скважинных данных с использованием множественных симуляций (скважинных данных, содержащих геометрию разрывов), создание модели неровностей на основе прогнозированного размещения, прогнозирование аппертурного изменения для заданного напряжения смыкания с использованием модели неровностей, определение проводимости разрывов на основе прогнозированного апертурного изменения, обоснование прогнозированного размещения путем сравнения множества симуляций, а также помещение проппанта в разрывы вместе жидкостью для воздействия на пласт путем закачивания такой жидкости для воздействия на пласт, содержащей проппант, в пласт месторождения на основании обоснованной проводимости разрывов.
В заключение, в другом аспекте реализации изобретения раскрытие сущности изобретения относится к способу стимулирования ствола скважины на буровой площадке. Буровая площадка имеет ствол скважины, проникающий в пласт, содержащий в себе разрывы. Способ содержит определение проппантных параметров разрывов путем прогнозирования размещения проппанта в разрывах на основе скважинных данных, при чем скважинные данные содержат геометрию разрывов, создание модели неровностей на основе прогнозированного размещения, прогнозирование аппертурного изменения для заданного напряжения смыкания с использованием модели неровностей, определение проводимости разрывов на основе прогнозированного апертурного изменения, а также размещение проппанта в разрывах вместе с жидкостью для воздействия на пласт путем закачивания жидкости для воздействия на пласт, содержащей в себе проппант, в пласт месторождения на основании обоснованной проводимости разрывов, а также извлечение жидкости из коллекторов, помещение ее в ствол скважины через удерживаемые от смыкания разрывы.
Это описание сущности изобретения предоставлено для введения разнообразных концепций, которые более детально описываются далее по тексту. Это описание сущности изобретения не предназначено для обозначения ключевых или существенных признаков заявленного изобретения, а также не предназначено для использования в качестве помощи в процессе ограничения объема заявленного предмета изобретения.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Варианты реализации способа для осуществления стимулирующих операций, включающих введение проппанта, описываются со ссылкой на следующие фигуры. Те же цифровые обозначения используются во всех фигурах для осуществления ссылок на схожие функции и компоненты. Способы реализации различных технологий далее будут описываться со ссылкой на прилагаемые чертежи. Следует иметь в виду, однако, что прилагаемые чертежи иллюстрируют только различные способы реализации, описанные в данном документе, и не предназначены для ограничения объема различных технологий, описанных в данном документе.
Фиг. 1.1-1.4 представляют собой схематические изображения буровой площадки, отображающие стимулирующие операции, включающие введение проппанта в пласт месторождения;
Фиг. 2 представляет собой блок-схему, отображающую способ выполнения стимулирующей операции;
Фиг. 3, 4, 5.1, 5.2 и 6 представляют собой блок-схемы, отображающие более детально различные аспекты способа выполнения разрывов;
Фиг. 7.1 и 7.2 представляют собой схематические диаграммы, отображающие модель неровностей расклиненного и нерасклиненного разрыва соответственно;
Фиг. 8.1-8.3 представляют собой схематические диаграммы, отображающие введение проппанта в разрыв;
Фиг. 9.1-9.4 представляют собой графики, отображающие спрогнозированный расклиненный разрыв с цилиндрическими колоннами гетерогенного проппанта при различных уровнях распределения и давления;
Фиг. 10.1-10.4 представляют собой графики, отображающие спрогнозированный расклиненный разрыв с нерасклиненными неровными разрывами при различных уровнях распределения и давления;
Фиг. 11.1-11.4 представляют собой графики, отображающие спрогнозированный расклиненный разрыв с непостоянным гетерогенным распределением проппанта в разрывах с различными уровнями давления;
Фиг. 12.1 и 12.2 представляют собой графики, отображающие напряжение смыкания и постепенное изменение проводимости разрывов соответственно для ряда проппантно-разрывных геометрий;
Фиг. 13 представляет собой схематическую диаграмму действия сил на прямоугольнике;
Фиг. 14 представляет собой схематическую диаграмму, отображающую поток через сужающийся разрыв.
Фиг. 15.1-15.3 представляют собой графики, сравнивающие 1-D и 2-D стимуляции.
Фиг. 16 представляет собой схематическую диаграмму, отображающую поток между параллельными пластинами через один из разрывов;
Фиг. 17 представляет собой схематическую диаграмму, отображающую 2-D расчетную область симметрической половины полного разрыва на Фиг. 16;
Фиг. 18.1-18.3 представляют собой графики, отображающие поток через определенный разрыв на Фиг. 16 с различными жидкостями;
Фиг. 19.1-19.3 представляют собой графики, сравнивающие 1-D и 2-D решения на различных углах для различных жидкостей;
Фиг. 20 представляет собой блок-схему, отображающую другой способ формирования проппантных параметров;
Фиг. 21 и 22 представляют собой схематическую диаграмму, отображающую цилиндрические проекции при разных моделях;
Фиг. 23 представляет собой Декартову сетку с указанным на ней давлением;
Фиг. 24.1 и 24.2 представляют собой различные схематические изображения одного из разрывов;
Фиг. 25.1 и 25.2 представляют собой пунктирные и линейные диаграммы, отображающие первое сравнение симуляторов;
Фиг. 26.1 и 26.2 представляют собой пунктирные и линейные диаграммы, отображающие второе сравнение симуляторов;
Фиг. 27.1 и 27.2 представляют собой графики, демонстрирующие апертуру, отображающую третье сравнение симуляторов;
Фиг. 28 представляет собой график, отображающий сравнение различных симуляторов;
Фиг. 29.1-29.3 представляют собой графики, отображающие сравнение симуляций при различных уровнях разрешения; и
Фиг. 30.1-30.3 представляют собой схематические диаграммы, отображающие введение гетерогенного проппанта для различных колонн.
ДЕТАЛЬНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
Последующее описание содержит аппараты, методы, приемы и последовательности команд, воплощающие способы предмета изобретения. Однако следует понимать, что описанные варианты осуществления изобретения могут применяться на практике без учета этих конкретных деталей.
По меньшей мере в одном аспекте настоящее раскрытие сущности изобретения описывает способ выполнения стимулирующих операций на буровой площадке. Стимулирование включает в себя формирование проппантных параметров путем прогнозирования введения проппанта в разрывы, формирование модели неровностей (в дальнейшем также именуемая модель на основе неровностей) на основе прогнозирования, прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей, а также определение проводимости разрывов на основе напряжения смыкания. Проппант может затем размещаться в разрывах путем закачивания жидкости для воздействия на пласт, содержащей проппант, в пласт месторождения на основе определенной проводимости разрывов. Пластовые жидкости могут затем извлекаться из расклиненного разрыва.
Может также рассматриваться независимо заданное изолированное, гетерогенное распределение проппанта. Прогнозирование может дополнительно обосновываться путем сравнения с другими прогнозами и/или измерениями. Введение проппанта и результативная проводимость в пределах шероховатого разрыва могут быть спрогнозированы при любом заданном напряжении смыкания. Шероховатый разрыв может быть представлен скоплением неровностей, которые могут распределяться на обычной решетке, присоединенной к двум деформируемым полупространствам.
Описываются по меньшей мере два подхода осуществления деформации. Первый подход предусматривает предварительное вычисление деформационных характеристик деформируемых полупространств, принимая в расчет эффективный прогноз деформации на обеих сторонах разрыва. Настоящее раскрытие сущности изобретения описывает способ автоматического обнаружения дополнительного контакта, в то время как разрыв закрывается в процессе увеличения напряжения смыкания (например, как в процессе обратного потока и извлечения). В дополнение, механический отклик неровностей может быть изменен с целью учета совокупного механического отклика поверхности шероховатого разрыва и проппанта, который может находиться в разрыве на таком определенном участке. Таким образом, может учитываться деформация любого сочетания шероховатости разрыва и гетерогенного размещения в разрыве.
Другой подход приближенно выражает детальные неровности с более грубым набором цилиндров для механического подсчета. В случае обеих механических моделей деформированное состояние затем преобразовывается в сеточную модель пористости, с помощью которой вычисляют проводимость разрыва во время обратного потока и извлечения. Этот альтернативный метод может быть более быстрым, чем первый метод и может обладать меньшей точностью. В некоторых случаях подходы можно сравнивать с целью обоснования и/или обнаружения проблем, таких как впрыскивание воды и взаимодействие множества жидкостей.
Способы прогнозирования введения проппанта могут предусматривать расчет взаимодействия между шероховатостью разрыва, обобщенной гетерогенной проппантной геометрией и проппантным соответствием. Такое введение может предназначаться для более эффективного стимулирования детальных, независимых проппантных размещений, включая естественную шероховатость естественных разрывов в деталях и фиксацию нелинейных жесткостных характеристик разрыва при его закрытии.
При введении могут использоваться ускоренные решения путем осуществления предварительного расчета механического отклика пласта месторождения на сетку для осуществления анализа. Такое введение может учитывать следующие механизмы: произвольное распределение проппанта в пределах разрыва; механическая деформация как проппанта, так и вмещающей породы; шероховатость поверхности разрыва в деталях; ответная реакция перераспределения давления во время осуществления дополнительного контакта между поверхностями разрыва; а также поток между деформированными поверхностями разрыва и в пределах гетерогенно расположенного проппанта в пределах промежутка между поверхностями.
Введение проппанта может быть использовано для равномерного заполнения разрыва проппантом с целью поддержания адекватного размера толщины трещины. Путем равномерного заполнения разрывов пластовые жидкости могут затем быть удалены обратно через проппант. Стратегии Введения Гетерогенного Проппанта (ВГП) нацелены на увеличение проводимости расклиненного разрыва путем выборочного помещения проппанта таким способом, чтобы такой разрыв оставался открытым в разрозненных местах, а пластовые жидкости могли быть перенесены через открытые каналы между проппантами. Примером ВГП технологии является HiWAY™, доступная для приобретения у компании SCHLUMBERGER™, Ltd., Houston, TX (см.: www.slb.com). Дополнительные описания проппантной технологии предоставляются, например, в US6776235, US8066068 и US8584755, которые были предварительно включены в настоящую заявку во всей полноте посредством ссылки.
ВГП может быть использовано с целью введения проппантов в разрывы в виде отдельных пробок. Смешивание проппантных пробок с чистыми может ограничиваться присутствием волокон. Указанные пробки могут быть перемещены вниз по стволу скважины и в разрывы с целью создания изолированных колонн, удерживающих разрыв под воздействием напряжения смыкания, и сохранения неприкосновенности гидроканалов в промежуточном пространстве.
В целях развития технологий и оптимизации могут разрабатываться инструменты прогнозирования проводимости гетерогенных расклиненных разрывов в процессе увеличения напряжения смыкания, возникающего в результате воздействия обратного потока и последующего извлечения. По меньшей мере в одном аспекте настоящего раскрытия сущности изобретения предоставляются средства прогнозирования введения проппанта и расчета результирующих проводимостей для произвольного распределения проппанта в пределах, например, фактических разрывов с неровными стенками.
I. ВПРЫСКИВАНИЕ И ВВЕДЕНИЕ ПРОППАНТА
Аспекты настоящего раскрытия сущности изобретения могут реализовываться на буровой площадке 100 такой, как площадка, изображенная на Фиг. 1.1. Буровая площадка 100 имеет ствол скважины 104, простирающийся из устья 108 на поверхности и через подземный пласт месторождения 102, указанный ниже. Система разрывов 106 простирается по стволу скважины 104. Насосная система 129 устанавливается в устье 108 для прокачивания жидкости через колонну труб 142.
Насосная система 129 изображена с возможностью управления наземным оператором 127 с целью фиксации эксплуатационных и операционных данных и/или выполнения операций в соответствии с установленным графиком закачки. Насосная система 129 закачивает жидкости с поверхности в ствол скважины 104 в процессе операций по образованию разрывов.
Насосная система 129 может содержать источник воды, представленный множеством резервуаров для воды 131, который подает воду в гель-гидратационную установку 133. Гель-гидратационная установка 133 комбинирует воду из резервуаров 131 с гелеобразующим веществом с целью получения геля. Гель затем помещается в смеситель 135, где он перемешивается с проппантом, извлекаемым из перевозчика проппанта 137, с целью получения жидкости для гидроразрыва пласта. Гелеобразующее вещество может быть использовано для увеличения вязкости жидкости для гидроразрыва пласта, а также для организации возможности растворения проппанта в жидкости для гидроразрыва пласта. Оно может также выступать в качестве понижающего трение агента с целью достижения более высокой интенсивности закачки с меньшим давлением трения.
Жидкость для гидроразрыва пласта затем закачивается из смесителя 135 в подготовочные грузовики 120 с плунжерными насосами, как указано сплошными линиями 143. Каждый подготовочный грузовик 120 принимает жидкость для гидроразрыва пласта под низким давлением и спускает ее в общий коллектор 139 (иногда называемый прицепом для транспортировки ракет или ракетой) под высоким давлением, как показано пунктирными линиями 141. Ракета 139 затем направляет жидкость для гидроразрыва пласта из подготовочных грузовиков 120 в ствол скважины 104, как указано сплошной линией 115. Один или более подготовочных грузовиков 120 может быть использован для поставки жидкости для гидроразрыва пласта на желаемом уровне.
Каждый подготовочный грузовик 120 может обычным образом эксплуатироваться с любой интенсивностью в пределах своей максимальной рабочей мощности. Эксплуатация подготовочных грузовиков 120 с интенсивностью меньше их рабочей мощности может спровоцировать выход одного насоса из строя и эксплуатацию остальных насосов с большей скоростью, с целью компенсации работы вышедшего из строя насоса. Компьютерная система контроля 149 может использоваться с целью управления всей насосной системой 129 в процессе осуществления операций по гидравлическому разрыву пласта.
С целью образования разрывов могут использоваться различные жидкости для гидроразрыва пласта, такие как обычная жидкость для воздействия на пласт, содержащая проппанты. Другие жидкости, такие как вязкие гели, "реагент на водяной основе" (который может содержать понижающий трение агент (полимер) и воду) могут также использоваться для осуществления гидравлического разрыва скважин сланцевого газа. Такие "реагенты на водяной основе" могут присутствовать в форме легкотекучей жидкости (например, с примерно такой же вязкостью, что и у воды) и могут использоваться для создания более сложных разрывов, таких как множественные микросейсмические разрывы, определяемые мониторингом.
Как дополнительно указывается на Фиг. 1.1, система трещин содержит разрывы, расположенные в различных положениях вокруг ствола скважины 104. Различные разрывы могут быть естественными разрывами 144, существующими до момента осуществления введения жидкостей, или гидравлическими разрывами 146, образованными возле пласта месторождения 102 в процессе осуществления введения.
Фиг. 1.2 демонстрирует часть 1.2 ствола скважины 104 Фиг. 1.1, отображающей введение проппанта 148 в пласт месторождения 102. Как схематически отображается на этой фигуре, проппант 148 может закачиваться в пласт месторождения 102 и распределяться по всей системе трещин 106. Как дополнительно схематически отображается на этой фигуре, проппант 148 может распространяться в виде кластеров (или пробок) 150, определяющих каналы 152 между разрывами 144/146.
Кластеры 150 могут переноситься в сеть трещин 106 таким образом, что части разрывов 144/146 раскрываются помощью проппанта 148 и части разрывов 144/146 остаются открытыми для прохождения потока в ствол скважины 102 (Фиг. 1.2) с целью извлечения жидкостей, как схематически отображается стрелками 152 на Фиг. 1.3.
Как демонстрируется на Фиг. 1.4, давление пласта месторождения может применяться по отношению к проппантным кластерам 150 в пределах разрывов 144/146. Изменение давлений (σэфф) может повлиять на поток жидкости, проходящий через определенный разрыв 144/146. Такой поток, именуемый проводимость, описывает легкость, с которой жидкость проходит через определенный разрыв 144/146, и может зависеть от проницаемости пласта месторождения, насыщения пласта месторождения и/или плотности и вязкости жидкости.
Фиг. 2 представляет собой блок-схему, отображающую способ 200 осуществления стимулирующих операций. Этот способ 200 может быть использован для определения проводимости и выполнения операций на основе определенной проводимости. Этот метод 200 включает сбор 254 скважинных данных. Скважинные данные могут быть получены с буровой площадки, имеющей ствол скважины, проникающий в подземный пласт месторождения, содержащий в себе разрывы. Как демонстрируется на Фиг. 1.1-1.4. скважинные данные могут содержать, например, данные акустики ствола скважины, данные микросейсмических событий, информацию о буровом оборудовании, технологические параметры и другие данные.
Этот способ 200 также может включать формирование 256 проппантных параметров. Проппантные параметры могут определяться на основе скважинных данных 254. Прогнозирование 256 может включать прогнозирование 260 введения проппантов в разрывы на основе скважинных данных, формирование 262 модели неровностей на основе проппантного прогнозирования, прогнозирования 264 апертурного изменения для заданного напряжения смыкания с использованием модели неровностей, а также определение 266 проводимости разрывов на основе апертурного изменения. Прогнозирование 264 и определение 266 могут повторяться 268 для различных напряжений смыкания.
Этот способ 200 также может включать 269 обоснование прогнозирования введения, размещение 270 проппанта в разрывах вместе с жидкостью для воздействия на пласт, а также извлечение 272 жидкости из пласта месторождения через определенные разрывы. Этот способ может применяться на буровой площадке 100 (см., например, Фиг. 1.1-1.4) с использованием изображенного на ней оборудования. Отдельные элементы этого способа могут применяться с использованием, например, насосной системы 129 с целью выполнения стимулирующих операций и контрольной системы 149 с целью осуществления введения проппанта. Отдельные элементы настоящего раскрытия сущности изобретения могут применяться с использованием процессора компьютерной системы.
Проводимость разрывов 266 может использоваться с целью определения способа впрыскивания и/или помещения проппанта для оптимального производства. Размещение 270 может применяться путем закачивания жидкости для воздействия на пласт, содержащей в себе проппант, в пласт месторождения на основе определенной проводимости разрывов 266, и извлечения 272 из пласта месторождения через определенный разрыв. Этот способ может также включать регулировку впрыскивания на основе новой информации и другие методы по желанию.
Этот способ 200 может применяться в любом порядке и повторяться по желанию. Фиг. 3-6 отображают различные элементы этого способа 200, показанного более детально.
1.1 Прогнозирование введения
Фиг. 3 демонстрирует другой вид на формирование 256 проппантных параметров Фиг. 2, показывающих Прогнозирование введения проппанта 260 более детально. Прогнозирование 260 может включать прогнозирование введения проппанта и других размещенных жидкостей в пределах шероховатого разрыва, такого как шероховатый разрыв Фиг. 1.3. Этот способ Фиг. 3 может также предоставлять детальный рабочий процесс для прогнозирования введения в пределах общего рабочего процесса проводимости разрывов.
Прогнозирование 260 может включать предоставление 357 разрывоапертурного распределения и 359 график закачки. Разрывоапертурное распределение 357 и график закачки 359 могут обеспечиваться информацией как части собранных скважинных данных (например, 254 Фиг. 2) или могут вводиться отдельно. Прогнозирование 260 может также включать определение траектории и расположения 361 Маркеров Лагранжа, проецирование 363 Маркеров Лагранжа на потоковую решетку и определение 365 проводимости сети и поля течения. Определение 361 может основываться на разрывоапертурном распределении 357 и графике закачки 359.
Могут определяться проводимость сети и новые поля течения 365. Определение 361, проектирование 363 и определение 365 могут повторяться 367 до момента завершения закачки. По завершении могут выполняться остаток прогнозирования 260 (например, 262-268) и/или способ 200 (например, 270, 272).
Предоставление разрывоапертурного распределения 357 может быть получено на основе реальных или синтетических методов. Например, трехмерная геометрия разрыва может быть приближена с помощью использования двухмерной системы мест расположения, когда известна локальная толщина трещин b(x,y):

где Δx представляет собой размер ячеек, используемых для расчетной сетки, а x и y являются координатами, лежащими в серединной плоскости разрыва, а i и j представляют собой индикаторы, определяющие i,j-ячейку. Для геометрии поверхности разрыва в равной степени могут использоваться измерения реальных разрывов для определения поверхностной геометрии или синтетические алгоритмы.
В последнем случае настоящее раскрытие сущности изобретения использует алгоритм создания искусственного разрыва. В процессе применения этого подхода используется квадратная матрица с тем же количеством ячеек, что и в желаемом разрыве, инициализируемая Гауссовскими нормально распределенными случайными числами. На матрице осуществляется преобразование Фурье A, и это преобразование затем корректируется с использованием степенного фильтра с числами высоких волн. Апертурное распределение затем получают путем осуществления обратного преобразования Фурье фильтруемого спектра. В равной степени с помощью измерения или синтеза может быть получено цифровое изображение поверхностей разрыва. Независимо от источника данных, поверхности разрыва могут быть приблизительно определены обычной решеткой точек, в которых известна апертура bij.
График закачки может быть предоставлен 359, например, на основе плана бурения для буровой площадки. График закачки может содержать предварительно существующие данные, предоставленные в качестве входных данных из внешних источников. На основе предоставленного графика закачки параметры проппанта в пределах разрыва могут быть подсчитаны с использованием методов введения частиц, таких как маркер Лагранжа для частиц, размещенных по всей расчетной области. Этот метод может применяться с использованием аспектов метода Крупных Частиц (КЧ), разработанного в докладе научной лаборатории Лос-Аламосo Harlow, F.H. LAMS-1956 (1955) под названием “Метод машинного расчета гидродинамических проблем”, содержание которого полностью включено в настоящую заявку посредством ссылки.
Маркеры Лагранжа (и/или их расположения) могут быть определены 361 путем закачивания и адвекции. Частицы могут переносить информацию, такую как информация о массе газа, геле, воде и проппанте в таких определенных местоположениях. В местах введения, данные правой части уравнения вносятся в уравнение потока и частицы маркера Лагранжа вводятся вместе с подходящим объемом фракций компонентов, вводимых в такое время.
Частицы Лагранжа могут также перемещаться с помощью адвекции вместе со скоростью течения местной жидкости в процессе определения 361. Например, если частица α занимает ячейку i, j изменение ее положения, Δxα, Δyα приводится в следующих уравнениях:

где 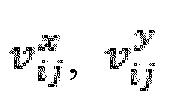 являются компонентами текущей скорости в ячейке i, j, а Δt является дискретным временным интервалом, используемым для интеграции. Другие переменные, зависящие от истории, также могут меняться на этом этапе осуществления метода. Например, фракция объема твердой фазы каждой частицы может быть изменена в связи с местным вычислением интенсивности вытекания жидкости.
являются компонентами текущей скорости в ячейке i, j, а Δt является дискретным временным интервалом, используемым для интеграции. Другие переменные, зависящие от истории, также могут меняться на этом этапе осуществления метода. Например, фракция объема твердой фазы каждой частицы может быть изменена в связи с местным вычислением интенсивности вытекания жидкости.
Обновленные состояния частиц Лагранжа могут быть спроецированы 363 на потоковую решетку. В пределах каждого временного интервала длины Δt, Частицы Лагранжа вносят вклад в объем фракций различных компонентов, где в пределах декартовой ячейки они располагаются внутри. Например, 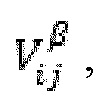 объемная концентрация компонентов β (где β соответствует одному из: вода, гель, проппант, и т.д.) в ячейке i, j может быть определена с использованием:
объемная концентрация компонентов β (где β соответствует одному из: вода, гель, проппант, и т.д.) в ячейке i, j может быть определена с использованием:

где Ωij представляет собой район, занятый ячейкой i, j:
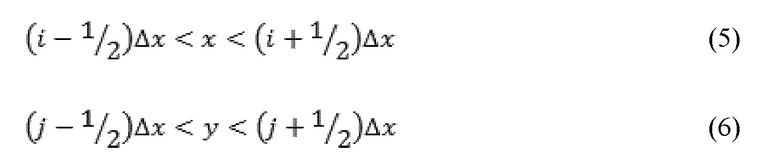
и 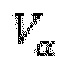 представляет собой объем частицы
представляет собой объем частицы 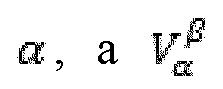 представляет собой объемную концентрацию частицы α занятой на стадии β. Таким образом, во всех точках решетки получают объем фракций всех видов жидкостей, вместе с другими параметрами, такими как фракция объема твердой фазы.
представляет собой объемную концентрацию частицы α занятой на стадии β. Таким образом, во всех точках решетки получают объем фракций всех видов жидкостей, вместе с другими параметрами, такими как фракция объема твердой фазы.
Параметры решетки, полученные таким образом, затем могут быть использованы с целью определения местных уровней проводимости 365 с использованием изображения потока жидкости между параллельными пластинами. Например, в случае использования жидкости Хершел-Бакли, проводимость элемента потока подсчитывается с использованием следующей взаимосвязи между притоком Q и градиентом давления в направлении расходомера Px:
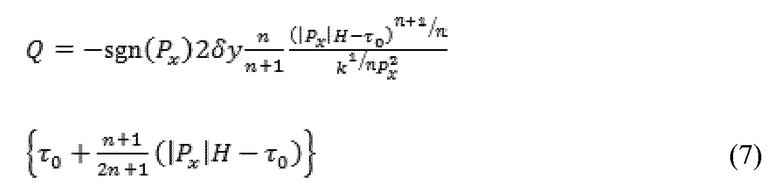
где τ0 представляет собой предел текучести жидкости, где k представляет собой коэффициент постоянства, n степенную экспоненту, H половину апертуры элемента, и 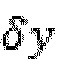 боковую длину элемента в направлении перпендикулярном потоку.
боковую длину элемента в направлении перпендикулярном потоку.
Проводимость сети и новое поле течения могут затем быть определены 365 для всех местоположений в пределах разрыва с использованием подхода, описанного в Разделе 1.4 (Подсчет проводимости разрывов, ниже). Если закачивание еще не завершено, процесс может повторяться (367) и новые поля течения могут затем использоваться с целью корректировки скоростей всех частиц Лагранжа в пределах разрыва, используемых в уравнениях (2) и (3) для адвективного перемещения частиц 361.
В конце графика закачки, месторасположения и плотность проппанта могут быть получены в пределах всех ячеек расчетной сетки. Эти результаты могут передаваться на следующую стадию, описанную Разделе 2 (Создание модели неровностей 262).
1.2 Создание модели неровностей
Фиг. 4 демонстрирует другую часть прогнозирования 256 Фиг. 2. В этом отношении, формирование 262 модели неровностей отображается более детально. Этот способ Фиг. 4 предоставляет детальное изображение создания модели неровностей в пределах общего способа проводимости разрывов 256. Формирование 262 включает разработку моделирования на основе шероховатостей сочетания шероховатости разрыва и введенного проппанта, что получается в равной степени на основе проппантных параметров 256 описанных в Разделе 1, в вышеуказанном тексте или других независимых источниках.
Как демонстрируется на примере Фиг. 4, формирование 262 содержит определение 469 разрыва апертурного распределения, определение 471 пространственное распределение проппанта, осуществление 473 смешивания материала, и формирование 475 моделирования шероховатостей сочетания шероховатости разрыва и проппанта.
Система геометрии, такая как распределение апертурного разрыва, может определяться 469 с помощью поверхностей разрыва в сочетании с размещением проппанта 471 между поверхностями разрыва. С механической точки зрения, разрыв затем представляется двумя эластичными полупространствами, разделенными совокупностью шероховатостей с длинами, 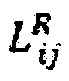 , с использованием той же дискретизации, как та, что используется при формировании 256 вышеуказанного Раздела 1.1.
, с использованием той же дискретизации, как та, что используется при формировании 256 вышеуказанного Раздела 1.1.
Фиг. 7.1 представляет собой схематическую диаграмму, отображающую нерасклиненный шероховатый естественный разрыв 744. Фиг. 7.2 демонстрирует поперечный вид в разрезе через модель неровностей в отношении шероховатого разрыва 744, содержащего проппант 745. Эти диаграммы демонстрируют поперечный вид в разрезе через модель неровностей в отношении нерасклиненного шероховатого разрыва 744. По меньшей мере в одном аспекте вышеуказанное описание вместе с Фигурами демонстрирует геометрию и локальные механические свойства разрыва, содержащего гетерогенное сочетание проппанта 475.
Вдоль разрыва 744 определяются длины шероховатостей Lij. Длины шероховатостей относятся к апертурам на основе следующего уравнения:

Далее настоящее раскрытие сущности изобретения рассматривает введение проппанта 745 в разрыв 744, заполнение промежутков между поверхностями породы как схематически демонстрируется на Фиг. 7.2. Настоящее раскрытие сущности изобретения подразумевает получение геометрии распределения проппанта на основе прогнозированного размещения 260 и возможность приблизительного определения с помощью дополнительных длин шероховатостей, 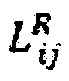 , по всей длине разрыва. Настоящее раскрытие сущности изобретения предполагает, что деформация проппанта является одноосевой (т.е. перпендикулярной x-y плоскости) и поэтому изменение высоты,
, по всей длине разрыва. Настоящее раскрытие сущности изобретения предполагает, что деформация проппанта является одноосевой (т.е. перпендикулярной x-y плоскости) и поэтому изменение высоты, 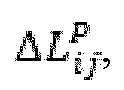 , проппанта в условиях давления определяется одноосевыми модулями проппанта
, проппанта в условиях давления определяется одноосевыми модулями проппанта 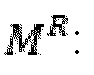

где σij представляет собой одноосевое давление в шероховатости i, j.
Одноосевой модуль для прогнозирования комбинированного отклика шероховатости твердой породы, 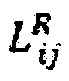 , и шероховатость проппанта,
, и шероховатость проппанта, 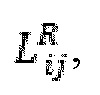 получают с помощью использования средней гармонической:
получают с помощью использования средней гармонической:

где 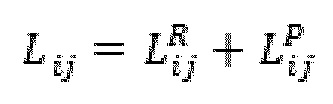 и MR представляют собой продольные модули пласта месторождения. Уравнение (10) может быть использовано в качестве алгоритма смешивания материалов с целью осуществления 473.
и MR представляют собой продольные модули пласта месторождения. Уравнение (10) может быть использовано в качестве алгоритма смешивания материалов с целью осуществления 473.
1.3 Прогнозирование апертурного изменения для заданного напряжения смыкания
В другом аспекте по меньшей мере одно раскрытие сущности изобретения рассматривает подходы прогнозирования 264 изменения в апертуре в связи с заданным напряжением смыкания. Первый подход, показанный на Фиг. 5.1, относится к “Декартовому прогнозированию апертурного изменения для заданного напряжение смыкания” (Декартов метод) и использует решеточный подход к решению механических уравнений эффективно на той же решетке, что и для потока с использованием предварительно рассчитанных фундаментальных функций. Второй подход, указанный на Фиг. 5.2, относится к “Прогнозированию апертурного изменения для заданного напряжение смыкания на основе цилиндров” (нелинейный цилиндрический метод), который приближенно показывает решетку неровностей с большими цилиндрическими неровностями для быстрого механического решения, которое затем проецируется обратно на таблицу неровностей.
1.3.1 Декартово прогнозирование апертурного изменения для заданного напряжения смыкания
С механической точки зрения, гетерогенный расклиненный разрыв рассматривается как два эластических полупространства материала, разделенного неровностями, чьи механические свойства получают путем создания модели неровностей 262. Как отображается на Фиг. 5.1, рассматривается метод декартового прогнозирования апертурного изменения для заданного напряжения смыкания в пределах общей обработки проводимости разрывов.
Как демонстрируется на Фиг. 5.1, прогнозирование 264 включает предварительное определение 581 таблиц влияния от неровности-к-неровности (взаимодействия), регулировку 583 дислокации в удаленных местах скважины, 585 формирование деформационного взаимодействия неровностей и полупространств на основе таблиц влияния от неровности-к-неровности, добавление 587 новых контактов, определение 589 нахождения разрыва в пределах допустимого заданного давления, а также определение 591 апертурного распределения от определенной неровности и деформации полупространства.
После формирования 585, может быть принято решение о добавлении или удалении новых контактов 587. В таком случае, формирование 585 может повторяться с добавлением новых контактов. В противном случае, формирование 264 может продолжиться до определения 589 и 591. Регулировка 583 может повторяться после определения 589, а формирования 585 может повторяться после добавления контактов 587.
Предварительное определение таблиц неровность-к-неровности 581 может быть достигнуто путем признания того, что если дана неровность, I, находящаяся в контакте с полупространствами, можно рассчитать радиальную зависимость отражения полупространства в связи с загрузкой неровности аналитически или численно. Аналитическая функция или числовой результат могут быть предварительно подсчитаны на решетке 581 при инициализации. Настоящее раскрытие сущности изобретения предполагает, что функция, α(x’,y’), которая дает увеличение отверстия на удельную нагрузку на единицу площади между полупространствами на дислокации x’,y’ в отношении к загруженной неровности. Следовательно, увеличение в открытии полупространства при неровности J в связи с нагрузкой fI, создаваемой на неровности I, может быть выражено как:
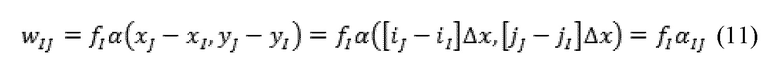
где

и 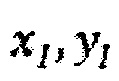 , и
, и 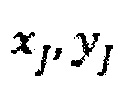 являются координатами неровности I и J соответственно, в то время как
являются координатами неровности I и J соответственно, в то время как 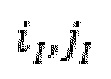 и
и 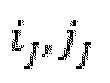 являются целочисленными координатами неровности I и J соответственно.
являются целочисленными координатами неровности I и J соответственно.
Настоящее раскрытие сущности изобретения предварительно определяет (или предварительно вычисляет) 581 показатель 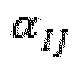 уравнения (12) сразу после инициализации стадии апертурного изменения. Настоящее раскрытие сущности изобретения получает распределение давления в пределах неровностей и сопряженной деформации окружающего материала путем обеспечения совместимости между напряжениями неровности и сопряженной деформацией. В особенности, в любом месте расположения, где неровность находится в контакте, изменение длины неровности и дополнительное открытие полупространства в месте расположения должны быть согласованными. Таким образом, деформированная неровность должна соответствовать деформированному промежутку:
уравнения (12) сразу после инициализации стадии апертурного изменения. Настоящее раскрытие сущности изобретения получает распределение давления в пределах неровностей и сопряженной деформации окружающего материала путем обеспечения совместимости между напряжениями неровности и сопряженной деформацией. В особенности, в любом месте расположения, где неровность находится в контакте, изменение длины неровности и дополнительное открытие полупространства в месте расположения должны быть согласованными. Таким образом, деформированная неровность должна соответствовать деформированному промежутку:

где D представляет собой промежуток, который будет находиться между полупространствами при отсутствии какой-либо контакта с неровностью, 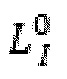 представляет собой ненагруженную длину неровности I.
представляет собой ненагруженную длину неровности I.
Дислокация в удаленных местах скважины D может быть скорректирована 583 с целью приближения к состоянию затребованной нагрузки в процессе создания неровности и взаимодействия деформации полупространства месторождения 585. Неровность и полупространственное взаимодействие 585 могут быть созданы путем признания того, что изменение по длине неровности I происходящее в связи с текущим напряжением, 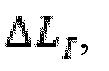 отображается в виде:
отображается в виде:

и линейная система уравнений, дающая возможность получения решения в отношении изменений в длине неровностей, 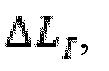 получается в виде:
получается в виде:
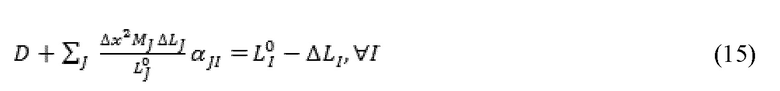
где 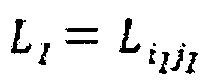 ,
, 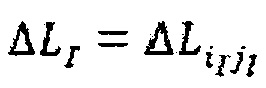 , и
, и  , и
, и 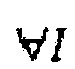 указывает, что уравнение (15) применимо ко всем значениям I.
указывает, что уравнение (15) применимо ко всем значениям I.
Решение этой системы предоставляет деформированное состояние разрыва 585. Как только получается такое деформированное состояние, настоящее раскрытие сущности изобретения осуществляет проверку наличия нового контакта между двумя поверхностями в связи с деформацией и выбирает новые перспективные неровности для контакта 587. Деформированное состояние затем подсчитывается заново, и процесс повторяется до обнаружения всех дополнительных точек контакта.
В этой точке текущее состояние напряжения, σn, подсчитывается путем деления общей силы на общую площадь, A, разрыва:

Позднее можно определить, нуждается ли промежуток, D в корректировке 583 вниз или вверх для аппроксимации σn к требуемому уровню нагрузки, и процедура повторяется до момента, когда σn признается достаточно близкой к уровню нагрузки, как демонстрируется на Фиг. 5.1.
1.3.2 Прогнозирование апертурного изменения для заданного напряжения смыкания с использованием цилиндрической модели неровностей
Используя альтернативный подход к механической деформации, решетка неровностей приблизительно определяется с помощью приблизительного набора цилиндрических неровностей. Фиг. 5.2 демонстрирует детальное изображение прогнозирования 264 для прогнозирования апертурного изменения для заданного напряжения смыкания в пределах формирование 256 на основе цилиндрической модели.
Как демонстрируется на Фиг. 5.2, прогнозирование 264 включает приближенное вычисление 580 решетки неровностей с необработанными цилиндрами, определение 582 для деформации цилиндра и полупространства согласующейся с приложенным давлением, добавление 584 точек соприкосновения и проектирование 587 апертурного изменения в связи с помещением цилиндров обратно на решетку неровностей. После решения 582, может приниматься решение о добавлении или удалении новых точек соприкосновения 584. В таком случае, решение 582 может повторяться. Если этого не происходит, может осуществляться проектирование 587.
Фиг. 8.1-8.3 представляют собой схематическое изображение, отображающее введение проппанта на трех стадиях (I), (II), и (III), соответственно. Эти Фигуры отображают преобразование (I) детальной модели неровностей (Фиг. 8.1 - две окружности и эллипс) в (II) приблизительное цилиндрическое моделирование (Фиг. 8.2), и затем обратное проецирование на (III) деформированные детальные модели неровностей как части рабочего процесса излома фракции на основе цилиндрического моделирования (Фиг. 8.3).
Фиг. 8.1 демонстрирует пример простой заданной декартовой сетки 848 проппанта, основанной на неровностях, распределенной в пределах разрыва 844. С использованием подхода, основанного на цилиндрах, эта сетка приблизительно определяется сочетанием цилиндров, которые имеют значительно большие размеры, чем размер индивидуальных неровностей. Например, Фиг. 8.2 демонстрирует грубое, основанное на цилиндрах, приближение к этому распределению с проппантом 848’, сгруппированным в кластеры 850. Деформация и взаимодействие между грубыми цилиндрами могут затем быть подсчитаны 582 использованием аналитических выражений, таких как аппроксимация в дальних участках скважины к деформации полупространства. Например, изменение в неровности, wIJ, в цилиндре I в связи с fj, общее усилие, оказываемое цилиндром J, может быть представлено:

где E и υ представляют собой модуль Янга и коэффициент Пуассона полупространства, и rIJ является расстоянием между двумя неровностями.
Определение деформации цилиндра и полупространства, согласующейся с приложенным давлением 582, может быть достигнуто путем сборки системы линейных уравнений для совместимости. В аппроксимации, основанной на методе цилиндров, количество уравнений может быть уменьшено на порядок величины или более в сравнении с декартовым механическим решением с целью улучшения эффективности.
Аналогично декартовому подходу, подход с использованием метода цилиндров в пределах разрыва может определять новые контактные точки на грубой решетке точек, именуемых “точками соприкосновения”. При обнаружении новых точек соприкосновения 584 в такое место расположения добавляется цилиндр, и расчет повторяется до момента достижения схождения (см. Фиг. 5.2).
Грубая аппроксимация может вызвать искусственную блокаду или возникновение каналов в области действия. Например, на Фиг. 8.2, открытый канал вдоль верха области был закрыт грубой аппроксимацией цилиндра. После получения деформированного состояния цилиндров, изменение в апертуре 587 может быть спроектировано обратно на оригинальную решетку неровностей (см. Фиг. 8.3).
Фиг. 8.3 демонстрирует изменение в апертуре для нагруженной проппантной колонны 848” в пределах разрыва 844. Таким образом, артефакты, такие как заблокированные каналы или новые отверстия, вызванные аппроксимацией грубого цилиндра, могут быть предотвращены от распространения обратно на сетку, используемую для подсчета проводимости, и изменение в апертуре в связи с напряжением может включаться.
1.4 Вычисление проводимости разрывов
Фиг. 6 предусматривает детальный способ для определения 266 расчета проводимости разрывов в пределах формирования 256. Как демонстрируется на Фиг. 6, определение 266 проводимости разрывов включает определение 688 заполненных проппантом и неконтактирующих неровностей, преобразование 690 определенных заполненных проппантом и неконтактирующих неровностей в потоковую сетку, и получение 692 проводимости разрывов путем решения сетки потока при текучем уровне напряжения.
Преобразование 690 может включать преобразование ячеек в сетку потока. Преобразование 690 может варьироваться в зависимости от состояния каждой ячейки. Поток из ячейки I, расположенной на iI,jI к ячейке J, расположенной на iJ, jJ может быть представлен:

где pI представляет собой давление в ячейке I и cIJ представляет проводимость между ячейкой I и ячейкой J. Этот метод для определения cIJ зависит от того, является ли ячейка заполненной проппантом.
Преобразование ячеек в сетку потока 690 в районах разрыва, не содержащих проппант, может быть подсчитано с использованием сетевой модели. См., например, работу Yang. G., Cook, N.H.W., Myer, L.R., Network Modeling Of Flow In Natural Fractures, Rock Mechanics as a Guide for Efficient Utilization of Natural Resources, p. 57-64 (1989), содержание которой полностью включено в настоящую заявку посредством ссылки. Путем использования этого подхода, разрывы могут быть представлены локально через проводящие трубы, при этом проводимость труб подсчитывается с использованием решения для потока между двумя параллельными пластинами. Следовательно, проводимость 692 между ячейками в пределах нерасклиненных областей разрыва приводится в виде:

где μ представляет собой вязкость жидкости и bIJ представляет среднее открытие двух ячеек:

где 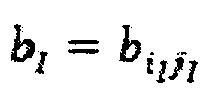 представляет собой открытие при неровности I.
представляет собой открытие при неровности I.
Преобразование ячеек в сетку потока 690 в пределах напряженных заполненных проппантом областях может обрабатываться другим способом. Можно предположить, что проницаемость уплотненного проппанта зависит от прилагаемого давления. По меньшей мере в одном аспекте реализации настоящее раскрытие сущности изобретения рассчитывает локальную проницаемость проппанта при наличии локального напряжения в разрыве и преобразовывает проницаемость в проводимость через допущение локального пористого Дарси потока с проницаемостью, зависящей от напряжения:

где

и k(σ) представляет собой проницаемость, зависящую от напряжения, и σI представляет локальное напряжение, получаемое во время закрытия разрыва в процессе стадии 264.
Получение проводимости разрывов 692 может быть достигнуто путем признания того, что результирующий поток в каждой ячейке отверстия равен нулю и формирование системы линейных уравнений для полей с неизвестным давлением представляется:
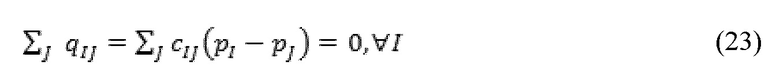
за исключением указанных месторасположений, где применяется условия давления на границах, и при известном p. Эта система уравнений решается для поля давления, p, которое потом заменяется обратно на уравнение локального потока с целью оценки проводимости разрыва 692.
Если вычисляется проводимость разрыва при напряжении дополнительного закрытия, настоящее раскрытие сущности изобретения возвращается к 264 прогнозированию апертурного изменения или заданного напряжения смыкания как демонстрируется на Фиг. 6. При таком способе настоящее раскрытие сущности изобретения получает проводимость естественного шероховатого разрыва под напряжением в присутствии произвольного распределения проппанта.
ПРИМЕР - Демонстрационное применение
Этот пример представляет практическое применение, включая ряд разрывов и проппантную геометрию в соответствии с по меньшей мере одним вариантом реализации настоящего изобретения. Предполагалось, что горная масса обладает модулем Янга, равным 20 ГПа, и коэффициентом Пуассона, равным 0,22. Проппант имел одноосевой модуль, равный 230 МПа и зависимость давления проницаемости, выраженную:

где k представляет собой Дарси и σ выражается в Па.
Фиг. 9.1-9.4 демонстрируют результаты, спрогнозированные настоящим раскрытием сущности изобретения при его применении для разрыва размером 10 квадратных метров, с отверстием равным 5 мм, содержащим круговые проппантные колонны с радиусом 2 м. Эти Фигуры демонстрируют апертурное распределение и распределение контактов в случае использования круговых колонн гетерогенного проппанта между плоскими поверхностями породы, как прогнозируется настоящим раскрытием сущности изобретения при 0 МПа и 10 МПа напряжения смыкания.
Фиг. 9.1-9.4 представляют собой графики 900.1-900.4, отображающие распределения 948, 948’ вдоль оси x (м) и оси y (м) в разрыве 944 между двумя плоским поверхностями породы. Фиг. 9.1 и 9.2 демонстрирует апертурное распределение 948 при 0,0 МПа и 10,0 МПа соответственно. Фиг. 9.3 и 9.4 демонстрируют распределение контакта 948’ при 0,0 МПа и 10,0 МПа соответственно.
Этот гетерогенный расклиненный разрыв был нагружен до напряжения смыкания в 10 МПа и жесткость разрыва, и проводимость разрывов были подсчитаны путем применения настоящего раскрытия. Эта процедура затем была повторена для серии разрывов с различными геометриями отверстия и проппантным распределением.
Фиг. 10.1-10.4 отображают апертурное распределение и контакт для неровного, естественного разрыва 944, как спрогнозировано настоящим раскрытием сущности изобретения при 0 МПа и 10 МПа напряжении смыкания. Фиг. 10.1-10.4 представляют собой графики 1000.1-1000.4, отражающие распределение 1048, 1048’ вдоль оси x (м) и y (м) в разрыве 944. Фиг. 10.1 и 10.2 демонстрирует апертурное распределение 1048 при 0,0 МПа и 10,0 МПа соответственно. Фиг. 10.3 и 10.4 демонстрирует распределение контакта 1048’ при 0,0 МПа и 10,0 МПа соответственно.
Фиг. 11.1-11.4 отображают разрыв 944, расклиненный сложным гетерогенным расположением проппанта. Фиг. 11.1-11.4 отображают апертурное распределение 1148 и распределение контакта 1148’ для произвольного, гетерогенного распределения в пределах неровного, естественного разрыва 944, как спрогнозировано настоящим раскрытием сущности изобретения для 0 МПа и 10 МПа напряжения смыкания. Фиг. 11.1-11.4 представляют собой графики 1100.1-1100.4, отражающие распределение 1148, 1148’ вдоль оси x (м) и оси y (м) в разрыве 944. Фиг. 11.1 и 11.2 демонстрируют апертурное распределение 1148 при 0.0 МПа и 10.0 МПа соответственно. Фиг. 11.3 и 11.4 демонстрируют распределение контакта 1148’ при 0,0 МПа и 10,0 МПа соответственно.
Для сравнения был простимулирован равномерно заполненный разрыв. Все измеряемые разрывы имели размеры 10 м по стороне и среднюю апертуру равную 5 мм. Поверхности естественных разрывов были получены через самоафинную схему создания ζ=0,8 и l=3,7×10-17. Последние могут быть предоставлены в соответствии со значениям, установленными далее в работе Drazer, G. and J. Koplik, Permeability of Self-Affine Rough Fractures, Physical Review E, 62(6):8076-8085 (2000), которые были предварительно включены в настоящую заявку во всей полноте посредством ссылки.
Фиг. 12.1 и 12.2 представляют собой графики 1200.1, 1200.2, демонстрирующие напряжение против дислокации и проводимости против откликов на напряжение, соответственно, прогнозированным для каждого разрыва данным раскрытием. Фиг. 12.1 предоставляет сравнение взаимосвязи между естественным закрытием (δn) и напряжением смыкания (σn) для ряда рассматриваемых геометрий проппантных разрывов. Таблица 1200.1 отображает естественное закрытие (δn) (м) (x-ось) и напряжение смыкания (σn) (Па) (y-ось) для различных размеров разрыва, включая круговой (1294.2), равномерно заполненный (1294.1), естественный нерасклиненный (1294.4), и естественный гетерогенный (1294.3) соответственно.
Фиг. 12.2 представляет сравнение постепенного изменения проводимости разрывов под напряжением смыкания для сочетаний проппанта и рассматриваемой геометрии разрыва. Таблица 1200.2 отображает проводимость (FC) (Дарси-м)) (y-ось) и отклик на напряжение (σn) (Па) (x-ось) для различных размеров разрыва, включая круговой (1294.1’), равномерно заполненный (1294.2’), естественный нерасклиненный (1294.3’), и естественный гетерогенный (1294.4’) соответственно.
Как ожидается, нерасклиненный разрыв в этом примере демонстрирует наивысшее закрытие при 10 МПа напряжения смыкания. В отличие от него, равномерно заполненный гладкий разрыв демонстрирует наименьшее закрытие с гетерогенно заполненным разрывом, демонстрирующим средний отклик. Проводимость нерасклиненного шероховатого разрыва быстро снижается в процессе увеличения напряжения смыкания. Как ожидалось, равномерно заполненный разрыв поддерживает сравнительно постоянную и низкую проводимость с увеличением напряжения с величиной, примерно равной 1,5 D-м=300 D×5×10-3 м. Гетерогенные расклиненные разрывы (как с гладкими, так и неровными стенками) демонстрируют высокую проводимость в течение широкого диапазона напряжений смыкания.
II. МОДЕЛИРОВАНИЕ ВВЕДЕНИЯ ПРОППАНТА В РАЗРЫВ
Фиг. 13-19.3 описывают дополнительные способы, относящиеся к прогнозированию 256 введения проппанта в разрывы и для 269 обоснования (или проверки) прогнозирования 256. Эти способы выполняются для введения проппанта и закачиваемых жидкостей в пределах шероховатого разрыва, как схематически демонстрируется на Фиг. 7.1 и 7.2. Способы могут использоваться как часть 260 прогнозирования введения проппанта, как описывается, например, касательно Фиг. 3. Способы могут включать аналитические, 1-D, 2-D и/или 3-D симуляции. Сравнение различных способов может быть использовано для обоснования 269.
2.1 Аналитические модели для решений в отношении потока между двумя пластинами
Аналитические решения, такие как модель Хершел-Балкли в отношении потока жидкости между бесконечными пластинами, могут быть использованы как основа для анализа потока жидкости между пластинами. Жидкость Хершел-Балкли представляет собой обобщенную модель, в которой неньютоновской жидкости напряжение, испытываемое жидкостью, относится к давлению по сложному, нелинейному способу. Можно предположить, что поток полностью развит локально. “Полностью развитый поток” означает поток, который имеет достаточное расстояние для развития таким образом, что локальная скорость жидкости через апертуру разрыва зависит от локального потока, и исключает детали поля скоростей набегающего потока. Отклонение от модели Хершел-Балкли могут быть продлены с использованием аналитических решения для степенного закона и Бингамовых жидкостей. Примеры аналитических решений описаны в работе Chhabra, R. P. & Richardson, J. F., Non-Newtonian Flow And Applied Rheology: Engineering Applications, 2-D ed. Elsevier (2008) (referred to herein as “Chhabra & Richardson”). Рассматривается диаграмма равновесия сил 1300 в отношении различных сил, действующих на прямоугольный жидкий элемент 1301, как демонстрируется на Фиг. 13.
Фиг. 13 отображает равновесие давления и вязкостного допустимого напряжения на прямоугольный участок в пределах пограничного потока между параллельными пластинами. Силы на Фиг. 13 представлены следующим:
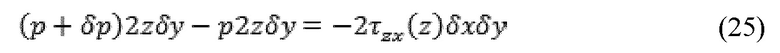
где δx представляет собой длину прямоугольника вдоль оси X, δy представляет длину прямоугольника вдоль оси Y, z представляет ½ ширину вдоль оси Z, ρ представляет плотность жидкости, p представляет давление, и τzx представляет допустимое напряжение. Из уравнения (25), может быть получено следующее уравнение:

Путем применения метода Хершел-Балкли относительно жидкости уравнение (26) представляет собой следующее:
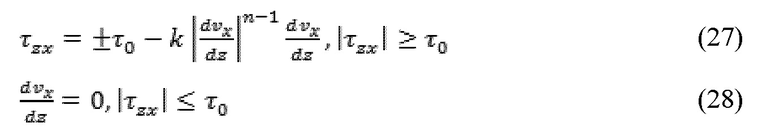
где vx представляет скорость, и k представляет коэффициент постоянства жидкости. Единицы коэффициента постоянства жидкости k зависят от значения n, как указано далее:

Учитывая, что допустимое напряжение, τzx равняется нулю на центральной линии CL, существует конечная область потока вытеснения возле центральной линии, где допустимое напряжение является недостаточным для сдвижения материала. Полуширина, zp, такой пробки получается путем вычисления для τzx = τ0 в уравнении (26) для получения следующего:

для потока, в особенности в пределах области z>0, и случай Px>0, соответствующий потоку справа налево на Фиг. 13. Предполагая, что условие прилипания на поверхности пластины 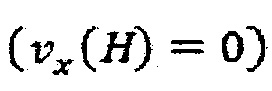 , υx будет иметь отрицательное значение и υx будет постепенно снижаться по абсолютной величине с увеличением z и
, υx будет иметь отрицательное значение и υx будет постепенно снижаться по абсолютной величине с увеличением z и 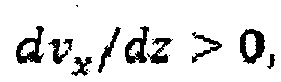 и τzx будет иметь отрицательное значение в соответствии с уравнением (26). Таким образом, для z>zp уравнения (27) становится:
и τzx будет иметь отрицательное значение в соответствии с уравнением (26). Таким образом, для z>zp уравнения (27) становится:

и соединяясь с уравнением (26), образуется следующее:

Уравнение (32) может быть преобразовано, как указано далее:

Уравнение (33) может быть интегрировано для получения следующего:

где C представляет собой постоянную интегрирования. C может быть выбрана для удовлетворения υx(H)=0 с целью предоставления следующего:
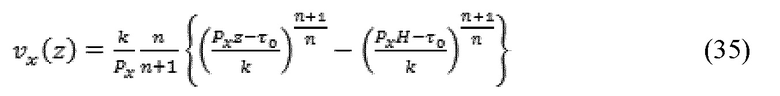
и скорость пробки, υp, получается, как указано далее:
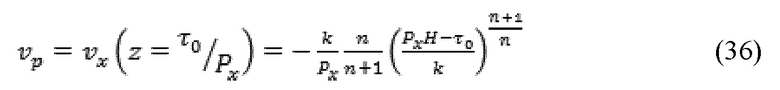
При условии, что Px > τ0/H, суммарный приток Qx в x-направлении через область ширины δy получается путем интегрирования через запертую и незапертую области разрыва, как указано далее:
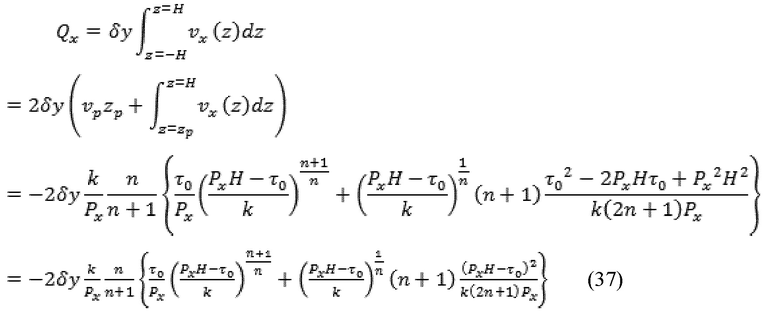
где H представляет собой высоту апертуры. Уравнение (37) может быть переписано, как указано далее:
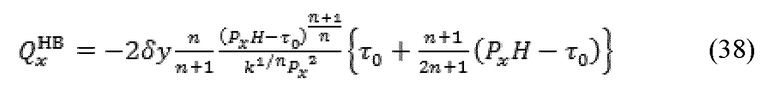
Уравнение (38) может быть написано в единицах толщины трещины, h = 2H, как указано далее:
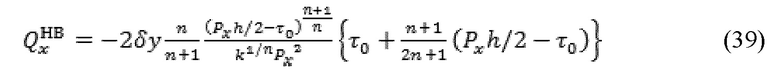
Этот результат соответствует случаю Px > 0. Таким образом, уравнение (39) может быть обобщенным для рассмотрения произвольного знака Px, как указано далее:
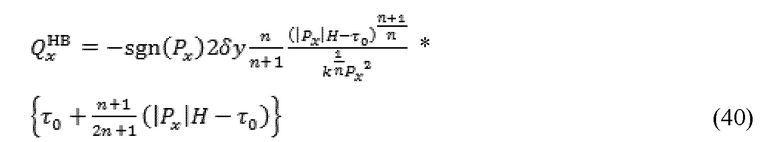
для 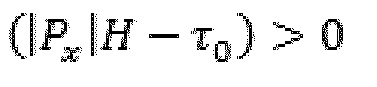
Критический градиент давления ниже, при котором останавливается поток, представляется:

где H = h/2.
Уравнение (40) выносит различные подклассы реологии жидкости в подходящих пределах, такие как ньютоновский, биндхемовский граничный случай, а также граничный случай степенного закона. Для граничного случая ньютоновской жидкости, где n=1 и τ0=0, уравнение (40) может быть переписано, как указано далее:
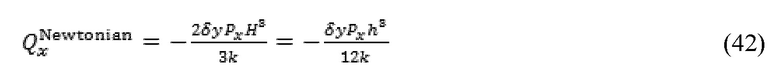
что соответствует “кубическому закону” для ньютоновского течения между двумя пластинами где k=μ. Замещая τ0=0 в уравнении (40), решение для граничного случая степенного закона предоставляется, как указано далее:
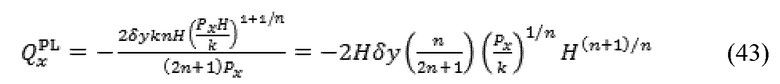
что соответствует Chhabra & Richardson. В заключение, рассматривая граничный случай бингамовской пластичной жидкости, n=1 в Уравнении (40) представляет следующее:
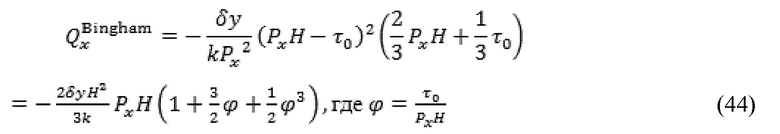
Уравнение (44) воспроизводит результат заявленный Chhabra & Richardson.
2.2 Решение для потока жидкости с использованием жидкости хершел-балкли между переменными пористыми пластинами
Поток множественных неньютоновских жидкостей в пределах изменяемой апертурный разрыв могут быть симулированным. Указанное включает Лагранжев подход, основанный на частицах, для отслеживания различных стадий в пределах разрыва. Результирующая симуляция может быть подтверждена путем сравнения с другими симуляциями для многофазового потока в разрывы с различными геометриями. Может быть получено согласие на широкий ряд впрыскиваемых жидкостей с вязкостью, разнящейся многими порядками величин.
Наш способ продолжается путем использования уравнения (40) для предоставления взаимосвязи между падением давления и потоком, объединенных с локальным ограничением потока, приводит к ряду нелинейных одновременных уравнений для неизвестного pi.
Решения могут быть получены путем итерационного решения линеаризованной формы уравнения (40). Заметьте, что при ограничении маленького τ0 и n≈1, значение 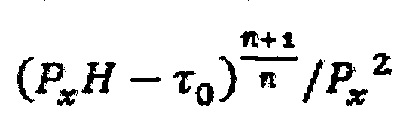 в уравнении (40) слабо зависит от Px. Это значение может быть факторизировано и выражено в единицах градиента давления из предыдущей итерации, как указано далее:
в уравнении (40) слабо зависит от Px. Это значение может быть факторизировано и выражено в единицах градиента давления из предыдущей итерации, как указано далее:
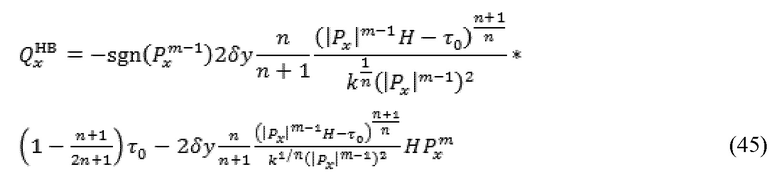
где верхний индекс m на Px относится к итерации давления упругости растворения. Первый показатель уравнение (45) не зависит от 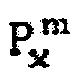 и станет показателем в правой части собранной линейной системы. Следовательно, линейная система, используя коэффициенты и вектор с правой стороны на основе решения предыдущей итерации,
и станет показателем в правой части собранной линейной системы. Следовательно, линейная система, используя коэффициенты и вектор с правой стороны на основе решения предыдущей итерации, 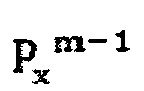 может быть собрана, и вычислена текущая итерация,
может быть собрана, и вычислена текущая итерация, 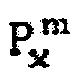 .
.
Другим способом рассмотрения уравнение (45) является то, что в пределах каждой итерации, поток локальной жидкости приблизительно определяется с помощью ньютоновской жидкости с локальными свойствами, продиктованными абсолютной величиной градиента давления из предыдущей итерации. Иными словами, серия линейных уравнений может быть собрана как указано далее с целью получения решения для неизвестного давления при текущей итерации, 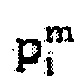 :
:
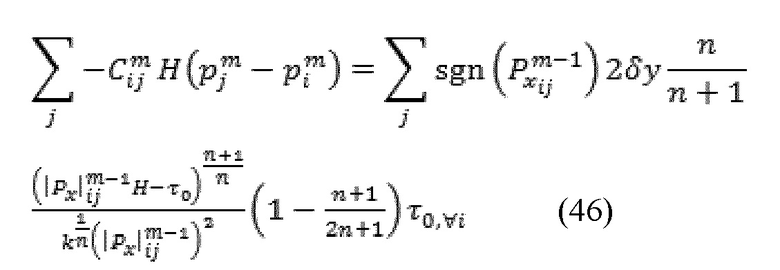
где эффективная проводимость при текущей итерации, 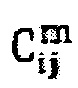 , использует информацию из предыдущей итерации, m-1, и представлена:
, использует информацию из предыдущей итерации, m-1, и представлена:

Может быть описано подходящее выражение для 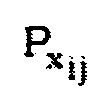 . Простая одномерная конечная разностная аппроксимация в единицах неизвестных давлений,
. Простая одномерная конечная разностная аппроксимация в единицах неизвестных давлений, 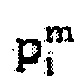 , приводит к следующему:
, приводит к следующему:

Эффективные линейные свойства каждой ячейки могут быть изотропными. Если используется аппроксимация, аналогичная уравнению (48), жидкость может развить анизотропию при движении потока под углом к сетчатым линиям.
В отличие от этого, тот же градиент давления, применяемый в любом направлении должен приводить к тому же потоку. Следовательно, значения градиента давления из предыдущей итерации могут быть включены в изотропный способ, с использованием подходящей матрицы конечной разницы градиента давления. Может быть внедрена разностная сетка стороны ячейки Δx с квадратными ячейками, как указано далее:
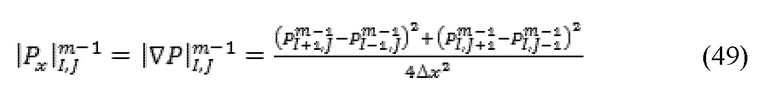
где I и J обозначают целочисленные координаты в x- и y-направлениях соответственно. Абсолютная величина градиента давления, используемая при оценке проводимости между ячейками i и j, использует среднюю абсолютную величину, как указано далее:

где I(I), J(i) обозначает целочисленные координаты ячейки i. Использованием этой аппроксимации, вклад, вносимый каждой ячейкой в эффективность проводимости между ячейками, является независимым от потокового направления.
Могут быть рассмотрены трудности подсчета, сопряженные с решением системы уравнений, таких как уравнение (46). Расчет проводимостей уравнения (47) и правосторонней части уравнения (46) включают деление на Px. Следовательно, как только Px достигает очень маленького значения, эти значения в системе уравнений разнятся. Этого можно быть избежать путем введения регуляризационного параметра 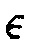 , который градуируется в соответствии с градиентом давления задачи, как указано далее:
, который градуируется в соответствии с градиентом давления задачи, как указано далее:

где 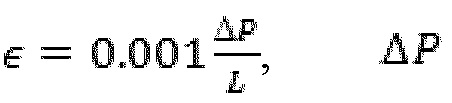 представляет собой общее падение давления по всему разрыву, и L представляет собой длину разрыва.
представляет собой общее падение давления по всему разрыву, и L представляет собой длину разрыва.
Второй трудностью, касающейся числового решения, является то, что уравнение (46) применяется исключительно между двумя ячейками когда 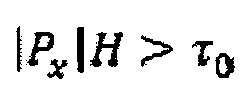 , иначе проводимость равняется нулю. Связи в гидродинамической сетке могут появляться и исчезать между итерациями, что может вызвать вопросы алгоритмической сложности и конвергенции. Даже когда, строго говоря, не существует потока в действительности, может предоставляться оценка локального градиента давления для целей установления удовлетворяет ли ячейка условию
, иначе проводимость равняется нулю. Связи в гидродинамической сетке могут появляться и исчезать между итерациями, что может вызвать вопросы алгоритмической сложности и конвергенции. Даже когда, строго говоря, не существует потока в действительности, может предоставляться оценка локального градиента давления для целей установления удовлетворяет ли ячейка условию 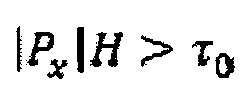 или нет на последующих интеграциях.
или нет на последующих интеграциях.
Для того чтобы иметь дело с такими вопросами, может вводиться неустойчивая, конечная проводимость параллельно с условием Хершел-Балкли. Это отвечает как цели регуляризации, так и цели обеспечения того, что локальная оценка градиента давления может быть в наличии в любое время. Эта проводимость градуируется толщиной трещин (h) и вязкостью жидкости (μ), как указано далее:

где α≈0,01. Это может вводить неустойчивую ошибку в решение для поля давления в процессе обеспечения того, что локальная оценка градиента давления присутствует пределах всех ячеек.
Процедура итерации предполагает существование первоначальной оценки Px в пределах каждой ячейки вычисления.
В процессе использования в пределах системы, развивающейся во времени, начальное приближение для каждого временного промежутка может быть взято из предыдущего временного промежутка. Для первой итерации при t=0 или в случаях, где изыскиваются стационарные решения, может быть выполнено начальное приближение поля давления путем замещения ньютоновской жидкости на разрыв. Будучи линейной проблемой, одна итерация может быть использована для получения решения при минимальных, поэтапных и вычисляемых затратах. Дли критериев конвергенции максимальное изменение в давлении от одной итерации к другой может представлять малую часть максимального давления в разрыве. В дополнение, уровни входящего и выходящего потока могут согласовываться в пределах допустимого отклонения, задаваемого пользователем.
2.3 Верификация модели
Нелинейные модели расширения могут быть подтверждены (или обоснованы) по сравнению с аналитическими или числовыми решениями для различных геометрий.
2.3.1 1-D Тестирование линейных потоков в сужающемся разрыве
В другом примере, 1-D поток в сужающемся разрыве с постоянным уровнем закачивания на левой кромке могут рассматриваться, как указано на Фиг. 14. Фиг. 14 представляет собой схематическую диаграмму 1400, отображающую подтверждение проверки равномерного, однонаправленного потока между суживающимися пластинами с постоянным закачиванием в входное отверстие 1403. Отображается поток во входное отверстие hi слева (x=0) и через проход 1406 между сужающимися пластинками 1405. Размеры пластинок 1405 отражаются как имеющие длину Lx, входное отверстие hi и выходное отверстие ho.
Разрыв (отражающийся открытием 1406) инициализируется водой, и вторая жидкость впрыскивается при x=0 с постоянным потоком. Скорость локального потока (v) повышается по направлению к выходному отверстию ho в связи с консервацией жидкости, предоставляя потенциальные вопросы для отслеживающего алгоритма фронта жидкости по мере ускорения поверхностного контакта между фазами.
В зависимости от отличий в свойствах жидкости, давление входного отверстия, 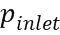 , может изменяться на многие порядки величины от абсолютной величины при впрыскивании второй жидкости. Путем сверки временных установок и абсолютной величины постепенного изменения, могут быть проверены интерфейс адвекции и решающее устройство давления в пределах этого абсолютизированного переменного разрыва отверстия.
, может изменяться на многие порядки величины от абсолютной величины при впрыскивании второй жидкости. Путем сверки временных установок и абсолютной величины постепенного изменения, могут быть проверены интерфейс адвекции и решающее устройство давления в пределах этого абсолютизированного переменного разрыва отверстия.
Это сочетание может быть симулировано с помощью постоянного закачивания в левую часть области определения (x=0) и нулевого давления на выходе (x=Lx_) при значении hi=0,25 в (0,64 см) и ho–0,125 в (0,32 см). 1-D конечная симуляция разницы может быть использована для прогнозирования давления входного отверстия для сравнения с 2-D моделью. При использовании 1-D симуляции может быть подсчитан впрыскиваемый объем и место расположения передней части жидкости, удовлетворяющее впрыскиваемому объему, может быть определено для заданного времени. 1-D область определения может быть дискретизирована и dp/dx могут быть подсчитаны путем инвертирования уравнения (45) в пределах каждой ячейки, и численного интегрирования инверсии из x=Lx, где p=0, обратно на входное отверстие для получения 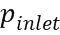 .
.
Таблица 1 отображает свойства жидкости для первоначальной поглотительной жидкости (“Жидкость 0”) и различных впрыскиваемых жидкостей (Жидкости 0-3), как указано далее:
В одном из примеров, были выполнены симуляции с низкой вязкостью ньютоновской жидкости, заполняющей разрыв (Жидкость 0 в Таблице 1) при t=0 и различных ньютоновских и неньютоновских жидкостях, вводимых на левой кромке (Жидкости 1 через 3 в Таблице 1). Жидкость 1 является ньютоновской жидкостью, обладающей высокой вязкостью; Жидкость 2 является степенной жидкостью; и Жидкость 3 является жидкостью Хершел-Балкли. Интенсивность закачивания равнялась 0,172 баррелям в минуту на каждые 10 футов (0,30 м) разрыва.
Соответствие между двумя числовыми решениями для каждой впрыскиваемой жидкости предоставлено, как демонстрируется на Фиг. 15.1-15.3. Фиг. 15.1-15.3 представляют собой графики 1500.1-1500.3, отображающие давление (p) (y-ось) по отношению к времени (t) (x-ось) для жидкостей 1-3 на Таблице 1 соответственно. Эти Таблицы демонстрируют сравнение между 2-D моделью и 1-D числовым решением для закачивания различных жидкостей, перечисленных в Таблице 1.
Как демонстрируется в каждой из Таблиц 1500.1-1500.3 2-D и 3-D симуляции жидкостей отмечаются линиями 1510.1 и 1510.2 соответственно. В то время, как первоначальное давление примерно равняется 1 кПa, конечное давление находится в пределах между примерно на один и три порядка абсолютной величины больше, в зависимости от свойств жидкости.
2.3.2 1-D тест радиального потока в постоянном разрыве отверстия
Другой тестовый сценарий рассматривает радиальный поток между двумя параллельными пластинами, как демонстрируется на Фиг. 16 и 17. Фиг. 16 представляет собой схематическую диаграмму 1600, отображающую параллельные пластины 1612, имеющие сквозное входное отверстие 1614. Эта Фигура демонстрирует геометрию подтверждения теста для радиально симметричного потока между двумя параллельными пластинами с постоянным закачиванием инжектором 1715 во входное отверстие в центре C0 при x=0, y=0). Несмотря на то что этот сценарий, как описывается, является радиально симметричным, расчетная сетка (или клеточная) не является радиально симметричной и может вызвать анизотропию, несмотря на попытки обеспечить, чтобы свойства жидкости являлись изотропными (см. Уравнение (49)).
2-D симуляция моделирует часть (например, одно крыло) предполагаемого симметричного разрыва с использованием области определения, описанной в Фиг. 16. Фиг. 17 представляет собой схематическую диаграмму 1700, отражающую 2-D расчетную область, симулируя одну симметричную половину (x>0) полной области разрыва при входном отверстии 1614’, разделенной пополам вдоль плоскости симметрии Ps и с закачиванием на центральной линии C0. Геометрия входного отверстия 1614’ имеет размеры Ly=290’ и Lx=145’ и клеточную сетку на 100 ячеек в вертикальном и 50 ячеек в горизонтальном направлении. Lx = радиус r кругового входного отверстия 1714’.
В этих случаях, разрыв на входном отверстии 1614’ был заполнен ньютоновской жидкостью с низкой вязкостью (например, Жидкость 0 в Таблице 1) при t=0, и различные ньютоновские и неньютоновские жидкости (например, Жидкости 1-3 в Таблице 1) были впрыснуты в центр C0 левой кромки со скоростью 5 баррелей в минуту (соответствующей потоку 10 баррелей в минуту в полном разрыве). Во избежание слишком высокого давления в пределах одной ячейки (и любыми сопряженными вопросами конвергенции) жидкость впрыскивалась в область меш 3 ячеек вдоль.
Фиг. 18.1-18.3 отражают три Таблицы 1800.1-1800.3, показывающие симуляцию для каждой из жидкостей 1-3 соответственно, проходящих через поделенное пополам входное отверстие 1614’ Фиг. 17. Каждая из трех Жидкостей 1-3 вытекала на протяжении 200 секунд, и конечные фронты жидкости демонстрируют отличную симметрию, как показано на Фиг. 18.1-18.3. Эти фигуры демонстрируют результаты 2-D симуляции при 200 секундах для закачивания Жидкости из Таблицы 1.
Для сравнения, 1-D симуляция следующая за алгоритмом, описанным в Разделе 2.3.1, была применена к той же проблеме. Фиг. 19.1-19.3 отображают Таблицы 1900.1-1900.3 давления p (y-ось) через радиус r (x-ось). Эти линии графиков в Таблицах 1900.1-1900.3, отображают сравнение результатов 1-D с 2-D симуляциями для закачивания жидкостей 1-3 из ТАБЛИЦЫ 1 вдоль 0°, 45° и 90° направлений (см. Фиг. 17) соответственно. При приближении симуляций к инжектору, симуляции захватывают сингулярность давления поля до переменных степеней. В дополнение, существует минимальная разница между полями давления, заявленными вдоль трех различных линий от инжектора.
III. ПРОГНОЗИРОВАНИЕ НЕЛИНЕЙНЫХ ДЕФОРМАЦИЙ И ГИДРАВЛИЧЕСКОЙ ПРОВОДИМОСТИ РАЗРЫВОВ ПРИ ОБЫЧНОМ НАПРЯЖЕНИИ
Данный Раздел III представляет другую версию 2056 этого способа формирования проппантных параметров 256. Как демонстрируется на блок-схеме Фиг. 20, этот способ 2056 включает те же параметры 260, 262, 266, 268 и 269, что были ранее описаны. По этой версии, прогнозирование 264 апертурного изменения для заданного напряжения смыкания с использованием линейной модели неровностей (см., например, Фиг. 5.1 и 5.2) было модифицировано для прогнозирования 2064 апертурного изменения с использованием нелинейных деформаций месторождения. Этот метод 2064 может включать прогнозирование апертурного изменения и проводимость с использованием нелинейной деформации месторождения и может применяться с использованием численного прогнозирования и/или аналитического подхода.
Численное прогнозирование может производиться с использованием численных моделей, включая пространственное распределение отклонений в отверстии. Такое прогнозирование может быть использовано для прогнозирования постепенного изменения закрытия разрыва и гидравлической проводимости под напряжением. Аналитические прогнозы могут также производиться путем удержания в открытом состоянии деформации месторождения и проводимости разрывов равнозначно путем естественных (неровностных) или искусственных (например, проппантных) способов.
Аналитический подход имеет целью соблюдение геометрии связи каналов в пределах разрыва в процессе предоставления эффективного решения для закрытия разрыва и проводимости разрывов. В дополнение, аналитический подход имеет целью уловить нелинейные результаты в связи с уплотнением материала, удерживающего разрыв в открытом состоянии, а также развитием дополнительных точек контакта в пределах каналов.
Проводимость разрывов может быть определена 266, как было описано ранее и/или как описывается далее по тексту в Разделе IV. Этот метод может быть обоснован (подтвержден) 269 как было описано ранее, или далее описано в Разделе V. Обоснование 269 может включать, например, сравнение с численными и аналитическими решениями для демонстрации хорошей многопоточной эксплуатации.
Как описывается в данном документе, нелинейное уплотнение неровностей, такое, которое приводит к сжиманию проппантного материала удовлетворению строго нелинейных структурных законов, относящихся к колоннам, могут рассматриваться с использованием расчетной модели касательно колонн и каналов между двумя полупространствами.
Предоставляется разработка правильной и эффективной численной модели для прогнозирования деформации месторождения и проводимости в равной степени естественного или искусственно расклиненного разрыва. Это достигается путем максимального использования двух внутренних способов моделирования колонн/каналов в пределах разрывов как: 1) мелкой расчетной сетки для симуляции потока во избежание случайного создания или разрушения каналов, и 2) упрощенных цилиндрических колонн для эффективного прогнозирования механических каналов в апертуре.
Модель деформации прогнозирует как снижение разрыва апертуры и нелинейных перераспределения нагрузки в связи с т очками соприкосновения, образующимися в каналах между колоннами. Модель деформации достигает быстрого решения путем упрощений в геометрии разрывов и через применение предобусловливателя, снижающего количество требуемых итераций. Проводимость разрывов может быть подсчитана на Декартовой сетке с использованием оригинального распределения апертуры с изменениями в апертуре, установленной в соответствии с результатами механической модели.
Примеры указывают на подтверждение характеристик кода по сравнению с аналитическими результатами и другим симулятором. Характеристика этого метода может позволить осуществлять симулирование множества сотен колонн/каналов в пределах множества разрывов в секунду. Сравнения с моделью более высокой точности указывают на нелинейные модели расширения с прогнозированием средней апертуры в пределах 5-10% и проводимость в пределах фактора 2-4. Нелинейные модели расширения могут быть использованы для предоставления эффективности и способствования более расширенному изучению параметров. Также может предоставляться нелинейность в конститутивной модели колонн в пределах разрыва, включая потенциальное распространение колонн. Будущее применение этого способа может рассматривать нелинейность в связи с распространением и уплотнением слабых проппантных колонн и вдавливанием проппанта в слабые пласты месторождения.
3.1 Введение
Гидравлическая проводимость разрывов при нагрузке может представлять интерес для ряда применений. Например, в геотермальных условиях может быть спрогнозировано деформированное состояние и сопряженная гидравлической проводимость естественных и гидравлически образованных разрывов на глубине. Примеры прогнозирования представлены в работе R. Jung, Goodbye or Back to The Future, in Effective And Sustainable Hydraulic Fracturing, Proceedings of the International Conference For Effective and Sustainable Hydraulic Fracturing (HF2013), InTech, pp. 95-121, г. Брисбен, Австралия, Май 20-22 (2013), которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
В случае хранения газа, осаждение и растворение минералов в пределах естественных разрывов, вместе с развитием эффективного состояния напряжения может привести к изменениям проводимости потенциальных каналов вытекания. См., например, работу J. P. Morris, J. W. Johnson, Predicting The Long-Term Evolution Of Fracture Transport Properties in Co2 Sequestration Systems, US Rock Mechanics/Geomechanics Symposium, pp. ARMA 11-399, June 26-29, г. Сан-Франциско (2011) (далее по тексту упоминаемая как “Morris (2011)),” которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
В дополнение, искусственные компоненты, такие как проппант, могут вводиться в гидравлической разрыв с целью поддержания проводимости при напряжении. См., например, работу L. R. Kern, T. K. Perkins, R. E. Wyant, The Mechanics Of Sand Movement In Fracturing, Transactions of the American Institute of Mining and Metallurgical Engineers 216 403-405 (1959); and C. Montgomery, Fracturing Fluids, Proceedings Of The Int’l Conf. For Effective And Sustainable Hydraulic Fracturing (HF2013), InTech, pp. 3-24, г. Брисбен, Австралия, Май 20-22 (2013), которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
В дальнейшем, некоторые классы технологии введения проппанта могут включать попытки стимулирования неоднородности в упорядочении проппанта с целью создания открытых каналов потока в пределах расклиненного разрыва (введение гетерогенного проппанта). См., например, работу A. Medvedev, K. Yudina, M. K. Panga, C. C. Kraemer, A. Pena, On The Mechanisms Of Channel Fracturing, SPE 163836; and J. P. Morris, N. Chugunov, G. Meouchy, Understanding Heterogeneously Propped Hydraulic Fractures Through Combined Fluid Mechanics, Geomechanics, And Statistical Analysis, 48th U.S. Rock Mechanics/Geomechanics Symposium, г. Миннеаполис, с. 2014-7408, Июнь 1-4, (2014) (далее по тексту упоминаемая как “Morris (2014)”), которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
Независимо от того, является ли она естественной или искусственно созданной, проводимость разрыва может преобладать над искусственно образованной канализированностью в пределах разрыва как в связи с пространственным распределением апертуры (в случае с естественными разрывами) и гетерогенностью в распределении проппанта (в случае с введением проппанта в процессе организации гидравлического разрыва). Например, экспериментальные исследования и исследования на моделях указывают, что индивидуальные естественные разрывы демонстрируют прогрессирующую сеть каналов при оказании нагрузки. См. работу: L. J. Pyrak-Nolte, L. R. Myer, N. G. W. Cook, P. A. Witherspoon, Hydraulic And Mechanical Properties Of Natural Fractures In Low Permeability Rock, G. Herget, S. Vongpaisal (Eds.), Proceedings of the Sixth International Congress on Rock Mechanics, Rotterdam: Balkema, 1987, pp. 225-231, Montreal, Canada, August 1987; and L. Pyrak-Nolte, J. Morris, Single fractures under normal stress: The relation between fracture specific stiffness and fluid flow, Int’l Jnl. of Rock Mechanics and Mining Sciences, 37 245-262 (2000) (далее по тексту упоминаем “Purak-Nolte (2000)”), которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
Наблюдения реактивного переноса в меняющихся скважинных разрывах могут также указывать, что апертурные изменения, искусственно образованные растворением, могут привести к образованию каналов, доминирующих над проводимостью разрыва. См., например, работу R. L. Detwiler, R. J. Glass, W. L. Bourcier, Experimental Observations of Fracture Dissolution: The Role Of Peclet Number On Evolving Aperture Variability, Geophys. Res. Lett, 30 (12) 1648 (2003), которые были предварительно включены в настоящую заявку во всей полноте посредством ссылки. Параметры закачивания могут контролировать присутствие или отсутствие каналов в пределах пачки расклинивающего агента, которые доминируют в технологиях выполнения введения гетерогенного проппанта. См., Morris (2011).
Решения могут быть разработаны для детальной деформации месторождения разрывов, принимая во внимание пространственное распределение материала в пределах разрыва. В некоторых случаях могут рассматриваться разрывы с двумя параллельными полупространствами, разделенными пространственным распределением контактных точек. См., например, работу J. A. Greenwood, J. B. P. Williamson, Contact Of Nominally Flat Surfaces, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 295 (1442) (1966) 300-319; and S. Brown, C. Scholz, Closure Of Random Elastic Surfaces In Contact, Jnl. Of Geophysical Research-Solid Earth And Planets 90 5531-5545 (1985), которые были предварительно включены в настоящую заявку во всей полноте посредством ссылки.
В некоторых случаях, контакт области деформируемых колонн, включая взаимодействие между колоннами, может рассматриваться в свете позволения каждому полупространству деформироваться в районе колонн. См., например, работу D. L. Hopkins, The Effect Of Surface Roughness on Joint Stiffness, Aperture, And Acoustic Wave Propagation, Ph.D. Thesis, University of California at Berkeley (1990) (далее по тексту - “Hopkins (1990)”), которая была предварительно включена в настоящую заявку во всей полноте посредством ссылки.
Указанные решения также могут включать рассмотрение регулярной сетки с маленькими контактными элементами (именуемыми отверстия) и эксплуатацию быстрых мультипольных методов. См., например, работу Purak-Nolte (2000). Сочетание мультипольных предельных элементов может быть использовано для стимулирования деформации скелета горной породы с отверстной механической моделью для фиксации детальной геометрии и механического отклика произвольного сочетания колонн и каналов. См., например, работу Purak-Nolte (2000) и Morris (2011). Могут также рассматриваться Деформации месторождения минерализованных колонн (см., например, Morris (2011)) и гетерогенных моделей проппанта в пределах разрыва (Morris 2014).
Деформации естественных каналов в пределах переменных отверстий разрыва могут быть спрогнозированы с использованием модели неровностей. См., например, работу Pyrak-Nolte (2000). В некоторых случаях, симуляция может включать расширенные вычислительные потребности при рассмотрении высоко субдискретизированных колонн/каналов. В некоторых случаях, симуляции могут предоставляться с повышенной вычислительной эффективностью, где количество колонн и сопряженных каналов остается маленьким. См., например, работу Hopkins (1990). Дополнительные вычислительные ресурсы могут быть внедрены в способы, содержащие использование большого количества отверстий для субдискретизации индивидуальных физических колонн и каналов. Использование большего количества колонн и каналов может привести к повышенной надежности модели. В некоторых случаях, при использовании слишком грубой модели для дискретизации разрыва, связи поля течения могут изменяться побочным введением численных артефактов, которые создают или удаляют каналы из модели. По той причине, что наличие или отсутствие каналов может повлиять на гидравлическую проводимость, изменения в потоковой геометрии могут повлиять на прогнозированное поле течения в пределах разрыва.
Для предоставления равновесия между увеличенными вычислительными ресурсами и необходимостью разрешения, может использоваться подход нелинейного увеличения. По мере увеличения разрешения, геомеханические расчеты могут использовать большинство вычислительных затрат и увеличенное разрешение могут потребоваться для правильного подсчета проводимости. Гибридный подход включает решение геoмеханической деформации на относительно грубой сетке, в то время как проводимость подсчитывается с использованием более усовершенствованной дискретизации. Гибридных подход имеет целью соответствовать геометрии и связываемости каналов в пределах разрыва (как естественного, так и искусственного), в то время как изменения также включаются в апертуру в связи с напряжением таким образом, что на то же количество вычислительных усилий, намного большее количество каналов могут быть включены в пределы одного подсчета.
Модели неровностей могут использоваться, включая линейный эластический конструктивный отклик для отверстий. См., например, работу Pyrak-Nolte (2000), Morris (2011), and Morris (2014). Расширение способов может быть реализовано с целью допущения эластического, идеально пластического поведения и/или с целью рассмотрения отказа материальной части. См. работы: P. Ameli, J. E. Elkhoury, J. P. Morris, R. L. Detwiler, Fracture Permeability Alteration Due to Chemical And Mechanical Processes: a Coupled Highresolution Model, Rock Mech Rock Eng., P. Ameli, J. E. Elkhoury, J. P. Morris, R. L. Detwiler, Fracture Permeability Alteration Due to Chemical And Mechanical Processes: a Coupled Highresolution Model, Rock Mech Rock Eng., DOI 10.1007/s00603-014-0575-z (2014); and E. A. Ejofodomi, G. Cavazzoli, J. Morris, R. Prioul, Application Of Channel Fracturing In The Vaca Muerta Shale Formation, SPE Latin American and Caribbean Petroleum Engr. Conf., pp. 169383-MS, Маракайбо, Венесуэла, Май 21-23 (2014), которые были предварительно включены в настоящую заявку во всей полноте посредством ссылки.
3.1.1 Нелинейный Метод Расширения
Этот нелинейный метод расширения может быть аналогичен нелинейному методу на Фиг. 5.2, за исключением того, что этот метод Фиг. 20 представляет дальнейшие детали нелинейных деформаций месторождения. Как указано далее в нижеприведенном разделе 2064 прогнозирование апертурного изменения проводимости с использованием нелинейных деформаций месторождения включает преобразование 2066 геометрии колонн/каналов в упрощенную аппроксимацию, такую как колонны или цилиндрическое представление (см. Раздел 4.3), и определение 2068 деформации разрыва (см. Раздел 4.4).
Преобразование 2066 может применяться с использованием механического подхода, содержащего геометрию колонн, или использование аналитического подхода, содержащего цилиндрическое приближенное проектирование на декартову сетку. Определение 2068 может применяться путем формирования деформации 2068.1 на основе цилиндрических колонн (см. Раздел 3.4.1), линеаризации 2068.2 отдельных элементов деформации цилиндрических колонн (см. Раздел 3.4.2), сборку 2068.3 линейной системы откликов цилиндрических колонн (см. Раздел 3.4.3), и рассмотрение 2068.4 точек соприкосновения (см. Раздел 3.4.4). Затем может быть определена проводимость разрывов 266 (см. Раздел IV). Для дополнительных точек соприкосновения, линеаризация 2068.2, сборка 2068.3, и решение 2068.4 могут повторяться.
В отношении разрыва с локальной системой координат x, y, интервал 0≤x≤Lx и 0≤y≤Ly, детальная геометрия колонн/каналов, характеризующая переменную топографию шероховатого разрыва или заполненное пространственное распределение проппанта в пределах разрыва предполагаются как таковые, что были предоставлены (см., например, Фиг. 7.1 и 7.2). Этот метод приближенно выражает детальную геометрию колонн с меньшим количеством грубых, цилиндрических колонн с целью ускорения геомеханических подсчетов. Может быть использована декартова сетка с более высоким разрешением для определения проводимости (см. нижеприведенный Раздел IV).
Выполнение этого метода продолжается путем прогрессивного добавления напряжения в разрыв с целью постепенного достижения требуемого уровня напряжения. В пределах каждого этапа увеличения напряжения, оценка, представленная нелинейной системой Уравнений, подвергается линеаризации (см. Раздел 3.4.2) для получения повторного Решения линейной системы, и для идентификации точек контакта (“точек соприкосновения”) (см. нижеприведенный Раздел 3.4.4). После достижения целевого уровня напряжения, подсчитываются окончательный размер толщины трещины и проводимость (см. нижеприведенный Раздел IV).
3.2 Преобразование из декартовой сетки в цилиндрическое представление
Точность прогнозирования проводимости зависит от наличия или отсутствия каналов в пределах неоднородного распределения проппанта или естественной шероховатости. Для ускорения геомеханического расчета используются сравнительно небольшое количество простых вычислительных элементов (цилиндрические колонны). В процессе аппроксимации геометрии канала с более крупными колоннами, могут вводиться или удаляться паразитные каналы.
На Фиг. 21 и 22 показаны схемы, изображающие модели 2100.1, 2100.2 имеющие и неимеющие канал соответственно. Эти цифры представляют два сценария, где преобразование в цилиндры может привести к ошибкам в оценке проводимости. В примере, показанном на Фиг. 21, начальная геометрия колонны включает в себя колонны, содержащие 2102.1 узкий канал, который 2104.1 удаляется в процессе пересчета на цилиндрическое представления 2102.1’.
В примере, показанном на 22, начальная геометрия колонны включает в себя две соседние колонны 2102.1 где шейка материала 2104.2 охватывает разрыв между ними. Преобразование на цилиндрическое приближении 2102.2’ удаляет материал 2104.2 из промежутка, создавая ложное канал.
Изменения в сети потока, охватывающих разрыв, может привести к много порядковым изменениям величины в прогнозировании проводимости. Чтобы избежать ложного создания или удаления каналов в рамках расчета проводимости, используются представление распределения материала в разрыве.
Фиг. 22 отображает схему, изображающую модель, используя множественные внутренние представления колонн/каналов. Обеспечивается естественная (произвольная) форма проппанта в форме колонны 2206. Создается аппроксимация с цилиндрами 2208.1 и проекция на декартовы (потоковые) сетки 2208.2. Аппроксимация 2208.1 цилиндра может быть быстро представлена геомеханически. Проекция 2208.2 может быть представлена проводимостью, соблюдающую геометрию и/или каналы.
Многочисленные внутренние представления включают механическую представление, делающее упрощающие предположения относительно колонны/геометрии канала (т.е. цилиндров) в целях достижения скорейшего решения, и аналитическое представление, использующее декартову сетку для фиксации геометрии колонны/канала, настолько точно, насколько это возможно для расчета проводимости. Механическое представление может включать заключение упрощающих предположений относительно пространственного распределения столбов и их геометрии в целях достижения скорейшего решения. Аналитическое представление может использовать более подробную сетку для фиксации геометрию канала как можно точнее для расчета проводимости.
Как показано стрелкой 2210, изменения в отверстии могут быть перенесены от геомеханических представлений 2208.1 до 2208.2 на декартовой сетке. Изменения в отверстия, предсказанные геомеханическим расчетом, могут быть перенесены на декартову сетку, как показано на схеме на Фиг. 23. Декартова сетка 2202 определяет множество прямоугольников (называемых ячейками), каждый из которых имеет ширину Δx и длину Δy. Габаритные размеры сетки равняются Lx на Ly с каждой ячейкой, имеющей Pij давление с потоками 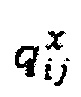 и
и 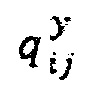 . Как показано на Фиг. 23, декартова сетка 2208.2 может быть использована для вычисления потока текучей среды. Давлениях pij является направленным к центру ячейки, в то время как потоки
. Как показано на Фиг. 23, декартова сетка 2208.2 может быть использована для вычисления потока текучей среды. Давлениях pij является направленным к центру ячейки, в то время как потоки 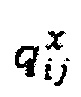 и
и 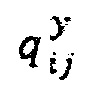 являются гранецентрированными. Таким образом, механическая деформация может быть предсказана без внесения изменений в сообщаемость канала.
являются гранецентрированными. Таким образом, механическая деформация может быть предсказана без внесения изменений в сообщаемость канала.
3.3 Прогнозирование деформации разрыва
Деформация разрыва 2068 может быть выполнена с использованием способов, описанных в отношении способа, показанного на 5.2. Например, деформация разрыва 2068 может включать определения 582 цилиндра и полупространства деформации в соответствии с приложенным напряжением и/или их расширением.
3.3.1 Модель деформации месторождения для цилиндрических колонн
Можно предположить, что детальное распределение канала было приближено к заданному числу колонн с мест расположения (xI, yI) и начальных радиусов (a0I) в пределах этого разрыва (например, при условии, что это происходило непосредственно на входе или через преобразование от подробной геометрии). Может рассматриваться линейный отклик такого набора колонн до заданного напряжения. См., например, Hopkins (1990). Можно также рассматривать более общий подход, включая нелинейное деформирование колонн.
Учитывая заданное напряжение смыкания σn для разрыва с размерами Lx и Ly, как показано на Фиг. 23, может быть предсказана результирующая деформация поверхности разрыва и колонн. Полная нормальная сила, Fn, применительно к разрыву может быть обеспечена следующим образом:

Каждая колонна, I, несет свою часть нагрузки, fI, такой как:

Окружающий пласт месторождения может быть смоделирован с двумя полупространствами. Предполагается также, что обе колонны и пласт месторождения могут деформироваться нелинейно с захватом сочетаний упругих и пластических эффектов. Для упрощения расчетов, что нелинейные эффекты в формировании предполагаются локализованными в зоне, сопоставимой с начальной апертурой разрыва. Следовательно, в дальней зоне взаимодействия между колонны могут быть приняты как линейно упругие. Локализованная нелинейная деформация формирования у колонны I и деформации колонны, включаются частично в деформированную высоту колонны lI. Высота, lI, и радиус, aI, из колонн может быть функцией от силы, которую несет колонна следующим образом:

Эти функции могут быть различными для каждой колонны в связи с отклонениями как в высотах колонн или неоднородности материала в пределах разрыва.
При напряжении смыкания, средняя деформированная высота каждой колонны, lI, может быть совместима со средней апертурой разрыва в месте расположения колонны. Это может быть выражено с помощью системы уравнений совместимости смещения следующим образом:

где локальная апертура является суммой невозмущенного промежутка полупространства, D, и способствованием локальной деформации вследствие воздействия всех колонн. Количество D представляет собой разделение упругих полупространств в отсутствии колонн для удержания их друг от друга. При уменьшении D, силы, оказываемые на столбы, увеличиваются. Предстоящим является определение значение D, вызывающее предписанный уровень давления внутри разрыва.
Предполагается функциональная форма lI (fI), моделирующая потенциально нелинейное поведение колонн. Этот термин может также включать нелинейность в результате местной неупругой деформации формирования под колонной. Предполагается, что влияющие условия, wIJ аппроксимируются с использованием упругих решений для деформации полупространства. Условие самостоятельного влияния, wII представляет собой среднюю дополнительную диафрагму в связи с распределением сил под неровностью I. Средняя деформация чувствительна к полной силе, fI, приложенной к колонне, и пространственному распределению этих сил по поверхности колонны.
Среднее смещение в окружности с равномерным распределением напряжения, 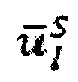 , представлено следующим образом:
, представлено следующим образом:

где Е является модулем Юнга и ν коэффициентом Пуассона. Среднее смещение при жестком круговом ударе, и 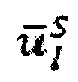 , обеспечиваются следующим образом:
, обеспечиваются следующим образом:

См.: K. Johnson, Контакт Mechanics, ninth printing 2003 ed., Cambridge University Press, 1985 (далее по тексту упоминаемая как “Johnson (1985)”).
Изменение величин апертуры вследствие смещения двух поверхностей является вдвое большим, чем перемещение отдельных поверхностей и может быть записано следующим образом:

где β является 1 для случая жесткой колонны и 32/3π2 ≈ 1,081 для случая равномерной загрузке колонны. Когда указано иное, β=1.
Может также предоставляться приближение для wIJ для случая I≠J. Поскольку детали точного распределения напряжения под каждой колонной не требуются, могут быть использованы приблизительное отклонение вне следа колонны в связи с нагрузкой на точку. Прогиб упругого полупространства за точечной нормальной нагрузкой, fJ обеспечивается следующим образом:
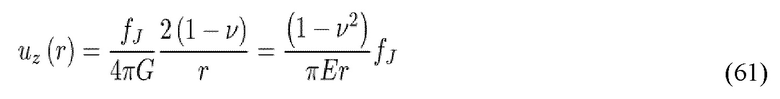
где G является модулем сдвига формирования. См. Johnson (1985). Следовательно, wIJ можно аппроксимировать с использованием суммы отклонения двух полупространств за точечной нормальной нагрузкой, fJ по месту расположения самой колонны, используя следующее:

где

Заметьте, что Уравнение (62) является идентичным влиянию на дальних участках скважины, отмеченной в Уравнении Pyrak-Nolte (2000):

где
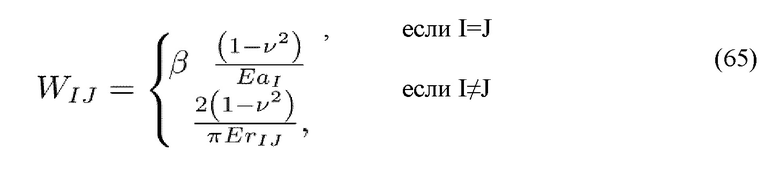
Уравнение дислокации совместимости (57) становится:

при условии ограничения на общий уровень напряжения, как описано в уравнении (54). Уравнение (66) является потенциально нелинейным в fJ, в зависимости от функциональной формы lI. Кроме того, WII условия включают aI, которая также может быть функцией fI.
3.3.2 Линеаризация функциональных форм для L и F/A
Условие lI на правой части уравнения (66) и fI/aI условие в wII вводят fI неявным образом. Следовательно, lI и fI/aI могут быть расширены следующим образом:

ClI является постоянной величиной, охватывающей линейную зависимость изменения ширины колонны с напряжением и индексом 0 указывающая на некоторое эталонное состояние. CfaI является постоянной величиной, которая может быть получена за счет расширения fI/aI с использованием начального наклона aI. Это может быть переписано следующим образом:
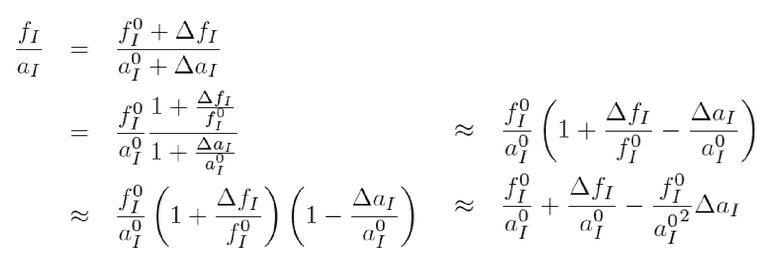
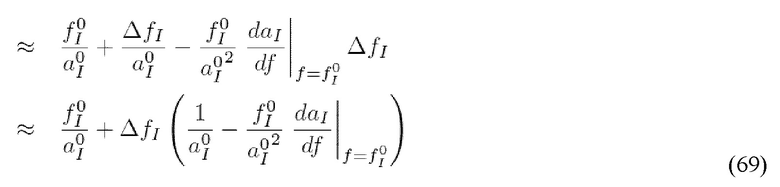
и, сравнивая с Уравнением (68) представляет следующее:

где начальный наклон aI может быть получен с помощью эксперимента или другого анализа. В часто предполагается линейной упругой случае, столбы могут не распространяться, а следовательно, da/df=0 и CfaI=1/a0I. Уравнение (66) можно переписать следующим образом:
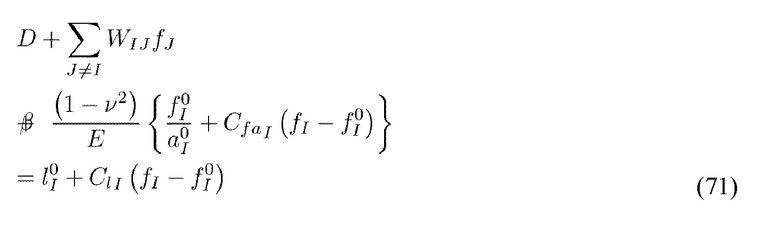
Решение для изменения силы и дислокации в удаленных местах скважины может быть многократно рассмотрено следующим образом:

под нарастающим напряжением, где верхний индекс 0 относится к решению от предыдущего напряженного состояния, уравнение (66) можно переписать следующим образом:
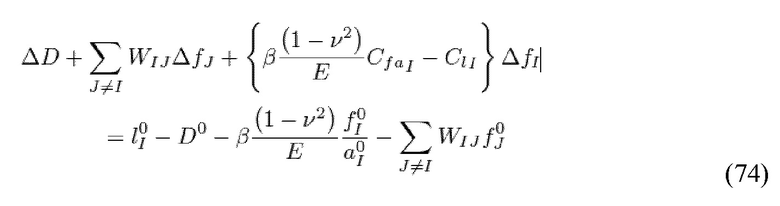
Следовательно, линейная система может быть решена следующим образом:


для неизвестных ΔfI и ΔD где
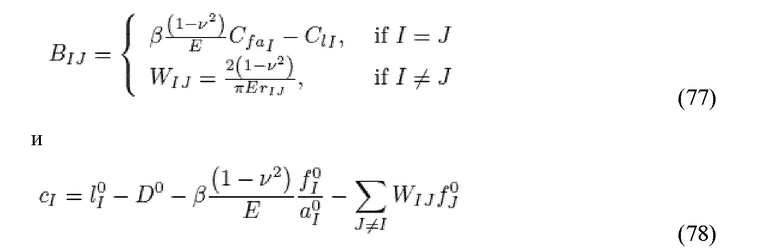
Для случая линейной упругой колонны, ClI можно соотнести обратно с продольным модулем.
Определение M представляет следующее:

где

Совмещение этих уравнений представляет следующее:
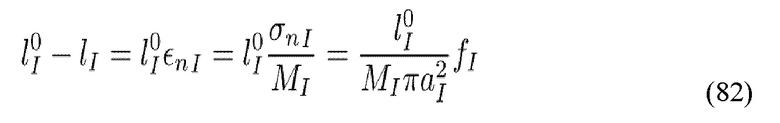
и, сравнение с Уравнением (67) представляет следующее:

В частности, в случае использования линейной упругой колонны. Способ, представленный здесь, остается целостным и рассматривает нелинейный случай.
3.3.3 Решение линеаризованных систем
В рамках каждого шага нелинейного прибавочного напряжения, обеспечивается повторяющееся решение с использованием решений с предыдущего нелинейной стадии в качестве начального приближения для решения каждой последующей итерации. Систему уравнений, описываемую уравнением (76), можно считать плотным с уменьшенным кондиционированием. Уравнения могут быть нормированы так, что все записи имеют одинаковую величину. Предположим, предусматривается n колонн, пронумерованных от 0 до n - 1, то n + 1 одновременные уравнения генерируются следующим образом:

где определяется следующее:
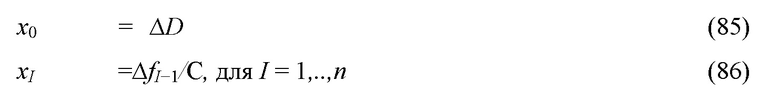
где

и
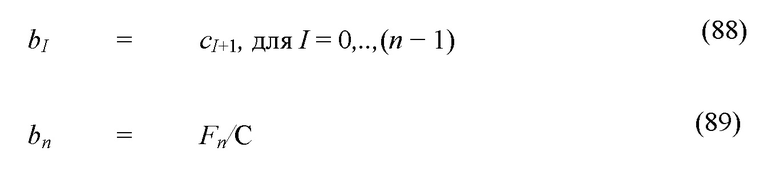
и
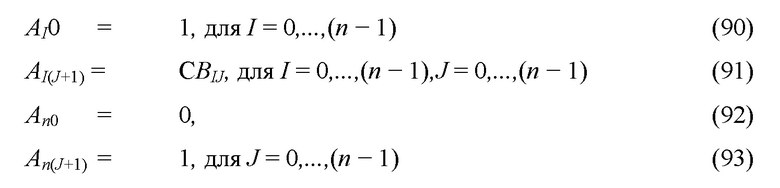
Таким образом, величина доминирующих условий в каждой линии линейных уравнений может иметь порядок 1. На практике самостоятельный вклад, BII, является большим, чем другой BIJ, который представляет перекрестные взаимодействия между колоннами.
Например, если все колонны имеют одинаковые свойства, то CBII = 1. Если остальные элементы вводных CBIJ обозначаются как 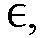 следующая матрица с единицами (1s) предоставляется в следующих местах расположения:
следующая матрица с единицами (1s) предоставляется в следующих местах расположения:

Асимметрия, введенная дополнительным уравнением для баланса сил, приводит к матрице с ограниченной кондиционирования. Следовательно, подходящий предобуславливатель, P, разработан таким образом, что P−1A имеет более низкое число предобусловливателя, чем А. Поскольку значения являются малыми, предобуславливатель получается, выбирая следующее:

с соответствующей инверсией, как указано далее:
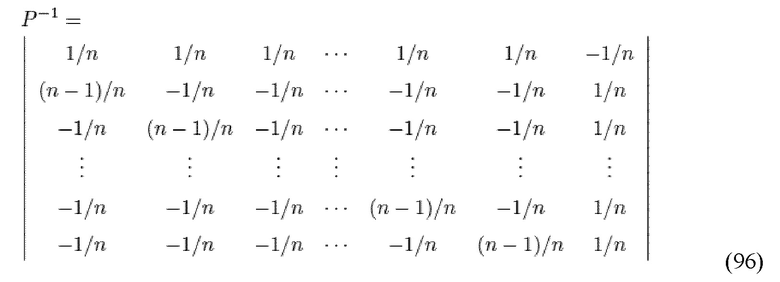
Итеративное решение касательно обусловленной системы может быть обеспечено следующим образом:

используя стабилизирующий способ бисопряженного градиента. См., например, H. A. van der Vorst, Bi-cgstab: A Fast And Smoothly Converging Variant of Bi-Cg For The Solution Of Nonsymmetric Linear Systems, SIAM J. Sci. Stat. Comput. 13 (2) 631644, doi:10.1137/0913035 (1992), полное содержание которого включено в данное описание в качестве ссылки.
3.3.4 Алгоритм точки соприкосновения
Точки соприкосновения могут быть добавлены с помощью способов, описанных со ссылкой на Фиг. 5.2 и/или как дополнительно описано в этом разделе. Для каждой дополнительной обнаруженной точки соприкосновения часть способа 256 на Фиг. 5.2, и/или 2056 на Фиг. 20 может быть повторена.
С возрастанием напряжения, приложенного к каналам внутри разрыва, у поверхностей разломов в пределах открытых каналов появляется возможность вступить в контакт в "точках соприкосновения". Присутствие таких точек может снизить проводимость внутри разрыва. Такие точки соприкосновения также могут подвергаться давлению, что приводит к нелинейности. Если пренебрегать напряжением, переносимым на точки соприкосновения, колонны вокруг несут нагрузку, а каналы могут закрыться преждевременно. При высоких уровнях давления, фракции общей нагрузки могут рассматриваться на таких точках соприкосновения. Как следствие, методы, которые пренебрегают механикой точек соприкосновения, могут недооценивать проводимость напряженного разрыва.
Механика точек соприкосновения может приниматься во внимание путем обработки как виртуальных колонн, которые вводятся в расчет напряжений, если контакт обнаружен по месту их нахождения. В начале расчета может быть идентифицирован список потенциальных точек соприкосновения для мониторинга на регулярной сетке. Расстояние между точками соприкосновения может быть выбрано автоматически в зависимости от размера колонн (например, такой размер, что 5 точек соприкосновения охватывают средний размер колонны). Любая точка прикосновения-кандидат, попадающая в пределы существующего компонента, может быть удалена из списка. Механика точек соприкосновения может включать создание списка точек прикосновения, постепенно обеспечивающих напряжение, определяющих деформацию 2068 с перечнем точек соприкосновения, регулируя (например, добавление/удаление) точки соприкосновения, удаление точек соприкосновения под давлением, сортировку списка точек перекрытия от большей к меньшей, добавляя часть мест в точках перекрытия в список точек соприкосновения в порядке от наибольшего перекрытия до наименьшего перекрытия, повторяя постепенно обеспечиваемое напряжение до момента достижения целевого уровня напряжения. Реализация механики точек соприкосновения продолжается путем повторения 2068.2 линеаризации, 2068.3 монтажа и 2068.4 решения (см. например, вышеуказанный раздел 3.4.2) для каждой точки соприкосновения.
IV. ОПРЕДЕЛЕНИЕ ПРОВОДИМОСТИ РАЗРЫВОВ
Проводимость разрыва может быть определена 266, как описано со ссылкой на Фиг. 2-6. Эти подходы включают получение состояния деформированной колонны (lI, aI, fI) и результирующую деформированную диафрагму разрыва при наборе произвольных точек в пределах разрыва. Средства для определения 266 влагопроводности деформированного разрыва (Фиг. 20) могут также включать растворение потока в разрыве, используя полностью 3-D численные методы. В тех случаях, когда необходимы сниженные приведенные вычислительные затраты, может производиться аппроксимация смазки внутри разрыва и уменьшение размерности численного решения касательно 2-D. См., например, Pyrak-Nolte (2000) и вышеуказанный Раздел 3.4.3 выше.
Давления pij в декартовой сетке (Фиг. 23) являются направленными к центру и индексируются с использованием i и j так, что:

Право текущие и восходящие объемные потоки (единицы объема в единицу времени) от ячейки i, j определены на лицевых сторонах ячеек (Фиг. 23) и обозначаются qijx и qijy соответственно.
Решение для поля давления пор может быть получено требованием сохранения массы жидкости в разрыве, в то время как поток индуцируется между входным и выходным давлением граничного условия. Суммарный объемный поток, входящий в ячейку i, j, можно отобразить

Потоки могут быть получены с использованием местных проводимостей для связывания падения давления для индуцирования потока:
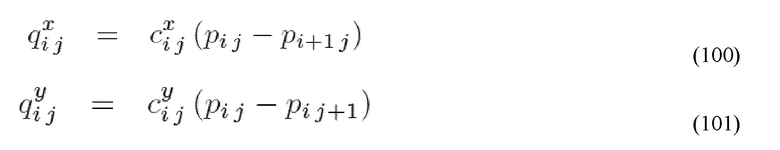
где проводимости, cxij и cyij, зависят от того, что занимает соответствующую ячейку. В том случае, если ячейка находится в пределах открытого канала, проводимость берется в виде приближения для потока между двумя пластинами. Если ячейка находится в пределах проппантной колонны, она рассматривается как пористая среда, и проводимость рассчитывается по закону Дарси. Если колонна представляет твердые породы, ячейка считается имеющей низкую проницаемость. См., например, Morris (2014). Проводимости используют средние показатели отверстий ячеек, соединенных следующим образом:
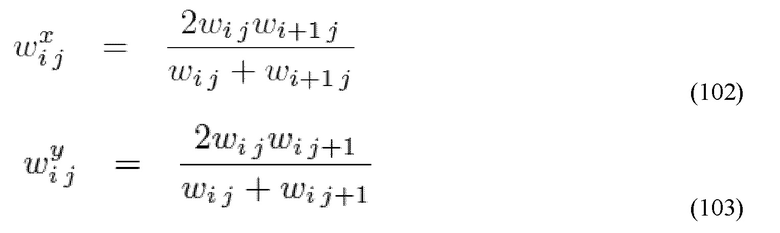
Проводимость в открытых ячейках задается по следующиму кубическому закону:
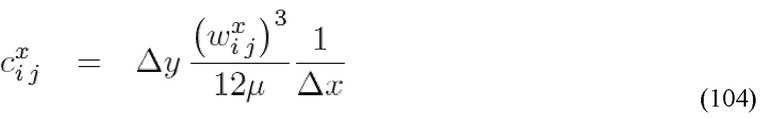
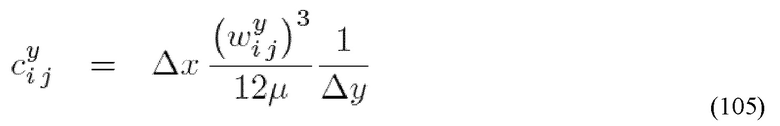
Аналогично, для клеток-ячеек в пределах колонн, средний коэффициент проницаемости для использования между двумя ячейками обеспечивается следующим образом:
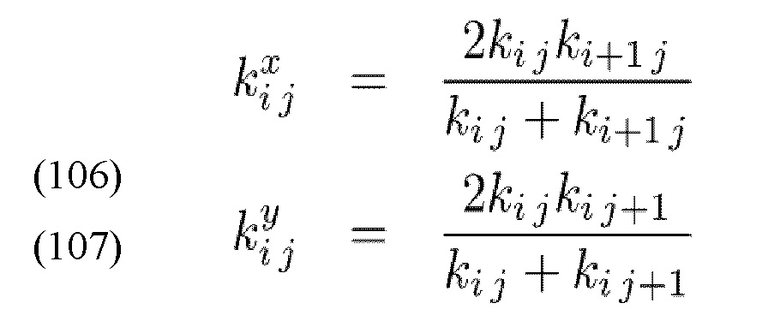
и проводимость вычисляется с использованием закона Дарси в отношении уплотненного материала следующим образом:

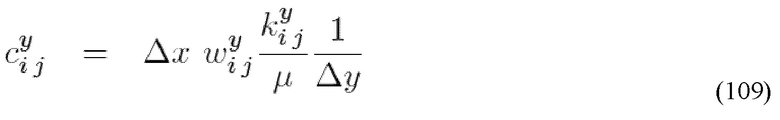
Для каждой некрайней точки условия, уравнение для поля давления, требующие сохранения массы могут быть получены:

Подставляя потоки граней элементарных ячеек, предусматривается следующее:
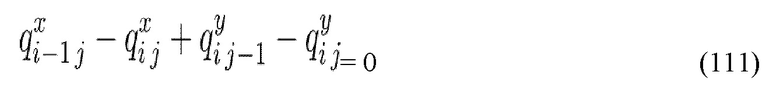
и выражая потоки с точки зрения торцевых проводимостей и перепадов давления, обеспечивается следующее:
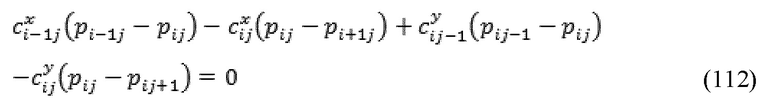
дискретное уравнение сохранения потока для ячеек i, j может быть получено следующим образом:
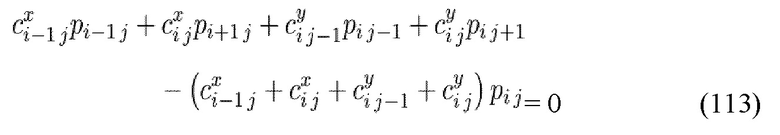
Для оценки х-проводимости система подвержена следующим граничным условиям:

в то время как для оценки у-проводимости система подвержена граничным условиям:

Граничные условия (либо Уравнения (114115) или уравнения (116117)) подставляются в систему уравнений (113) и собраны в линейную систему:

до прохождения системы к линейному решателю. Для получения поля давления используется прямой разреженный решатель.
Как только были получены давление, Pij, торцевые потоки могут быть вычислены из (100101), а затем могут быть вычислены общие входные и выходные потоки. Из этих полных потоков, может быть выведена проводимость трещины.
V. ОБОСНОВАНИЕ
Элемент (проверка) может быть определена 269, как описано со ссылкой на Фиг. 2-6. Обоснование также может быть выполнено с использованием методов, описанных в разделах III и IV. Обоснование 269 может быть выполнено, чтобы проверить проводимость разрыва 266. Обоснования также могут быть выполнены, чтобы проверить методы, используемые при моделировании. Примеры обоснований предоставляются.
5.1 Обоснование Проводимости
Обоснование 269 может быть выполнено для проверки определенной проводимости разлома 266. Рассматриваются две проблемы касательно обоснования участием потока внутри открытого, нерасклиненного разрыва и потока через равномерно расклиненный разрыв. Разрыв может быть увязан с примерно квадратными элементами. Для того чтобы проверить реализацию уравнений для Δx6= Δy и Lx6 = Ly, рассматривается дискретизация разрыва со свойствами, перечисленными в нижеприведенной таблице 2, что включает высокий формат отношения области и нетипично высокий коэффициент аспекта вычислительных элементов.
В Таблице 3 приведены геометрические свойства разрыва, используемого для проверки реализации способа для потока через открытый разрыв и поток через однородно расклиненный разрыв. Соотношение элементов выбрано намеренно, чтобы быть нереально высоким, чтобы проверить надежность реализации способа.
5.1.1 Пример - Проводимость - Сквозной Поток через Открытый Канал
Поток между двумя пластинами задается по следующим кубическому закону:

где L и W являются длинами разрыва в направлении, параллельном и перпендикулярном потоку, соответственно, w это разрыв между пластинами, Δp, выражает падением давления в направлении потока и μ является вязкостью жидкости. Когда модель на Фиг. 20 используется для вычисления проводимости открытого разрыва, дискретизированного в соответствии с Таблицей 2, получают сравнение с аналитическими результатами, полученными с помощью уравнения (119), как показано в Таблице 3 ниже:
Таблица 4 приводит сравнение между аналитическим решением для потока между двумя пластинами, используя дискретизацию, описанную в Таблице 3. Между кодом и аналитическим решением наблюдается погрешность менее 0,01%, предполагая, что реализация является точной для обеих неквадратных областей и неквадратных элементов потока.
5.1.2 Пример - Проводимость - сквозной поток через канал заполненный проницаемым материалом
Игнорируя краевые эффекты, поток через прямоугольную кубовидную проницаемую среду, зажатую между двумя пластинами, определяется по формуле:

где L и W являются длинами разрыва в направлении, параллельном и перпендикулярном потоку, соответственно, ж это разрыв между пластинами, Δp, является падением давления в направлении потока, μ является вязкостью жидкости и к магнитной проницаемостью пористой среды.
Подобным образом, как и в предыдущем разделе, считается, что поток проходит через ту же геометрию разрыва (Таблица 3). На этот раз поток содержит 300 D проницаемости материала (например, сжатый песок используют для поддержания гидроразрывов). Потому что проблема является линейной, любой конечный выбор проницаемости подходит для целей проверки уравнения.
В нижеприведенной Таблице 4 ниже показывается, что результаты согласуются с 6 значащими значениями, предполагая реализацию потока через пористую среду даже для высокого аспекта элементов отношения и вычислительных областей:
Таблица 4 приводит сравнение между кодом и аналитическим решением для потока между двумя пластинами, расклиненными однородно с 300 D проницаемого материала (например, проппанта), используя дискретизацию, приведенную в Таблице 3.
5.1.3 Пример - Проводимость - Конвергенция Для Гетерогенного Заполненного Разрыва
Применение метода к гетерогенному расположению проппанта в разрыве может быть проверено. Может быть установлено какое количество ячеек необходимо на каждой колонне, чтобы сделать достаточно точный прогноз проводимости разрыва. Чтобы это проверить, были дискретизированы системы колонн, показанных на Фиг. 24.1 и 24.2, с увеличением числа клеток потока, na, охватывая радиус а = 1м из колонн.
На Фиг. 24.1 показана схема, изображающая разрыв 2412.1, показывающий систему гетерогенного проппанта 2414.1 рассматриваемую для конвергенции потока исследования. На Фиг. 24.2 показана схема, изображающая декартову сетку 2412.2, отображающую дискретизацию соответствующего na = 4, где 4 ячейки используются через радиус каждой колонны 3414.2. В таблице 5 ниже сравнивается предсказанная проводимость для диапазона дискретизаций разрыва:
В Таблице 5 представлены результаты конвергенции исследования для вычисления расхода с увеличением числа элементов, охватывающих радиус а=1м, из колонн, показанных на Фиг. 24.1 и 24.2.
Даже при относительно грубых сетках (например, na=4, как изображено справа на Фиг. 24.2), достигаются прогнозы проводимости, которые находятся в пределах 5% самого высокого рассматриваемого разрешения (na = 128). Таким образом, теперь предполагается, что na = 4.
5.2 Обоснование моделей путем сравнения
Обоснование 269 может быть выполнено для того, чтобы сравнить различные методы, используемые в данном документе. Такие валидации могут включать в себя сравнение одного или более из моделирований и/или результатов, представленных здесь.
5.2.1 Пример - Модель сравнения для линейных геoмеханических деформаций
Моделирование с использованием аналитического метода может сравниваться с более подробными моделями "неровности", которая сама по себе была подтверждена и проверена в отношении многочисленных аналитических решений. См., например, Morris (2014) и Pyrak-Nolte (2000).
Методы повышенной точности могут предполагать, что особенности конструкции корпуса разрыва представлены обычной сеткой "неровностей" одинакового радиуса, имеющих разную высоту и механические свойства. Это позволяет модели неровности осуществлять дискретизацию сложных форм. Более быстрая модель позволяет иметь круглые колонны разного радиуса и произвольного месторасположения. Для оказания помощи в прямом сравнении между кодами, можно рассматривать разное количество колонн, организованных по обычной сетке с шагом 0,5 м в разрыве, охватывающем 5 м на стороне со свойствами в нижеприведенной Таблице 6:
Таблица 6 предоставляет механические и геометрические свойства разрыва, использованные для нижеуказанных первой, второй и третьей проблем верификации.
Выбор β может быть сделан, чтобы сравнить то, что предполагается с внутренней моделью неровности. Сетка модели неровность использует размер 0,5 м, в то время как наша модель работает быстро, используя радиус колонны 0,282095 м для получения колонны с той же площадью, что и 0,5 м на 0,5 м неровностей.
В таблице 7 ниже изображает относительную погрешность между моделью неровностей и способом, предусмотренным в настоящем документе для трех проблем верификации 1-3.
Модель неровностей использует более точную функциональную форму для деформации, а не аппроксимацию дальних частей скважины. Следовательно, наибольшее количество погрешностей в точках, близких к колонне. Таблица 7 сообщает, что относительная погрешность моделирования указывает на то, что в среднем погрешность составляет менее 0,1%, и указывает на то, что максимальная ошибка составляет 1,5%.
Первая проблема верификации рассматривает одну колонну, расположенную в точке х=1,25, у=3,75 с начальной высотой 5 мм, под действием напряжению смыкания равному 0,75 МПа. Модель неровности показана на Фиг. 25.1, наряду со сравнением двух подходов, как показано на Фиг. 25.2.
Фиг. 25.1 представляет собой график 2500.1, имеющий размеры у (м) (ось у) от х (м) (ось х) и отображающий точку неровностей на основе 2516 контакта для первой задачи проверки. Фиг. 25.2 представляет собой график, изображающий 2500.2 диафрагмы (мм) (Y-ось) в зависимости от х (м) (ось х). График 2500.2 является сравнением между моделью неровностей (RapidSHAC) и нелинейной моделью расширения с использованием методов, указанных здесь, в отношении нескольких различных внешних линий (SHAC в у = 1,75, 3,25, и 3,75) в пределах области.
Соответствие между сравниваемыми моделями является почти точным около центра колонны и на одинаковых расстояниях от колонны. Однако модель неровности использует более точную функциональную форму для деформации, а не только приближение дальних участков скважины. Следовательно, наибольшее количество погрешностей в точках, близких к колонне. Таблица 8 сообщает, что относительная погрешность моделирования указывает на то, что в среднем погрешность между двумя методами составляет менее чем 0:1%, а максимальная полученная погрешность составляет 1:5%.
Вторая проблема обоснования рассматривала три колонны 5 мм в высоту, расположенные в координатах (х, у)=(1:25; 3:75), (3:25; 3:25) и (2:75; 1:75), подвергающиеся давлению смыкания, равному 3 МПа. Модель неровности показана на Фиг. 26.1, наряду со сравнением двух моделей, как показано на Фиг. 26.2.
Фиг. 26.1 представляет собой график, 2600.1, имеющий координаты у (м) (Y-ось) в зависимости от х (м) (ось х) и изображающий контактные точки неровности 2616 на второй проблеме обоснования. Фиг. 26.2 представляет собой график, изображающий 2600,2 диафрагмы (мм) (Y-ось) в зависимости от х (м) (ось х). График 3600,2 представляет сравнение между моделью неровностей (RapidSHAC) и нелинейной моделью расширения, указанной здесь, для нескольких различных внешних линий (SHAC в у = 1,75, 3,25, и 3,75) в пределах области. Стоит повторно отметить, что соответствие между ними двумя находится почти точно в центре колонны и на равных расстояниях от колонны, с крупнейшим расхождением в областях, ближайших к колоннам.
Третья проблема обоснования рассматривает те же самые три колонны с различными высотами для дальнейшего тестирования нелинейной модели расширения. Колоннам, расположенным на (х, у)=(1,25; 3,75), (3,25; 3,25), и (2,75; 1,75) были приданы высоты 4 мм, 5 мм, и 5,5 мм соответственно и были подвергнуты напряжению смыкания 2 МПа.
Вычислительная модель неровностей показана на Фиг. 27.1 и 27.2 вместе со сравнением двух моделей. Фиг. 27.1 представляет собой график, 2700.1, имеющий координаты Y (м) (Y-ось) в зависимости от х (м) (ось х), изображающий сравнение между симуляциями неровностей с высокой разрешающей способностью, имеющих среднюю апертуру 2,07 мм и проводимость 58,3 D·м.
Фиг. 27.2 представляет собой график, 2700.2, имеющий координаты Y (м) (Y-ось) в зависимости от х (м) (ось х), изображающий нелинейное расширение модели прогнозирования распределения диафрагмы, имеющей среднюю апертуру 1,97 мм и проводимость 25,9 D·м в пределах разрыва с необычным геометриями колонн. Поз.2700.1, 2700.2 указывают на соответствие между двумя прогнозами изменения диафрагмы внутри областей канала.
Стоит повторно отметить, что соответствие между ними двумя находится почти точно в центре колонны и на равных расстояниях от колонны, с крупнейшим расхождением в областях, ближайших к колоннам.
В целом, нелинейная модель расширений показывает соответствие с моделью неровностей для ожидаемых районов области, и в других местах расхождения находятся в пределах нескольких процентов относительной погрешности.
5.2.2 Пример - Модель сравнения для геометрий сложных колонн
Подход, основанный на неровностях, представляет проппант с использованием декартовой сетки для обоих потоков и проводимости. См., например, Pyrak-Nolte (2000). В этом разделе, метод нелинейного расширение, используя баллоны для геомеханики и сетки для потока, сравнивается с мелкоотверстными моделями неровностей для более общих геометрий колонн. Результаты сравнения, показанные на Фиг. 28, указывают на согласование двух методов.
Фиг. 28 представляет собой график, 2800, изображающий сравнение между двумя моделями Фиг. 27.1 и 27.2. Фиг. 28 иллюстрирует сравнение между моделью неровности и нелинейной моделью расширения для нескольких различных внешних линий в пределах области для обоснования проблемы 3.
Нижеприведенные Таблицы 8 и 9 отображают параметры моделирования, в том числе механические и геометрические свойства разрыва, используемые для проблемы обоснования общей геометрия колонн (вышеуказанный раздел 5.2.1).
Моделирование неровности спрогнозировало окончательную среднюю апертуру 2,07 мм, по сравнению с нашим модельным прогнозом 1,97 мм. Кроме того, моделирование неровности предсказало проводимости 58,3 D·м в отличие от нового быстротекущего прогноза 25,9 D·м.
В целом, средняя диафрагма обладает точностью, приблизительно равной 5%, тогда как проводимость согласуется в пределах фактора примерно равного 2. Расчет проводимости чувствителен к небольшим изменениям в отверстие или геометрии, указывая на то, что согласование является приемлемым.
5.2.3 Пример - модель сравнение для нелинейных проблем содержащие точки соприкосновения
Механика точек соприкосновения может быть удовлетворена с помощью тонкой дискретизации поверхностей разрушения и обнаружения контакта. См., Pyrak-Nolte (2000). Изменение апертуры предсказало нелинейный подход к расширению с и без точек соприкосновения по сравнению с подходом на основе неровностей на Фиг. 29.1-29.3 касательно двух колонн, подвергнутых нагрузке, достаточной для частичного закрытия каналов между ними.
Фиг. 29.1-29.3 представляют собой графики, имеющие 2900.1-2900.3 у (м) (Y-ось) против х (м) (ось х), изображающие сравнение между неровностями моделирования с высокой разрешающей способностью, имеющие среднюю апертуру 2,07 мм и проводимость 58,3 D·м. Фиг. 29.1 показывает неровности на основе моделирования с высоким разрешением (1,1 мм средней диафрагмой и 19 D·м проводимостью), Фиг. 29.2 демонстрирует нелинейную модель расширения без точек соприкосновения (0,71 мм средняя апертура и 0,0012 D·м проводимость), и Фиг. 29.3 показывает нелинейную модель расширения с точками соприкосновения (0,9 мм средняя апертура и 4,6 D·м проводимость). Эти модели, как показано на графиках 2900,1-0,3, указывают на соглашение между прогнозами диафрагмы и проводимостью при условии принятия в расчет механики точек соприкосновения.
Таблица 10 демонстрирует параметры моделирования, в том числе механические и геометрические свойства разрыва, используемого для проверки проблемы точек соприкосновения.
Таблица 10 демонстрирует численные результаты расчетов. В этом примере, игнорирование точками соприкосновения привело к 5-порядковому уменьшению предсказанной проводимости по сравнению с подходом на основе неровностей. Таблица 11 приводит сравнение между моделью неровности и нелинейной моделью расширения, разработанной для испытания с точками соприкосновения.
При включении точек соприкосновения в пределах фактора, примерно равного 4 предсказания на основе неровности, расчет проводимости может быть чувствителен к небольшим изменениям в отверстии или геометрии. Следовательно, этот уровень может считаться приемлемым.
5.3 Сравнение функционирования
Эффективность различных моделей может быть подвергнута сравнению. Для облегчения применения метода по отношению к большому количеству разрывов, код, используемый в различных симуляциях, может быть распараллелен через многопоточности, такую как многопоточность OpenMP. Модель может быть применена ко многим (потенциально сотням) отдельных трещин, содержащих десятки или сотни колонн/каналов. Расчеты для каждого разрыва могут рассматриваться отдельно и осуществляться в потокобезопасном виде.
5.3.1 Пример - расчет деформации функционирования
Методы неровностей могут рассмотреть полностью произвольные комбинации геометрии колонны с шероховатостью разрыва и подробных дополнительных точках соприкосновения в условиях нагрузки. См., например, Pyrak-Nolte (2000) и Morris (2014). Десять или более элементов неровностей могут использоваться вдоль одной колонны или канала, с целью фиксации механических деформаций. Модели могут использовать более ограниченную внутреннюю дискретизацию колонн и могут быть более эффективными, чем метод неровности на основе случая круговых колонн.
Выполнение расчета деформации с использованием модели нелинейного расширения настоящего изобретения может быть подвергнуто сравнению с моделью неровности (см., например, Morris (2014)) для одного разрыва, содержащего 330 круглых колонн. Обе модели могут быть запущены однопоточно с целью упрощения сравнения производительности при ядре 2,4 ГГц. Время выполнения требует модели неровности, как показано в таблице 12 ниже:
элементы)2
Таблица 12 обеспечивает время выполнения для решения гидроразрыва с 330 колоннами с моделью неровностей с увеличением разрешения. В отличие от этого, при сопоставимой проблеме, быстро работающая модель, представленная в этой заявке, продемонстрировала результат выполнения, равный примерно 0,1 с.
Для осуществления решений по 10 элементам по всей колонне, модель неровности принимает в течение 40 минут. Затраты расчета неровности примерно пропорциональна квадрату числа элементов. Для сопоставимой проблемы с участием 330 колонн, метод нелинейного обобщения занимает около 0,1 с.
5.3.2 Пример - объединенная деформация и функционирование расчета проводимости
В качестве примера, нелинейная модель расширений в однопоточном режиме была использована для моделирования трех HPP геометрий, показанных на Фиг. 30.1-30.3. Эти результаты дают графики 3000.1-3000.3, содержащие 100, 400 и 900 колонны, соответственно, в пределах одного разрыва. На Фиг. 30.1-30.3 изображают системы гетерогенных проппантных колонн, рассмотренных исследованиями скорости работы программы.
Полученные значения выполнения приведены в Таблице 13 следующим образом.
Таблица 13 описывает производительность многопоточности для задачи с 64 разрывами с 400 колоннами в каждом (всего 25 600 колонн). NThreads отображает количество потоков и TWall отображает так называемое принятое "стенное (фактическое) время".
Для идеальной параллелизации фактическое время обратно пропорционально числу витков резьбы. Следовательно, произведение, NThreadsTWall, в идеале должно быть постоянным. Результаты показывают масштабирование с потерей эффективности против однопоточного способа в 36%, при увеличении количества потоков от 1 до 8 для этой конкретной проблемы. Таблица 14 показывает единое резьбовое исполнение нелинейной модели расширения для увеличения числа колонн в пределах разрыва при ядре 2,4 ГГц. Время выполнения на ядре 2,4 ГГц является вопросом секунд.
Для исследования многопоточного функционирования проблемы, в том числе 64 разрывов, содержащих 400 колонн, были рассмотрены с использованием 1, 2, 4 и 8 порожденных процессов, работающих на ядрах 2,4 ГГц. Таблица 14 ниже указывает время исполнения, достигнутое путем присвоения каждому потоку равного количества разрывов для расчета.
Эти результаты отражают масштабирование с потерей примерно 1/3 эффективности при масштабировании от 1 до 8 порожденных процессов.
Предшествующее описание было представлено со ссылкой на некоторые варианты осуществления. Специалисты в данной области техники и технологии, в которой относится данное изобретение, поймут, что модификации и изменения в описанных структурах и способах функционирования могут быть осуществлены без существенного отклонения от принципа и объема данного способа. Например, в то время как система и способ, представленные здесь, были описаны с конкретной ссылкой на операции гидроразрыва, можно понять, что система и способ также могут применяться к другим стимулирующим операциям для пластов, таким как кислотная обработка. Кроме того, в то время как лишь ограниченное число реализаций изобретения были использованы в качестве примеров, следует понимать, что любое количество реализаций изобретения может быть выполнено и оценено. Соответственно, вышеприведенное описание не следует рассматривать как относящееся исключительно к конкретным структурам и рабочим процессам, описанным и показанным на прилагаемых чертежах, а следует рассматривать как согласуемое и поддерживающее последующую формулу изобретения, которая должна рассматриваться во всем своем полном и самом надлежащем объеме.
При разработке любого такого фактического варианта осуществления, многочисленных вариантов реализаций, должны быть приняты конкретные решения для достижения конкретных целей разработчика, такие как соответствие с ограничениями, связанными с системой и бизнес-операциями, которые различаются от одного варианта реализации к другому. Кроме того, следует понимать, что такие усилия по разработке могут быть сложными и занимать много времени, но, тем не менее, будут являться обычными действиями для специалистов в этой области техники, использующих преимущества данного изобретения. Кроме того, состав, используемый/описываемый в этом документу, может также содержать некоторые другие компоненты, отличающиеся от упоминавшихся. В этом подробном описании каждое числовое значение следует читать один раз как содержащее поправку "приблизительно" (если такое изменение уже не было прямо внесено), а затем прочитать снова, без такой поправки, если иное не указано в контексте. Кроме того, в данном подробном описании, следует понимать, что считается, что диапазон концентраций, указанный или описанный как полезный, подходящий или подобный этому, включает в себя любую и каждую концентрацию в диапазоне, в том числе конечные точки и должен рассматриваться, как указанный. Например, «диапазон от 1 до 10» следует рассматривать как указание на каждый и все возможные номера вдоль промежутка между примерно 1 и примерно 10. Таким образом, даже если конкретные точки данных в пределах диапазона или отсутствие точек данных в пределах диапазона четко определены или относятся только к нескольким конкретным, следует понимать, что изобретатели оценивают и понимают, что любые и все точки данных в диапазоне, должны рассматриваться как указанные, и что изобретатели обладали знаниями в отношении всего диапазона и всех точек в пределах диапазона.
Заявления, сделанные в данной заявке, только лишь предоставляют информацию, связанную с настоящим изобретением и не могут являться известным уровнем техники, а также могут описывать некоторые варианты осуществления, иллюстрирующие изобретение.
Хотя всего несколько примеров вариантов осуществления были описаны подробно выше, специалисты в данной области техники легко поймут, что возможны множественные модификации в примерах вариантов осуществления без существенного отклонения от системы и способа для выполнения стимулирующих операции в стволе скважины. Соответственно, все такие модификации считаются включенными в объем настоящего изобретения, как указано в нижеследующей формуле изобретения. В формуле изобретения считается, что пункты, описывающие средство-плюс-функцию, охватывают конструкции, описанные в данном документе, как выполняющие указанную функцию, а не только структурные эквиваленты, но и эквивалентные структуры. Таким образом, хотя гвоздь и винт могут не являться структурными эквивалентами, поскольку гвоздь использует цилиндрическую поверхность для скрепления деревянных частей вместе, в то время как винт использует винтовую поверхность, в среде скрепления деревянных частей гвоздь и винт могут быть эквивалентными структурами. Прямым намерением заявителя является желание не обращаться к 35 U.S.C. § 112, пункт 6, в отношении любых ограничений любой формулы изобретения, содержащейся в данном документе, за исключением тех, в которых формула изобретения прямо использует слова «средство для» месте с соответствующей функцией.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ГИДРОРАЗРЫВА ПРОДУКТИВНОГО ПЛАСТА | 2011 |
|
RU2453695C1 |
| Способ сохранения безопасного диапазона проводимости трещины при выводе на режим скважины с ГРП | 2020 |
|
RU2745684C1 |
| СПОСОБ ИНТЕНСИФИКАЦИИ РАБОТЫ СКВАЖИНЫ | 2013 |
|
RU2536524C1 |
| СПОСОБ ГИДРОРАЗРЫВА ПОДЗЕМНОГО ПЛАСТА (ВАРИАНТЫ) | 2006 |
|
RU2404359C2 |
| СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА | 2011 |
|
RU2453694C1 |
| Способ определения геометрии трещин ГРП с учетом разделения и взаимодействия потоков жидкости ГРП между трещинами | 2022 |
|
RU2786303C1 |
| СПОСОБ ВЫПОЛНЕНИЯ СТИМУЛИРУЮЩИХ ОПЕРАЦИЙ С РАЗМЕЩЕНИЕМ СМЕСИ ПРОППАНТОВ | 2023 |
|
RU2833624C1 |
| Способ интенсификации работы скважины | 2019 |
|
RU2720717C1 |
| СПОСОБ ИНТЕНСИФИКАЦИИ РАБОТЫ СКВАЖИНЫ | 2014 |
|
RU2551586C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБЫ ПРОГНОЗИРОВАНИЯ РИСКОВ ГИДРОРАЗРЫВА ПЛАСТА | 2017 |
|
RU2730576C1 |
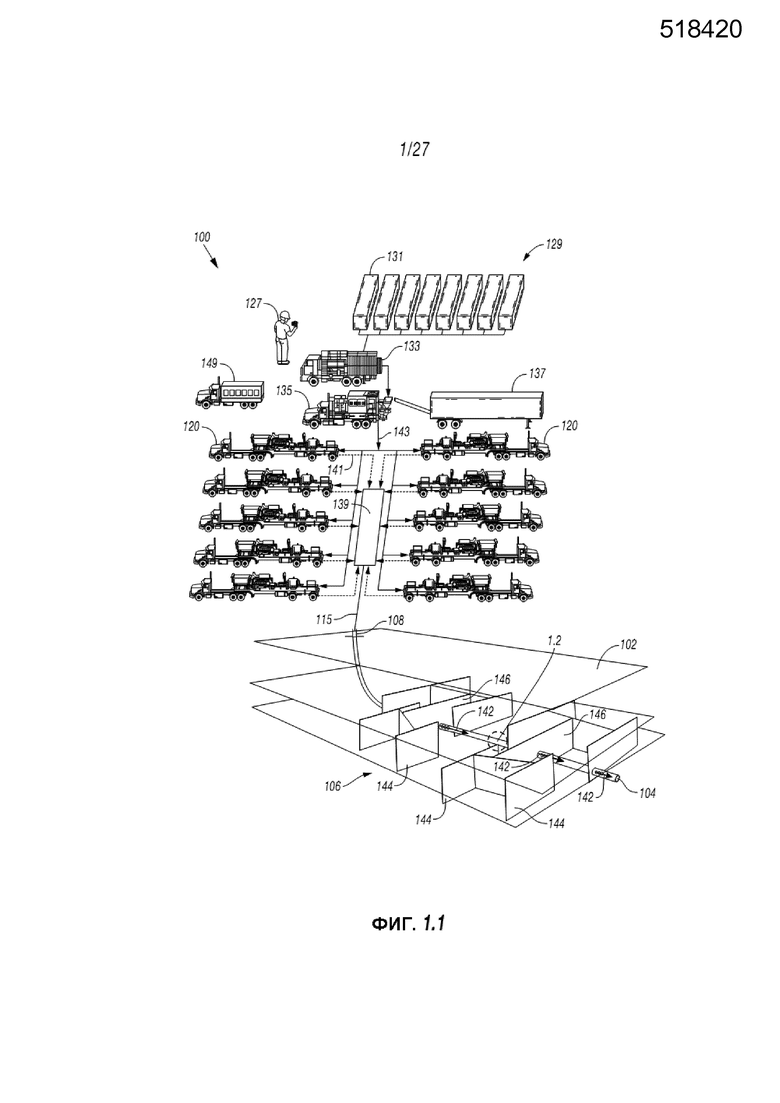
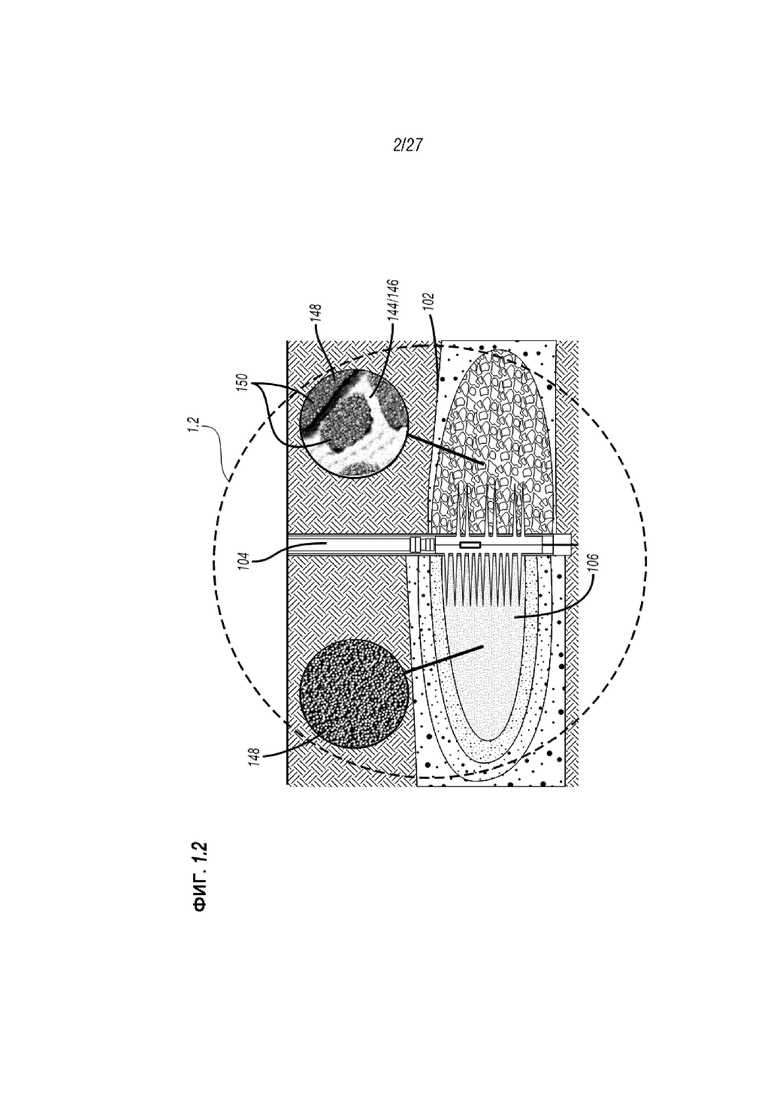
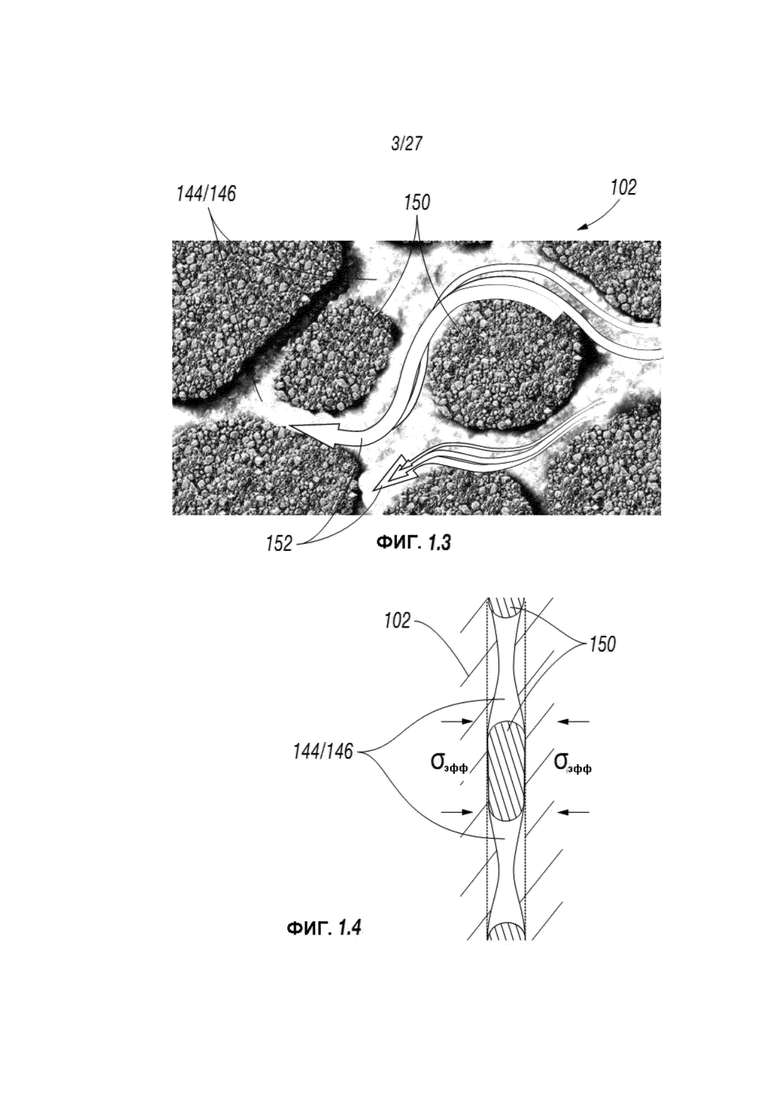
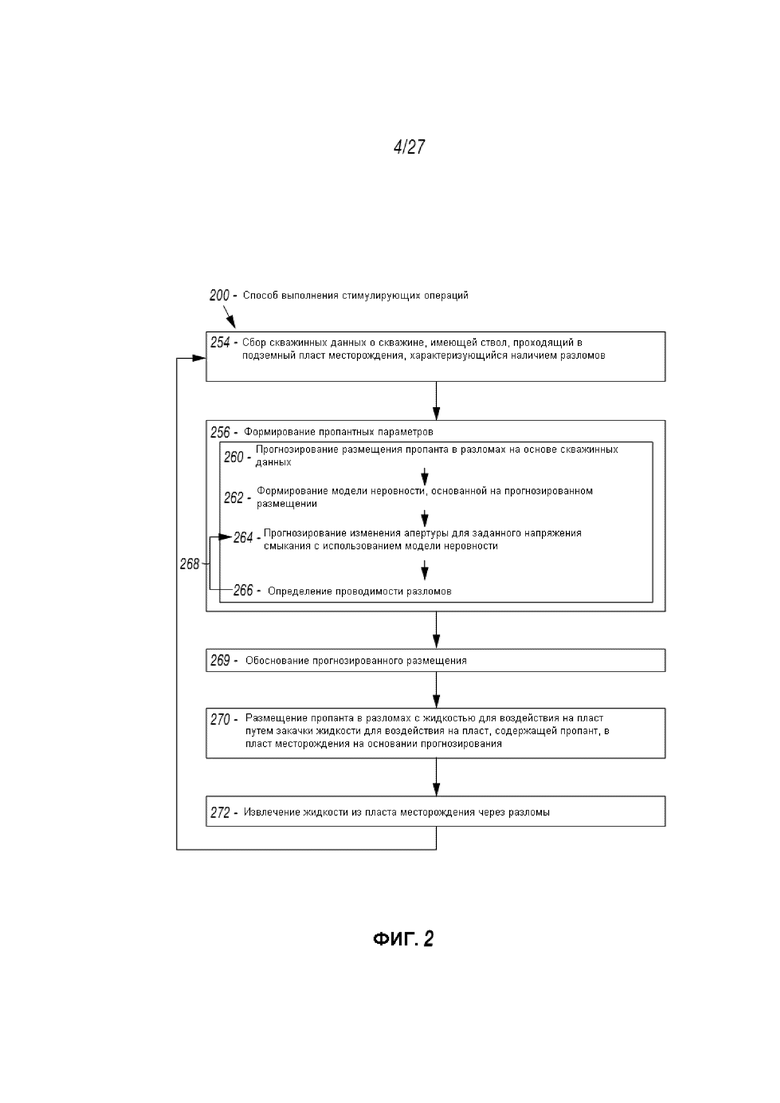
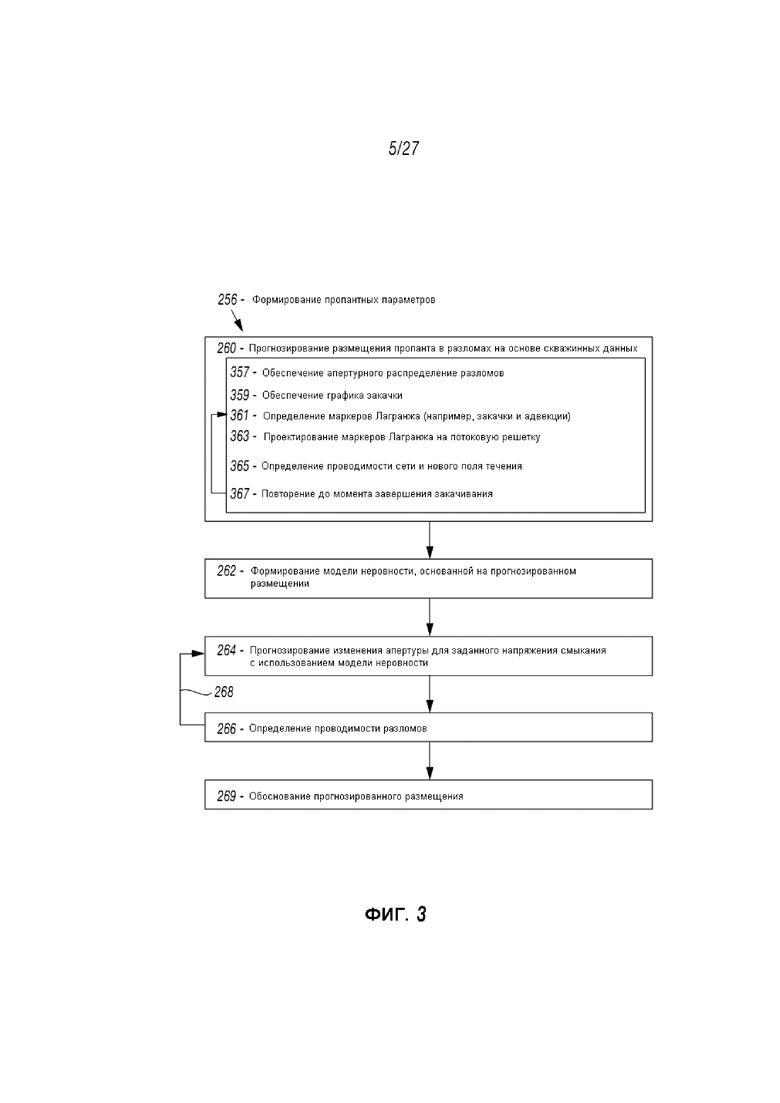
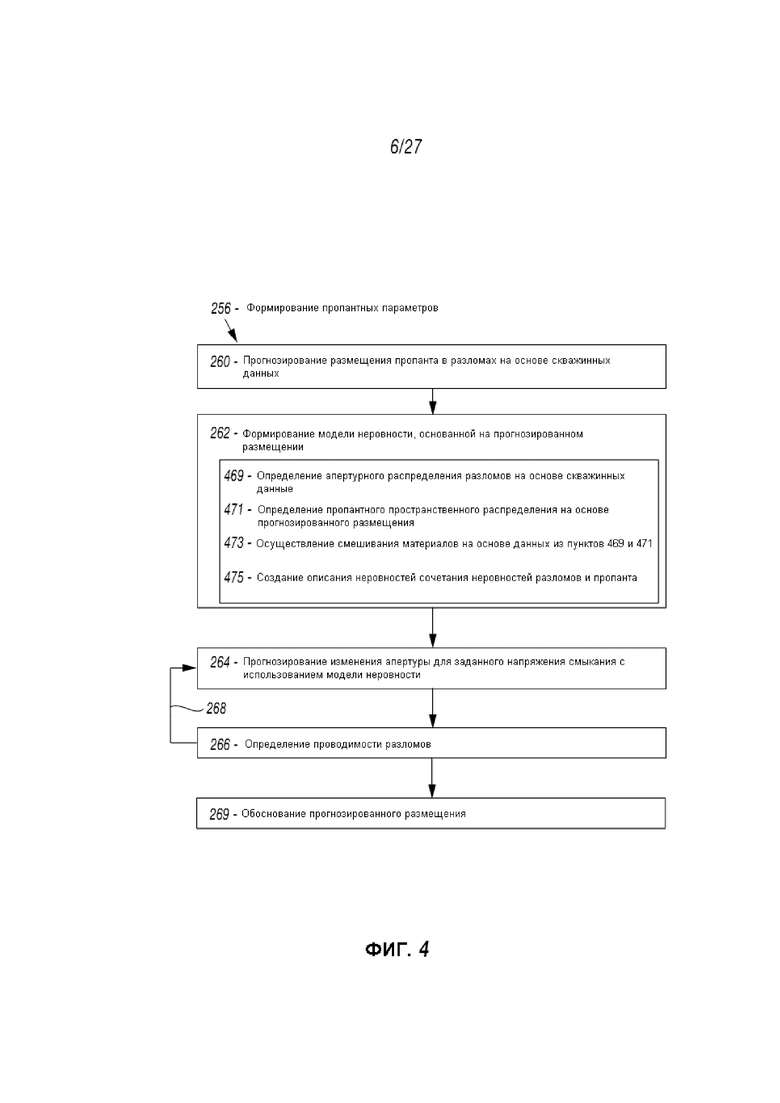
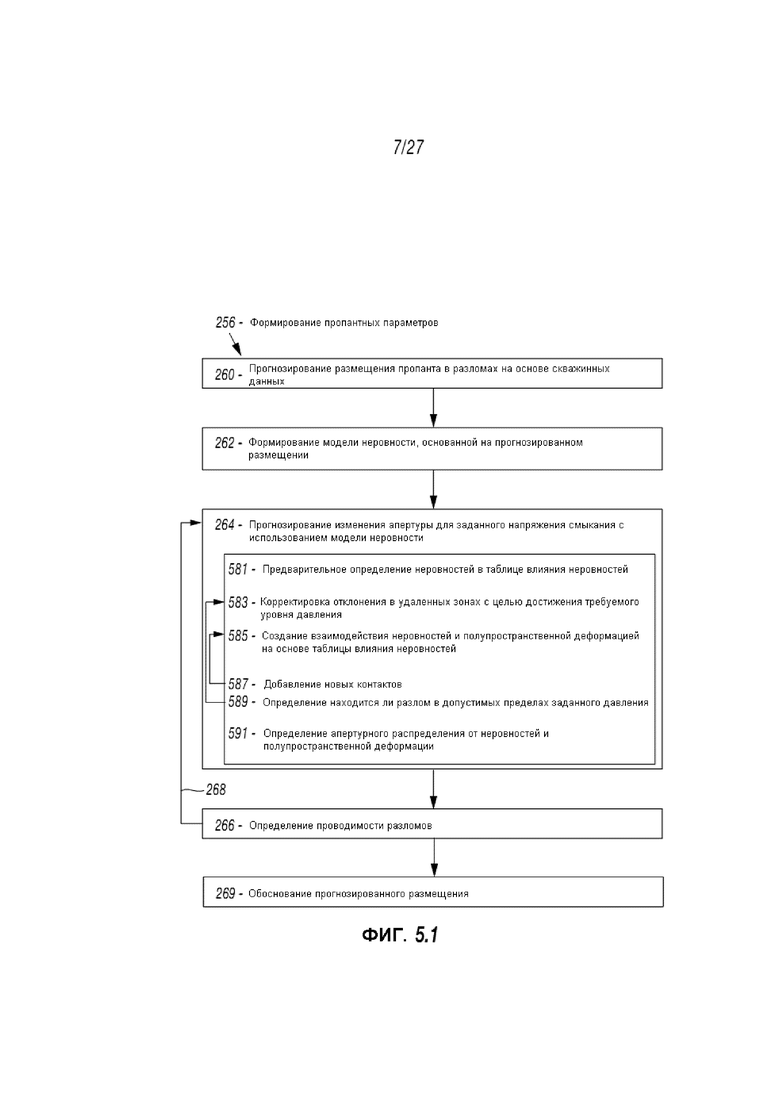
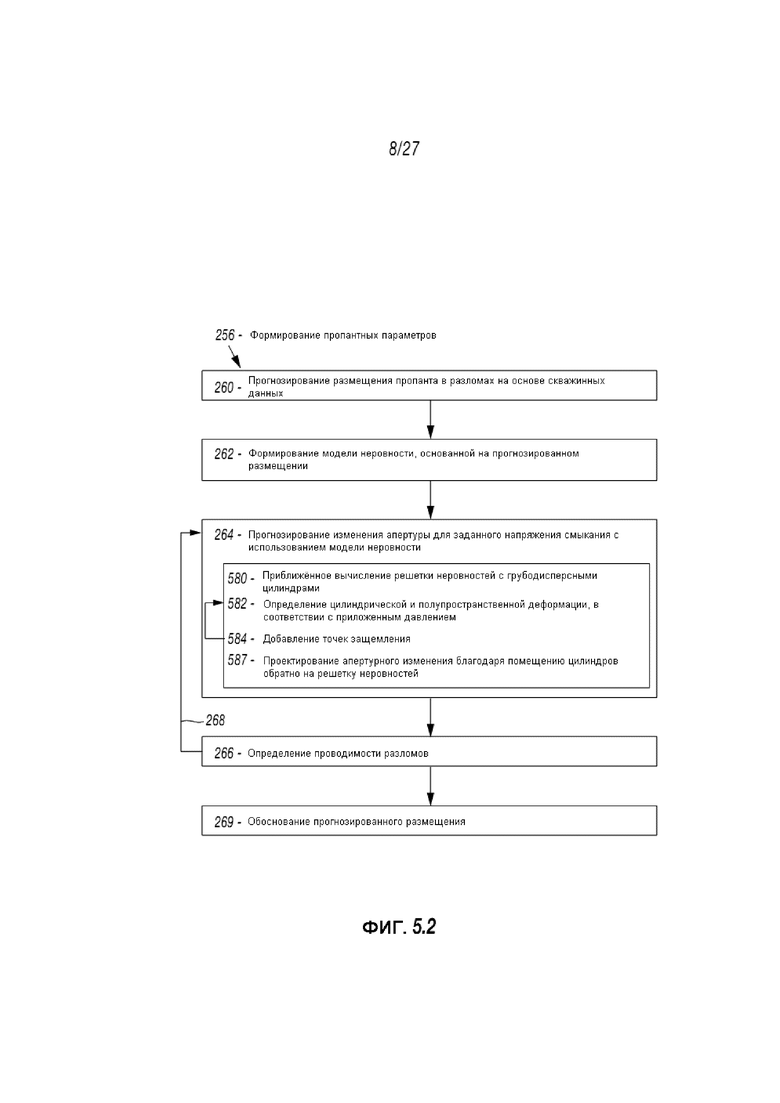
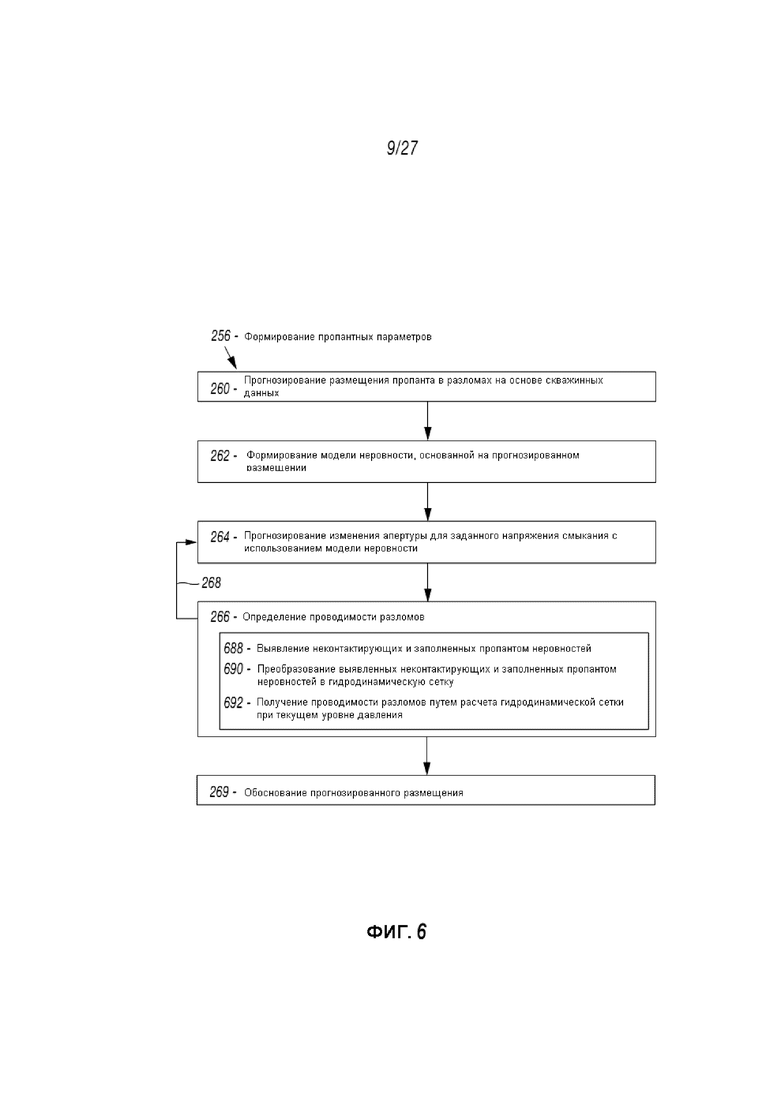
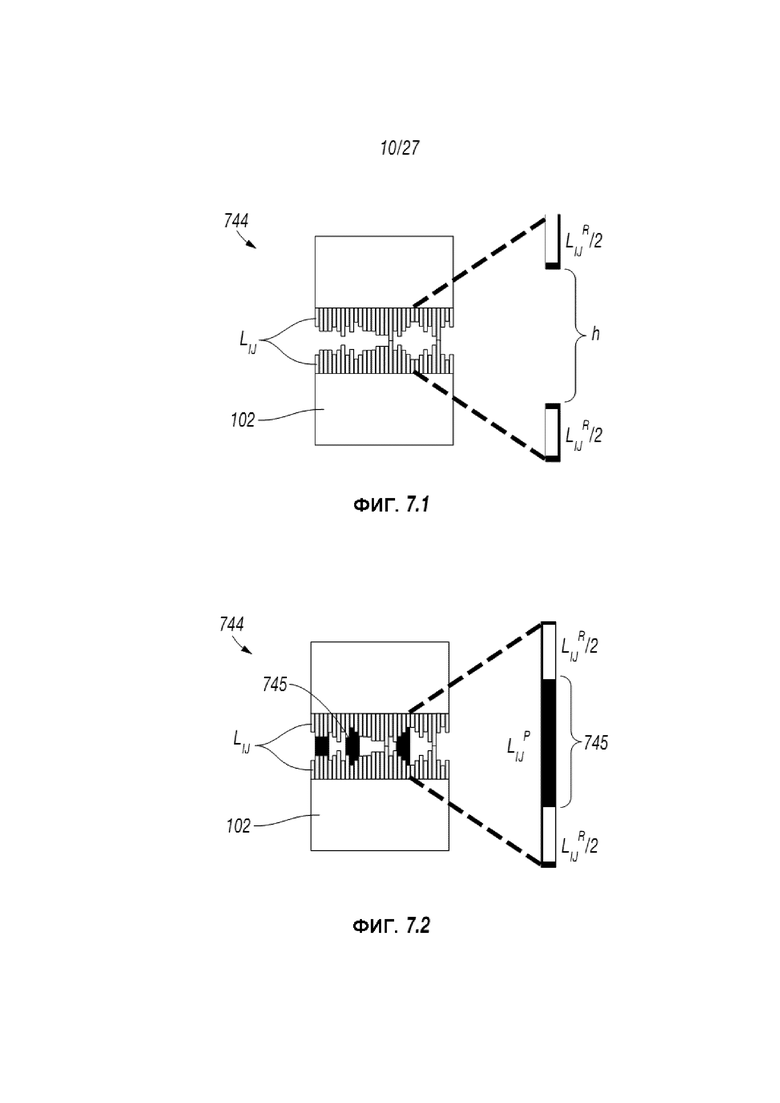
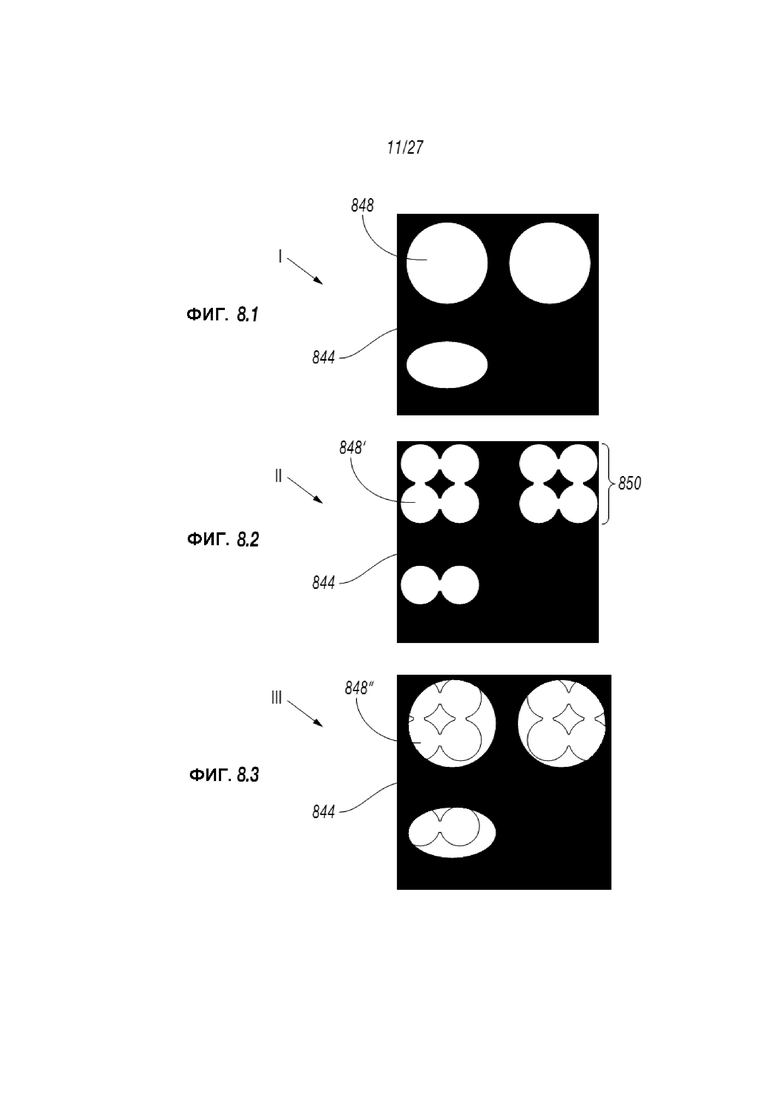
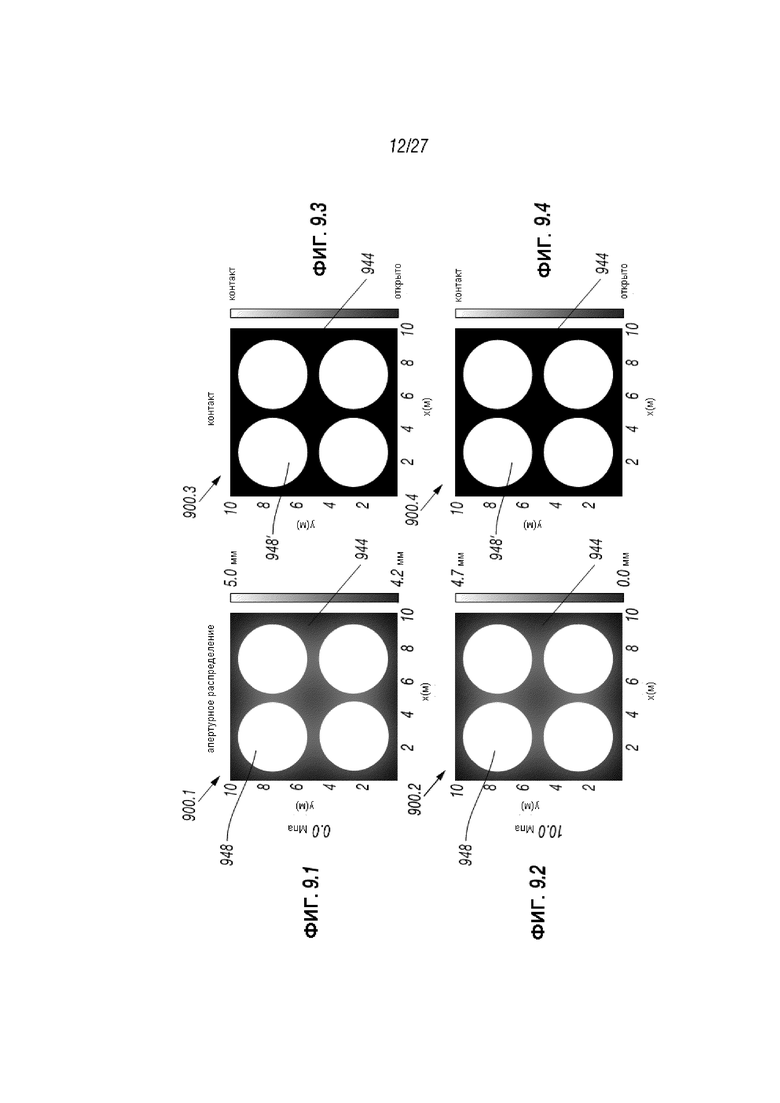

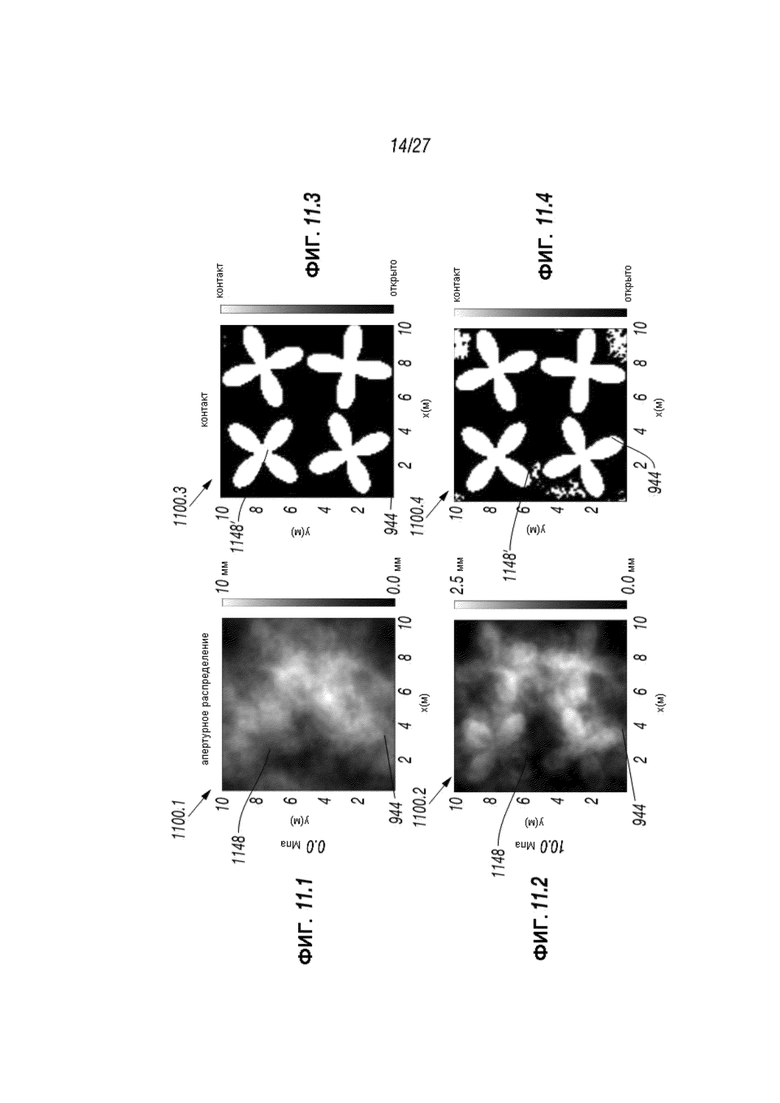
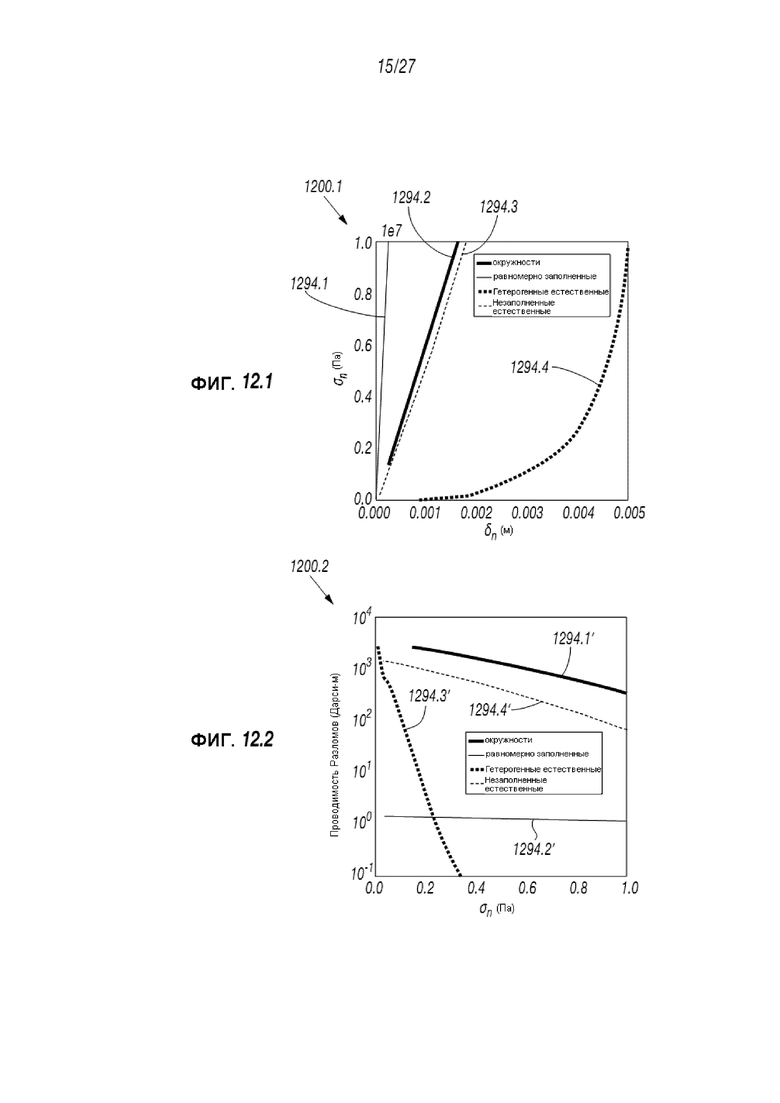
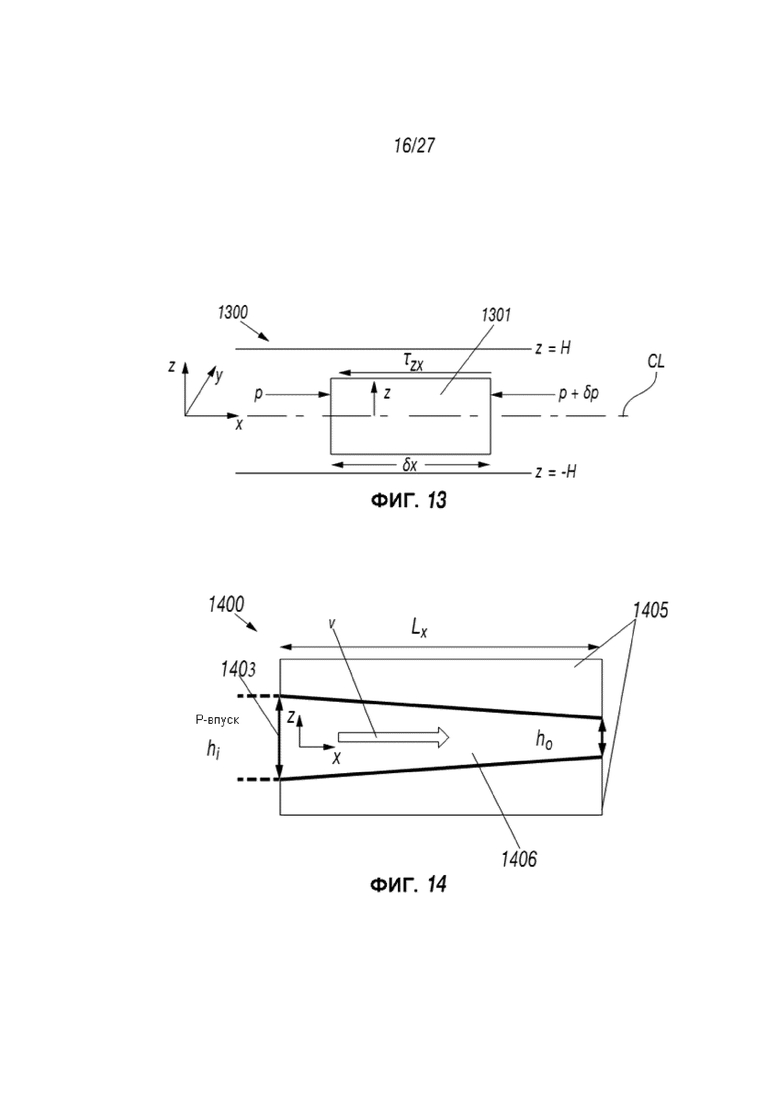
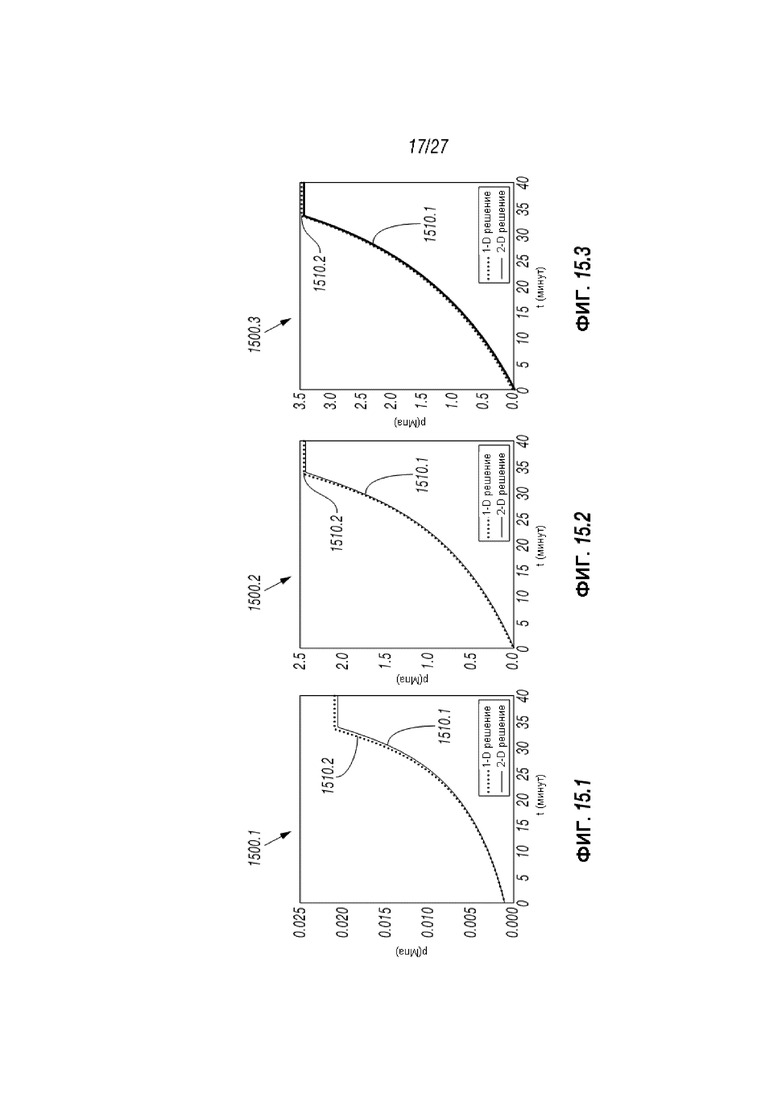
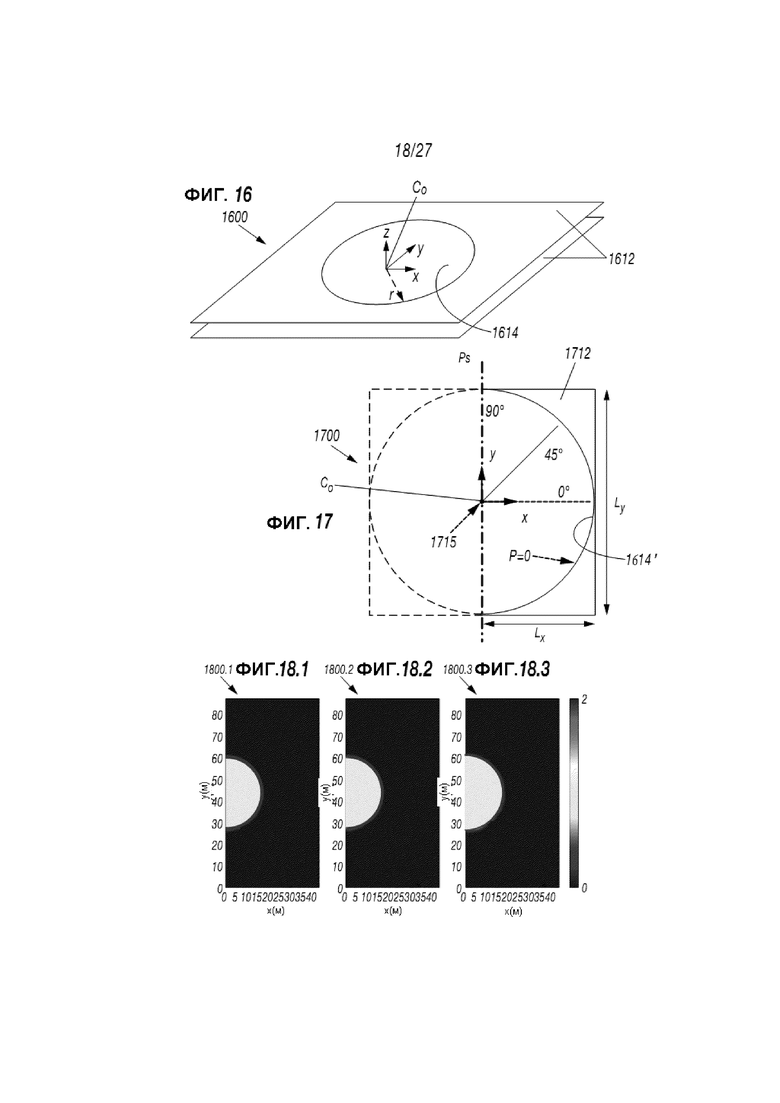
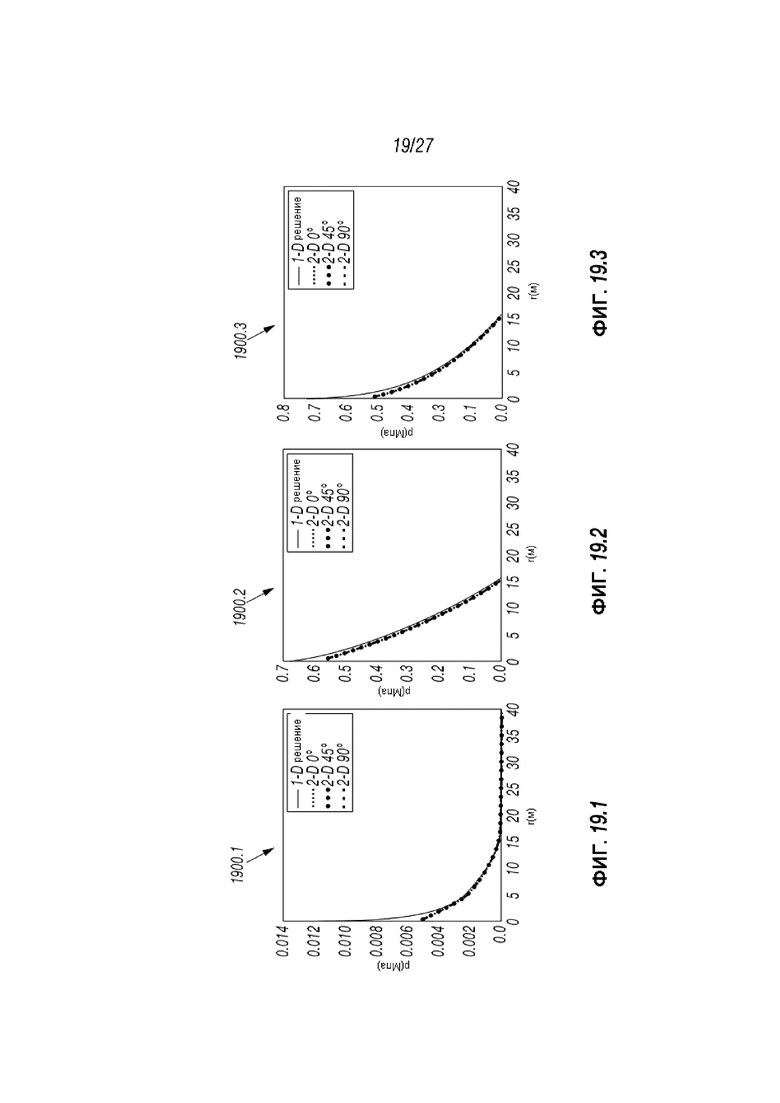
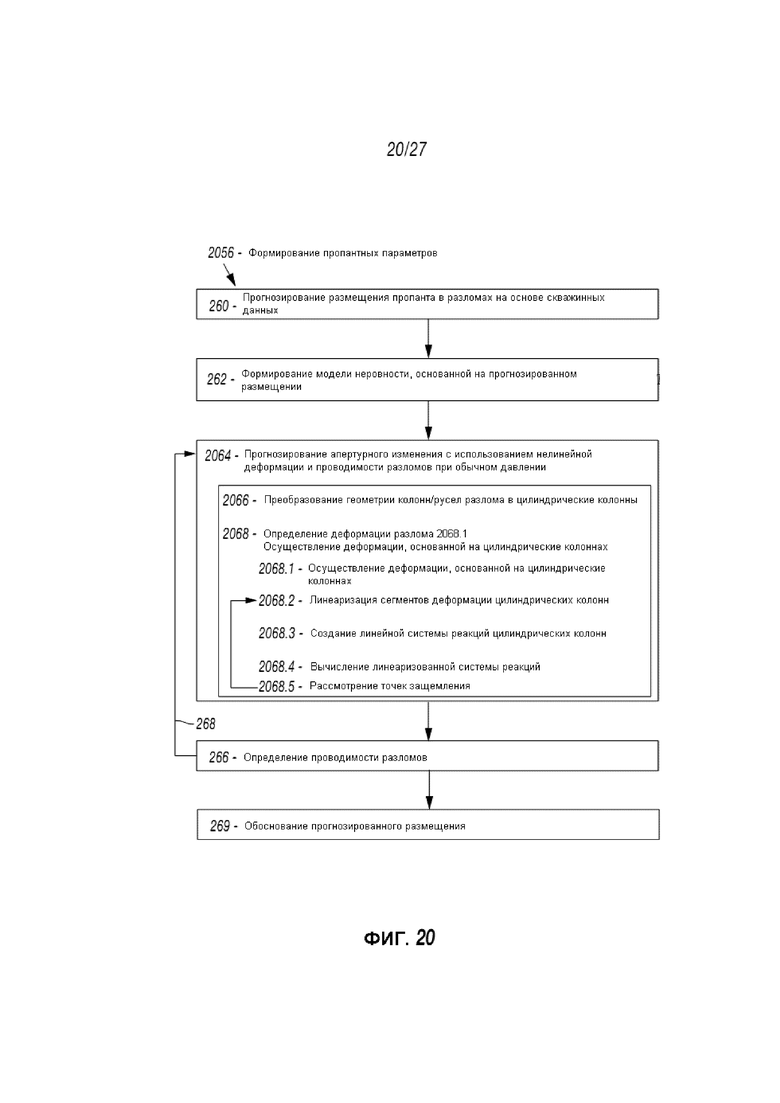
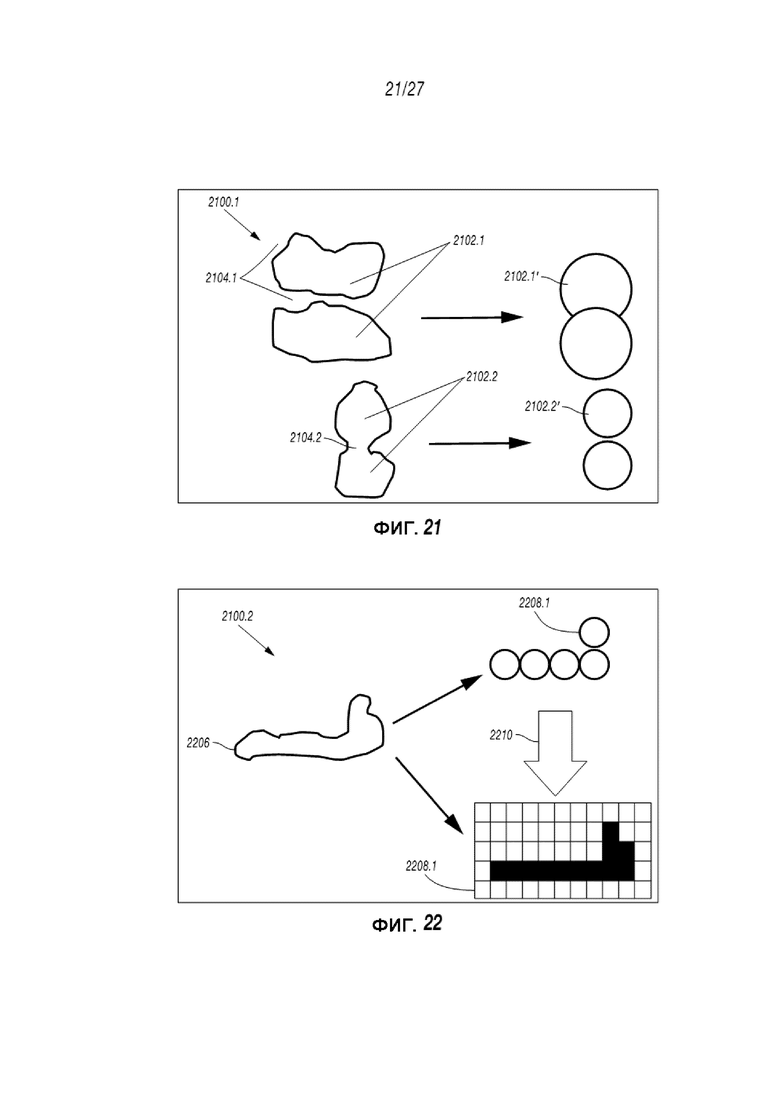
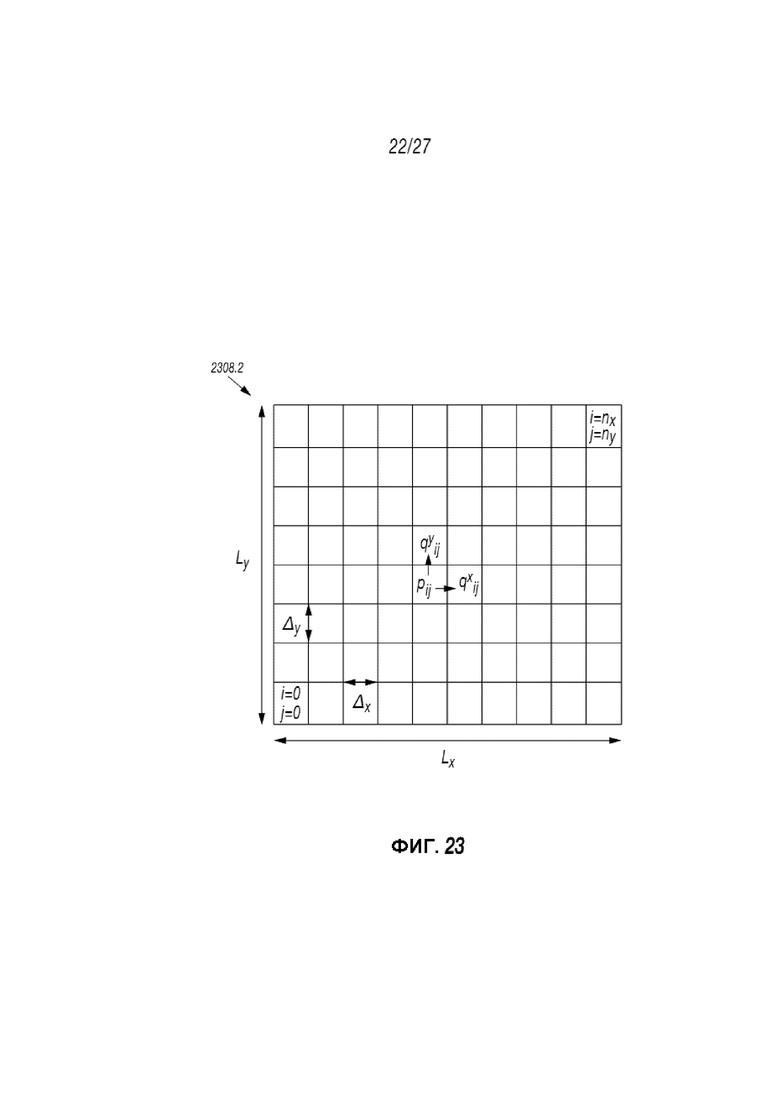
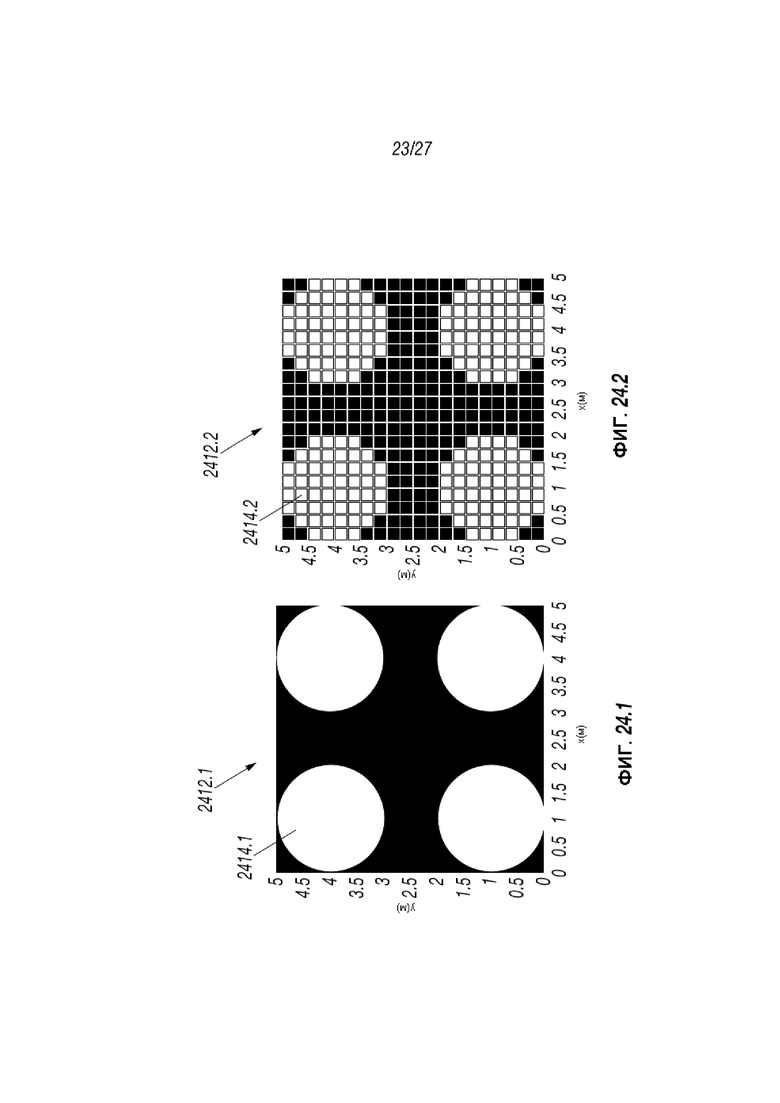
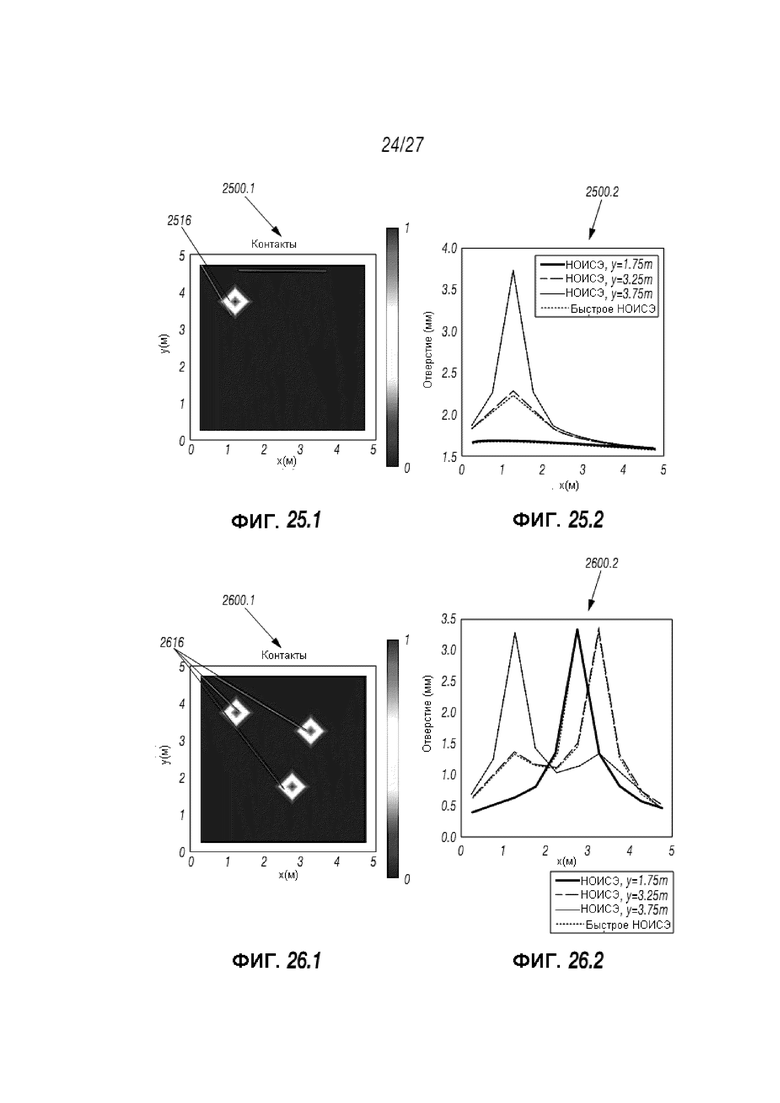
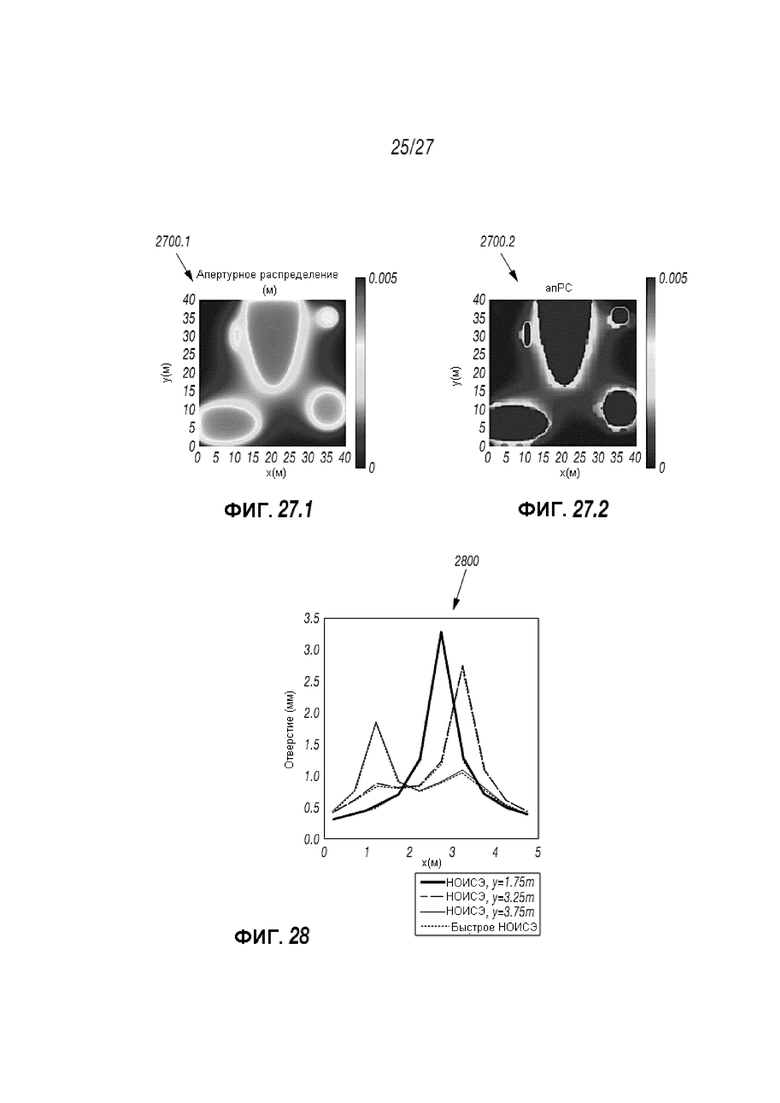
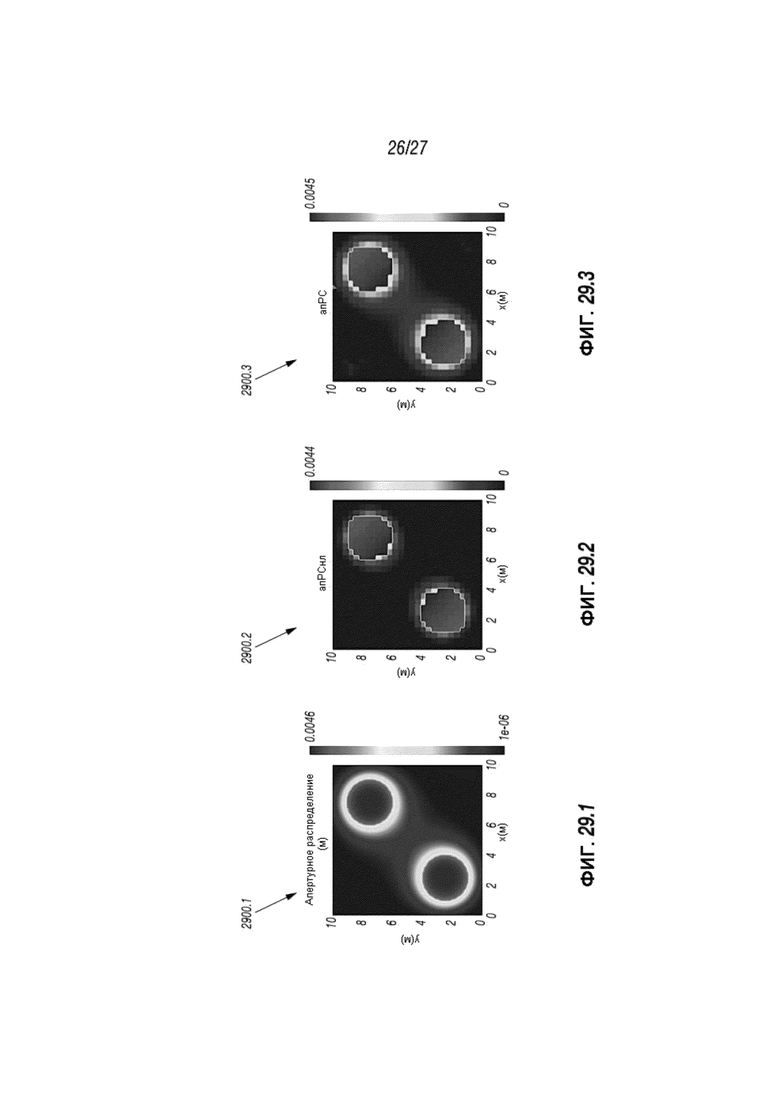
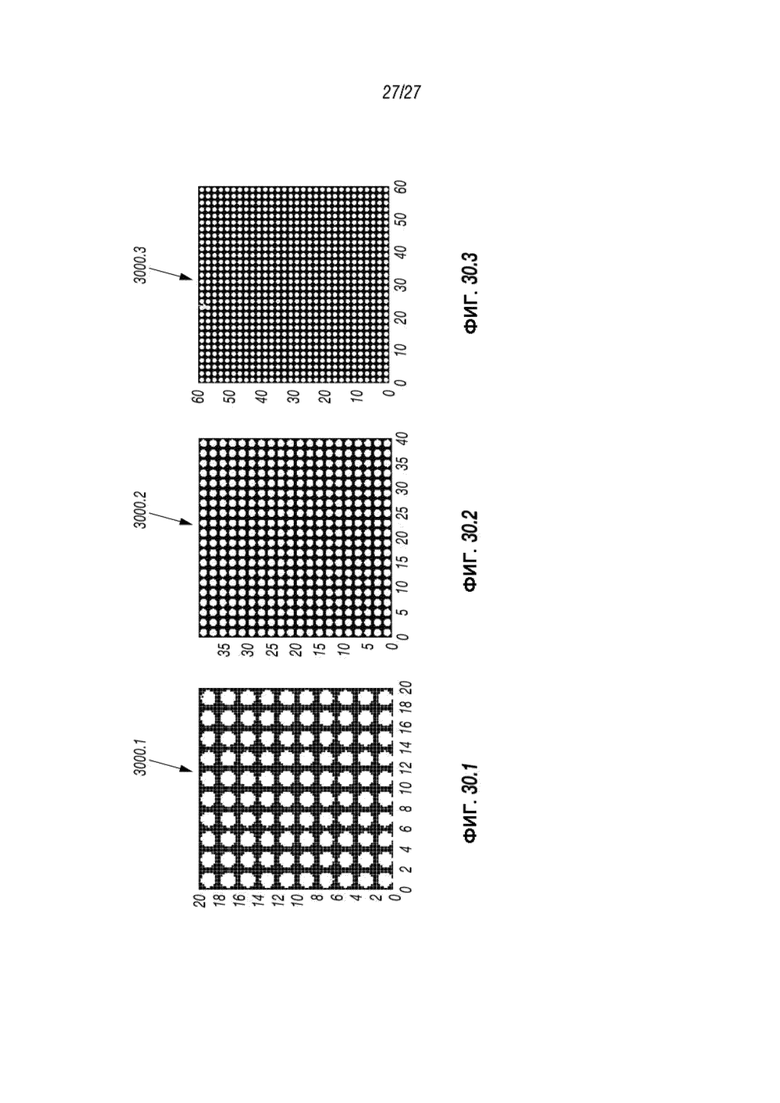
Группа изобретений относится к вариантам способа выполнения стимулирующих операций с размещением проппанта на буровой площадке. Буровая площадка имеет ствол скважины, проникающий в пласт месторождения, имеющий разрыв. Этот метод включает прогнозирование введения проппантных параметров в разрывы на основе скважинных данных, формирование модели неровностей на основе прогнозированного размещения, прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей, а также определение проводимости разрывов на основе прогнозированного апертурного изменения. Этот способ также включает размещение в разрывах жидкости для воздействия на пласт путем закачивания такой жидкости, содержащей в себе проппант, в пласт месторождения на основе определенной проводимости разрывов и извлечения из коллекторов и закачивание в ствол скважины через расклиненный разрыв. Технический результат заключается в повышении эффективности стимулирующих операций. 3 н. и 21 з.п. ф-лы, 61 ил., 14 табл.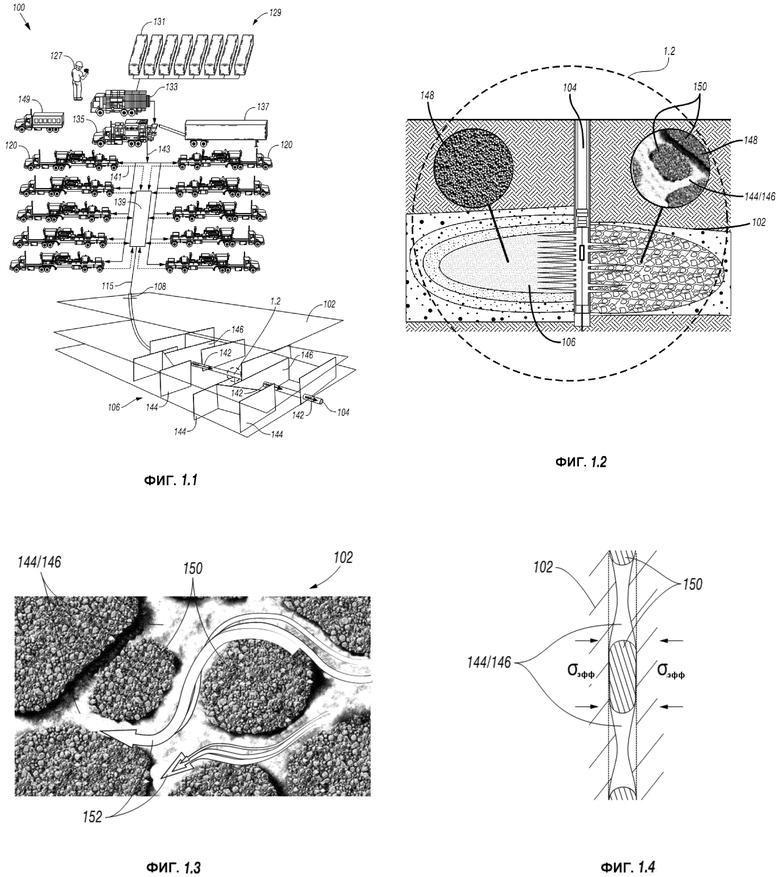
1. Способ выполнения стимулирующих операций на буровой площадке, при этом буровая площадка имеет ствол скважины, проникающий в пласт месторождения, содержащий в себе разрывы, этот способ включает:
прогнозирование введение проппанта в разрыв на основе скважинных данных, при этом скважинные данные содержат геометрию разрывов;
формирование модели неровностей на основе прогнозированного размещения;
прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей;
определение проводимости разрывов на основе прогнозированного апертурного изменения; и
размещение проппанта в разрывах вместе с жидкостью для воздействия на пласт путем закачивания такой жидкости, содержащей в себе проппант, в пласт месторождения на основе определенной проводимости разрывов.
2. Способ по п.1, дополнительно включающий сбор скважинных данных на буровой площадке.
3. Способ по п.1, дополнительно включающий извлечение жидкости через определенные разрывы.
4. Способ по п.1, при котором прогнозирование введения включает:
предоставление распределения апертурного разрыва и график закачки;
определение маркеров Лагранжа;
проецирование маркеров Лагранжа на потоковую решетку; и
определение проводимости сети и поля течения на основе потока между параллельными пластинами.
5. Способ по п.4, дополнительно включающий повторение прогнозирования введения до момента завершения закачки.
6. Способ по п.4, отличающийся тем, что маркеры Лагранжа представлены закачкой, адвекцией или их сочетанием.
7. Способ по п.1, отличающийся тем, что формирование модели неровностей включает:
определение разрыва апертурного распределения на основе скважинных данных;
определение проппантного пространственного распределения на основе прогнозированного размещения;
формирование смешивания материалов на основе определенного разрыва и определенного проппантного пространственного распределения; и
формирование неровностного описания сочетания шероховатостей разрыва и проппанта на основе смешивания материалов.
8. Способ по п.1, отличающийся тем, что прогнозирование апертурного изменения включает:
предварительно рассчитанную неровность на основе таблиц влияния неровностей;
регулировку дислокации в удаленных местах скважины на основе предварительно рассчитанной неровности;
формирование взаимодействия деформации неровности и полупространства с использованием таблиц неровностей и на основе скорректированной дислокации в удаленных местах скважины;
определение, находится ли неровность в пределах допустимых отклонений от состояния целевой нагрузки; и
определение апертурного распределения от определенной неровности и скорректированной дислокации в удаленных местах скважины.
9. Способ по п.8, дополнительно включающий добавление новых контактов и повторение формирования с дополнительными контактами.
10. Способ по п.1, отличающийся тем, что прогнозирование апертурного изменения включает:
предварительное определение таблиц влияния от неровности к неровности;
регулировку дислокации в удаленных местах скважины для приближения к состоянию целевой нагрузки;
формирование взаимодействия деформации неровности и полупространства с использованием таблиц неровностей и на основе скорректированной дислокации в удаленных местах скважины;
добавление новых контактов;
определение, находится ли разрыв в пределах допустимых отклонений от состояния целевой нагрузки; и
определение апертурного распределения от определенной неровности и полупространственной деформации.
11. Способ по п.1, отличающийся тем, что прогнозирование апертурного изменения включает:
приближенное вычисление решетки неровностей с необработанными цилиндрами;
определение цилиндрической и полупространственной деформации, согласующейся с приложенным давлением;
добавление точек соприкосновения; и
проектирование апертурного изменения благодаря помещению цилиндров обратно на решетку неровностей.
12. Способ по п.1, отличающийся тем, что прогнозирование апертурного изменения включает:
преобразование геометрии разрывов в цилиндрические колонны; и
определение деформации разрывов.
13. Способ по п.12, отличающийся тем, что определение деформации разрывов включает:
формирование деформации на основе цилиндрических колонн;
линеаризацию частей деформации цилиндрических колонн;
сборку линейной системы откликов цилиндрических колонн; и
решение линеаризованной системы откликов.
14. Способ по п.1, отличающийся тем, что определение проводимости разрывов включает:
определение заполненных проппантом и неконтактирующих отверстий;
преобразование определенных заполненных проппантом и неконтактирующих отверстий в гидродинамическую сетку; и
получение проводимости разрывов путем решения гидродинамической сетки при текущем уровне напряжения.
15. Способ по п.1, дополнительно включающий добавление точек соприкосновения и повторение определения проводимости разрывов для каждой точки соприкосновения.
16. Способ по п.1, дополнительно включающий обоснование определенной проводимости разрывов.
17. Способ по п.16, отличающийся тем, что обоснование включает осуществление прогнозирования введения с использованием множественных симуляций и сравнение множественных симуляций.
18. Способ выполнения стимулирующих операций на буровой площадке, при этом буровая площадка содержит ствол скважины, проникающий в пласт месторождения, имеющего в себе разрыв, при этом способ включает:
определение проппантных параметров разрывов путем прогнозирования введение проппанта в разрывы на основе скважинных данных с использованием множественных симуляций, при этом скважинные данные включают геометрию разрывов;
формирование модели неровностей на основе прогнозированного размещения;
прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей;
определение проводимости разрывов на основе прогнозированного апертурного изменения;
обоснование прогнозированного размещения путем сравнения множественных симуляций; и
размещение проппанта в разрывах вместе с жидкостью для воздействия на пласт путем закачивания такой жидкости, содержащей в себе проппант, в пласт месторождения на основе обоснованной проводимости разрывов.
19. Способ по п.18, отличающийся тем, что множественные симуляции включают по меньшей мере одно аналитическое решение,
степенное решение, решение с использованием бингамовых жидкостей и их сочетание.
20. Способ по п.18, отличающийся тем, что обоснование включает отслеживание интерфейса между множественными стадиями в пределах разрывов.
21. Способ по п.18, отличающийся тем, что множественные симуляции включают множество 1-D, 2-D и 3-D симуляций, а также их сочетания.
22. Способ по п.18, отличающийся тем, что множественные симуляции включают 2-D симуляцию, определение дополнительно содержащего расширения 2-D модели для ньютоновской жидкости.
23. Способ по п.18, отличающийся тем, что обоснование включает использование нелинейной модели расширения, содержащей решение геомеханической деформации на необработанной решетке и при которой определение проводимости разрывов выполняется с использованием обработанной дискретизации.
24. Способ стимулирования ствола скважины на буровой площадке, при этом буровая площадка имеет ствол скважины, проникающий в пласт месторождения, содержащий в себе разрывы, при этом способ включает:
определение проппантных параметров разрывов путем:
прогнозирования введение проппанта в разрывы на основе скважинных данных, при этом скважинные данные включают геометрию разрывов;
формирование модели неровностей на основе прогнозированного размещения;
прогнозирование апертурного изменения для заданного напряжения смыкания с использованием модели неровностей; и
определение проводимости разрывов на основе прогнозированного апертурного изменения; и
размещение проппанта в разрывы вместе с жидкостью для воздействия на пласт путем закачивания такой жидкости, содержащей в себе проппант, в пласт месторождения на основе обоснованной проводимости разрывов; и
извлечение жидкости из коллекторов и закачивание ее через ствол скважины через расклиненный разрыв.
| СПОСОБ ДИАГНОСТИКИ ПРОЦЕССОВ ГИДРОРАЗРЫВА ПЛАСТА В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ С ИСПОЛЬЗОВАНИЕМ КОМБИНИРОВАНИЯ ТРУБНЫХ ВОЛН И МИКРОСЕЙСМИЧЕСКОГО МОНИТОРИНГА | 2010 |
|
RU2455665C2 |
| EA 200701755 A1, 28.04.2008 | |||
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ | 2007 |
|
RU2349740C2 |
| СПОСОБ ОБРАБОТКИ СЕЙСМИЧЕСКИХ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2009 |
|
RU2412454C2 |
| МОДЕЛИРОВАНИЕ ПЕРЕХОДНОГО РЕЖИМА КНБК/БУРИЛЬНОЙ КОЛОННЫ В ПРОЦЕССЕ БУРЕНИЯ | 2008 |
|
RU2461707C2 |
| WO 2012090175 A2, 05.07.2012. | |||
Авторы
Даты
2018-06-26—Публикация
2014-08-25—Подача