Изобретение относится к области контрольно-измерительной техники, может быть использовано для одновременного определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур в сверхвысокочастотном диапазоне, и может найти применение для неразрушающего контроля электрофизических параметров производимых диэлектрических подложек и структур для устройств СВЧ-электроники.
При разработке радиоэлектронных устройств и систем важную роль играет информация о свойствах используемых для их создания материалов именно на тех частотах, на которых функционируют разрабатываемые устройства. Анизотропия свойств материалов приводит также к необходимости выбора электродинамической конфигурации измерительной системы таким образом, чтобы структура электромагнитного поля в проектируемом устройстве и применяемой измерительной системы были идентичны. Одним из наиболее распространенных элементов сверхвысокочастотной электроники является коаксиальная линии передачи, отличающаяся широкополосностью, стабильностью характеристик в широком диапазоне частот, технологичностью производства. Измерение электрофизических параметров диэлектриков, применяемых в коаксиальной линии передачи, представляется достаточно трудоемким процессом в силу особенностей конструкции самой линии передачи и неоднозначностей, возникающих при использовании математических соотношений, описывающих распространение электромагнитной волны в линии.
Известен способ определения комплексной диэлектрической проницаемости диэлектрических материалов (A. M. Nicolson, G. F. Ross, Measurement of the intrinsic properties of materials by time-domain techniques, IEEE Trans. on Instrum. Meas., vol. IM-19, Nov 1970, pp. 377-82; W. B. Weir, Automatic measurement of complex dielectric constant and permeability at microwave frequencies, Proc. IEEE, vol. 62, no. 1, pp. 33-36, Jan. 1974.), основанный на измерении всех четырех S-параметров заполненного воздухом отрезка линии передачи, содержащего исследуемый образец, а также группового времени задержки сигнала для устранения неоднозначности в определении фазы. В случае коаксиальной линии передачи, исследуемый образец имеет форму шайбы, полностью заполняющей пространство между внутренним и внешним проводниками коаксиальной линии с воздушным заполнением. Отклонения от идеальной цилиндрической формы учитываются посредством введения поправочных коэффициентов в формулы расчета комплексной диэлектрической проницаемости.
Однако данный способ ограничен в применении для длинных образцов диэлектрических материалов с низкой величиной потерь в сверхвысокочастотном диапазоне. Длины исследуемых образцов должны составлять менее половины длины волны, так как на частотах, при которых длина образца кратна целому числу полуволн на измеряемых диэлектрических спектрах возникают искажения, связанные с неопределенностью в измерении фазы в минимуме коэффициента отражения сверхвысокочастотного сигнала.
Известен способ определения комплексной диэлектрической проницаемости диэлектрических материалов (P. G. Bartley, and S. B. Begley, “A New Technique for the Determination of the Complex Permittivity and Permeability of Materials Proc. IEEE Instrument Meas. Technol. Conf., pp. 54-57, 2010.), реализующий итерационную процедуру минимизации разницы между экспериментально измеренными S-параметрами содержащей исследуемый образец линии передачи и теоретически рассчитанными в предположении, что зависимость диэлектрической проницаемости исследуемого образца от частоты представляет собой полином n-ой степени от частоты. В ходе процедуры минимизации степень полинома повышается до тех пор, пока не будет обеспечено минимальное отличие между экспериментальными и расчетными характеристиками или для такого обеспечения достигнуто заранее предустановленное максимально возможное значение порядка полинома.
Однако данный способ требует наличия дополнительной информации о строении и свойствах исследуемых образцов, и он не применим для измерения тех типов материалов, чьи электрофизические параметры не могут быть представлены в виде полиноминальной зависимости от частоты.
Известен способ определения диэлектрической проницаемости и тангенса угла диэлектрических потерь жидких диэлектриков (Коаксиальные брэгговские СВЧ-структуры в сенсорных системах Морозов Г.А., Морозов О.Г., Насыбуллин А.Р., Севастьянов А.А., Фахрутдинов Р.В. Физика волновых процессов и радиотехнические системы. 2014. Т. 17. № 3. С. 65-70.) с использованием брэгговской сверхвысокочастотной структуры на коаксиальном кабеле, представляющей собой стандартный сверхвысокочастотный коаксиальный кабель с периодически высверленными во внешнем проводнике вертикальными полостями цилиндрической формы, которые заполняются исследуемыми жидкостями. Теоретическое описание коэффициентов отражения и прохождения сверхвысокочастотного излучения, взаимодействующего с брэгговской структурой, и расчет диэлектрической проницаемости и тангенса угла диэлектрических потерь проводится с привлечением программ трехмерного электродинамического моделирования.
Однако данный способ отличается как значительной трудоемкостью при создании бездефектной брэгговской структуры в коаксиальном кабеле, так и повышенными затратами времени и вычислительных ресурсов для определения значений электрофизических параметров при обработке экспериментальных результатов.
Наиболее близким по сущности к предлагаемому является способ, реализованный в устройстве для измерения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь жидкостей (RU 2419099 от 20.05.2011), содержащем фотонный кристалл в микрополосковом исполнении с периодическим изменением диэлектрической проницаемости подложки, в котором дополнительно создано нарушение периодичности в виде отрезка микрополосковой линии передачи с воздушным заполнением, играющее роль измерительной кюветы для жидких диэлектриков. По спектрам прохождения сверхвысокочастотного излучения, взаимодействующего с микрополосковым фотонным кристаллом, содержащим исследуемый жидкий диэлектрик, на частоте пика пропускания в фотонной запрещенной зоне в ходе решения обратной задачи по методу наименьших квадратов определяются значения искомых параметров.
Однако в данном способе используется открытая сверхвысокочастотная линия передачи, что приводит к необходимости учета потерь на излучение и снижения влияния внешних воздействий, таких как, например, температура, на результаты измерений. Конструкция микрополоскового типа фотонного кристалла, в отличие от волноводного и коаксиального, является неразъемной и не позволяет изменять его конфигурацию для смещения частотного положения окна прозрачности в фотонной запрещенной зоне, и, следовательно, реализовать возможность измерения параметров материалов на различных частотах. В микрополосковой линии распространяется квази-ТЕМ волна и силовые линии электрического поля проходят не только в диэлектрике, но и вне его. Поэтому для строгого теоретического описания спектров отражения и прохождения сверхвысокочастотного излучения в случае использования микрополосковой линии в качестве сенсора необходимо или проведение строгого электродинамического моделирования, или введение поправочных коэффициентов в используемые соотношения.
Техническая проблема состоит в обеспечении возможности одновременного определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических материалов, используемых при проектировании СВЧ-узлов на основе коаксиальной линии передачи.
Технический результат заключается в расширении функциональных возможностей одновременного определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур, применяемых в качестве диэлектрического наполнения сверхвысокочастотных коаксиальных кабелей.
Техническая проблема достигается тем, что в способе определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур, включающий размещение диэлектрической структуры в области нарушения периодичности СВЧ фотонного кристалла, облучение фотонного кристалла, содержащего измеряемую диэлектрическую структуру, электромагнитным излучением сверхвысокочастотного диапазона, измерение частотных зависимостей коэффициентов прохождения и отражения в запрещенной зоне в окрестности дефектной моды, расчет с помощью ЭВМ искомых значений, при которых теоретические частотные зависимости коэффициентов отражения и прохождения электромагнитного излучения наиболее близки к измеренным, из решения системы дифференциальных уравнений, согласно изобретению, в качестве фотонного кристалла используют коаксиальный сверхвысокочастотный фотонный кристалл, представляющий собой последовательно соединенные отрезки коаксиальной линии передачи, пространство между внешним и внутренним проводником каждого отрезка полностью заполнено диэлектриком, при этом относительная диэлектрическая проницаемость диэлектрического заполнения периодически изменяется вдоль направления распространения электромагнитной волны, подбирают значения длин и относительных диэлектрических проницаемостей диэлектрических заполнений чередующихся отрезков коаксиальной линии передачи таким образом, чтобы обеспечить кратность их электрических длин, приводящую к формированию фотонных запрещенных зон равной глубины на частотных зависимостях коэффициентов прохождения электромагнитного излучения, нарушение периодичности СВЧ фотонного кристалла создают в центральном отрезке коаксиального фотонного кристалла, что приводит к формированию дефектных мод в нескольких фотонных запрещенных зонах, рассчитывают распределение поля электромагнитной волны внутри коаксиального фотонного кристалла вдоль направления распространения электромагнитной волны на частотах, соответствующих дефектным модам в фотонных запрещенных зонах, фиксируют узлы и пучности стоячей электромагнитной волны внутри коаксиального фотонного кристалла, выбирают дефектную моду, на частоте которой в области расположения диэлектрической структуры в центральном отрезке коаксиального фотонного кристалла наблюдается пучность стоячей волны.
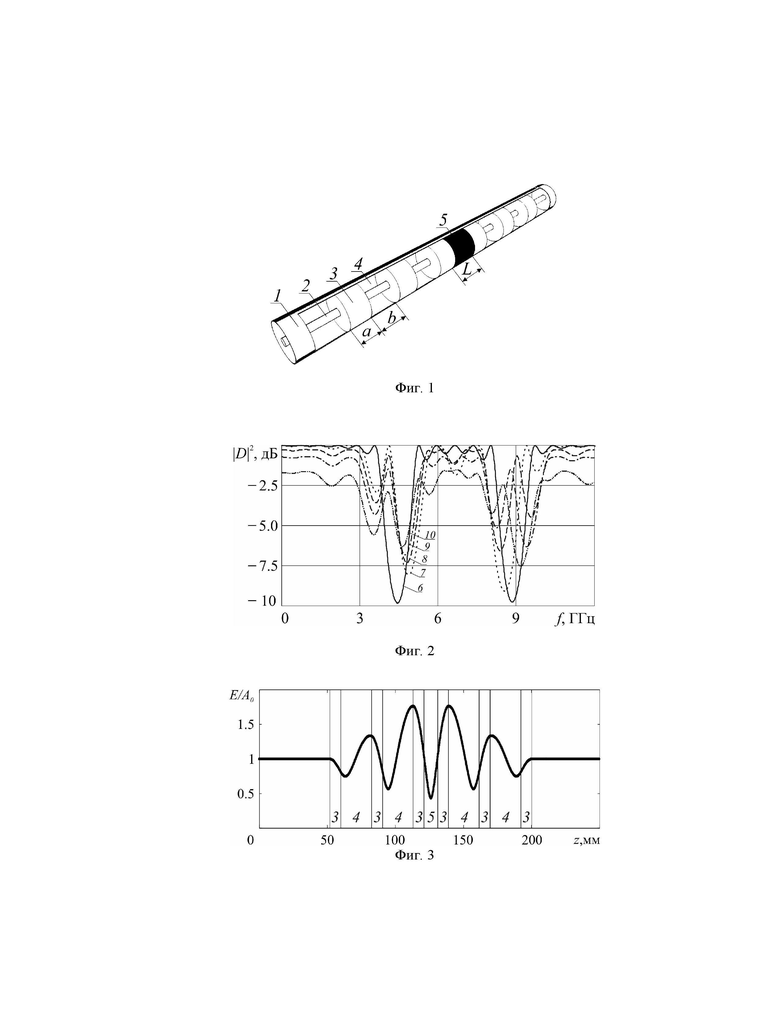
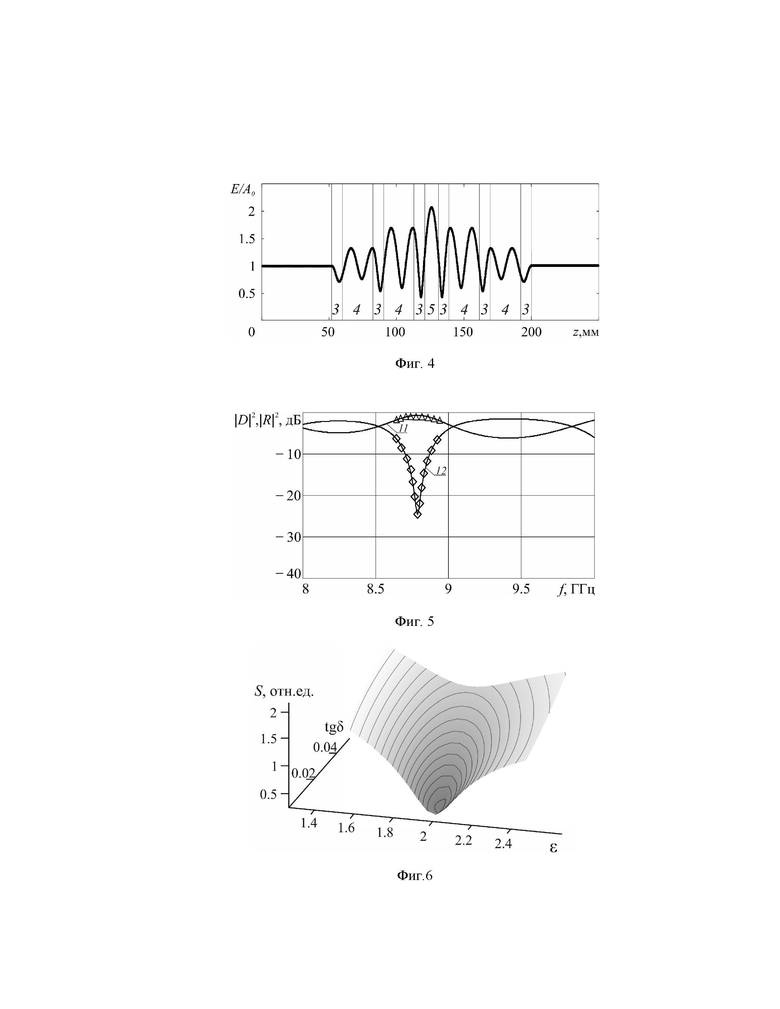
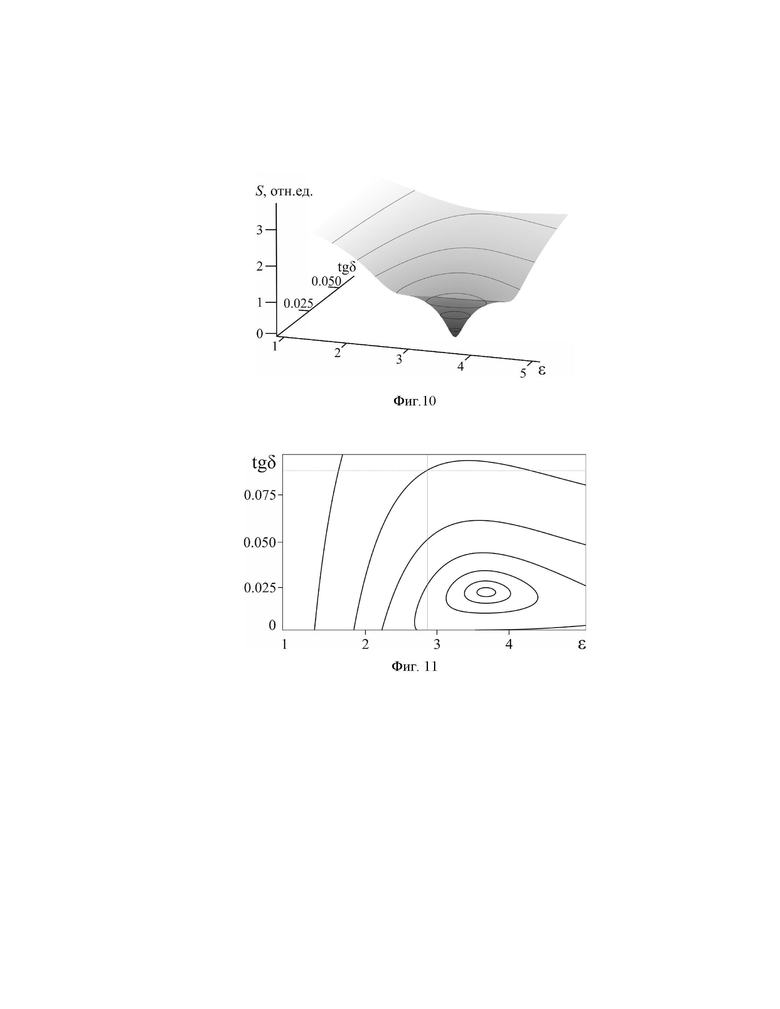
Изобретение поясняется чертежами, где на фиг. 1 приведено схематическое изображение конструкции одномерного коаксиального фотонного кристалла, содержащего измеряемый диэлектрик в нарушенном центральном отрезке, на фиг. 2 приведены частотные зависимости коэффициентов прохождения сверхвысокочастотного излучения без нарушения периодичности и с нарушением периодичности в виде ряда измеряемых диэлектриков, помещенных в центральный отрезок коаксиального фотонного кристалла, на фиг. 3 приведено распределение напряженности электрического поля электромагнитной волны вдоль структуры коаксиального фотонного кристалла на резонансной частоте 4.113 ГГц дефектной моды, на фиг. 4 приведено распределение напряженности электрического поля электромагнитной волны вдоль структуры коаксиального фотонного кристалла на резонансной частоте 9.382 ГГц дефектной моды, на фиг. 5 приведены исходные тестовые (◊◊◊ и Δ) и рассчитанные (линии) с использованием результатов решения обратной задачи частотные зависимости коэффициентов отражения и прохождения для коаксиального фотонного кристалла с с нарушением периодичности в виде тестового образца на резонансной частоте дефектной моды 8.786 ГГц во второй запрещенной зоне, на фиг. 6 приведен вид функционала S(e, tgδ) в пространстве (e, tgδ, S(e, tgδ)) для образца длиной L=10 мм с относительной диэлектрической проницаемостью e=2 и тангенсом угла диэлектрических потерь tg=0.005 на резонансной частоте f2=8.786 ГГц, соответствующей дефектной моде во второй запрещенной зоне, на фиг. 7 приведены контурные карты в плоскости искомых параметров (e, tgδ) для образца с относительной диэлектрической проницаемостью e=2 и тангенсом угла диэлектрических потерь tg=0.005 на резонансной частоте f2=8.786 ГГц, соответствующей дефектной моде во второй запрещенной зоне, на фиг. 8 представлены экспериментально измеренные частотные зависимости коэффициентов прохождения сверхвысокочастотного коаксиального фотонного кристалла без нарушения периодичности и с нарушением периодичности в виде центрального (6-го слоя) с различными значениями комплексной диэлектрической проницаемости, на фиг. 9 экспериментальные (◊◊◊ и Δ) и рассчитанные (линии) с использованием результатов решения обратной задачи частотные зависимости коэффициентов отражения и прохождения для коаксиального фотонного кристалла с нарушением периодичности в виде образца из текстолита на резонансной частоте f2=8.378 ГГц во второй запрещенной зоне, на фиг. 10 приведен вид функционала S(e, tgδ) в пространстве (e, tgδ, S(e, tgδ)) для образца из текстолита на резонансной частоте f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне, на фиг. 11 приведены контурные карты в плоскости искомых параметров (e, tgδ) для образца из текстолита на резонансной частоте f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне
Позициями на чертежах обозначены:
а и b – длины отрезков коаксиальной линии передачи с различными значениями диэлектрической проницаемости диэлектрического заполнения;
L – длина нарушенного отрезка;
D – коэффициент прохождения сверхвысокочастотного излучения;
R – коэффициент прохождения сверхвысокочастотного излучения;
f – частота;
A0–амплитуда падающей электромагнитной волны;
E – амплитуда стоячей волны в фотонном кристалле;
z – координата;
e – относительная диэлектрическая проницаемость;
tgδ – тангенс угла диэлектрических потерь;
S(e, tgδ) – функционал, определяющий различие между рассчитанными и измеренными частотными зависимостями коэффициентов отражения и прохождения;
1 и 2 – внешний и внутренний проводники коаксиальной линии;
3 и 4 – диэлектрические элементы, образующие периодическую структуру;
5 –нарушение периодичности в виде измеряемого диэлектрика;
кривая 6 – теоретически рассчитанная амплитудно-частотная характеристика коэффициента прохождения для коаксиального фотонного кристалла без нарушений;
кривые 7–10 – теоретически рассчитанные амплитудно-частотные характеристики коэффициента прохождения для коаксиального фотонного кристалла с нарушением периодичности в виде измеряемого образца длиной L=10 мм со значениями относительной диэлектричесой проницаемости и тангенса угла диэлектрических потерь: 7 – e=1.0, tgδ=0; 8 – e=1.5, tgδ=0.013; 9 – e=2.0, tgδ=0.03; 10 – e=3.0, tgδ=0.057;
кривая 11– амплитудно-частотная характеристика коэффициента прохождения, рассчитанная с использованием результатов решения обратной задачи на резонансной частоте f2=8.786 ГГц, соответствующей дефектной моде во второй запрещенной зоне,
кривая, обозначенная символами ◊◊◊ – исходная тестовая амплитудно-частотная характеристика коэффициента прохождения;
кривая 12 – амплитудно-частотная характеристика коэффициента отражения, рассчитанная с использованием результатов решения обратной задачи на резонансной частоте f2=8.786 ГГц, соответствующей дефектной моде во второй запрещенной зоне,
кривая, обозначенная символами ΔΔΔ – исходная тестовая амплитудно-частотная характеристика коэффициента отражения;
кривая 13 – экспериментальная амплитудно-частотная характеристика коэффициента прохождения для коаксиального фотонного кристалла без нарушений;
кривые 14–17 – экспериментальные амплитудно-частотные характеристики коэффициента прохождения для коаксиального фотонного кристалла с нарушением периодичности в виде центрального (6-го слоя) с различными значениями комплексной диэлектрической проницаемости: 14 – фторопласт; 15 – капролон; 16 – эбонит; 17 – текстолит;
кривая 18 – амплитудно-частотная характеристика коэффициента прохождения, рассчитанная с использованием результатов решения обратной задачи на резонансной частоте f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне;
кривая, обозначенная символами ◊◊◊ – экспериментальная амплитудно-частотная характеристика коэффициента прохождения вблизи резонансной частоты f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне;
кривая 19 – амплитудно-частотная характеристика коэффициента отражения, рассчитанная с использованием результатов решения обратной задачи на резонансной частоте f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне;
кривая, обозначенная символами ΔΔΔ – экспериментальная амплитудно-частотная характеристика коэффициента отражения вблизи резонансной частоты f2=8.378 ГГц, соответствующей дефектной моде во второй запрещенной зоне.
Для расчета коэффициента прохождения и отражения электромагнитной волны в коаксиальном фотонном кристалле использовалась матрица передачи  четырехполюсника сложной структуры, представляющего собой каскадное соединение элементарных четырехполюсников с известными матрицами передачи, которые имеют вид:
четырехполюсника сложной структуры, представляющего собой каскадное соединение элементарных четырехполюсников с известными матрицами передачи, которые имеют вид:
где T'i и T"i,j — матрицы передачи четырехполюсников, описывающих соответственно i-ый отрезок и прямое соединение i-го и (i+1)-го отрезков коаксиальной линии передачи.
Выражения для матриц передачи T'i и T"i,j соответствующих элементарных четырехполюсников имеют вид:
Здесь li — длина i-го отрезка, γi — постоянная распространения электромагнитной волны в i-ом отрезке, 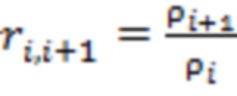 , где ρi— волновое сопротивление i-го отрезка коаксиальной линии передачи с диэлектрической проницаемостью наполнения ε, рассчитываемое по формуле:
, где ρi— волновое сопротивление i-го отрезка коаксиальной линии передачи с диэлектрической проницаемостью наполнения ε, рассчитываемое по формуле:
Постоянная распространения gi имеет вид:
где ai=ami+adi — постоянная затухания i-го отрезка коаксиальной линии, равная сумме постоянных затухания в металлических проводниках ami и в диэлектрическом наполнении adi; bi=2p/li – фазовая постоянная, где li – длина электромагнитной волны в i-ом отрезке коаксиальной линии.
Постоянные затухания ami, adi имеют вид:
где μ – магнитная проницаемость диэлектрического наполнения, RS– удельное поверхностное сопротивление проводника, tgδ – тангенс угла диэлектрических потерь.
Коэффициенты прохождения и отражения СВЧ мощности определяются через элементы матрицы передачи T по известным соотношениям:
Сопротивление нагрузки на входе и выходе фотонной структуры составляло 50 Ω.
Расчет распределения поля электромагнитной волны вдоль коаксиального фотонного кристалла проводится с помощью трехмерного электродинамического моделирования по методу конечных элементов.
Решение обратной задачи по определению относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектриков по частотным зависимостям коэффициентов прохождения и отражении основано на использование метода наименьших квадратов, при реализации которого находится такое значение параметров e'иск и⋅eʺиск, при котором сумма квадратов разностей S(e, tgδ) расчетных |D(e, tgδ, f)|2, |R(e, tgδ, f)|2 и экспериментальных (исходных) |Dэксп|2 и |Rэксп|2 значений квадратов модулей коэффициентов прохождения и отражения
становится минимальной. Здесь K – число измеренных значений коэффициентов прохождения и отражения.
Искомые значения параметров исследуемого образца определяются численным методом в результате решения системы дифференциальных уравнений:
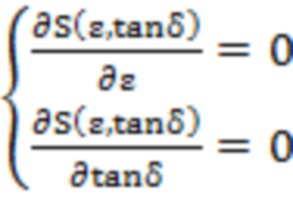 .
.
Пример реализации способа определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрической структуры.
Вначале проводился расчет частотных зависимостей коэффициентов отражения и прохождения 11-ти слойного сверхвысокочастотного коаксиального фотонного кристалла без нарушения периодичности и с нарушением периодичности в виде центрального (6-го слоя) (фиг. 1) с различными значениями комплексной диэлектрической проницаемости в диапазоне 0...12 ГГц приведены на фиг. 2.
Параметры структуры фотонного кристалла были выбраны таким образом, что электрические длины четных элементов, составляющих фотонный кристалл, оказываются кратными длинам нечетных элементов (кратность равна 2).
Как следует из результатов расчета при выбранных параметрах структуры фотонного кристалла в диапазоне частот 0...12 ГГц на АЧХ наблюдаются две запрещенные зоны равной глубины, разделенные разрешенной зоной (кривая 6 на фиг. 2).
При создании нарушения периодичности в виде измененной длины и диэлектрической проницаемости центрального (6-го слоя) (фиг. 1) в первой и второй запрещенных зонах возникают дефектные моды, частотное положение f1 и f2 и форма которых зависят от значения диэлектрической проницаемости вносимого нарушения. При этом оказывается, что изменения резонансной частоты Df1 и Df2 дефектных мод при изменении диэлектрической проницаемости образца, выполняющего роль нарушения в центральном слое, различны. Для выяснения причин различной чувствительности дефектных мод к изменению диэлектрической проницаемости были выполнены расчеты распределения напряженности электрического поля E(z) электромагнитной волны вдоль структуры фотонного кристалла на резонансных частотах f1 и f2 дефектных мод с использованием программы трехмерного электродинамического моделирования HFSS. Результаты расчета распределения напряженности электрического поля E(z) электромагнитной волны вдоль структуры одномерного сверхвысокочастотного коаксиального фотонного кристалла представлены на фиг. 3 и 4. Как следует из результатов расчета на частоте дефектной моды f1=4.113 ГГц в области расположения дефекта наблюдается узел стоячей волны, а на частоте дефектной моды f2=9.382 ГГц в области расположения дефекта наблюдается пучность стоячей волны.
Анализируя распределение электрического поля на частотах дефектных мод f1 и f2 внутри фотонного кристалла, можно сделать вывод, что причиной слабой чувствительности дефектной моды в первой запрещенной зоне на частоте f1 и высокой чувствительности дефектной моды во второй запрещенной зоне на частоте f2 к изменению диэлектрической проницаемости вносимого нарушения является возникновение в области расположения дефекта на частоте f1 узла стоячей волны и на частоте f2 пучности стоячей волны.
Для отработки метода измерений решалась тестовая задача, которая заключалась в следующем: задавались относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь исследуемого диэлектрика и рассчитывались частотные зависимости коэффициентов пропускания и отражения исследуемой структуры, то есть решалась прямая задача. Эти частотные зависимости с погрешностью ± 5% выбирались в качестве исходных при решении обратной задачи по нахождению комплексной диэлектрической проницаемости исследуемого диэлектрика, считающейся в этом случае неизвестной величиной и подлежащей определению. Сравнение результатов решения обратной задачи с исходными значениями комплексной диэлектрической проницаемости исследуемого диэлектрика позволяет оценить погрешность предложенного метода измерений.
Функционал S(e, tgδ) (фиг. 4) на резонансных частотах f1=4.094 ГГц и f2=8.786 ГГц, соответствующих дефектным модам в первой и второй запрещенных зонах, для образца длиной L=10 мм с относительной диэлектрической проницаемостью e=2 и тангенсом угла диэлектрических потерь tg=0.005, как следует из результатов расчета, обладают глобальным минимумом в пространстве координат (e, tgδ, S(e, tgδ)), а контурные карты (фиг. 5) характеризуются наличием замкнутых траекторий вблизи минимума, что подтверждает возможность однозначно определять относительную диэлектрическую проницаемость и тангенс угла диэлектрических потерь из решения системы дифференциальных уравнений.
Значения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь, определенные из решения обратной задачи с использованием системы дифференциальных уравнений, составили e=1.896, tg=0.0074 на резонансной частоте дефектной моды в первой разрешенной зоне и e=1.994, tg=0.006 на резонансной частоте дефектной моды во второй разрешенной зоне.
Относительная погрешность определения относительной диэлектрической проницаемости на резонансной частоте дефектной моды в первой разрешенной зоне составила 5.2% и 0.3% на резонансной частоте дефектной моды во второй разрешенной зоне. При этом относительные погрешности определения тангенса угла диэлектрических потерь на резонансных частотах дефектной моды в первой и второй разрешенных зонах составляют 48% и 20%, соответственно.
Экспериментально в диапазоне частот 0–12 ГГц измерялись амплитудно-частотные характеристики коэффициентов отражения и прохождения сверхвысокочастотного излучения, взаимодействующего с 11-слойным коаксиальным фотонным кристаллом, нечетные слои которого были выполнены из коаксиальных отрезков с диэлектрическим заполнением (фторопласт, длина 8 мм), а четные – коаксиальных отрезков с воздушным заполнением (длина 22.56 мм). Результаты измерений демонстрируют наличие на амплитудно-частотной характеристике в диапазоне частот 0–12 ГГц двух запрещенных зон равной глубины, разделенных разрешенной зоной (кривая 13 на фиг. 8).
Исследуемые диэлектрические образцы, выполненные в виде цилиндрических втулок (внешний диаметр 7 мм, внутренний диаметр 3 мм), помещались в коаксиальный фотонный кристалл в качестве центрального (шестого) отрезка. Исследуемые образцы были выполнены из фторопласта (длина 10.47 мм), капролона (длина 10.65 мм), эбонита (длина 10.16 мм) и текстолита (длина 10.25 мм).
Как следует из результатов эксперимента (фиг. 8) при измерении образцов, выполненных из фторопласта, капролона, эбонита и текстолита, в первой и второй запрещенных зонах коаксиального фотонного кристалла появляются дефектные моды на частотах 4.066 ГГц и 8.716 ГГц (фторопласт), 4.049 ГГц и 8.677 ГГц (капролон), 4.074 ГГц и 8.651 ГГц (эбонит), 4.016 ГГц 8.378 ГГц (текстолит), соответственно.
Из результатов компьютерного моделирования, изменение резонансной частоты f1 дефектной моды в первой запрещенной зоне при изменении относительной диэлектрической проницаемости нарушенного слоя является незначительным по сравнению с изменением дефектной моды во второй запрещенной зоне. В связи с этим для реализации способа измерения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь исследуемых в эксперименте диэлектриков была выбрана дефектная мода во второй запрещенной зоне.
Результаты измерений относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь выбранных диэлектриков приведены в таблице 1.
На фиг. 9 представлены амплитудно-частотные характеристики коэффициентов прохождения и отражения, экспериментальные (◊◊◊ и Δ) и рассчитанные (линии) при значениях e и tgδ, приведенных в таблице 1 для образца из текстолита, которые были определены при решении обратной задачи) на резонансной частоте f2=8.378 ГГц, соответствующей дефектной моде во второй фотонной запрещенной зоне.
Сравнение результатов теоретического расчета и эксперимента демонстрирует их качественное и количественное совпадение. Функционал S(e, tgδ) (фиг. 10) и его контурная карта для случая измерения образца, выполненного из текстолита, со значениями относительной диэлектрической проницаемости e=3.682 и тангенса угла диэлектрических потерь tg=0.022, обладает ярко выраженным глобальным минимумом в пространстве координат (e, tgδ, S(e, tgδ)), а контурная карта характеризуется наличием замкнутых траекторий вблизи минимума, что подтверждает возможность однозначно определять относительную диэлектрическую проницаемость и тангенс угла диэлектрических потерь.
Таблица 1 Результаты измерений
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ТАНГЕНСА УГЛА ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ ЖИДКОСТИ | 2010 |
|
RU2419099C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЭЛЕКТРОФИЗИЧЕСКИХ ПАРАМЕТРОВ СТРУКТУРЫ "НАНОМЕТРОВАЯ МЕТАЛЛИЧЕСКАЯ ПЛЕНКА - ПОЛУПРОВОДНИКОВАЯ ИЛИ ДИЭЛЕКТРИЧЕСКАЯ ПОДЛОЖКА" | 2007 |
|
RU2349904C1 |
| Зонд для измерения диэлектрической проницаемости диэлектрических пластин методом СВЧ-спектроскопии | 2023 |
|
RU2803975C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МЕТАЛЛОДИЭЛЕКТРИЧЕСКИХ СТРУКТУР | 2013 |
|
RU2534728C1 |
| СПОСОБ ИЗМЕРЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2548064C1 |
| ВОЛНОВОДНАЯ СТРУКТУРА С РАЗРЕШЕННЫМИ И ЗАПРЕЩЕННЫМИ ЗОНАМИ | 2014 |
|
RU2575995C2 |
| СВЧ фотонный кристалл | 2017 |
|
RU2658113C1 |
| СВЕРХВЫСОКОЧАСТОТНОЕ УСТРОЙСТВО ДЛЯ НЕРАЗРУШАЮЩЕГО ИЗМЕРЕНИЯ ЭЛЕКТРОФИЗИЧЕСКИХ ПАРАМЕТРОВ ДИЭЛЕКТРИЧЕСКИХ МАТЕРИАЛОВ | 2001 |
|
RU2188433C1 |
| СВЧ фотонный кристалл | 2018 |
|
RU2698561C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ПОЛУПРОВОДНИКОВЫХ СТРУКТУР | 2015 |
|
RU2622600C2 |

Изобретение относится к области контрольно-измерительной техники и предназначено для одновременного определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур в сверхвысокочастотном диапазоне, и может найти применение для неразрушающего контроля электрофизических параметров производимых диэлектрических подложек и структур для устройств СВЧ-электроники. Технический результат заключается в расширении функциональных возможностей одновременного определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур, применяемых в качестве диэлектрического наполнения сверхвысокочастотных коаксиальных кабелей. Изобретение представляет собой способ определения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрических структур, включающий размещение диэлектрической структуры в области нарушения периодичности СВЧ фотонного кристалла, облучение фотонного кристалла, содержащего измеряемую диэлектрическую структуру, электромагнитным излучением сверхвысокочастотного диапазона, измерение частотных зависимостей коэффициентов прохождения и отражения в запрещенной зоне в окрестности дефектной моды, расчет с помощью ЭВМ искомых значений, при которых теоретические частотные зависимости коэффициентов отражения и прохождения электромагнитного излучения наиболее близки к измеренным, при этом, в качестве фотонного кристалла используют коаксиальный сверхвысокочастотный фотонный кристалл, представляющий собой последовательно соединенные отрезки коаксиальной линии передачи, пространство между внешним и внутренним проводником каждого отрезка полностью заполнено диэлектриком, при этом относительная диэлектрическая проницаемость диэлектрического заполнения периодически изменяется вдоль направления распространения электромагнитной волны, подбирают значения длин и относительных диэлектрических проницаемостей диэлектрических заполнений чередующихся отрезков коаксиальной линии передачи таким образом, чтобы обеспечить кратность их электрических длин, приводящую к формированию фотонных запрещенных зон равной глубины на частотных зависимостях коэффициентов прохождения электромагнитного излучения, нарушение периодичности СВЧ фотонного кристалла создают в центральном отрезке коаксиального фотонного кристалла, что приводит к формированию дефектных мод в нескольких фотонных запрещенных зонах, рассчитывают распределение поля электромагнитной волны внутри коаксиального фотонного кристалла вдоль направления распространения электромагнитной волны на частотах, соответствующих дефектным модам в фотонных запрещенных зонах, фиксируют узлы и пучности стоячей электромагнитной волны внутри коаксиального фотонного кристалла, выбирают дефектную моду, на частоте которой в области расположения диэлектрической структуры в центральном отрезке коаксиального фотонного кристалла наблюдается пучность стоячей волны. 2 з.п. ф-лы, 1 табл., 11 ил.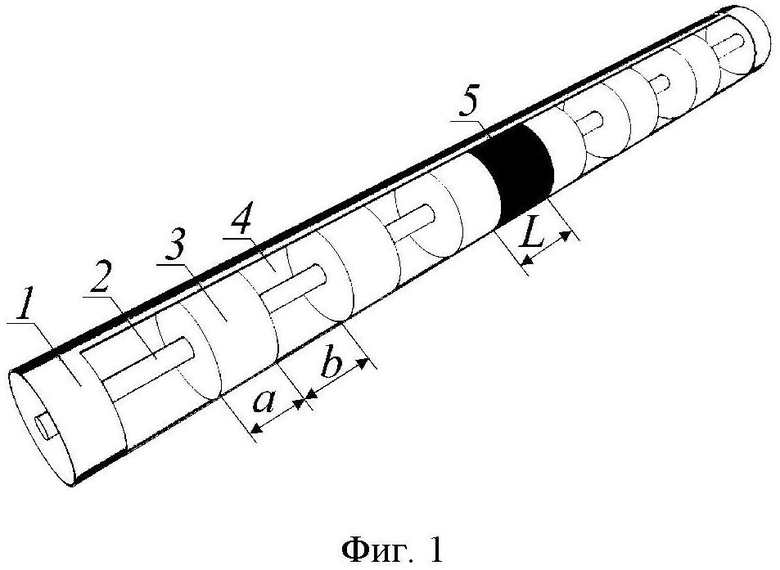
1. Способ определения диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрической структуры, включающий размещение диэлектрической структуры в области нарушения периодичности СВЧ фотонного кристалла, облучение фотонного кристалла электромагнитным излучением СВЧ-диапазона, измерение частотных зависимостей коэффициентов прохождения и отражения в запрещенной зоне в окрестности дефектной моды, расчет искомых значений, при которых теоретические частотные зависимости коэффициентов отражения и прохождения электромагнитной волны наиболее близки к измеренным, отличающийся тем, что в качестве фотонного кристалла используют коаксиальный СВЧ фотонный кристалл, в котором при размещении диэлектрической структуры формируются дефектные моды в нескольких запрещенных зонах, рассчитывают на частотах, соответствующих дефектным модам, распределение поля стоячей электромагнитной волны внутри фотонного кристалла, фиксируют её узлы и пучности, для определения диэлектрической проницаемости и тангенса угла диэлектрических потерь диэлектрической структуры выбирают ту из частот, на которой в области расположения структуры наблюдается пучность стоячей волны.
2. Способ по п. 1, отличающийся тем, что коаксиальный СВЧ фотонный кристалл представляет собой последовательно соединенные отрезки коаксиальной линии передачи, пространство между внешним и внутренним проводником каждого отрезка полностью заполнено диэлектриком, при этом относительная диэлектрическая проницаемость диэлектрического заполнения периодически изменяется вдоль направления распространения электромагнитной волны.
3. Способ по п. 1, отличающийся тем, что подбирают значения длин и относительных диэлектрических проницаемостей диэлектрических заполнений чередующихся отрезков коаксиальной линии передачи таким образом, чтобы обеспечить кратность их электрических длин, приводящую к формированию фотонных запрещенных зон равной глубины на частотных зависимостях коэффициентов прохождения электромагнитного излучения.
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ И ТОЛЩИНЫ ПОЛУПРОВОДНИКОВЫХ ПЛАСТИН ИЛИ НАНОМЕТРОВЫХ ПОЛУПРОВОДНИКОВЫХ СЛОЕВ В СТРУКТУРАХ "ПОЛУПРОВОДНИКОВЫЙ СЛОЙ - ПОЛУПРОВОДНИКОВАЯ ПОДЛОЖКА" | 2012 |
|
RU2517200C2 |
| СПОСОБ ИЗМЕРЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2548064C1 |
| Устройство для измерения тангенса угла диэлектрических потерь и определения относительной диэлектрической проницаемости | 1987 |
|
SU1597777A1 |
| Способ определения диэлектрической проницаемости и тангенса угла потерь диэлектрика | 1988 |
|
SU1539681A1 |
| US 9335273 B2 10.05.2016. | |||
Авторы
Даты
2020-03-13—Публикация
2019-06-25—Подача