Изобретение относится к способам регистрации изображений, сформированных с помощью пучка протонов, и может найти применение при исследовании материалов и объектов с использованием радиографических способов регистрации изображений, использующих заряженные частицы.
Задачей, стоящей в рассматриваемой области техники, является получение высококачественного изображения области исследования. Способы настройки систем получения изображения являются неотъемлемой частью решения данной задачи.
Во всех видах радиографии (рентгенографии, протонографии или нейтронографии) при прохождении пучка частиц через вещество происходит выбывание первичных частиц из пучка по экспоненциальному закону, то есть количество частиц N на выходе из объекта толщиной L зависит от начального количества частиц N0 следующим образом:
N=N0⋅exp(-L/λ),
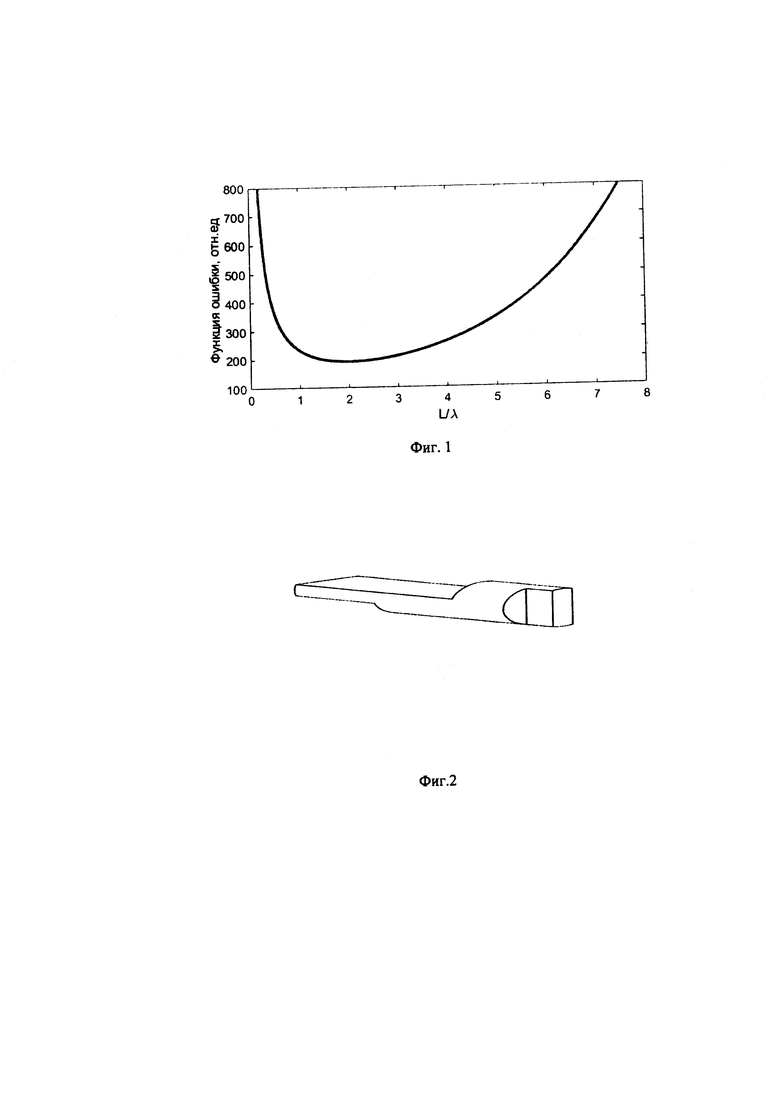
где λ - длина взаимодействия первичной частицы с веществом. В [The Proton Radiography Concept, H.-J. Ziock, K.J. Adams et.al., LA-UR-98-1368 (1998)] показано, что если исходить из данной простой экспоненциальной зависимости коэффициента прохождения через вещество, то функция ошибки восстановления массовой толщины будет иметь вид, представленный на фиг 1. В частности, оптимальным с точки зрения разрешения по массовой толщине при исследовании объектов толщиной Lopt=2⋅λ будет наблюдаться максимальная контрастная чувствительность. Для всех остальных толщин ошибка будет возрастать и при толщине L<Lopt/4 или L>2.5⋅Lopt ошибка восстановления массовой толщины возрастет более чем в 2 раза. В свинце, например, длина взаимодействия для рентгеновского излучения с энергией 5 МэВ (при которой длина взаимодействия максимальна) составляет 23 г/см2, а для протонов высоких энергий - 194 г/см2 [тот же источник]. Поэтому для больших толщин просвечиваемых объектов (сотни г/см2) гораздо выгоднее использовать протонное излучение, чем рентгеновское. Казалось бы, протоны высоких энергий имеют преимущество только при больших толщинах, когда величина ошибки в несколько раз ниже, чем для рентгеновского излучения. Однако, в протонной радиографии, в отличие от других видов радиографии, после размещения объекта исследования стоит магнитооптическая система (МОС), которая является ключевой системой протонографического комплекса и влияет на общий коэффициент пропускания. МОС включает магнитные линзы и коллиматор и фокусирует протонный пучок, рассеявшийся в исследуемом объекте, находящемся в объектной плоскости, на сцинтиллятор (в плоскость регистрации). Соответственно, от настройки МОС протонографического комплекса зависит качество проводимых исследований. Наиболее распространенным вариантом МОС является так называемая оптика, состоящая из четырех квадрупольных магнитных линз, чередующихся друг с другом (фокусирующая - дефокусирующая - фокусирующая -дефокусирующая) и расположенных симметрично относительно центральной плоскости - плоскости Фурье и обладает тем свойством, что протоны в ней сортируются по углам рассеяния в исследуемых объектах (устанавливаемых в объектной плоскости): отклонение протонов от оси МОС в плоскости Фурье пропорционально углу рассеяния протонов в объекте. Поэтому, устанавливая в этой плоскости коллиматоры различного диаметра, можно блокировать протоны, рассеянные больше чем на определенный угол. При установке коллиматоров различного диаметра в плоскости Фурье меняется вид общего коэффициента пропускания (см., например, [Charged particle radiography; С.L. Morris et al., 2012, LA-UR 12-01545]), поэтому, подобрав коллиматор оптимального диаметра, можно получить общий коэффициент пропускания, минимизирующий ошибку восстановления массовой толщины для конкретного объекта с конкретной массовой толщиной. Таким образом, протонная установка является универсальной: на одной и той же установке можно исследовать процессы пылеобразования с характерными массовыми толщинами в сотни мг/см2 и, одновременно, тяжелые объекты с массой в несколько сот г/см2.
Известны способы настройки МОС путем подбора оптимального диаметра коллиматора, для чего определяют общий коэффициент пропускания Ktot, учитывая неупругое ядерное рассеяние (НЯР) и многократное кулоновское рассеяние (МКР) протонного пучка [Flash radiography with 24 GeV/c protons, С.L. Morris et al, JOURNAL OF APPLIED PHYSICS 109, 104905 (2011)] и [The optimum angle-cut of collimator for the dense objects in high-energy proton radiography, XU Hai-Bo ZHENG Na, (Institute of Applied Physics and Computational Mathematics, Beijing 100094, China), 2015], последний источник выбран в качестве ближайшего аналога. Способ настройки МОС включает в себя расчетное получение полного коэффициента пропускания Ktot (L,∅) в зависимости от толщины объекта L и от диаметра используемого коллиматора ∅, расчет по нему функции ошибки ε (∅; L=Lobj) в зависимости от диаметра используемого коллиматора для исследуемой толщины объекта Lobj. Тогда значение диаметра коллиматора, при котором функция ошибки минимальна, и будет оптимальным.
Поскольку общий коэффициент пропускания Ktot зависит от вида коллиматора, установленного в плоскости Фурье, то координата xfour в этой плоскости для согласованного с магнитной системой пучка определяется углом рассеяния протонов в объектной плоскости θscatt по формуле: xfour ≈ β0θscatt, где β0 - параметр МОС. Если считать, что отклонение протонов от прямолинейной траектории обусловлено только МКР, то угловое распределение рассеянных протонов имеет форму гауссиана [Bartels J., Haidt D., Zichichi A. The European Physical Journal C, v. 15, 2000.], и, воспользовавшись тем, что θscatt ~ 1 мрад << 1 рад, мы получим, что пространственное распределение протонов в плоскости Фурье также имеет вид гауссиана:
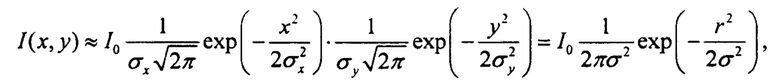
где I0 - общая интенсивность пучка, σ=σx=σу=β0σθ. Согласно [Bartels J et al]
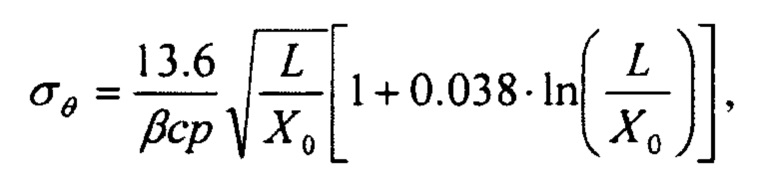
где X0 - радиационная длина материала образца, р-импульс протона, выраженный в еденицах МэВ/с, a L - толщина образца.
В общем случае для комбинированного коллиматора в Фурье-плоскости, состоящего из ферма-коллиматора радиуса r1 и обычного коллиматора радиуса r2 (т.е. проходят только те протоны, для которых в Фурье-плоскости r1<r<r2), теоретический коэффициент пропускания МОС определяется выражением:
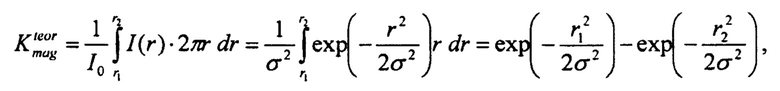
а общий коэффициент пропускания через объект и через МОС (с учетом неупругого ядерного взаимодействия):
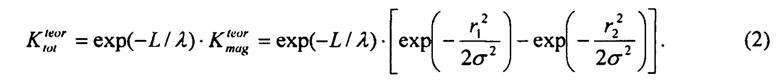
Плотностное разрешение, в целом, определяется статистикой, т.е. количеством протонов, падающих на один разрешающий элемент. Пусть у нас есть просвечиваемый объект и фиксированное количество протонов в облучающем его пучке. Поставим перед собой задачу подобрать оптимальный коллиматор с точки зрения получения максимального плотностного разрешения.
Допустим теперь, что у нас есть два элемента объекта толщиной L и L+h и пусть на каждый из этих элементов падает N0 протонов. Количество протонов, в среднем проходящих через эти элементы равно:
N1=N(L)=N0Ktot(L), N2=N(L+h)=N0Ktot(L+h),
где Ktot=Kobj⋅Kmag=exp(-L/λ)⋅Kmag - общий коэффициент пропускания протонов объектом и каналом. Разность количества протонов, проходящих через два этих элемента:
ΔN=N1-N2=N0(Ktot(L)-Ktot(L+h)).
Статистическая ошибка определения AN равна сумме квадратов ошибок каждого члена:
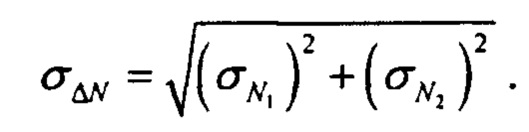
Относительная ошибка определения ΔN равна:
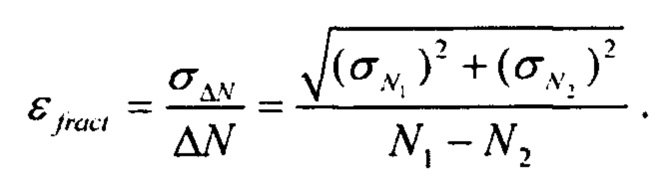
При большом количестве протонов N0 количество прошедших и зарегистрированных протонов по центральной предельной теореме будет распределено по нормальному закону со среднеквадратичным отклонением 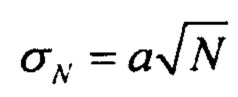 , где коэффициент а≥1 зависит от регистрирующей системы. Тогда:
, где коэффициент а≥1 зависит от регистрирующей системы. Тогда:
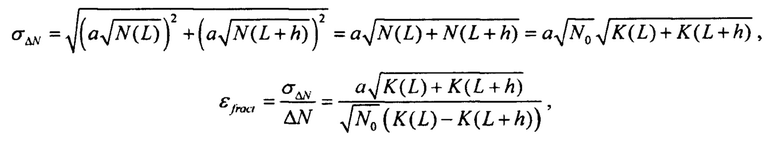
или, для конкретной установки с определенным количеством протонов в банче и определенной системой регистрации (то есть, зафиксировав параметры а и N0) можно ввести более универсальную величину:
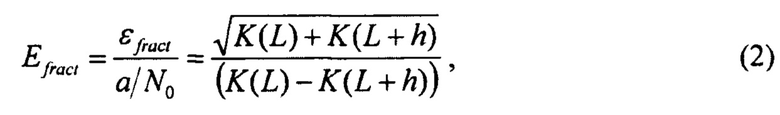
где K=Ktot - величина, которая зависит только от коэффициента пропускания.
Оптимальный диаметр коллиматора для той или иной толщины объекта будет минимизировать величину Efract (или, что то же самое εfract) при этой толщине. В качестве величины h можно выбрать h=0.01L, т.е. будем исходить из требования различать перепад толщины в один процент.
К недостаткам данного способа можно отнести то, что при выборе оптимального коллиматора не учитывают упругое ядерное рассеяние (УЯР) протонного пучка, вызывающее дополнительное рассеяние. Тем не менее, УЯР является значимым процессом и его влияние на общий коэффициент пропускания установки составляет, в некоторых случаях, десятки процентов.
Техническим результатом заявляемого способа является повышение точности настройки МОС, и, как следствие, получение более информативных протонограмм.
Указанный технический результат достигается за счет того, что в способе настройки МОС протонографического комплекса по первому варианту, заключающемся в подборе оптимального диаметра входящего в МОС коллиматора с точки зрения получения максимальной контрастной чувствительности изображений, для чего определяют общие коэффициенты пропускания МОС - Ktot, (L,∅) для коллиматоров разных диаметров ∅ в зависимости от толщины объекта L, учитывая НЯР и МКР протонного пучка, и расчет по найденным коэффициентам функции ошибки ε (∅; L=Lobj) для коллиматоров разных диаметров при заданной толщине исследуемого объекта Lobj, оптимальным диаметром коллиматора выбирают тот, при котором функция ошибки минимальна, новым является то, что при определении общих коэффициентов пропускания МОС - Ktot (L,∅) дополнительно учитывают УЯР высокоэнергетичных протонов, для чего в объектной плоскости МОС размещают радиографический клин, состоящий, не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, пропуская пучок протонов через объектную плоскость, получают изображения, обрабатывая которые восстанавливают общие коэффициенты пропускания Ktot для каждой ступени радиографического клина по ее центральной части, строят кривую коэффициента пропускания K(L) для каждого коллиматора и вычисляют относительную ошибку εfract определения количества прошедших протонов через ступень определенной толщины для всего набора коллиматоров, и тот коллиматор, для которого данная ошибка минимальна, выбирают в качестве оптимального по размерам для данной толщины объекта.
Указанный технический результат достигается также за счет того, что в способе настройки МОС протонографического комплекса по второму варианту, заключающемся в подборе оптимального диаметра входящего в МОС коллиматора с точки зрения получения максимальной контрастной чувствительности изображений, для чего определяют общие коэффициенты пропускания МОС - Ktot (L,∅) для коллиматоров разных диаметров ∅ в зависимости от толщины объекта L, учитывая НЯР и МКР протонного пучка и расчет по найденным коэффициентам функции ошибки ε (∅; L=Lobj) для коллиматоров разных диаметров при заданной толщине исследуемого объекта Lobj, оптимальным диаметром коллиматора выбирают тот, при котором функция ошибки минимальна, новым является то, что при определении общих коэффициентов пропускания МОС - Ktot (L,∅) дополнительно учитывают УЯР высокоэнергетичных протонов, для чего в объектной плоскости МОС размещают радиографический клин, состоящий, не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, пропуская пучок протонов через объектную плоскость, получают изображения, обрабатывая которые восстанавливают общие коэффициенты пропускания Ktot для каждой ступени по ее центральной части для двух коллиматоров, диаметры которых, а соответственно при этом и коэффициенты пропускания существенно отличаются друг от друга, далее по нижеприведенной формуле определяют общий расчетный коэффициент пропускания Кtot:
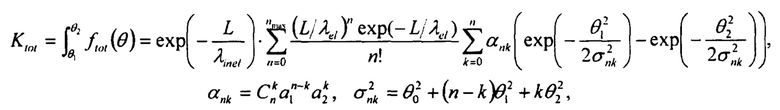
где 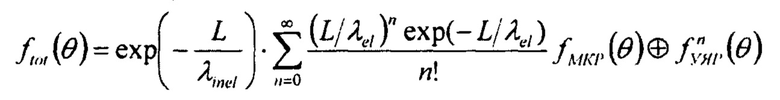 - распределение полного угла рассеяния протонов при прохождении через слой вещества толщиной L, exp(-L/λinel) - протоны, прошедшие через объект/слой вещества; λel - длина упругого и квазиупругого ядерного взаимодействия; λinel - длина неупругого ядерного взаимодействия; ƒмкр,
- распределение полного угла рассеяния протонов при прохождении через слой вещества толщиной L, exp(-L/λinel) - протоны, прошедшие через объект/слой вещества; λel - длина упругого и квазиупругого ядерного взаимодействия; λinel - длина неупругого ядерного взаимодействия; ƒмкр, 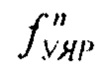 - свертки из n распределений углов МКР и УЯР;
- свертки из n распределений углов МКР и УЯР; 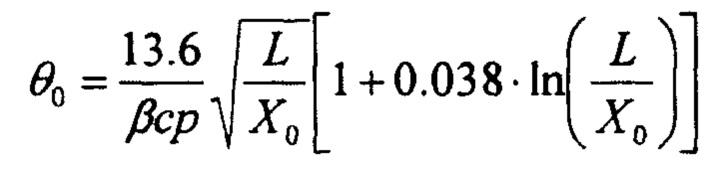 ; Х0 - радиационная длина материала образца, р-импульс протона, выраженный в единицах МэВ/с, a L - толщина объекта, при этом, варьируя коэффициенты λel и λinel, подбирают их таким образом, чтобы экспериментальные коэффициенты пропускания наилучшим образом аппроксимировали указанную формулу, далее, минимизируя величину относительной ошибки εfract определения количества прошедших протонов через объект толщиной L для конкретной установки с определенным количеством протонов в пучке и определенной системой регистрации с известными параметрами а и N0, из соотношения
; Х0 - радиационная длина материала образца, р-импульс протона, выраженный в единицах МэВ/с, a L - толщина объекта, при этом, варьируя коэффициенты λel и λinel, подбирают их таким образом, чтобы экспериментальные коэффициенты пропускания наилучшим образом аппроксимировали указанную формулу, далее, минимизируя величину относительной ошибки εfract определения количества прошедших протонов через объект толщиной L для конкретной установки с определенным количеством протонов в пучке и определенной системой регистрации с известными параметрами а и N0, из соотношения 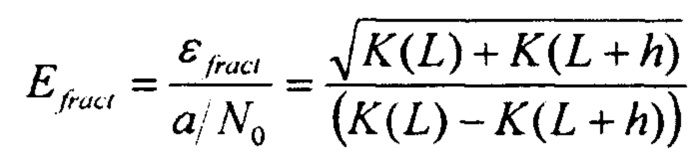 , h=0.01L и вычисленным коэффициентом К=Кtot подбирают диаметр оптимального коллиматора.
, h=0.01L и вычисленным коэффициентом К=Кtot подбирают диаметр оптимального коллиматора.
На фиг. 1 показана функция ошибки восстановления массовой толщины; на фиг. 2 - радиографический клин.
Можно воспользоваться следующим способом оптимизации коллиматора (по варианту 1). Допустим, что нам необходимо оптимизировать толщину коллиматора для объекта толщиной Lobj. Из формулы (2) следует, что величина ошибки определения толщины просвечиваемого объекта зависит только от общего коэффициента пропускания МОС при данном коллиматоре. Зависимость данного коэффициента от толщины исследуемого объекта измеряют экспериментально, с помощью радиографического клина. Перед проведением эксперимента с объектом, в объектной плоскости устанавливают радиографический клин из вещества, из которого изготовлен объект. Клин состоит из нескольких ступеней, с максимальной массовой толщиной большей, чем максимальная массовая толщина объекта (фиг. 2). Ширина ступеней в перпендикулярном пучку направлению выбирают, исходя из минимизации вклада от размытия, вызванного конвертором [по аналогии с железным тест-объектом в виде клина с поперечными размерами 30×30 мм2 по патентному документу RU 2529454, публик. 27.09.2014]: не менее 20 мм, причем по этим же соображениям наиболее толстые ступени необходимо располагать в центре объектной плоскости. Количество ступеней должно обеспечить детальное описание кривой пропускания, в настоящее время используют не менее 9 ступеней. Пропускают пучок протонов через объектную плоскость и МОС, включающую магнитные линзы и коллиматор, и с помощью системы регистрации изображений последовательно получают протонограммы клина, используя коллиматоры разного диаметра. Далее, по процедуре, описанной в патентном документе RU 2604723 [«Способ получения и обработки изображений, сформированных с помощью протонного излучения», публик. от 10.12.2016], осуществляют обработку полученных протонограмм путем использования реперов и преобразования полученных изображений к одному ракурсу. При обработке восстанавливают коэффициент пропускания для каждой ступени по ее центральной части. Таким образом, получают совокупность точек «толщина ступени» - «коэффициент пропускания», по которой при помощи сплайнов строят кривую пропускания K(L) для нескольких коллиматоров. Далее, фиксируя небольшую толщину h (например, h-0.01L), по формуле (2) вычисляют ошибку определения толщины для толщины Lobj для всех коллиматоров. Тот коллиматор, для которого данная ошибка будет минимальна, и будет оптимальным.
Выбор оптимального коллиматора с учетом УЯР можно осуществить альтернативным способом (по варианту 2), основанным на теоретическом подходе. Он подразумевает вычисление полного коэффициента пропускания расчетным путем, с учетом УЯР, НЯР и МКР с предварительной экспериментальной проработкой. Данный способ обладает большей универсальностью и может быть использован для расчета коэффициентов пропускания, и, соответственно, оптимизации коллиматора, для комбинации веществ, что особенно важно, учитывая, что исследуемые в протонной радиографии объекты, как правило, состоят из нескольких слоев, изготовленных из различных веществ.
Рассмотрим процесс рассеяния протонов в веществе более детально. Дополнительно к МКР, при прохождении протона через слой вещества может возникнуть одно или несколько дискретных процессов упругого ядерного рассеяния, в результате каждого из которых протон приобретет дополнительный угол рассеяния, описываемый некоторым распределением ƒУЯР(θ). Акты УЯР независимы друг от друга, вероятность возникновения УЯР на элементарном участке длины равна
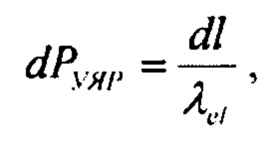
где λel - длина упругого и квазиупругого ядерного взаимодействия, поэтому количество n актов УЯР высокоэнергетических протонов на толщине L вещества распределено согласно статистике Пуассона:
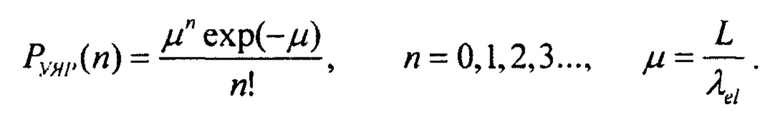
В случае одного акта УЯР общий угол отклонения будет равен свертке распределения угла МКР и УЯР, то есть:
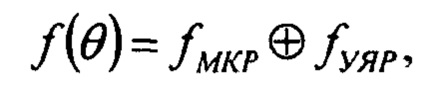
а в случае n УЯР:
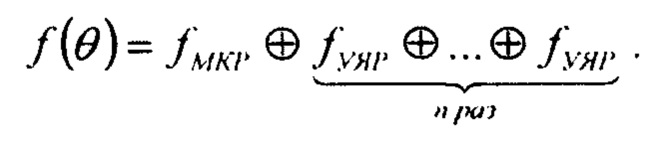
Таким образом, обозначив через 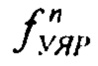 свертку из n распределений углов упругого ядерного рассеяния, получим для полного угла рассеяния протонов при прохождении через слой вещества толщиной L:
свертку из n распределений углов упругого ядерного рассеяния, получим для полного угла рассеяния протонов при прохождении через слой вещества толщиной L:
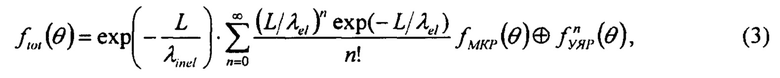
где λinel - длина неупругого ядерного взаимодействия. Величины λel и λinel получают экспериментальным путем, хотя их можно взять из справочников, но при этом нужно учитывать следующее. Данные величины измерялись экспериментально для ограниченного количества элементов и для ограниченного количества энергий налетающих протонов, поэтому для интересующей нас области значения получаются с помощью интерполяции, что приводит к некоторой ошибке этих данных для конкретного изотопа и для конкретной энергии налетающего протона. А также данные, приведенные в различных справочниках, зачастую отличаются друг от друга. Даже на таком широко распространенном ресурсе, как Particle Data Group (http://pdg.lbl.gov/) данные по пробегам до сих пор уточняются от выпуска к выпуску. Так, например, в 2002 году табличное значение для сечения неупругого ядерного взаимодействия для свинца составляло 194 г/см2 [(Review of Particle Physics, K. Hagiwara et al, Phys. Rev. D 66, 010001 (2012)], а в 2018 году данное значение составило 199.6 г/см2 [«Review of Particle Physics, M. Tanabashi et al, Phys. Rev. D 98, 030001 (2018)].
В выражении (3) учитывается тот факт, что при прохождении высокоэнергетических протонов через слой вещества только часть из них, а именно ехр(-L/λinel), преодолевает объект. Остальные протоны выбывают за счет неупругих ядерных взаимодействий, то есть либо исчезают, порождая значительное количество вторичных частиц, либо неупруго рассеиваются, теряя значительную часть энергии (и также порождая вторичные частицы).
В рамках предлагаемого варианта заявляемого способа была использована параметризация из [Estimation of radiation problems around high energy accelerators using calculations of the hadronic cascade in matter; J. Ranft; Particle Accelerators, 1972, v. 3, pp 129-161]:
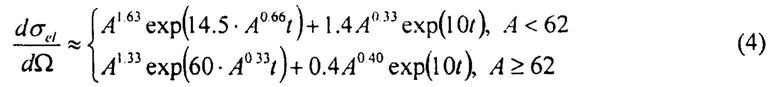
где t=~2p2(1-cosθ)≈-р2θ2, p - импульс частицы, ГэВ/с.
Таким образом, угловую зависимость упругого и квазиупругого ядерного рассеяния можно представить в виде выражения:
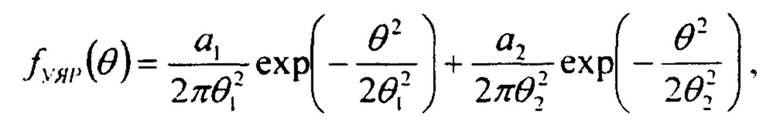
параметры в котором берутся из выражения (4). С другой стороны, многократное кулоновское рассеяние можно представить в виде:
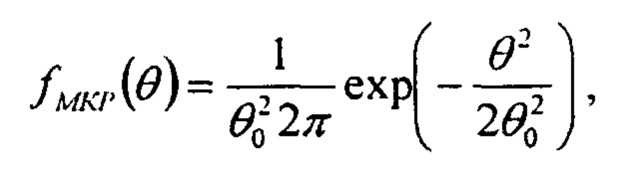
где 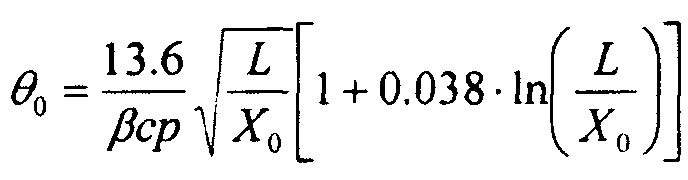 , Х0 - радиационная длина материала образца, р - импульс протона, выраженный в единицах МэВ/с, a L - толщина образца.
, Х0 - радиационная длина материала образца, р - импульс протона, выраженный в единицах МэВ/с, a L - толщина образца.
Для свертки двух одномерных гауссианов имеем:
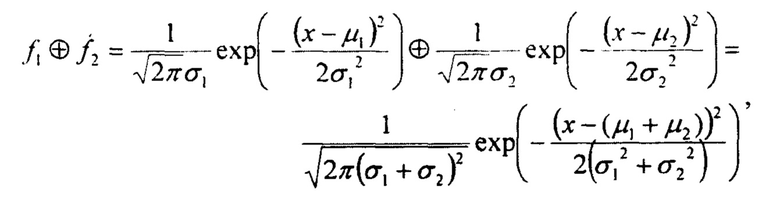
то есть среднее и среднеквадратичное отклонение свертки двух гауссианов равно:
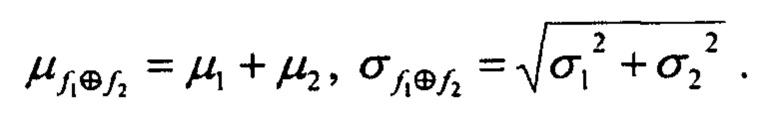
В случае осесимметричных гауссианов, то есть когда у них среднеквадратические отклонения по осям Ох и Оу равны, те же самые формулы можно написать и для двумерного случая, то есть:
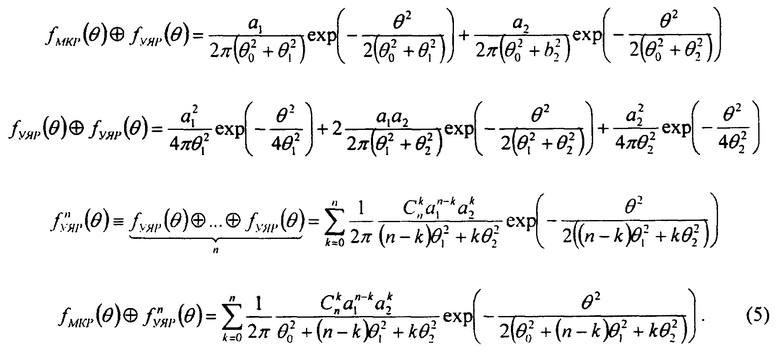
Таким образом, используя формулы (3)-(5), можно полностью описать процесс упругого и неупругого рассеяния высокоэнергетичных протонов в среде.
Учет упругого ядерного рассеяния можно применить для того, чтобы усовершенствовать алгоритм выбора коллиматора, оптимального для получения максимального разрешения по массовой толщине.
Учитывая формулу (1) для общего коэффициента прохождения можно написать:
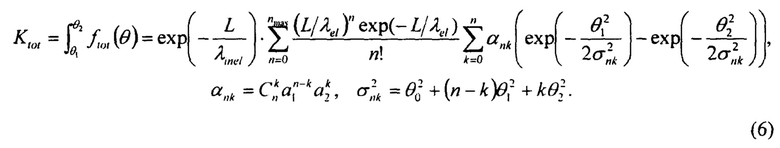
В формуле (6) в пределах суммирования стоит nmax вместо ∞, что объясняется следующим. Максимальная толщина просвечиваемых объектов в протонной радиографии составляет 300-400 г/см3. Это соответствует 1-1.5 длин упругого ядерного рассеяния. Количество ядерных взаимодействий распределено согласно статистике Пуассона (формула 2). То есть, например, в случае максимального значения толщины объекта L/λel=1.5 вероятность того, что произойдет 5 случаев упругого ядерного взаимодействия, составляет 1.41%, 6 случаев - 0.35%, а вероятность возникновения более 6 таких взаимодействий - 0.09%. Таким образом, без большой потери точности в формуле (6) можно выбрать в качестве nmax, например, 6 взаимодействий. При менее толстых объектах nmax можно выбирать еще меньше.
Как упоминалось выше, коэффициенты λel и λinel в формуле (6) получают экспериментальным путем. Измерять их напрямую, ставя прямые эксперименты по измерению поглощения и углов рассеяния протонов на различных веществах, - это длительный и дорогостоящий процесс, неоправданный для нужд протонной радиографии, поэтому применяют следующий косвенный метод измерения. Перед пропусканием пучка протонов через объектную плоскость магнитооптической системы в ней размещают радиографический клин, состоящий не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, далее при обработке изображений восстанавливают коэффициент пропускания Ktot для каждой ступени по ее центральной части для двух коллиматоров, диаметры которых, а соответственно при этом и коэффициенты пропускания Ktot существенно отличаются друг от друга, например, в два раза, далее по формуле (6) определяют общий коэффициент пропускания Кtot. Для чего методами фитирования, варьируя искомые коэффициенты λel и λinel, подобирают их таким образом, чтобы найденные Ktot вписывались в формулу (6). При этом подобранные коэффициенты могут быть использованы для расчета Кtot, для заданного вещества при других коллиматорах, а также для комбинации веществ.
Минимизируя величину относительной ошибки из (2) по диаметру коллиматора для определенной толщины Lobj с коэффициентом пропускания, учитывающим упругое ядерное рассеяние из (6), мы получаем диаметр оптимального коллиматора.
При применении заявляемого способа настройки магнитооптической системы по учету упругого ядерного рассеяния повышается качество настройки МОС и информативность протонограмм.
Использование: для настройки магнитооптической системы протонографического комплекса. Сущность изобретения заключается в том, что осуществляют подбор оптимального диаметра входящего в магнитооптическую систему коллиматора с точки зрения получения максимальной контрастной чувствительности изображений, для чего определяют общие коэффициенты пропускания магнитооптической системы Ktot (L,∅) для коллиматоров разных диаметров ∅ в зависимости от толщины объекта L, учитывая неупругое ядерное рассеяние и многократное кулоновское рассеяние протонного пучка, и производят расчет по найденным коэффициентам функции ошибки ε (∅; L=Lobj) для коллиматоров разных диаметров при заданной толщине исследуемого объекта Lobj, оптимальным диаметром коллиматора выбирают тот, при котором функция ошибки минимальна, причем при определении общих коэффициентов пропускания магнитооптической системы Ktot (L,∅) дополнительно учитывают упругое ядерное рассеяние высокоэнергетичных протонов, для чего в объектной плоскости магнитооптической системы размещают радиографический клин, состоящий не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, пропуская пучок протонов через объектную плоскость, получают изображения, обрабатывая которые восстанавливают общие коэффициенты пропускания Ktot для каждой ступени радиографического клина по ее центральной части, строят кривую коэффициента пропускания K(L) для каждого коллиматора и вычисляют относительную ошибку εfract определения количества прошедших протонов через ступень определенной толщины для всего набора коллиматоров, и тот коллиматор, для которого данная ошибка минимальна, выбирают в качестве оптимального по размерам для данной толщины объекта. Технический результат: обеспечение возможности получения высококачественного изображения области исследования. 2 н.п. ф-лы, 2 ил.
1. Способ настройки магнитооптической системы протонографического комплекса, заключающийся в подборе оптимального диаметра входящего в магнитооптическую систему коллиматора с точки зрения получения максимальной контрастной чувствительности изображений, для чего определяют общие коэффициенты пропускания магнитооптической системы Ktot (L,∅) для коллиматоров разных диаметров ∅ в зависимости от толщины объекта L, учитывая неупругое ядерное рассеяние и многократное кулоновское рассеяние протонного пучка, и производят расчет по найденным коэффициентам функции ошибки ε (∅; L=Lobj) для коллиматоров разных диаметров при заданной толщине исследуемого объекта Lobj, оптимальным диаметром коллиматора выбирают тот, при котором функция ошибки минимальна, отличающийся тем, что при определении общих коэффициентов пропускания магнитооптической системы Ktot (L,∅) дополнительно учитывают упругое ядерное рассеяние высокоэнергетичных протонов, для чего в объектной плоскости магнитооптической системы размещают радиографический клин, состоящий не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, пропуская пучок протонов через объектную плоскость, получают изображения, обрабатывая которые восстанавливают общие коэффициенты пропускания Ktot для каждой ступени радиографического клина по ее центральной части, строят кривую коэффициента пропускания K(L) для каждого коллиматора и вычисляют относительную ошибку εfract определения количества прошедших протонов через ступень определенной толщины для всего набора коллиматоров, и тот коллиматор, для которого данная ошибка минимальна, выбирают в качестве оптимального по размерам для данной толщины объекта.
2. Способ настройки магнитооптической системы протонографического комплекса, заключающийся в подборе оптимального диаметра входящего в магнитооптическую систему коллиматора с точки зрения получения максимальной контрастной чувствительности изображений, для чего определяют общие коэффициенты пропускания магнитооптической системы Ktot (L,∅) для коллиматоров разных диаметров ∅ в зависимости от толщины объекта L, учитывая неупругое ядерное рассеяние и многократное кулоновское рассеяние протонного пучка, и производят расчет по найденным коэффициентам функции ошибки ε (∅; L=Lobj) для коллиматоров разных диаметров при заданной толщине исследуемого объекта Lobj, оптимальным диаметром коллиматора выбирают тот, при котором функция ошибки минимальна, отличающийся тем, что при определении общих коэффициентов пропускания магнитооптической системы Ktot (L,∅) дополнительно учитывают упругое ядерное рассеяние высокоэнергетичных протонов, для чего в объектной плоскости магнитооптической системы размещают радиографический клин, состоящий не менее чем из девяти ступеней, устанавливая клин наиболее толстыми ступенями в центре объектной плоскости, пропуская пучок протонов через объектную плоскость, получают изображения, обрабатывая которые восстанавливают общие коэффициенты пропускания Ktot для каждой ступени по ее центральной части для двух коллиматоров, диаметры которых, а соответственно при этом и коэффициенты пропускания существенно отличаются друг от друга, далее по нижеприведенной формуле определяют расчетный общий коэффициент пропускания Кtot:
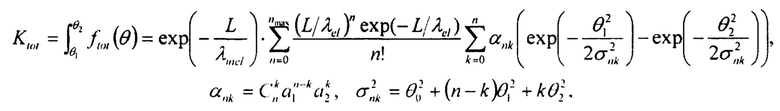
где 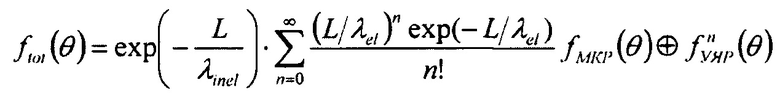 - распределение полного угла рассеяния протонов при прохождении через слой вещества толщиной L, exp(-L/λinel) - протоны, прошедшие через объект/слой вещества; λel - длина упругого и квазиупругого ядерного взаимодействия; λinel - длина неупругого ядерного взаимодействия; ƒмкр,
- распределение полного угла рассеяния протонов при прохождении через слой вещества толщиной L, exp(-L/λinel) - протоны, прошедшие через объект/слой вещества; λel - длина упругого и квазиупругого ядерного взаимодействия; λinel - длина неупругого ядерного взаимодействия; ƒмкр, 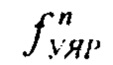 - свертки из n распределений углов многократного кулоновского рассеяния и упругого ядерного рассеяния;
- свертки из n распределений углов многократного кулоновского рассеяния и упругого ядерного рассеяния; 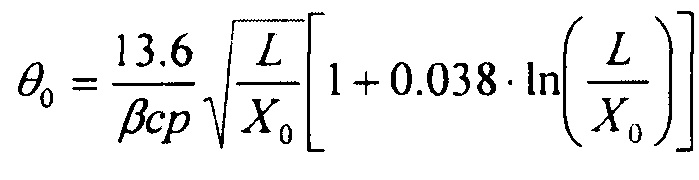 ; Х0 - радиационная длина материала образца, р - импульс протона, выраженный в единицах МэВ/с, a L - толщина объекта, при этом, варьируя коэффициенты λе1 и λinel, подбирают их таким образом, чтобы экспериментальные коэффициенты пропускания наилучшим образом аппроксимировали указанную формулу, далее, минимизируя величину относительной ошибки εfract определения количества прошедших протонов через объект толщиной L для конкретной установки с определенным количеством падающих протонов N0, с известным коэффициентом a≥1, зависящим от регистрирующей системы, вычисленным коэффициентом К=Кtot из соотношения
; Х0 - радиационная длина материала образца, р - импульс протона, выраженный в единицах МэВ/с, a L - толщина объекта, при этом, варьируя коэффициенты λе1 и λinel, подбирают их таким образом, чтобы экспериментальные коэффициенты пропускания наилучшим образом аппроксимировали указанную формулу, далее, минимизируя величину относительной ошибки εfract определения количества прошедших протонов через объект толщиной L для конкретной установки с определенным количеством падающих протонов N0, с известным коэффициентом a≥1, зависящим от регистрирующей системы, вычисленным коэффициентом К=Кtot из соотношения 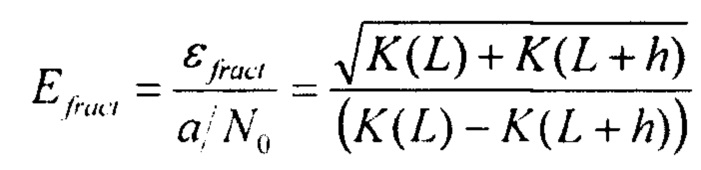 , h=0.01L, подбирают диаметр оптимального коллиматора.
, h=0.01L, подбирают диаметр оптимального коллиматора.
| УСТРОЙСТВО И СПОСОБЫ:НАСТРОЙКИ МАГНИТНОЙ СИСТЕМЫ ФОРМИРОВАНИЯ ПУЧКА ПРОТОНОВ В ОБЪЕКТНОЙ ПЛОСКОСТИ ПРОТОНОГРАФИЧЕСКОГО КОМПЛЕКСА, СОГЛАСОВАНИЯ МАГНИТНОЙ ИНДУКЦИИ МАГНИТООПТИЧЕСКОЙ СИСТЕМЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ И КОНТРОЛЯ НАСТРОЙКИ МНОГОКАДРОВОЙ СИСТЕМЫ РЕГИСТРАЦИИ ПРОТОННЫХ ИЗОБРАЖЕНИЙ | 2012 |
|
RU2515222C1 |
| УСТРОЙСТВО РЕГИСТРАЦИИ ИЗОБРАЖЕНИЙ, СФОРМИРОВАННЫХ С ПОМОЩЬЮ ИЗЛУЧЕНИЯ | 2010 |
|
RU2446613C2 |
| СПОСОБ ИССЛЕДОВАНИЯ МАТЕРИАЛОВ ПРИ УДАРНО-ВОЛНОВОМ НАГРУЖЕНИИ С ПОМОЩЬЮ ПРОТОНОГРАФИИ | 2010 |
|
RU2426100C1 |
| РАДИОГРАФИЧЕСКИЙ КОМПЛЕКС НА ОСНОВЕ ПРОТОННОГО УСКОРИТЕЛЯ ДЛЯ ИССЛЕДОВАНИЯ БЫСТРОПРОТЕКАЮЩИХ ПРОЦЕССОВ | 2010 |
|
RU2431133C1 |
| WO 2003107088 A3, 24.12.2003. | |||
Авторы
Даты
2020-07-21—Публикация
2019-12-16—Подача