Изобретение относится к области спектрального анализа и может найти применение в областях техники, в которых используется спектральный анализ, в частности в радиотехнике, и может найти применение в устройствах связи и в измерительной технике.
Известен способ Эйлера-Фурье представления функции в виде тригонометрического ряда (см., например, М.Я. Выгодский «Справочник по высшей математике». М. 1965 г., стр. 607), недостатком которого является осуществление спектрального анализа на кратных частотах.
Известны способ и устройство энергетического обнаружения сигнала с компенсацией комбинационных составляющих помехи и сигнала и помехи (патент РФ №2683021), недостатком которых является отсутствие возможности осуществления спектрального анализа.
Известен способ спектрального анализа электрических сигналов (патент РФ №2431853), в котором анализируемый электрический сигнал подают одновременно на гребенку фильтров, настроенных на различные частоты и измеряют сигналы на выходах этих фильтров, причем до проведения измерений диапазон контролируемых частот разбивают на элементы разрешения с шагом дискретизации, соответствующим желаемым точности и разрешению спектрального анализа. Недостатком данного способа является сложность технической реализации и недостаточно высокая скорость обмена информацией, при реализации данного способа в устройствах связи.
Известен способ спектрального анализа сигналов (патент РФ №2127888), в котором при дискретизации и квантовании сигнала создают последовательности дискретных значений сигнала с различными частотами следования отсчетов в каждой из них. При этом дискретные значения этих последовательностей фильтруют с помощью цифровых полосовых фильтров и цифровых фильтров нижних частот. Сигналы с выходов цифровых полосовых фильтров подвергают обработке, связанной с определением амплитудных значений, а на их основе и остальных информативных параметров полосовых сигналов. Недостатком данного способа является то, что способ предназначен для использования при спектральном анализе сигналов с постоянной относительной разрешающей способностью по частоте, а также большая вычислительная сложность и, соответственно, трудность технической реализации в системах связи.
Известен способ спектрального анализа сигналов (патент РФ №2229725), в котором формируют опорный синусоидальный сигнал, который многократно сдвигают по фазе относительно анализируемого периодического многочастотного сигнала. Оба сигнала представляются отсчетами мгновенных значений для одних и тех же моментов времени tj=t1, t2,..., tN, где N - число разбиений на периоде Т. Далее находят точки совместного решения а(b0) при различных круговых частотах опорного сигнала и фазах опорного сигнала, строят вольт-амперные характеристики и определяют их площадь FBAX min, причем вывод о присутствии гармонической составляющей с некоторой круговой частотой и фазой в анализируемом сигнале а(tj) делают, исходя из условия FBAX=0. Затем определяют максимальную площадь вольт-амперной характеристики FВАХ max К при φК ±90° и находят амплитуду К-ой спектральной составляющей. По значениям ωК, φК и Amk судят о спектральном составе анализируемого сигнала а(tj). Недостатком данного способа является большая вычислительная сложность и, соответственно, трудность технической реализации в системах связи.
Наиболее близким способом по технической сущности к предлагаемому является способ спектрального анализа многочастотных периодических сигналов, представленных цифровыми отсчетами (Функциональный контроль и диагностика электротехнических систем и устройств по цифровым отсчетам мгновенных значений тока и напряжения. /под редакцией Е.И. Гольдштейна - Томск: Изд. «Печатная мануфактура», 2003, с.92-94), выбранный в качестве прототипа, заключающийся в том, что для исходного сигнала a(ti), заданного отсчетами мгновенных значений в моменты времени
t1, t2, …,tj, …, tN;
t2-t1 =t3-t2=tN-tN-1= … =Δt;
Δt=Т/N,
где Δt - шаг дискретизации;
N - количество точек за время T,
для последовательности частот ω1, ω2, …, ωj, …, ω n, определяют мгновенную спектральную плотность (МСП) по выражениям:
S(ωj)= 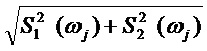
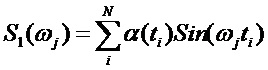

где S1(ωj) и S2(ωj) - синусная и косинусная составляющие мгновенной спектральной плотности.
Частоте ωk=fk*2π, рад,(4)
где fk - частота, Гц,
содержащейся в исходном сигнале а(ti), соответствует экстремум функции S(ωj). Таким образом, находят последовательность частот ω1, ω2, …, ωj, …, ωn, содержащихся в сигнале. Для найденных частот находят амплитуду Amk и фазу φk частотной составляющей ωk находят по формулам:
Amk=2 (S(ωk))/N;(5)
Φk=arctg(S2(ωk)/S1(ωk)),(6)
далее по значениям Amj, ωj, φj судят о спектральном составе исходного сигнала a(ti).
Недостатком известного способа является его недостаточно высокая эффективность в условиях наличия помех.
Задача предлагаемого способа – повышение эффективности спектрального анализа произвольного ряда гармонических сигналов.
Для решения поставленной задачи предлагается способ спектрального анализа многочастотных периодических сигналов с использованием компенсации комбинационных составляющих, заключающийся в том, что для исходного сигнала a(ti), заданного отсчетами мгновенных значений в моменты времени
t1, t2, …,tj, …, tN; t2-t1 =t3-t2=tN-tN-1= … =Δt; Δt=Т/N,
где Δt - шаг дискретизации;
N - количество точек за время T,
для последовательности частот ω1, ω2, …, ωi, …, ωn, (опорные частоты) определяют мгновенную спектральную плотность (МСП) по выражениям:
S(ωj)= 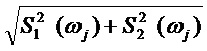
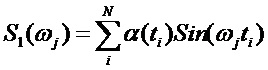

где S1(ωj) и S2(ωj) - синусная и косинусная составляющие мгновенной спектральной плотности, согласно изобретению, каждый результат преобразования сигнала и помехи, которые образуются после умножения входного сигнала на синус и косинус опорных частот, разделяют на две одинаковые составляющие, обработку полученных сигналов осуществляют одинаково в соответствующих линейках – каждый из полученных сигналов разветвляют на две одинаковые составляющие, первую составляющую фильтруют фильтром нижних частот (ФНЧ), полоса которого согласована с полосой анализируемого сигнала, одновременно вторую составляющую фильтруют полосовым фильтром, полоса пропускания которого выбирается так, что верхняя частота полосового фильтра соответствует верхней частоте анализируемого сигнала, нижнюю частоту полосового фильтра устанавливают равной некоторому заранее заданному значению, выбор ФНЧ и полосового фильтра осуществляют с идентичными в максимальной степени фазо-частотными характеристиками и так, что амплитудно-частотная характеристика (АЧХ) полосового фильтра в области частот близких к нулю имеет максимально-возможную крутизну, в области частот, начиная со значения, для которого разность значений АЧХ ФНЧ и полосового фильтра становится меньше некоторой заранее заданной величины, обеспечивают идентичность их АЧХ в максимальной степени, сигналы, прошедшие ФНЧ и полосовой фильтр, вычитают один из другого, результат вычитания преобразуют в цифровой вид, по данным значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют МСП для каждой опорной частоты и запоминают эти значения пропорциональные амплитуде сигналов, из полученных значений находят МСП с максимальным значением, определяют значение порога путем умножения найденного максимального значения МСП на коэффициент, значение которого устанавливают заранее, полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой, рассчитанные значения МСП, считают амплитудой сигнала с соответствующей частотой, определяют дискретные значения фаз, используемые при проведении спектрального анализа φ1, φ2, …, φj …, φm, таким образом, чтобы:
φ2-φ1= Δφ; φ3-φ2= Δφ; …; φm-φ(m-1) =Δφ, Δφ =2π/m,
где Δφ – шаг дискретизации фазы;
m – количество значений фаз, используемое при ее дискретизации,
определяют отсчеты для каждого значения частоты исходного сигнала a(ti), заданного отсчетами мгновенных значений, для которых проводят анализ и каждого значения фазы, с использованием способа выбора отсчетов, при использовании которого «расстояние» между моментами времени взятия отсчетов и рассчитанными значениями времени взятия отсчетов было минимальным, для каждой частоты и каждого значения фазы рассчитывают сумму абсолютных значений отсчетов, для каждой частоты находят сумму отсчетов с максимальным значением, запоминают соответствующие значения фазы как фазу сигнала с соответствующей частотой.
Способ заключается в следующем.
Последовательность опорных частот ω1, ω2, …, ωi, …, ωn, формируют, исходя из необходимой точности анализа спектра анализируемого сигнала. Например, путем формирования сетки частот по принципу задания расстояния между соседними частотами как какой-либо процент от предыдущего значения частоты, то есть
Fi= F(i-1)+ F(i-1)Kp/100, (7)
где: Fi, F(i-1) – i-ое и (i-1)–ое значения частот, соответственно;
Kp – процент от предыдущего значения частоты.
При этом: F1= Fmin;
Fn ≤ Fmax.
Здесь Fmin – минимальное значение частоты спектра сигнала,
Fmax – максимальное значение частоты спектра сигнала,
n – число опорных частот, используемых при проведении спектрального анализа.
Аддитивную смесь периодических сигналов с различными частотами и помех умножают в блоках умножения, которые могут быть выполнены, например в виде смесителей, на опорные сигналы.
Дальнейшую обработку осуществляют с использованием способа компенсации шумов преобразования – гармоник разностной частоты (комбинационные составляющие), например способом, описанном в патенте РФ №2683021.
Для обработки одной частоты используют две линейки устройства. То есть, если используют k опорных частот, то число линеек равно
N=2*k.
Принятую аддитивную смесь сигнала и помехи подают на первые входы блоков умножения 1.1-1.n, на вторые входы которых подают соответствующие опорные сигналы, например,
Uоп1=sin(x1);
Uоп2=cos(x1).
….
Uоп(n-1)=sin(xk);
Uопn=cos(xk).
Результаты умножения сигнала и помехи на соответствующие опорные сигналы обрабатывают одинаково. Разветвляют на две одинаковые составляющие, первую составляющую фильтруют фильтром нижних частот (ФНЧ), полоса которого согласована с полосой сигнала, одновременно вторую составляющую фильтруют полосовым фильтром, полоса пропускания которого выбирается так, что верхняя частота полосового фильтра соответствует верхней частоте сигнала, нижнюю частоту полосового фильтра устанавливают согласованно с значениями разности между соседними опорными частотами. Нижнюю частоту полосового фильтра устанавливают равной некоторому заранее заданному значению. Данное значение определяют на этапе разработки экспериментальным путем или методом математического моделирования как значение, обеспечивающие максимальную эффективность спектрального анализа.
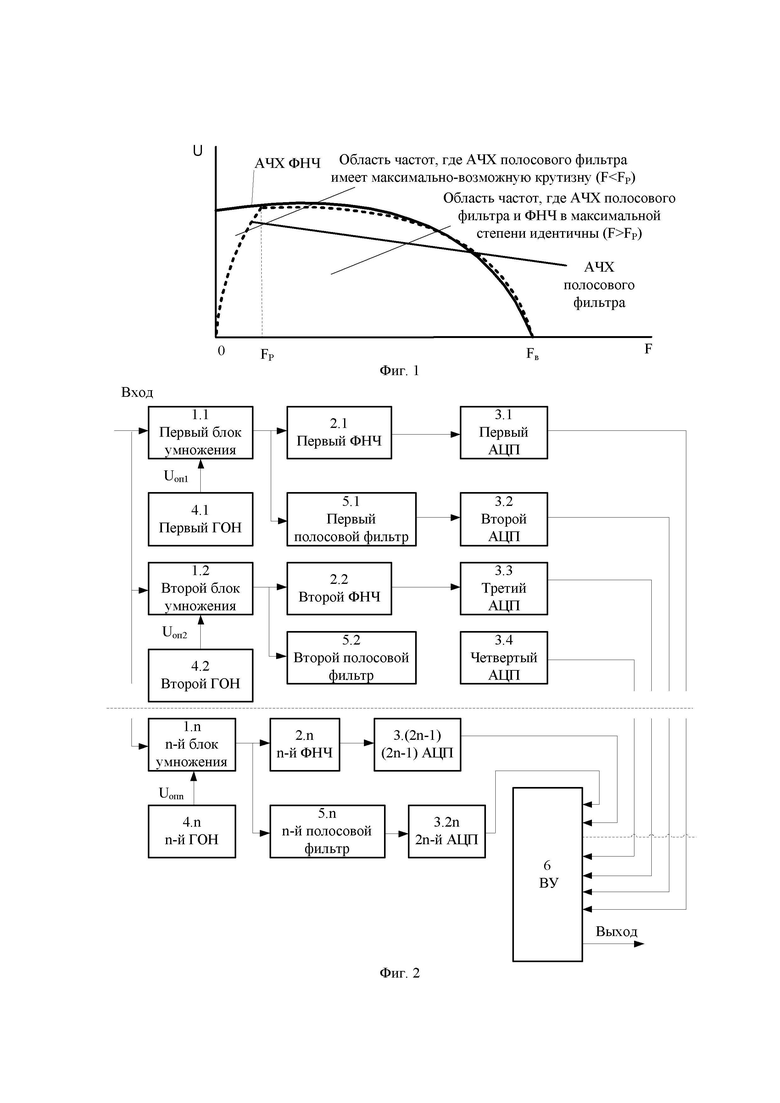
Выбор ФНЧ и полосового фильтра осуществляют с идентичными в максимальной степени фазо-частотными характеристиками и так, что АЧХ полосового фильтра в области частот близких к нулю имеет максимально-возможную крутизну, в области частот, начиная со значения, для которого разность значений АЧХ ФНЧ и полосового фильтра становится меньше некоторой заранее заданной величины, обеспечивают идентичность их АЧХ в максимальной степени (иллюстративный пример приведен на фиг. 1).
Сигналы, прошедшие ФНЧ и полосовой фильтр, вычитают один из другого. Полученные сигналы преобразуют в цифровой вид в соответствующих аналого-цифровых преобразователях (АЦП).
По значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют мгновенную спектральную плотность (МСП) для каждой опорной частоты и запоминают эти значения пропорциональные амплитуде сигналов, из полученных значений находят МСП с максимальным значением, определяют значение порога путем умножения найденного максимального значения МСП на коэффициент, значение которого устанавливают заранее.
Значение данного коэффициента определяют на этапе разработки экспериментальным путем или методом математического моделирования как значение, обеспечивающее максимальную эффективность спектрального анализа.
Полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой.
Рассчитанные значения МСП, считают амплитудой сигнала с соответствующей частотой.
Определяют дискретные значения фаз, используемые при проведении спектрального анализа φ1, φ2, …, φj …, φm, таким образом, чтобы:
φ2-φ1= Δφ; φ3-φ2= Δφ; …; φm-φ(m-1) =Δφ, Δφ =2π/m,
где Δφ – шаг дискретизации фазы;
m – количество значений фаз, используемое при ее дискретизации.
Количество значений фаз, используемое при ее дискретизации, определяют на этапе разработки экспериментальным путем или методом математического моделирования как значение, обеспечивающее максимальную эффективность спектрального анализа.
Для каждого сигнала, присутствующего в исходном многочастотном сигнале, находят значения фаз следующим образом.
В соответствии с частотой, которая была определена как частота сигнала, и для каждого значения фазы определяют отсчеты исходной аддитивной суммы сигнала и помехи. При представлении сигнала отсчетами мгновенных значений используют способ выбора отсчетов, при применении которого необходимый отсчет определяют как отсчет, для которого «расстояние» между моментом времени взятия отсчета и рассчитанным значением времени взятия отсчета является минимальным.
Для каждой частоты и каждого значения фазы рассчитывают сумму абсолютных значений отсчетов и находят сумму отсчетов с максимальным значением. Запоминают соответствующее значение фазы.
Ниже приведены результаты моделирования процесса спектрального анализа произвольного ряда гармонических сигналов при использовании предлагаемого способа.
Результаты оценки эффективности предлагаемого способа получены методом математического моделирования на ЭВМ с использованием системы MATLAB – свидетельство о государственной регистрации программы для ЭВМ «Программа оценки эффективности способа спектрального анализа многочастотных периодических сигналов с использованием квадратурных составляющих и компенсацией комбинационных составляющих» № 2019660813.
Сумма гармоник помехи при моделировании представлена в виде совокупности гармонических колебаний со случайными значениями амплитуд (Usi) и фаз (ϕsi), которые распределены по нормальному (амплитуды) и равномерному (фазы) законам, соответственно
U=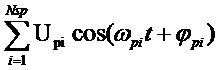
где: ωsi φsi 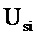
Ns – число гармонических сигналов.
При моделировании:
– диапазон изменения частоты речевого сигнала: 300 Гц – 3400 Гц;
– амплитуды, частоты и фазы речевых сигналов представлены как случайные величины, значения амплитуд, фаз и значение частоты гармоники с наименьшим значением распределены по равномерному закону.
Моделирование проведено для следующих значений параметров
– число реализаций –500;
– число гармоник сигнала – 5;
– число гармоник помехи – 30;
– число временных шагов – 250;
– число отсчетов при определении фазы – 8;
– число опорных частот – 51;
– количество значений фаз, используемое при ее дискретизации – 36;
– коэффициент, определяющий частоту дискретизации – 9000;
– значение первой опорной частоты – 300 Гц;
– коэффициент, определяющий шаг изменения опорной частоты шаг изменения опорной частоты – 1,05;
– шаг изменения частоты гармоник сигнала 200;
– диапазон изменения амплитуд сигналов – от 1 до 2;
– значение порога для амплитуды гармоник – 0,5;
– значение полосы частот полосового фильтра с максимальной крутизной АЧХ – 200 Гц.
Результаты моделирования процесса спектрального анализа произвольного ряда гармонических сигналов для различных значений отношения мощностей сигнала и помехи приведены в таблице.
На основе анализа данных, приведенных в таблице, установлено, что среднее значение ошибки определения частоты не превосходит 350 Гц, среднее значение ошибки определения фазы не превосходит 1 радиан для значений отношения мощностей сигнала и помехи не менее 1.
Следует отметить, что увеличение значений ошибок определения частоты, фазы и амплитуды при увеличении мощности помехи связано с тем, что некоторые гармоники помехи воспринимаются как сигнал.
Структурная схема устройства, при использовании которого может быть реализован предлагаемый способ, приведена на фиг. 2, где обозначено:
1.1 – 1.n – блоки умножения с первого по n-ый;
2.1 – 2.n – фильтры нижних частот (ФНЧ) с первого по n-ый;
3.1 – 3.n – устройства вычитания с первого по n-ый;
4.1 – 4.n – аналого-цифровые преобразователи (АЦП) с первого по n-ый;
5.1 – 5.n – полосовые фильтры с первого по n-ый;
6, 8 – первое и второе вычислительные устройства (ВУ);
7 – (n+1)-ый АЦП.
Устройство содержит n параллельных линеек, каждая из которых состоит из соответствующих последовательно соединенных блока умножения 1, ФНЧ 2, устройства вычитания 3 и АЦП 4, при этом полосовой фильтр 5 включен между выходом блока умножения 1 и вторым входом устройства вычитания 3. Устройство так же содержит (n+1)-ый АЦП 7, выход которого соединен с (n+1)-ым входом первого ВУ 6. Входы n блоков умножения 1.1 – 1.n объединены и являются входом устройства. Вход (n+1)-го АЦП 7 подключен ко входу устройства. Выходы n АЦП 4.1 – 4.n соединены с соответствующими входами с первого по n-ый вычислительного устройства 6, выход которого является выходом устройства. Вторые входы блоков умножения 1.1 – 1.n являются входами для опорных сигналов.
Устройство работает следующим образом.
Для обработки одной поднесущей используют две линейки устройства. То есть, если используют k поднесущих, то число линеек равно
N=2*k.
Принятую аддитивную смесь сигнала и помехи подают на первые входы блоков умножения 1.1-1.n, на вторые входы которых подают соответствующие опорные сигналы, например,
Uоп1=sin(x);
Uоп2=cos(x).
….
Uоп(n-1)=sin(x);
Uопn=cos(x).
Принятую аддитивную смесь сигнала и помехи подают на первые входы блоков умножения 1.1-1.n, на вторые входы которых подают соответствующие опорные сигналы.
Результат умножения сигнала и помехи на опорные сигналы разветвляют на две одинаковые составляющие. Первую составляющую фильтруют ФНЧ 2.1 – 2.n, полоса каждого из которых согласована с полосой сигнала. Одновременно вторую составляющую фильтруют полосовыми фильтрами 5.1 – 5.n, полоса пропускания каждого из которых выбирается так, что верхняя частота полосовых фильтров 5.1 – 5.n соответствует верхней частоте сигнала, нижнюю частоту полосовых фильтров 5.1 – 5.n устанавливают согласованно с значениями разности между соседними опорными частотами.
Значение нижней частоты полосовых фильтров 5.1 – 5.n определяют на этапе разработки экспериментальным путем или методом математического моделирования как значение, обеспечивающее максимальную эффективность спектрального анализа.
Выбор ФНЧ 2.1 – 2.n и полосовых фильтров 5.1 – 5.n осуществляют с идентичными в максимальной степени фазо-частотными характеристиками и так, что АЧХ полосовых фильтров 5.1 – 5.n в области частот близких к нулю имеет максимально-возможную крутизну, в области частот, начиная со значения, для которого разность значений АЧХ ФНЧ 2.1 – 2.n и полосовых фильтров 5.1 – 5.n становится меньше некоторой заранее заданной величины (Fр), обеспечивают идентичность их АЧХ в максимальной степени (иллюстративный пример приведен на фиг. 1).
Сигналы, прошедшие ФНЧ 2.1 – 2.n и полосовые фильтры 5.1 – 5.n, , вычитают один из другого. То есть из сигнала первого ФНЧ 2.1 вычитают сигнал первого полосового фильтра 5.1, из сигнала второго ФНЧ 2.2 вычитают сигнал второго полосового фильтра 5.2 и т.д.
Полученные сигналы преобразуют в цифровой вид в соответствующих АЦП 4.1 – 4.n. Данные сигналы в цифровом виде подают в ВУ 6.
В ВУ 6 по данным значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют мгновенную спектральную плотность (МСП) для каждой опорной частоты и запоминают эти значения пропорциональные амплитуде сигналов, из полученных значений находят МСП с максимальным значением, определяют значение порога путем умножения найденного максимального значения МСП на коэффициент, значение которого устанавливают заранее, полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой.
Рассчитанные значения МСП, считают амплитудой сигнала с соответствующей частотой.
В (n+1)-ом АЦП 7 аддитивную смесь сигнала и помехи преобразуют в цифровой вид, при этом отсчеты берут с частотой обеспечивающей необходимую точность решения задачи.
Данные отсчеты подают на (n+1)-ый вход второго ВУ 8, где с использованием результата определения частот входного сигнала определяют значения фазы для каждого сигнала описанным выше способом.
Результаты моделирования процесса спектрального анализа приведены выше.
Блоки умножения 1.1 – 1.n могут быть выполнены, например,
в виде преобразователя частоты (смесителя), см., например, учебное
пособие «Основы теории радиотехнических систем». Учебное пособие. //В.И. Борисов, В.М. Зинчук, А.Е. Лимарев, Н.П. Мухин. Под ред. В.И. Борисова. Воронежский научно-исследовательский институт связи, 2004», стр. 186 – 189.
АЦП 4.1 – 4.n и (n+1)-ый АЦП 7 могут быть выполнены, например, на микросхеме AD7495BR фирмы Analog Devices.
Первое 6 и второе 8 вычислительные устройства могут быть выполнены, например, в виде единого микропроцессорного устройства с соответствующим программным обеспечением, например процессора серии TMS320VC5416 фирмы Texas Instruments, или в виде программируемой логической интегральной схемы (ПЛИС), с соответствующим программным обеспечением, например ПЛИС XCV400 фирмы Xilinx.
Таким образом, заявляемый способ может быть реализован описанным устройством.
Изобретение относится к области спектрального анализа и может найти применение в устройствах связи и в измерительной технике. Техническим результатом является повышение эффективности спектрального анализа в условиях наличия помех за счет компенсации шумов преобразования. Способ спектрального анализа многочастотных периодических сигналов с использованием компенсации комбинационных составляющих заключается в том, что для исходного сигнала a(ti), заданного отсчетами мгновенных значений в заданные моменты времени для последовательности частот ω1, ω2, …, ωi, …, ωn, (опорные частоты) определяют мгновенную спектральную плотность (МСП). Для достижения технического результата каждый результат преобразования сигнала и помехи, которые образуются после умножения входного сигнала на синус и косинус опорных частот, разделяют на две одинаковые составляющие. Обработку полученных сигналов осуществляют одинаково в соответствующих линейках – каждый из полученных сигналов разветвляют на две одинаковые составляющие. Первую составляющую фильтруют фильтром нижних частот (ФНЧ), полоса которого согласована с полосой сигнала. Одновременно вторую составляющую фильтруют полосовым фильтром, полоса пропускания которого выбирается так, что верхняя частота полосового фильтра соответствует верхней частоте анализируемого сигнала, нижнюю частоту полосового фильтра устанавливают равной некоторому заранее заданному значению. Сигналы, прошедшие ФНЧ и полосовой фильтр, вычитают один из другого. По значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют мгновенную спектральную плотность (МСП) для каждой опорной частоты, пропорциональную амплитуде сигнала. Полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой. Значения фаз определяют с использованием метода когерентного накопления. 2 ил., 1 табл.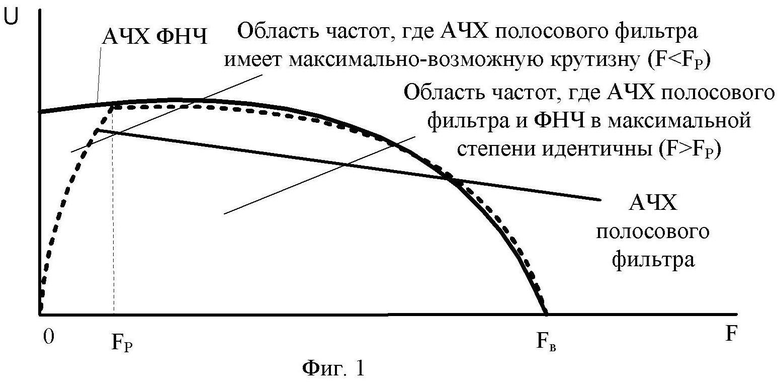
Способ спектрального анализа многочастотных периодических сигналов с использованием компенсации комбинационных составляющих, заключающийся в том, что для исходного сигнала a(ti), заданного отсчетами мгновенных значений в моменты времени
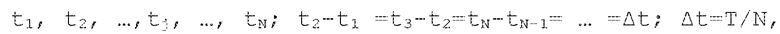
где 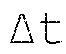 - шаг дискретизации;
- шаг дискретизации;
N - количество точек за время T,
для последовательности частот 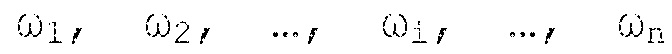 (опорные частоты), определяют мгновенную спектральную плотность (МСП) по выражениям:
(опорные частоты), определяют мгновенную спектральную плотность (МСП) по выражениям:
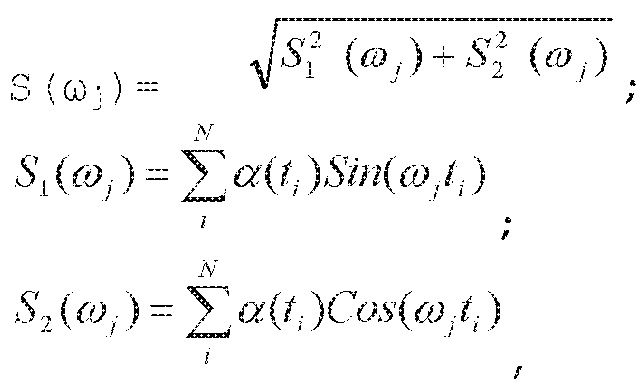
где 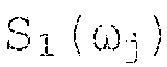 и
и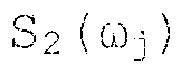 - синусная и косинусная составляющие мгновенной спектральной плотности, отличающийся тем, что каждый результат преобразования сигнала и помехи, которые образуются после умножения входного сигнала на синус и косинус опорных частот, разделяют на две одинаковые составляющие, обработку полученных сигналов осуществляют одинаково в соответствующих линейках – каждый из полученных сигналов разветвляют на две одинаковые составляющие, первую составляющую фильтруют фильтром нижних частот (ФНЧ), полоса которого согласована с полосой анализируемого сигнала, одновременно вторую составляющую фильтруют полосовым фильтром, полоса пропускания которого выбирается так, что верхняя частота полосового фильтра соответствует верхней частоте анализируемого сигнала, нижнюю частоту полосового фильтра устанавливают равной некоторому заранее заданному значению, выбор ФНЧ и полосового фильтра осуществляют с идентичными в максимальной степени фазочастотными характеристиками и так, что амплитудно-частотная характеристика (АЧХ) полосового фильтра в области частот близких к нулю имеет максимально-возможную крутизну, в области частот, начиная со значения, для которого разность значений АЧХ ФНЧ и полосового фильтра становится меньше некоторой заранее заданной величины, обеспечивают идентичность их АЧХ в максимальной степени, сигналы, прошедшие ФНЧ и полосовой фильтр, вычитают один из другого, результат вычитания преобразуют в цифровой вид, по данным значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют МСП для каждой опорной частоты и запоминают эти значения пропорциональные амплитуде сигналов, из полученных значений находят МСП с максимальным значением, определяют значение порога путем умножения найденного максимального значения МСП на коэффициент, значение которого устанавливают заранее, полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой, рассчитанные значения МСП, считают амплитудой сигнала с соответствующей частотой, определяют дискретные значения фаз, используемые при проведении спектрального анализа
- синусная и косинусная составляющие мгновенной спектральной плотности, отличающийся тем, что каждый результат преобразования сигнала и помехи, которые образуются после умножения входного сигнала на синус и косинус опорных частот, разделяют на две одинаковые составляющие, обработку полученных сигналов осуществляют одинаково в соответствующих линейках – каждый из полученных сигналов разветвляют на две одинаковые составляющие, первую составляющую фильтруют фильтром нижних частот (ФНЧ), полоса которого согласована с полосой анализируемого сигнала, одновременно вторую составляющую фильтруют полосовым фильтром, полоса пропускания которого выбирается так, что верхняя частота полосового фильтра соответствует верхней частоте анализируемого сигнала, нижнюю частоту полосового фильтра устанавливают равной некоторому заранее заданному значению, выбор ФНЧ и полосового фильтра осуществляют с идентичными в максимальной степени фазочастотными характеристиками и так, что амплитудно-частотная характеристика (АЧХ) полосового фильтра в области частот близких к нулю имеет максимально-возможную крутизну, в области частот, начиная со значения, для которого разность значений АЧХ ФНЧ и полосового фильтра становится меньше некоторой заранее заданной величины, обеспечивают идентичность их АЧХ в максимальной степени, сигналы, прошедшие ФНЧ и полосовой фильтр, вычитают один из другого, результат вычитания преобразуют в цифровой вид, по данным значениям, соответствующим синусной и косинусной составляющей одной частоты, определяют МСП для каждой опорной частоты и запоминают эти значения пропорциональные амплитуде сигналов, из полученных значений находят МСП с максимальным значением, определяют значение порога путем умножения найденного максимального значения МСП на коэффициент, значение которого устанавливают заранее, полученные значения МСП сравнивают с порогом, по результатам сравнения делают вывод о наличии или об отсутствии сигнала с соответствующей частотой, рассчитанные значения МСП, считают амплитудой сигнала с соответствующей частотой, определяют дискретные значения фаз, используемые при проведении спектрального анализа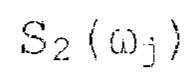 таким образом, чтобы:
таким образом, чтобы:
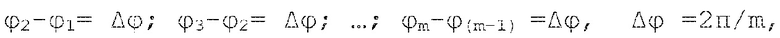
где 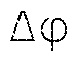 – шаг дискретизации фазы;
– шаг дискретизации фазы;
m – количество значений фаз, используемое при ее дискретизации,
определяют отсчеты для каждого значения частоты исходного сигнала a(ti), заданного отсчетами мгновенных значений, для которых проводят анализ и каждого значения фазы, с использованием способа выбора отсчетов, при использовании которого «расстояние» между моментами времени взятия отсчетов и рассчитанными значениями времени взятия отсчетов было минимальным, для каждой частоты и каждого значения фазы рассчитывают сумму абсолютных значений отсчетов, для каждой частоты находят сумму отсчетов с максимальным значением, запоминают соответствующие значения фазы как фазу сигнала с соответствующей частотой.
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ПЕРИОДИЧЕСКИХ МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ ИНТЕРГАРМОНИКИ И ЗАДАННЫХ ЦИФРОВЫМИ ОТСЧЕТАМИ | 2007 |
|
RU2360260C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ПЕРИОДИЧЕСКОГО МНОГОЧАСТОТНОГО СИГНАЛА | 2002 |
|
RU2229725C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ЭЛЕКТРИЧЕСКОГО СИГНАЛА | 2010 |
|
RU2431853C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1994 |
|
RU2086991C1 |
| WO 2003046586 A1, 05.06.2003 | |||
| CN 107843767 A, 27.03.2018. | |||
Авторы
Даты
2020-08-14—Публикация
2019-11-20—Подача