Изобретение относится к нефтегазодобывающей области, операциям гидравлического разрыва (гидроразрыва) пласта, в частности к моделированию трещин гидроразрыва пласта относительно горизонтального ствола скважины. Изобретение может быть использовано при моделировании разработки коллекторов нефти и газа горизонтальными скважинами с одностадийным гидроразрывом пласта (ГРП) и многостадийным гидроразрывом пласта (МГРП).
Гидроразрыв пласта представляет собой процесс, при котором флюид (нефть или газ) под высоким давлением нагнетают в пласт для образования и/или удлинения трещин, которые проникают в пласт, что обеспечивает возможность дополнительного стока нефти или газа к скважине. В результате ГРП повышается дебит добывающих скважин или приёмистость нагнетательных скважин. Корректное моделирование трещин ГРП является крайне важным, так как повышается качество планирования разработки месторождений нефти и газа.
Известен способ моделирования эффектов ГРП на полномасштабных моделях при помощи метода создания дополнительных соединений (Шахов Д.С., Ярышев М.Г. Моделирование эффектов ГРП на полномасштабных моделях при помощи метода создания дополнительных соединений//Бурение и нефть. – 2014 - №12.), согласно которому задают геометрию трещины, находят ячейки модели, вскрываемые плоскостью трещины, в которых создают дополнительные соединения. В каждой из вскрытых ячеек рассчитывают коэффициент соединения, для определения которого определяют значение безразмерного коэффициента продуктивности для скважины с заданными параметрами трещины ГРП. Далее выполняют переход от безразмерного коэффициента продуктивности для всей скважины с ГРП к коэффициентам соединения отдельных ячеек, затем моделируют трещину ГРП.
Общими признаками известного способа с заявленным способом является определение ячеек, по которым проходит трещина ГРП и моделирование трещины ГРП. Однако, в данном способе не осуществляется определение отрицательного скин-фактора для каждой модели вертикальной скважины, находящейся в ячейки. Недостатком способа является невысокая точность моделирования трещины ГРП.
Известен способ и система моделирования гидравлического разрыва на основе анализа скин-фактора для вертикальной скважины (заявка на изобретение США US 2017/0218729 A1). Согласно способу возможность осуществления гидравлического разрыва пласта можно оценить, проанализировав скин-фактор вертикальной скважины. Рассматриваются две трёхмерные модели: базовый случай без трещин и комплексный случай с трещинами. Базовый случай моделируется изменением проницаемости матрицы, в то время как случай с трещинами моделируется с разными наборами изменяющихся длин, ширины и проницаемости трещин и проницаемости матрицы. Два случая анализируются и определяется скин-фактор. Обобщенную корреляцию для определения скин-фактора получают путем применения метода многомерной регрессии к полученным скин-факторам и их соответствующим переменным.
Способ включает в себя моделирование первого участка, содержащего пласт без трещин, определение параметров пласта, затем вычисляют первый индекс продуктивности для первого набора точек данных; моделирование второй модели пласта, который включает в себя трещину, вычисление второго индекса продуктивности второй модели для второго набора точек данных; вычисление скин-фактора на основе вычислений первого и второго наборов точек данных, выполнение регрессионного анализа с использованием подмножества второго набора точек данных для получения скин-фактора.
Вариант осуществления данного способа подразумевается в считываемом компьютере носителе, содержащем программу, которая содержит команды по выполнению вышеописанного способа.
Общими признаками изобретения по заявке на изобретение США №US 2017/0218729 A1 с предлагаемым изобретением является расчет скин-фактора, моделирование трещины ГРП. Недостатком способа является длительное моделирование трещины ГРП, за счет моделирования трещин в ячейках с малой размерностью.
В заявленном техническом решении рассматривается моделирование как конечной, так и бесконечной проводимости трещины гидроразрыва пласта продольного и поперечного расположения относительно горизонтального ствола скважины с учетом схождения (конвергенции) линий тока при их схождении в самой трещине, а также определение инерциальных потерь давления для газовой фазы (газового типа флюида). То есть рассмотрены всевозможные варианты ГРП в зависимости от типа флюида (нефть или газ), типа проводимости трещины ГРП (бесконечная или конечная), а также расположение трещины относительно горизонтального ствола скважины (вдоль или поперек).
Технической проблемой предлагаемого изобретения является совершенствование моделирования эффекта применения одностадийного и многостадийного ГРП при разработке коллекторов нефти и газа горизонтальными скважинами с гидроразрывом пласта.
Технический результат – повышение точности моделирования эффекта применения одностадийного и многостадийного гидроразрыва пласта (трещина ГРП) при разработке коллекторов нефти и газа горизонтальными скважинами с гидроразрывом пласта, уменьшение времени моделирования трещины ГРП, а также универсальность применения способа для моделирования трещин ГРП различного типа проводимости (например, конечный/бесконечный), трещин ГРП, которые могут иметь разное расположение относительно горизонтального ствола скважины (например, поперек/ вдоль), также для скважин с различными типами флюида скважины (газ и нефть).
Технический результат достигается за счет того, что способ моделирования
трещин гидроразрыва пласта включает следующие этапы выполнения:
- получают значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины (формируют траекторию трещины ГРП);
- строят гидродинамическую модель (ГДМ) пласта с использованием ячеек заданной геометрии;
- определяют ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определяют длины участков (отрезков) трещины ГРП в ячейках гидродинамической модели пласта;
- в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта;
- для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках;
- моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
Таким образом, технический результат достигается за счет того, что моделирование трещины ГРП проводят с помощью моделей вертикальных скважин с отрицательным скин-фактором в каждой пересекаемой трещиной ячейке гидродинамической модели. При моделировании трещины ГРП в гидродинамической модели предлагаемым способом непосредственно трещина не моделируется, а используются мнимые модели вертикальных скважин с отрицательным скин-фактором, рассчитанным на основе параметров трещины, для ячеек гидродинамической модели, которые пересекает траектория трещины ГРП. В результате получают симуляцию работы трещины ГРП (моделирование притока) в ячейках гидродинамической модели. При явном (прямом) моделировании самой трещины ГРП, ячейки, в которые попала трещина ГРП, будут иметь дополнительно ячейки маленькой размерности (толщиной в несколько миллиметров), отвечающие пространству трещины ГРП и имеющие маленький объем. Соответственно, чем меньше размерность ячеек, тем больше потребуется расчетных шагов и времени для моделирования. При моделировании трещины ГРП с использованием моделей вертикальных скважин, ячейки, которые пересекла трещина ГРП, будут иметь большую размерность (большой объем). Это позволяет существенно сэкономить время как на подготовку данных для гидродинамического моделирования, так и на проведение непосредственных гидродинамических расчетов ввиду исключения из модели ячеек очень низкой размерности.
Учет конвергенции линий тока, например в случае конечной проводимости трещины ГРП, позволяет учитывать дополнительные потери давления, что позволяет проводить более точное гидродинамическое моделирование трещины ГРП.
Модель вертикальной скважины или мнимая (псевдо) вертикальная скважина в ячейке гидродинамической модели – это модель вертикальной скважины, которая используется для симуляции работы трещины гидроразрыва пласта в ячейке гидродинамической модели пласта. Модель вертикальной скважины с произвольным радиусом (как правило используется 0,1 метр (аналог реальной скважины)) располагают в центре ячейке гидродинамической модели. При расчете отрицательного скин-фактора используют произвольный радиус мнимой вертикальной скважины, а также используют параметры ячейки гидродинамической модели, в которой расположена мнимая вертикальная скважина. Отрицательный скин-фактор, рассчитанный для мнимой вертикальной скважины в ячейке гидродинамической модели, позволяет достичь такую же продуктивность (точность), как у траектории трещины ГРП, находящейся в данной ячейки.
Траекторию трещины ГРП могут отражать в виде плоскости в гидродинамической модели пласта (или линия в двумерном изображении), которая отражает длину и расположение трещины ГРП. Также траекторию трещины ГРП могут не отражать в гидродинамической модели пласта, однако ее траекторию (расположение и дину) учитывают для дальнейшего моделирования. То есть траектория трещины ГРП, в независимости от того отражена она в гидродинамической модели пласта или нет, дает информацию о расположении трещины в ячейках гидродинамической модели (сколько ячеек пересекла траектория трещины ГРП, как траектория трещины ГРП пересекла каждую ячейку (целую ячейку или ее часть)).
Данный способ универсален для всевозможных вариантов ГРП в зависимости от типа флюида (нефть или газ), типа проводимости трещины ГРП (бесконечная или конечная), а также расположение трещины относительно горизонтального ствола скважины (вдоль или поперек).
Также технический результат достигается за счет того, что система моделирования трещин гидроразрыва пласта содержит по меньшей мере один процессор, который выполняет следующие этапы:
- получает значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины (формируется траекторию трещины ГРП);
- строит гидродинамическую модель пласта с использованием ячеек заданной геометрии;
- определяет ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определяет длины участков (отрезков) трещины ГРП в ячейках гидродинамической модели пласта;
- в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагает модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта;
- для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывает отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках;
- моделирует трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
Также технический результат достигается за счет того, что машиночитаемый носитель содержит компьютерную программу, при исполнении которой на компьютере процессор выполняет следующие операции:
- получение значения длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данных о расположении этой трещины (формируется траектория трещины ГРП);
- построение гидродинамической модели пласта с использованием ячеек заданной геометрии;
- определение ячеек гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определение длины участков (отрезков) трещины ГРП в ячейках гидродинамической модели пласта;
- расположение модели вертикальной скважины, выполненной с возможностью симуляции трещины гидроразрыва пласта, в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП;
- расчёт отрицательного скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта;
- моделирование трещины ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
Также технический результат может достигаться за счет того, что способ моделирования трещин гидроразрыва пласта для случая расположения трещины поперек ствола добывающей горизонтальной скважины и конечного типа проводимости трещины, при котором:
- получают значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины (формируют траекторию трещины ГРП);
- строят гидродинамическую модель пласта с использованием ячеек заданной геометрии;
- определяют ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определяют длины участков (отрезков) трещины ГРП в ячейках гидродинамической модели пласта;
- в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта;
- для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках;
- определяют эффективную безразмерную проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине;
- моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
Также технический результат может достигаться за счет того, что система и машиночитаемый носитель моделирования трещин гидроразрыва пласта для случая расположения трещины поперек ствола добывающей горизонтальной скважины и конечного типа проводимости трещины, которые содержат этапы аналогично способу, описанному выше.
В одном из вариантов реализации после расчёта отрицательного скин-фактора (S) для каждой модели вертикальной скважины дополнительно могут рассчитать минимальный отрицательный скин-фактор (MinS), и затем моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), при этом если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS, и при моделировании трещины ГРП дополнительно учитывают множитель коэффициента продуктивности горизонтальной скважины.
В одном из вариантов реализации, а именно для случая газового типа флюида скважины дополнительно могут определить D-фактор (динамический скин-фактор), который учитывают при моделировании трещины ГРП. Ввиду того, что D-фактор влияет на значение дебита скважины, который в свою очередь определяет скорость движения фильтрующейся газовой фазы в трещине ГРП, используемой для вычисления D-фактора, то для его вычисления используют итеративный подход.
Расчет D-фактора позволяет учесть инерциальные потери давления в трещине ГРП при движении газовой фазы на высоких скоростях в трещине, что также влияет на точность моделирования трещины ГРП.
В варианте реализации в случае бесконечного типа проводимости трещины ГРП для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, могут рассчитать отрицательный скин-фактор (S) по формуле:
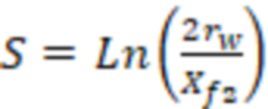 , где
, где
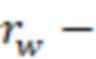
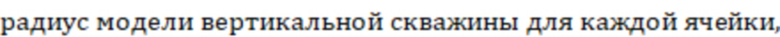
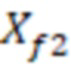 – полудлина участка трещины ГРП.
– полудлина участка трещины ГРП.
В варианте реализации в случае конечного типа проводимости трещины ГРП для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, могут рассчитать отрицательный скин-фактор (S) по формуле:
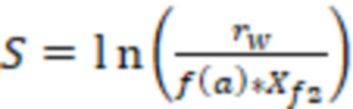 , где
, где
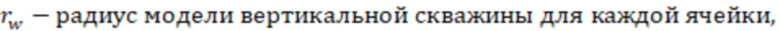
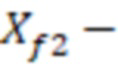 полудлина участка трещины ГРП,
полудлина участка трещины ГРП,
f(a) – зависимость эффективного радиуса модели вертикальной скважины для каждой ячейки от относительного емкостного параметра. Зависимость эффективного безразмерного радиуса скважины f(a) от относительного емкостного параметра определяют по графику, приведенному на фиг. 11 в статье «Effect of Vertical Fractures jn Reservoir Behavior – Incompressible Fluid Case» (Влияние вертикальных трещин на поведение коллектора - случай несжимаемой жидкости) (https://www.onepetro.org/download/journal-paper/SPE-1575-G?id=journal-paper%2FSPE-1575-G, fig. 11).
Дополнительно могут определить относительный емкостной параметр по формуле
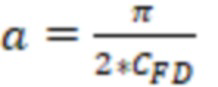 , где
, где
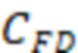 – безразмерная проводимость трещины гидроразрыва пласта.
– безразмерная проводимость трещины гидроразрыва пласта.
Дополнительно могут определить относительный емкостной параметр по формуле:
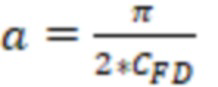 , где
, где
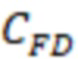 – безразмерная проводимость трещины ГРП.
– безразмерная проводимость трещины ГРП.
Безразмерную проводимость трещины ГРП могут определить по формуле:
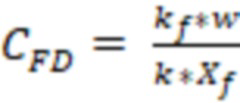 , где
, где
 ,
,
 ,
,
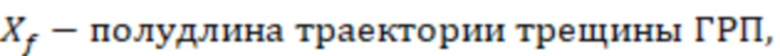
 .
.
В одном из вариантов реализации, а именно в случае прохождения траектории трещины ГРП поперек ствола горизонтальной скважины и конечного типа проводимости трещины ГРП дополнительно могут определить эффективную безразмерную проводимость трещины ГРП 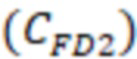 с учетом схождения (конвергенции) линий тока в трещине ГРП, которую учитывают при расчете отрицательного скин-фактора (S).
с учетом схождения (конвергенции) линий тока в трещине ГРП, которую учитывают при расчете отрицательного скин-фактора (S).
Эффективную безразмерную проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине ГРП могут определить по формуле:
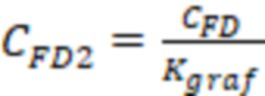 , где
, где
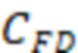 – безразмерная проводимость трещины гидроразрыва пласта,
– безразмерная проводимость трещины гидроразрыва пласта,
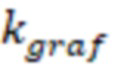 – коэффициент снижения продуктивности скважины.
– коэффициент снижения продуктивности скважины.
То есть в одном из вариантов реализации, а именно в случае прохождения траектории трещины ГРП поперек ствола горизонтальной скважины и конечного типа проводимости трещины определяют эффективную безразмерную проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине, например, по формуле 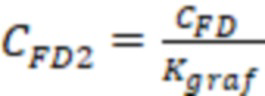 . Затем полученный значение
. Затем полученный значение 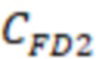 используют для определения относительного емкостного параметра
используют для определения относительного емкостного параметра 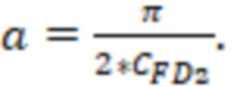 Затем значение емкостного параметра используют при расчёте отрицательного скин-фактора (S).
Затем значение емкостного параметра используют при расчёте отрицательного скин-фактора (S).
D-фактор (динамический скин-фактор) для газового типа флюида горизонтальной скважины могут определить по формуле:
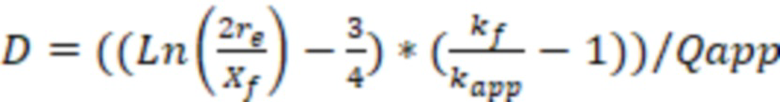 , где
, где
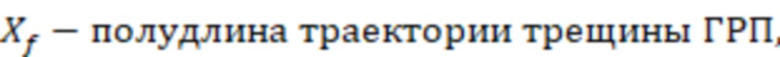
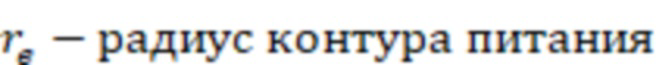 ,
,
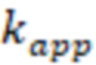 - проницаемость трещины ГРП с учетом инерциальных потерь,
- проницаемость трещины ГРП с учетом инерциальных потерь,
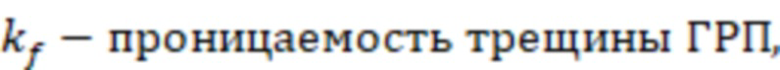
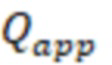 - дебит газа.
- дебит газа.
Проницаемость трещины ГРП с учетом инерциальных потерь могут определить по формуле:
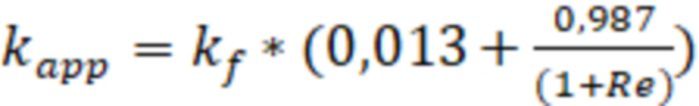 , где
, где 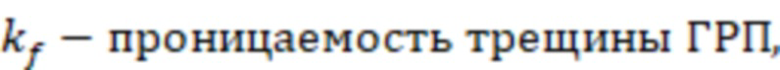
Re – число Рейнольдса.
Число Рейнольдса могут определить по формуле:
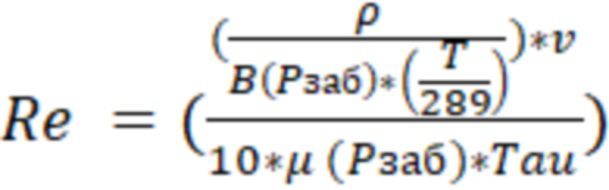 , где
, где

B – объемный коэффициент газа 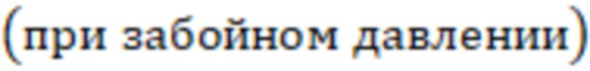 ,
,
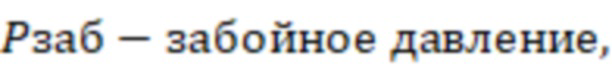

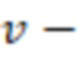 скорость фильтрации газа в трещине ГРП,
скорость фильтрации газа в трещине ГРП,
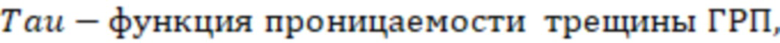
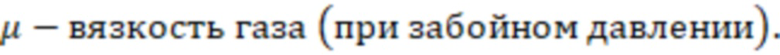

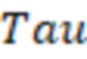 могут определить по графику (Барри Р.Д., Конвей М.В. Полная модель течения Дарси, Форхгеймера и транс-Форхгеймера в пористых средах // Международное общество инженеров нефтегазовой промышленности SPE, январь, 2004 - фиг. 13).
могут определить по графику (Барри Р.Д., Конвей М.В. Полная модель течения Дарси, Форхгеймера и транс-Форхгеймера в пористых средах // Международное общество инженеров нефтегазовой промышленности SPE, январь, 2004 - фиг. 13).
В одном из реализации способа, скорость фильтрации газа в трещине ГРП, траектория которой проходит поперек ствола горизонтальной скважины, могут определить по формуле:
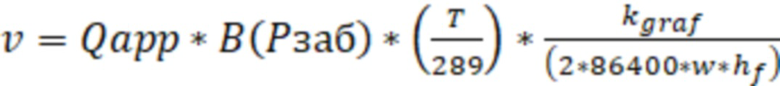 , где
, где
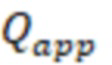 - дебит газа,
- дебит газа,
B – объемный коэффициент газа 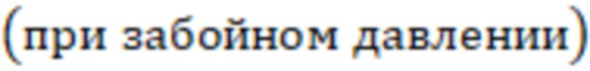 ,
,
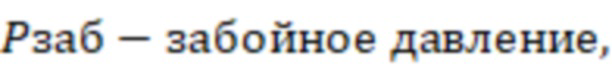

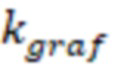 – коэффициент снижения продуктивности скважины,
– коэффициент снижения продуктивности скважины,
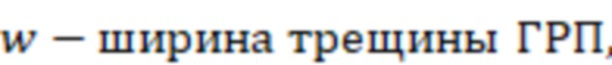
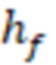 - высота трещины ГРП (это высота нефтегазового резервуара (коллекторная)).
- высота трещины ГРП (это высота нефтегазового резервуара (коллекторная)).
Коэффициент снижения продуктивности скважины могут определить с использованием значений отношения длины траектории трещины ГРП к ее высоте (фиг.6). График, учитывающий конвергенцию линий тока, был получен путем многократного гидродинамического моделирования и построен в безразмерных координатах. По оси «x» - отношение длины трещины ГРП к ее высоте в пласте, по оси «y» - коэффициент снижения продуктивности скважины, который учитывает конвергенцию линий тока. Значения линий графика соответствуют отношению высоте трещины ГРП в пласте к радиусу горизонтальной скважины, в которую осуществляется движение флюида (нефти, газа) трещины. Учет конвергенции линий тока в трещине ГРП повышает точность гидродинамического моделирования при поперечном расположении трещин горизонтальному стволу скважин.
В одном из реализации способа, скорость фильтрации газа в трещине ГРП, траектория которой проходит вдоль ствола газовой горизонтальной скважины, могут определить по формуле:
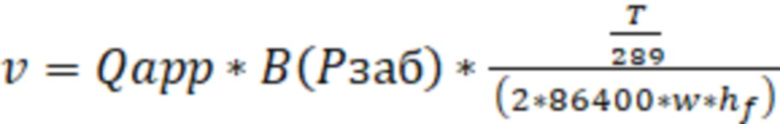 , где
, где
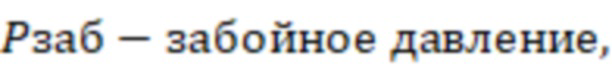
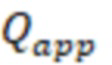 - дебит газа,
- дебит газа,
B – объемный коэффициент газа 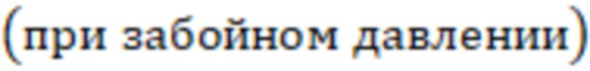 ,
,

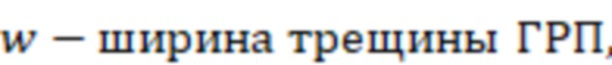
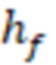 - высота трещины ГРП.
- высота трещины ГРП.
В одном из реализации способа дебит газа могут определить по формуле:
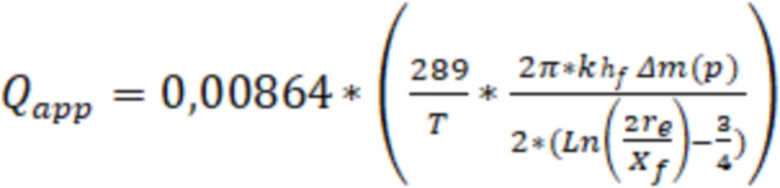 , где
, где

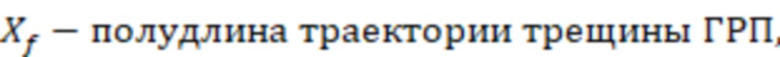
 ,
,
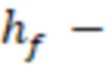 высота трещины ГРП,
высота трещины ГРП,
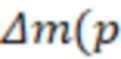 ) – депрессия псевдодавления,
) – депрессия псевдодавления,
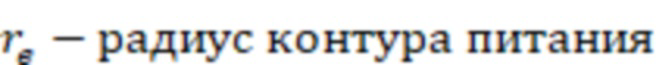 .
.
В одном из вариантов реализации дополнительно могут пересчитать дебит газа до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от дебита газа на последнем шаге пересчета менее, чем на 1%, при этом дебит газа пересчитывают по формуле:
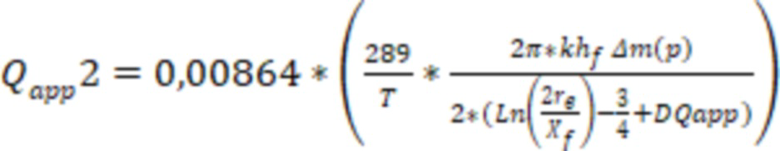 , где
, где
DQapp=Sин – скин-фактор за счет инерциальных потерь движения газа в трещине ГРП,

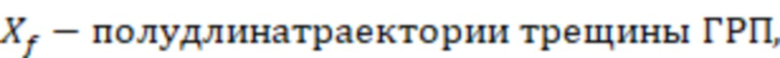
 ,
,
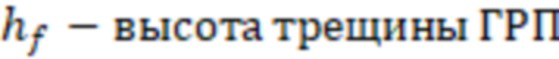 ,
,
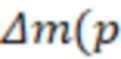 ) – депрессия псевдодавления,
) – депрессия псевдодавления,
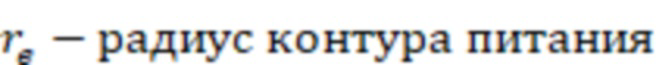 ,
,
при этом по каждому полученному значению дебита газа пересчитывают D-фактор, последнее значение которого учитывают при моделировании трещины ГРП. То есть по полученным значениям дебита газа по формуле:
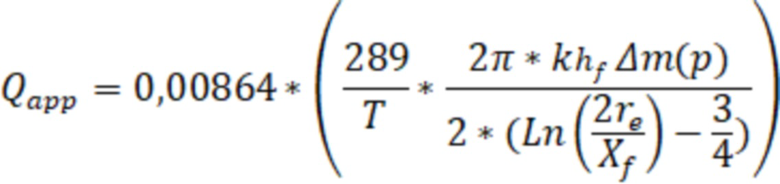
и D-фактора по формуле:
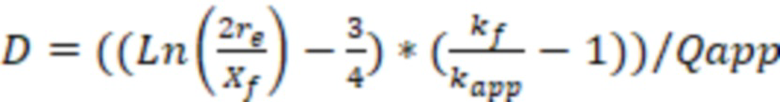 ), начинают пересчитывать дебит газа, используя полученное значение D-фактоор, а затем пересчитывают D-фактор, используя уже пересчетное значение дебита газа. И так делают до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от значения дебита газа на последнем шаге пересчета менее, чем на 1%. И при этом при моделировании трещины ГРП учитывают последнее полученное значение D-фактора. Расчет D-фактора позволяет учесть инерциальные потери давления в трещине ГРП при движении газовой фазы на высоких скоростях в трещине.
), начинают пересчитывать дебит газа, используя полученное значение D-фактоор, а затем пересчитывают D-фактор, используя уже пересчетное значение дебита газа. И так делают до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от значения дебита газа на последнем шаге пересчета менее, чем на 1%. И при этом при моделировании трещины ГРП учитывают последнее полученное значение D-фактора. Расчет D-фактора позволяет учесть инерциальные потери давления в трещине ГРП при движении газовой фазы на высоких скоростях в трещине.
Минимальный отрицательный скин-фактор (MinS) могут определить по формуле:
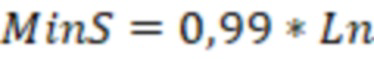 (
(
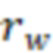 /
/
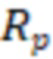 ), где
), где
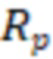 – радиус Писмана,
– радиус Писмана,
 .
.
Радиус Писмана могут определить по формуле:
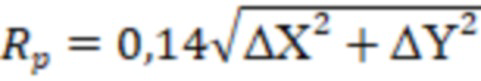 , где
, где
ΔX 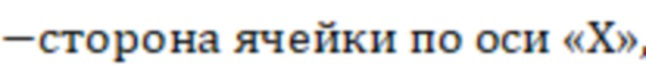
ΔY 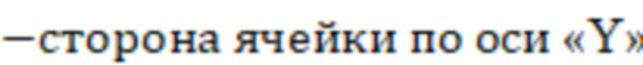 .
.
Множитель коэффициента продуктивности горизонтальной скважины могут определить по формуле:
Кмнож прод. = (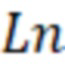 (
(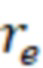 /
/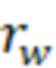 )-3/4+
)-3/4+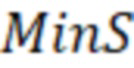 )/(
)/(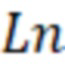 (
(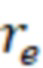 /
/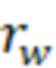 )-3/4+
)-3/4+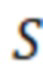 ), где
), где
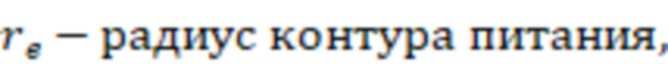
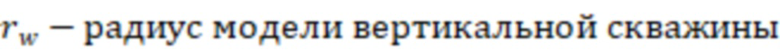 для каждой ячейки,
для каждой ячейки,
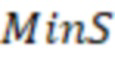 – минимальный отрицательный скин-фактор (MinS),
– минимальный отрицательный скин-фактор (MinS),
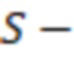 отрицательный скин-фактор.
отрицательный скин-фактор.
Сущность предлагаемого изобретения поясняется фигурами:
Фиг. 1 – схема расположения траектории продольной трещины ГРП относительно горизонтальной скважины;
Фиг. 2 - схема расположения траектории поперечной трещины ГРП относительно горизонтальной скважины;
Фиг. 3 – схема траектории трещины ГРП, пересекающая несколько ячеек гидродинамической модели;
Фиг. 4 – схема конвергенции линий тока в поперечной трещине ГРП;
Фиг. 5 – график определения относительного емкостного параметра;
Фиг. 6 – график определения коэффициента учета конвергенции линии тока;
Фиг. 7 – график определения 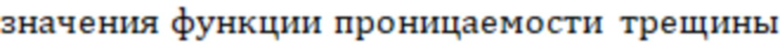
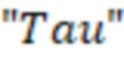 .
.
На фиг. 1-4 приняты следующие обозначения:
1 – горизонтальная добывающая/нагнетательная скважина;
2 – траектория трещины ГРП;
3 – ячейки гидродинамической модели;
4 – модели (мнимые) вертикальные скважины;
5 – конвергенция линий тока;
6 – зависимость эффективного радиуса модели вертикальной скважины для каждой ячейки от относительного емкостного параметра;
7, 8, 9, 10, 11 – зависимости коэффициента снижения продуктивности скважины за счет конвергенции (схождения) линий тока (значения отношения высоты трещины ГРП в пласте к радиусу горизонтальной скважины, равные 800, 400, 200, 100 и 50, соответственно);
12 – зависимость функции проницаемости трещины ГРП.
Заявленный способ реализуется следующим образом.
Получают значение длины трещины гидроразрыва пласта (ГРП) 2, пересекающей горизонтальную скважину 1, и данные о расположении этой трещины 2 (траектория трещины ГРП). Далее строят гидродинамическую модель пласта с использованием ячеек 3 заданной геометрией. Ячейки 3 имеют объемную геометрию. После чего определяют ячейки 3 гидродинамической модели пласта, по которым проходит траектория трещины ГРП 2 и определяют длины участков трещины ГРП 2 в ячейках 3 гидродинамической модели пласта. В каждой ячейке 3 гидродинамической модели пласта, по которой проходит траектория трещины ГРП 2, располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины ГРП 2. Для каждой модели вертикальной скважины 4, которые расположены в ячейках 3 гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек 3 и длинам участков трещины ГРП 2 в соответствующих ячейках 3. В результате моделируют трещину ГРП 2 с использованием моделей вертикальных скважин 4 с учетом отрицательного скин-фактора (S). Моделирование трещины ГРП предлагаемым способ возможно в любом гидродинамическом симуляторе (программном комплексе, предназначенным, в том числе, для построения геологический моделей).
На фиг. 1 показано расположение трещины ГРП (траектория трещины ГРП) 2 вдоль горизонтальной скважины 1. Траектория трещины ГРП 2 пересекает три ячейки гидродинамической модели 3, и для моделирования используют три мнимые вертикальными скважинами 4 с отрицательными скин-факторами.
На фиг. 2 показано расположение трещины ГРП (траектория трещины ГРП) 2 поперек горизонтальной скважины 1. Траектория трещины ГРП 2 пересекает три ячейки гидродинамической модели 3, и для моделирования используют три мнимые вертикальные скважины 4 с отрицательными скин-факторами с учетом конвергенции (схождения) линий тока.
На фиг. 3 показано, что траектория трещины ГРП 2 пересекает несколько ячеек 3 гидродинамической модели и для каждой ячейки 3 вычисляется длина и полудлина трещины ГРП 2, которая в нее попадает. То есть, длина трещины ГРП 2 (ее траектория) равна 2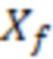 , а полудлина -
, а полудлина - 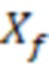 . В каждой ячейке 3 гидродинамической модели длина попавшего участка (отрезка) трещины ГРП 2 равна 2
. В каждой ячейке 3 гидродинамической модели длина попавшего участка (отрезка) трещины ГРП 2 равна 2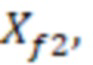 а полудлина -
а полудлина - 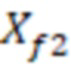 . Например, длина трещины ГРП 2
. Например, длина трещины ГРП 2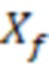 = 200 м., полудлина трещины ГРП = 100 м. В гидродинамической модели трещина ГРП 2 пересекла, например, (согласно фиг.3), четыре целых ячейки 3 гидродинамической модели, и две половины ячейки 3. То есть длина участков трещины ГРП 2 для четырех ячеек 3 гидродинамической модели, которых пересекла трещина ГРП 2, составит 2
= 200 м., полудлина трещины ГРП = 100 м. В гидродинамической модели трещина ГРП 2 пересекла, например, (согласно фиг.3), четыре целых ячейки 3 гидродинамической модели, и две половины ячейки 3. То есть длина участков трещины ГРП 2 для четырех ячеек 3 гидродинамической модели, которых пересекла трещина ГРП 2, составит 2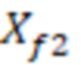 = 40 м, а полудлина участков трещины ГРП 2 для данных ячеек -
= 40 м, а полудлина участков трещины ГРП 2 для данных ячеек - 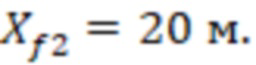 А для двух ячеек гидродинамической модели, которые траектория трещины ГРП 2 пересекла лишь их половину, длина участков трещины ГРП составит 2
А для двух ячеек гидродинамической модели, которые траектория трещины ГРП 2 пересекла лишь их половину, длина участков трещины ГРП составит 2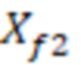 = 20 м, а полудлина участков трещины ГРП для данных ячеек -
= 20 м, а полудлина участков трещины ГРП для данных ячеек - 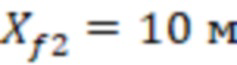 .
.
На фиг. 4 показано, что в случае поперечной трещины ГРП 2 возникает схождение (конвергенция) линий тока 5 к скважине 1, что приводит к дополнительным потерям давления.
По фиг. 5 можно определить эффективный безразмерный радиус скважины (зависимость 6) в зависимости от относительного емкостного параметра, который учитывает конечную проводимость трещины ГРП. С использованием эффективного безразмерного радиуса скважины возможно определить отрицательный скин-фактор для мнимой вертикальной скважины 4 (модели вертикальной скважины) в каждой пересекаемой трещиной ГРП 2 ячейки 3 гидродинамической модели.
По графику на фиг. 6 можно определить коэффициент снижения продуктивности скважины за счет конвергенции (схождения) линий тока. График был получен путем многократного гидродинамического моделирования в диапазоне параметров по данным фактических месторождений, и построен в безразмерных координатах. По оси «x» - отношение длины трещины ГРП к ее высоте в пласте, по оси «y» - коэффициент снижения продуктивности скважины, значения линий графика соответствуют отношению высоте трещины ГРП в пласте к радиусу горизонтальной скважины (зависимости 7, 8, 9, 10, 11), в которую осуществляется движение флюида трещины. На основе данных фактических месторождений отношение высоты трещины ГРП 2 в пласте к радиусу горизонтальной скважины установлено в диапазоне от «50» до «800».
По фиг. 7 можно определить значение функции проницаемости трещины ГРП – «Tau» (зависимость 12). Данный параметр используется при вычислении числа Рейнольдса при движении флюида в пористой среде проппанта трещины ГРП. Данный график был получен лабораторным путем ((Барри Р.Д., Конвей М.В. Полная модель течения Дарси, Форхгеймера и транс-Форхгеймера в пористых средах // Международное общество инженеров нефтегазовой промышленности SPE, январь, 2004 - фиг. 13).
Рассмотрим более подробно реализацию способа.
Реализация способа возможна со следующими параметрами: тип флюида горизонтальной добывающей/нагнетательной скважины – жидкость или газ; тип проводимости трещины ГРП - бесконечная или конечная; расположение трещины ГРП относительно ствола горизонтальной добывающей/нагнетательной скважины, например, вдоль или поперек.
1. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины – жидкость, тип проводимости трещины ГРП – бесконечная, расположение трещины ГРП относительно добывающей горизонтальной скважины 1 – вдоль (фиг.1).
Получают значение о длине трещины ГРП (2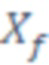 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией.
Определяют ячейки 3 гидродинамической модели, по которым проходит траектория трещины ГРП 2. Затем определяют длины участков трещины ГРП 2, расположенные в ячейках 3 гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2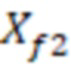 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 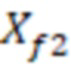 равна полудлине участка трещины ГРП 2 в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке 3 в зависимости от расположения трещины ГРП 2 относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине участка трещины ГРП 2 в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке 3 в зависимости от расположения трещины ГРП 2 относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
Затем для каждой модели вертикальной скважины 4, которые расположены в ячейках 3 гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек 3 и длинам участков трещины ГРП 2 в соответствующих ячейках 3.
При бесконечной проводимости трещины ГРП 2 отрицательный скин-фактор в случае добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле:
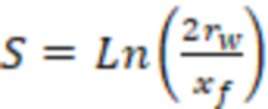 , где
, где
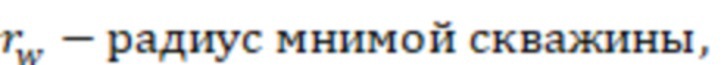
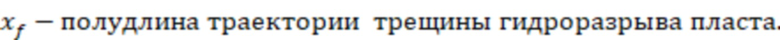
Далее могут определить допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле 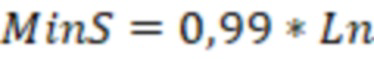 (
( /
/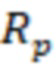 ),
),
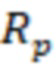 – радиус Писмана,
– радиус Писмана,
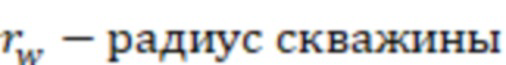 .
.
Радиус Писмана могут определить по формуле 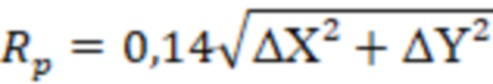 ,
,
где ΔX 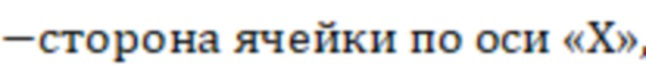
ΔY 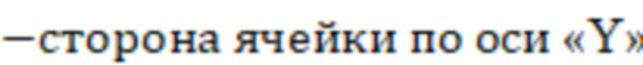 (Фиг.3).
(Фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно могут учитывать множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. =(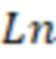 (
(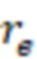 /
/ )-3/4+
)-3/4+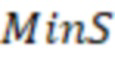 )/(
)/(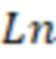 (
(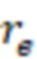 /
/ )-3/4+
)-3/4+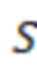 ), где
), где

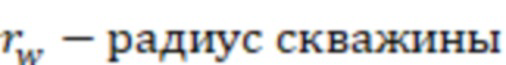 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S). Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины.
2. Рассмотрим реализацию способа со следующими параметрами: тип флюида
добывающей/нагнетательной скважины – жидкость, тип проводимости трещины ГРП 2 – конечная, расположение трещины ГРП 2 относительно добывающей горизонтальной скважины 1 – вдоль (фиг.1).
Получают значение о длине трещины ГРП (2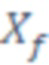 ) и об ее расположении (формируют траекторию трещины ГРП 2). Затем строят гидродинамическую модель пласта с использованием ячеек 3 с заданной геометрией.
) и об ее расположении (формируют траекторию трещины ГРП 2). Затем строят гидродинамическую модель пласта с использованием ячеек 3 с заданной геометрией.
Определяют ячейки 3 гидродинамической модели, которые пересекает траектория трещины ГРП 2. Затем определяют длины участков трещины ГРП 2, расположенные в ячейках 3 гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2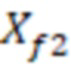 (фиг. 4) в каждой ячейке 3, где
(фиг. 4) в каждой ячейке 3, где 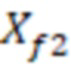 равна полудлине трещины ГРП 2 в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке 3 в зависимости от расположения трещины ГРП 2 относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной 2 ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине трещины ГРП 2 в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке 3 в зависимости от расположения трещины ГРП 2 относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной 2 ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
Затем для каждой модели вертикальной скважины 4, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек 3 и длинам участков трещины ГРП 2 в соответствующих ячейках 3.
При конечной проводимости трещины 2 расчетный отрицательный скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут рассчитать по формуле:
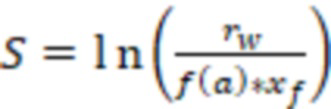 , где
, где
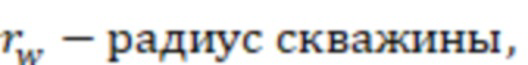
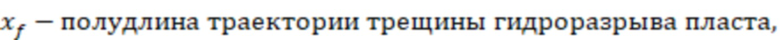
f(a) – зависимость эффективного безразмерного радиуса скважины от относительного емкостного параметра, которую могут определить по графику на фиг. 5 (зависимость 6).
Относительный емкостной параметр могут определить по формуле 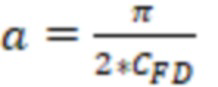 , где
, где
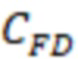 – безразмерная проводимость трещины гидроразрыва пласта.
– безразмерная проводимость трещины гидроразрыва пласта.
Безразмерную проводимость трещины гидроразрыва пласта могут определить по формуле 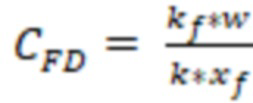 ,
,
где 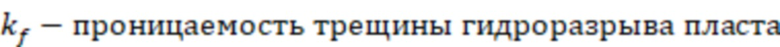 ,
,
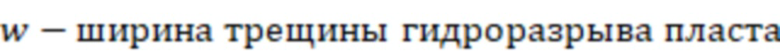 ,
,
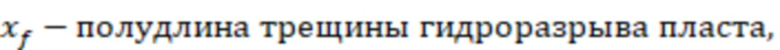
 .
.
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле 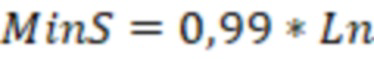 (
( /
/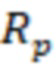 ),
),
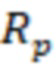 – радиус Писмана,
– радиус Писмана,
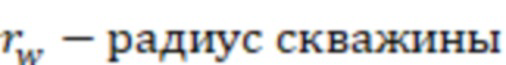 .
.
Радиус Писмана могут определить по формуле 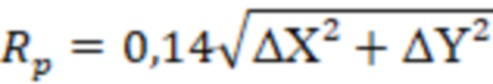 ,
,
где ΔX 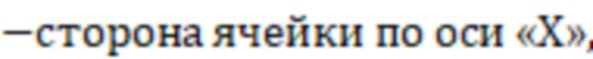
ΔY 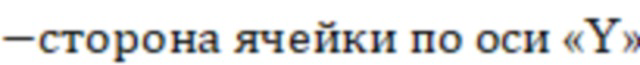 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. =(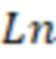 (
(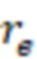 /
/ )-3/4+
)-3/4+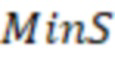 )/(
)/(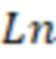 (
(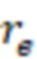 /
/ )-3/4+
)-3/4+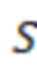 ), где
), где

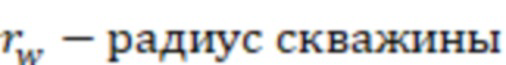 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S). Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины.
3. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины – газ, тип проводимости трещины ГРП – бесконечная, расположение трещины ГРП 2 относительно добывающей горизонтальной скважины 1 – вдоль (фиг.1).
Получают значение о длине трещины ГРП (2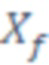 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией.
Определяют ячейки гидродинамической модели, которые пересекает траектория трещины ГРП. Затем определяют длины участков трещины ГРП, расположенные в ячейках гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2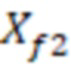 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 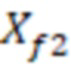 равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
Затем для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках.
При бесконечной проводимости трещины расчетный отрицательный скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле:
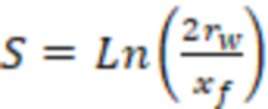 ,
,
где 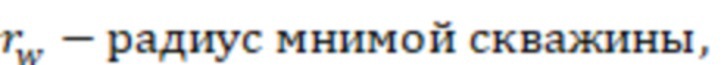
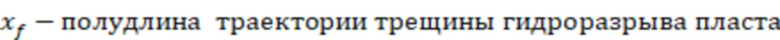 .
.
Затем могут определить D-фактор для газовой скважины, который учитывают при моделировании трещины ГРП. D-фактор могут определить по формуле:
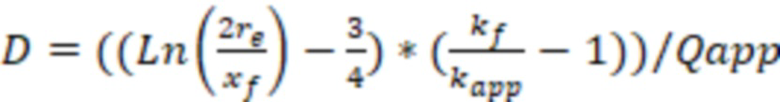 ,
,
где

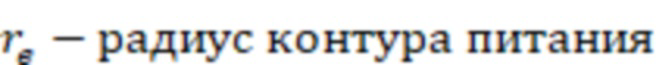 ,
,
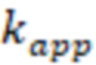 - проницаемость трещины учетом инерциальных потерь,
- проницаемость трещины учетом инерциальных потерь,
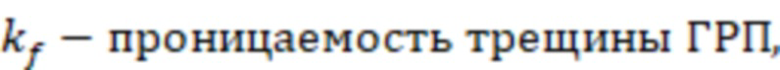
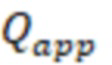 - дебит газа.
- дебит газа.
Проницаемость трещины с учетом инерциальных потерь могут определить по формуле:
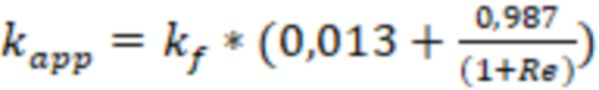 ,
,
где 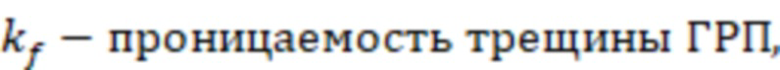
Re – число Рейнольдса.
Число Рейнольдса могут определить по формуле:
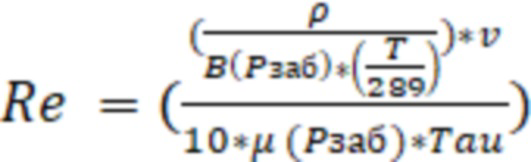 ,
,
где 
B – объемный коэффициент газа (при забойном давлении),
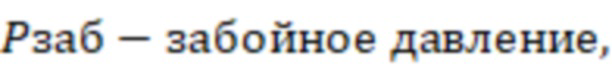
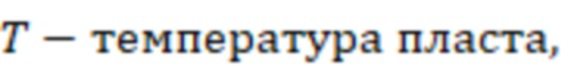
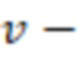 скорость фильтрации газа в трещине гидроразрыва пласта,
скорость фильтрации газа в трещине гидроразрыва пласта,

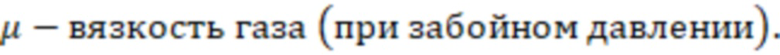
Скорость фильтрации газа в трещине ГРП, при ее расположении вдоль ствола газовой скважины, могут определить по формуле:
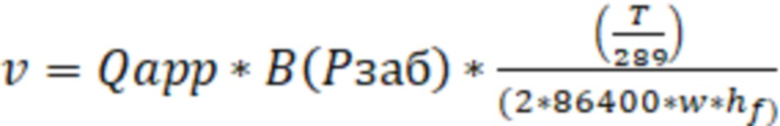 ,
,
где 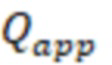 - дебит газа,
- дебит газа,
B – объемный коэффициент газа (при забойном давлении),
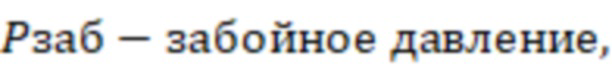
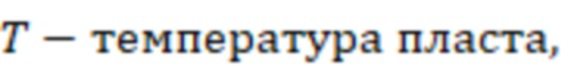
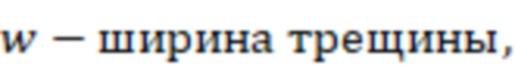
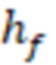 - высота трещины.
- высота трещины.
Значение 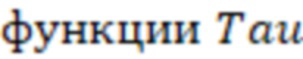 от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
Дебит газа могут определить по формуле:
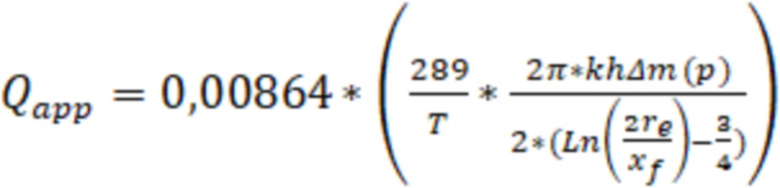 ,
,
где 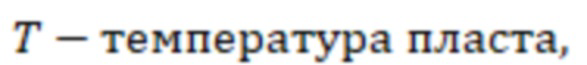
 ,
,
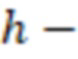 эффективная высота пласта (равна высоте трещины в пласте
эффективная высота пласта (равна высоте трещины в пласте 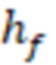 ),
),
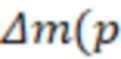 ) – депрессия псевдодавления,
) – депрессия псевдодавления,

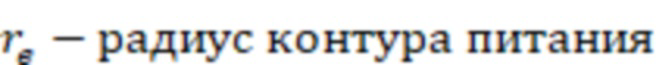 .
.
После расчета D-фактора в первой итерации повторяют расчет дебита газа трещины ГРП с учетом полученного значения D-фактора и первого значения дебита газа:
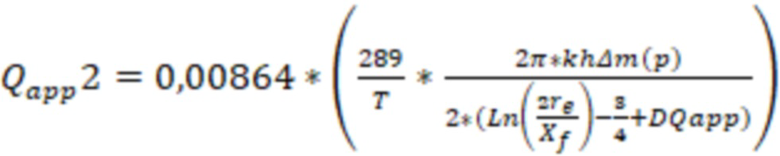 ,
,
где DQapp=Sин – скин-фактор за счет инерциальных потерь движения газа в трещине ГРП. То есть пересчитывают дебит газа добавив дополнительную компоненту в знаменатель. Затем пересчитывают скорость фильтрации газа в трещине ГРП и D-фактор. Такой пересчет делают до тех пор, пока дебит газа на предыдущем шаге расчета не будет отличаться от дебита на последнем шаге расчета менее, чем на 1%. Для моделирования используют последнее полученное значение D-фактора.
Далее могут определить допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
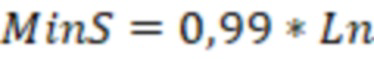 (
(
 /
/
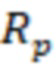 ),
),
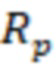 – радиус Писмана,
– радиус Писмана,
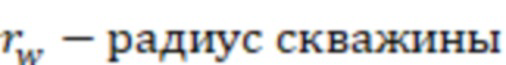 .
.
Радиус Писмана могут определить по формуле:
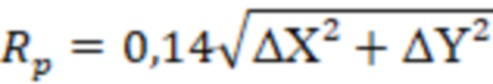 ,
,
где ΔX 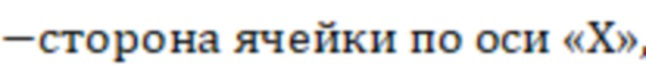
ΔY 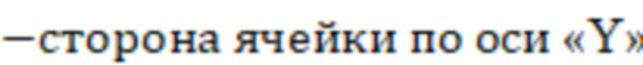 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. =(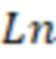 (
(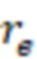 /
/ )-3/4+
)-3/4+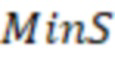 )/(
)/(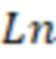 (
(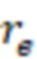 /
/ )-3/4+
)-3/4+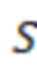 ), где
), где

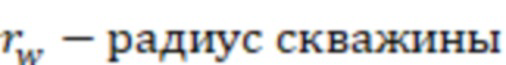 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), определенным D-фактором. Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины и D-фактор.
4. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины – газ, тип проводимости трещины ГРП – конечная, расположение трещины ГРП относительно добывающей горизонтальной скважины – вдоль (фиг.1).
Получают значение о длине трещины ГРП (2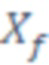 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП 2.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП 2.
Затем определяют длины участков трещины ГРП, расположенные в ячейках гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2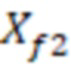 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 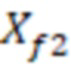 равна полудлине участка трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине участка трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
Затем для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках. При конечной проводимости трещины расчетный отрицательный скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле: 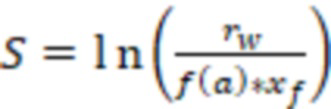 , где
, где
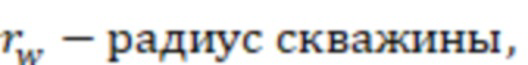
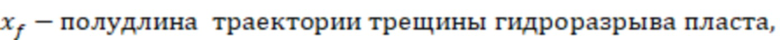
f(a) – зависимость эффективного безразмерного радиуса скважины от относительного емкостного параметра, которую определяют по графику на фиг. 5 (зависимость 6).
Относительный емкостной параметр могут определить по формул
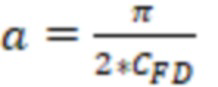 ,
,
где 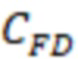 – безразмерная проводимость трещины гидроразрыва пласта.
– безразмерная проводимость трещины гидроразрыва пласта.
Безразмерную проводимость трещины гидроразрыва пласта могут определить по формуле:
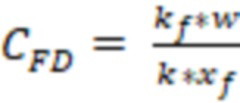 ,
,
где 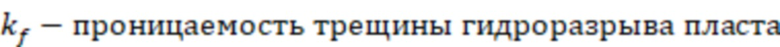 ,
,
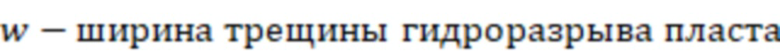 ,
,
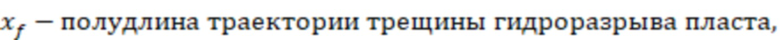
 .
.
Затем определяют D-фактор для газовой скважины. D-фактор могут определить по формуле:
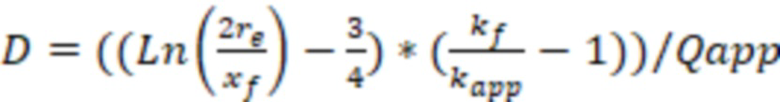 ,
,
где
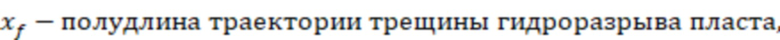
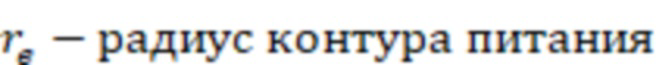 ,
,
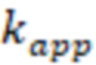 - проницаемость трещины c учетом инерциальных потерь,
- проницаемость трещины c учетом инерциальных потерь,
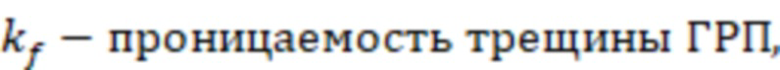
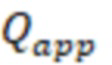 - дебит газа.
- дебит газа.
Проницаемость трещины с учетом инерциальных потерь могут определить по формуле:
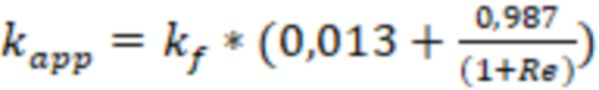 , где
, где
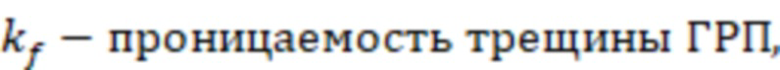
Re – число Рейнольдса.
Число Рейнольдса могут определить по формуле:
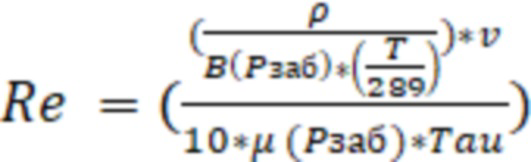 ,
,
где 
B – объемный коэффициент газа (при забойном давлении),
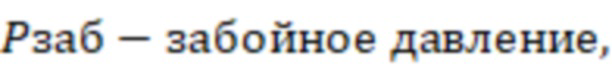
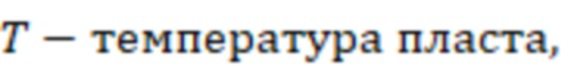
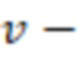 скорость фильтрации газа в трещине гидроразрыва пласта,
скорость фильтрации газа в трещине гидроразрыва пласта,

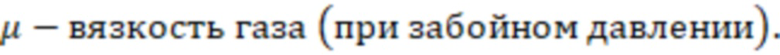
Значение 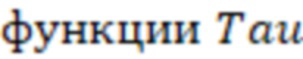 от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
Скорость фильтрации газа в трещине ГРП, при ее расположении вдоль ствола газовой скважины, могут определить по формуле:
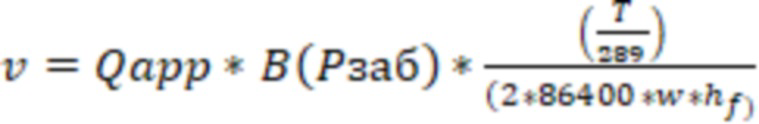 ,
,
где 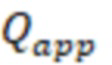 - дебит газа,
- дебит газа,
B – объемный коэффициент газа (при забойном давлении),
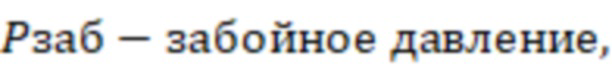
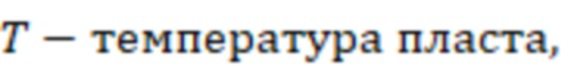
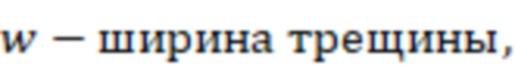
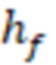 - высота трещины.
- высота трещины.
Дебит газа могут определить по формуле:
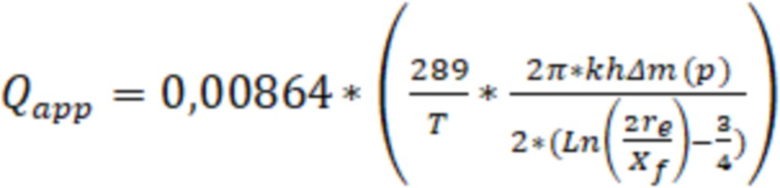 ,
,
где 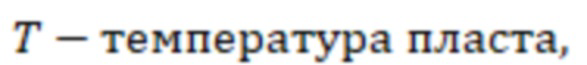
 ,
,
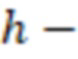 эффективная высота пласта (равна высоте трещины в пласте
эффективная высота пласта (равна высоте трещины в пласте 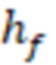 ),
),
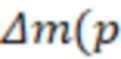 ) – депрессия псевдодавления,
) – депрессия псевдодавления,
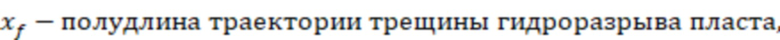
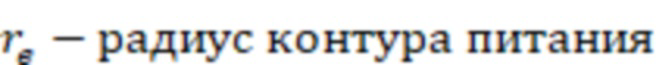 .
.
После расчета D-фактора в первой итерации повторяют расчет дебита газа трещины ГРП с учетом полученного значения D-фактора и первого значения дебита газа:
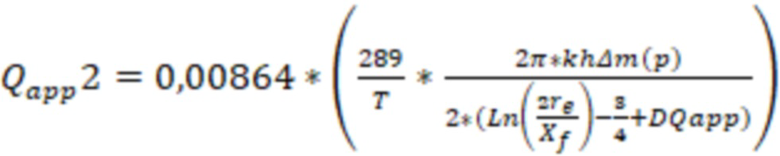 ,
,
где DQapp=Sин – скин-фактор за счет инерциальных потерь движения газа в трещине ГРП. То есть пересчитывают дебит газа добавив дополнительную компоненту в знаменатель. Затем пересчитывают скорость фильтрации газа в трещине ГРП и D-фактор. Такой пересчет делают до тех пор, пока дебит газа на предыдущем шаге расчета не будет отличаться от дебита на последнем шаге расчета менее, чем на 1%. Для моделирования используют последнее полученное значение D-фактора.
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
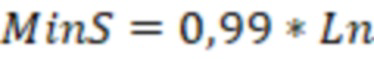 (
(
 /
/
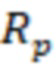 ),
),
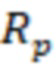 – радиус Писмана,
– радиус Писмана,
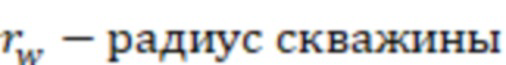 .
.
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. = (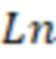 (
(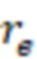 /
/ )-3/4+
)-3/4+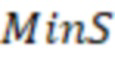 )/(
)/(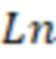 (
(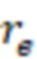 /
/ )-3/4+
)-3/4+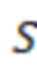 ),
),
где 
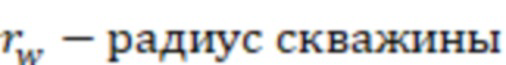 .
.
Радиус Писмана могут определить по формуле:
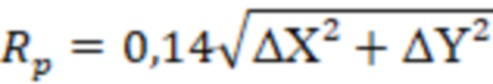 ,
,
где ΔX 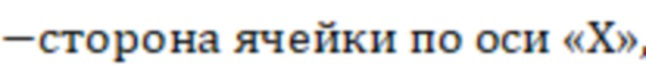
ΔY 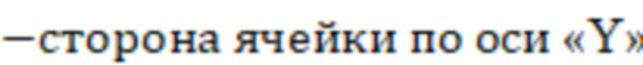 (фиг.3).
(фиг.3).
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), определенным D-фактором. Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины и D-фактор.
5. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины – жидкость, тип проводимости трещины ГРП – бесконечная, расположение трещины ГРП относительно добывающей скважины – поперек (фиг.2).
Получают значение о длине трещины ГРП 2 (2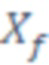 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП 2.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП 2.
Затем определяют длины участков трещины ГРП, расположенные в ячейках гидродинамической модели пласта (фиг. 3). Полученные длины участков принимают за 2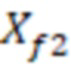 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 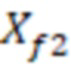 равна полудлине участка трещины ГРП в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине участка трещины ГРП в данной ячейке 3. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта.
Затем для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках.
При бесконечной проводимости трещины расчетный отрицательный скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле:
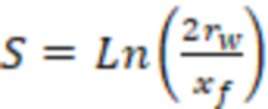 ,
,
где 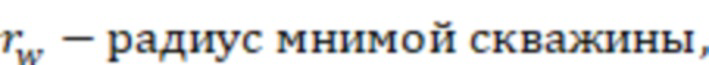
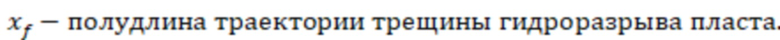
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
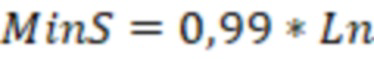 (
(
 /
/
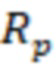 ),
),
где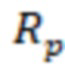 – радиус Писмана,
– радиус Писмана,
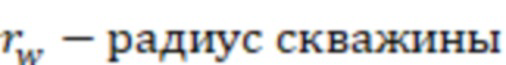 .
.
Радиус Писмана могут определить по формуле:
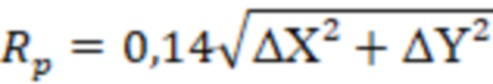 ,
,
где ΔX 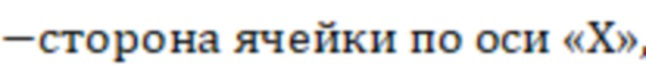
ΔY 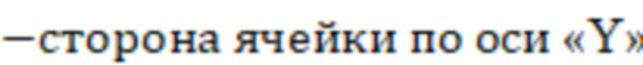 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. =(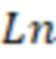 (
(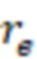 /
/ )-3/4+
)-3/4+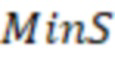 )/(
)/(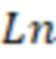 (
(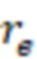 /
/ )-3/4+
)-3/4+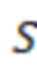 ),
),
где 
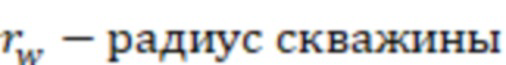 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), определенным D-фактором. Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины и D-фактор.
6. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины – жидкость, тип проводимости трещины ГРП – конечная, расположение трещины ГРП относительно добывающей горизонтальной скважины – поперек (фиг.2).
Получают значение о длине трещины ГРП 2 (2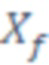 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, которые пересекает траектория трещины ГРП.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, которые пересекает траектория трещины ГРП.
Затем определяют длины участков трещины ГРП, расположенные в ячейках гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2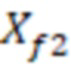 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 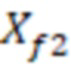 равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
При конечной проводимости трещины скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле:
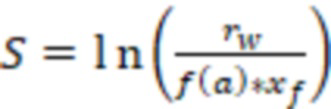 ,
,
где 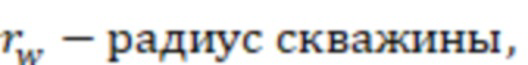
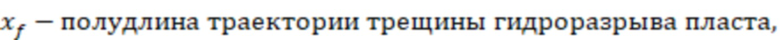
f(a) – зависимость эффективного безразмерного радиуса скважины от относительного емкостного параметра, которую можно определить по графику на фиг. 5 (зависимость 6).
Относительный емкостной параметр могут определить по формуле:
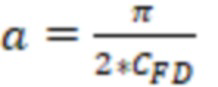 ,
,
где 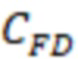 – безразмерная проводимость трещины гидроразрыва пласта.
– безразмерная проводимость трещины гидроразрыва пласта.
Безразмерную проводимость трещины гидроразрыва пласта могут определить по формуле:
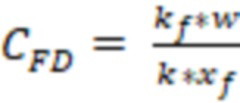 ,
,
где 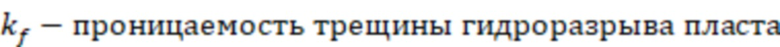 ,
,
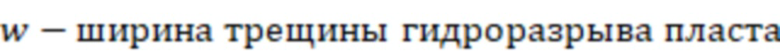 ,
,
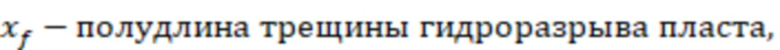
 .
.
Учитывая, что трещина ГРП расположена поперек, необходимо учесть сходимость линий тока в трещине к стволу скважины (фиг. 4). Для этого определяют эффективную безразмерную проводимость трещины ГРП с учетом схождения линий тока в трещине, которая расположена поперек ствола добывающей скважины, по формуле:
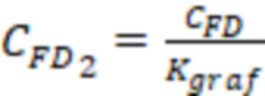 ,
,
где 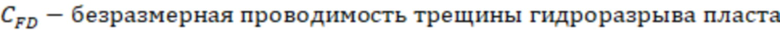 ,
,
 – коэффициент снижения продуктивности скважины.
– коэффициент снижения продуктивности скважины.
Затем данное полученное значение подставляют в формулу определения относительного емкостного параметра, то есть:
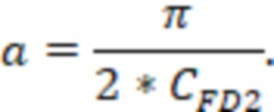
Коэффициент снижения продуктивности скважины могут определить по графику на фиг. 6 (зависимости 7, 8, 9, 10, 11).
Зависимость эффективного безразмерного радиуса скважины от относительного емкостного параметра могут определить по графику на фиг. 5 (зависимость 6).
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
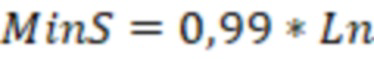 (
(
 /
/
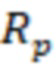 ),
),
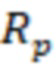 – радиус Писмана,
– радиус Писмана,
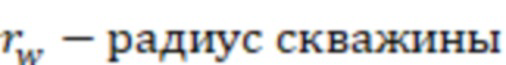 .
.
Радиус Писмана могут определить по формуле:
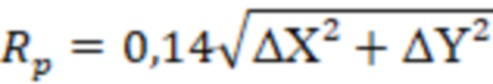 ,
,
где ΔX 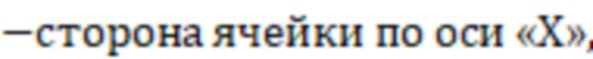
ΔY 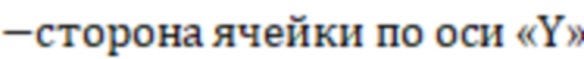 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле
Кмнож прод. =(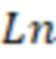 (
(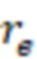 /
/ )-3/4+
)-3/4+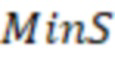 )/(
)/(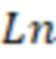 (
(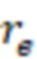 /
/ )-3/4+
)-3/4+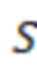 ),
),
Где 
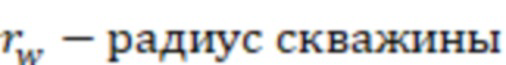 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S). Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины.
7. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины 1 – газ, тип проводимости трещины ГРП – бесконечная, расположение трещины ГРП относительно добывающей горизонтальной скважины – поперек (фиг.2).
Получают значение о длине трещины ГРП 2 (2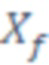 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП.
Затем определяют длины участков трещины ГРП, расположенные в ячейках 3гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2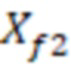 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 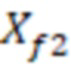 равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
При бесконечной проводимости трещины скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле: 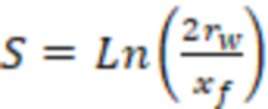 ,
,
где 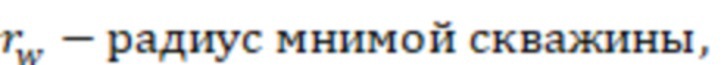
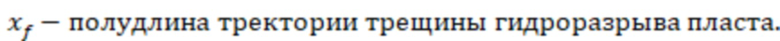
Затем определяют D-фактор для газовой скважины, который учитывают при моделировании трещины ГРП. D-фактор могут определить по формуле:
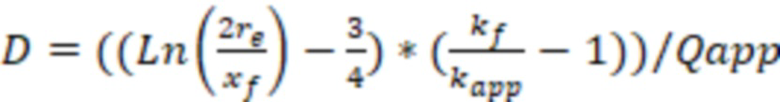 ,
,
где 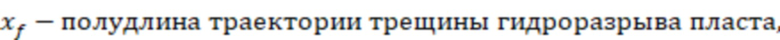
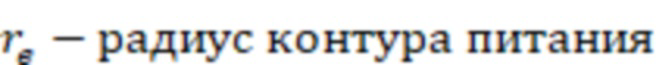 ,
,
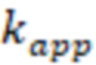 - проницаемость трещины учетом инерциальных потерь,
- проницаемость трещины учетом инерциальных потерь,
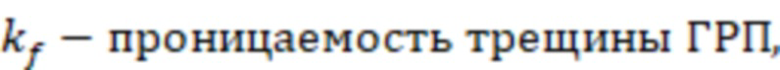
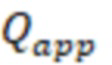 - дебит газа.
- дебит газа.
Проницаемость трещины с учетом инерциальных потерь могут определить по формуле:
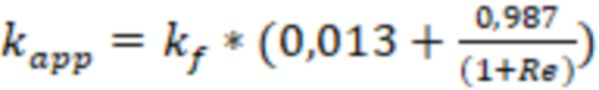 ,
,
где 
Re – число Рейнольдса.
Число Рейнольдса могут определить по формуле:
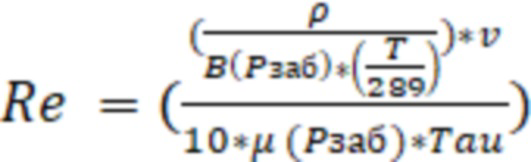 ,
,
где 
B – объемный коэффициент газа (при забойном давлении),
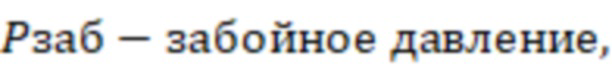
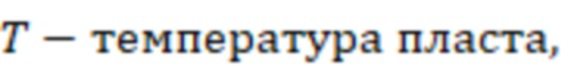
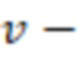 скорость фильтрации газа в трещине гидроразрыва пласта,
скорость фильтрации газа в трещине гидроразрыва пласта,

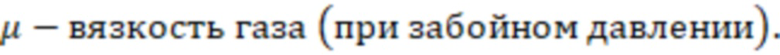
Значение 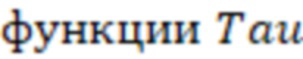 от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
Скорость фильтрации газа в трещине ГРП, при ее расположении поперек ствола газовой скважины, могут определить по формуле:
 ,
,
где 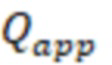 - дебит газа,
- дебит газа,
B – объемный коэффициент газа (при забойном давлении),
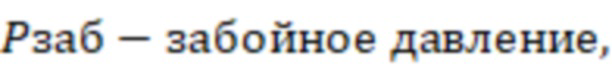
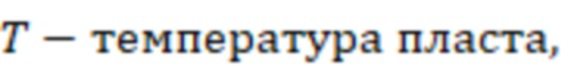
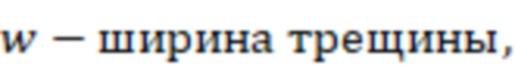
 – коэффициент снижения продуктивности скважины,
– коэффициент снижения продуктивности скважины,
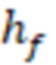 - высота трещины.
- высота трещины.
Коэффициент снижения продуктивности скважины (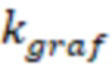 ) могут определить по графику на фиг. 6 (зависимости 7, 8, 9, 10, 11).
) могут определить по графику на фиг. 6 (зависимости 7, 8, 9, 10, 11).
Дебит газа могут определить по формуле:
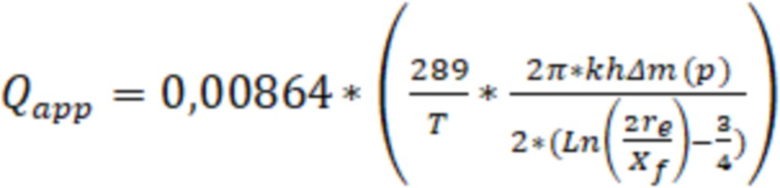 ,
,
где 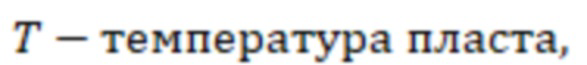
 ,
,
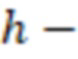 эффективная высота пласта (равна высоте трещины в пласте
эффективная высота пласта (равна высоте трещины в пласте 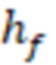 ),
),
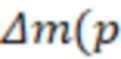 ) – депрессия псевдодавления,
) – депрессия псевдодавления,
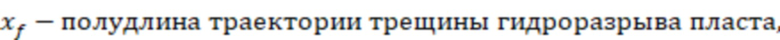
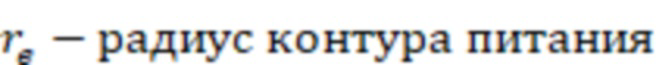 .
.
После расчета D-фактора в первой итерации повторяют расчет дебита газа трещины ГРП с учетом полученного значения D-фактора и первого значения дебита газа:
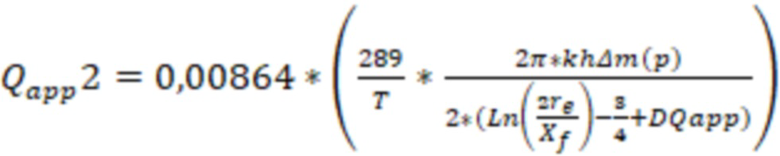 ,
,
где DQapp=Sин – скин-фактор за счет инерциальных потерь движения газа в трещине ГРП. То есть пересчитывают дебит газа добавив дополнительную компоненту в знаменатель.
Затем пересчитывают скорость фильтрации газа в трещине ГРП и D-фактор. Такой пересчет делают до тех пор, пока дебит газа на предыдущем шаге расчета не будет отличаться от дебита на последнем шаге расчета менее, чем на 1%. Для моделирования используют последнее полученное значение D-фактора.
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
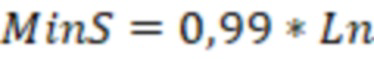 (
(
 /
/
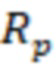 ),
),
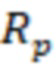 – радиус Писмана,
– радиус Писмана,
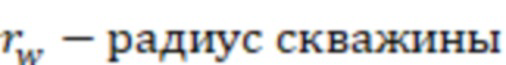 .
.
Радиус Писмана могут определить по формуле:
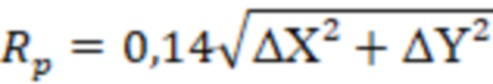 ,
,
где ΔX 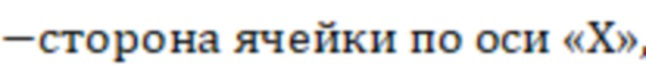
ΔY 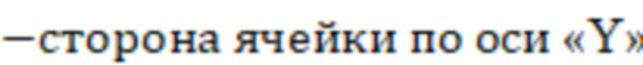 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. =(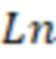 (
(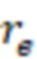 /
/ )-3/4+
)-3/4+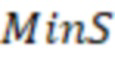 )/(
)/(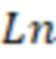 (
(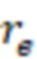 /
/ )-3/4+
)-3/4+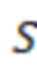 ),
),

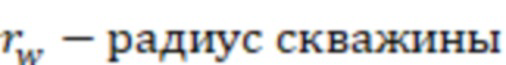 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S). Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины.
8. Рассмотрим реализацию способа со следующими параметрами: тип флюида добывающей/нагнетательной скважины 1 – газ, тип проводимости трещины ГРП – конечная, расположение трещины ГРП относительно добывающей горизонтальной скважины – поперек (фиг.2).
Получают значение о длине трещины ГРП 2 (2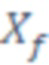 ) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП.
) и об ее расположении (формируют траекторию трещины ГРП). Затем строят гидродинамическую модель пласта с использованием ячеек с заданной геометрией. Определяют ячейки гидродинамической модели 3, по которым проходит траектория трещины ГРП.
Затем определяют длины участков трещины ГРП, расположенные в ячейках гидродинамической модели пласта (фиг. 3). Полученные длины принимают за 2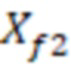 (фиг. 4) в каждой ячейке, где
(фиг. 4) в каждой ячейке, где 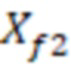 равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
равна полудлине трещины ГРП в данной ячейке. Данное значение может иметь различные значения в каждой пересекаемой ячейке в зависимости от расположения трещины ГРП относительно используемой сетки гидродинамической модели. Затем в каждой пересекаемой трещиной ячейке 3 гидродинамической модели пласта располагают модель вертикальной скважины 4, выполненную с возможностью симуляции трещины гидроразрыва пласта.
При конечной проводимости трещины расчетный отрицательный скин-фактор для добывающих/нагнетательных скважин (жидкость или газ) могут определить по формуле: 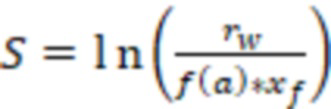 ,
,
где 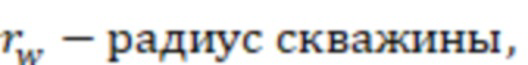
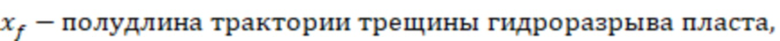
f(a) – зависимость эффективного безразмерного радиуса скважины от относительного емкостного параметра, который можно определить по графику на фиг. 5 (зависимость 6).
Относительный емкостной параметр могут определить по формуле:
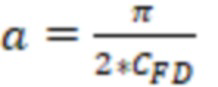 ,
,
где 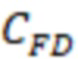 – безразмерная проводимость трещины гидроразрыва пласта.
– безразмерная проводимость трещины гидроразрыва пласта.
Безразмерную проводимость трещины гидроразрыва пласта могут определить по формуле:
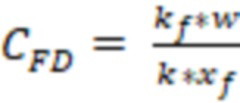 ,
,
где 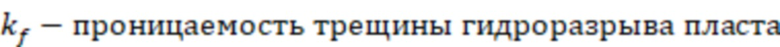 ,
,
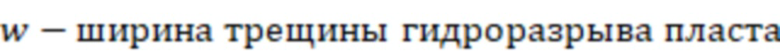 ,
,
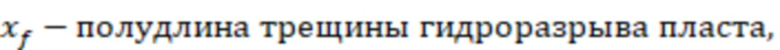
 .
.
Учитывая, что трещина ГРП расположена поперек, необходимо учесть сходимость линий тока в трещине к стволу скважины (фиг. 4). Для этого определяют эффективную безразмерную проводимость трещины ГРП с учетом схождения (конвергенции) линий тока 5 в трещине, которая расположена поперек ствола скважины 1, по формуле:
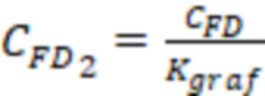 ,
,
где 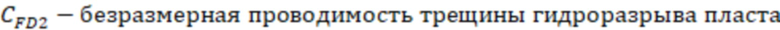 ,
,
 – коэффициент снижения продуктивности скважины. Полученное значение безразмерной проводимости трещины ГРП используют для определения емкостного параметра.
– коэффициент снижения продуктивности скважины. Полученное значение безразмерной проводимости трещины ГРП используют для определения емкостного параметра.
Коэффициент снижения продуктивности скважины могут определить по графику на фиг. 6 (зависимости 7, 8, 9, 10, 11).
Затем определяют D-фактор для газовой скважины. D-фактор могут определить по формуле:
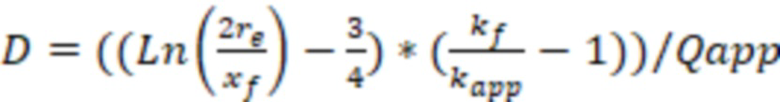 ,
,
Где 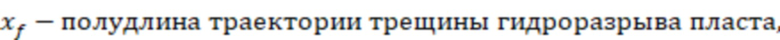
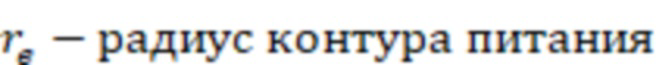 ,
,
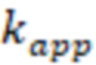 - проницаемость трещины учетом инерциальных потерь,
- проницаемость трещины учетом инерциальных потерь,
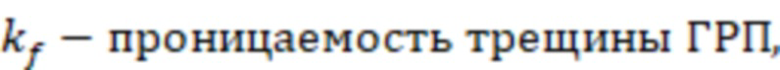
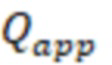 - дебит газа.
- дебит газа.
Проницаемость трещины с учетом инерциальных потерь могут определить по формуле:
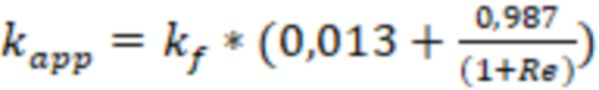 ,
,
где 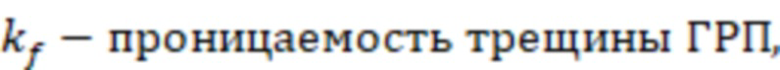
Re – число Рейнольдса.
Число Рейнольдса могут определить по формуле:
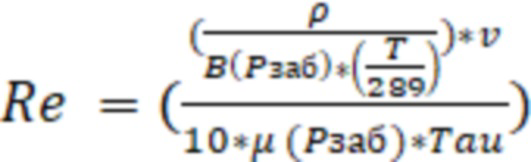 ,
,
где 
B – объемный коэффициент газа (при забойном давлении),
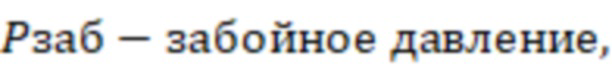
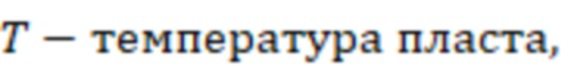
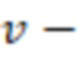 скорость фильтрации газа в трещине гидроразрыва пласта,
скорость фильтрации газа в трещине гидроразрыва пласта,

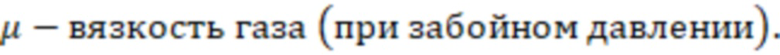
Значение 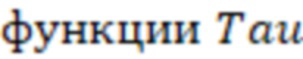 от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
от проницаемости могут определить по графику на фиг. 7 (зависимость 12).
Скорость фильтрации газа в трещине ГРП, при ее расположении поперек ствола газовой скважины, могут определить по формуле:
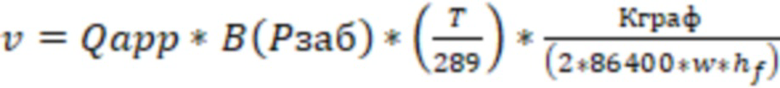 ,
,
где 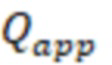 - дебит газа,
- дебит газа,
B – объемный коэффициент газа (при забойном давлении),
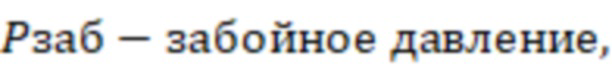
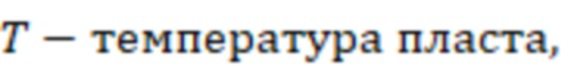
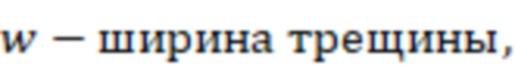
 – коэффициент снижения продуктивности скважины,
– коэффициент снижения продуктивности скважины,
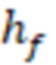 - высота трещины.
- высота трещины.
Дебит газа могут определить по формуле:
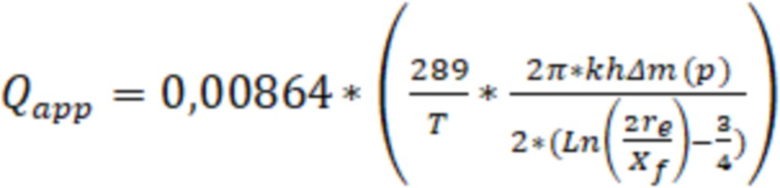 ,
,
где 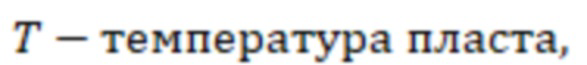
 ,
,
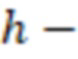 эффективная высота пласта (равна высоте трещины в пласте
эффективная высота пласта (равна высоте трещины в пласте 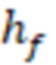 ),
),
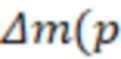 ) – депрессия псевдодавления,
) – депрессия псевдодавления,
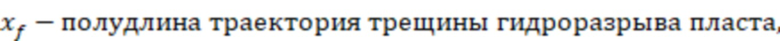
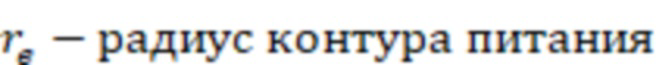 .
.
После расчета D-фактора в первой итерации повторяют расчет дебита газа трещины ГРП с учетом полученного значения D-фактора и первого значения дебита газа:
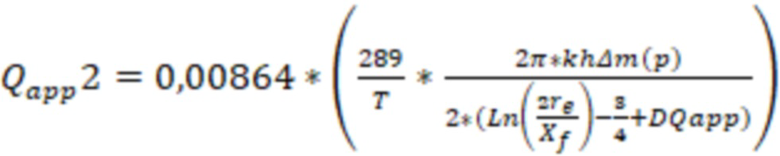 ,
,
где DQapp=Sин – скин-фактор за счет инерциальных потерь движения газа в трещине ГРП. То есть пересчитывают дебит газа добавив дополнительную компоненту в знаменатель. Затем пересчитывают скорость фильтрации газа в трещине ГРП и D-фактор. Такой пересчет делают до тех пор, пока дебит газа на предыдущем шаге расчета не будет отличаться от дебита на последнем шаге расчета менее, чем на 1%. Для моделирования трещины ГРП используют последнее полученное значение D-фактора.
Далее определяют допустимый минимальный скин-фактор. Допустимый минимальный скин-фактор могут определить по формуле:
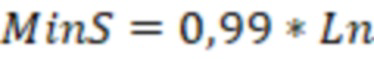 (
(
 /
/
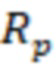 ),
),
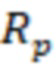 – радиус Писмана,
– радиус Писмана,
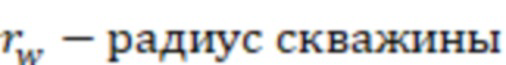 .
.
Радиус Писмана могут определить по формуле:
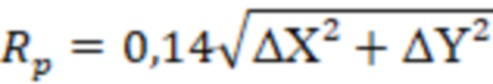 ,
,
где ΔX 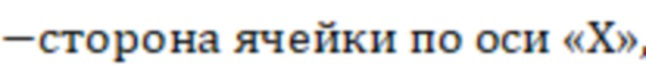
ΔY 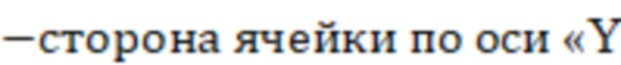
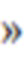 (фиг.3).
(фиг.3).
Если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины.
Дополнительный множитель продуктивности мнимой вертикальной скважины могут определить по формуле:
Кмнож прод. = (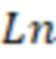 (
(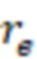 /
/ )-3/4+
)-3/4+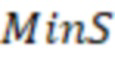 )/(
)/(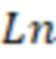 (
(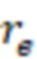 /
/ )-3/4+
)-3/4+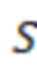 ),
),
Где 
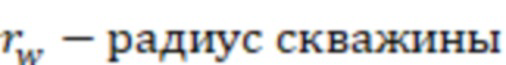 .
.
Затем моделируют трещину гидроразрыва пласта с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), определенным D-фактором. Или если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS и при моделировании дополнительно учитывают множитель коэффициента продуктивности скважины, то есть в этом случае для моделирования используют S, равным значению MinS, а также используют множитель коэффициента продуктивности скважины и D-фактор.
Рассмотрим примеры реализации способа.
Пример 1. Тип флюида добывающей/нагнетательной горизонтальной скважины 1 – жидкость, тип проводимости трещины ГРП 2 – бесконечная, расположение трещины ГРП 2 относительно добывающей горизонтальной скважины 1 – вдоль. Получают длину трещины. Например, полученная длина трещины ГРП составляет 150 метров. Строят ГДМ с геометрией ячейки: длина квадратной сетки гидродинамической модели (ГДМ) составляет 50 метров. Направление трещины ГРП 2 параллельное одной из сторон ячеек 3 гидродинамической модели (ГДМ) (фиг.1).
Определяют ячейки 3, по которым проходит траектория трещины ГРП. Таким образом, 150 метровая трещина ГРП размещается в трех ячейках по 50 метров (Х - 50, Y - 50, так как горизонтальные разрезы мнимых вертикальных скважин идентичные (постоянные), Z не учитывается) в гидродинамической модели. Определяют длины участков трещины ГРП в ячейках 3 (в трех ячейках). Длина участков трещины ГРП в каждой ячейке 3 – 50 метров. Полудлина участков трещины ГРП 2 в каждой из ячеек 3 составляет 25 метров. В каждой ячейке 3, по которым проходит траектория трещины ГРП, располагают модель вертикальной скважины. Тогда для моделирования трещины ГРП потребуется использование трех мнимых вертикальных скважин с расчетным отрицательным скин-фактором.
Рассчитывают отрицательный скин-фактор (S) для каждой модели вертикальной скважины 4. Пусть радиус мнимых вертикальных скважин 4 составляет 0.1 метра (аналог реальной скважины), тогда отрицательный скин-фактор для каждой из мнимых вертикальных скважин 4 составит:
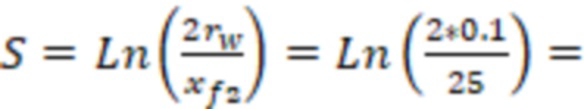 -4.83
-4.83
Далее определим радиус Писмана и допустимый минимальный скин-фактор:
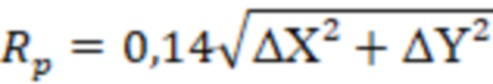 =0,14
=0,14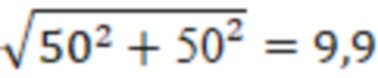
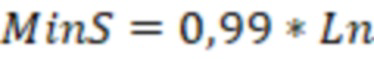 (
(
 /
/
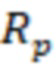 )=0,99*
)=0,99*
 (
(
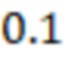 /
/
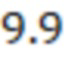 )=-4.55
)=-4.55
Так как отрицательный скин-фактор S (-4,83) меньше минимально допустимого отрицательного скин-фактора MinS для ячеек 3 гидродинамической модели (-4,55), то он не может использоваться напрямую для расчетов. Поэтому мнимым вертикальным скважинам 4 присваивается минимально допустимый отрицательный скин-фактор (-4,55) и рассчитывается дополнительно множитель продуктивности для мнимых вертикальных скважин 4. Радиус контура питания скважины (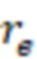 ) принимается как половина расстояния между соседними скважинами. Пусть он равен 400 метров, тогда
) принимается как половина расстояния между соседними скважинами. Пусть он равен 400 метров, тогда
Кмнож прод. = (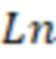 (
(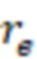 /
/ )-3/4+
)-3/4+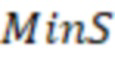 )/(
)/(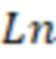 (
(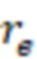 /
/ )-3/4+
)-3/4+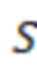 ) =
) =
= (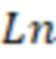 400/0,1)-3/4-4,55)/(
400/0,1)-3/4-4,55)/(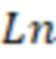 (
(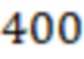 /
/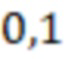 )-3/4-4,83) =
)-3/4-4,83) =
= 2,99405/2,71405 = 1,1
Моделируют трещину ГРП, например, в гидродинамическом симуляторе tNavigator (производитель – компания «Rock Flow Dynamics») с использованием моделей вертикальных скважин с учётом отрицательного скин-фактора. Таким образом, для моделирования в выбранной гидродинамической модели трещины гидроразрыва пласта 2 длиной 150 метров бесконечной проводимости, расположенной вдоль ствола горизонтальной нефтяной скважины требуется задать 3 мнимые вертикальные скважины 4 с отрицательными скин-факторами в (-4,55) и дополнительным множителем продуктивности мнимых вертикальных скважин в «1,1». Таким образом, использование мнимых вертикальных скважин в ячейках 3 с отрицательным скин-фактором (-4,55) и множителем продуктивности (1,1) существенно сократит время моделирования трещины ГРП (как на подготовку данных для моделирования, так и на проведение непосредственных гидродинамических расчетов (моделирования)) ввиду того, что ячейки, которые пересекла траектория трещины ГРП и в которых расположены мнимые вертикальные скважины имеют большую размерность (большой объем).
Пример 2. Рассмотрим еще один пример для случая, когда тип флюида добывающей/нагнетательной горизонтальной скважины – газ, тип проводимости трещины ГРП – конечная, расположение трещины ГРП относительно добывающей горизонтальной скважины – поперек. Получают значение длины трещины ГРП 2. Например, длина трещины ГРП составляет 150 метров. Сроят ГДМ пласта с ячейками заданной геометрии: длина квадратной сетки ГДМ составляет 50 метров. Направление трещины ГРП поперечное направлению горизонтальной скважине (фиг.2).
Определяют ячейки ГДМ пласта, по которым проходит траектория трещины ГРП 2. Таким образом, 150 метровая трещина ГРП также размещается в трех ячейках 3 по 50 метров в ГДМ. Определяют длины участков трещины ГРП в ячейках 3 (в трех ячейках). Длина участков трещины ГРП в каждой ячейке 3 – 50 метров. Полудлина трещины ГРП 2 в каждой из ячеек 3 составляет 25 метров. Располагают модель вертикальной скважины в каждой ячейке ГДМ пласта, по которым проходит траектория трещины ГРП. Тогда для моделирования трещины ГРП 2 потребуется использование трех мнимых вертикальных скважин 4 с расчетным отрицательным скин-фактором. Пусть для моделирования радиус мнимых вертикальных скважин 4 составляет 0,1 метра.
Так как трещина 2 по условию имеет конечную проводимость, но необходимо рассчитать безразмерную проводимость трещины ГРП (CFD). Пусть проницаемость трещины ГРП (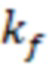 ) составляет 100 000 милиДарси, проницаемость пласта (
) составляет 100 000 милиДарси, проницаемость пласта (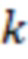 ) составляет 1 милиДарси, ширина трещины (
) составляет 1 милиДарси, ширина трещины (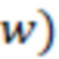 0,005 метра. Тогда безразмерная проводимость трещины составит:
0,005 метра. Тогда безразмерная проводимость трещины составит:
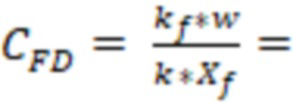
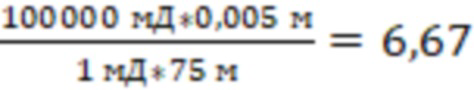
Причем 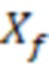 соответствует полудлине трещине ГРП (длина которой составляет 150 м).
соответствует полудлине трещине ГРП (длина которой составляет 150 м).
Далее необходимо учесть, что трещина 2 расположена поперек ствола горизонтальной скважины 1 и имеет место конвергенция линий тока в трещине 2 к стволу скважины 1. Для того, чтобы учесть конвергенцию линий тока необходимо знать высоту трещины ГРП 2 в продуктивной толще пласта (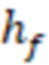 ). Примем ее равной 40 метров. Тогда в соответствии с фиг. 6 значение оси абсцисс составит:
). Примем ее равной 40 метров. Тогда в соответствии с фиг. 6 значение оси абсцисс составит:
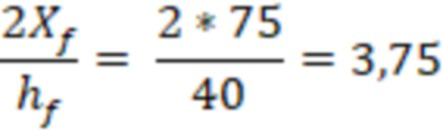
Определим значение зависимость высоты трещины ГРП к радиусу мнимой скважины:
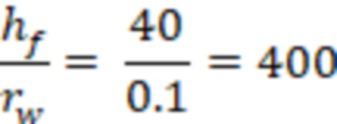
Значение 400 соответствует зависимости 8 на фиг. 6. Причем в расчете участвует полудлина трещины ГРП в 75 метров без разбивки на ячейки, так как определяется общий коэффициент понижения безразмерной проводимости трещины за счет схождения линий тока во всей области трещины ГРП 2 (Kgraf). Далее данный коэффициент понижения безразмерной проводимости трещины 2 используется в расчетах для каждой ячейки 3 гидродинамической модели, пересекаемой трещиной ГРП 2. Тогда согласно фиг. 6 (зависимость 8) К(graf) составляет 14.
В этом случае эффективная безразмерная проводимость трещины ГРП 2 составит
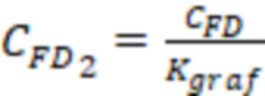 =
= 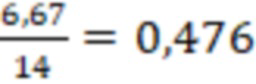
Так как трещина 2 имеет конечную проводимость, то относительный емкостной параметр равен:
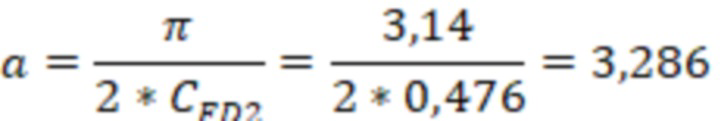
Рассчитывают отрицательней скин-фактор для каждой модели вертикальной скважины. По фиг. 5 при относительном емкостном параметре, равном 3.286, f(a) составит 0,123. Тогда расчетный отрицательный скин-фактор в каждой ячейке 3 составит:
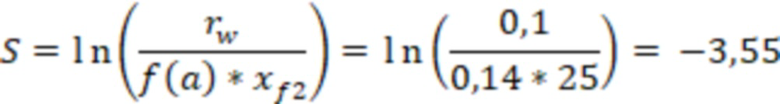
Далее определим радиус Писмана и допустимый минимальный скин-фактор:
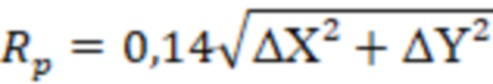 =0,14
=0,14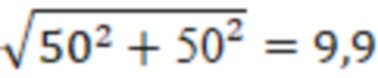
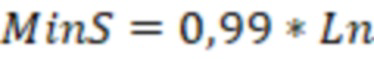 (
(
 /
/
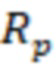 )=0,99*
)=0,99*
 (
(
 /
/
 )=-4.55
)=-4.55
Так как расчетный скин-фактор (-3,55) больше минимально допустимого отрицательного скин-фактора для ячеек гидродинамической модели (-4,55), то он может использоваться напрямую для расчетов без дополнительного множителя продуктивности.
Далее для определения D-фактора проводят серию итерационных расчетов по цепочке:
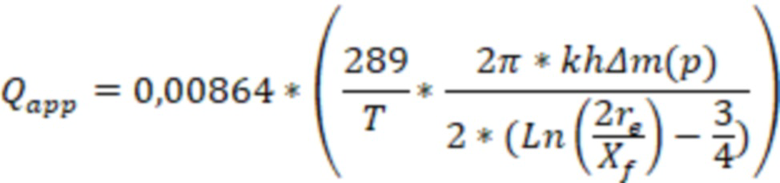
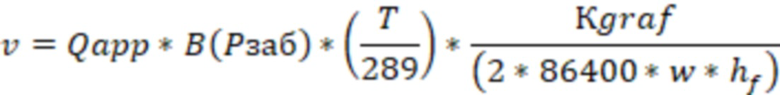
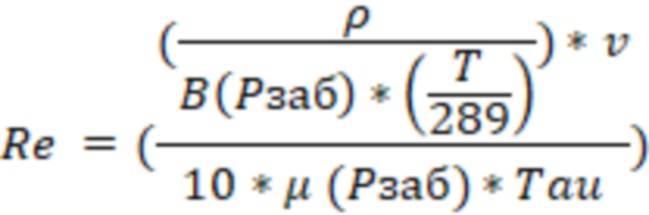
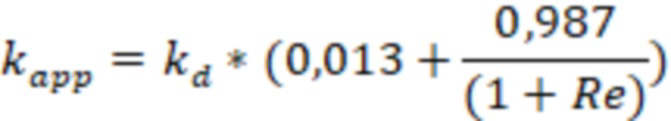
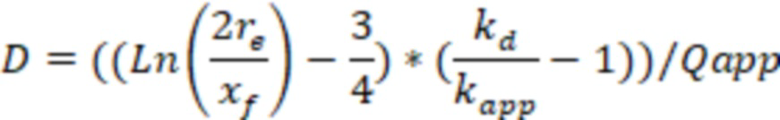
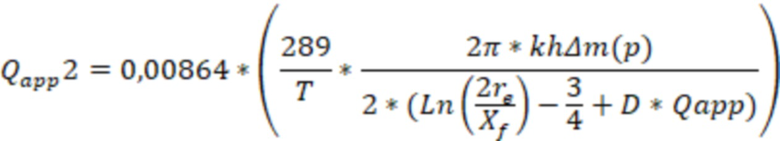
Итерацию проводят до тех пор, пока разница между расчетным дебитом на последнем этапе и предыдущем не будет менее 1%. В моделирование принимается последний расчетный D-фактор.
Примем, что проницаемость трещины ГРП равна также 100 000 милиДарси, тогда функция проницаемости трещины (Tau) равна 15 (фиг. 7, зависимость 12).
Для итеративных расчетов примем следующие параметры:
- радиус мнимой вертикальной скважины 0,1 метра (rw);
- полная полудлина трещины ГРП 75 метров (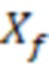 );
);
- ширина трещины 0,005 метров (w);
- проницаемость трещины (проппанта) 100 000 милиДарси (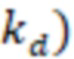 ;
;
- проницаемость пласта 1 милиДарси (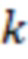 );
);
- высота трещины в пласте 40 метров (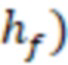 ;
;
- температура пласта 90 градусов Цельсия (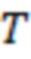 );
);
- плотность газа 0,9 кг/м3 ( );
);
- пластовое давление 350 атм (Рпласт);
- забойное давление 300 атм (Pзаб);
- радиус контура питания 400 метров (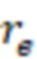 );
);
- объемный коэффициент газа при забойном давлении 0,00406 м3/м3 (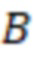 );
);
- вязкость газа при забойном давлении 0,02352 сантиПуаз (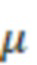 ).
).
Также было рассчитано псевдодавление 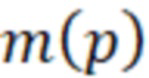 при забойном (Pзаб) и пластовом (Рпласт)давлениях по формуле:
при забойном (Pзаб) и пластовом (Рпласт)давлениях по формуле:
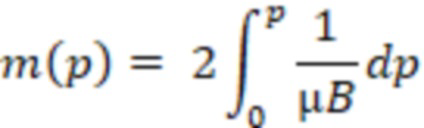
Результаты приведены в таблице 1.
Таблица 1
 ), сП
), сП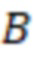 ), м3/м3
), м3/м3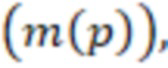 атм/сП *м/м3
атм/сП *м/м3
Таким образом, 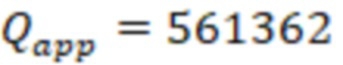 м3/сут, который определили по формуле:
м3/сут, который определили по формуле:
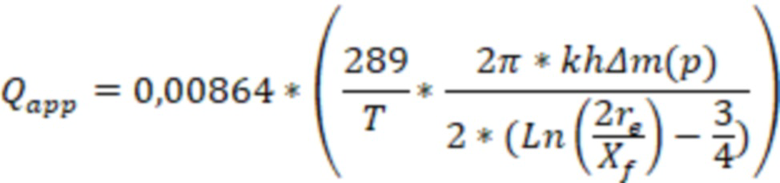
Так как расчеты по определению D-фактора имеют большой массив, то их выполнение было автоматизировано в специальном программном продукте Smart Frac Test 2.0 (регистрационный номер свидетельства о государственной регистрации программы для ЭВМ №2019665566), часть выгрузки результатов из которого приведена ниже:
Итерация №1:
Значение функции (Tau) на 1-й итерации = 15 1/см (см-1)
Скорость фильтрации газа (поперек) на 1-й итерации (v) = 1,15 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 1-й итерации (Re) = 57,93
Проницаемость трещины с учетом инерциальных потерь на 1-й итерации(kapp) = 2974,90мД
D-фактор на 1-й итерации (D) = 9,31сут/м3
Скин-фактор за счёт инерционных потерь (DQapp= Sин) = 52,7417
Дебит газа (Qapp) = 16840,86 м3/сут
ΔQapp =100% - ( 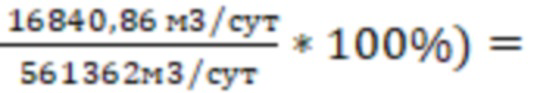 97%
97%
Итерация №2:
Значение функции (Tau) на 2-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 2-й итерации (v) = 0,034 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 2-й итерации (Re) = 1,7233
Проницаемость трещины с учетом инерциальных потерь на 2-й итерации(kapp) = 37542,47 мД
D-фактор на 2-й итерации (D) = 0,00016 сут/м3
Скин-фактор за счёт инерционных потерь (DQapp = Sин) = 2,69
Дебит газа (Qapp) = 212527,00 м3/сут
Δ Qapp = 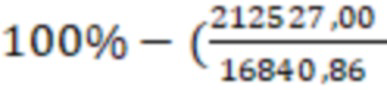 *100%)=1162%
*100%)=1162%
Итерация №3:
Значение функции (Tau) на 3-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 3-й итерации (v) = 0,43 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 3-й итерации (Re) = 21,75
Проницаемость трещины с учетом инерциальных потерь на 2-й итерации(kapp) = 5638,87 мД
D-фактор на 3-й итерации (D) = 0,00012 сут/м3
Скин за счёт инерционных потерь (DQapp = Sин) = 27,061
Дебит газа (Qapp) = 31921,49 м3/сут
ΔQapp = 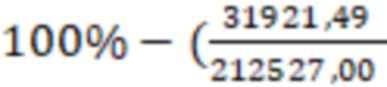 *100%)=85%
*100%)=85%
Итерация №23:
Значение функции (Tau) на 23-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 23-й итерации (v) = 0,15 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 23-й итерации (Re) = 7,561
Проницаемость трещины с учетом инерциальных потерь на 23-й итерации(kapp) = 12828,97 мД
D-фактор на 23-й итерации (D) = 0,00015 сут/м3
Скин-фактор за счёт инерционных потерь (DQapp= Sин) = 10,9881
Дебит газа (Qapp) = 72624,47 м3/сут
ΔQapp = 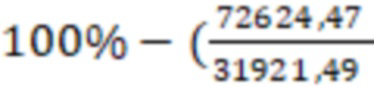 *100%) = 127,5%
*100%) = 127,5%
Итерация №24:
Значение функции (Tau) на 24-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 24-й итерации (v) = 0,15 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 24-й итерации (Re) = 7,43
Проницаемость трещины с учетом инерциальных потерь на 24-й итерации(kapp) = 13005,88 мД
D-фактор на 24-й итерации (D) = 0,00015 сут/м3
Скин-фактор за счёт инерционных потерь (DQapp= Sин) = 10,81
Дебит газа (Qapp) = 73626,008 м3/сут
ΔQapp =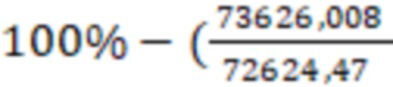 *100%) = 1,4%
*100%) = 1,4%
Итерация №25:
Значение функции (Tau) на 25-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 25-й итерации (v) = 0,15 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 25-й итерации (Re) = 7,53
Проницаемость трещины с учетом инерциальных потерь на 25-й итерации(kapp) = 12865,31 мД
D-фактор на 25-й итерации (D) = 0,00015 сут/м3
Скин-фактор за счёт инерционных потерь (DQapp= Sин) = 10,95
Дебит газа (Qapp) = 72830,20 м3/сут
Δ Qapp = 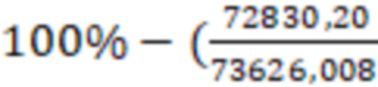 *100%) = 1,1%
*100%) = 1,1%
Итерация №26:
Значение функции (Tau) на 26-й итерации = 15 1/см
Скорость фильтрации газа (поперек) на 26-й итерации = 0,15 м/с
Значение Δm(p) = 4257217,71 – 3139954,26 = 1117263,45
Число Рейнольдса на 26-й итерации (Re) = 7,45
Проницаемость трещины с учетом инерциальных потерь на 26-й итерации(kapp) = 12976,73 мД
D-фактор на 26-й итерации (D)= 0,0001489 сут/м3
Скин-фактор за счёт инерционных потерь = 10,84
Дебит газа Qapp = 73460,96 м3/сут
ΔQapp = 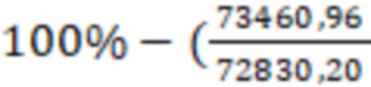 *100%) = 0,9%
*100%) = 0,9%
Понадобилось 26 итераций, чтобы определить D-фактор на уровне 0,0001489 сут/м3.
Моделируют трещину ГРП, например, в гидродинамическом симуляторе tNavigator (производитель – компания «Rock Flow Dynamics»). В итоге для моделирования в гидродинамической модели поперечной трещины ГРП 2 конечной проводимости длиною в 150 метров для горизонтальной газовой скважины 1 требуется задать три мнимые вертикальные скважины 4 с отрицательными скин-факторами, равными -3,55, и D-фактором, равным 0,0001489 сут/м3.
Таким образом, использование мнимых вертикальных скважин в ячейках 3 с отрицательными скин-факторами (-3,55) и D-фактором (0,0001489) существенно сократит время моделирования трещины ГРП (как на подготовку данных для моделирования, так и на проведение непосредственных гидродинамических расчетов (моделирования)) ввиду того, что ячейки, которые пересекла траектория трещины ГРП и в которых расположены мнимые вертикальные скважины имеют большую размерность (большой объем), А также данный способ учитывает конвергенцию (схождение) линий тока при конечной проводимости трещины ГРП, что позволяет учитывать дополнительные потери давления, благодаря чему повышается точность моделирования трещины ГРП. Также учитывается D-фактор, который позволяет учесть инерциальные потери давления в трещине ГРП при движении газа на высоких скоростях в трещине, что также влияет на точность моделирования ГРП.
Таким образом, вышеописанный способ универсален для всевозможных вариантов ГРП в зависимости от типа флюида (нефть или газ), типа проводимости трещины ГРП (бесконечная или конечная), а также расположение трещины относительно горизонтального ствола скважины (вдоль или поперек).
Реализация систем и машиночитаемых носителей осуществляется аналогично способам, описанным выше. Получение значения длины трещины ГРП 2 и данные о ее расположении могут быть определены, как заранее измеренные фактические значения, или как вывод проектных значений из базы данных.
Таким образом, с помощью применения заявленного изобретения достигается повышение точности моделирования эффекта применения одностадийного и многостадийного гидроразрыва пласта при разработке низкопроницаемых коллекторов горизонтальными скважинами с гидроразрывом пласта, уменьшение времени моделирования трещины ГРП.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ исследования горизонтальных скважин с многостадийным гидравлическим разрывом пласта в низкопроницаемых коллекторах | 2019 |
|
RU2734202C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБЫ ПРОГНОЗИРОВАНИЯ РИСКОВ ГИДРОРАЗРЫВА ПЛАСТА | 2017 |
|
RU2730576C1 |
| СПОСОБ ВЫВОДА НА РЕЖИМ СКВАЖИНЫ, ПРОБУРЕННОЙ В ЕСТЕСТВЕННО ТРЕЩИНОВАТОМ ПЛАСТЕ | 2019 |
|
RU2717019C1 |
| СПОСОБ ВЫБОРА СИСТЕМЫ РАЗРАБОТКИ МЕСТОРОЖДЕНИЯ | 2018 |
|
RU2692369C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДРЕНИРУЕМОЙ ШИРИНЫ ТРЕЩИНЫ ГИДРОРАЗРЫВА И СТЕПЕНИ ОСЕДАНИЯ ПРОППАНТА В НЕЙ | 2015 |
|
RU2585296C1 |
| СПОСОБ ОПТИМИЗАЦИИ ДОБЫЧИ ПЛАСТОВОГО ФЛЮИДА ИЗ СКВАЖИНЫ ПОСЛЕ КИСЛОТНОГО ГИДРОРАЗРЫВА ПЛАСТА | 2020 |
|
RU2759621C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЛЬТРАЦИОННЫХ СВОЙСТВ СОВМЕСТНО РАБОТАЮЩИХ ПЛАСТОВ (ВАРИАНТЫ) | 2011 |
|
RU2476670C1 |
| Способ определения геометрии трещин ГРП с учетом разделения и взаимодействия потоков жидкости ГРП между трещинами | 2022 |
|
RU2786303C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОФИЛЯ ПРИТОКА И ПАРАМЕТРОВ ОКОЛОСКВАЖИННОГО ПРОСТРАНСТВА В МНОГОПЛАСТОВОЙ СКВАЖИНЕ | 2009 |
|
RU2505672C1 |
| СПОСОБ ОСУЩЕСТВЛЕНИЯ ГИДРАВЛИЧЕСКОГО РАЗРЫВА ПЛАСТА И ВЫВОДА СКВАЖИНЫ НА РЕЖИМ | 2022 |
|
RU2798193C1 |
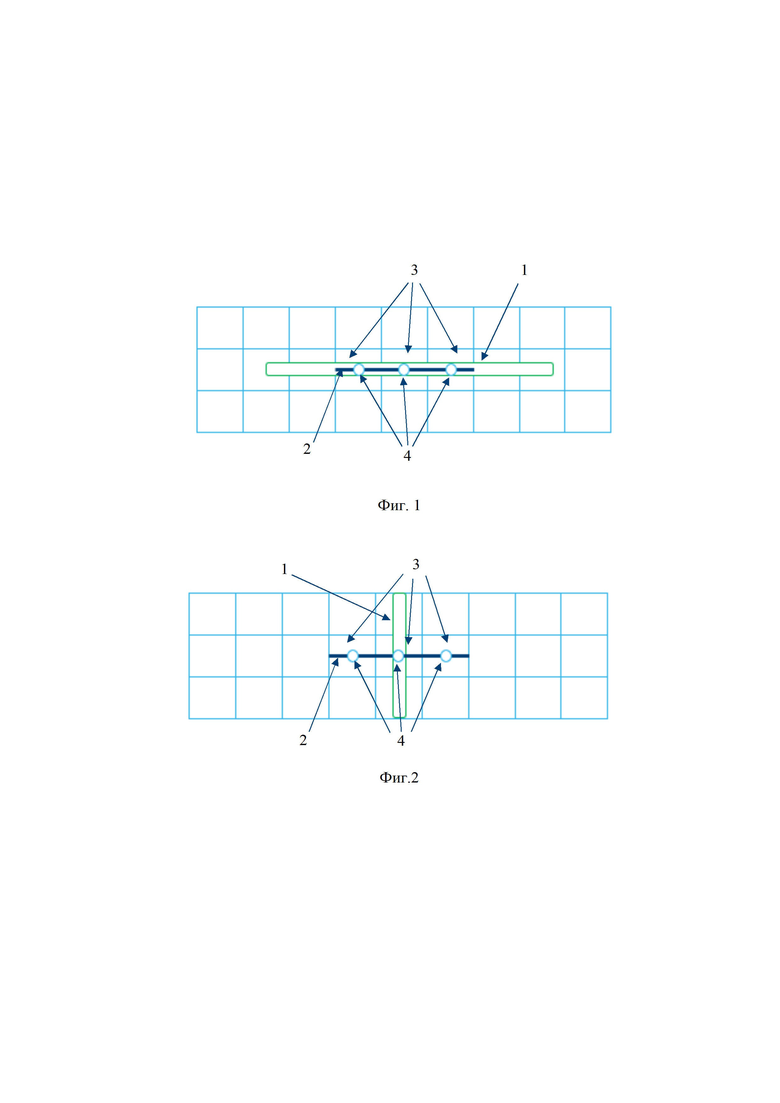
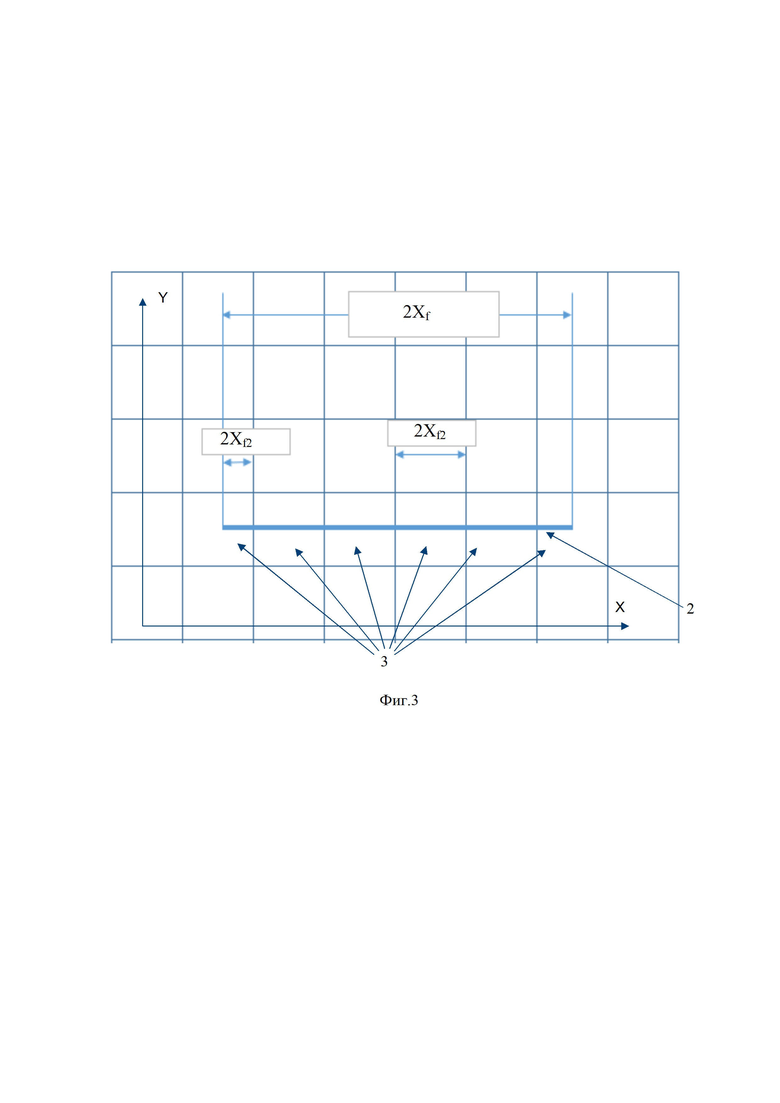
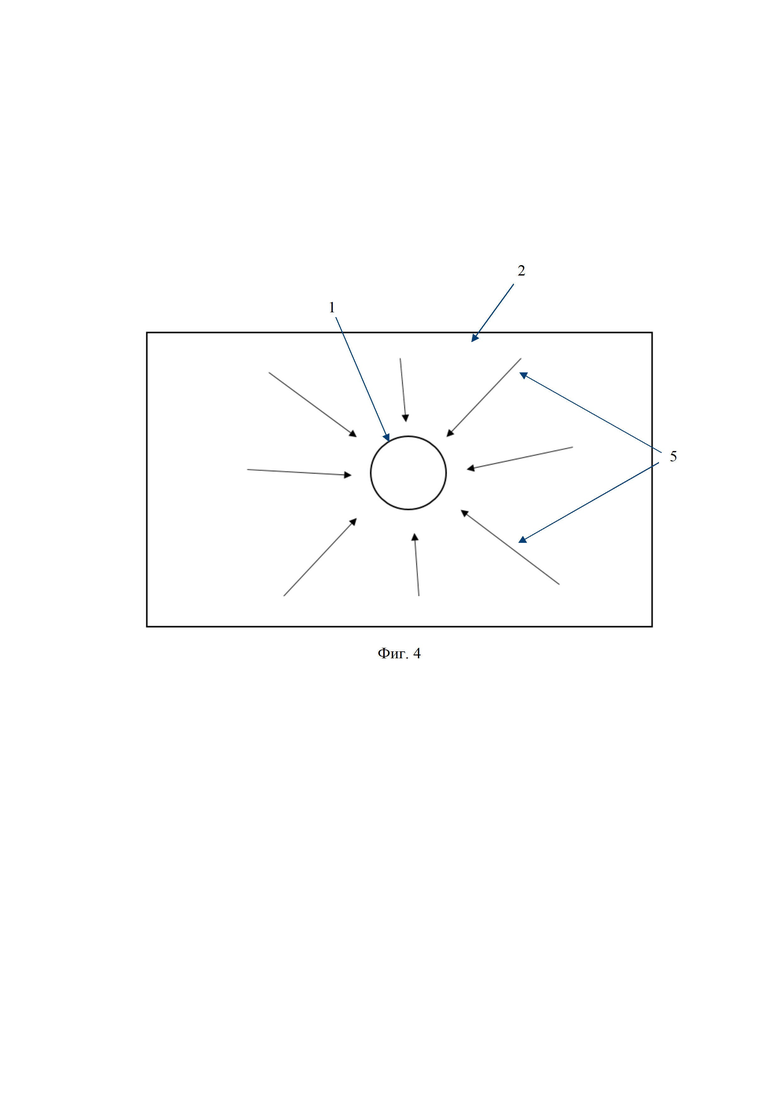
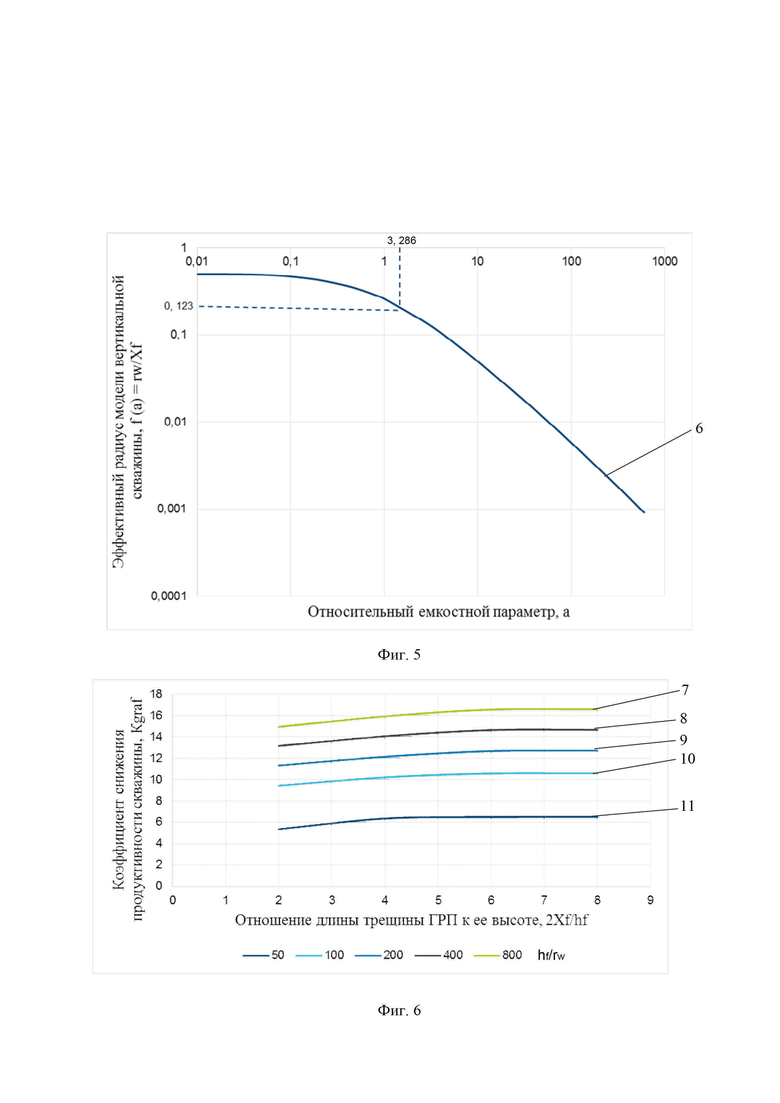
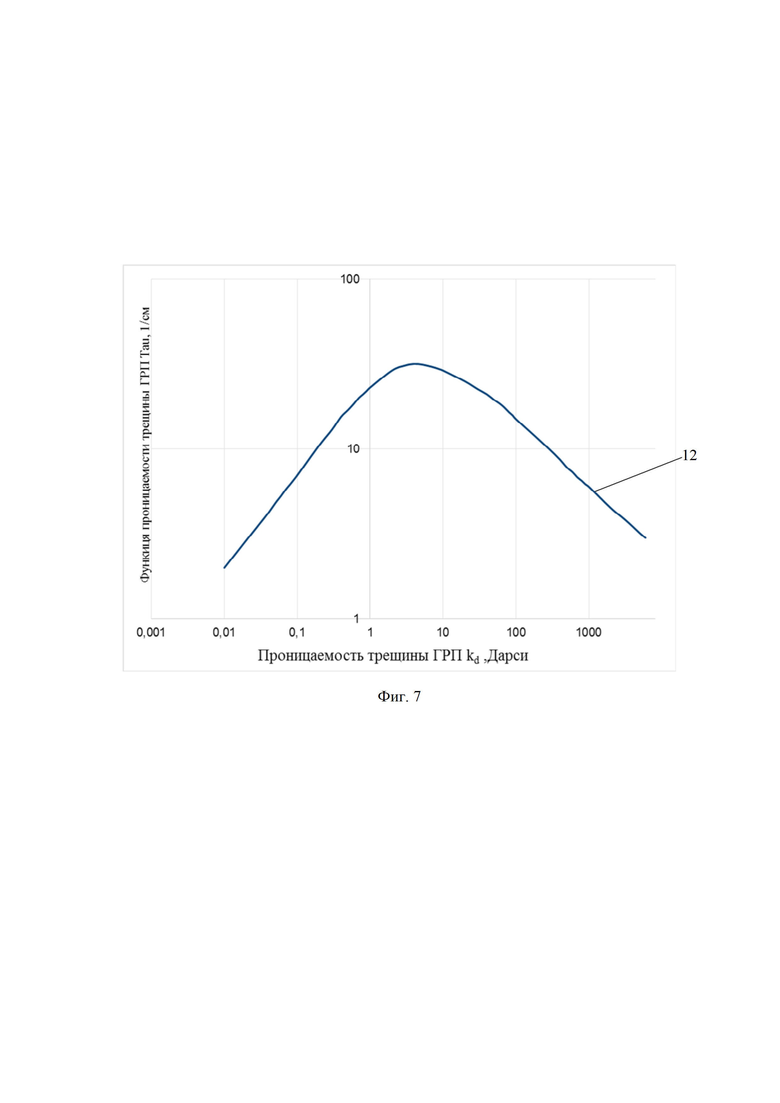
Изобретение относится к нефтегазодобывающей области, операциям гидравлического разрыва (гидроразрыва) пласта, в частности к моделированию трещин гидроразрыва пласта относительно горизонтального ствола скважины. Согласно способу моделирования трещин гидроразрыва пласта получают значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины. Строят гидродинамическую модель пласта с использованием ячеек заданной геометрии. Определяют ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП. Определяют длины участков трещины ГРП в ячейках гидродинамической модели пласта. В каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта. Для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках; моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора. Технический результат - повышение точности моделирования эффекта применения одностадийного и многостадийного гидроразрыва пласта (трещина ГРП) при разработке коллекторов нефти и газа горизонтальными скважинами с гидроразрывом пласта, уменьшение времени моделирования трещины ГРП, а также универсальность применения способа для моделирования трещин ГРП различного типа проводимости (например, конечный/бесконечный), трещин ГРП, которые могут иметь разное расположение относительно горизонтального ствола скважины (например, поперек/вдоль), также для скважин с различными типами флюида скважины (газ и нефть). 3 н. и 57 з.п. ф-лы, 7 ил., 1 табл.
1. Способ моделирования трещин гидроразрыва пласта, при котором
- получают значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины;
- строят гидродинамическую модель пласта с использованием ячеек заданной геометрии;
- определяют ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определяют длины участков трещины ГРП в ячейках гидродинамической модели пласта;
- в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагают модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта;
- для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках;
- моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
2. Способ моделирования трещин гидроразрыва пласта по п. 1, при котором после расчета отрицательного скин-фактора (S) для каждой модели вертикальной скважины дополнительно рассчитывают минимальный отрицательный скин-фактор (MinS) и затем моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), при этом если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS, и при моделировании трещины ГРП дополнительно учитывают множитель коэффициента продуктивности горизонтальной скважины.
3. Способ моделирования трещин гидроразрыва пласта по п. 1, при котором, в случае газового типа флюида горизонтальной скважины, дополнительно определяют D-фактор (динамический скин-фактор), который учитывают при моделировании трещины ГРП.
4. Способ моделирования трещин гидроразрыва пласта по п.1, при котором, в случае бесконечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по формуле:
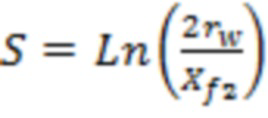 , где
, где
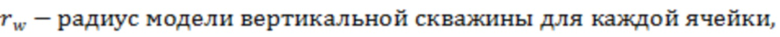
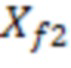 - полудлина участка трещины ГРП.
- полудлина участка трещины ГРП.
5. Способ моделирования трещин гидроразрыва пласта по п. 1, при котором, в случае конечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по формуле:
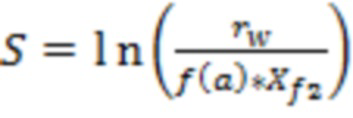 , где
, где
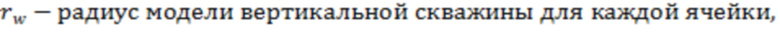
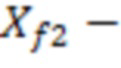 полудлина участка трещины ГРП,
полудлина участка трещины ГРП,
f(a) - зависимость эффективного радиуса модели вертикальной скважины для каждой ячейки от относительного емкостного параметра.
6. Способ моделирования трещин гидроразрыва пласта по п. 5 при котором дополнительно определяют относительный емкостной параметр по формуле:
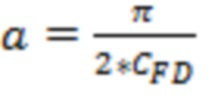 , где
, где
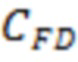 - безразмерная проводимость трещины ГРП.
- безразмерная проводимость трещины ГРП.
7. Способ моделирования трещин гидроразрыва пласта по п. 6, при котором безразмерную проводимость трещины ГРП определяют по формуле:
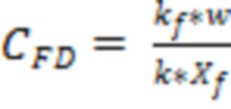 , где
, где
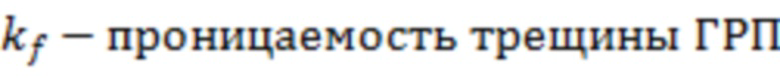 ,
,
 ,
,
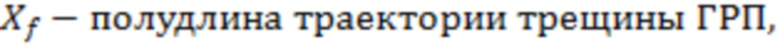
 .
.
8. Способ моделирования трещин гидроразрыва пласта по п. 1, при котором, в случае прохождения траектории трещины ГРП поперек ствола горизонтальной скважины и конечного типа проводимости трещины ГРП, дополнительно определяют эффективную безразмерную проводимость трещины ГРП 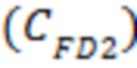 с учетом схождения (конвергенции) линий тока в трещине ГРП, которую учитывают при расчете отрицательного скин-фактора (S).
с учетом схождения (конвергенции) линий тока в трещине ГРП, которую учитывают при расчете отрицательного скин-фактора (S).
9. Способ моделирования трещин гидроразрыва пласта по п. 8, при котором эффективную безразмерную проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине ГРП определяют по формуле:
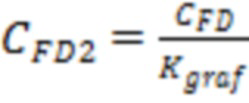 , где
, где
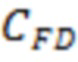 - безразмерная проводимость трещины ГРП,
- безразмерная проводимость трещины ГРП,
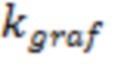 - коэффициент снижения продуктивности скважины.
- коэффициент снижения продуктивности скважины.
10. Способ моделирования трещин гидроразрыва пласта по п. 3, при котором D-фактор для газового типа флюида горизонтальной скважины определяют по формуле:
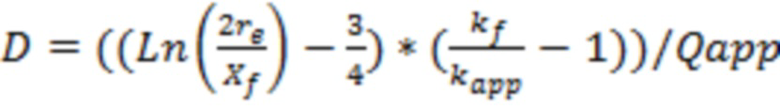 , где
, где
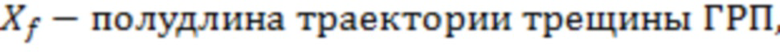
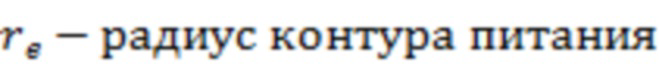 ,
,
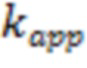 - проницаемость трещины ГРП с учетом инерциальных потерь,
- проницаемость трещины ГРП с учетом инерциальных потерь,
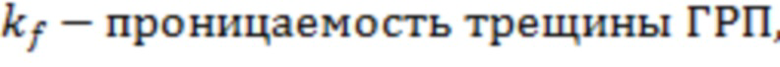
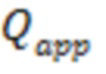 - дебит газа.
- дебит газа.
11. Способ моделирования трещин гидроразрыва пласта по п. 10, при котором определяют проницаемость трещины ГРП с учетом инерциальных потерь по формуле:
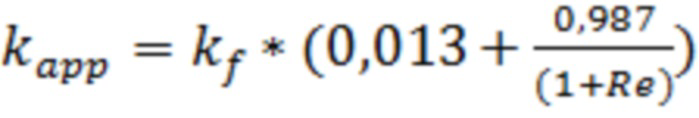 , где
, где
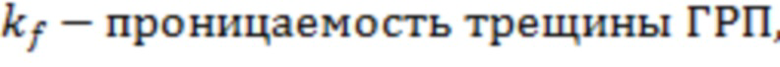
Re - число Рейнольдса.
12. Способ моделирования трещин гидроразрыва пласта по п. 11, при котором определяют число Рейнольдса по формуле:
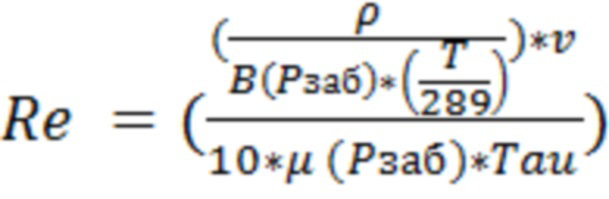 , где
, где

B - объемный коэффициент газа 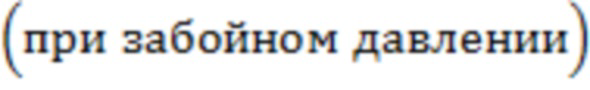 ,
,
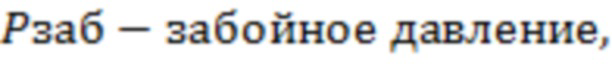

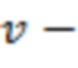 скорость фильтрации газа в трещине ГРП,
скорость фильтрации газа в трещине ГРП,
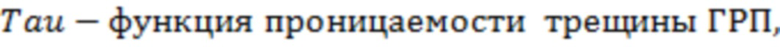
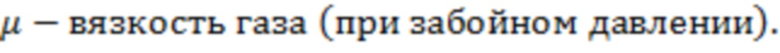
13. Способ моделирования трещин гидроразрыва пласта по п. 12, при котором скорость фильтрации газа в трещине ГРП, траектория которой проходит поперек ствола горизонтальной скважины, определяют по формуле:
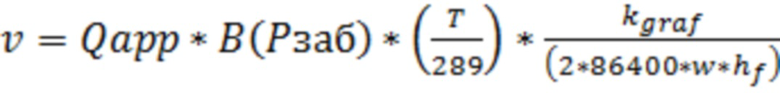 , где
, где
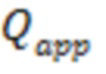 - дебит газа,
- дебит газа,
B - объемный коэффициент газа 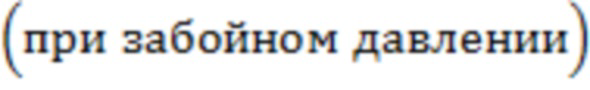 ,
,
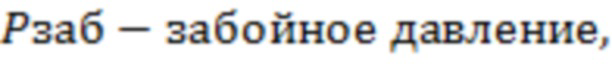

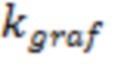 - коэффициент снижения продуктивности скважины,
- коэффициент снижения продуктивности скважины,
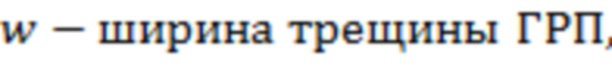
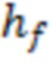 - высота трещины ГРП.
- высота трещины ГРП.
14. Способ моделирования трещин гидроразрыва пласта по пп. 9 и 13, при котором определяют коэффициент снижения продуктивности скважины с использованием значений отношения длины траектории трещины ГРП к ее высоте.
15. Способ моделирования трещин гидроразрыва пласта по п. 12, при котором скорость фильтрации газа в трещине ГРП, траектория которой проходит вдоль ствола газовой горизонтальной скважины, определяют по формуле:
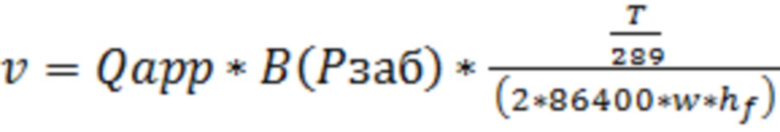 , где
, где
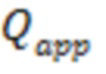 - дебит газа,
- дебит газа,
B - объемный коэффициент газа 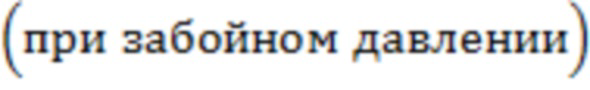 ,
,

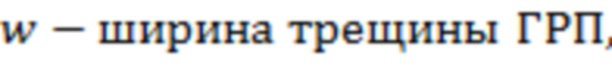
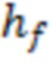 - высота трещины ГРП.
- высота трещины ГРП.
16. Способ моделирования трещин гидроразрыва пласта по любому из пп. 10, 13, 15, при котором дебит газа определяют по формуле:
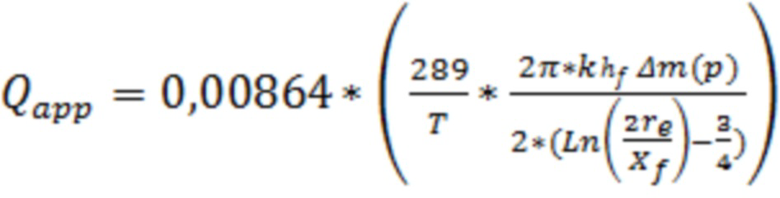 , где
, где

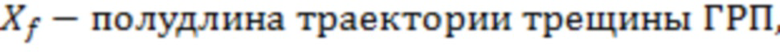
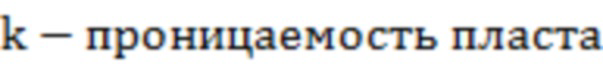 ,
,
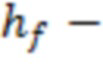 высота трещины ГРП,
высота трещины ГРП,
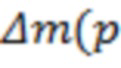 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
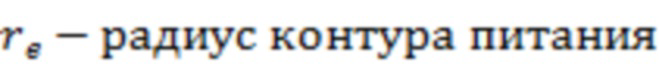 .
.
17. Способ моделирования трещин гидроразрыва пласта по п. 16, при котором дополнительно пересчитывают дебит газа до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от дебита газа на последнем шаге пересчета менее чем на 1%, при этом дебит газа пересчитывают по формуле:
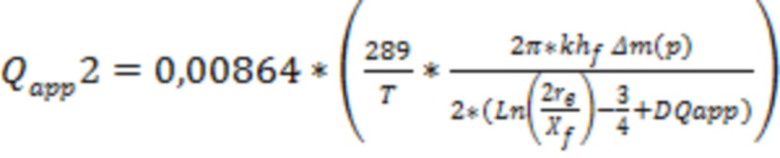 , где
, где
DQapp=Sин - скин-фактор за счет инерциальных потерь движения газа в трещине ГРП,

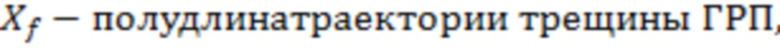
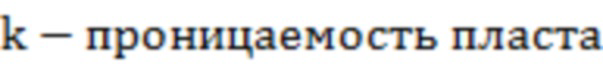 ,
,
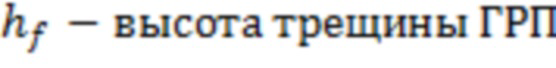 ,
,
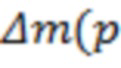 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
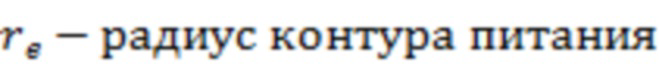 ,
,
при этом по каждому полученному значению дебита газа пересчитывают D-фактор, последнее значение которого учитывают при моделировании трещины ГРП.
18. Способ моделирования трещин гидроразрыва пласта по п. 2, при котором минимальный отрицательный скин-фактор (MinS) определяют по формуле:
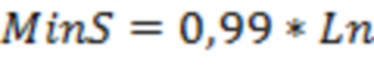 (
(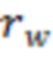 /
/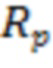 ), где
), где
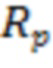 - радиус Писмана,
- радиус Писмана,
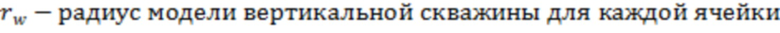 .
.
19. Способ моделирования трещин гидроразрыва пласта по п. 18, при котором радиус Писмана определяют по формуле:
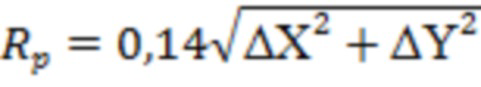 , где
, где
ΔX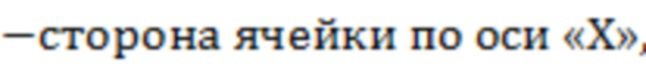
ΔY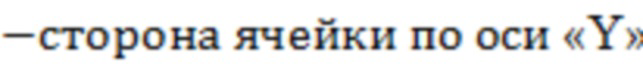 .
.
20. Способ моделирования трещин гидроразрыва пласта по п. 2, при котором множитель коэффициента продуктивности горизонтальной скважины определяют по формуле:
Кмнож. прод = ( (
(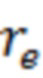 /
/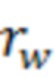 )-3/4+
)-3/4+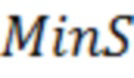 )/(
)/( (
(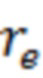 /
/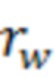 )-3/4+
)-3/4+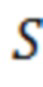 ), где
), где

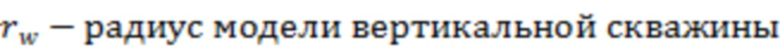 для каждой ячейки,
для каждой ячейки,
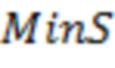 - минимальный отрицательный скин-фактор (MinS),
- минимальный отрицательный скин-фактор (MinS),
 отрицательный скин-фактор.
отрицательный скин-фактор.
21. Система моделирования трещин гидроразрыва пласта, содержащая по меньшей мере один процессор, который выполняет следующие этапы:
- получает значение длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данные о расположении этой трещины;
- строит гидродинамическую модель пласта с использованием ячеек заданной геометрии;
- определяет ячейки гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определяет длины участков трещины ГРП в ячейках гидродинамической модели пласта;
- в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП, располагает модель вертикальной скважины, выполненную с возможностью симуляции трещины гидроразрыва пласта;
- для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывает отрицательный скин-фактор (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках;
- моделирует трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
22. Система моделирования трещин гидроразрыва пласта по п. 21, при которой после расчета отрицательного скин-фактора (S) для каждой модели вертикальной скважины дополнительно рассчитывается минимальный отрицательный скин-фактор (MinS) и затем моделирует трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), при этом если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимается равным MinS, и при моделировании трещины ГРП дополнительно учитывается множитель коэффициента продуктивности горизонтальной скважины.
23. Система моделирования трещин гидроразрыва пласта по п. 21, при которой, в случае газового типа флюида горизонтальной скважины, дополнительно определяется D-фактор (динамический скин-фактор), который учитывается при моделировании трещины ГРП.
24. Система моделирования трещин гидроразрыва пласта по п. 21, при которой, в случае бесконечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывается отрицательный скин-фактор (S) по формуле:
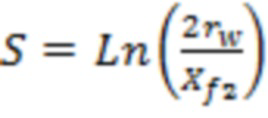 , где
, где
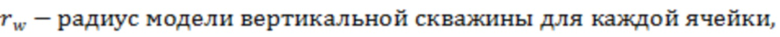
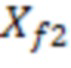 - полудлина участка трещины ГРП.
- полудлина участка трещины ГРП.
25. Система моделирования трещин гидроразрыва пласта по п. 21, при которой, в случае конечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывается отрицательный скин-фактор (S) по формуле:
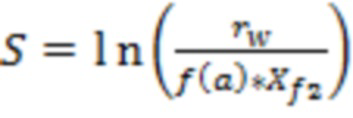 , где
, где
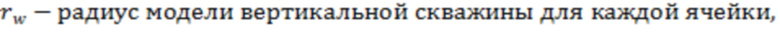
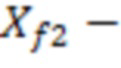 полудлина участка трещины ГРП,
полудлина участка трещины ГРП,
f(a) - зависимость эффективного радиуса модели вертикальной скважины для каждой ячейки от относительного емкостного параметра.
26. Система моделирования трещин гидроразрыва пласта по п. 25, при которой дополнительно определяется относительный емкостной параметр по формуле:
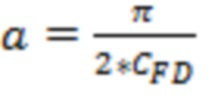 , где
, где
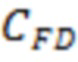 - безразмерная проводимость трещины ГРП.
- безразмерная проводимость трещины ГРП.
27. Система моделирования трещин гидроразрыва пласта по п. 26, при которой безразмерная проводимость трещины гидроразрыва пласта определяется по формуле:
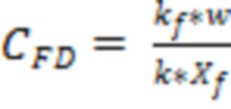 , где
, где
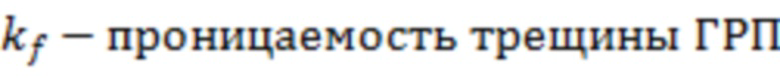 ,
,
 ,
,
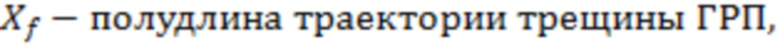
 .
.
28. Система моделирования трещин гидроразрыва пласта по п. 21, при которой, в случае конечного типа проводимости трещины ГРП, дополнительно определяется эффективная безразмерная проводимость трещины ГРП 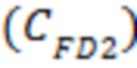 с учетом схождения (конвергенции) линий тока в трещине ГРП, которая учитывается при расчете отрицательного скин-фактора (S).
с учетом схождения (конвергенции) линий тока в трещине ГРП, которая учитывается при расчете отрицательного скин-фактора (S).
29. Система моделирования трещин гидроразрыва пласта по п. 28, при которой эффективная безразмерная проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине ГРП определяется по формуле:
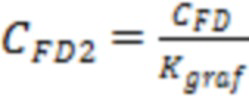 , где
, где
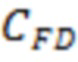 - безразмерная проводимость трещины ГРП,
- безразмерная проводимость трещины ГРП,
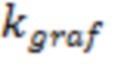 - коэффициент снижения продуктивности скважины.
- коэффициент снижения продуктивности скважины.
30. Система моделирования трещин гидроразрыва пласта по п. 23, при которой D-фактор для газового типа флюида горизонтальной скважины определяется по формуле:
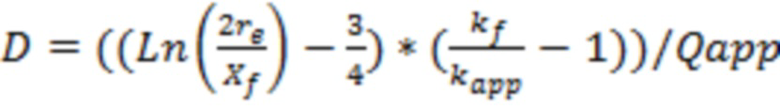 , где
, где
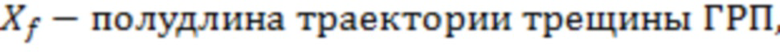
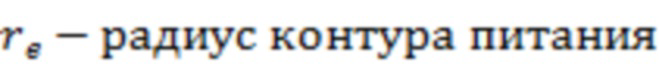 ,
,
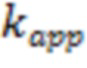 - проницаемость трещины ГРП с учетом инерциальных потерь,
- проницаемость трещины ГРП с учетом инерциальных потерь,
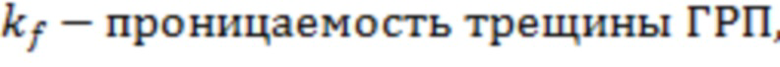
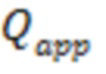 - дебит газа.
- дебит газа.
31. Система моделирования трещин гидроразрыва пласта по п. 30, при которой определяется проницаемость трещины ГРП с учетом инерциальных потерь по формуле:
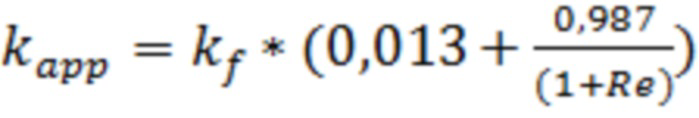 , где
, где
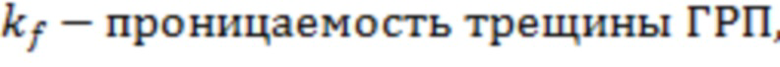
Re - число Рейнольдса.
32. Система моделирования трещин гидроразрыва пласта по п. 31, при которой определяется число Рейнольдса по формуле:
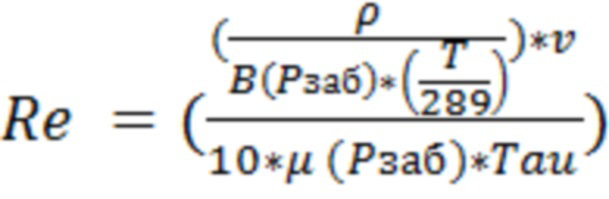 , где
, где

B - объемный коэффициент газа 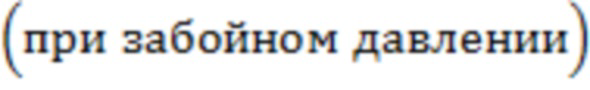 ,
,
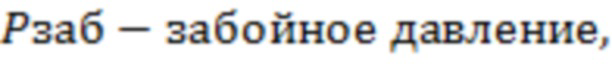

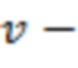 скорость фильтрации газа в трещине ГРП,
скорость фильтрации газа в трещине ГРП,
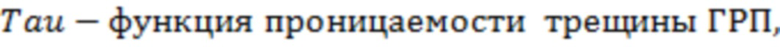
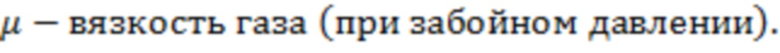
33. Система моделирования трещин гидроразрыва пласта по п. 32, при которой скорость фильтрации газа в трещине ГРП, траектория которой проходит поперек ствола горизонтальной скважины, определяется по формуле:
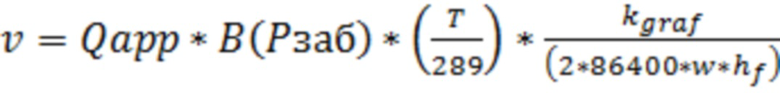 , где
, где
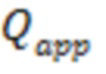 - дебит газа,
- дебит газа,
B - объемный коэффициент газа 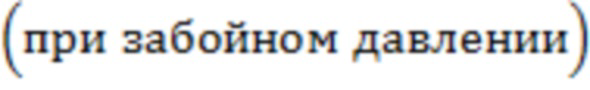 ,
,
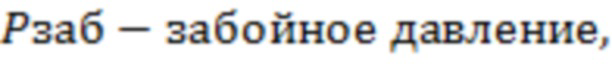

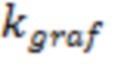 - коэффициент снижения продуктивности скважины,
- коэффициент снижения продуктивности скважины,
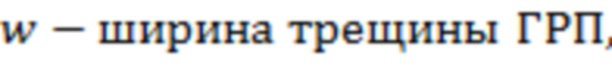
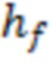 - высота трещины ГРП.
- высота трещины ГРП.
34. Система моделирования трещин гидроразрыва пласта по пп. 29 и 33, при которой определяется коэффициент снижения продуктивности скважины с использованием значений отношения длины траектории трещины ГРП к ее высоте.
35. Система моделирования трещин гидроразрыва пласта по п. 32, при которой скорость фильтрации газа в трещине ГРП, траектория которой проходит вдоль ствола газовой горизонтальной скважины, определяется по формуле:
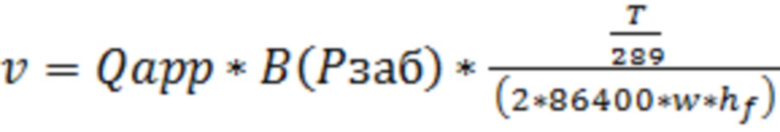 , где
, где
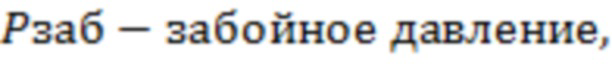
B - объемный коэффициент газа 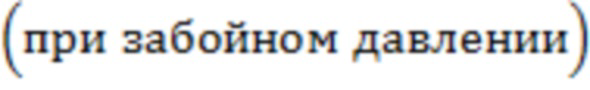 ,
,
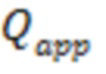 - дебит газа,
- дебит газа,

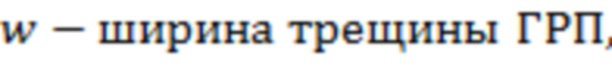
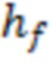 - высота трещины ГРП.
- высота трещины ГРП.
36. Система моделирования трещин гидроразрыва пласта по любому из пп. 30, 33, 35, при которой дебит газа определяется по формуле:
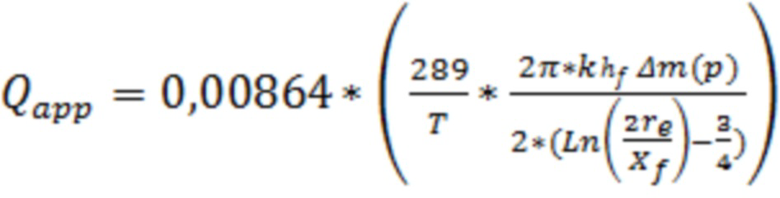 , где
, где

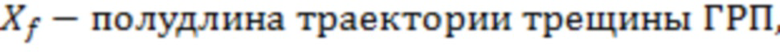
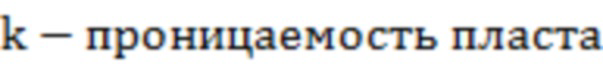 ,
,
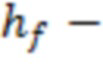 высота трещины ГРП,
высота трещины ГРП,
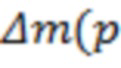 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
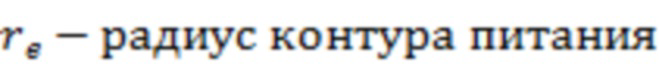 .
.
37. Система моделирования трещин гидроразрыва пласта по п. 36, при которой пересчитывается дебит газа до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от дебита газа на последнем шаге пересчета менее чем на 1%, при этом дебит газа пересчитывают по формуле:
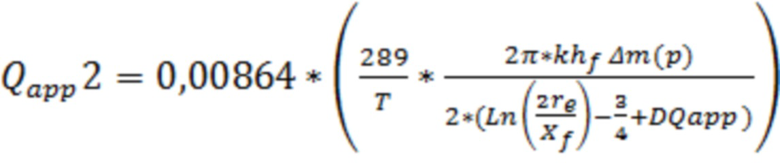 , где
, где
DQapp=Sин - скин-фактор за счет инерциальных потерь движения газа в трещине ГРП,

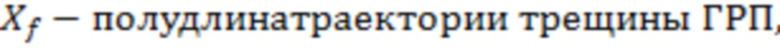
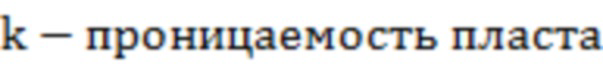 ,
,
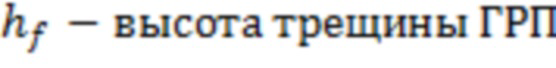 ,
,
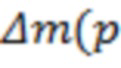 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
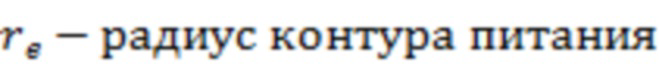 ,
,
при этом по каждому полученному значению дебита газа пересчитывается D-фактор, последнее значение которого учитывает при моделировании трещины ГРП.
38. Система моделирования трещин гидроразрыва пласта по п. 22, при которой минимальный отрицательный скин-фактор (MinS) определяется по формуле:
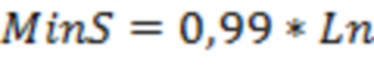 (
(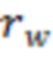 /
/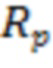 ), где
), где
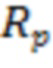 - радиус Писмана,
- радиус Писмана,
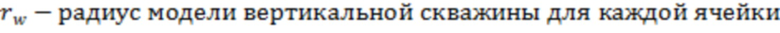 .
.
39. Система моделирования трещин гидроразрыва пласта по п. 38, при которой радиус Писмана определяется по формуле:
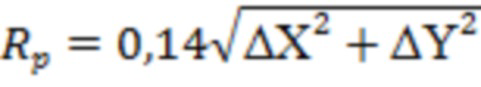 , где
, где
ΔX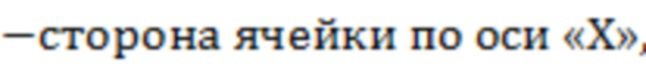
ΔY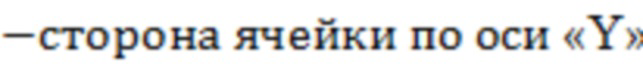 .
.
40. Система моделирования трещин гидроразрыва пласта по п. 22, при которой множитель коэффициента продуктивности горизонтальной скважины определяется по формуле:
Кмнож. прод = ( (
(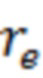 /
/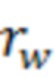 )-3/4+
)-3/4+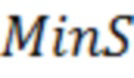 )/(
)/( (
(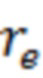 /
/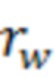 )-3/4+
)-3/4+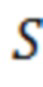 ), где
), где

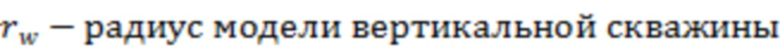 для каждой ячейки,
для каждой ячейки,
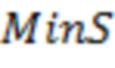 - минимальный отрицательный скин-фактор (MinS),
- минимальный отрицательный скин-фактор (MinS),
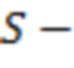 отрицательный скин-фактор.
отрицательный скин-фактор.
41. Машиночитаемый носитель, содержащий компьютерную программу, при исполнении которой на компьютере процессор выполняет следующие операции:
- получение значения длины трещины гидроразрыва пласта (ГРП), пересекающей горизонтальную скважину, и данных о расположении этой трещины;
- построение гидродинамической модели пласта с использованием ячеек заданной геометрии;
- определение ячеек гидродинамической модели пласта, по которым проходит траектория трещины ГРП;
- определение длины участков трещины ГРП в ячейках гидродинамической модели пласта;
- расположение модели вертикальной скважины, выполненной с возможностью симуляции трещины гидроразрыва пласта, в каждой ячейке гидродинамической модели пласта, по которой проходит траектория трещины ГРП;
- расчет отрицательного скин-фактора (S) по геометрии ячеек и длинам участков трещины ГРП в соответствующих ячейках для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта;
- моделирование трещины ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S).
42. Машиночитаемый носитель по п. 41, в котором после расчета отрицательного скин-фактора (S) для каждой модели вертикальной скважины дополнительно рассчитывается минимальный отрицательный скин-фактор (MinS) и затем моделируют трещину ГРП с использованием моделей вертикальных скважин с учетом отрицательного скин-фактора (S), при этом если отрицательный скин-фактор (S) меньше значения минимального отрицательного скин-фактора (MinS), то S принимают равным MinS, и при моделировании трещины ГРП дополнительно учитывается множитель коэффициента продуктивности горизонтальной скважины.
43. Машиночитаемый носитель по п. 41, в котором, в случае газового типа флюида горизонтальной скважины, дополнительно определяется D-фактор (динамический скин-фактор), который учитывают при моделировании трещины ГРП.
44. Машиночитаемый носитель по п. 41, в котором, в случае бесконечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывают отрицательный скин-фактор (S) по формуле:
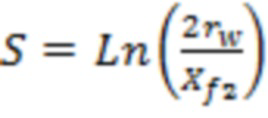 , где
, где
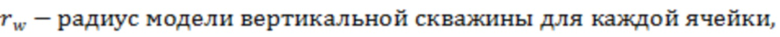
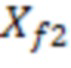 - полудлина участка трещины ГРП.
- полудлина участка трещины ГРП.
45. Машиночитаемый носитель по п. 41, в котором, в случае конечного типа проводимости трещины ГРП, для каждой модели вертикальной скважины, которые расположены в ячейках гидродинамической модели пласта, рассчитывается отрицательный скин-фактор (S) по формуле:
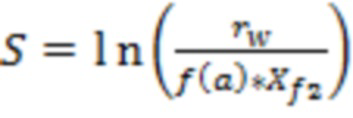 , где
, где
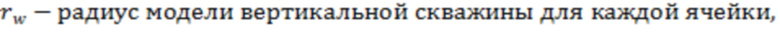
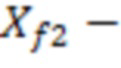 полудлина участка трещины ГРП,
полудлина участка трещины ГРП,
f(a) - зависимость эффективного радиуса модели вертикальной скважины для каждой ячейки от относительного емкостного параметра.
46. Машиночитаемый носитель по п. 45, в котором дополнительно определяется относительный емкостной параметр по формуле:
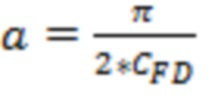 , где
, где
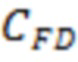 - безразмерная проводимость трещины ГРП.
- безразмерная проводимость трещины ГРП.
47. Машиночитаемый носитель по п. 46, в котором безразмерная проводимость трещины ГРП определяется по формуле:
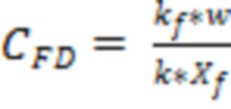 , где
, где
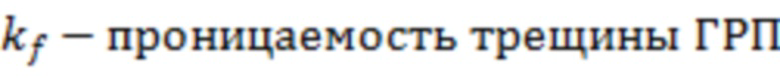 ,
,
 ,
,
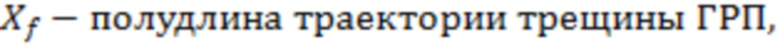
 .
.
48. Машиночитаемый носитель по п. 46, в котором, в случае конечного типа проводимости трещины ГРП, дополнительно определяется эффективная безразмерная проводимость трещины ГРП 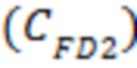 с учетом схождения (конвергенции) линий тока в трещине ГРП, которая учитывается при расчете отрицательного скин-фактора (S).
с учетом схождения (конвергенции) линий тока в трещине ГРП, которая учитывается при расчете отрицательного скин-фактора (S).
49. Машиночитаемый носитель по п. 48, в котором эффективная безразмерная проводимость трещины ГРП с учетом схождения (конвергенции) линий тока в трещине ГРП определяется по формуле:
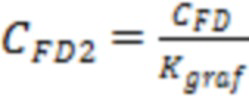 , где
, где
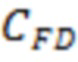 - безразмерная проводимость трещины ГРП,
- безразмерная проводимость трещины ГРП,
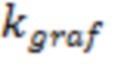 - коэффициент снижения продуктивности скважины.
- коэффициент снижения продуктивности скважины.
50. Машиночитаемый носитель по п. 43, в котором D-фактор для газового типа флюида горизонтальной скважины определяется по формуле:
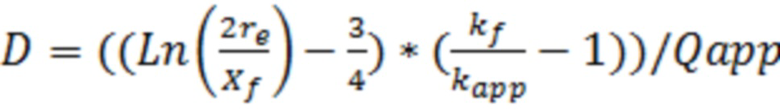 , где
, где
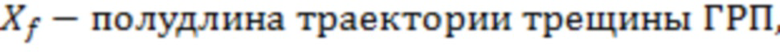
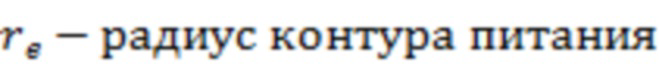 ,
,
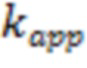 - проницаемость трещины ГРП с учетом инерциальных потерь,
- проницаемость трещины ГРП с учетом инерциальных потерь,
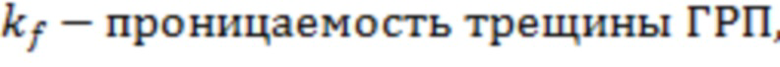
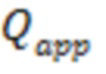 - дебит газа.
- дебит газа.
51. Машиночитаемый носитель по п. 50, в котором определяется проницаемость трещины ГРП с учетом инерциальных потерь по формуле:
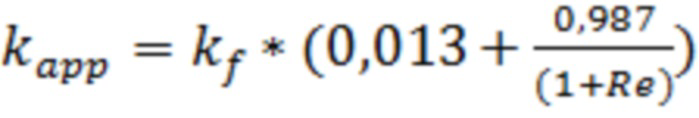 , где
, где
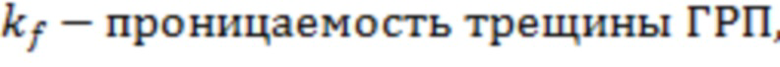
Re - число Рейнольдса.
52. Машиночитаемый носитель по п. 51, в котором определяется число Рейнольдса по формуле:
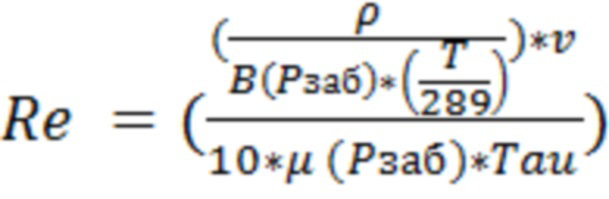 , где
, где

B - объемный коэффициент газа 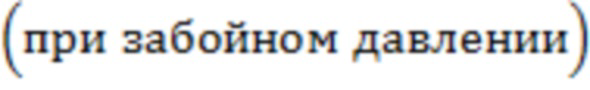 ,
,
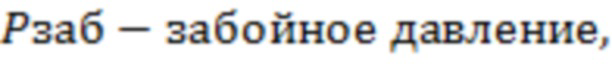

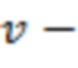 скорость фильтрации газа в трещине ГРП,
скорость фильтрации газа в трещине ГРП,
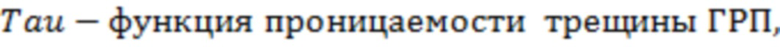
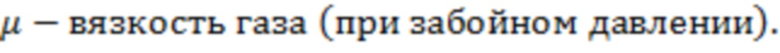
53. Машиночитаемый носитель по п. 52, в котором скорость фильтрации газа в трещине ГРП, траектория которой проходит поперек ствола горизонтальной скважины, определяется по формуле:
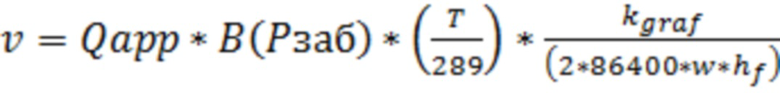 , где
, где
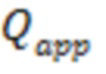 - дебит газа,
- дебит газа,
B - объемный коэффициент газа 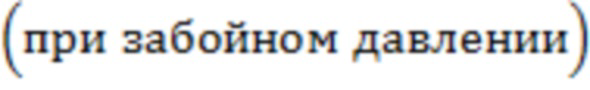 ,
,
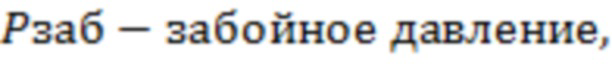

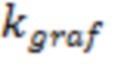 - коэффициент снижения продуктивности скважины,
- коэффициент снижения продуктивности скважины,
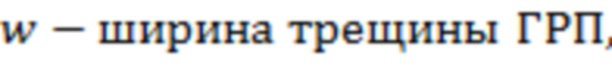
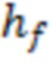 - высота трещины ГРП.
- высота трещины ГРП.
54. Машиночитаемый носитель по пп. 49 и 53, в котором определяется коэффициент снижения продуктивности скважины с использованием значений отношения длины траектории трещины ГРП к ее высоте.
55. Машиночитаемый носитель по п. 52, в котором скорость фильтрации газа в трещине ГРП, траектория которой проходит вдоль ствола газовой горизонтальной скважины, определяют по формуле:
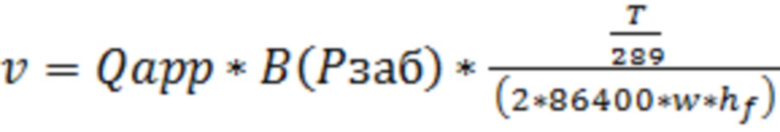 , где
, где
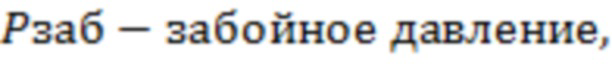
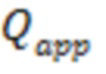 - дебит газа,
- дебит газа,

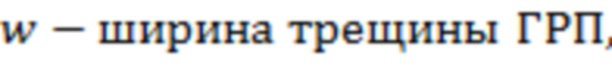
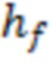 - высота трещины ГРП.
- высота трещины ГРП.
56. Машиночитаемый носитель по любому из пп. 50, 53, 55, в котором дебит газа определяется по формуле:
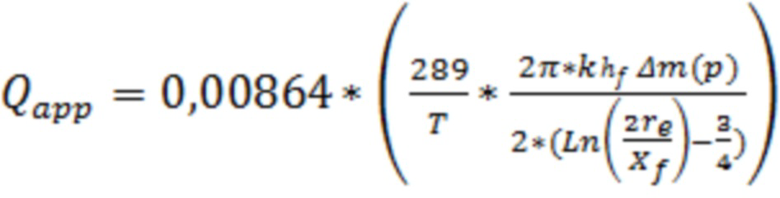 , где
, где

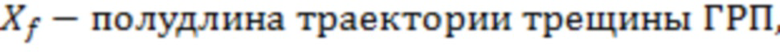
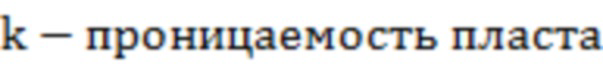 ,
,
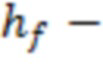 высота трещины ГРП,
высота трещины ГРП,
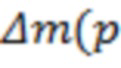 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
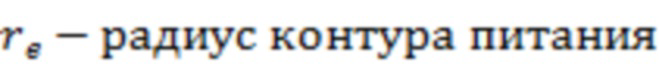 .
.
57. Машиночитаемый носитель по п. 56, в котором дополнительно пересчитывается дебит газа до тех пор, пока значение дебита газа на предыдущем шаге пересчета не будет отличаться от дебита газа на последнем шаге пересчета менее чем на 1%, при этом дебит газа пересчитывается по формуле:
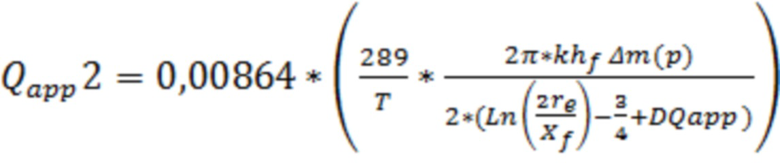 , где
, где
DQapp=Sин - скин-фактор за счет инерциальных потерь движения газа в трещине ГРП,

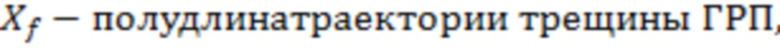
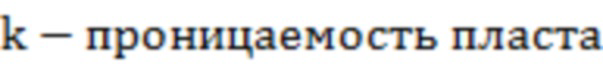 ,
,
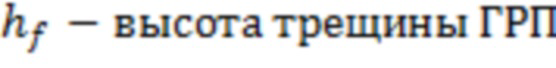 ,
,
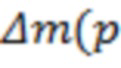 ) - депрессия псевдодавления,
) - депрессия псевдодавления,
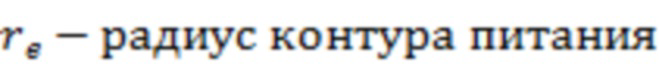 ,
,
при этом по каждому полученному значению дебита газа пересчитывается D-фактор, последнее значение которого учитывается при моделировании трещины ГРП.
58. Машиночитаемый носитель по п. 42, в котором минимальный отрицательный скин-фактор (MinS) определяется по формуле:
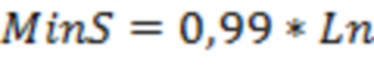 (
(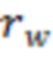 /
/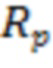 ), где
), где
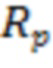 - радиус Писмана,
- радиус Писмана,
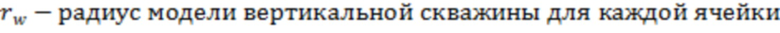 .
.
59. Машиночитаемый носитель по п. 58, в котором радиус Писмана определяется по формуле:
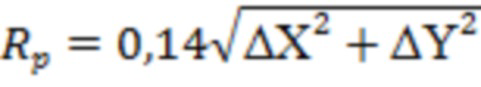 , где
, где
ΔX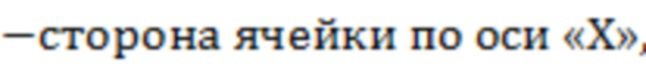
ΔY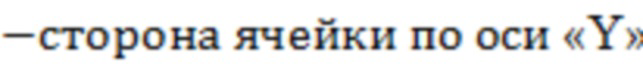 .
.
60. Машиночитаемый носитель по п. 42, в котором множитель коэффициента продуктивности горизонтальной скважины определяется по формуле:
Кмнож. прод = ( (
(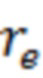 /
/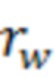 )-3/4+
)-3/4+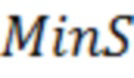 )/(
)/( (
(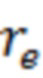 /
/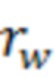 )-3/4+
)-3/4+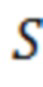 ), где
), где

 для каждой ячейки,
для каждой ячейки,
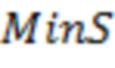 - минимальный отрицательный скин-фактор (MinS),
- минимальный отрицательный скин-фактор (MinS),
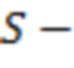 отрицательный скин-фактор.
отрицательный скин-фактор.
| US 20170218729 A1, 03.08.2017 | |||
| СПОСОБ ПРОГНОЗИРОВАНИЯ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБЫ ПРОГНОЗИРОВАНИЯ РИСКОВ ГИДРОРАЗРЫВА ПЛАСТА | 2017 |
|
RU2730576C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИИ ТРЕЩИН ПРИ ГИДРОРАЗРЫВЕ ПЛАСТА (ГРП) | 2018 |
|
RU2695411C1 |
| US 7925482 B2, 12.04.2011 | |||
| ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПЛОСКОСТЕЙ РАЗВИТИЯ ТРЕЩИН | 2013 |
|
RU2592751C1 |
| US 20200190977 A1, 18.06.2020 | |||
| CA 2914348 A1, 14.12.2016 | |||
| CA 3012203 A1, 24.01.2019. | |||
Авторы
Даты
2021-03-22—Публикация
2020-09-17—Подача