Изобретения относятся к измерительной технике при измерении температуры на различных глубинах электропроводящих сред. Предлагаемые способ измерения пространственного распределения температуры и устройство для его осуществления могут быть использованы при производстве материалов и сплавов, в металлургии, в высокотемпературных камерах сгорания, при производстве датчиков температуры, для контроля температуры электропроводящих твёрдых объектов и жидкостей.
Известен способ, реализующий устройство измерения пространственного распределения температуры (Патент RU (11) №2079822, опубликовано 1997, МПК G01K 7/00), основанный на измерении тока насыщения полупроводниковых термочувствительных элементов, размещенных в интересующих точках измерения температурного поля.
Наиболее близким к предлагаемому способу пространственного распределения температуры является способ измерения пространственного распределения температуры (Патент RU (11) № 2206878, опубликовано 20.06.2003, МПК G01K 7/00) Известный способ заключается в измерении пространственного распределения температуры путем помещения в контролируемые точки N термочувствительных датчиков, соединенных параллельно двухпроводной линией, подачи на один из входов линии сигнала переменного напряжения и регистрации входного переменного тока Iвх(t) двухпроводной линии, в качестве термочувствительных датчиков используют кварцевые пьезорезонансные датчики с различными резонансными частотами ωр1, ωр2, ... ωрi, ... ωрN, в качестве сигнала переменного напряжения, подаваемого на один из входов двухпроводной линии используют сигнал с частотной модуляцией в диапазоне резонансных частот пьезорезонансных датчиков, после регистрации входного переменного тока Iвх(t) вычисляют его амплитудно-частотный спектр S(ω), осуществляют первое измерение резонансных частот кварцевых пьезорезонансных датчиков ω0р1, ω0р2, ... ω0рi, ... ω0рN, по положению максимумов амплитудно-частотного спектра S(щ), генерируют многочастотный сигнал, состоящий из N сигналов с девиацией частоты, в пределах диапазона температурного изменения резонансных частот датчиков ω0р1, ω0р2, ... ω0рi, ... ω0рi , который подают на один из входов двухпроводной линии, регистрируют входной переменный ток Iвх(t) двухпроводной линии, вычисляют его амплитудно-частотный спектр S(ω), осуществляют второе измерение резонансных частот кварцевых пьезорезонансных датчиков ωTр1, ωTр2, ... ωTрi, ... ωTрN по положению максимумов амплитудно-частотного спектра S(ω), исходя из которых определяют искомую температуру в контролируемых точках по предварительно экспериментально найденным или теоретически известным зависимостям резонансной частоты кварцевых пьезорезонансных датчиков от температуры ωрi(t).
Наиболее близким к предлагаемому устройству измерения пространственного распределения температуры и для осуществления предлагаемого способа является устройство измерения пространственного распределения температуры (Патент RU (11) № 2206878, опубликовано 20.06.2003, МПК G01K 7/00 (2000.01)), которое содержит N термочувствительных датчиков, параллельно соединенных двухпроводной линией, соединенной с регистратором, который соединен с источником переменного напряжения, причем, в качестве термочувствительных датчиков использованы кварцевые пьезорезонансные датчики с различными резонансными частотами ωр1, ωр2, ... ωрi, ... ωрN, в качестве источника переменного напряжения использован генератор многочастотного сигнала, регистратор содержит последовательно соединенные схему согласования, регистратор амплитуды переменного тока, анализатор спектра, блок обработки и индикации, блок обработки и индикации соединен с генератором многочастотного сигнала
Основным недостатком указанного способа измерения пространственного распределения температуры и устройства для его осуществления, выбранных в качестве прототипов, является необходимость помещения пьезорезонансных датчиков непосредственно в область измерения, при этом тепловое распределение внутри объекта исследования вблизи температурных датчиков может искажаться и вносить погрешность в результаты измерения пространственного распределения температуры. В предлагаемом способе измерения данный недостаток отсутствует, так как термочувствительным элементом является непосредственно сам элемент объема исследуемого объекта. При этом его электрофизические и термочувствительные характеристики зависят только от материала объекта исследования и как следствие – такой способ измерения является неразрушающим методом измерения.
Техническая проблема заключается в создании способа измерения пространственного распределения температуры и устройства, для его осуществления которые позволяют осуществлять измерение распределения температуры по глубине объекта исследования.
Техническим результатом в предлагаемых способе измерения пространственного распределения температуры и устройстве для его осуществления является возможность измерения распределения температуры по глубине электропроводящего объекта исследования.
Технический результат в способе измерения пространственного распределения температуры, включающем подачу на исследуемый объект частотно-модулированного электрического тока в полосе частот, достигается тем, что на исследуемый электропроводящий объект через поверхностные электроды подают частотно-модулированный электрический ток с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, формируя тем самым скин-слой переменной толщины δ, проникающий на глубину δmin≤δ≤δmax исследуемого объекта, где δmin - минимальная толщина скин-слоя, соответствующая частоте ωmax, δmax - максимальная толщина скин-слоя, соответствующая частоте ωmin, измеряют в полосе частот ωmin≤ω≤ωmax частотную характеристику импеданса Z(jω), по которой определяют распределение удельной электрической проводимости по глубине σ(δ), и по найденному распределению σ(δ) и по предварительно экспериментально найденным или теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(T) судят о пространственном распределении температуры по глубине Т(δ) в исследуемом объекте.
Технический результат в устройстве для измерения пространственного распределения температуры (для осуществления предлагаемого способа), содержащем генератор сигналов, соединенный с блоком обработки, достигается тем, что генератором сигналов является генератор сигналов с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, блоком обработки является вычислитель частотной характеристики импеданса Z(jω), выход генератора сигналов является выходом для соединения с электропроводящим исследуемым объектом с помощью первого электрода, а второй вход вычислителя частотной характеристики импеданса Z(jω) является входом для соединения с электропроводящим исследуемым объектом посредством второго электрода, выход вычислителя частотной характеристики импеданса Z(jω) соединен со входом вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ).
На фиг.1 изображена структурная схема устройства для осуществления способа измерения пространственного распределения температуры с электропроводящим объектом исследования.
На фиг. 2 приведена функциональная схема устройства, разъясняющая осуществление способа измерения пространственного распределения температуры по глубине с подключенным электропроводящим объектом исследования.
На фиг. 3 приведена эквивалентная электрическая схема представления электропроводящего объекта исследования на основе А - матриц.
На фиг. 4 изображен алгоритм работы вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ).
Структурная схема устройства для осуществления способа измерения пространственного распределения температуры с электропроводящим объектом исследования, изображенная на фиг.1, включает: 1 - Генератор сигналов, 2 - Объект исследования, 3 - Первый электрод, 4 - Вычислитель частотной характеристики импеданса Z(jω), 5 - Второй электрод, 6 - Вычислитель распределения удельной электрической проводимости по глубине σ(δ) и пространственного распределения температуры Т(δ).
Функциональная схема устройства, разъясняющая осуществление способа измерения пространственного распределения температуры по глубине, приведенная на фиг. 2, включает: 1 - Генератор сигналов, 2 – Подключенный к схеме измерения электропроводящий объект исследования 2 со скин-слоем, 3 - Первый электрод, 4 - Вычислитель частотной характеристики импеданса Z(jω). 5 - Второй электрод, 6 - Вычислитель распределения удельной электрической проводимости по глубине σ(δ) и пространственного распределения температуры Т(δ).
В примере конкретной реализации устройство для измерения пространственного распределения температуры (для осуществления предлагаемого способа), представленного на фиг. 1, 2 содержит генератор сигналов 1 с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, выход генератора сигналов 1 соединен с электропроводящим исследуемым объектом 2, представленного на фиг. 3 в виде электрической схемы на основе А - матриц, с помощью первого электрода 3, и с вычислителем частотной характеристики импеданса Z(jω)4, выход генератора сигналов 1 также соединен со входом вычислителя частотной характеристики импеданса Z(jω) 4, второй вход которого соединен с электропроводящим исследуемым объектом 2 посредством второго электрода 5, выход вычислителя частотной характеристики импеданса Z(jω) 4 соединен со входом вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ) 6.
В примере конкретной реализации в качестве генератора сигналов 1 может быть использован стандартный высокочастотный генератор, например, высокочастотный генератор российского производства АКИП-3417, Г4-194 и др. В качестве вычислителя частотной характеристики импеданса Z(jω) 4 могут быть использованы векторные анализаторы импеданса, например, измеритель импеданса E4990A фирмы Keysight. В качестве вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры T(δ) 6 могут быть использованы ЭВМ или микроконтроллер с программой согласно алгоритму, приведенному на фиг.4. Объектом исследования может быть любой объект или конструкция, изготовленные из электропроводящего материала (металлы, сплавы, композиты из углеволокна и т.п.), в которых необходимо измерить или контролировать профиль температуры по глубине. Например, конструкция из легированной стали при аргоновой сварке либо при кузнечной (горновой) сварке давлением, в процессе которой необходимо точно контролировать температуру сварного шва.
На фиг. 3 изображена эквивалентная электрическая схема представления электропроводящего объекта исследования 2 на основе А - матриц. Схема содержит генератор сигналов 1, который подключен с помощью электродов 3 и 5 к объекту исследования 2. При подаче сигналов с частотой ωmin≤ω≤ωmax в объекте исследования последовательно формируются N скин-слоёв, соответствующих частотам ω1, ω2, ω3… ωN с толщиной д1, д2, д3,…дN. с шагом Δδ
 , (1)
, (1)
где N – необходимое количество точек измерения профиля температуры T(δ). В пределах Δδ каждый i-й элементарный участок можно представить в виде RL-цепи, представленных на схеме резисторами Ri и индуктивностями Li (Фиг. 3), образующими резистивно-индуктивную RL-структуру с распределёнными параметрами. Сопротивление i-го элементарного участка цепи равно:
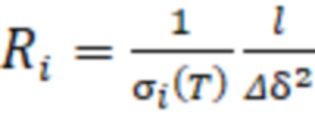 , (2)
, (2)
где  – удельная электропроводность материала i-го участка объекта исследования, зависящая от температуры T,
– удельная электропроводность материала i-го участка объекта исследования, зависящая от температуры T,  поперечное сечение элементарного участка, l – расстояние между электродами. Импеданс реактивной составляющей i-го участка равен:
поперечное сечение элементарного участка, l – расстояние между электродами. Импеданс реактивной составляющей i-го участка равен:
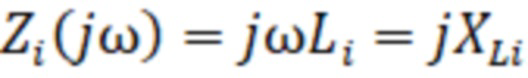 , (3)
, (3)
где j – мнимая единица,  – индуктивность i-го слоя материала объекта,
– индуктивность i-го слоя материала объекта, - реактивное сопротивление индуктивной составляющей.
- реактивное сопротивление индуктивной составляющей.
Электрическая цепь на фиг 3. представляет собой цепь с распределёнными параметрами, в которых для металлических проводников [Л.А. Вайнштейн Электромагнитные волны. М.: Радио и связь, 1990г. – С. 94]
 . (4)
. (4)
Для магнитных электропроводящих материалов с магнитной проницаемостью  правая часть выражения (4) возрастает в
правая часть выражения (4) возрастает в  раз.
раз.
Каждый i-й элементарный участок  схемы можно описать А-матрицей по формуле [Каганов З.Г. Электрические цепи с распределенными параметрами и цепные схемы. М.: Энергоатомиздат, 1990. – С. 25]
схемы можно описать А-матрицей по формуле [Каганов З.Г. Электрические цепи с распределенными параметрами и цепные схемы. М.: Энергоатомиздат, 1990. – С. 25]
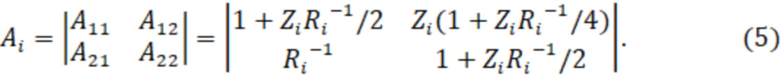
Результирующая матрица  всей цепи описывается как произведение всех матриц Аi
всей цепи описывается как произведение всех матриц Аi
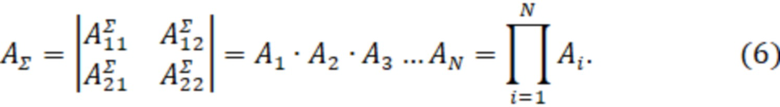
Из элементов результирующей матрицы  можно определить входной импеданс [Каганов З.Г. Электрические цепи с распределенными параметрами и цепные схемы. М.: Энергоатомиздат, 1990. – С. 24] по формуле
можно определить входной импеданс [Каганов З.Г. Электрические цепи с распределенными параметрами и цепные схемы. М.: Энергоатомиздат, 1990. – С. 24] по формуле

где  - волновое сопротивление
- волновое сопротивление

Здесь  индуктивность и сопротивление при однородном распределении температуры
индуктивность и сопротивление при однородном распределении температуры 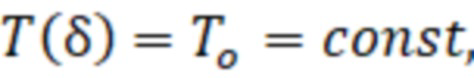 которые находятся из формулы (6) и (7) при предварительном калибровочном измерении.
которые находятся из формулы (6) и (7) при предварительном калибровочном измерении.
При произвольном распределении температуры по глубине 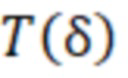 электрическая проводимость меняется в соответствии с профилем температуры
электрическая проводимость меняется в соответствии с профилем температуры  , так как электропроводность металлов и других проводящих материалов всегда зависит от температуры.
, так как электропроводность металлов и других проводящих материалов всегда зависит от температуры.
В случае, когда температура в объекте измерения постоянна по глубине  , то удельная электропроводность материала объекта постоянна
, то удельная электропроводность материала объекта постоянна 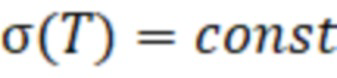 по глубине. Следовательно, все матрицы одинаковы
по глубине. Следовательно, все матрицы одинаковы  и результирующая матрица цепи согласно (6) будет равна:
и результирующая матрица цепи согласно (6) будет равна:
 . (9)
. (9)
На максимальной частоте измерения  глубина проникновения будет равна
глубина проникновения будет равна 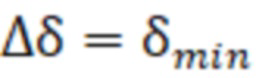 и результирующая матрица цепи будет равна матрице
и результирующая матрица цепи будет равна матрице  (фиг. 3).
(фиг. 3).
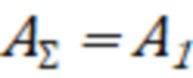 . (10)
. (10)
При частоте  результирующая матрица
результирующая матрица  цепи при глубине проникновения
цепи при глубине проникновения 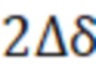 будет равна произведению двух первых матриц
будет равна произведению двух первых матриц
 (11)
(11)
Тогда из данного выражения матрица 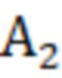 будет равна
будет равна
 , (12)
, (12)
где 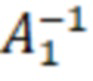 обратная матрица
обратная матрица  .
.
Таким образом, можно последовательно вычислить все матрицы от  и их элементы для частот ωN, ωN-1, ωN-2… ω1 в диапазоне частот от
и их элементы для частот ωN, ωN-1, ωN-2… ω1 в диапазоне частот от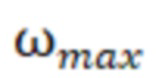 до
до  и определить значения
и определить значения 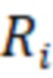 и соответственно
и соответственно 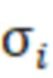 по формуле (2) для различных глубин.
по формуле (2) для различных глубин.
Глубина проникновения δ электрического тока с частотой ω пропорциональна

Чем меньше частота щ, тем на большую глубину проникает переменный ток. Например, согласно [Волин М.Л. Паразитные процессы в радиоэлектронной аппаратуре. Изд. 2-е перераб, и доп. М.: Радио и связь, 1981. – С. 65] для частот 100 Гц и 10 МГц толщина скин-слоя д для различных металлов различна и соответственно для меди составляет 6,6 мм и 0,02 мм, для алюминия - 8,5 мм и 0,025 мм, для различных марок стали – ориентировочно лежит в диапазоне от 1 мм до 0,002 мм. Если проводить измерение на N частотах ω1, ω2, ω3…ωN, то глубина проникновения в электропроводящий материал объекта будет равна соответственно δ1, δ2, δ δ3 … δ N. Выбирая необходимый шаг по частоте Δω можно добиться необходимой пространственной разрешающей способности Δδ измерений профиля температуры T(δ). Оценку пространственной разрешающей способности можно получить как полный дифференциал из соотношения (13):

Тогда необходимое количество точек измерения с заданной пространственной разрешающей способности  будет равно
будет равно

где  – максимальная толщина скин слоя на минимальной частоте
– максимальная толщина скин слоя на минимальной частоте . Для постоянства разрешающей способности
. Для постоянства разрешающей способности  =const необходимо частоту ωi и переменный шаг по частоте
=const необходимо частоту ωi и переменный шаг по частоте 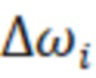 выбирать из соотношений:
выбирать из соотношений:


На фиг. 4 изображен алгоритм работы вычислителя удельной электрической проводимости σ(δ) и пространственного распределения температуры T(δ) 6. Он реализует расчет распределения по глубине δ удельной электрической проводимости σ(δ) и температуры T(δ) по измеренной частотной характеристике импеданса Z(jω) 4. Первой функцией данного алгоритма является считывание импеданса Z(jω) с вычислителя частотной характеристики импеданса 4. Далее вычисляются значения частот ω1, ω2, ω3… ωN таким образом, чтобы согласно (15), (16), (17) толщины соответствующих скин-слоёв были кратны Δδ, 2Δδ ,3Δδ, … NΔδ. Далее рассчитываются значения элементов А11, А21, А12, А22. матрицы A1 первого элемента структуры при частотах ωN. Затем последовательно вычисляются
А1, А2, А3 … АN – матрицы структуры объекта исследования 2. В расчёте каждого Ai элемента используется значение матрицы предыдущего Ai-1 элемента. Далее вычисляется проводимость σi скин-слоя Δδi от элемента Ri матрицы Ai. Затем по найденным значениям σi и известной зависимости σ=f(T). удельной электрической проводимости от температуры вычисляется распределение температуры Т(δi). Для наглядного отображения зависимости температуры по глубине предлагается графическое представление.
Рассмотрим осуществление предлагаемого способа измерения пространственного распределения температуры с помощью устройства для его осуществления, структурная схема которого изображена на фиг. 1. Вычислитель распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры T(δ) 6 работает согласно алгоритму работы, приведенному на фиг. 4. Способ измерения пространственного распределения температуры заключается в том, что на исследуемый электропроводящий объект 2 подают с генератора сигналов 1 с помощью поверхностных электродов, в примере конкретной реализации посредством первого электрода 3, частотно-модулированный электрический ток с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, формируя тем самым скин-слой переменной толщины δ, проникающий на глубину δmin≤δ≤δmax исследуемого объекта, где δmin - минимальная толщина скин-слоя, соответствующая частоте ωmax, δmax - максимальная толщина скин-слоя, соответствующая частоте ωmin. Далее, измеряют с помощью вычислителя частотной характеристики импеданса Z(jω) 4, на вход которого поступает сигнал с электропроводящего исследуемого объекта 2 посредством второго электрода 5 в полосе частот ωmin≤ω≤ωmax частотную характеристику импеданса Z(jω). Далее, по ней с помощью вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ) 6 определяют распределение удельной электрической проводимости по глубине σ(δ) и по найденному распределению σ(δ) и по предварительно экспериментально найденным или теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(T) судят о пространственном распределении температуры Т(δ) в исследуемом объекте.
Рассмотрим осуществление предлагаемого способа измерения пространственного распределения температуры по глубине. Решение данной задачи возможно при использовании известного физического эффекта - возникновения скин-слоя в поверхностном слое проводника при пропускании переменного тока высокой частоты  . Суть эффекта заключается в оттеснении протекающего электрического тока проводника и, как следствие, зависимость его импеданса
. Суть эффекта заключается в оттеснении протекающего электрического тока проводника и, как следствие, зависимость его импеданса  от частоты
от частоты 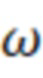
 (18)
(18)
где  – комплексное значение напряжения,
– комплексное значение напряжения,  – комплексное значение тока. Толщина скин-слоя δ является функцией частоты
– комплексное значение тока. Толщина скин-слоя δ является функцией частоты 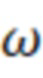 и уменьшается с ее повышением по выражению:
и уменьшается с ее повышением по выражению:
 , (19)
, (19)
где у – удельная электрическая проводимость материала, µ - относительная магнитная проницаемость вещества, µ0 – магнитная постоянная, 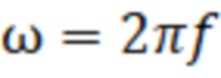 – угловая частота. Таким образом, подбирая частоту
– угловая частота. Таким образом, подбирая частоту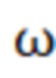 переменного тока, можно сформировать практически любую толщину δ скин-слоя, необходимую для зондирования глубинных электрических параметров материала.
переменного тока, можно сформировать практически любую толщину δ скин-слоя, необходимую для зондирования глубинных электрических параметров материала.
По теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(T) [Справочник по электротехническим материалам / Под ред. Ю.В. Корицкого, В.В. Пасынкова, Б.М. Тареева. – М.: Энергоиздат, 1988. т.3. – C.239-289.] по найденному распределению проводимости 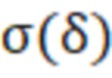 определяют распределение температуры T(д) по глубине д. Для металлов и сплавов зависимость удельного сопротивления от температуры
определяют распределение температуры T(д) по глубине д. Для металлов и сплавов зависимость удельного сопротивления от температуры  , как правило, является линейной и выражается формулой:
, как правило, является линейной и выражается формулой:
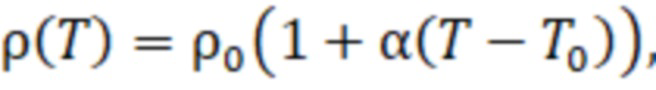 (20)
(20)
где  – удельное сопротивление материала при температуре
– удельное сопротивление материала при температуре  , α - температурный коэффициент сопротивления материала. Следовательно, температуру Ti каждого i-го слоя (i=1,2,3…N) можно определить по электропроводности
, α - температурный коэффициент сопротивления материала. Следовательно, температуру Ti каждого i-го слоя (i=1,2,3…N) можно определить по электропроводности  из формулы
из формулы
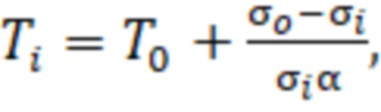 (21)
(21)
где 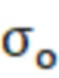 - известная электропроводность материала объекта при температуре
- известная электропроводность материала объекта при температуре  .
.
Подставляя в (21) найденное по приведённому алгоритму значение электропроводности, рассчитывается температура на глубине Ti.
Значение температурного коэффициента сопротивления α для неизвестного материала можно определить экспериментально по формуле (21) или другими известными методами.
По сравнению с прототипом в предлагаемых технических решениях в способе измерения пространственного распределения температуры и устройстве для его осуществления технический результат будет достигнут за счет того, что на исследуемый электропроводящий объект через поверхностные электроды подают частотно-модулированный электрический ток с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, формируя тем самым скин-слой переменной толщины δ, проникающий на глубину δmin≤δ≤δmax исследуемого объекта, где δmin - минимальная толщина скин-слоя, соответствующая частоте ωmax, δmax - максимальная толщина скин-слоя, соответствующая частоте ωmin, измеряют в полосе частот ωmin≤ω≤ωmax частотную характеристику импеданса Z(jω), по которой определяют распределение удельной электрической проводимости по глубине σ(δ), и по найденному распределению σ(δ) и по предварительно экспериментально найденным или теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(T) судят о пространственном распределении температуры по глубине Т(δ) в исследуемом объекте. А в устройстве для реализации предложенного способа за счет того, что генератором сигналов является генератор сигналов с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, блоком обработки является вычислитель частотной характеристики импеданса Z(jω), выход генератора сигналов является выходом для соединения с электропроводящим исследуемым объектом с помощью первого электрода, а второй вход вычислителя частотной характеристики импеданса Z(jω) является входом для соединения с электропроводящим исследуемым объектом посредством второго электрода, выход вычислителя частотной характеристики импеданса Z(jω) соединен со входом вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСТАЦИОНАРНОГО ТЕПЛОВОГО ПОТОКА | 2022 |
|
RU2787301C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСТАЦИОНАРНОГО ТЕПЛОВОГО ПОТОКА | 2022 |
|
RU2787300C1 |
| Способ определения концентрации газа | 2020 |
|
RU2739719C1 |
| СПОСОБ ИССЛЕДОВАНИЯ КОЛЕБАНИЙ | 1994 |
|
RU2097710C1 |
| ТЕРМОАНЕМОМЕТРИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ СКОРОСТИ ПОТОКА ЖИДКОСТИ ИЛИ ГАЗА (ЕГО ВАРИАНТЫ) | 1992 |
|
RU2018850C1 |
| СПОСОБ ПОЛУЧЕНИЯ ТОМОГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ МАГНИТНОЙ ИНДУКЦИОННОЙ ТОМОГРАФИИ | 1996 |
|
RU2129406C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОФИЛЯ ЛЕГИРОВАНИЯ ПОЛУПРОВОДНИКА | 1980 |
|
SU1028203A1 |
| Способ классификации биологических объектов на основе многомерного биоимпедансного анализа и устройство для его реализации | 2020 |
|
RU2752594C1 |
| СПОСОБ ЭЛЕКТРОМАГНИТНОГО ЗОНДИРОВАНИЯ ЗЕМНОЙ КОРЫ С ИСПОЛЬЗОВАНИЕМ НОРМИРОВАННЫХ ИСТОЧНИКОВ ПОЛЯ | 1996 |
|
RU2093863C1 |
| СПОСОБ ОЦЕНКИ ТЕМПЕРАТУРЫ В НЕДРАХ ЗЕМЛИ | 2006 |
|
RU2326413C1 |



Изобретения относятся к измерительной технике при измерении температуры на различных глубинах электропроводящих сред. Предлагаемые способ измерения пространственного распределения температуры и устройство для его осуществления могут быть использованы при производстве материалов и сплавов, в металлургии, в высокотемпературных камерах сгорания, при производстве датчиков температуры, для контроля температуры электропроводящих твёрдых объектов и жидкостей. Заявлен способ измерения пространственного распределения температуры, согласно которому на исследуемый электропроводящий объект через поверхностные электроды подают частотно-модулированный электрический ток с полосой частот ωmin≤ω≤ωmax, формируя тем самым скин-слой переменной толщины δ, проникающий на глубину δmin≤δ≤δmax исследуемого объекта. Измеряют в полосе частот ωmin≤ω≤ωmax частотную характеристику импеданса Z(jω), по которой определяют распределение удельной электрической проводимости по глубине σ(δ). По найденному распределению σ(δ) и по предварительно экспериментально найденным или теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(T) судят о пространственном распределении температуры по глубине Т(δ) в исследуемом объекте. Также предложено устройство для осуществления предлагаемого способа, в котором генератором сигналов является генератор сигналов с полосой частот ωmin≤ω≤ωmax, блоком обработки является вычислитель частотной характеристики импеданса Z(jω). Выход генератора сигналов является выходом для соединения с электропроводящим исследуемым объектом с помощью первого электрода, а второй вход вычислителя частотной характеристики импеданса Z(jω) является входом для соединения с электропроводящим исследуемым объектом посредством второго электрода. Выход вычислителя частотной характеристики импеданса Z(jω) соединен со входом вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры T(δ). Технический результат - обеспечение возможности измерения распределения температуры по глубине электропроводящего объекта исследования. 2 н.п. ф-лы, 4 ил.
1. Способ измерения пространственного распределения температуры, включающий подачу на исследуемый объект частотно-модулированного электрического тока в полосе частот, отличающийся тем, что на исследуемый электропроводящий объект через поверхностные электроды подают частотно-модулированный электрический ток с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, формируя тем самым скин-слой переменной толщины δ, проникающий на глубину δmin≤δ≤δmax исследуемого объекта, где δmin - минимальная толщина скин-слоя, соответствующая частоте ωmax, δmax - максимальная толщина скин-слоя, соответствующая частоте ωmin, измеряют в полосе частот ωmin≤ω≤ωmax частотную характеристику импеданса Z(jω), по которой определяют распределение удельной электрической проводимости по глубине σ(δ), и по найденному распределению σ(δ) и по предварительно экспериментально найденным или теоретически известным зависимостям электрической проводимости материала объекта исследования от температуры σ=f(Т) судят о пространственном распределении температуры по глубине Т(δ) в исследуемом объекте.
2. Устройство для осуществления способа измерения пространственного распределения температуры по п.1, содержащее генератор сигналов, соединенный с блоком обработки, отличающееся тем, что генератором сигналов является генератор сигналов с полосой частот ωmin≤ω≤ωmax, где ωmin - минимальная частота, ωmax - максимальная частота, блоком обработки является вычислитель частотной характеристики импеданса Z(jω), выход генератора сигналов является выходом для соединения с электропроводящим исследуемым объектом с помощью первого электрода, а второй вход вычислителя частотной характеристики импеданса Z(jω) является входом для соединения с электропроводящим исследуемым объектом посредством второго электрода, выход вычислителя частотной характеристики импеданса Z(jω) соединен со входом вычислителя распределения удельной электрической проводимости σ(δ) и пространственного распределения температуры Т(δ).
| СПОСОБ ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2206878C1 |
| УСТРОЙСТВО ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ | 1994 |
|
RU2079822C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ (ВАРИАНТЫ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2194956C1 |
| Устройство для многоточечного измерения температуры | 1983 |
|
SU1177684A1 |
| СПОСОБ ИЗМЕРЕНИЯ СРЕДНЕЙ ТЕМПЕРАТУРЫ НЕОДНОРОДНОЙ СРЕДЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2495390C1 |
| JP 2011137738 A, 14.07.2011 | |||
| JP 2017166840 A, 21.09.2017. | |||
Авторы
Даты
2021-07-13—Публикация
2020-12-18—Подача