Изобретение относится к измерительной технике и может найти применение в экспериментальной гидро- и газодинамике, теплофизике, океанологии, а также в промышленных технологиях, связанных с необходимостью исследования полей фазовой оптической плотности в газовых, конденсированных и реагирующих средах, пламенах и струях.
Известен способ визуализации полей фазовой оптической фазовой плотности в газовых и конденсированных средах [Дубнищев Ю.Н., Арбузов В.А., Арбузов Э.В., Сотников В.В. Патент на изобретение №2681672 «Способ визуализации полей фазовой оптической плотности в газовых и конденсированных средах» Гос. рег. РФ 12.03.2019]. Согласно этому способу, в исследуемую среду направляют зондирующее световое поле, сформированное пространственно-совмещенными пучками, волновые числа которых находятся в соотношении 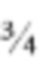 и соответствуют разным rgb-компонентам чувствительности пиксельной структуры фотоматрицы цифровой камеры. Последовательно выполняют гильберт-фильтрацию фурье-спектра фазовых возмущений зондирующего светового поля, индуцированных исследуемой средой, и обратное фурье-преобразование фильтрованного оптического поля. Формируют его изображение на фотоматрице видеокамеры и анализируют покадровую последовательность изображений поля оптической фазовой плотности. Основным недостатком этого способа является влияние дифракционных возмущений структуры зондирующего поля, индуцированных исследуемой средой, на гильберт-визуализацию полей фазовой оптической плотности.
и соответствуют разным rgb-компонентам чувствительности пиксельной структуры фотоматрицы цифровой камеры. Последовательно выполняют гильберт-фильтрацию фурье-спектра фазовых возмущений зондирующего светового поля, индуцированных исследуемой средой, и обратное фурье-преобразование фильтрованного оптического поля. Формируют его изображение на фотоматрице видеокамеры и анализируют покадровую последовательность изображений поля оптической фазовой плотности. Основным недостатком этого способа является влияние дифракционных возмущений структуры зондирующего поля, индуцированных исследуемой средой, на гильберт-визуализацию полей фазовой оптической плотности.
Устройство, реализующее этот способ, содержит последовательно расположенные: источник зондирующего светового поля в виде пространственно-совмещенных световых пучков, волновые числа которых находятся в соотношении 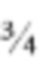 и соответствуют разным rgb-компонентам чувствительности фотоматрицы цифровой камеры, формирователь зондирующего поля, оптический фурье-анализатор, в частотной плоскости которого установлен гильберт-фильтр, оптический фурье-преобразователь, частотная плоскость которого совмещена с фотоматрицей видеокамеры. Недостатком этого устройства является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт-визуализацию полей фазовой оптической плотности.
и соответствуют разным rgb-компонентам чувствительности фотоматрицы цифровой камеры, формирователь зондирующего поля, оптический фурье-анализатор, в частотной плоскости которого установлен гильберт-фильтр, оптический фурье-преобразователь, частотная плоскость которого совмещена с фотоматрицей видеокамеры. Недостатком этого устройства является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт-визуализацию полей фазовой оптической плотности.
В другом известном способе [J.K.T. Eu, A.W. Lohmann. Isotropic Hilbert spatial filtering // Opt. Communications. - 1973. - Vol. 9, No 3. - P. 257-262] или, в более современной интерпретации, [Ананьин М.А., Хонина С.Н. Моделирование оптической обработки изображений с использованием вихревого пространственного фильтра // Компьютерная оптика. - 2009. - Т. 33, №4. С. 466-472], также выполняется гильберт-визуализация визуализация полей фазовой оптической плотности. Формируется фурье-спектр фазовых возмущений зондирующего поля, индуцируемых исследуемой средой. Выполняется изотропное преобразование Гильберта фурье-спектра фазовых возмущений. Основным недостатком этого способа является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт- визуализацию полей фазовой оптической плотности.
Устройство, реализующее этот способ, содержит последовательно расположенные формирователь зондирующего светового поля, оптический фурье-анализатор, в частотной плоскости которого установлен гильберт-фильтр. Последовательно с гильберт-фильтром помещен регистратор фильтрованного изображения в координатном пространстве. Недостатком этого устройства является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт-визуализацию полей фазовой оптической плотности.
Кроме того, известен способ изотропной гильберт-визуализации полей фазовой оптической плотности [Оптические методы исследования потоков / Ю.Н. Дубнищев, В.А. Арбузов, П.П. Белоусов, П.Я. Белоусов Новосибирск: Сиб. унив. изд-во, 2003. 418 с.], являющийся прототипом способа. В этой книге на стр. 363-365 приведено описание способа изотропной гильберт-визуализации полей фазовой оптической плотности, который осуществляется за счет применения кольцевого источника и выполнения пространственно-частотного фильтра в виде коаксиальной фазовой пластинки Кастлера, В исследуемую среду направляется осесимметричное зондирующее поле, структура которого является ганкель-образом кольцевого светового источника. Фурье-спектр фазовых возмущений зондирующего светового поля, индуцируемых исследуемой средой, формируется в частотной плоскости оптической системы, являющейся плоскостью изображения кольцевого источника. После выполнения изотропной гильберт-фильтрации световое поле подвергается обратному фурье-преобразованию и проектируется на фотоматрицу видеокамеры. Визуализированное поле оптических фазовых неоднородностей фиксируется видеокамерой и подвергается компьютерной обработке. Основным недостатком этого способа является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт- визуализацию полей фазовой оптической плотности. Такие возмущения возникают из-за дифракции на неоднородностях исследуемой среды, что искажает пространственную структуру зондирующего поля, нарушая изотропность гильберт-фильтрации. Изотропность нарушается из-за искажений формы и смещения изображения кольцевого источника относительно гильберт-фильтра в частотной плоскости, что приводит к ошибкам в диагностике полей фазовой оптической плотности.
Устройство, реализующее этот способ, являющееся прототипом устройства, содержит последовательно расположенные кольцевой источник излучения, формирователь зондирующего светового поля, оптический фурье-анализатор, в частотной плоскости которого помещен изотропный гильберт-фильтр в виде коаксиальной фазовой пластинки Кастлера. Последовательно с гильберт-фильтром помещен регистратор фильтрованного изображения на фотоматрице видеокамеры, подключенной к компьютеру. Основным недостатком этого устройства является влияние дифракционных возмущений структуры зондирующего поля исследуемой средой на гильберт-визуализацию полей фазовой оптической плотности.
Задачей (техническим результатом) предлагаемого изобретения является повышение точности и расширение функциональных возможностей на гильберт-визуализацию пространственной структуры поля оптической фазовой плотности в конденсированных, газовых и реагирующих (пламя) средах. Решение поставленной задачи достигается тем, что в известном способе зондирующее поле в исследуемой среде формируют в виде одного или нескольких пространственно-сконфигурированных монохроматических или полихроматических бесселевых пучков. Фурье-спектр этих пучков оптически сопряжен с фазовой структурой изотропного гильберт-фильтра. Цветовая структура соответствует спектральной чувствительности пиксельной структуры фотоматрицы. В устройстве, реализующем способ гильберт-визуализации полей фазовой оптической плотности, между источником и формирователем зондирующего поля помещен формирователь сконфигурированных бесселевых пучков, фурье-спектр которых соответствует фазовой структуре изотропного гильберт-фильтра. Формирователь сконфигурированных бесселевых пучков выполнен в виде последовательно расположенных формирователя концентрических r, g и b пучков и аксикона. Формирователь сконфигурированных бесселевых пучков содержит ступенчатый аксикон, согласованный с концентрической структурой r, g и b пучков.
На Фиг. 1 показана структурная схема устройства, реализующего предложенный способ по п. 1 и 2.
На Фиг. 2 показана структурная схема устройства, реализующего предложенный способ по п. 3.
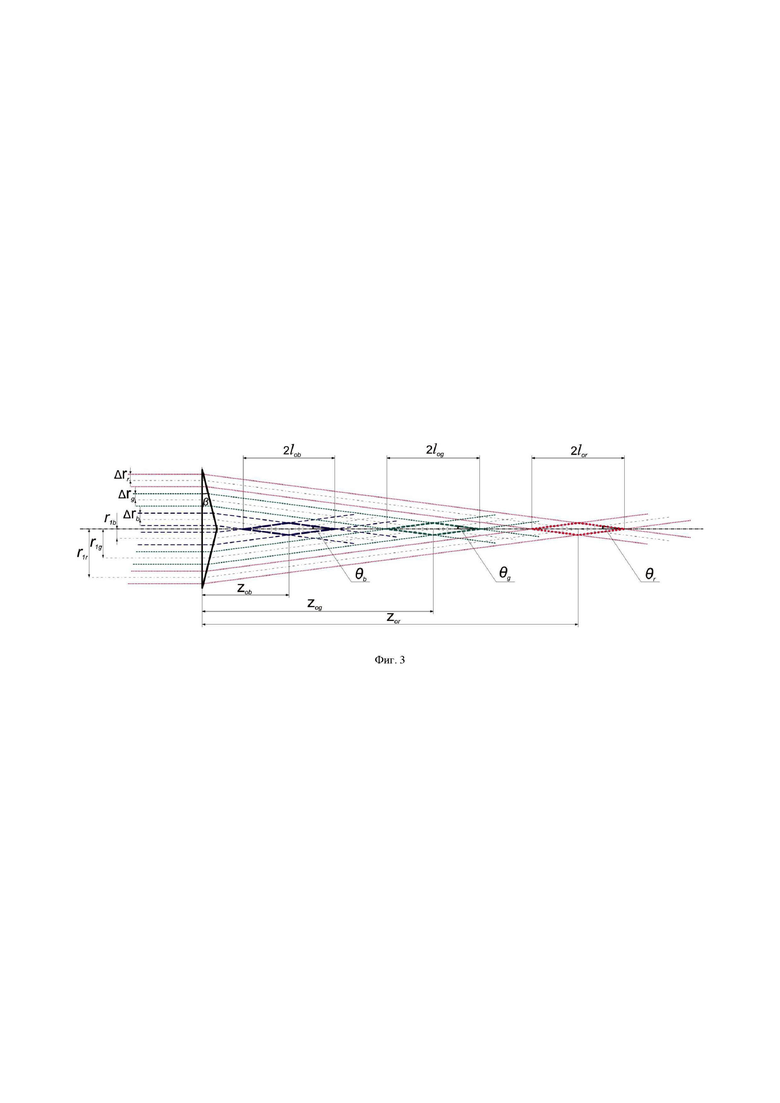
На Фиг. 3 показана структурная схема аксиконного формирователя последовательно расположенных r, g и b бесселевых пучков в устройстве по п. 3.
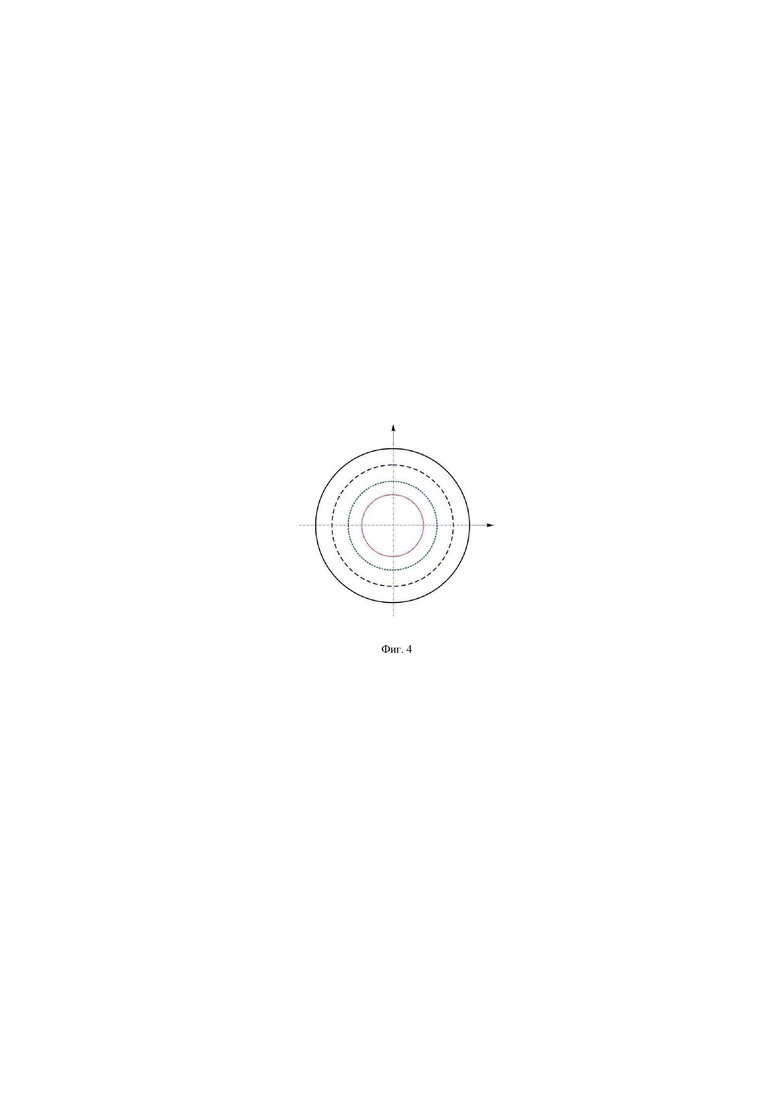
На Фиг. 4 показана структурная схема r, g и b гильберт-фильтра.
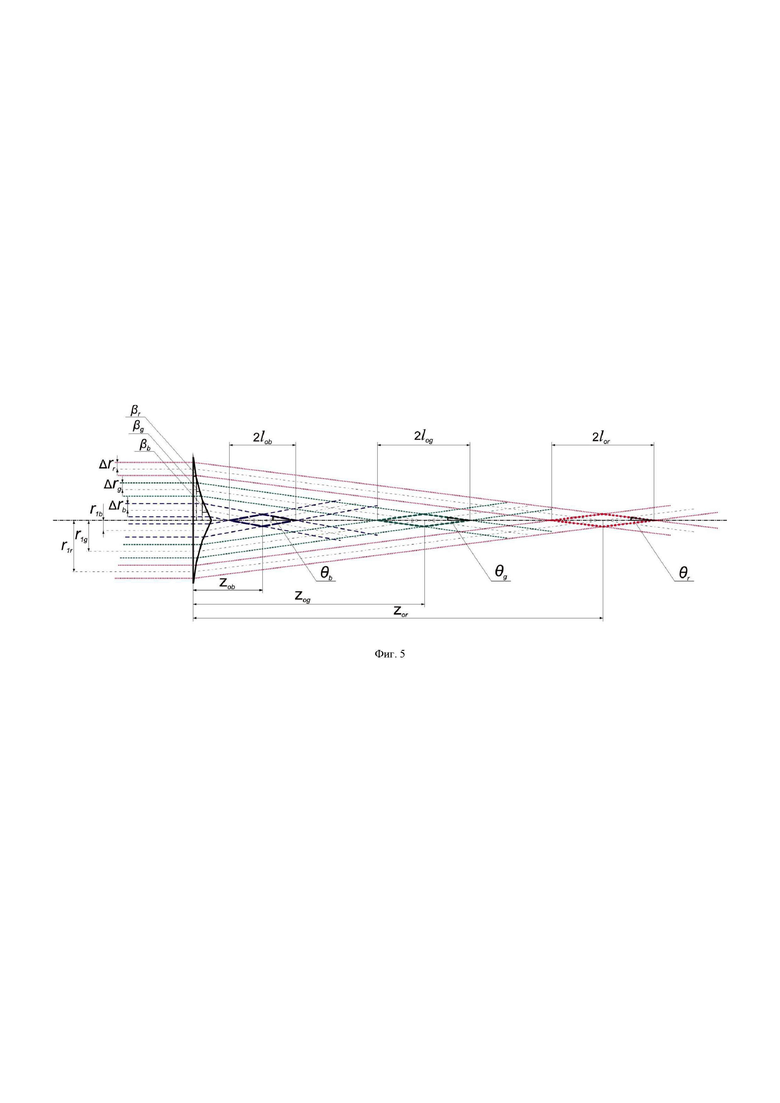
На Фиг. 5 показана структурная схема аксиконного ступенчатого формирователя последовательно расположенных r, g и b бесселевых пучков.
Устройство, реализующее предлагаемый способ, содержит последовательно расположенные источник светового излучения 1, аксикон 2, фурье-сопряженные объективы 3 и 4, объектив 5, в фурье-плоскости которого установлен гильберт-фильтр 6, объектив 7 и цифровую видеокамеру (камкодер) 8, подключенную к компьютеру 9. Способ осуществляется следующим образом. 1. Источник 1 формирует световой пучок, падающий на аксикон 2, параметры которого

где θ - угловой параметр бесселева пучка I0(kr1sinθ), заданный аксиконом,
β - угол между основанием и образующей конической поверхности аксикона,
n - показатель преломления материала, из которого выполнен аксикон.
Примем амплитуду волны единичной. Тогда комплексная амплитуда поля непосредственно за аксиконом:
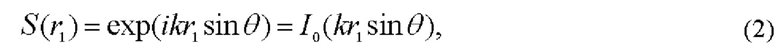
где I0(kr1sinθ) - функция Бесселя нулевого порядка,
k=2π/λ - волновое число,
λ - длина волны источника излучения,
r1 - полярный радиус.
Здесь мы воспользовались известным разложением функции exp(ikr1sinθ) в ряд Фурье, ограничившись первым членом [Дубнищев ЮН. Теория и преобразование сигналов в оптических системах. СПб.: Издательство «Лань», 2011. - 368 с.]. При малом θ sinθ≈θ и (2) принимает вид:
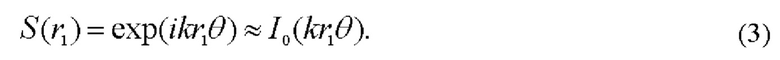
Комплексная амплитуда поля в передней фурье-плоскости объектива 3 описывается с точностью до комплексного множителя бесселевым пучком (3).
Объектив 3 выполняет ганкель-преобразование поля, заданного в передней фурье-плоскости:

где w1 - полярный радиус в частотной плоскости объектива 3, w1=kr1/ƒ1 (ƒ1 - фокусное расстояние объектива 3). Ганкель-образ 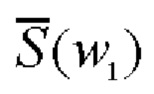 и фурье-спектр S(w1) связаны соотношением
и фурье-спектр S(w1) связаны соотношением

С учетом (4) и (5) находим выражение для комплексной амплитуды поля в задней фурье-плоскости объектива 3. Для этого воспользуемся известным [Папулис А. Теория систем и преобразований в оптике. М.: Издательство «МИР», 1971. 495 с.] преобразованием Ганкеля

где δ(w1-а) - дельта-функция.
Согласно Фиг. 1, а=kθ и, следовательно,
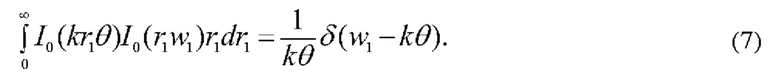
Из (7) и (3) для комплексной амплитуды поля в задней фурье-плоскости объектива 3 с точностью до постоянного комплексного множителя имеем:

Как видно из (8), в задней фурье-плоскости объектива 3 формируется кольцевая структура, радиус которой определяется из свойств дельта-функции, имеющей ненулевое значение при

Объектив 4, фокусное расстояние которого ƒ2, выполняет обратное преобразование Ганкеля для поля с комплексной амплитудой (8):

или, с учетом (8) и с точностью до постоянного комплексного множителя,
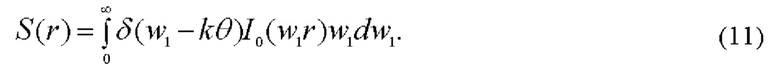
Здесь r - полярный радиус бесселева пучка, сформированного объективом 4. Воспользовавшись фильтрующим свойством дельта-функции,
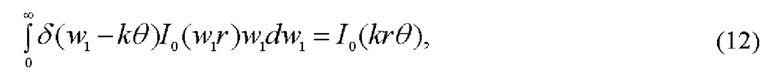
получаем из (11) и (12) с точностью до комплексного множителя для амплитуды зондирующего поля:

Расходимость зондирующего поля оценивается областью существования главного (нулевого) максимума функции Бесселя I0(krθ) в (13). Как известно [Андре Анго. Математика для электро- и радиоинженеров. М.: Издательство «Наука». Главная редакция физико-математической литературы. 1965. 779 с.], полуширина главного максимума функции Бесселя нулевого порядка (12) составляет 2,4:

Учитывая

где ƒ2/ƒ1 - поперечный коэффициент увеличения конфокальной системы, состоящей из объективов 3 и 4, условие (14) можно записать в виде:

Согласно (15) и (16), радиус сечения бесселева пучка, сформированного в исследуемой среде, оценивается как радиус бесселева пучка r1, умноженный на коэффициент передачи (увеличения) оптической системы, состоящей из объективов 3 и 4. Соответственно, угол расходимости зондирующего бесселева пучка, как следует из (13) и (16),

Продольный размер зондирующего поля 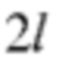 определяется как
определяется как

где 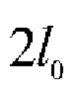 - продольный размер бесселева пучка, сформированного аксиконом,
- продольный размер бесселева пучка, сформированного аксиконом,
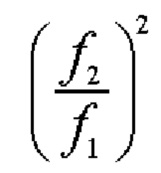 - продольный коэффициент увеличения конфокальной системы,
- продольный коэффициент увеличения конфокальной системы,

r0 - радиус аксикона.
Как следует из (13)-(17), объектив 4 формирует в исследуемой среде зондирующее поле, которое с точностью до комплексного множителя описывается бесселевым пучком с плоским волновым фронтом и комплексной амплитудой:

Опущенный комплексный множитель пропорционален экспоненте, мнимый показатель которой является линейной функцией координат оптической оси объектива 4, формирующего зондирующее поле. Это поле возмущается фазовыми неоднородностями exp[iψ(r)] исследуемой среды
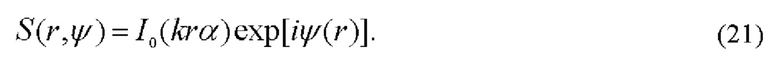
Объектив 5 выполняет фурье-преобразование возмущенного зондирующего поля. Фурье-спектр этого поля S(w) формируется в задней фурье-плоскости объектива 5:
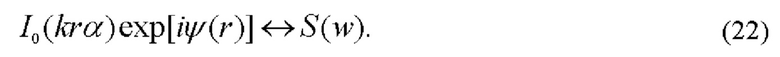
В осесимметричной оптической системе фурье-преобразование (22) реализуется через преобразование Ганкеля:
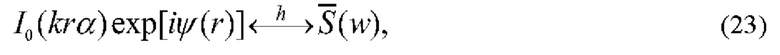
где 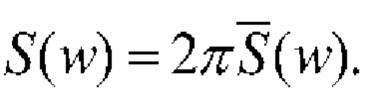
В приближении малых фазовых возмущений 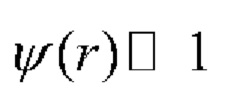

С учетом (24), фурье-спектр S(w) с точностью до постоянного множителя пропорционален ганкель-образу возмущенного зондирующего поля:
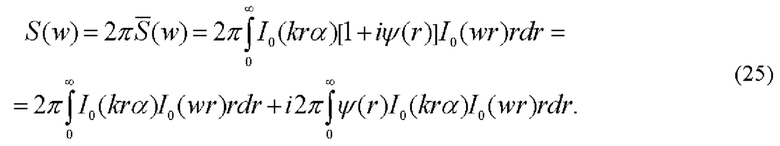
Для первого интеграла в (25) имеем:
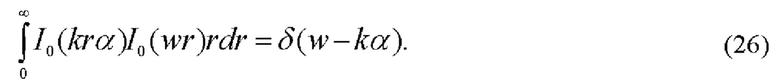
Выражение (26) описывает тонкое кольцо как ганкель-образ бесселева пучка. Кольцевая структура δ(w-kα), сформированная в фурье-плоскости объектива 5, разграничивает области положительных (w>kα) и отрицательных (w<kα) пространственных частот.
Ганкель-образ фазовых возмущений определяется вторым интегралом в (25):
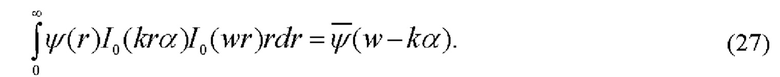
Фурье-спектр этих возмущений пропорционален ганкель-образу (27):
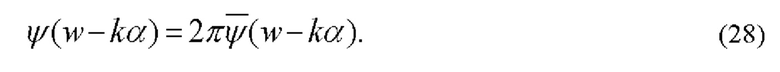
Для визуализации полей фазовой оптической плотности (28) в частотной плоскости установлен гильберт-фильтр с когерентной передаточной функцией
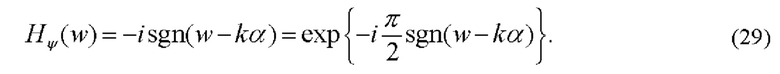
Формула (29) описывает фазочастотную характеристику (ФЧХ) фильтра при амплитудно-частотной характеристике (АЧХ), равной единице. Фурье-спектр поля непосредственно за гильберт-фильтром определяется произведением фурье-спектра фазовых возмущений (28) на когерентную передаточную функцию (29):
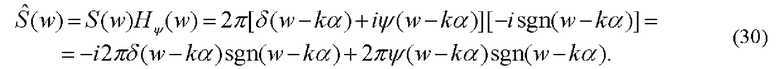
По свойствам дельта-функции,
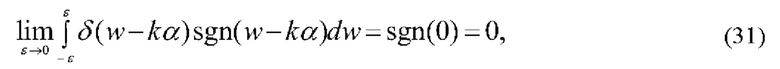
где 2ε - толщина границы раздела положительных и отрицательных пространственных частот в структуре гильберт-фильтра.
Отсюда в (30)

С учетом (32) фурье-спектр поля непосредственно за гильберт-фильтром является гильберт-сопряженным фурье-спектром фазовых возмущений, индуцированных исследуемой средой:
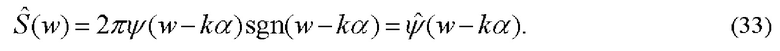
Здесь 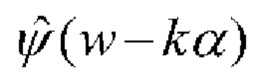 гильберт-спектр фазовых возмущений.
гильберт-спектр фазовых возмущений.
Объектив 7 выполняет обратное фурье-преобразование гильберт-сопряженного фурье-спектра фазовых возмущений. Воспользовавшись свойством фурье-преобразования (теорема смещения), получаем для гильберт-образа фазовых возмущений:
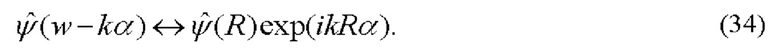
Здесь R - полярный радиус цилиндрической системы координат в плоскости фотоматрицы видеокамеры, регистрирующей гильберт-изображение I(R) поля оптической фазовой плотности исследуемой среды:

Гильберт-изображение поля фазовых возмущений (35) обрабатывается компьютером 9, подключенным к видеокамере 8. Таким образом, устройство по п. 1 и 2 реализует предложенный способ гильберт-визуализации полей фазовой оптической плотности газовых и конденсированных сред.
2. Обратимся к Фиг. 2. Здесь источник формирует концентрическую кольцевую r, g и b структуру излучения. Устройство содержит такую же, как и на Фиг. 1, конфигурацию последовательно расположенных элементов: источник светового излучения 1, аксикон 2, объективы 3 и 4, фурье-объектив 5, гильберт-фильтр 6, фурье-объектив 7 и видеокамеру 8, подключенную к компьютеру 9.
Аксикон 2 в этом устройстве преобразует, как показано на Фиг. 3, падающие на него поля с концентрической кольцевой r, g и b структурой излучения в соосную последовательность r, g и b бесселевых пучков.
Для суперпозиции таких rgb-компонент, сформированных аксиконом, с точностью до комплексных по аналогии с (3) множителей, имеем:
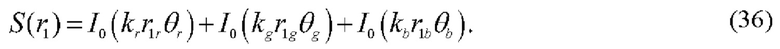
В (36) индексы r, g и b указывают на соответствие параметров бесселевых пучков r-, g- и b-спектральным интервалам.
Центральные сечения этих бесселевых пучков расположены на расстояниях z0r, z0g и z0b от аксикона:

Здесь θr, θg и θb - угловой параметр бесселева пучка, заданный аксиконом с учетом дисперсии. Размеры бесселевых пучков вдоль оптической оси соответственно равны 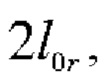
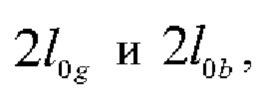 где
где

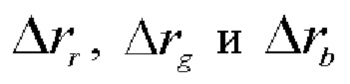 радиусы бесселевых пучков (красного, зеленого и синего соответственно).
радиусы бесселевых пучков (красного, зеленого и синего соответственно).
В задней фурье-плоскости объектива 3 формируются фурье-спектры комплексных амплитуд этих бесселевых пучков. По аналогии с (8), с точностью до комплексных множителей имеем:
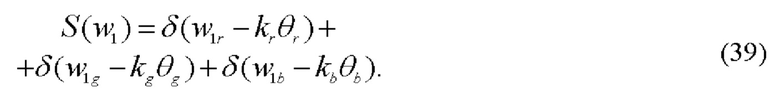
Радиусы кольцевых структур в (39) определяются из свойств дельта-функции: она имеет в (39) ненулевое значение при аргументе, равном нулю,

Объектив 4 выполняет обратное преобразование Ганкеля фурье-спектров бесселевых пучков (39):
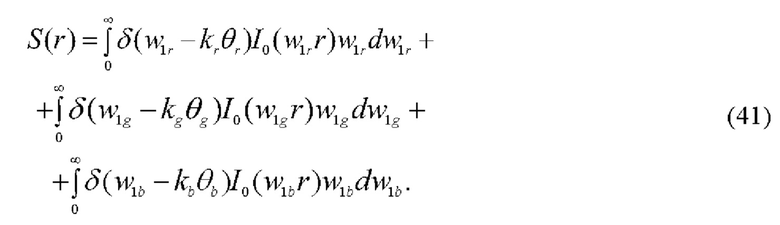
где r - текущее значение радиуса в r, g и b бесселевых пучках.
Воспользовавшись фильтрующим свойством дельта-функции, получаем из (41) для зондирующего поля:
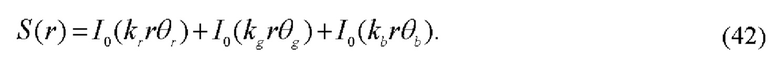
Как видно из (42), зондирующее поле представляет из себя суперпозицию трех последовательно расположенных бесселевых пучков с амплитудами I0(krrθr), I0(kgrθg) и I0(kbrθb). Кривизна волнового фронта этих волн в сечении, ограниченном существованием главного максимума амплитуд хроматических составляющих, описываемых функциями Бесселя нулевого порядка (42), равна нулю.
Поперечный размер зондирующего поля находится из условий, аналогичных (14):
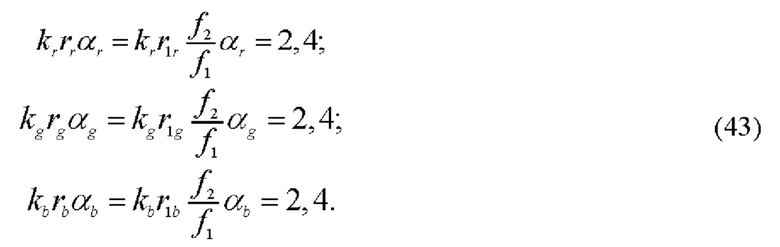
Здесь, как и в (15), ƒ2/ƒ1 - коэффициент увеличения конфокальной системы, состоящей из объективов 3 и 4 с фокусными расстояниями ƒ1 и ƒ2. Отсюда находим радиусы сечений r, g и b зондирующего поля:

Продольные размеры r, g и b бесселевых зондирующих полей 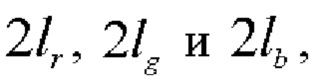 сформированных объективами 3 и 4, определяются, согласно (18) и (19), формулами:
сформированных объективами 3 и 4, определяются, согласно (18) и (19), формулами:
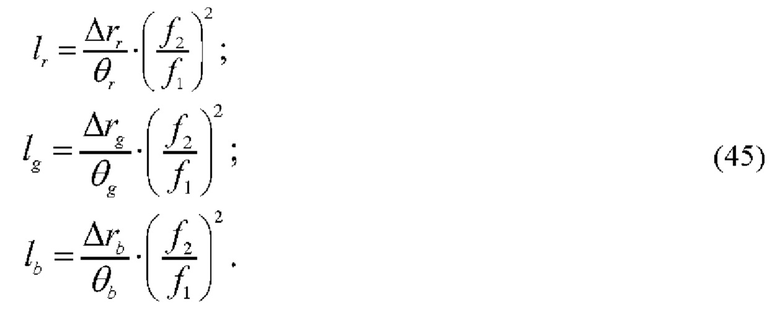
Соответственно, для углов расходимости зондирующих бесселевых пучков по аналогии с (17) имеем:

Объектив 4 формирует в исследуемой среде r, g и b зондирующие поля, которые с точностью до комплексных множителей описываются по аналогии с (20) бесселевыми пучками:

Исследуемая среда индуцирует фазовые возмущения rgb-структуры зондирующего поля (47). Возмущенное исследуемой средой зондирующее поле по аналогии с (21) можно с точностью до постоянных комплексных множителей описать выражением:
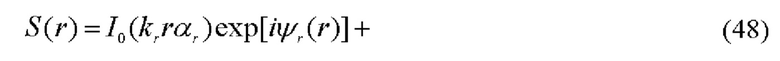
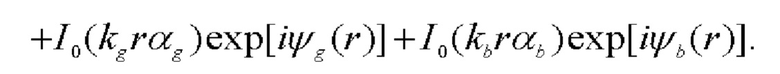
Фурье-спектр возмущенного зондирующего поля формируется в задней фурье-плоскости объектива 5. По аналогии с (23), для фурье-спектра возмущенного исследуемой средой зондирующего поля имеем:
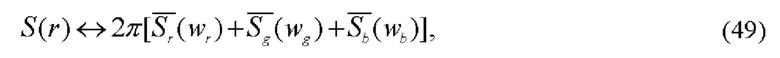
где 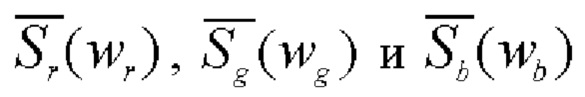 ганкель-образы возмущенных rgb-зондирующих полей:
ганкель-образы возмущенных rgb-зондирующих полей:
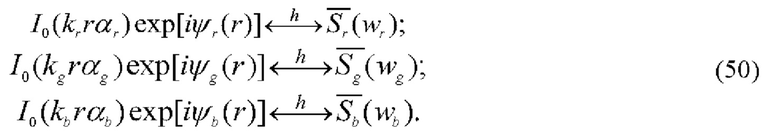
В приближении малых фазовых возмущений (24) для фурье-спектров rgb-полей фазовой оптической плотности (50) имеем по аналогии с (30):
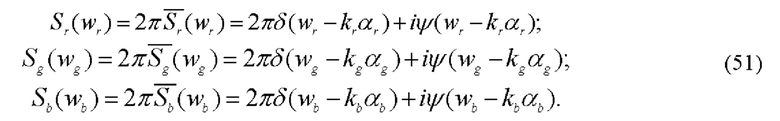
Дельта-функции в (51) разграничивают области положительных (wr>krαr, wg>kgαg и wb>kbαb) и отрицательных (wr<krαr, wg<kgαg и wb<kbαb) пространственных частот в фурье-плоскости 6. Функции iψ(wr-krθr), iψ(wg-kgθg) и iψ(wb-kbθb) - описывают фурье-спектры фазовых возмущений, индуцированных исследуемой средой в зондирующих полях, сформированных r, g и b бесселевыми пучками (47).
Для визуализации полей фазовой оптической плотности (51) в частотной плоскости 6 устанавливается гильберт-фильтр с когерентной передаточной функцией, которая, по аналогии с (29), описывается выражением:
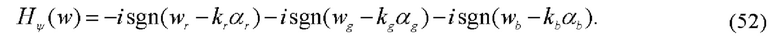
Структура гильберт-фильтра, реализующего изотропную гильберт-фильтрацию с когерентной передаточной функцией (52), показана на Фиг. 4.
Фурье-спектр поля непосредственно за гильберт-фильтром определяется, как и в (33), произведением фурье-спектра фазовых возмущений (51) на когерентную передаточную функцию гильберт-фильтра (52):
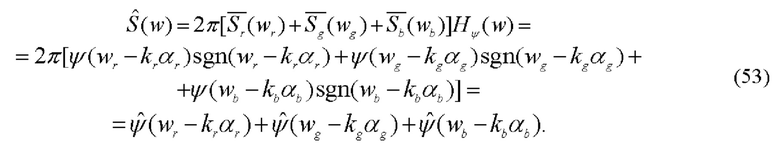
Фурье-объектив 7 выполняет, по аналогии с (34), обратное фурье-преобразование гильберт-сопряженных фурье-спектров фазовых возмущений (53):
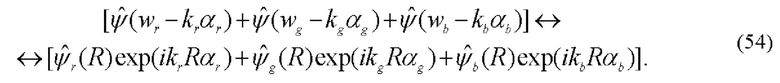
Здесь R полярный радиус в координатной плоскости фото матрицы 8.
Фотоматрица видеокамеры регистрирует изображения гильберт-визуализированных полей фазовой оптической плотности исследуемой среды (54), локализованных в пределах зондирующих r, g и b бесселевых пучков (47):
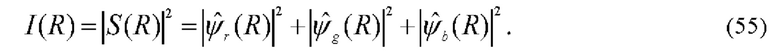
Изображения визуализированных полей фазовой оптической плотности исследуемой среды в пространственных фрагментах, ограниченных зондирующими rgb-бесселевыми пучками, обрабатываются компьютером 9, подключенным к видеокамере. Устройство по п. 3 реализует предложенный способ гильберт-визуализации полей фазовой оптической плотности газовых и конденсированных сред.
На Фиг. 2 показана упрощенная схема устройства по п. 2, реализующего предложенный способ. В этом устройстве перед аксиконом установлен источник светового поля, имеющего кольцевую концентрическую r, g и b конфигурацию, оптически сопряженную со структурой гильберт-фильтра. Гильберт-фильтр имеет концентрическую rgb-структуру.
Обозначения оптических элементов на Фиг. 2 та же, что и на Фиг. 1. В такой системе аксиконом 2 формируется три разнесенных по оптической оси r, g, b бесселевых пучка, которые объективами 3 и 4 направляются в исследуемую среду. Структура фильтра 6, реализующего изотропную гильберт-фильтрацию, оптически сопряжена со структурой фурье-спектра бесселевых пучков, локализованной в задней фурье-плоскости объектива 3.
На Фиг. 3 показана схема аксиконного формирователя бесселевых пучков для устройства п. 2, реализующего способ. Структура полихроматического гильберт-фильтра, используемого в этом устройстве, представлена на Фиг. 4. Фиг. 5 иллюстрирует формирование бесселевых пучков ступенчатым аксиконом в устройстве, показанном на Фиг. 2. В этом устройстве ступенчатым аксиконом формируются три пространственно разнесенных по оси бесселевых пучка, которые объективами 3 и 4 направляются в исследуемую среду. Структура фильтра 6, реализующего изотропную гильберт-фильтрацию, оптически сопряжена со структурой фурье-спектра бесселевых пучков, локализованных в задней фурье-плоскости объектива 3.
Технический результат предлагаемого изобретения заключается в расширении функциональных возможностей гильберт-визуализации на получение информации о пространственной структуре полей фазовой оптической плотности в конденсированных, газовых и реагирующих средах. Он достигается тем, что зондирующее поле в исследуемой среде формируется в виде пространственно сконфигурированных монохроматических или полихроматических бесселевых пучков, фурье-спектр которых оптически сопряжен с фазовой структурой изотропного гильберт-фильтра, а цвет соответствует спектральной чувствительности фотоматрицы видеокамеры. Повышение точности визуализации фазовых возмущений в исследуемой среде обеспечивается низкой расходимостью волнового фронта бесселевых пучков, образующих структуру зондирующего поля. Отсюда следует преимущество предлагаемого способа и устройств, его реализующих, по сравнению с известными аналогами и прототипом, в которых зондирующее поле формируется гауссовыми или апертурно ограниченными пучками, дифракционная расходимость которых выше расходимости бесселевых пучков.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВИЗУАЛИЗАЦИИ ПОЛЕЙ ФАЗОВОЙ ОПТИЧЕСКОЙ ПЛОТНОСТИ В ГАЗОВЫХ И КОНДЕНСИРОВАННЫХ СРЕДАХ | 2018 |
|
RU2681672C1 |
| ЦВЕТНОЙ ВИЗУАЛИЗАТОР ПОЛЕЙ ОПТИЧЕСКОЙ ПЛОТНОСТИ | 1995 |
|
RU2101744C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОЛЯ СКОРОСТЕЙ В ГАЗОВЫХ И КОНДЕНСИРОВАННЫХ СРЕДАХ | 2015 |
|
RU2621466C2 |
| ЛАЗЕРНЫЙ ДОПЛЕРОВСКИЙ ИЗМЕРИТЕЛЬ СКОРОСТИ | 2016 |
|
RU2638110C1 |
| Устройство для визулизации оптических неоднородностей | 1974 |
|
SU522482A1 |
| Устройство для формирования бесселевых пучков электромагнитного излучения в однородной прозрачной среде | 1990 |
|
SU1753446A1 |
| Способ измерения скорости | 1983 |
|
SU1093974A1 |
| Устройство для визуализации сечений оптических неоднородностей | 1975 |
|
SU538324A1 |
| Способ измерения скорости потоков | 1980 |
|
SU957107A1 |
| Лазерный доплеровский измеритель скорости | 2019 |
|
RU2707957C1 |
Изобретение относится к измерительной технике и может найти применение в экспериментальной гидро- и газодинамике, теплофизике, океанологии, а также в промышленных технологиях, связанных с необходимостью исследования полей фазовой оптической плотности в газовых, конденсированных и реагирующих средах, пламенах и струях. Заявленный способ визуализации полей фазовой оптической плотности газовых и конденсированных сред состоит в том, что в исследуемую среду направляют зондирующее световое поле, формируют пространственно-частотный фурье-спектр возмущений, индуцированных в зондирующем световом поле исследуемой средой, последовательно выполняют изотропную гильберт-фильтрацию пространственно-частотного фурье-спектра возмущённого поля, обратное фурье-преобразование, проектируют гильберт-образ возмущений светового поля на фотоматрицу видеокамеры и подвергают компьютерной обработке покадровую последовательность изображений. Причем зондирующее поле формируют в исследуемой среде в виде пространственно-сконфигурированных монохроматических или полихроматических бесселевых пучков. Устройство, реализующее способ, содержит последовательно расположенные световой источник, формирователь зондирующего светового поля, фурье-объектив, в частотной плоскости которого помещён изотропный гильберт-фильтр, и цифровую видеокамеру, подсоединённую к компьютеру. Световым источником является источник сконфигурированных бесселевых пучков, фурье-спектр которых согласован с фазовой структурой изотропного гильберт-фильтра. Устройство может быть выполнено, например, так, что формирователь сконфигурированных бесселевых пучков выполнен в виде последовательно расположенных формирователя концентрических кольцевых r, g, b пучков и аксикона, выполненного ступенчатым. Технический результат - повышение точности и расширение функциональных возможностей на гильберт-визуализацию пространственной структуры поля оптической фазовой плотности в конденсированных, газовых и реагирующих (пламя) средах. 2 н. и 2 з.п. ф-лы, 5 ил.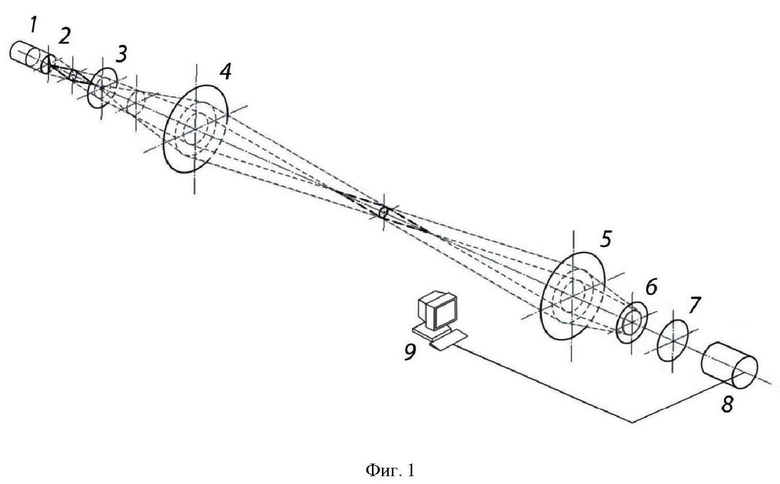
1. Способ визуализации полей фазовой оптической плотности газовых и конденсированных сред, состоящий в том, что в исследуемую среду направляют зондирующее световое поле, формируют пространственно-частотный фурье-спектр возмущений, индуцированных в зондирующем световом поле исследуемой средой, последовательно выполняют изотропную гильберт-фильтрацию пространственно-частотного фурье-спектра возмущённого поля, обратное фурье-преобразование, проектируют гильберт-образ возмущений светового поля на фотоматрицу видеокамеры и подвергают компьютерной обработке покадровую последовательность изображений, отличающийся тем, что зондирующее поле формируют в исследуемой среде в виде пространственно-сконфигурированных монохроматических или полихроматических бесселевых пучков.
2. Устройство, реализующее способ визуализации полей фазовой оптической плотности в газовых или конденсированных средах по п. 1, содержащее последовательно расположенные световой источник, формирователь зондирующего светового поля, фурье-объектив, в частотной плоскости которого помещён изотропный гильберт-фильтр, и цифровую видеокамеру, подсоединённую к компьютеру, отличающееся тем, что световым источником является источник сконфигурированных бесселевых пучков, фурье-спектр которых согласован с фазовой структурой изотропного гильберт-фильтра.
3. Устройство по п. 2, отличающееся тем, что источник сконфигурированных бесселевых пучков выполнен в виде последовательно расположенных источника концентрических кольцевых r, g, b пучков и аксикона.
4. Устройство по п. 3, отличающееся тем, что аксикон ступенчатый.
| Оптические методы исследования потоков / Ю.Н | |||
| Дубнищев, В.А | |||
| Арбузов, П.П | |||
| Белоусов, П.Я | |||
| Белоусов Новосибирск: Сиб | |||
| унив | |||
| изд-во, 2003, стр | |||
| Способ получения бензонафтола | 1920 |
|
SU363A1 |
| СПОСОБ ВИЗУАЛИЗАЦИИ ПОЛЕЙ ФАЗОВОЙ ОПТИЧЕСКОЙ ПЛОТНОСТИ В ГАЗОВЫХ И КОНДЕНСИРОВАННЫХ СРЕДАХ | 2018 |
|
RU2681672C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОЛЯ СКОРОСТЕЙ В ГАЗОВЫХ И КОНДЕНСИРОВАННЫХ СРЕДАХ | 2015 |
|
RU2621466C2 |
| СПОСОБ ПОЛУЧЕНИЯ НА ПРЕДМЕТЕ УКРАШЕНИЯ | 2006 |
|
RU2388614C2 |
| US 20130057675 A1, 07.03.2013 | |||
| ЦВЕТНОЙ ВИЗУАЛИЗАТОР ПОЛЕЙ ОПТИЧЕСКОЙ ПЛОТНОСТИ | 1995 |
|
RU2101744C1 |
| RU 95108833 A1, 20.12.1996. | |||
Авторы
Даты
2021-07-26—Публикация
2020-10-28—Подача