ОБЛАСТЬ ИЗОБРЕТЕНИЯ
Предложен новый способ оценки распределения энергии квантов излучения, например фотонов, падающих на детектор в спектроскопических системах, таких как рентгеновская или гамма-резонансная спектроскопия. Способ особенно полезен для режимов скорости счета, когда возникает проблема наложения импульсов. Ключевым этапом при выводе формулы оценки в одном из вариантов осуществления изобретения является новая формулировка проблемы, как проблемы разложения составного пуассоновского процесса. Способ можно применять к детекторам излучения любой формы, детектирующим кванты или другие корпускулы излучения, такие как рентгеновские лучи, гамма-лучи или другие фотоны, нейтроны, атомы, молекулы или сейсмические импульсы. Применение таких детекторов для спектроскопии хорошо известно. Такие применения широко описаны в уровне техники, в том числе в международных патентных заявках PCT/AU2005/001423, PCT/AU2009/000393, PCT/AU2009/000394, PCTAU2009/000395, PCT/AU2009/-001648, PCT/AU2012/000678, PCT/AU2014/050420, PCT/AU2015/050752, PCT/AU-2017/050514 и PCT/AU2017/050512, каждая из которых полностью включена в настоящий документ с целью описания потенциальных применений настоящего изобретения и любого другого справочного материала, необходимого для понимания настоящего изобретения.
1 ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ
Рентгеновская и гамма-спектроскопия лежат в основе широкого спектра научных, промышленных и коммерческих процессов. Одна из целей спектроскопии - оценить распределение энергии фотонов, падающих на детектор. С точки зрения обработки сигналов задача состоит в том, чтобы преобразовать поток импульсов, выдаваемых детектором, в гистограмму области под каждым импульсом. Импульсы генерируются в соответствии с распределением Пуассона, частота которых соответствует интенсивности рентгеновских или гамма-лучей, используемых для облучения образца. Увеличение интенсивности приводит к увеличению числа импульсов в секунду в среднем и, следовательно, сокращению времени до получения точной гистограммы. При таких применениях, как сканирование багажа в аэропортах, это напрямую увеличивает пропускную способность. Наложение импульсов происходит, когда два или более импульсов перекрываются по времени. По мере увеличения скорости счета (среднего числа импульсов в секунду) увеличивается и частота наложения импульсов. Это увеличивает сложность определения числа присутствующих импульсов и области под каждым импульсом. В пределе проблема плохо обусловлена: если два импульса начинаются практически в одно и то же время, их суперпозиция неотличима от одного импульса. Отклик детектора рентгеновского или гамма-излучения на падающие фотоны можно смоделировать как суперпозицию сверток функций 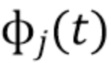 формы импульса с импульсными дельта-функциями,
формы импульса с импульсными дельта-функциями,
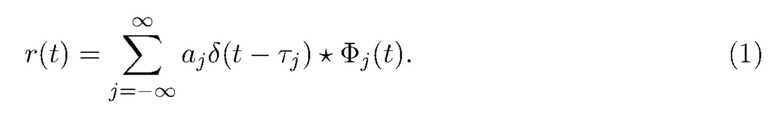
Времена прибытия …, 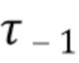 ,
, 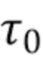 ,
, 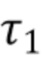 , … неизвестны и образуют процесс Пуассона. Каждое прибытие фотона моделируется дельта-функцией в момент времени
, … неизвестны и образуют процесс Пуассона. Каждое прибытие фотона моделируется дельта-функцией в момент времени 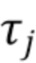 , с амплитудой
, с амплитудой 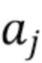 , которая пропорциональна энергии фотона и вызывает отклик
, которая пропорциональна энергии фотона и вызывает отклик 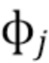 детектора с формой импульса. Амплитуды
детектора с формой импульса. Амплитуды 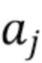 являются реализациями одинаково распределенных случайных величин
являются реализациями одинаково распределенных случайных величин 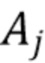 , общая функция
, общая функция 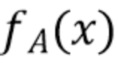 плотности вероятности которых неизвестна. Функция
плотности вероятности которых неизвестна. Функция 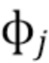 формы импульса определяется геометрией детектора и взаимодействием с фотоном. В некоторых системах изменение формы импульса минимально и им можно пренебречь, в то время как в других системах (например, HPGe) формы отдельных импульсов могут значительно отличаться друг от друга [1]. Предполагается, что импульсы всех форм являются причинно-обусловленными, т. е.
формы импульса определяется геометрией детектора и взаимодействием с фотоном. В некоторых системах изменение формы импульса минимально и им можно пренебречь, в то время как в других системах (например, HPGe) формы отдельных импульсов могут значительно отличаться друг от друга [1]. Предполагается, что импульсы всех форм являются причинно-обусловленными, т. е. 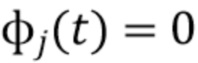 для
для 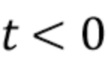 , с одной модой, конечной энергии, и экспоненциально затухают к нулю при
, с одной модой, конечной энергии, и экспоненциально затухают к нулю при 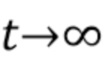 . Интеграл от функций формы импульса нормирован на единицу, т. е.
. Интеграл от функций формы импульса нормирован на единицу, т. е. 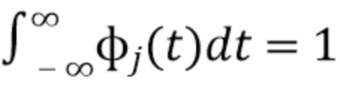 так, чтобы площадь под импульсом была равна
так, чтобы площадь под импульсом была равна 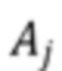 . Наблюдаемый сигнал состоит из выходного сигнала детектора, искаженного шумом, т. е.
. Наблюдаемый сигнал состоит из выходного сигнала детектора, искаженного шумом, т. е.
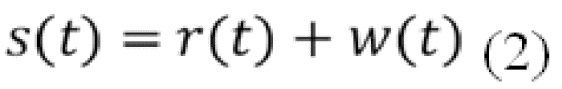
Математическая цель коррекции наложения импульсов состоит в том, чтобы оценить 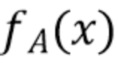 , заданной равномерно квантованной версией
, заданной равномерно квантованной версией 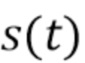 конечной длины. Мы предполагаем, что распределение шума
конечной длины. Мы предполагаем, что распределение шума 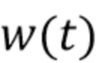 является гауссовым с нулевым средним и известной дисперсией
является гауссовым с нулевым средним и известной дисперсией 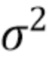 . Мы также предполагаем, что времена прибытий фотонов образуют однородный пуассоновский процесс с известной скоростью, состоящий из отклика
. Мы также предполагаем, что времена прибытий фотонов образуют однородный пуассоновский процесс с известной скоростью, состоящий из отклика 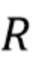 детектора, искаженного процессом
детектора, искаженного процессом 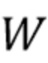 шума, где
шума, где 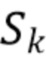 ,
, 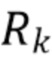 , и
, и 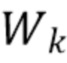 , представляют k-е элементы каждой серии и где
, представляют k-е элементы каждой серии и где 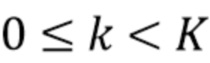 . Пусть
. Пусть 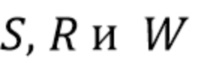 будут равномерно квантованными временными интервалами, соответствующими этим сигналам,
будут равномерно квантованными временными интервалами, соответствующими этим сигналам,
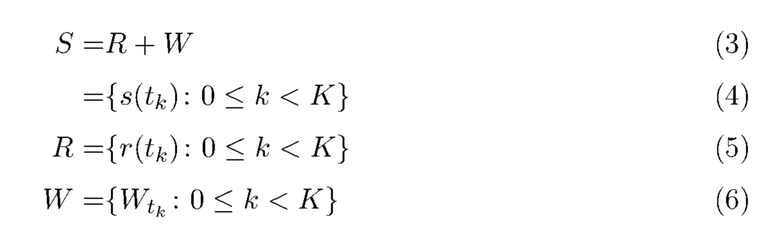
где 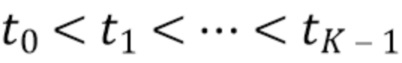
Краткое изложение методик обработки импульсов: на протяжении десятилетий было предложено множество подходов для решения проблемы наложения импульсов. Подходы можно в целом разделить на два типа: основанные на временных интервалах и основанные на энергетических областях. Популярной стратегией является попытка детектировать, когда на временном интервале произошло наложение, и либо отклонить, либо вводить поправку на затронутые импульсы. Ранние спектроскопические системы использовали подход, основанный на режекции, наряду с согласованной фильтрацией. Недостатком этого подхода является то, что все большая часть импульсов отбраковывается по мере роста вероятности наложения. Система быстро утрачивает чувствительность, устанавливая верхний предел скорости счета [1]. Число стратегий, которые компенсируют или корректируют наложение, растет с увеличением дешевой вычислительной мощности. К ним относятся подгонка шаблона [2], вычитание базовой линии [3], адаптивная фильтрация [4, 5], разреженная регрессия [6, 7] и многое другое. Все эти подходы пытаются идентифицировать и скомпенсировать наложение на временном интервале и, как правило, лучше всего подходят для систем со слабым изменением формы импульса. Сложность этих подходов значительно возрастает с увеличением изменчивости между формами импульсов 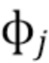 . Можно показать, что любой способ, который пытается охарактеризовать отдельные импульсы, будет страдать от наложений. Лучшее, что могут дать эти подходы, - это уменьшить вероятность возникновения наложений. Подходы, основанные на энергии, пытаются решить проблему наложения на основе статистики сочетания импульсов, а не отдельных импульсов. Обычно они работают с гистограммами расчетной энергии (области под кластерами импульсов). Ранние работы Wielopolski и Gardner [8] и более поздние расширения их идеи [9] работают в основном в энергетических областях с использованием стратегий, основанных на сочетании. Trigano и др. [10, 11] оценивают спектр налетающих частиц, используя плотность безусловного распределения из совместного распределения статистических свойств кластеров импульсов переменной длины, где детектируются начало и конец каждого кластера. Это избавляет от необходимости идентифицировать отдельные импульсы и устойчиво к изменению формы импульса. Ilhe и др. [12] исследуют экспоненциальные процессы дробового шума, ограничивая форму импульса простой экспонентой, чтобы получить удобные результаты. Дальнейшая работа [13] была проделана, чтобы сделать возможным более широкий диапазон форм импульсов. В обоих случаях требуется знание формы импульса, а также оценки характеристической функции и ее производной.
. Можно показать, что любой способ, который пытается охарактеризовать отдельные импульсы, будет страдать от наложений. Лучшее, что могут дать эти подходы, - это уменьшить вероятность возникновения наложений. Подходы, основанные на энергии, пытаются решить проблему наложения на основе статистики сочетания импульсов, а не отдельных импульсов. Обычно они работают с гистограммами расчетной энергии (области под кластерами импульсов). Ранние работы Wielopolski и Gardner [8] и более поздние расширения их идеи [9] работают в основном в энергетических областях с использованием стратегий, основанных на сочетании. Trigano и др. [10, 11] оценивают спектр налетающих частиц, используя плотность безусловного распределения из совместного распределения статистических свойств кластеров импульсов переменной длины, где детектируются начало и конец каждого кластера. Это избавляет от необходимости идентифицировать отдельные импульсы и устойчиво к изменению формы импульса. Ilhe и др. [12] исследуют экспоненциальные процессы дробового шума, ограничивая форму импульса простой экспонентой, чтобы получить удобные результаты. Дальнейшая работа [13] была проделана, чтобы сделать возможным более широкий диапазон форм импульсов. В обоих случаях требуется знание формы импульса, а также оценки характеристической функции и ее производной.
2 СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Мы выбрали подход коррекции наложений, основанный на энергии, чтобы i) избежать ограничений, связанных с детектированием отдельных импульсов [14], и ii) иметь возможность обрабатывать изменение формы импульса без чрезмерного увеличения сложности вычислений. Вместо того, чтобы использовать подходы совместного распределения [10, 11] или дробового процесса [12], мы перерабатываем проблему наложения как проблему «разложения» составного пуассоновского процесса. Составной пуассоновский процесс - это случайный процесс с дискретным временем, каждый компонент которого состоит из суммы случайного числа независимых одинаково распределенных случайных величин, где число случайных величин в каждой сумме распределено по Пуассону [15]. «Разложение» составного пуассоновского процесса - это задача использования случайных сумм для оценки распределения, из которого были взяты случайные величины. Buchmann и Grübel [16] сформулировали разложение сложных пуассоновских процессов в контексте страховых требований и теории очередей. Разложение равномерно квантованных сложных пуассоновских процессов привлекло некоторое внимание в последнее время [16, 17, 18, 12, 19]. Контекст этих выводов часто предполагает (резонно), что каждое событие поддается детектированию (т.е. нет двусмысленности относительно числа событий), или что формулы оценки плотности обусловлены по меньшей мере одним событием, происходящим при каждом наблюдении [20]. Эти предположения содержат ограничивающий параметр при решении проблемы спектроскопических наложений.
Исследованию непараметрического разложения без обусловливания детектирования событий уделялось относительно мало внимания в литературе. Gugushvili [18] предлагает непараметрическую формулу параметра ядра для задачи разложения в присутствии гауссовского шума. В вариантах осуществления изобретения авторы изобретения предположили, что после того, как получен способ выбора параметра ядра плотности полосы пропускания, наряду со способом преобразования наблюдаемого выходного сигнала детектора для соответствия математической модели, эту формулу параметра можно легко расширить и применить при новой формулировке проблемы спектроскопических наложений.
В соответствии с первым широким аспектом изобретения предлагается способ определения спектра энергий отдельных квантов излучения, принимаемых детектором излучения, содержащий этапы: (1) получения временного ряда цифровых наблюдений от детектора излучения, содержащего импульсы, соответствующие детектированию отдельных квантов; (2) вычисления спектрально-зависимых статистических данных из сигнала детектора, при этом спектрально-зависимые статистические данные задают отображение в виде карты из плотности амплитуд импульсов в спектрально-зависимые статистические данные; (3) определения спектра путем оценки плотности амплитуд импульсов путем применения инверсии отображения в виде карты к спектрально-зависимым статистическим данным.
В вариантах осуществления спектрально-зависимые статистические данные могут основываться на сумме цифровых наблюдений на множестве временных интервалов, и отображение в виде карты может быть задано с использованием аппроксимируемого составного пуассоновского процесса, который может быть дополнен смоделированным шумом. Отображение в виде карты можно выразить как отношение между характеристическими функциями амплитуд, спектрально-зависимыми статистическими данными и смоделированным шумом. Характеристические функции спектрально-зависимых статистических данных могут быть вычислены с использованием гистограммы суммы цифровых наблюдений, к которой применяется обратное преобразование Фурье. Вычисление характеристической функции амплитуд может содержать использование фильтра нижних частот.
В первом варианте осуществления упомянутое множество временных интервалов не перекрываются и имеют постоянную длину L и каждый интервал выбирается, чтобы охватить ноль или более приближенно целые кластеры импульсов. Этого можно достичь через требование максимального значения сигнала детектора в начале и в конце каждого временного интервала. В этом варианте осуществления составной пуассоновский процесс может быть задан как сумма амплитуд импульсов на каждом временном интервале. Отображение в виде карты может быть выражено, как задано в уравнениях (40) и (41), которые могут быть дополнены оконными функциями.
Во втором варианте осуществления множество интервалов содержит первый набор неперекрывающихся временных интервалов постоянной длины L, выбранных без учета совокупности кластеров импульсов, и второй набор неперекрывающихся временных интервалов постоянной длины L1 меньшей L, также выбранных без учета совокупности кластеров импульсов. L является по меньшей мере такой же, как длительность импульсов и предпочтительно, чтобы L1 была меньше длительности импульсов. В этом варианте осуществления составной пуассоновский процесс может быть задан, как в Разделе 6. Отображение в виде карты может быть выражено, как задано в Разделе 6. Второй вариант осуществления может использовать процессы и вычисления для каждого набора временных интервалов, как задано для набора временных интервалов в первом варианте осуществления.
В вариантах осуществления используется определяемая данными стратегия, которая приводит к почти оптимальному выбору параметра ядра, который минимизирует интегральную квадратичную ошибку (ISE) оцененной функции плотности вероятности энергий падающих фотонов.
Согласно второму широкому аспекту изобретения предлагается способ оценки скорости счета отдельных квантов излучения, принимаемых детектором излучения, содержащий этапы: (1) получения временного ряда цифровых наблюдений от детектора излучения, содержащего импульсы, соответствующие детектированию отдельных квантов; (2) вычисления спектрально-зависимых статистических данных из сигнала детектора, при этом спектрально-зависимые статистические данные используют интервалы постоянной длины L и постоянной длины L1, как описано выше в отношении 1-го широкого аспекта; (3) определения оценки характеристической функции составного пуассоновского процесса, используя формулу (109); (4) оценки скорости счета из оценки характеристической функции. Этап (4), описанный выше, может быть достигнут с помощью процедуры оптимизации или некоторых других средств для подгонки кривой, оценки смещения постоянного тока из логарифма оценки характеристической функции или подгонки кривой к логарифму оценки характеристической функции.
Остальная часть это заявки организована следующим образом. Разделы 3, 4 и 5 относятся к 1-му варианту осуществления 1-го аспекта изобретения. В разделе 3 представлены предварительные сведения, определены обозначения, очерчены математическая модель и дан вывод формулы оценки 1-го варианта осуществления, в том числе модификаций. В разделе 4 показаны характеристики модифицированной формулы оценки 1-го варианта осуществления как для смоделированных, так и для экспериментальных данных, а также обсуждаются результаты. В Разделе 5 дается заключение для 1-го варианта. В Разделе 6 описан 2-й вариант осуществления со ссылкой на 1-й вариант, где это уместно. В Разделе 7 описан 2-й аспект изобретения, новый способ оценки скорости счета.
3 ВЫВОД ФОРМУЛЫ ОЦЕНКИ ПЕРВОГО ВАРИАНТА ОСУЩЕСТВЛЕНИЯ
Общий подход, который мы применяем к решению проблемы наложения, основан на следующей стратегии; i) получение статистических данных из 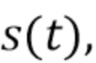 которая чувствительна к распределению энергий падающих фотонов, и оценка этих статистических данных, с использованием наблюдаемой квантованной версии
которая чувствительна к распределению энергий падающих фотонов, и оценка этих статистических данных, с использованием наблюдаемой квантованной версии 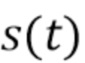 конечной длины, ii) получение отображения в виде карты плотности энергии падающих фотонов в статистические свойства наблюдаемых статистических данных, iii) оценка плотности энергии падающих фотонов посредством инвертирования отображения в виде карты. В Разделе 3.1 описывается наш выбор статистических данных. В Разделе 3.2 утверждается, что эти статистические данные (приблизительно) имеют то же распределение, что и составной пуассоновский процесс. В Разделе 3.3 вводится способ разложения для восстановления спектра из этих статистических данных. Он основан на алгоритме разложения из [18], но доработан для получения почти оптимальных характеристик с точки зрения интегральной квадратичной ошибки. Наш подход к проблеме наложения следует общей теме нахождения некоторых статистических данных
конечной длины, ii) получение отображения в виде карты плотности энергии падающих фотонов в статистические свойства наблюдаемых статистических данных, iii) оценка плотности энергии падающих фотонов посредством инвертирования отображения в виде карты. В Разделе 3.1 описывается наш выбор статистических данных. В Разделе 3.2 утверждается, что эти статистические данные (приблизительно) имеют то же распределение, что и составной пуассоновский процесс. В Разделе 3.3 вводится способ разложения для восстановления спектра из этих статистических данных. Он основан на алгоритме разложения из [18], но доработан для получения почти оптимальных характеристик с точки зрения интегральной квадратичной ошибки. Наш подход к проблеме наложения следует общей теме нахождения некоторых статистических данных 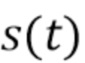 , которые чувствительны к лежащему в их основе спектру, оценки этих статистических данных из квантованной версии
, которые чувствительны к лежащему в их основе спектру, оценки этих статистических данных из квантованной версии 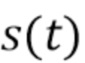 за конечное время, а затем инвертирования карты, которая описывает статистические свойства этих статистических данных с учетом лежащего в их основе спектра, тем самым производя оценку спектра.
за конечное время, а затем инвертирования карты, которая описывает статистические свойства этих статистических данных с учетом лежащего в их основе спектра, тем самым производя оценку спектра.
3.1 Выбор статистических данных
Мы хотим получить оценки энергии фотонов из наблюдаемого сигнала, приведенного в (2). В типичных современных спектроскопических системах выходной сигнал 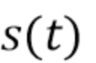 детектора равномерно дискретизируется посредством АЦП. Без потери общности мы предполагаем, что исходные наблюдения, доступные алгоритму, следующие:
детектора равномерно дискретизируется посредством АЦП. Без потери общности мы предполагаем, что исходные наблюдения, доступные алгоритму, следующие: 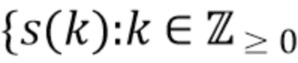 }. Поскольку идентификация отдельных импульсов может быть затруднена, вместо этого мы ищем интервалы фиксированной длины
}. Поскольку идентификация отдельных импульсов может быть затруднена, вместо этого мы ищем интервалы фиксированной длины 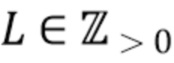 , содержащие ноль или более кластеров импульсов. А именно, мы задаем эти интервалы как
, содержащие ноль или более кластеров импульсов. А именно, мы задаем эти интервалы как 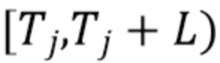 , где
, где
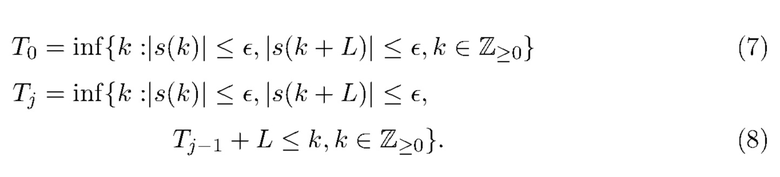
Здесь 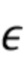 выбирается как компромисс между ошибками в оценке энергии и вероятностью создания интервала. Значение
выбирается как компромисс между ошибками в оценке энергии и вероятностью создания интервала. Значение 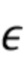 должно быть достаточно малым, чтобы гарантировать, что ошибка в оценке полной энергии фотонов, прибывающих в течение каждого интервала, будет достаточно низкой, но при этом достаточно большой по отношению к дисперсии шума, чтобы гарантировать получение большого числа интервалов. Хотя вероятность разделения наблюдаемых данных на интервалы приближается к нулю по мере того, как скорость счета стремится к бесконечности, этот подход утрачивает чувствительность при более высоких скоростях счета по сравнению со стратегиями режекции наложения, основанными на отдельных импульсах, поскольку разрешено наложение нескольких фотонов на каждом интервале. Раздел 4.2 описывает выбор
должно быть достаточно малым, чтобы гарантировать, что ошибка в оценке полной энергии фотонов, прибывающих в течение каждого интервала, будет достаточно низкой, но при этом достаточно большой по отношению к дисперсии шума, чтобы гарантировать получение большого числа интервалов. Хотя вероятность разделения наблюдаемых данных на интервалы приближается к нулю по мере того, как скорость счета стремится к бесконечности, этот подход утрачивает чувствительность при более высоких скоростях счета по сравнению со стратегиями режекции наложения, основанными на отдельных импульсах, поскольку разрешено наложение нескольких фотонов на каждом интервале. Раздел 4.2 описывает выбор 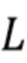 и
и 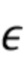 для реальных данных. Каждый интервал содержит неизвестное случайное число импульсов и может содержать ноль импульсов.
для реальных данных. Каждый интервал содержит неизвестное случайное число импульсов и может содержать ноль импульсов.
Мы оцениваем полную энергию фотона 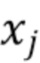 в интервале
в интервале 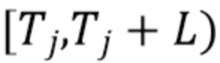 , используя дискретизированные исходные наблюдения. Поскольку площадь под каждым импульсом пропорциональна энергии фотона
, используя дискретизированные исходные наблюдения. Поскольку площадь под каждым импульсом пропорциональна энергии фотона 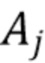 , заданной в (1), положим
, заданной в (1), положим

Число прибытий фотонов, энергия каждого прибывающего фотона и выходной шум детектора на каждом интервале 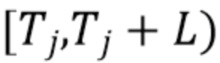 предполагаются случайными и независимыми от других интервалов. Для форм импульсов с экспоненциальным затуханием небольшое количество энергии фотонов, прибывающих в некоторый интервал, может быть записано в следующий интервал. Величина утечки пропорциональна
предполагаются случайными и независимыми от других интервалов. Для форм импульсов с экспоненциальным затуханием небольшое количество энергии фотонов, прибывающих в некоторый интервал, может быть записано в следующий интервал. Величина утечки пропорциональна 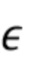 и пренебрежимо мала для достаточно малых
и пренебрежимо мала для достаточно малых 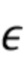 . Следовательно, оценки
. Следовательно, оценки 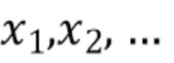 можно рассматривать как реализацию слабозависимого стационарного процесса, в котором каждая оценка одинаково распределена в соответствии со случайной величиной
можно рассматривать как реализацию слабозависимого стационарного процесса, в котором каждая оценка одинаково распределена в соответствии со случайной величиной 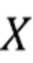 . Эта зависимость проиллюстрирована на Фиг. 1 для случая отсутствия шума с использованием типичной формы импульса.
. Эта зависимость проиллюстрирована на Фиг. 1 для случая отсутствия шума с использованием типичной формы импульса.
3.2 Аппроксимация через составной пуассоновский процесс
В этом подразделе мы описываем распределение 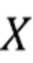 через
через 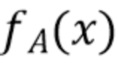 . Затем мы его инвертируем в разделе 3.3, чтобы получить формулу оценки плотности
. Затем мы его инвертируем в разделе 3.3, чтобы получить формулу оценки плотности 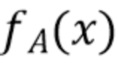 . Используя (9), (2), (1) и тот факт, что
. Используя (9), (2), (1) и тот факт, что 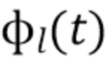 является причинно-обусловленной, мы имеем
является причинно-обусловленной, мы имеем
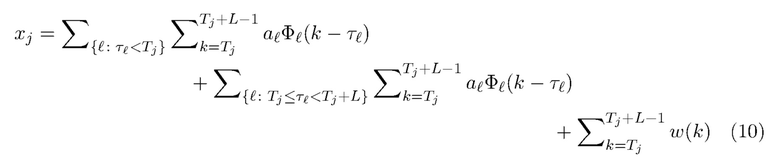
Как поясняется ниже, это упрощается до

где
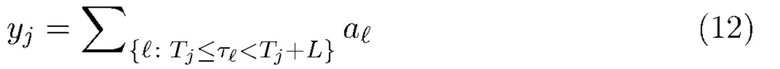
и

И 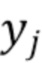 и
и 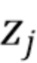 представляют собой н.о.р. (независимую и одинаково распределенную) последовательность случайных величин. Обозначим их распределения через
представляют собой н.о.р. (независимую и одинаково распределенную) последовательность случайных величин. Обозначим их распределения через 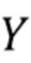 и
и 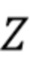 . Распределение
. Распределение 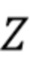 полностью определяется из распределения
полностью определяется из распределения 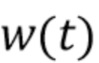 , которое предполагается гауссовым с нулевым средним и известной дисперсией
, которое предполагается гауссовым с нулевым средним и известной дисперсией 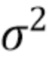 . Более того,
. Более того, 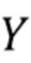 является составным пуассоновским процессом, поскольку число членов в суммировании (число прибытий фотонов в интервале длины
является составным пуассоновским процессом, поскольку число членов в суммировании (число прибытий фотонов в интервале длины 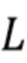 ) имеет статистику Пуассона. Уравнения (11) - (13) обосновываются следующим образом. Первый член (10) представляет утечку из более ранних интервалов и приблизительно равен нулю. Это легко показать для нормально распределенного шума, выполнив разложение в ряд Тейлора в окрестности=
) имеет статистику Пуассона. Уравнения (11) - (13) обосновываются следующим образом. Первый член (10) представляет утечку из более ранних интервалов и приблизительно равен нулю. Это легко показать для нормально распределенного шума, выполнив разложение в ряд Тейлора в окрестности= 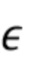 0.
0.
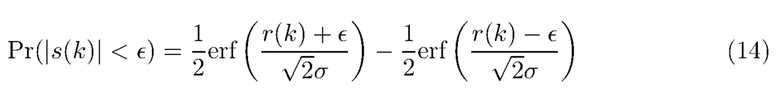
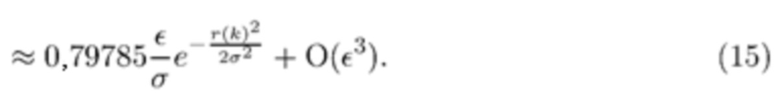
Таким образом, существует конечная, но малая вероятность того, что некоторая энергия, принадлежащая предыдущему интервалу, будет включена в текущую оценку. На практике этот вклад сопоставим с шумом при достаточно малых 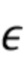 . Третий член в (10) равен нулю, поскольку
. Третий член в (10) равен нулю, поскольку 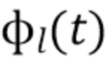 является причинно-обусловленной. Второй член в (10) можно записать как
является причинно-обусловленной. Второй член в (10) можно записать как
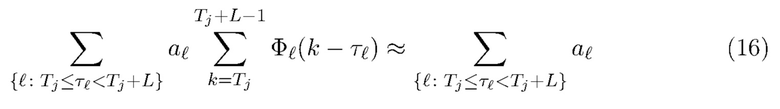
где мы предполагаем, что формы импульсов достаточно гладкие, так что 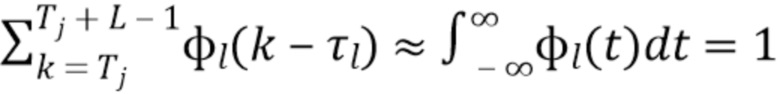 . Она аппроксимирует полную энергию всех фотонов, прибывающих в интервале
. Она аппроксимирует полную энергию всех фотонов, прибывающих в интервале 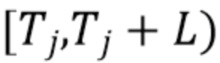 . Пусть
. Пусть 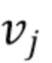 обозначает число прибытий фотонов в интервале
обозначает число прибытий фотонов в интервале 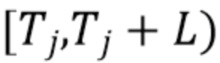 . Мы предполагаем, что
. Мы предполагаем, что 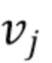 является реализацией однородного пуассоновского процесса с параметром скорости λ, где λ выражается через ожидаемое число фотонов на интервал длины
является реализацией однородного пуассоновского процесса с параметром скорости λ, где λ выражается через ожидаемое число фотонов на интервал длины 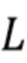 . В дальнейшем будем предполагать, что (11) выполняется точно, и писать
. В дальнейшем будем предполагать, что (11) выполняется точно, и писать
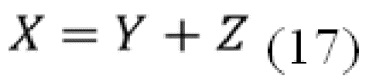
Наконец, запишем 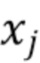 как
как
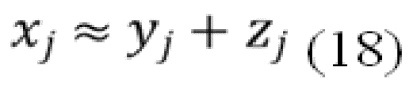
где мы предполагаем, что 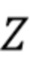 имеет известную дисперсию
имеет известную дисперсию 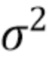 . В этом подразделе мы моделируем статистику Раздела 3.1, используя составной пуассоновский процесс. Это позволяет нам вывести формулу оценки плотности
. В этом подразделе мы моделируем статистику Раздела 3.1, используя составной пуассоновский процесс. Это позволяет нам вывести формулу оценки плотности 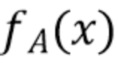 через наблюдаемые величины. Число фотонов, прибывающих в интервале
через наблюдаемые величины. Число фотонов, прибывающих в интервале 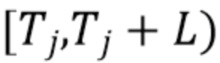 , является пуассоновской случайной величиной, которую мы обозначаем
, является пуассоновской случайной величиной, которую мы обозначаем 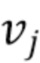 . Полная энергия в интервале
. Полная энергия в интервале 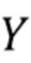 может быть смоделирована как составной пуассоновский процесс, т. е.
может быть смоделирована как составной пуассоновский процесс, т. е.
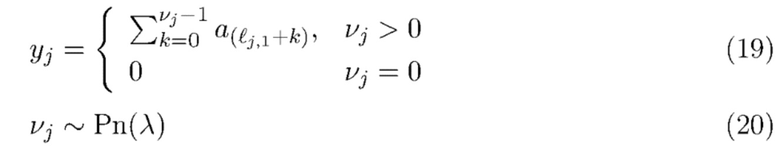
где 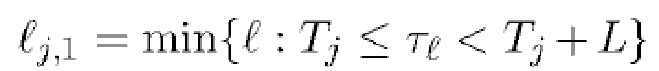 - индекс времени прибытия первого фотона в интервале, предполагается, что времена прибытия упорядочены, а
- индекс времени прибытия первого фотона в интервале, предполагается, что времена прибытия упорядочены, а 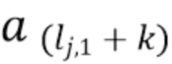 , представляющие энергию фотона, являются независимыми реализациями случайной величины
, представляющие энергию фотона, являются независимыми реализациями случайной величины 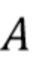 с функцией плотности
с функцией плотности 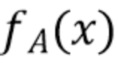 .
. 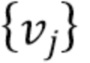 образуют однородный пуассоновский процесс с параметром скорости λ. Коэффициент Пуассона λ выражается через ожидаемое число фотонов на интервале длины
образуют однородный пуассоновский процесс с параметром скорости λ. Коэффициент Пуассона λ выражается через ожидаемое число фотонов на интервале длины 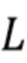 .
.

Связь между реализациями 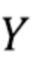 и дискретизированным откликом детектора проиллюстрирована на Фиг.1. Наблюдаемое
и дискретизированным откликом детектора проиллюстрирована на Фиг.1. Наблюдаемое 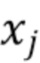 можно аппроксимировать через
можно аппроксимировать через 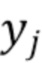 , подставив (2) в (9),
, подставив (2) в (9),
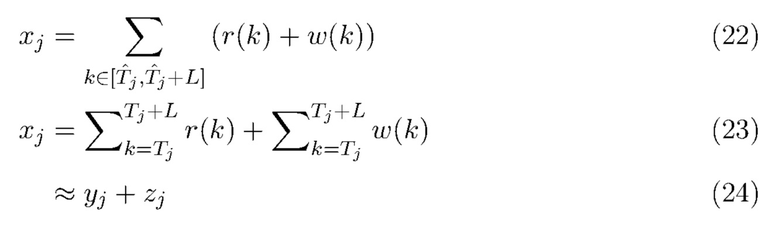
где 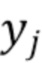 - реализация ненаблюдаемой случайной величины
- реализация ненаблюдаемой случайной величины 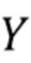 , которая представляет энергию фотона в интервале отклика детектора с дискретным временем,
, которая представляет энергию фотона в интервале отклика детектора с дискретным временем,

где 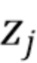 - реализация
- реализация 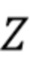 , независимой случайной величины, представляющей ошибки в процессе выборки и оценке
, независимой случайной величины, представляющей ошибки в процессе выборки и оценке 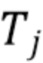 . Мы предполагаем, что Z имеет известную дисперсию
. Мы предполагаем, что Z имеет известную дисперсию 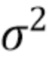 . С учетом этих определений
. С учетом этих определений 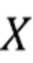 и
и 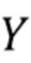 число интервалов, которые могут быть найдены на конечной длине выходного сигнала детектора, является случайной величиной
число интервалов, которые могут быть найдены на конечной длине выходного сигнала детектора, является случайной величиной 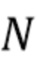 . При высоких скоростях счета этот подход утрачивает чувствительность, поскольку вероятность разделения наблюдаемых данных на интервалы приближается к нулю. Начало утраты чувствительности происходит при более высоких скоростях счета по сравнению со стратегиями, основанными на режекции накопления, поскольку на каждом интервале разрешается накопление нескольких фотонов. Предположим, что временной ряд, заданный в (3) - (6), был равномерно квантован. Без ограничения общности, предположим, что интервалы единичной выборки начинаются с
. При высоких скоростях счета этот подход утрачивает чувствительность, поскольку вероятность разделения наблюдаемых данных на интервалы приближается к нулю. Начало утраты чувствительности происходит при более высоких скоростях счета по сравнению со стратегиями, основанными на режекции накопления, поскольку на каждом интервале разрешается накопление нескольких фотонов. Предположим, что временной ряд, заданный в (3) - (6), был равномерно квантован. Без ограничения общности, предположим, что интервалы единичной выборки начинаются с 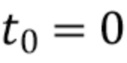 , т. е.
, т. е. 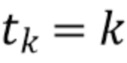 ,
, 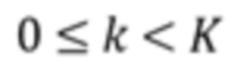 . Пусть R - случайный процесс с дискретным временем, представляющий дискретизированный отклик (1) детектора. Пусть
. Пусть R - случайный процесс с дискретным временем, представляющий дискретизированный отклик (1) детектора. Пусть 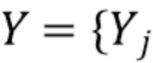 : 0
: 0 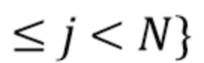 - случайный процесс с дискретным временем, компоненты
- случайный процесс с дискретным временем, компоненты 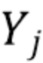 которого представляют полную энергию фотонов, прибывающих в течение фиксированного интервала времени. Составной пуассоновский процесс можно использовать для моделирования
которого представляют полную энергию фотонов, прибывающих в течение фиксированного интервала времени. Составной пуассоновский процесс можно использовать для моделирования 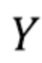 т. е.,
т. е.,
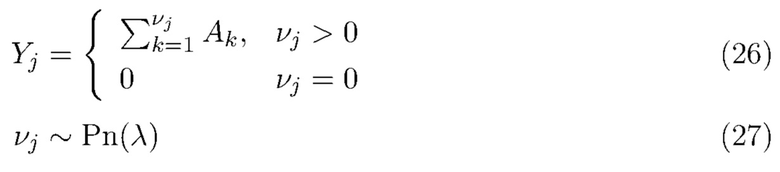
где 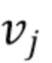 - независимая пуассоновская случайная величина, а
- независимая пуассоновская случайная величина, а 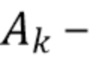 независимые одинаково распределенные случайные величины с функцией плотности
независимые одинаково распределенные случайные величины с функцией плотности 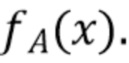
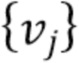 образуют однородный пуассоновский процесс с параметром скорости λ. Процесс
образуют однородный пуассоновский процесс с параметром скорости λ. Процесс 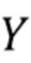 нельзя наблюдать непосредственно. Предположим, что форма импульса
нельзя наблюдать непосредственно. Предположим, что форма импульса 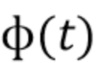 имеет конечный носитель. Пусть
имеет конечный носитель. Пусть 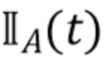 - индикаторная функция для множества
- индикаторная функция для множества 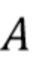 . Пусть длительность импульса
. Пусть длительность импульса 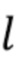 дается выражением
дается выражением 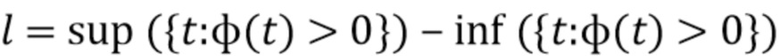 . Пусть
. Пусть 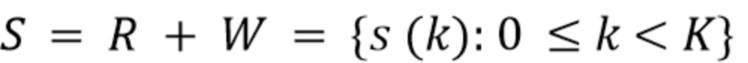 - случайный процесс с дискретным временем, представляющий наблюдаемый вывод детектора, заданный формулой (2). Он состоит из отклика детектора
- случайный процесс с дискретным временем, представляющий наблюдаемый вывод детектора, заданный формулой (2). Он состоит из отклика детектора 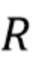 , искаженного шумовым процессом
, искаженного шумовым процессом 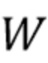 . Без ограничения общности мы предполагаем единичные интервалы выборки. Из наблюдений
. Без ограничения общности мы предполагаем единичные интервалы выборки. Из наблюдений 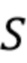 формируем процесс
формируем процесс 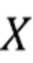 , где
, где

и где 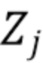 - случайная величина из независимого шумового процесса с известной дисперсией
- случайная величина из независимого шумового процесса с известной дисперсией 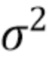 . Простая модель для проверки теории получается, когда мы полагаем форму импульса
. Простая модель для проверки теории получается, когда мы полагаем форму импульса 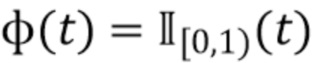 в (1), и в этом случае мы полагаем
в (1), и в этом случае мы полагаем 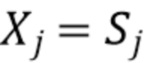 а
а 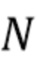 - просто длина
- просто длина 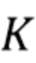 выборки. Для реальных данных получить
выборки. Для реальных данных получить 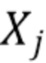 из
из 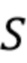 сложнее. В этом случае мы разбиваем процесс
сложнее. В этом случае мы разбиваем процесс 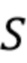 на неперекрывающиеся блоки длины
на неперекрывающиеся блоки длины 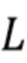 , где
, где 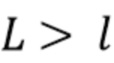 . Коэффициент Пуассона λ выражается в фотонах на блок. Начало каждого блока
. Коэффициент Пуассона λ выражается в фотонах на блок. Начало каждого блока 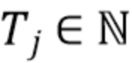 выбирается таким образом, чтобы полная энергия любого импульса полностью содержалась в блоке, в который он прибывает
выбирается таким образом, чтобы полная энергия любого импульса полностью содержалась в блоке, в который он прибывает
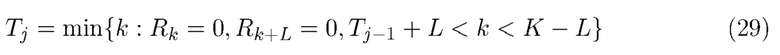
На Фиг.1 показано, что
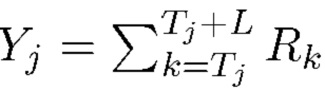 .
.
Мы полагаем
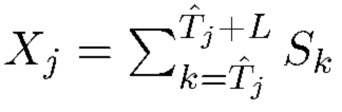

где 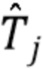 - оценка
- оценка 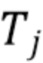 , в Разделе 4.2 описывается выбор
, в Разделе 4.2 описывается выбор 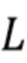 и
и 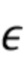 для реальных данных. При таком определении
для реальных данных. При таком определении 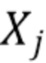 число компонентов в
число компонентов в 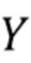 становится случайной величиной для заданной длины
становится случайной величиной для заданной длины 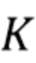 выборки. При высоких скоростях счета этот подход утрачивает чувствительность, поскольку вероятность создания блока приближается к нулю. Начало утраты чувствительности происходит при более высоких скоростях счета по сравнению со стратегиями, основанными на режекции накопления, поскольку в каждом блоке разрешается накопление нескольких фотонов. Пусть
выборки. При высоких скоростях счета этот подход утрачивает чувствительность, поскольку вероятность создания блока приближается к нулю. Начало утраты чувствительности происходит при более высоких скоростях счета по сравнению со стратегиями, основанными на режекции накопления, поскольку в каждом блоке разрешается накопление нескольких фотонов. Пусть 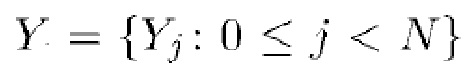 - случайный процесс с дискретным временем, компоненты которого
- случайный процесс с дискретным временем, компоненты которого 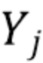 задаются формулами
задаются формулами
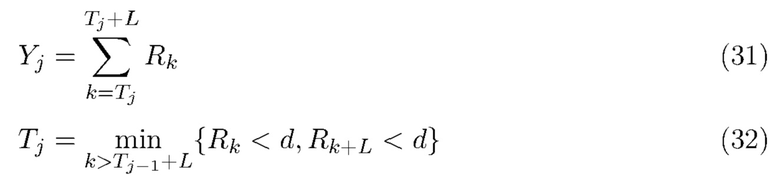
где 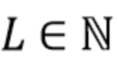 - константа, выбранная таким образом, что h и d - небольшое пороговое значение, близкое к нулю. Таким образом, случайная величина
- константа, выбранная таким образом, что h и d - небольшое пороговое значение, близкое к нулю. Таким образом, случайная величина 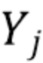 представляет собой полную энергию фотонов, прибывающих в течение фиксированного интервала времени длиной
представляет собой полную энергию фотонов, прибывающих в течение фиксированного интервала времени длиной 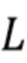 . Значение d гарантирует, что сигнал, связанный с прибытием фотонов, очень мал в начале и в конце каждого интервала. Это проиллюстрировано на Фиг. 1. Составной пуассоновский процесс можно использовать для моделирования
. Значение d гарантирует, что сигнал, связанный с прибытием фотонов, очень мал в начале и в конце каждого интервала. Это проиллюстрировано на Фиг. 1. Составной пуассоновский процесс можно использовать для моделирования 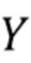 , т. е.
, т. е.
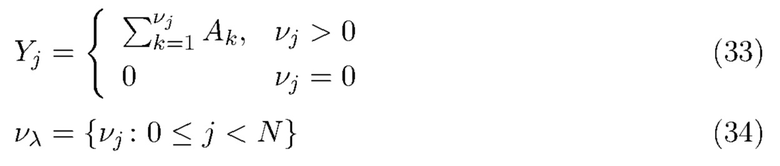

где 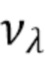 - однородный пуассоновский процесс с параметром скорости λ, а
- однородный пуассоновский процесс с параметром скорости λ, а 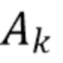 € независимые одинаково распределенные случайные величины с функцией плотности
€ независимые одинаково распределенные случайные величины с функцией плотности 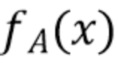 . Пусть
. Пусть 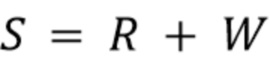 - случайный процесс с дискретным временем, представляющий дискретизированный выходной сигнал детектора, заданный формулой (2). Он состоит из отклика детектора
- случайный процесс с дискретным временем, представляющий дискретизированный выходной сигнал детектора, заданный формулой (2). Он состоит из отклика детектора 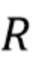 , искаженного шумовым процессом
, искаженного шумовым процессом 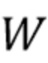 . Процесс
. Процесс 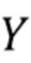 нельзя наблюдать непосредственно. Используя (2), (25) и (32), мы моделируем наблюдения процессом
нельзя наблюдать непосредственно. Используя (2), (25) и (32), мы моделируем наблюдения процессом 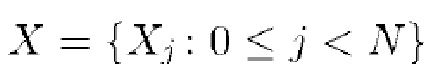 , т. е.
, т. е.
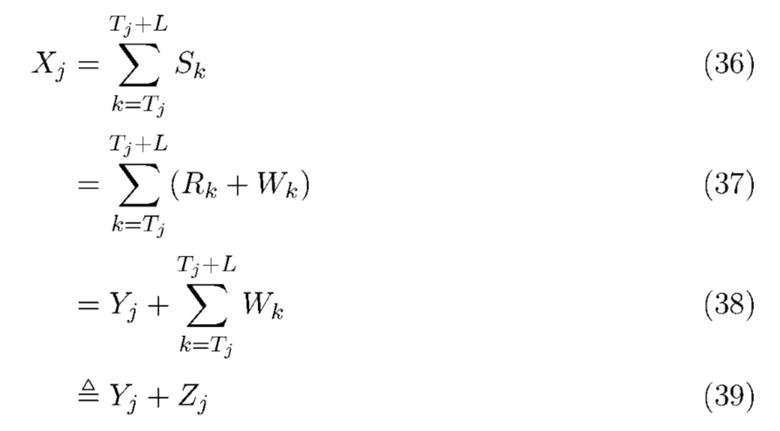
где 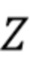 шумовой процесс с известной дисперсией
шумовой процесс с известной дисперсией 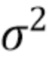 . Все случайные величины
. Все случайные величины 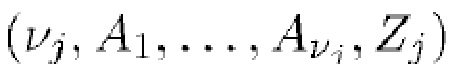 , участвующие в моделировании данного наблюдения
, участвующие в моделировании данного наблюдения 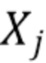 , считаются независимыми. Пусть
, считаются независимыми. Пусть 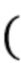
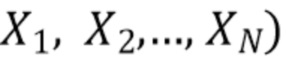 -
- 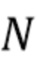 независимых одинаково распределенных наблюдений. Пусть
независимых одинаково распределенных наблюдений. Пусть 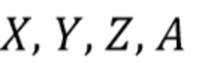 - наборы
- наборы 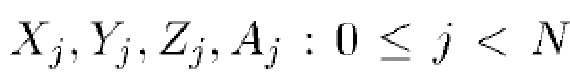 . Пусть соответствующие характеристические функции будут
. Пусть соответствующие характеристические функции будут 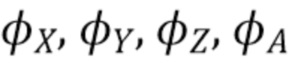 .
.
3.3 Основная форма оценки
Мы стремимся инвертировать отображение в виде карты распределения энергии 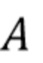 фотонов в распределение
фотонов в распределение 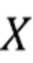 . Наша стратегия состоит в том, чтобы сначала получить характеристическую функцию
. Наша стратегия состоит в том, чтобы сначала получить характеристическую функцию 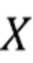 исходя из
исходя из 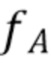 , а затем инвертировать отображение в виде карты, предполагая, что скорость счета и характеристики шума известны. Пусть
, а затем инвертировать отображение в виде карты, предполагая, что скорость счета и характеристики шума известны. Пусть 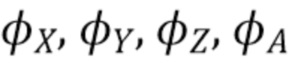 - характеристические функции
- характеристические функции 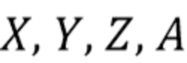 . Хорошо известно [15], что для составного пуассоновского процесса
. Хорошо известно [15], что для составного пуассоновского процесса 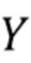 со скоростью
со скоростью 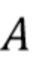 ,
,

и поскольку 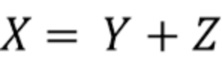 , то
, то

Учитывая наблюдения 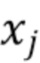 , мы можем сформировать эмпирическую оценку
, мы можем сформировать эмпирическую оценку 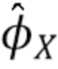 характеристической функции
характеристической функции 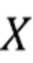 . Рассматривая ее как истинную характеристическую функцию, мы можем инвертировать (40), (41), чтобы получить характеристическую функцию
. Рассматривая ее как истинную характеристическую функцию, мы можем инвертировать (40), (41), чтобы получить характеристическую функцию 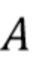 , а затем выполнить преобразование Фурье, чтобы найти спектр амплитуды
, а затем выполнить преобразование Фурье, чтобы найти спектр амплитуды 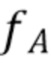 . В частности, используя (40), (41) и предположение, что
. В частности, используя (40), (41) и предположение, что 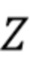 является гауссовым, которое используется для обеспечения того, что
является гауссовым, которое используется для обеспечения того, что 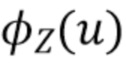 будет отлична от нуля
будет отлична от нуля 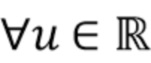 , полагаем, что
, полагаем, что 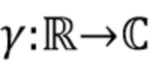 будет кривой, описываемой
будет кривой, описываемой

Временно полагая  , взяв «выделенный логарифм» (43) и переставив, мы имеем
, взяв «выделенный логарифм» (43) и переставив, мы имеем

В идеале 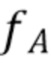 восстанавливается преобразованием Фурье
восстанавливается преобразованием Фурье
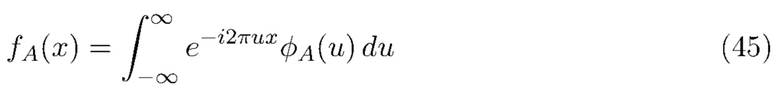
Основная форма предлагаемой нами формулы оценки дана в (88) и выводится из (45) с помощью последовательности этапов. Сначала по данным оценивается 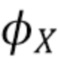 (Этап 1). Простая подстановка этой оценки для
(Этап 1). Простая подстановка этой оценки для 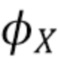 в (42) не дает оптимальной оценки интегральной средней квадратической погрешности (ISE), равной γ. Приблизительная ISE получается из приблизительной оценки распределения ошибок
в (42) не дает оптимальной оценки интегральной средней квадратической погрешности (ISE), равной γ. Приблизительная ISE получается из приблизительной оценки распределения ошибок 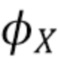 (Этап 2). Затем мы определяем чувствительную оконную функцию
(Этап 2). Затем мы определяем чувствительную оконную функцию 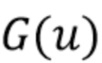 (на этапе 3) и оцениваем γ как
(на этапе 3) и оцениваем γ как

Оконная функция 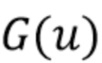 предназначена для минимизации приблизительной ISE между
предназначена для минимизации приблизительной ISE между 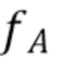 и нашей оценкой
и нашей оценкой 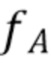 на основе (44), (45) и (46), но с заменой γ в (44) на (46). Аналогичная идея используется для оценки
на основе (44), (45) и (46), но с заменой γ в (44) на (46). Аналогичная идея используется для оценки 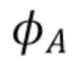 из (44): весовая функция
из (44): весовая функция 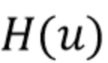 находится (на этапе 4) таким образом, что замена
находится (на этапе 4) таким образом, что замена 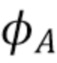 в (45) на
в (45) на

дает лучшую оценку 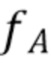 , чем использование невзвешенной оценки
, чем использование невзвешенной оценки 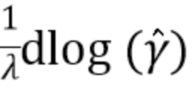 . Наконец, весовая функция
. Наконец, весовая функция 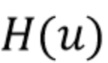 модифицируется (на этапе 5), чтобы учесть в интеграле в (45), который на практике приходится заменять конечной суммой. В следующих подразделах подробно рассматриваются эти пять этапов.
модифицируется (на этапе 5), чтобы учесть в интеграле в (45), который на практике приходится заменять конечной суммой. В следующих подразделах подробно рассматриваются эти пять этапов.
3.4 Оценка 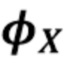
Для оценки 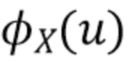 требуется оценка
требуется оценка 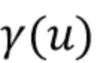 . В этом подразделе мы задаем модель гистограммы и описываем нашу оценку
. В этом подразделе мы задаем модель гистограммы и описываем нашу оценку 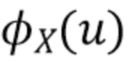 на основе гистограммы значений
на основе гистограммы значений 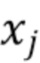 . Предположим, что
. Предположим, что 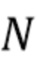 интервалов (и соответствующие значения
интервалов (и соответствующие значения 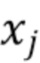 ) были получены из выборки данных конечной длины. Хотя эмпирическая характеристическая функция
) были получены из выборки данных конечной длины. Хотя эмпирическая характеристическая функция
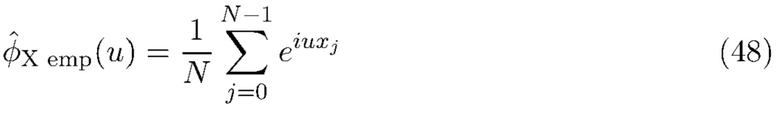
обеспечивает последовательную, асимптотически нормальную оценку характеристической функции [21], она имеет недостаток, заключающийся в быстром росте вычислительной нагрузки по мере увеличения числа точек данных 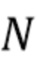 и необходимого числа точек оценки
и необходимого числа точек оценки 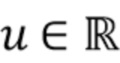 . Вместо этого мы используем оценку на основе гистограммы, которая требует меньших вычислительных затрат. Предположим, что гистограмма наблюдаемых значений
. Вместо этого мы используем оценку на основе гистограммы, которая требует меньших вычислительных затрат. Предположим, что гистограмма наблюдаемых значений 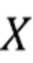 представлена вектором
представлена вектором 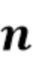 размерностью
размерностью 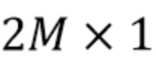 , где подсчет в m-м столбике гистограммы дается выражением
, где подсчет в m-м столбике гистограммы дается выражением
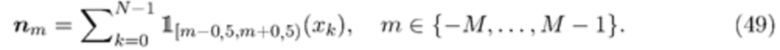
Все столбики гистограммы имеют одинаковую ширину. Ширина столбика выбирается в зависимости от величины значений 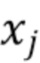 . Поскольку результат выбора другой ширины столбика просто эквивалентен масштабированию значений
. Поскольку результат выбора другой ширины столбика просто эквивалентен масштабированию значений 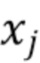 , мы предполагаем, что ширина столбика равна единице без потери общности. Столбики распределяются поровну между неотрицательными и отрицательными значениями данных. Число столбиков 2
, мы предполагаем, что ширина столбика равна единице без потери общности. Столбики распределяются поровну между неотрицательными и отрицательными значениями данных. Число столбиков 2 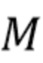 гистограммы влияет на оценку по-разному, что обсуждается в следующих подразделах. На данный момент достаточно предположить, что 2
гистограммы влияет на оценку по-разному, что обсуждается в следующих подразделах. На данный момент достаточно предположить, что 2 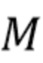 достаточно велико, чтобы гистограмма включала все значения
достаточно велико, чтобы гистограмма включала все значения 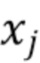 . Мы оцениваем
. Мы оцениваем 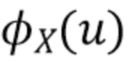 , формируя гистограмму масштабированных значений
, формируя гистограмму масштабированных значений 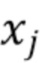 и применяя обратное дискретное преобразование Фурье, т. е.
и применяя обратное дискретное преобразование Фурье, т. е.
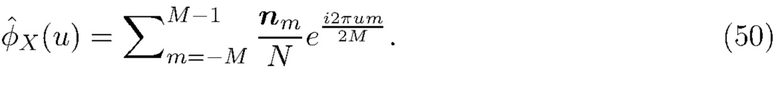
Это хорошее приближение к эмпирической характеристической функции, но где члены 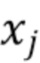 округлены до ближайшего центра столбика гистограммы (а
округлены до ближайшего центра столбика гистограммы (а 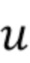 сокращено в 2
сокращено в 2 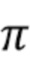 раз). Член
раз). Член 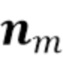 просто подсчитывает число округленных членов с одинаковым значением. Ясно, что эту функцию можно успешно вычислить в определенных дискретных точках
просто подсчитывает число округленных членов с одинаковым значением. Ясно, что эту функцию можно успешно вычислить в определенных дискретных точках 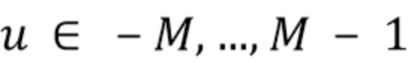 с помощью быстрого преобразования Фурье (БПФ).
с помощью быстрого преобразования Фурье (БПФ).
3.5 Распределение ошибок 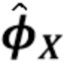
Конструкция фильтров 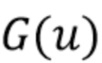 и
и 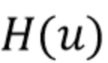 в (46) и (47) основана на статистических данных ошибок между
в (46) и (47) основана на статистических данных ошибок между 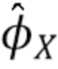 и истинной характеристической функцией. В этом подразделе мы задаем и описываем характеристики этих ошибок. Мы предполагаем, что функция плотности
и истинной характеристической функцией. В этом подразделе мы задаем и описываем характеристики этих ошибок. Мы предполагаем, что функция плотности 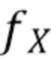 достаточно гладкая (т.е.
достаточно гладкая (т.е. 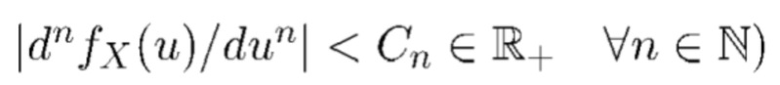 и что ширина столбиков гистограммы достаточно мала (относительно стандартного отклонения аддитивного шума
и что ширина столбиков гистограммы достаточно мала (относительно стандартного отклонения аддитивного шума 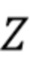 ), так что ошибки, вносимые округлением значений
), так что ошибки, вносимые округлением значений 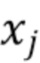 до центра каждого столбика гистограммы, приблизительно равномерно распределены по каждому столбику, имеют нулевое среднее значение и малы по сравнению с пиковым расширением, вызванным
до центра каждого столбика гистограммы, приблизительно равномерно распределены по каждому столбику, имеют нулевое среднее значение и малы по сравнению с пиковым расширением, вызванным 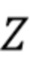 . Другими словами, источник ошибки, возникающий из-за разбивки значений
. Другими словами, источник ошибки, возникающий из-за разбивки значений 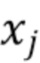 , считается весьма незначительным. Из-за того, что как статистический характер подсчета Пуассона, так и ожидаемое число отсчетов в каждом столбике не является целым
, считается весьма незначительным. Из-за того, что как статистический характер подсчета Пуассона, так и ожидаемое число отсчетов в каждом столбике не является целым 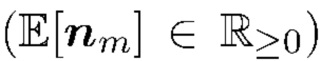 , существуют расхождения между наблюдаемым числом отсчетов в любом данном столбике гистограммы и ожидаемым числом отсчетов для этого столбика. Мы объединяем эти два источника ошибок в нашей модели и называем их «гистограммным шумом». Подчеркнем, что этот шум отличается от аддитивного шума
, существуют расхождения между наблюдаемым числом отсчетов в любом данном столбике гистограммы и ожидаемым числом отсчетов для этого столбика. Мы объединяем эти два источника ошибок в нашей модели и называем их «гистограммным шумом». Подчеркнем, что этот шум отличается от аддитивного шума 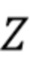 , смоделированного в (11), который вызывает разброс пиков на гистограмме. Пусть вероятность того, что реализация
, смоделированного в (11), который вызывает разброс пиков на гистограмме. Пусть вероятность того, что реализация 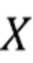 попадет в m-й интервал, равна
попадет в m-й интервал, равна
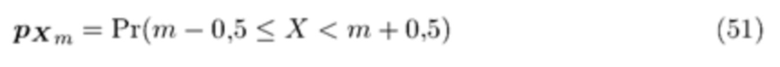
Пусть нормализованная ошибка гистограммы 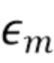 в m-м интервале будет разницей между наблюдаемым числом
в m-м интервале будет разницей между наблюдаемым числом 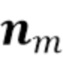 и ожидаемым числом
и ожидаемым числом 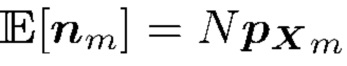 в m-ом столбике относительно общего числа отсчетов на гистограмме
в m-ом столбике относительно общего числа отсчетов на гистограмме 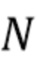 , т.е.
, т.е.

Используя (50), (51) и (52), имеем
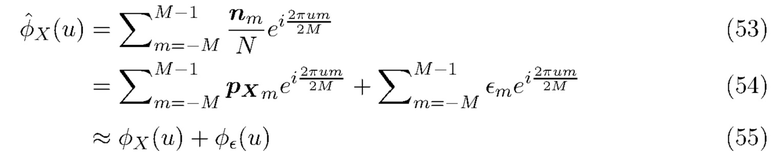
Если гистограмма моделируется как вектор Пуассона, покажем, что
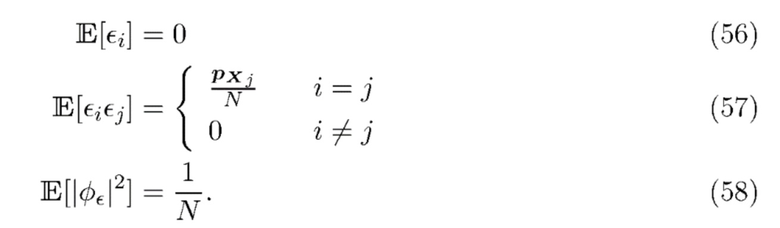
Поскольку характеристики гистограммного шума могут быть выражены через общее число наблюдаемых интервалов 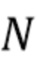 , влияние использования данных наблюдений конечной длины можно учесть путем включения этой информации в структуру
, влияние использования данных наблюдений конечной длины можно учесть путем включения этой информации в структуру 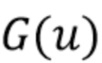 и
и 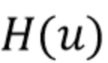 .
.
3.6 Оценка γ
После получения 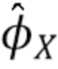 следующая задача - оценить γ. Вместо того, чтобы подставлять
следующая задача - оценить γ. Вместо того, чтобы подставлять 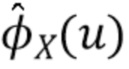 вместо
вместо 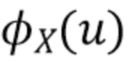 в (42), мы вместо этого используем (46) в качестве оценки, что требует выбора оконной функции
в (42), мы вместо этого используем (46) в качестве оценки, что требует выбора оконной функции 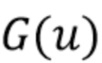 . В этом подразделе мы попытаемся найти функцию
. В этом подразделе мы попытаемся найти функцию 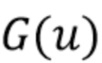 , близкую к оптимальной. Когда рассматривается распределение ошибок в
, близкую к оптимальной. Когда рассматривается распределение ошибок в 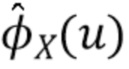 , оконная функция
, оконная функция 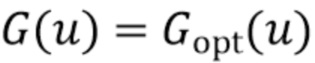 , которая приводит к наименьшей оценке ISE формы, данной в
, которая приводит к наименьшей оценке ISE формы, данной в
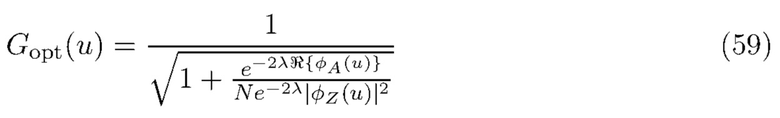
где 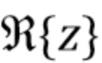 обозначает действительную составляющую
обозначает действительную составляющую 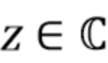 . Мы не можем вычислить
. Мы не можем вычислить 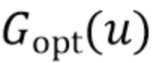 , поскольку
, поскольку 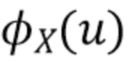 неизвестно, поэтому вместо этого мы пытаемся найти приближение. Пусть
неизвестно, поэтому вместо этого мы пытаемся найти приближение. Пусть
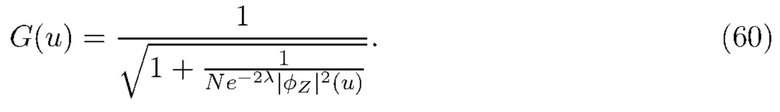
Это оправдано рассмотрением величины относительной ошибки между функциями 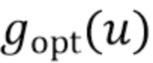 и
и 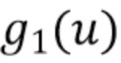 , где
, где
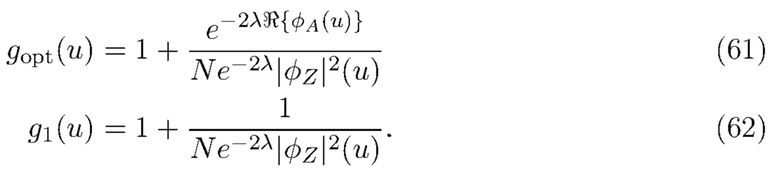
Величина относительной ошибки определяется выражением
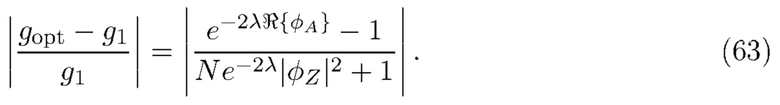
Поскольку 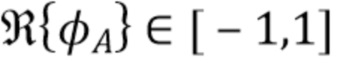 , мы видим, что правая часть (63) максимальна, когда
, мы видим, что правая часть (63) максимальна, когда 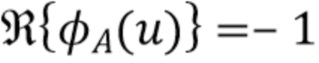 . Таким образом, относительная ошибка ограничивается соотношением
. Таким образом, относительная ошибка ограничивается соотношением
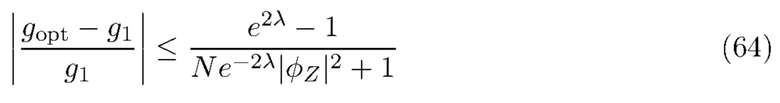
что делает справедливым приближение, когда λ мало, или когда 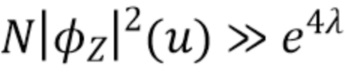 . Кроме того, отметим, что полученная оценка достаточно консервативна. Распределение энергии фотонов в спектроскопических системах обычно можно смоделировать как сумму
. Кроме того, отметим, что полученная оценка достаточно консервативна. Распределение энергии фотонов в спектроскопических системах обычно можно смоделировать как сумму 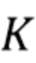 гауссовых пиков, где
гауссовых пиков, где 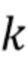 -й пик имеет местоположение
-й пик имеет местоположение 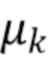 и масштаб
и масштаб 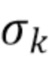 , т. е.
, т. е.
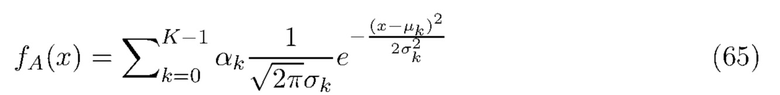
где 
Следовательно, характеристическая функция будет иметь вид
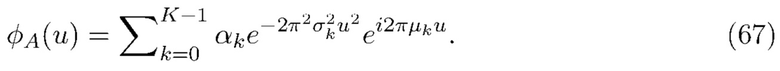
т. е., колебания внутри оболочки, которое затухает как 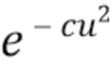 при некотором
при некотором 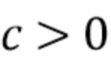 . Оценка сверху, данная в (64), весьма консервативна, поскольку
. Оценка сверху, данная в (64), весьма консервативна, поскольку 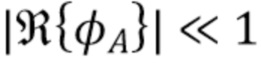 для большинства значений
для большинства значений 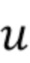 . Ошибка аппроксимации будет значительно меньше в большинстве точек оценки по всему спектру. Выбрав
. Ошибка аппроксимации будет значительно меньше в большинстве точек оценки по всему спектру. Выбрав 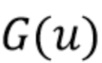 , мы можем составить оценку γ, используя (46). Оконная функция снижает влияние гистограммного шума, возникающего из-за конечного числа выборок данных. Для больших значений
, мы можем составить оценку γ, используя (46). Оконная функция снижает влияние гистограммного шума, возникающего из-за конечного числа выборок данных. Для больших значений 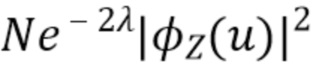 влияние оконной функции незначительно, и оценка, по существу, такая же, как при использовании (42) напрямую. Однако в областях, где
влияние оконной функции незначительно, и оценка, по существу, такая же, как при использовании (42) напрямую. Однако в областях, где

влияние оконной функции становится значительным и, таким образом, ограничивает нашу оценку γ. Используя тот факт, что шум 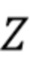 является гауссовским (так что
является гауссовским (так что 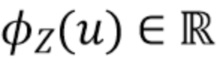 и, следовательно,
и, следовательно, 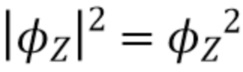 ), и поскольку
), и поскольку 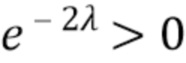 , мы видим, что
, мы видим, что
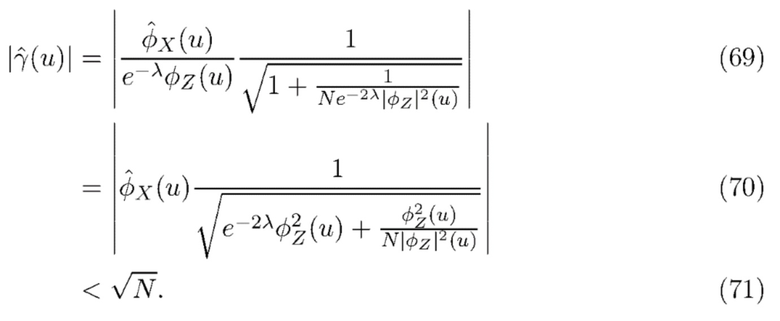
Это гарантирует, что аргумент «выделенного логарифма» в (47) остается конечным, даже если 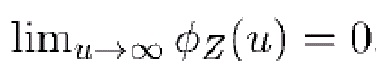 .
.
3.7 Оценка 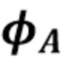
После получения 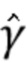 переходим к оценке
переходим к оценке 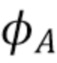 , используя (47). Для этого требуется другая оконная функция
, используя (47). Для этого требуется другая оконная функция 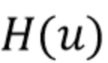 . В этом подразделе мы найдем функцию
. В этом подразделе мы найдем функцию 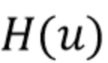 для оценки
для оценки 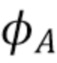 , которая близка к оптимальной для ISE. Для удобства обозначений начнем с определения функции
, которая близка к оптимальной для ISE. Для удобства обозначений начнем с определения функции 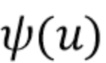

ISE минимизируется, когда 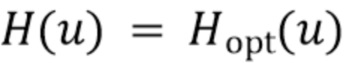 , где оптимальный фильтр
, где оптимальный фильтр 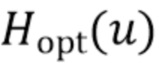 задается формулой
задается формулой
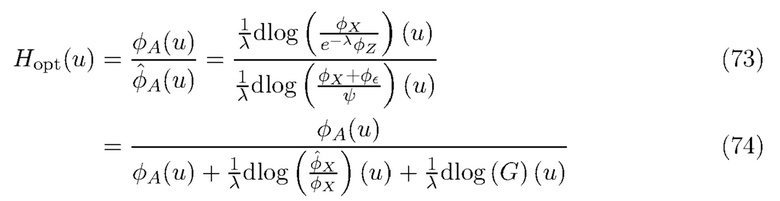
Опять же, мы не можем вычислить оптимальный фильтр, используя (73) - (74), поскольку 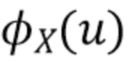 ,
, 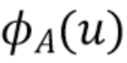 и
и 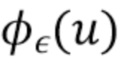 неизвестны. Вместо этого мы делаем следующие наблюдения, чтобы получить приближение для оптимального по ISE фильтра.
неизвестны. Вместо этого мы делаем следующие наблюдения, чтобы получить приближение для оптимального по ISE фильтра.
3.7.1 Начальные наблюдения
Оптимальный фильтр остается близким к единице, пока оценка 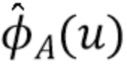 остается близкой к истинному значению
остается близкой к истинному значению 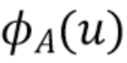 . Это всегда будет иметь место при малых значениях
. Это всегда будет иметь место при малых значениях 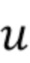 , поскольку
, поскольку

Кроме того, уравнение (73) показывает, что если  , то
, то 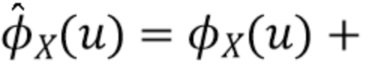
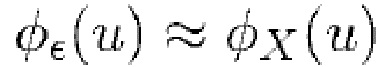 поэтому
поэтому 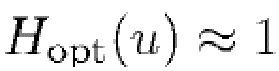 . Для больших значений
. Для больших значений 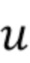 , когда величина
, когда величина 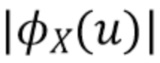 становится сравнимой или меньшей, чем
становится сравнимой или меньшей, чем 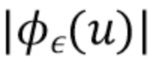 , в формуле оценки
, в формуле оценки 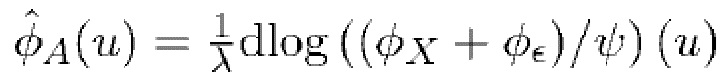 преобладает шум и она больше не дает полезных оценок
преобладает шум и она больше не дает полезных оценок 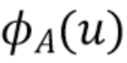 . В крайнем случае
. В крайнем случае  , поэтому
, поэтому 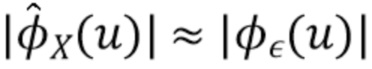 и, следовательно,
и, следовательно,

Окно 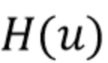 должно исключать эти области из оценки, поскольку смещение, вносимое при этом, будет меньше дисперсии нефильтрованного шума. К сожалению, оценка
должно исключать эти области из оценки, поскольку смещение, вносимое при этом, будет меньше дисперсии нефильтрованного шума. К сожалению, оценка 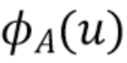 может сильно ухудшиться задолго до того, как будет достигнуто это граничное условие, поэтому (77) не особенно полезно. Более полезный способ определения того, когда начинает преобладать шум, заключается в следующем.
может сильно ухудшиться задолго до того, как будет достигнуто это граничное условие, поэтому (77) не особенно полезно. Более полезный способ определения того, когда начинает преобладать шум, заключается в следующем.
3.7.2 Функция конструкции фильтра
Дальнейшее преобразование (67) показывает, что для типичных спектроскопических систем величина 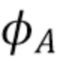 будет иметь вид
будет иметь вид
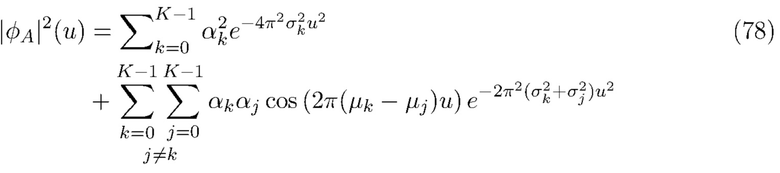
а именно: средняя составляющая, которая затухает в соответствии с шириной пиков 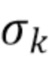 , и более быстро затухающая колебательная составляющая, которая изменяется в зависимости от расположения спектральных пиков
, и более быстро затухающая колебательная составляющая, которая изменяется в зависимости от расположения спектральных пиков 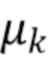 . При проектировании окна
. При проектировании окна 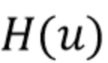 мы заинтересованы в ослаблении областей в
мы заинтересованы в ослаблении областей в 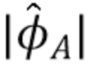 , где
, где 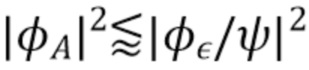 , то есть, где мощность сигнала меньше, чем гистограммный шум, который был усилен удалением
, то есть, где мощность сигнала меньше, чем гистограммный шум, который был усилен удалением 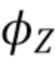 во время оценки γ. Чтобы получить оценку
во время оценки γ. Чтобы получить оценку 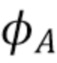 , фильтр
, фильтр 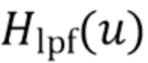 нижних частот гауссовой формы сворачивается с
нижних частот гауссовой формы сворачивается с 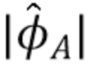 для ослабления всех, кроме медленно изменяющихся крупномасштабных характеристик
для ослабления всех, кроме медленно изменяющихся крупномасштабных характеристик 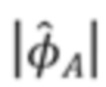 . Мы обозначаем это
. Мы обозначаем это 
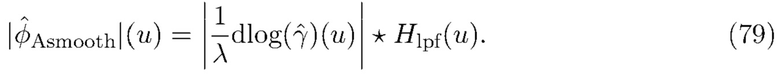
Мы видим, что 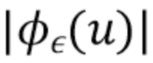 имеет распределение Рэлея с масштабным коэффициентом
имеет распределение Рэлея с масштабным коэффициентом 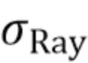 =
= 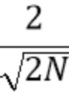 . Следовательно
. Следовательно
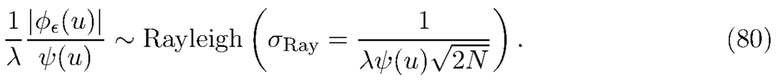
Хорошо известно, что кумулятивная функция распределения случайной величины с распределением Рэлея 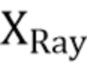 имеет вид
имеет вид
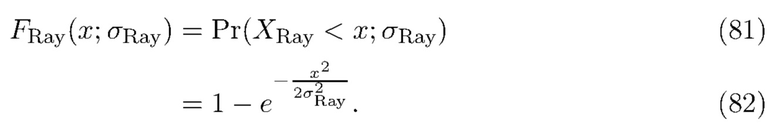
Следовательно, чтобы облегчить вычисление окна 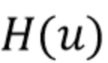 , мы воспользуемся функцией
, мы воспользуемся функцией
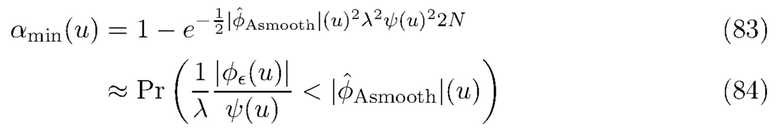
для управления формой 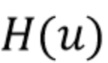 . Функция
. Функция 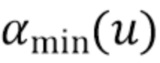 обеспечивает индикацию того, насколько мы можем быть уверены в том, что оценка
обеспечивает индикацию того, насколько мы можем быть уверены в том, что оценка 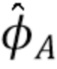 содержит больше энергии сигнала, чем энергии шума. Приближение в (84) возникает из того факта, что
содержит больше энергии сигнала, чем энергии шума. Приближение в (84) возникает из того факта, что 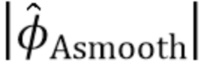 также является случайной величиной, на которую слегка влияет шум
также является случайной величиной, на которую слегка влияет шум 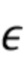 . Иногда - особенно для больших значений
. Иногда - особенно для больших значений 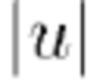 - гистограммный шум может приводить к достаточно большим значениям
- гистограммный шум может приводить к достаточно большим значениям 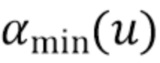 , чтобы дать ложное чувство уверенности и потенциально позволить зашумленным результатам искажать оценку
, чтобы дать ложное чувство уверенности и потенциально позволить зашумленным результатам искажать оценку 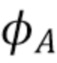 . Чтобы преодолеть эту проблему, функция была изменена так, чтобы она была одномодальной по
. Чтобы преодолеть эту проблему, функция была изменена так, чтобы она была одномодальной по 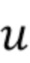
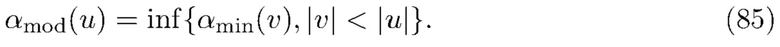
Эта модификация была оправдана в предположении, что гауссовский шум вызывает уменьшение 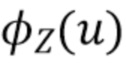 по
по 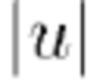 . Следовательно, мы ожидаем, что
. Следовательно, мы ожидаем, что 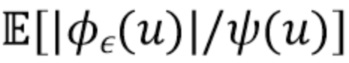 будет увеличиваться по
будет увеличиваться по 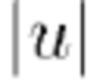 . Если мы проигнорируем локальные колебания
. Если мы проигнорируем локальные колебания 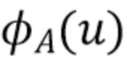 , которые связаны с положениями пиков в
, которые связаны с положениями пиков в 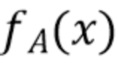 , огибающая, аппроксимируемая сглаженным
, огибающая, аппроксимируемая сглаженным 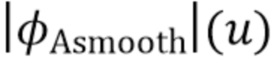 , не будет увеличиваться по
, не будет увеличиваться по 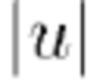 . Уравнение (74) указывает, что оптимальное окно имеет вид
. Уравнение (74) указывает, что оптимальное окно имеет вид 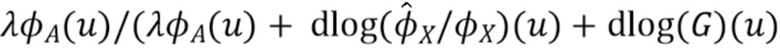 , поэтому общая форма окна будет уменьшаться по
, поэтому общая форма окна будет уменьшаться по 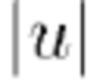 . Следовательно, если оцененная характеристическая функция в области некоторого
. Следовательно, если оцененная характеристическая функция в области некоторого 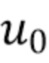 (где отношение сигнал шум высокое) определила, что значение окна должно быть
(где отношение сигнал шум высокое) определила, что значение окна должно быть 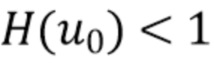 , то резонно отклонить предположение, что в области
, то резонно отклонить предположение, что в области 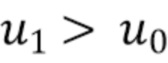 (где отношение сигнал/шум будет хуже), что
(где отношение сигнал/шум будет хуже), что 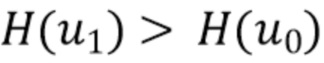 . Зная, что
. Зная, что 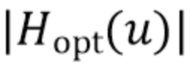 должен быть близок к единице для малых
должен быть близок к единице для малых 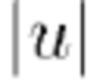 , близок к нулю для больших
, близок к нулю для больших 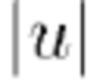 и должен «спадать» при уменьшении отношения сигнал/шум - мы рассматриваем две потенциальные оконные функции как приближения к
и должен «спадать» при уменьшении отношения сигнал/шум - мы рассматриваем две потенциальные оконные функции как приближения к 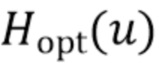 .
.
3.7.3 Прямоугольное окно
Индикаторная функция дает очень простую оконную функцию

Пороговое значение 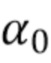 определяет точку, в которой происходит отсечка, и которое может быть выбрано вручную по желанию (например,
определяет точку, в которой происходит отсечка, и которое может быть выбрано вручную по желанию (например, 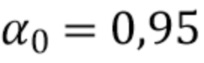 ). Как только порог выбран, оценка демонстрирует аналогичные характеристики ISE независимо от местоположения пиков в спектрах падающего излучения. Вместо того, чтобы требовать от пользователя выбора ширины окна в зависимости от падающего спектра (Gugushvili [18] предложил непараметрическую оценку для общей задачи разложения, в которой использовалась прямоугольная оконная схема. При этом требуется ручной выбор ширины окна, которая зависит от
). Как только порог выбран, оценка демонстрирует аналогичные характеристики ISE независимо от местоположения пиков в спектрах падающего излучения. Вместо того, чтобы требовать от пользователя выбора ширины окна в зависимости от падающего спектра (Gugushvili [18] предложил непараметрическую оценку для общей задачи разложения, в которой использовалась прямоугольная оконная схема. При этом требуется ручной выбор ширины окна, которая зависит от 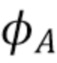 ), ширина окна автоматически выбирается на основании данных через
), ширина окна автоматически выбирается на основании данных через 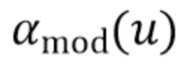 . Хотя простота является основным преимуществом прямоугольного окна, область резкого перехода представляет собой плохую модель для области спада оптимального фильтра. Вторая форма фильтра пытается улучшить это.
. Хотя простота является основным преимуществом прямоугольного окна, область резкого перехода представляет собой плохую модель для области спада оптимального фильтра. Вторая форма фильтра пытается улучшить это.
3.7.4 Логистическое окно
Окно, основанное на логистической функции, пытается смоделировать более плавный спад. Это дается
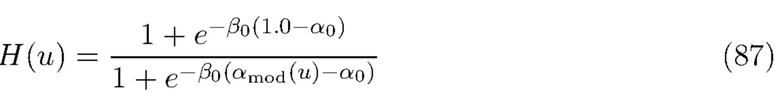
где 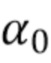 снова действует как порог принятия гипотезы о том, что энергия сигнала больше, чем энергия шума в оценке
снова действует как порог принятия гипотезы о том, что энергия сигнала больше, чем энергия шума в оценке 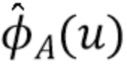 . Скорость спада фильтра в окрестности пороговой области управляется параметром
. Скорость спада фильтра в окрестности пороговой области управляется параметром 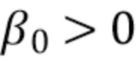 . Это обеспечивает более плавную переходную область, чем прямоугольное окно, уменьшая колебания Гиббса в окончательной оценке
. Это обеспечивает более плавную переходную область, чем прямоугольное окно, уменьшая колебания Гиббса в окончательной оценке 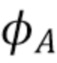 . Еще раз, хотя параметры
. Еще раз, хотя параметры 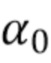 ,
, 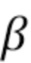 выбираются вручную, они гораздо меньше зависят от
выбираются вручную, они гораздо меньше зависят от 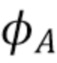 и могут использоваться для обеспечения фильтрации, близкой к оптимальной, для самых разных спектров падающих импульсов. Типичные использованные значения были
и могут использоваться для обеспечения фильтрации, близкой к оптимальной, для самых разных спектров падающих импульсов. Типичные использованные значения были 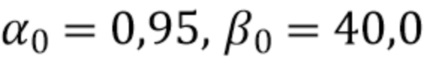 . Характеристики функций прямоугольного и логистического окон сравниваются в разделе 4.
. Характеристики функций прямоугольного и логистического окон сравниваются в разделе 4.
3.8 Оценка 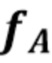
После конструирования оконной функции 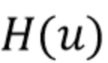 и, следовательно, средства оценки
и, следовательно, средства оценки 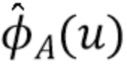 , последняя задача состоит в том, чтобы оценить
, последняя задача состоит в том, чтобы оценить 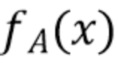 путем обращения преобразования Фурье. В этом подразделе описывается несколько проблем, связанных с численной реализацией. Во-первых, невозможно вычислить
путем обращения преобразования Фурье. В этом подразделе описывается несколько проблем, связанных с численной реализацией. Во-первых, невозможно вычислить 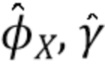 (u) и
(u) и 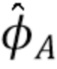 численно на всей действительной прямой. Вместо этого мы оцениваем их в дискретных точках на конечном интервале. Конечный интервал выбирается достаточно большим, чтобы возникла допустимо небольшая ошибка в результате исключения значений сигнала за пределами интервала. Это оправдано, поскольку
численно на всей действительной прямой. Вместо этого мы оцениваем их в дискретных точках на конечном интервале. Конечный интервал выбирается достаточно большим, чтобы возникла допустимо небольшая ошибка в результате исключения значений сигнала за пределами интервала. Это оправдано, поскольку 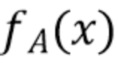 является смесью гауссовых распределений, поскольку величины
является смесью гауссовых распределений, поскольку величины 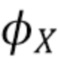 и
и 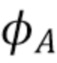 будут убывать как
будут убывать как 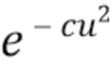 для некоторого
для некоторого 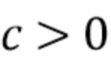 . Быстрое преобразование Фурье (БПФ) используется для вычисления
. Быстрое преобразование Фурье (БПФ) используется для вычисления 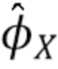 в дискретных точках и, следовательно, также определяет точки, в которых оцениваются
в дискретных точках и, следовательно, также определяет точки, в которых оцениваются 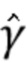 (u) и
(u) и 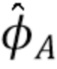 . Аналогичным образом, БПФ используется для определения окончательной оценки
. Аналогичным образом, БПФ используется для определения окончательной оценки 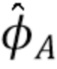 в дискретных точках. Чтобы использовать БПФ, сигналы вне интервала должны быть достаточно малыми, чтобы уменьшить влияние наложения спектров. Точки оценки также должны быть достаточно плотными, чтобы избежать неоднозначности «обращения фазы» при оценке
в дискретных точках. Чтобы использовать БПФ, сигналы вне интервала должны быть достаточно малыми, чтобы уменьшить влияние наложения спектров. Точки оценки также должны быть достаточно плотными, чтобы избежать неоднозначности «обращения фазы» при оценке 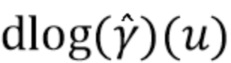 . Обе эти цели могут быть достигнуты путем увеличения числа столбиков 2M в гистограмме (заполнение нулями) до тех пор, пока не будет достигнуто достаточно большое число столбиков. По мере увеличения
. Обе эти цели могут быть достигнуты путем увеличения числа столбиков 2M в гистограмме (заполнение нулями) до тех пор, пока не будет достигнуто достаточно большое число столбиков. По мере увеличения 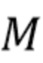 плотность дискретизации
плотность дискретизации 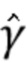 увеличивается, что позволяет детектировать и управлять свертыванием фазы. Большее значение M также позволяет пренебречь наложением (вызванных хвостами
увеличивается, что позволяет детектировать и управлять свертыванием фазы. Большее значение M также позволяет пренебречь наложением (вызванных хвостами 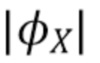 гауссовой формы). Обычно значение
гауссовой формы). Обычно значение 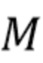 выбиралось как наименьшая степень двойки, достаточно большая, чтобы ненулевые значения гистограммы были ограничены индексами «нижней половины», то есть
выбиралось как наименьшая степень двойки, достаточно большая, чтобы ненулевые значения гистограммы были ограничены индексами «нижней половины», то есть 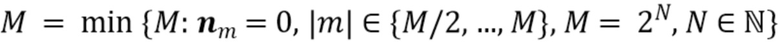 . Во-вторых, «выделенный логарифм» в (47) не определен если
. Во-вторых, «выделенный логарифм» в (47) не определен если 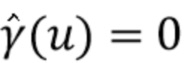 . При оценке γ
. При оценке γ 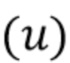 по данным существует небольшая, но ненулевая вероятность того, что оценка будет равна нулю. В этом случае «выделенный логарифм» в (47) не определен и метод не работает. По мере увеличения
по данным существует небольшая, но ненулевая вероятность того, что оценка будет равна нулю. В этом случае «выделенный логарифм» в (47) не определен и метод не работает. По мере увеличения 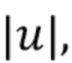
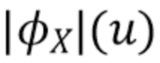 уменьшается и может приближаться
уменьшается и может приближаться 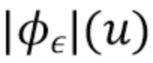 . Когда
. Когда 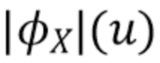 и
и 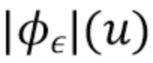 имеют одинаковые величины, вероятность того, что
имеют одинаковые величины, вероятность того, что 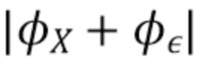 (и, следовательно,
(и, следовательно, 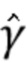 ) будет близка к нулю, может стать значительной. Фильтр
) будет близка к нулю, может стать значительной. Фильтр 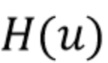 должен спадать быстрее, чем
должен спадать быстрее, чем 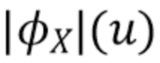 приближается к
приближается к 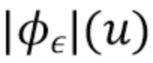 , чтобы уменьшить влияние, которое это может оказать на оценку. В идеале
, чтобы уменьшить влияние, которое это может оказать на оценку. В идеале 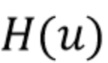 должно быть равно нулю в областях, где шум может привести к тому, что
должно быть равно нулю в областях, где шум может привести к тому, что 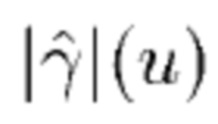 будет близко к нулю. Gugushvili показал [18], что для прямоугольного окна вероятность невыполнения инверсии приближается к нулю, поскольку длина набора данных увеличивается
будет близко к нулю. Gugushvili показал [18], что для прямоугольного окна вероятность невыполнения инверсии приближается к нулю, поскольку длина набора данных увеличивается 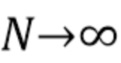 .
.
3.9 Дискретное обозначение
Мы сделаем небольшое отступление, чтобы ввести дополнительные обозначения. В остальной части документа полужирным шрифтом будет обозначаться вектор 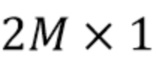 , соответствующий дискретно выбранной версии названной функции, например,
, соответствующий дискретно выбранной версии названной функции, например, 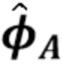 представляет вектор
представляет вектор 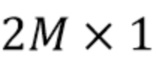 , значения которого задаются характеристической функцией
, значения которого задаются характеристической функцией 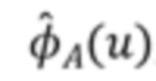 , вычисленной в точках
, вычисленной в точках 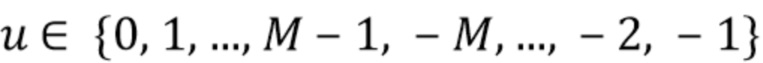 . Обозначение
. Обозначение 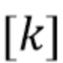 в квадратных скобках используется для индексации определенного элемента в векторе, например,
в квадратных скобках используется для индексации определенного элемента в векторе, например, 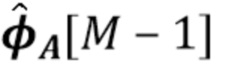 имеет значение
имеет значение 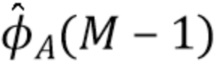 . Мы также используем отрицательные индексы для доступа к элементам вектора способом аналогичным способу в языке программирования Python. Отрицательные индексы следует интерпретировать относительно длины вектора, т.е.
. Мы также используем отрицательные индексы для доступа к элементам вектора способом аналогичным способу в языке программирования Python. Отрицательные индексы следует интерпретировать относительно длины вектора, т.е. 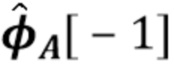 относится к последнему элементу в векторе (что эквивалентно
относится к последнему элементу в векторе (что эквивалентно 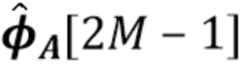 .
.
3.10 Сущность оценки
Используемую нами процедуру оценки можно свести к следующим этапам.
1. Разбейте выбранный временной ряд на интервалы, используя (8).
2. Рассчитайте значение 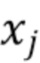 для каждого интервала согласно (9).
для каждого интервала согласно (9).
3. Сгенерируйте гистограмму 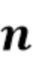 из значений
из значений 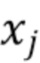 .
.
4. Вычислите 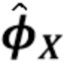 , используя обратное БПФ, для эффективной оценки (50) в различных точках выборки.
, используя обратное БПФ, для эффективной оценки (50) в различных точках выборки.
5. Вычислите 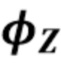 и
и 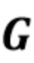 в соответствующих точках.
в соответствующих точках.
6. Вычислите 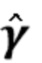 по (46), используя
по (46), используя 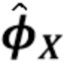 ,
, 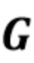 и
и 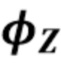 .
.
7. Вычислите 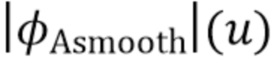 , версию
, версию 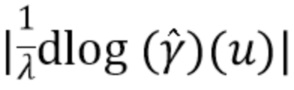 с фильтром нижних частот.
с фильтром нижних частот.
8. Вычислите 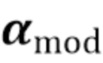 с помощью (83) и (85).
с помощью (83) и (85).
9. Вычислите 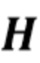 , используя
, используя 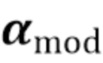 и (86) или (87).
и (86) или (87).
10. Вычислите 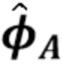 с помощью (47), используя
с помощью (47), используя 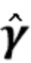 и
и 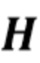 . Если какой-либо элемент
. Если какой-либо элемент 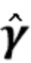 равен нулю, а соответствующий элемент
равен нулю, а соответствующий элемент 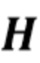 отличен от нуля, оценка не удалась, поскольку «выделенный логарифм» не определен.
отличен от нуля, оценка не удалась, поскольку «выделенный логарифм» не определен.
11. Вычислите 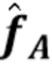 , используя БПФ для
, используя БПФ для 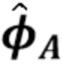 в соответствии с
в соответствии с
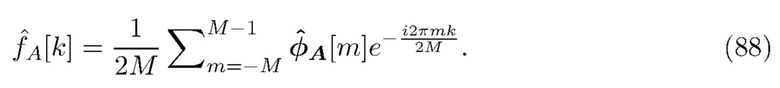
3.11 Показатели эффективности
Эффективность оценки измеряется с использованием интегральной квадратичной ошибки (ISE). ISE измеряет общее соответствие оценочной плотности.
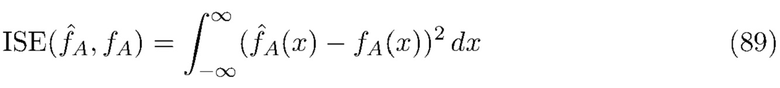
Дискретная мера ISE определяется выражением
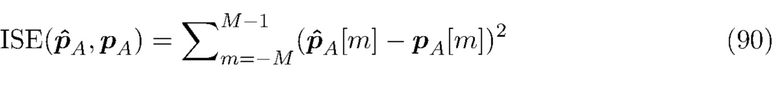
где 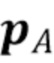 - это вектор размером
- это вектор размером 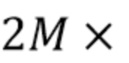 1, элементы которого содержат вероятностную меру в области каждого столбика гистограммы, т.е.
1, элементы которого содержат вероятностную меру в области каждого столбика гистограммы, т.е.
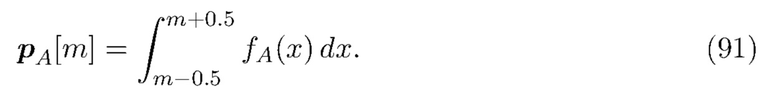
Вектор 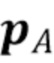 представляет собой соответствующий оцененный вектор вероятностной меры.
представляет собой соответствующий оцененный вектор вероятностной меры.
4 ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ ПЕРВОГО ВАРИАНТА ОСУЩЕСТВЛЕНИЯ
Эксперименты проводились с использованием смоделированных и реальных данных.
4.1 Моделирование
Для этих расчетов использовалась идеальная плотность, использованная Trigano и др. [11]. Она состоит из смеси шести гауссовых и одного гамма-распределения для имитации комптоновского фона. Плотность смеси определяется как
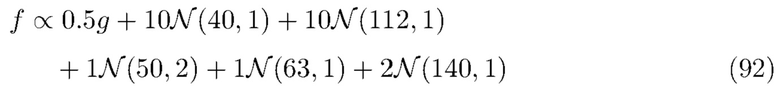
где 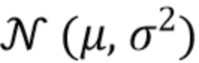 - плотность нормального распределения со средним
- плотность нормального распределения со средним 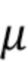 и дисперсией
и дисперсией 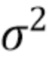 . Плотность гамма-распределения определяется выражением
. Плотность гамма-распределения определяется выражением 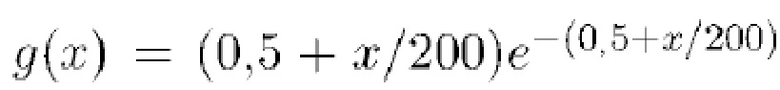 . Плотность была выбрана в 8192 равноотстоящих целочисленных точках, чтобы получить дискретный вектор
. Плотность была выбрана в 8192 равноотстоящих целочисленных точках, чтобы получить дискретный вектор 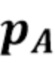 вероятностной меры. БПФ использовалось для получения
вероятностной меры. БПФ использовалось для получения 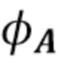 , дискретного вектора значений
, дискретного вектора значений 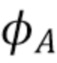 .
.
Для эксперимента была выбрана конкретная скорость λ счета, соответствующая ожидаемому числу событий за интервал наблюдения. Ожидаемая плотность наложения была получена с помощью (40). Т.е. дискретный вектор 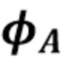 , был пропорционально изменен в отношении λ, возведен в степень, затем пропорционально изменен в отношении
, был пропорционально изменен в отношении λ, возведен в степень, затем пропорционально изменен в отношении 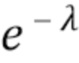 и, наконец, было применено БПФ.
и, наконец, было применено БПФ.
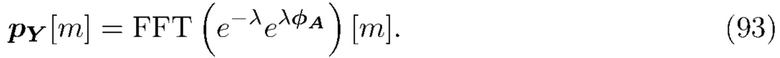
Уравнение (93) было свернуто с гауссианом для моделирования эффекта шума 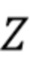 , размывающего наблюдаемый спектр.
, размывающего наблюдаемый спектр.

Это представляет собой ожидаемую плотность наблюдаемого спектра, включая наложения и аддитивный шум. Гистограммы наблюдений были построены с использованием случайных величин, которые были распределены согласно (94). Эксперименты параметризовались парой 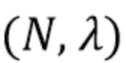 , где
, где 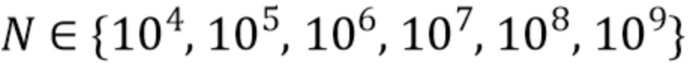 и
и 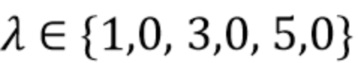 . Для каждой пары параметров
. Для каждой пары параметров 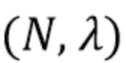 была сделана тысяча наблюдаемых гистограмм. Оценки вектора
была сделана тысяча наблюдаемых гистограмм. Оценки вектора 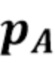 вероятностной меру были сделаны с использованием (88) с использованием как (86), так и (87) для
вероятностной меру были сделаны с использованием (88) с использованием как (86), так и (87) для 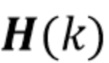 . Пороговое значение
. Пороговое значение 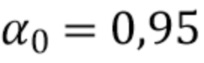 использовалось для обеих форм окон и
использовалось для обеих форм окон и 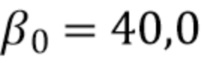 для логистической формы. Дискретная мера ISE ошибки между каждой оценкой
для логистической формы. Дискретная мера ISE ошибки между каждой оценкой 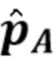 и истинным вектором
и истинным вектором 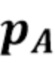 записывалась. Для сравнения с результатами асимптотической полосы пропускания оценки были сделаны с использованием прямоугольного окна, ширина полосы которого была выбрана в соответствии с условием 1.3, указанным Gugushvili в [18], т.е.
записывалась. Для сравнения с результатами асимптотической полосы пропускания оценки были сделаны с использованием прямоугольного окна, ширина полосы которого была выбрана в соответствии с условием 1.3, указанным Gugushvili в [18], т.е. 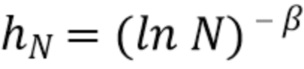 где
где 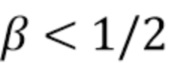 . Подчеркнем, что
. Подчеркнем, что 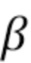 фильтра Gugushvili не следует путать с
фильтра Gugushvili не следует путать с 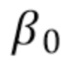 из (87). Критерий асимптотической полосы пропускания реализован с использованием
из (87). Критерий асимптотической полосы пропускания реализован с использованием
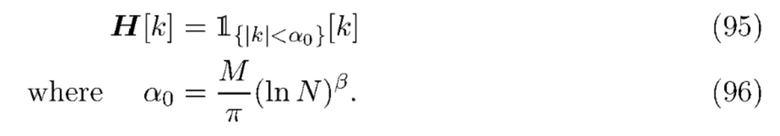
Были опробованы три значения для 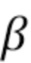 из Gugushvili, а именно
из Gugushvili, а именно 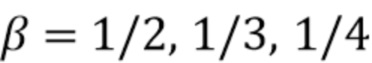 .
.
Оценки также были сделаны с использованием прямоугольного фильтра (95) с фиксированной полосой пропускания различных значений 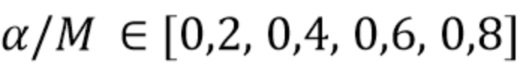 . Наконец, данные временного ряда были созданы в соответствии с (1) с идеализированной прямоугольной формой импульса и 107 импульсами, энергии которых были распределены в соответствии с (92). Длительность импульса и скорость счета были выбраны так, чтобы коэффициент Пуассона был
. Наконец, данные временного ряда были созданы в соответствии с (1) с идеализированной прямоугольной формой импульса и 107 импульсами, энергии которых были распределены в соответствии с (92). Длительность импульса и скорость счета были выбраны так, чтобы коэффициент Пуассона был 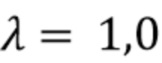 . Алгоритм, описанный Trigano и др. [11], использовался для оценки лежащей в их основе амплитудной плотности из двумерной гистограммы, содержащей 32×1024 (длительность x энергия) столбиков - этот выбор столбиков, как сообщается, дает наилучшую точность и разумное время выполнения. Производительность и время обработки основного алгоритма были записаны для сравнения с предложенным нами алгоритмом. На Фиг. 2 показана типичная оценка
. Алгоритм, описанный Trigano и др. [11], использовался для оценки лежащей в их основе амплитудной плотности из двумерной гистограммы, содержащей 32×1024 (длительность x энергия) столбиков - этот выбор столбиков, как сообщается, дает наилучшую точность и разумное время выполнения. Производительность и время обработки основного алгоритма были записаны для сравнения с предложенным нами алгоритмом. На Фиг. 2 показана типичная оценка 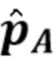 , сделанная управляемым данными фильтром логистической формы для эксперимента с парой параметров
, сделанная управляемым данными фильтром логистической формы для эксперимента с парой параметров 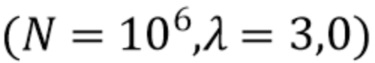 . Также нанесены истинный вектор
. Также нанесены истинный вектор 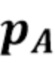 (тонкая сплошная линия) и наблюдаемая гистограмма
(тонкая сплошная линия) и наблюдаемая гистограмма 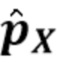 (нижняя кривая, содержащая некоторый шум). На наблюдаемой гистограмме хорошо видны пики наложения. Хотя расчетная плотность страдает от звона (из-за явления Гиббса), в противном случае она оценивает истинную плотность и исправляет наложение, которое присутствовало на наблюдаемой гистограмме. На Фиг. 3 показана типичная оценка, сделанная в той же рабочей точке, что и на Фиг. 2, но с помощью оценки, использующей прямоугольный фильтр, в котором полоса пропускания была выбрана с использованием (96) и
(нижняя кривая, содержащая некоторый шум). На наблюдаемой гистограмме хорошо видны пики наложения. Хотя расчетная плотность страдает от звона (из-за явления Гиббса), в противном случае она оценивает истинную плотность и исправляет наложение, которое присутствовало на наблюдаемой гистограмме. На Фиг. 3 показана типичная оценка, сделанная в той же рабочей точке, что и на Фиг. 2, но с помощью оценки, использующей прямоугольный фильтр, в котором полоса пропускания была выбрана с использованием (96) и 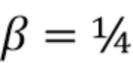 . Это соответствует рабочей области на Фиг. 6, где характеристика фильтра с фиксированной полосой пропускания (
. Это соответствует рабочей области на Фиг. 6, где характеристика фильтра с фиксированной полосой пропускания (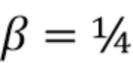 ) приближается к характеристикам фильтров, управляемых данными. Очевидно, что, несмотря на корректировку наложения, полученная оценка содержит больше шума. На Фиг. 4 показаны плотности распределения измерений ISE в зависимости от отсчетов образцов, с использованием прямоугольного фильтра и различных фиксированных полос пропускания. Линии были нанесены между математическими ожиданиями (MISE mean integrated squared error - средний интегральный квадрат ошибки) для облегчения визуализации. Результаты для управляемого данными прямоугольного фильтра (86), также были нанесены на график и соединены более толстой кривой. Они ясно показывают слабость фильтрации с фиксированной полосой пропускания. Для любой фиксированной полосы пропускания ISE уменьшается по мере увеличения отсчетов образцов, в конечном итоге асимптотически, поскольку смещение становится доминирующим источником ошибки. В этой точке (которая зависит от шума и полосы пропускания) ISE остается в основном постоянной, несмотря на увеличение отсчетов образцов. Фиксированная полоса пропускания исключает использование некоторых оценок
) приближается к характеристикам фильтров, управляемых данными. Очевидно, что, несмотря на корректировку наложения, полученная оценка содержит больше шума. На Фиг. 4 показаны плотности распределения измерений ISE в зависимости от отсчетов образцов, с использованием прямоугольного фильтра и различных фиксированных полос пропускания. Линии были нанесены между математическими ожиданиями (MISE mean integrated squared error - средний интегральный квадрат ошибки) для облегчения визуализации. Результаты для управляемого данными прямоугольного фильтра (86), также были нанесены на график и соединены более толстой кривой. Они ясно показывают слабость фильтрации с фиксированной полосой пропускания. Для любой фиксированной полосы пропускания ISE уменьшается по мере увеличения отсчетов образцов, в конечном итоге асимптотически, поскольку смещение становится доминирующим источником ошибки. В этой точке (которая зависит от шума и полосы пропускания) ISE остается в основном постоянной, несмотря на увеличение отсчетов образцов. Фиксированная полоса пропускания исключает использование некоторых оценок 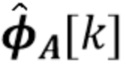 в окончательных расчетах, даже если они имеют высокое отношение сигнал/шум (SNR). На Фиг. 4 также показаны результаты, полученные с помощью прямоугольного фильтра с предложенным нами выбором полосы пропускания на основе данных. Эта кривая находится близко к точке перегиба каждой кривой фиксированной полосы пропускания. Это указывает на то, что полоса пропускания, выбранная для прямоугольного фильтра, управляемого данными, близка к оптимальному значению полосы пропускания (для прямоугольного фильтра) во всем диапазоне отсчетов образцов. На Фиг. 5-7 показаны плотности распределения меры ISE как функции общего числа оценок
в окончательных расчетах, даже если они имеют высокое отношение сигнал/шум (SNR). На Фиг. 4 также показаны результаты, полученные с помощью прямоугольного фильтра с предложенным нами выбором полосы пропускания на основе данных. Эта кривая находится близко к точке перегиба каждой кривой фиксированной полосы пропускания. Это указывает на то, что полоса пропускания, выбранная для прямоугольного фильтра, управляемого данными, близка к оптимальному значению полосы пропускания (для прямоугольного фильтра) во всем диапазоне отсчетов образцов. На Фиг. 5-7 показаны плотности распределения меры ISE как функции общего числа оценок 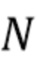 в каждой гистограмме при трех скоростях счета
в каждой гистограмме при трех скоростях счета 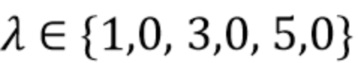 . Кривые MISE для логистических и прямоугольных фильтров ниже, чем кривые, полученные с использованием полосы пропускания, заданной формулой (96), для большей части области, представляющей интерес для применения. Существуют различные области, где полоса пропускания, не управляемая данными (
. Кривые MISE для логистических и прямоугольных фильтров ниже, чем кривые, полученные с использованием полосы пропускания, заданной формулой (96), для большей части области, представляющей интерес для применения. Существуют различные области, где полоса пропускания, не управляемая данными (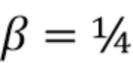 ), дает характеристики, аналогичные полосе пропускания, управляемой данными, однако они не поддерживаются для всего диапазона отсчетов образцов. Логистическая форма фильтра имеет несколько лучшие характеристики, чем прямоугольная форма фильтра, хотя различия между двумя фильтрами кажутся относительно незначительными для меры ISE. В Таблице 1 сравниваются результаты предложенного алгоритма и алгоритма, недавно описанного в [11]. ISE для обоих способов были похожи в исследуемой рабочей точке
), дает характеристики, аналогичные полосе пропускания, управляемой данными, однако они не поддерживаются для всего диапазона отсчетов образцов. Логистическая форма фильтра имеет несколько лучшие характеристики, чем прямоугольная форма фильтра, хотя различия между двумя фильтрами кажутся относительно незначительными для меры ISE. В Таблице 1 сравниваются результаты предложенного алгоритма и алгоритма, недавно описанного в [11]. ISE для обоих способов были похожи в исследуемой рабочей точке 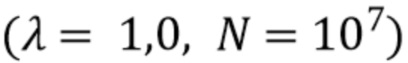 , однако предлагаемый нами алгоритм требует значительно меньше вычислений.
, однако предлагаемый нами алгоритм требует значительно меньше вычислений.
Таблица 1: Сравнение с алгоритмом, описанным в [11]
4.2 Реальные данные
Оценка применялась к реальным данным, чтобы оценить их полезность в практических приложениях. Пороговое значение 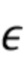 , найденное в (8), было выбрано равным примерно половине стандартного отклонения аддитивного шума
, найденное в (8), было выбрано равным примерно половине стандартного отклонения аддитивного шума 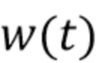 . Это обеспечило достаточно высокую вероятность создания интервалов, но при этом гарантировало, что ошибки в оценке энергии интервала были низкими. Значение длины
. Это обеспечило достаточно высокую вероятность создания интервалов, но при этом гарантировало, что ошибки в оценке энергии интервала были низкими. Значение длины 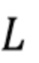 интервала было выбрано примерно в четыре раза больше «длины» типичного импульса, то есть в четыре раза больше длины интервала
интервала было выбрано примерно в четыре раза больше «длины» типичного импульса, то есть в четыре раза больше длины интервала 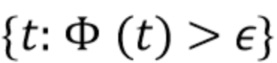 . Гистограмма энергии была получена для образца марганца с номинальной скоростью потока фотонов 105 событий в секунду. Небольшая отрицательная асимметрия присутствовал в форме основных пиков наблюдаемой гистограммы, что свидетельствует о том, что на систему повлиял составной источник шума. Это едва заметно на Фиг. 8. Шум был смоделирован как бимодальная гауссова смесь, а не как один гауссовский пик. Простая процедура оптимизации методом наименьших квадратов использовалась для подгонки параметров
. Гистограмма энергии была получена для образца марганца с номинальной скоростью потока фотонов 105 событий в секунду. Небольшая отрицательная асимметрия присутствовал в форме основных пиков наблюдаемой гистограммы, что свидетельствует о том, что на систему повлиял составной источник шума. Это едва заметно на Фиг. 8. Шум был смоделирован как бимодальная гауссова смесь, а не как один гауссовский пик. Простая процедура оптимизации методом наименьших квадратов использовалась для подгонки параметров 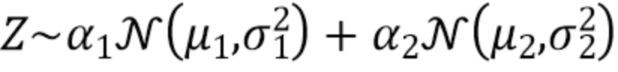 бимодального гауссовского распределения к пику шума, расположенному у столбика с нулевым индексом. Подходящее значение λ было выбрано вручную. Для оценки истинной плотности использовался логистический фильтр с полосой пропускания, управляемой данными. На Фиг. 8 показаны графики наблюдаемых и оцененных векторов вероятностной меры. Основные пики (столбики 450 ~ 600) были усилены, в то время как наложение было ослаблено, но не полностью удалено. Пики наложения первого порядка уменьшены. Отношение максимума к наложению (отношение высоты основного пика к высоте первого пика наложения) увеличилось с около 6 до около 120. Эти улучшения сопоставимы с другими современными системами (например, [11]). Имеется несколько возможных причин, по которым не удается оценка, чтобы полностью разложить наложение. Точность оценки зависит от правильного моделирования пика гауссова шума. Бимодальная гауссова смесь моделировала пик шума таким образом, что максимальная ошибка составляла менее 1% от пика плотности шума. Учитывая, что остаточные наложенные пики в оцененном спектре составляют менее 1% от основного пика, чувствительность оценки к ошибкам в моделировании шума могла в некоторой степени этому способствовать. Вторая причина неразложенного наложения может быть связана с неопределенностью в оценке наблюдаемого спектра. Некоторые из остаточных пиков наложения относительно близки к низу наблюдаемой гистограммы. Остаточные пики могут быть просто артефактом оценки, вызванным шумом. Наконец, математическая модель может быть слишком простой аппроксимацией наблюдаемого спектра. Процесс детектирования включает в себя многочисленные эффекты второго порядка, которые не были включены в модель (например, баллистический дефицит, истощение запаса заряда, коррелированный шум, нелинейности и т. д. …). Эти незначительные эффекты могут ограничить точность оценки поправки наложения.
бимодального гауссовского распределения к пику шума, расположенному у столбика с нулевым индексом. Подходящее значение λ было выбрано вручную. Для оценки истинной плотности использовался логистический фильтр с полосой пропускания, управляемой данными. На Фиг. 8 показаны графики наблюдаемых и оцененных векторов вероятностной меры. Основные пики (столбики 450 ~ 600) были усилены, в то время как наложение было ослаблено, но не полностью удалено. Пики наложения первого порядка уменьшены. Отношение максимума к наложению (отношение высоты основного пика к высоте первого пика наложения) увеличилось с около 6 до около 120. Эти улучшения сопоставимы с другими современными системами (например, [11]). Имеется несколько возможных причин, по которым не удается оценка, чтобы полностью разложить наложение. Точность оценки зависит от правильного моделирования пика гауссова шума. Бимодальная гауссова смесь моделировала пик шума таким образом, что максимальная ошибка составляла менее 1% от пика плотности шума. Учитывая, что остаточные наложенные пики в оцененном спектре составляют менее 1% от основного пика, чувствительность оценки к ошибкам в моделировании шума могла в некоторой степени этому способствовать. Вторая причина неразложенного наложения может быть связана с неопределенностью в оценке наблюдаемого спектра. Некоторые из остаточных пиков наложения относительно близки к низу наблюдаемой гистограммы. Остаточные пики могут быть просто артефактом оценки, вызванным шумом. Наконец, математическая модель может быть слишком простой аппроксимацией наблюдаемого спектра. Процесс детектирования включает в себя многочисленные эффекты второго порядка, которые не были включены в модель (например, баллистический дефицит, истощение запаса заряда, коррелированный шум, нелинейности и т. д. …). Эти незначительные эффекты могут ограничить точность оценки поправки наложения.
5 СУЩНОСТЬ ПЕРВОГО ВАРИАНТА ОСУЩЕСТВЛЕНИЯ
Мы взяли оценку, предложенную Gugushvili [18] для разложения в условиях гауссова шума, и адаптировали ее для коррекции наложения импульсов в рентгеновской спектроскопии. Мы предложили управляемый данными механизм выбора полосы пропускания, который легко реализуется и обеспечивает значительное ISE/MISE в широком диапазоне отсчетов образцов, представляющих интерес для спектроскопических приложений (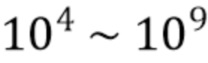 отсчетов). Выбор прямоугольной полосы пропускания, управляемый данными, близок к оптимальному (для прямоугольных фильтров) и в интересующем диапазоне превосходит выбор полосы пропускания, основанный на асимптотических результатах или фиксированной полосе пропускания. Хотя первоначальные результаты кажутся многообещающими, требуется дальнейшая работа для повышения производительности при практическом внедрении. Оценка по-прежнему содержит «звенящие» артефакты, связанные с феноменом Гиббса. Дополнительная форма фильтра пытается уменьшить это, есть и другие формы, которые ближе к оптимальной MSE.
отсчетов). Выбор прямоугольной полосы пропускания, управляемый данными, близок к оптимальному (для прямоугольных фильтров) и в интересующем диапазоне превосходит выбор полосы пропускания, основанный на асимптотических результатах или фиксированной полосе пропускания. Хотя первоначальные результаты кажутся многообещающими, требуется дальнейшая работа для повышения производительности при практическом внедрении. Оценка по-прежнему содержит «звенящие» артефакты, связанные с феноменом Гиббса. Дополнительная форма фильтра пытается уменьшить это, есть и другие формы, которые ближе к оптимальной MSE.
6 ВТОРОЙ ВАРИАНТ ОСУЩЕСТВЛЕНИЯ
В этом разделе дается сущность оценки спектра 2-го варианта осуществления. Второй вариант осуществления решает проблему первого варианта осуществления, который требует, чтобы каждым интервалом были приближенно охвачены целые кластеры. Во втором варианте осуществления при желании можно использовать всю серию данных, и перекрытие компенсируется введением двух интервалов разной длины 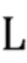 и
и  .
.
Нам необходимо ввести несколько дополнительных терминов, не упомянутых в первом варианте осуществления. В частности, 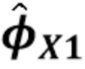 Оценка спектра основывается на
Оценка спектра основывается на
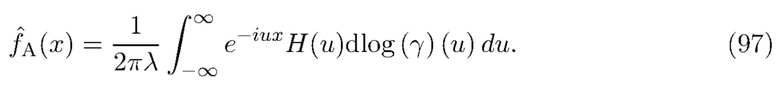
Введение фильтра 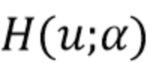 позволяет решить несколько возникающих проблем реализации. Процедуру оценки, которую мы используем, можно резюмировать в следующих этапах.
позволяет решить несколько возникающих проблем реализации. Процедуру оценки, которую мы используем, можно резюмировать в следующих этапах.
1. Разделите выбранный временной ряд на интервалы фиксированной длины 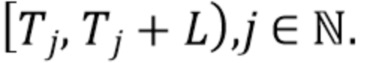
2. Вычислите значение 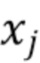 для каждого интервала в соответствии с
для каждого интервала в соответствии с 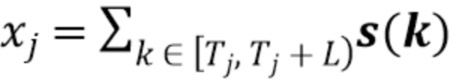 .
.
3. Создайте гистограмму 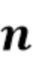 из значений
из значений 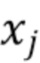 .
.
4. Рассчитайте 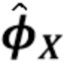 , используя обратное БПФ для
, используя обратное БПФ для 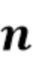 .
.
5. Разделите выбранный временной ряд на другой набор интервалов длиной 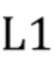 и, выполнив аналогичные вычисления, получите
и, выполнив аналогичные вычисления, получите 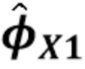 .
.
6. Вычислите 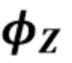 и
и 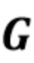 .
.
7. Вычислите 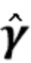 , используя
, используя 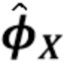 ,
, 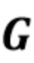 ,
, 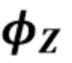 и
и 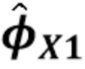 ,
,

8. Вычислите 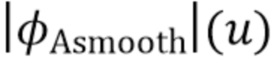 , версию
, версию 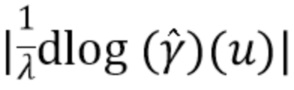 с фильтром нижних частот.
с фильтром нижних частот.
9. Вычислите 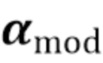 .
.
10. Вычислите 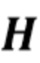 , используя
, используя 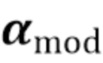 .
.
11. Вычислите 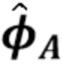 , используя
, используя 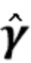 и
и 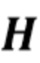 . Если какой-либо элемент
. Если какой-либо элемент 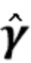 равен нулю, а соответствующий элемент
равен нулю, а соответствующий элемент 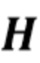 отличен от нуля, оценка не удалась, поскольку «выделенный логарифм» не определен.
отличен от нуля, оценка не удалась, поскольку «выделенный логарифм» не определен.
12. Вычислите 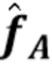 , используя БПФ для
, используя БПФ для 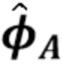 в соответствии с
в соответствии с
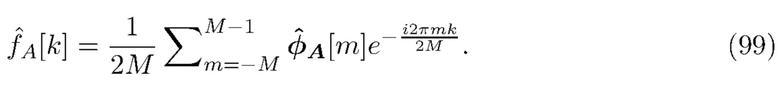
6.1 Детали алгоритма
Разделите выходной поток детектора на набор неперекрывающихся интервалов длиной 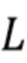 , т.е.
, т.е. 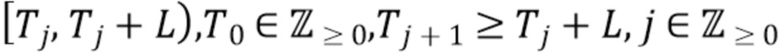 . Пусть
. Пусть 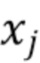 будет суммой выходных отсчетов детектора в j-м интервале, т.е.
будет суммой выходных отсчетов детектора в j-м интервале, т.е.

Предполагая, что 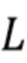 больше длительности импульса, j-й интервал может содержать «полные» импульсы, а также импульсы, которые были усечены по окончании интервала. Можно показать, что
больше длительности импульса, j-й интервал может содержать «полные» импульсы, а также импульсы, которые были усечены по окончании интервала. Можно показать, что 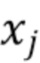 состоит из суперпозиции энергии «полных» импульсов, которые мы обозначаем
состоит из суперпозиции энергии «полных» импульсов, которые мы обозначаем 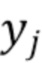 , энергий усеченных импульсов, которые мы обозначаем
, энергий усеченных импульсов, которые мы обозначаем 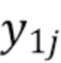 , и шума
, и шума 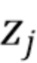 .
.
Пусть выходной поток детектора разделен на второй набор неперекрывающихся интервалов 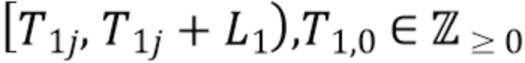 ,
, 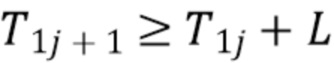 ,
, 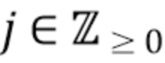 , где
, где 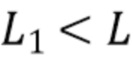 . Пусть
. Пусть 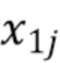 задается формулой
задается формулой

Если 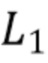 выбрано немного меньше длительности импульса, член
выбрано немного меньше длительности импульса, член 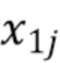 не будет содержать «полных» импульсов, а будет состоять из суперпозиции только энергий усеченных импульсов
не будет содержать «полных» импульсов, а будет состоять из суперпозиции только энергий усеченных импульсов 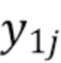 и шума
и шума 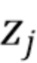 . Число усеченных импульсов в любом интервале имеет распределение Пуассона. Имеем
. Число усеченных импульсов в любом интервале имеет распределение Пуассона. Имеем

Мы можем разложить полную энергию в интервале 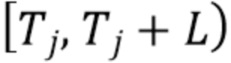 на энергетический вклад
на энергетический вклад 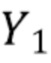 от импульсов, которые были усечены, и энергетический вклад
от импульсов, которые были усечены, и энергетический вклад 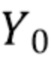 от импульсов, которые полностью содержатся в интервале
от импульсов, которые полностью содержатся в интервале 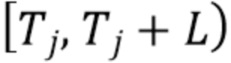 , т.е.
, т.е.

где Z0 представляет шум в областях, где импульсы полностью содержатся в интервале (длины 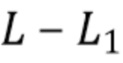 ), а
), а 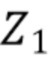 представляет шум в областях, где импульсы усечены (длина
представляет шум в областях, где импульсы усечены (длина 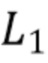 ). Следовательно,
). Следовательно,

Объединяя (103) с (105), получаем

Перестановка дает

Мы можем оценить 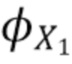 аналогично тому, как мы оценили
аналогично тому, как мы оценили 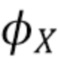 , или каким-либо другим способом, например, с помощью эмпирической характеристической функции или путем выполнения БПФ на нормализованной гистограмме значений
, или каким-либо другим способом, например, с помощью эмпирической характеристической функции или путем выполнения БПФ на нормализованной гистограмме значений 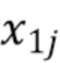 .
.
При выполнении операции разложения коэффициент 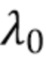 Пуассона для уменьшенной длины интервала
Пуассона для уменьшенной длины интервала 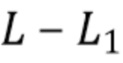 используется для учета подинтервала, на котором возникает составной пуассоновский процесс
используется для учета подинтервала, на котором возникает составной пуассоновский процесс 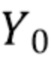 .
.
6.2 Визуализация внутренних величин
Чтобы помочь читателю понять, на Фиг. 9 показаны различные величины, полученные в процессе оценки. Верхняя синяя кривая (со значением около 0,3 в нулевом столбике) обозначает 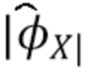 , оценочную характеристическую функцию наблюдаемого спектра. Коричневая кривая используется для представления истинного значения
, оценочную характеристическую функцию наблюдаемого спектра. Коричневая кривая используется для представления истинного значения 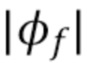 , которую отчетливо видно как нижнюю кривую с периодическими нулями в области [6000, 10000]. Величина
, которую отчетливо видно как нижнюю кривую с периодическими нулями в области [6000, 10000]. Величина 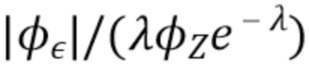 показана прозрачным красным цветом и возникает как «шум», средняя плотность которого достигает пика около столбика № 8000. Ожидаемое значение
показана прозрачным красным цветом и возникает как «шум», средняя плотность которого достигает пика около столбика № 8000. Ожидаемое значение 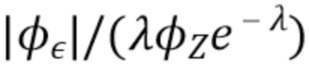 показано черной штриховой линией. Это получается с использованием (75), известного значения λ и допущения гауссовского шума с известным
показано черной штриховой линией. Это получается с использованием (75), известного значения λ и допущения гауссовского шума с известным 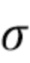 для получения
для получения 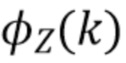 . Величина
. Величина 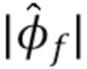 показана прозрачной синей кривой. Это едва заметно, так как она близко совмещается с
показана прозрачной синей кривой. Это едва заметно, так как она близко совмещается с 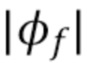 в интервалах [0, 4000], [12000, 16000] и близко с
в интервалах [0, 4000], [12000, 16000] и близко с 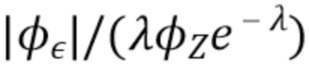 в интервале [5000, 11000]. Обратите внимание, кажется, что цвет
в интервале [5000, 11000]. Обратите внимание, кажется, что цвет 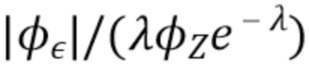 , меняется с красного на фиолетовый в интервале [5000, 11000], поскольку оба прозрачных графика перекрываются. Сплошная черная линия показывает
, меняется с красного на фиолетовый в интервале [5000, 11000], поскольку оба прозрачных графика перекрываются. Сплошная черная линия показывает 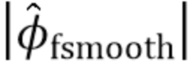 , версию
, версию 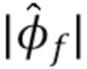 с фильтром нижних частот. Фильтрация нижних частот удаляет любые локальные колебания в
с фильтром нижних частот. Фильтрация нижних частот удаляет любые локальные колебания в 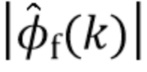 благодаря локализации пиков, как описано в параграфе о сглаживании в начале этого раздела. Член
благодаря локализации пиков, как описано в параграфе о сглаживании в начале этого раздела. Член  служит оценкой
служит оценкой 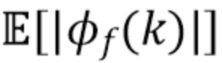 . Можно видеть, что
. Можно видеть, что 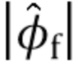 обеспечивает достаточно хорошую оценку
обеспечивает достаточно хорошую оценку 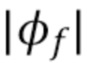 в области, где
в области, где 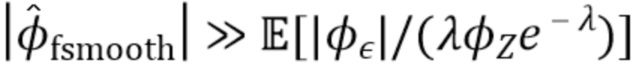 . По мере того, как эти две величины приближаются друг к другу, качество оценки ухудшается до тех пор, пока в нем в конечном итоге не будет преобладать шум. Фильтр
. По мере того, как эти две величины приближаются друг к другу, качество оценки ухудшается до тех пор, пока в нем в конечном итоге не будет преобладать шум. Фильтр 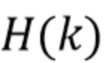 должен содержать хорошие оценки
должен содержать хорошие оценки 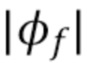 , при исключении плохих оценок. Чтобы найти области, в которых получены хорошие оценки
, при исключении плохих оценок. Чтобы найти области, в которых получены хорошие оценки 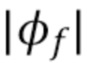 , мы обращаемся к вопросу: учитывая
, мы обращаемся к вопросу: учитывая 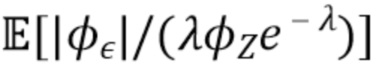 , какова вероятность того, что вычисленные значения
, какова вероятность того, что вычисленные значения 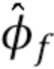 в локальной области в значительной степени связаны с шумом?
в локальной области в значительной степени связаны с шумом?
7 ОЦЕНКА СКОРОСТИ СЧЕТА
Предыдущая оценка предполагала, что λ было известно. Оценка λ может быть получена без предварительного знания следующим образом.
1. Используя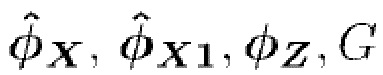 из предыдущего раздела, вычислите
из предыдущего раздела, вычислите
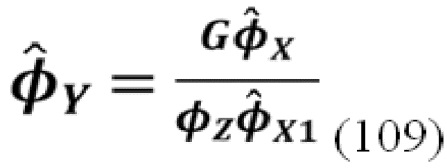
2. Используя 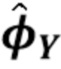 , оцените скор
, оцените скор
ость счета. Это можно сделать несколькими способами.
3. Один из способов - использовать процедуру оптимизации или другие средства для подгонки кривой 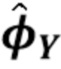 . Подбираемые параметры можно использовать для оценки скорости счета.
. Подбираемые параметры можно использовать для оценки скорости счета.
4. Другой способ включает в себя оценку смещения 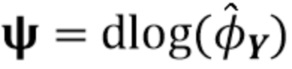 постоянного тока. Это можно сделать путем усреднения подходящего числа точек
постоянного тока. Это можно сделать путем усреднения подходящего числа точек 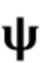 . Точки, полученные путем фильтрации с помощью
. Точки, полученные путем фильтрации с помощью 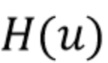 в предыдущем разделе, обычно подходят, хотя меньшее число точек также может дать адекватную оценку.
в предыдущем разделе, обычно подходят, хотя меньшее число точек также может дать адекватную оценку.
5. Другой способ включает в себя использование механизма оптимизации или других средств для подгонки кривой к 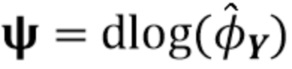 . Подходящая параметризованная кривая для подгонки
. Подходящая параметризованная кривая для подгонки 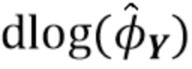 дается
дается
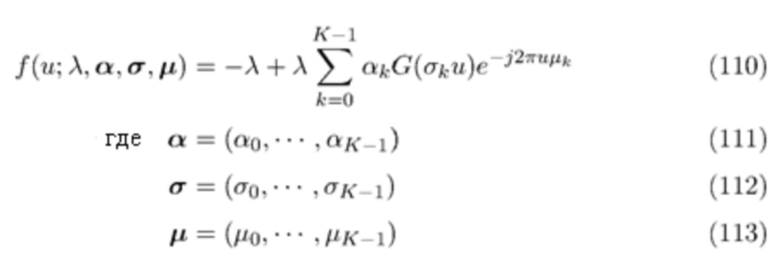
и где 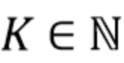 выбирается так, чтобы кривая соответствовала с достаточной точностью. Параметр λ дает оценку скорости счета. От механизма оптимизации не требуется придавать одинаковый вес в каждой точке
выбирается так, чтобы кривая соответствовала с достаточной точностью. Параметр λ дает оценку скорости счета. От механизма оптимизации не требуется придавать одинаковый вес в каждой точке 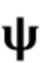 .
.
8 ОПИСАНИЕ ФИГУР
Следующие фигуры помогают понять процесс. На Фиг. 1 показана одна из возможных схем, используемых для разделения выходного сигнала детектора. На иллюстрации показан дискретизированный отклик детектора на три падающих фотона. Для большей ясности фигуры были удалены эффекты шума. Выходной отклик был разделен на несколько областей равной длины 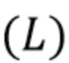 . Число импульсов, прибывающих в каждую область, неизвестно системе обработки. Один импульс прибыл в первый интервал. Два импульса прибыло во второй интервал. В третьем интервале импульсов не было. Полная энергия фотонов, прибывающих в каждый интервал, вычисляется как интересующая статистика, представляя собой сумму всех значений выборки на каждом интервале. Интервалы не синхронизируются по времени с прибытиями импульсов. На Фиг. 2 показан результат процедуры оценки. Истинная плотность вероятности энергии падающего фотона показана черной линией. Скорость прибытия фотонов такова, что в среднем за любой заданный интервал
. Число импульсов, прибывающих в каждую область, неизвестно системе обработки. Один импульс прибыл в первый интервал. Два импульса прибыло во второй интервал. В третьем интервале импульсов не было. Полная энергия фотонов, прибывающих в каждый интервал, вычисляется как интересующая статистика, представляя собой сумму всех значений выборки на каждом интервале. Интервалы не синхронизируются по времени с прибытиями импульсов. На Фиг. 2 показан результат процедуры оценки. Истинная плотность вероятности энергии падающего фотона показана черной линией. Скорость прибытия фотонов такова, что в среднем за любой заданный интервал 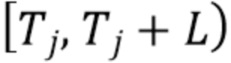 прибывают три фотона. Стандартное отклонение аддитивного шума в выходном сигнале детектора
прибывают три фотона. Стандартное отклонение аддитивного шума в выходном сигнале детектора 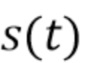 равно ширине одного столбика гистограммы. Был собран миллион интервалов. Была построена гистограмма полной энергии на каждом интервале. Это показано синей линией. Эффекты наложения очевидны, особенно вокруг столбиков 75, 150 и 225. Красная трассировка показывает оценку истинного спектра падающей энергии после обработки данных системой. Хотя в оценке присутствует некоторый шум, эффекты наложения были устранены. Ожидается, что оценка правильно восстановит в среднем истинный спектр падающего излучения. Этот результат был получен с использованием внутреннего фильтра, полоса пропускания которого определялась автоматически из данных. На Фиг. 3 показаны те же величины, что и на Фиг. 2, при тех же рабочих условиях, однако в этом случае ширина полосы внутреннего фильтра была определена с использованием асимптотических результатов из литературы. Хотя оценочная плотность вероятности падающих энергий была восстановлена, дисперсия значительно больше по сравнению с Фиг. 2. На Фиг. 8 показана работа системы на реальных данных. Синяя трассировка показывает плотность вероятности наблюдаемых значений энергии, а красная трассировка показывает оцененную истинную плотность вероятности энергий падающих фотонов. Черной трассировки нет, поскольку истинная плотность вероятности неизвестна. В этом эксперименте в качестве источника фотонов использовалась рентгеновская флуоресценция образца марганца. Скорость прибытия фотонов составляла около 105 фотонов в секунду. Длина интервала выбиралась такой, чтобы среднее время между фотонами соответствовало длине двух интервалов. Было собрано достаточно данных и разделено, чтобы сформировать на 5,9×106 интервалов. Стандартное отклонение аддитивного шума соответствует 4,7 столбикам гистограммы. Процесс оценки явно уменьшил пики наложения и увеличил истинные пики. На Фиг. 9 показаны различные величины, полученные во время моделирования системы, описанной во 2-м варианте осуществления. Это описано в разделе 5.1 Визуализация внутренних величин. Фиг. 9-12 относятся ко второму варианту осуществления. На Фиг. 10 показаны наблюдаемая и истинная плотность вероятности входных энергий фотонов для эксперимента, из которого были получены Фиг. 9-13. Черная трассировка показывает истинную плотность вероятности. Красная трассировка показывает ожидаемую плотность, когда три фотона прибывают в среднем в течение заданного интервала времени. Синяя трассировка показывает фактическую наблюдаемую плотность. В наблюдаемой плотности можно увидеть наложение до десятого порядка. Фиг. 10 включает в себя несколько графиков типичной спектроскопической системы. Фактическая плотность падающих фотонов («Идеальная плотность») показана сплошной темной линией. Наблюдаемая гистограмма, полученная путем разделения данных временного ряда, показана темно-синим цветом. Очевидно искажение спектра, вызванное наложением импульсов. На Фиг. 13 показаны различные внутренние величины с использованием логарифмической вертикальной оси. Темно-синяя кривая, которая опускается в центре графика, -
равно ширине одного столбика гистограммы. Был собран миллион интервалов. Была построена гистограмма полной энергии на каждом интервале. Это показано синей линией. Эффекты наложения очевидны, особенно вокруг столбиков 75, 150 и 225. Красная трассировка показывает оценку истинного спектра падающей энергии после обработки данных системой. Хотя в оценке присутствует некоторый шум, эффекты наложения были устранены. Ожидается, что оценка правильно восстановит в среднем истинный спектр падающего излучения. Этот результат был получен с использованием внутреннего фильтра, полоса пропускания которого определялась автоматически из данных. На Фиг. 3 показаны те же величины, что и на Фиг. 2, при тех же рабочих условиях, однако в этом случае ширина полосы внутреннего фильтра была определена с использованием асимптотических результатов из литературы. Хотя оценочная плотность вероятности падающих энергий была восстановлена, дисперсия значительно больше по сравнению с Фиг. 2. На Фиг. 8 показана работа системы на реальных данных. Синяя трассировка показывает плотность вероятности наблюдаемых значений энергии, а красная трассировка показывает оцененную истинную плотность вероятности энергий падающих фотонов. Черной трассировки нет, поскольку истинная плотность вероятности неизвестна. В этом эксперименте в качестве источника фотонов использовалась рентгеновская флуоресценция образца марганца. Скорость прибытия фотонов составляла около 105 фотонов в секунду. Длина интервала выбиралась такой, чтобы среднее время между фотонами соответствовало длине двух интервалов. Было собрано достаточно данных и разделено, чтобы сформировать на 5,9×106 интервалов. Стандартное отклонение аддитивного шума соответствует 4,7 столбикам гистограммы. Процесс оценки явно уменьшил пики наложения и увеличил истинные пики. На Фиг. 9 показаны различные величины, полученные во время моделирования системы, описанной во 2-м варианте осуществления. Это описано в разделе 5.1 Визуализация внутренних величин. Фиг. 9-12 относятся ко второму варианту осуществления. На Фиг. 10 показаны наблюдаемая и истинная плотность вероятности входных энергий фотонов для эксперимента, из которого были получены Фиг. 9-13. Черная трассировка показывает истинную плотность вероятности. Красная трассировка показывает ожидаемую плотность, когда три фотона прибывают в среднем в течение заданного интервала времени. Синяя трассировка показывает фактическую наблюдаемую плотность. В наблюдаемой плотности можно увидеть наложение до десятого порядка. Фиг. 10 включает в себя несколько графиков типичной спектроскопической системы. Фактическая плотность падающих фотонов («Идеальная плотность») показана сплошной темной линией. Наблюдаемая гистограмма, полученная путем разделения данных временного ряда, показана темно-синим цветом. Очевидно искажение спектра, вызванное наложением импульсов. На Фиг. 13 показаны различные внутренние величины с использованием логарифмической вертикальной оси. Темно-синяя кривая, которая опускается в центре графика, - 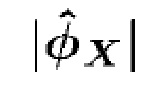 . Зеленая величина, которая пересекает график по горизонтали,
. Зеленая величина, которая пересекает график по горизонтали, 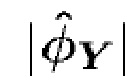 . Верхняя голубая кривая, спускающаяся в центре графика, -
. Верхняя голубая кривая, спускающаяся в центре графика, - 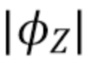 . На Фиг. 11 показана траектория кривой γ в комплексной плоскости. На Фиг. 12 показаны внутренние величины, аналогичные Фиг. 9, однако есть некоторые дополнительные сигналы. Горизонтальная красная трассировка, которая в основном представляет собой шум, и соответствующая черная штриховая линия представляют
. На Фиг. 11 показана траектория кривой γ в комплексной плоскости. На Фиг. 12 показаны внутренние величины, аналогичные Фиг. 9, однако есть некоторые дополнительные сигналы. Горизонтальная красная трассировка, которая в основном представляет собой шум, и соответствующая черная штриховая линия представляют 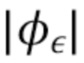 , величину характеристической функции гистограммного шума. Прозрачный зеленый график, образующий «зашумленный пик» в центре фигуры, представляет собой оценку
, величину характеристической функции гистограммного шума. Прозрачный зеленый график, образующий «зашумленный пик» в центре фигуры, представляет собой оценку 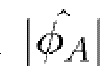 . Эта величина была выделена синим цветом на Фиг. 9 и была едва видна, поскольку была скрыта
. Эта величина была выделена синим цветом на Фиг. 9 и была едва видна, поскольку была скрыта 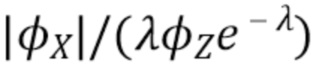 , что не показано на Фиг. 12. Горизонтальная трассировка со средним значением -3 представляет собой график
, что не показано на Фиг. 12. Горизонтальная трассировка со средним значением -3 представляет собой график 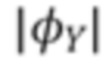 . Голубая трассировка, которая начинается со значения нуля в нулевом столбике и падает до минимума около столбика 8000, представляет собой
. Голубая трассировка, которая начинается со значения нуля в нулевом столбике и падает до минимума около столбика 8000, представляет собой 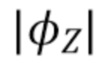 , величину характеристической функции аддитивного гауссовского шума. Фиг. 13 относится ко второму широкому аспекту вычисления скорости счета. На ней показаны внутренние количества, используемые при расчете
, величину характеристической функции аддитивного гауссовского шума. Фиг. 13 относится ко второму широкому аспекту вычисления скорости счета. На ней показаны внутренние количества, используемые при расчете 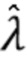 . Голубая трассировка, которая начинается с нулевого значения в нулевом столбике и падает до минимума около столбика 8000, представляет собой
. Голубая трассировка, которая начинается с нулевого значения в нулевом столбике и падает до минимума около столбика 8000, представляет собой 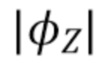 , величину характеристической функции аддитивного гауссовского шума. Темно-синя трассировка, которая падает до минимума в центре фигуры, представляет собой
, величину характеристической функции аддитивного гауссовского шума. Темно-синя трассировка, которая падает до минимума в центре фигуры, представляет собой 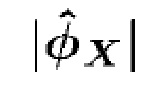 , оценка характеристической функции наблюдаемых данных. Желто-зеленая горизонтальная трассировка со средним значением -3, представляет собой оценку
, оценка характеристической функции наблюдаемых данных. Желто-зеленая горизонтальная трассировка со средним значением -3, представляет собой оценку 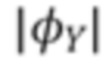 .
.
Список литературы
[1] G. F. Knoll, Radiation Detection and Measurement, 3rd Edition. New York: Wiley,2000.
[2] P. A. B. Scoullar and R. J. Evans, “Maximum likelihood estimation techniques for high rate, high throughput digital pulse processing,” in 2008 IEEE Nuclear Science Symposium Conference Record, pp. 1668-1672, Oct. 2008.
[3] M. Haselman, J. Pasko, S. Hauck, T. Lewellen, and R. Miyaoka, “FPGA-based pulse pile-up correction with energy and timing recovery,” IEEE Transactions on Nuclear Science, vol. 59, pp. 1823-1830, Oct. 2012.
[4] T. Petrovic, M. Vencelj, M. Lipoglavsek, R. Novak, and D. Savran, “Efficient re duction of piled-up events in gamma-ray spectrometry at high count rates,” IEEE Transactions on Nuclear Science, vol. 61, pp. 584-589, Feb. 2014.
[5] B. A. VanDevender, M. P. Dion, J. E. Fast, D. C. Rodriguez, M. S. Taubman, C. D. Wilen, L. S. Wood, and M. E. Wright, “High-purity germanium spectroscopy at rates in excess of 106 events/s,” IEEE Transactions on Nuclear Science, vol. 61, pp. 2619-2627, Oct. 2014.
[6] Y. Sepulcre, T. Trigano, and Y. Ritov, “Sparse regression algorithm for activity esti mation in spectrometry,” IEEE Transactions on Signal Processing, vol. 61, pp. 4347-4359, Sept. 2013.
[7] T. Trigano, I. Gildin, and Y. Sepulcre, “Pileup correction algorithm using an iterated sparse reconstruction method,” IEEE Signal Processing Letters, vol. 22, pp. 1392-1395, Sept. 2015.
[8] L. Wielopolski and R. P. Gardner, “Prediction of the pulse-height spectral distortion caused by the peak pile-up effect,” Nuclear Instruments and Methods, vol. 133, pp. 303-309, Mar. 1976.
[9] N. P. Barradas and M. A. Reis, “Accurate calculation of pileup effects in PIXE spectra from first principles,” X-Ray Spectrometry, vol. 35, pp. 232-237, July 2006.
[10] T. Trigano, A. Souloumiac, T. Montagu, F. Roueff, and E. Moulines, “Statistical pileup correction method for HPGe detectors,” IEEE Transactions on Signal Processing, vol. 55, pp. 4871-4881, Oct. 2007.
[11] T. Trigano, E. Barnt, T. Dautremer, and T. Montagu, “Fast digital filtering of spectrometric data for pile-up correction,” IEEE Signal Processing Letters, vol. 22, pp. 973-977, July 2015.
[12] P. Ilhe, E. Moulines, F. Roueff, and A. Souloumiac, “Nonparametric estimation of mark's distribution of an exponential shot-noise process,” Electronic Journal of Statistics, vol. 9, no. 2, pp. 3098-3123, 2015.
[13] P. Ilhe, F. Roueff, E. Moulines, and A. Souloumiac, “Nonparametric estimation of a shot-noise process,” in 2016 IEEE Statistical Signal Processing Workshop (SSP), pp. 1-4, June 2016.
[14] C. McLean, M. Pauley, and J. H. Manton, “Limitations of decision based pile-up correction algorithms,” in 2018 IEEE Statistical Signal Processing Workshop (SSP), pp. 693-697, June 2018.
[15] D. Snyder and M. Miller, Random Point Processes In Time And Space. New York: Springer-Verlag, 2, revised ed., Sept. 2011.
[16] B. Buchmann and R. Grubel, “Decompounding: An estimation problem for Poisson random sums,” Annals of Statistics, pp. 1054-1074, 2003.
[17] B. van Es, S. Gugushvili, and P. Spreij, “Deconvolution for an atomic distribution,” Electronic Journal of Statistics, vol. 2, pp. 265-297, 2008.
[18] S. Gugushvili, Non-Parametric Inference for Partially Observed Levy Processes. PhD, University of Amsterdam, Thomas Stieltjes Institute, 2008.
[19] S. Said, C. Lageman, N. Le Bihan, and J. H. Manton, “Decompounding on compact Lie groups,” IEEE Transactions on Information Theory, vol. 56, pp. 2766-2777, June 2010.
[20] B. van Es, S. Gugushvili, and P. Spreij, “A kernel type nonparametric density esti mator for decompounding,” Bernoulli, vol. 13, pp. 672-694, Aug. 2007.
[21] J. Yu, “Empirical characteristic function estimation and its applications,” Econo metric Reviews, vol. 23, pp. 93-123, Dec. 2004.
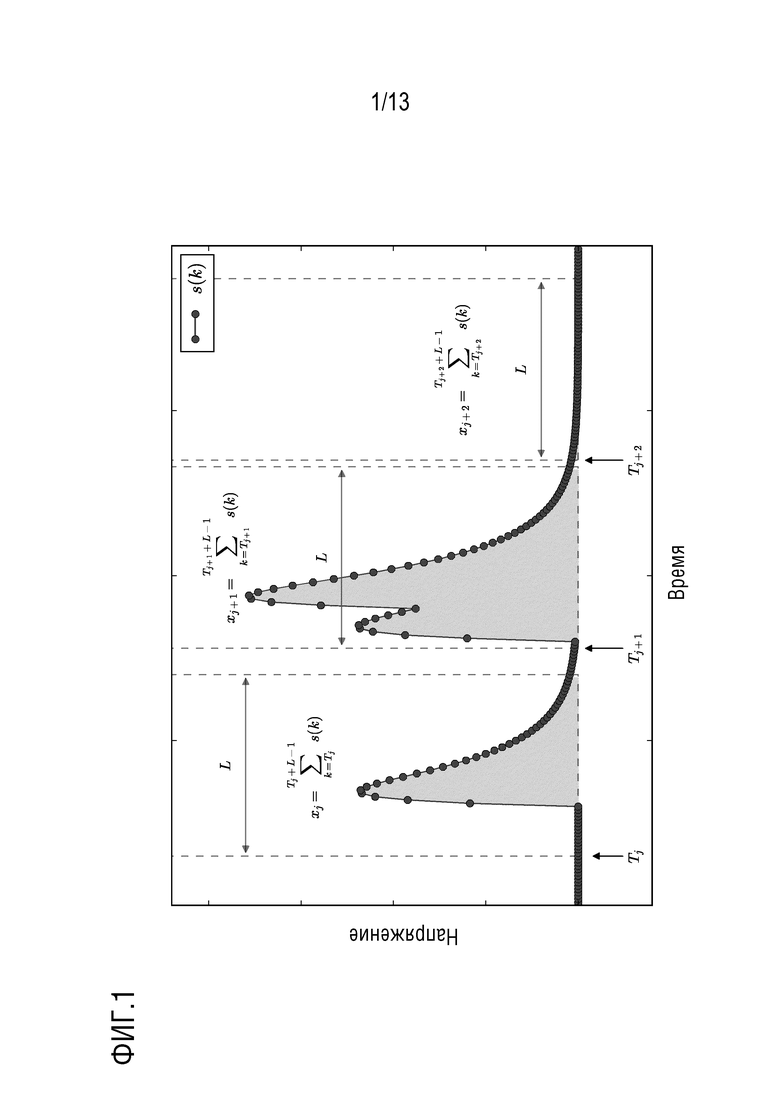
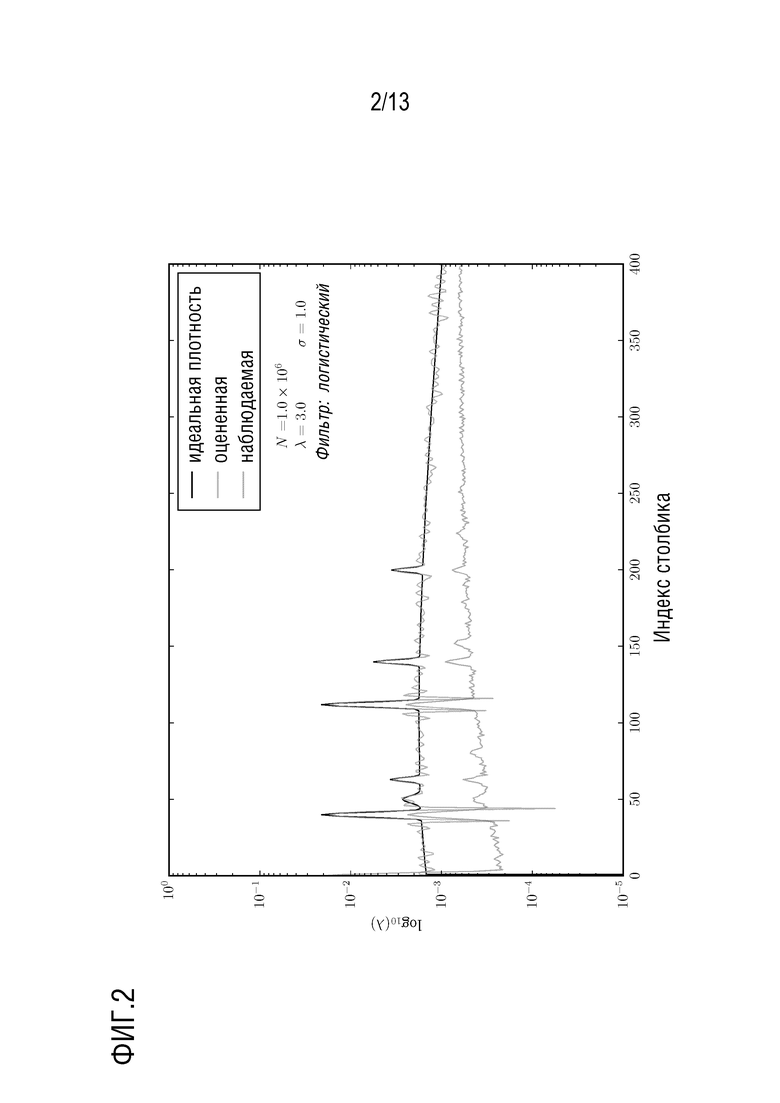
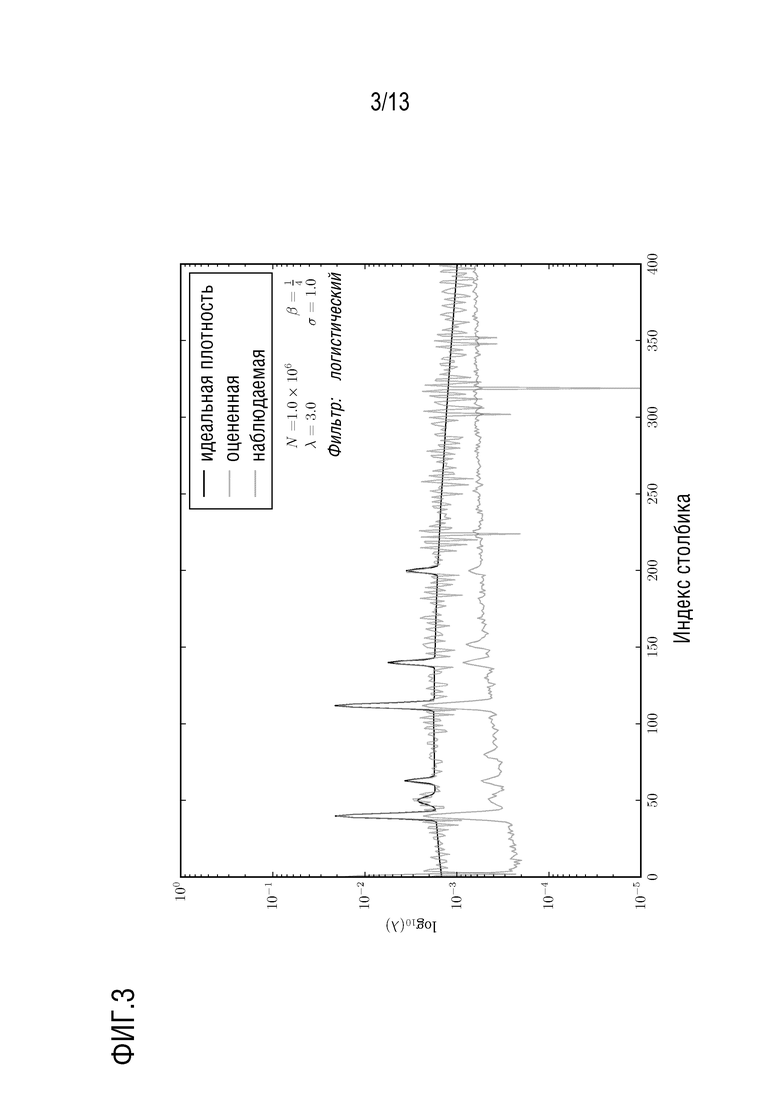
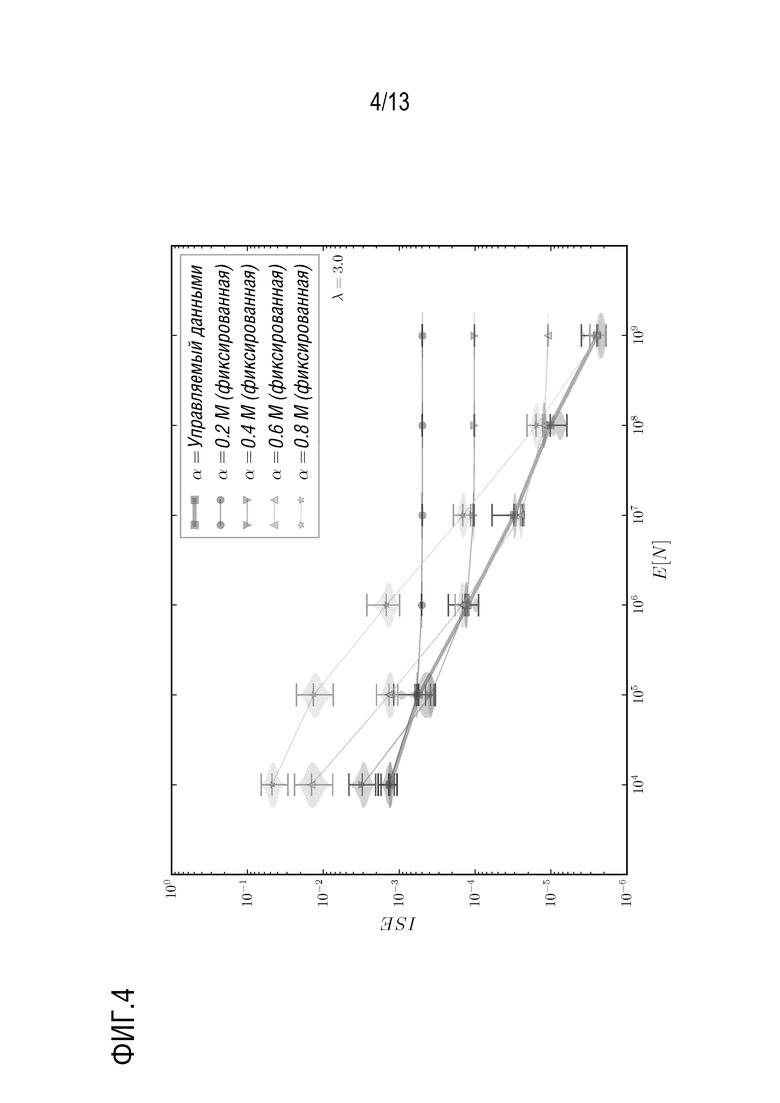
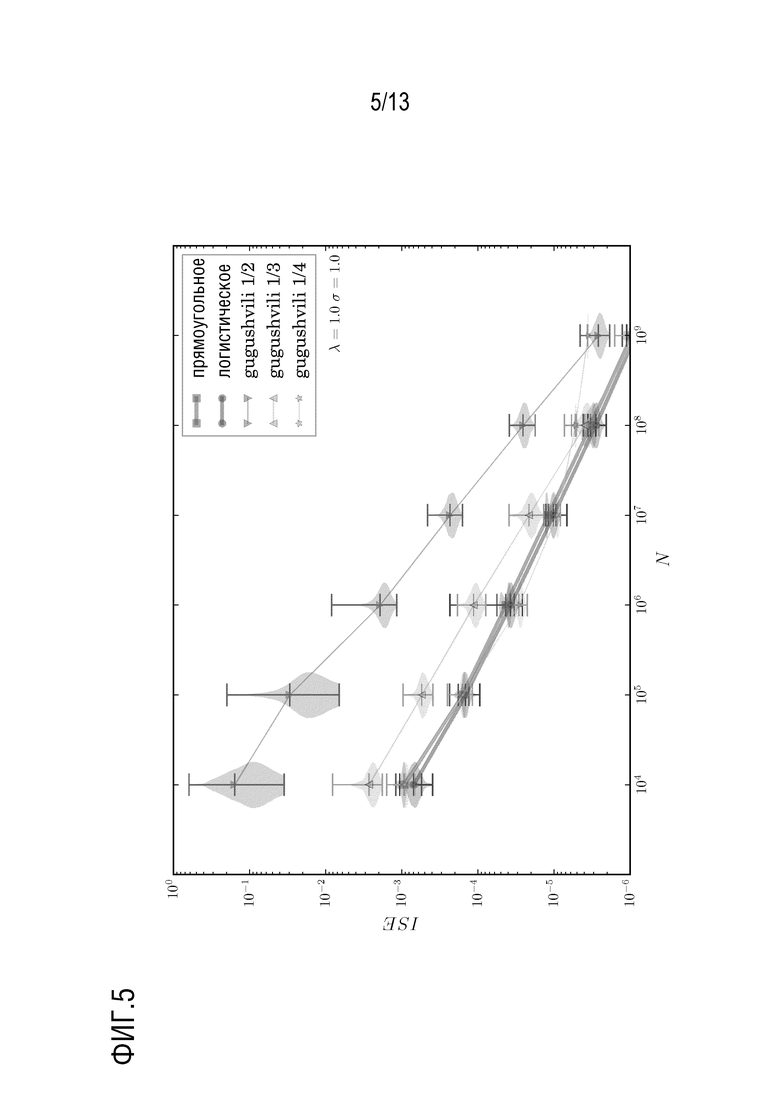
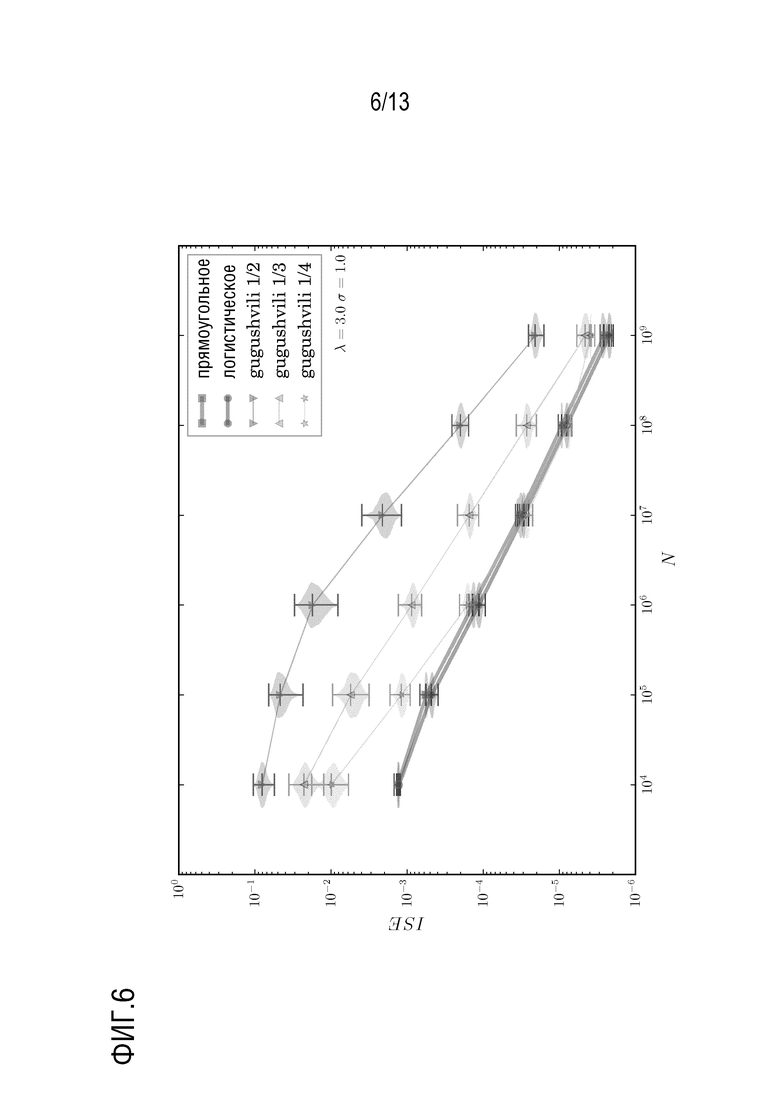
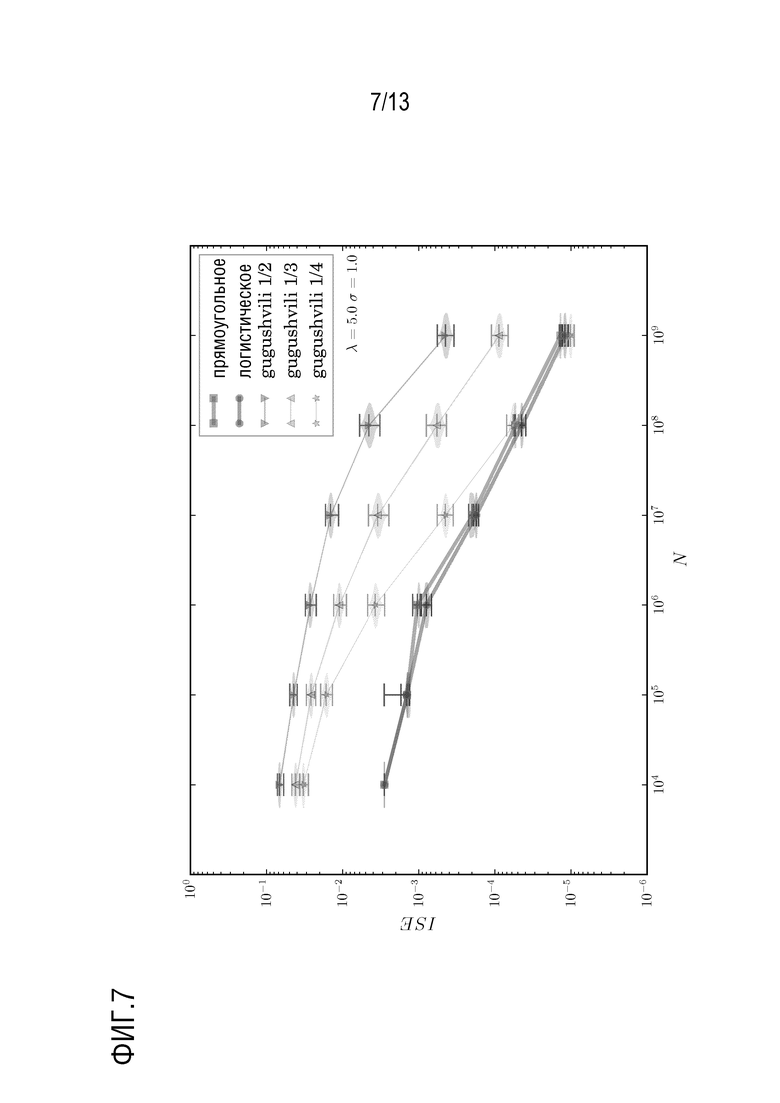
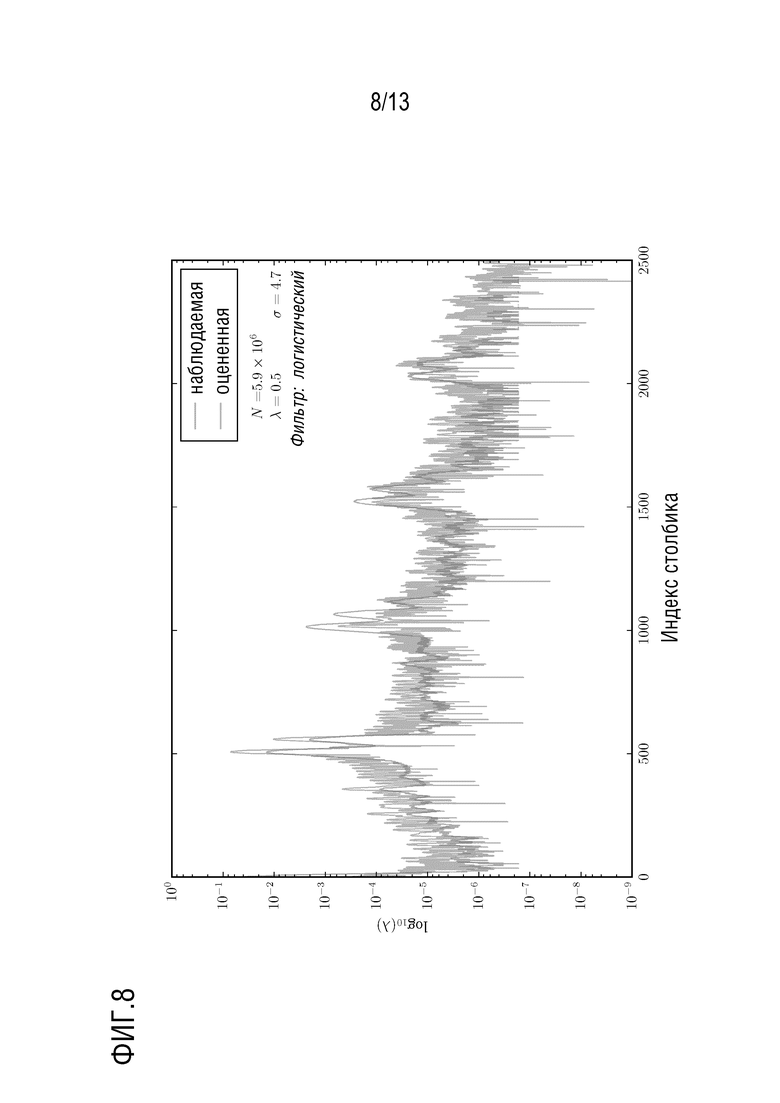
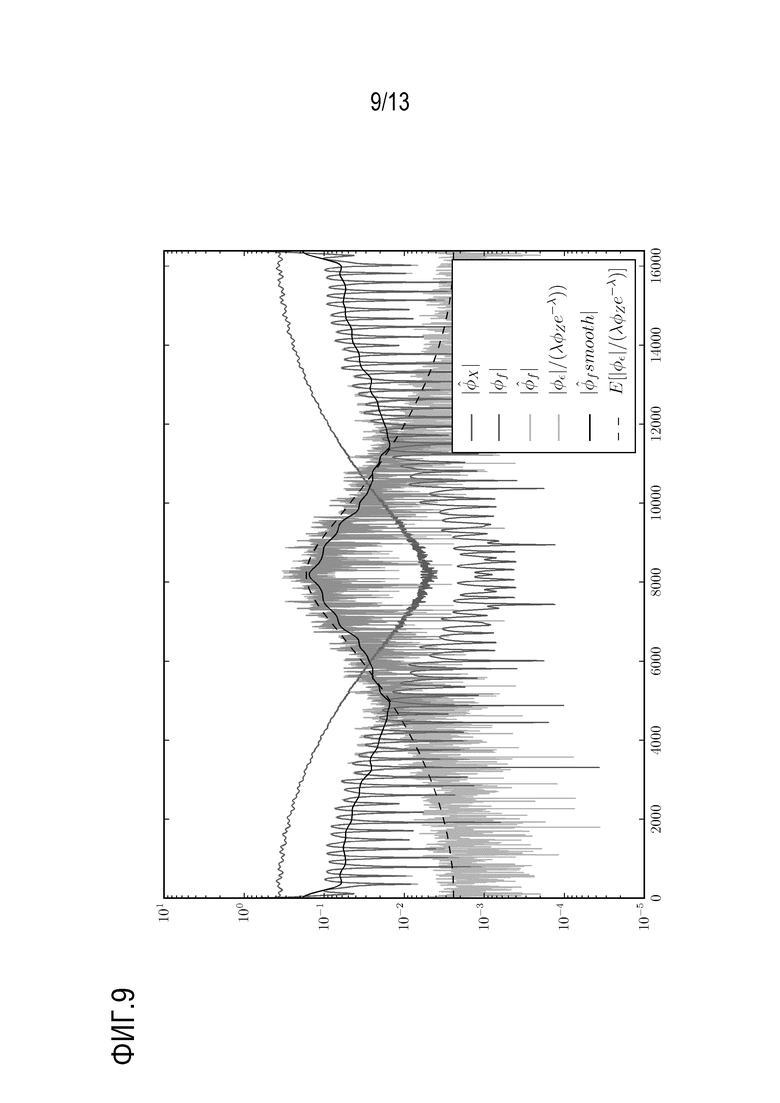
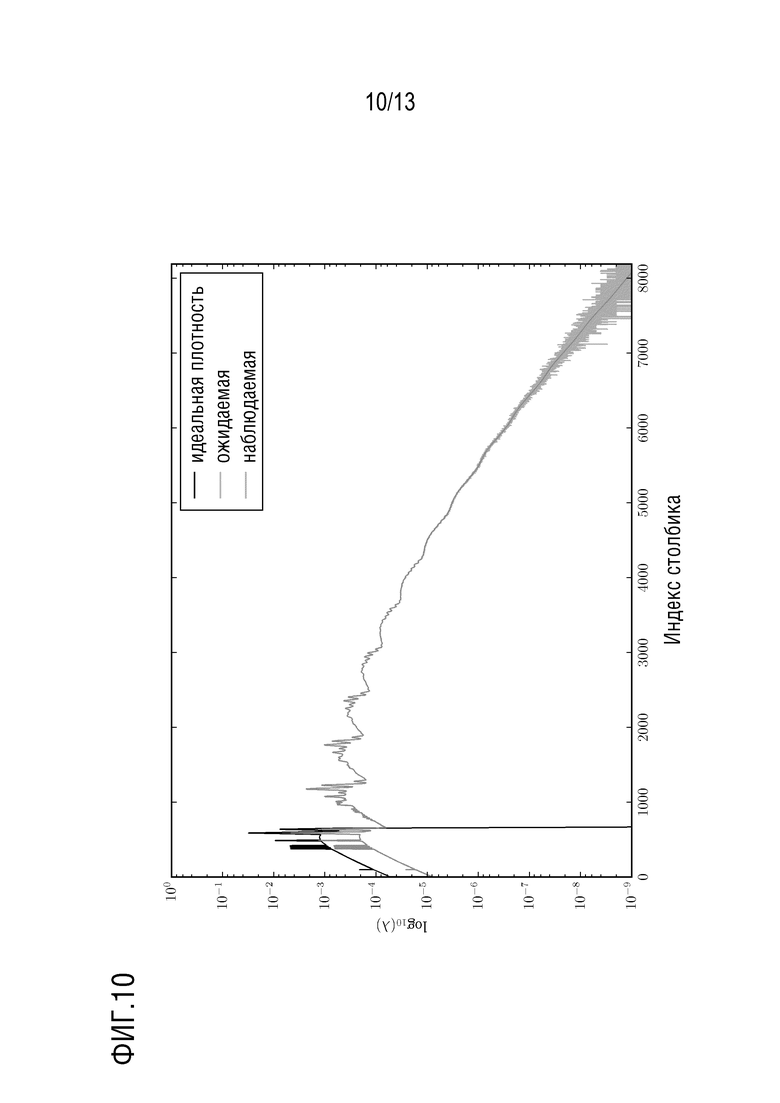
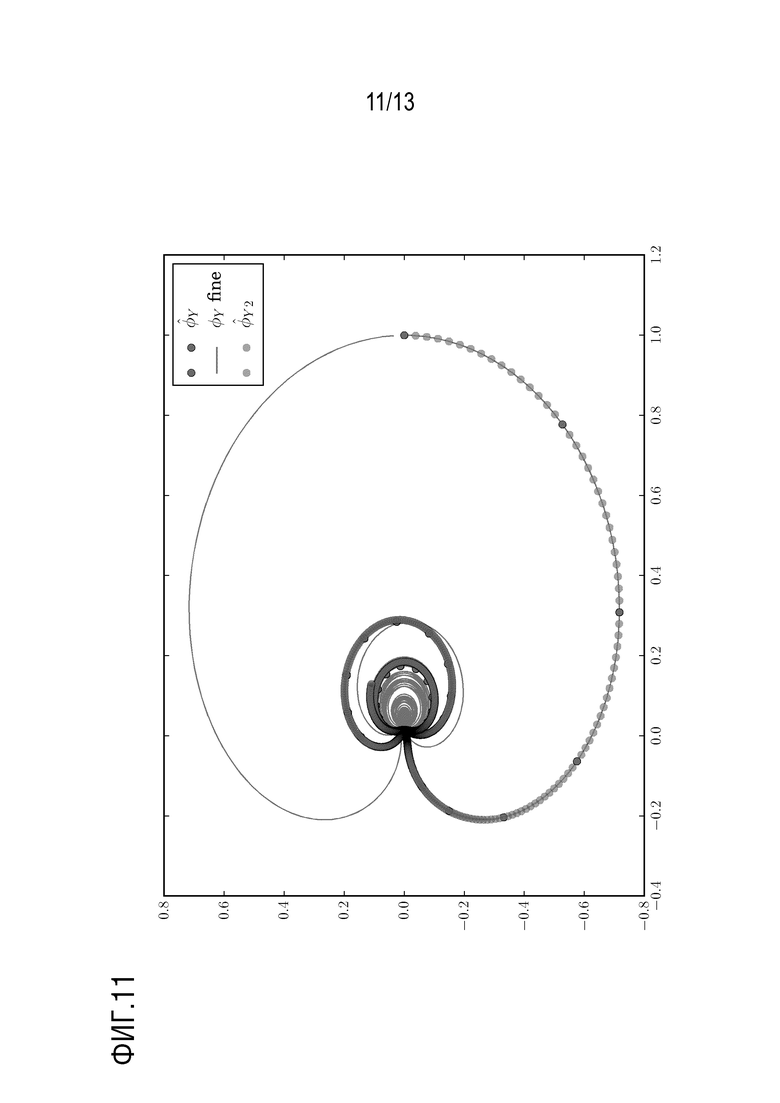
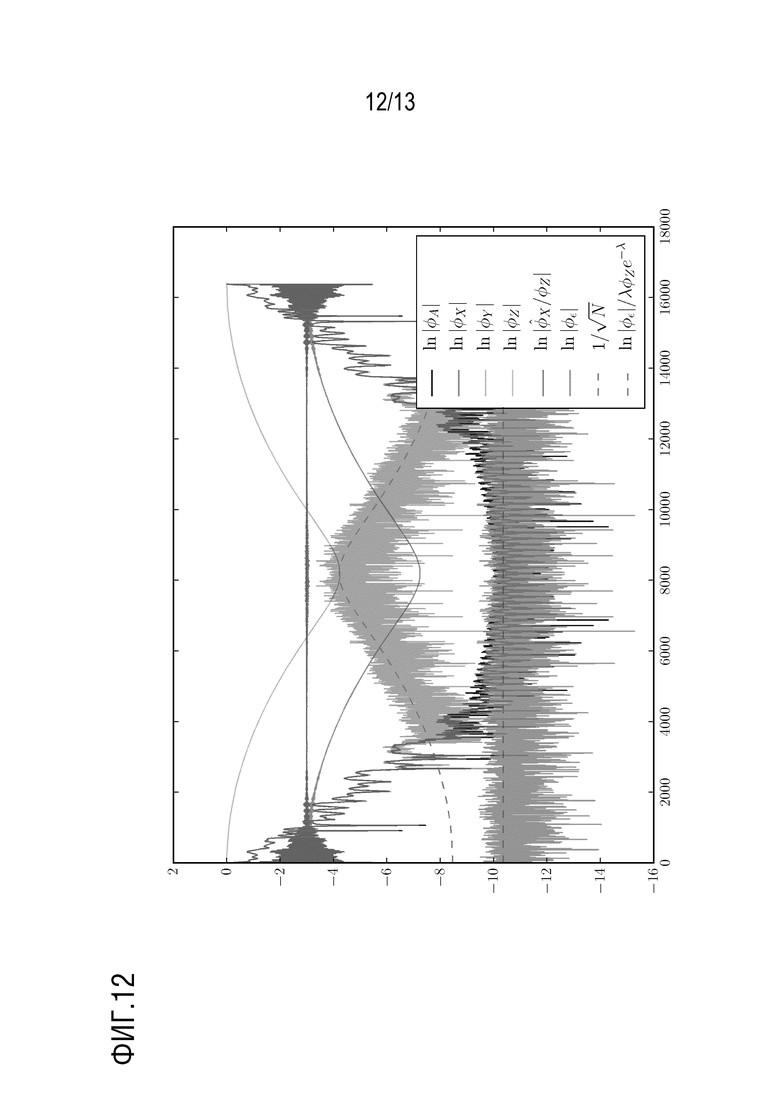
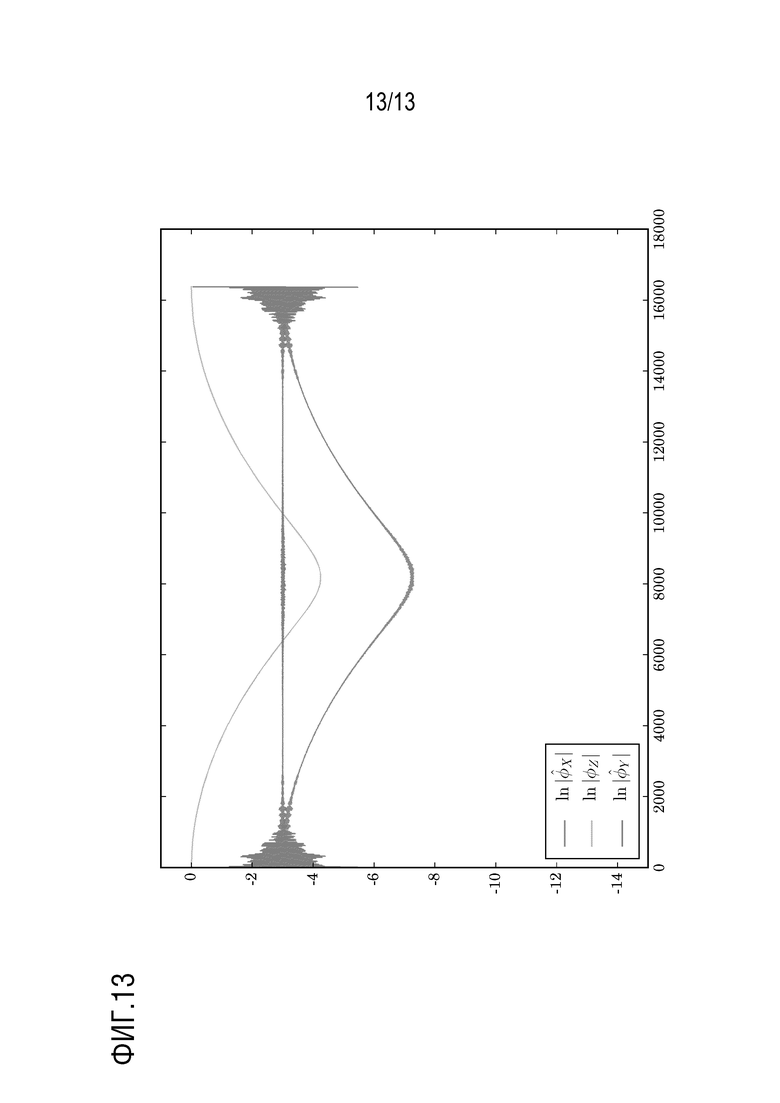
Группа изобретений относится к области спектроскопии. Спектрально-зависимые статистические данные вычисляются из временного ряда цифровых наблюдений от детектора излучения, задавая отображение в виде карты из плотности амплитуд импульсов в спектрально-зависимые статистические данные. Спектр определяется путем оценки плотности амплитуд импульсов путем применения инверсии отображения в виде карты к спектрально-зависимым статистическим данным. Статистические данные могут быть основаны на первом наборе неперекрывающихся временных интервалов постоянной длины L, по меньшей мере такой же, как длительность импульсов, без учета совокупности кластеров импульсов; и втором наборе неперекрывающихся временных интервалов постоянной длины L1, меньшей L, также без учета совокупности кластеров импульсов. Технический результат – возможность получения спектра энергий из отображения плотности амплитуд. 3 н. и 9 з.п. ф-лы, 13 ил.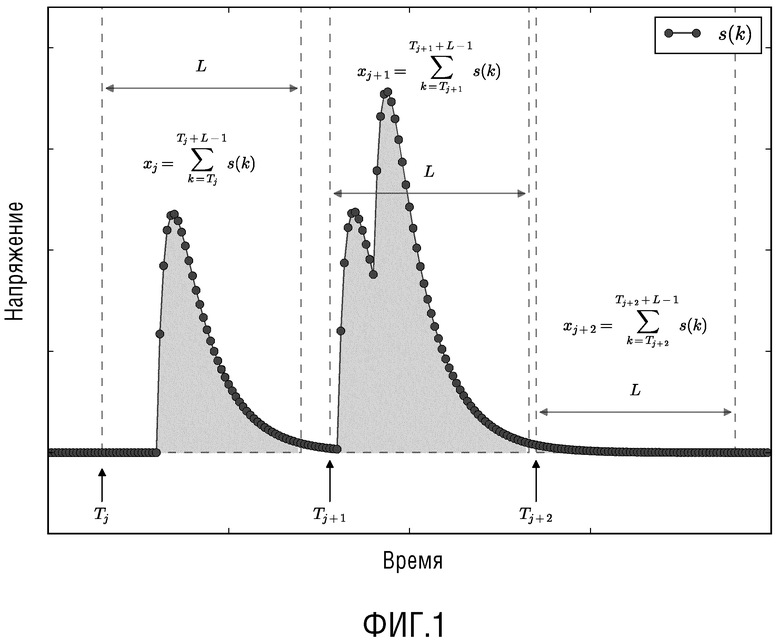
1. Способ определения спектра энергий отдельных квантов излучения, принимаемых детектором излучения, содержащий этапы:
(1) получение временного ряда цифровых наблюдений от детектора излучения, содержащего импульсы, соответствующие детектированию отдельных квантов;
(2) вычисление спектрально-зависимых статистических данных из сигнала детектора и задание отображения в виде карты из плотности амплитуд импульсов в спектрально-зависимые статистические данные с использованием аппроксимируемого составного пуассоновского процесса,
отличающийся
(3) основыванием спектрально-зависимых статистических данных на сумме цифровых наблюдений на множестве временных интервалов;
(4) выбором каждого из упомянутого множества временных интервалов, чтобы охватить ноль или более приближенно целые кластеры импульсов, и заданием упомянутого множества временных интервалов неперекрывающимися и имеющими постоянную длину L; и
(5) определением спектра путем оценки плотности амплитуд импульсов с применением инверсии отображения в виде карты к спектрально-зависимым статистическим данным.
2. Способ по п. 1, дополнительно содержащий требование максимального значения сигнала детектора в начале и в конце каждого временного интервала.
3. Способ по п. 1 или 2, дополнительно содержащий задание аппроксимируемого составного пуассоновского процесса как суммы амплитуд импульсов в каждом временном интервале.
4. Способ определения спектра энергий отдельных квантов излучения, принимаемых детектором излучения, содержащий этапы:
(1) получение временного ряда цифровых наблюдений от детектора излучения, содержащего импульсы, соответствующие детектированию отдельных квантов;
(2) вычисление спектрально-зависимых статистических данных из сигнала детектора и задание отображения в виде карты из плотности амплитуд импульсов в спектрально-зависимые статистические данные с использованием аппроксимируемого составного пуассоновского процесса,
отличающийся
(3) основыванием спектрально-зависимых статистических данных на сумме цифровых наблюдений на множестве временных интервалов;
(4) выбором упомянутого множества временных интервалов включающим: первый набор неперекрывающихся временных интервалов постоянной длины L без учета совокупности кластеров импульсов и второй набор неперекрывающихся временных интервалов постоянной длины L1 меньшей L, также без учета совокупности кластеров импульсов, причем L является по меньшей мере такой же, как длительность импульсов; и
(5) определением спектра путем оценки плотности амплитуд импульсов с применением инверсии отображения в виде карты к спектрально-зависимым статистическим данным.
5. Способ по п. 4, дополнительно содержащий выбор L1 меньшей длительности импульсов.
6. Способ по п. 4 или 5, дополнительно содержащий использование определяемой данными стратегии, выбранной так, чтобы приводить к почти оптимальному выбору параметра ядра, который минимизирует интегральную квадратичную ошибку оцененной функции плотности вероятности энергий отдельных квантов излучения.
7. Способ по любому из пп. 1-6, дополнительно содержащий дополнение аппроксимируемого составного пуассоновского процесса смоделированным шумом.
8. Способ по п. 7, дополнительно содержащий выражение отображения в виде карты как отношения между характеристическими функциями амплитуд, спектрально-зависимыми статистическими данными и смоделированным шумом.
9. Способ по п. 1, дополнительно содержащий вычисление характеристических функций спектрально-зависимых статистических данных путем применения обратного преобразования Фурье к гистограмме суммы цифровых наблюдений.
10. Способ по п. 8 или 9, дополнительно содержащий вычисление характеристических функций амплитуд с использованием фильтра нижних частот.
11. Способ оценки скорости счета отдельных квантов излучения, принимаемых детектором излучения, содержащий этапы:
(1) получение временного ряда цифровых наблюдений от детектора излучения, содержащего импульсы, соответствующие детектированию отдельных квантов;
(2) вычисление спектрально-зависимых статистических данных из сигнала детектора на основе суммы цифровых наблюдений на множестве временных интервалов, задание отображения в виде карты из плотности амплитуд импульсов в спектрально-зависимые статистические данные с использованием аппроксимируемого составного пуассоновского процесса,
отличающийся
(3) выбором упомянутого множества временных интервалов включающим: первый набор неперекрывающихся временных интервалов постоянной длины L, выбранных без учета совокупности кластеров импульсов, и второй набор неперекрывающихся временных интервалов постоянной длины L1 меньшей L, также выбранных без учета совокупности кластеров импульсов, причем L является по меньшей мере такой же, как длительность импульсов;
(4) определением оценки 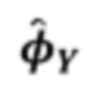 характеристической функции аппроксимируемого составного пуассоновского процесса с использованием
характеристической функции аппроксимируемого составного пуассоновского процесса с использованием
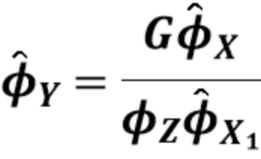
где 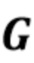 - оконная функция,
- оконная функция, 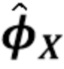 - оценка характеристической функции суммы цифровых наблюдений на каждом неперекрывающемся временном интервале в первом наборе,
- оценка характеристической функции суммы цифровых наблюдений на каждом неперекрывающемся временном интервале в первом наборе, 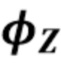 - характеристическая функция смоделированного шумового процесса, и
- характеристическая функция смоделированного шумового процесса, и 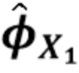 - оценка характеристической функции суммы цифровых наблюдений на каждом неперекрывающемся временном интервале во втором наборе;
- оценка характеристической функции суммы цифровых наблюдений на каждом неперекрывающемся временном интервале во втором наборе;
(5) оценкой скорости счета из оценки характеристической функции.
12. Способ по п. 11, дополнительно содержащий оценку скорости счета с использованием процедуры оптимизации или других средств для подгонки кривой, оценку смещения постоянного тока из логарифма оценки характеристической функции или подгонки кривой к логарифму оценки характеристической функции.
| US 2018204356 A1, 19.07.2018 | |||
| SHOTA GUGUSHVILI: "Decompounding under Gaussian noise" | |||
| MATHEMATICS, CORNELL UNIVERSITY LIBRARY, 201 OLIN LIBRARY CORNELL UNIVERSITY ITHACA, NY 14853, 5 November 2007 (2007-11-05), p | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| US 2012041700 A1, 16.02.2012 | |||
| СПОСОБ И УСТРОЙСТВО ДЛЯ ВЫДЕЛЕНИЯ СИГНАЛОВ В ДАННЫХ | 2014 |
|
RU2681377C1 |
Авторы
Даты
2023-08-30—Публикация
2020-03-23—Подача