Изобретение относится к способам прогнозирования вспышек на Солнце на основании исследований изменения энтропии измеряемых полей, которое возникает вследствие активизации процессов подготовки указанных вспышек на протяжении интервала времени порядка нескольких суток перед ними.
Из уровня техники известны способы прогнозирования вспышек, основанные на применение измерения излучения Солнца в радио-, ультрафиолетовом и рентгеновском диапазонах длин волн.
Например, из уровня техники известен способ определения координат всплесков радиоизлучения Солнца (см. SU 1053030, опубл. 07.11.1983) на радиотелескопах с шириной направленности больше диаметра Солнца, заключающийся в приеме сигналов на первой несущей частоте сигнала радиоизлучения Солнца при круговом сканировании диаграммы направленности вокруг Солнца, измерение амплитуд и двух составляющих первой гармоники частоты сканирования без всплеска и во время всплеска.
Данный способ имеет схожий характер с заявленным, однако имеет различное назначение и не прогнозирует вспышки на Солнце, а только определяет местоположение уже произошедшей вспышки.
Наиболее близким аналогам по техническому исполнению, но не по назначению, является способ регистрации вспышек на Солнце и комплекс для его реализации (см. RU 2715837 C1, опубл. 03.03.2020). Предложен способ регистрации сильных солнечных вспышек на основе комплекса, объединяющего сеть приемных устройств автоматического наблюдения за потоком радиоизлучения Солнца, и критериев интенсивности потока и энергии всплесков радиоизлучения Солнца на выбранных длинах волн с регулярной корректировкой по произошедшим событиям, использованием калибровок регистрируемых характеристик и валидации критериев сильных вспышек. В состав комплекса регистрации интенсивности и энергии всплесков радиоизлучения Солнца входит не менее одного комплекта антенных и радиоприемных устройств, скоммутированных с блоком анализа и калибровки регистрируемых сигналов на базе процессора с устройством отображения информации (ПЭВМ оператора), с пунктами регистрации радиоизлучения солнечных вспышек, Центром сбора и обработки информации, электронными архивами гелиогеофизических данных. Изобретение позволяет повысить надежность и оперативность регистрации сильных солнечных вспышек с помощью сравнительно дешевых наземных радиотехнических устройств.
Указанный способ также не предназначен для прогнозирования вспышек на Солнце.
Техническим результатом заявленного изобретения является устранение недостатков аналогов и создания достоверного и простого способа прогнозирования солнечных вспышек на основе выявления феноменов с высоким уровнем детерминированности.
Заявленный технический результат достигается посредством способа прогнозирования вспышек на Солнце на основе выявления феноменов с высоким уровнем детерминированности, характеризующегося тем, что он основан на анализе изменений статистики полей, измеряемых в период времени, который полагаем предшествующим вспышке, и обладающих свойством формирования линейных структур рассматриваемых статистических зависимостей, изменения полей регистрируют с помощью космических или наземных телескопов, проводящих измерения потока рентгеновского, радио, УФ-излучения, с максимально возможным временным разрешением, которое, желательно, должно быть не хуже чем 1 секунда, поскольку точность и устойчивость применяемой методики являются обратно пропорциональными указанному временному разрешению, на достаточно протяженном интервале времени перед моментом вспышки, который, в частности, может составлять величину от десяти до двадцати суток, в частности с помощью работающего на орбите космического телескопа Geostationary Operational Environmental Satellite (GOES), передающего рентгеновские данные в диапазонах 1-8 Å и 0,5-4 Å на приемо-передающее земное устройство, осуществляют их анализ при помощи компьютера с выявлением возникновения линейных структур, вдоль которых располагались несколько направляющих точек в виде граничных точек локальных трендов, то есть достаточно больших и прямолинейных сегментов изучаемой зависимости, которые начинаются и заканчиваются в точках экстремумов, существенно отстоящих по времени от моментов достижения равных значений указанной зависимости, данные линейные структуры представляют при помощи компьютера либо в форме каналов в виде пар прямых линий, соединяющих указанные точки, эти прямые почти параллельны: угол между их направлениями удовлетворяет соотношению ∆α≤1,5° при условии нормирования горизонтальной координаты на величину интервала времени от начала измерений до момента указанной вспышки, максимальной по энергии, а вертикальной координаты – на максимум значений применяемого статистического функционала в период времени от начала измерений до момента указанной вспышки, максимальной по энергии, либо в виде прямых, проведенных через две направляющие точки и проходящих мимо третьей такой точки при выраженном в процентах отношении δ≤1,2% минимального расстояния от данной точки к отвечающему ей значению рассматриваемого статистического функционала, определение высокой вероятности возникновения предстоящей в течение нескольких десятков часов вспышки высокой энергии по усилению концентрации моментов регистрации фактов возникновения линейных по времени границ для вариаций энтропии в системе и/или моментов регистрации фактов возникновения «односторонних» линейных по времени границ для уровня энтропии в системе, или моментов регистрации фактов выхода энтропии измеряемого процесса за пределы указанных границ.
В частном варианте выполнения способ обозначает завершение процесса подготовки вспышки после двукратного изменения свойств статистики потока измеряемого солнечного излучения, в ходе которого минимум два раза был отмечен факт критического состояния системы в виде осцилляции рассматриваемой статистической зависимости между квазипараллельными прямыми, формирующими границы канала.
В частном варианте выполнения способ также обозначает завершение процесса подготовки вспышки, в ходе которого отмечен факт критического состояния в форме произошедшего с высокой точностью трехкратного отражения рассматриваемой зависимости от прямой линии.
В частном варианте выполнения способа время «итогового рывка» к моменту достижения критического состояния составляет порядка 5–8 часов.
В результате проведенных вычислений удалось выявить феномен процессов с высокой степенью детерминированности, возникающих за короткий промежуток времени перед солнечным событием.
Способ проиллюстрирован следующими рисунками:
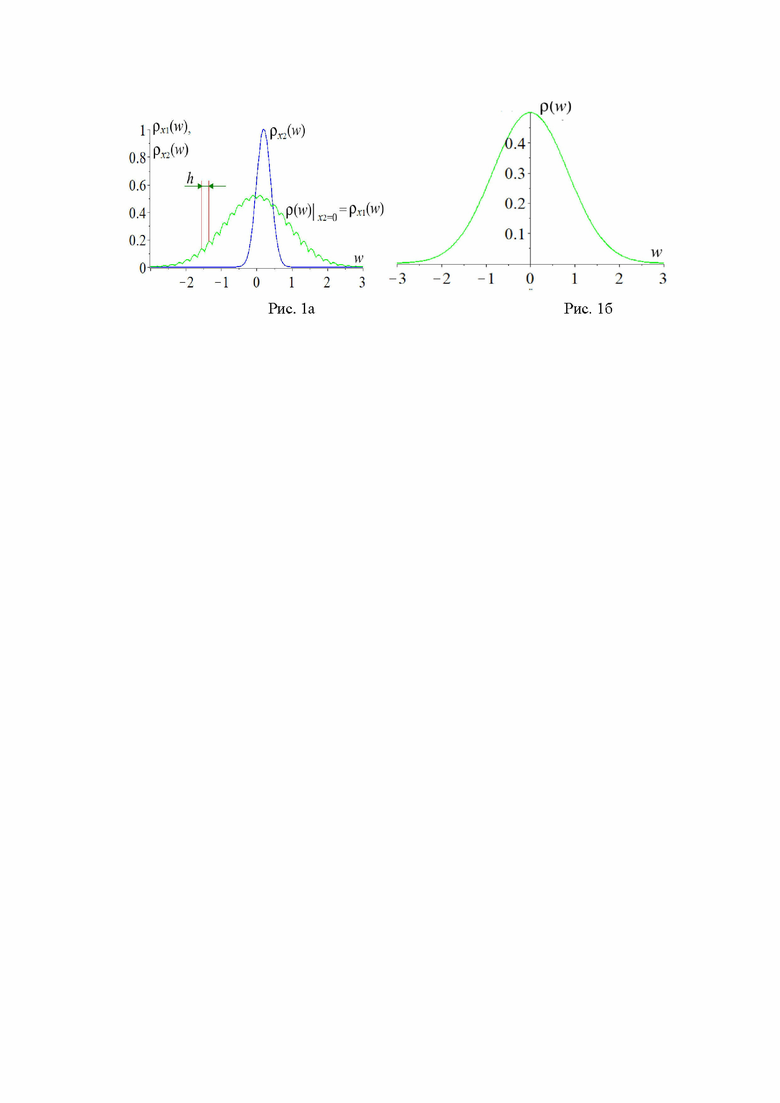
Рис.1 – Схематическое изображение эмпирической плотности вероятности измеренного случайного процесса 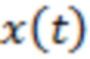 для одного сегмента реализации в отсутствие (широкая кривая на фиг. 1a) и при наличии (рис. 1б) в сумме (1) независимого случайного слагаемого
для одного сегмента реализации в отсутствие (широкая кривая на фиг. 1a) и при наличии (рис. 1б) в сумме (1) независимого случайного слагаемого 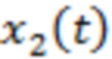 . На рис. 1а узкая синяя кривая соответствует схематической плотности вероятности значений процесса
. На рис. 1а узкая синяя кривая соответствует схематической плотности вероятности значений процесса 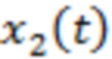 .
.
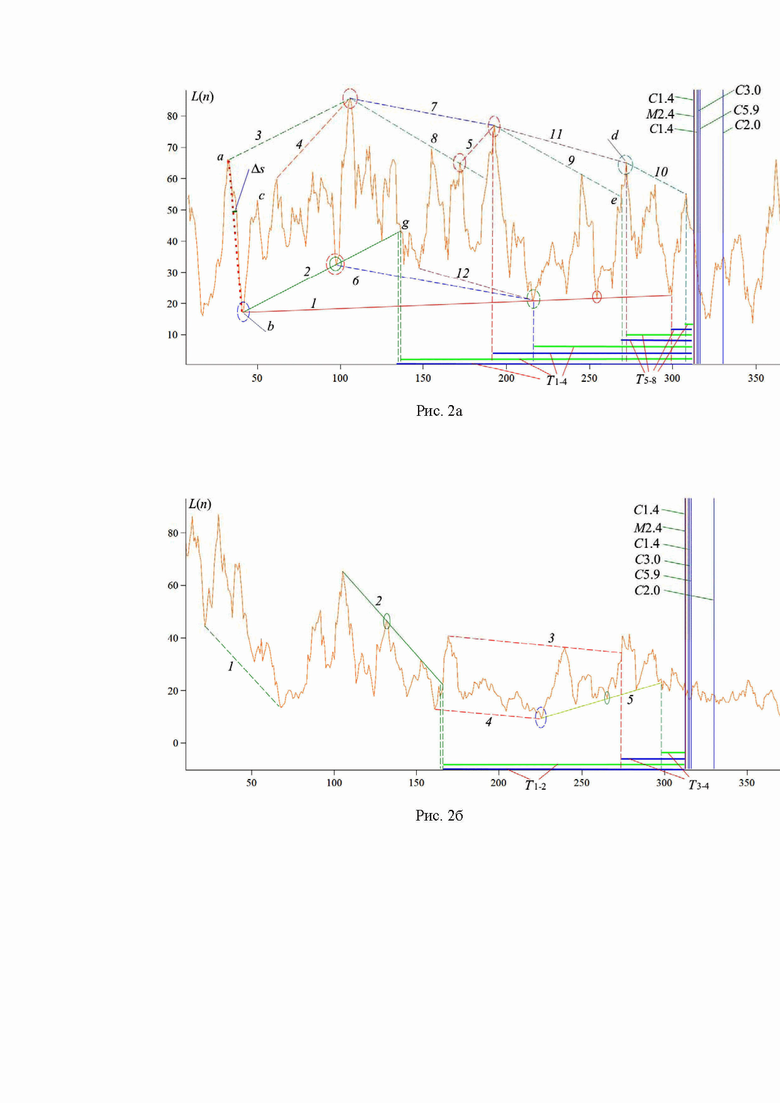
Рис. 2 – Зависимость L(n), построенная по измерениям потока рентгеновского излучения за период с 1 по 16 июля 2017 года в диапазоне длин волн 0.5-4 Å (рис. 2а) и 1-8 Å (рис. 2б).
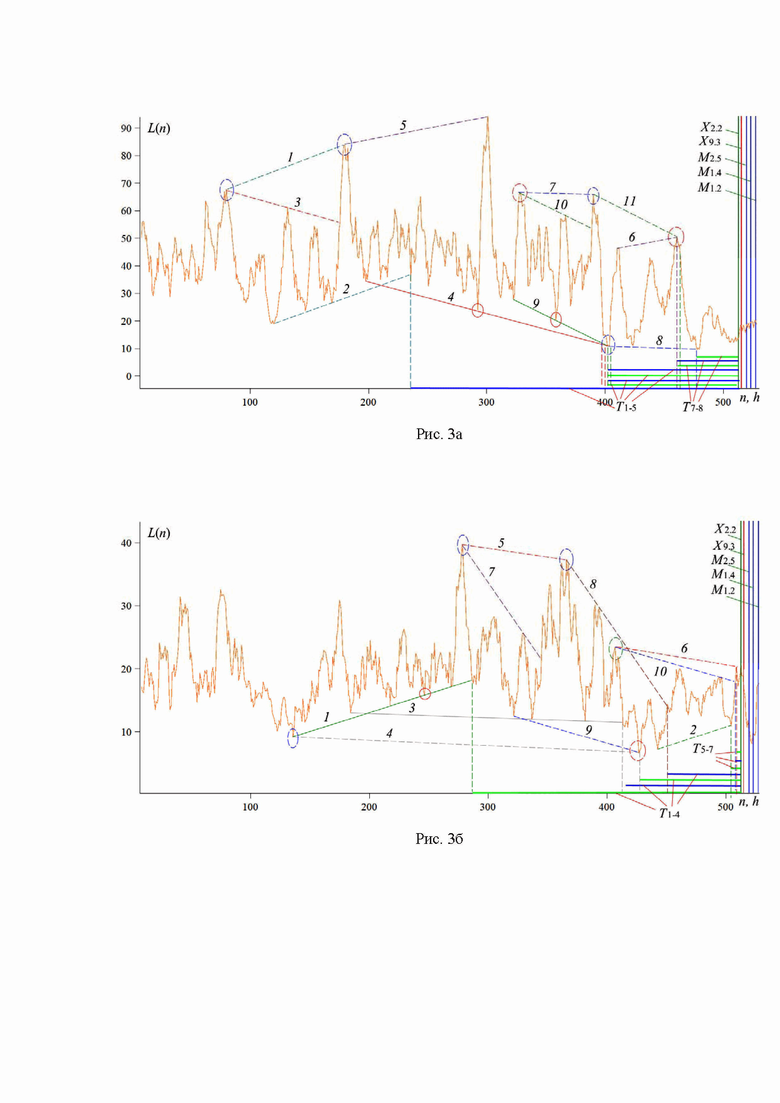
Рис. 3. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 15 августа по 6 сентября 2017 года в диапазоне длин волн 0.5-4 Å (рис. 3а) и 1-8 Å (рис. 3б).
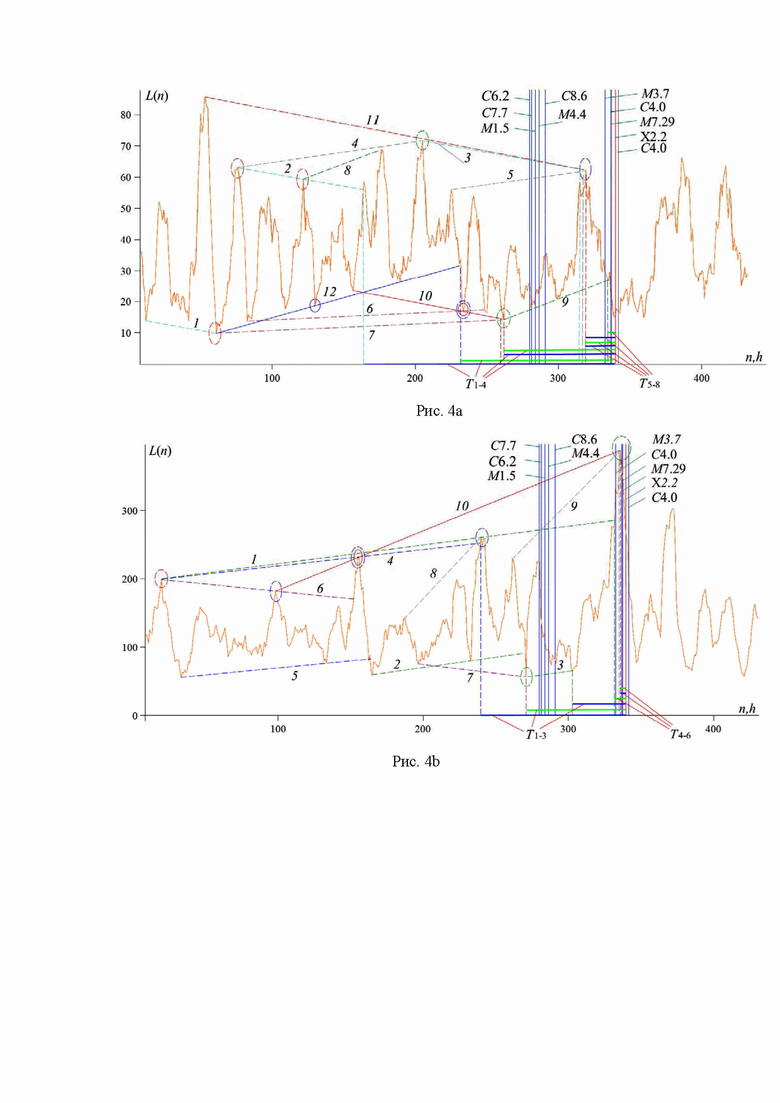
Рис. 4. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 6 по 23 апреля 2022 года в диапазоне длин волн 0.5-4 Å (рис. 4а) и 1-8 Å (рис. 4б).
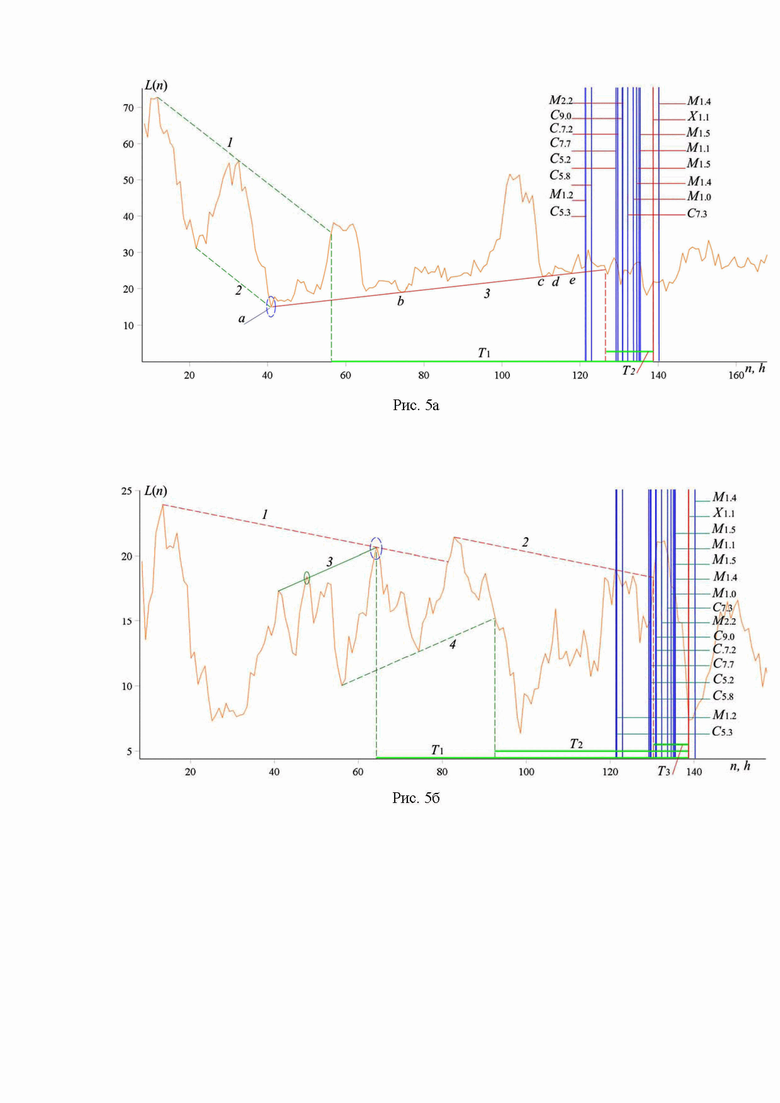
Рис. 5. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 6 по 12 февраля 2023 года в диапазоне длин волн 0.5-4 Å (рис. 5а) и 1-8 Å (рис. 5б).
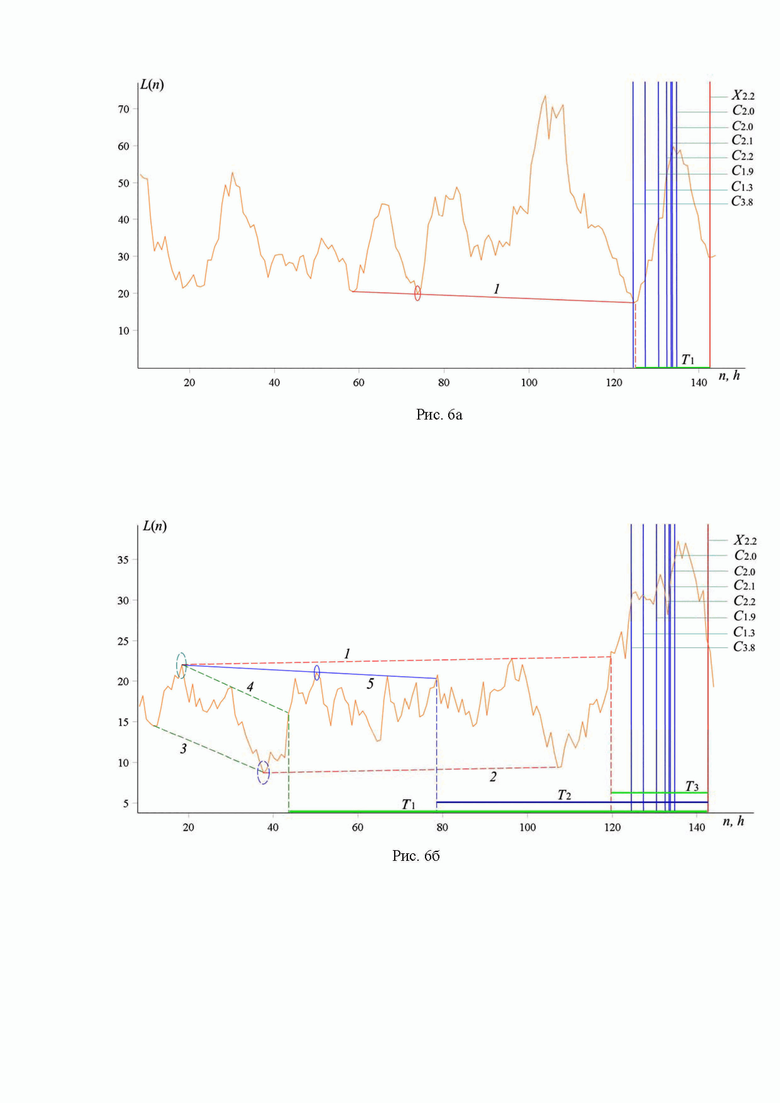
Рис. 6. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 13 по 18 февраля 2023 года в диапазоне длин волн 0.5-4 Å (рис. 6а) и 1-8 Å (рис. 6б).
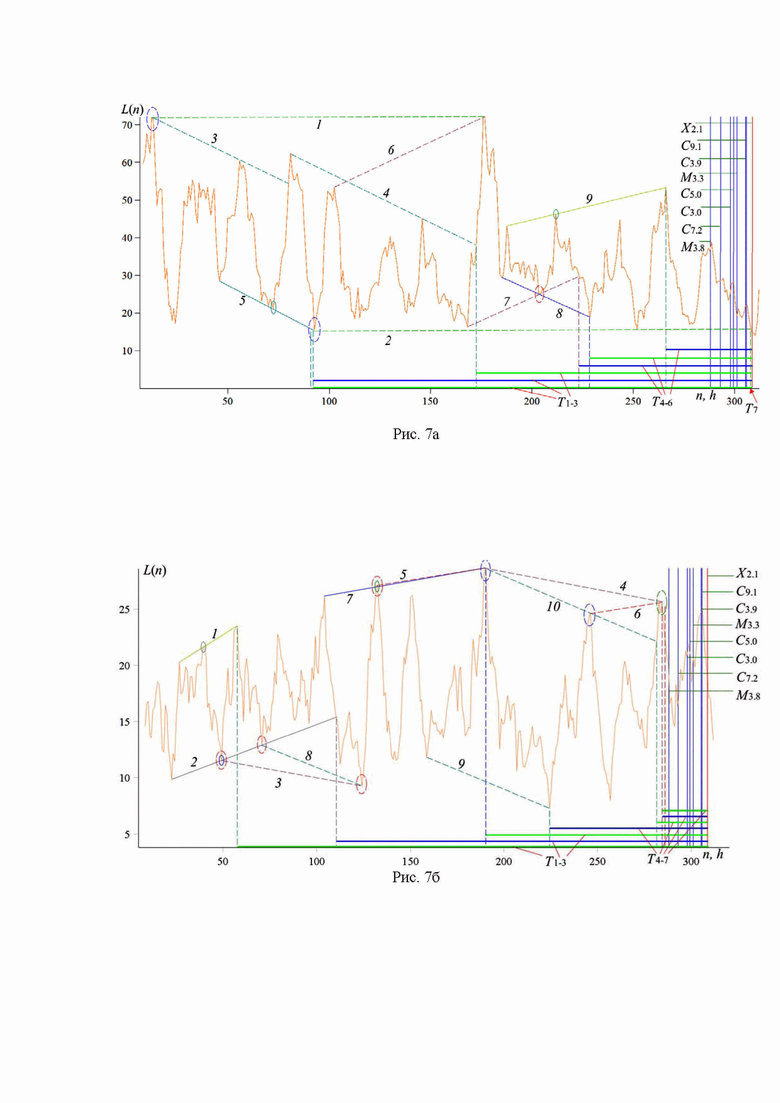
Рис. 7. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 19 февраля по 3 марта 2023 года в диапазоне длин волн 0.5-4 Å (рис. 7а) и 1-8 Å (рис. 7б).
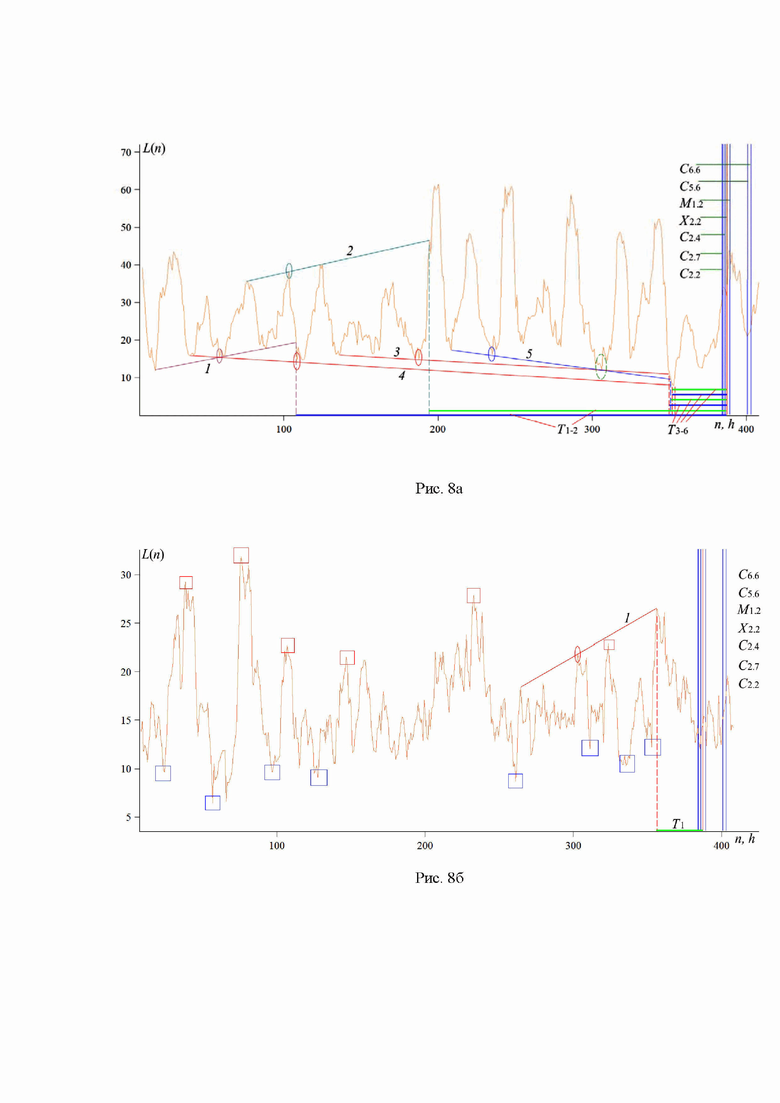
Рис. 8. Зависимость L(n), построенная по измерениям потока рентгеновского излучения магнитного поля за период с 14 по 30 марта 2023 года в диапазоне длин волн 0.5-4 Å (рис. 8а) и 1-8 Å (рис. 8б).
Далее раскрыт один из вариантов осуществления способа прогнозирования вспышек на Солнце на основе выявления феноменов с высоким уровнем детерминированности.
Предлагаемый способ основан на анализе изменений статистики полей, измеряемых в период времени, который полагаем предшествующим вспышке, и обладающих свойством формирования линейных структур, подобных рассматриваемым далее. Таким полем может являться регистрируемый с помощью космических и/или наземных телескопов непрерывный поток солнечного рентгеновского, радио, УФ-излучения с временным разрешением не хуже чем 1 секунда, измеряемый на интервале времени порядка восемнадцати суток перед моментом вспышки.
Техническими средствами, с помощью которых осуществляется метод может являться, работающий на орбите Солнечный рентгеновский датчик (Solar X-Ray Sensor) космического телескопа Geostationary Operational Environmental Satellite (GOES), передающий непрерывные данные рентгеновских наблюдений Солнца в стандартных спектральных диапазонах GOES 1-8 Å и 0,5-4 Å со спутника на станцию управления и сбора данных наземного сегмента, где полученные данные затем обрабатываются, хранятся и распространяются среди пользователей. А также компьютер, реализующий программу обработки данных.
Классификация солнечных вспышек основана на данных измерения потока мягкого рентгеновского излучения с помощью космического аппарата GOES в диапазонах 1-8 Å и 0.5-4 Å. Для анализа использовались данные солнечного рентгеновского излучения с космического аппарата GEOS. Во всех случаях при проведении статистического анализа с помощью методики рассматриваются данные измерений космического телескопа Geostationary Operational Environmental Satellite в рентгеновских диапазонах 0,5-4 Å, и 1,0-8.0 Å. Применяемая методика прогнозирования вспышек на Солнце связана со статистическим эффектом уменьшения амплитуды мелкомасштабных вариаций плотности вероятности любого случайного процесса при появлении в его составе даже небольшого дополнительного члена, который можно считать независимым или слабозависимым от фонового шума. Этот термин относится к совокупности обычно наблюдаемых процессов (включая, в частности, шум измерительного оборудования). Мы считаем, что такие явления не связаны или слабо связаны с возмущениями, которые соответствуют процессам подготовки взрывов, которые в дальнейшем происходят в солнечной фотосфере. Стоит отметить важное условие использования метода – наличие рядов данных с временным разрешением 1 секунда. Такие данные GOES стали возможны с февраля 2017 года.
Во временном ряду данных рентгеновского излучения GOES имеются длительные интервалы медленного изменения между дискретными вспышками. Это убедительно свидетельствует о существовании двух различных источников коронального энерговыделения: вспышечного и стационарного (Hudson, 2011). В настоящее время стандартной моделью развития вспышек и корональных выбросов массы (КВМ) является модель «CSHKP» (Svestka & Cliver, 1992), сущность которой состоит в крупномасштабном токовом слое, в котором магнитное пересоединение приводит в движение потоки, высвобождающие энергию.
Далее во всех случаях при проведении статистического анализа использовались данные измерений спутника GOES, которые обеспечивают потоки солнечного рентгеновского излучения для диапазонов длин волн от 0.5 до 4 Å (см. рис. 2а-8а) и от 1 до 8 Å (см. рис. 2б-8б). На всех рисунках первая точка кривой  соответствует моменту времени
соответствует моменту времени 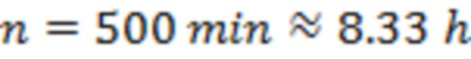 с учетом усреднения по первым
с учетом усреднения по первым 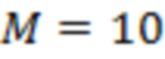 отрезкам реализации (все такие отрезки имеют продолжительность 3000 секунд, каждая из которых соответствует одному измерению), см. (7).
отрезкам реализации (все такие отрезки имеют продолжительность 3000 секунд, каждая из которых соответствует одному измерению), см. (7).
Более подробно излагая предлагаемый подход, будем считать, что любое физическое поле 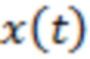 , связанное с излучением Солнца, может быть представлено в виде следующей суммы:
, связанное с излучением Солнца, может быть представлено в виде следующей суммы:

В (1) случайная величина (СВ) 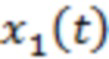 – фоновый шум, то есть совокупность обычно наблюдаемых случайных процессов, включая сюда шум самой измерительной аппаратуры. Тогда как случайный процесс
– фоновый шум, то есть совокупность обычно наблюдаемых случайных процессов, включая сюда шум самой измерительной аппаратуры. Тогда как случайный процесс 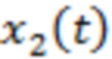 полагаем вызванным интенсивными явлениями, происходящими во время «итоговой подготовки» приближающейся вспышки. По аналогии с работами, относящимися к поиску предвестников землетрясений (Volvach et al., 2022a, b, c, d; Volvach et al., 2023a ,b; Kogan et al.,2021; Kogan, 2015), в роли основной гипотезы в этой статье принимается предположение о статистической независимости (или слабой зависимости) двух этих случайных слагаемых.
полагаем вызванным интенсивными явлениями, происходящими во время «итоговой подготовки» приближающейся вспышки. По аналогии с работами, относящимися к поиску предвестников землетрясений (Volvach et al., 2022a, b, c, d; Volvach et al., 2023a ,b; Kogan et al.,2021; Kogan, 2015), в роли основной гипотезы в этой статье принимается предположение о статистической независимости (или слабой зависимости) двух этих случайных слагаемых.
С целью получения статистики значений СВ 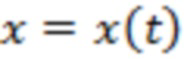 разделим весь интервал времени измерений случайного процесса
разделим весь интервал времени измерений случайного процесса 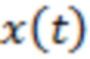 на отдельные отрезки реализации c одинаковой продолжительностью. На рис. 1а схематически изображена экспериментальная плотность вероятности
на отдельные отрезки реализации c одинаковой продолжительностью. На рис. 1а схематически изображена экспериментальная плотность вероятности 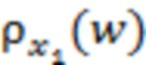 для значений случайного процесса
для значений случайного процесса 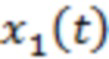 на заданном отрезке реализации (кривая 1), которая совпадала бы с плотностью вероятности
на заданном отрезке реализации (кривая 1), которая совпадала бы с плотностью вероятности 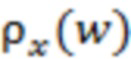 при тожественном отсутствии на этом отрезке слагаемого
при тожественном отсутствии на этом отрезке слагаемого 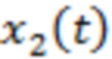 . Здесь же также схематически приведена экспериментальная плотность вероятности
. Здесь же также схематически приведена экспериментальная плотность вероятности 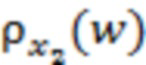 (кривая 2) для этого же отрезка реализации, которая отвечала бы значениям процесса
(кривая 2) для этого же отрезка реализации, которая отвечала бы значениям процесса 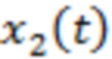 , если бы их можно было каким-то образом измерить. (На рисунке 1а и на приведенном далее рис. 1б для повышения наглядности рассматривается случай непрерывных распределений случайных слагаемых в равенстве (1), хотя при проведении измерений обычно имеют место их дискретные варианты; кроме того, с той же целью на этих схематических рисунках допускается приближенное выполнение условия нормировки). На рис. 1а обе рассматриваемые кривые являются «шероховатыми», то есть содержащими большое число мелкомасштабных малых флуктуаций. Это свойство является следствием присутствия в эмпирических распределениях
, если бы их можно было каким-то образом измерить. (На рисунке 1а и на приведенном далее рис. 1б для повышения наглядности рассматривается случай непрерывных распределений случайных слагаемых в равенстве (1), хотя при проведении измерений обычно имеют место их дискретные варианты; кроме того, с той же целью на этих схематических рисунках допускается приближенное выполнение условия нормировки). На рис. 1а обе рассматриваемые кривые являются «шероховатыми», то есть содержащими большое число мелкомасштабных малых флуктуаций. Это свойство является следствием присутствия в эмпирических распределениях 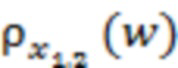 случайной составляющей, связанной с ограниченным числом отсчетов.
случайной составляющей, связанной с ограниченным числом отсчетов.
Плотность вероятности 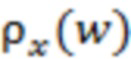 для суммы (1) двух независимых случайных величин может быть записана в форме свертки вида:
для суммы (1) двух независимых случайных величин может быть записана в форме свертки вида:

Из анализа интеграла (2) следует, что если ширина распределения 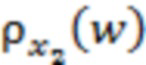 хотя бы в несколько раз превосходит период указанных мелкомасштабных флуктуаций зависимости
хотя бы в несколько раз превосходит период указанных мелкомасштабных флуктуаций зависимости 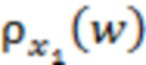 , то, как несложно понять, в результате выполнения свертки (2) произойдет усреднение этих мелкомасштабных возмущений, следствием чего станет уменьшение их амплитуды, понимаемой как величина эффективного отклонения от нулевого уровня соответствующих флуктуаций. На рис. 1б приведено схематическое изображение зависимости
, то, как несложно понять, в результате выполнения свертки (2) произойдет усреднение этих мелкомасштабных возмущений, следствием чего станет уменьшение их амплитуды, понимаемой как величина эффективного отклонения от нулевого уровня соответствующих флуктуаций. На рис. 1б приведено схематическое изображение зависимости 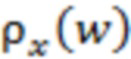 , отвечающей таким условиям. Принципиально важным является вывод, что подобное изменение амплитуды малых флуктуаций при появлении в системе «дополнительного» независимого случайного слагаемого вполне может быть зафиксировано, в частности, с помощью математических методов наподобие преобразования Фурье.
, отвечающей таким условиям. Принципиально важным является вывод, что подобное изменение амплитуды малых флуктуаций при появлении в системе «дополнительного» независимого случайного слагаемого вполне может быть зафиксировано, в частности, с помощью математических методов наподобие преобразования Фурье.
С целью более подробного обоснования указанного свойства, состоящего в высокой вероятности значительного уменьшения эффективной амплитуды рассматриваемых мелкомасштабных вариаций экспериментальной плотности вероятности (применительно к ее дискретной форме) при существовании в (1) независимого случайного процесса 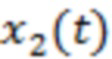 , для каждого отрезка реализации разобьем область значений измеряемой случайной величины
, для каждого отрезка реализации разобьем область значений измеряемой случайной величины 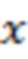 на
на 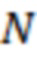 интервалов равной ширины
интервалов равной ширины 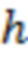 :
:
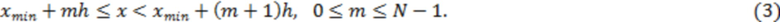
В (3) слагаемое 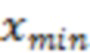 равно минимуму
равно минимуму 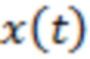 на соответствующем отрезке реализации, а целочисленный множитель
на соответствующем отрезке реализации, а целочисленный множитель 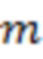 является номером ячейки разбиения области значений случайной величины
является номером ячейки разбиения области значений случайной величины 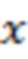 , принадлежащим интервалу
, принадлежащим интервалу 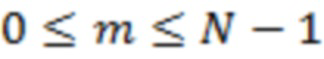 .
.
Тогда дискретные плотности вероятности 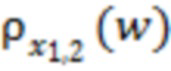 могут быть записаны в виде
могут быть записаны в виде
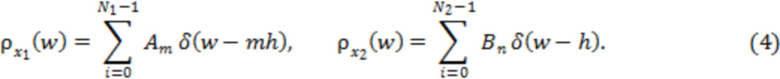
Здесь 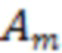 и
и  – вероятности попадания в ячейку (3) номер
– вероятности попадания в ячейку (3) номер  для значений случайных величин
для значений случайных величин 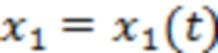 и соответственно
и соответственно 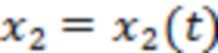 , если бы их можно было бы измерить по отдельности, а
, если бы их можно было бы измерить по отдельности, а 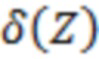 – дельта-функция Дирака. Пусть
– дельта-функция Дирака. Пусть 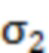 – дисперсия значений случайной величины
– дисперсия значений случайной величины 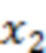 для заданного отрезка реализации. Тогда общее число
для заданного отрезка реализации. Тогда общее число 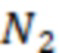 слагаемых во второй сумме в (4) будет определяться с учетом условия, что ширина
слагаемых во второй сумме в (4) будет определяться с учетом условия, что ширина 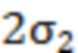 распределения
распределения 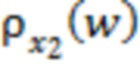 удовлетворяет соотношению
удовлетворяет соотношению

Для процесса 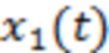 общее число
общее число 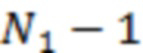 существенных ячеек в (4) считаем лишь немногим меньшим, чем
существенных ячеек в (4) считаем лишь немногим меньшим, чем 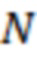 в (3), тогда как для
в (3), тогда как для 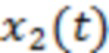 аналогичную величину
аналогичную величину 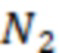 полагаем меньшей, чем
полагаем меньшей, чем 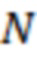 , как минимум в несколько раз. При этом выполняется соотношение
, как минимум в несколько раз. При этом выполняется соотношение 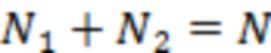 .
.
Сопоставляя (2) и (4), получаем:
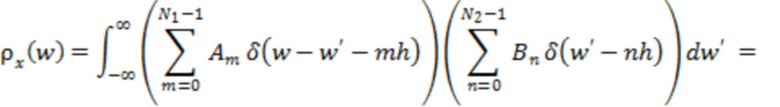
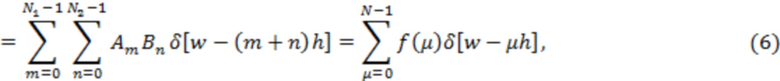
где 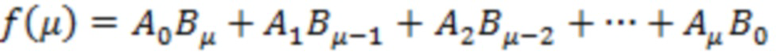 . Для суммы
. Для суммы 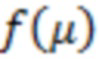 коэффициенты
коэффициенты 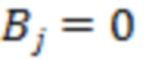 при
при 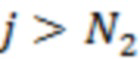 . Нетрудно понять, что значения
. Нетрудно понять, что значения 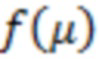 равны вероятности попадания измеренных значений случайного процесса
равны вероятности попадания измеренных значений случайного процесса 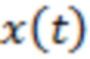 в ячейку вида (3) с номером
в ячейку вида (3) с номером 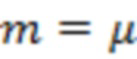 .
.
Пусть для случайного процесса 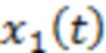 известны два соседних интервала области значений вида (3) с номерами
известны два соседних интервала области значений вида (3) с номерами 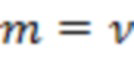 и
и 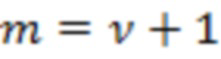 , для которых разность
, для которых разность 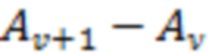 является максимальной по модулю применительно к рассматриваемому отрезку реализации. Запишем аналогичную разность
является максимальной по модулю применительно к рассматриваемому отрезку реализации. Запишем аналогичную разность 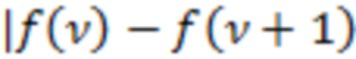 | для этих же двух же интервалов в (3) при условии существования в (1) на этом же отрезке реализации независимого случайного процесса
| для этих же двух же интервалов в (3) при условии существования в (1) на этом же отрезке реализации независимого случайного процесса 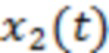 :
:
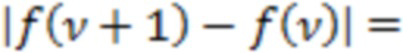
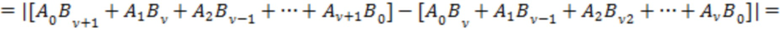
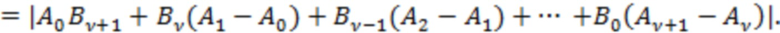
В данном случае в последнем равенстве первое слагаемое 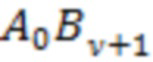 под знаком модуля является пропорциональным вероятности попадания значений фонового шума
под знаком модуля является пропорциональным вероятности попадания значений фонового шума 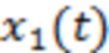 в первую ячейку распределения (3). Распределение значений фонового шума, описываемое слагаемыми
в первую ячейку распределения (3). Распределение значений фонового шума, описываемое слагаемыми 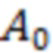 ,
, 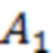 …
… 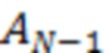 , является гауссовой плотностью вероятности. При
, является гауссовой плотностью вероятности. При 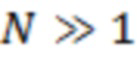 значение
значение 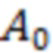 отвечает редко встречающимся значениям, расположенным в области самого начала «хвоста» данного распределения. Поэтому данным слагаемым будем пренебрегать, и в результате получаем:
отвечает редко встречающимся значениям, расположенным в области самого начала «хвоста» данного распределения. Поэтому данным слагаемым будем пренебрегать, и в результате получаем:
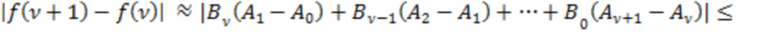
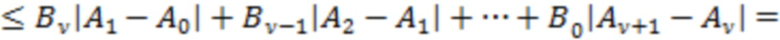
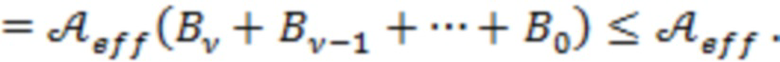
Здесь 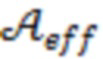 – эффективное значение для совокупности множителей
– эффективное значение для совокупности множителей 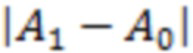 ,
, 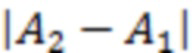 , …
, …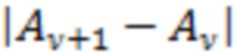 , отвечающее формулировке теоремы о среднем для дискретных сумм. Кроме того, в (6) учтено, что сумма вероятностей
, отвечающее формулировке теоремы о среднем для дискретных сумм. Кроме того, в (6) учтено, что сумма вероятностей 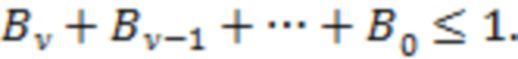
Легко показать, что значение 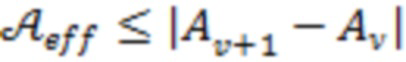 , причем знак равенства здесь возможен либо при условии
, причем знак равенства здесь возможен либо при условии 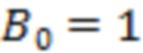 и
и 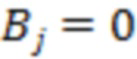 ,
, 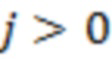 (вероятность его выполнения мала с учетом (5)), либо в крайне маловероятном случае
(вероятность его выполнения мала с учетом (5)), либо в крайне маловероятном случае 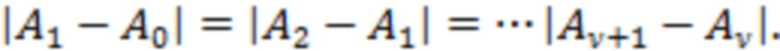
Укажем также, что в (6) в общем случае также с высокой вероятностью для большинства отрезков реализации переход от оценки модуля суммы вида 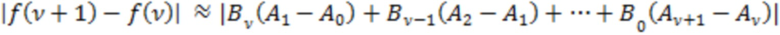 к рассмотрению суммы абсолютных величин
к рассмотрению суммы абсолютных величин 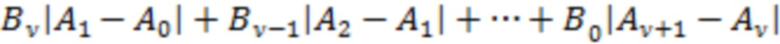 означает резкое ужесточение условий проведения расчетов. Поскольку совпадение знаков всех разностей вида
означает резкое ужесточение условий проведения расчетов. Поскольку совпадение знаков всех разностей вида 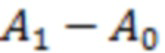 ,
, 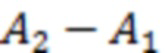 , …
, … 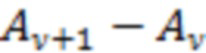 , при котором два рассматриваемых выше выражения тоже будут совпадать друг с другом, для абсолютного большинства отрезков реализации также относится к редко происходящим событиям.
, при котором два рассматриваемых выше выражения тоже будут совпадать друг с другом, для абсолютного большинства отрезков реализации также относится к редко происходящим событиям.
Таким образом, в результате проведенных расчетов приходим к выводу, что при появлении в (1) случайного слагаемого 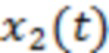 , которое удовлетворяет (5) и является независимым или слабо зависимым от фонового шума
, которое удовлетворяет (5) и является независимым или слабо зависимым от фонового шума 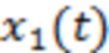 , с высокой вероятностью будет иметь место уменьшение амплитуды мелкомасштабных вариаций измеряемого случайного поля
, с высокой вероятностью будет иметь место уменьшение амплитуды мелкомасштабных вариаций измеряемого случайного поля 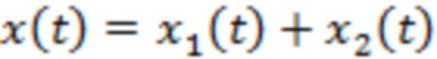 . Поскольку эта амплитуда для процесса
. Поскольку эта амплитуда для процесса 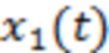 характеризуется модулями разностей вида
характеризуется модулями разностей вида 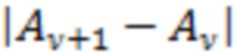 , тогда как в случае «суммарного» процесса
, тогда как в случае «суммарного» процесса 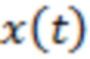 подобная величина определяется меньшими значениями вида
подобная величина определяется меньшими значениями вида 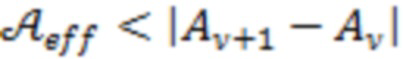 . Проводимые далее численные расчеты основаны на рассматриваемых вероятностных эффектах. При этом степень отличия свойств статистики измеряемых потоков рентгеновского излучения Солнца в обычном состоянии и в периоды, предшествующие сильным вспышкам, оказывается достаточной для определения предвестников с помощью методики, использующей изложенные выше теоретические результаты.
. Проводимые далее численные расчеты основаны на рассматриваемых вероятностных эффектах. При этом степень отличия свойств статистики измеряемых потоков рентгеновского излучения Солнца в обычном состоянии и в периоды, предшествующие сильным вспышкам, оказывается достаточной для определения предвестников с помощью методики, использующей изложенные выше теоретические результаты.
Далее с целью дополнительного усиления обсуждаемого статистического феномена вместо непосредственно измеряемого поля 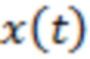 перейдем к рассмотрению зависимости
перейдем к рассмотрению зависимости 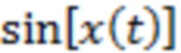 , обладающей интегрируемыми особенностями плотности вероятности
, обладающей интегрируемыми особенностями плотности вероятности 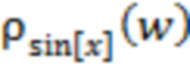 вида
вида 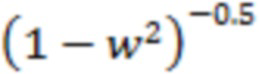 при
при 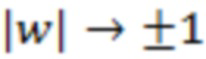 . Из проведенных вычислений следует, что их влияние приведет к усилению различия (вблизи точек указанных особенностей) величины эффективной амплитуды рассматриваемых мелкомасштабных флуктуаций для тех отрезков реализации, для которых существует независимое слагаемое
. Из проведенных вычислений следует, что их влияние приведет к усилению различия (вблизи точек указанных особенностей) величины эффективной амплитуды рассматриваемых мелкомасштабных флуктуаций для тех отрезков реализации, для которых существует независимое слагаемое 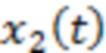 , по сравнению с отрезками, для которых оно тождественно отсутствует. Например, при условии
, по сравнению с отрезками, для которых оно тождественно отсутствует. Например, при условии 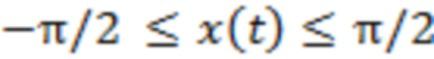 получаем
получаем 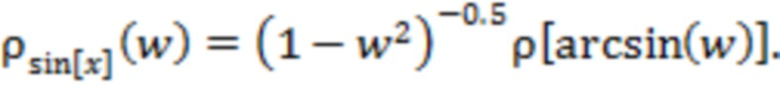 Поскольку случайные флуктуации, присущие зависимости
Поскольку случайные флуктуации, присущие зависимости 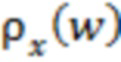 и связанные с ограниченным числом отсчетов, будут иметь место и для
и связанные с ограниченным числом отсчетов, будут иметь место и для 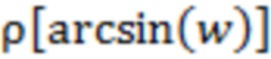 , то рассматриваемое отличие величины мелкомасштабных возмущений для указанных двух типов отрезков реализации с высокой вероятностью будет иметь место.
, то рассматриваемое отличие величины мелкомасштабных возмущений для указанных двух типов отрезков реализации с высокой вероятностью будет иметь место.
В результате мы приходим к выводу, что появление в (1) слагаемого 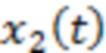 , связанного с подготовкой предстоящей вспышки, при выполнении (5) со статистически значимой вероятностью способно привести к существенному изменению величины и в целом свойств функционала вида
, связанного с подготовкой предстоящей вспышки, при выполнении (5) со статистически значимой вероятностью способно привести к существенному изменению величины и в целом свойств функционала вида
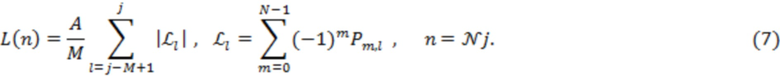
В (7) 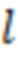 – номер отрезка реализации, множитель
– номер отрезка реализации, множитель 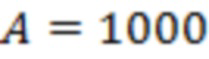 введен с целью перехода к удобной для анализа области значений данного функционала,
введен с целью перехода к удобной для анализа области значений данного функционала, 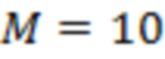 – ширина интервала усреднения по последовательным отрезкам реализации, индекс
– ширина интервала усреднения по последовательным отрезкам реализации, индекс 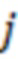 отвечает моменту времени завершения отрезка реализации с этим номером, продолжительность любого такого отрезка составляет
отвечает моменту времени завершения отрезка реализации с этим номером, продолжительность любого такого отрезка составляет 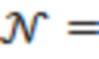 3000 секунд, каждой из которых сопоставляется одно измерение. При этом коэффициенты
3000 секунд, каждой из которых сопоставляется одно измерение. При этом коэффициенты 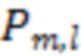 есть вероятности попадания значений СВ
есть вероятности попадания значений СВ 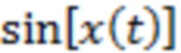 в ячейку номер
в ячейку номер 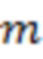 статистики вида
статистики вида
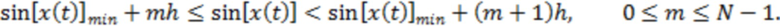 (8)
(8)
В (8) множитель 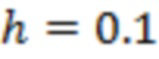 есть ширина интервала дискретизации, определяющая их общее число
есть ширина интервала дискретизации, определяющая их общее число 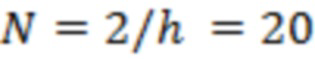 (заметим, что для всех отрезков реализации можем считать
(заметим, что для всех отрезков реализации можем считать 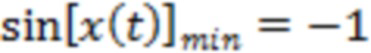 ). Проведенные в данной статье вычисления могут рассматриваться как проверка эффективности использования функционала
). Проведенные в данной статье вычисления могут рассматриваться как проверка эффективности использования функционала  в роли индикатора приближения моментов времени начала солнечных событий.
в роли индикатора приближения моментов времени начала солнечных событий.
Отметим, что аргумент  зависимости
зависимости  в (7) отвечает дискретным значениям времени. Тем не менее с учетом большого, порядка нескольких сотен, точек, через которые проходят кривые
в (7) отвечает дискретным значениям времени. Тем не менее с учетом большого, порядка нескольких сотен, точек, через которые проходят кривые  на рис. 1–7, оказывается возможным с высокой точностью оценивать время пересечения этой кривой с рассматриваемыми далее линейными объектами.
на рис. 1–7, оказывается возможным с высокой точностью оценивать время пересечения этой кривой с рассматриваемыми далее линейными объектами.
Как несложно понять, возрастание и, наоборот, убывание амплитуды независимого случайного процесса 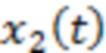 с высокой вероятностью приводит к уменьшению и, соответственно, к увеличению значений
с высокой вероятностью приводит к уменьшению и, соответственно, к увеличению значений  . Это означает, в частности, что точки тех экстремумов данного функционала, которые определяют начало и завершение наиболее существенных периодов подготовки приближающейся вспышки, соответствуют моментам времени критических состояний системы. В рамках проведенных в статье вычислений указанные периоды отвечают локальным трендам кривых
. Это означает, в частности, что точки тех экстремумов данного функционала, которые определяют начало и завершение наиболее существенных периодов подготовки приближающейся вспышки, соответствуют моментам времени критических состояний системы. В рамках проведенных в статье вычислений указанные периоды отвечают локальным трендам кривых  . При этом введенные в рассмотрение каналы и скользящие границы, как видно из приложенных рисунков и отвечающих им расчетов, «опираются» на граничные точки соответствующих локальных трендов. Как следует из приведенных рисунков, моменты возникновения, или, наоборот, прерывания указанных геометрических объектов на декартовой плоскости
. При этом введенные в рассмотрение каналы и скользящие границы, как видно из приложенных рисунков и отвечающих им расчетов, «опираются» на граничные точки соответствующих локальных трендов. Как следует из приведенных рисунков, моменты возникновения, или, наоборот, прерывания указанных геометрических объектов на декартовой плоскости 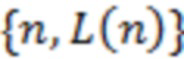 с высокой вероятностью «притягиваются» к времени начала соответствующих вспышек.
с высокой вероятностью «притягиваются» к времени начала соответствующих вспышек.
С учетом проведенных расчетов укажем также, что рассматриваемый эффект уменьшения мелкомасштабных флуктуаций эмпирической плотности вероятности (см. рис. 1а, б) означает приближение к некоторому (неизвестному в общем случае) «идеальному» распределению, которое вообще лишено случайных отклонений. Такого рода плотность вероятности должна была бы отвечать неограниченно большому числу отсчетов, которое могло бы быть получено только за бесконечно большое время измерений. Важно отметить, что применение функционала  к такому «идеальному» распределению, лишенному случайных флуктуаций, приведет к значениям, близким к нулю. Например, если в (7) коэффициенты
к такому «идеальному» распределению, лишенному случайных флуктуаций, приведет к значениям, близким к нулю. Например, если в (7) коэффициенты 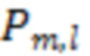 соответствуют «строго регулярному» распределению Гаусса, то при
соответствуют «строго регулярному» распределению Гаусса, то при 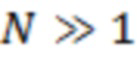 (см. (3), (7) и (8)) значения функционала
(см. (3), (7) и (8)) значения функционала  будут экспоненциально малы. В результате получаем, что величина зависимости
будут экспоненциально малы. В результате получаем, что величина зависимости  определяется размахом указанных случайных флуктуаций эмпирической плотности вероятности. Следовательно, поскольку их эффективная амплитуда уменьшается при появлении независимого случайного члена в составе измеряемого поля, связанного с влиянием процесса подготовки предстоящей вспышки, применяемый функционал оказывается чувствительным к процессам, происходящим в период времени до наступления рассматриваемых солнечных событий. Доказательством правильности разработанной логики являются как общие результаты данной статьи, так и, в частности, появление глобального минимума зависимости
определяется размахом указанных случайных флуктуаций эмпирической плотности вероятности. Следовательно, поскольку их эффективная амплитуда уменьшается при появлении независимого случайного члена в составе измеряемого поля, связанного с влиянием процесса подготовки предстоящей вспышки, применяемый функционал оказывается чувствительным к процессам, происходящим в период времени до наступления рассматриваемых солнечных событий. Доказательством правильности разработанной логики являются как общие результаты данной статьи, так и, в частности, появление глобального минимума зависимости  практически на всех рисунках от нескольких часов до двух-трех суток до основной рассматриваемой вспышки.
практически на всех рисунках от нескольких часов до двух-трех суток до основной рассматриваемой вспышки.
Пользуясь «энтропийным» языком, следует также отметить, что рассматриваемый ниже фоновый поток рентгеновского излучения можно отнести к равновесным или квазиравновесным процессам. В то время как явления, связанные с «окончательной подготовкой» солнечной вспышки, очевидно, являются неравновесными процессами. Поэтому их влияние в общем случае должно приводить к увеличению уровня энтропии, что, как показано выше, вызывает уменьшение значений  . При этом в качестве случайной составляющей, независимой или слабо зависящей от фонового шума, рассматривается излучение тех активных областей, в которых происходит «окончательная подготовка» предстоящей вспышки.
. При этом в качестве случайной составляющей, независимой или слабо зависящей от фонового шума, рассматривается излучение тех активных областей, в которых происходит «окончательная подготовка» предстоящей вспышки.
В итоге подчеркнем, что с математической точки зрения принцип действия предлагаемой методики состоит в оценке степени равномерности вероятностного распределения на малых интервалах области значений измеряемого сигнала. Это означает, что статистический функционал  характеризует уровень хаоса и, следовательно, величину энтропии для измеряемого физического поля.
характеризует уровень хаоса и, следовательно, величину энтропии для измеряемого физического поля.
В данном случае в роли случайного процесса 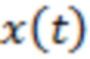 рассматривается совокупность измерений интенсивности излучения Солнца для двух рассматриваемых ниже энергетических диапазонов.
рассматривается совокупность измерений интенсивности излучения Солнца для двух рассматриваемых ниже энергетических диапазонов.
Введем несколько определений. Локальными трендами (ЛТ) будем именовать участки кривой  , для которых выполняются указанные далее условия. (Примером локального тренда, в частности, является участок
, для которых выполняются указанные далее условия. (Примером локального тренда, в частности, является участок 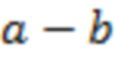 кривой
кривой  на рис. 2).
на рис. 2).
(а) Точки начала и завершения ЛТ (назовем их направляющими точками) отвечают экстремумам зависимости  .
.
(б) Выполняется соотношение

где 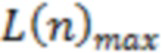 и
и 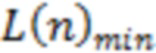 – максимум и минимум зависимости
– максимум и минимум зависимости  в указанных точках границ ЛТ (например, точки
в указанных точках границ ЛТ (например, точки 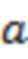 и
и 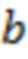 на рис. 2), а
на рис. 2), а 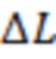 , по аналогии с (Volvach et al., 2022a, b, c, d) – аналогичная разность максимума и минимума (точки
, по аналогии с (Volvach et al., 2022a, b, c, d) – аналогичная разность максимума и минимума (точки 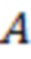 и соответственно
и соответственно 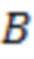 на рис. 2) значений функционала
на рис. 2) значений функционала  на интервале от начала отсчета и до момента начала вспышки (в данном случае значение
на интервале от начала отсчета и до момента начала вспышки (в данном случае значение 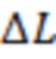 оказывается тем же самым в пределах всей рассматриваемой на соответствующем рисунке области определения аргумента
оказывается тем же самым в пределах всей рассматриваемой на соответствующем рисунке области определения аргумента  ).
).
(в) На декартовой плоскости 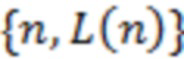 геометрическое отклонение
геометрическое отклонение 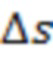 кривой
кривой  от отрезка прямой линии, соединяющей граничные точки и обладающего длиной
от отрезка прямой линии, соединяющей граничные точки и обладающего длиной 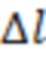 , удовлетворяет условию
, удовлетворяет условию

(Выбор единиц геометрической длины осей абсцисс и ординат, влияющий на определение значений 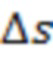 и
и 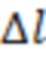 , будет прокомментирован далее.)
, будет прокомментирован далее.)
На рис. 2 такой отрезок, изображенный удлиненным пунктиром, соединяет точки 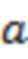 и
и 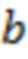 границ локального тренда; здесь же показано указанное максимальное отклонение
границ локального тренда; здесь же показано указанное максимальное отклонение 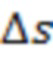 .
.
(г) Для точки как начала, так и завершения ЛТ при условии, что время от начала измерений до наиболее мощной вспышки составляет 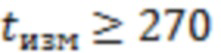 часов, минимальное расстояние
часов, минимальное расстояние 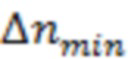 по горизонтали от данной точки до кривой
по горизонтали от данной точки до кривой  должно удовлетворять неравенству
должно удовлетворять неравенству

Если 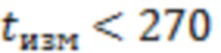 часов, то значение
часов, то значение 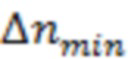 уменьшается пропорционально продолжительности
уменьшается пропорционально продолжительности 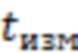 .
.
Условия (10)–(12) означают, что локальные тренды – это достаточно большие и квазипрямолинейные участки кривой  , граничные точки которых являются экстремумами, которые существенно отдалены по горизонтали от других точек этой кривой. Примерами ЛТ являются, в частности, участки
, граничные точки которых являются экстремумами, которые существенно отдалены по горизонтали от других точек этой кривой. Примерами ЛТ являются, в частности, участки 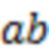 (он уже отмечен ранее) и
(он уже отмечен ранее) и 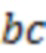 этой кривой на рис. 2а. Кроме того, также в виде примера на рис. 8б красными и синими сплошными прямоугольниками выделены те направляющие точки, через которые не проведены и которые не тестируются определяемыми далее линейными объектами, построенными на этом рисунке. (Как указано выше, все локальные тренды и начинаются, и заканчиваются в направляющих точках.)
этой кривой на рис. 2а. Кроме того, также в виде примера на рис. 8б красными и синими сплошными прямоугольниками выделены те направляющие точки, через которые не проведены и которые не тестируются определяемыми далее линейными объектами, построенными на этом рисунке. (Как указано выше, все локальные тренды и начинаются, и заканчиваются в направляющих точках.)
Определим канал как пару квазипараллельных прямых, каждая из которых проведена через две соответствующие направляющие точки и угол 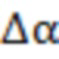 между направлениями которых удовлетворяет условию
между направлениями которых удовлетворяет условию

Значение 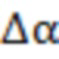 определяется с помощью метода скалярного произведения для векторов, проведенных на декартовой плоскости
определяется с помощью метода скалярного произведения для векторов, проведенных на декартовой плоскости 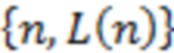 через указанные пары направляющих точек, определяющих направление границ канала.
через указанные пары направляющих точек, определяющих направление границ канала.
При этом горизонтальные координаты этих точек координаты этих точек нормируются на длительность интервала времени (в часах) от начала рассматриваемых измерений и до момента 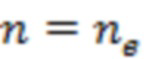 начала наиболее мощной вспышки, а вертикальные – на максимум
начала наиболее мощной вспышки, а вертикальные – на максимум 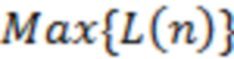 зависимости
зависимости  на том же промежутке времени. Значения
на том же промежутке времени. Значения 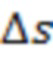 и
и 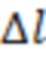 в (11) вычисляются при этих же условиях. Введение данной нормировки необходимо для устранения возможного произвола (при определении значений
в (11) вычисляются при этих же условиях. Введение данной нормировки необходимо для устранения возможного произвола (при определении значений 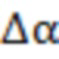 ,
, 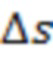 и
и 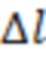 ), связанного с выбором единичного масштаба по осям абсцисс и ординат. Указанная нормировка эквивалентна переходу к проведению соответствующих расчетов при условии одинаковой геометрической длины интервалов
), связанного с выбором единичного масштаба по осям абсцисс и ординат. Указанная нормировка эквивалентна переходу к проведению соответствующих расчетов при условии одинаковой геометрической длины интервалов 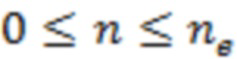 и
и 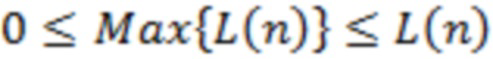 для соответствующих осей координат.
для соответствующих осей координат.
Кроме того, с целью дополнительной минимизации вероятности случайного возникновения указанных линейных объектов, будем рассматривать только те каналы, для которых хотя бы одна граница проходит либо через один из трех наиболее высоких максимумов, либо через один из трех самых глубоких минимумов рассматриваемой зависимости  на временном интервале до момента начала вспышки, энергия которой является максимальной в соответствующей серии. Введение данного ограничения связано со статистическим смыслом функционала
на временном интервале до момента начала вспышки, энергия которой является максимальной в соответствующей серии. Введение данного ограничения связано со статистическим смыслом функционала  , минимумы и максимумы которого с высокой вероятностью отвечают максимумам и соответственно минимумам «дополнительного» независимого случайного процесса
, минимумы и максимумы которого с высокой вероятностью отвечают максимумам и соответственно минимумам «дополнительного» независимого случайного процесса 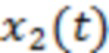 , значения которого полагаем пропорциональными возрастанию амплитуды процессов подготовки приближающейся вспышки.
, значения которого полагаем пропорциональными возрастанию амплитуды процессов подготовки приближающейся вспышки.
Кроме того, полагаем, что для любого канала отношение  большего и меньшего интервалов времени между парами точек, через которые проведены его границы, удовлетворяет условию
большего и меньшего интервалов времени между парами точек, через которые проведены его границы, удовлетворяет условию

(д) Рассмотрим определение тестирования, которое означает либо пересечение кривой  и рассматриваемой прямой линии (например, границы канала), либо (применительно к любой направляющей точке
и рассматриваемой прямой линии (например, границы канала), либо (применительно к любой направляющей точке 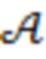 с координатами
с координатами 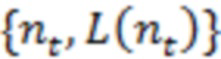 и независимо от указанного пересечения или его отсутствия) взаимное прохождение этой прямой при
и независимо от указанного пересечения или его отсутствия) взаимное прохождение этой прямой при 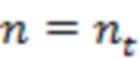 на таком расстоянии
на таком расстоянии 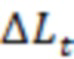 по вертикали от данной точки
по вертикали от данной точки  , что коэффициент отклонения
, что коэффициент отклонения 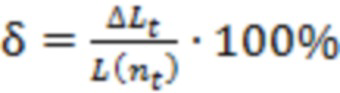 удовлетворяет условию
удовлетворяет условию

Время последнего тестирования кривой  границ канала рассматривается как момент фиксации предвестника приближающейся вспышки высокого уровня энергии. Укажем, в частности, что граница канала прерывается в точке ее пересечения с кривой
границ канала рассматривается как момент фиксации предвестника приближающейся вспышки высокого уровня энергии. Укажем, в частности, что граница канала прерывается в точке ее пересечения с кривой  при нарушении условия (15).
при нарушении условия (15).
(е) Будем называть скользящей границей (СГ) прямую линию, которая проведена через две направляющие точки и при этом происходит тестирование этой прямой со стороны кривой  еще как минимум в одной направляющей точке (которую назовем дополнительной) при выполнении (15). Момент последнего тестирования СГ со стороны кривой
еще как минимум в одной направляющей точке (которую назовем дополнительной) при выполнении (15). Момент последнего тестирования СГ со стороны кривой  также полагаем временем выявления предвестника. Укажем, что далее при построении каналов и СГ применительно к совокупности точек кривой
также полагаем временем выявления предвестника. Укажем, что далее при построении каналов и СГ применительно к совокупности точек кривой 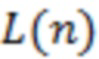 , для которых выполняется условие (15), будут учитываться только направляющие точки. Отметим, что для скользящих границ, изображенных на всех приведенных далее рисунках, коэффициенты отклонения
, для которых выполняется условие (15), будут учитываться только направляющие точки. Отметим, что для скользящих границ, изображенных на всех приведенных далее рисунках, коэффициенты отклонения  в большинстве случаев оказываются существенно меньше 1% (см. (15)). Как и в случае границ канала, полагаем, в частности, что скользящая граница прерывается в точке ее пересечения с кривой
в большинстве случаев оказываются существенно меньше 1% (см. (15)). Как и в случае границ канала, полагаем, в частности, что скользящая граница прерывается в точке ее пересечения с кривой  при нарушении (15).
при нарушении (15).
Таким образом, как для границ каналов, так и для скользящих границ точкой последнего тестирования является либо точка пересечения с кривой  при нарушении условия (15), либо последняя направляющая точка, для которой (15) оказывается справедливым.
при нарушении условия (15), либо последняя направляющая точка, для которой (15) оказывается справедливым.
Считаем, что для любой СГ отношение наибольшего и наименьшего интервалов времени между любыми последовательными парами из трех указанных соседних направляющих точек (через две из которых эта прямая проведена, а третья является дополнительной), также должно удовлетворять (14). Другими словами, интервалы между указанными соседними направляющими точками должны быть взаимно соизмеримыми.
Границы каналов будем изображать наклонными пунктирными прямыми, а скользящие границы – сплошными наклонными прямыми линиями.
Более подробное теоретическое описание применяемого математического аппарата на примере прогнозирования землетрясений дано в (Volvach et al., 2022a).
Отметим, что определения локальных трендов (ЛТ), скользящих границ, дополнительных и опорных точек в целом совпадают с (Volvach et al., 2022a). Основное отличие от указанной работы состоит в том, что для каналов и скользящих границ момент фиксации предвестника соответствует максимально удаленной во времени точке тестирования. Например, на рис. 2а такими точками являются точка  четвертого тестирования для канала 11–12 (то есть время регистрации предвестника совпадает с моментом возникновения этого канала) и точка
четвертого тестирования для канала 11–12 (то есть время регистрации предвестника совпадает с моментом возникновения этого канала) и точка  пятого тестирования для канала 8-9 (момент выхода «вверх» кривой
пятого тестирования для канала 8-9 (момент выхода «вверх» кривой 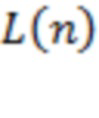 из данного канала). Для скользящих границ момент регистрации предвестника соответствует третьей направляющей точке (см. прямую 10 на рис. 4а), если далее для соответствующей прямой линии отсутствуют точки тестирования со стороны кривой
из данного канала). Для скользящих границ момент регистрации предвестника соответствует третьей направляющей точке (см. прямую 10 на рис. 4а), если далее для соответствующей прямой линии отсутствуют точки тестирования со стороны кривой 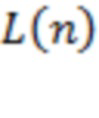 .
.
Введение этих условий позволяет сравнивать в каждом рассматриваемом случае от одного-двух до не более десяти рассматриваемых линейных объектов. Такое их количество упрощает анализ свойств статистического функционала 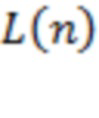 и позволяет выделить зоны концентрации рассматриваемых ниже предвестников. На всех рисунках дополнительные точки выделены сплошными эллипсами, а критические точки (где одновременно имеет место тестирование кривой
и позволяет выделить зоны концентрации рассматриваемых ниже предвестников. На всех рисунках дополнительные точки выделены сплошными эллипсами, а критические точки (где одновременно имеет место тестирование кривой 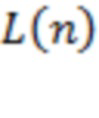 двух и более каналов и/или скользящих границ) – штриховыми эллипсами.
двух и более каналов и/или скользящих границ) – штриховыми эллипсами.
Моменты фиксации предшественников указаны вертикальными пунктирными линиями. Если время регистрации нескольких предшественников совпадает, то они обозначаются на рисунках соответствующим количеством близко расположенных вертикальных пунктирных линий одинаковой высоты. Любой интервал 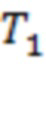 ,
, 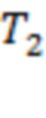 ,
, 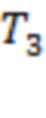 … обозначает время от регистрации предвестника либо до первой вспышки Х-класса, либо, при отсутствии таких событий, до самой сильной вспышки.
… обозначает время от регистрации предвестника либо до первой вспышки Х-класса, либо, при отсутствии таких событий, до самой сильной вспышки.
Мы проверили метод на самых мощных вспышках. Вспышки Х-класса отбирались с 2017 г., включая все имеющиеся на сегодняшний день вспышки на 2023 г. Вспышка 14 июля 2017 г. была выбрана как уникальная по продолжительности с мощным выбросом корональной массы и предшествовавшая каскадам вспышек Х-класса, произошедшим затем в сентябре 2017. Следует отметить, что помимо вспышки М-класса 14 июля 2017 г., вместе со вспышками Х-класса в 2017-2023 гг., вспышки С- и М-класса, произошедшие в 2017-2023 гг., рассматривались как кластерные события. Укажем, что на рис. 2 - 7 сплошными вертикальными линиями отмечены моменты начала вспышек (красным цветом отмечена самая сильная из них), а по оси абсцисс отложено время в часах.
На рис. 2 по измерениям за период 00:00:00 01.07.2017 – 23:59:59 16.07.2017 (время UTC) построена зависимость 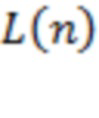 , которая используется для поиска предвестников последовательности вспышек класса
, которая используется для поиска предвестников последовательности вспышек класса 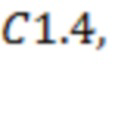
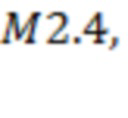
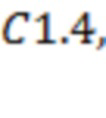
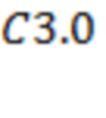 ,
, 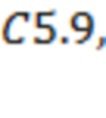
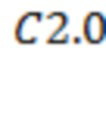 . Моменты их начала соответствуют 14.07.2017 в 0:27, 0:46, 2:30, 3:12, 4:07 и, соответственно, 22:18. Для рис. 2а получаем
. Моменты их начала соответствуют 14.07.2017 в 0:27, 0:46, 2:30, 3:12, 4:07 и, соответственно, 22:18. Для рис. 2а получаем 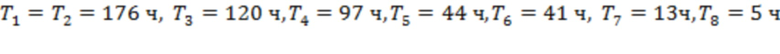 .
.
Интервалы 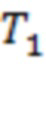 ,
, 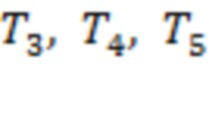 ,
, 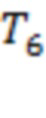 и
и 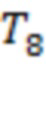 соответствуют последнему тестированию для каналов 2–3, 4–5, 6–7, 8–9, 11–12 и 9–10, а интервалы
соответствуют последнему тестированию для каналов 2–3, 4–5, 6–7, 8–9, 11–12 и 9–10, а интервалы 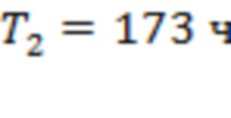 и
и 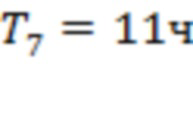 – для скользящих границ в виде прямых 2 и 1. Точка g соответствует последнему тестированию для прямой 2 и одновременно моменту выхода кривой
– для скользящих границ в виде прямых 2 и 1. Точка g соответствует последнему тестированию для прямой 2 и одновременно моменту выхода кривой 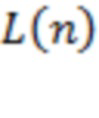 из канала 2–3. Четыре из восьми моментов регистрации предвестников сосредоточены в интервале 44 часа до начала солнечных событий. Для Рис. 2b интервалы
из канала 2–3. Четыре из восьми моментов регистрации предвестников сосредоточены в интервале 44 часа до начала солнечных событий. Для Рис. 2b интервалы 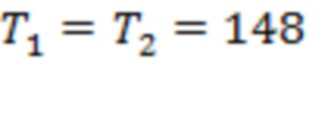 ч,
ч, 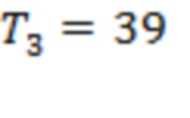 ч и
ч и 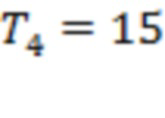 ч. Значения T1 и T3 соответствуют последнему тестированию для границ каналов 1–2 и 3–4, тогда как T2 и T4 – для скользящих границ 2 и 5. Два из четырех предвестников регистрируются в пределах 39 часов до первой вспышки.
ч. Значения T1 и T3 соответствуют последнему тестированию для границ каналов 1–2 и 3–4, тогда как T2 и T4 – для скользящих границ 2 и 5. Два из четырех предвестников регистрируются в пределах 39 часов до первой вспышки.
На рис. 3 зависимость 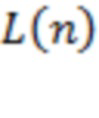 построена по измерениям за 00:00 15.08.2017 – 23:59 06.09.2017. (Изучаются вспышки классов Х2.2, Х9.3, М2.5, М1.4 и М1.2, время начала 06.09.2017 в 8:57, 11:53, 15:51, 19:21 и 23:33 соответственно.) Для рис. 3а получаем T1=279 ч, T2= T3= T4=T5=113 ч (наиболее удаленные точки каналов 3–4 и 9–10 совпадают с точками последнего тестирования для скользящих границ 4 и 9 соответственно),
построена по измерениям за 00:00 15.08.2017 – 23:59 06.09.2017. (Изучаются вспышки классов Х2.2, Х9.3, М2.5, М1.4 и М1.2, время начала 06.09.2017 в 8:57, 11:53, 15:51, 19:21 и 23:33 соответственно.) Для рис. 3а получаем T1=279 ч, T2= T3= T4=T5=113 ч (наиболее удаленные точки каналов 3–4 и 9–10 совпадают с точками последнего тестирования для скользящих границ 4 и 9 соответственно), 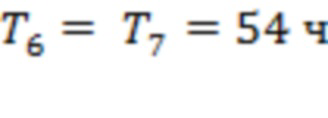 и
и 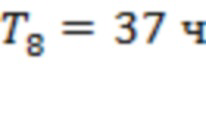 . Здесь
. Здесь  и
и  соответствуют точкам последнего тестирования для каналов 1–2, 3–4, 9–10, 5–6, 10–11 и 7–8, а T2 и T4 – для скользящих границ 4 и 9. Три из восьми моментов регистрации предвестников сосредоточены на интервале длительностью 54 часа до начала вспышечной серии.
соответствуют точкам последнего тестирования для каналов 1–2, 3–4, 9–10, 5–6, 10–11 и 7–8, а T2 и T4 – для скользящих границ 4 и 9. Три из восьми моментов регистрации предвестников сосредоточены на интервале длительностью 54 часа до начала вспышечной серии.
Для рис. 3b значения 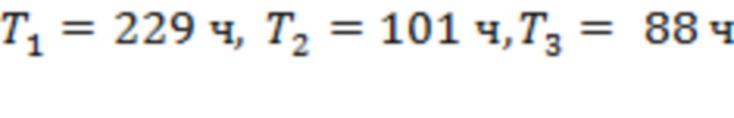 ,
, 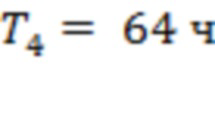 ,
, 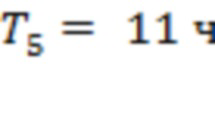 ,
, 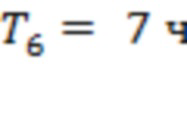 и
и 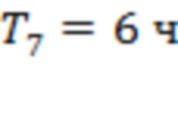 . Интервалы
. Интервалы 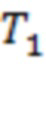 и
и 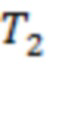 отвечают точкам последнего тестирования для скользящих границ 1 и 3, тогда как промежутки времени
отвечают точкам последнего тестирования для скользящих границ 1 и 3, тогда как промежутки времени 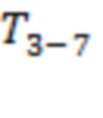 соответствуют подобным точкам для каналов 3–4, 7–8, 1–2, 9–10 и 5–6. Четыре из семи моментов регистрации предвестников сосредоточены на 64-часовом интервале до начала первой вспышки.
соответствуют подобным точкам для каналов 3–4, 7–8, 1–2, 9–10 и 5–6. Четыре из семи моментов регистрации предвестников сосредоточены на 64-часовом интервале до начала первой вспышки.
Рис. 4 соответствует измерениям за 00:00 06.04.2022 – 23:59 23.04.2022. Мы изучаем вспышки класса С7.7, С6.2, М1.5 и М4.4 (начало 17.04.2022 в 16.02, 17:50, 19:52 и 22:28), С8.6 (начало 18.04.2022 в 03:01), М3.7 (начало 19.04.2022 в 22.39) и С4.0, М7.29, Х2.2 и С4.0 (начало 20.04.2022 в 00.46, 01.20, 03.41 и 05.35). В отличие от рис. 2 и 3, где значения интервалов 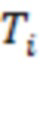 соответствовали первой вспышке класса X, которая не была самой большой по мощности, в данном случае промежутки времени
соответствовали первой вспышке класса X, которая не была самой большой по мощности, в данном случае промежутки времени 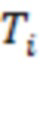 отвечают моменту начала единственной (и наиболее мощной изо всей серии) вспышке класса Х2.2. На рис. 4а интервалы
отвечают моменту начала единственной (и наиболее мощной изо всей серии) вспышке класса Х2.2. На рис. 4а интервалы 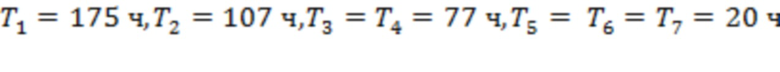 и
и 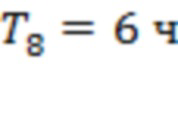 . Интервалы T2 и T4 соответствуют точкам последнего тестирования для скользящих границ 12 и 10, тогда как T1, T3 и
. Интервалы T2 и T4 соответствуют точкам последнего тестирования для скользящих границ 12 и 10, тогда как T1, T3 и 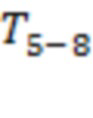 отвечают аналогичным моментам времени для каналов 1–2, 6–7, 4–5, 2–3, 10–11 и 8–9. Четыре из восьми моментов регистрации предвестников сосредоточены на интервале в 20 часов до начала события. Для рис. 4b получаем
отвечают аналогичным моментам времени для каналов 1–2, 6–7, 4–5, 2–3, 10–11 и 8–9. Четыре из восьми моментов регистрации предвестников сосредоточены на интервале в 20 часов до начала события. Для рис. 4b получаем 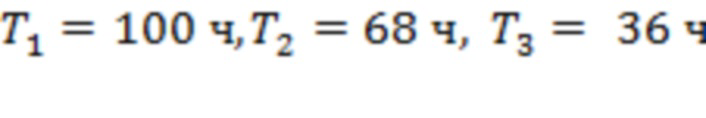 ,
, 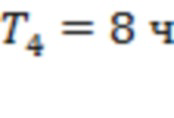 ,
, 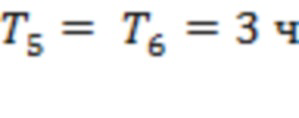 . Интервалы
. Интервалы 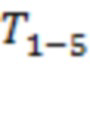 соответствуют времени последнего тестирования для каналов 4–5, 6–7, 2–3, 1–2 и 8–9, а промежуток времени
соответствуют времени последнего тестирования для каналов 4–5, 6–7, 2–3, 1–2 и 8–9, а промежуток времени 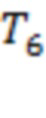 отвечает скользящей границе 10. Четыре из шести моментов регистрации предвестников сосредоточены на интервале в 36 часов до начала события.
отвечает скользящей границе 10. Четыре из шести моментов регистрации предвестников сосредоточены на интервале в 36 часов до начала события.
Рис. 5 соответствует измерениям за 00:00 02.06.2023 – 23:59 02.12.2023. Здесь исследуется серия вспышек классов С5.3, М1.2,С5.8, С5.2, С7.7, С7.2, С9.0, С5.8, М2.2, М1.4, М1.5, М1.1, М1.5, Х1.1 и М1.4 (начало 02.11.2023 в 01.19, 01.34, 02.55, 09.10, 09.27, 09.42, 10.48, 10.59, 12.13, 13.42, 14.29, 15.05, 1 5.18, 15.28, 18.40 и 20.11). В данном случае рассматриваемый интервал измерений составляет всего 7 дней, что связано с отсутствием данных на 5 февраля 2023 г. На рис. 5 значения интервалов  соответствуют моменту начала самой мощной вспышки класса Х1.1.
соответствуют моменту начала самой мощной вспышки класса Х1.1.
На рис. 5а интервалы 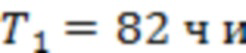
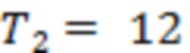 часов. Интервалы
часов. Интервалы 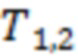 соответствуют точкам последнего тестирования для канала 1–2 и, соответственно, ограничительной линии 3. Последний линейный объект соответствует введенному в (Volvach et al., 2022a) определению касательной прямой, проведенной через две направляющие точки зависимости
соответствуют точкам последнего тестирования для канала 1–2 и, соответственно, ограничительной линии 3. Последний линейный объект соответствует введенному в (Volvach et al., 2022a) определению касательной прямой, проведенной через две направляющие точки зависимости  (точки
(точки 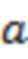 и
и 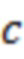 на рис. 5а) и реализующей тестирование кривой
на рис. 5а) и реализующей тестирование кривой  еще как минимум в двух точках ее экстремумов (в данном случае точки
еще как минимум в двух точках ее экстремумов (в данном случае точки 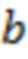 и
и 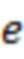 ). Эти точки в общем случае могут не являться направляющими (как и указанные точки
). Эти точки в общем случае могут не являться направляющими (как и указанные точки 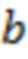 и
и 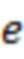 ), однако должны удовлетворять условию существенно более жесткому, чем (15). При этом хотя бы одна из них (точка
), однако должны удовлетворять условию существенно более жесткому, чем (15). При этом хотя бы одна из них (точка 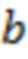 на этом рисунке) должна располагаться между двумя направляющими точками и удовлетворять, в соответствии с (14), как и «обычная» дополнительная точка, отношению расстояний до этих двух точек с параметром ζ ≤ 7/2, принятым в данной статье. В данном случае для точек
на этом рисунке) должна располагаться между двумя направляющими точками и удовлетворять, в соответствии с (14), как и «обычная» дополнительная точка, отношению расстояний до этих двух точек с параметром ζ ≤ 7/2, принятым в данной статье. В данном случае для точек 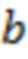 и
и 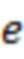 введенный в (15) коэффициенты отклонения составляют
введенный в (15) коэффициенты отклонения составляют
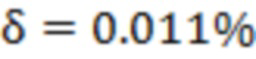 и соответственно
и соответственно 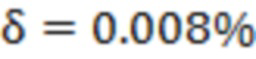 , что является заведомо много меньшими значениями по сравнению с правой частью (15). Поскольку для точки
, что является заведомо много меньшими значениями по сравнению с правой частью (15). Поскольку для точки 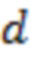 получаем
получаем 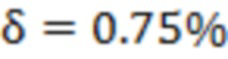 , что также удовлетворяет (15), то приходим к выводу, что прямая 3, выполняющая, как следует из рис. 5а, функцию ограничительного барьера для значений зависимости
, что также удовлетворяет (15), то приходим к выводу, что прямая 3, выполняющая, как следует из рис. 5а, функцию ограничительного барьера для значений зависимости  , удовлетворяет указанному определению касательной прямой. Кроме того, в качестве дополнительного ужесточения вводится также выполняемое здесь требование, чтобы продолжительность существования касательной прямой, от ее начала до момента последнего тестирования, составляла бы не менее половины всего интервала времени от начала измерений и до момента возникновения основной рассматриваемой вспышки.
, удовлетворяет указанному определению касательной прямой. Кроме того, в качестве дополнительного ужесточения вводится также выполняемое здесь требование, чтобы продолжительность существования касательной прямой, от ее начала до момента последнего тестирования, составляла бы не менее половины всего интервала времени от начала измерений и до момента возникновения основной рассматриваемой вспышки.
На рис. 5б интервалы 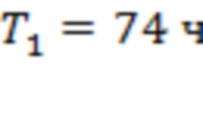 ,
, 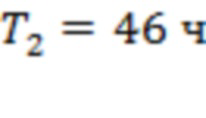 и
и 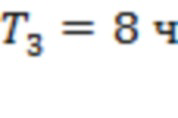 соответствуют точкам последнего тестирования для скользящей границы 3 и каналов 3–4 и 1–2 соответственно. На рис. 5а, б в общей совокупности зарегистрировано 5 предвестников, три из которых расположены в интервале не более 46 часов до рассматриваемой основной вспышки. Несмотря на малое число присутствующих на рис. 5 линейных объектов, в обоих случаях, и на рис. 5а, и на рис. 5б, имеет место критическая точка.
соответствуют точкам последнего тестирования для скользящей границы 3 и каналов 3–4 и 1–2 соответственно. На рис. 5а, б в общей совокупности зарегистрировано 5 предвестников, три из которых расположены в интервале не более 46 часов до рассматриваемой основной вспышки. Несмотря на малое число присутствующих на рис. 5 линейных объектов, в обоих случаях, и на рис. 5а, и на рис. 5б, имеет место критическая точка.
Рис. 6а, б соответствует измерениям за 00:00 13.02.2023 – 23:59 18.02.2023. В этот период имели место вспышки класса С3.8, С1.3, С1.9, С2.2, С2.1, С2.0, С2.0 и Х2.2 (начало 17.02.2023 в 04.31, 07.19, 10.29, 12.29, 13.24, 13.44, 14.43 и 22.38). Здесь значения интервалов Ti отвечают моменту начала самой мощной вспышки класса Х2.2. На рис. 6а единственный интервал T1=18 ч соответствует точке последнего тестирования скользящей границы 1. На рис. 6б интервалы T1=99 ч и T3=23 ч соответствуют точкам последнего тестирования для каналов 3–4 и 1–2 соответственно, а интервал T2=64 ч отвечает аналогичной точке для скользящей границы 5. Как и для рис. 5, интервал времени рассматриваемых измерений в данном случае относительно невелик, по сравнению со случаями рис. 2–4, и составляет 6 суток. Это связано с необходимостью учета влияния вспышки класса Х1.1. Она произошла 11 февраля 2023 года, и связанные с ней последствия должны были повлиять на статистику измерений солнечной фотосферы как минимум еще на одни сутки. Поэтому в данном случае были приняты к рассмотрению результаты измерений только начиная с 13.02.2023.
Рис. 7 соответствует измерениям за 00:00 19.02.2023 – 23:59 03.03.2023. Мы изучаем вспышки класса М3.8, С7.2, С3.0, С5.0, М3.3, С3.9, С9.1 и Х2.1 (начало 03.03.2023 в 00.05, 04.58, 09.58, 11.26, 13.10, 17.26, 17.48 и 20.42). Здесь значения интервалов Ti отвечают моменту начала самой мощной вспышки класса Х2.1.
На рис. 7а интервалы 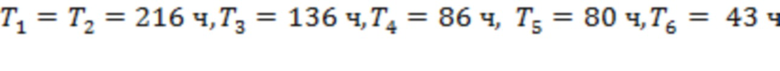 и
и 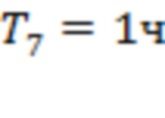 соответствуют времени начала самой мощной вспышки класса Х2.1. Интервалы
соответствуют времени начала самой мощной вспышки класса Х2.1. Интервалы 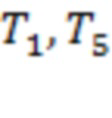 и
и 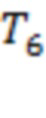 отвечают точкам последнего тестирования для скользящих границ 5, 8 и 9, а
отвечают точкам последнего тестирования для скользящих границ 5, 8 и 9, а 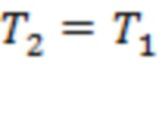 ,
, 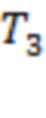 ,
, 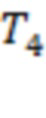 и
и 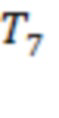 соответствуют аналогичным точкам для каналов 3–5, 3–4, 6 –7 и 1–2. (Точка начала интервала T7 отмечена красной стрелкой.) Три из семи моментов регистрации предвестников сосредоточены на промежутке времени в 80 часов до начала события. Для рис. 7b мы получаем
соответствуют аналогичным точкам для каналов 3–5, 3–4, 6 –7 и 1–2. (Точка начала интервала T7 отмечена красной стрелкой.) Три из семи моментов регистрации предвестников сосредоточены на промежутке времени в 80 часов до начала события. Для рис. 7b мы получаем 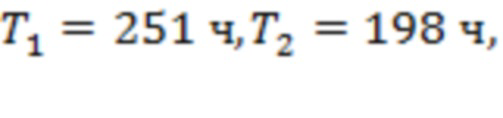
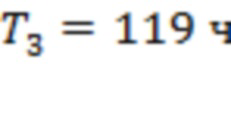 ,
, 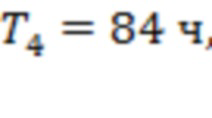
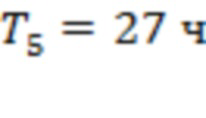 и
и 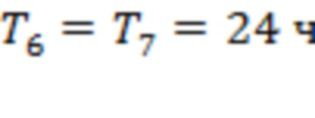 . Интервалы
. Интервалы  и
и 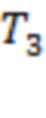 соответствуют точкам последнего тестирования для скользящих границ 1, 2 и 7, тогда как
соответствуют точкам последнего тестирования для скользящих границ 1, 2 и 7, тогда как 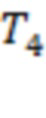 ,
, 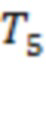 и
и 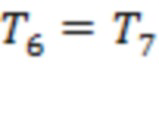 отвечают аналогичным точкам для каналов 8–9, 9–10, 3–4 и 5–6. Три из семи моментов регистрации предвестников отстоят от начала рассматриваемой вспышки более чем на 27 часов.
отвечают аналогичным точкам для каналов 8–9, 9–10, 3–4 и 5–6. Три из семи моментов регистрации предвестников отстоят от начала рассматриваемой вспышки более чем на 27 часов.
Рис. 8 соответствует измерениям за 00:00 14.03.2023 – 23:59 30.03.2023. Рассматриваемые вспышки относятся к классам С2.2, С2.7, С2.4, Х2.2, М1.2, С5.6 и С6.6 (начало 29.03.2023 в 00.38, 01.02, 22.03, 18.05, 16.47, 18.58 и 19.14). Значения интервалов Ti отвечают моменту начала самой мощной вспышки класса Х2.2. На рис. 8а интервалы 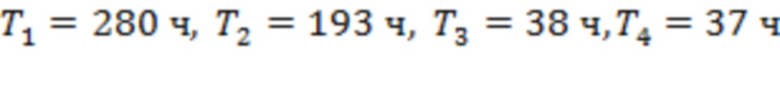 и
и 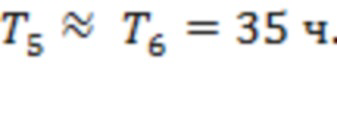
Промежутки времени 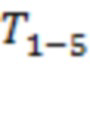 соответствуют точкам последнего тестирования скользящих границ 1, 2, 3, 5 и 4, а интервал
соответствуют точкам последнего тестирования скользящих границ 1, 2, 3, 5 и 4, а интервал 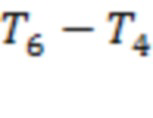 отвечает подобной точке для канала 3–4. Четыре из шести моментов регистрации предвестников отстоят не более чем на 38 часов от момента начала события. На рис. 8б интервал
отвечает подобной точке для канала 3–4. Четыре из шести моментов регистрации предвестников отстоят не более чем на 38 часов от момента начала события. На рис. 8б интервал 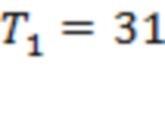 ч соответствует точке последнего тестирования для скользящей границы 1. На этом рисунке красными и, соответственно, синими прямоугольниками отмечены те максимумы и, соответственно, минимумы зависимости L(n), которые являются направляющими точками в дополнение к тем точкам (двум направляющим и одной дополнительной), через которые проводится рассматриваемая прямая 1. Их число остается достаточно ограниченным даже в случае такой сильно «зубчатой», как в данном случае, кривой L(n).
ч соответствует точке последнего тестирования для скользящей границы 1. На этом рисунке красными и, соответственно, синими прямоугольниками отмечены те максимумы и, соответственно, минимумы зависимости L(n), которые являются направляющими точками в дополнение к тем точкам (двум направляющим и одной дополнительной), через которые проводится рассматриваемая прямая 1. Их число остается достаточно ограниченным даже в случае такой сильно «зубчатой», как в данном случае, кривой L(n).
Литература
Hudson H.S., 2011. Global Properties of Solar Flares. Space Sci Rev., 158, 5–41.
Kogan L.P., 2015. Change in statistical functionals of critical frequency prior to strong earth-quakes. Geomagnetism and Aeronomy, 55, № 4. 507—520.
Kogan L.P., Bubukin I.T., Shtenberg V.B., 2021. To the question of calculating the probability of strong earthquakes in real time. Chaos, Solitons and Fractals. 145. 110807.
Svestka, Z., Cliver, E.W., 1992. History and basic characteristics of eruptive flares, in IAU Colloq. 133: Eruptive Solar Flares, ed. by Z. Svestka, B.V. Jackson, M.E. Machado. Lecture Notes in Physics, 399, 1.
Volvach A.E., Kogan L.P., Kanonidi K.H., Nadezhka L.I., Bubukin I.T., Shtenberg V.B., Gordetsov A.S., Krasnikova O.V., Kislitsyn D.I., 2022a. Changes in the properties of the statistics of physical and biophysical fields as earthquake precursor. Communications in Nonlinear Science and Numerical Simulation, 108. 106200. https://doi.org/10.1016/j.cnsns.2021.106200.
Volvach A.E., Kogan L.P., Kanonidi K.H., Nadezhka L.I., Bubukin I.T., Boborikina O.V., Shtenberg V.B., Biazitov D.T., 2022b. A Possible Relationship between the Sets of Quasi-Linear Local Trends Statistically Detected in the Variations of the Magnetic Field Parameters before Earthquakes in Seismicly Active Zones of the Black Sea, Caucasus, and Western Asia. Geodynamics & Tectonophysics 13(5), 0680.
Volvach A.E., Kogan L.P., Kanonidi K.H., Bubukin I.T., Shtenberg V.B., Volvach L.N., Biazitov D.T., 2022c. Statistical precursors of a strong earthquake on April 6, 2009 on the Apennine Peninsula. Heliyon 8(8), e10200.
Volvach A., Kogan L., Kanonidi K., Nadezhka L., Bubukin I., Boborykina O., Shtenberg V. & Biazitov D., 2022d. On the statistical precursors that preceded the earthquake of magnitude 6.0 on September 27, 2021, on the island of Crete. Arabian Journal of Geosciences 15, 1358.
Volvach A., Kogan L., Kanonidi K., Bubukin I., Shtenberg V., Volvach L., 2023a. About Statistical Precursor Earthquakes on October 12, 2021 with a Magnitude of 6.4 on the Island of Crete. Romanian Journal of Physics 68, 801.
Volvach A.E., Kogan L.P., Kanonidi K.H., Bubukin I.T., Boborikina O.V., Shtenberg V.B., Volvach L.N., 2023b. On a comparison of the properties of a statistical functional from measurements of the magnetic field in the mid of the Russian continental platform and in a seismicly active region. Geomagnetism and Aeronomy 63(2), 1.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения вероятности возникновения землетрясений на основе выявления феноменов с высоким уровнем детерминированности | 2021 |
|
RU2778972C1 |
| СПОСОБ ПРОГНОЗА ГЕОЭФФЕКТИВНЫХ СОЛНЕЧНЫХ ВСПЫШЕК | 2012 |
|
RU2491583C1 |
| СПОСОБ РЕГИСТРАЦИИ ВСПЫШЕК НА СОЛНЦЕ И КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2019 |
|
RU2715837C1 |
| НАУКАСТИНГ ПОЯВЛЕНИЯ ГЕОЭФФЕКТИВНЫХ ПОТОКОВ ПРОТОНОВ В ОКОЛОЗЕМНОМ КОСМИЧЕСКОМ ПРОСТРАНСТВЕ | 2011 |
|
RU2485557C1 |
| СПОСОБ КРАТКОСРОЧНОГО ПРОГНОЗА ВРЕМЕНИ РЕГИСТРАЦИИ ЯВЛЕНИЯ КОРОНАЛЬНОГО ВЫБРОСА МАССЫ (КВМ) | 2016 |
|
RU2630535C2 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ СЕЙСМИЧЕСКОГО СОБЫТИЯ | 2011 |
|
RU2581119C2 |
| СПОСОБ КРАТКОСРОЧНОГО ПРОГНОЗА МОЩНЫХ СОЛНЕЧНЫХ ВСПЫШЕК | 2009 |
|
RU2419821C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО МОНИТОРИНГА И ПРОГНОЗА ТЕКТОНИЧЕСКИХ ПРОЦЕССОВ С ВЫБОРОМ МЕСТА И ВРЕМЕНИ ВОЗДЕЙСТВИЯ НА ЗЕМЛЕТРЯСЕНИЯ И ВУЛКАНЫ | 2011 |
|
RU2488853C2 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАИБОЛЕЕ ОПАСНЫХ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 1997 |
|
RU2124744C1 |
| Способ краткосрочного прогноза землетрясений | 2016 |
|
RU2645878C1 |
Изобретение относится к области геофизики. Способ прогнозирования вспышек на Солнце на основе выявления феноменов с высоким уровнем детерминированности основан на анализе изменений статистики полей, измеряемых в период времени, который полагаем предшествующим вспышке, и обладающих свойством формирования линейных структур, подобных рассматриваемым далее. Таким полем может являться регистрируемый с помощью космических и/или наземных телескопов непрерывный поток солнечного рентгеновского, радио-, УФ-излучения с временным разрешением не более чем 1 секунда, измеряемый на интервале времени порядка восемнадцати суток перед моментом вспышки. Технический результат – повышение достоверности и упрощение способа прогнозирования солнечных вспышек. 8 ил.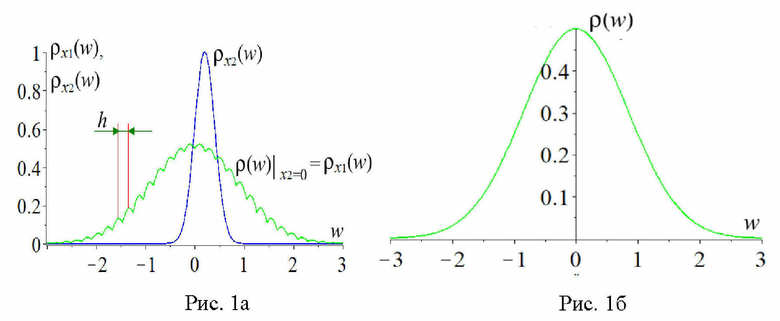
Способ прогнозирования вспышек на Солнце, основанный на выявлении феноменов с высоким уровнем детерминированности, характеризующийся тем, что способ основан на анализе изменений статистики полей, измеряемых в период времени, который полагают предшествующим вспышке, при регистрации которых строят зависимость их флуктуаций во времени и выявляются ее квазилинейные участки, изменения полей регистрируют с помощью космических или наземных телескопов, поток рентгеновского, радио-, УФ-излучения с максимально возможным временным разрешением не более чем 1 секунда, в частности, с помощью работающего на орбите космического телескопа Geostationary Operational Environmental Satellite (GOES), передающего данные на приемо-передающее земное устройство в диапазонах 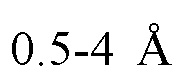 и
и 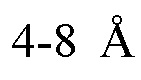 осуществляют их анализ при помощи компьютера с выявлением возникновения участков кривой, вдоль которых располагались несколько точек, которые являются граничными точками изучаемой зависимости энергии вспышек от времени, данные линейные структуры представляют при помощи компьютера либо в форме каналов в виде пар прямых линий, соединяющих указанные точки, эти прямые почти параллельны: угол между их направлениями удовлетворяет Δα≤1,5° при условии нормирования горизонтальной координаты на величину интервала времени от начала измерений до момента указанной вспышки, максимальной по энергии, а вертикальной координаты – на максимум значений применяемого статистического функционала, характеризующего энергии вспышек во времени, в период времени от начала измерений до момента указанной вспышки, максимальной по энергии, в виде прямых, проведенных через две точки, и проходящих мимо третьей точки, расположенной на минимальном расстоянии δ≤1,2% от отвечающего ей значения вышеуказанного статистического функционала, определение высокой вероятности возникновения предстоящей в течение нескольких десятков часов вспышки высокой энергии по усилению концентрации моментов регистрации фактов возникновения линейных по времени границ для вариаций во времени энтропии энергии вспышек и/или моментов регистрации фактов возникновения линейных вышеупомянутых границ или моментов регистрации фактов выхода вышеуказанной энтропии за пределы границ.
осуществляют их анализ при помощи компьютера с выявлением возникновения участков кривой, вдоль которых располагались несколько точек, которые являются граничными точками изучаемой зависимости энергии вспышек от времени, данные линейные структуры представляют при помощи компьютера либо в форме каналов в виде пар прямых линий, соединяющих указанные точки, эти прямые почти параллельны: угол между их направлениями удовлетворяет Δα≤1,5° при условии нормирования горизонтальной координаты на величину интервала времени от начала измерений до момента указанной вспышки, максимальной по энергии, а вертикальной координаты – на максимум значений применяемого статистического функционала, характеризующего энергии вспышек во времени, в период времени от начала измерений до момента указанной вспышки, максимальной по энергии, в виде прямых, проведенных через две точки, и проходящих мимо третьей точки, расположенной на минимальном расстоянии δ≤1,2% от отвечающего ей значения вышеуказанного статистического функционала, определение высокой вероятности возникновения предстоящей в течение нескольких десятков часов вспышки высокой энергии по усилению концентрации моментов регистрации фактов возникновения линейных по времени границ для вариаций во времени энтропии энергии вспышек и/или моментов регистрации фактов возникновения линейных вышеупомянутых границ или моментов регистрации фактов выхода вышеуказанной энтропии за пределы границ.
| СПОСОБ РЕГИСТРАЦИИ ВСПЫШЕК НА СОЛНЦЕ И КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2019 |
|
RU2715837C1 |
| СПОСОБ ПРОГНОЗА ГЕОЭФФЕКТИВНЫХ СОЛНЕЧНЫХ ВСПЫШЕК | 2012 |
|
RU2491583C1 |
| СПОСОБ КРАТКОСРОЧНОГО ПРОГНОЗА ВРЕМЕНИ РЕГИСТРАЦИИ ЯВЛЕНИЯ КОРОНАЛЬНОГО ВЫБРОСА МАССЫ (КВМ) | 2016 |
|
RU2630535C2 |
| CN 111965733 A, 20.11.2020. | |||
Авторы
Даты
2024-05-02—Публикация
2023-08-15—Подача