Способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице Российский патент 2024 года по МПК G01N15/10 

Настоящее изобретение относится к способам определения резонансной моды Ми высокого порядка при суперрезонансе в сферической мезоразмерной диэлектрической однородной частице и может быть использовано, например, для оптической генерации сверхсильных магнитных полей, генерации фотонно-магнитных наноструй, для получения биоизображений небольших биологических объектов, таких как, например, вирус, для лазерного наноструктурирования небольшими микро/наночастицами, в различных датчиках, например, для измерения показателя преломления, температуры, плотности и т.д.

Известно, что диэлектрические сферы с определенными параметрами размера и изготовленные из материала с малыми потерями, например, стекла, кварца, фторопласта, могут стимулировать гигантскую напряженность поля в сингулярностях, а затем образовывать две круглые горячие точки вокруг полюсов сферы и поддерживать так называемые «суперрезонансные моды» [Z. B. Wang, B. Luk’yanchuk, L. Yue, B. Yan, J. Monks, R. Dhama, O. V. Minin, I. V. Minin, S. M. Huang, and A. A. Fedyanin, High order Fano resonances and giant magnetic fields in dielectric microspheres, // Scientific Reports 9, 20293 (2019); L. Yue, B. Yan, J. N. Monks, R. Dhama, C. Jiang, O. V. Minin, I. V. Minin, and Z. Wang. Full three-dimensional Poynting vector analysis of great field-intensity enhancement in a specifically sized spherical-particle. // Sci Rep 9, 20224 (2019); L. Yue, Z. Wang, B. Yan, J. Monks, Y. Joya, R. Dhama, O.V. Minin, and I. V. Minin, Super-Enhancement Focusing of Teflon Spheres // Ann. Phys. (Berlin) 532, 2000373 (2020)], что отличается от других типов резонансов [Conwell, P., Barber, P., Rushforth, C. Resonant spectra of dielectric spheres, // J. Opt. Soc. Am. A, 1(1), 62 (1984); P. Chýlek, J. D. Pendleton, and R. G. Pinnick, Internal and near-surface scattered field of a spherical particle at resonant conditions, // Appl. Opt. 24, 3940-3942 (1985); Y. Duan, G. Barbastathis, and B. Zhang, Classical imaging theory of a microlens with super-resolution, // Opt. Lett. 38, 2988-2990 (2013); S. Zhou, Y. Deng, W. Zhou, M. Yu, H. P. Urbach, Y. Wu. Effects of whispering gallery mode in microsphere super resolution imaging. // Appl. Phys. B 123, 236 (2017)] в таких частицах. Суперрезонансом называется резонанс, соответствующий максимальной интенсивности рассеянного поля из всего спектра резонансных линий в заданном диапазоне параметров размера Ми сферы.

Напряженность электромагнитного поля в горячих точках внутри диэлектрической сферы может на несколько порядков, примерно на 10³-10¹⁰, превышать напряженность электромагнитного поля в освещающей волне. Особенностью этого типа резонанса является то, что величина напряженности магнитного поля может существенно превышать величину напряженности электрического поля в горячих точках.

Этот суперрезонанс связан с внутренними модами Ми высокого порядка и имеет место при определенных значениях параметра размера частиц q (параметр Ми), определяемого как q=2πR/λ, где R - радиус частицы, а λ - длина волны излучения, показатель преломления сферической частицы n, зависит от ее сферичности и т.д., которые могут быть непосредственно получены из строгой аналитической теории Ми [Mie, G. Beiträge zur optik trüber medien, speziell kolloidalermetallösungen, // Ann. Phys. 30, 3, 377-445 (1908)].

Суть нового физического эффекта - оптического суперрезонанса заключается в следующем: в диэлектрических мезоразмерных частицах, облучаемых электромагнитной волной с плоским фронтом и когда параметр размера частицы q превышает некоторое значение, зависящее от ее показателя преломления, возникают оптические вихри [Wang Z., Luk’yanchuk B., L. Yue L., B. Yan B., J. Monks J., R. Dhama R., Minin O. V., Minin I. V., Huang S., Fedyanin A. High order Fano resonances and giant magnetic fields in dielectric microspheres. // Sci Rep. 2019; 9: 20293.]. Следовательно, в соответствии с законом Био- Савара, соответствующие кольцевые токи, возникающие в оптических вихрях, создают магнитные поля. Моделирование на основе теории Лоренца-Ми показало, что внутри мезомасштабной слабодиссипативной диэлектрической частицы, размещенной в вакууме, магнитное поле может быть потенциально усилено более, чем на 3-4 порядка.

Известен способ Лоренца-Ми получения распределения интенсивностей электромагнитных полей в сферической диэлектрической частице [Mie G. Beitrage zur Optik truber Medien speziell kolloidaler Goldlosungen (Сontributions to the optics of diffuse media, especially colloid metal solutions). Ann. Physik. 1908; 25, 377-445; Bohren C. and Huffman D. Absorption and Scattering of Light by Small Particles (WILEY-VCH Verlag). 1998.]. Способ заключается в формировании линейно поляризованной волны с плоским волновым фронтом, освещении ею сферической однородной диэлектрической частицы, выполненной из прозрачного для освещающей волны материала, рассеяния плоской, линейно поляризованной электромагнитной волны на однородной сферической частице, представления рассеянных волн в виде бесконечного ряда парциальных волн, каждая из которых представляется в виде суммы электрической и магнитной моды, представления соответствующих эффективностей внешнего и внутреннего рассеяния через две пары комплексных парциальных коэффициентов рассеяния, которые выражаются через комбинации сферических функций Неймана, Бесселя и их производных.

Известен способ получения распределения интенсивностей электромагнитных полей в сферической диэлектрической частице расположенной на подложке по патенту WO 2007/061383 Al Determination of Field Distribution, включающий создание падающей волны в виде лазерного пучка, определение электрического вектора поля и магнитного вектора поля внутри и снаружи частицы, выбранного из группы, состоящей из: электромагнитного поля и электрического поля и магнитного поля и определение дополнительных рассеянных полей внутри и снаружи частицы за счет отражения падающей волны от подложки, а распределение поля представляет собой, по меньшей мере одно, выбранное из группы, состоящей из: распределения электрического поля, распределения магнитного поля, распределения векторного поля Пойнтинга и других величин электромагнитного поля, которые могут быть получены из электрического вектора поля и векторного магнитного поля, при этом распределения полей представляют собой векторные поля, которые могут быть определены из потенциалов Дебая.

Достоинством способов является возможность определения интенсивностей электромагнитных полей как внутри частицы, так и вне ее для частиц с характерными размерами от q~1 до q~100.

Недостатком известных способов является определение моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице за счет последовательного перебора значений параметра Ми и расчета распределения электромагнитного поля внутри частицы.

Известен способ определения резонансных мод Ми высокого порядка в сферической диэлектрической частице при суперрезонансе, заключающийся в облучении электромагнитным излучением сферической диэлектрической мезоразмерной частицы, определения электрического вектора поля и магнитного вектора поля внутри и снаружи частицы на основе расчета по теории Ми, последовательного перебора диаметров диэлектрической частицы до появления резонансных мод Ми с максимальными уровнями напряженности электрического и магнитного полей [Z. B. Wang, B. Luk’yanchuk, L. Yue, B. Yan, J. Monks, R. Dhama, O. V. Minin, I. V. Minin, S. M. Huang, and A. A. Fedyanin, High order Fano resonances and giant magnetic fields in dielectric microspheres, // Scientific Reports 9, 20293 (2019); L. Yue, B. Yan, J. N. Monks, R. Dhama, C. Jiang, O. V. Minin, I. V. Minin, and Z. Wang. Full three-dimensional Poynting vector analysis of great field-intensity enhancement in a specifically sized spherical-particle. // Sci Rep 9, 20224 (2019); L. Yue, Z. Wang, B. Yan, J. Monks, Y. Joya, R. Dhama, O.V. Minin, and I. V. Minin, Super-Enhancement Focusing of Teflon Spheres // Ann. Phys. (Berlin) 532, 2000373 (2020)].

Недостатком способа является определение резонансных мод Ми высокого порядка для сферической диэлектрической частицы при суперрезонансе за счет последовательного перебора диаметров сферической диэлектрической частицы по максимальным уровням напряженности электрического и магнитного полей.

В качестве прототипа выбран способ определения резонансных мод Ми высокого порядка для сферической диэлектрической частицы при суперрезонансе по патенту РФ 2786780, заключается в изготовлении сферической диэлектрической частицы из прозрачного материала для используемого излучения, облучении диэлектрической частицы лазерным излучением, при этом облучение диэлектрической частицы осуществляют перестраиваемым источником излучения, формировании освещающей волны с плоским волновым фронтом, регистрировании электромагнитного излучения в горячих точках вокруг полюсов сферы вдоль направления распространения излучения и преобразовании регистрируемого излучения в электрический сигнал, определении резонансных мод Ми высокого порядка при суперрезонансе по уровню максимального сигнала при различных длинах волн освещающего излучения.

Недостатком способа является определение резонансных мод Ми высокого порядка для сферической диэлектрической частицы при суперрезонансе за счет последовательного перебора длины волны освещающего излучения по максимальным уровням напряженности электрического и магнитного полей.

Задачей заявляемого технического решения является разработка способа быстрого определения резонансной моды Ми высокого порядка при суперрезонансе в сферической мезоразмерной диэлектрической однородной частице.

Это достигается тем, что применяемый способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице, заключающийся в изготовлении сферической диэлектрической частицы из прозрачного материала для используемого излучения, облучении диэлектрической частицы лазерным излучением, формировании освещающей волны с плоским волновым фронтом, определения суперрезонанса мод Ми высокого порядка по уровню максимального сигнала при различных длинах волн освещающего излучения, новым является то, что сферическую диэлектрическую частицу выполняют из материала с относительным показателем преломления не более 2, с диаметром D не менее 10λ/π и определяют на внешнем поверхностном слое внутри диэлектрической сферы в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе из условия локализации суперрезонанса по достижению глобального минимума модулей знаменателей парциальных коэффициентов Ми (c_l,d_l) для сферической диэлектрической однородной частицы.

Авторам неизвестны технические решения, содержащие сходные отличительные признаки и их использование для заявленной цели быстрого определения резонансных мод Ми высокого порядка для сферической диэлектрической частицы при суперрезонансе.

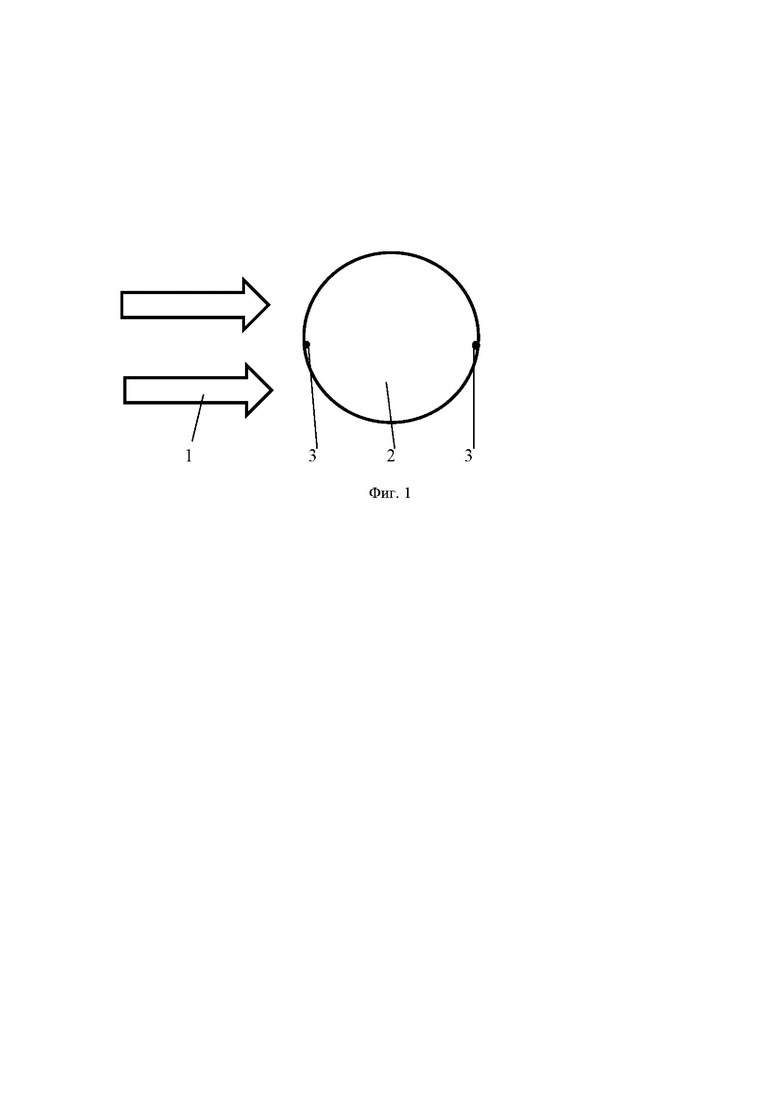
На Фиг. 1 показана схема устройства, реализующее предлагаемый способ.

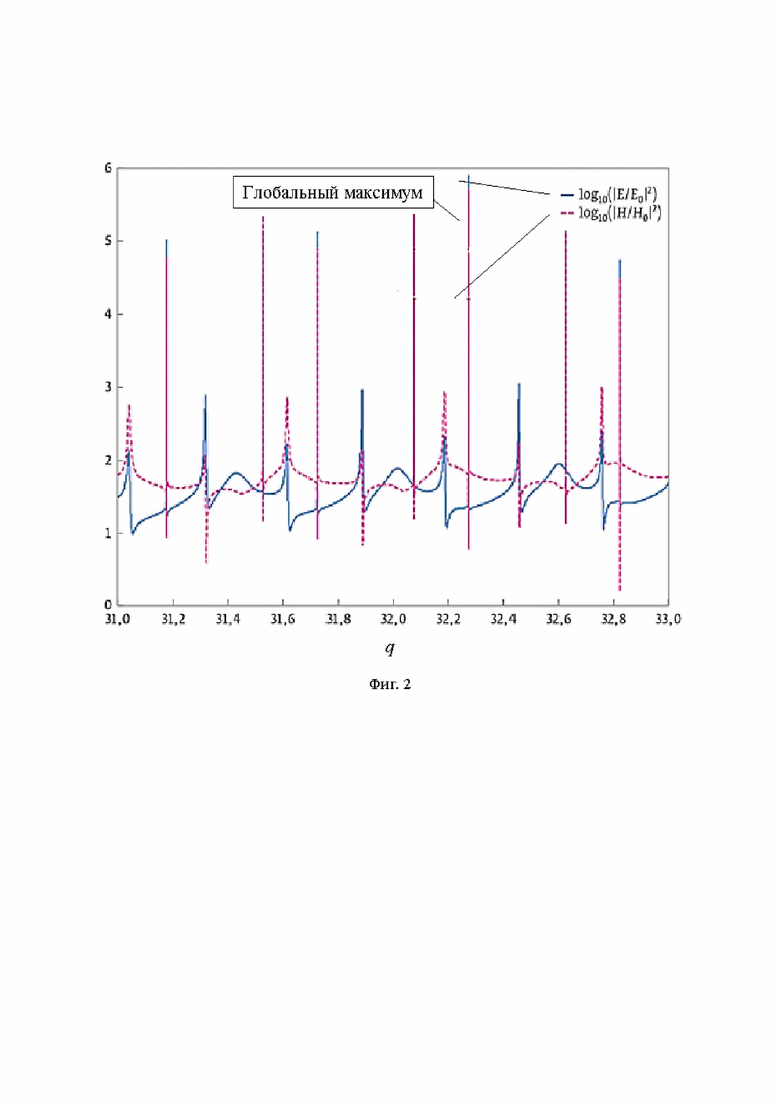
На Фиг. 2 приведен пример зависимости магнитных и электрических полей формируемых на поверхности сферической диэлектрической частицы с показателем преломления 1,9, параметром Ми около 30 и расположенной в воде. Оптический контраст сферы равен 1,43. На рисунке видно чередование преимущественных магнитного и электрического резонансов. Типичный диапазон размерных параметров, необходимый для получения таких резонансов, зависит от показателей преломления частицы и окружающей среды.

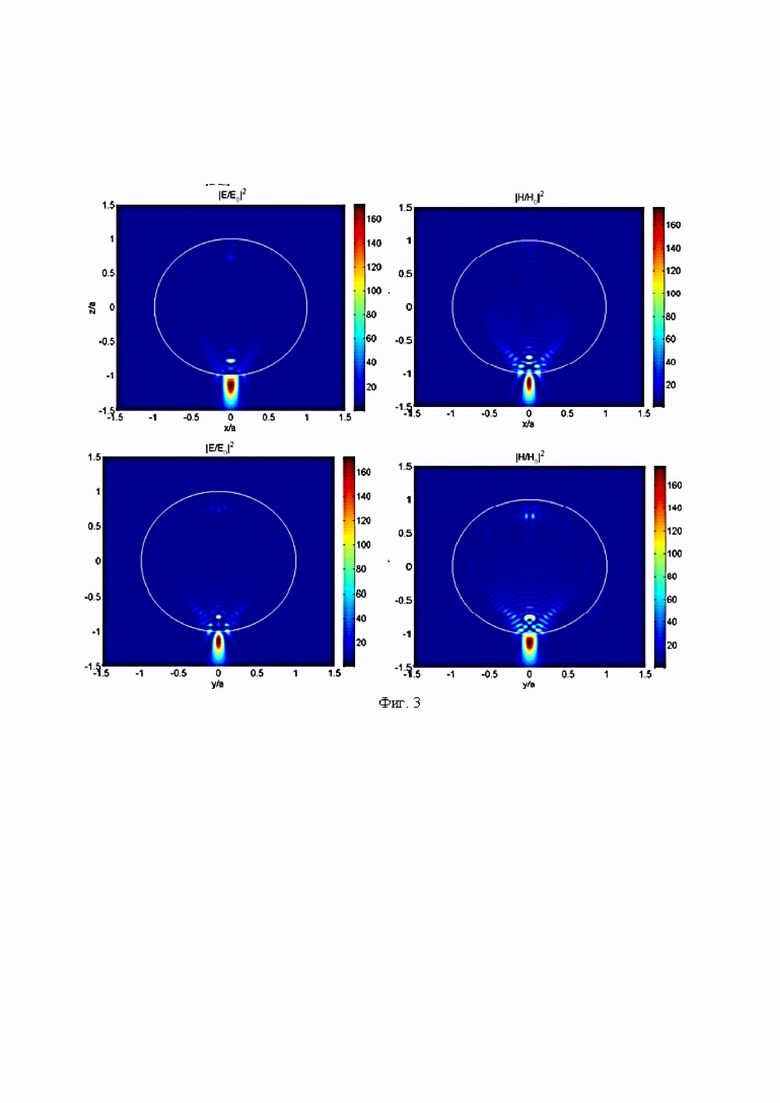
На Фиг. 3 приведены примеры распределения нормируемых на интенсивность освещающей волны с длиной волны 0,532 мкм и относительным показателем преломления материала сферической однородной диэлектрической частицы равным 1,5 с параметром Ми q=30,9 формирование «фотонной струи» для компонент электрического и магнитного полей.

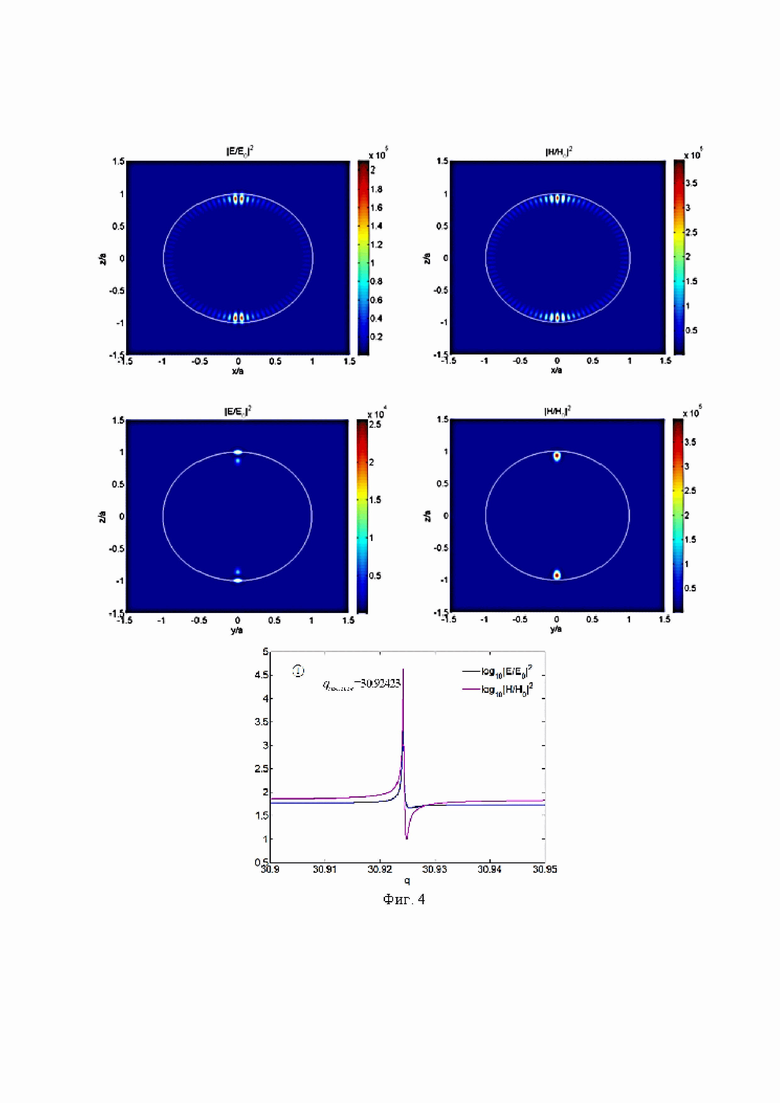
На Фиг. 4 приведены примеры распределения нормируемых на интенсивность освещающей волны с длиной волны 0,532 мкм и относительным показателем преломления материала сферической однородной диэлектрической частицы равным 1,5 с параметром Ми q=30,92423 распределения нормированных на падающую волну интенсивностей магнитного поля в линейной шкале и выделена суперрезонансная мода для этой частицы.

На Фиг. 5 приведены примеры распределения нормируемых на интенсивность освещающей волны с длиной волны 0,532 мкм и относительным показателем преломления материала сферической однородной диэлектрической частицы равным 1,5 с параметром Ми q=30,92423 распределения нормированных на падающую волну интенсивностей магнитного поля в логарифмической шкале.

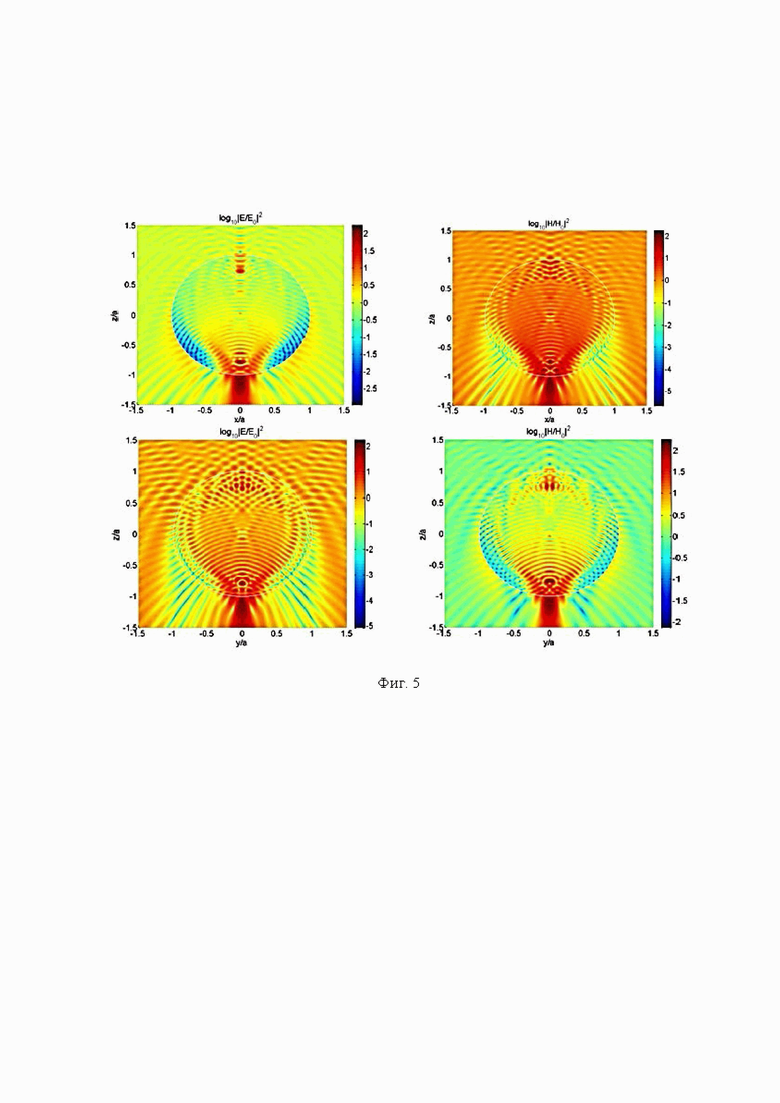
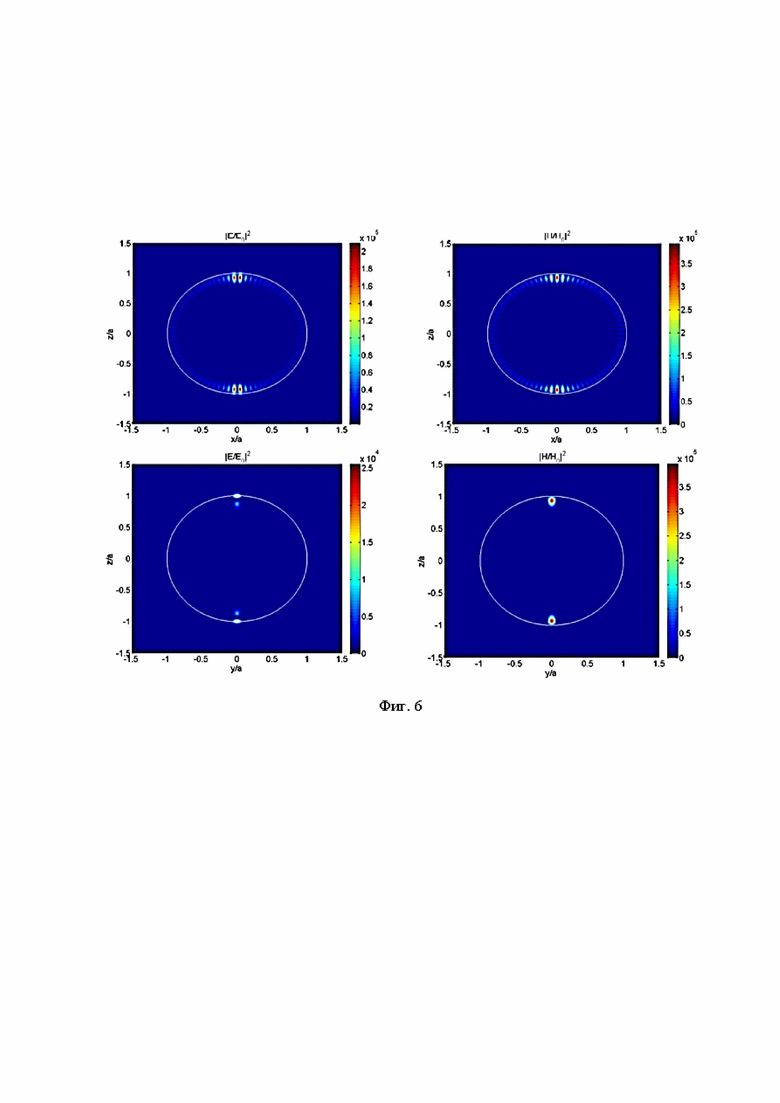
На Фиг. 6 приведены примеры распределения нормируемых на интенсивность освещающей волны с длиной волны 0,532 мкм и относительным показателем преломления материала сферической однородной диэлектрической частицы равным 1,5 с параметром Ми q=30,92423 распределения нормированных на падающую волну интенсивностей магнитного поля в линейной шкале.

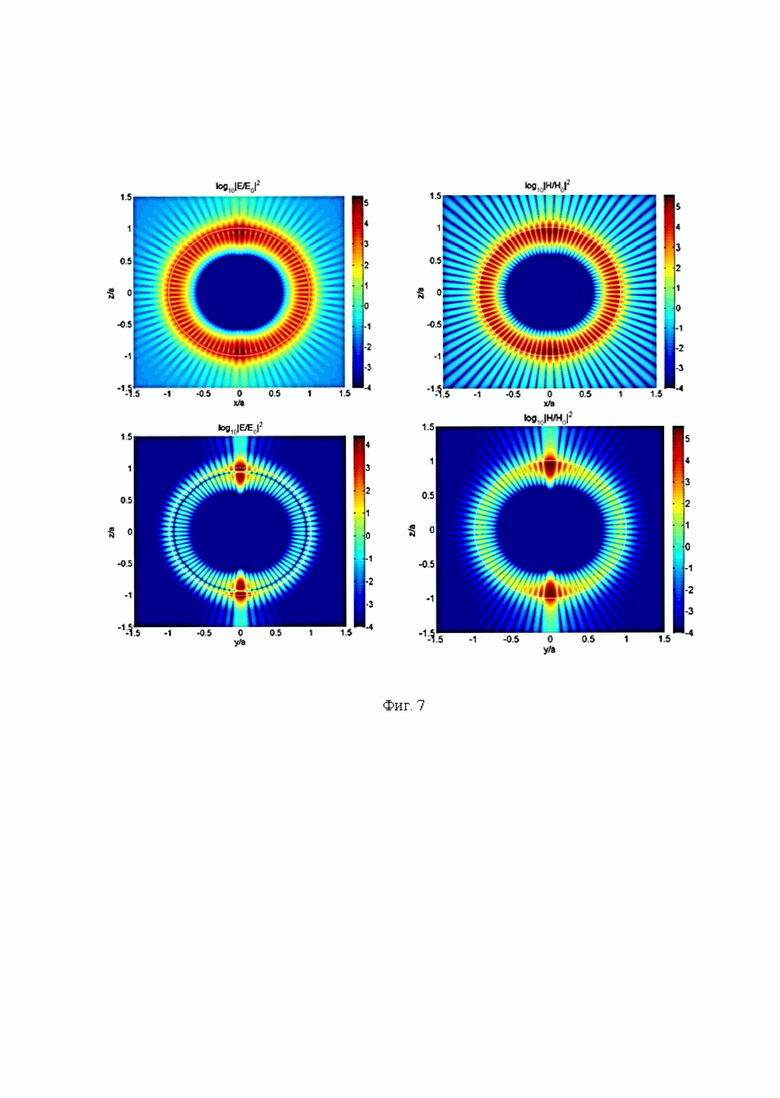
На Фиг. 7 приведены примеры распределения нормируемых на интенсивность освещающей волны с длиной волны 0,532 мкм и относительным показателем преломления материала сферической однородной диэлектрической частицы равным 1,5 с параметром Ми q=30,92423 распределения нормированных на падающую волну интенсивностей магнитного поля в логарифмической шкале. Показана структура резонансной Моды.

Обозначения: 1 - плоская электромагнитная волна; 2 - сферическая диэлектрическая однородная частица; 3 - «горячие» точки, области экстремальных значений электрического и магнитного полей.

Электромагнитное излучение, сформированное источником электромагнитного излучения, например, лазером работающем в видимом, ИК или мазером в Трц или микроволновом диапазонах [Е. Гулевич, Н. Кондратюк, А. Протасеня Перестраиваемые источники лазерного излучения УФ, видимого, ближнего и среднего ИК диапазона // Фотоника 3/2007, с. 30-33; Патенты РФ 2202844, 2351045, 2037916, 2084996; Патент США 4376917], формирует освещающую волну с плоским волновым фронтом 1, которое облучает диэлектрическую однородную сферическую мезоразмерную частицу 2, изготовленную из диэлектрика прозрачного для используемого излучения, например, из стекла, кварца, полимеров.

Сферическая диэлектрическая частица 2 выполнена из материала с относительным показателем преломления не более 2 и с диаметром D не менее 10λ/π, т.е. являясь мезоразмерной частицей. В результате дифракции и интерференции волн на сферической диэлектрической частице 2 формируют области с максимальными значениями электрического и магнитного полей (горячие точки 3). Горячие точки 3 формируются вокруг полюсов диэлектрической сферической частицы 2 вдоль направления падения электромагнитной волны с плоским фронтом 1. В окрестности горячих точек 3 наблюдается высокая степень локализации магнитных и электрических полей, превышающая дифракционный предел, как внутри частицы, так и на ее поверхности. Последнее связано с образованием областей, в которых локальные волновые векторы могут на порядки превышать волновой вектор падающего излучения из-за наличия оптических нановихрей.

Из технической литературы известно, что в отличие от диэлектрических частиц с радиусом существенно меньше длины волны излучения (в которых оптические свойства обычно обусловлены, как правило, первыми тремя резонансами Ми) [A. Kuznetsov, A. Miroshnichenko, M. Brongersma, Y. Kivshar, and B. Luk‘yanchuk, Optically resonant dielectric nanostructures // Science 354, 6314, aag2472 (2016); S. Kruk and Y. Kivshar, Functional metaoptics and nanophotonics governed by Mie resonances // ACS Photonics 4, 2638 (2017); N. Bonod and Y. Kivshar. All-dielectric Mie-resonant metaphotonics // C. R. Physique, 21, (4-5), 425 (2020).], в диэлектрических частицах c размером более длины волны и до характерных размеров, где начинает работать геометрическая оптика (мезоразмерные частицы), наблюдаются резонансы Ми высокого (<5) порядка, что приводит к специфическим оптическим явлениям, обусловленными интерференцией широкого спектра всех внутренних мод с одиночной модой внутреннего резонанса высокого порядка. В свою очередь, эти интерференционные эффекты приводят, в частности, к формированию оптических вихрей внутри частицы [X. Cai, J. Wang, M. Strain, B. Johnson-Morris, J.. Zhu, M. Sorel, J. L. O’Brien, M. Thompson, and S. Yu, Integrated Compact Optical Vortex Beam Emitters // Science 338, 363 (2012)] с характерными размерами существенно меньше дифракционного предела и к формированию двух горячих точек вокруг полюсов сферической частицы вдоль направления распространения излучения. При облучении диэлектрической мезоразмерной частицы 2 электромагнитным излучением 1 в ней могут сформироваться суперрезонансные моды Ми высокого порядка с формированием горячих точек 3 вокруг полюсов сферы 2 вдоль направления распространения излучения.

В диэлектрических частицах с низким показателем преломления (менее 2) [Boris S. Luk’yanchuk, Ramón Paniagua-Domínguez, Igor Minin, Oleg Minin, and Zengbo Wang. Refractive index less than two: photonic nanojets yesterday, today and tomorrow // Optical Materials Express Vol. 7, Issue 6, pp. 1820-1847 (2017) •https://doi.org/10.1364/OME.7.001820.] был обнаружен и наблюдался ряд интересных явлений и применений, например, формирование «фотонных» струй или оптические сингулярности сложной внутренней структуры, которые образуют две горячие точки вблизи полюсов частиц [Yue L., Yan B., Monks J., Dhama R., Jiang C., Minin O.V., Minin I.V. & Wang Z. Full three-dimensional Poynting vector flow analysis of great field-intensity enhancement in specifically sized spherical-particles // Sci. Rep. 2019. Vol.9. P.20224.], формирование мод шепчущей галереи, преодолевающий дифракционный предел, ведущий к получению изображений со сверхвысоким разрешением [Yue L., Yan B., Monks J., Dhama R., Jiang C., Minin O.V., Minin I.V. & Wang Z. Full three-dimensional Poynting vector flow analysis of great field-intensity enhancement in specifically sized spherical-particles // Sci. Rep. 2019. Vol.9. P.20224] и т.д. Открыт т.н. эффект суперрезонанса [Z. B. Wang, B. Luk’yanchuk, L. Yue, B. Yan, J. Monks, R. Dhama, O. V. Minin, I. V. Minin, S. M. Huang, and A. A. Fedyanin, High order Fano resonances and giant magnetic fields in dielectric microspheres // Scientific Reports 9, 20293 (2019); L. Yue, Z. Wang, B. Yan, J. Monks, Y. Joya, R. Dhama, O.V. Minin, and I. V. Minin, Super-Enhancement Focusing of Teflon Spheres // Ann. Phys. (Berlin) 532, 2000373 (2020); Yue L., Yan B, Monks J, Wang Z, Minin I.V., and Minin O.V. Loss impact on super resolution photonic jet produced by a Teflon sphere // Proc. Progress in Electromagnetics Research Symposium, St Petersburg, 22-25 May 2017, Russia. 2017. P.1377.].

С увеличением показателя преломления материала сферы уменьшается номер резонансной моды и растет максимально достижимая интенсивность поля в резонансе. Однако для показателя преломления больше двух локализация поля смещается по направлению от внешней границы сферы к ее центру, что качественно можно объяснить на основе формулы для фокуса сферической линзы.

Определяют на внешнем поверхностном слое внутри диэлектрической сферы 2 в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе из условия локализации суперрезонанса по достижению глобального минимума знаменателей парциальных коэффициентов Ми для сферической диэлектрической однородной частицы.

В соответствии с теорией Ми (часто называемой теорией Лоренца-Ми) [Mie G. Beitrage zur Optik truber Medien speziell kolloidaler Goldlosungen (Сontributions to the optics of diffuse media, especially colloid metal solutions) // Ann. Physik. 1908; 25, 377-445; Bohren C. and Huffman D. Absorption and Scattering of Light by Small Particles (WILEY-VCH Verlag). 1998.] рассеяние плоской, линейно поляризованной электромагнитной волны на однородной сферической частице представляется в виде бесконечного ряда парциальных волн, каждая из которых представляется в виде суммы электрической и магнитной моды. В сферических координатах 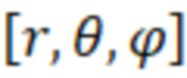компоненты поля плоской волны с линейной поляризацией могут быть записаны как [Bohren C. and Huffman D. Absorption and Scattering of Light by Small Particles. WILEY-VCH Verlag. N.Y. 1998. 530 p.]:

$$E_r=e^{i{k}_{m}r\cos \theta }\sin \theta \cos \varphi ,$$

$$H_r=\sqrt{{\epsilon }_m}{e}^{i{k}_{m}r\cos \theta }\sin \theta \sin \varphi$$

$$E_{\theta }=e^{i{k}_{m}r\cos \theta }\cos \theta \cos \phi ,$$

$$H_{\theta }=\sqrt{{\epsilon }_m}{e}^{i{k}_{m}r\cos \theta }\cos \theta \sin \varphi$$

$$$$ $$E_{\varphi }=-e^{i{k}_{m}r\cos \theta }\sin \varphi ,$$

$$H_{\varphi }=-\sqrt{{\epsilon }_m}{e}^{i{k}_{m}r\cos \theta }\sin \varphi$$ .

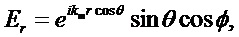
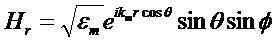
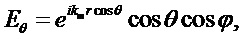
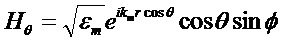
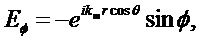
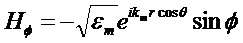
Внутреннее поле немагнитной сферы определяется из выражений:

$$E_r^{(p)}=\frac{\cos \phi }{{(k_{p}r)}^2}{\displaystyle \sum _{n=1}^{\infty }n(n+1)}{}^{e}A{}_n{\Psi }_n(k_{p}r)P_n^{(l)}(\cos \theta )$$ ,

$$E_{\theta }^{(p)}=\frac{\cos \phi }{k_{p}r}{\displaystyle \sum _{n=1}^{\infty }\left[{}^{e}A{}_n{\Psi }_n^{/}(k_{p}r)P_n^{{(l)}^{/}}(\cos \theta )\sin \theta -i{}^{m}A{}_n{\Psi }_n(k_{p}r)\frac{P_n^{(l)}(\cos \theta )}{\sin \theta }\right]}$$ ,

$$E_{\varphi }^{(p)}=\frac{\sin \varphi }{k_{p}r}{\displaystyle \sum _{n=1}^{\infty }\left[{}^{e}A{}_n{\Psi }_n^{/}(k_{p}r)\frac{P_n^{(l)}(\cos \theta )}{\sin \theta }-i{}^{m}A{}_n{\Psi }_n(k_{p}r)P_n^{{(l)}^{/}}(\cos \theta )\sin \theta \right]}$$ ,

$$H_r^{(p)}=\frac{\sqrt{{\epsilon }_m}\sin \phi }{{(k_{p}r)}^2}{\displaystyle \sum _{n=1}^{\infty }n(n+1)}{}^{m}A{}_n{\Psi }_n(k_{p}r)P_n^{(l)}(\cos \theta )$$ ,

$$H_{\theta }^{(p)}=i\frac{\sin \varphi }{k_{0}r}{\displaystyle \sum _{n=1}^{\infty }\left[{}^{e}A{}_n{\Psi }_n^{}(k_{p}r)\frac{P_n^{(l)}(\cos \theta )}{\sin \theta }+i{}^{m}A{}_n{\Psi }_n^{/}{}_{}(k_{p}r)P_n^{{(l)}^{/}}(\cos \theta )\sin \theta \right]}$$ ,

$$H_{\varphi }^{(p)}=i\frac{\cos \varphi }{k_{0}r}{\displaystyle \sum _{n=1}^{\infty }\left[{}^{e}A{}_n{\Psi }_n^{}(k_{p}r)P_n^{{(l)}^{/}}(\cos \theta )\sin \theta +i{}^{m}A{}_n{\Psi }_n^{/}{}_{}(k_{p}r)\frac{P_n^{(l)}(\cos \theta )}{\sin \theta }\right]}$$ ,

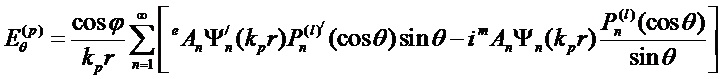
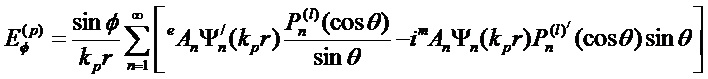
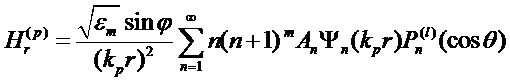
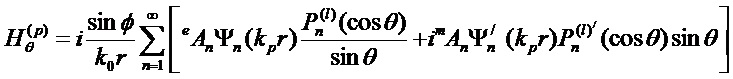
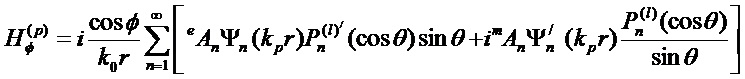
Соответствующие эффективности внешнего и внутреннего рассеяния математически связаны с выражениями для двух пар комплексных парциальных коэффициентов рассеяния (a_l, b_l) и (c_l, d_l)_, соответственно, которые, в свою очередь, выражаются через комбинации сферических функций Неймана, Бесселя и их производных. Коэффициенты рассеяния для вычисления полей могут быть представлены в виде:

$${}^{e}B{}_n=i^{n+1}\frac{2n+1}{n(n+1)}{a}_{n,}$$ ,$${}^{m}B{}_n=i^{n+1}\frac{2n+1}{n(n+1)}{b}_{n,}$$$${}^{e}A{}_n=i^{n+1}\frac{2n+1}{n(n+1)}{c}_{n,}$$$${}^{m}A{}_n=i^{n+1}\frac{2n+1}{n(n+1)}{d}_n$$, (1)

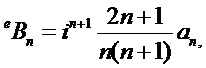
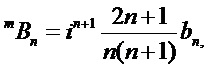
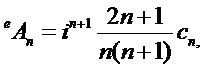
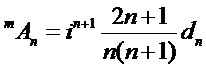
где [Seoungjun Lee, Lin Li and Zengbo Wang. Optical resonances in microsphere photonic nanojets // Journal of Optics, 16 (2014) 015704 (8pp)]:

$$a_n=\frac{y{{\psi }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)-x{\psi }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)}{y{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)-x{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)}$$ ,

$$b_n=\frac{y{\psi }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)-x{\psi }_n\left(y\right){{\psi }^{\prime }}_n\left(x\right)}{y{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)-x{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)}$$ ,

$$c_n=\frac{y{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(x\right)-y{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(x\right)}{y{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)-x{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)}$$ ,

$$d_n=\frac{y{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(x\right)-y{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(x\right)}{y{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)-x{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)}$$ . (2)

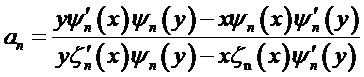
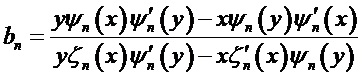
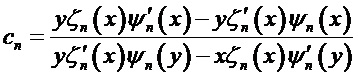
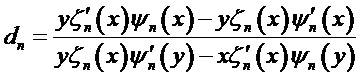
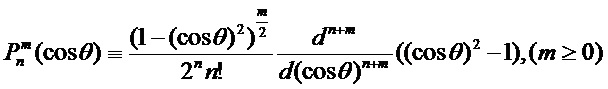
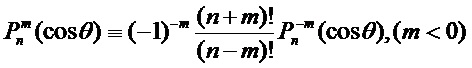
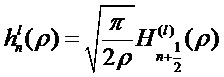
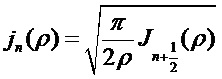
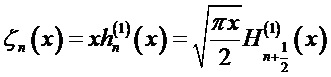
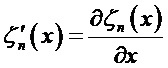
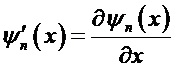
Здесь: x=k_ma и y=k_pa (индексы m и p соответствуют среде и частице, соответственно, k, a - волновое число и радиус сферической частицы), $$P_n^m(\cos \theta )\equiv \frac{{(1-{(\cos \theta )}^2)}^{\frac{m}{2}}}{2^{n}n!}\frac{d^{n+m}}{d{(\cos \theta )}^{n+m}}({(\cos \theta )}^2-1),(m\ge 0)$$, $$P_n^m(\cos \theta )\equiv {(-1)}^{-m}\frac{(n+m)!}{(n-m)!}{P}_n^{-m}(\cos \theta ),(m<0)$$ - функции Лаггера,

$$h_n^l(\rho )=\sqrt{\frac{\pi }{2\rho }}{H}_{n+\frac{1}{2}}^{(l)}(\rho )$$ - сферическая функция Ханкеля и

$$$$ $$j_n(\rho )=\sqrt{\frac{\pi }{2\rho }{J}_{n+\frac{1}{2}}(\rho )}$$ - сферическая функция Бесселя, $${\zeta }_n\left(x\right)=x{h}_n^{\left(1\right)}\left(x\right)=\sqrt{\frac{\pi x}{2}}{H}_{n+\frac{1}{2}}^{\left(1\right)}\left(x\right)$$, $${\psi }_n\left(x\right)=\rho j_n\left(x\right)=\sqrt{\frac{\pi x}{2}}{J}_{n+\frac{1}{2}}\left(x\right)$$, а $${{\zeta }^{\prime }}_n\left(x\right)=\frac{\partial {\zeta }_n\left(x\right)}{\partial x}$$, $${{\psi }^{\prime }}_n\left(x\right)=\frac{\partial {\psi }_n\left(x\right)}{\partial x}$$ - производные соответствующих функций.

В теории Ми знаменатели амплитуд (a_l, c_l) и (b_l, d_l) одинаковы, т.е. положения этих резонансов близки, однако числители коэффициентов (c_l, d_l) никогда не стремятся к нулю. В результате значения амплитуд $$c_l$$ и $$d_l$$ не ограничиваются единицей, как амплитуды $$a_l$$ и $$b_l$$ в (2) [Wang Z., Luk’yanchuk B., Yue L., Yan B., Monks J., Dhama R., Minin O.V., Minin I.V., Huang S., Fedyanin A. High order Fano resonances and giant magnetic fields in dielectric microspheres // Sci Rep. 2019. V.9. P. 20293.], а увеличиваются с ростом значений параметра размера Ми и показателя преломления. Полная эффективность внутреннего рассеяния может быть представлена суммой частичных эффективностей внутреннего рассеяния:

$${}^{}Q{}_{\mathrm{int}}={\displaystyle \sum _{n=1}^{\infty }\left({}^{e}F{}_n+{}^{m}F{}_n\right)}$$ , где $${}^{e}F{}_n=\frac{2(2n+1)}{y^2}{\left|c_n\right|}^2$$, $${}^{m}F{}_n=\frac{2(2n+1)}{y^2}{\left|d_n\right|}^2$$. (3)

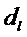
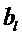
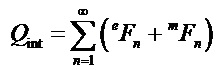
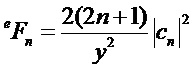
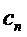
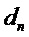
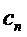
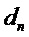
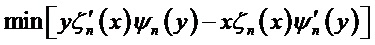
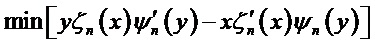
Анализ амплитуд коэффициентов рассеяния Ми (c_n, d_n) при суперрезонансе показывает, что основным фактором, ответственным за это явление, является сильное рассеяние одиночной моды высокого порядка во внутреннем электрическом или магнитном поле частицы. При резонансе (ТЕ или ТМ) модуль соответствующего парциального коэффициента ($$c_n$$ или $$d_n$$) резко возрастает. Например, из выражения для парциальных коэффициентов $$c_n$$ и $$d_n$$ (2) для достижения резонанса можно записать необходимые условия:

$$\min \left[y{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)-x{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)\right]$$ , (4)

$$\min \left[y{\zeta }_n\left(x\right){{\psi }^{\prime }}_n\left(y\right)-x{{\zeta }^{\prime }}_n\left(x\right){\psi }_n\left(y\right)\right]$$ .

Заметим, что для недиссипативных сфер (без потерь на поглощение) мнимая часть парциальных коэффициентов при резонансе равна нулю. Как следует из приведенных соотношений, четыре переменные - параметр размера Ми, номер резонансной моды и показатели преломления среды и материала сферы (через параметр Ми y (1)) являются величинами, правильный выбор которых позволит минимизировать условия (4). Чем точнее будут минимизированы значения (4) (для ТЕ и ТМ волн в зависимости от необходимости), тем точнее будет локализован соответствующий резонанс.

Глобальный минимум - это точка, в которой функция достигает наименьшего значения на всем допустимом пространстве значений и, следовательно, определяет параметры суперрезонанса из всех возможных резонансов в диэлектрической сфере при облучении ее электромагнитной волной с плоским фронтом. Определяя глобальный минимум функции (4) для соответствующих параметров Ми, показателя преломления и длины волны облучающей сферу позволяет определить условие наступления суперрезонанса, определить необходимую резонансную моду. Определить глобальный минимум функции возможно различными способами, например, аналитически или, например, применяя известные методы [А. И. Косолап. Поиск глобального минимума методом точной квадратичной регуляризации // Scientific Journal «ScienceRise» №5/3(5)2014; Патент РФ 2336553; заявка на изобретение РФ 2005114911А].

Чем точнее будут минимизированы значения (4) (для ТЕ и ТМ резонансов в зависимости от необходимости), тем точнее будет локализован соответствующий резонанс. Зависимость ширины и интенсивности резонансной линии от точности параметра размера Ми для электрического поля ранее была продемонстрирована в [P. Chyiek, J. D. Pendleton, and R. G. Pinnick. Internal and near-surface scattered field of a spherical particle at resonant conditions. Appl. Opt., 24(23), 3940 (1985)]. Соответственно, чем точнее локализован резонанс, тем меньше будет ширина резонансной линии и выше ее интенсивность. Отметим, что с ростом показателя преломления материала сферы уменьшается номер резонансной моды и растет максимально достижимая интенсивность поля в резонансе. Однако для показателя преломления больше двух локализация поля смещается по направлению от внешней границы сферы к ее центру, что качественно можно объяснить на основе формулы для фокуса сферической линзы. В свою очередь, увеличение размера сфер приводит к возбуждению более выраженных сверхрезонансных мод с более сильной локализацией поля [I. V. Minin, O. V. Minin, Z. Song. High-Order Fano Resonance in a Mesoscale Dielectric Sphere with a Low Refractive Index. JETP Letters, 2022, Vol. 116, No. 3, pp. 144-148.].

Изготовление стеклянных шариков возможно по способу предложенному, например, в патенте РФ 2081858. Известен метод вынужденного капиллярного распада струй, который может быть использован для изготовления диэлектрических микрошариков [Патент РФ 2315061, патент US 5380496, В. В. Блаженков, А. Ф. Гиневский, В. А. Григорьев, А. С. Дмитриев, О генерации упорядоченных потоков монодисперсных капель методом вынужденного капиллярного распада струй // Докл. АН СССР, 313:6 (1990), 1412-1417]. Например, стеклошарики (микрошарики из стекла) с показателем преломления 1,56-1,62 выпускаются промышленностью диаметром от единиц до 500 мкм. В оптическом диапазоне приемлемыми материалами с небольшой диссипацией (коэффициент поглощения на уровне 10^-7) является боросиликатное стекло [O. V. Minin, I. V. Minin, Z. Song. Superresonance in Micron Borosilicate Glass Sphere in Optical Range. // Optoelectron. Instrument. Proc. 2022, Vol. 58, No. 5, pp. 514-519.] и полиэстер, облученный ионами H+ [Z. Kaňuchová, G.A. Baratta, M. Gorozzo, G. Strazzulla. Space weathering of asteroidal surfaces. Influence on the UV-Vis spectra. // Astronomy & Astrophysics. - 2010. - Vol. 517. - A60.].

Пример. Была изготовлена сферическая диэлектрическая частица из прозрачного материала для используемого излучения с показателем преломления m=1,33 и диаметром d=12 мкм, которая освещалась циркулярно-поляризованной электромагнитной волной с плоским фронтом.

Определяют на внешнем поверхностном слое внутри диэлектрической сферы в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе.

Выражение для внутреннего Е и рассеянного Е^sc электрических полей при падении на однородную сферу с радиусом а₀ и комплексным показателем преломления m_a=n_a-ik_a плоской циркулярно-поляризованной электромагнитной волны с вектором электрического поля Eⁱ(z,t)=E₀[e_x+ie_y]e^iw0t-ik0t (начало координат помещено в центр частицы) в сферических координатах имеют вид [Фемптосекундная атмосферная оптика / Д.В. Алексимов и др.; Рос. Акад. Наук, Сиб. Отд-ние, Ин-т лазерной физики, ин-т оптики атмосферы. - Новосибирск: Изд-во СО РАН, 2010. - 238 с. ]:

$$\begin{array}{l}E(r,\theta ,\phi ;t)=e^{iwt}\frac{E_0}{k_{a}r}{\displaystyle \sum _{n=1}^{\infty }{R}_m}\left[c_n(m{x}_a)Y_{nl}(\theta ,\phi ){\psi }_n(k_{a}r)+\frac{1}{k_a}{d}_n(m{x}_a)\nabla \times \left[Y_{nl}(\theta ,\phi ){\psi }_n(k_{a}r)\right]\right],\\ \end{array}$$

$$\begin{array}{l}{E}^{sc}(r,\theta ,\phi ;t)=e^{iwt}\frac{E_0}{k_{a}r}{\displaystyle \sum _{n=1}^{\infty }{R}_m}\left[a_n(m_0{x}_a)Y_{nl}(\theta ,\phi ){\xi }_n(k_{a}r)+\frac{1}{k_a}{b}_n(m_0{x}_a)\nabla \times \left[Y_{nl}(\theta ,\phi ){\xi }_n(k_{a}r)\right]\right].\\ \end{array}$$

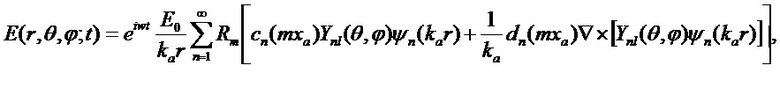
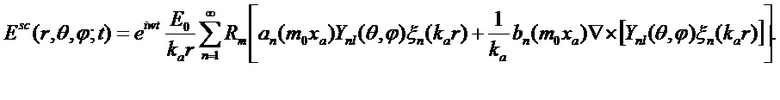
Амплитуды парциальных гармоник (коэффициенты Ми) математически связаны с выражениями для двух пар комплексных парциальных коэффициентов рассеяния (a_l, b_l) и (c_l, d_l)_, соответственно, которые, в свою очередь, выражаются через комбинации сферических функций Неймана, Бесселя и их производных и определяются выражениями:

$$a_n=\frac{{\psi }_n^{/}(x_a){\psi }_n(m{x}_a)-m{\psi }_n(x_a){\psi }_n^{/}(m{x}_a)}{{\xi }_n^{/}(x_a){\psi }_n(m{x}_n)-m{\xi }_n(x_a){\psi }_n^{/}(m{x}_a)}$$ , $$b_n=\frac{{\psi }_n^{}(x_a){\psi }_n^{/}{}_{}(m{x}_a)-m{\psi }_n^{/}{}_{}(x_a){\psi }_n^{}(m{x}_a)}{{\xi }_n^{}(x_a){\psi }_n^{/}{}_{}(m{x}_a)-m{\xi }_n^{/}(x_a){\psi }_n(m{x}_a)},$$

$$c_n=\frac{-m}{{\xi }_n^{/}(x_a){\psi }_n^{}{}_{}(m{x}_a)-m{\xi }_n^{}(x_a){\psi }_n^{/}(m{x}_a)}$$ , $$d_n=\frac{m}{{\xi }_n^{}(x_a){\psi }_n^{/}{}_{}(m{x}_a)-m{\xi }_n^{/}(x_a){\psi }_n^{}(m{x}_a)}$$.

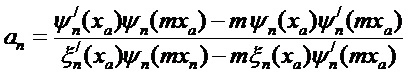
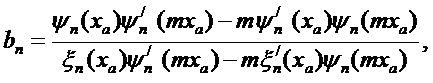
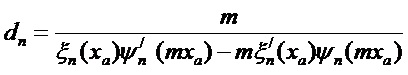
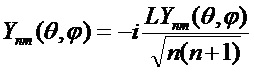
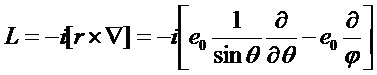
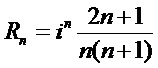
Здесь: k_a =m₀k₀ - волновое число внутри частицы; m=m_a/m₀ относительный показатель преломления (m₀ - показатель преломления окружающей среды); r,θ,ϕ - сферические координаты; ψ_n, ξ_n - сферические функции Рикатти-Бесселя; $$Y_{nm}(\theta ,\phi )=-i\frac{L{Y}_{nm}(\theta ,\phi )}{\sqrt{n(n+1)}}$$ - векторные сферические функции, Y_nm(θ,ϕ) - сферические функции, $$L=-i[r\times \nabla ]=-i\left[e_0\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }-e_0\frac{\partial }{\phi }\right]$$ - оператор углового момента; E₀ - амплитуда электрического поля падающей на частицу электромагнитной волны; $$R_n=i^n\frac{2n+1}{n(n+1)}$$. Штрихи означают производные по аргументу, указанному под знаком функции.

Из выражений для коэффициентов c_n и d_n следует, что амплитуда этих коэффициентов будет максимальной при минимуме знаменателей.

Из выражения для парциальных коэффициентов c_n и d_n следует, что резонансные значения параметра дифракции x_nj, могут быть определены из следующего условия для ТЕ_n резонансов или ТМ_n резонансов соответственно:

$$\min =\left[{\xi }_n^{/}(x_a){\psi }_n(m{x}_a)-m{\xi }_n(x_a){\psi }_n^{/}(m{x}_a)\right]$$

и

$$\min =\left[{\xi }_n^{}(x_a){\psi }_n^{/}(m{x}_a)-m{\xi }_n^{/}(x_a){\psi }_n^{}(m{x}_a)\right]$$ .

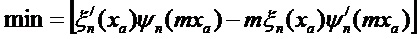
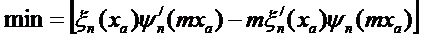
Из свойств функции Бесселя следует, что число корней этих уравнений для каждого конкретного значения индекса n бесконечно и, следовательно, бесконечен и поэтому ищется глобальный минимум знаменателей соответствуюих парциальных коэффициентов.

Расчет дает для сферической частицы на длине волны около λ = 0,534 мкм резонансная мода имеет высокий номер 86 с параметром размера πd/λ ~70,6. При этом возможна генерация электрического и магнитного полей с интенсивностями в полюсах сферы около 10⁶-10⁷.

Таким образом, в предлагаемом способе определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице из материала с относительным показателем преломления не более 2, с диаметром D не менее 10λ/π и определения на внешнем поверхностном слое внутри диэлектрической сферы в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе возможно быстрое определение резонансной моды в зависимости от параметра Ми и относительного показателя преломления материала диэлектрической частицы.

Изобретение относится к способам определения резонансной моды Ми высокого порядка. Способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице, заключается в изготовлении сферической диэлектрической частицы из прозрачного материала для используемого излучения, облучении диэлектрической частицы лазерным излучением с плоским волновым фронтом, определения суперрезонанса мод Ми высокого порядка по уровню максимального сигнала при различных длинах волн, при этом сферическую диэлектрическую частицу выполняют из материала с относительным показателем преломления не более 2, с диаметром D не менее 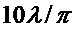и определяют на внешнем поверхностном слое внутри диэлектрической сферы в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе из условия локализации суперрезонанса по достижению глобального минимума модулей знаменателей парциальных коэффициентов Ми (c_l,d_l) для сферической диэлектрической однородной частицы. Технический результат - быстрое определение резонансной моды Ми высокого порядка при суперрезонансе в сферической мезоразмерной диэлектрической однородной частице. 7 ил.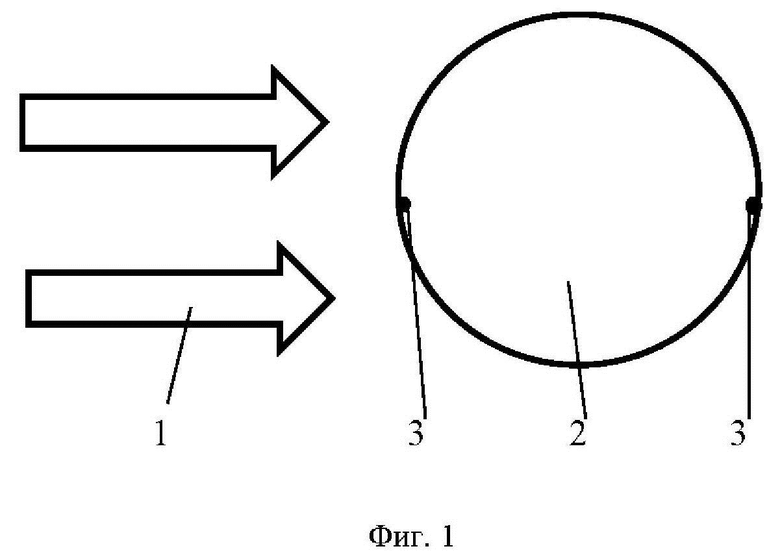

Способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице, заключающийся в изготовлении сферической диэлектрической частицы из прозрачного материала для используемого излучения, облучении диэлектрической частицы лазерным излучением, формировании освещающей волны с плоским волновым фронтом, определения суперрезонанса мод Ми высокого порядка по уровню максимального сигнала при различных длинах волн освещающего излучения, отличается тем, что сферическую диэлектрическую частицу выполняют из материала с относительным показателем преломления не более 2, с диаметром D не менее 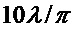и определяют на внешнем поверхностном слое внутри диэлектрической сферы в области полюсов сферы вдоль направления распространения излучения моды Ми высокого порядка при суперрезонансе из условия локализации суперрезонанса по достижению глобального минимума модулей знаменателей парциальных коэффициентов Ми (c_l,d_l) для сферической диэлектрической однородной частицы.