Предлагаемое техническое решение относится к области строительства и может быть использовано в качестве стержневых и балочных элементов при разработке несущих конструкций зданий и сооружений различного назначения. В частном случае это могут быть поясные и решетчатые элементы ферм покрытий, балки перекрытий, стеновые ригели или кровельные прогоны.
Известным техническим решением является прокатной зетовый равнополочный профиль со стенкой, наклонной к параллельным полкам под тупым углом [Мисник Г.И., Торицын И.В. Зетовый профиль // Патент №2135308. 27.08.1999]. Очертания такого профиля рациональны для его прокатки в горячедеформированном состоянии, а также использования в машиностроении. Для строительства применим сортовой гнутый профиль проката. По определению он образован стенкой и двумя полками, расположенными по разные стороны от стенки под прямым углом, и в зависимости от размеров полок может быть равнополочным или неравнополочным [ГОСТ 14350-80. Профили проката гнутые. Термины и определения. М.: Издательство стандартов, 1980. С. 16].
Другое известное решение (принятое за аналог) представляет собой зетовый (Z-образный) равнополочный профиль со стенкой, наклонной к параллельным полкам под острым углом. Он реализован в прогонной конструкции крутоуклонной кровли [Юрьев А.Г., Зинькова В.А. Нелинейные задачи косого изгиба // Вестник БГТУ им В.Г. Шухова. 2023, №11. С. 37-45]. Недостаток технического решения из аналога заключается в повышенных толщинах его стенки и полок.
Наиболее близким к предлагаемому (принятым в качестве прототипа) является техническое решение также в виде зетового (Z-образного) равнополочного профиля со стенкой, наклонной к параллельным полкам под острым углом. Однако в отличие от аналога тонкостенность прототипа позволяет рассчитывать его по средней линии сечения [Волков В.П., Волкова О.В. Определение геометрических характеристик тонкостенного Z-образного стержня (Электронный ресурс) // Моделирование и механика конструкций. 2015. №1. URL: http://mechanics.pguas.m/Plone/nomera-zhurnala/nol/stroitelnaya-mechanika/opredelenie-geometricheskih-harakteristik4onkostermogo-sterzhnya/at_downloao7file]. Этот профиль с целью расширения области его рационального применения можно дополнительно проработать, оптимизируя основные геометрические (статические) характеристики. При этом для решения оптимизационных задач целесообразно использовать критерии максимальной жесткости (или минимальной гибкости), максимальной прочности на изгиб, а также равной устойчивости, одинаковой из силовой плоскости несущей конструкции и в таковой плоскости.
Техническим результатом предлагаемого решения является расширение области его рационального применения.
Указанный результат достигается тем, что в зетовом (Z-образном) равнополочном профиле со стенкой, наклонной к параллельным полкам под острым углом, отношение габаритов ширины и высоты по средней линии сечения составляет 1/6,031 и 2,332/1 при равной устойчивости из плоскости и в плоскости конструкции, 1/2,071 при максимальной жесткости (минимальной гибкости), 1/4,008 при максимальной прочности.
Предлагаемый зетовый (Z-образный) равнополочный профиль с наклонной стенкой обладает достаточно универсальным техническим решением, с реализацией которого его равноустойчивая модификация эффективна в ферменных конструкциях, максимально прочная модификация - в балочных конструкциях, а максимально жесткая (минимально гибкая) - и в ферменных, и в балочных. Такое решение способствует расширению области его рационального применения.
Предлагаемое техническое решение поясняется графическими материалами, где на
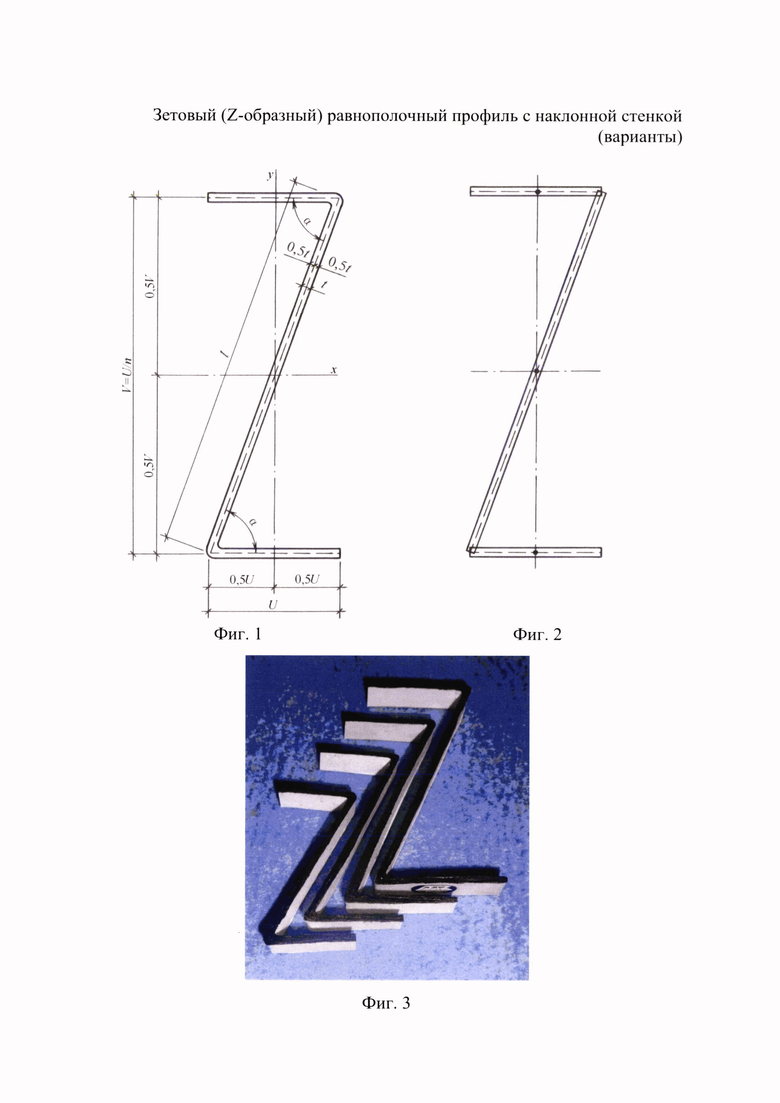
- фиг. 1 показан зетовый (Z-образный) равнополочный профиль с наклонной стенкой (пунктиром обозначена средняя линия тонкостенного сечения);
- фиг. 2 - расчетная схема поперечного сечения зетового профиля;
- фиг. 3 - снимок среза разнокалиберных зетовых профилей;
- фиг. 4 - графики изменений основных расчетных параметров зетового профиля в зависимости от роста отношения габаритов его ширины и высоты.
Для вывода приведенных отношений и количественной оценки ресурсов несущей способности зетового профиля целесообразно рассчитать площадь А, а также моменты инерции его сечения IX и IY относительно главных центральных осей, где ось ординат проходит через середины обеих полок профиля. Здесь очевидно, что сечение такого профиля можно считать составной фигурой, включающей пару горизонтальных прямоугольников размерами txU, удаленных друг от друга по вертикали на высоту V и соединенных наклонным прямоугольником размерами t×l. Расчетные выкладки при этом допустимо выполнять по средней линии тонкостенного сечения без учета его угловых закруглений и без учета численных величин, содержащих значения толщины, возведенной во вторую и третью степень (t2, t3) [Марутян А.С. Оптимизация конструкций из трубчатых (гнутосварных) профилей квадратных (прямоугольных) и ромбических сечений // Строительная механика и расчет сооружений, 2016, №1. С. 30-38].
С учетом принятых расчетно-теоретических предпосылок значения геометрических (статических) характеристик поперечного сечения зетового профиля можно определять по формулам:
- площадь
A=tU(2+(1+1/n)1/2);
- момент инерции относительно оси абсцисс
Ix,=tU3, (0,5/n2+(1+1/n)1/2/12);
- момент инерции относительно оси ординат Iy=tU3(1/6+(1+1/n)1/2/(12n2)), где п - отношение габаритов ширины и высоты по средней линии тонкостенного сечения, n=U/V;
I - длина наклонной стенки,
l=(U+V)1/2=U(1+1/n)1/2; а - угол наклона стенки к полкам,
sin2α=1/(n2+1), cos2α=n2/(n2+1), sin2α+cos2α=1. Приведенные формулы целесообразно протестировать с использованием расчетных параметров зетового профиля из аналога: b=11,2 см - ширина основной части полки профиля; h=20 см - высота сечения по его наружной линии; t=2,5 см - толщина профиля; t1=3,3 см - горизонтальная проекция полутолщины профиля; А=122 см2 - площадь сечения; Ix=6667 см4 и Iy=4282 см4 - осевые моменты инерции сечения.
Тестовый расчет можно представить в следующем виде:
U=b+t1=11,2+3,3=14,5 см;
V=h-t=20-2,5=17,5 см;
n=U/V;=14,5/17,5=0,8285714=l/l,2068965;
A=tU(2+(1+1/n)1/2)=2,5×14,5(2+(1+1/0,8285714)1/2)=129,32 см2 (106,0%);
Ix=tU3(0,5/n2+(1+1/n)1/2/12)=
=2,5×14,53(0,5/0,82857142+(1+1/0,8285714)1/2/12)=
=6546,3 см4 (98,19%); Iy=tU3(l/6+(1+1/n) 1/2/(12n2))+At12=
=2,5×14,53(1/6+(1+1/0,8285714)1/2/(12×0,82857142))+129,32×3,32=4128,5 см4 (96,42%), где за эталонные (100-процентные) показатели приняты соответствующие параметры из технического решения аналога.
Если учесть, что зетовый профиль из аналога является толстостенным, то полученные результаты теста можно признать достаточно корректными для дальнейшего использования расчетных формул в решении оптимизационных задач.
Предлагаемый зетовый профиль равноустойчив относительно силовой плоскости несущей конструкции при нулевой разнице значений осевых моментов его сечения, то есть Ix-Iy=0.
Тогда подставив выражения осевых моментов инерции, можно получить уравнение шестой степени
1/n6-37/n4+23/n2-3=0 с корнями
1/n1=-6,0307443; 1/n2=-0,6667773; 1/n3=-0,4307338; 1/n4=0,4307337; 1/n5=0,6667773; 1/n6=6,0307442. Из полученных шести корней практический интерес вызывают, прикладное значение имеют четвертый и шестой, а пятый корень является лишним, поскольку при избавлении от квадратных радикалов обе части уравнения возведены во вторую степень.
При 1/n6=6,0307442 предлагаемый зетовый профиль равноустойчив относительно силовой плоскости несущей конструкции и имеет следующие расчетные параметры:
n=1/6,0307442=0,1658170≈1/6,031;
A=8,1130904tU; U=0,1232575A/t; V=0,7433344A/t;
IX=18,694361tU3=0,0350066A3/t2; Iy=18,694360tU3=0,0350066A3/t2;
Ix/Iy=1,0;
Wx=6,1996862tU2=0,0941881A2/t; Wy=37,38872tU2=0,5680248A2/t;
ix=1,5179663U=0,1871007А/t; iy=1,5179663U=0,1871007A/t;
ix/iy=1,0.
При 1/n4=0,4307337 предлагаемый зетовый профиль также равноустойчив относительно силовой плоскости несущей конструкции и имеет следующие расчетные параметры:
n=1/0,4307337=2,321620=2,322/1;
A=3,0890189tU; U=0,3237273A/t; V=0,13994402A/t;
Ix=0,1835172tU3=0,0062260A3/t2; Iy=0,1835056tU3=0,0062256A3/t2;
Ix/Iy=1,0000632≈1,0;
Wx=0,8521144tU2=0,0893010A2/t; Wy=0,3670112tU2=0,0384625A2/t;
ix=0,2437406U=0,0789054A/t; iy=0,2437328U=0,0789029A/t; ix/iy=1,000032≈1,0.
Чтобы найти экстремальное значение жесткостной характеристики, коей является момент инерции сечения относительно оси абсцисс Ix=Ix,max, его формулу необходимо продифференцировать по переменной п и, приравняв к нулю производную (dIx/dn=0), получить разрешающее уравнение. Поскольку степень этого уравнения превысила десятую степень полиномиального уравнения, экстремум определен по методике последовательных приближений.
Жесткость предлагаемого зетового профиля в силовой плоскости несущей конструкции максимальна, а гибкость соответственно минимальна при
n=0,2494874=1/4,0082184≈1/4,008;
A=6,1310790tU; U=0,1631034A/t; V=0,6537540A/t;
Ix,max=8,3771639tU3=0,0363484A3/t2;Iy=5,6974287tU3=0,0247303A3/t2;
Wx=4,1799935tU2=0,1111991A2/t; Wy=11,394857tU2=0,3031341A2/t;
ix,max=1,1689072U=0,1906527A/t; iy=0,9639865=0,1572294A/t. Чтобы найти экстремальное значение прочностной характеристики, коей является момент сопротивления сечения относительно оси абсцисс Wx=Wx,max, его формулу необходимо продифференцировать по переменной n и, приравняв к нулю производную (dWx/dn=0), получить разрешающее уравнение. Поскольку и в этом расчетном случае степень этого уравнения превысила десятую степень полиномиального уравнения, экстремум определен по методике последовательных приближений.
Прочность на изгиб предлагаемого зетового профиля в силовой плоскости несущей конструкции максимальна при
n=0,4828125=1/2,0711974≈1/2,071;
A=4,2999692tU; U=0,2325598A/t; V=0,4816772A/t;
Ix=2,3365934tU3=0,0293891A3/t2;Iy=0,9888784tU3=0,0124378A3/t2;
Wx,max=2,2562730tU2=0,1220284A2/t; Wy=1,9777568tU2=0,1069651A2/t;
ix=0,7371551U=0,1714326A/t; iy=0,4795553=0,1115252A/t. Практическую реализацию предлагаемого зетового профиля можно показать на примере базового объекта в виде 5-метровой конструкции прогона из прямоугольного гнутосварного профиля сечением 166×90х3 мм, основные расчетные параметры которого в силовой плоскости составляют 4=563 см4, Wx=67,8 см3, ix=6,08 см и приняты в качестве эталонных (100опроцентных) показателей [Брудка Я., Лубиньски М. Легкие стальные конструкции. М.: Стройиздат, 1974. С. 201-202].
5-метровая конструкция прогона из равноустойчивого зетового профиля (n=1/6,031) в силовой плоскости имеет следующие основные расчетные параметры:
V=0,7433344×15,0/0,3=37,16672=37,2 см (224,1%);
Ix=0,0350066×15,03/0,32=1312,7475≈1312 см4 (233,2%);
Wx=0,0941881×15,02/0,3t=70,641075≈70,64 см3 (104,2%);
ix=0,1871007×15,0/0,3=9,355035≈9,36 см (153,9%). 5-метровая конструкция прогона из зетового профиля с максимальной жесткостью или минимальной гибкостью (n=1/4,008) в силовой плоскости имеет следующие основные расчетные параметры:
V=0,6537540×15,0/0,3=32,6877=32,7 см (197,0%);
Ix=0,0363484×15,03/0,32=1363,065≈1363 см4 (242,1%);
Wx=0,1111991×15,02/0,3t=83,399325≈83,4 см3 (123,0%);
ix=0,1906527×15,0/0,3=9,532635≈9,53 см (156,7%). 5-метровая конструкция прогона из зетового профиля с максимальной прочностью на изгиб (n=1/2,071) в силовой плоскости имеет следующие основные расчетные параметры:
V=0,4816772×15,0/0,3=24,08386≈24,1 см (145,2%);
Ix=0,0293891×15,03/0,32=1102,0912≈1102 см4 (195,7%);
Wx=0,1220284×15,070,3t=91,5213≈91,5 см3 (135,0%);
ix=0,1714326×15,0/0,3=8,57163≈8,57 см (140,0%). Из сравнения расчетных параметров базового объекта и предлагаемого зетового профиля следует, что, если строительная высота в силовой плоскости несущей конструкции у зетового профиля возросла в 1,45…2,24 раза, то момент инерции увеличился в 1,96...2,33 раза, момент сопротивления - в 1,04…1,35 раза, радиус инерции - в 1,40…1,56 раза. Полученный результат подтверждает рациональность нового технического решения для перспективного применения в практике строительства.
| название | год | авторы | номер документа |
|---|---|---|---|
| Н-ОБРАЗНЫЙ ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ С ПЕРФОРИРОВАННОЙ ПОЛКОЙ | 2019 |
|
RU2714033C1 |
| ДВУТАВРОВЫЙ ГНУТОСВАРНОЙ ПРОФИЛЬ | 2018 |
|
RU2686762C1 |
| С-ОБРАЗНЫЙ ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ С ПЕРФОРИРОВАННОЙ СТЕНКОЙ | 2019 |
|
RU2725340C1 |
| ДВУТАВРОВЫЙ ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ (ВАРИАНТЫ) | 2018 |
|
RU2680560C1 |
| КОНСОЛЬНАЯ БАЛКА РЕГУЛЯРНО-ПЕРЕМЕННОЙ ВЫСОТЫ ИЗ ПРОФИЛЬНЫХ ТРУБ (ГНУТОСВАРНЫХ ПРОФИЛЕЙ) | 2018 |
|
RU2701404C1 |
| ПЛОСКООВАЛЬНЫЙ ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ | 2017 |
|
RU2653209C1 |
| СПОСОБ ПЕРЕПРОФИЛИРОВАНИЯ КРУГЛОЙ ТРУБЫ В ШЕСТИУГОЛЬНУЮ РАВНОБЕДРЕННУЮ | 2022 |
|
RU2794269C1 |
| СПОСОБ ПЕРЕПРОФИЛИРОВАНИЯ КРУГЛОЙ ТРУБЫ В ВОСЬМИУГОЛЬНУЮ | 2022 |
|
RU2795544C1 |
| ПЯТИУГОЛЬНЫЙ ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ | 2017 |
|
RU2645318C1 |
| ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ | 2017 |
|
RU2641333C1 |

Изобретение относится к области строительства и может быть использовано в качестве стержневых и балочных элементов при разработке несущих конструкций зданий и сооружений различного назначения. Техническим результатом изобретения является расширение области его рационального применения. В зетовом (Z-образном) равнополочном профиле со стенкой, наклонной к параллельным полкам под острым углом, отношение габаритов его ширины и высоты по средней линии сечения составляет 1/6,031 и 2,332/1 при равной устойчивости из плоскости и в плоскости конструкции, 1/2,071 при максимальной жесткости, минимальной гибкости, 1/4,008 при максимальной прочности. 4 ил.
Зетовый (Z-образный) равнополочный профиль со стенкой, наклонной к параллельным полкам под острым углом, отличающийся тем, что отношение габаритов его ширины и высоты по средней линии сечения составляет 1/6,031 и 2,332/1 при равной устойчивости из плоскости и в плоскости конструкции, 1/2,071 при максимальной жесткости, минимальной гибкости, 1/4,008 при максимальной прочности.
| ЗЕТОВЫЙ ПРОФИЛЬ | 1998 |
|
RU2135308C1 |
| ЗЕТОВЫЙ (Z-ОБРАЗНЫЙ) ГНУТОЗАМКНУТЫЙ ПРОФИЛЬ | 2018 |
|
RU2683839C1 |
| WO 2014109698 A1, 17.07.2014 | |||
| 0 |
|
SU196689A1 | |
Авторы
Даты
2024-09-27—Публикация
2024-04-11—Подача