Изобретение относится к нефтедобывающей промышленности, а именно к области интерпретации геофизических исследований скважин (ГИС) и предназначено для определения условной проницаемости коллекторов в условиях слоистого анизотропного разреза.
Известен способ определения величины анизотропии проницаемости с помощью построения карт градиента проницаемости. (Вершинин И.С.«Оценка анизотропии проницаемости многопластового сложнопостроенного нефтяного месторождения Крапивинское»). Для этого автором предлагается вычислить средние значения коэффициентов проницаемости во всех скважинах, провести построение карты средних значений проницаемости с интерполяцией данных в межскважинное пространство, далее по направлениям X (DX) и Y (DY) вычислить первую производную проницаемости и рассчитать угловые характеристики полученных векторов.
Стоит отметить, что описанный способ не учитывает модель слоистой анизотропии, в результате чего не удается получить рассчитанные кривые вертикальной и горизонтальной проницаемости.
Техническим результатом настоящего изобретения является повышение точности и достоверности определения коэффициента проницаемости коллекторов в условиях сложнопостроенных слоистых отложений.
Указанный технический результат достигается тем, что способ определения условной проницаемости скважин на основе модели слоистой анизотропии, характеризуется тем, что для расчета используют приближения Voigt и Reuss и осреднение Hill, при этом производят отбор стандартных цилиндрических образцов керна из полноразмерного керна, проводят на них лабораторные исследования по определению коэффициентов пористости и проницаемости, и по результатам лабораторных исследований керна проводят построение графика зависимости Кпр=f(Кп) и расчет проницаемости по приближению Reuss и Voigt на каждом шаге пористости, причем предварительно определяют кривую пористости согласно методике интерпретации ГИС на месторождении, при этом решение сводится к следующим формулам:
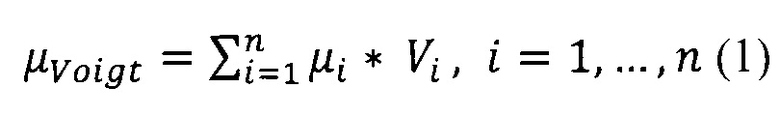
где μVoigt - приближение проницаемости по Voigt, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
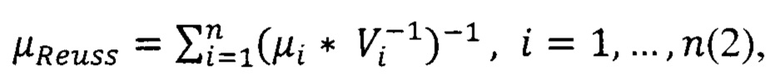
где μReuss - приближение проницаемости по Reuss, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
Осреднение по Hill:
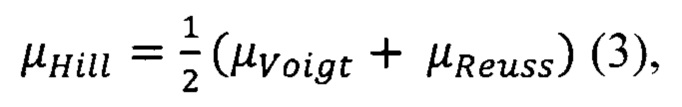
причем в результате расчета на каждом шаге пористости получают функции верхнего и нижнего пределов проницаемости, а для определения условной проницаемости при наклоне оси скважины 90 градусов к плоскости напластования (вертикальная скважина) используется осреднение Hill, а в условиях наклона оси скважины 180 градусов к плоскости напластования (горизонтальная скважина) используется приближение Reuss.
На Фиг. 1 представлена геометрическая интерпретация фильтрации флюидов в вертикальных и горизонтальных скважинах.
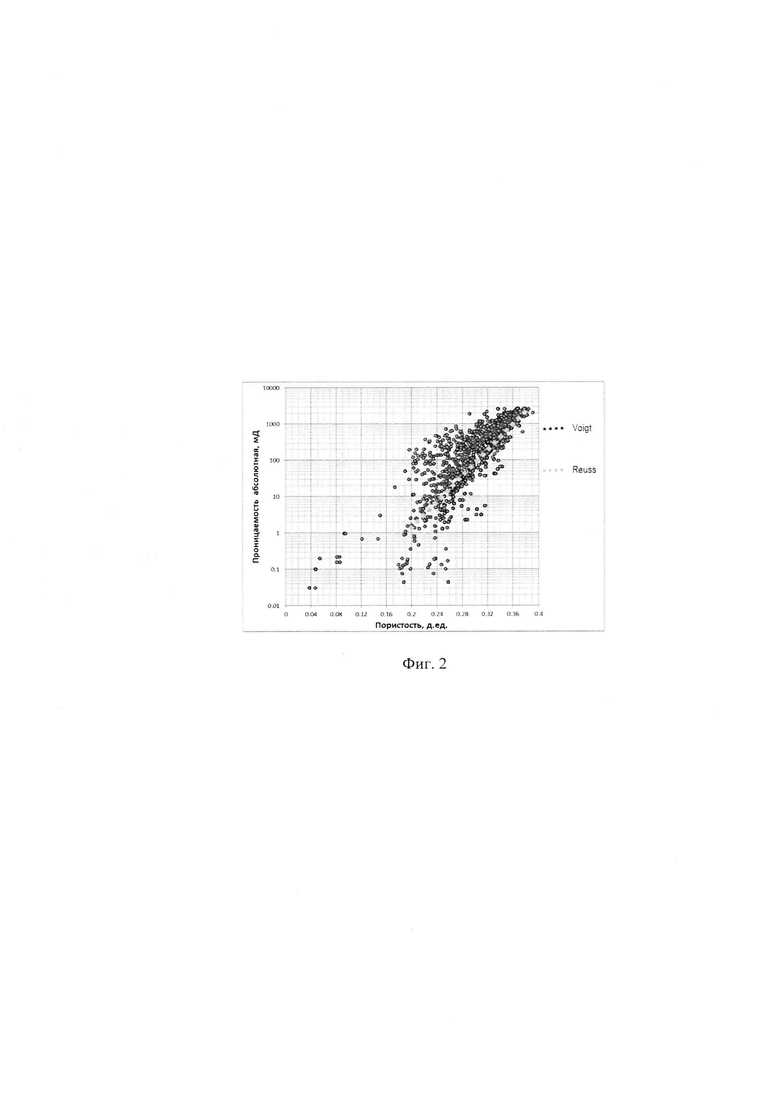
На Фиг. 2 показаны функции Voigt (красная) и Reuss (зеленая) для одного из литотипов. Синими точками показаны фактические данные керна для всех литотипов.
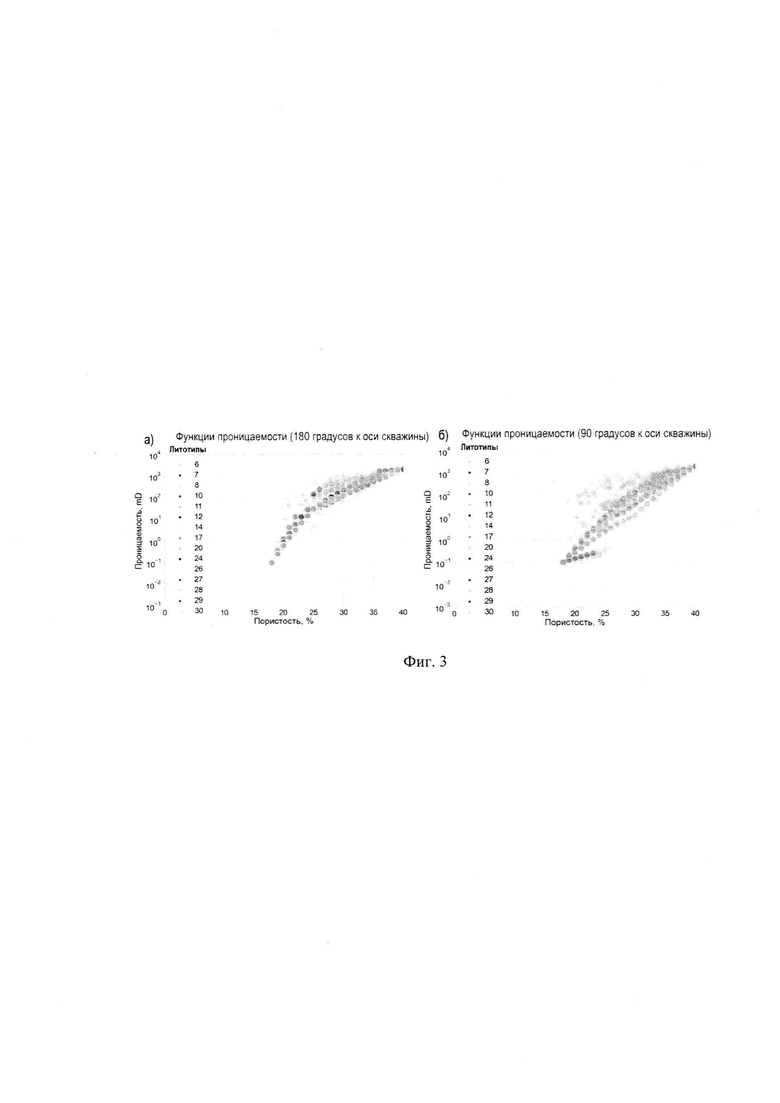
На Фиг. 3 показаны графики зависимости коэффициента проницаемости от пористости; а - функции проницаемости по Voigt для каждого литотипа, б - функции проницаемости по Reuss для каждого литотипа. Оранжевыми прозрачными точками показаны фактические данные керна.
На Фиг. 4 показан планшет с результатами определения проницаемости по вертикальной скважине. В последнем треке показана проницаемость по Hill (синяя) и фактические данные керна (красные точки).
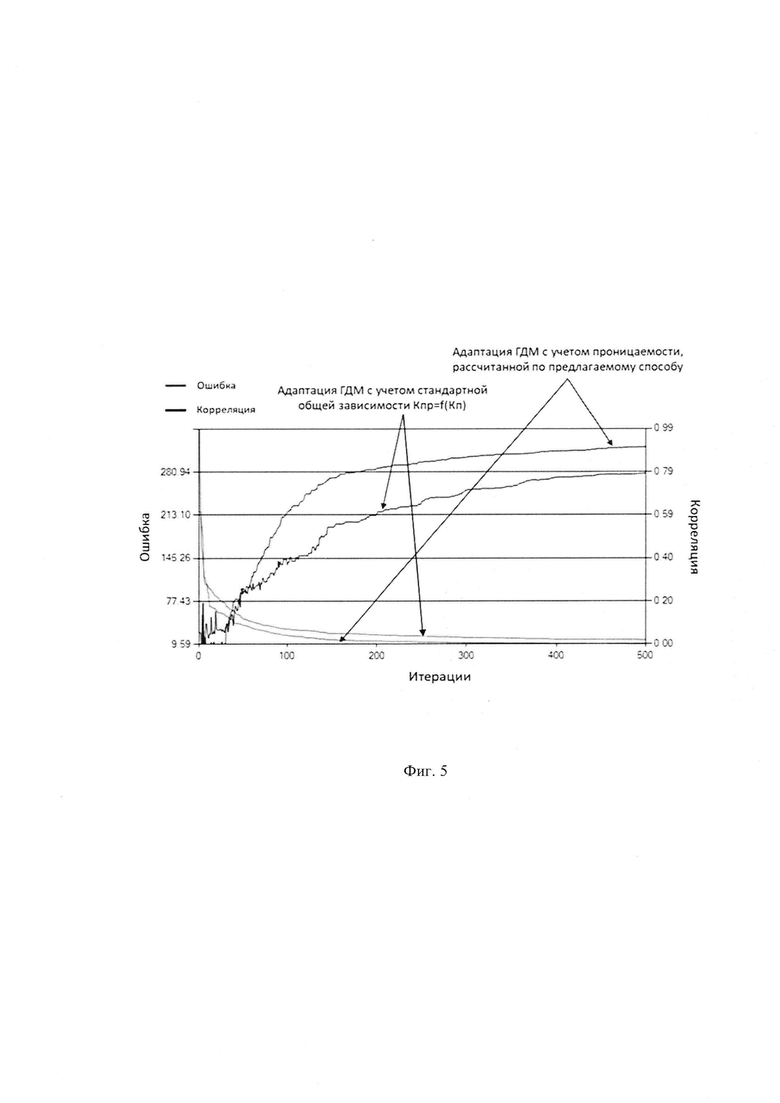
На Фиг. 5 показаны графики ошибки решения и коэффициента корреляции при адаптации гидродинамической модели ГДМ.
Особенностью предлагаемого способа является рассмотрение проницаемости как тензорной величины. Причины рассмотрения проницаемости именно как тензорного свойства, а не как скалярной характеристики среды, заключаются в следующем. В анизотропных средах векторы скорости фильтрации и градиента давления в общем случае не направлены по одной прямой (за исключением главных осей тензора проницаемости), а значения проницаемости и фильтрационного сопротивления могут изменяться для различных направлений. Поэтому в условиях анизотропной среды понятие проницаемости нуждается в обобщении.
Модель среды анизотропного коллектора предлагается описывать тензором вида:
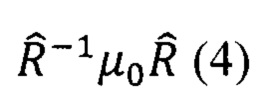
где 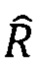 - матрица поворота вокруг оси, параллельной границе пласта, μ0 - тензор проницаемости в главных осях, описывающий трансверсально-изотропную среду. Тензор проницаемости параметризуется тремя величинами: продольной и поперечной проводимостью, а также углом между осями анизотропии и скважины.
- матрица поворота вокруг оси, параллельной границе пласта, μ0 - тензор проницаемости в главных осях, описывающий трансверсально-изотропную среду. Тензор проницаемости параметризуется тремя величинами: продольной и поперечной проводимостью, а также углом между осями анизотропии и скважины.
Исходя из вышеописанного, среднее значение проницаемости в неоднородном слоистом пласте не может быть определено арифметическим способом. Поэтому для расчета проницаемости слоистого коллектора предлагается использовать приближения Voigt и Reuss, а также осреднение по Hill. Приближение Voigt описывает изотропную среду. Приближение Reuss описывает анизотропную среду (далее в тексте приближение Reuss называется также «нижней границей проницаемости» и «вертикальной проницаемостью»).
Реализация настоящего способа сводится к следующим формулам:
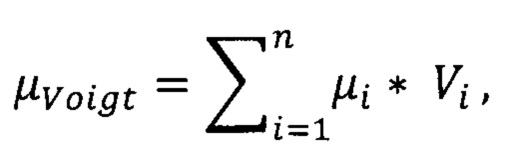 i=1, …, n
i=1, …, n
где μVoigt - приближение проницаемости по Voigt, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
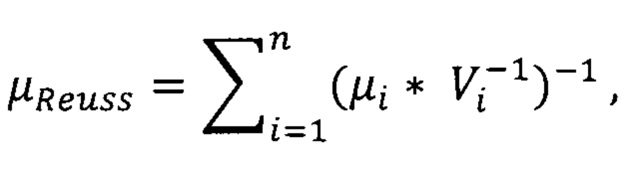 i=1, …, n
i=1, …, n
где μReuss - приближение проницаемости по Reuss, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
Осреднение по Hill:
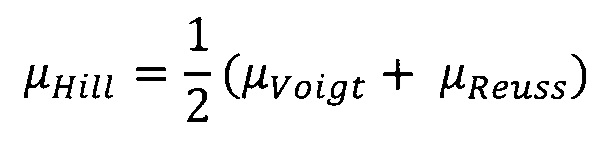
причем в результате расчета на каждом шаге пористости получают функции верхнего и нижнего пределов проницаемости, а для определения условной проницаемости при наклоне оси скважины 90 градусов к плоскости напластования (вертикальная скважина) используется осреднение Hill, а в условиях наклона оси скважины 180 градусов к плоскости напластования (горизонтальная скважина) используется приближение Reuss.
Расчет проницаемости проводится по следующим формулам:
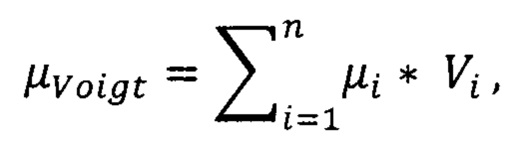 i=1, …, n
i=1, …, n
где μVoigt - приближение проницаемости по Voigt, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.
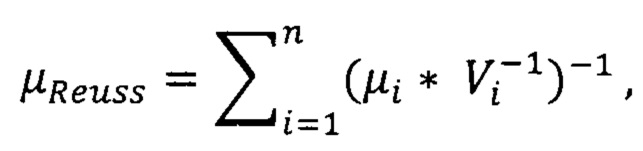 i=1, …, n
i=1, …, n
где μReuss - приближение проницаемости по Reuss, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.
В частном случае переслаивания двух типов пород уравнения (2) и (3) можно представить в следующем виде:
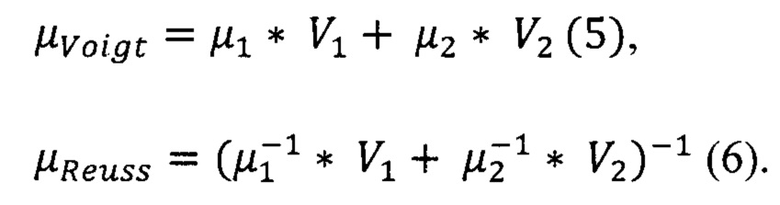
Для расчета проницаемости в скважинах, пересекающих пласт перпендикулярно плоскости напластования предлагается использовать осреднение Hill:
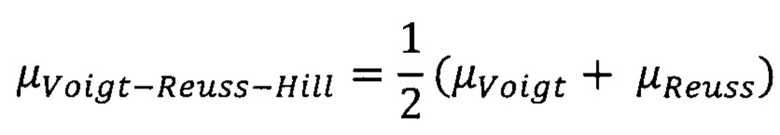
Для скважин, проводка которых осуществлена вдоль плоскости напластования (горизонтальные скважины), для расчета проницаемости предлагается использовать приближение Reuss, соответствующее нижней границе на Фиг. 2.
Ниже описаны операции и последовательность их выполнения при реализации предлагаемого способа. Для наглядности апробация методики проведена на реальном примере - тонкое переслаивание песчаников, алевролитов и аргиллитов сеномана на одном из месторождений в ЯНАО.
1. Для расчетов необходимы следующие исходные данные:
• Результаты лабораторных исследований коэффициентов пористости и проницаемости на стандартных цилиндрических образцах керна;
• Рассчитанная по ГИС кривая коэффициента пористости;
• Результаты литотипизации разреза (опционально).
2. Строят график зависимости Кпр=f(Кп) по данным лабораторных исследований керна.
По каждому литотипу (при отсутствии литотипизации для всех данных в целом) проводится расчет проницаемости по приближению Reuss и Voigt на каждом шаге пористости (шаг 0.01 д.ед.) по формулам 1 и 2.
3. В результате расчета на каждом шаге пористости получаются функции верхнего и нижнего пределов проницаемости. На Фиг. 2 показан пример функций Voigt и Reuss для одного из литотипов.
Функции верхнего и нижнего пределов проницаемости для всех выделенных литотипов показаны на Фиг. 3. На Фиг. 3 (а) показаны функции верхнего предела проницаемости - Voigt; на Фиг. 3 (б) - функции «вертикальной» проницаемости (Reuss). Фактические данные керна показаны оранжевыми прозрачными точками, цветные точки - расчетные функции для каждого литотипа.
4. Для расчета итоговых кривых условной проницаемости по данным ГИС на каждом шаге глубины для каждого кластера (литотипа) используются установленные на предыдущем этапе функции. Далее, используя осреднение Hill, определяется проницаемость вертикальных скважин. Проницаемость горизонтальных скважин определяется через приближение Reuss (нижняя граница проницаемости).
Авторами впервые на основе модели слоистой анизотропии проведен расчет условного коэффициента проницаемости коллекторов, в том числе для скважин с наклоном пласта 180 градусов к оси скважины (горизонтальные).
Достоверность расчета Кпр в вертикальной скважине с применением предлагаемого способа подтверждается сопоставлением результатов с данными керна, Фиг. 4. В последнем треке показана кривая проницаемости по осреднению Hill (синяя) и фактические данные керна (красные точки). Соответствие данных керна и ГИС говорит о корректности результатов применения предлагаемого способа.
Достоверность расчета Кпр в горизонтальных скважинах (с применением приближения Reuss) подтверждается коэффициентом корреляции при адаптации гидродинамической модели (ГДМ), Фиг. 4. На графике показаны кривые коэффициента корреляции и ошибки решения при адаптации ГДМ. Наглядно видно, что при использовании предлагаемого способа определения проницаемости коэффициент корреляции при адаптации ГДМ (черная линия) достигает 0.92, а ошибка (красная линия) асимптотически стремится к нулю. Чем выше коэффициент корреляции и ниже ошибка, тем выше достоверность расчетов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДИФФЕРЕНЦИАЦИИ ПУСТОТНОСТИ НЕОДНОРОДНЫХ КАРБОНАТНЫХ ПЛАСТОВ | 2021 |
|
RU2771802C1 |
| Способ построения геологических и гидродинамических моделей месторождений нефти и газа | 2020 |
|
RU2731004C1 |
| Способ построения геолого-гидродинамических моделей неоднородных пластов с тонким линзовидным переслаиванием песчано-алевритовых и глинистых пород | 2017 |
|
RU2656303C1 |
| СПОСОБ ПОСТРОЕНИЯ ГЕОЛОГО-ГИДРОДИНАМИЧЕСКИХ МОДЕЛЕЙ ДВОЙНОЙ СРЕДЫ ЗАЛЕЖЕЙ БАЖЕНОВСКОЙ СВИТЫ | 2014 |
|
RU2601733C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНИЗОТРОПИИ ПРОНИЦАЕМОСТИ ГОРНЫХ ПОРОД | 2020 |
|
RU2752913C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНИЗОТРОПИИ ПРОНИЦАЕМОСТИ ПЛАСТА | 2008 |
|
RU2374442C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕФТЕНАСЫЩЕННЫХ ПЛАСТОВ | 2012 |
|
RU2487239C1 |
| Способ локализации перспективных зон в нефтематеринских толщах | 2021 |
|
RU2762078C1 |
| Способ определения текущей нефтенасыщенности разрабатываемого пласта в работающих интервалах скважины с последующим восстановлением поля текущей нефтенасыщенности | 2020 |
|
RU2737453C1 |
| Способ определения фильтрационных свойств кавернозно-трещиноватых коллекторов | 2023 |
|
RU2817122C1 |


Изобретение относится к области интерпретации геофизических исследований скважин и предназначено для определения условной проницаемости коллекторов в условиях слоистого анизотропного коллектора. Для определения условной проницаемости применяются приближения Reuss (при наклоне оси скважины 180 градусов к плоскости напластования) и Voigt, а также осреднение по Hill (при наклоне оси скважины 90 градусов к плоскости напластования). Входными данными для реализации предлагаемого способа являются результаты определения ФЕС на образцах керна, непрерывная кривая пористости, а также результаты кластеризации разреза по ГИС. Техническим результатом является повышение точности и достоверности определения коэффициента проницаемости коллекторов в условиях сложнопостроенных слоистых отложений. 5 ил.
Способ определения условной проницаемости скважин на основе модели слоистой анизотропии, характеризующийся тем, что для расчета используют приближения Voigt и Reuss и осреднение Hill, при этом производят отбор стандартных цилиндрических образцов керна из полноразмерного керна, проводят на них лабораторные исследования по определению коэффициентов пористости и проницаемости, и по результатам лабораторных исследований керна проводят построение графика зависимости Кпр=f(Кп) и расчет проницаемости по приближению Reuss и Voigt на каждом шаге пористости, причем предварительно определяют кривую пористости согласно методике интерпретации ГИС на месторождении, при этом решение сводится к следующим формулам:
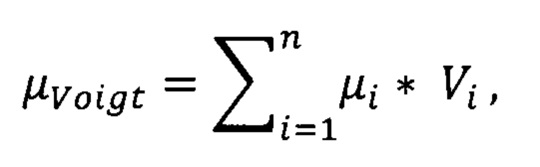 i=1, …, n,
i=1, …, n,
где μVoigt - приближение проницаемости по Voigt, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
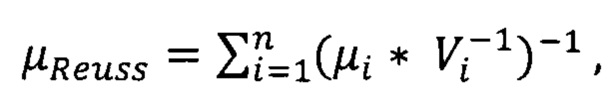 i=1, …, n;
i=1, …, n;
где μReuss - приближение проницаемости по Reuss, μi - значение проницаемости i-го компонента, Vi - пропорция содержания i-го компонента в разрезе в д.ед.;
осреднение по Hill:
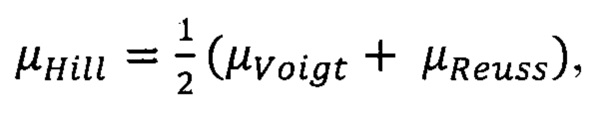
причем в результате расчета на каждом шаге пористости получают функции верхнего и нижнего пределов проницаемости, а для определения условной проницаемости при наклоне оси скважины 90 градусов к плоскости напластования для вертикальной скважины используется осреднение Hill, а в условиях наклона оси скважины 180 градусов к плоскости напластования для горизонтальной скважины используется приближение Reuss.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ АНИЗОТРОПИИ ПЛАСТА | 1992 |
|
RU2039235C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНИЗОТРОПИИ ПРОНИЦАЕМОСТИ ПЛАСТА В ЛАБОРАТОРНЫХ УСЛОВИЯХ | 2009 |
|
RU2407889C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНИЗОТРОПИИ ПОРОВОГО ПРОСТРАНСТВА И ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ ТЕНЗОРА ПРОНИЦАЕМОСТИ ГОРНЫХ ПОРОД НА КЕРНЕ | 2012 |
|
RU2492447C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АНИЗОТРОПИИ ПРОНИЦАЕМОСТИ ГОРНЫХ ПОРОД | 2020 |
|
RU2752913C1 |
| CN 0110552690 A, 10.12.2019 | |||
| CN 109577969 A, 05.04.2019. | |||
Авторы
Даты
2024-10-09—Публикация
2023-10-26—Подача