Изобретение относится к области электрических машин и может быть использовано для уменьшения их потерь холостого хода.
Известна формула определения толщины листов магнитопровода трансформаторов [Цыкин Г.С.Трансформаторы низкой частоты. Связьиздат, 1955, страница 225, формула ХIII.5], полученная из условия допустимого падения проницаемости листовых магнитных материалов из-за вытеснения магнитного потока к поверхности листа вихревыми токами. Согласно этой формуле, толщина листа (мм) не должна превышать
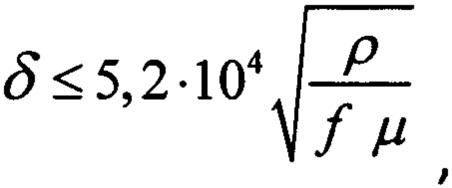
где ρ - удельное электросопротивление, Ом см
μ - магнитная проницаемость материала, ƒ - частота, Гц
При этом автор подчеркивает, что на практике желательно применять для сердечника материал в два-три раза меньшей толщины, чем дает данная формула. Вторая расчетная формула получена на основании геометрических данных сердечника и проницаемости материала [см. там же, формула XIII. 8]
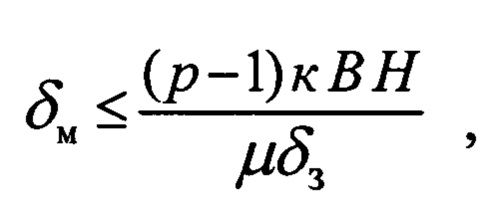
где δ3 - толщина зазора между отдельными пластинами;
В,H- размеры сторон сердечника;
p=μ/μк - отношение проницаемости материала к его кажущейся проницаемости, определенное через геометрические размеры пластин и зазоров;
к - коэффициент, зависящий от соотношения размеров пластины (для Ш - образных пластин к = 0,2 - 0,25).
Известные формулы получены на основе допустимой проницаемости материала листов, ограничивают толщину листов только по верхнему пределу и являются неточными.
Известен способ определения оптимальной толщины листов магнитопровода трансформатора, заключающийся в проведении измерения потерь в магнитопроводе опытом холостого хода на двух частотах для двух значений толщины листов и вычисление оптимального значения толщины листов по формуле, содержащей значения этих толщин, значения измеренных потерь и отношение частот [Патент РФ 2752353].
Недостаток известного способа заключается в сложности получения строго синусоидального напряжения с частотой, отличающейся от стандартной. Электронные преобразователи частоты вносят искажения в форму кривой подводимого первичного напряжения, в результате чего измеренные потери в стали будут содержать погрешность.
Изобретение решает задачу повышения точности и снижения трудоемкости определения толщины листов (пластин) магнитопровода, при которой потери в нем (потери в стали) минимальны, т.к. частоту подводимого напряжения изменить гораздо сложнее, чем изменить его величину.
Техническим результатом от использования изобретения является возможность снижения магнитных потерь в трансформаторе за счет более точного определения оптимальной толщины листов (пластин) магнитопровода на основании результатов четырех измерений и расчета по выведенной формуле.
Это достигается тем, что в способе определения оптимальной толщины листов магнитопровода трансформатора, заключающемся в измерении потерь в магнитопроводе опытом холостого хода на двух частотах для двух значений толщины листов, согласно изобретению, измерения потерь опытом холостого хода проводят при номинальном и пониженном напряжениях для двух значений толщины листов, а оптимальную толщину листов при работе трансформатора с номинальным напряжением определяют по формуле
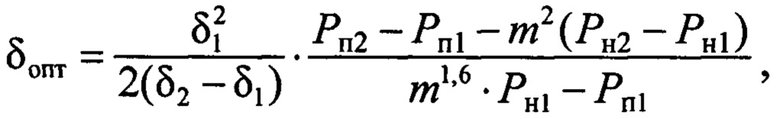
где Рн1 - потери в магнитопроводе с толщиной листов δ1 при номинальном напряжении
PП1 - потери в магнитопроводе с толщиной листов δ1 при пониженном напряжении
РН2 - потери в магнитопроводе с толщиной листов δ2 при номинальном напряжении
РП2 - потери в магнитопроводе с толщиной листов δ2 при пониженном напряжении UП;
m=UП/UH
Заявляемый способ определения оптимальной толщины листов (пластин), при которой потери в магнитопроводе минимальны, отличается расчетом толщины листов по результатам четырех опытов холостого хода: двух опытов при номинальном и пониженном напряжениях для листов одной толщины и двух опытов при номинальном и пониженном напряжениях для листов другой толщины.
Формула, связывающая значение оптимальной толщины листов с четырьмя измеренными значениями потерь в магнитопроводе (в стали), двумя значениями толщины листов и отношением напряжений, при которых проводились измерения, выведена автором впервые.
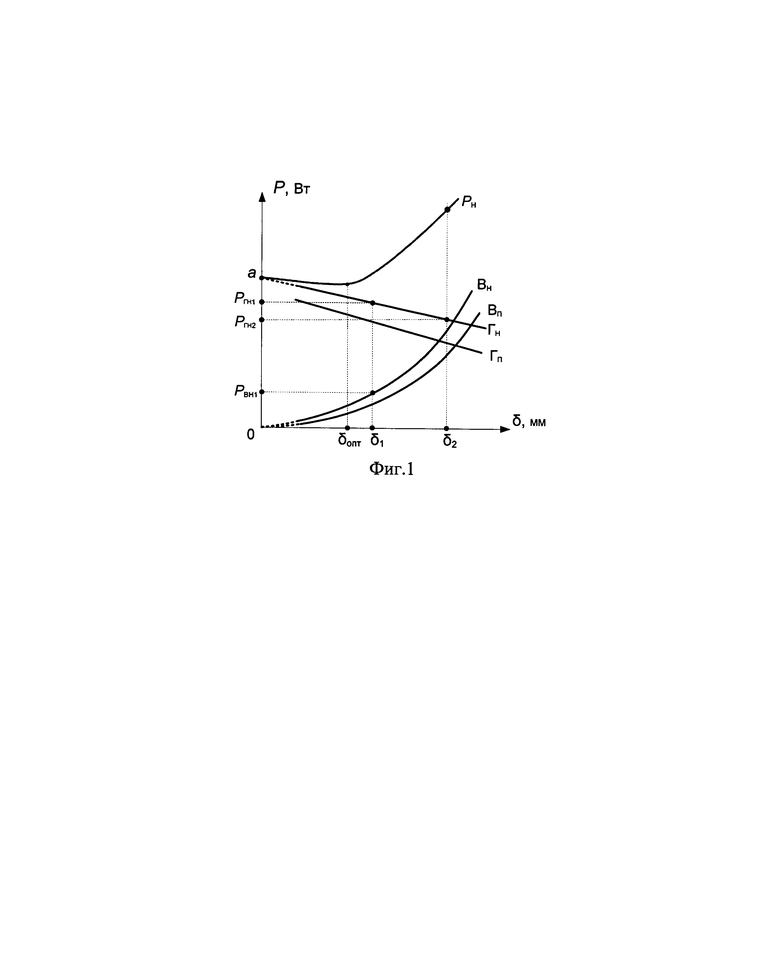
На чертеже представлены зависимости потерь в магнитопроводе от толщины листов, из которых он набран: P1 - полные потери в магнитопроводе при номинальном напряжении; Гн - потери на гистерезис при номинальном напряжении; ГП - потери на гистерезис при пониженном напряжении; Вн - потери на вихревые токи при номинальном напряжении; Вп - потери на вихревые токи при пониженном напряжении.
На чертеже отражено то, что при определенной толщине листов значения линии Гн в m1,6 раз превышают значения линии Гп, а значения кривой Вн в m2 раз превышают значения кривой Вп, т.к. потери на гистерезис пропорциональны магнитной индукции в степени 1,6, а потери на вихревые токи - второй степени. Магнитная индукция, в свою очередь, пропорциональна приложенному первичному напряжению.
Чем меньше толщина листов (пластин) магнитопровода, тем больше коэрцитивная сила, площадь петли и потери на гистерезис [см., например, Богородицкий Н.П. и др. Электротехнические материалы. - Л. Энергоатомиздат, 1985. - 304 с, страница 272,]. Кроме того, в процессе доводки до требуемой толщины пластин на холодных листах их толщина уменьшается, сталь уплотняется, что также приводит к росту потерь на гистерезис [Цыкин Г.С.Трансформаторы низкой частоты. Связьиздат, 1955, страница 229].
Для толщин более 0,08 мм зависимость потерь на гистерезис Рг от толщины листов δ можно выразить в виде линейной функции

где a - коэффициент, определяющий начальные потери на гистерезис, Вт;
b - коэффициент наклона прямой, Вт/мм.
Потери на вихревые токи Рв зависят от квадрата толщины листов магнитопровода [см., например, Общая электротехника: под. ред. А.Т. Блашкина. - Л.: Энергоатомиздат, 1986.-392 с, страница 198]

где с - коэффициент квадратичной функции, Вт/мм2.
Зависимость полных потерь в стали P1 при номинальном первичном напряжении от толщины листов, из которых набран магнитопровод
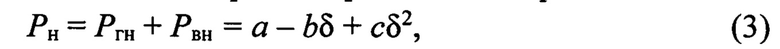
где Ргн- потери на гистерезис при номинальном напряжении;
Рвн- потери на вихревые токи при номинальном напряжении;
Оптимальное значение толщины листов δопт, при котором суммарные потери в магнитопроводе минимальны, найдем через производную Рн, приравняв ее нулю 
Коэффициент наклона линии Гн (см. чертеж) 
Коэффициент квадратичной функции

Подставим (5), (6) в (4), получим оптимальное значение толщины листов на частоте f1

где Ргн1 - потери на гистерезис при номинальном напряжении для толщины листов δ1;
Ргн2 - потери на гистерезис при номинальном напряжении для толщины листов δ2;
Рвн1 - потери на вихревые токи при номинальном напряжении для толщины листов δ1;
Данные потери определяем по результатам четырех опытов холостого хода (по показаниям ваттметра) из выражений [Патент РФ 2755053]
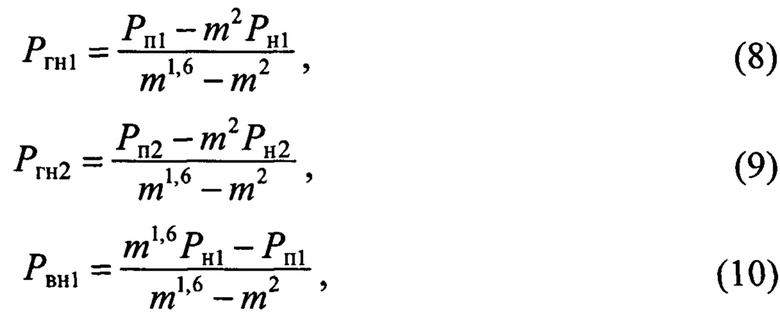
где Рн1 - потери в магнитопроводе с толщиной листов δ1 при номинальном напряжении UН;
PП1 - потери в магнитопроводе с толщиной листов δ1 при пониженном напряжении UП;
Рн2 - потери в магнитопроводе с толщиной листов δ2 при номинальном напряжении UН;
Рп2 - потери в магнитопроводе с толщиной листов 82 при пониженном напряжении UП;
m=UП/UH.
Подставив (8), (9), (10) в (7), получим расчетную формулу оптимальной толщины листов магнитопровода по критерию минимума потерь в нем
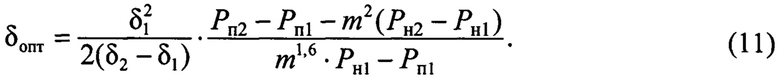
Способ осуществляют следующим образом.
Для трансформатора, магнитопровод которого собран из листов толщиной δ1, проводят опыт холостого хода при номинальном первичном напряжении UH, с помощью ваттметра измеряют потери холостого хода Рн1. Затем понижают подводимее первичное напряжение до значения UП, которое на 5… 10% отличается от значения UH, и измеряют потери холостого хода PП1-. Затем листы толщиной δ1 в магнитопроводе заменяют на листы толщиной δ2 и повторяют оба опыта холостого хода при напряжениях UH и UП измеряя с помощью ваттметра потери холостого хода соответственно Рн2 и Рп2. Далее вычисляют оптимальную толщину листов магнитопровода по выражению (11).
Осуществление способа рассмотрим на примере сухого однофазного трансформатора OCMl-1,6 М мощностью 1600 В А.
В опытах холостого хода, проведенных на частоте 50 Гц, были зафиксированы следующие показания ваттметра (тип Д5105, класс точности 0,1): потери холостого хода при номинальном первичном напряжении 220 В для сердечника из листов толщиной δ1=0,35 мм составили Рн1=20 Вт, потери при пониженном до 198 В первичном напряжении - PП1=16,6 Вт. Для сердечника из листов толщиной δ2=0,5 мм потери холостого хода при номинальном напряжении 220 В составили Рн2=24,2 Вт, при пониженном до 198 В напряжении - Рп2=20,2 Вт.Коэффициент 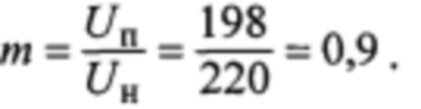
Оптимальную толщину листов трансформатора определим по формуле
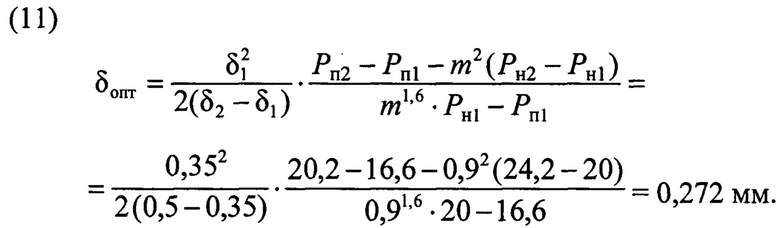
Потери на гистерезис и вихревые токи определим из выражений (7), (8),
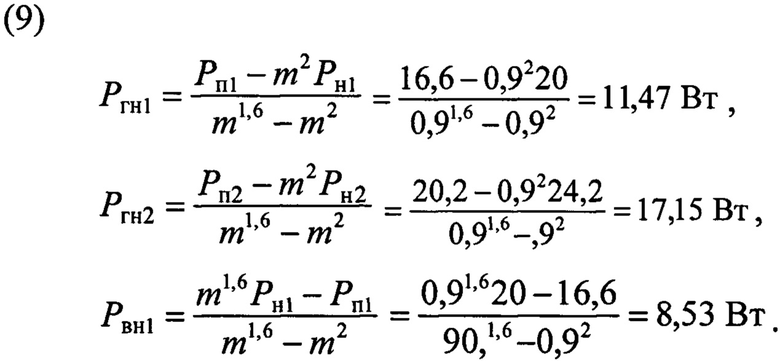
Коэффициент наклона линии Гн определим из выражения (5)
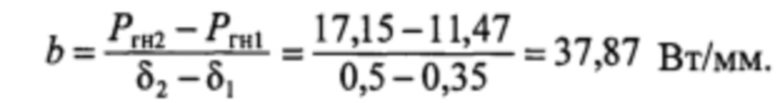
Коэффициент, определяющий начальные потери на гистерезис при номинальном напряжении определим с использованием линии Гн (см. чертеж) 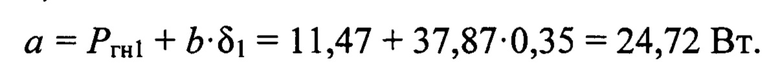
Это теоретическая величина, т.к. при толщинах менее 0,08 мм зависимость Рг(δ) становится нелинейной.
Коэффициент квадратичной функции определим из выражения (6)
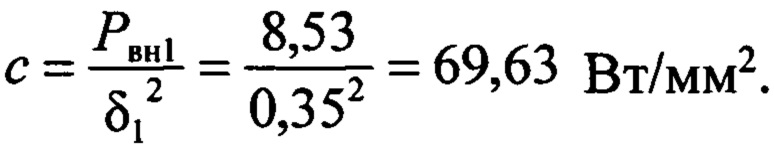
Полные потери в стали при номинальном напряжении для толщины листов 0,35 мм, согласно (3)
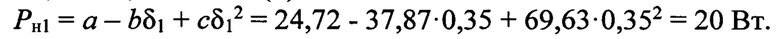
Полные потери в стали при номинальном напряжении для толщины листов 0,272 мм
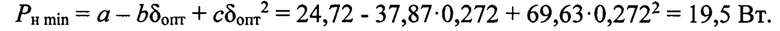
При данной толщине листов потери в стали данного трансформатора составляют 19,5 Вт, что на 2,5% меньше, чем при толщине листов 0,35 мм, и на 18,5% меньше, чем при толщине листов 0,5 мм. Это значение полных потерь является минимальным для всех остальных толщин листов данного магнитопровода. Например, для толщины листов 0,1 мм полные потери составят
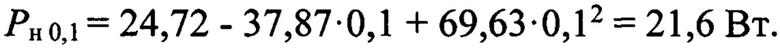
Разнообразие толщин производимых в настоящее время лент и листов электротехнической стали позволяет перейти на толщину листов наиболее близкую к оптимальной. Изобретение позволяет повысить точность и снизить трудоемкость определения оптимальной толщины листов сердечника магнитопровода, при которой магнитные потери в трансформаторе будут минимальны.
Изобретение относится к области электротехники, а именно к электрическим машинам, и может быть использовано для уменьшения их потерь холостого хода. Техническим результатом является возможность снижения магнитных потерь в трансформаторе за счет оптимизации толщины листов магнитопровода. Способ определения оптимальной толщины листов магнитопровода трансформатора заключается в измерении потерь в магнитопроводе опытом холостого хода для двух значений толщины листов на одной частоте при номинальном и пониженном напряжениях для двух значений толщины листов. Оптимальную толщину листов при работе трансформатора с номинальным напряжением определяют по формуле
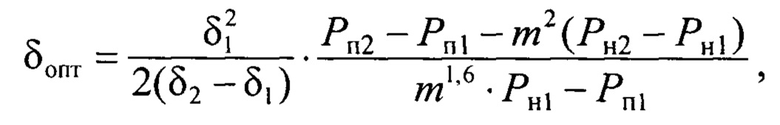
где Рн1 - потери в магнитопроводе с толщиной листов δ1 при номинальном напряжении Uн; Рп1 - потери в магнитопроводе с толщиной листов δ1 при пониженном напряжении Uп; Рн2 - потери в магнитопроводе с толщиной листов δ2 при номинальном напряжении Uн; Рп2 - потери в магнитопроводе с толщиной листов δ2 при пониженном напряжении Uп; m=Uп/Uн. 1 ил.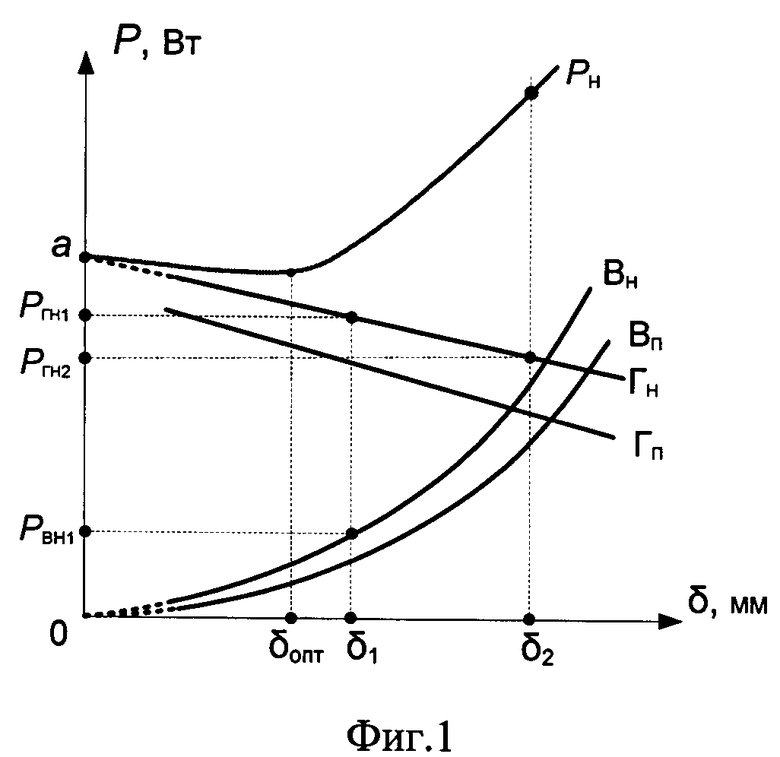
Способ определения оптимальной толщины листов магнитопровода трансформатора, заключающийся в измерении потерь в магнитопроводе опытом холостого хода для двух значений толщины листов, отличающийся тем, что измерения потерь опытом холостого хода проводят на одной частоте при номинальном и пониженном напряжениях для двух значений толщины листов, а оптимальную толщину листов при работе трансформатора с номинальным напряжением определяют по формуле
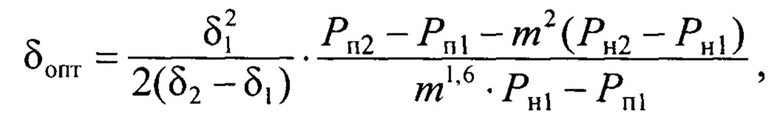
где Рн1 - потери в магнитопроводе с толщиной листов δ1 при номинальном напряжении Uн;
Рп1 - потери в магнитопроводе с толщиной листов δ1 при пониженном напряжении Uп;
Рн2 - потери в магнитопроводе с толщиной листов δ2 при номинальном напряжении Uн;
Рп2 - потери в магнитопроводе с толщиной листов δ2 при пониженном напряжении Uп;
m=Uп/Uн.
| Способ определения оптимальной толщины листов магнитопровода трансформатора | 2020 |
|
RU2752353C1 |
| Способ определения показателя степени магнитной индукции в потерях на гистерезис для стали сердечника трансформатора | 2021 |
|
RU2764780C1 |
| Способ определения магнитных потерь в трансформаторе | 2020 |
|
RU2755053C1 |
| Устройство для измерения толщины листа | 1988 |
|
SU1610262A1 |
| Устройство для неразрушающего контроля | 1986 |
|
SU1415043A1 |
| US 3405353 А, 08.10.1968. | |||
Авторы
Даты
2025-02-17—Публикация
2023-10-23—Подача