Изобретение относится к генерации пачечного телекоммуникационного трафика и может быть использовано при анализе очередей в других системах массового обслуживания.
Появление сетей передачи данных с коммутацией пакетов показало, что пуассоновские модели потоков не являются адекватными, и потребовало разработки новых моделей, основанных на не пуассоновских распределениях. Исследуются потоки с распределениями Вейбулла, Эрланга, Парето, Гамма-распределениями и др. Все интервалы времени, представляемые данными распределениями вероятностей, по-прежнему считались взаимно независимыми. Это позволяло применить хорошо разработанный аппарат теории очередей для анализа сетей с пакетной коммутацией. Описание сложных коррелированных потоков в современных телекоммуникационных сетях часто производилось с использованием «фрактальных» процессов. Сотни работ посвящены анализу «самоподобного» трафика. Однако ощутимых практических результатов указанные исследования не дали. Недостаточная эффективность представления трафика моделями «самоподобных» процессов привела к созданию целого класса моделей потоков, управляемых цепью Маркова. Этапы развития указанных моделей представлены в обзоре [1]. В нашей стране они были названы МС-потоками, а в США эволюционировали от «разносторонних (versatile) потоков», через «N-потоки (потоки Ньютса)» [2] до марковских входных потоков (MAP - Markovian Arival Process) и их обобщения - групповых марковских входных потоков (BMAP - Batch Markovian Arival Process) [3-10]. Появилось большое число различных генераторов подобных потоков с заданными характеристиками.
Наиболее близким по технической сущности является генератор неординарного пуассоновского потока событий [12]. В таком потоке выполняются свойства стационарности и отсутствия последействия, но не выполняется свойство ординарности. Это - пуассоновский поток независимых событий, каждое из которых заключается в одновременном появлении «пачки» из независимых случайно распределенных чисел заявок на обслуживание.
Предлагаемое решение проблемы состоит в том, что каждый временной интервал между двумя соседними пачками группового пуассоновского потока увеличивается на одинаковый, постоянный промежуток времени.
Сущность предлагаемого решения состоит в том, что добавляется еще одна степень свободы изменения характеристик потока.
Техническим результатом предлагаемого изобретения является повышение точности аппроксимации зависимостей средних значений очередей пачечного телекоммуникационного трафика на интервале больших загрузок.
Нами показано [11], что среднее значение очереди 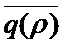 в одноканальной системе массового обслуживания с таким входным потоком заявок определяется соотношением
в одноканальной системе массового обслуживания с таким входным потоком заявок определяется соотношением
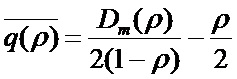 ,
,
где  - дисперсия чисел заявок на интервалах времени обслуживания одной заявки, а
- дисперсия чисел заявок на интервалах времени обслуживания одной заявки, а 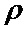 - коэффициент загрузки в системе. Так же, как и для обычного пуассоновского потока дисперсия изменяется линейно по отношению к
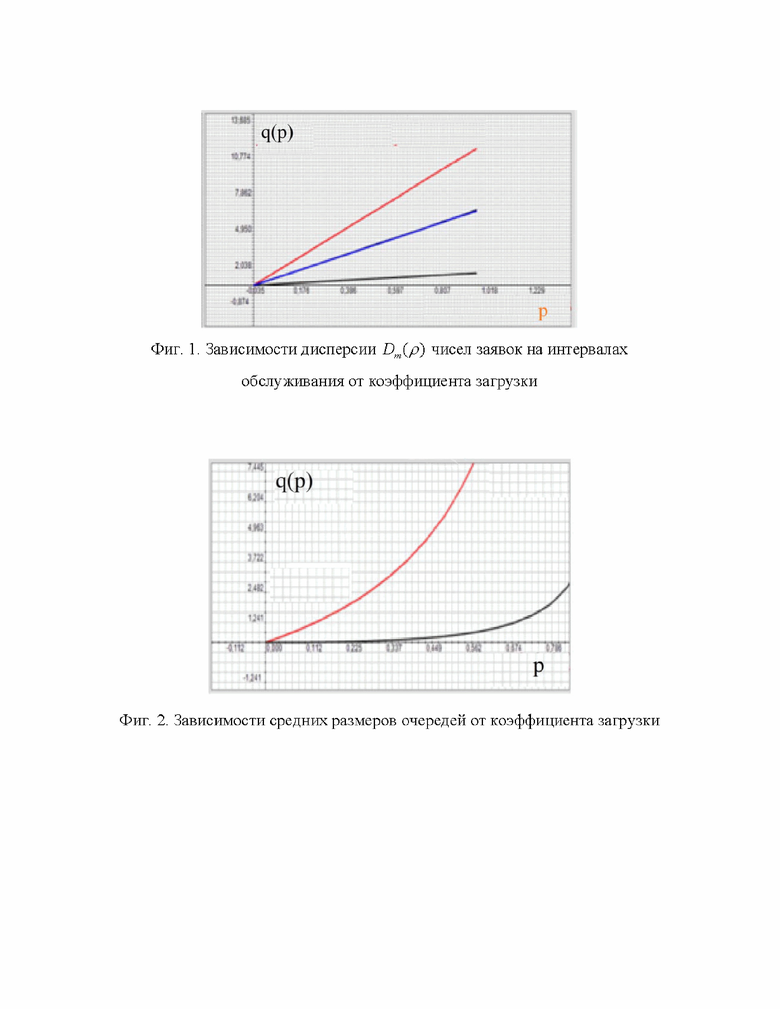
- коэффициент загрузки в системе. Так же, как и для обычного пуассоновского потока дисперсия изменяется линейно по отношению к 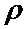 , однако, наклон линии изменения дисперсии зависит напрямую от чисел заявок в пачках, как это показано на Фиг. 1.
, однако, наклон линии изменения дисперсии зависит напрямую от чисел заявок в пачках, как это показано на Фиг. 1.
Верхний график соответствует групповому пуассоновскому потоку с числом заявок в пачке, равным 12. Нижний график соответствует обычному пуассоновскому потоку, с одной заявкой в пачке.
На Фиг. 2 показаны зависимости средних размеров очередей 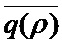 от коэффициента загрузки, полученные в результате имитационного моделирования обоих указанных потоков. Верхний график - групповой поток, нижний график - пуассоновский поток. Из рисунка следует, что групповой пуассоновский поток обеспечивает возможность получения высоких углов наклона зависимости среднего значения очереди от коэффициента загрузки, свойственные трафику, имеющему пачечный характер. Таким образом, групповой пуассоновский поток хорошо аппроксимирует средние значения очередей пачечного трафика, при сравнительно малых значениях коэффициента загрузки системы массового обслуживания. Однако, для такого потока, при аппроксимации пачечного трафика, отсутствует возможность изменения размеров очередей в районе больших коэффициентов загрузки при неизменном наклоне кривой в районе малых загрузок.
от коэффициента загрузки, полученные в результате имитационного моделирования обоих указанных потоков. Верхний график - групповой поток, нижний график - пуассоновский поток. Из рисунка следует, что групповой пуассоновский поток обеспечивает возможность получения высоких углов наклона зависимости среднего значения очереди от коэффициента загрузки, свойственные трафику, имеющему пачечный характер. Таким образом, групповой пуассоновский поток хорошо аппроксимирует средние значения очередей пачечного трафика, при сравнительно малых значениях коэффициента загрузки системы массового обслуживания. Однако, для такого потока, при аппроксимации пачечного трафика, отсутствует возможность изменения размеров очередей в районе больших коэффициентов загрузки при неизменном наклоне кривой в районе малых загрузок.
Для устранения указанного недостатка предлагается генератор потоков, в котором каждый временной интервал между двумя соседними пачками группового пуассоновского потока увеличивается на одинаковый промежуток времени.
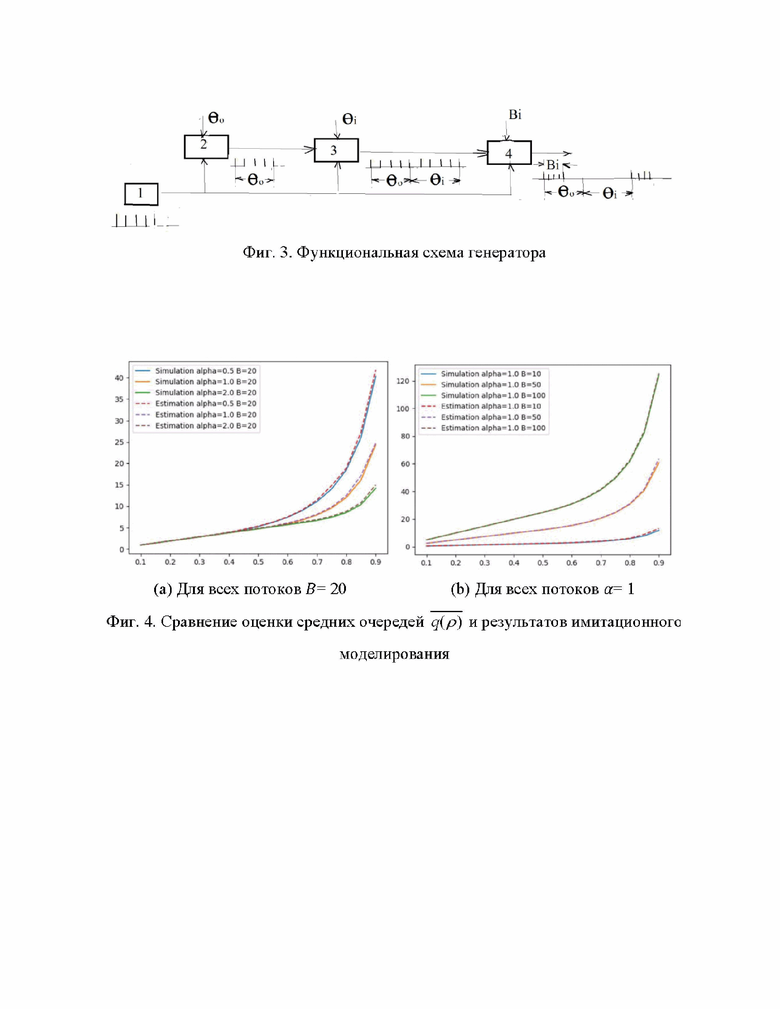
Предлагаемый генератор функционирует следующим образом (Фиг. 3).
1 - генератор тактовых импульсов;
2 - первый формирователь - генерирует задаваемые постоянные интервалы времени;
3 - второй формирователь - генерирует задаваемые, экспоненциально распределенные, независимые интервалы времени;
4 - формирователь пачек с заданным числом заявок.
Генератор тактовых импульсов-1 генерирует поток импульсов высокой частоты, определяющих масштаб времени последовательности событий. Формирователь постоянных временных интервалов-2 получает заданные значения 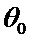 постоянных интервалов времени, выражаемые в числе тактовых импульсов, и формирует указанные интервалы времени. В качестве формирователя может использоваться, например, счетчик чисел импульсов с предварительной установкой числа импульсов в цикле. После окончания цикла, в течение которого формируется заданный интервал времени
постоянных интервалов времени, выражаемые в числе тактовых импульсов, и формирует указанные интервалы времени. В качестве формирователя может использоваться, например, счетчик чисел импульсов с предварительной установкой числа импульсов в цикле. После окончания цикла, в течение которого формируется заданный интервал времени 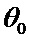 , управление передается формирователю-3, который генерирует экспоненциально распределенные интервалы времени
, управление передается формирователю-3, который генерирует экспоненциально распределенные интервалы времени  с заданным математическим ожиданием
с заданным математическим ожиданием 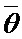 . В результате, временные интервалы между соседними событиями представляют собой сумму постоянных интервалов времени
. В результате, временные интервалы между соседними событиями представляют собой сумму постоянных интервалов времени 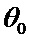 и независимых интервалов времени
и независимых интервалов времени 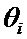 , имеющих экспоненциальное распределение вероятностей. Далее, управление передается формирователю пачек-4, который формирует числа заявок в пачках
, имеющих экспоненциальное распределение вероятностей. Далее, управление передается формирователю пачек-4, который формирует числа заявок в пачках 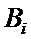 с заданным законом распределения вероятностей. В начале каждого интервала времени между соседними событиями формирователь пачек заявок-4 формирует короткие последовательности тактовых импульсов, числа которых определяются значениями чисел заявок в пачках
с заданным законом распределения вероятностей. В начале каждого интервала времени между соседними событиями формирователь пачек заявок-4 формирует короткие последовательности тактовых импульсов, числа которых определяются значениями чисел заявок в пачках 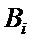 .
.
Для упрощения рассуждений, примем, что размеры всех пачек одинаковые и обозначим числа заявок в одной пачке через 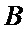 . Обозначим
. Обозначим 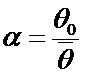 ,
, 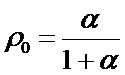 ,
, 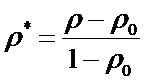 ,
, 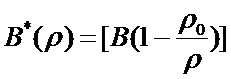 , где
, где 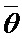 - математическое ожидание интервалов времени
- математическое ожидание интервалов времени 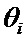 , а скобки […] означают наименьшее целое число, больше или равное выражению в них.
, а скобки […] означают наименьшее целое число, больше или равное выражению в них.
Для средних значений очередей в одноканальной системе массового обслуживания с групповыми квазипуассоновскими потоками нами получено оценочное соотношение
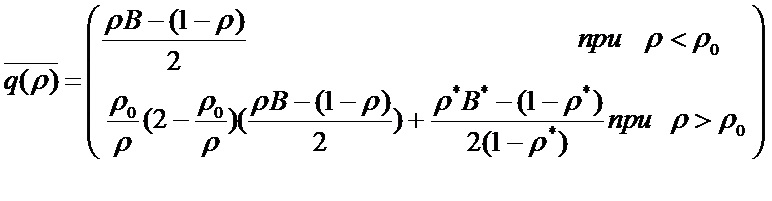
На Фиг. 4 представлены зависимости 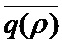 , полученные в результате имитационного моделирования (сплошные линии) и в результате расчетов по приведенной выше оценочной формуле (пунктирные линии).
, полученные в результате имитационного моделирования (сплошные линии) и в результате расчетов по приведенной выше оценочной формуле (пунктирные линии).
Приближение получается хорошее.
С помощью изменения коэффициента 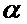 возможно изменение значения очередей при больших загрузках. На Фиг. 4 (a) показаны зависимости
возможно изменение значения очередей при больших загрузках. На Фиг. 4 (a) показаны зависимости 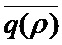 для различных значений коэффициентов
для различных значений коэффициентов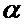 =0,5 (верхняя кривая),
=0,5 (верхняя кривая), 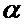 =1 (средняя кривая) и
=1 (средняя кривая) и 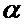 =2 (нижняя кривая). При этом, значение размеров пачек оставались постоянными (В=20), и при малых загрузках кривые практически совпадали. На Фиг. 4 (b) показаны зависимости
=2 (нижняя кривая). При этом, значение размеров пачек оставались постоянными (В=20), и при малых загрузках кривые практически совпадали. На Фиг. 4 (b) показаны зависимости 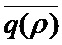 для различных значений чисел заявок в пачках В=100 (верхняя кривая), В=50 (средняя кривая), В=10 (нижняя кривая). Изменением B достигается изменение угла наклона кривых на малых нагрузках. Таким образом, нами генерируется новый вид потоков, являющихся моделью пачечного трафика телекоммуникационных систем. Указанный генератор обеспечивает качественную аппроксимацию и получение весьма простых зависимостей для расчета средних значений очередей в системах массового обслуживания.
для различных значений чисел заявок в пачках В=100 (верхняя кривая), В=50 (средняя кривая), В=10 (нижняя кривая). Изменением B достигается изменение угла наклона кривых на малых нагрузках. Таким образом, нами генерируется новый вид потоков, являющихся моделью пачечного трафика телекоммуникационных систем. Указанный генератор обеспечивает качественную аппроксимацию и получение весьма простых зависимостей для расчета средних значений очередей в системах массового обслуживания.
С помощью предлагаемого генератора группового квазипуассоновского потока производилась, например, успешная аппроксимация очередей для потоков пакетов видеокодеков Н.264. Реальный поток видеокодеков Н.264 аппроксимировался групповым квазипуассоновским потоком, а затем, все расчеты производились с использованием характеристик этого группового потока.
ЛИТЕРАТУРА
1. Вишневский В.М., Дудин А.Н. Системы массового обслуживания с коррелированными входными потоками и их применение для моделирования телекоммуникационных сетей // Автоматика и телемеханика, 2017. - №8. - С. 3-59.
2. Neuts M.F. Versatile Markovian point process // Journal of Applied Probability, 1979. - Vol. 16. - Issue 4. - P. 764-779. - DOI: https://doi.org/10.2307/3213143.
3. Ramaswami V. The N/G/1 queue and its detailed analysis // Advances in Applied Probability, 1980. - Vol. 12. - Issue 1. - P. 222-261. - DOI: https://doi.org/10.2307/1426503.
4. Lakatos L., Szeidl L., Telek M. Introduction to Queueing Systems with Telecommunication Applications // Springer Science+Business Media, 2013. - 388 p. - DOI: https://doi.org/10.1007/978-1-4614-5317-8.
5. Lema M.A., Pardo E., Galinina O., Andreev S., Dohler M. Flexible Dual-Connectivity Spectrum Aggregation for Decoupled Uplink and Downlink Access in 5G Heterogeneous Systems // IEEE Journal on Selected Areas in Communications, 2016. - Vol. 34. - Issue 1. - P. 2851-2865. - DOI: https://doi.org/10.1109/JSAC.2016.2615185.
6. Niknam S., Nasir A.A., Mehrpouyan H., Natarajan B. A Multiband OFDMA Heterogeneous Network for MillimeterWave 5G Wireless Applications // IEEE Access, 2016. - Vol. 4. - P. 5640-5648. - DOI: https://doi.org/10.1109/ACCESS.2016.2604364.
7. Vishnevsky V., Larionov A., Frolov S. Design and Scheduling in 5G Stationary and Mobile Communication Systems Based on Wireless Millimeter-Wave Mesh Networks // Distributed Computer and Communication Networks, 2014.- Vol. 279.- P. 11-27.- DOI: https://doi.org/10.1007/978-3-319-05209-0_2.
8. Vishnevsky V.M., Larionov A.A., Ivanov R.E., Dudin M. Applying graph-theoretic approach for time-frequency resource allocation in 5G MmWave backhaul network // Advances in Wireless and Optical Communications (RTUWO), 2016. - P. 221-224. - DOI: https://doi.org/10.1109/RTUWO.2016.7821888.
9. Leland W.E., Taqqu M.S., Willinger W., Wilson D.V. On the Self-Similar Nature of Ethernet Traffic // IEEE/ACM Transactions on Networking, 1994. - Vol. 2. - № 1. - P. 1-15.
10. Цыбаков Б.С. Модель телетрафика на основе самоподобного случайного процесса // Радиотехника, 1999. - № 5. - C. 24-31.
11. Лихтциндер Б.Я. Интервальные характеристики групповых пуассоновских моделей трафика телекоммуникационных систем //Инфокоммуникационные технологии, 2020. - Т. 18. - № 3. - С. 302-311.
12. Лихтциндер Б.Я., Моисеев В.И.Алгоритмы генерации групповых потоков случайных событий // Инфокоммуникационные технологии, 2023. - Т. 21, № 1. - С. 14-21.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения параметров телетрафика | 2023 |
|
RU2813666C1 |
| Устройство для моделирования импульсных помех | 1982 |
|
SU1094037A1 |
| Генератор пачек случайных импульсов | 1980 |
|
SU940282A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ АГРЕГИРОВАНИЯ ВХОДЯЩИХ ПАКЕТОВ В ОПТИЧЕСКИЕ ПАЧКИ ДЛЯ СЕТИ С КОММУТАЦИЕЙ ОПТИЧЕСКИХ ПАЧЕК | 2004 |
|
RU2355128C2 |
| СПЕКТРОМЕТРИЧЕСКИЙ СПОСОБ ИЗМЕРЕНИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ И РЕАЛИЗУЮЩАЯ ЕГО СПЕКТРОМЕТРИЧЕСКАЯ СИСТЕМА | 2002 |
|
RU2269798C2 |
| Способ скорейшего обнаружения момента возникновения перегрузки пуассоновского IP телетрафика | 2019 |
|
RU2728948C1 |
| Генератор квазипуассоновского импульсного потока | 1984 |
|
SU1195432A1 |
| Генератор псевдослучайных нестационарных импульсов | 1980 |
|
SU900419A1 |
| ГЕНЕРАТОР ПУАССОНОВСКОГО ИМПУЛЬСНОГО ПОТОКА | 2003 |
|
RU2246174C1 |
| Генератор пуассоновского потока импульсов | 1991 |
|
SU1786648A1 |
Изобретение относится к анализу пачечного телекоммуникационного трафика и может быть использовано при анализе очередей в других системах массового обслуживания. Технический результат заключается в повышении точности аппроксимации зависимостей средних значений очередей пачечного телекоммуникационного трафика на интервале больших загрузок. Для этого в генераторе группового квазипуассоновского потока пакетов телекоммуникационного трафика первый формирователь постоянных временных интервалов получает заданные значения постоянных интервалов времени, выражаемые в числе тактовых импульсов, затем управление передается во второй формирователь временных интервалов, генерирующий экспоненциально распределенные интервалы времени с заданным математическим ожиданием, в котором каждый интервал времени между соседними событиями в потоке образуется путем суммирования постоянного интервала времени, генерируемого первым формирователем временных интервалов, и экспоненциально распределенного интервала времени, генерируемого вторым формирователем временных интервалов, затем управление передается формирователю пачек заявок. 5 ил.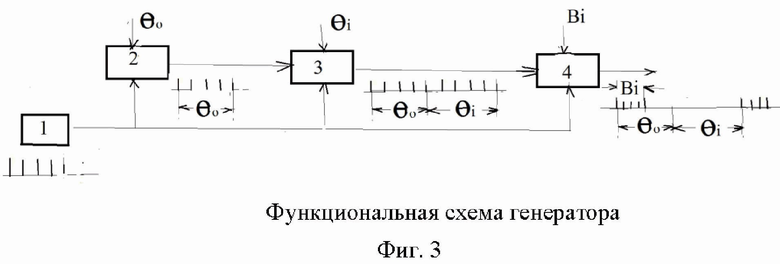
Генератор группового квазипуассоновского потока пакетов телекоммуникационного трафика, генерирующий пуассоновский поток независимых событий, каждое из которых заключается в одновременном появлении «пачки» случайно распределенных чисел заявок на обслуживание, содержащий тактовый генератор, формирователи временных интервалов и формирователь пачек заявок, отличающийся тем, что первый формирователь постоянных временных интервалов получает заданные значения постоянных интервалов времени, выражаемые в числе тактовых импульсов, затем управление передается во второй формирователь временных интервалов, генерирующий экспоненциально распределенные интервалы времени с заданным математическим ожиданием, в котором каждый интервал времени между соседними событиями в потоке образуется путем суммирования постоянного интервала времени, генерируемого первым формирователем временных интервалов, и экспоненциально распределенного интервала времени, генерируемого вторым формирователем временных интервалов, затем управление передается формирователю пачек заявок.
| Генератор квазипуассоновского импульсного потока | 1984 |
|
SU1195432A1 |
| Генератор пуассоновского потока импульсов | 1990 |
|
SU1739490A1 |
| Генератор пуассоновского потока импульсов | 1990 |
|
SU1739489A1 |
| ГЕНЕРАТОР ПУАССОНОВСКОГО ИМПУЛЬСНОГО ПОТОКА | 2003 |
|
RU2246174C1 |
| JP 9312667 A, 02.12.1997 | |||
| US 8391145 B2, 05.03.2013. | |||
Авторы
Даты
2025-04-29—Публикация
2024-09-10—Подача