S






| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения параметров графа | 1988 |
|
SU1603396A1 |
| Устройство для исследования параметров графа | 1986 |
|
SU1392574A1 |
| Устройство для моделирования графов | 1984 |
|
SU1228111A1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ СУБОПТИМАЛЬНОГО РАЗМЕЩЕНИЯ И ЕГО ОЦЕНКИ | 2001 |
|
RU2193796C2 |
| Устройство для анализа графов | 1990 |
|
SU1817104A1 |
| УСТРОЙСТВО АНАЛИЗА ПЕРЕКРЫТИЙ КАНАЛОВ ПРИ РАЗМЕЩЕНИИ ПАРАЛЛЕЛЬНЫХ ПОДПРОГРАММ В МНОГОПРОЦЕССОРНЫХ СИСТЕМАХ | 2011 |
|
RU2460126C1 |
| Устройство для определения параметров графа | 1990 |
|
SU1705839A1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ЗАДАЧ НА ГРАФАХ | 1996 |
|
RU2100838C1 |
| УСТРОЙСТВО ДЛЯ АНАЛИЗА СТРУКТУРЫ ОРИЕНТИРОВАННОГО ГРАФА | 1991 |
|
RU2023300C1 |
| Устройство для подсчета минимального значения интенсивности размещения в многопроцессорных кубических циклических системах при однонаправленной передаче информации | 2018 |
|
RU2688236C1 |


Изобретение относится к вычислительной технике и может быть использовано для создания цифровых и аналоговых вычислительных устройств для решения задач на графах. Целью изобретения является сокращение аппаратурных затрат при определении вершин, входящих в окрестность центра графа. Устройство содержит блок 1 определения кратчайшего пути, времяимпульсный интегрирующий преобразователь 2, блок 3 синхронизации и накапливающий блок 4 логического сложения. Перед началом работы по входу 8 задают порог интегрирования преобразователя 2 (т.е. задают радиус окрестности). По одному из входов 9 задают центр, для которого будут отыскивать вершины его окрестности. После подачи импульсного сигнала уровня логической единицы на вход 5 пуска блок 3 синхронизации формирует последовательность сигналов уровня логической единицы, которая позволяет проверить принадлежность вершин окрестностям. 28 ил.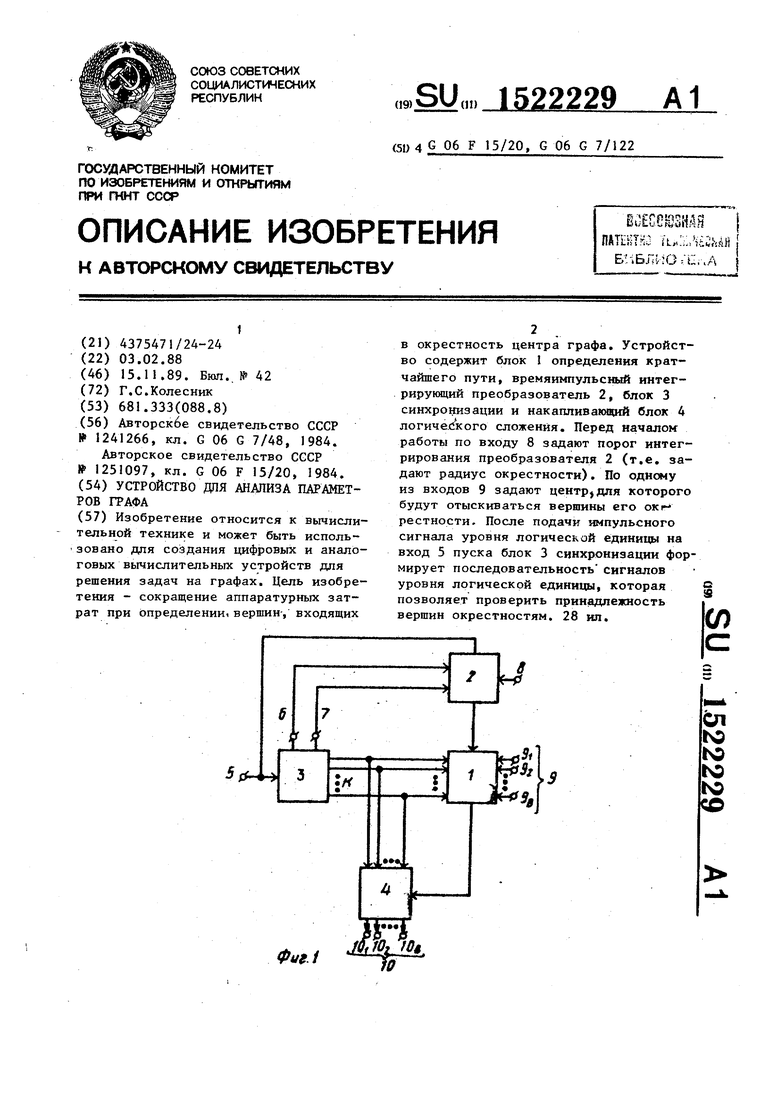
-J
, JfJOi fO Фu.i 31522229
Изобретение относится к вычислительной технике и может быть использовано для создания цифровых и анало- говых вычислительных и моделирующих устройств для решения задач на гра- фах, .
Цель изобретения - сокращение аппаратурных затрат при определении вершин, входящих в окрестность цент- JQ ра графа,
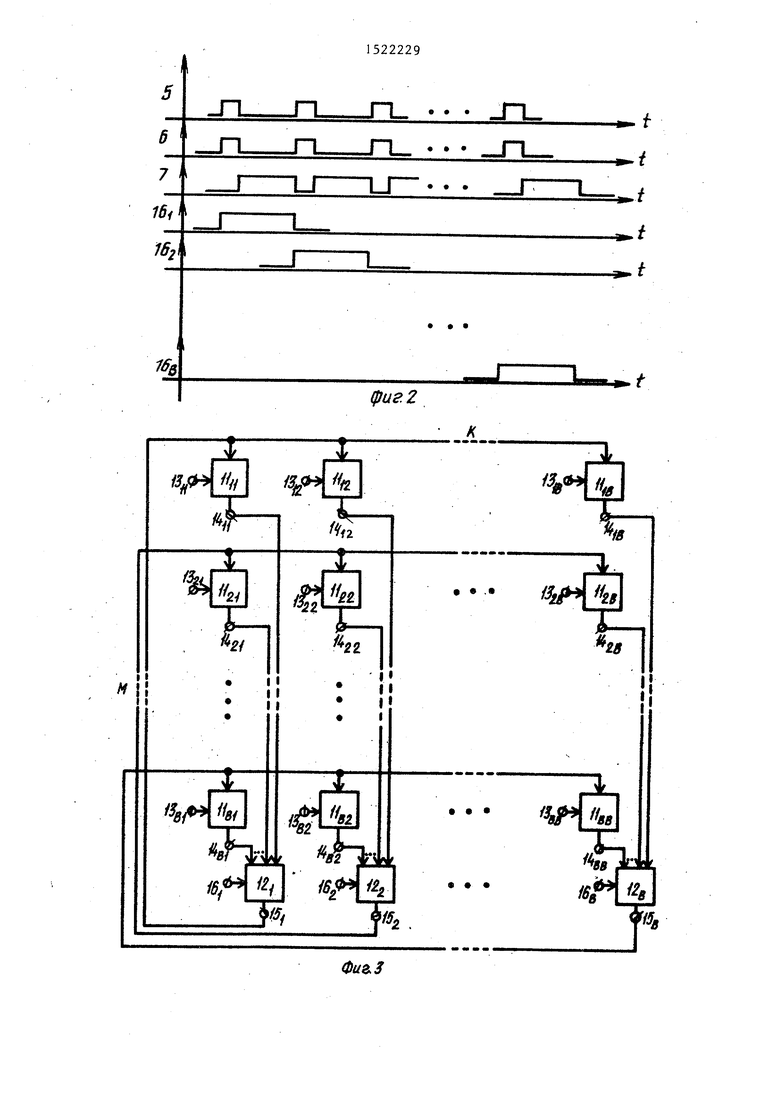
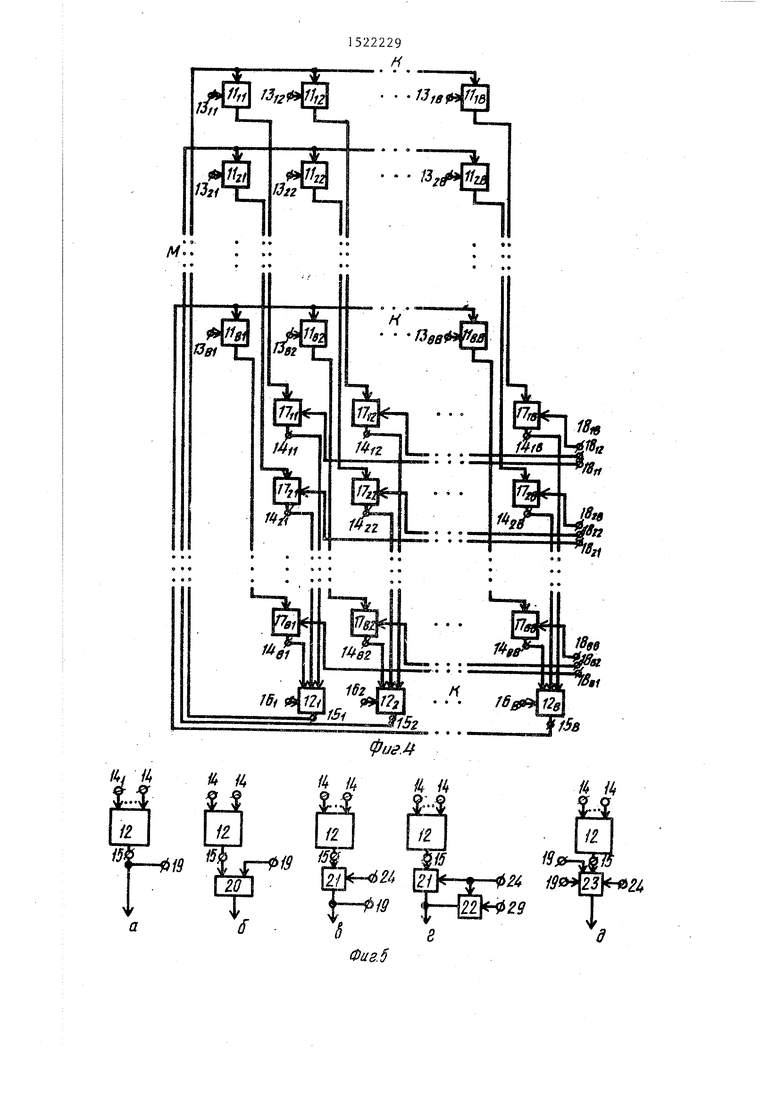
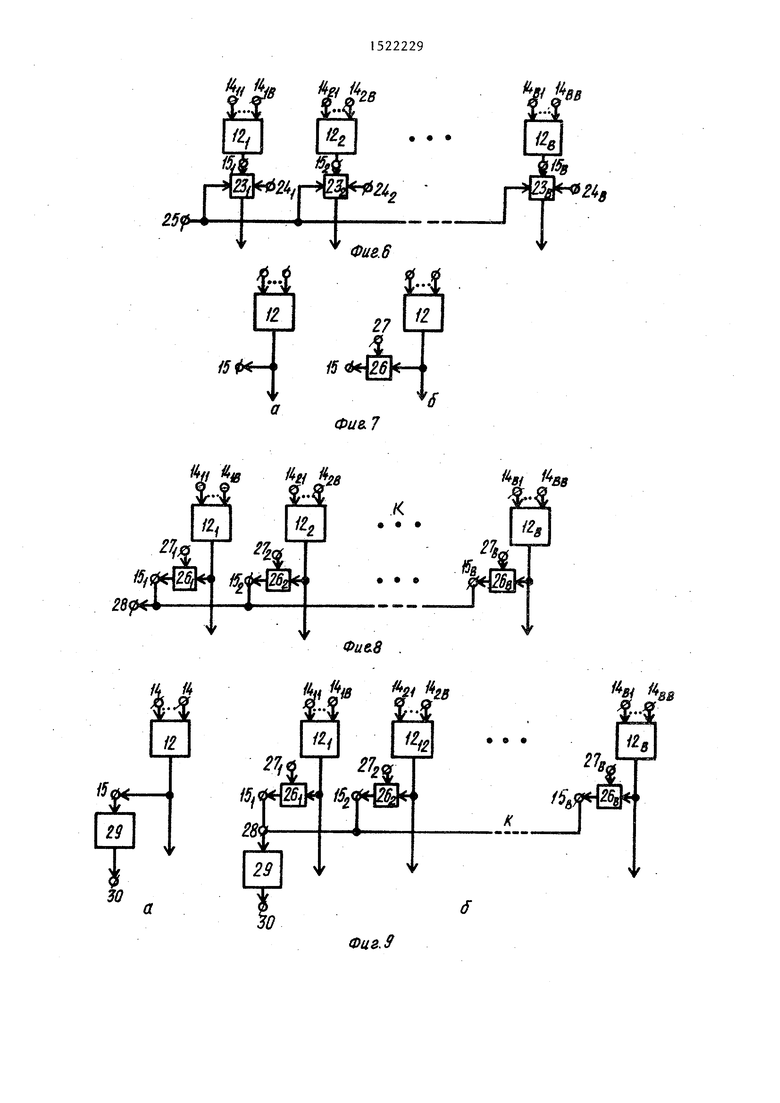
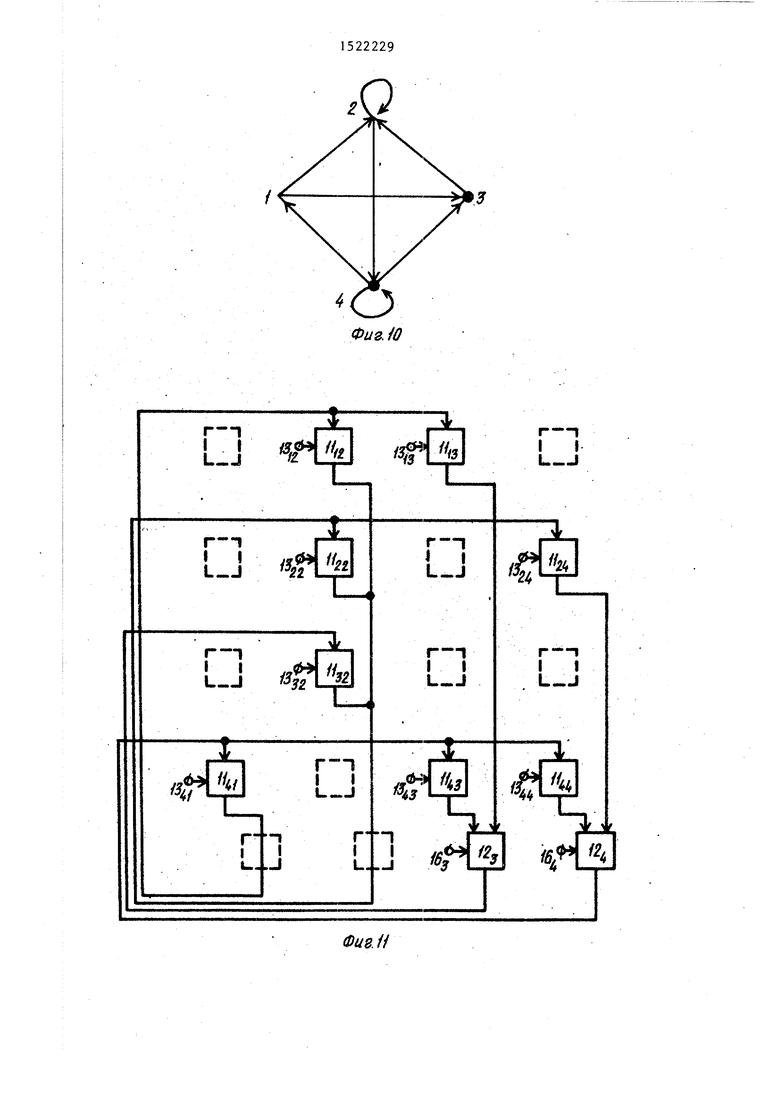
На фиг,1 представлена функциональная схема устройства; на фиг.2 - временная диаграмма работы блока синхронизации; на фиг.З функцио- 55 нальная схема базовой модели ориентированного графа (орграфа); на фиг,4 - функциональная схема универсальной модели орграфа; на фиг,5 - способ имитации состояния функциональной 20 модели вершины (МВ) и функциональной модели дуги (ФМД); на фиг.6 - способ задания начальных вершин орграфа; на фиг.7 - способ регистрации состояния ФМВ и ФМД; на фиг.8 - спо- 25 соб задания конечных вершин орграфа; на фиг,9 - способ регистрации событий, связанных с моделированием вершин и дуг орграфа; на фиг,10 - пример топологии орграфа; на фиг.И д пример структурной оптимизации базовой модели орграфа; на фиг,12 пример структурной оптимизации универсальной модели орграфа на фиг. 13- 5- примеры модульной оптимизации з нивер- сальной модели орграфа; на фиг,16 - функциональная схема базовой модели неориентированного графа; на фиг„17 его универсальная модель; на способ имитации состояния ФМР; на фиг.19 - способ имитации состояния ФМВ; на фиг.20 способ задания начальных вершин (ребер) неориентированного графа; на фиг.21 - способ регистрации состояния вершин (ребер) неориентированного графа; на фиг,22 - способ задания конечных вершин (пег бер) неориентированного графа; на фиг. - способ регистрации событий, связанных с состоянием ШВ и ФМР; на фиг.24 - пример топологии неориентированного графа; на фиг,25 - пример структурной оптимизации базовой модели неориентированного графа; ка фиг,26 - пример структурной оптимизации универсальной модели неориентированного графа; на фиг.27 - пример модульной оптимизации универсальной модели неориентированного графа;; на
35
40
50
55
Q
5 0 5 д
5
0
0
5
фиг.,28 - пример функциональной схемы блока определения кратчайшего пути.
Устройство содержит блок 1 определения кратчайшего пути, времяимпульс- ньш интегрирующий преобразователь 2, блок 3 синхронизации и накапливающий блок 4 логического сложения. Кроме того, на фиг,1 обозначены: вход 5 пуска устройства, первьш 6 и второчи 7 выходы блока 3 синхронизации, вход 8 задания радиуса окрестности радиуса устройства, входы 9 задания центра графа устройства и выходы 10 признаков принадлежности вершин составу вершин окрестности центра графа устройства.
Устройство работает следуюшда образом.
Перед началом ра;боты по входу 8 задают порог интегрирования преобразователя 2 (тем самым задают величину радиуса окрестностей графа). По одному из входов 9 задают конечную вершину графа (т.е. определяют центр, для которого будут определяться окрестности) .
После выдачи на вход 5 пуска устройства импульса уровня лог. 1 блок 3 синхронизации начинает формирование последовательности сигналов, предусмотренной временной диаграммой его работы (фиг.2), Сигнал на выходе 6 блока 3 устанавливает в О преобразова гель 2 сигнал на первом выходе группы блока 3 задает начальную вершину Графа (т.е. вершину, проверка которой на принадлежность составу вершин окрестности графа изводится в первом такте работы). Чб рез время, доетатсчное для установки в О преобразователя 2 блок 3 снимает сигнал с выхода 6. Потенциал уровня лог. 1 с выхода 7 блока 3 разрешает работу .преобразователя 2. Последний формирует на своем информационном выходе линейно возрастающий сигнал (напрш ер цифровой код или напряжение) который имитирует состояние начальной вершины графа Через время, достаточное дкя достижения порога, сигнал уровня лог. 1 с выхода признака достижения порога преобразователя 2 разрешает очередной такт работы блока 3 синхронизации. По- спедний формирует последовательность сигнапов, предусмотренную временной диаграммой его работы. Сигнал с выхода 6 блока 3 устанавливает в О преобразователь 2, сигнал на втором выходе группы блока 3 задает начальную вершину графа (т.е. вершину (вторую), проверка которой на принадлежность со- составу вершин окрестности центра графа производится во втором такте работы). Далее работа устройства повторяется до полного перебора всех В вершин графа. Если в каком-либо такте работы устройства моделирование конечной вершины графа будет закончено (конечная вершина будет достигнута из начальной), на выходе признака
окончания моделирования конечной вер- 15 их наличия в моделируемом орграфе шины модели 1 появляется потенциал уровня лог. О. По этому сигналу накапливающий блок 4 логического сложения произведет сложение (по ИЛИ) инзначительно усложняет моделировани особенно в орграфах с большим коли чеством вершин (в случае отсутстви каких-либо дуг в орграфе приходитс
значительно усложняет моделирование, особенно в орграфах с большим количеством вершин (в случае отсутствия каких-либо дуг в орграфе приходится
формации, накопленной в предыдущих ЦИК-20 задавать бесконечно большие параметлах работы, с текущими сигналами с выходов группы блока 3 (т.е. присоединение вершины, опрошенной в данном такте работы, к составу вершин, принадлежащих окрестности центра графа).
Рассмотрим конструкцию блока определения кратчайшего пути.
Часто дпя решения критических задач (определения кратчайшего или /, : длиннейшего пути, максимального или минимального потока и.т.п.) в системах, описываемых графами, используют их (т.е. систем) матричные модели. Поскольку модели систем,описьшаемых ориентированными графами (орграфами) и неориентированными графами (графами), имеют некоторые отличия, они разбираются отдельно.
ры, например бесконечно большие времена задержек или бесконечно большие пороги срабатьшания, а при отсутствии взвешенных вершин - бесконечно ма- 25 лые параметры моделирования).
Указанного недостатка в значительной мере лишена представленная универсальная модель орграфа (фиг.4). По сравнению с базовой моделью орграфа в нее введена матрица из ВхВ ключей 17 (в общем случае любых коммутационных элементов, начиная от коммутационных (распаянных) перемычек, устанавливаемых между информационш м входом и выходом ключа непосредственно перед моделированием, и кончая злектронными ключами с многоразряд30
35
Рассмотрим моделирование систем, опи- ными входом и выходом), причем выход
.сываемых орграфами (т.е. моделироваг- ние орграфов).
Представленная на фиг.3 базовая модель орграфа содержит матрицу из ВхВ функциональных моделей 11 дуг и группу из В функциональных моделей 12 вершин, причем вход 13 задания параметров моделирования (К,М)-й дуги модели орграфа (К 1,...,В; М 1,...В, где В - количество вершин в графе) , подключен к одноименному входу К-й модели 11 М-й строки матрицы, выход з значения функций которой является выходом 14 состояния (К,М)-й дуги модели орграфа и подключен к входу М-го аргумента К-й модели 12 группы, выход значения функции которой является выходом 15 состояния К-й вершины модели орграфа и подключен к выходам аргумента всех моделей 11 К-й строки
40 значения функции (К,М)-й ФМД П матрицы подключен к инфо1 {ациониому входу (К,М)-го ключа 17 матрицы, информационный выход которого является выходом состояния (К,М)-й дуги моде45 |пи орграфа и подключен к входу М-го аргумента К-й ФМВ 12 группы, управляющий вход (вход включения) (К,М)-го ключа 17 матрицы является входом 18 признака наличия (К,М)-й Дуги моде-
50 ли орграфа. Остальные связи универсальной модели полностью соответствуют связям базовой модели орграфа. Подавая на входы 18 потенциалы, уровня лог. 1 (например, с соответст55 вующих выходов блока задания матрицы ск-:жности) , можно легко изменить топологию орграфа, не перенастраивая 1МД 1 1 , что особенно удобно. Когда исследуются части орграфа.
матрицы, вход 16 задания параметров моделирования К-й вершины модели орграфа подключен к одноименному входу модели 12.
Поскольку (К,М)-я ФМД 11 матрицы соответствует (К,М)-му элементу матрицы смежности графа, базовая модель орграфа позволяет моделировать оргра фь1 произвольной топологии, количество вершин в которых не пр евышает В. Однако необходимость каждый раз перед началом работы задавать параметры всех дуг и вершин независимо от
их наличия в моделируемом орграфе
значительно усложняет моделирование, особенно в орграфах с большим количеством вершин (в случае отсутствия каких-либо дуг в орграфе приходится
задавать бесконечно большие параметры, например бесконечно большие времена задержек или бесконечно большие пороги срабатьшания, а при отсутствии взвешенных вершин - бесконечно ма- лые параметры моделирования).
Указанного недостатка в значительной мере лишена представленная универсальная модель орграфа (фиг.4). По сравнению с базовой моделью орграфа в нее введена матрица из ВхВ ключей 17 (в общем случае любых коммутационных элементов, начиная от коммутационных (распаянных) перемычек, устанавливаемых между информационш м входом и выходом ключа непосредственно перед моделированием, и кончая злектронными ключами с многоразряд
значения функции (К,М)-й ФМД П матрицы подключен к инфо1 {ациониому входу (К,М)-го ключа 17 матрицы, информационный выход которого является выходом состояния (К,М)-й дуги моде|пи орграфа и подключен к входу М-го аргумента К-й ФМВ 12 группы, управляющий вход (вход включения) (К,М)-го ключа 17 матрицы является входом 18 признака наличия (К,М)-й Дуги моде-
ли орграфа. Остальные связи универсальной модели полностью соответствуют связям базовой модели орграфа. Подавая на входы 18 потенциалы, уровня лог. 1 (например, с соответствующих выходов блока задания матрицы ск-:жности) , можно легко изменить топологию орграфа, не перенастраивая 1МД 1 1 , что особенно удобно. Когда исследуются части орграфа.
Моделирование орграфа рассмотрим на примере решения задачи определения величины кратчайшего пути.
Пусть в качестве ФМД 11 используются элементы задержки, причем вход элемента задержки является в. данном случае входом аргумента ФМД 11, выход - выходом значения функции, а вход задания величины задержки - вхо- дом задания параметров моделирования; в качестве ФМВ 12 используется элемент ИЛИ, Причем его входы являются в данном, случае входами аргументов ФМВ 12, а выход - выходом значе- НИН функции ФМВ 12. Пусть требуется определить величину кратчайшего пути меАду начальной (Н-й) и конечной (Е-й) вершинами.
Перед началом работы задают топо- логию орграфа и устанавливают величины задержек пропорциональными весам соответствующих дуг графа. На Н-й выход 15 модели орграфа (т.е. применительно к данному случаю на выход Н-го элемента ИЛИ) подают импульсный сигнал или потенциал уровня лог. 1 (т.е. имитируют исполнение начальной вершины орграфа), который поступает, на входы всех ФМД 11 Н-й строки матрицы,(т.е. на входы всех элементов задержки данной строки). По окончании моделирования дуг (т.е. по появлению задержанных на величину веса соответ ствуюшлх дуг сигналов уровня лог. 1 на выходе элементов задержки) сигналы с выходов соответствующих им ФМВ 12 (т.е. фактически с выходов элементов ИЛИ) поступают на входы ФМД 11 следующих строк матрицы и т.д. до тех пор, пока сигнал уровня лог. 1 не появится на выходе Е-й ФМВ 12 (Е-го элемента ИЛИ), что свидетельствует об окончании моделирования Е-й вершины. Время, прошедшее от момента имитации исполнения начальной вершины до момента окончания моделирования конечной вершины графа соответствует величине кратчайшего пути между этими вершинами. .
Пусть в качестве ФМД 11 используются пороговые элементы, причем вход порогового элемента является в данном случае входом аргумента ФМД 11, выход - выходом значения функции, а вход задания величины порога - входо задания параметров моделирования. В качестве ФМВ 12 в этом случае могут быть использованы блоки выбора максимума, причем его информационные входы являются входами аргументов ФМВ информационный выход - выходом значения функции ФМВ 12,Пусть требуется определить величину кратчайшего пути между начальной Н-й и конечной Е-й вершинами орграфа.
Перед началом работы задают тополгию графа и устанавливают величин порогов пропорциональными весам соответствующих дуг графа. На Н-й выход 15 модели орграфа подают возрас- таюший по значению сигнал, например цифровой код или напряжение (т.е. имитируют исполнение начальной вершины: орграфа), который (сигнал) поступает на входы всех ШД Н-й строки матрицы (т.е. на входь всех пороговых элементов данной строки). По окончании моделирования дуг (т.е. по достижении сигнала на входах пороговых элементов величины порога) сигналы с выходов ФМД 11 (численно равные разности между значением сигнала на его входе и значением соответствующего ему порога) поступают на входы соответствующих им ФМВ 12 и выхода - на входы ШД 1 I следующих строк матрицы и т.д. до т ех пор, пока сигнал на выходе Е-й ФМВ 12 не станет больще О, что свидетельствует об окончании моделирования оргра- фа. Разность значений сигналов на вьгходах И-и «и Е-й ФМВ 12 соответствует величине кратчайшего пути между этими вершинами.
Таким образом, независимо от способа представления аргументов и значений функций на выходах и входах ШД 11 и ФМВ 12, а также независимо от осуществляемых ими Функциональных преобразований функциональная схема модели орграфа и ее работа не изменяются, что оправдывает терминологию выбранную для описания моделей дуг, моделей вершин и их функциональных входов. Аргументы и значения функций ШД 11 и ФМВ 12 могут быть представлены любыми аналоговыми величинами (значением напряжения, тока, частоты рь1азы и т.п.) или цифровыми кодами (числовым - в любой системе счислени кодоимпульсным, числоимпульсом, амплитудно-импульсным и т,п.).
Очень часто элементная база, выбранная для моделирования дуг и вершин орграфа, не допускает подключени входа 19 имитации исполнения вершины
(дуги) непосредственно к выходу МВФ 12 .(ФМЦ 11), как показано на фиг.5а. В этом случае используют развязывающие элементы (элемент ИЛИ 20 на фиг.56), а при наличии в орграфе циклов и петель, когда на выходе развязывающего элемента может образоваться логическая сумма сигналов имитации исполнения вершины (дуги) и сигналов ее собственного состояния, используют ключи 21, 22 или коммутаторы 23. При подаче на вход 24 признака имитации исполнения вершины (дуги) сигнала уровня лог. 1 ключи 21 и 22 обеспечивают отключение выхода ФМБ 12 (ФМД П) от входа 19 и подключение входа 19 к входам всех ЩЦ 11 (к одному из входов ФМВ 12) -соответствующей строки матрицы (соответствующего ФМВ 12 группы)(фиг.5в,г) или изменения направления коммутации (фиг.5д).
Объединение вторых информационных направлений всех коммутаторов 23, всех 12 группы (всех ФМД II матрицы) (фиг.6) позвовтяет ввести понятие - вход 25 имитации исполнения начальной вершины. В этом случае входы 24 признаков имитации исполнения вершин (дуг) орграфа допустимо называть входами задания начальных вершин (дуг) орграфа.
Регистрация состояния ФМВ 12 (ШД 1 1) иногда также требует отключения выхода 15 (14) от выхода значения функции ФМВ 12 (ФМД 11). В этом случае выход 15 (14) подключают к выходу ФМВ 12 (ФМД II) через нормально разомкнутый ключ 26. Подавая на .вход 27 опроса состояния вершины (дуги) сигнал уровня лог. 1, подключают выход ФМВ 12 (ФМД 11) к выходу 15 состояния вершины (дуги) модели орграфа. Объединяя по ИЛИ (на фиг.8 показано монтажное ИЛИ) информационные выходы всех ключей 26, можно ввести понятие - выход 28 состояния конечной вершины (дуги) графа. В этом случае входы 27 опроса состояния вершин (дуг) модели орграфа допустимо называть входами задания конечной вершины (дуги) орграфа.
Решение некоторых задач требует регистрации каких-либо характерчых состояний ФМВ 12 и ФМД 1I например начало моделирования вершины (дуги), окончание моделирования, переход через минимум или максимум значения функции на выходе ШД 11 или ФМВ 12,
10
20
25
}530
35
40
45
0
5
и т.п. в этом случае к выходам 15 (14) ФМВ 12 (фиг.9а) подключают блоки 29 сравнения, настроенные на фиксацию .с: определенного состояния, выхоДы признаков отношения (равно, не равно, больше, меньше и т о п.) которых являются выходами 30 событий модели орграфа. Подключение блока 29 сравнения к выходу 28 состояния конечной вершины (дуги) орграфа позволяет фиксировать события, связанные с конечной вершиной орграфа (фиг.96).
Аппаратные средства моделей орграфов можно значительно упростить используя метод структурной оптимизации.
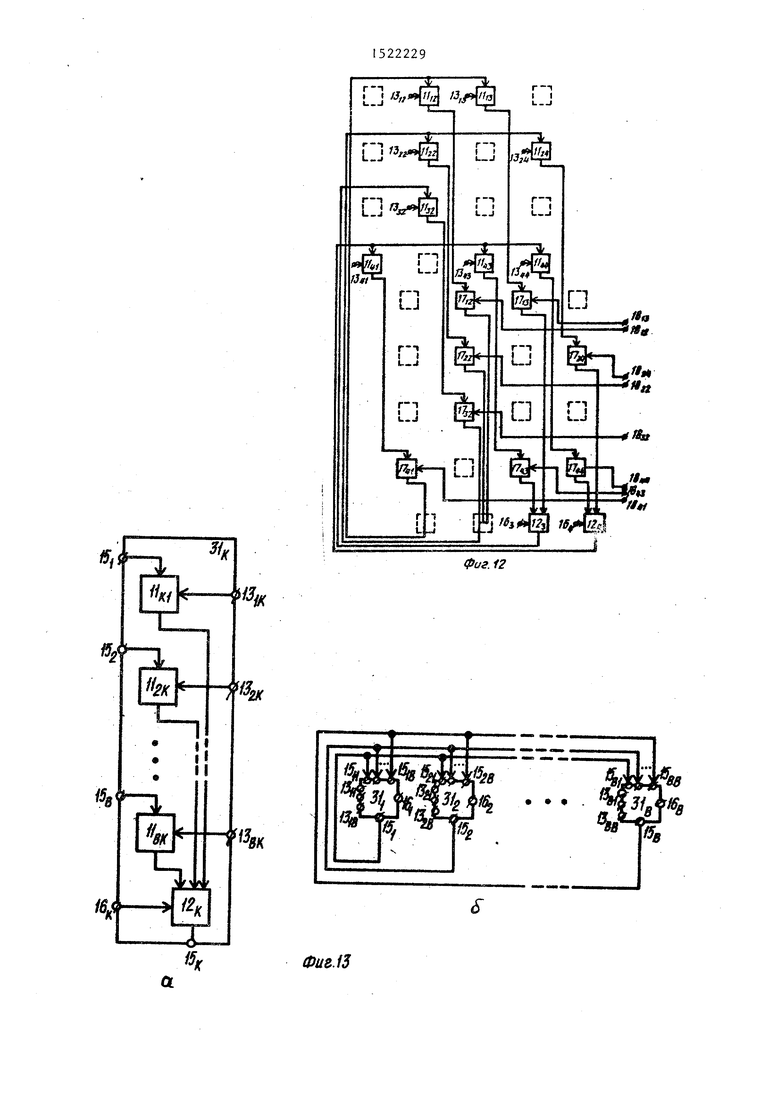
Метод структурной оптимизации предполагает исключение всех аппаратных средств устройства, которые не используются при данном его применении. Например, если автомобиль применяют как укрытие от непогоды, из его состава могут быть исключены колеса и двигатель. Применительно к моделированию орграфов это означает, что из состава модели могут быть исключены все «ИЩ 1 1 , ФМВ 12 и любые другие элементы, структура совокупности которых отражает топологию орграфа, ко- торые не предусмотрены топологией конкретного орграфа. Например, для орграфа, топология которого представлена на фиг.10, структурная оптимизация базовой и универсальной модели показана на фиг.II и 12 соответственно. Обычно в этом случае говорят,что модели дуг 1 и 12 вершин соединены в соответствии с топологией орграфа. Пунктиром показаны 11 и «ШВ 12 и ключи 1 7,которые исключены из базовойи универсальной моделей орграфа в результате их структурной оптимизации .
Конструктивно аппаратные средства моделей орграфов, как и любых других устройств, могут быть выполнены в виде модулей, которые соединяют между собой в соответствии с требованиями конкретной задачи. В модуль может быть выделена любая повторяющаяся часть аппаратных средств .. Например, на фиг.1 За показан модуль 31, в состав которого введены ФМВ 12 и все соответствующие ей «ЙМД 11. В этом случае базовая модель орграфа принимает вид, показанный на фиг.136. На фиг.14а показан модуль 32, в состав которого введены все ФМД 11, соответ-
ствующие дугам ,инцидентным К-й вершине графа. В этом случае базовая модель орграфа принимает вид, показанный на фиг.1Аб. На фиг.15а показан модуль 33, в состав которого введены ключ 17 и ФМД 11, соответствующие (К,М)-й дуге графа. В этом случае ., универсальная модель орграфа принимает вид, показанный на фиг.156.
Среди преимуществ модульной организации аппаратуры можно указать следующие:
возможность сокращения аппаратурных затрат за счет замены совокупности аппаратуры, выделенной в модуль ее моделью (например, цифровой);
повышение эффективности структурной оптимизации модульно организованного устройства, так как, исключая из его состава модули в соответствии с Методом структурной оптимизации, фактически подвергают структурной оптимизации все блоки, включенные в состав модуля.
Рассмотрим моделирование систем, описываемых неориентированными графами (т.е.моделирование неориентированных графов).
Неориентированные грифы можно исследовать на моделях орграфов, В этом случае каждое ребро неориентированного графа представляется как две противоположно направленные дуги и ,- каждой дуге ставят в соответствие ФМД 11.
Однако для моделирования неориентированных графов используют модели неориентированных ребер и вершин.
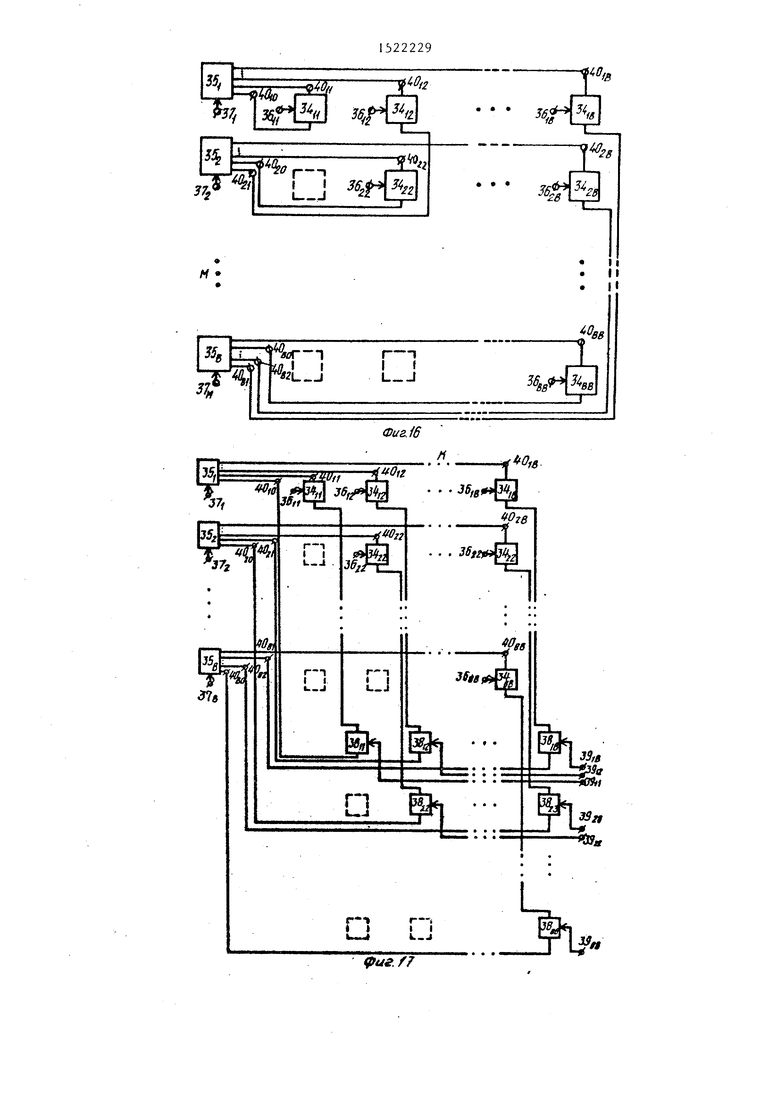
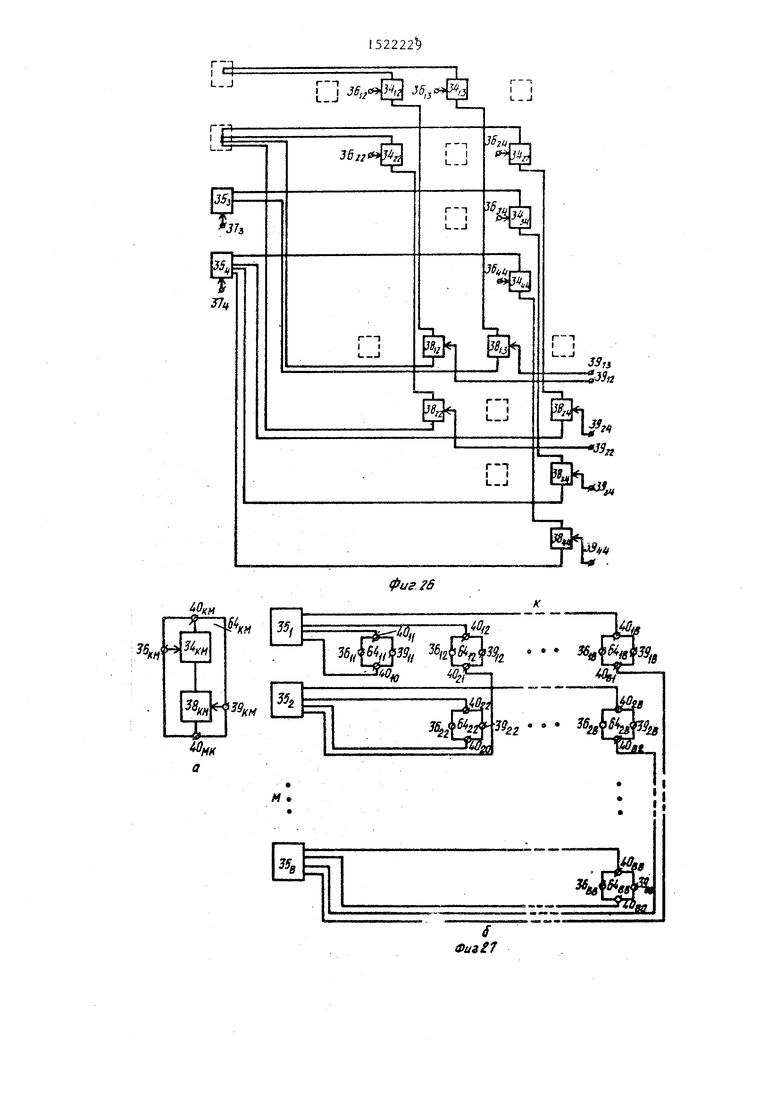
Представленная на фиг.16 базовая модель неориентированного графа (графа) содержит матрицу из 1/2 В(В+1) функциональных моделей 34 ребер (ФМР 34) и группу из В функциональных моделей 35 вершин (ФМВ 35), причем вход 36 з.адания параметров моделирования (К,М)-го ребра графа (К . ... М,...,В; М 1,.,.,Б) подключен к одноименному входу (К,М)-й ФМР 34 матрицы, первьш вход аргумента (вход значения функции) которой подключен к К-му входу аргумента (выход значения функции) М-й ФМВ 35 группы, второй вход .аргумента (выход значения
10
20
фиг . 16 показаны те ФМР 34, которые исключены из модели графа в силу симметрии его матрицу. смежности.
Необходимость задания перед началом работы параметров всех ФМР 34 матрицы при изменении топологии графа является недостатком базовой моде ли графа. В значительной мере он оп- ;ределен в универсальной модели графа 1функциональная схема которой предста лена на фиг.7. По сравнению с базовой моделью в универсальную модель графа введена матрица из 1/2 В(В+1)
15 ключей 38, причем второй вход аргуме та (выход значения функции)(К,М)-и ФМ 34 матрицы подключен к первому Информационному входу/выходу (К,М)-го ключа матрицы, второй информационный вход/выход которого подключен к ()-му входу аргумента (выходу зна чения функции)К-й ФМВ 35 группы, вход 39 признака наличия (К,М)-го ребра модели графа подключен к управляюще25 му входу (к входу включения)(К,М)-го ключа 38 матрицы. Остальные конструктивные признаки базовой и универсальной моделей совпадают. Подавая на входы 39 потенциалы уровня лог, 1, например, с выходов блока задания матрицы смежности, задают топологию моделиру ем ог о г р афа.
Процесс моделирования графа ничем не отличается от процесса моделировакия орграфа. Точно так же имитируют исполнение вершины или ребра графа и регистрируют изменения параметров дру гих вершин и ребер. Однако поскольку ФМР 36 и ФМВ 35 двунаправлены имитировать исполнение вершины (ребра) приходится на каждом из ее входов (выходов). С этой целью к выходам 40 состояния (К,М)-й ФМР 34 по М-й и вершинам модели графа подключают вхо ды 41 имитации исполнения ребра по М-й и К-й вершинам модели графа (фиг,18а). Если элементная база, выбранная для моделирования графа,или его топология (с циклами и петлямиЗЕ не допускает подключения входов/выходов ШР 34 к соответствующим входам 41, используют ключи 42-45 или коммутаторы 46 и 47. При подаче сигнала уровня лог. 1 на вход 48 приз30
35
40
45
50
функции) (К,М) -и тР 34 матрицы под- 55 имитации исполнения (К,М)-реб- ключен к (М-1)-му входу К-й ФМВ 35, Р- модели графа ключи 42 и 43 отклю- вход задания параметров моделирования которой является одноименным входом 37 модели графа. Пунктиром на
входы/выходы ФМР 34 от входов 41 ключи 44 и 45 подключают входы 41 к соответствукщим входам 40 (фиг.186,в
0
фиг . 16 показаны те ФМР 34, которые исключены из модели графа в силу симметрии его матрицу. смежности.
Необходимость задания перед началом работы параметров всех ФМР 34 матрицы при изменении топологии графа является недостатком базовой модели графа. В значительной мере он оп- ;ределен в универсальной модели графа, 1функциональная схема которой представлена на фиг.7. По сравнению с базовой моделью в универсальную модель графа введена матрица из 1/2 В(В+1)
5 ключей 38, причем второй вход аргумента (выход значения функции)(К,М)-и ФМ 34 матрицы подключен к первому Информационному входу/выходу (К,М)-го ключа матрицы, второй информационный вход/выход которого подключен к ()-му входу аргумента (выходу значения функции)К-й ФМВ 35 группы, вход 39 признака наличия (К,М)-го ребра модели графа подключен к управляюще5 му входу (к входу включения)(К,М)-го ключа 38 матрицы. Остальные конструктивные признаки базовой и универсальной моделей совпадают. Подавая на входы 39 потенциалы уровня лог, 1, например, с выходов блока задания матрицы смежности, задают топологию моделиру ем ог о г р афа.
Процесс моделирования графа ничем не отличается от процесса моделирова кия орграфа. Точно так же имитируют , исполнение вершины или ребра графа и регистрируют изменения параметров других вершин и ребер. Однако поскольку ФМР 36 и ФМВ 35 двунаправлены имитировать исполнение вершины (ребра) приходится на каждом из ее входов (выходов). С этой целью к выходам 40 состояния (К,М)-й ФМР 34 по М-й и вершинам модели графа подключают входы 41 имитации исполнения ребра по М-й и К-й вершинам модели графа (фиг,18а). Если элементная база, выбранная для моделирования графа,или его топология (с циклами и петлямиЗЕ не допускает подключения входов/выходов ШР 34 к соответствующим входам 41, используют ключи 42-45 или коммутаторы 46 и 47. При подаче сигнала уровня лог. 1 на вход 48 приз0
5
0
5
0
имитации исполнения (К,М)-реб- Р- модели графа ключи 42 и 43 отклю-
входы/выходы ФМР 34 от входов 41 , ключи 44 и 45 подключают входы 41 к соответствукщим входам 40 (фиг.186,в)
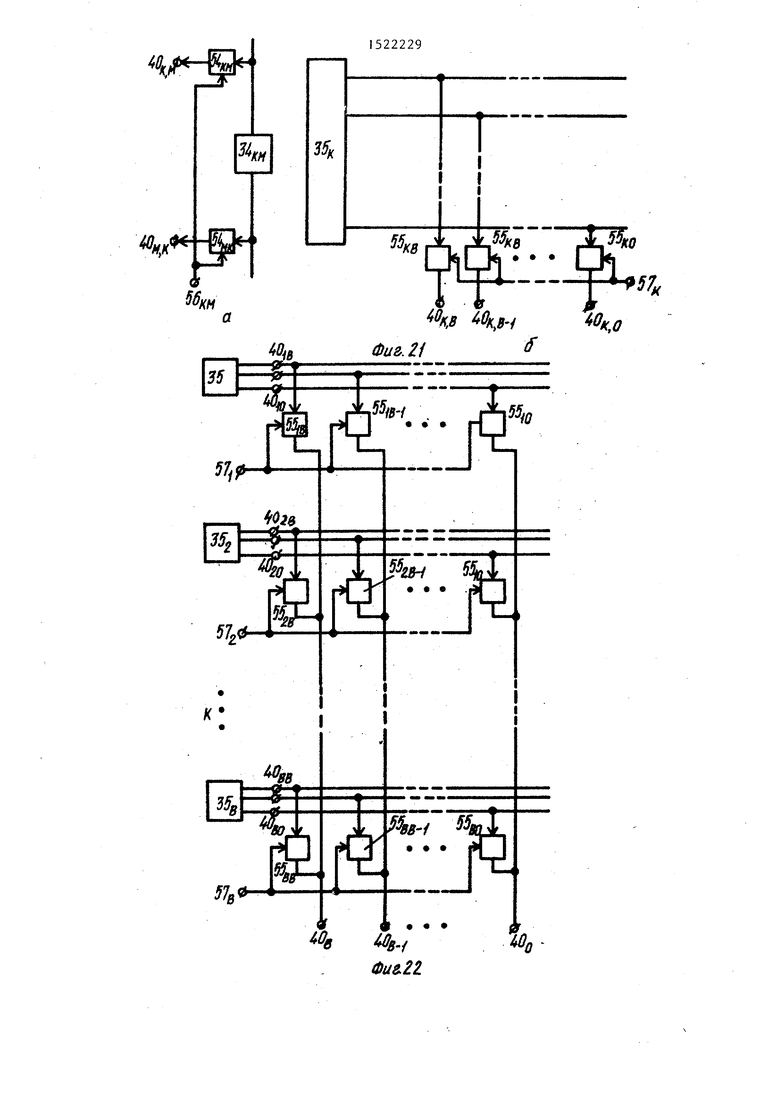
а коммутаторы 46 и 47 изменяют на- - правление коммутации (фиг.18г). Варианты схем для имитации исполнения взвешенных вершин показаны на фиг.19а-г. Точно так же при подаче сцгиала на вход 48 признака имитации исполнения вершины модели графа ключи 49 группы отключают входы/выходы ФМВ 35, ключи 50 группы подключают входы 51 имитации исполнения К-й вершины по М-му ребру модели графа к соответствующим выходам 40, а коммутаторы 52 группы изменяют направление, отключая входы/выходы ФМВ 35 от выходов 40 и подключая к выходам 40 соответствующие входы 51. Во всех случаях нулевой индекс в обозначении входов относится к обозначению петли, принадпежащей вершине, обозначен- JQ на выходе признака отношения (Больной вторым индексом того же цифрового обозначения входа.
Объединение вторых информационньрс направлений коммутаторов 46 и вторых информационных направлений коммутаторов 47 (т.е.объединение всех однотипных входов 41 имитации исполнения ребер) (фиг.20) позволяет ввести понятие входов 53 имитации исполнения начального ребра модели графа по К-й и М-й вершинам графа, В этом случае входы 48 признаков имитации исполнения ребер допустимо назьшать входами задания начальных ребер (фиг.20).
Такие же понятия могут быть введены и для имитации исполнания начальных вершин графа.
Регистрация состояния «ШР 34 по каждой из инцидентных верншк и состояния ШВ 35 по каждому инцидентному ребру ийогда также требует отключения выходов 40 от каждого из входов/выходов ШР 34 и ФМВ 35. С этой целью используют ключи 54 и 55. Подавая на вход 56 опроса состояния (К,М)-й ФМР 34 или вход 57 опроса состояния К-й ФМВ 35 модели графа потенциал уровня лог. I, подключают входы/ звыходы ФМР : 34 и ШВ 35 к соответствующим выходам 40. Объединяя по ИЛИ (на фиг.22 показано монтажное ИЛИ) информационные выходы ключей 55 с одноименными индексами, можно ввес.ти понятие выхода 40 состояния конечной вершины графа по К-му ребру моделк графа. В этом случае входы 57 опроса состояния вершин модели графа допусткше.
25
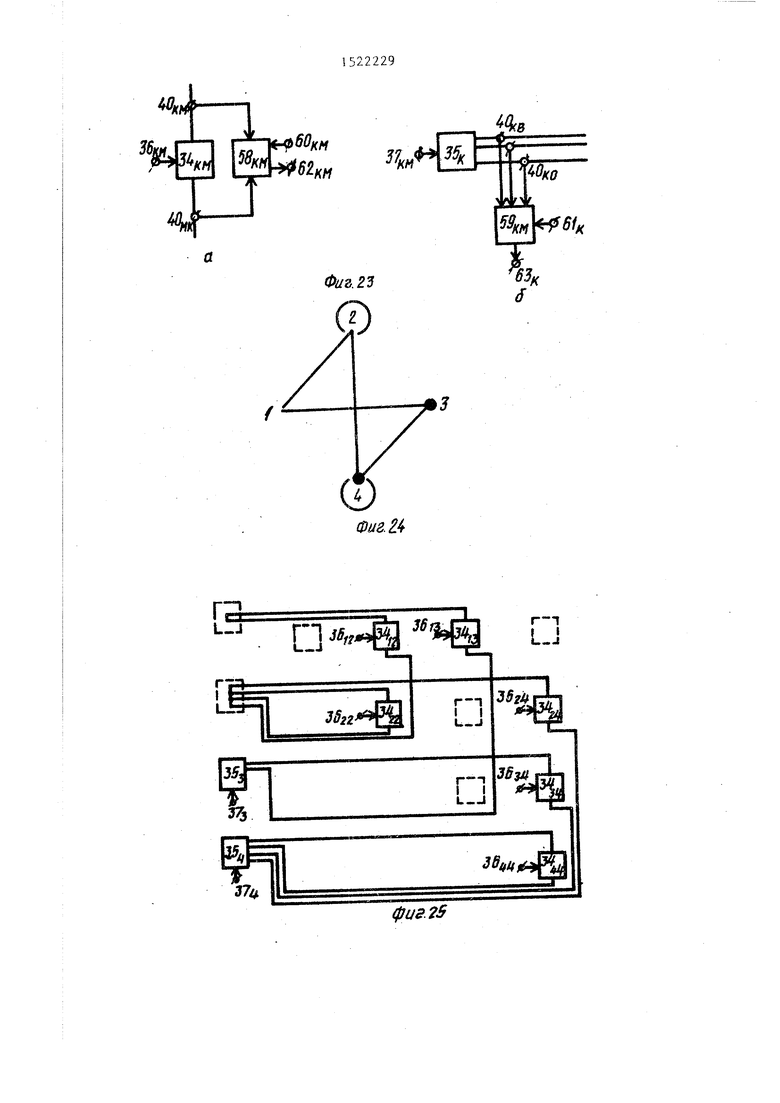
Меньше, Равио и т.п.) блока 58 и/или 59 сравнения, который является выходом 62 и/илн 63 осуществ- ления события модели графа (фиг.23а,б
Аппаратшле средства моделей графов можно значительно упростить, используя метод структурной оптимизации, Например, для графа, топология которого представлена на фиг.24 (цифрами
30 обозначены номера вершин, взвешенные вершины изображены в вк;; а жкрной точки) , структурная оптимизация базовой и универсальной моделей графа показана на фиг.25 и 26 соответ ственнсу Обычно в .этом случае говорят, что ФМР 34 и ФМВ 35 соединены в ссютветст- ВИИ с топологией графа. Пунктиром на фиг.25 и 26 показаны 34 и {B35s которые исключены из базовой и уни4Q версальной моделей графа в результате их структурной оптимизации.
Конструктивно аппаратные средства моделей графов могут быть выполнены в виде модулей. В модуль может быть введена любая повторяющаяся часть аппаратных средств. На фиг.27а показан модуль 64, в состав которого введены Ф№ 34 и ключ 38. В эгом случае универсапьная модель графа принимает вид, показанкый на фиг.276.
Таким образом, методы и средства моделирования, оптимизации и построения моделей графов практически ничем не отличаются от аналогичных методов и средств моделей орграфов, если не с... ,ать использование элементов,двунаправленных по своим входам/выходам и исключение.всех подциагональных элементов из структуры соответствую45
50
55
5
МО называть входами задания конечной вершкны грзфа.
Таким же образом можно задавать конечные ребра графа
Решение некоторых задач требует регистрации некоторых характерных состояний ФМР 34 и ФМВ 35, например - начало моделирования вершины (ребра), окончания моделирования и т.п. В этом случае ко всем или некоторьм выходам 40 состояния ФМР 34 и/или ФМВ 35 подключают блоки 58 и/или 59 сравнения. По входам 60 и/или 61 задают значения параметров по Каждому выходу 40, совокупность которых (параметров) служит признаком осуществления события, о появлении которой говорит появление сигнала уровня лог. 1
JQ на выходе признака отношения (Больше.
25
Меньше, Равио и т.п.) блока 58 и/или 59 сравнения, который является выходом 62 и/илн 63 осуществ- ления события модели графа (фиг.23а,б).
Аппаратшле средства моделей графов можно значительно упростить, используя метод структурной оптимизации, Например, для графа, топология которого представлена на фиг.24 (цифрами
0 обозначены номера вершин, взвешенные вершины изображены в вк;; а жкрной точки) , структурная оптимизация базовой и универсальной моделей графа показана на фиг.25 и 26 соответ ственнсу Обычно в .этом случае говорят, что ФМР 34 и ФМВ 35 соединены в ссютветст- ВИИ с топологией графа. Пунктиром на фиг.25 и 26 показаны 34 и {B35s которые исключены из базовой и униQ версальной моделей графа в результате их структурной оптимизации.
Конструктивно аппаратные средства моделей графов могут быть выполнены в виде модулей. В модуль может быть введена любая повторяющаяся часть аппаратных средств. На фиг.27а показан модуль 64, в состав которого введены Ф№ 34 и ключ 38. В эгом случае универсапьная модель графа принимает вид, показанкый на фиг.276.
Таким образом, методы и средства моделирования, оптимизации и построения моделей графов практически ничем не отличаются от аналогичных методов и средств моделей орграфов, если не с... ,ать использование элементов,двунаправленных по своим входам/выходам и исключение.всех подциагональных элементов из структуры соответствую5
0
5
щих неориентированным графам аппаратных средств.
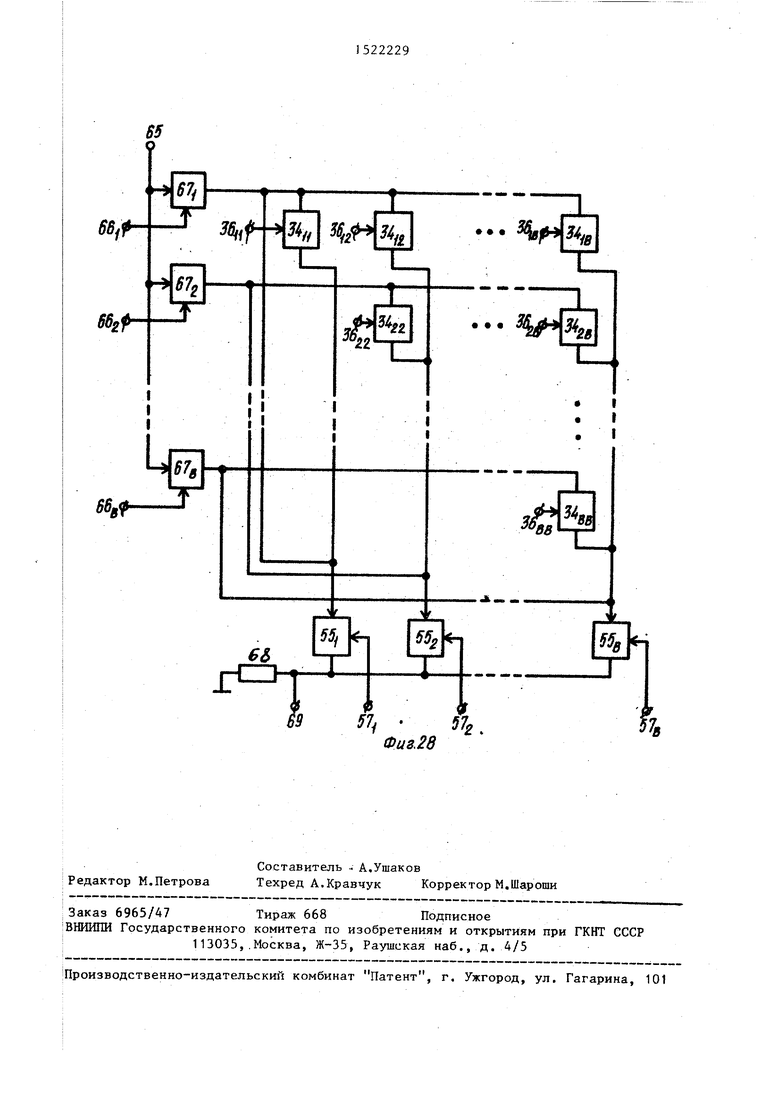
В соответствии с изложенным блок 1 определения кратчайших путей для неориентированного графа без взвешенных ребер может быть выполнен по схеме, показанной на фиг.28.
В том случае, если ФМР 34 выполнены в виде двунаправленных пороговых элементов и перед началом работы по входам 36 задан порог срабатьгоания каждой ФМР 34, то при подаче возрастающего сигнала на вход 65 имитации исполнения начальной вершины указанный сигнал через один из ключей 67, открытый подачей на его управляющий вход сигнала уровня лог. 1 с одноименного входа 66 задания начальной вершины графа, поступает на ФМР 34, соответствующие ребрам, инцидентным начальной вершине. Когда значение сигнала на входе 65 превысит величину кратчайшего пути из начальной в конечную вершину графа, ФМР 34 (т.е. фактически, пороговые элементы) срабатьгоают и на резисторе 68 образуется падение напряжения, которое в качестве признака окончания моделирования конечной вершины графа поступает на выход 69 блока 1. формула изобретени
Устройство для анализа параметров графа, содержащее блок определения кратчайшего пути и времяимпульсный интегрирующий преобразователь, информационный выход которого подключен к входу имитации состояния начальной
вершины блока определения кратчайшего пути, входы задания конечной вершины графа которого являются входами задания центра графа устройства, отличающееся тем, что, с целью сокращения аппаратурных затрат при определении вершин, входящих в окрестность центра графа, в него введены блок синхронизации и накапливающий блок логического сложения, причем вход задания радиуса окрестности графа устройства подключен к входу задания- порога интегрирования время5 импульсного интегрирующего преобразо вателя, выход признака достижения порога которого подключен к входу пуска устройства и к тактовому входу блока синхронизации, первый и второй вьпсоды которого подключены к входу установки в О и к входу разрешения работы времяимпульсного интегрирующего преобразователя соответственно, К-й выход группы блока синхронизации (,..,,Bj где В - количество вершин в графе) подключен к К-му разряду информационного входа накапливающего блока логического сложения и к К-му входу задания начальной вершины блока определения кратчайшего пути, выход признака окончания моделирования конечной вершины графа которого подалючен к тактовому входу накапливающего блока логического сложения,
С К-й разряд информационного выхода которого является выходом признака принадлежности К--й вершины составу верпшн окрестности центра графа устройства.
0
5
0
% /4
/f
Ж
19
а
фигЛ
Фг )-0f4
X
м
/f
i5
r
a
Ф1/&7
%A
«v
ф//в .
/4 «
M
«« % %
;f 1-
/f
fr-
Фиг. 6
Z
%
Фив.
Фив. 11
Фив. 0
I1
I I I1
5,J
/5.
8
/5
K
15,
Фuг.fЗ
j I3n
I-I I I
L--I
Фиг. 12
6
«xf «
Фае. 15
М
I М
It
gruf. f
4а
щ
40и
5
Фиг18 5 4
И It 11
54г
J
t 0
%
Д
Фив./9
Фиг.20
%м
(Р
Af
5
1Л,
./i
К.О
МО
g б
8В
3ft
В
IB
40g
1522229
4
(I
5-/
Фи&22
40,
5ft
w
AW
KM
rs
L-J
П
rp
ДДгг
4,
/(«
Т
63,
f
Jff
LJ
П
3S2J
г
т i1
3BtfH
(pus. 5
JK
Н%«
3
KI4
Щ2
(щ %fe|% %t
.З Л-4Л --.
J Л
4j
39,
KM
%/f
a
м
Jfg -
т
№
фиг 26
%t
АЛ
J Л
4j
и
f
Щ
%f- - % %
t
57ee f
%
л:.
У
3
2В
I
I I
ВВ
57 572 Физ.28
| Устройство для исследования параметров графов | 1984 |
|
SU1241266A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для определения параметров графов | 1984 |
|
SU1251097A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-11-15—Публикация
1988-02-03—Подача