Изобретение относится к автоматике и вычислительной технике и может быть использовано для создания генераторного оборудования многоканальных систем связи.
Известен блок формирования функций Уолша, содержащий источник постоянного напряжения, n-разрядный счетчик (где 2П - число формируемых функций Уолша) и (п-1) групп умножителей по (2-1) умножителей в каждой группе (где i - порядковый номер группы, I 1 ,п-1), причем первый вход умножителя первой группы подключен к выходу первого разряда счетчика (нумерация разрядов со стороны старшего разряда счетчика), первые входы умножителей 1-й группы, кроме первой, подключены к выходам с первого по 1-й разрядов счетчика и к выходам умножителей групп с первой по (Н)-ю, вторые входы умножителей 1-й группы подключены к выходу (1+1)-го разряда счетчика, счетный вход счетчика является тактовым
входом блока формирования функций Уолша, а выход источника постоянного напряжения, выходы разрядов счетчика и выходы умножителей являются выходами блока формирования функций Уолша.
Однако известный блок формирования функций Уолша формирует систему функций Уолша, которая обладает большой эффективной шириной спектра, что ограничивает класс решаемых задач.
Наиболее близким к предлагаемому по технической сущности является генератор дискретных ортогональных функций, содержащий тактовый генератор, блок формирования функций Уолша, состоящий из источника постоянного напряжения, п-раз- рлдного счетчика (где 2П - число формируемых функций Уолша) и (п-1) групп умножителей по (21 - 1) умножителей в каждой группе (где I - порядковый номер группы, i 1,п-1), формирователь импульсов, триггер, два ключа, сумматор и 2П дополниС
ел
OD S
тельных умножителей (2П - число генерируемых функций), причем первый вход умножителя первой группы подключен к выходу первого разряда счетчика (нумерация разрядов со стороны старшего разряда счетчи- ка), первые входы умножителей i-й группы, кроме первой, подключены к выходам с первого по 1-й разрядов счетчика и к выходам умножителей групп с первой по (1-1)-ю, вторые входы умножителей i-й группы подклю- чены к выходу ( разряда счетчика, счетный вход счетчика является тактовым входом блока формирования функций Уол- ша, а выход источника постоянного напряжения, выходы разрядов счетчика и выходы умножителей являются выходами блока формирования функций Уолша, выход тактового генератора подключен к тактовому входу блока формирования функций Уолша, выход второй функции Уолша блока форми- рования функций Уолша соединен с входом формирователя импульсов и с информационным входом первого ключа, выход 2а-й функции Уолша блока формирования функций Уолша соединен с информационным входом второго ключа, выход формирователя импульсов подключен к счетному входу триггера, прямой и инверсный выходы триггера подключены к управляющим входам первого и второго ключей соответственно, выходы первого и второго ключей подключены к входам сумматора, выход сумматора подключен к первым входам всех дополнительных умножителей, выходы блока формирования функций Уолша подключены к вторым входам дополнительных умножителей, выходы дополнительных умножителей являются выходами генератора дискретных ортогональных функций.
Однако известный генератор дискрет- ных ортогональных функций обладает значительной сложностью.
Целью изобретения является упрощение генератора.
Поставленная цель достигается тем, что в генераторе дискретных ортогональных функций, содержащем тактовый генератор, формирователь импульсов, триггер, два ключа, сумматор, (п+1) умножителей и блок формирования функций Уолша, включаю- щий n-разрядный счетчик и (п-1) групп умножителей по (2-1) умножителей в каждой группе (2П - число генерируемых функций, i - 1.П-1), причем выход тактового генератора соединен со счетным входом счетчика, вы- ход первого разряда которого соединен с информационным входом первого ключа и входом формирователя импульсов, выход которого соединен со счетным входом триггера, инверсный и прямой выходы которого
соединены соответственно с управляющими входами первого и второго ключей, выходы которых соединены с входами сумматора, выход которого соединен с первыми входами всех п-Н умножителей, а информационный вход второго ключа соединен с выходом п-го разряда счетчика, второй вход первого умножителя соединен с первым выходом блока формирования функций Уолша и с шиной единичного потенциала, первые входы умножителей i-й группы соединены с выходом (i+1)-ro разряда счетчика, второй вход умножителя первой группы соединен с выходом второго умножителя jerrapbie входы умножителей j-й группы (j 2,п-1) соединены с выходами с второго по (1+1)-й умножителей и выходами умножителей с первой по (И)-ю групп, второй вход k-ro умножителя (k 2, п+1) соединен с выходом (k-1)-ro разряда счетчика, выходы умножителей и умножителей с первой по (п-1)-ю групп являются выходами генератора.
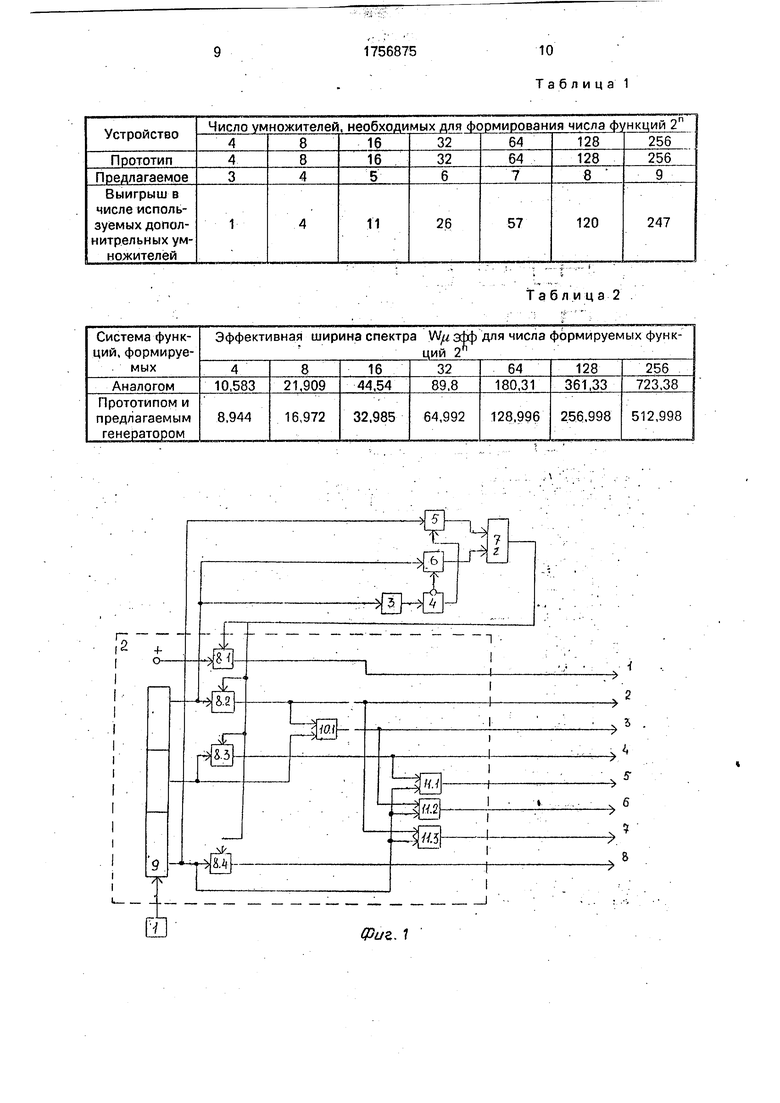
На фиг. 1 представлена структурная схема генератора дискретных ортогональных функций для случая п 3; на фиг. 2 - временные диаграммы, иллюстрирующие процесс формирования предлагаемым генератором дискретной функции Ф(5, в}; на фиг. 3 - временные диаграммы функций Уолша, формируемых аналогом; на фиг. А - временные диаграммы дискретных ортогональных функций, формируемых прототипом и предлагаемым генератором.
Генератор дискретных ортогональных функций содержит тактовый генератор 1, блок 2 формирования функций Уолша, формирователь 3 импульсов, триггер 4, ключи 5 и 6, двухвходовый сумматор 7, умножители 8.1 -8.4.
Блок 2 формирования функций Уолша состоит из счетчика 9, умножителя 10.1 первой и умножителей 11.1 - 11.3 второй группы.
Система функций Уолша содержит функции, имеющие число блоков г 1,2N
(где блок - последовательность одинаковых элементов). Вследствие этого значение максимальной эффективности ширины спектра сигнала, входящего в систему, определяется с учетом ft N (фиг. 3)
... ., «2 2ft-1 N-
(D
где N - число элементов фазоманипулиро- ванного сигнала; A t - длительность элемента сигнала.
-В прототипе для уменьшения числа блоков в функциях до значений
N
N + 2
P--TI или ц--2
используется умножение всех функций Уол- ша на одну и ту же функцию Ф(0, в).
Поскольку функции, формируемые прототипом, имеют максимальное число блоков
N 4-2
fi , значение максимальной эффективной ширины спектра сигнала, входящего в систему функций, формируемых прототипом, определяется в соответствии с (1) и оказывается значительно меньшей, чем у аналога.
Однако для .этой цели в прототипе используется 2П умножителей, поскольку каждая из 2П функций Уолша умножается на функцию Ф(0, в, т.е.
(2)
Так как все 2 функций Уолша, кроме Wal(0, в), формируются из п функций Раде- махера посредством их перемножения, то для получения функций Ф(1, в) достаточно осуществить умножение функции Ф(0, в) на каждую из п функций Радемахера и в дальнейшем использовать эти произведения для формирования дискретных ортогональных функций Ф(1, в). В этом случае число умножителей окажется равным (п+1) с учетом умножителя, необходимого для формирования из функции Wal(0, в) функции Ф(0,
0).
Для различного числа функций, формируемых прототипом и предлагаемым гене- ратором, было рассчитано число умножителей 8, входящих в состав их схем. Результаты расчетов представлены в табл. 1.
Как следует из расчетов, представленных в табл. 1, при увеличении числа формируемых функций выигрыш в числе используемых умножителей стремится к 100%.
Результаты расчетов эффективной ширины спектра систем функций-, формируемых аналогом, прототипом и предлагаемым генератором, представлены в табл. 2,
По результатам табл. 2 видно, что эффективная ширина спектра системы сигна- 5 лов, формируемых прототипом и предлагаемым генератором, существенно меньше, чем у сигналов, формируемых аналогом.
Генератор дискретных ортогональных 10 функций работает следующим образом.
Исходное состояние триггера 4 - единичное. Потенциалы с прямого и инверсного выходов триггера 4 поступают на управляющие входы ключей 5 и 6. Таким 15 образом, ключ 5 открыт, а ключ 6 закрыт. Под действием импульсов с выхода тактового генератора 1, поступающих на счетный вход счетчика 9, на выходах разрядов счетчика 9 формируются функции Радемахера 0 п( в). гг( в)гп( в.
Функция Радемахера гп (в), формируемая на выходе n-го разряда счетчика 9, представляет собой функцию Уолша Wal(2 -1, в ), которая при упорядочении по Уолшу 5 формируется на 2п-м выходе блока формирования функции Уолша в прототипе. Эта функция через открытый ключ 5 поступает на вход сумматора 7 и формируется на его выходе.
Функция Радемахера п( в), формируемая на выходе первого разряда счетчика 9, представляет собой функцию Уолша Wa(1, в), которая при упорядочении по Уолшу формируется на втором выходе блока формирования функций Уолша в прототипе. Эта функция поступает на вход закрытого ключа 6 и вход формирователя 3 импульсов. В момент смены знака этой функции срабатывает формирователь 3 импульсов. Импульс, поступающий с его выхода, изменяет состояние триггера 4, а следовательно, и состояние ключей 5 и 6. В результате функция п (в) через открытый ключ б поступает на вход сумматора 7 и формируется на его выходе. Таким образом, в течении 2 тактов на выходе сумматора 7 формируется функция Ф(0, в), первый полупериод которой представляет собой первый полупериод функции Гп( #)(или Wal(2n-1, в)), а второй полупериод представляет собой второй полупериод функции п( #)(или Wai(1, 0)).
Функция Ф (0, $) умножается в (п+1) умножителях на функции Радемахера п( в). rz( 0),...,гп( $)и на постоянное напряжение, представляющее собой функцию Уолша Wal(0, в).
Следовательно, на выходе умножителя 8.1 в котором осуществляется умножение
0
5
0
5
0
5
функции Ф(0, в) на постоянное напряжение, формируется функция Ф(0, 0).
На выходе второго умножителя 8.2 формируется функция
Ф(0,6) -п(6$ Ф(0,0) WalO.fl-cDO.fl
из соотношений (1) и (2).
На выходе умножителя 10.1 первой группы формируется функция
Ф(0.6) -п(6) -Г2(65 Ф(0,- Wal(2,0) - Ф(2, 6)
из соотношений (1) и (2) и т.д.
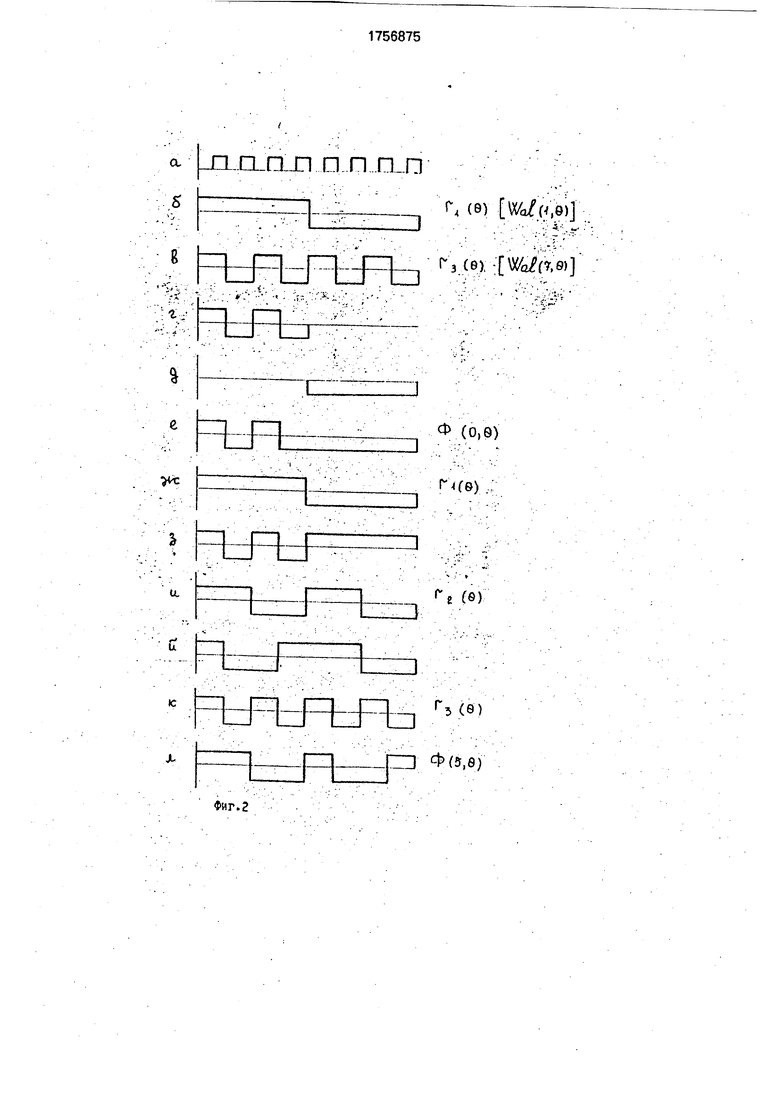
На фиг. 2 приведены временные диаграммы, иллюстрирующие процесс формирования предлагаемым генератором функции Ф(5, 0) для случая п 3, на которых показано временное состояние:
а - выхода тактового генератора 1; б - выхода первого разряда счетчика 9, на котором формируется функция Радема- хера п( в), являющаяся функцией Уолша Wal(1, 0);
в - выхода третьего разряда счетчика 9, на котором формируется функция Радема- хера гз( 0), являющаяся функцией Уолша Wal(7,0);
г- выхода ключа 5; д - выхода ключа 6;
е - выхода сумматора 7, на котором формируется функция Ф(0, в}, поступающая на второй вход умножителя 8,2;
ж - выхода первого разряда счетчика 9, на котором формируется функция п( в), поступающая на первый вход умножителя 8.2; з - выхода умножителя 8.2, сигнал с которого поступает на первый вход умножителя 10.1 первой группы;
и - выхода второго разряда счетчика 9, на котором формируется функция Г2( 0, поступающая на второй вход умножителя 10.1 первой группы;
и - выхода умножителя 10.1 первой группы, сигнал с которого поступает на первый вход умножителя 11.2 второй группы;
к - выхода третьего разряда счетчика 9, на котором формируется функция гз( 0, поступающая на второй вход умножителя 11.2 второй группы;
л - выхода умножителя 11.2 второй группы, на котором формируется функция Ф(5, в).
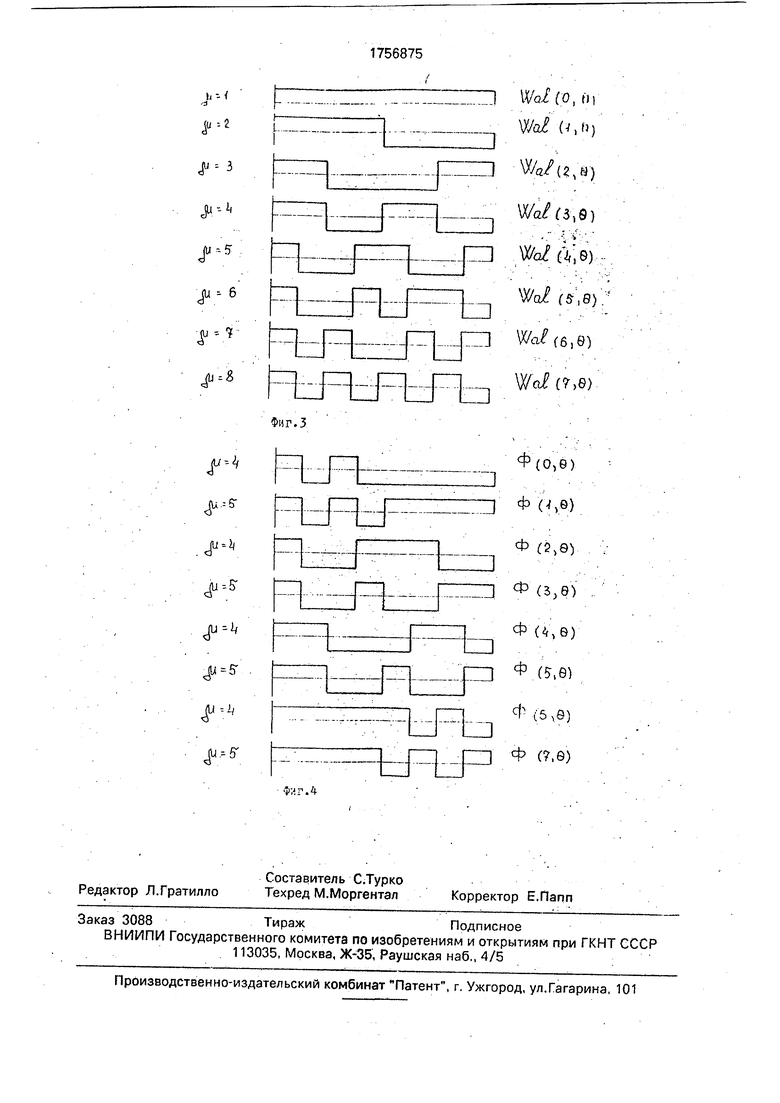
На фиг. 3 приведены функции Уолша Wal(l, 0), формируемые аналогом для случая 2П 8. На фиг. 4 приведены функции Ф(1,
в), формируемые прототипом и предлагаемым генератором
Таким образом, предлагаемый генератор дискретных ортогональных функций
формирует те же функции Ф(1, в), что и прототип. При этом для формирования 2П дискретных ортогональных функций в прототипе используется 2П умножителей 8. В предлагаемом генераторе для формирования 2П дискретных ортогональных функций используется только n-И умножителей 8. Выигрыш в числе умножителей 8 равен (2П- -п-1) и при увеличении п стремится к 100%. Использование изобретения позволяет
создавать генераторное оборудование многоканальных систем связи, обеспечивающее значительное упрощение генератора функций.
20
Формула изобретения
Генератор дискретных ортогональных функций, содержащий тактовый генератор, деформирователь импульсов, триггер, два
ключа, сумматор (п+1) умножителей и блок формирования функций Уолша, включающий n-разрядн.ый счетчик, (п-1) групп умножителей по (21 -1) умножителей в каждой группе (2П - число генерируемых функций,
1,п-1), причем выход тактового генератора соединен со счетным входом счетчика, выход первого разряда которого соединен с информационным входом первого ключа и входом формирователя импульсов, выход
которого соединен со счетным входом триггера, инверсный и прямой выходы которого соединены соответственно с управляющими входами первого и второго ключей, еыхо- ды которых соединены с входами
сумматора, выход которого соединен с первыми входами всех п+1 умножителей, а информационный вход второго ключа соединён с выходом n-го разряда счетчика, второй вход первого умножителя соединен
с вторым выходом блока формирования функций Уолша и шиной единичного уровня, первые входы умножителей i-й группы соединен с выходом (i-M)-ro разряда счетчика, отличающийся тем, что, с целью
упрощения, второй вход умножителя первой группы соединен с выходом второго умножителя, вторые входы умножителей j-й группы 0 2,п-1) соединены с выходами с второй по (1+1)-й умножителей и выходами
умножителей с первой по (И)-ную групп, второй вход k-ro умножителя (k 2,п+1) соединен с выходом (k-1)-ro разряда счетчика, выходы умножителей и умножителя с первой по (п-1)-ю групп являются выходами генератора.
1756875
10 Таблица 1



| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПОСЛЕДОВАТЕЛЬНОСТЕЙ КОДА ДЖЕФФИ | 2016 |
|
RU2620988C1 |
| Генератор дискретных ортогональных функций | 1989 |
|
SU1783506A1 |
| ГЕНЕРАТОР ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 2017 |
|
RU2634234C1 |
| ГЕНЕРАТОР ПОСЛЕДОВАТЕЛЬНОСТЕЙ КОДА СТИФФЛЕРА | 2017 |
|
RU2668742C1 |
| Устройство для моделирования дискретных ортогональных сигналов | 1989 |
|
SU1686428A1 |
| ГЕНЕРАТОР ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 1991 |
|
RU2022332C1 |
| ГЕНЕРАТОР ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 2011 |
|
RU2446437C1 |
| Генератор дискретных ортогональных функций | 1989 |
|
SU1686429A1 |
| ШИРОКОПОЛОСНАЯ СИСТЕМА РАДИОСВЯЗИ | 2009 |
|
RU2411654C1 |
| Генератор дискретных ортогональных функций | 1990 |
|
SU1784958A1 |
Изобретение относится к автоматике и вычислительной технике и может быть использовано для создания генераторного оборудования многоканальных систем связи. Цель изобретения - упрощение генератора. Генератор дискретных ортогональных функций содержит тактовый генератор, блок формирования функций Уолша, состоящий из источника постоянного напряжения, n-разрядного счетчика (где 2П - число генерируемых функций) и (п-1) групп умножителей по (2-1) умножителей в каждой группе (где i - порядковый номер группы, i 1 ,п-1), формирователь импульсов, триггер, два ключа, сумматор и (п+1) дополнительных умножителей. 4 ил.,2 табл.
Таблица 2
Фиг. 7
а JjTLTLrLD П.П ГШ
б
1 j
8
I
TZ
с
а
Г, (б) №/fl,9)
А ...
и
Гэ.О). - Wotoe)
Ф (0,9)
П(6).
13
е (б)
Z1
Г3(9)
Ф(5,б)
| Хармут Х.Ф | |||
| Передача информации ортогональными функциями | |||
| М.: Связь, 1975, с | |||
| Приспособление для соединения пучка кисти с трубкою или втулкою, служащей для прикрепления ручки | 1915 |
|
SU66A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Генератор дискретных ортогональных функций | 1986 |
|
SU1386981A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1992-08-23—Публикация
1990-09-04—Подача