Струнный гальванометр, шлейфный осцилло граф и обычный гальванометр, как измерительные приборы и как модуляторы света, обладают тем недостатком, что со5ственный период их, определяющийся упругостью и массой их подвижных электрических систем, лежит в области звуковых частот; это ставит предел частоте регистрируемых ими процессов.
Предлагаемое изобретение для уменьшения периода собственных колебаний такого рода подвижных систем (струна, шлейф струнного осциллографа нли рамка гальванометра) использует уже известный способ измерения механических параметров движущихся систем, помещенных в магнитном поле, основанный на том, что параллельно указанной системе присоединяют контур, ооладающий самоиндукцией или емкостью.
Согласно предлагаемому изоб,1етению, с целью устранения ьлияния соост1енного активного сопротивления аодиижной системы, последовательно с нею ьключают некоторое отрицательное сопротивление.
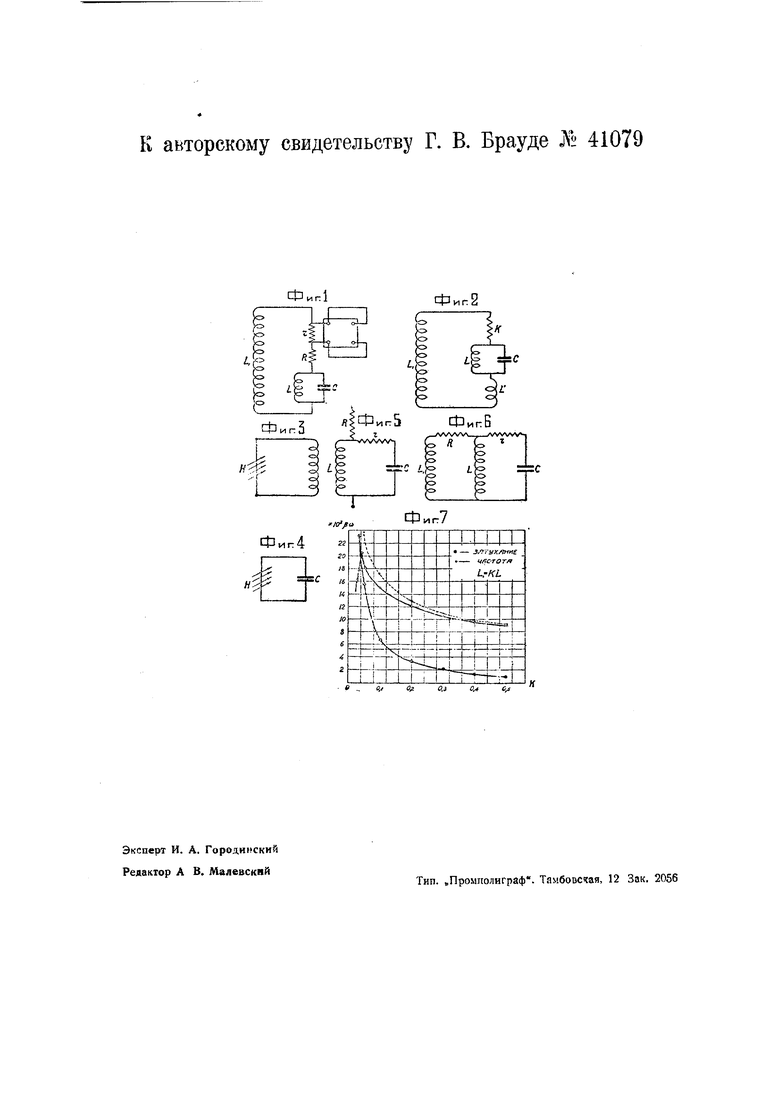
На чэртеже фиг. 1 изображает схему устройства для осуществления предлагаемого способа; фиг. 2 - схему видоизмененного устройства; фиг. Зи4 - схемы проводника, замкнутого на самоиндукцию или емкость; фиг. 5 и 6 - эквивалентную электрическую схему струны, например, струнного гальванометра; фиг. 6 - видоизменение схемы по фиг. 5 и фиг. 7 - крииые затухания и частоты системы по фиг. 6.
Для уяснения сущности п:)едлагаемого способа рассмотрим силы, действующие на проводник, находящийся в магнитном поле, в том случае, когда к нему присоединена самоиндукция (фиг. 3).
При движении проводника в магнитном поле
(513)
в нем индуктируется электродвижущая сила, проdy
порциональная скорости эта электродвижущая сила вызовет ток через самоиндукцию, приключенную к проводнику, причем напряжение на концах этой самоиндукции, пропорциональное
di скорости изменения силы тока L-, должно быть
равно электродвижущей силе, индуцируемой в проводнике. Таким образом, через самоиндукцию, а следовательно и через проводник пройдет ток, скорость изменення которого пропорциональна скорости проводника; сам же ток будет пропорционален перемещению проводника. От взаимодействия этого тока с магнитным полем в проводнике возникнет пропорциональная перемещению пондремоторная сила, которая, склады ваясь с упругой силой, возникающей при перемещении в системе, составленной из таких проводников, и также пропорциональной этому перемещению, будет увеличивать собственную частоту системы (уменьшать ее период).
Простейшей системой такого рода является струна струнного гальванометра.
Повышение собственной частоты струны всего на 30-40% дает возможность устранить искажения, появляющиеся при звукозаписи, посредством струнного осциллографа; повышение частоты в несколько раз дает возможность применить струну в качгстве м; щного модулятора снета при оптической телефонии, а поьышение собственной частоты струны в десятки раз дает возможность применить ее в качестве мощного модулятора в телевидении (осуществить телевидение на большом вкране).
В дальнейшем исследование проведено на примере струны, причем полученные вывты могут быть легко распространены и на другие подвижные электрические системы, помещенные в постоянное магнитное поле.
Несмотря на справедливость изложенных вышэ соображений, их совершенно недостаточно для осуществления существенного ьозд йствия на сооственный период струнного резонатора. Оказывается необходимым более глубокое теоретическое рассмотрение этого вопроса.
Автором было показано (Журнал прикладной физики, том 6, вып. 6, 1929 г,}, что струна в магнитном поле представляет для переменного тока сопротивление, зависящее от частоты, причем постоянная часть ее сопротивления, не зависящая от частоты, представляет собой ее собственное омичгское сопротивление, перзменная же ее часть имеет максимум при резонансе с основной частотой струны и вообще изменяется частотой по своей величине и фазе так же, как сопротивление параллельного колебательного контура. Сопротивление при резонансе в случае равномерного магнитного поля выражается следующей формулой
где / -длина струны,- Н- сила магнитного поля, р-плотность материала струны, /-площадь поперечного сечения, - затухание струны.
Эквивалентная электрическая схема струны может быть таким образом представлена в виде параллельного колебательного контура, соединенного последовательно с собственным омическим сопротивлением струны (фиг. 5). Исходя из приьеденного кыще выражения для величины сопротивления сгруны (переменной ее части) при резонансе, можно вычислить посгоянные эквивалентной электрической схемы струны.
У сгруны длины /, площади поперечного сечэния /, плотности р, с коэфициентом затухания р, натянутой силой Р и помещенной в магнитное поле силой Н сопротивление при резонансе
4/ /Я
712 р/р
собственная часига
-
I у pf V LC
затухание
Р
2 L
где i -эквивалентная самоиндукция струны, С-эквивалентная емкость струны и г-соп:)0тиьление, эквиьалентноа потерям энергии струны при колебаниях (не имеет никакого отношения к собственному омическому сопротивлению R струны).
Из этих уравнений получается следующее ыражение эквивалентных электрических постоянных струны через ее механические :йостоянные и силу магнитн)го поля
16Э/ №
8Р т
712 р/
С
-л: р
г 7f4 р
8/ Я2
Очевидно, что при приключении к сх мг, изобран{еН11ой на фиг 5, некоторой самоиндукции L (фиг. 6) собственная частота всей схемы уьеличится. Весь ьопрос в стгпени этого увеличения. При омическом сопротивлении струны такой величины, что им можно пренебречь по срав ei.Hio с величинами реактивных сопротивлз1 Ий эквивалентной схемы струны, собственная частота струны может повышаться приключением к ней самоиндукции в любой степени вплоть до бесконечности (при LI 0). Наоборот при омическом сопротивлении R такой ьеличины, что по сравнению с ним можно пренебречь реактивными сопротивлениями эквивалентной схемы струны, приключение к нзй самоиндукции любой величины не изменит существенно собственной частоты струны.
Таким образом, для того, чтобы посредством приключения к струне самоиндукции существенно увеличить собственную частоту колебания струны, необходимо, чтобы струна обладала возможно меньшим собственным омическим сопротивлением и одноврзменно возможно оольшими реактивными сопротивлениями. В употребляющихся осциллографах это условие обычно не соблюдено и поэтому измзнить сущесгьенно их собствен ый период указанным выше методом в большей части невозможно. Принимая во BI имание, что емкостное сопротивление CTpyi ы об,)атно a.joпорционально плотности струны р, а омическое соп.ютивление прямт пропо щно.я .ьпо уде :ьному сопротивлению струны о, необходимо материал для струны ьыб,;ать такой, чтобы произведение его плотности на yдeльнoJ сопротивление было наименьшим. Такими материалами являются, например, алюминий, дюралюминий, серебро.
Если струну, обладающую таким омическим сопротивлением и массой, поместить в магнитное поле такой силы, что уже нельзя будет пренебречь ее реактивными сопротивлениями по сравнению с омическим, то период собственных колебаний струны уже может быть существенно изменен.
Легко, однако, видеть, что величина этого изменения ограничена, так как приключение к системе бесконечно малой самоиндукции в случае, когда омичэское сопротивление является конечной величиной, не вызо1ет увеличения частоты системы до бесконечности, а, наоборот, уменьщит ее частоту, увеличив только ее затухание. 1аким образом, при уменьшении величины самоиндукции, приключенной к системе, собственная частота ее будет в начале расти и затем, достигнув при некоторой величине самоиндукции максимума, начнет уменьшаться, причем затухание системы будет непрерывно расти. Величина самоиндукции, приключенной к системе для увелич-ння ее соостаенной частоты, им JOT оптимум.
Все вышесказанное можно вывести из диференциальною уравнения системы, откуда можно вычислить оптимальную величин самоиндукции, величину возможного увеличения частоты и получающееся при этом затухание системы. Написав уравнения Кирхгофа для схемы, изображенной на фиг. б, и, пренебрегая г, в ъиау незначительности ьеличины затухания струны, получае.м следующее дифе,}енциаль;юе ураснение:
А -г-/. dl R
г 0 1 ЛЗ Г di2 Г 1C ut Т LC
Соответст1ующеэ этому лиферекциальному уравнению характеристическое уравнение 3-й степени
L,x + Rx + - х +
трудно поддается аналитическому исследованию, но из него lio всяком случае легко вытекают все вышеописанные выводы; кроме того, вычисляя комплексные корни этого уравнения для различных значений параметров с.чемы, можно графически иccлeдoLarь поведение системы. На прилагаемом графике (фиг. 7) представлена зависимость собстиенной частоты (мнимая часть комплексного корня) и затухания (вещественная часть комплексного корня) струны из алюминия длиной 9 см, диаметром 0,2 мм, с собственной круговой частотой 5200, помещенной в магнитное поле в 15000 Н, обладающей следующими эквивалентными электрическими постоянными;
L б. С 6.10- F; R ОД Q (г 2000 пренебрегаем)
в зависимости от величины приключенной к ней самоиндукции LI. Из графика видно, что частота сг.уны дейстьите.шно, изменяясь с изменением ij, достигает при некотором оптимальном значении i, 0,04L максимальной ьеличины в 20400, преьышающей собственную частоту струны почти в 4 раз:. Но при этом затухание струны резко возрастает таким образом, что повышать частоту струны больше чем в 2-3 раза не имеет смысла. Там же на графике пунктиром нанесена кривая изменения частоты струны в том случае, если бы у струны i;e было совсем собственною омического сопротивления.
По данным автора, эксперимент подтверждает теоретический расчет не только качественно, но и по порядку получающихся количественных изменений частоты и затухания. 1 очного количественного соьпадания и нельзя ожидать ввиду того, что П1;и построении эквивалентной схемы струны мы пренебрегли величиной и гармониками струны. При учете этих последних эквивалентная система струны не могла бы быть представлена как один параллельный колебательный контур, а должна была бы представлять соб&й ряд последовательно соединенных параллельных колебательных контуров.
Из исследования характеристического уравнения также следует, что возможное увеличение собственной частоты струны падает вместе с уменьшением длины струны, например, если при длине CTpyjibi в 9 см возмок;ное увеличение частоты составляет 200-300%, то при длине в 2 слс возможное увеличение частоты составляет уже всего 30-40%. Это также подтверждается
экспериментом. Таким образом, описанный метод, хотя и существенно расщиряет диапазон звуковых частот, записываемых струной и, таким образом, может быть с применен при звукозаписи, лля мощной модуляции света при оптической телефонии и в измерительной технике, но не в состоянии сам по себе отдалить собственный период струны в область ультразвуковых частот, что необходимо для применения его в телевидении. Сделать это вышеописанным методом возможно только при омическом сопротивлении R, меньшем собственного омического сопротивления струны, чего можно достигнуть, компенсируя собственное омическое сопротивление струны посредством обратной связи. Осуществить такую обратную связь, которая во всем диапазоне частот компенсировала бы собственное омическое сопротивление струны R, можно, например, включив последовательно со струной активное сопротивление г (фиг. 1), с концов которого напряжение подается к входу лампового усилителя, ток с выхода которого (усилителя) подается обратно с обратным знаком на сопротивление г. Сопротивление такой системы г
где р - крутизна усилителя. При
равно
1гр
S -- -f- -Q- оно будет равно - /. Это отрицательное сопротивление таким образом полностью скомпенсирует собственное активное сопротивление R, последовательно с которым оно соединено. Практически, понятно, скомпенсировать полностью собственное активное сопротивление струны невозможно, можно только его уменьшить. Но уменьшение его даже только в 10 раз, что вполне допускает устойчивость и амплитудная характеристика ламповых схем, позволяет, как показыьает расчет, в десятки раз повысить собственную частоту струны приключением к ней соответствующей малой самоиндукции. Таким образом открывается возможносгь использования струны, как мощного модулятора света в телевидении.
Однако, при уменьшении величины самоиндукции LI, приключенной к струне, начинает, наконец, сказываться собственная самоиндукция струны, как провода, которая до сихпор не рассматривалась. Эта самоиндукция L, включенная последовательно с самоиндукцией Z-i (фиг. 2), оказывается, наконец, больше самоиндукции LI, и тогда уже дальнейшее уменьшение величины LI не будет влиять на собственную частоту . Собственную самоиндукцию струны, как провода, можно однако, свести к мннимуму, если один из подводящих к струне проводов распо;.ожить параллельно струне на небольшом от нее расстоянии, образуя вместе со струной бифиляр. Таким образом, магнитное поле подводящего провода уничтожает магнитное поле собственной самоиндукции струны.
С уменьшением величины самоиндукции LI станоьится все труднее подводить к струне ток необходимой для ее возбуждения величины, так как эта самоиндукция шунтирует струну. Выходом нз положения является кспользовапие этой самоиндукции, как вторичной обмотки понижающего трансформатора, питающего струну. Этот выход наиболее целесообразен тогда, когда нсточНИКОМ тока является лампа, внутреннее сопротивление которой во много раз больше сопротивления струны. Другим выходом из положения ягляется возбуждение струны, на некоторую часть которой нанесен слой фер;)омагнитно10 материала, с помощью отдельною электромагнита, в обмотке которого течет переменный ток, возбуждающий таким образом струну. Как было уже сказано, выводы, прилученные при детальном иссл довании стру1 ы, могут бы.ь распространены и на другие подьижиые электрические системы, помещенные в постоянное магнитное ПОЛ . Очевидно, что и в случае шлейфа осциллографа, рамки гальванометра и других подвижных систем материал проводников, составляющих их, необходимо подбирать таким, чтобы произведение его плотности на удельное сопротивление было наименьшим, компенсировать их омическое сопротивление посредством обратных связей и т. д. Собственная самоиндукция этнх систем (не имеющая никакого отношения к их эквивалентной самоиндукции, связанной с механическими постоянным.) может также компенсироваться акало ичко случаю струны, посредством связи ее с некоторой другой самоиндукцией, магкитное поле которой уничтожило бы магнитное поле собственной самоиндукции системы. Ьсли в случае струны такой самоиндукцией можег служить подводящий провод, то, в случае использования рамки гальванометра, можно включить особую неподвижную обмотку, магнитное поле которой противоположно направлено магнитному полю самоиндукции рамки. В случае осциллографа компенсация собственной самоиндукции уже почти осуществлена в виду конструкции шлейфа. Гак же, как в сл чае струны, возбуждать колебания этих систем можно в сдучаа необходимости посредством взаимодействия между переменным магнитным полем особого электромагнита и 1анасенным на часть подвижной системы ферромагнитным материалом. Методом, аналогичным вышеописанному, можно не увеличивать, но уменьшать собственную частоту подвижной электрической системы, помещенной в постоянное магнитное поле, увеличивая инерцию (массу) системы. Для этого необходимо приключить к системе емкость. Действительно, в случае, когда к проводнику приключгна емкость (фиг. 4). электродвижущая сила, индуцируемая в проводнике при его движении в MaiHHTHoM поле, будет пгопорцио.;альна скорости проводника и силе магнитного поля, dv т, е. будет равна Н . Эта электродвижущая сила вызовет ток через емкость, причем напряжение на концах этой емкости будет пропорцнонально интегралу тока, т. е. равно LJ,.., i/ idf., откуда Я Через емкость, a следовательно, и через проводник пойдет ток, пропорциональный ускорению струны. От взаимодействия этого тока с MSIBHTным полем в проводнике возникнет пондремоторная сила rfsy , также пропорциональная ускорению. Складываясь с инерционной силой (также пропорциональной ускорению), она будет увеличивать эквивалентную массу (инерцию) проводника. Система, состоящая из таких проводников, будет, таким образом, уменьшать свою собственную частоту; Логко убедиться в том, что выводы, сделанные для случая повышения собственной частоты с 1СТйМы, прилпжимы и к случаю понижения собст еннпй частоты системы. И в этом случае для максимального воздейгтьия на собственную частоту Системы (в сто, ону ее понижения), необг ходнмо подбирать материал проводника так, чтобы произведение его плотности на удельное сопротивление было наименьшим, компенсировать омическое сопротивление посредством обратной связи и т. д. Предмет изобретения. 1.Способ изменения механических свойств подвижной системы электрических приборов, помешесной в постоянном магнитном поле, осноьанный на том, ч;о паралл -льно указанной системе присоединяют контур, обладающий самоиндукцией или емкостью, отличающийся тем, что с целью устранения ьличния собственного активного сопротивления подвижной системы последовательно с нею включают некоторое отрицательное сопротивление. 2.Устройство для осуществления способа по п. 1, отличающееся применением включенного Г10С едокательно с под1ижьсй системой прчбора активного сопротивления, к концам которого паралле.1Ь о присоединекы входные и выходные зажимы катодного усилителя, парамет ы которого подобраны таким oi-pajoM, чти напряжение меж1у ко цами сопротивления гаы о и противоположно по знаку сумме падений напря/лений на указанном сопротив;1ении и на концах обмотки подьижной системы измерительного прибора. 3.Видоизмененне устрсйстьа по п, 2, отличающееся применением тра; сформатора, ne.jвич;;ая обмотка которо.о включена в измеряемую цепь, а вторичная, предразначе ная для пятаиия подвижной системы измерительного прибора использована одноьремгнно в качестве включен ной пара.лельно прибору самоиндукции, предназначен ой для повышения собственной частоты его колебаний.
Фип1
Н
в 0 OfO,
Фиг2



| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения силы магнитного поля | 1929 |
|
SU24927A1 |
| Способ изменения емкости или самоиндукции электрической цепи | 1931 |
|
SU48618A1 |
| Устройство для получения пилообразных колебаний | 1945 |
|
SU72697A1 |
| Способ устранения шума в усилителе | 1941 |
|
SU64435A1 |
| Способ измерения деформаций при помощи струнного осциллятора | 1929 |
|
SU24670A1 |
| Устройство для выделения сигналов изображения в системе телевидения | 1936 |
|
SU57685A2 |
| Способ устранения шума в усилителе | 1933 |
|
SU35908A1 |
| Генератор электрических колебаний, управляемых струной | 1929 |
|
SU24458A1 |
| Электрический фильтр | 1931 |
|
SU24933A1 |
| Способ коррекции сложных схем | 1940 |
|
SU63797A1 |


Авторы
Даты
1935-01-31—Публикация
1932-10-11—Подача