Гармонические синусоидальные незатухающие колебания, широко используемые в радиотехнике, генерируются в системах, необходимыми составными частями которых являются:
1) источник энергии (постоянная энергия которого преобразуется в энергию переменную);
2)двухполюсник с падающей характеристикой (V) (лампа, искра и т. д};
3)контур, состоящий из самоиндукции и емкости.
Первые два элемента необходимы для того, чтобы создать в третьем эле менте незатухающие электрические колебания, которые могут рассматриваться как периодическое преобразование энергии из потенциальнойформы в форму кинетическую. Последнее обстоятельство требует наличия двух резервуаров энергии или, вернее, резервуаров энергии двух типов, т. е. емкости С и самоиндукции L.
Существуют системы, довольствующиеся одним резервуаром энергии-либо емкостью, либо самоиндукцией,-и дающие тем не менее периодические колебания. Таковы, например, системы Лбрагама-Блоха, Хесснера, Ватанабе и др-. но колебания, генерируемые указанными системами, являются колебаниями релаксационного типа. Даже в тех из этих систем, в которых генерируются почти синусоидальные колебания, происходят процессы, которые ио-гут быть сформулированы, как периодическое срывание и восстановление некоторых определенных первоначальных условий.
Предлагаемое устройство предназна чено для генерирования синусоидальных незатухающих колебаний -без использования емкости.. Недостающий резервуар энергии-емкость С-заменяется контуром, состоящим из самоиндукции L и активного сопротивления /.
Для того, чтобы получить представление о процессах, происходящих в предлагаемом устройстве, достаточно проанализировать систему двух связанных контуров I и //, состоящих каждый из активного сопротивления Ri и, соответственно, и катушки самоиндукции LI и,х:оответственно,2, причем коэфициент взаимоиндукции катущек L и LI райен М.
Диференциальные уравнения, управляющие системой, напишутся так:
dk
0 dr
dt
dk
. 0
dt
Решая совместно эту систему уравнений, получается уравнение второго порядка:
Н-«- +
dt
где
LiR2 + bi Ri и L2 - AJ2
g
b, b2 -jf2
Решение этого уравнения будет, как известно, иметь вид:
(i )/l-r),
Г -у +
.+«. (
функция, характеризующая ток h в контуре //, будет иметь такой же вид.
Я2
При в системе возможны затухающие колебания, ибо «- величина положительная. Величину а можно сделать отрицательной. Это легко выпол,нить, заменив одно из сопротивлений/ i или лампой с падающей характеристикой (. но тогда р станет величиной отрицательной и в системе не будет колебаний.
Система будет генерировать незатухающие синусоидальные колебания в том случае, если, кроме условия отрицательности одного из сопротивлений, будет иметь место еще условие Af2 LiZ/2. Это-то, на первый взгляд, невыполнимое условие, и выполняется в предлагаемом устройстве.
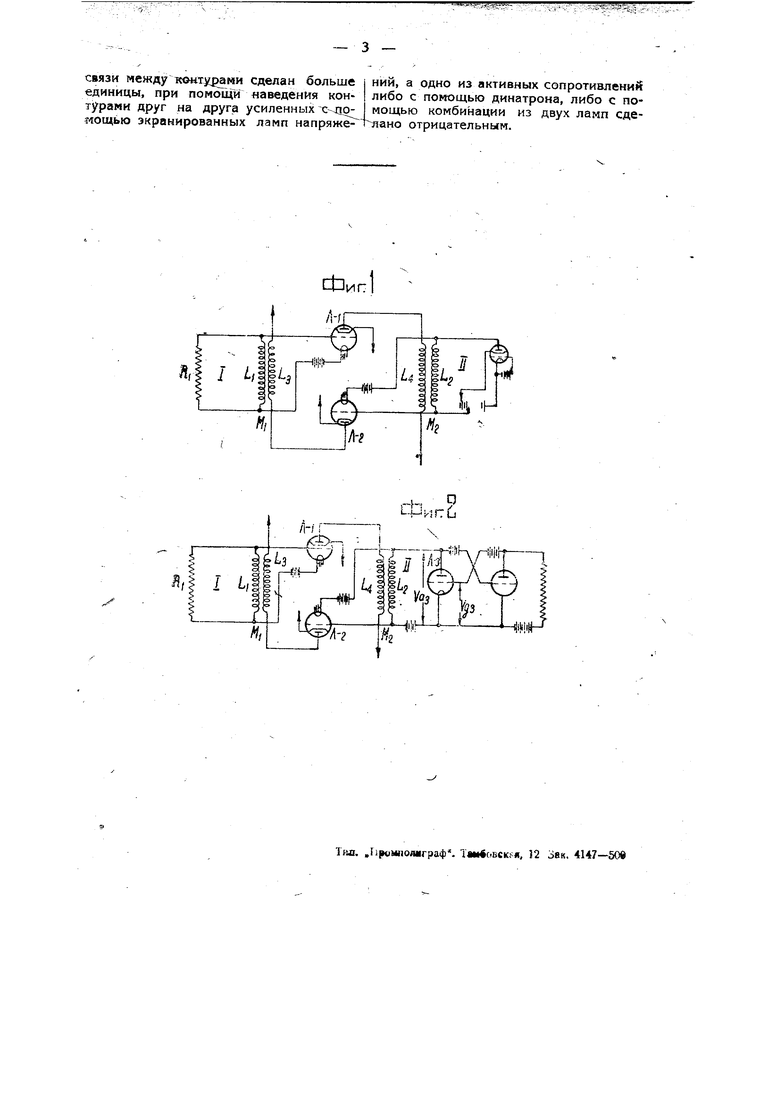
Устройство может быть выполнено в виде двух вариантов, изображенных на чертеже (фиг. 1 и 2).
Увеличение взаимоиндукции достигается в обеих схемах путем симметричного усиления наводимых контурами друг в друге напряжений. Применение экранированных ламп позволяет сохранить при этом необходимую фазу.
Схемы отличаются друг от друга способом получения отрицательного сопротивления. В варианте по фиг. 1 акт.ивное сопротивление сделано отрицательным с помощью динатрона, в варианте по фиг. 2 это достигается комбинацией двух обыкновенных ламп. Лампа Л-3 будет являться отрицательным сопротивлением в том случае, если U DZ что очень легко выполнить. Анализ предлагаемых схем с помощью Линейных диференциальных уравнений, при вполне допустимом пренебрежении обратным действием анодов экранированных ламп, приводит к следующему выражению для круговой частоты генерируемых колебаний
RI
L, L2 +Ml M25iS2/,
где R - сопротивление контура
- абсолютное значение отрицательного сопротивления LI - самоиндукция контура I
..11
MI - взаимоиндукциякатушек
LI и //2
М2 - взаимоиндукциякатушек
il и /,2
Si - крутизна лампы ЛЛ 52- „„ Л-2.
Можно, не составляя нелинейного уравнения, утверждать, что амплитуда колебаний, несмотря на наличие отрицательного сопротивления, д0стигнет с течением времени вполне определенной величины. Это будет вызвано, как и в обычных схемах, криволинейностью ламповой характеристики лампы .
Отдельные источники питания для ламп ЛЛ и Л-2 не являются обязательными.
Физический смысл колебаний в предлагаемой системе заключается в том, что энергия перемещается периодически из контура 1 в контур 11 и наоборот.
П,редмет изобретения.
Устройство для генерации синусоидальных колебаний с помощью системы, состоящей из двух связанных контуров, каждый из которых состоит из самоиндукции и активного сопротивления, отличающееся тем, что коэфициент
связи между KOHTj ми сделан больше единицы, при помощи наведения контурами друг на друга усиленных с-лр 1ощью экранированных ламп напряжёНИИ, а одно из активных сопротивлений либо с помощью динатрона, либо с помощью комбинации из двух ламп сдеhnaHO отрицательным.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для быстродействующей телеграфии | 1935 |
|
SU48635A1 |
| Устройство для коррекции формы радиотелеграфных сигналов | 1936 |
|
SU48628A1 |
| Катодное генераторное реле | 1921 |
|
SU797A1 |
| КОММУТАЦИОННЫЙ СПОСОБ ВОЗБУЖДЕНИЯ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2386207C2 |
| АППАРАТ ДЛЯ ЭЛЕКТРИЧЕСКОЙ ТЕЛЕСКОПИИ | 1925 |
|
SU5592A1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕНЕНИЯ ДЕЙСТВУЮЩИХ ВЕЛИЧИН ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ | 1931 |
|
SU27721A1 |
| МУЗЫКАЛЬНЫЙ ПРИБОР С КАТОДНЫМИ ЛАМПАМИ | 1921 |
|
SU890A1 |
| Способ модуляции | 1925 |
|
SU7006A1 |
| Ламповый генератор | 1939 |
|
SU61417A1 |
| Ламповый генератор | 1933 |
|
SU43380A1 |

k 1|
М,
Фиг 6

Авторы
Даты
1936-08-31—Публикация
1936-05-08—Подача