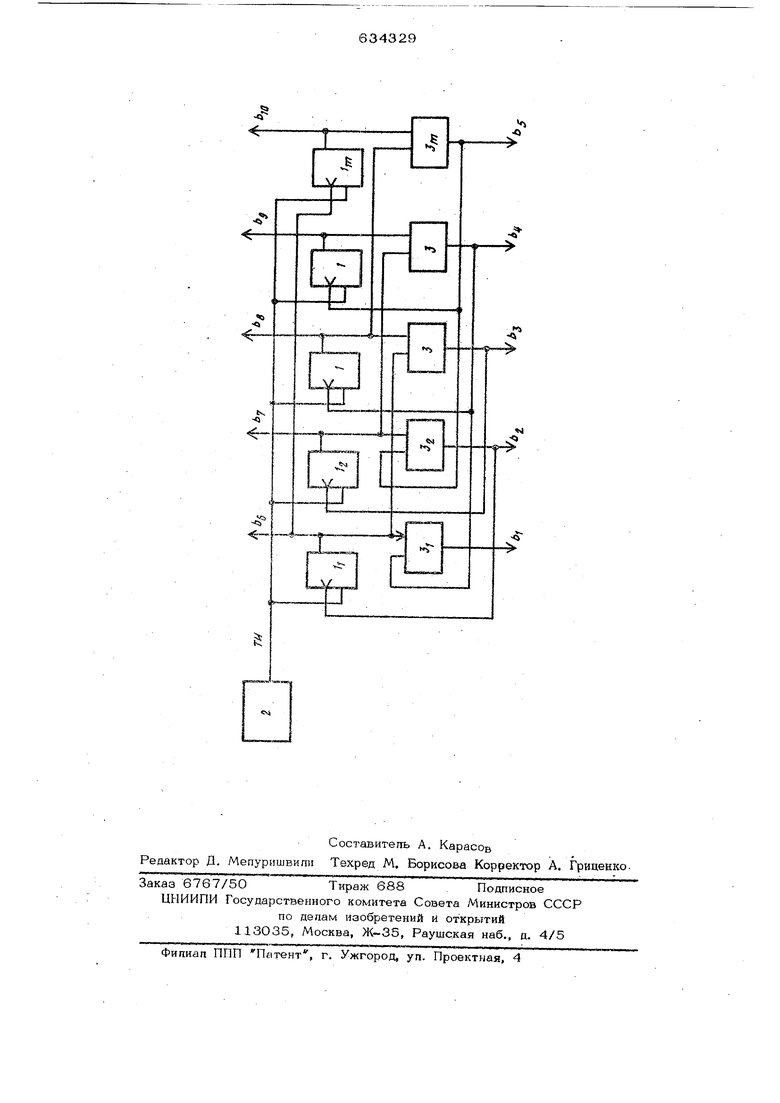
Изобретение относится к области вычислительной техники и может быть иопопьзовано дгш повышения эффективности больших ЦВМ, для расширения воэможности малых ЦВМ при вероятностном модели ровании, а также в качестве основного бпока стохастических ЭВМ. Известны генераторы псевдослучайных чисел, основанные на применении регистров сдвига. Простейшим генератором псевдослучайных чисел на базе регистра сдвига является последовательный генератор псевдо случайных чисел (ГПСЧ) i. В таком генераторе очередное двоичное число образуется на выходе 8 разрядов регистра сдвига через ii импульсов сдвига. Частота выборки псевдослучайных чисел в N раз меньше, чем тактовая частота. Другой из известных генераторов псевдослучайных чисел для повьлиения бьютродействия на один разряд содержит m t-m-/ Г--) триггеров, что обуспав -. пивает его аппаратурную избыточность 21 Наиболее бшгзким техническим решением к данному изобретению является генератор псевдосдучайных чисел, содержащий т сумматоров по модупю /ша и гП триггеров, входы синхроннэацик которых подкгаочены к выходу генератс а тактовых HMnym.coBfpj. Недостатком этого генератс а также является аппаратурная избыточность. Целью изобретения явп51ется упрощение гевератора. Дпя достижения постав пенной иеяи единичные выходы триггеров подключены к первым входам сумматсфов по модупю два соответственно, вторые вхощл старших сумматоров по модулю два ктаочены / к единичным выходам i младших триггеров соответственно, счетные входы 2 i - m старших триггеров соединетны с единичными выходами 2 i m младших триггеров соответственно, счетные входы2т-2 младших триггеров соединены с выходами2n)-2i старших сумм торов по модулю два соответственно, вто4 рые входы in- 1 мпадших сумматоров по модулю два подключены к выходам m - { старших сумматоров по модулю даа соответственно. Бпок-схема генератора дпя случая ТИ 5 (т -число разрядов генератора) приведена на чертеже. Генератор содержит тТ триггеров 1, входы синхронизации которых подключены к генератору тактовых импульсов 2, т сумматоров по модулю два 3, первые входы которых соединены с единичными выходами триггеров, а вторые входы i старших сумматоров по модулю два соединены с единичными выходами млад- ших триггеров, вторые входы-т-i младших сумматоров по модулю два соединены с Ш выходами старших сумматоров по моду лю язва, счетные входы 2 - m старших тригге ров соединены с единичными выходами 2i -1 младших триггеров, а счетные входы 2т - 2 « млaдшvlx триггеров соединены с выходами 2т-21 старших сумматоров по модулю два. Работает генератор следующим образом. Начальное псевдослучайное число иО /иО vOл о имеет вид )- 2 Щт7 разрядность регистра сдвига,на базе которого основан гечератор. ЧислоЬ° 1321 ,., Ь снимается с выходов сумматоров ПО модулю два слева направо, а число ..,b2j«c выходов триггеров со счетным входом. При поступлении тактового импульса состояние триггеров и соответственно состояние выходов сумматоров по модулю два изменяется. По истечении переходных процессов на выходах сумматоров по модулю два и выходах триггеров получается очередное псевдослучайное число J j sbjbgM.bg При поступлении очередного тактового импульса получается следующее число Ё „ и т. д. Из функционирования многоканального генератора псевдослучайных чисел очевидно, что данное устройство имеет максимальное быст родействие, т. е. за один такт получается следующее число. В данном случае быстродействие определяется только элементной базой. Структурный состав генератора показьшает, что при минимальных затратах оборудования попучает ся 2 m разрядное псевдослучайное число. Данньпй генератор, как и все генераторы на базе регистра сдвига с сумматором по модулю два, генерирует М- последовательность, свойства которой хорошо изучены. Аналитически функциональные связи для построения многоканального генерато а псевдослучайных чисел пля любого значения легко определить из следующей системы уравнений (1): , к-И , «. К m-j Oam-jQ m Uj jrO,i.2,...rn-l дИ+14 4m-j b2m-i® 2Ui; .i,,... гт7-1 где D.j - содержимое или значение m разряда ГСП Ч в К+1 такт работы устройства. Для пояснения аналитической зависимости (1) и функционирования генератора на чертеже приведена конкретная структура для m 5. Легко видеть, что функциональные связи структуры подчиняются вышеприведенной системе уравнений (1). Так, например, для m 5, i 3 система уравнений (1) имеет вид ЧоЬ.о® Ьб bg b ® bj be b4 b2 bf bg ,&b t72 что полностью соответствует функциональным связям между узлами многоканального генератора псевдослучайных чисел, приведенного на чертеже. Все известные генераторы псевдослучайных чисел на базе рюгистра сдвига имеют одинаковые статистические свойства, отражающие равномерность и случайность появления двоичных цифр. Все эти свойства определ5Ш)тся свойствами последовательного генератора, что доказьгоается в ряде литературных источников. Предлагаемый многоканальньтй генератор псевдослучайных чисел обладает аналогичными Свойствами в силу того, что генерирует идентичную последовательность псевдослучайных чисел, как и последовательный генератор. Справедливость этого утверждения подтверждается функционированием последовательного генератора и предлагаемого генератора. Для генератора, приведенного на чертеже, последовательность псевдослучайных чисел будет иметь вид: Ъ ЪгЬзЬ ЬзЬ Ь Ъ Ъ Ью 1 1 О О i i о 1 О I О 1 L о О О i 1 причем очередное чиспо получается за один такт, и разрядность этого числа равняется 1О, т. е. в общем случае 2 Дня последовательного генератора посл довательность состояний триггеров буд иметь вид: Очевидно, что очередным псевдослучайным числом может являеться только тако число, которое получается через N : 10 тактов, т. е. очередным после. яв1 1rjляется число с i -з вьгщеприведенного fe I к tr легко видеть, чтос,,(, иЕ, fe,, , нополучение сопряжено с большими временными затратами. Таким образом, введение новых функциональных связей и сумматоров по модулю два позволяет получить быстродействующий, высоко экономичньШ многоканаль ный генератор псевдослучайных чисел. Если в прототипе удельные затраты обору дования на один разряд составляли один триггер со счетным входом, то в предлагаемом генераторе 1/2 триггера плюс 1/ сумматора по модулою два. И в то же время быстродействие такого генератора максимально. Патентный поиск пока96зап, что прелпагаемый многоканапьный генератор псевдоспучайньгх чисеп имеет максимальное быстродействие (т. е. это устройство однотактное) и самые минимальные удегаьньге затраты оборудования по сравнению с известными. форму па изобретения Генератор псевдослучайных чисеп, содержащий гтт сумматоров по модулю два и fYl триггеров, входы синхронизации которых подключены к выходу генератора тактовых импульсов, отличающийс я тем, что, с цепью упрощения генератора, единичные выходы триггеров подключены к первым входам сумматоров по модулю два соответственно, вторые входы 4 старших сумматоров по ива подключены к единичным выходам младших триггеров соответственно, счетные входы 2 - т старших триггеров соединены с единичными выходами 21-тмпада1их триггеров соответственно, счетные входы 2т- 2 I младших триггеров соединены с выходами 2т-2 старших сумматоров по модулю два соответственно, вторые входы 1 - младших сумматоров по модулю два подключены к выходам m-i старших сумматоров по модулю два соответственно. Источники информации, принятые во внимание при экспертизе; 1.Яковлев В. В.,Федоров Р. Ф. , Стахастические вычислительные машины. Л., Машиностроение, 1974, с. 246253. 2.Авторское свидетельство СССР №468231, кп. Q 06 F 1/О2, 14.О9.73. 3.Авторское свидетельство СССР N«543962, кл. q О7 С 15/ОО, 16,06.75.


| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор псевдослучайных чисел | 1980 |
|
SU907548A1 |
| Генератор псевдослучайных чисел | 1977 |
|
SU708381A1 |
| Генератор псевдослучайной последовательности | 1981 |
|
SU1024918A1 |
| Генератор псевдослучайных чисел | 1979 |
|
SU868734A1 |
| Генератор псевдослучайных чисел | 1981 |
|
SU1005045A1 |
| Генератор псевдослучайных чисел | 1981 |
|
SU1001097A1 |
| Генератор псевдослучайных чисел | 1975 |
|
SU543962A1 |
| Генератор псевдослучайных чисел | 1977 |
|
SU739602A1 |
| Генератор псевдослучайных чисел | 1981 |
|
SU1013955A1 |
| Генератор псевдослучайных чисел | 1980 |
|
SU903872A1 |


Авторы
Даты
1978-11-25—Публикация
1976-10-27—Подача