(54) УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ПРОИЗВОЛЬНЫХ ЭЖМЕРТОВ ПОЖЙ ГАЛУА GF(p)





| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения произвольных элементов полей Галуа GF (р @ ) | 1989 |
|
SU1709297A2 |
| Устройство для формирования элементов расширенных полей Галуа GF ( @ ) и кодовых последовательностей на их основе | 1987 |
|
SU1441413A1 |
| Четырехзначный умножитель элементов поля Галуа GF(2 @ ) | 1990 |
|
SU1737443A1 |
| Устройство для умножения произвольных элементов расширенных полей Галуа GF(Р @ ) | 1985 |
|
SU1334143A1 |
| Параллельное устройство для умножения в конечных полях | 1986 |
|
SU1383338A1 |
| Устройство для формирования элементов мультипликативных групп полей Галуа @ | 1984 |
|
SU1236497A1 |
| Параллельно-последовательное устройство для умножения в конечных полях | 1986 |
|
SU1399725A1 |
| Способ защиты информации в облачных вычислениях с использованием гомоморфного шифрования | 2017 |
|
RU2691874C2 |
| Устройство для умножения элементов поля Галуа GF(2 @ ) при образующем полиноме F(х)=х @ +Х @ +х @ +х @ +1 | 1989 |
|
SU1716504A1 |
| Устройство для реализации переключательных функций в поле галуа GF /2 /. | 1984 |
|
SU1234861A1 |

t
Изобретение относится к вычислительной технике и может быть использовано в специализированных вычислительных устройствах и микропроцессорах для умножения элементов расширения полей GF(P), а также в системах кодирования, yQтpoйcтвax обнаружения и исправления ошибок кодов, построение которых базируется на теории полей GF().
Известны умножители элементов поля GF(2), построение которых основывается на специальных уравнениях полей GF() и базируется на разделении элементов поля GF(2) при помощи генератора полиномов GF() О .
Однако данные умножители представляют значительную сложность и неприспособленность к большим полям GF(2) и не позволяют умножать произвольные элементы расширенных полей при любом простом Р 2, т.е. полей GF(PN, где п 1,2,3...
Наиболее близким по технической сущности к предлагаемому является устройство для умножения произвольных элементов полей Галуа GF(P), при Р 2, которое обеспечивает систематический комбинационнологический подход к умножению произвольных элементов F(x) и P(x)(F(x)tix, P(X)PIX, ,,..., m-l) поля GF( p первообразным полиномом g(x)g x (i 0,1,... m).
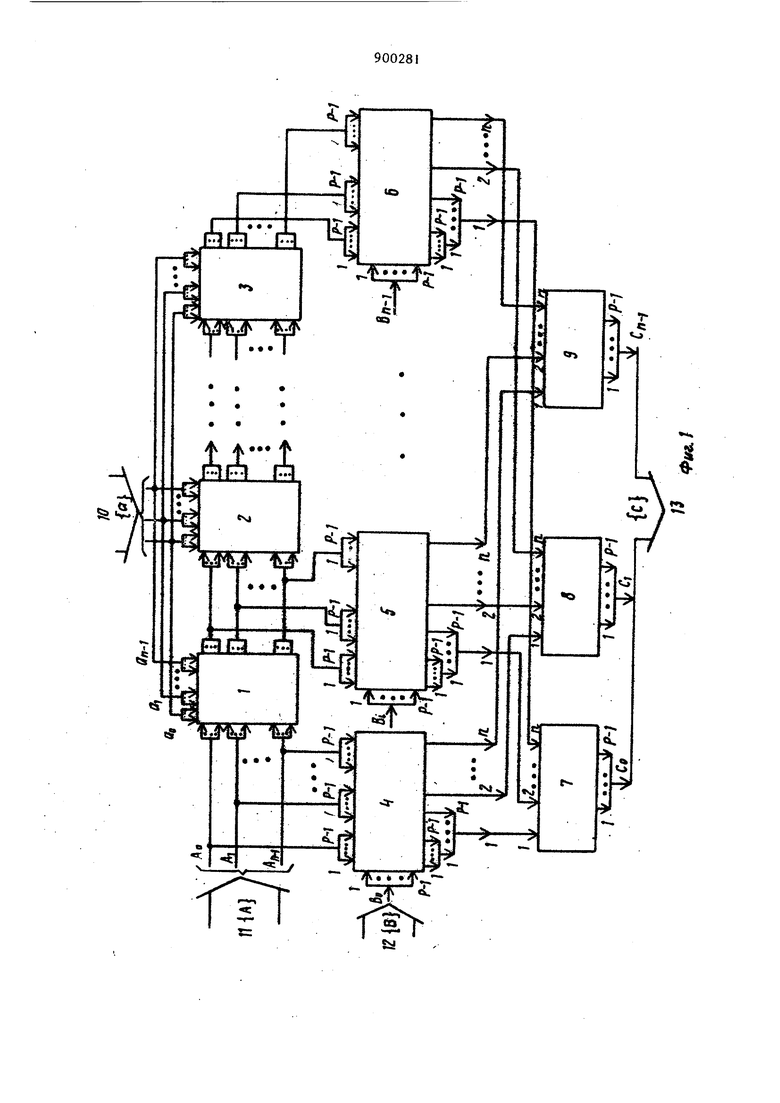
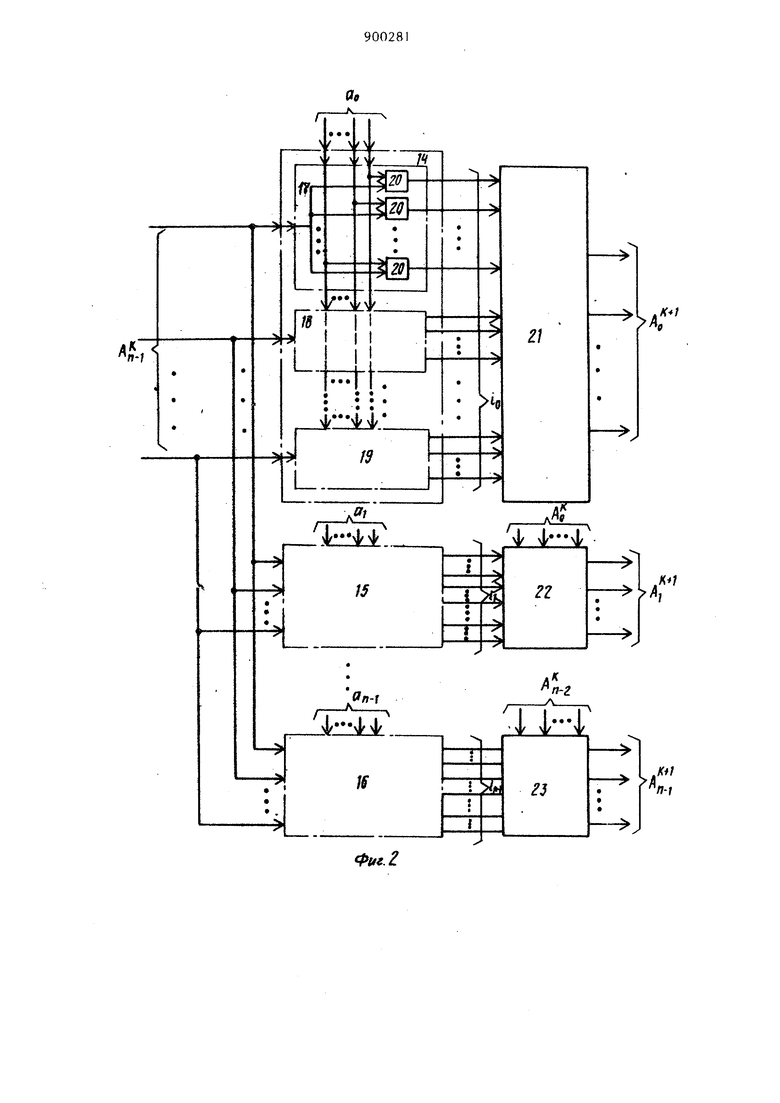
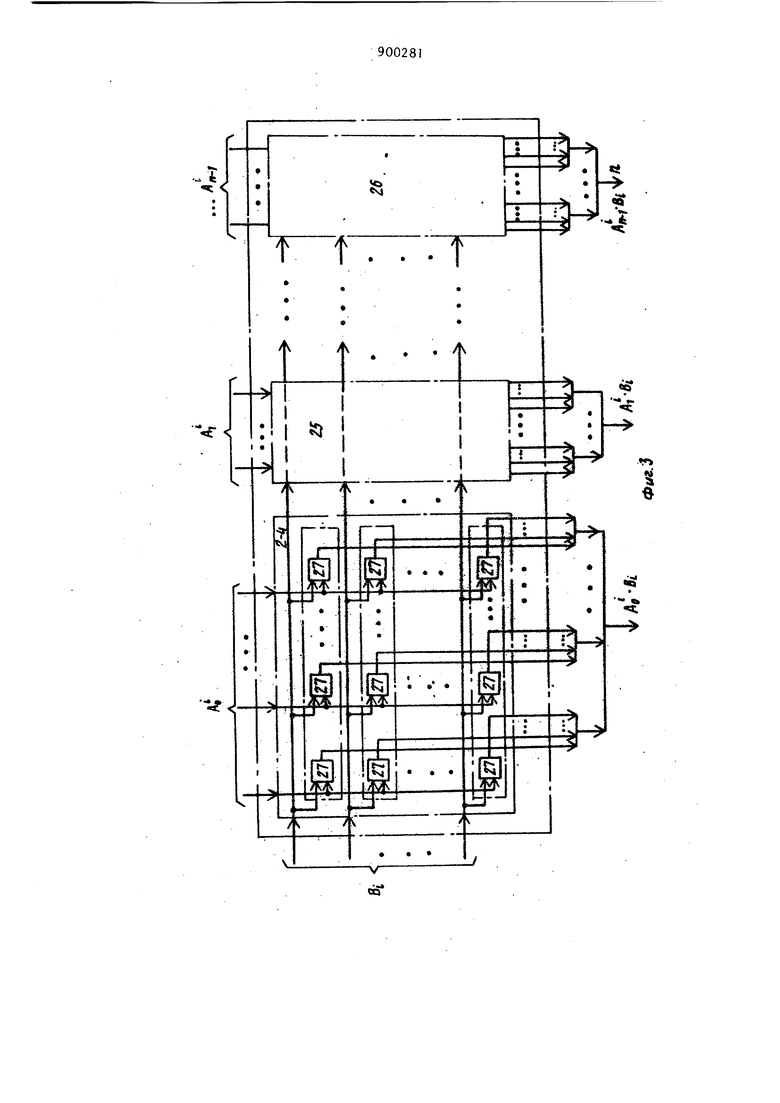
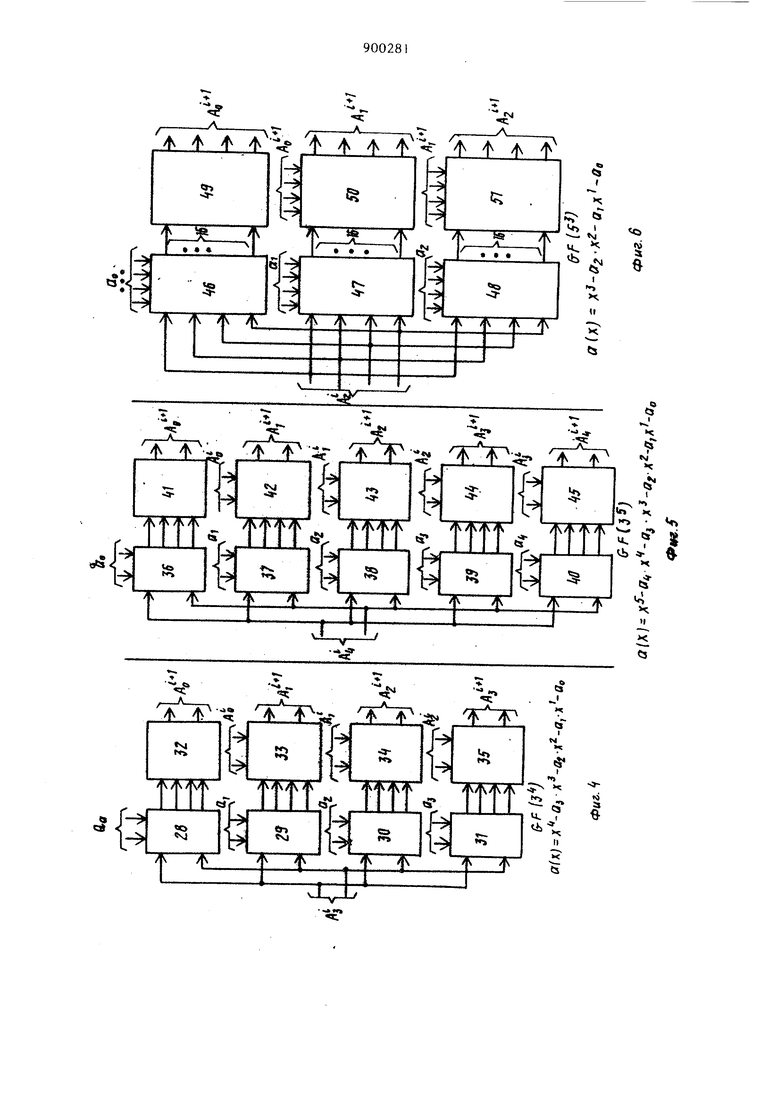
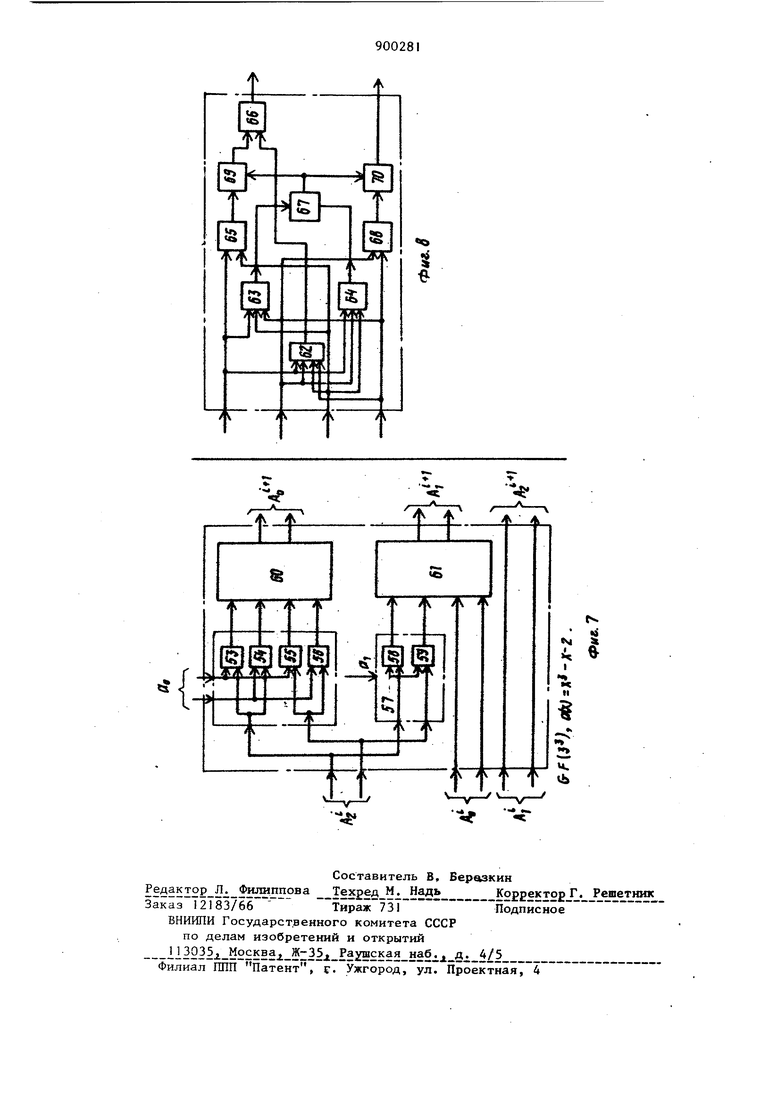
Это устройство содержит (m-l) упорядоченных блоков умножения. На первый из них поступают сигналы элемента F(x) поля, а на остальные подаются выходные сигналы предшествуюш,их. В каждом блоке умножения вход умножается на X для создания результирующего сигнала с модулем д(х). На вход i-ro формирователя частичных произведений соединенного с (i-l)-M блоком умножения, поступают сигналы (x), i-й формирователь частичных пронзведений осуществляет логическое умноже ние на Р и выдает частичное произве дение РХ F. Выходные сигналы m формирователей частичных произведений поступают на входы m суммирующих блоков для образования сигналов, соответствующих произведению РХ F по модулю д(х). Каждый суммирующий блок оперирует с соответствующими компонентами частичных произведений логических схем t2l. Недостатком известного устройства является то, что оно не позволяет умножить произвольные элементы расши ренных полей GFtP) при произвольных простом и п, а также любых перво образных неприводимых над GF(P) поли номов степени п. Цель изобретения - расширение функциональных возможностей за счет обеспечения умножения произвольных элементов А(х) и В{х) расширенных полей Галуа GF(P) при произвольных простых ии и различных производя щих полиномах а{х), где a(x) j xJ , ,l,...n; А(х)(А4 х, 8(x) Bi ,i,...n-l, А, Bj, , 0,1 ,.. .p-i; р-простое чис ло. Эта цель достигается тем, что в устройстве для умножения произвольных элементов полей Галуа GFCp), содержащем п модульных блоков умноже ния , п блоков формирования частичных произведений и И блоков суммирования причем входы первых групп модульных блоков умножения соединены со входами производтпдего полинома устройства входы второй группы первого модульио го блока умножения соединены со вхо дами первой группы первого блока фор мирования частичных произведений и со входами первой группы произвольных элементов полей Галуа Gf(р) устройства, выходы каждого j - го { j 1,..., n-l) модульного блока умножения соединены со входами первой группы (j-H)-ro блока формирования частичных произведений, входы второй группы каждого блока формирования частичных произведений соедине ны с соответствующими входами второй группы произвольных элементов полей Галуа GFCp) устройства, входы каждого к-го (,...,п) блока суммирования соединены с к-ми выходами блоков формирования частичных произведений выходы блоков суммирования являются ьыходами устройства, каждый вход производящего полинома и каждый вход первой и второй групп произвольных элементов полей Галуа GFip) устройства содержит (р-1) шин, каждый вход и выход каждого модульного блока умножения, блока формирования частичных произведений и блока суммирования содержит (р-1) щин, каждый модульный блок умножения является блоком умножения по модулю а (х), р, а{х)|а ,I,...,п где а{х)а ,I,...,п-1; О,1,...,р-1, каждый бло блок формирования частичных произведений содержит и узлов формирования частичных произведений, выполненных в виде матриц элементов И, первые входы которых соединены с шинами соответствующего входа первой группы узла формирования частичных произведений, а вторые входы соединены с шинами входа второй группы узла формирования частичных произведений, каждый блок суммирования является сумматором по модулю р. На фяг. I представлена функциональная схема устройства; на фиг. 2 - схема модульного блока умножения; на фиг. 3 - схема блока формирования частичных произведений; на фиг. 4 |схема модульного блока умножения по модулю а(х) Р для поля СР(з) и а(х) -х -а з -а х-а х-Зо ; на фиг. 5 то же, по модулю a(, Р для поля 6F(3) и a(x)x -a x-aJx-aJX -a;j на фиг. 6 - то же, по модулю а (х). Р для поля GF(5) и а(х) J , на фиг. 7 - то же х -а,х-а по модулю a(xi, Р для поля GF(3) и а(х)«х -х-2; на фиг. 8 представлена схема блока суммирования по модулю три для поля GF(3). Устройство для умножения произвольных элементов расширенных полей Галуа GF() (фиг. 1) содержит модульные блоки 1-3 умножения по модулю (х);|Р, блоки 4-6 формирования частичных произведений, блоки 7-9 суммирования по модулю Р, входы 10 производящего полинома а(х), входы 11 и 12 произвольных элементов А(х) и В(х), выходы 13, на щины которых поступают коэффициенты полинома элемента с(х)А(х)« B(x)(modd а(х) Р), Модульный блок , 2 или 3 умножения по модулю а(х),Р (фиг. 2) содержитгруппы 14-16 логических узлов 17-19, элементы И 20, блоки 21-23 5 суммириваиня ни мидулю Р, при этом каждая группа 14, 15 или 16 содержи (р-1) логических узлов 17-19, каждый из которь х содержит а t элементов И 20. Узел формирования частичных произведений (фиг, З) содержит матрицы 24-26 элементов И 27. Модульный блок 1, 2 или 3 умноже ния по модулю а(х)Р для поля GF(3 и а(х)х -Эух -aj, х -а х-Эд (фиг. А) содержит группы 28-31 логических узлов элементов И, блоки 32-35 суммирования по модулю три. Модульный блок 1, 2 или 3 умноженин по модулю а(х. Р для поля GF(3) и а(х).х«-а,-х-а. -а, (фиг. 5) содержит группы 36-40 логических узлов элементов И и блоки 41-45 суммирования по модулю три Модульный блок 1, 2 или 3 умножения по модулю а(х)1 Р для поля GF (5) и а(х)х -а Х -а -х-Зо (фиг. содержит группы 46-48 логических узлов элементов И, а также блоки 49 51 суммирования по модулю пять. Модульный блок 1, 2 или 3 умноже ния по модулю а(х}| Р для поля GF(3) и а(х) (фиг.7) содержит группу 52 элементов И 53-56, группу 57 элементов И 58 и 59 и блоки 60 и 61 суммирования по модулю три. Блок 7, 8 или 9 суммирования по модулю три для поля GF(3) (фиг.8) содержит элементы И 62-64, элементы ИЛИ 65-68, элементы запрета 69 и 70 Из теорииполей ) известно, что если 9 - первообразный элемент поля GF(P) , то все элементы поля GF(P) являются степенями О, т.е. GF(P)l9, Q,.... (modda(x) Р). При этом а(х) является первообразны |неприводимым гад GF(P) полиномом ст Пени п и а (9)0. Таким образом, любой элемент :поля GF(P) может быть найден путем возведени Xf 9 в степень i-1 и приведения A по modda(x), Р, т.е. двойному модулю, в случае, если известен А - -и элемент поля, то для нахождения А-го элемента достаточно -и элемент умножить на к и результат привести nomodda(x) Р,т.е А x(TOdda(x),P). Элементы поля GF(3) вычислены согласно формулам, приведенным выше 16 GF(3), , , а(х), ас,2, , aj,0. х- -|А9 х +2х-И . д« .хА 2x + 2x-f2 . x2+x+2А А« xU2А + 2х А 2 А 2х+2 А 2хЧх+2 А 2х А 2хЧ2х 2х А 2х -ь2х-|-1 А х+2х+2 А 2х-И Ав 2x-t-x Например, 6-И элемент А вычисляется путем умножения элемента А на X и приведения результата по двойному модулю а(х) А.х()jf )(modda(x, Р). Таким образом, для отыскания всех элементов (поли номов) по л я GF(P) необходимо рекуррентно умножать ранее вычисленный предшествующий элемент (полином) иа X и результат приводить по modda(x)P. Эта операция тождественна сдвигу влево полинома предьщущего элемента (т.е. увеличение на единицу степени х каждого члена полинома) и, если наибольшая степень при X равна п,то из результата необходимо вычитать полином а(х) столько раз, чтобы результат вычитания не имел степени х равной п, а затем результат прив-ести по модулю Р, Существует более упрощенное рекуррентное правило вычисления элементов полей GF(P ). Рассмотрим некоторые примеры иа поле GF(3 ). Чтобы получить значения коэффициентов при степенях xjx x элемента ,А(т.е. АС , А , А ) достаточно jпровести следующие операции с коэффициентами А , А , А элемента А и первообразного полинома а(х), умножая А на а и приводя результат по модулю , получаем АО 1( (mod 3), умножая Ag на а и прибавляя к результату А получаем (после приведения по модудво ) А 1(А, (mod3) , умножая Aj на а, и прибавляя к результату AJ, (после приведения по модулю ) получаем А 1 (А|-а, 1). Таким образом, А . Например, коэффициенты полинома А вычисляются следующим обпазом. , 2,Aj.A% 0. Коэффициенты полинома вычисляются следующим образом: А Af. (niod3) , А А а +А 3EO(mod3) , А . aj,. Таким образом, данное рекуррентное правило сводится к тому, что ко эффициенты каждого последующего пол нома-элемента А поля GF(P) вычис ляются с использованием коэффициентов предыдутпего полинома-элемента А и первообразного, полинома а(х) по правилу 5Ац, . а (modp) ,А эА,. а + АГ «Aj (modp). Данное правило лежит в основе по строения и функционирования модульн го блока I, 2 или 3 умножения по модулю a()) Р. Данный блок осуществляет умножение полинома-элемента на X и приведение результата по modda x)/ Р, тем самьм осуществля ется получение элемента А -го. Де ствительно, группы 14-16 логических узлов 17-19, кажд1 из которых состоит из аj элементов И 20, осуществляют умножение коэффициента А|,.| полинома А-го на коэффициенты ао 04 ««(а,, , путем размножения каждого входа входной шины, отображакицей коэффициент А,, в aj раз в логических узлах 17-19 каждой групп 14-16. Если А(, 2, то сигнал существует на первьос двух входах шины , , если то сигнал на Р-1 входах шины А. и т.д. Если aje2, то сигнал существует на первы двух входах шины, отображакнцей коэффициент aj и т.д. Таким образом, число активных {на которых существуют сигналы) выходов каждой группы 14-16 равно про изведению активных входов шин Аи-Ч и aJ. Так как любой коэф циент А(, не превш1ает Р-1, а коэффициент а| не превьявает Р-, то число всех выходов каждой группы в общем случае не превышает ij(Pl) . Блоки 21-23 суммирования по модулю Р (фиг. 2) представляют дешифсост. I выхода I
1
2 3 4 5 6 7
входы
4 О О
3 О О О 1 I 1 1
О О
1 I о раторы, так как осуществляют операцию преобразования сигналов на своих входах в сигналы на своих выходах. Для блока 21 число входов определяется лишь числом выходов группы 14, для блока 22 число входов дополняется числом входов шины , ;для блока 23 число входов дополняется числом входов шины Число выходов блоков 21-23 равно Р-1. Таким образом, блоки 21-23 дополнительно осуществляют операцию сложения результат умножения .к . . .к Ац., .фJ с AJ , Функциональные схемы модульных блоков I, 2 или 3 умножения по модуJBO a{x), Р для различных конкретных полей 6Р(з)са(х).а.х -а -хGF(3)ca(x).x«-a,.x-а.х«-а х-ао; GF(5)ca(x)«x-a5tX -a,x-ao представлены на фиг. 4-6. Эти функциональные схемы отображают конкретное построегше для конкретных пол%й GF функциональной схемы общего случая, представленной на фиг. 2. Для поля GF{3) с а(х) (фиг. 7) функциональная схема модульного блока 1, 2 или 3 умножения по модулю а(х)х-х-2, . Так как а., то группа элементов И, осуществляющая умножение Ад на отсутствует, отсутствует из-за ненадобности и третий блок суммирования по модулво . Так как ад 2, то группа 52 содержит четыре элемента И 53-56, а группа 57 - два элемента И 58 и 59. Блоки суммирования 7-9 по модулю Р для любых полей GFCP) представляют дешифраторы. Схема блока су1да4ирования по модулю Р 3 для поля SF(3) (фиг. 8) реализует приведение по модулю три сигналов на своихчетырех входах в сигналы на своих двух выходах (см. таблицу). 99 Рассмотрим процедуру умножения двух любых элементов Ахи В(х)поля GF(Р ) , Умножение двух полиномэлементов А(Х) и В(х) можно осуществить путем суммирования по mod Р частичных произведений полинома А(Х) на слагаемые полинома В(х), т.е. произведений вида А (х)А(х) Bi-x), приведенных по modda(x) Р., Умножение А(х) на х и приведение результата по modda(x) Р осуществлено при помощи одного модульного блока 1 умножения по модулю а(х) Р, а умноже дае А(Х) на х (равнозначно умножению (х) на х) и приведени результата по nx3dda(x)|P, осуществляется при помощи цепочки, состояв шей из модульных блоков 2 и 3 умнож ния по модулю а(х) Р, выходы каждого предыдущего при этом соединяются со входами каждого последующего. Умножение произведения А(Х)Х , приведенного по modda, на коэффициент Bi можно осуществить при помо щи блоков 4-6 формирования част11чны произведений, функциональная схема которых представлена на фиг. 3. Дан ная операция осуществляется путем размножения каждого входа шины Aj,,| раз j-и матрицей 24-26 элементов И К каждой j-й матрице 24-26 элементов И 27 подведено Р-1 шин, отображающих коэффициент А и Р-1 шин, отображающих коэффициент Bt, при этом каждая j-я матрица 24-26 элеме тов И 27 имеет () грутш, по (Р-1) выходов, отобраркающих произве дение коэффициентов А В . Каждый i-й блок 4-6 имеет п матриц 24-26 элементов И 27 и тем самым - п выходов по (P-I) шин в каждом выход Таким образом, выходные шины кажд го i-ro блока 4-6 отображают частичное произведение А(Х)(В(х). Суммирование по mod р частичных Произведений осуществляется в блоках 7-9 суммирования по модулю Р. При этом ко входам блока 7 подведены первые выходы блоков 4-6, ко входам блока 8 - вторые выходы блоков 4-6, а ко входам блока 9 п-6 выходы блоков 4-6. Первые выходы блоков 4-6 отображают коэффициенты частичных произведений при степени х, вторые выходь блоков 4-6 - коэффициенты частичных произведений при степени х и т.д. Таким образом, блок 7 осуществляет суммирование (приведение) по модулю Р коэффициентов при х всех частичных произведений, блок 8 осуществляет суммирование по модулю Р коэффициентов при Х всех частичных произведений, а блок 9 - коэффициентов при всех частичных произведений. Блоки 7-9 могут быть выполнены в виде дешифраторов. Выходы блоков 7-9 отображают коэффициенты соответственно Со, С,,..., С, полинома, представляющего собой результат умножения по modda(х), Р полиномов-элементов А(Х) и В(х) поля GF(P). Предлагаемое устройство обеспечивает умножение произвольных элементов А(Х) и В(х) полей GF() при любых значениях простого числа Р, .степени п и первообразных неприводимых полиномов а(х) . Формула изобретения Устройство для умножения произволь ных элементов полей Галуа GF() , содержащее п модульных блоков- умножения, п блоков формирования частичных произведений и п блоков суммирования, причем входы первых групп модульных блоков умноженяя соединены со входами производящего полинома устройства, входы второй группы первого модульного блока умножения соединены со. входами первой группы первого блока формирования частичных произведений и со входами первой группы произвольных элементов полей Галуа GF(P) устройства, выходы каждого j-ro (,...,п-1) модульного блока умножения соединены со входами первой группы ()-ro блока формирования частичных произведений, входы второй группы каждого блока формирования частичных произведений соединены с соответствующими входами второй группы произвольных элементов поЛей Галуа GFCp) устройства, входы каждого к-го (,...,n) блока суммирования соединены с к-ми выходами блоков формирования частичных произведений, выходы блоков суммирования являются выходами устройства, отличающееся тем, что, с целью расширения функциональных возможностей устройства за счет обеспечения функциональных возможностей устройства за счет обеспечения умножения произвольных элементов полей Галуа GF(p) при произвольных простых и п и различных производящих полиномах, калэдый вход производящей полинома и каждый вход первой и второй групп произвольных элементов полей Галуа GF(p) устройства содержит () шин, каящый вход и выход каждог модульного блока умножения, блока формирования частичных произведений и блока суммирования содержит () ШИН| каждый модульный блок умножения является блоком умножения по модулю а(х),р, где а(х) (а ,l,..., п-1; , 1,... ,, каждый блок формирования частичных произведений содержит П узлов формирования частичных произведений, выполненных в виде матриц элементов И, первые входы которых соединены с шинами соответствующего входа первой группы узла формирования частичных произведений, а вторые входы соединены с шинами входа второй группы узла формирования частичных произведений, ка дый блок суммирования является сумматором по модулю Р.
Источники информации, принятые во внимание при экспертизе
1u formation and Control, 61, 1963, pp. 79-98,
Д
Kfl
К П-1
иг.2.
«
Ч
«
т - ъ
з:
- /
/ ф f t tg ф /fv ф 4 ф ф /fv ф
t3
а
I
Ч
«
1
4s tvi
51 в
QS I
f К
U
IK Cs
к
:s
в
Авторы
Даты
1982-01-23—Публикация
1979-07-30—Подача