Изобретение относится к автоматике и вычислительной технике и может быть использовано при контроле и диагностике отказов комбинационных логических схем (КЛС) и узлов.
Целью изобретения является повышение достоверности контроля КЛС.
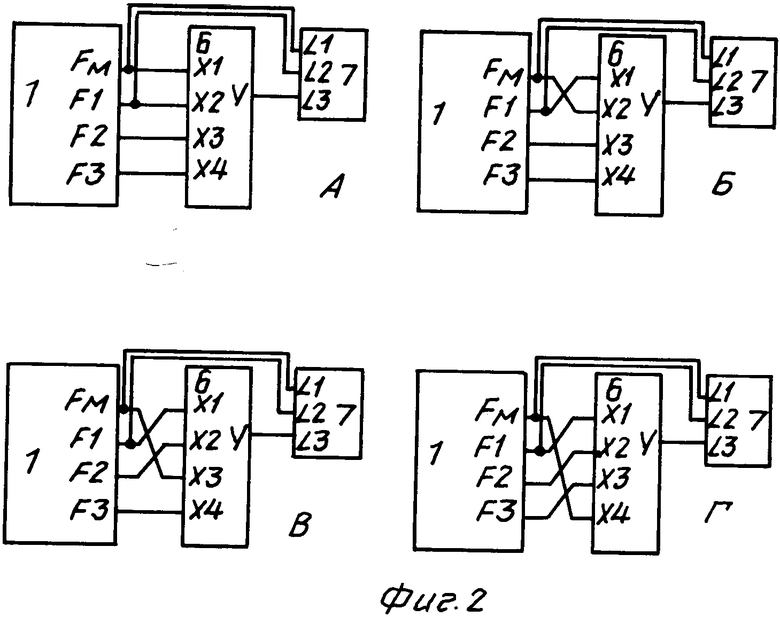
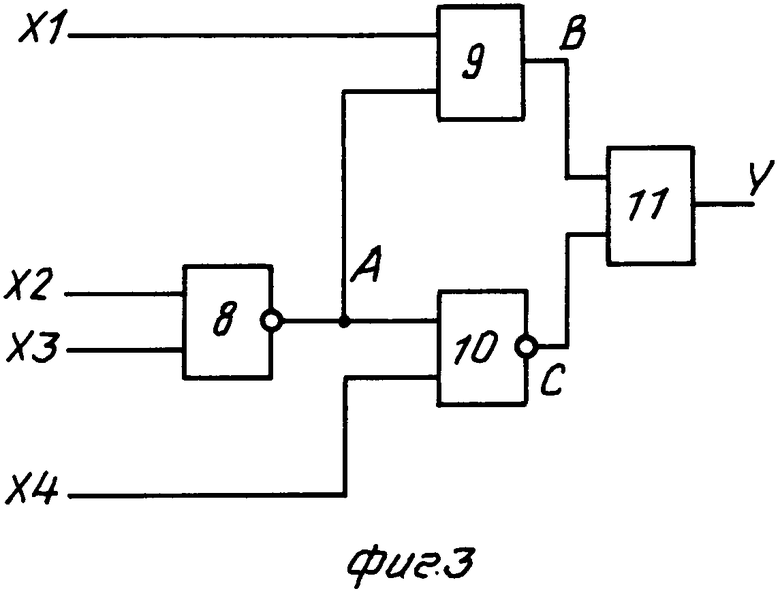
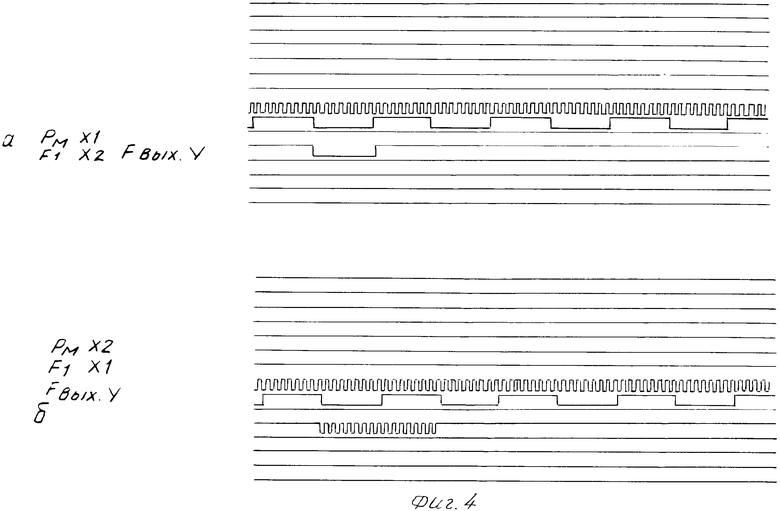
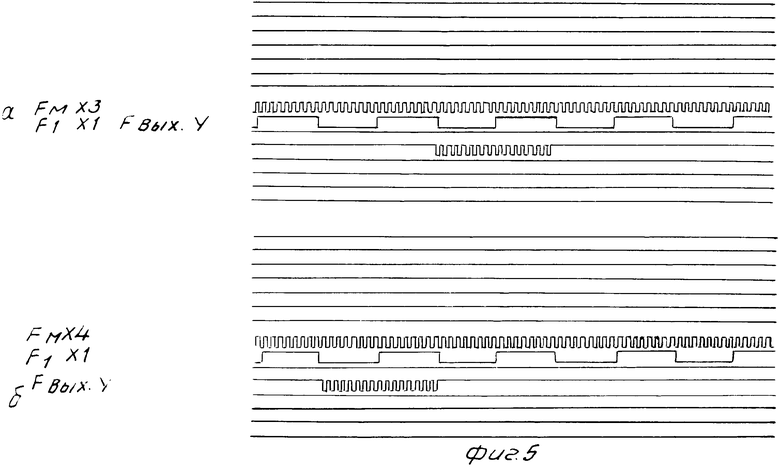
На фиг.1 представлена структурная схема подключения устройств для проведения процедуры диагностирования; на фиг.2 представлены схемы подключения экспериментального устройства на разных стадиях проведения процедуры диагностирования; на фиг. 3 представлена диагностируемая схема (объект эксперимента); на фиг.4 представлены временные диаграммы, полученные с помощью логического анализатора (ЛА) при экспериментальном подключении устройства, представленного на фиг.2б,а; на фиг.5 - временные диаграммы, полученные с помощью ЛА при экспериментальном подключении устройства, представленного на фиг.2в,г.
Представленные на фиг.1 устройства, с помощью которых реализован способ, содержат блок 1 воздействия (БВ), состоящий из генератора (Г) 2 - простейшего генератора прямоугольных импульсов, который может быть выполнен как с использованием простых логических элементов с применением положительной обратной связи, так и с использованием стандартных микросхем типа ГГ1, и счетчиков-делителей 3, 4, 5 - группы четырехразрядных двоичных счетчиков, удовлетворяющих частотным требованиям подающегося на вход синхронизации счетчика 3 сигнала, подключенных для счета на возрастание (убывание) таким образом, что сигнал "Переполнение" предыдущего счетчика подается на вход синхронизации последующего. Количество счетчиков зависит от количества входных полюсов объекта 6 эксперимента (ОЭ) так, что на каждые от одного до четырех входных полюсов приходится один счетчик. ОЭ 6 может быть любая КЛС, где Х - входные полюса ОЭ, а Y - выходной полюс. ЛА 7 - прибор для отслеживания цифровых сигналов (регистратор логических перепадов), где L - входные каналы ЛА. Можно использовать любой ЛА с количеством входных каналов не менее трех, способный производить отслеживание в асинхронном режиме (т.е. с внутренней частотой синхронизации).
На фиг.3 представлена КЛС, она же ОЭ 6, каждым элементом которой могут быть логические элементы типа И, ИЛИ, И-НЕ, ИЛИ-НЕ, НЕ. Причем если ОЭ 6 имеет несколько выходных полюсов Y, то вся процедура диагностирования делится на этапы, каждый из которых включает в себя работу только с одним из этих полюсов.
Пример конкретного выполнения процедуры диагностирования.
Для эксперимента в качестве ОЭ 6 берут схему с неисправностью Const 1 в точке В, представленную на фиг.3, выполненную на микросхемах 155 серии, где логический элемент ИЛИ-НЕ 8 - К155ЛЕ1, логический элемент И 9 - К155ЛИ1, логический элемент И-НЕ 10 - К155ЛА3, логический элемент И 11 - К155ИЛ1, имеющую четыре входных полюса Х1-Х4 и один выходной полюс Y. БВ 1 выполнен из генератора 2 - К531ГГ1 и двух счетчиков 3, 4 - К155ИЕ7. В качестве ЛА 7 используют систему экспериментального логического анализа (СЭЛА - 1), разработанную и созданную в НИИ автоматики и электромеханики, г.Томск. Определяют коэффициенты прозрачности для моделей, соответствующих различным неисправностям данной КЛС.
Из дискретной математики известно понятие булева производная или булева разность. Она обозначается как D (i/F) и является в математической форме записью наборов, на которых переменная с i-го входа передается на выход или, как говорят, которые "очувствляют" путь с i-го входа на выход.
Введенный интегральный диагностический параметр, коэффициент прозрачности i-го входа на выход связан с булевой производной следующим соотношением: он равен отношению единичных наборов булевой производной к количеству возможных подаваемых наборов 2 ** (N-1). Имеют ввиду, что булева производная принимает значение 1 на наборе по N-1 входам при условии "проявления" модулирующего сигнала i-го входа на выходе схемы.
В дальнейшем для КЛС рассматривают векторный, т.е. многомерный, коэффициент прозрачности, состоящий из коэффициентов прозрачности всех входов схемы.
Так как при существенной неисправности в схеме меняется функция, реализованная этой схемой, то естественно ожидать, что различным функциям соответствуют различные коэффициенты прозрачности. Это предположение подтверждается экспериментально.
На основании вышесказанного предлагаетcя использовать эту характеристику для различения существенных неисправностей схемы. Достоинством такого подхода является, с одной стороны, то, что имеется возможность вычисления этого коэффициента прозрачности непосредственно по модели, а с другой стороны, этот параметр довольно просто получить экспериментально.
Процедура определения коэффициента прозрачности для моделей, соответствующих различным неисправностям исследуемой схемы и заполнению эталонной таблицы, выглядит следующим образом.
Строят по структурной схеме ортогональную дизъюнктивно-нормальную форму (ДНФ), которая получается путем суперпозиции функций, описывающих каждый элемент в виде ортогональной ДНФ (ДНФ, в которой все конъюнкции попарно ортогональны).
Находят булеву производную функции D (i/F) относительно i-го входа (причем F может быть как исправной, так и неисправной функцией), по формуле
D(i/F)=F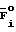 F
F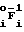 .
.
Используя свойства ортогональной ДНФ, определяют количество единиц ДНФ этой булевой производной.
Путем деления количества единиц булевой производной на 2 ** (N-1) - количество возможных входных наборов на N-1 входных полюса определяют коэффициент прозрачности i-го входа на выход. Таким образом, определяют весь мерный вектор коэффициентов прозрачности.
Для каждой новой вводимой в модель неисправности определяют свой многомерный коэффициент прозрачности, который заносят в эталонную таблицу.
Конкретный пример получения коэффициента прозрачности для модели КЛС, представленной на фиг.3.
Определяют ДНФ данной исправной функции
F=BΛC=(x1ΛA)Λ(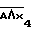 )=x1(
)=x1(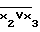 )((
)((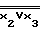 )V
)V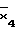 )=
)=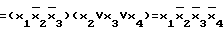
По формуле D(i/F)=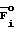 F
F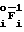 определяют булевы производные D (i/F):
определяют булевы производные D (i/F):
D(1/F)=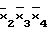 ;
;
D(2/F)=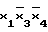 ;
;
D(3/F)=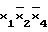 ;
;
D(4/F)=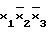 .
.
Определяют количество единиц каждой булевой производной:
D1(F) = 1;
D2(F) = 1;
D3(F) = 1;
D4(F) = 1 и векторный коэффициент прозрачности для исправной схемы
[1/8, 1/8, 1/8, 1/8].
Данная процедура может быть автоматизирована и выполняться за короткий промежуток времени.
Определяют коэффициент прозрачности для модели КЛС соответствующей неисправности Const 1 в точке В.
Определяют ДНФ функции
F′= V
V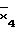 =(
=(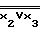 )V
)V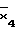 =x2Vx3V
=x2Vx3V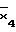 ..
..
Определяют булевы производные по формуле
D(i/F)=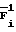 F
F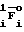 :
:
D(1/F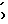 =0;
=0;
D(2/F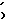 =(
=(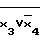 )=
)=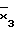 x4;
x4;
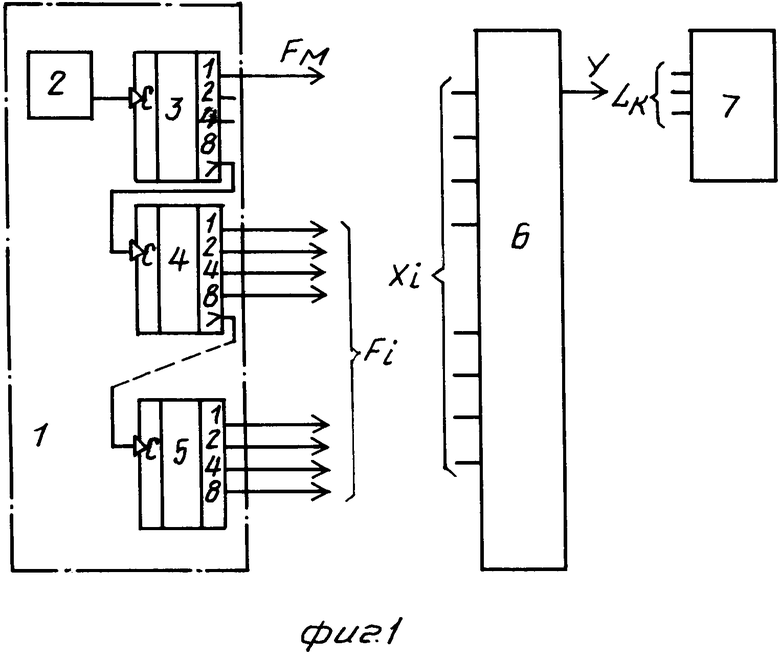
D(2/F = x
= x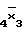 =x1x
=x1x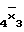 V
V 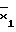 x
x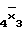 ;
;
D(3/F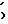 =(
=(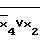 )=x
)=x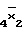 =x
=x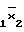 x4V
x4V 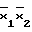 x4;
x4;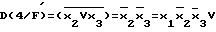
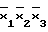 .
.
Получают коэффициент прозрачности
[0, 1/4, 1/4, 1/4].
Рассмотрим классы эквивалентности неисправностей данной схемы (неисправностей, для которых нет разделяющих тестов).
Неисправностям Const 0 в точке С, Const 0 в точке Х1, Const 1 в точке Х2, Const 1 в точке Х3, Const 1 в точке Х4, Const 0 в точке F, Const 1 в точке F, Const 0 в точке А, Const 0 в точке В отсутствует коэффициент прозрачности [0, 0, 0, 0].
Неисправностям Const 1 - в точке В, Сonst 1 - в точке Х1 соответствует коэффициент прозрачности [0, 1/4, 1/4, 1/4] и т.д.
Приступают к определению коэффициента прозрачности реальной схемы.
Внутреннюю частоту ЛА 7 устанавливают равной 1 МГц. Частоту генератора 2 БВ 1 устанавливают равной 0,5 МГц, следовательно, сигнал Fмимеет частоту 0,25 МГц, которая удовлетворяет условию разрешающей способности асинхронного режима ЛА быть минимум в 4 раза меньше внутренней частоты ЛА и не превышает предельной рабочей частоты микросхем 155 серии, равной 100 МГц. Сигнал Fм модулирующей частоты снимается с первого выхода счетчика 3, его частота в 2 раза меньше частоты генератора 2, которая подается на вход синхронизации этого счетчика. Остальные частоты F1 снимаются, начиная с первого выхода счетчика 4. Таким образом, частота сигнала F1 (1 = 1) в 16 раз меньше частоты сигнала Fм, что позволяет производить анализ количества перепадов на выходном полюсе ОЭ 6, равных не менее 16, за время, равное полупериоду сигнала частоты F1 (1 = 1). Частота сигнала F1 (1 = 1) не обязательно должна быть в 16 раз меньше частоты сигнала Fм. Для того, чтобы оценка количества перепадов была достоверной, частота сигнала F1(1 = 1) должна быть минимум в 4 раза меньше частоты сигнала Fм. Условие разрешающей способности асинхронного режима ЛА быть минимум в 4 раза меньше внутренней частоты ЛА вытекает из следующих соображений.
Сущность асинхронного режима ЛА заключается в записи последовательности логических сигналов в память ЛА синхронно с внутренней частотой синхроимпульсов СИ ЛА, т. е. по каждому синхроимпульсу СИ в память ЛА (по одному входному каналу) записывается бит информации. Записываемый сигнал как бы "режется" частотой СИ, и записана будет та информация, которая находилась на входе ЛА в момент прихода синхроимпульса СИ. Очевидно, что чем чаще "режут" входной сигнал, тем полнее имеют информацию о нем. Но слишком большая частота "разрезания" требует больших объемов памяти ЛА и применения высокочастотной элементной базы для создания ЛА. Чтобы получить минимально полную достоверную информацию об отслеживаемом сигнале, имеющей вид меандра, производят отслеживание в асинхронном режиме, входной сигнал должен быть "разрезан" 4 раза - в начале и конце нулевого полупериода и в начале и конце единичного полупериода. Отсюда и условие - удовлетворять разрешающей способности асинхронного режима ЛА, т.е быть минимум в 4 раза меньше внутренней частоты ЛА.
Производят подключение экспериментального устройства, как показано на фиг.2а-г так, чтобы производился полный перебор подачи сигнала Fмпоочередно на каждый из четырех входных полюсов ОЭ 6, а на остальные три свободные полюса сигналов F1 (1 = 1, 2, 3). Причем в каждом эксперименте сигналы Fм, F1 (1 = 1), Y отслеживаются ЛА 7.
Сигнал Fм подают на вход Х1 ОЭ 7 и L1 ЛА 7, сигнал F1 подают на вход Х2 ОЭ 6 и L1 ЛА 7, сигнал F2 - на входной полюс Х3 ОЭ 6, сигнал F3- на входной полюс Х4 ОЭ 6, сигнал Y - на входной полюс L3 ЛА 7.
Подают питание на БВ 1 и ОЭ 6 и проводят эксперимент, результатом которого является получение квазивременной диаграммы на фиг.4а.
Производят подключение экспериментального устройства, как показано на фиг. 2б. Сигнал Fм подают на вход Х2 ОЭ 6 и L1 ЛА 7, сигнал F1 - на вход Х1 ОЭ 6 и L1 ЛА 7, сигнал F2 - на входной полюс Х3 ОЭ 6, сигнал F3- на входной полюс Х4 ОЭ 6, сигнал ОЭ 6 Y - на входной полюс L3 ЛА 7.
Подают питание на БВ 1 и ОЭ 6 и проводят эксперимент, результатом которого является получение квазивременной диаграммы на фиг.4б.
Производят подключение экспериментального устройства, как показано на фиг. 2в. Сигнал Fм подают на вход Х3 ОЭ 6 и L1 ЛА 7, сигнал F1 - на вход Х1 ОЭ 6 и L1 ЛА 7, сигнал F2 - на входной полюс Х2 ОЭ 6, сигнал F3- на входной полюс Х4 ОЭ 6, сигнал ОЭ 6 Y - на входной полюс L3 ЛА 7.
Подают питание на БВ 1 и ОЭ 6 и проводят эксперимент, результатом которого является получение квазивременной диаграммы на фиг.5а.
Проводят подключение экспериментального устройства, как показано на фиг. 2г. Сигнал Fм подают на вход Х4 ОЭ 6 и L1 ЛА 7, сигнал F1 - на вход Х1 ОЭ 6 и L1 ЛА 7, сигнал F2 - на входной полюс Х2 ОЭ 6, сигнал F3 - на входной полюс Х3 ОЭ 6, сигнал ОЭ 6 Y - на входной полюс L3 ЛА 7.
Подают питание на БВ 1 и ОЭ 6 и проводят эксперимент, результатом которого является получение квазивременной диаграммы на фиг.5б.
Процедура переключений при подаче сигналов с БВ может быть автоматизирована.
Оценивают количество перепадов из нуля в единицу на выходном полюсе Y ОЭ 6 (фиг.4а) за промежуток времени, равный полупериоду частоты сигнала F1. Из фиг.4б видно, что на полюсе Y за два из восьми промежутков времени, равных полупериоду частоты сигнала F1, наблюдается больше двух перепадов из нуля в единицу, следовательно, можно сделать выводы, что коэффициент прозрачности К2 = 1/4.
Оценивают количество перепадов из нуля в единицу на выходном полюсе Y ОЭ 6 (фиг.5а) за промежуток времени, равный полупериоду частоты сигнала F1. Из фиг.5а видно, что на полюсе Y за два из восьми промежутков времени, равных полупериоду частоты сигнала F1, наблюдается больше двух перепадов из нуля в единицу, следовательно, можно сделать вывод, что коэффициент прозрачности K3 = 1/4.
Оценивают количество перепадов из нуля в единицу на выходном полюсе Y ОЭ 6 (фиг.5б) за промежуток времени, равный полупериоду частоты сигнала F1. Из фиг. 5б видно, что на полюсе Y за два из восьми промежутков времени, равных полупериоду частоты сигнала F1, наблюдается больше двух перепадов из нуля в единицу, следовательно, можно сделать вывод, что коэффициент прозрачности K4 = 1/4.
Комплексный или векторный коэффициент прозрачности K = [0, 1/4, 1/4, 1/4].
Проводят сравнение его с коэффициентами прозрачности для моделей неисправностей, он совпадает с коэффициентом прозрачности, соответствующим классу эквивалентных неисправностей, которому принадлежит и введенная в реальную схему неисправность Const 1 в точке В.
По сравнению с прототипом достоверность процедуры контроля и диагностики КЛС, осуществляемой предложенным способом, повышается вследствие того, что для получения эталонной библиотеки при использовании других способов диагностики (реализуемых другими диагностическими параметрами) должно быть проведено большое количество экспериментов, что из-за увеличения вероятности ошибки при больших объемах измерений в процессе проведения подготовительной процедуры ведет к уменьшению достоверности последующих диагностических процедур, а предложенный способ позволяет, производя минимальные вычисления, по структуре КЛС получить параметр диагностирования теоретически, что исключает экспериментальную погрешность и ошибку и позволяет сократить время проведения подготовительной процедуры диагностирования (заполнение эталонной таблицы) за сет исключения из этой процедуры механических операций и участия человека.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА БЕСПЕРЕБОЙНОГО ЭЛЕКТРОПИТАНИЯ | 1993 |
|
RU2037936C1 |
| ЧАСТОТНО-РЕГУЛИРУЕМЫЙ ЭЛЕКТРОПРИВОД | 1988 |
|
RU2014722C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКТИРОВКИ ПОКАЗАНИЙ ИНТЕГРИРУЮЩЕГО РАСХОДОМЕРА | 1992 |
|
RU2010165C1 |
| ЧАСТОТНО-РЕГУЛИРУЕМЫЙ ЭЛЕКТРОПРИВОД | 1989 |
|
RU2069033C1 |
| УСТРОЙСТВО ДЛЯ УПРАВЛЕНИЯ M-ФАЗНЫМ ИНВЕРТОРОМ | 1990 |
|
RU2013851C1 |
| ВЕНТИЛЬНЫЙ ЭЛЕКТРОДВИГАТЕЛЬ | 1991 |
|
RU2007010C1 |
| ВЕНТИЛЬНЫЙ ЭЛЕКТРОПРИВОД | 1990 |
|
RU2012991C1 |
| СИСТЕМА БЕСПЕРЕБОЙНОГО ЭЛЕКТРОПИТАНИЯ | 1988 |
|
RU2043686C1 |
| УСТРОЙСТВО ДЛЯ РЕГУЛИРОВАНИЯ ТЕМПЕРАТУРЫ | 1992 |
|
RU2037870C1 |
| ФОРМИРОВАТЕЛЬ ПИЛООБРАЗНОГО НАПРЯЖЕНИЯ | 1991 |
|
RU2019910C1 |
Изобретение относится к вычислительной технике и позволяет с высокой достоверностью осуществлять контроль комбинационных логических схем (КЛС). Способ основан на измерении числа логических перепадов на выходных полюсах логических схем. Отличается тем, что для модулей, соответствующих различным неисправностям диагностируемой КЛС, определяют коэффициенты прозрачности i-го входа на выход, подают на вход Xi исследуемой логической схемы меандр частоты Fм, имеющей значение, удовлетворяющее разрешающей способности регистратора логических перепадов, на N - 1 оставшихся входов меандры частот, наибольшая из которых должна иметь длительность полупериода импульса, не менее чем в 2 раза большую длительности периода частоты Fм , а коэффициент прозрачности реальной логической схемы определяют из соотношения Z/2 (N - 1), где Z - количество интервалов времени, в которых обнаружено более двух логических периодов; N - количество входных полюсов исследуемой схемы. Диагностику осуществляют путем сравнения коэффициентов прозрачности, полученных для модулей схем с различными неисправностями, с коэффициентом прозрачности, полученным экспериментально. 5 ил.
СПОСОБ ДИАГНОСТИКИ КОМБИНАЦИОННЫХ ЛОГИЧЕСКИХ СХЕМ, основанный на измерении количества логических перепадов на выходных полюсах исследуемой схемы, отличающийся тем, что, с целью повышения достоверности анализа, для моделей, соответствующих различным неисправностям диагностируемой комбинационной логической схемы, определяют коэффициенты прозрачности i-го входа на выход (i = 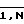 ), , каждый из которых равен отношению единичных наборов булевой производной к количеству возможных подаваемых на N-1 входных полюсов этой схемы наборов, число которых определяется по формуле 2**(N-1) , подают на вход Xi исследуемой комбинационной логической схемы меандр частоты Fm, имеющей значение, удовлетворяющее разрешающей способности регистратора логических перепадов и не превышающее допустимой рабочей частоты исследуемой схемы, а на N-1 оставшихся входов - меандры частот, наибольшая из которых Fl (l= 1) должна иметь длительность полупериода импульса, не менее чем в 2 раза большую длительности периода частоты Fm, а остальные частоты Fl (l =
), , каждый из которых равен отношению единичных наборов булевой производной к количеству возможных подаваемых на N-1 входных полюсов этой схемы наборов, число которых определяется по формуле 2**(N-1) , подают на вход Xi исследуемой комбинационной логической схемы меандр частоты Fm, имеющей значение, удовлетворяющее разрешающей способности регистратора логических перепадов и не превышающее допустимой рабочей частоты исследуемой схемы, а на N-1 оставшихся входов - меандры частот, наибольшая из которых Fl (l= 1) должна иметь длительность полупериода импульса, не менее чем в 2 раза большую длительности периода частоты Fm, а остальные частоты Fl (l = 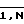 ) должны быть кратны наибольшей, при этом выходной сигнал фиксируют регистратором логических перепадов, определяют коэффициент прозрачности реальной логической схемы из соотношения
) должны быть кратны наибольшей, при этом выходной сигнал фиксируют регистратором логических перепадов, определяют коэффициент прозрачности реальной логической схемы из соотношения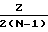 ,,
,,
где Z - количество интервалов времени для выходного сигнала Y, равных полупериоду сигнала Fl (l=1), в которых обнаружено более двух логических перепадов, N - количество входных полюсов исследуемой схемы,
а диагностику осуществляют путем сравнения коэффициентов прозрачности, полученных для моделей схем с различными неисправностями, с коэффициентом прозрачности, полученным экспериментально.
| Устройство для анализа состояний логических схем | 1987 |
|
SU1499350A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1994-07-30—Публикация
1991-01-22—Подача