Изобретение относится к технике измерений на сверхвысоких частотах и может быть использовано при измерении комплексных коэффициентов отражения, комплексных коэффициентов передачи, полных сопротивлений СВЧ-устройств различного целевого назначения.
В технике измерений на СВЧ широко используется способ, основанный на анализе амплитудного распределения поля вдоль линии передачи (метод измерительной линии). Недостатком этого способа является низкая производительность измерений.
Этот недостаток устранен в способе, основанном на анализе амплитудного распределения поля в дискретных точках линии передачи (так называемый многозондовый метод). Недостатком этого способа является малая широкополосность и, как следствие, низкая точность при работе в полосе частот.
Этот недостаток устранен в способе калибруемого двенадцатиполюсника. Суть способа заключается в том, что осуществляется измерение мощностей на выходах линейного калибруемого двенадцатиполюсника и по ним вычисляют измеряемые параметры. Причем предварительно в процессе калибровки по образцовым мерам на каждой частоте определяют и запоминают эквивалентные параметры многополюсника, которые используются в дальнейшем для расчета измеряемых параметров.
Наиболее близким по технической сущности является способ, который заключается в том, что измеряют мощности на выходах линейного калибруемого двенадцатиполюсника, к которому подключены источник гармонических колебаний и измеряемое устройство, а реальную и мнимую части комплексного параметра рассчитывают по формулам
X = R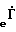 =
= 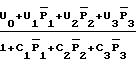 (1)
(1)
Y = I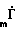 =
= 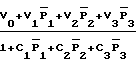 (2) где
(2) где 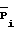 =
= 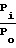 =
= 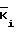
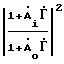 , i = 1,2,3 . (3)
, i = 1,2,3 . (3)
Рi - мощности, измеренные на выходах линейного двенадцатиполюсника;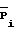 - ноpмированные значения мощностей, причем нормировка осуществляется относительно мощности на выходе индексом "0" (Ро);
- ноpмированные значения мощностей, причем нормировка осуществляется относительно мощности на выходе индексом "0" (Ро);
Аi, 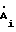 ,
, 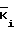 - эквивалентные параметры, характеризующие i-й выход двенадцатиполюсника;
- эквивалентные параметры, характеризующие i-й выход двенадцатиполюсника;
Un,Vn,Сn - константы, которые однозначно связаны с эквивалентными параметрами двенадцатиполюсника, эти константы рассчитываются на этапе калибровки и запоминаются.
Недостаточно высокая точность определения комплексных параметров по способу-прототипу связана с тем, что существенный вклад в результирующую погрешность вносят шумы. Из-за влияния шумов, возникающих при обработке сигналов, снимаемых с датчиков мощности, измерение мощностей Рiосуществляется с погрешностями, а это в соответствии с формулами (1) и (2) приводит к ошибке в определении составляющих комплексного параметра.
Целью изобретения является повышение точности.
Это достигается тем, что при способе определения комплексных параметров СВЧ-устройств, заключающемся в измерении мощностей на выходах линейного калибруемого двенадцатиполюсника, к которому подключены источник гармонического сигнала и измеряемое устройство, формируют три независимые импульсные последовательности из отсчетов измеренных мощностей путем их перестановок во времени, путем дискретного преобразования Фурье определяют аргументы первого коэффициента разложения этих последовательностей Ψ1, Ψ2, Ψ3 и рассчитывают реальную и мнимую части комплексного параметра 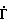 по формулам
по формулам
X = R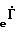 =
= 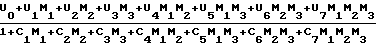 (4)
(4)
Y = I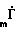 =
= 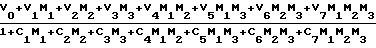 (5)
(5)
где Мi=tg Ψ i (i=1,2,3);
Сm,Um,Vm (m=0...7) - постоянные величины, определяемые при калибровке.
Таким образом, в отличие от прототипа исходными данными для определения комплексных параметров являются не измеренные мощности, а аргументы коэффициентов разложения Фурье, которые оказываются менее чувствительными к шумам. Это и приводит к новому свойству, заключающемуся в повышении точности определения комплексных параметров. Данное свойство обеспечивается введением заявленных отличительных признаков и без этих признаков не может быть получено.
Таким образом, отличительные признаки заявленного технического решения являются существенными.
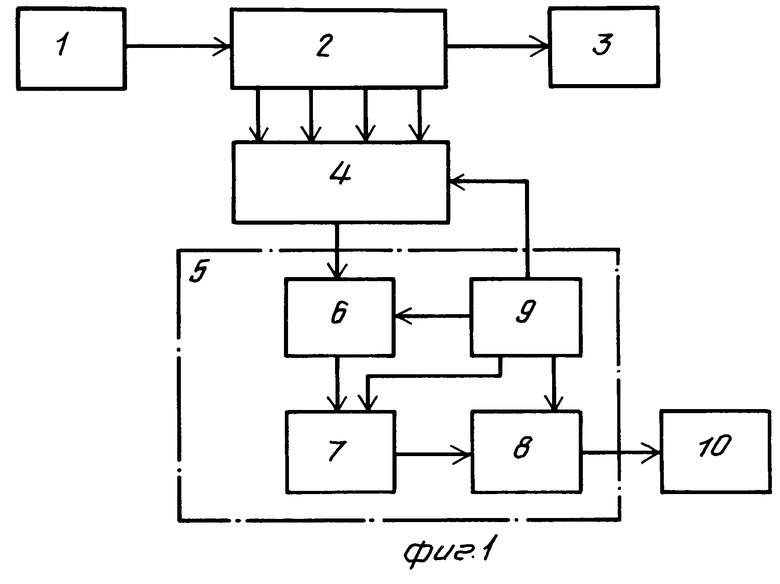
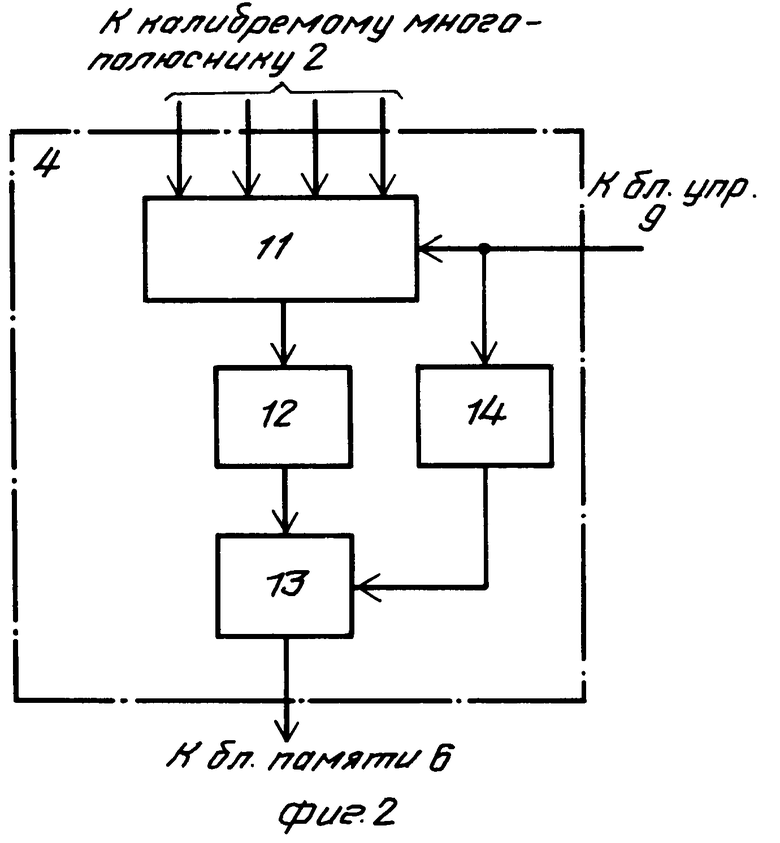
На фиг. 1 изображена структурная схема одного из вариантов устройства для измерения комплексного коэффициента отражения на основе калибруемого двенадцатиполюсника; на фиг.2 - структурная схема возможной реализации блока измерения мощности; на фиг.3 - эпюры дискретных сигналов, полученных из отсчетов мощностей путем их перестановок во времени.
Устройство для измерения комплексного коэффициента отражения содержит СВЧ-генератор 1, выход которого через линейный калибруемый двенадцатиполюсник 2 подключен к входу измеряемой нагрузки 3. Четыре измерительных выхода калибруемого двенадцатиполюсника 2 подключены к блоку измерения мощности 4. Выход блока измерения мощности 4 соединен с входом вычислительно-управляющего устройства 5, в состав которого входят последовательно соединенные блок памяти 6, блок 7 дискретного преобразования Фурье и решающее устройство 8, а также блок управления 9, выходы которого соединены с блоком измерения мощности 4, блоком памяти 6, блоком 7 дискретного преобразования Фурье и решающим устройством 8. Выход решающего устройства 8 соединен с индикаторным блоком 10.
СВЧ-генератор 1 предназначен для формирования гармонических колебаний соответствующей частоты. В качестве СВЧ-генератора 1 может быть реализован любой генератор соответствующего диапазона волн из группы приборов Г4 либо генератор качающейся частоты из комплекта панорамных приборов (группы приборов Р2 и Р4).
Линейный калибруемый двенадцатиполюсник 2 предназначен для формирования измерительных сигналов. Возможны различные конструктивные варианты на основе как направленных, так и ненаправленных элементов.
Блок измерения мощности 4 предназначен для измерения уровней мощности сигналов, поступающих с измерительных выходов калибруемого двенадцатиполюсника 2. Одна из возможных реализаций блока измерения мощности 4 приведена на фиг. 2. Блок состоит из СВЧ-коммутатора 11, датчика мощности 12, аналого-цифрового преобразователя 13 (АЦП), элемента задержки 14.
Блок измерения мощности работает следующим образом. Блок управления 9 осуществляет последовательное переключение каналов СВЧ-коммутатора 11. При этом вход датчика мощности 12 поочередно подключается к выходам калибруемого двенадцатиполюсника 2. В качестве датчика мощности может быть использован квадратичный СВЧ-детектор либо термисторный (болометрический) преобразователь, включенный в мост. Напряжения, пропорциональные уровням мощностей, поступают поочередно на вход АЦП 12, который осуществляет преобразование этих напряжений в цифровой код, поступающий далее в вычислительно-управляющее устройство 5. Запуск АЦП 13 осуществляется с некоторой задержкой относительно момента переключения СВЧ-коммутатора 11. Задержка обеспечивается с помощью элемента задержки 14, который легко реализуется на логических схемах.
Вычислительно-управляющее устройство 5 с входящими в него блоком памяти 6, блоком 7 дискретного преобразования Фурье, решающим устройством 8 и блоком управления 9 предназначен для формирования дискретных последовательностей, определения аргументов коэффициентов разложения Фурье этих последовательностей и вычисления действительной и мнимой частей комплексного коэффициента отражения по формулам (4), (5).
Вычислительно-управляющее устройство 5 может быть реализовано на основе управляющей микроЭВМ типа "ДВК", "Электроника-60" и др. Возможна реализация этого блока на основе микропроцессорного вычислителя.
Индикаторный блок 10 предназначен для отображения результатов измерения в удобной форме. Для этих целей могут быть использованы цифровые, аналоговые, осциллографические и прочие индикаторы.
Устройство для измерения комплексного коэффициента отражения работает следующим образом.
Гармонический сигнал от СВЧ-генератора 1 через калибруемый двенадцатиполюсник 2 поступает на измеряемый двухполюсник 3 с комплексным коэффициентом отражения 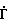 . При этом в линии передачи формируется режим смешанных волн. На измерительных выходах калибруемого двенадцатиполюсника 2 появляются сигналы. Эти сигналы поступают на входы блока измерения мощности 4, в котором по командам из блока управления 9 осуществляется поочередное измерение мощностей и преобразование их в цифровые коды. Эти коды поступают в блок памяти 6, где осуществляется их запоминание. Далее по командам из блока управления 9 запомненные значения мощностей в требуемой последовательности и полярности (см.фиг.3) подаются в блок 7 дискретного преобразования Фурье. В этом блоке для каждой из трех последовательностей определяются аргументы первого коэффициента разложения. Полученные значения аргументов поступают далее в решающее устройство 8, где по формулам (4), (5) рассчитываются действительная и мнимая части комплексного коэффициента отражения. По полученным значениям в решающем устройстве при необходимости могут быть вычислены модуль и аргумент комплексного коэффициента отражения. С выхода решающего устройства 8 сигналы поступают в индикаторный блок 10, где осуществляется индикация в удобной форме.
. При этом в линии передачи формируется режим смешанных волн. На измерительных выходах калибруемого двенадцатиполюсника 2 появляются сигналы. Эти сигналы поступают на входы блока измерения мощности 4, в котором по командам из блока управления 9 осуществляется поочередное измерение мощностей и преобразование их в цифровые коды. Эти коды поступают в блок памяти 6, где осуществляется их запоминание. Далее по командам из блока управления 9 запомненные значения мощностей в требуемой последовательности и полярности (см.фиг.3) подаются в блок 7 дискретного преобразования Фурье. В этом блоке для каждой из трех последовательностей определяются аргументы первого коэффициента разложения. Полученные значения аргументов поступают далее в решающее устройство 8, где по формулам (4), (5) рассчитываются действительная и мнимая части комплексного коэффициента отражения. По полученным значениям в решающем устройстве при необходимости могут быть вычислены модуль и аргумент комплексного коэффициента отражения. С выхода решающего устройства 8 сигналы поступают в индикаторный блок 10, где осуществляется индикация в удобной форме.
При осуществлении предложенного способа выполняют следующие операции:
устанавливают требуемую частоту СВЧ-генератора 1;
осуществляют измерение мощностей на измерительных выходах линейного калибруемого двенадцатиполюсника 2;
запоминают измеренные значения мощностей;
формируют три независимые импульсные последовательности из отсчетов измеренных мощностей путем их перестановок во времени;
осуществляют дискретное преобразование Фурье, в результате которого определяют аргументы первого коэффициента разложения этих последовательностей;
рассчитывают реальную и мнимую части комплексного параметра по формулам (4), (5).
Рассмотрим предложенный способ определения комплексных параметров СВЧ-устройств.
Отсчеты мощностей Рi (i=0,1,2,3), измеренных на выходах двенадцатиполюсника 2, могут быть сформированы во временные четырехточечные последовательности путем перестановок по времени. Причем общее число перестановок из N элементов равно N! . В нашем случае N=4 (число измерительных выходов двенадцатиполюсника 2). Таким образом число перестановок будет N!=4!=24. Из этих перестановок только 3 последовательности будут обладать свойством независимости с точки зрения аргументов коэффициентов разложения, в чем легко убедиться. Эти последовательности приведены на фиг.3, выглядят следующим образом: Р0, -Р1, -Р2, Р3; Р0, -Р1, -Р3, Р2; Р0, -Р2, -Р1, Р3.
Проведем дискретное преобразование Фурье (ДФП) этих последовательностей. В общем случае комплексные коэффициенты ДФП равны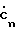 =
= 
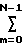 Xm·e-j
Xm·e-j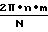 (6)
(6)
Хm - отсчеты дискретного сигнала;
n - номер коэффициента ДПФ;
m - номер отсчета.
Проведем расчет первого (n=1) коэффициента разложения для нашего случая (N=4)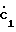 =
= 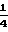
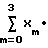 e
e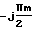 =
= 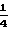
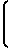 xo+x1e
xo+x1e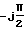 + x2e-jπ + x3e
+ x2e-jπ + x3e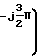 (7)
(7)
Применяя формулу Эйлера, получим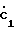 =
= 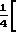 (xo-x2)+j(x3-x1)
(xo-x2)+j(x3-x1)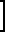 (8) Определим аргумент коэффициента разложения
(8) Определим аргумент коэффициента разложения
Ψ1= arctg 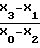 (9) Теперь определим Ψ1 для трех последовательностей, представленных на фиг.3. Подставляя в формулу (9) соответствующие отсчеты мощностей, получим
(9) Теперь определим Ψ1 для трех последовательностей, представленных на фиг.3. Подставляя в формулу (9) соответствующие отсчеты мощностей, получим
Ψ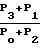 (10)
(10)
Ψ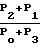 (11)
(11)
Ψ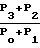 (12) В соотношениях (10)-(12) возьмем тангенсы от обеих частей, а также разделим числители и знаменатели дробей на Ро. Введем обозначения tg Ψ1(i)=Мi (i=1,2,3). При этом получим
(12) В соотношениях (10)-(12) возьмем тангенсы от обеих частей, а также разделим числители и знаменатели дробей на Ро. Введем обозначения tg Ψ1(i)=Мi (i=1,2,3). При этом получим
M1= 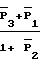 (13)
(13)
M2= 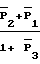 (14)
(14)
M3= 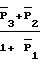 (15) где
(15) где 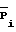 - нормированные значения мощностей, определяемые соотношением (3).
- нормированные значения мощностей, определяемые соотношением (3).
Подставляя соотношение (3) в формулы (13)-(15), получим систему из трех уравнений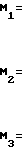
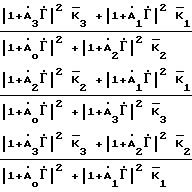
 (16)
(16)
Введем обозначения:  =
=  e jϕ;
e jϕ; 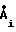 = =
= =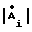 ejαi. Подставим эти значения в систему (16). Взяв модули и возведя их в квадрат, получим после преобразований
ejαi. Подставим эти значения в систему (16). Взяв модули и возведя их в квадрат, получим после преобразований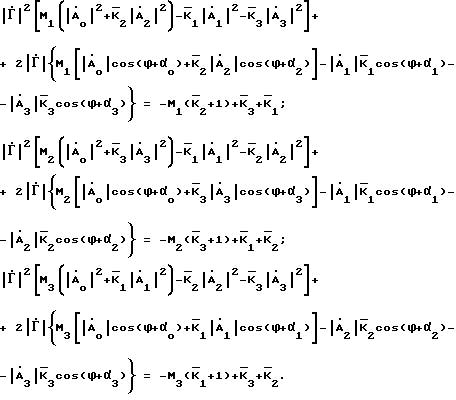
 (18)
(18)
Полученная система уравнений является нелинейной относительно 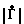 и ϕ . Однако ее можно свести к линейной относительно квадрата модуля |
и ϕ . Однако ее можно свести к линейной относительно квадрата модуля |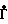 |2, действительной Х=
|2, действительной Х= 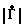 cos ϕ и мнимой Y=
cos ϕ и мнимой Y=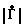 sin ϕ частей ком- плексного коэффициента отражения. Для этого воспользуемся формулой для косинуса суммы и проведем перегруппировку. В результате система (18) может быть записана в виде
sin ϕ частей ком- плексного коэффициента отражения. Для этого воспользуемся формулой для косинуса суммы и проведем перегруппировку. В результате система (18) может быть записана в виде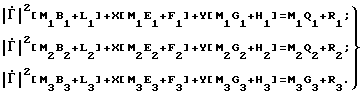 (19) где
(19) где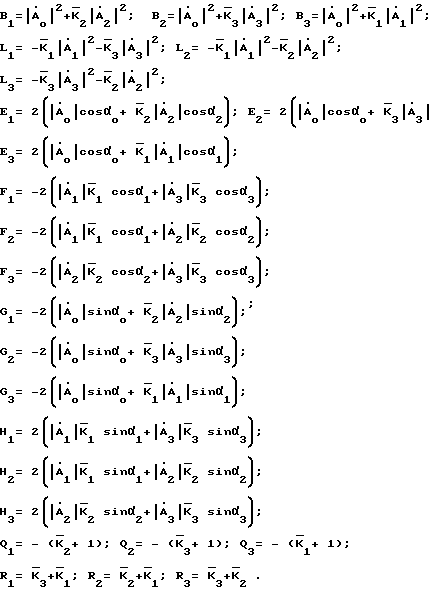 cos
cos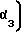 ;
; 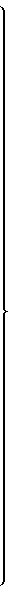

Систему уравнений (19) решим относительно X и Y /используя правило Крамера.Решение имеет вид
X = 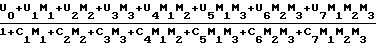 (21)
(21)
Y = 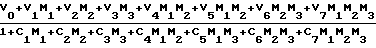 (22) где
(22) где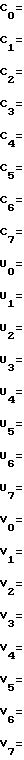

 Таким образом, формулы (21) и (22) определяют реальную и мнимую части комплексного параметра. Причем в этих формулах Сm,Um,Vm являются постоянными величинами, однозначно через соотношения (23) и (20) связанными с эквивалентными параметрами двенадцатиполюсника 2. Коэффициенты Сm,Um,Vm определяются при калибровке измерителя, которая проводится по образцовым мерам перед измерениями. Коэффициенты Сm,Um,Vm(m=0...7) в данном случае не совпадают с коэффициентами Сn,Un,Vn(n=0...3) для способа-прототипа ни численно, ни количественно. Одинаковые буквы для обозначения коэффициентов выбраны для удобства восприятия. В дальнейшем в обозначениях введем следующие индексы: индекс "1" будем относить к предложенному способу, а индекс "2" - к способу-прототипу.
Таким образом, формулы (21) и (22) определяют реальную и мнимую части комплексного параметра. Причем в этих формулах Сm,Um,Vm являются постоянными величинами, однозначно через соотношения (23) и (20) связанными с эквивалентными параметрами двенадцатиполюсника 2. Коэффициенты Сm,Um,Vm определяются при калибровке измерителя, которая проводится по образцовым мерам перед измерениями. Коэффициенты Сm,Um,Vm(m=0...7) в данном случае не совпадают с коэффициентами Сn,Un,Vn(n=0...3) для способа-прототипа ни численно, ни количественно. Одинаковые буквы для обозначения коэффициентов выбраны для удобства восприятия. В дальнейшем в обозначениях введем следующие индексы: индекс "1" будем относить к предложенному способу, а индекс "2" - к способу-прототипу.
Докажем достижение положительного эффекта.
Случайные среднеквадратичные погрешности при косвенных измерениях для предложенного способа и способа-прототипа определим в виде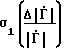 =
= 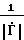
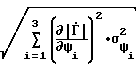 ; (24)
; (24)
σ1(Δϕ)=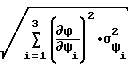 ; (25)
; (25)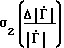 =
= 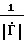
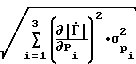 ; (26)
; (26)
σ2(Δϕ)=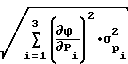 ; (27) где
; (27) где 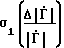 , σ1(Δϕ) - относительная погрешность определения модуля и абсолютная погрешность определения фазы для предложенного способа;
, σ1(Δϕ) - относительная погрешность определения модуля и абсолютная погрешность определения фазы для предложенного способа;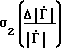 , σ2(Δϕ) - то же самое для способа-прототипа;
, σ2(Δϕ) - то же самое для способа-прототипа;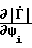 ,
, 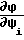 - коэффициенты чувствительности предложенного способа по параметру Ψi;
- коэффициенты чувствительности предложенного способа по параметру Ψi;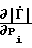 ,
, 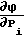 - коэффициенты чувствительности способа-прототипа по параметру Рi.
- коэффициенты чувствительности способа-прототипа по параметру Рi.
Модуль и фазу комплексного параметра определим через действительную и мнимую части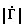 =
= 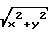 (28)
(28)
ϕ = arctg Y/X . (29) Используя выражения (28)-(29), (21)-(22), (1)-(2), определим коэффициенты чувствительности. Для удобства представим Х=а/f; Y= b/f. Тогда после дифференцирования получим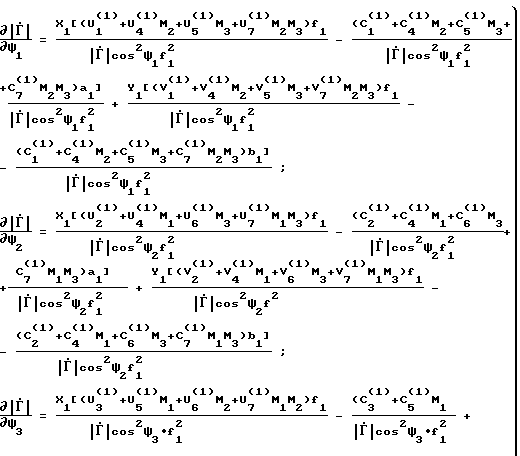
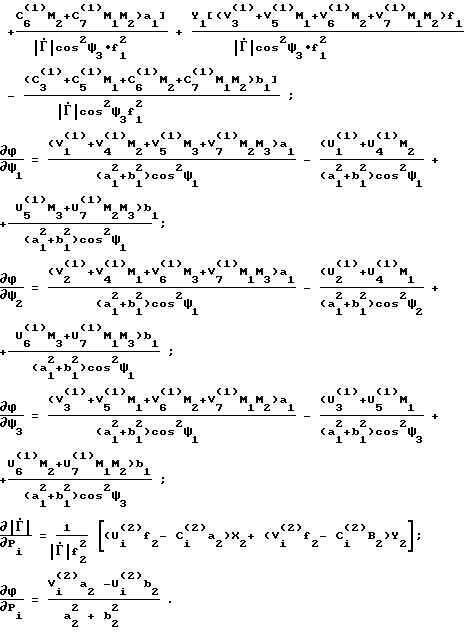

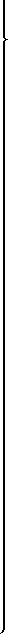

Теперь определим дисперсии σΨi2 и σрi2. Для этого предположим, что сигналы, снимаемые с датчика мощности, усиливаются усилителем с прямоугольной АЧХ коэффициентом усиления Ко и полосой пропускания от нуля до ωm, где ωm = 2 π fm - максимальная частота. Предположим, что в системе действует белый шум с энергетическим спектром Wо. Тогда для способа-прототипа дисперсия σрi2 будет равна
σ
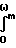 K
K WoK
WoK
Поскольку результат измерения в способе-прототипе и в предложенном способе не зависит от абсолютного уровня сигналов, то коэффициент Коможно выбрать любым. Для удобства в дальнейшем положим Ко=1.
В предложенном способе после усиления осуществляется операция ДПФ, которая обладает фильтрующим свойством. Амплитудно-частотная характеристика ДПФ имеет вид
K(n, ω)= 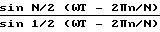 , (32) где N - число отсчетов дискретного сигнала;
, (32) где N - число отсчетов дискретного сигнала;
n - номер коэффициента ДПФ;
Т=1/2fm - интервал дискретизации, определяемый по теореме Котельникова.
Для нашего случая N=4, n=1, тогда получим
K(1,ω)= 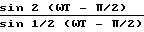 (33) Последнее выражение преобразуем к виду
(33) Последнее выражение преобразуем к виду
K(1, ω)= K cos
cos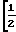 (ωT-π/2)
(ωT-π/2) cos(ωT-π/2) (34) где К'о=4 - коэффициент передачи устройства ДПФ на частоте первой гармоники дискретного сигнала.
cos(ωT-π/2) (34) где К'о=4 - коэффициент передачи устройства ДПФ на частоте первой гармоники дискретного сигнала.
Энергетический спектр шума после фильтрации
W(ω) = WoK2(1, ω)= Wo(K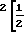 (ωT-π/2)
(ωT-π/2)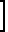 cos2(ωT-π/2) (35) Считая, что после фильтрации процесс становится узкополосным, используемым следующее соотношение для энергетического спектра фазы:
cos2(ωT-π/2) (35) Считая, что после фильтрации процесс становится узкополосным, используемым следующее соотношение для энергетического спектра фазы:
WΨi(Ω)= 2W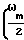 +
+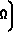 /A
/A
WΨi(Ω)= 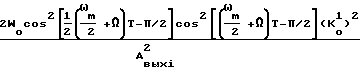
С учетом того/что ωmT/2 = π/2,а также Aвых1/K = Aвхi- амплитуда первой гармоники/ приведенная к входу устройства ДПФ/получим
= Aвхi- амплитуда первой гармоники/ приведенная к входу устройства ДПФ/получим
WΨi(Ω) = 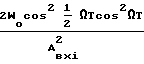 (37) Определим дисперсию выходного процесса, воспользовавшись соотношением
(37) Определим дисперсию выходного процесса, воспользовавшись соотношением
σ
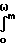 WΨi(Ω)dΩ (38)
WΨi(Ω)dΩ (38)
Подставляя выражение (37) в выражение (38) получим
σ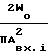
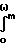 cos2
cos2 ΩT cos2ΩTdΩ (39)
ΩT cos2ΩTdΩ (39)
Проведем замену переменной 1/2 ΩT = Z.Это приводит к следующему:
σ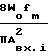
 cos2Zcos22ZdZ
cos2Zcos22ZdZ
Подынтегральную функцию представим в виде
Cos2Z·Cos22Z= Cos2Z(Cos2Z- Sin2Z)=
= Cos6Z + Cos2Z Sin4Z- 2Cos4Z Sin2Z (41)
При этом интеграл (40) сводится к трем известным берущимся интегралам. После некоторых преобразований получим
σ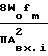
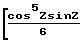 +
+ 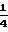 Z+
Z+ 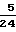 sin2Z +
sin2Z +
+ 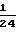 sin4Z -
sin4Z -  sin3Z cos3Z
sin3Z cos3Z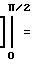
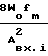 ·π/8 =
·π/8 = 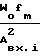 (42)
(42)
Подставив формулы (31) и (42) в формулы (24)-(27), получим формулы для расчета погрешностей.
Сравнение результатов (оценку эффективности) осуществим путем использования отношений погрешностей способа-прототипа и предложенного способа. В результате получим
Эг= 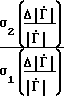 =
= 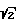
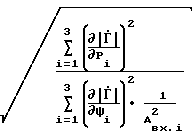 (43)
(43)
Эϕ= 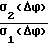 =
= 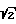
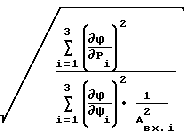 (44)
(44)
Амплитуды Авх.i для каждой из дискретных последовательностей определяются как
Aвх.1= 2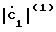 = 0,5
= 0,5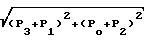
Aвх.2= 2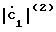 = 0,5
= 0,5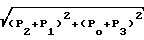 (45)
(45)
Aвх.3= 2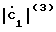 = 0,5
= 0,5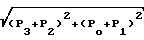
Ввиду громоздкости вычислений расчеты по оценке эффективности предложенного способа были проведены на ЭВМ lВМ РS/ХТ. Программа позволяет в диалоговом режиме задать любые параметры измерительного двенадцатиполюсника и параметры нагрузки. После чего осуществляется расчет обобщенных коэффициентов С,V,U для предложенного способа и способа-прототипа, расчет коэффициентов чувствительности и расчет эффективности по формулам (43), (44).
Проведены многочисленные расчеты для различных моделей двенадцатиполюсников. Эти расчеты подтверждают повышение точности предложенного способа определения комплексных параметров. В качестве примера в табл.1,2,3 приведены результаты расчета эффективности для случая, когда в двенадцатиполюснике использован один направленный и три ненаправленных датчика. Расчеты проведены для различных значений модуля и фазы коэффициента отражения нагрузки.
Из таблиц следует, что предложенный способ обеспечивает повышение точности измерения модуля комплексного параметра практически во всем диапазоне изменения модуля и фазы. Так, при 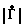 =1 точность повышается максимум в 5,24 раза (при ϕ =270о), при
=1 точность повышается максимум в 5,24 раза (при ϕ =270о), при 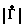 =0,3 - в 2,97 раза (при ϕ =90о), при
=0,3 - в 2,97 раза (при ϕ =90о), при 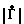 = 0,1 - в 2,14 раза (при ϕ =90о). При других значениях фазы точность измерения модуля также возрастает, исключая значения фазы, близкие 0 и 360о, где точности одинаковы (Эг=1). Во всех случаях отсутствует повышение точности измерения фазы, практически во всем диапазоне изменения модуля и фазы погрешности определения фазы для предложенного способа и способа-прототипа приблизительно одинаковы (Э ϕ ≈ 1). Это объясняется тем, что для обоих способов коэффициенты чувствительности таковы, что реальная и мнимая части комплексного параметра отклоняются в одном направлении, так как фаза определяется отношением мнимой и реальной частей, то это не приводит к существенному ее изменению в обоих случаях.
= 0,1 - в 2,14 раза (при ϕ =90о). При других значениях фазы точность измерения модуля также возрастает, исключая значения фазы, близкие 0 и 360о, где точности одинаковы (Эг=1). Во всех случаях отсутствует повышение точности измерения фазы, практически во всем диапазоне изменения модуля и фазы погрешности определения фазы для предложенного способа и способа-прототипа приблизительно одинаковы (Э ϕ ≈ 1). Это объясняется тем, что для обоих способов коэффициенты чувствительности таковы, что реальная и мнимая части комплексного параметра отклоняются в одном направлении, так как фаза определяется отношением мнимой и реальной частей, то это не приводит к существенному ее изменению в обоих случаях.
Таким образом предложенный способ обеспечивает повышение точности определения комплексных параметров. Это объясняется тем, что исходными данными для определения комплексных параметров являются не измеренные мощности, а аргументы (фазы) коэффициентов разложения Фурье дискретных последовательностей, которые оказываются менее чувствительными к шумам.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОЛУЧЕНИЯ СЕЙСМИЧЕСКОГО РАЗРЕЗА | 1991 |
|
RU2022310C1 |
| ИЗМЕРИТЕЛЬ S-ПАРАМЕТРОВ НЕВЗАИМНОГО СВЧ-ЧЕТЫРЕХПОЛЮСНИКА | 1992 |
|
RU2010248C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ В БОРТОВОЙ ЧЕТЫРЕХКАНАЛЬНОЙ ДОПЛЕРОВСКОЙ РЛС | 2014 |
|
RU2572357C1 |
| ПАНОРАМНЫЙ ИЗМЕРИТЕЛЬ КОЭФФИЦИЕНТА СТОЯЧЕЙ ВОЛНЫ И ОСЛАБЛЕНИЯ | 1991 |
|
RU2026562C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ВРЕМЕНИ ЗАПАЗДЫВАНИЯ ОДНОГО СИГНАЛА ОТНОСИТЕЛЬНО ДРУГОГО СИГНАЛА | 1990 |
|
RU2032924C1 |
| СПОСОБ ВЫРАВНИВАНИЯ КАНАЛОВ МНОГОКАНАЛЬНОЙ ПРИЕМНОЙ СИСТЕМЫ (ВАРИАНТЫ) | 2004 |
|
RU2289885C2 |
| КОМПЕНСАЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ РАЗНОСТИ ФАЗ СЛУЧАЙНЫХ СИГНАЛОВ | 2002 |
|
RU2227306C2 |
| ДИСКРЕТНЫЙ СОГЛАСОВАННЫЙ ФИЛЬТР | 1990 |
|
RU2011291C1 |
| Способ дистанционного контроля уровня и плотности жидкости в резервуаре | 2015 |
|
RU2614343C1 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ КАЛИБРОВКИ УРОВНЯ ВЫХОДНОГО СИГНАЛА ГЕНЕРАТОРОВ СВЧ- И КВЧ-ДИАПАЗОНОВ | 2012 |
|
RU2507674C2 |

Использование: для измерения с высокой точностью комплексных параметров СВЧ-устройств. Сущность изобретения: формируют три независимые импульсные последовательности из отсчетов измеренных мощностей путем их перестановок во времени, путем дискретного преобразования Фурье определяют аргументы первого коэффициента разложения этих последовательностей Ψ1 Ψ2, Ψ3 и расчитывают реальную и мнимую части комплексного параметра Г по соответствующим формулам. 3 ил., 3 табл.
СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСНЫХ ПАРАМЕТРОВ СВЧ-УСТРОЙСТВ, заключающийся в подаче гармонического сигнала на вход линейного калибруемого многополюсника и измерении мощностей на выходах линейного калибруемого многополюсника, к которому подключено измеряемое устройство, отличающийся тем, что, с целью повышения точности, формируют три независимые импульсные последовательности из отсчетов измеренных мощностей путем их перестановок во времени, определяют начальные фазы первых гармоник спектра этих последовательностей Ψ1, Ψ2, Ψ3 и расчитывают реальную Re и мнимую части Im комплексного параметра 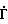 по формулам
по формулам
R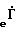 =
= 
I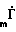 =
= 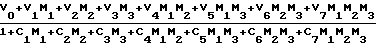 ;
;
где Mi = tgΨi(i = 1, 2, 3) ;
Cm, Um, Vm (m = 0, - ,7) - постоянные величины, определяемые при калибровке.
| Li | |||
| S., Bosisio R, G, Calibration of multiport refletometers by means of four Open / short cuirtuits | |||
| IEEE | |||
| Frans | |||
| MTT, v.30, n 7, p.p.1085-1089, 1982. |
Авторы
Даты
1994-10-30—Публикация
1991-04-26—Подача